Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Soft micron-sized polypeptide microgels: preparation, crosslink density, topography and nanomechanics in swollen state†
Oleksii
Kotko
 ab,
Petr
Šálek
ab,
Petr
Šálek
 *a,
Jana
Dvořáková
*a,
Jana
Dvořáková
 a,
Miroslava Dušková
Smrčková
a,
Miroslava Dušková
Smrčková
 a,
Ján
Šomvársky
c,
Jean Jacques
Bonvent
d,
Sérgio
Brochsztain
d,
Miroslav
Šlouf
a,
Ján
Šomvársky
c,
Jean Jacques
Bonvent
d,
Sérgio
Brochsztain
d,
Miroslav
Šlouf
 a and
Vladimír
Proks
a and
Vladimír
Proks
 a
a
aInstitute of Macromolecular Chemistry, Czech Academy of Sciences, Heyrovského nám. 2, 162 00 Prague 6, Czech Republic. E-mail: salek@imc.cas.cz; Fax: +420 296 809 410; Tel: +420 296 809 225
bDepartment of Physical and Macromolecular Chemistry, Faculty of Science, Charles University, Hlavova 8, 128 00 Prague 2, Czech Republic
cDepartment of Macromolecular Physics, Faculty of Mathematics and Physics, Charles University, V Holešovičkách 2, 180 00 Prague 8, Czech Republic
dUniversidade Federal do ABC, Av. dos Estados, 5001. Bairro Santa Terezinha, Santo Andre, SP, Brazil
First published on 25th June 2024
Abstract
We report an innovative preparation of soft micron-sized polypeptide microgels by horseradish peroxidase (HRP)-mediated crosslinking in inverse suspension. The prepared microgels were based on poly[N5-((2-hydroxypropyl)-L-glutamine)-ran-(N5-propargyl-L-glutamine)-ran-(N5-(6-aminohexyl)-L-glutamine)]-ran-(N5-[2-((4-hydroxyphenyl)ethyl)-L-glutamine)] (P2HPG-Tyr) polymer precursor. We tested effects of three different surfactants, namely, sorbitan monooleate (SPAN 80), polyoxyethylenesorbitan trioleate (TWEEN 85), and dioctyl sulfosuccinate sodium salt (AOT), on microgelation in inverse suspension without or with a pre-emulsification step. The prepared P2HPG-Tyr microgels were investigated using light and cryogenic microscopy. The HRP-mediated crosslinking in inverse suspension employing SPAN 80 and one hour pre-emulsification yielded high-quality, spherical, and colloidally stable ∼80 μm P2HPG-Tyr microgels. Innovatively, we immobilized these large swollen P2HPG-Tyr microgels on mica and glass substrates for subsequent topography and surface nanomechanical measurements of these hydrated and swollen microgels using atomic force microscopy (AFM) in peak force quantitative nanomechanical mapping (PF-QNM) mode. The topography analyses revealed surface irregularities of the developed P2HPG-Tyr microgels consisting of small holes with diameters ranging from 80 to 200 nm. The PF-QNM proved the viscoelasticity and softness of P2HPG-Tyr microgels documented with Young's modulus in the range of tens of kPa derived from force-separation curves. Finally, the crosslink density was evaluated using two methods of calculation, revealing comparable concentrations of elastically active network chains (EANCs) in the range from 0.489 × 10−3 to 0.812 × 10−3 mol cm−3.
Introduction
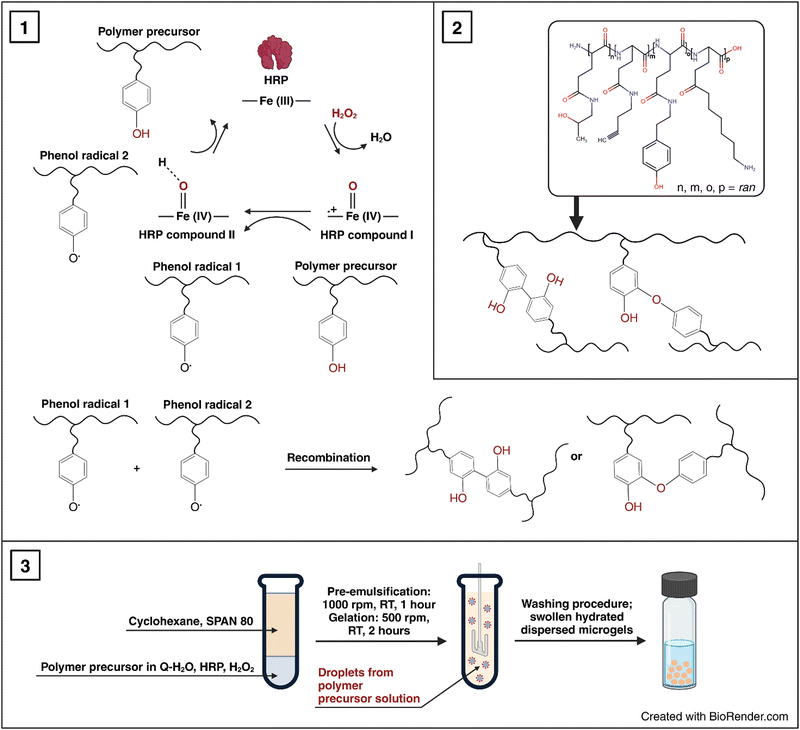
Microgels are crosslinked colloidal particles with sizes ranging from 100 nm to hundreds of microns built from various monomers and synthetic or natural polymers. They can be physically or covalently crosslinked depending on a constituent and a preparation procedure. Thus, they also exhibit swelling capability in aqueous media, and they may optionally possess stimuli-responsive behavior as a result of pH and temperature changes.1 Therefore, microgels have been investigated for different applications in biomedicine, pharmaceuticals, biotechnologies, and the food industry.2 Microgels can be fabricated from various materials. N-Isopropylacrylamide (NIPAM) and polyethylene oxide derivatives are the mostly used building materials for their fabrication.3 Microgels can also be prepared from other synthetic monomers and polymers or natural polymers including 2-hydroxyethyl methacrylate, proteins and polysaccharides to better meet requirements for future application.2,4 In particular, biopolymer-based microgels from chitosan, hyaluronan, dextran, pullulan, alginate, and whey protein have been abundantly explored for biomedical applications due to their non-cytotoxic, biodegradable, and physicochemical properties allowing external stimuli-induced structure change in microgels, water uptake, and even controlled payload release.5,6 These microgel systems can be employed for the delivery of bioactive compounds such as proteins (e.g. albumin, insulin), peptides and antigens, nucleic acids DNA and RNA, hydrophobic drugs, enzyme immobilization, cell encapsulation, application in photodynamic therapy, and fat replacers in food industry and biosensors3,7–10 There are various physical and chemical strategies to produce microgels, such as precipitation polymerization, emulsion methods, reversible addition–fragmentation transfer polymerization, microfluidic methods, extrusion, inverse suspension polymerization, and self-assembly.5,11 Besides, enzyme-mediated methods have been also applied for the fabrication of various hydrogel materials typically represented with horseradish peroxidase (HRP)-induced crosslinking in the presence of hydrogen peroxide as the enzyme substrate. The reaction is based on the catalytic crosslinking of polymers, such as alginate, hyaluronic acid, gelatin, dextran, poly(ethylene glycol), poly(glutamic acid), substituted with the reactive phenol groups of tyrosine or tyramine units.12–15Fabrication conditions, composition, and physico-chemical properties of the final product predetermine the architecture and nature of microgels, which then define structure, mass density, softness, and mechanical properties. In other words, it refers to how the microgel internal structure and cross-linked network interact with the environment and macromolecular system and respond to external stimuli.16 Therefore, the mechanical properties, swelling, and softness of microgels are crucial parameters for potential applications in industry, biotechnology, and biomedicine. In particular, tailored soft microgels have become very attractive for bioapplications, such as tissue engineering, delivery systems, or cell encapsulation, because they meet the specific requirements for the mechanical properties of these soft hydrogel materials.17,18 Nevertheless, the research community has been facing a formidable challenge in quantifying the mechanical properties of soft or even ultra-soft hydrogel materials in a hydrated state, which has rarely been described in the literature in much detail.17,19,20 Particularly, this challenge is particularly profound for soft microgels because they operate in the nano- and microscale size ranges.18,21 According to the literature, a modulus of soft hydrogel materials is typically accepted in the range from ∼200 Pa to 100 kPa and that of ultra-soft hydrogel materials is in the range of ≤200 Pa.19,20
The mechanical properties of soft hydrated microgels can be characterized using a few established methods, including microfluidic-based approaches, micropipette aspiration, glass-capillary approach, and atomic force microscopy (AFM).20,22 AFM belongs to fundamental methods used to measure elasticity and nano- and micromechanical properties of soft microgels with Young's modulus (E), frequency-dependent loss (G′), and storage moduli (G′′).23 A significant advantage of AFM is the possibility of performing measurements under ambient conditions in a liquid environment, which is more suitable for the characterization of soft hydrogel materials. However, the accuracy of moduli measurements in a liquid environment may suffer from hydrodynamic forces between the AFM cantilever, probe and analyzed samples.24 In particular, AFM allows imaging of surface topography, as well as detection and capture of forces between the tip and the sample via peak force quantitative nanomechanical mapping (PF-QNM) mode. PF-QNM is an AFM imaging mode that tracks the surface of the sample while simultaneously acquiring the individual force curves for each intermittent individual tap of the surface of the sample using the AFM tip. The force curves can be later analyzed to obtain mechanical data, such as Young's modulus and/or reduced modulus. PF-QNM is advantageous for the analysis of hydrated soft materials, such as microgels, because it controls the forces between the AFM tip and the sample, thus reducing the deformation of the sample and the tip wear. However, this measurement is difficult to perform for the analysis of large swollen microgels in a liquid environment, where the stable fixation of the sample to the substrate and the immobility of the sample during measurement are very complicated. Moreover, there are very few publications that address this problem and propose effective solutions.
In this study, we aimed to prepare soft micron-sized polypeptide P2HPG-Tyr microgels using HRP-mediated crosslinking in inverse suspension. The effects of various microgelation conditions, including surfactant type and pre-emulsification step, were tested on P2HPG-Tyr microgel morphology, size, and particle size distribution, and the prepared microgels were studied using a light microscopy technique. We discovered that pre-emulsification is a crucial step in stabilizing the inverse suspension and obtaining spherical and colloidally stable ∼80 μm P2HPG-Tyr microgels. The next aim was to evaluate the nanomechanical properties of the developed P2HPG-Tyr microgels in the hydrated state. Therefore, they were successfully immobilized on mica and glass substrates. Then, topography and nanomechanical analyses of P2HPG-Tyr microgels swollen in Q-H2O or PBS buffer were performed by PF-QNM, providing topography images and Young's moduli derived from force-separation curves. The results demonstrated the surface irregularity, viscoelasticity and softness of the developed P2HPG-Tyr microgels.
Experimental
Materials
Benzene, cyclohexane (CHX), chloroform, N,N-dimethylformamide (DMF), 1,4-dioxane, methanol, tetrahydrofuran, and toluene were obtained from Lach-Ner (Czech Republic). The solvents were purified and dried by standard procedures before use. Dioctyl sulfosuccinate sodium salt, 96% (AOT), was purchased from Alfa Aesar (Germany). Aminopropan-2-ol (Alfa Aesar) was purified by vacuum distillation. (3-Aminopropyl)triethoxysilane (APTES), 1,6-diaminohexane, HBr 33 wt% in acetic acid, 30% hydrogen peroxide solution (w/w) in water containing stabilizer (H2O2), horseradish peroxidase type VI (HRP), propargylamine, polyoxyethylensorbitan trioleate (TWEEN 85), sodium methoxide, sorbitan monooleate (SPAN 80), triphosgene, and tyramine were purchased from Sigma-Aldrich (Czech Republic) and were used without purification. γ-Benzyl-L-glutamate (BLG) 99% was purchased from Emmenar Bio-Tech (India) and recrystallized from a hot water/ethanol mixture. OxymaPure was purchased from Irish Biotech (Germany).Synthesis of the microgel precursor
The polyamino acid-based precursor poly(N5-(2-hydroxypropyl)-L-glutamine-ran-N5-propargyl-L-glutamine-ran-N5-(2-(4-hydroxyphenyl)ethyl)-L-glutamine) denoted as P2HPG-Tyr was prepared from poly(γ-benzyl-L-glutamate) (PBLG) (Mw = 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900, Mn = 25
900, Mn = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800, Đ = 1.70), including the synthesis of the N-carboxyanhydride of BLG, which was followed by solution ring-opening polymerization and by a series of post-polymerization modifications of the PBLG, according to our previously published procedure.25 The resulting P2HPG-Tyr precursor was characterized using 1H NMR spectroscopy (600 MHz, 25 °C, D2O): 7.1 ppm (2H, s, aromatic), 6.8 ppm (2H, s, aromatic), 4.1–4.4 (1H, s, NHC
800, Đ = 1.70), including the synthesis of the N-carboxyanhydride of BLG, which was followed by solution ring-opening polymerization and by a series of post-polymerization modifications of the PBLG, according to our previously published procedure.25 The resulting P2HPG-Tyr precursor was characterized using 1H NMR spectroscopy (600 MHz, 25 °C, D2O): 7.1 ppm (2H, s, aromatic), 6.8 ppm (2H, s, aromatic), 4.1–4.4 (1H, s, NHC![[H with combining low line]](https://www.rsc.org/images/entities/i_char_0048_0332.gif) CO), 4.0 ppm (2H, s, NHCH2CCH), 3.9 ppm (1H, s, C
CO), 4.0 ppm (2H, s, NHCH2CCH), 3.9 ppm (1H, s, C![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2CH(OH)CH3), 3.7 ppm (2H, m, CONHCH2(CH2)5NH2), 3.4 ppm (2H, s, CONHCH2CH2 next to aromatic ring), 3.1 ppm (2H, d, CONHC
2CH(OH)CH3), 3.7 ppm (2H, m, CONHCH2(CH2)5NH2), 3.4 ppm (2H, s, CONHCH2CH2 next to aromatic ring), 3.1 ppm (2H, d, CONHC![[H with combining low line]](https://www.rsc.org/images/entities/i_char_0048_0332.gif) 2CH(OH)CH3), 2.9 ppm (2H, m, CONH(CH2)5CH2NH2), 2.6 ppm (2H, s, CONHCH2CH2 next to aromatic ring), 2.2–2.5 ppm (2H, s, CHCH2C
2CH(OH)CH3), 2.9 ppm (2H, m, CONH(CH2)5CH2NH2), 2.6 ppm (2H, s, CONHCH2CH2 next to aromatic ring), 2.2–2.5 ppm (2H, s, CHCH2C![[H with combining low line]](https://www.rsc.org/images/entities/i_char_0048_0332.gif) 2CO), and 1.9–2.2 ppm (2H, s, CHC
2CO), and 1.9–2.2 ppm (2H, s, CHC![[H with combining low line]](https://www.rsc.org/images/entities/i_char_0048_0332.gif) 2CH2CO), 1.2–1.3 ppm (8H, m, CONHCH2(CH2)4CH2NH2), 1.1 ppm (3H,s, C
2CH2CO), 1.2–1.3 ppm (8H, m, CONHCH2(CH2)4CH2NH2), 1.1 ppm (3H,s, C![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2CH(OH)CH3) (Fig. S1, ESI†), UV-vis and fluorescence spectroscopy, and size exclusion chromatography (SEC) (see ESI† for the details of analysis).
2CH(OH)CH3) (Fig. S1, ESI†), UV-vis and fluorescence spectroscopy, and size exclusion chromatography (SEC) (see ESI† for the details of analysis).
The number-average molecular weight of the P2HPG-Tyr was Mn = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100, the weight-average molecular weight was Mw = 29
100, the weight-average molecular weight was Mw = 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and the dispersity was Đ = 1.31 (Shimadzu HPLC-SEC system equipped with UV detector (Shimadzu, Japan), differential refractive index detector (Wyatt Optilab T-rEX), and multi-angle light scattering detector DAWN EOS (Wyatt Technology), Superose 6 column). The concentrations of tyramine and propargyl units were 0.69 (11 w%) and 0.14 mmol g−1 (2 w%), respectively. The content of the primary amine groups was around 0.02 mmol g−1 determined by the commonly used reaction with fluorescamine.
000, and the dispersity was Đ = 1.31 (Shimadzu HPLC-SEC system equipped with UV detector (Shimadzu, Japan), differential refractive index detector (Wyatt Optilab T-rEX), and multi-angle light scattering detector DAWN EOS (Wyatt Technology), Superose 6 column). The concentrations of tyramine and propargyl units were 0.69 (11 w%) and 0.14 mmol g−1 (2 w%), respectively. The content of the primary amine groups was around 0.02 mmol g−1 determined by the commonly used reaction with fluorescamine.
Preparation of microgels
P2HPG-Tyr was microgelated into the form of micron-sized microgels according to the modified procedure.26 In a typical experiment, P2HPG-Tyr (0.072 g) was dissolved in Q-H2O (1.4 g) in a 30-mL glass reaction vessel with an anchor-type stirrer for 24 h at room temperature under stirring (150 rpm). HRP (0.180 mg) was dissolved in Q-H2O (0.328 g) and mixed with the previous solution. The concentration of HRP in the aqueous solution was 26 U mL−1. A given surfactant (15–20 wt% of surfactants) was dissolved in CHX (8.2 g) and mixed with the water phase. Then, the inverse suspension was microgelated after the addition of H2O2 (6.4 μL) for 2 h under stirring (500 rpm). The microgel was collected by sedimentation and washed five times with CHX (20 mL each cycle), five times with EtOH (20 mL each cycle), and five times with deionized water (20 mL each cycle) to completely remove the residual surfactant. Finally, the microgel was freeze-dried from deionized water.In the subsequent experiments, the microgelation procedure started with a pre-emulsification step for 1 h under stirring (1000 rpm), after which the stirring speed was reduced to 500 rpm and microgelation was initiated by the addition of H2O2 (6.4 μL).
Characterization of microgels
The size and size distribution of swollen microgels in aqueous media (Q-H2O, PBS buffer with pH 7.4) were analyzed using an Opton III light microscope (Oberkochen, Germany). The number-weighted mean diameter (Dn), volume-weighted mean diameter (Dw), and dispersity (Đ = Dw/Dn) were calculated using ImageJ software by counting at least 100 hydrogel microgels on light microscopy images using the following equations: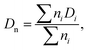 | (1) |
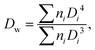 | (2) |
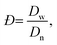 | (3) |
Immobilization of swollen P2HPG-Tyr microgels to substrates
To prevent any movement of the microgel particles during AFM measurements, the microgel particles were immobilized on (3-aminopropyl)triethoxysilane (APTES)-modified glass and mica substrates. Glass substrates and freshly cleaved mica substrates were sonicated in excess of CHCl3 for 30 minutes and then placed vertically in 0.1 M solution of APTES in toluene for 24 hours. Modification of glass and mica substrates by APTES was confirmed by contact angle measuring device OCA 20 (DataPhysics Instruments GmbH) at room temperature. Simultaneously, 2 mg of dry lyophilized microgel particles were dispersed and reswollen in 200 μL of Q-H2O or PBS buffer (pH 7.4) overnight. Subsequently, dispersions of reswollen microgel particles were drop-casted on APTES-modified glass and mica substrates and placed in a vacuum oven for 96 hours at 55 °C. Finally, APTES-modified glass and mica substrates with immobilized microgel particles were placed in excess of Q-H2O and PBS buffer with pH 7.4 in a multi-well plate to reswell and kept in the fridge at 8 °C.Determination of topography and nanomechanical properties by atomic force microscopy
AFM measurements were carried out using a Bruker Dimension Icon Scanning Probe Microscope equipped with a NanoScope V controller and Dimension Direct Drive Fluid Cantilever holder in Q-H2O and PBS buffer with pH 7.4 at room temperature. Bruker SAA-SPH-1UM probes with cylindrical tips (nominal spring constant of 0.25 N m−1 and nominal tip radius of 0.95 μm) were used for the measurements. The probes were factory-precalibrated, and their real spring constants were determined as 0.25 N m−1 and 0.206 N m−1. Before each experiment, the deflection sensitivity of the cantilevers was calibrated in Q-H2O and PBS buffer with pH 7.4 on a glass reference sample.Bruker PF-QNM mode was employed to determine topography, Young's modulus (E) and reduced modulus (E*) of the reswollen microgel particles. Topography images of each sample were captured. The scan sizes were 5 × 5 μm, and the scan rate ranged from 0.1 Hz to 0.2 Hz. For each sample, 500 pairs of extend and retract force curves in trace and retrace directions were collected by real-time High Speed Data Capture interface on the center of the particles with a particle size of 80 μm (in Q-H2O) and 74 μm (in PBS buffer with pH 7.4). The force curves were analyzed using NanoScope Analysis 1.50 software. The E and E* values were collected from 500 pairs of retract force-separation curves for each sample. Then, the values were averaged, and their standard deviations (SD) were calculated.
To obtain the E values of the samples, the retract force-separation curves were fitted by the following equation according to the Hertz model:
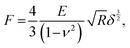 | (4) |
To obtain the E* values, the retract force-separation curves were fitted by applying the following equation using the Derjaguin–Muller–Toporov model:
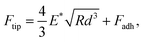 | (5) |
Cryogenic scanning electron microscopy (Cryo-SEM)
The samples for Cryo-SEM were prepared in three ways. The first method of sample preparation started with the deposition of a thin layer of microparticle suspension on an aluminum stub, which was manually roughened with a sandpaper. The roughening was important to maintain the liquid layer thinness and stability during the following vitrification procedure. The stub with the solution was vitrified in liquid nitrogen slush (LNS) using a Cryo-SEM preparation system (PP3010 system; Quorum Technologies Ltd, United Kingdom) attached to a FEGSEM microscope (MAIA3; TESCAN, Czech Republic). The frozen sample was inserted into an intermediate chamber, where a part of the vitrified ice was sublimed off (−90 °C for 15 min in high vacuum conditions, p ∼ 10−3 Pa). Then, the stub was cooled back to liquid nitrogen temperature and inserted into the microscope chamber. In the microscope chamber, the frozen microparticles were observed (without any sputtering) using secondary electron imaging mode at an accelerating voltage of 1 kV. The second method of sample preparation was similar to the first one, but instead of a thin liquid layer, we vitrified a droplet of the microparticle suspension. The droplet was fractured in the intermediate chamber using micromanipulators; part of the ice was sublimed off (−90 °C for 10 min at p ∼ 10−3 Pa), and the fracture surface with the microparticles was observed in the same way described above. The third method of sample preparation was similar to the second one, but the frozen sample was fractured in a capillary as follows: at the very beginning, the solution was partially evaporated (to obtain a sufficiently high concentration of microparticles) and put into copper capillary made of two parts glued together (the high concentration of microparticles was necessary so that the microparticles were in the whole volume, not only on the bottom of the capillary). The capillary was frozen in the LNS and broken in the middle, i.e. in the glued part. The fracture surface was sputtered with a thin platinum layer (the samples fractured in capillaries tend to charge; the sputter coater is a part of the above-described cryo-SEM preparation system; the thickness of the Pt layer is ca. 5 nm). The fracture surface was observed without any preliminary sublimation using secondary electron imaging, as described above.Results and discussion
Based on our previous studies on the HRP/H2O2-mediated nanogelations of various polypeptides, we used this method to prepare soft micron-sized polypeptide P2HPG-Tyr microgels.26,27 P2HPG-Tyr microgels were prepared by HRP/H2O2-mediated microgelation in inverse suspension according to the slightly modified procedure for the preparation of P2HPG-Tyr nanogels.26 The P2HPG-Tyr polymer precursor with 11 wt% tyramine units (Tyr) had a number-average molecular weight Mn = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100, weight-average molecular weight Mw = 29
100, weight-average molecular weight Mw = 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and dispersity Đ = 1.31. Then, this polymer precursor was used for the preparation of P2HPG-Tyr microgels, and the effects of three surfactants and pre-emulsification step on size, size distribution, morphology of final microgels and yields of microgelations were investigated (as listed in Table 1) according to Scheme 1. The selection of tested surfactants (SPAN 80, TWEEN 85, and AOT) and their concentrations was based on the results of our previous study about P2HPG-Tyr nanogelation.26
000, and dispersity Đ = 1.31. Then, this polymer precursor was used for the preparation of P2HPG-Tyr microgels, and the effects of three surfactants and pre-emulsification step on size, size distribution, morphology of final microgels and yields of microgelations were investigated (as listed in Table 1) according to Scheme 1. The selection of tested surfactants (SPAN 80, TWEEN 85, and AOT) and their concentrations was based on the results of our previous study about P2HPG-Tyr nanogelation.26
| Microgels | Surfactant | Surfactant concentration (wt%) | Pre-emulsification | Dispersant for image analysis | D n (μm) | D w (μm) | Đ | Yield (%) |
|---|---|---|---|---|---|---|---|---|
| AOT – dioctyl sulfosuccinate sodium salt; Dn – number-average diameter; Dw – weight-average diameter; Đ – dispersity; SPAN 80 - sorbitan monooleate; TWEEN 85 – polyoxyethylensorbitan trioleate | ||||||||
| M1 | SPAN 80 | 20 | No | Q-H2O | 47 | 128 | 2.7 | 67 |
| M2 | SPAN 80 | 20 | 1000 rpm/1 h | Q-H2O | 80 | 127 | 1.6 | 57 |
| M3 | TWEEN 85 | 15 | no | Q-H2O | 45 | 104 | 2.3 | 84 |
| M4 | TWEEN 85 | 15 | 1000 rpm/1 h | Q-H2O | 25 | 36 | 1.4 | 90 |
| M5 | AOT | 15 | no | Q-H2O | 33 | 59 | 1.8 | 64 |
| M6 | AOT | 15 | 1000 rpm/1 h | Q-H2O | 11 | 17 | 1.6 | 50 |
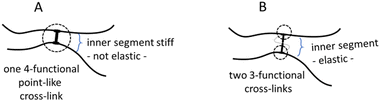
First, we tested 20 wt% SPAN 80 as a steric stabilizer for the microgelation without the pre-emulsification step of P2HPG-Tyr. The final microgels (M1) were mainly coagulated and contained only a small number of 47 μm microgels (Fig. 1(a)). According to the literature, we decided to include the mechanical pre-emulsification step in the microgelation process to form a stable inverse suspension that can subsequently be microgelated by H2O2 addition.28Fig. 1(b) depicts that the mechanical pre-emulsification step significantly affected the microgelation of P2HPG-Tyr in the presence of 20 wt% SPAN 80. The individual and spherically shaped M2 microgels (swollen in Q-H2O) with Dn = 80 μm and Dw = 127 μm, and broad particle size distribution (Đ = 1.6) were formed.
The results indicated that the pre-emulsification step enabled the molecules of SPAN 80 to cover the droplets and, thus, effectively stabilize inverse suspension against undesired coalescence. Nevertheless, the microgelation yielded 57% of the product, indicating that not all the amounts of P2HPG-Tyr polymer precursor were incorporated into the final microgels due to the partial coalescence of droplets during microgelation. Besides, we suppose that the lower microgelation yield would be due to the hydrophobic character of SPAN 80 and its high concentration and higher viscosity, as already observed in our previous study on the preparation of polypeptide nanogels.26 Second, the microgelation was carried out in the presence of 15 wt% TWEEN 85 steric stabilizer (M3), resulting in aggregated 45 μm microgels (Fig. 1(c)). The pre-emulsification step helped to ensure the colloidal stability of the inverse suspension because individual spherical M4 microgels were fabricated with Dn = 25 μm, Dw = 36 μm, and Đ = 1.4 in the swollen state (Fig. 1(d)). The yield of microgelation was calculated as 90%, suggesting that TWEEN 85 effectively prevented undesired coalescence of droplets compared to stabilization using 20 wt% SPAN 80 (M4). However, during this microgelation, we encountered one major problem: the reproducibility of the preparation of microgels in the presence of TWEEN 85. We suppose that TWEEN 85 might have negatively affected the enzymatic activity of HRP; therefore, the microgels could not be reproducibly prepared. Third, 15 wt% AOT was used as a steric stabilizer for microgelation. The stabilization of inverse suspension was slightly improved by AOT because more individual P2HPG-Tyr microgels (M5) were obtained (Fig. 1(e)). Besides a few irregular objects, M5 contained spherical microgels (swollen in Q-H2O) with Dn = 33 μm, Dw = 59 μm, and Đ = 1.8. Surprisingly, the pre-emulsification step had a deteriorating effect on the microgelation of P2HPG-Tyr in the presence of 15 wt% AOT (M6). Fig. 1(f) depicts mainly aggregated products with few number of 11 μm microgels. The microgelation in the presence of the AOT surfactant also resulted in low yields, which was probably due to electrostatic repulsion between the AOT surfactant and P2HPG-Tyr polymer precursor.26
Our results clearly demonstrated that the pre-emulsification step contributed to the formation of a more colloidally stable inverse suspension, which was then more effectively microgelated, and individual P2HPG-Tyr microgels were fabricated in the presence of SPAN 80 as a steric stabilizer (M2). We also evaluated morphology, particle size and particle size distribution of M2 swollen in PBS buffer with pH 7.4. As observed in aqueous M2 suspension, M2 microgels swollen in PBS buffer maintained their spherical shape and smooth surface. The change in pH to 7.4 also led to narrowing of the particle size distribution (Đ = 1.4) and a decrease in M2 diameter to Dn = 74 μm and Dw = 103 μm (Fig. 2) due to stronger hydrophobic interactions and hydrogen bonding between P2HPG-Tyr chains in M2.29
Immobilization of swollen P2HPG-Tyr microgels on substrates
With the idea of evaluating the surface and nanomechanical properties of the developed P2HPG-Tyr microgels by PF-QNM, it was crucial to firmly immobilize hydrated M2 microgel samples to each substrate. Thus, the undesired movement of samples on a substrate and during contact with the tip in liquid environments can be avoided. We selected two substrates, mica and glass substrates, which were modified with APTES. APTES is a known agent for the immobilization and AFM measurements of microgels or biological samples.30,31 The surface can be considered hydrophilic when the water contact angle (WCA) is <90°.32 The WCAs of APTES-modified mica and glass substrates were 47° and 38.8°, respectively, and they were lower than the WCAs of unmodified substrates possessing WCAs 56.9° and 59.2°, respectively. These results indicate the overall higher hydrophilicity of both APTES-modified substrates. Then, swollen M2 was successfully and firmly immobilized on each substrate via the hydroxy and carboxy groups on the P2HPG-Tyr polymer chains (Scheme 2).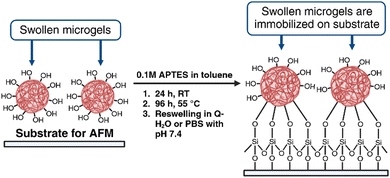 | ||
| Scheme 2 Immobilization of swollen P2HPG-Tyr microgels on APTES-modified mica and glass substrates (created with BioRender.com). | ||
Determination of topography and nanomechanical properties by atomic force microscopy
Because AFM has been extensively used for the topography and mechanical measurements of soft materials, we employed this technique in the PF-QNM imaging mode to investigate our developed P2HPG-Tyr microgels. PF-QNM was used to determine the topography of swollen M2 in Q-H2O and PBS (pH 7.4) immobilized on APTES-modified mica and glass substrates. To obtain E and E* moduli, we acquired 500 pairs of force curves on the centre of the M2 microgels with Dn = 80 μm (in Q-H2O) and 74 μm (in PBS with pH 7.4) for each sample during topography investigations.Fig. 3(a)–(d) shows AFM images of swollen M2 under various conditions. Interestingly, PF-QNM topography analyses revealed that M2 surface irregularities in both environments were not visible during light microscopy analyses due to a lack of necessary magnification. These observations were attributed to dimples in swollen M2. In general, AFM does not belong to the standard techniques for the characterization of porous structures. However, it can provide relevant information about surface properties of hydrated and swollen hydrogel samples under optimized, reliable, and stable conditions as it was, for example, demonstrated with carboxymethyl guar gum and agarose hydrogels.33,34 M2 is composed of covalently crosslinked P2HPG-Tyr polymer chains via dityramine crosslinks into 3D P2HPG-Tyr network.25 When M2 was swollen, it was permeated with a solvent enabling a conformational change from collapsed to extended state.17 According to PF-QNM analyses, M2 showed surface irregularities consisting of small holes with depths ranging from 80 to 200 nm in diameter. A similar observation of irregular surface structure was found with swollen poly(2-hydroxyethyl methacrylate) hydrogels with various crosslinking densities.35 Moreover, our assumption can be supported by the fact that Fig. 3(a)–(d) illustrates that the PF-QNM analyses were performed on the spherical surface of a single M2 microgel because the color change from dark to bright can be observed in the images, as illustrated in Fig. 3(b)–(d). In other words, the surface irregularities were visible only in the central region of the PF-QNM images. Therefore, we can rule out the possibility that light areas represent small microgels surrounding the studied ∼80 μm M4 microgel (in Q-H2O) or ∼74 μm M2 microgel (in PBS buffer) because they are observed as light-colored objects in dark areas. Nevertheless, the size of the irregularities is too small in comparison to the diameter of M2, and it is still possible to consider the investigated surfaces of M2 as smooth.
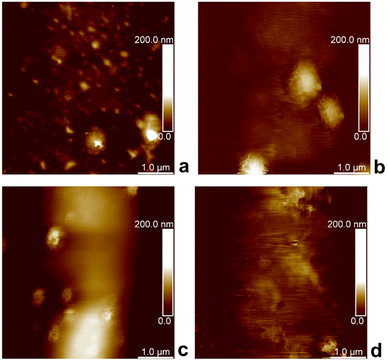 | ||
| Fig. 3 PF-QNM topography height images of P2HPG-Tyr microgels on mica substrate (a), (b) and glass substrate (c), (d), swollen in Q-H2O (a), (c), and PBS buffer (b), (d). | ||
Verification of morphology using cryogenic scanning electron microscopy
The morphology of swollen M2 microgels was visualized and verified by cryogenic scanning electron microscopy (Cryo-SEM). The samples for Cryo-SEM were prepared in multiple ways, as described in the Experimental section. The most illustrative Cryo-SEM results are shown in Fig. 4(a) and (b). The figure displays the frozen M2 microparticles on an aluminium stub after the sublimation of ice. The Cryo-SEM micrographs confirmed that the microparticles of M2 were spherical and smooth. This agreed well with the light microscopy results (Fig. 1(b) and 2). The slightly smaller size of the microparticles in Cryo-SEM micrographs (Fig. 4(a) and (b)) in comparison with light micrographs (Fig. 2) can be attributed to the shrinkage of the microgels after ice sublimation. | ||
| Fig. 4 Cryo-SEM micrographs showing the morphology of frozen M2 microgels at (a) lower magnification and (b) higher magnification. | ||
Determination of nanomechanical properties
To evaluate the surface nanomechanical properties of swollen M2, we performed PF-QNM measurements using a spherical tip that is more suitable for the characterization of soft materials.36Fig. 5(a)–(d) shows the force–separation curves of swollen M2 microgels immobilized on two different substrates, mica and glass, in Q-H2O and PBS buffer at pH 7.4. On the extended curve in Fig. 5(a), there is an attractive interaction at ∼180 nm between the swollen M2 in Q-H2O and the tip. The interaction between the tip and the swollen M2 then becomes slightly repulsive and is followed by the strong attraction of the tip to the sample. After the tip touches the surface, the attractive forces increase to approximately 1.8 nN. On the retract curve, the interactive forces decrease gradually, while the obvious hysteresis and slight adhesion are attributed to viscoelastic relaxation and squeezing out of Q-H2O from swollen M2.37
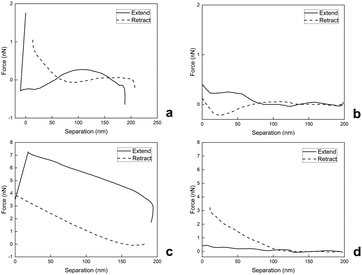 | ||
| Fig. 5 Force–separation curves of swollen M4 on mica (a), (b) and glass (c), (d) substrates in Q-H2O (a), (c) and PBS buffer with pH 7.4 (b), (d). | ||
On the extended curve depicted in Fig. 5(b), there is weak repulsion from 200 nm to 190 nm, followed by gradual weak attraction, depicted from 190 nm to 0 nm. During retraction, the swollen M2 adheres and is stretched by the retracting tip with almost no attractive or repulsive interaction afterwards.
Fig. 5(c) demonstrates strong and gradual attraction until ∼20 nm of the extended curve and rapid drop due to the repulsion of the tip from the surface, while the retract curve illustrates the continuous decrease in tip-sample interaction until there is no repulsion or attraction. During the nanomechanical measurement of swollen M2 in Q-H2O, we also observed hysteresis due to the viscoelastic behavior and drainage of Q-H2O.37
As depicted in Fig. 5(d), the tip-to-sample approach occurs with weak repulsion, which is then followed by the gradual weak attraction mostly visible in the 125-nm to 0-nm part of the separation axis; the retract curve shows a continuous decrease with no repulsion or attraction.
As our observations revealed, the nanomechanical properties of swollen M2 were sensitive to aqueous environments with different pH and salinity levels. PF-QNM analyses of swollen M4 in Q-H2O on mica and glass substrates demonstrated softer behaviors documented with E values (Table 2). It was also obvious that swollen M2 was more load-dependent during analyses in Q-H2O in comparison with PF-QNM analyses in PBS buffer with pH 7.4. The force–separation curves demonstrated that PBS-swollen M2 was not so responsive to contact with the tip and had stiffer behavior documented with increased E values on the glass substrate in PBS (Table 2). Simultaneously, the PBS-swollen M2 on mica demonstrated slightly lower E values than the Q-H2O-swollen M2 on mica (Table 2). However, the lower tip-sample interactions, which were observed during PF-QNM analysis of PBS-swollen M2 on mica (Fig. 5(b)), suggest that lower tip-sample interaction yields lower E values. This analysis also confirmed the viscoelasticity of swollen M2 because the E* values shifted to higher values compared to the E values (Table 2).
| Substrate | Environment | Young's modulus (E ± SD) [kPa] | Reduced Young's modulus (E* ± SD) [kPa] |
|---|---|---|---|
| Mica | Q-H2O | 40.2 ± 16.2 | 53.6 ± 21.6 |
| Glass | Q-H2O | 50.9 ± 14.9 | 67.8 ± 19.8 |
| Mica | PBS buffer | 35.7 ± 15.1 | 47.6 ± 20.1 |
| Glass | PBS buffer | 60.9 ± 13.4 | 81.2 ± 17.8 |
In summary, the calculated Young's moduli were in the range of tens of kPa, indicating soft hydrogel materials. For example, Dvořáková et al. prepared the injectable hydrogels from a P2HPG-Tyr polymer precursor modified with integrin-binding arginine–glycine–aspartic acid peptide by varying the concentrations of the P2HPG-Tyr precursors and horseradish peroxidase as well as the nH2O2/nTyr ratio. The mechanical properties of the injectable hydrogels were characterized by oscillatory rheology measurements with storage moduli ranging from 1 to 4 kPa, indicating ultra-soft hydrogel materials.15 In general, there is clear and practical evidence that the softness of hydrogel materials is influenced by crosslink density.
Determination of microgels crosslinking density
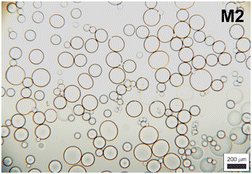
To gain more insight into the hydrogel structure, we aimed to characterize the crosslink density of the developed soft microgels as a key parameter of their macromolecular network. It is important to note that we define the network density as the concentration of the “elastically active network chains”, EANCs38 in a given reference volume, for which the volume of dry hydrogel is chosen. To arrive at the value of crosslink density, νe, given typically in [mol cm−3], we used an advanced statistical simulation based on the theory of branching processes (TBP). A scheme of the chemical composition of the primary chains and tyramine links is depicted in Scheme 1, and a schematic explanation of how the primary chains and crosslinks are arranged in a 3D infinite network is presented in Fig. 6(A). The calculation of νe is described in hereinafter and amended in ESI.†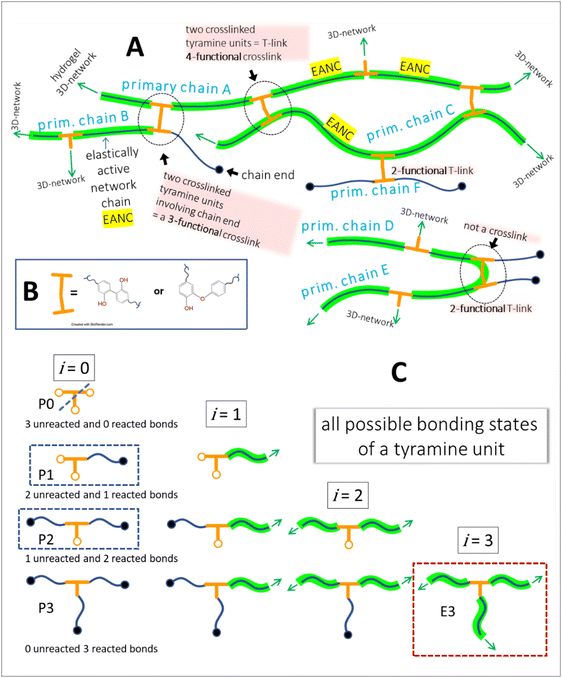 | ||
| Fig. 6 A – hydrogel network structure formed by crosslinking of primary polyfunctional P2HPG-Tyr chains via linking of tyramine units, i.e. the depicted network is crosslinked with the dityramine crosslinks. Example A is given for the situation depicted in Fig. 7(A), i.e. the dityramine bonds issue maximally 4 bonds to the hydrogel 3D network structure, and the internal dityramine chains are not considered elastically active; insert B shows the two possible chemical structures of dityramine links; and panel C shows a single tyramine unit in its all possible bonding states as treated by the theory of branching processes found in the crosslinking system: in the starting backbone chains, the units P0 with three unreacted bonds do not exist, while the units P1 with only one connection to backbone chains are possible (outermost units) and the units P2 represent the most probable state of tyramines in initial system, i.e. the T-units are incorporated in the primary P2HPG-Tyr chains. Unit E3 demonstrates that the trifunctional fully reacted tyramine unit embedded in the hydrogel network, an elastically active crosslink depicted in Fig. 7(B). | ||
The tyramines are crosslinking the P2HPG-Tyr primary chains by their mutual coupling. The formed dityramine bonds can attain two possible chemical types, as depicted in the insert in Scheme 1 and Fig. 6. The two possible types of dityramine links are similar in size. However, the biphenyl-containing units presumably possess higher rigidity. It has already been reported in the literature that the major part of dityramine bonds attains the biphenyl structure, i.e. the more rigid bonds prevail.39
Thus, for the calculation of the concentration of EANCs, we consider both situations delimiting the possible real behavior of gels: i/the dityramine links between the backbone chains are considered single four-functional crosslinks of a rigid nature, and their internal segment does not contribute to the number of elastically active chains (Fig. 7(A)), or, ii/the connecting dityramine link is considered sufficiently flexible and contributing to elasticity of the network; then, each tyramine unit provides a three-functional crosslink (Fig. 7(B)).
Later, we also briefly address the rather general issue of the minimal chain length between the elastically active crosslinks to exert the rubbery elasticity.
In the scheme in Fig. 6, the general structure of the hydrogel network is shown and the basic structural features of the network are illustrated. The primary P2HPG-Tyr chains are combined through 4-functional, 3-functional, and bifunctional dityramine links, and some chains can be attached as monofunctional parts through a monofunctional “T-link”. (The adjective “functional” describes the number of connections of the given unit with the infinite network, as illustrated in Fig. 6(C)). In the “monofunctional case” (not shown in Fig. 6(A)), indeed, the attached part of the material forms a dangling chain and does not contribute to the elastic response.
First, the crosslink densities of hydrogels in both limiting states were inferred from the system's starting composition and from the parameters determined during the characterization of the P2HPG-Tyr polymer precursor (such as the molecular weight of the precursor – Mn = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 g mol−1, the content of the crosslinking units (tyramines) – 10.8 wt%; thus, the average number of crosslinkable units per chain is 12).
100 g mol−1, the content of the crosslinking units (tyramines) – 10.8 wt%; thus, the average number of crosslinkable units per chain is 12).
Let us distinguish units in which all chains are composed by the number of issuing bonds to an infinite network (arrows in Fig. 6), i = 0, 1, 2,…, (cf. unit states in Fig. 6(C)) with molar concentrations ci and molar fractions ni = ci/c, where 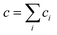 and Mi is molar mass. Crosslinks are units with at least 3 issuing bonds to an infinite network, i ≥ 3. In our case, i = 3 belongs to reacted tyramine units (see unit E3 in Fig. 6(C)) or 4 belongs to dityramine bonds. Each bond issued from a crosslink represents 1/2 of an elastically active network chain. Therefore, the number (of moles) of EANCs (per unit volume), i.e., the molar concentration of EANCs is
and Mi is molar mass. Crosslinks are units with at least 3 issuing bonds to an infinite network, i ≥ 3. In our case, i = 3 belongs to reacted tyramine units (see unit E3 in Fig. 6(C)) or 4 belongs to dityramine bonds. Each bond issued from a crosslink represents 1/2 of an elastically active network chain. Therefore, the number (of moles) of EANCs (per unit volume), i.e., the molar concentration of EANCs is 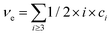 . However, molar concentrations ci are not known or measurable directly, whereas the molar fractions, ni, are. Molar concentration c can be obtained from the specific gravity,
. However, molar concentrations ci are not known or measurable directly, whereas the molar fractions, ni, are. Molar concentration c can be obtained from the specific gravity, 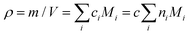 , where m and V are the mass and volume of the whole system, respectively, and νe can be expressed in terms of hydrogel composition ni as follows:
, where m and V are the mass and volume of the whole system, respectively, and νe can be expressed in terms of hydrogel composition ni as follows:
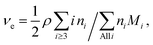 | (6) |
To calculate the crosslink density for situation A in Fig. 7, let us assume that the average number of 3-functional T-links (such as the units P2 or less likely P1 in Fig. 6(C)) is 12 per a primary chain of 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 g mol−1. Because the two 3-functional crosslinks are consumed for one 4-functional dityramine bond, the number obtained by the application of eqn (6) is further divided by a factor of two; thus, the value of νe,4 is 0.542 × 10−3 mol of EANCs per 1 cm3 of the dry network.
100 g mol−1. Because the two 3-functional crosslinks are consumed for one 4-functional dityramine bond, the number obtained by the application of eqn (6) is further divided by a factor of two; thus, the value of νe,4 is 0.542 × 10−3 mol of EANCs per 1 cm3 of the dry network.
In situation B of Fig. 7, the number of 3-functional crosslinks is equal to the number of fully reacted tyramines connected to the infinite network, such as units E3 in Fig. 6(C). Then, corresponding to the conversion of tyramine coupling reactions close to 1, the final νe,3 is 0.812 × 10−3 mol cm−3. Subsequently, the difference between the limiting network structures with either crosslink type Δν is 33% (related to the value higher of the two values, νe,3).
A more refined way leading to a value of νe corrected for all possible bonding states of crosslinking units was based on the schooled application of the statistical theory of branching processes (TBP).40 The application of TBP on multifunctional crosslinking chains is explained in detail in the work.41 Briefly, applying the TBP, one examines all the possible connections between units existing at a given state of the crosslinking process. The units are distinguished according to their number of bonds in all reaction states: unreacted bonds, bonds reacted but issued to a finite structure, and bonds reacted and issued to an infinite network structure. See Fig. 6(C) for an example of a single tyramine unit. The TBP algorithms provide the average concentrations of given units in the system, while the inactive structures that are statistically present in every real network are not counted. In other words, the calculation considers the loss of units in the dangling chains (example in Fig. 6(A): primary chain F and other chain ends) and in the possible sol part.
A mathematical tool enabling this analysis is the probability generating function (PGF) derived in this case for the given case of multifunctional chains. The PGF provided the result through a solution of a system of differential equations. A detailed discussion of these derivations exceeds the scope of this paper but will be made available to the reader on request. We used a script written in the software Wolfram Mathematica 14: the solution of the simulation of the network state at a complete conversion (α = 1) gave the values of νe,3 = 0.677 × 10−3 mol cm−3 and νe,4 = 0.489 × 10−3 (see Table 3 for a summary). The estimate from the system composition is very reasonable. Moreover, the simple estimate gives higher values because it does not count off the elastically inactive bonds, unlike TBP. Particularly, the units situated in the dangling chains or appearing in the chain ends negatively contribute to the value of νe. Thus, the TBP shows, by a statistical treatment of the given system, that approximately 10 (for fe = 4) and 17% (for fe = 3) of bonds belonging to crosslinkers are connected with elastically inactive material. The set of results in Table 3 provides good evidence of the relevancy of the estimates. It is also worth mentioning that (1) the value of νe determined for the hydrogels corresponds to the crosslink density of moderately crosslinked synthetic hydrogels based on poly(2-hydroxyl methylmethacrylate)42 or falls within a range of crosslink densities of chemically similar hydrogels based on a copolymer of four types of (meth)acrylamide units crosslinked with aromatic azo bonds designed previously for drug delivery application.43
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 g mol−1 and number of tyramine units per chain 12
100 g mol−1 and number of tyramine units per chain 12
| Method of calculation | Crosslink density νe [mol cm−3] | |||
|---|---|---|---|---|
| Parameters | ν e,4 f e = 4 | ν e,3 f e = 3 | (νe,3 − νe,4)/νe,3 | |
| Composition of hydrogel eqn (6) | Chain length, g mol−1 number of tyramine units per chain maximal functionality of crosslink | 0.542 × 10−3 | 0.812 × 10−3 | 0.333 |
| Theory of branching processes | 0.489 × 10−3 | 0.677 × 10−3 | 0.277 | |
| Interaction parameter χ | ||||
|---|---|---|---|---|
| Parameters | ν e,4 f e = 4 | ν e,3 f e = 3 | χ ν e,4 = χνe,3 | |
| Swelling of hydrogel eqn (8) | φ 2 | 0.094 | 0.404 | |
| φ 0 | 0.04 → 0.094 | |||
| front factors A, B | A = 1, B = 2/4 | A = 1, B = 2/3 | ||
| V s, cm3 mol−1 | 54 | |||
| v e – TBP | 0.489 × 10−3 | 0.677 × 10−3 | ||
A legitimate question arises if all the segments constituting the hydrogel network are long enough to return the elastic work. In other words, are the chain segments between the branched sides exerting entropic elasticity? The distribution of crosslinkable units along the backbone of the random copolymer is indeed statistical. This means that some tyramine units can be placed tightly next to each other or separated by 1,2,3…Nmax units. The average length of chains between the two tyramine units in the P2HPG-Tyr backbone is 8 units. Let us analyse the behaviour of the N-jointed polymer segments within the basic polymer physics paradigm of the freely jointed model44 and calculate the distribution of the distances between the chain ends from the minimal number of two segments. The result is quite remarkable, and the end-to-end distance (ETED) of already 3 jointed segments revealed maxima on the ETED distribution curve (Fig. S2 in ESI†). This means that if such a chain is strained using force and its ends are displaced outside of the maximum intensity of ETED counts, the ends tend to “come back” to their most probable distance once the displacement is no longer maintained by force. Therefore, it follows that 3 segments already possess entropic elasticity. Moreover, the distribution function does not dramatically differ with the number of segments (Fig. S2 in ESI†). Indeed, the length of a “typical” segment in a real system, which could perhaps substitute one bond in a freely jointed model, is the subject of a complex assessment. It is quite clear that due to the limited rotation and various stiff structures, such characteristic segments must be longer than a single covalent bond. In our copolymer, each incorporated unit is contributed by two or three covalent σ-bonds into the P2HPG-Tyr backbone. Let us consider the backbone sequence of a monomer unit to be a stiff segment. The reasoning above and the results of the calculation of ETED show that all connections between tyramine units from the N ≥ 3 can be considered elastically active. The molar fraction of these connections is more than 98 molar% of all connections between tyramine branch points; see Table SI in ESI.† Thus, the resulting values of crosslink densities can be taken as very close approximations, and a correction for the fraction of elastically inactive chains was not adopted.
Finally, we considered calculating hydrogel network parameters based on their physical behavior, specifically on their equilibrium swelling tackled experimentally. We characterized the swelling of microgel particles from their dry and swollen diameters obtained from the light scattering experiment, resulting in a volume fraction of swelling φ2 = 0.094. The equilibrium swelling volume fraction is defined as follows:
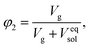 | (7a) |
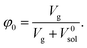 | (7b) |
The balance between the number of solvent molecules penetrating the network chains, process driven osmotically, and the network elastic retraction force driven by the entropy of the network chains determines the equilibrium swelling for a given solvent and temperature. The retraction force is proportional to the concentration of EANCs. Therefore, we should be able to calculate the concentration of the retracting chains, νe, using the well-known swelling equation, the Flory–Huggins–Rehner model, in the following form:45
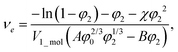 | (8a) |
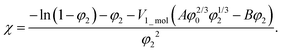 | (8b) |
The outcome of the relation above was very interesting: when the value of φ0 was 0.04 (in consent with real preparatory conditions). For the case of trifunctional crosslinks and experimental φ2 of 0.094, swelling eqn (8,a) surprisingly provided a negative value of crosslink density for a range of χ. Because the Flory–Huggins–Rehner model is derived from thermodynamic principles and the well-established rubbery elasticity theory, we attribute this limiting behaviour of eqn (8) to an existing physical effect, unknown at the current time. Tentatively, it seems that the formation of a network at φ0 = 0.04 would not be physically possible for the given composition. In fact, when the network is formed in such a highly diluted system, the precursors separated in space must come together to make crosslinks, while the solvent volume exceeds the maximum network capacity obtained from φ2. When the first network is formed, the excess solvent is excluded from the crosslinking system. Thus, in eqn (8b), we use the value 0.094 for φ0 to approximate our experimental circumstances. Interestingly, the obtained χ did not depend on functionality, i.e. on parameter B, and was 0.404 for both considered structures. This value of the constant interaction parameter falls within a sound range for aqueous hydrogel and will serve as a starting point in future investigations of the swelling behaviour of the novel P2HPG-Tyr-based networks.
Conclusions
This study reported the successful preparation of polypeptide P2HPG-Tyr microgels by HRP-mediated crosslinking in an inverse suspension. We found that the pre-emulsification step supported the formation of a stable inverse suspension stabilized with 20 wt% SPAN 80, which was then microgelated by the addition of H2O2 as a substrate for HRP. The prepared P2HPG-Tyr microgels were investigated using light microscopy, showing their regular and spherical shape and smooth surfaces. P2HPG-Tyr microgels swollen in Q-H2O had a diameter Dn = 80 μm with a broad particle size distribution documented with Đ = 1.6. They exhibited a decrease in their diameter in PBS buffer (pH 7.4) to Dn = 74 μm and slightly narrowed particle size distribution (Đ = 1.4) due to stronger hydrophobic interactions and hydrogen bonding between P2HPG-Tyr chains within the individual microgels at higher pH. Cryo-SEM confirmed the spherical shape and smooth surface of the P2HPG-Tyr microgels. Despite the difficult handling and immobilization of similar microgels in a swollen state, we successfully immobilized the developed P2HPG-Tyr microgels in the swollen state on APTES-modified mica and glass substrates. These immobilized P2HPG-Tyr microgels were then characterized in terms of surface morphology and nanomechanical properties using AFM in PF-QNM mode. The topography analyses revealed irregularities on the P2HPG-Tyr microgel surfaces in a swollen state consisting of holes with diameters ranging from 80 to 200 nm. The final nanomechanical measurements showed the viscoelastic behavior and softness of the P2HPG-Tyr microgels with observed drainage of dispersants during PF-QNM analyses. Both Q-H2O- and PBS buffer-swollen microgels exhibited Young's moduli in the range of tens of kPa derived from force–separation curves. Finally, the concentration of EANCs, “crosslink density”, of the developed soft microgels was calculated using two methods: Composition of Hydrogels, and Theory of Branching Processes. These calculations provided EANC values that were in good agreement and ranged from 0.489 × 10−3 to 0.812 × 10−3 mol cm−3. We hope that these findings will inspire further studies of large soft microgels and their nanomechanical properties in the swollen state, as well as further investigation of hydrogel swelling behaviour by adopting a complex multidisciplinary approach discussed in this article.Author contributions
Oleksii Kotko – conceptualization; methodology; investigation; preparation and characterization of microgels; contact angle measurements, immobilization of microgels, AFM measurements; data evaluation; article writing; Petr Šálek – conceptualization, methodology, investigation, data evaluation, article writing; Jana Dvořáková – preparation and characterization of P2HPG-Tyr polymer precursor, article writing; Miroslava Dušková – crosslinking density calculation; article writing; Ján Šomvársky – crosslinking density calculation, derivation of statistical model of networks; Jean Jacques Bonvent – AFM measurements, article writing; Sérgio Brochsztain – APTES modification of substrates, article writing; Miroslav Šlouf – Cryo-SEM analyses, article writing; Vladimír Proks – article writing; funding acquisition, microgel immobilization.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
Financial support from the Czech Science Foundation (no. 21-06524S), Horizon 2020 research and innovation program of the European Union Maria Sklodowska-Curie (grant agreement 823883-NanoPol-MSCA-RISE-2018) and The project National Institute for Cancer Research (Programme EXCELES, ID project no. LX22NPO5102) – Funded by the European Union – Next Generation EU are gratefully acknowledged. Miroslav Šlouf would like to thank Veronika Gajdosova and Pavel Nemecek for numerous sample preparations for Cryo-SEM and for the repeated Cryo-SEM measurements.References
- Y. Wang, L. Guo, S. Dong, J. Cui and J. Hao, Adv. Colloid Interface Sci., 2019, 266, 1–20 CrossRef CAS PubMed.
- P. D. Thornton, G. McConnell and R. V. Ulijn, Chem. Commun., 2005, 5913–5915 RSC.
- M. Malmsten, H. Bysell and P. Hansson, Curr. Opin. Colloid Interface Sci., 2010, 15, 435–444 CrossRef CAS.
- J. P. Newsom, K. A. Payne and M. D. Krebs, Acta Biomater., 2019, 88, 32–41 CrossRef CAS PubMed.
- J. K. Oh, D. I. Lee and J. M. Park, Prog. Polym. Sci., 2009, 34, 1261–1282 CrossRef CAS.
- Y. Chu, Y. Jo and L. Chen, Food Hydrocolloids, 2022, 124, 107316 CrossRef CAS.
- Y. Pan, Y. Qi, X. Li, S. Luan and Y. Huang, Adv. Funct. Mater., 2021, 31, 2105742 CrossRef CAS.
- M. Nöth, E. Gau, F. Jung, M. D. Davari, I. El-Awaad, A. Pich and U. Schwaneberg, Green Chem., 2020, 22, 8183–8209 RSC.
- Q. Feng, D. Li, Q. Li, X. Cao and H. Dong, Bioact. Mater., 2022, 9, 105–119 CAS.
- B. Kew, M. Holmes, M. Stieger and A. Sarkar, Trends Food Sci. Technol., 2020, 106, 457–468 CrossRef CAS PubMed.
- H. Wu, L. Gong, X. Zhang, F. He and Z. Li, Chem. Eng. J., 2021, 411, 128539 CrossRef CAS.
- E. Gantumur, S. Skai, M. Nakahata and M. Taya, Soft Matter, 2019, 15, 2163–2169 RSC.
- H. Wei, J. Xie, X. Jiang, T. Ye, A. Chang and W. Wu, Macromolecules, 2014, 47, 6067–6076 CrossRef CAS.
- O. Hasturk, K. E. Jordan, J. Choi and D. L. Kaplan, Biomaterials, 2020, 232, 119720 CrossRef CAS PubMed.
- J. Dvořáková, J. Trousil, B. Podhorská, Z. Mikšovská, O. Janoušková and V. Proks, Biomacromolecules, 2021, 22, 1417–1431 CrossRef PubMed.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS PubMed.
- F. Scheffold, Nat. Commun., 2020, 11, 4315 CrossRef CAS PubMed.
- M. Yuan, X. Ju, R. Xie, W. Wang and L. Chu, Particuology, 2015, 19, 164–172 CrossRef CAS.
- A. Aufderhorst-Roberts, D. Baker, R. J. Foster, O. Cayre, J. Mattson and S. D. Connell, Nanoscale, 2018, 10, 16050–16061 RSC.
- A. Hussain, J. Rahmannezhad, G. M. Choi, S. G. Kim, W. R. Hwang, J. Yoon and H. S. Lee, Phys. Fluids, 2023, 35, 122001 CrossRef CAS.
- Y. Xu, H. Zhu, A. Denduluri, Y. Ou, N. A. Erkamp, R. Qi, Y. Shen and T. P. J. Knowles, Small, 2022, 18, 2200180 CrossRef CAS PubMed.
- I. H. Oevreeide, R. Szydlak, M. Luty, H. Ahmed, V. Prot, B. H. Skallerud, J. Zemła, M. Lekka and B. T. Stokke, Gels, 2021, 7, 64 CrossRef CAS PubMed.
- C. D. Markert, X. Guo, A. Skardal, Z. Wang, S. Bharadwaj, Y. Zhang, K. Bonin and M. Guthold, J. Mech. Behav. Biomed. Mater., 2013, 27, 115–127 CrossRef CAS PubMed.
- A. M. Joshua, G. Cheng and E. V. Lau, Appl. Surf. Sci. Adv., 2023, 17, 100448 CrossRef.
- J. Dvořáková, P. Šálek, L. Korecká, E. Pavlova, P. Černoch, O. Janoušková, B. Koutníková and V. Proks, J. Appl. Polym. Sci., 2020, 137, 1–10 CrossRef.
- D. Oleshchuk, P. Šálek, J. Dvořáková, J. Kučka, E. Pavlova, P. Francová, L. Šefc and V. Proks, Mater. Sci. Eng., C, 2021, 126, 111865 CrossRef CAS PubMed.
- S. Hladysh, D. Oleshchuk, J. Dvořáková, A. Golunova, P. Šálek, J. Pánek, O. Janoušková, D. Kaňková, E. Pavlova and V. Proks, Eur. Polym. J., 2021, 148, 110347 CrossRef CAS.
- G. T. Vladisavljević, I. Kobayashi and M. Nakajima, Microfluid. Nanofluid., 2012, 13, 151–178 CrossRef.
- M. A. Pujana, L. Pérez-Álvarez, L. C. C. Iturbe and I. Katime, Eur. Polym. J., 2014, 61, 215–225 CrossRef.
- G. Li, I. Varga, A. Kardos, I. Dobryden and P. M. Claesson, Langmuir, 2021, 37, 1902–1912 CrossRef CAS PubMed.
- C. Herranz-Diez, Q. Li, C. Lamprecht, C. Mas-Moruno, S. Neubauer, H. Kessler, J. M. Manero, J. Guillem-Martí and C. Selhuber-Unkel, Colloids Surf., B, 2015, 136, 704–711 CrossRef CAS PubMed.
- A. Samanta, Q. Wang, S. K. Shaw and H. Ding, Mater. Des., 2020, 192, 108744 CrossRef CAS.
- A. M. A. Hasan, M. Keshawy and M. E. S. Abdel-Raouf, Mater. Chem. Phys., 2022, 278, 125521 CrossRef CAS.
- I. Jaywardena, P. Turunen, B. C. Garms, A. Rowan, S. Corrie and L. Grøndahl, Mater. Adv, 2023, 4, 669–682 RSC.
- G. Li, I. Dobryden, E. J. Salayar-Sandoval, M. Johansson and P. M. Claesson, Soft Matter, 2019, 15, 7704–7714 RSC.
- A. V. Petrunin, M. M. Schmidt, R. Schweins, J. E. Houston and A. Scotti, Langmuir, 2023, 39, 7530–7538 CrossRef CAS PubMed.
- L. Nyström, R. Álvarez-Asencio, G. Frenning, B. R. Saunders, M. W. Rutland and M. Malmsten, ACS Appl. Mater. Interfaces, 2016, 8, 27129–27139 CrossRef PubMed.
- K. Dušek and M. Dušková-Smrčková, Prog. Polym. Sci., 2000, 25, 1215–1260 CrossRef.
- J. W. Bae, J. H. Choi, Y. Lee and K. D. Park, J. Tissue Eng. Regen. Med., 2015, 9, 1225–1232 CrossRef CAS PubMed.
- K. Dušek and M. Dušková-Smrčková, Polymer Networks in book Macromolecular Engineering, Precise Synthesis, Materials Properties, Applications, ed. K. Matyjaszewski, Y. Gnanou and L. Liebler, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2007 Search PubMed.
- J. Šomvarsky, K. te Nijenhuis and M. Ilavský, Macromolecules, 2000, 33, 3659–3670 CrossRef.
- M. Dušková-Smrčková, H. Valentová, A. Ďuračková and K. Dušek, Macromolecules, 2010, 43, 6450–6462 CrossRef.
- P. Chivukula, K. Dušek, D. Wang, M. Dušková-Smrčková, P. Kopečková and J. Kopeček, Biomaterials, 2006, 27, 1140–1151 CrossRef CAS PubMed.
- M. Rubinstein and R. H. Colby, Polym. Phys., 2003, Oxford University Press, Oxford, UK Search PubMed.
- K. Dušek, M. Dušková-Smrčková and C. B. Douglas, Swelling of Coating Films in book Protective Coatings, ed. M. Wen and K. Dušek, Springer International Publishing, Berlin, Germany, 2017 Search PubMed.
- M. Dušková-Smrčková and K. Dušek, ACS Macro Lett., 2019, 8, 272–278 CrossRef PubMed.
- L. R. G. Treloar, The Physics of Rubber Elasticity, Oxford University Press, Oxford, UK, 3rd edn, 1975 Search PubMed.
- K. Dušek, Collect. Czech. Chem. Commun., 1969, 34, 3309–3317 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00356j |
| This journal is © The Royal Society of Chemistry 2024 |