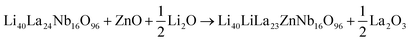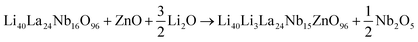Experimental and computational study of Zn doping in Li_5+xLa₃Nb_2−xZr_xO₁₂ garnet solid state electrolytes

Abstract

While garnet Li ion conductors are attracting considerable interest as potential solid state electrolytes for Li ion batteries, a key challenge is to improve the conductivity, which is associated with the Li content in the structure, and the density of the sintered electrolyte membranes. In this work we show that Zn can be doped on the 16a octahedral Nb site increasing the Li content, while also leading to substantially improved sintering in Li_5+xLa₃Nb_2−xZr_xO₁₂. As a result of the enhanced sintering, and the increase in Li content, the conductivities were significantly enhanced on Zn doping, up to 2.1 × 10⁻⁴ S cm⁻¹ at 25 °C for Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂. Computational modelling supports favourable doping of Zn on the Nb site with 3 Li interstitials as per experimental findings. Furthermore, it suggests Li ion diffusion via a knock-on mechanism, but crucially the saturation of sites closest to the Zn means that migration barriers are similar for doped and pure systems, with the increased Li ion conductivity attributed to larger pre-factors due to increased number of Li ions in the doped material. A challenge with these Zn doped garnet is the reduction of Zn in contact with Li metal. Nevertheless, surface fluorination or employing the Zn doped garnet as a buffer layer with an alternative garnet electrolyte is shown to be effective to inhibit dendrite growth, and stable cycling exceeding 250 hours is demonstrated.

---

Introduction

State-of-the-art lithium ion batteries (LIBs) dominate the energy storage market due to their high energy density and long cycle life compared to other energy storage systems.¹ However, commercial LIBs often use liquid electrolytes (such LiPF₆ in EC/DEC organic solvent), which have a variety of safety, thermal and toxicity concerns, some of which are uniquely problematic in the emerging electric vehicle market.^2,3 It is thought these concerns can be addressed by use of an all-solid-state battery (ASSB), where the flammable electrolyte is replaced with an inorganic solid-state electrolyte (SSE). Additionally, ASSBs would also allow higher energy density cells by enabling the use of high-performance cathode materials and anodic lithium metal. Therefore SSEs have attracted considerable attention in the field of next generation LIBs.^4,5 Over the last few decades, various potential SSEs have been investigated, including LISICON,^6–8 NASICON,^9,10 perovskites,¹¹ garnet,¹² Thio-LISICON,¹³ argyrodite¹⁴ and anti-perovskites.¹⁵ However, of all the systems reported, the lithium garnet systems are among the few which encompass both good electrochemical stability and high room temperature Li⁺ ion conductivity. Hence the garnet solid-state electrolytes are envisaged as promising candidates for all-solid-state batteries.

The ideal garnet has a general formula A₃B₂C₃O₁₂ where A, B and C are 8, 6 and 4 oxygen coordinated metal ions. The garnet has a cubic structure (Ia3̄d), which contains a framework of corner-linked tetrahedra and octahedra with the larger A ions located in cavities.^12,16 In 2003, the first report of high Li⁺ ion conductivity was made by Thangadurai et al. for La₃M₂Li₅O₁₂ (M = Nb, Ta). Later studies into the conductivity mechanism revealed lithium ions were located in the tetrahedral site (24d), as well as distorted interstitial octahedral sites (48g and 96h).¹⁷ Further work determined that, in addition to lithium content, the lithium ion distribution is key in understanding, and optimizing, the Li⁺ ion conductivity of garnet SSEs.¹⁸ Subsequent work has employed a variety of aliovalent doping strategies to improve the conductiviry, including substitution at the A site (Ca, Ba), B site (Zr, Hf, Sn) and C site (Al, Ga).^19–30

The maximum lithium content was demonstrated to be 7 as shown for Li₇La₃Zr(Hf, Sn)₂O₁₂ garnets, although in these system the lithium ions are ordered in three fully occupied sites (tetrahedral 8a and octahedral 16f and 32g sites), leading to tetragonal systems with lower conductivity.^31–33 High temperature X-ray diffraction studies show a reversible tetragonal to cubic phase transition in Li₇La₃Zr₂O₁₂ at 750 °C,³⁴ with the transition temperature decided by the average size of the B site cations. This cubic phase with much higher conductivity can be obtained at lower temperature by the incorporation of lithium vacancies, either through Li loss during high temperature synthesis or reaction with alumina crucibles resulting in Al incorporation. In addition, proton/lithium exchange in tetragonal garnet has also been shown to form cubic symmetry, whereby moisture reacts to form a LiOH surface layer, which subsequently reacts with CO₂ to form a Li₂CO₃ insulating layer.^35,36

The quest to utilise these electrolytes in practical ASSBs has meant that interfacial issues, like high electrolyte–cathode/anode interfacial resistance, dendrite propagation through the solid state electrolyte, have attracted more attention in recent years.^37–43 It has been noted that the Li stripping process can induce the emergence of local defects, such as voids at the SSE/Li interface, leading to a diminished contact area between the SSE and Li. This decrease in contact area is likely to result in increased polarisation and a localised rise in current density, which subsequently initiates and promotes the growth of dendrites within the solid-state electrolyte. To minimise interfacial impedance and encourage dendrite-resistant lithium deposition and dissolution, extensive efforts have been made to tailor the interfaces of solid-state electrolytes (SSE).⁴⁴ A practical strategy to improve the Li and garnet interface contact involves removing surface contaminants, achievable through acid treatment, heat treatment with carbon or the addition of a highly conducting material.^45–49 The interfacial resistance can be negated somewhat via a surface coating that subsequently forms a Li metal alloy, which also prevents dendrite growth by acting as a buffer layer.^50–53 Polymer–garnet ceramic composites have also been examined to address the interfacial problems while also eliminating high temperature sintering.^54–56 Furthermore, employing a reducible interlayer that promotes mixed conduction at the interface, like Ce or Pr doped garnet, has demonstrated effectiveness in addressing interfacial challenges.^57–60

There has been prior work on Zn²⁺ incorporation Li₇La₃Zr₂O₁₂, where substitution on the 24d tetrahedral Li⁺ site was reported.⁶¹ Attempts to dope Zn on the 96d octahedral site to give a Li excess material of formula Li_7+2xLa₃Zr_2−xZn_xO₁₂ was also investigated, but impurities were observed for all samples and no conclusive confirmation of Zn incorporation on the Zr site.⁶² This can be explained by the inability to accommodate more than 7 Li ions in these garnet systems. However, no attempts have been made to dope Zn on the 16a octahedral site in garnets with Li contents lower than 7. In this work, Zn²⁺ dopant was therefore used to substitute onto the 16a octahedral Nb⁵⁺ ions for the first time in Li_5+xLa₃Nb_2−xZr_xO₁₂ and the corresponding effects on chemical, physical and electrochemical properties were studied. These studies show the first successful Zn incorporation onto this site, revealing that Zn-doped garnets exhibit a marked increase in density alongside enhanced Li⁺ ion conductivity, attributed to the subsequent rise in Li content. The electrochemical performance was evaluated through a trilayer design or surface modification strategy, illustrating enhanced critical current density and improved long-term stability. Computational modelling studies are also reported, evaluating the efficacy of the Zn doping strategy.

Experimental

Synthesis

Li₂CO₃ (99.9%, Alfa Aesar), ZrO₂ (99.9%, Sigma Aldrich), La₂O₃ (99.9%, Sigma Aldrich), Nb₂O₅ (99%, Sigma Aldrich) and ZnO (99%, Sigma Aldrich) were used as starting materials. Li₂CO₃ was dried at 180 °C while ZnO, ZrO₂ and Nb₂O₅ were dried at 900 °C before use. Li_5+3xLa₃Nb_2−xZn_xO₁₂: x = 0, 0.1, 0.2, 0.3, 0.4, 0.6, Li_6+3xLa₃ZrNb_1−xZn_xO₁₂: x = 0, 0.2 and Li_5−2yZn_yLa₃Nb₂O₁₂: y = 0.2, 0.4 samples were prepared via the solid state route by intimate grinding of stoichiometric amounts of reagents. The powders were then initially heated to 650 °C for 12 hours at 5 °C min⁻¹. To compensate for Li loss during the heat treatment/sintering, 10–15% excess Li₂CO₃ were then added to the powders, which were subsequently ball milled (ZrO₂ containers and balls) with hexane for 30 minutes (FRITSCH Pulverisette 7 classic line planetary ball mill). The fine powders were uniaxially pressed into pellets, placed onto ZrO₂ pellets to prevent Al contamination and reheated at 950–1050 °C for 12 hours at 5 °C min⁻¹ to yield the final product.

Characterisation of materials

X-ray diffraction data were collected using a Bruker D8 X-ray diffractometer (XRD) (CuKα radiation) with a linear position sensitive detector. Patterns were recorded over 2θ range 15° to 80° with a 0.02° step size. Structural refinement was carried out using the GSAS suite of Rietveld refinement software.

Scanning electron microscopy (SEM, Philips/FEI XL 30S FEG) was employed to examine the microstructure. Before being coated with carbon, bulk samples were polished and thermally etched at 90% of the sintering temperature for 1 h. Powder samples were fixed on conductive carbon tapes. An accelerating voltage of 5 kV and an effective spot size of 3 mm was used. The distribution of elements was probed with an energy dispersive X-ray spectroscopy (EDX) detector.

Pellets for impedance measurements were sintered at 1000–1100 °C for 4 hours at a heating rate of 5 °C min⁻¹ in dry N₂. The pellet was placed on, and covered with, mother powders to suppress Li₂O loss and prevent any reaction with the Al₂O₃ crucible. Au paste was painted on both sides of the pellet and heated at 850 °C for 1 hour. Impedance data were recorded in air with a HP 4192 analyser with 100 mV A.C. applied voltage over the frequency range 1 to 10⁷ Hz.

Electrochemical characterisation

Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂(LLZNZ) was chosen as the target electrolyte material due to its high lithium ion conductivity. A challenge with these electrolytes in contact with Li metal is reduction of Zn, resulting in the formation of Li/Zn alloys leading to cell shorting. To facilitate the prevention of this cell shorting, the LLZNZ pellets was modified in the following routes: (1) LLZNZ||L_i6.4La₃Zr_1.4Nb_0.6O₁₂(LLZN)||LLZNZ (0.2 mm||0.4 mm||0.2 mm) thickness was pressed into a sandwich pellet at 0.2 tons using the uniaxial press and followed by sintering at 1050 °C for 12 h. (2) The sintered Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂(LLZNZ) pellet was covered with PTFE powder on both sides and heated at 400 °C for 12 h in a dry room (named as LLZNZ-PTFE). Li||LLZNZ||Li, Li||sandwich||Li and Li||LLZNZ-PTFE||Li symmetric cells were hot pressed at 175 °C/1 h and assembled using the Swagelok cell inside an argon filled glove box. These symmetric cells were cycled at various current densities to assess electrochemical stability at room temperature using a BioLogic VMP3 multichannel potentiostat. EIS data were collected through an impedance analyser connected to the BioLogic VMP3 multichannel potentiostat, operating at 100 mV across a frequency spectrum of 1 to 10⁶ Hz.

Computational methodology

Structural and defect modelling

The plane-wave DFT code VASP⁶³ has been used for the defect modelling. The projector-augmented wave (PAW) method⁶⁴ describes the interaction between core and valence electrons using pseudopotentials. Unless stated, all calculations used the hybrid-DFT functional HSE06,⁶⁵ with a plane wave energy cutoff of 500 eV. A K-point sampling of 2 × 2 × 2 was chosen to ensure energies converge to <1 meV per atom. Structural relaxations for all defects were calculated with the optimized cell parameters for stoichiometric LLNO (a = 12.75, b = 12.73 and c = 12.72). The force tolerance for convergence was 0.01 eV Å⁻¹ per atom for the geometry optimizations, and the energy tolerance for convergence was 10⁻⁶ eV for the hybrid single-point energy calculations.

Molecular dynamics

Potential-based molecular dynamics were employed in this study. The advantage of combining potential-based methods is to allow us to study much larger systems for nanosecond time scales, which would be unfeasible for DFT calculations. It is necessary to rigorously prior parameterize the ion–ion interactions appropriate to describe the material in question in line with experimental observations. The large-scale atomic/molecular massively parallel simulator (LAMMPS) code⁶⁶ was used for the interatomic potential verification.

The interatomic potential models of Wang et al.⁶⁷ and Jackson et al.⁶⁸ all listed in Table 1 were used to model pure LLNO; in this potential model the species are assigned a full formal charge and the shell model of Dick and Overhauser⁶⁹ is used to represent ionic polarizability. Short-range interactions were represented by Buckingham potential with a cutoff of 10 Å.

Table 1 Buckingham interatomic potential parameters used in this work: (La³⁺–O²⁻, Li⁺–O²⁻ and O²⁻–O²⁻)⁶⁷, (Nb⁵⁺–O²⁻)⁶⁸ and (Zn²⁺–O²⁻)⁷⁰

Interaction	A (eV)	ρ (Å)	C (eV Å^6)
La^3+–O^2−	4579.23	0.3040	0.0
Nb^5+–O^2−	1425.00	0.3650	0.0
Li^+–O^2−	632.10	0.2906	0.0
Zn^2+–O^2−	529.70	0.3581	0.0
O^2−–O^2−	22764.30	0.1490	27.63

---

Species	Shell charge (e)	Spring constant (eV Å^−2)
O^2−	−2.760	30.20

---

Results and discussion

Phase formation

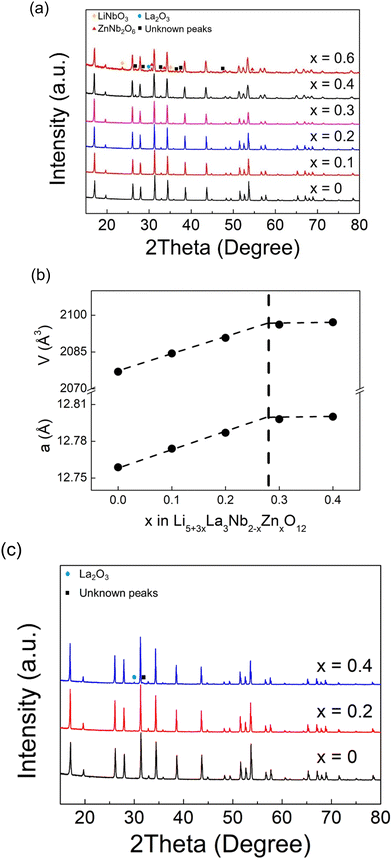
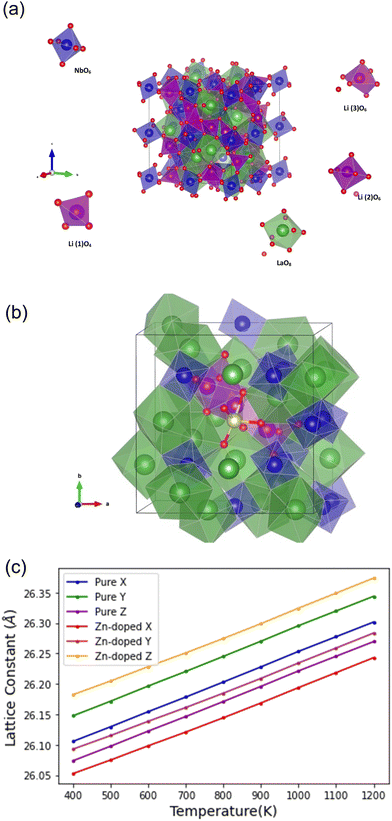
Li₅La₃Nb₂O₁₂ can be indexed using a cubic Ia3̄d cell as previously reported for cubic garnet electrolytes. Given the lower charge of Zn (2+) versus Nb (5+), for charge balance the incorporation of an extra 3 Li⁺ are required, giving a general formula Li_5+3xLa₃Nb_2−xZn_xO₁₂. Thus, Zn doping leads to a significant increase in the Li content of the sample (3 extra Li⁺ ions introduced per 1 Zn²⁺ incorporation in place of Nb⁵⁺). As shown in Fig. 1(a), the XRD patterns for Li_5+3xLa₃Nb_2−xZn_xO₁₂ show single phase samples for x = 0–0.2 compositions, with a linear increase in cell parameters as a function of composition until x = ∼0.3 (Fig. 1(b)), implying the formation of a solid solution across this range and corresponding to Vegard's law. The observed cell expansion is in agreement with replacing Nb⁵⁺ ions with larger Zn²⁺ ions (ionic radius of 0.64 and 0.74 for Nb⁵⁺ and Zn²⁺ respectively in a 6-oxygen coordinated octahedral site). Above x = 0.3, LiNbO₃, ZnNb₂O₆, La₂O₃ impurity phases became increasingly apparent. Hence x = ∼0.3 is thought to be the Zn limit for these systems, which is supported by the lack of any significant change in cell parameters for compositions between x = 0.4 and 0.6.

Fig. 1 (a) XRD patterns of Li_5+3xLa₃Nb_2−xZn_xO₁₂: x = 0, 0.1 0.2, 0.3, 0.4 Triangle, diamond, circular and rectangle labels represent for ZnNb₂O₆, LiNbO₃, La₂O₃ and unknown peaks respectively. (b) Variation of lattice parameter a and volume V for Li_5+3xLa₃Nb_2−xZn_xO₁₂ with composition x. (c) XRD patterns of Li_5−2yZn_yLa₃Nb₂O₁₂: y = 0, 0.2, 0.4. circular and rectangle labels represent for La₂O₃ and unknown peak respectively.

Zn substitution at the Li sites was also investigated, taking into account of higher charge of Zn (2+) versus Li (1+), this substitution necessitates the formation of a lithium vacancy for the charge balance, resulting in the general formula Li_5−2yZn_yLa₃Nb₂O₁₂. As shown in Fig. 1(c), the XRD patterns for Li_5−2yZn_yLa₃Nb₂O₁₂ indicate a single phase for y = 0.2, with cell parameters increasing as a function of the composition up to approximately y = 0.3 (Fig. S1, ESI†), suggesting the formation of a solid solution. Given the similar ionic radius of Zn²⁺ (0.74) and Li⁺ (0.76) in a 6-oxygen coordinated octahedral site, the expansion in cell parameters is primarily attributed to the formation of lithium vacancies, which aligns with previous increased lattice volume on Zn-doped LLZO.⁶¹ A La₂O₃ impurity phase and an unknown peak were observed for the composition at y = 0.4.

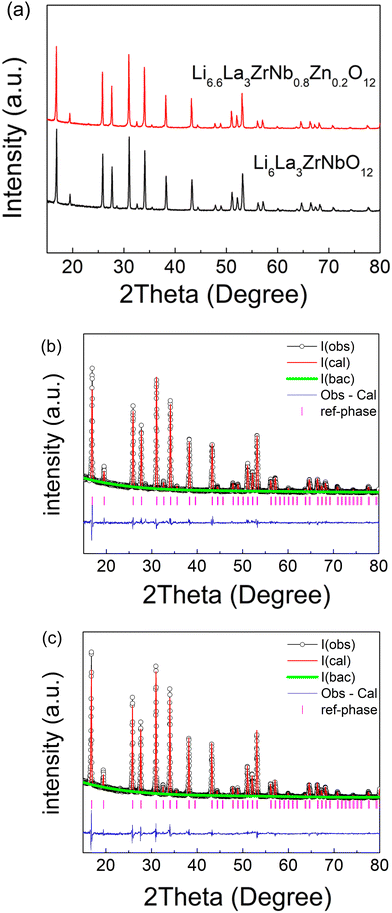
While the results show that the Li content can be increased by Zn doping on the Nb site in Li₅La₃Nb₂O₁₂, it can only successfully achieved for x ⩽ 0.3 leading to a Li content less than 6. To this end, given the need for high Li content for high conductivities in these garnets systems, further work focused on Zn doping on a garnet with higher initial Li content. Optimum garnet Li conductivities are typically found in compositions with Li content between ∼6.4–6.6. Therefore, Zn doping in the Li₆La₃ZrNbO₁₂ system was subsequently investigated to see if sintering and Li ion conductivity could be improved. As shown in Fig. 2(a), a single cubic phase was observed for Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂ (LLZNZ). Structure refinement of these phases were carried out using XRD data to confirm the replacement of Zn²⁺ on Nb⁵⁺ site. The starting model is derived from the literature.⁷¹ As XRD is insensitive to lithium in the presence of heavy elements, the atomic coordinates, occupancies and U_isos of lithium atoms were constrained as the same. Given that Zr⁴⁺ and Nb⁵⁺ are isoelectronic, a constraint between Nb1 and Zr1 was set with the occupancies of these in accordance to the chemical composition for (1 : 1 for Li₆La₃ZrNbO₁₂). The Uiso parameters of all atoms were initially set to a typical value of 0.01 Å. The scale factor, background (6 terms of shifted Chebyshev function) and lattice parameters were refined at the beginning, followed by peak profile parameters and 2θ zero error, which were refined and fixed at the converged value. Finally, the atomic coordinates of O1, U_isos of La1, Nb1(Zr1) were refined together in the last step. The refined parameters for Li₆La₃ZrNbO₁₂ are summarised in Table 2. A similar refinement strategy was applied to Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂, with Zn1 added as the same atomic position as Zr1/Nb1 with the total occupancy for Zn1 + Nb1 = 0.5. This refinement gave occupancies of 0.40(1) for Nb1 and 0.10(1) for Zn1 which is consistent with the expected composition. The final refined parameters for Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂ are shown in Table 3.

Fig. 2 (a) XRD patterns for Li₆La₃ZrNbO₁₂ and Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂. (b) Observed, calculated and difference profiles from Rietveld refinement for Li₆La₃ZrNbO₁₂. (c) Observed, calculated and difference profiles from Rietveld refinement for Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂.

Table 2 Refined structural parameters for Li₆La₃ZrNbO₁₂ using XRD data

Atom	x	y	z	Mult.	Occupancy	u iso × 100 (Å^2)
a = 12.8885(2) Å, V = 2140.98(8) Å^3; χ^2 = 2.538, Rwp = 9.28%, Rp = 7.45%.
La1	0.125	0	0.25	24	1	1.0(1)
Nb1	0	0	0	16	0.5	0.9(2)
Zr1	0	0	0	16	0.5	0.9(2)
O1	0.2858(6)	0.1022(8)	0.1980(7)	96	1	2.3(4)
Li1	0.25	0.875	0	24	0.674	0.1
Li2	0.125	0.6773	0.5727	48	0.22	0.1
Li3	0.0937	0.6888	0.5817	96	0.218	0.1

---

Table 3 Refined structural parameters for Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂ using XRD data

Atom	x	y	z	Mult.	Occupancy	u iso × 100 (Å^2)
a = 12.9081(1) Å, V = 2150.71(5) Å^3; χ^2 = 3.755, Rwp = 9.81%, Rp = 8.06%.
La1	0.125	0	0.25	24	1	2.1(1)
Zr1	0	0	0	16	0.5	0.1
Nb1	0	0	0	16	0.40(1)	0.1
Zn1	0	0	0	16	0.10(1)	0.1
O1	0.2849(5)	0.1028(7)	0.1966(6)	96	1	4.4(4)
Li1	0.25	0.875	0	24	0.568	0.1
Li2	0.125	0.6690	0.5810	48	0.249	0.1
Li3	0.0908	0.6892	0.5771	96	0.283	0.1

---

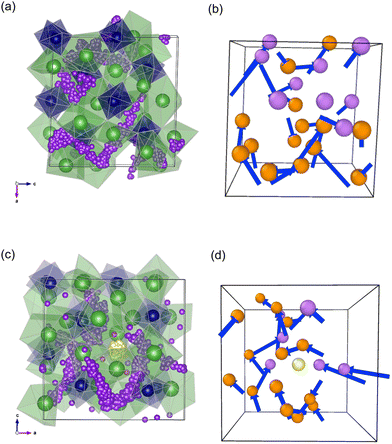
Computational modelling was used to further validate Zn doping in Li₅La₃Nb₂O₁₂ and examine defect formation energies of zinc on the Nb site (Zn_Nb). In addition the possibility of Zn doping on the La site was investigated (Zn_La) forming either lithium interstitials or oxygen vacancies and interstitials, (V_O and O_i) for charge compensation. Doping mechanisms considered are listed in Table 4. The solution energies from Table 4 indicate that Zn prefers to occupy the Nb site for either charge compensation but it is more favourable for creating lithium interstitials than oxygen vacancies, in line with experimental findings. Fig. 3(a) illustrates zinc doping (yellow atom) on the niobium site and the three lithium octahedral interstitials nearest neighbour to the Zn, which is more favourable than the Li interstitials being further away from the Zn. The nearest neighbour distances are 3.27, 2.36 and 3.49 Å. The difference in energy is 2.98 eV.

Table 4 Doping mechanisms for Zn on both the La and Nb sites, with the formation of Li interstitials or oxygen vacancies

Mechanism	Solution energy (eV)
(1)	0.98
(2) Li40La24Nb16O96 + 2ZnO → Li40La22Zn2Nb16O95 + La2O3	1.37
(3)	0.64
(4) Li40La24Nb16O96 + 2ZnO → Li40La24Nb14Zn2O93 + Nb2O5	1.06

---

Fig. 3 (a) Crystal structure of cubic Li₅La₃Nb₂O₁₂ with 3 Li coordination sites, tetrahedral Li(1) and octahedral Li(2) and Li(3). Key: purple polyhedral (Li), green polyhedral (La), blue polyhedral (Nb). (b) Crystal structure of Li₅La₃Nb₂O₁₂ doped with Zn (yellow) and three Li interstitials (purple) with Li–Zn distances of 3.27, 2.36 and 3.49 Å. (c) Time average lattice parameters of pure and Zn-doped LLNO as a function of temperature each simulated for 2 ns using NPT ensemble.

Potential-based molecular dynamics (MD) were employed in this study to investigate any phase changes at higher temperature. The advantage of combining potential-based methods is to allow us to study much larger systems for nanosecond time scales which would be infeasible for DFT. The Interatomic potentials used are listed in the methodology section in Table 1. A 2 × 2 × 2 supercell expansion of the 176-atom cubic unit cell for pure LLNO containing a total of 1408 atoms was simulated using classical MD. The simulations were conducted using a 1 fs time step and Nosé–Hoover thermostats barostat⁷² within the LAMMPS code.

A zinc doped system was setup with a Zn : Nb ratio of 8 : 120 resulting in a material with a total of 24 Li interstitials, with the formula Li_5+3xLa₃Nb_2−xZn_xO₁₂ (where x = 0.63) similar to the experimental setup. The pure and zinc-doped systems were simulated at five different temperatures (range 500 to 1100 K). At each temperature studied the systems were equilibrated time for 0.5 nanoseconds before a total of 2.5 ns of data was collected under an isobaric–isothermal ensemble (NPT). The average lattice vectors were extracted and are presented as a function of simulation temperature in Fig. 3(c). The simulated lattice parameters suggest that the LLNO system remains in the cubic phase and experiences uniform expansion with increasing temperature, exhibiting no phase transition.

Conductivity results

To achieve high density garnet pellets, ceramic sintering techniques with additional driving force for sintering, such as hot-pressing and spark plasma sintering^73,74 or sintering aids (e.g. Al₂O₃, Ga₂O₃, Li₃BO₄, Li₄SiO₄) as a densification strategy,^75,76 have previously been applied in the literature. However, these are either costly or lead to the generation of a non-stoichiometric garnet and potentially other impurity phases. In this work, the relative densities of both the Zn doped Li₅La₃Nb₂O₁₂ and Li₆La₃ZrNbO₁₂ pellets (Table 5) show dramatic improvement compared with undoped samples: the relative densities of Li_5.6La₃Nb_1.8Zn_0.2O₁₂ and Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂ increased to 87% and 90% compared to Li₅La₃Nb₂O₁₂ and Li₆La₃ZrNbO₁₂ (61% and 59%) under the same synthesis/sintering conditions. Therefore Zn doping showed advantages as an alternative low cost and more homogeneous way of densifying the garnet, which is consistent with prior studies in other fields (e.g. perovskite proton conductors).^77,78

Table 5 Relative densities for Zn-doped Li₅La₃Nb₂O₁₂ or Li₆La₃ZrNbO₁₂ pellets

Composition	Condition (h)	Relative density (%)
Li5La3Nb2O12	1100/4	61.0
Li5.6La3Nb1.8Zn0.2O12	1100/4	87.1
Li6.2La3Nb1.6Zn0.4O12	1100/4	87.2
Li6La3ZrNbO12	1100/6	59.0
Li6.6La3Nb0.8Zn0.2ZrO12	1100/6	90.3

---

The surface microstructure of a LLZNZ pellet was characterised by SEM, as shown in Fig. 4(a). A dense garnet pellet with a few small pores was observed, confirming Zn ions are a good densification dopant for garnet solid state electrolyte materials. The grain size distribution for LLZNZ is in the range ∼2–10 μm with no detection of impurities at the grain boundary. The EDX mapping (Fig. 4(b)) shows a homogeneous distribution of La, Zr, Nb, Zn and O through the sample consistent with its incorporation into the structure in agreement with the Rietveld refinement data.

Fig. 4 SEM and EDX elemental mappings of Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂.

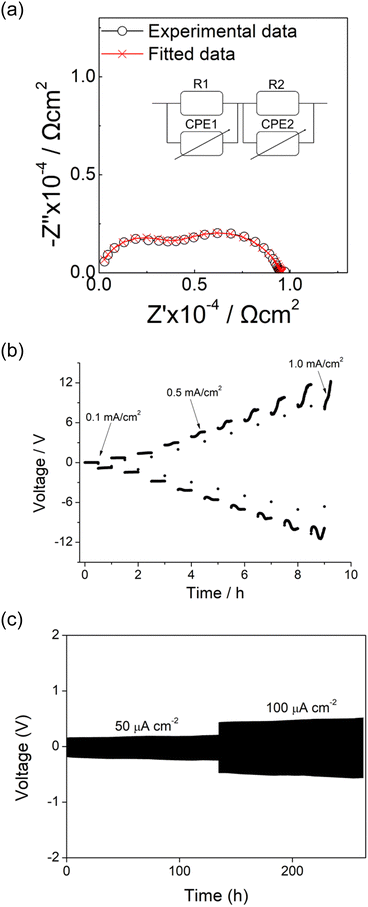
Typical impedance data for Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂ are shown in Fig. 5. In the Z* complex plot (Fig. 5(a)), a high frequency arc which passes the origin point and a low frequency spike were observed. A resistor R1 in parallel with a constant phase element CPE1 were used to fit the semicircle while another CPE2 which is in series with R1/CPE1 accounted for the sharp spike. The corresponding spectroscopic C′ plot (Fig. 5(b)) shows a high frequency plateau with a capacitance of 8.7 pF cm⁻¹ which is a typical value for the bulk response with an associated permittivity of 10–20 (assuming A/l = 10).⁷⁹ At lower frequencies, a plateau with a capacitance of 1.3 μF cm⁻¹ was observed; this high capacitance is a good indication of double layer effect at the sample – electrode interface with Li⁺ ion conduction in this case. Plots of log Y′ as a function of log f (Fig. 5(c)) show a frequency independent plateau at intermediate frequency, which corresponds to the bulk conductivity. A dispersion at high frequency related to the Jonscher's power law and a curvature at low frequency representing the blockage of Li ions at the electrode – sample interface are detected.⁸⁰

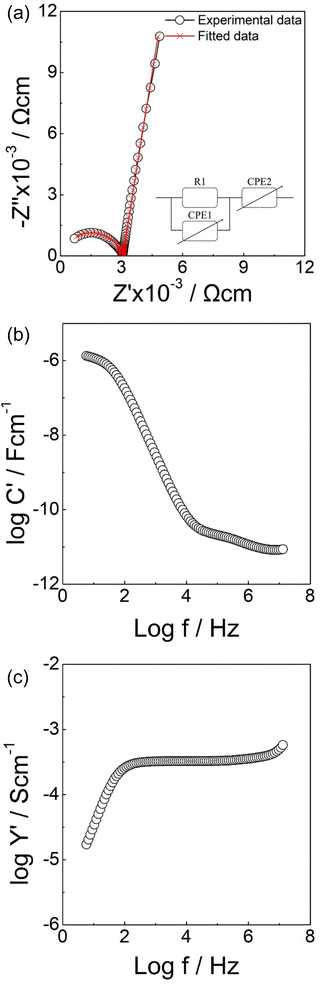Fig. 5 Impedance data of Li_6.6La₃ZrNb_0.8Zn_0.2O₁₂. (a) Complex Z* plot (b) Spectroscopic plot of C′ (c) Spectroscopic plot of Y′.

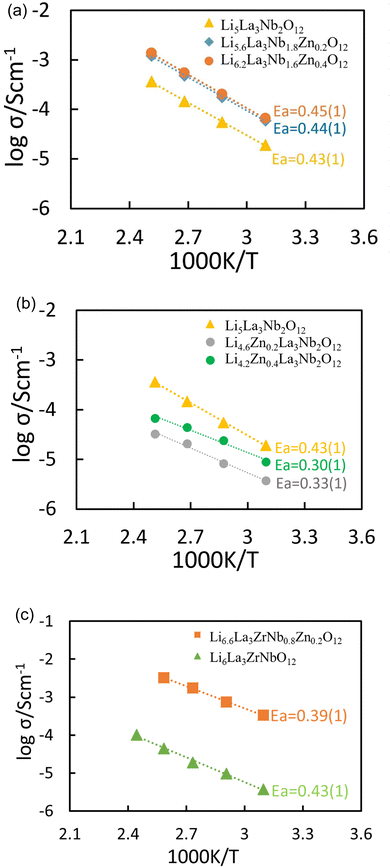
From the Arrhenius plot (Fig. 6(a)), the conductivities observed in Li₅La₃Nb₂O₁₂ doped with Zn on the Nb site, exhibit an improvement over the undoped Li₅La₃Nb₂O₁₂, attributed to the increased lithium content. Conversely, the substitution of Zn on the Li site, resulting in the formation of lithium vacancies, is associated with a reduction in conductivity when compared to the undoped variant, as shown in Fig. 6(b). This phenomenon is ascribed to the direct correlation between lithium concentration and conductivity within garnet-type materials. Similar enhanced conductivities are observed for Zn doping on Nb site in Li₆La₃ZrNbO₁₂. As shown in Fig. 6(c), the conductivity of LLZNZ reached 2.1 × 10⁻⁴ S cm⁻¹ at 25 °C with an associated activation energy of 0.39(1) eV. Such a Li ion conductivity is ∼ two orders more than the undoped Li₆La₃ZrNbO₁₂ that was prepared and sintered under the same conditions.

Fig. 6 (a) Arrhenius conductivity plots for Li_5+3xLa₃Nb_2−xZn_xO₁₂. (b) Arrhenius conductivity plots for Li_5−2yZn_yLa₃Nb₂O₁₂ (c) Arrhenius conductivity plots for Zn-doped Li₆La₃ZrNbO₁₂. Unit of activation energy is set as eV.

Computational modelling of the Li ion diffusion in pure and Zn-doped LLNO systems were conducted using classical MD. A 1 fs timestep was used with the Nosé–Hoover thermostat. A constant volume canonical ensemble (NVT) was conducted on the NPT simulated structures accounting for any temperature related volume expansion. A temperature range of 500–1100 K was simulated for 2 ns. The mean squared displacements MSD of all species were calculated using eqn (5).

MSD(t) = (r_i(t) − r_i(0))² (5)

In eqn (5), r_i(t) is the position of atom i at time t. For lithium, the MSDs are averaged over all lithium ions in the system. Additionally, a shifting time origin, r_i(0), is also employed over the last 1.5 ns to further improve statistics. Using eqn (6) the diffusion coefficients for both systems at all temperatures simulated are calculated and listed in Table 6.

MSD(t) = 6Dt + C (6)

Table 6 Diffusion coefficients (cm² s⁻¹) of Pure and Zn doped LLNO

Temperature (K)	Undoped LLNO	Zn doped LLNO
500	1.52 × 10^−7	2.10 × 10^−7
700	1.90 × 10^−6	1.82 × 10^−6
900	7.07 × 10^−6	5.72 × 10^−6
1100	1.49 × 10^−5	1.31 × 10^−5

---

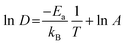From the MSDs, it is also possible to extract activation energies for lithium diffusion. An Arrhenius plot (ln D vs. 1000/T) for the pure a LLNO systems is presented in Fig. S2 (ESI†). The activation energies for lithium diffusion (E_a) are extracted by using eqn (7).

The activation energies of a pure and Zn-doped system are 0.36 eV and 0.32 eV respectively. The simulated diffusion coefficients and migration barriers suggest no improvement in ionic conductivities on Zn doping, however the experimentally observed increase in conductivity is attributed to an increase in prefactors, which is kept constant for the simulated values. The migration barriers are similar to experimental values which show a small drop in barriers on Zn doping. On closer observation, the nearest neighbour Li positions to the Zn atoms diffuse the least over both the NPT and NVT simulations, suggesting they are not involved in the diffusion mechanisms. As suggested by the doping mechanisms investigated the Li interstitials prefer to be closest to the Zn rather than further away and, once they are locked in, do not participate in the overall Li ion diffusion. AIMD simulations also show similar results although these were only run for 8 ps but validate that this is not an effect of the potential model. From the diffusion pathways shown in Fig. 7, a knock-on mechanism is suggested for Li ion diffusion mechanism.

Fig. 7 Schematic of lithium-diffusion pathways pure (top) and Zn-doped LLNO. Left and right images show pathways of Li diffusion at 1000 K respectively. Images on the right show knock-on mechanism where the orange circles are octahedral sites and the purple are tetrahedral sites. Other species are omitted for clarity.

Electrochemical properties

Initially, the Li_6.6La₃Nb_0.8Zn_0.2ZrO₁₂ pellet was tested on its own as a potential solid electrolyte in contact with Li metal. The Li_6.6La₃Nb_0.8Zn_0.2ZrO₁₂ pellet was subjected to hot pressing alongside lithium metal at 175 °C. However, a notable change in colour from white to black was observed during the hot pressing process after 10–20 minutes, indicative of dendrite growth attributed to Zn reduction and the formation of Li–Zn alloys. Electrochemical impedance spectroscopy (EIS) measurements of the Li||LLZN||Li cell exhibited pronounced short-circuit behaviour, with the total area-specific resistance (ASR) being less than 50 Ω cm², as shown in the Fig. S3 (ESI†). Therefore, this system cannot be used on its own as a solid state electrolyte in contact with Li metal.

Nevertheless, whilst Li_6.6La₃Nb_0.8Zn_0.2ZrO₁₂ has been associated with triggering short circuits in lithium symmetric cells, the utilisation of Li–Zn alloys in the literature has proven effective in addressing interfacial issues.^81–83 Therefore, we investigated the retention for this garnet to be used as an interlayer with another garnet phase. This approach centres on designing a trilayer sandwich pellet that utilises Li_6.6La₃Nb_0.8Zn_0.2ZrO₁₂ as a buffer layer, enveloping both sides of an alternative garnet material; here Li_6.4La₃Nb_0.6Zr_1.4O₁₂ was used. The electrochemical impedance spectroscopy analysis of the Li||sandwich||Li symmetric cell is depicted in Fig. 8(a). The circuit model for the lithium symmetric cell was constructed using two parallel resistor and constant phase element (CPE) in series in series, corresponding to the bulk conductivity and interlayer response, respectively; the sandwich cells exhibit a bulk area-specific resistance of 3500 Ω cm² and 3000 Ω cm² for the Zn-doped Li_6.4La₃Nb_0.6Zr_1.4O₁₂ layer. As Zn can react with Li metal to form Li–Zn alloys, the interfacial resistance will be negligible in this case. To ascertain the critical current density of the symmetric cell, current densities ranging from 0.1 mA cm⁻² to 1 mA cm⁻² were applied, as illustrated in Fig. 8(b). With the increase in current densities, the voltage escalated without any significant voltage drops, indicating that the sandwich configuration with the Zn-doped garnet interlayer plays a crucial role in dendrite formation prevention. The long-term cycling performance of the Li||sandwich||Li symmetric cell at 50 and 100 μA cm² is presented in Fig. 8(c). The voltage plateaus with an overpotential of 0.18 V at 50 μA cm² and 0.46 V at 100 μA cm² were observed. The cell exhibited long-term cycling stability for approximately 250 hours, albeit with a slightly rising overpotential.

Fig. 8 (a) Electrochemical impedance spectra Li||sandwich||Li symmetric cells. (b) Constant current cycling testing of Li||sandwich||Li cell from 0.1 mA cm⁻² to 1 mA cm⁻². (c) Charge – discharge voltage profile of the Li||sandwich||Li symmetry cell at room temperature with 50 and 100 μA cm⁻² current densities.

Therefore, Li_6.6La₃Nb_0.8Zn_0.2ZrO₁₂ has been shown to effectively act as a buffer layer for the sandwich pellet to mitigate dendrite growth. As an alternative approach to allow the use of the Zn doped garnet as an electrolyte, we employed a cost-effective fluorination technique using PTFE,⁴⁸ a method we have previously developed, to treat the pellet and thus address the issue of dendrite intercalation. Using such an approach (with Li_6.4Al_0.2La₃Zr₂O₁₂ garnet electrolyte), we have previously shown that there is a homogeneous distribution of all elements (including F) across the pellet with no obvious change of XRD after the PTFE treatment. This fluorinated coating layer acts as a superior buffer that prevents full dendrite penetration at high current densities. Similar improvement by such an approach was observed in this case. The EIS of the Li||LLZNZ-PTFE||Li symmetric cell is shown in Fig. S4(a) (ESI†). The data consists of three components where the total ASR of the bulk and grain boundary is ∼3600 Ω cm² and interfacial ASR is about 550 Ω cm². Long term cycling performance of the Li||LLZNZ-PTFE||Li symmetry cell is shown in Fig. S4(b) (ESI†). Despite the fluctuations in voltage, potentially attribute to the uneven distribution during the fluorination process, the cell demonstrated long-term cycling stability exceeding 160 hours, illustrating that the fluorination layer limited Zn reduction.

Conclusion

In conclusion, the successful synthesis of Zn-doped Li₅La₃Nb₂O₁₂ and Li₆La₃ZrNbO₁₂ through a conventional solid-state process has been achieved. Zn doping led to a significant increase in the relative density of both systems (90%), indicating that Zn is a good densification dopant for garnet materials. The conductivities in both systems were enhanced on Zn doping, with that of LLZNZ increasing to 2.1 × 10⁻⁴ S cm⁻¹ at 25 °C, which is more than ∼ two orders of magnitude of Li₆La₃ZrNbO₁₂ prepared/sintered under the same conditions. Computational modelling suggests favourable doping of Zn on the Nb site with 3 Li interstitials as per experimental findings. The diffusion of Li ions appears to follow a knock-on mechanism and the enhancement in Li ion conductivity in the doped material is attributed to larger pre-factors, stemming from the increased presence of Li ions. A challenge, however, is the reduction of Zn in contact with Li metal. Nevertheless, utilizing the Zn-doped garnet as a buffer layer with another garnet phase has proven effective in hindering dendrite growth up to a current density of 1 mA cm⁻². Moreover, the long-term cycling stability of a Li||sandwich||Li symmetric cell was demonstrated over 250 hours. Alternatively surface fluorination by heating with PTFE can help to limit Zn reduction. Thus, Zn doping represents a good method for enhancing ionic conductivity of garnet materials and boosting the critical current density, paving the way for potential applications in all-solid-state batteries.

Author contributions

Bo Dong: conceptualization, data curation, formal analysis, investigation, methodology, visualization, writing – original draft, writing – review & editing. Bassey Oboho: data curation, formal analysis, investigation, methodology, visualization, writing – original draft, writing – review & editing. Linhao Li: data curation, formal analysis, writing – original draft. Xiao Tao: data curation, formal analysis, writing – original draft. Pengcheng Zhu: data curation, formal analysis, writing – original draft. Mark P. Stockham: data curation, formal analysis, writing – original draft. Chuan Li: data curation, formal analysis, writing – original draft. Roger Smith: data curation, formal analysis, writing – original draft. Yongliang Li: data curation, formal analysis, writing – original draft. Yulong Ding: data curation, formal analysis, writing – original draft. Pooja Goddard: conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, writing – original draft, writing – review & editing. Peter R. Slater: conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, writing – original draft, writing – review & editing.

Data availability

Research data supporting this manuscript can be found at https://doi.org/10.25500/edata.bham.00001134.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

We would like to thank EPSRC (grant EP/R024006/1: ICSF Wave 1: GENESIS: Garnet Electrolytes for New Energy Storage Integrated Solutions) for financial support. We would like to thank the Faraday Institution CATMAT (FIRG016, EP/S003053/1) and NEXTRODE (FIRG015) projects for funding. We would like to thank the University of Birmingham for the studentship funding of Mark Stockham.

References

1. J. B. Goodenough and K. S. Park, The Li-ion rechargeable battery: a perspective, J. Am. Chem. Soc., 2013, 135(4), 1167–1176.
2. J.-M. Tarascon and M. Armand, Issues and challenges facing rechargeable lithium batteries, Nature, 2001, 414(6861), 359–367.
3. P. G. Bruce, B. Scrosati and J. M. Tarascon, Nanomaterials for rechargeable lithium batteries, Angew. Chem., Int. Ed., 2008, 47(16), 2930–2946.
4. J. Janek and W. G. Zeier, A solid future for battery development, Nat. Energy, 2016, 1(9), 1–4.
5. A. Manthiram, X. Yu and S. Wang, Lithium battery chemistries enabled by solid-state electrolytes, Nat. Rev. Mater., 2017, 2(4), 16103.
6. P. G. Bruce and A. R. West, The A–C Conductivity of Polycrystalline LISICON, Li_2+2xZn_1−xGeO₄, and a Model for Intergranular Constriction Resistances, J. Electrochem. Soc., 1983, 130.
7. B. Dong, R. Jarkaneh, S. Hull, N. Reeves-McLaren, J. J. Biendicho and A. R. West, Synthesis, structure and electrical properties of N-doped Li₃VO₄, J. Mater. Chem. A, 2016, 4(4), 1408–1413.
8. B. Dong, J. Yan, B. Walkley, K. K. Inglis, F. Blanc, S. Hull and A. R. West, Synthesis and characterisation of the new oxyfluoride Li⁺ ion conductor, Li₅SiO₄F, Solid State Ionics, 2018, 327, 64–70.
9. M. A. Subramanian, R. Subramanian and A. Clearfield, Lithium ion conductors in the system AB(IV)₂(PO₄)₃ (B = Ti, Zr AND Hf), Solid State Ionics, 1986, 18, 562.
10. V. Thangadurai, A. K. Shukla and J. Gopalakrishnan, New lithium-ion conductors based on the NASICON structure, J. Mater. Chem., 1999, 9, 739.
11. Y. Harada, T. Ishigaki, H. Kawai and J. Kuwano, Lithium ion conductivity of polycrystalline perovskite La_0.67−xLi_3xTiO₃ with ordered and disordered arrangements of the A-site ions, Solid State Ionics, 1998, 108, 407–413.
12. V. Thangadurai, S. Narayanan and D. Pinzaru, Garnet-type solid-state fast Li ion conductors for Li batteries: critical review, Chem. Soc. Rev., 2014, 43(13), 4714–4727.
13. R. Kanno and M. Murayama, Lithium Ionic Conductor Thio-LISICON The Li₂S–GeS₂–P₂S₅ System, J. Electrochem. Soc., 2001, 148.
14. J. Percival, D. Apperley and P. R. Slater, Synthesis and Structural Characterisation of the Li Ion Conducting Garnet-Related Systems, Li₆ALa₂Nb₂O₁₂ (A = Ca, Sr), Solid State Ionics, 2008, 179(27–32), 1693–1696.
15. Y. Zhao and L. L. Daemen, Superionic conductivity in lithium-rich anti-perovskites, J. Am. Chem. Soc., 2012, 134(36), 15042–15047.
16. S. Ramakumar, C. Deviannapoorani, L. Dhivya, L. S. Shankar and R. Murugan, Lithium garnets: Synthesis, structure, Li⁺ conductivity, Li⁺ dynamics and applications, Prog. Mater. Sci., 2017, 88, 325–411.
17. V. Thangadurai, H. Kaack and W. Weppner, Novel Fast Lithium Ion Conduction in Garnet-Type Li₅La₃M₂O₁₂ (M = Nb, Ta), J. Am. Ceram. Soc., 2003, 86(3), 437–440.
18. E. J. Cussen, Structure and ionic conductivity in lithium garnets, J. Mater. Chem., 2010, 20(25), 5167–5173.
19. V. Thangadurai and W. Weppner, Li₆ALa₂Ta₂O₁₂ (A = Sr, Ba): Novel Garnet-Like Oxides for Fast Lithium Ion Conduction, Adv. Funct. Mater., 2005, 15(1), 107–112.
20. J. Percival and P. R. Slater, Identification of the Li sites in the Li ion conductor, Li₆SrLa₂Nb₂O₁₂, through neutron powder diffraction studies, Solid State Commun., 2007, 142(6), 355–357.
21. J. Percival, E. Kendrick and P. R. Slater, Synthesis and conductivities of the garnet-related Li ion conductors, Li₅Ln₃Sb₂O₁₂ (Ln = La, Pr, Nd, Sm, Eu), Solid State Ionics, 2008, 179(27–32), 1666–1669.
22. M. A. Howard, O. Clemens, E. Kendrick, K. S. Knight, D. C. Apperley, P. A. Anderson and P. R. Slater, Effect of Ga incorporation on the structure and Li ion conductivity of La₃Zr₂Li₇O₁₂, Dalton Trans., 2012, 41(39), 12048–12053.
23. Y. Li, J.-T. Han, C.-A. Wang, H. Xie and J. B. Goodenough, Optimizing Li⁺ conductivity in a garnet framework, J. Mater. Chem., 2012, 22(30), 15357–15361.
24. J. Wolfenstine, J. Ratchford, E. Rangasamy, J. Sakamoto and J. L. Allen, Synthesis and high Li-ion conductivity of Ga-stabilized cubic Li₇La₃Zr₂O₁₂, Mater. Chem. Phys., 2012, 134(2–3), 571–575.
25. M. A. Howard, O. Clemens, K. S. Knight, P. A. Anderson, S. Hafiz, P. M. Panchmatia and P. R. Slater, Synthesis, conductivity and structural aspects of Nd₃Zr₂Li_7−3xAl_xO₁₂, J. Mater. Chem. A, 2013, 1(44), 14013–14022.
26. T. Thompson, J. Wolfenstine, J. L. Allen, M. Johannes, A. Huq, I. N. David and J. Sakamoto, Tetragonal vs. cubic phase stability in Al – free Ta doped Li₇La₃Zr₂O₁₂ (LLZO), J. Mater. Chem. A, 2014, 2(33), 13431–13436.
27. M. P. Stockham, A. A. Griffiths, B. Dong and P. R. Slater, Assessing the Importance of Cation Size in the Tetragonal-Cubic Phase Transition in Lithium-Garnet Electrolytes, Chem. – Eur. J., 2021, 27(27), 1–10.
28. M. P. Stockham, B. Dong, M. S. James, Y. Li, Y. Ding and P. R. Slater, Water based synthesis of highly conductive Ga_xLi_7−3xLa₃Hf₂O₁₂ garnets with comparable critical current density to analogous Ga_xLi_7−3xLa₃Zr₂O₁₂ systems, Dalton Trans., 2021, 50(7), 2364–2374.
29. M. P. Stockham, B. Dong, M. S. James, Y. Li, Y. Ding, E. Kendrick and P. R. Slater, Evaluation of Ga_0.2Li_6.4Nd₃Zr₂O₁₂ garnets: exploiting dopant instability to create a mixed conductive interface to reduce interfacial resistance for all solid state batteries, Dalton Trans., 2021, 50(39), 13786–13800.
30. B. Dong, L. L. Driscoll, M. P. Stockham, E. Kendrick and P. R. Slater, Low temperature synthesis of garnet solid state electrolytes: Implications on aluminium incorporation in Li₇La₃Zr₂O₁₂, Solid State Ionics, 2020, 350, 115317.
31. J. Awaka, N. Kijima, H. Hayakawa and J. Akimoto, Synthesis and structure analysis of tetragonal Li₇La₃Zr₂O₁₂ with the garnet-related type structure, J. Solid State Chem., 2009, 182(8), 2046–2052.
32. J. Percival, E. Kendrick, R. I. Smith and P. R. Slater, Cation ordering in Li containing garnets: synthesis and structural characterisation of the tetragonal system, Li₇La₃Sn₂O₁₂, Dalton Trans., 2009,(26), 5177–5181.
33. J. Awaka, N. Kijima, K. Kataoka, H. Hayakawa, K.-I. Ohshima and J. Akimoto, Neutron powder diffraction study of tetragonal Li₇La₃Hf₂O₁₂ with the garnet-related type structure, J. Solid State Chem., 2010, 183(1), 180–185.
34. G. Larraz, A. Orera and M. L. Sanjuán, Cubic phases of garnet-type Li₇La₃Zr₂O₁₂: the role of hydration, J. Mater. Chem. A, 2013, 1(37), 11419–11428.
35. L. Truong, M. Howard, O. Clemens, K. S. Knight, P. R. Slater and V. Thangadurai, Facile proton conduction in H⁺/Li⁺ ion-exchanged garnet-type fast Li-ion conducting Li₅La₃Nb₂O₁₂, J. Mater. Chem. A, 2013, 1(43), 13469–13475.
36. R. H. Brugge, A. K. O. Hekselman, A. Cavallaro, F. M. Pesci, R. J. Chater, J. A. Kilner and A. Aguadero, Garnet Electrolytes for Solid State Batteries: Visualization of Moisture-Induced Chemical Degradation and Revealing Its Impact on the Li-Ion Dynamics, Chem. Mater., 2018, 30(11), 3704–3713.
37. F. M. Pesci, R. H. Brugge, A. K. O. Hekselman, A. Cavallaro, R. J. Chater and A. Aguadero, Elucidating the role of dopants in the critical current density for dendrite formation in garnet electrolytes, J. Mater. Chem. A, 2018, 6(40), 19817–19827.
38. A. G. Squires, D. O. Scanlon and B. J. Morgan, Native Defects and Their Doping Response in the Lithium Solid Electrolyte Li₇La₃Zr₂O₁₂, Chem. Mater., 2019, 32(5), 1876–1886.
39. Y. Xiao, Y. Wang, S.-H. Bo, J. C. Kim, L. J. Miara and G. Ceder, Understanding interface stability in solid-state batteries, Nat. Rev. Mater., 2019, 5(2), 105–126.
40. X. He, X. Ji, B. Zhang, N. D. Rodrigo, S. Hou, K. Gaskell, T. Deng, H. Wan, S. Liu, J. Xu, B. Nan, B. L. Lucht and C. Wang, Tuning Interface Lithiophobicity for Lithium Metal Solid-State Batteries, ACS Energy Lett., 2021, 7(1), 131–139.
41. Y. Chen, J. Qian, X. Hu, Y. Ma, Y. Li, T. Xue, T. Yu, L. Li, F. Wu and R. Chen, Constructing a Uniform and Stable Mixed Conductive Layer to Stabilize the Solid-State Electrolyte/Li Interface by Cold Bonding at Mild Conditions, Adv. Mater., 2023, 35(18), e2212096.
42. C. Zhu, T. Fuchs, S. A. L. Weber, F. H. Richter, G. Glasser, F. Weber, H. J. Butt, J. Janek and R. Berger, Understanding the evolution of lithium dendrites at Li(6.25)Al(0.25)La(3)Zr(2)O(12) grain boundaries via operando microscopy techniques, Nat. Commun., 2023, 14(1), 1300.
43. J. Zhao, Y. Tang, Q. Dai, C. Du, Y. Zhang, D. Xue, T. Chen, J. Chen, B. Wang, J. Yao, N. Zhao, Y. Li, S. Xia, X. Guo, S. J. Harris, L. Zhang, S. Zhang, T. Zhu and J. Huang, In situ Observation of Li Deposition-Induced Cracking in Garnet Solid Electrolytes, Energy Environ. Mater., 2021, 5(2), 524–532.
44. J. Kasemchainan, S. Zekoll, D. Spencer Jolly, Z. Ning, G. O. Hartley, J. Marrow and P. G. Bruce, Critical stripping current leads to dendrite formation on plating in lithium anode solid electrolyte cells, Nat. Mater., 2019, 18(10), 1105–1111.
45. Y. Li, X. Chen, A. Dolocan, Z. Cui, S. Xin, L. Xue, H. Xu, K. Park and J. B. Goodenough, Garnet Electrolyte with an Ultralow Interfacial Resistance for Li-Metal Batteries, J. Am. Chem. Soc., 2018, 140(20), 6448–6455.
46. Y. Ruan, Y. Lu, X. Huang, J. Su, C. Sun, J. Jin and Z. Wen, Acid induced conversion towards a robust and lithiophilic interface for Li–Li₇La₃Zr₂O₁₂ solid-state batteries, J. Mater. Chem. A, 2019, 7(24), 14565–14574.
47. H. Xie, C. Li, W. H. Kan, M. Avdeev, C. Zhu, Z. Zhao, X. Chu, D. Mu and F. Wu, Consolidating the grain boundary of the garnet electrolyte LLZTO with Li₃BO₃ for high-performance LiNi_0.8Co_0.1Mn_0.1O₂/LiFePO₄ hybrid solid batteries, J. Mater. Chem. A, 2019, 7(36), 20633–20639.
48. B. Dong, A. R. Haworth, S. R. Yeandel, M. P. Stockham, M. S. James, J. Xiu, D. Wang, P. Goddard, K. E. Johnston and P. R. Slater, Halogenation of Li₇La₃Zr₂O₁₂ solid electrolytes: a combined solid-state NMR, computational and electrochemical study, J. Mater. Chem. A, 2022, 10(20), 11172–11185.
49. P. Ghorbanzade, A. Pesce, K. Gómez, G. Accardo, S. Devaraj, P. López-Aranguren and J. M. López del Amo, Impact of thermal treatment on the Li-ion transport, interfacial properties, and composite preparation of LLZO garnets for solid-state electrolytes, J. Mater. Chem. A, 2023, 11(22), 11675–11683.
50. X. Han, Y. Gong, K. K. Fu, X. He, G. T. Hitz, J. Dai, A. Pearse, B. Liu, H. Wang, G. Rubloff, Y. Mo, V. Thangadurai, E. D. Wachsman and L. Hu, Negating interfacial impedance in garnet-based solid-state Li metal batteries, Nat. Mater., 2017, 16(5), 572–579.
51. J. Dai, C. Yang, C. Wang, G. Pastel and L. Hu, Interface Engineering for Garnet-Based Solid-State Lithium-Metal Batteries: Materials, Structures, and Characterization, Adv. Mater., 2018, 30(48), e1802068.
52. N. J. Taylor, S. Stangeland-Molo, C. G. Haslam, A. Sharafi, T. Thompson, M. Wang, R. Garcia-Mendez and J. Sakamoto, Demonstration of high current densities and extended cycling in the garnet Li₇La₃Zr₂O₁₂ solid electrolyte, J. Power Sources, 2018, 396, 314–318.
53. J. Wang, S. Zhang, H. Zhao, J. Liu, M.-A. Yang, Z. Li and K. Świerczek, Construction of an intimately riveted Li/garnet interface with ultra-low interfacial resistance for solid-state batteries, J. Mater. Chem. A, 2024, 12(8), 4903–4911.
54. W. Zhou, Z. Wang, Y. Pu, Y. Li, S. Xin, X. Li, J. Chen and J. B. Goodenough, Double-Layer Polymer Electrolyte for High-Voltage All-Solid-State Rechargeable Batteries, Adv. Mater., 2019, 31(4), e1805574.
55. H. Duan, Y. X. Yin, Y. Shi, P. F. Wang, X. D. Zhang, C. P. Yang, J. L. Shi, R. Wen, Y. G. Guo and L. J. Wan, Dendrite-Free Li-Metal Battery Enabled by a Thin Asymmetric Solid Electrolyte with Engineered Layers, J. Am. Chem. Soc., 2018, 140(1), 82–85.
56. R. Subramani, Y.-H. Tseng, Y.-L. Lee, C.-C. Chiu, S.-S. Hou and H. Teng, High Li⁺ transference gel interface between solid-oxide electrolyte and cathode for quasi-solid lithium-ion batteries, J. Mater. Chem. A, 2019, 7(19), 12244–12252.
57. G. V. Alexander, C. Shi, J. O’Neill and E. D. Wachsman, Extreme lithium-metal cycling enabled by a mixed ion- and electron-conducting garnet three-dimensional architecture, Nat. Mater., 2023, 22(9), 1136–1143.
58. M. P. Stockham, B. Dong, Y. Ding, Y. Li and P. R. Slater, Evaluation of the effect of site substitution of Pr doping in the lithium garnet system Li₅La₃Nb₂O₁₂, Dalton Trans., 2020, 49(30), 10349–10359.
59. B. Dong, S. R. Yeandel, P. Goddard and P. R. Slater, Combined Experimental and Computational Study of Ce-Doped La₃Zr₂Li₇O₁₂ Garnet Solid-State Electrolyte, Chem. Mater., 2019, 32(1), 215–223.
60. B. Dong, M. P. Stockham, P. A. Chater and P. R. Slater, X-ray pair distribution function analysis and electrical and electrochemical properties of cerium doped Li₅La₃Nb₂O₁₂ garnet solid-state electrolyte, Dalton Trans., 2020, 49(33), 11727–11735.
61. Y. Chen, E. Rangasamy, C. Liang and K. An, Origin of High Li⁺ Conduction in Doped Li₇La₃Zr₂O₁₂ Garnets, Chem. Mater., 2015, 27(16), 5491–5494.
62. E. Hanc, W. Zając, L. Lu, B. Yan, M. Kotobuki, M. Ziąbka and J. Molenda, On fabrication procedures of Li-ion conducting garnets, J. Solid State Chem., 2017, 248, 51–60.
63. G. Kresse and J. Hafner, Ab initio molecular-dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(1), 14251–14269.
64. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979.
65. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125(22), 224106.
66. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimp-ton, LAMMPS – a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171.
67. Y. Wang, A. Huq and W. Lai, Insight into lithium distribution in lithium-stuffed garnet oxides through neutron diffraction and atomistic simulation: Li_7−xLa₃Zr_2−xTa_xO₁₂ (x = 0–2) series, Solid State Ionics, 2014, 255, 39–49.
68. R. A. Jackson and M. E. G. Valerio, A new interatomic potential for the ferroelectric and paraelectric phases of LiNbO₃, J. Phys.: Condens. Matter, 2005, 17, 837.
69. B. Dick Jr. and A. Overhauser, Theory of the dielectric constants of alkali halide crystals, Phys. Rev., 1958, 112, 90.
70. D. J. Binks, Computational Modelling of Zinc Oxide and Related Oxide Ceramics, PhD thesis, University of Surrey, Harwell, 1994.
71. M. P. O’Callaghan and E. J. Cussen, Lithium dimer formation in the Li-conducting garnets Li(5 + x)Ba(x)La(3 − x)Ta₂O₁₂ (0 < x < or =1.6), Chem. Commun., 2007,(20), 2048–2050.
72. S. Nose, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519.
73. J. L. Allen, J. Wolfenstine, E. Rangasamy and J. Sakamoto, Effect of substitution (Ta, Al, Ga) on the conductivity of Li₇La₃Zr₂O₁₂, J. Power Sources, 2012, 206, 315–319.
74. S.-W. Baek, J.-M. Lee, T. Y. Kim, M.-S. Song and Y. Park, Garnet related lithium ion conductor processed by spark plasma sintering for all solid state batteries, J. Power Sources, 2014, 249, 197–206.
75. S. Ohta, S. Komagata, J. Seki, T. Saeki, S. Morishita and T. Asaoka, All-solid-state lithium ion battery using garnet-type oxide and Li₃BO₃ solid electrolytes fabricated by screen-printing, J. Power Sources, 2013, 238, 53–56.
76. N. Janani, C. Deviannapoorani, L. Dhivya and R. Murugan, Influence of sintering additives on densification and Li⁺ conductivity of Al doped Li₇La₃Zr₂O₁₂ lithium garnet, RSC Adv., 2014, 4(93), 51228–51238.
77. A. Azad and J. Irvine, High density and low temperature sintered proton conductor BaCe_0.5Zr_0.35Sc_0.1Zn_0.05O_3–δ, Solid State Ionics, 2008, 179(19–20), 678–682.
78. P. Babilo and S. M. Haile, Enhanced Sintering of Yttrium-Doped Barium Zirconate by Addition of ZnO, J. Am. Ceram. Soc., 2005, 88(9), 2362–2368.
79. J. T. S. Irvine, D. C. Sinclair and A. R. West, Electroceramics: Characterization by Impedance Spectroscopy, Adv. Mater., 1990, 2(3), 132–138.
80. B. Dong, S. Hull and A. R. West, Phase Formation, Crystallography, and Ionic Conductivity of Lithium Manganese Orthosilicates, Inorg. Chem., 2019, 58(1), 715–723.
81. Z. Wan, K. Shi, Y. Huang, L. Yang, Q. Yun, L. Chen, F. Ren, F. Kang and Y.-B. He, Three-dimensional alloy interface between Li_6.4La₃Zr_1.4Ta_0.6O₁₂ and Li metal to achieve excellent cycling stability of all-solid-state battery, J. Power Sources, 2021, 505, 230062.
82. G. V. Alexander, O. V. Sreejith, M. S. Indu and R. Murugan, Interface-Compatible and High-Cyclability Lithiophilic Lithium–Zinc Alloy Anodes for Garnet-Structured Solid Electrolytes, ACS Appl. Energy Mater., 2020, 3(9), 9010–9017.
83. Y. Zhong, Y. Xie, S. Hwang, Q. Wang, J. J. Cha, D. Su and H. Wang, A Highly Efficient All-Solid-State Lithium/Electrolyte Interface Induced by an Energetic Reaction, Angew. Chem., Int. Ed., 2020, 59(33), 14003–14008.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00429a

---