Open Access Article
Open Access ArticleEntropy engineering in I–V–VI2 family: a paradigm to bestow enhanced average ZT in the entire operating temperature regime†
Ranita
Basu
 *ab,
U. Sandhya
Shenoy
*ab,
U. Sandhya
Shenoy
 c,
Ankita
Pathak
ab,
Shweta
Singh
bd,
P.
Jha
c,
Ankita
Pathak
ab,
Shweta
Singh
bd,
P.
Jha
 ab,
D. Krishna
Bhat
ab,
D. Krishna
Bhat
 e,
Hirakendu
Basu
e,
Hirakendu
Basu
 bd and
Ajay
Singh
ab
bd and
Ajay
Singh
ab
aTechnical Physics Division, Bhabha Atomic Research Centre, Mumbai 400085, India. E-mail: ranitapaul@gmail.com; ranitab@barc.gov.in; Tel: (+91)2225593217
bHomi Bhabha National Institute, Training School Complex, Anushaktinagar, Mumbai 400094, India
cDepartment of Materials Science and Engineering, Institute of Engineering and Technology, Srinivas University, Mukka 574146, Mangalore, Karnataka, India
dAnalytical Chemistry Division, Bhabha Atomic Research Centre, Mumbai 400085, India
eDepartment of Chemistry, National Institute of Technology Karnataka, Surathkal, Srinivasnagar 575025, Mangalore, Karnataka, India
First published on 28th August 2024
Abstract
The design and development of n-type alloys in the mid-temperature regime (500–700) K with enhanced thermoelectric performance is of utmost necessity for the fabrication of thermoelectric devices. In this regard, the I–V–VI2 family reveals superior thermoelectric performance, owing to the fact that group V elements have non-bonded electrons and high Z (atomic number), with a high Grüneisen parameter, which cause amplified anharmonicity and subsequently low intrinsic lattice thermal conductivity. However, the irony is that the well-studied alloy of this family, AgBiSe2, undergoes phase transition in the operating temperature range. Thus, of paramount importance is restricting the phase transition and bringing it down below room temperature (RT), along with stabilizing a highly symmetrical crystal structure in the extended operating temperature range. Efforts were made to synthesize a cubic n-type AgBiSeS alloy belonging to the I–V–VI2 compounds (unlike AgBiSe2) that is stabilized throughout the temperature range, as the S element aids in strengthening of the chemical bonds. In addition, the alloy was further stabilized by forming a solid solution with PbSe, which aids in increasing the configurational entropy and thereby increases the chemical space of the system. The resultant alloys possess intrinsically low lattice thermal conductivity ranging from 0.38–0.74 W m−1 K−1 in the entire operating range. Consequently, the peak ZT was reported as ∼0.6 at 780 K, with an average ZT value of 0.3 for the alloy (AgBiSeS)0.5(PbSe)0.5 within 300–823 K. Although the reported ZT is low, the methodology of entropy-driven structural stabilization in the operating temperature regime was adapted to attain a highly symmetrical, stable structure for practical applications.
1. Introduction
In today's environment of looming global energy scarcity, the pursuit of unconventional power generation methods is of extreme importance. One of the promising alternatives is thermoelectric power generation. Its ability to recover waste heat (which accounts for about two-thirds of the consumed fossil fuel) and convert it to electrical energy makes it suitable for manifold industrial applications. Moreover, thermoelectric (TE) modules involve no moving parts, which makes them portable and highly reliable and increases their operational life.1–6 Their reliability has been shown in space applications, where they have operated without failure for more than 30 years.7,8 The particular demand from energy system developers and industrial component manufacturers for high-temperature thermo-generators has significantly accelerated institutional and governmental research efforts worldwide. However, today's available devices cannot be applied at temperatures higher than 250 °C, yet the largest part of recoverable waste heat is available at those temperatures. Thus, an urgent need in research progress is required to explore technically viable solutions at elevated temperatures. Nevertheless, low conversion efficiency and high cost limit their usage in niche applications. With substantial improvement in the figure-of-merit (ZT), which requires untangling two unfavorably coupled properties, thermoelectric materials can be used in more advanced applications, which include harvesting waste heat from power plants and engines or cooling computer chips. The dimensionless ZT of the material is given by: ZT = (α2σ/(κe + κl))T, where α, σ, κe, and κl are the Seebeck coefficient, electrical conductivity, electronic thermal conductivity and lattice thermal conductivity, respectively. Thus, (i) decoupling of α, σ, and κe through band engineering to improve the power factor9,10 and (ii) phonon engineering through lattice defects11 and embedding nanostructures which destroy the path required for the propagation of the phonons12 are the two mainstream stratagems for boosting the thermoelectric performance. In the past decade, several new thermoelectric elements were designed and discovered, and notably, entropy engineering has evolved as an exemplar shifting methodology which integrates the phase, band and phonon engineering via multicomponent alloying. Entropy engineering is actually a hybrid of the research fields in conventional thermoelectrics and high-entropy alloys (HEAs).13–15 Here, the participation of the multiple elements tends to form high-symmetry crystal structures, i.e., face-centered cubic lattice or body-centered cubic lattice, which are otherwise thermoelectrically preferred due to the introduction of high band degeneracy, Nv, and thus leads to a high Seebeck coefficient, α. This can also be explained from the fact that the influence of entropy of mixing, −TΔSconf, counterbalances the strain energy and hence stabilizes the crystalline single-phase solid solution.16 The influence of the enhanced entropy effect is so influential that in some instances, a single-phase alloy is formed, violating the classic Hume–Rothery rules. Thus, the hypotheses of “enhanced entropy” and configurational entropy-stabilized compounds are useful to elucidate the stability challenge. Nevertheless, the entropy-driven, structurally stabilized single phase provides a beneficial path to strengthen the electrical transport properties with some incremental compromise in the carrier mobility.17According to a well-recognized report, high-performance thermoelectric materials, in principle, are degenerate semiconductors possessing high crystal symmetry and the lowest lattice thermal conductivity. Traditional thermoelectric materials with rock salt cubic structure (SG: Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), for instance, PbTe,18–20 SnTe21–24 and PbSe,14,25,26 were intensely studied in the past owing to their superior thermoelectric performance. These alloys possess multiple valleys, having carrier pockets with a copious number of equivalent positions in a typical reciprocal space benefitting from high crystal symmetry. In order to explore new thermoelectric materials, researchers are now inclined towards extending their interest to the ternary I–V–VI2 alloys with crystal structure similar to AgSbTe2.27–30 This alloy is considered as an isoelectronic structural analog of the champion thermoelectric alloy, PbTe. AgSbTe2 crystallizes in rock-salt structure at room temperature and has appeared to be a promising thermoelectric material due to low lattice thermal conductivity, restricted by the Sb lone pair electrons. Moreover, Roychowdhury et al. have demonstrated that by optimizing the electronic and phonon transport properties simultaneously, Cd-doped AgSbTe2 exhibits a near-room-temperature ZT of ∼1.5 and a max ZT of 2.6 at 573 K, which is one of the highest ever reported among the state-of-the-art bulk TE alloys from room temperature to 573 K.29 Nevertheless, AgSbTe2 shows p-type conduction intrinsically and is difficult to tune into n-type via the addition of dopants. Moreover, the n-type counterpart of AgSbTe2 with a similar rock salt crystal structure is absent in the ternary I–V–VI2 family. This largely restricts the realistic application of this particular family of materials for the fabrication of thermoelectric modules, which demands both n- and p-type legs manufactured from alloys with similar physical and chemical properties.31
m), for instance, PbTe,18–20 SnTe21–24 and PbSe,14,25,26 were intensely studied in the past owing to their superior thermoelectric performance. These alloys possess multiple valleys, having carrier pockets with a copious number of equivalent positions in a typical reciprocal space benefitting from high crystal symmetry. In order to explore new thermoelectric materials, researchers are now inclined towards extending their interest to the ternary I–V–VI2 alloys with crystal structure similar to AgSbTe2.27–30 This alloy is considered as an isoelectronic structural analog of the champion thermoelectric alloy, PbTe. AgSbTe2 crystallizes in rock-salt structure at room temperature and has appeared to be a promising thermoelectric material due to low lattice thermal conductivity, restricted by the Sb lone pair electrons. Moreover, Roychowdhury et al. have demonstrated that by optimizing the electronic and phonon transport properties simultaneously, Cd-doped AgSbTe2 exhibits a near-room-temperature ZT of ∼1.5 and a max ZT of 2.6 at 573 K, which is one of the highest ever reported among the state-of-the-art bulk TE alloys from room temperature to 573 K.29 Nevertheless, AgSbTe2 shows p-type conduction intrinsically and is difficult to tune into n-type via the addition of dopants. Moreover, the n-type counterpart of AgSbTe2 with a similar rock salt crystal structure is absent in the ternary I–V–VI2 family. This largely restricts the realistic application of this particular family of materials for the fabrication of thermoelectric modules, which demands both n- and p-type legs manufactured from alloys with similar physical and chemical properties.31
To confront this challenge, AgBiSe2 was discovered from the same I–V–VI2 family as a matched n-type counterpart. However, AgBiSe2 undergoes polymorphic transition twice in the operating temperature regime: (i) 390–525 K, from hexagonal (α) to rhombohedral (β), and (ii) from rhombohedral (β) to cubic (γ) in the temperature span of 560–585 K.32–36 These phase transitions impose a serious threat because as far as thermoelectric modules are concerned, sudden changes in the crystal structure and lattice constants would engender high internal stress in the device.37 This phase transition can be averted largely by considering the Ag–Bi–Se–S system, which is intrinsically n-type with NaCl crystal structure, and thus the thermoelectric community deviated their focus from the parent compound. AgBiSeS (or BiAgSeS) belongs to the extensively studied parent compound AgBiSe2 alloy (I–V–VI2 system) and has been described as an established n-type alternative with the unusually low thermal conductivity of 0.29 W m−1 K−1 at 823 K due to the presence of heavy-mass elements and frail inter-atomic bonding.38 The cubic daughter alloy AgBiSeS is stabilized owing to the S residing at the Se site and imparts modifications in the bond length and bond angle, which eventually can cause distortion in the crystal structure and thus reduce the lattice thermal conductivity.39 Hu et al. mentioned that AgBiSeS crystallizes in cubic phase at high temperature, and room-temperature cubic phase is vulnerable towards synthetic procedures. Utmost care was taken to synthesize AgBiSeS in order to retain the cubic structure.40 Furthermore, it was manifested that enhancing the configurational entropy of AgBiSeS via entropy engineering can ascertain the cubic structure in the entire operating temperature range and averts the sudden spike in internal thermal stress.41 In this regard, AgBiSeS was alloyed with PbSe because it aids in the enhancement of chemical space. PbSe was chosen for alloying, as it is a well-proven high-performance thermoelectric material, along with compensating the loss of Se in the synthetic procedure. AgBiSeS shows n-type conduction, and to maintain the conduction type on alloying and to avoid the energy barrier due to the formation of p–n junction, n-type PbSe was chosen. This paradigm utilizes multiple elements to occupy the indistinguishable atomic sites and eventually augment the stability of the highly symmetrical crystal structure.
2. Experimental
The synthetic procedure, characterization techniques and the computational details employed in this study are described in ESI† (S1.0).3. Results and discussions
3.1. Influence of the alloying of PbSe on the structural and chemical properties of AgBiSeS
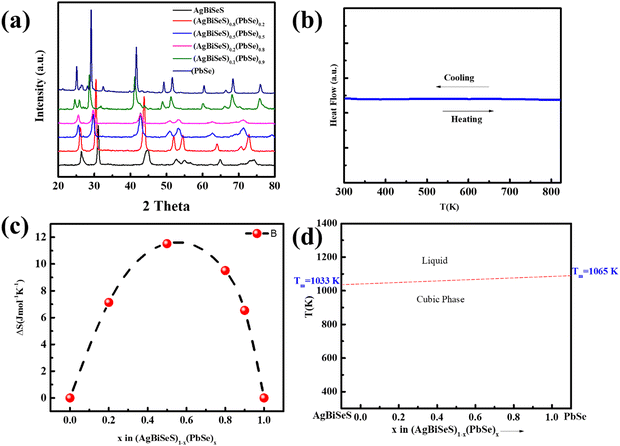
Fig. 1(a) shows the room-temperature powder XRD pattern of (AgBiSeS)1−x(PbSe)x for the melt-alloyed and hot-pressed samples. The samples crystallize in cubic rock salt (NaCl) structure, and the major Bragg peaks match well with the simulated AgBiSeS structure. AgBiSeS, which belongs to the I–V–VI2 compounds (unlike AgBiSe2) due to its S element, has strengthened chemical bonds, and thus, the cubic structure is stabilized.40 Moreover, the XRD pattern demonstrates that the cubic structure is retained even upon alloying with PbSe. The slight shifting of the peaks to lower 2θ degree with the increase in the PbSe content indicates competition for the cationic site by the large Pb2+ ion. In other words, the experimental observation can be attributed to the overall compensation by the replacement of the cationic site (Ag–Bi disordered occupation) by the larger ionic radius of Pb, and the anionic site by more Se atoms. As aforementioned, the vulnerability of the cubic phase of AgBiSeS at RT towards the methodology adapted for synthesis demands highly sensitive DSC measurement to be carried out in order to ascertain that no phase transition takes place in the operating temperature regime. The measurement manifested high thermal stability with no thermal sign (endothermic or exothermic peak) owing to entropy engineering (Fig. 1(b)). The thermal stability of the PbSe-alloyed AgBiSeS with the composition (AgBiSeS)0.5(PbSe)0.5 was further confirmed by high-temperature XRD plot (Fig. S1, ESI†). According to the laws of thermodynamics, entropy (S) is considered as a gauge to understand the microscopic configuration of the arrangement, and relying on the Boltzmann hypothesis, for a multispecies system, the entropy of mixing is given by: where R is the universal gas constant and xi is defined as the molar concentration of the ith constituent.42 Although for pristine AgBiSeS, ΔSmix = 0, with the increasing concentration of PbSe, the configurational entropy increases and attains maximum for x = 0.5 and then decreases. Fig. 1(c) shows the plot of calculated ΔSmixvs. x for the (AgBiSeS)1−x(PbSe)x solid solution, and Fig. 1(d) demonstrates the schematic of temperature vs. composition plot, or more precisely, the phase diagram inferred from powder XRD and DSC analysis. The plot depicts that the novel engineered alloy is stabilized due to enhanced configurational entropy.
where R is the universal gas constant and xi is defined as the molar concentration of the ith constituent.42 Although for pristine AgBiSeS, ΔSmix = 0, with the increasing concentration of PbSe, the configurational entropy increases and attains maximum for x = 0.5 and then decreases. Fig. 1(c) shows the plot of calculated ΔSmixvs. x for the (AgBiSeS)1−x(PbSe)x solid solution, and Fig. 1(d) demonstrates the schematic of temperature vs. composition plot, or more precisely, the phase diagram inferred from powder XRD and DSC analysis. The plot depicts that the novel engineered alloy is stabilized due to enhanced configurational entropy.
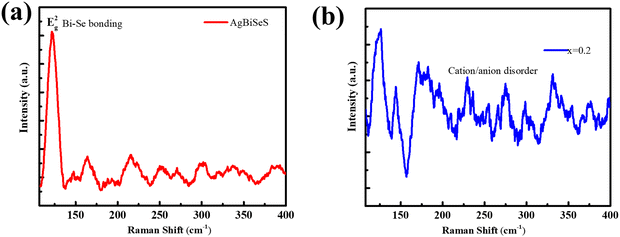
A topical analysis of the cubic stabilized pristine dimetal chalcogenide, AgBiSeS, exhibits a Raman active mode Eg2 for Bi–Se bonding at ∼121.6 cm−1 that demonstrates the presence of macroscopic polarizability in the molecule (Fig. 2(a)). Actually, in cubic AgBiSeS, having cubic structure at room temperature and enhanced configurational entropy in comparison to AgBiSe2 (theoretical and structural analyses unveiled the presence of two Raman active modes in the hexagonal lattice of AgBiSe2 at room temperature owing to the presence of two types of Bi atom at 124 cm−1 and 157 cm−1 assigned to Eg and A1g modes), the cationic disorder due to Ag vacancy and BiAg antisite defect fetch only one Raman peak at room temperature.43 However, metal ions or cations exist in altogether disordered state at ambient temperature on alloying due to the increase in configurational entropy and presence of antisite defects. This makes the exchange of metal ions inevitable, or in other words, the formation of vacancies (vacancy defects) acts like a passage in the exchange of the metal ions and thus plays a major role.44 To rephrase, the cationic intermixing or disordering causes no macroscopic polarizability and evades the Raman peak, owing to the absence of long-range ordering of atoms (which is a basis of the Raman peak) (Fig. 2(b)).
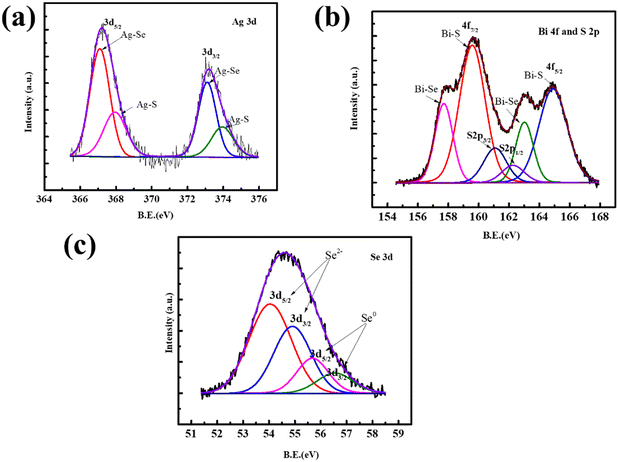
The enclosed bonding nature of pristine AgBiSeS, as shown in Fig. 3(a), and of (AgBiSeS)1−x(PbSe)x (x = 0.2) (Fig. S2, ESI†), was further corroborated by X-ray photoelectron spectroscopy (XPS). The elements Ag, Bi, Pb, Se and S were clearly spotted in the survey scan, and to identify the chemical state, high-resolution spectra were acquired for the aforementioned elements. In the Ag 3d XPS spectrum, the Ag 3d5/2 can be deconvoluted by the Ag curve fitting software into two peaks. The peaks centred at 367.1 eV (3d5/2) and 373.1 eV (3d3/2) are attributed to +1 oxidation state and assigned to the Ag–Se bond.45 Similarly, the peaks at 367.94 eV (3d5/2) and 373.94 eV (3d3/2) correspond to Ag–S bond.46 The high-resolution scan of Bi 4f (Fig. 3(b)) shows two strong, broad peaks with binding energies of 157.7 eV and 163.02 eV corresponding to Bi 4f7/2 and 4f5/2, respectively, which are assigned to the Bi–Se bond, with Bi primarily in the +3 oxidation state.47 In addition, the peaks at 159.6 eV and 164.9 eV correspond to Bi 4f7/2 and 4f5/2, respectively, of the Bi–S bond.48 The occurrence of spin orbit separation (∼1.2 eV) between S 2p3/2 (161.1eV) and S 2p1/2 (162.3 eV) peaks corroborate the presence of S in the form of S2− in the alloy (Fig. 3(b)). The high-resolution scan for 3d Se corresponds to selenides as well as Se in elemental state (Fig. 3(c)). Analogous to sulphides, the existence of spin orbit separation of (∼0.86 eV) between Se 3d5/2 (54.05 eV) and Se 3d3/2 (54.91 eV) confirms the presence of selenides in the alloy. However, commenting on the exact chemical environment of the Se is difficult because the binding energy values corresponding to Bi–Se and Ag–Se are close by and beyond the resolution of our instrument. Moreover, suppressing the loss of Se vapor is also enabled by the presence of elemental Se in the alloy. To corroborate the XPS analysis, analogous to AgBiSeS, Huang et al. reported the cubic structure of AgBiSeTe at room temperature and studied the local structure using X-ray absorption fine structure spectroscopy (XAFS). They explicitly mentioned that the local structure of Bi in AgBiSeTe is more disordered in comparison to AgBiSe2 and AgBiTe2, although the antisite disorder prevails in all the alloys. In addition, when the radial distribution function is compared for the Bi L3-edge and Se K-edge for AgBiSe1−xTex (x = 0, 0.5, 1.5 and 2) using extended X-ray absorption fine structure spectroscopy (EXAFS), the analysis revealed that the Bi–Te bond crops up and intensifies with increasing Te content. However, when probed at the Se K-edge, all the peaks are well aligned for the first shell and correspond to Se–Bi or Se–Ag bonds.49 Using similar analogy, it can be interpreted that when probed at the Bi L3-edge in AgBiSeS, there will be pronounced Bi–S bond, whereas probing at the Se K-edge will show Se–Bi or Se–Ag bonds. Thus, the depiction of the schematic representation of the arrangement of atoms is shown in Fig. S3 (ESI†).
As aforementioned, unlike AgBiSe2, S residing at the Se (Fig. S3, ESI†) site will modify the bond length and bond angle, and thus, the bond heterogeneity will eventually contribute to the reduction of lattice thermal conductivity.
3.2. Electronic transport behaviour and electronic structure calculation
The temperature-dependent Seebeck coefficient (Fig. 4(a)) was recorded from 300 to 823 K, and the negative value for both pristine AgBiSeS and PbSe indicates n-type conduction (Fig. S4(a), ESI†). Interestingly, the Seebeck coefficient for AgBiSeS was very high, ∼−620 μV K−1 at 300 K, and it decreases with temperature to ∼−150 μV K−1 at 825 K. Jang et al. explained that in the ABX2 system, it is the B-site cation which dictates the conduction type. For Sb-based alloys, i.e., B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Sb, the alloy imparts p-type conduction, whereas for Bi-based alloys, i.e., B
Sb, the alloy imparts p-type conduction, whereas for Bi-based alloys, i.e., B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Bi, the alloys show n-type conduction. Thus, the n-type conduction in AgBiSeS is presumably due to the BiAg, i.e., Bi- on Ag antisite defect, and the enhanced Seebeck coefficient is due to the high effective mass (m*).50 Moreover, the decrease in Seebeck coefficient with increase in temperature can be ascribed to the effect of bipolar conduction, i.e., the presence of contrasting charge carriers or two different electron bands with varied effective mass (violation of single parabolic mode).38 In other words, calculation of the effective mass in n-type AgBiSeS is complex owing to non-parabolicity of the conduction band in the proximity of Fermi level. Nevertheless, in the interest of simplicity and to acquire a rough estimation of the effective mass of the carriers, the single parabolic band model was considered.
Bi, the alloys show n-type conduction. Thus, the n-type conduction in AgBiSeS is presumably due to the BiAg, i.e., Bi- on Ag antisite defect, and the enhanced Seebeck coefficient is due to the high effective mass (m*).50 Moreover, the decrease in Seebeck coefficient with increase in temperature can be ascribed to the effect of bipolar conduction, i.e., the presence of contrasting charge carriers or two different electron bands with varied effective mass (violation of single parabolic mode).38 In other words, calculation of the effective mass in n-type AgBiSeS is complex owing to non-parabolicity of the conduction band in the proximity of Fermi level. Nevertheless, in the interest of simplicity and to acquire a rough estimation of the effective mass of the carriers, the single parabolic band model was considered.
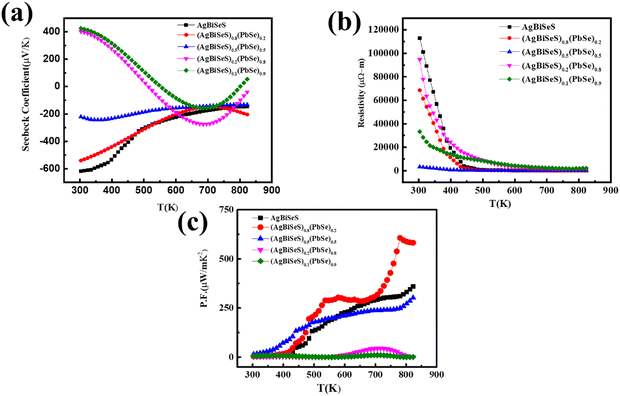 | ||
| Fig. 4 Temperature-dependent (a) Seebeck coefficient; (b) electrical resistivity and (c) power factor of the alloy system (AgBiSeS)1−x(PbSe)x. | ||
Moreover, to validate the assumption, m* was evaluated using the following equations utilizing experimental Seebeck coefficient, S and carrier density (nH) measured at 300 K (eqn (1)–(3)):
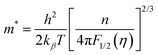 | (1) |
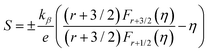 | (2) |
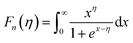 | (3) |
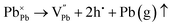 | (4) |
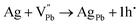 | (5) |
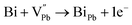 | (6) |
To further explain the unusual trend in the case of x ≥ 0.8, we simulated these materials. As the electronic structure of a material is known to have huge influence on the transport properties, we determined the electronic structure of pristine and alloyed PbSe. Although DFT is known to underestimate the band gap due to the approximations, it can provide a qualitative insight.53 Cubic PbSe showed a principal band gap of 0.16 eV at Γ point (Fig. 5(a)), which is comparable to the values in a previous report.54 The folding of L point onto the Γ point leads to the appearance of the principal band gap here, as is seen in previous reports of other thermoelectric materials where the same dimensions of supercell were used.55,56 A band offset of 0.23 eV is estimated between the valence sub-bands at Γ point and Z + δ point in Z → R direction, along with an offset of 0.46 eV between the conduction sub-bands, respectively. The valence and conduction sub-bands with heavy hole nature appear at Z + δ point in Z → R direction in the supercell used, due to folding of the Σ point of the primitive cell's Brillouin zone onto it.57,58 To further understand the contributions from various atoms, we studied the pDOS (Fig. 5(b)). Se ‘p’ orbitals form most of the valence band, while ‘p’ orbitals of Pb form the conduction band, with the Fermi level lying in the mid-gap area.
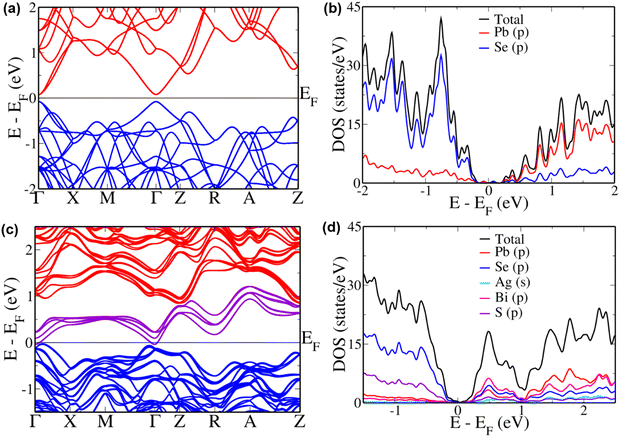 | ||
| Fig. 5 Electronic structures and pDOS of (a) and (b) PbSe and (c) and (d) AgBiSeS alloyed PbSe. Energies are shifted with respect to Fermi level, which is set to zero. | ||
The alloying of AgBiSeS in PbSe was simulated in a disordered way to mimic the experimental configuration (Fig. 5(c) and (d)). The electronic structure shows a drastic change, with the appearance of new sets of bands traversing across the band gap, touching the valence band at Γ point and conduction band at Z point. The conduction and valence band edges move 0.87 eV apart, with the hybrid band having a width of 1.25 eV. When we examine the pDOS for its content in this area, we see that the ‘p’ orbitals of Bi and Se hybridize, resulting in increased density of states in this region. Meanwhile, ‘p’ orbitals of Se and S show major contribution in the valence band region, and the ‘p’ orbitals of Pb show a considerable contribution 1 eV above the Fermi level. A previous report suggested that Bi does not exert much influence on the electronic structure or pDOS of PbSe, and the present work shows that in the presence of Ag and S, it greatly distorts the DOS.59 Hybridizing with the anionic orbitals of the host and distorting the DOS is a well-known feature exhibited by Bi in host systems like GeTe and SnTe.60,61 Although Ag is known to increase the band gap in the systems mentioned above, in the present scenario, it has little to no influence.62 We do see a cumulative convergence of the valence sub-bands in the alloyed composition leading to an increase in the number of contributing valleys to the p-type transport. For the improvement of n-type transport, we see the flattening of the conduction bands observed similar to the case of Cd-doped PbSe.54
The temperature-dependent electrical resistivity (ρ) of pristine AgBiSeS and those of the (AgBiSeS)1−x(PbSe)x composites are shown in Fig. 4(b). At ambient temperature (i.e. 300 K), the ρ value for AgBiSeS is found to be 112![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 792 μΩ m, which decreases to 59 μΩ m at 823 K—a reduction in resistivity by 99.9%. This typically indicates semiconductor behaviour, where the degenerate behaviour supersedes the intrinsic excitation and so prevails for all the new alloys formed by using AgBiSeS and PbSe. Moreover, the resistivity plot demonstrates that the resistivities of the entropy-engineered new multinary alloys are lower than that of pristine AgBiSeS. This is attributed to the fact that PbSe, being a degenerate semiconductor, injects electrons in the system and thus optimizes the carrier concentration. However, for x = 0.5, there is a competition between the formation of donor type charged antisite defects BiAg and AgPb. Consequently, in the presence of two donor atoms Bi and Ag, the resistivity drops down in comparison to other alloy systems. Nevertheless, pristine PbSe exhibits the behaviour of a degenerate semiconductor, where the resistivity increases with the increase in temperature (Fig. S4(b), ESI†). The calculated power factor for AgBiSeS and the (AgBiSeS)1−x(PbSe)x composites are shown in Fig. 4(c).
792 μΩ m, which decreases to 59 μΩ m at 823 K—a reduction in resistivity by 99.9%. This typically indicates semiconductor behaviour, where the degenerate behaviour supersedes the intrinsic excitation and so prevails for all the new alloys formed by using AgBiSeS and PbSe. Moreover, the resistivity plot demonstrates that the resistivities of the entropy-engineered new multinary alloys are lower than that of pristine AgBiSeS. This is attributed to the fact that PbSe, being a degenerate semiconductor, injects electrons in the system and thus optimizes the carrier concentration. However, for x = 0.5, there is a competition between the formation of donor type charged antisite defects BiAg and AgPb. Consequently, in the presence of two donor atoms Bi and Ag, the resistivity drops down in comparison to other alloy systems. Nevertheless, pristine PbSe exhibits the behaviour of a degenerate semiconductor, where the resistivity increases with the increase in temperature (Fig. S4(b), ESI†). The calculated power factor for AgBiSeS and the (AgBiSeS)1−x(PbSe)x composites are shown in Fig. 4(c).
3.3. Temperature-dependent thermal transport behaviour
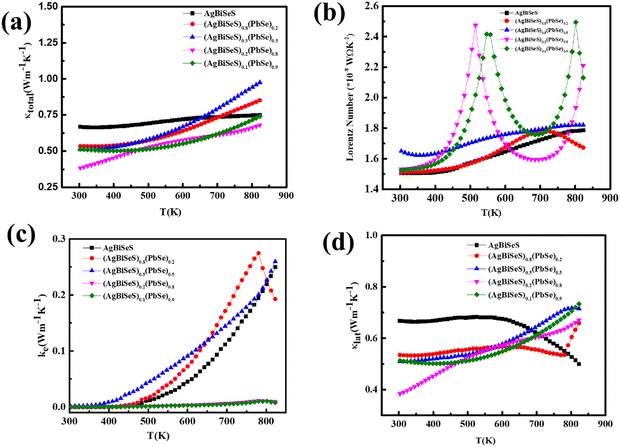
Considering the temperature-dependent thermal transport behaviour, the total thermal conductivities (κ) of the pristine AgBiSeS and the solid solutions (AgBiSeS)1−x(PbSe)x, respectively are shown in Fig. 6(a). (Temperature-dependent thermal diffusivity plots of pristine AgBiSeS, PbSe and solid solution of (AgBiSeS)1−x(PbSe)x are shown in Fig. S5, ESI†). Pan et al. reported that AgBiSe2 has a κ value of 0.65 W m−1 K−1,33 whereas Hu et al. reported a similar composition exhibited the κ of 0.55 W m−1 K−1.40 The total thermal conductivities of the alloys remain significantly flat, demonstrating glass-like behaviour. In the present study, pristine AgBiSeS displays an ultra-low total thermal conductivity of 0.69–0.74 W m−1 K−1 in the temperature regime of 300–823 K, whereas PbSe exhibits values ranging from 3.16–1.89 W m−1 K−1 (Fig. S4(d), ESI†). It is noteworthy that AgBiSeS as well as the composites exhibit ultra-low total thermal conductivity over the entire temperature range. Primarily, the total thermal conductivity is constituted by the contributions from the lattice and electronic thermal conductivity. In principle, the lattice thermal conductivity (κlat) is estimated by directly subtracting the electronic contribution (κele) from the total thermal conductivity as κtotal = κlat + κele. The electronic contribution κele, can be estimated using the Widemann Franz Law, κele = LσT, where L is the Lorentz number, σ is the electrical conductivity and T is the temperature. The common practice in thermoelectrics is to consider L = 2.44 × 10−8 W Ω K−2 (degenerate limit). Moreover, the Widemann Franz Law is valid for degenerate semiconductors and metals. Thus, utmost care should be taken while estimating κele, and so, L was obtained based on the thermopower measured. Kim et al. explicitly mentioned that remarkable divergence from the degenerate limit (∼40% or greater for Kane bands) are known to arise for non-degenerate semiconductors, and eventually L congregates to 1.5 × 10−8 W Ω K−2 (in the case of acoustic phonon scattering). In this regard, L was estimated using the equation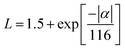 .63 The L estimated using this eqn. for AgBiSeS and (AgBiSeS)1−x(PbSe)x (x = 0.2, 0.5, 0.8, 0.1) alloy systems was found to be ∼1.5 × 10−8 W Ω K−2. However, for the degenerate semiconductor PbSe, L was estimated to be ∼2.44 × 10−8 W Ω K−2 (Fig. S3(e), ESI†). The L vs. T plot for the compositions under study and the calculated κelevs. T are shown in Fig. 6(b) and (c), respectively.
.63 The L estimated using this eqn. for AgBiSeS and (AgBiSeS)1−x(PbSe)x (x = 0.2, 0.5, 0.8, 0.1) alloy systems was found to be ∼1.5 × 10−8 W Ω K−2. However, for the degenerate semiconductor PbSe, L was estimated to be ∼2.44 × 10−8 W Ω K−2 (Fig. S3(e), ESI†). The L vs. T plot for the compositions under study and the calculated κelevs. T are shown in Fig. 6(b) and (c), respectively.
Nevertheless, it is the lattice thermal conductivity which plays the key role in the total thermal conductivity of the alloy without PbSe. When calculated, it shows that without PbSe, where the electronic contribution to κtotal is ∼52%, (Fig. S4(d), ESI†), AgBiSeS imparts only 0.006% at RT. On increasing the concentration of PbSe (x = 0.2) in the alloy, the electronic contribution increases marginally; however, at x = 0.5, the electronic contribution to κtotal is ∼0.3%. For the compositions x = 0.8 and 0.9, electronic thermal conductivity is almost temperature independent throughout the temperature range. Fig. 6(d) displays the lattice thermal conductivity as a function of T. Previous reports pertaining to I–V–VI2 compounds demonstrate that highly symmetrical rock-salt cubic structures exhibit low κlat in comparison to other crystal structures, which can be correlated to the intense anharmonicity appearing from the existence of the lone pair electron.64 Nielsen et al. demonstrated using DFT calculations that the rock salt structure of the I–V–VI2 family develops soft phonon modes owing to the intense hybridization and repulsion among the lone-pair electrons of the cations (group V) and the anions (group VI) having valence p orbitals.65 Consequently, the presence of stereochemically active non-bonded electrons or lone pairs in the sp-hybridized bonding orbitals cause the occurrence of high Grüneisen parameter, which causes amplified anharmonicity and subsequently low intrinsic lattice thermal conductivity.66 This is analogous to AgSbTe2, where the valence configuration of Sb (i.e. 5s25p3, the 5s orbital being significantly low in energy compared to the 5p orbital) fails to undergo hybridization and thus prevents the formation of sp3 bonds among Sb and Te. Thus, the crystal co-ordination swaps from tetrahedral geometry (AgInTe2) to octahedral geometry (AgSbTe2), and the group V cation exhibits +3 oxidation state and develops polar covalent bond with the group VI anion (chalcogens) by sharing the p-electrons. However, the s2 electrons remain isolated as non-bonding electrons or lone pairs. Eventually, it couples or gets repelled from the valence bands of the d-orbital of noble metals (such as Ag) and the p-orbitals of chalcogen and undergoes deformation (s-orbital of group V) by lattice vibrations, causing strong anharmonicity. In a similar group (Vb), Bi exhibits a large atomic radius (=143 pm) in comparison to Sb (=133 pm),67 and consequently, it can be assumed or is rather reasonable that the electron cloud encasing the Bi atoms would be higher than Sb. This infers that non-bonded or lone-pair electrons on Bi probably cause more disproportionate electron density, leading to enhanced lattice vibrations. Hence, it can be speculated that pristine AgBiSeS, without PbSe, exhibits ultra-low lattice thermal conductivity owing to enhanced bond anharmonicity related to Bi3+ ion and is analogous to the aforementioned Sb3+ ion.
3.4. Microstructural analysis
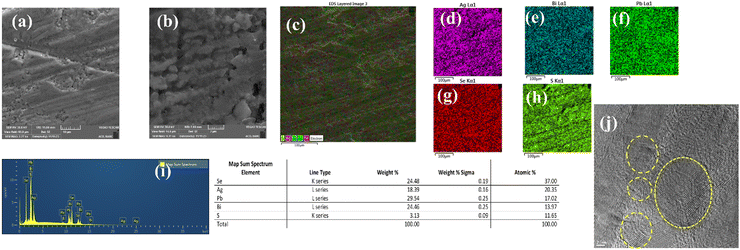
Scanning electron micrographs of the (AgBiSeS)0.5(PbSe)0.5 are depicted in Fig. 7(a) and (b). The image shows the sample is highly dense. EDS mapping of the randomly selected region corroborates the homogeneous distribution of the constituent elements and is devoid of any precipitation or phase segregation Fig. 7(c)–(i). (The SEM micrographs along with EDS mapping of other compositions are shown in Fig. S6, ESI†). However, further investigation of the microstructure using high-resolution transmission electron microscopy (HRTEM) depicts the presence of defects at various length scales (majority being point defects due to atomic mass mismatch, Fig. 7(j)). Thus, in spite of the subdued effect of the stereochemical activity of the lone pair on Bi owing to the increase of the chemical space due to entropy engineering, the eventual generation of point defects in conjunction with lattice anharmonicity scatters the phonons extensively and thus reduces the lattice thermal conductivity drastically.Consequently, besides being intrinsically a low-thermal-conductivity alloy, the presence of all-scale hierarchical architecture further slashes the thermal conductivity.
3.5. ZT optimisation
Interestingly, the intrinsic low lattice thermal conductivity attributed to the stereochemical activity of the lone pair on Bi (group Vb) and the large Grüneisen parameter with intentional architecturing in the dimension of the defects, along with entropy-driven structural stabilization, has led to a peak ZT of ∼0.6 at 780 K (Fig. 8(a)) and an average ZT value of 0.3 for the alloy (AgBiSeS)0.5(PbSe)0.5 within 300–823 K (Fig. 8(b)). To ascertain the repeatability and reproducibility of the (AgBiSeS)0.5(PbSe)0.5 composite, samples with nomenclature S1–S6 were measured, and the plot is given in Fig. S7 (ESI†).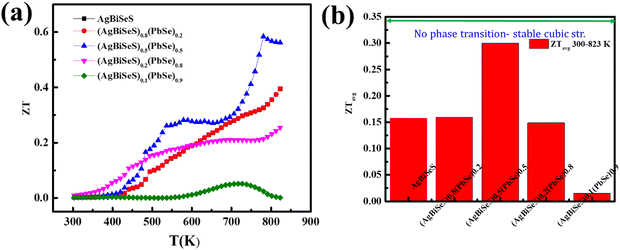 | ||
| Fig. 8 (a) ZT vs. T plot of the alloy system and (b) ZTavgvs. composition in the temperature range of 300–823 K. | ||
4. Conclusion
In conclusion, the stabilized n-type cubic phase of AgBiSeS was synthesized with utmost care, utilizing the concept of phase boundary mapping, as the practical application of thermoelectricity has no space for polymorphism in the operating temperature regime. This excellent dynamical stability was possible owing to the substitution of Se by the highly electronegative S atom, which aids in chemical bond strengthening. This highly susceptible cubic AgBiSeS was further stabilized by entropy-driven solid solution alloying with PbSe. The various analytical techniques corroborate the absence of phase transformation and support the compound as an excellent alternative for an n-type alloy in the mid-temperature (300–823) K regime. Ultra-low lattice thermal conductivity was achieved due to high Grüneisen parameter and bond anharmonicity, in addition to all-scale hierarchical architecturing. Thus, entropy engineering has led to a highly symmetrical cubic structure with diminished thermal conductivity, paving a new path for the design and development of new thermoelectric materials.5. Author contributions
Ranita Basu: conceptualization, methodology, funding acquisition, investigation, resources, supervision, writing – review and editing; U. Sandhya Shenoy and D. Krishna Bhat: DFT analysis, validation and writing draft, funding acquisition; Ankita Pathak – XPS analysis; Shweta Singh and Hirakendu Basu: morphological and compositional analysis; P. Jha: Raman spectroscopy measurements, and Ajay Singh: Resources.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There is no conflict of interest.Acknowledgements
The author (USS) acknowledges the grant from Science and Engineering Research Board, Department of Science and Technology, Government of India under the SRS scheme.References
- H. J. Goldsmid and G. S. Nolas, A review of the new thermoelectric materials, Proceedings ICT2001, 20 International Conference on Thermoelectrics (Cat. No. 01TH8589), Beijing, China, 2001, pp. 1–6 Search PubMed.
- W. Liu, Q. Jie, H. Seok Kim and Z. Ren, Current progress and future challenges in thermoelectric power generation: from materials to devices, Acta Mater., 2015, 87, 357–376 CrossRef CAS.
- D. K. Aswal, R. Basu and A. Singh, Key issues in development of thermoelectric power generators: high figure-of-merit materials and their highly conducting interfaces with metallic interconnects, Energy Convers. Manage., 2016, 114, 50–67 CrossRef.
- X.-L. Shi, J. Zou and Z.-G. Chen, Advanced Thermoelectric Design: From Materials and Structures to Devices, Chem. Rev., 2020, 120, 7399–7515 CrossRef CAS PubMed.
- R. Basu, Thermoelectric Modules: Key Issues in Architectural Design and Contact Optimization, ChemNanoMat, 2023, 9, 1–20 CrossRef.
- Y. Tian, G.-K. Ren, Z. Wei, Z. Zheng, S. Deng, L. Ma, Y. Li, Z. Zhou, X. Chen, Y. Shi and Y.-H. Lin, Advances of thermoelectric power generation for room temperature: applications, devices, materials and beyond, Renewable Energy, 2024, 226, 120443 CrossRef.
- J. Li, Q. Xiang, R. Ze, M. Ma, S. Wang, Q. Xie and Y. Xiang, Thermal and electrical analysis of SiGe thermoelectric unicouple filled with thermal insulation materials, Appl. Therm. Eng., 2018, 134, 266–274 CrossRef CAS.
- R. Basu and A. Singh, High temperature Si–Ge alloy towards thermoelectric applications: a comprehensive review, Mater. Today Phys., 2021, 21, 100468 CrossRef CAS.
- C. Xiao, Z. Li, K. Li, P. Huang and Y. Xie, Decoupling Interrelated Parameters for Designing High Performance Thermoelectric Materials, Acc. Chem. Res., 2014, 47, 1287–1295 CrossRef CAS PubMed.
- Y. Pei, H. Wang and G. J. Snyder, Band Engineering of Thermoelectric Materials, Adv. Mater., 2012, 24, 6125–6135 CrossRef CAS PubMed.
- W. Kim, Strategies for engineering phonon transport in thermoelectrics, J. Mater. Chem. C, 2015, 3, 10336–10348 RSC.
- A. Seif, W. DeGottardi, K. Esfarjani and M. Hafezi, Thermal management and non-reciprocal control of phonon flow via optomechanics, Nat. Commun., 2018, 9, 1207 CrossRef PubMed.
- Q. Tang, B. Jiang, K. Wang, W. Wang, B. Jia, T. Ding, Z. Huang, Y. Lin and J. He, High-entropy thermoelectric materials, Joule, 2024, 8, 1641–1666 CrossRef CAS.
- B. Jiang, Y. Yu, H. Chen, J. Cui, X. Liu, L. Xie and J. He, Entropy engineering promotes thermoelectric performance in p-type chalcogenides, Nat. Commun., 2021, 12, 3234 CrossRef CAS PubMed.
- R. Basu and A. Singh, A comprehensive review of entropy engineered GeTe: an antidote to phase transformation, Energy Adv., 2024, 3, 689–711 RSC.
- P.-C. Wei, C.-N. Liao, H.-J. Wu, D. Yang, J. He, G. V. Biesold-McGee, S. Liang, W.-T. Yen, X. Tang, J.-W. Yeh, Z. Lin and J.-H. He, Thermodynamic Routes to Ultralow Thermal Conductivity and High Thermoelectric Performance, Adv. Mater., 2020, 32, 1906457 CrossRef CAS PubMed.
- R. K. Pittkowski, C. M. Clausen, Q. Chen, D. Stoian, W. van Beek, J. Bucher, R. L. Welten, N. Schlegel, J. K. Mathiesen, T. M. Nielsen, J. Du, A. W. Rosenkranz, E. D. Bojesen, J. Rossmeisl, K. M. O. Jensen and M. Arenz, The more the better: on the formation of single-phase high entropy alloy nanoparticles as catalysts for the oxygen reduction reaction, EES Catal., 2023, 1, 950–960 RSC.
- A. D. LaLonde, Y. Pei, H. Wang and G. Jeffrey Snyder, Lead telluride alloy thermoelectrics, Mater. Today, 2011, 14, 526–532 CrossRef CAS.
- P. Kumar Sharma, T. D. Senguttuvan, V. Kumar Sharma and S. Chaudhary, Revisiting the thermoelectric properties of lead telluride, Mater. Today Energy, 2021, 21, 100713 CrossRef.
- Y. Pei, N. A. Heinz, A. LaLonde and G. Jeffrey Snyder, Combination of large nanostructures and complex band structure for high performance thermoelectric lead telluride, Energy Environ. Sci., 2011, 4, 3640–3645 RSC.
- R. Moshwan, L. Yang, J. Zou and Z.-G. Chen, Eco-Friendly SnTe Thermoelectric Materials: Progress and Future Challenges, Adv. Funct. Mater., 2017, 27, 1703278 CrossRef.
- Y. Zhang, J. Sun, J. Shuai, X. Tang and G. Tan, Lead-free SnTe-based compounds as advanced thermoelectrics, Mater. Today Phys., 2021, 19, 100405 CrossRef CAS.
- S. Ahmad, A. Singh, S. Bhattacharya, M. Navaneethan, R. Basu, R. Bhatt, P. Sarkar, K. N. Meshram, K. P. Muthe, S. Vitta and D. K. Aswal, Remarkable improvement of thermoelectric figure-of-merit in SnTe through in situ-created Te nanoinclusions, ACS Appl. Energy Mater., 2020, 3, 7113–7120 CrossRef CAS.
- S. Mandava, R. Basu, B. Khasimsaheb, S. Bathula, A. Singh and S. Neeleshwar, A synergistic approach to achieving the high thermoelectric performance of La-doped SnTe using resonance state and partial band convergence, Mater. Adv., 2021, 2, 4352–4361 RSC.
- G. Tan, S. Hao, S. Cai, T. P. Bailey, Z. Luo, I. Hadar, C. Uher, V. P. Dravid, C. Wolverton and M. G. Kanatzidis, All-Scale Hierarchically Structured p-Type PbSe Alloys with High Thermoelectric Performance Enabled by Improved Band Degeneracy, J. Am. Chem. Soc., 2019, 141, 4480–4486 CrossRef CAS PubMed.
- Y. Lee, S.-H. Lo, C. Chen, H. Sun, D.-Y. Chung, T. C. Chasapis, C. Uher, V. P. Dravid and M. G. Kanatzidis, Contrasting role of antimony and bismuth dopants on the thermoelectric performance of lead selenide, Nat. Commun., 2014, 5, 3640 CrossRef CAS PubMed.
- Y. Wu, P. Qiu, Y. Yu, Y. Xiong, T. Deng, O. Cojocaru-Mirédin, M. Wuttig, X. Shi and L. Chen, High-performance and stable AgSbTe2-based thermoelectric materials for near room temperature applications, J. Materiomics, 2022, 8, 1095–1103 CrossRef.
- T. Ghosh, S. Roychowdhury, M. Dutta and K. Biswas, High-Performance Thermoelectric Energy Conversion: A Tale of Atomic Ordering in AgSbTe2, ACS Energy Lett., 2021, 6, 2825–2837 CrossRef CAS.
- S. Roychowdhury, T. Ghosh, R. Arora, M. Samanta, L. Xie, N. Kumar Singh, A. Soni, J. He, U. V. Waghmare and K. Biswas, Enhanced atomic ordering leads to high thermoelectric performance in AgSbTe2, Science, 2021, 371, 722–727 CrossRef CAS PubMed.
- Y. Zhang, Z. Li, S. Singh, A. Nozariasbmarz, W. Li, A. Genç, Y. Xia, L. Zheng, S. H. Lee, S. K. Karan, G. K. Goyal, N. Liu, S. M. Mohan, Z. Mao, A. Cabot, C. Wolverton, B. Poudel and S. Priya, Defect-Engineering-Stabilized AgSbTe2 with High Thermoelectric Performance, Adv. Mater., 2023, 35, 2208994 CrossRef CAS PubMed.
- R. Freer and A. V. Powell, Realising the potential of thermoelectric technology: a Roadmap, J. Mater. Chem. C, 2020, 8, 441–463 RSC.
- S. N. Guin, V. Srihari and K. Biswas, Promising thermoelectric performance in n-type AgBiSe2: effect of aliovalent anion doping, J. Mater. Chem. A, 2015, 3, 648–655 RSC.
- L. Pan, D. Berardan and N. Dragoe, High Thermoelectric Properties of n-Type AgBiSe2, J. Am. Chem. Soc., 2013, 135, 4914 CrossRef CAS PubMed.
- T. Deng, J. Recatala-Gomez, M. Ohnishi, D. V. Maheswar Repaka, P. Kumar, A. Suwardi, A. Abutaha, I. Nandhakumar, K. Biswas, M. B. Sullivan, G. Wu, J. Shiomi, S.-W. Yang and K. Hippalgaonkar, Electronic transport descriptors for the rapid screening of thermoelectric materials, Mater. Horiz., 2021, 8, 2463–2474 RSC.
- T. Zhao, H. Zhu, B. Zhang, S. Zheng, N. Li, G. Wang, G. Wang, X. Lu and X. Zhou, High thermoelectric performance of tellurium-free n-type AgBi1−xSbxSe2 with stable cubic structure enabled by entropy engineering, Acta Mater., 2021, 220, 117291 CrossRef CAS.
- N. Li, G. Wang, Z. Zhou, G. Wang, G. Han, X. Lu and X. Zhou, IV-VI/I–V–VI2 Thermoelectrics: Recent Progress and Perspectives, Adv. Funct. Mater., 2024, 2405158 CrossRef.
- X. Wu, Y. Lin, C. Liu, Y. Wang, H. Li, B. Ge and W. Liu, A high performance eco-friendly MgAgSb-based thermoelectric power generation device near phase transition temperatures, Energy Environ. Sci., 2024, 17, 2879–2887 RSC.
- Y.-L. Pei, H. Wu, J. Sui, J. Li, D. Berardan, C. Barreteau, L. Pan, N. Dragoe, W.-S. Liu, J. He and L.-D. Zhao, High thermoelectric performance in n-type BiAgSeS due to intrinsically low thermal conductivity, Energy Environ. Sci., 2013, 6, 1750–1755 RSC.
- Q. Xia, P. Ying, Z. Han, X. Li, L. Xu and J. Cui, Chemical Composition Engineering Leading to the Significant Improvement in the Thermoelectric Performance of AgBiSe2-Based n-Type Solid Solutions, ACS Appl. Energy Mater., 2021, 4, 2899–2907 CrossRef CAS.
- Y. Hu, S. Yuan, H. Huo, J. Xing, K. Guo, X. Yang, J. Luo, G.-H. Rao and J.-T. Zhao, Stabilized cubic phase BiAgSe2−xSx with excellent thermoelectric properties via phase boundary engineering, J. Mater. Chem. C, 2021, 9, 6766 RSC.
- H. Zhu, T. Zhao, B. Zhang, Z. An, S. Mao, G. Wang, X. Han, X. Lu, J. Zhang and X. Zho, Entropy Engineered Cubic n-Type AgBiSe2 Alloy with High Thermoelectric Performance in Fully Extended Operating Temperature Range, Adv. Energy Mater., 2020, 11, 2003304 CrossRef.
- C. A. Gearhart, Einstein before 1905: the early papers on statistical mechanics, Am. J. Phys., 1990, 58, 468–480 CrossRef.
- C. Xiao, X. Qin, J. Zhang, R. An, J. Xu, K. Li, B. Cao, J. Yang, B. Ye and Y. Xie, High thermoelectric and reversible p–n–p conduction type switching integrated in dimetal chalcogenide, J. Am. Chem. Soc., 2012, 134, 18460–18465 CrossRef CAS PubMed.
- Y. Yin, R. M. Rioux, C. K. Erdonmez, S. Hughes, G. A. Somorjai and A. Paul Alivisatos, Formation of Hollow Nanocrystals Through the Nanoscale Kirkendall Effect, Science, 2004, 304, 711–714 CrossRef CAS PubMed.
- W.-T. Chang, S. Sharma, J.-H. Liao, S. Kahlal, Y.-C. Liu, M.-H. Chiang, J.-Y. Saillard and C. W. Liu, Heteroatom-Doping Increases Cluster Nuclearity: From an [Ag20] to an [Au3Ag18] Core, Chem. – Eur. J., 2018, 24, 14352 CrossRef CAS PubMed.
- A. Arulraj, N. Ilayaraja, V. Rajeshkumar and M. Ramesh, Direct Synthesis of cubic shaped Ag2S on Ni mesh as Binder-free Electrodes for Energy Storage Applications, Sci. Rep., 2019, 9, 10108 CrossRef PubMed.
- S. Gautam, V. Aggarwal, B. Singh, V. P. S. Awana, R. Ganesan and S. S. Kushvaha, Signature of weak-antilocalization in sputtered topological insulator Bi2Se3 thin films with varying thickness, Sci. Rep., 2022, 12, 9770 CrossRef CAS PubMed.
- B. Weng, X. Zhang, N. Zhang, Z.-R. Tang and Y.-J. Xu, Two-Dimensional MoS2 Nanosheet-Coated Bi2S3 Discoids: Synthesis, Formation Mechanism, and Photocatalytic Application, Langmuir, 2015, 31, 4314–4322 CrossRef CAS PubMed.
- W. Huang, Y. Zhu, Y. Liu, S. Tao, C. Yang, Q. Diao, Z. Hong, H. Han, L. Liue and W. Xu, Long-range ordering and local structural disordering of BiAgSe2 and BiAgSeTe thermoelectrics, Phys. Chem. Chem. Phys., 2021, 23, 24328 RSC.
- H. Jang, M. Y. Toriyama, S. Abbey, B. Frimpong, J. P. Male, G. Jeffrey Snyder, Y. Sik Jung and M.-W. Oh, Suppressing Charged Cation Antisites via Se Vapor Annealing Enables p-Type Dopability in AgBiSe2–SnSe Thermoelectrics, Adv. Mater., 2022, 34, 2204132 CrossRef CAS PubMed.
- R. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., 1976, 32, 751 CrossRef.
- Q. Tian, P. Li, L. Zhang, Y. Tian, L.-J. Yin, L. Zhang and Z. Qin, Native Pb vacancy defects induced p-type characteristic in epitaxial monolayer PbSe, Appl. Phys. Lett., 2023, 123, 051903 CrossRef CAS.
- U. S. Shenoy and D. K. Bhat, Electronic Structure Modulation of Pb0.6Sn0.4Te via Zinc Doping and Its Effect on the Thermoelectric Properties, J. Alloys Compd., 2021, 872, 159681 CrossRef CAS.
- X. Qian, H. Wu, D. Wang, Y. Zhang, J. Wang, G. Wang, L. Zheng, S. J. Pennycook and L. D. Zhao, Synergistically optimizing interdependent thermoelectric parameters of n-type PbSe through alloying CdSe, Energy Environ. Sci., 2019, 12, 1969–1978 RSC.
- D. K. Bhat and U. S. Shenoy, Mg/Ca Doping Ameliorates the Thermoelectrics Properties of GeTe: Influence of Electronic Structure Engineering, J. Alloys Compd., 2020, 834, 155989 CrossRef.
- U. S. Shenoy and D. K. Bhat, Vanadium: A Protean Dopant in SnTe for Augmenting its Thermoelectric Performance, ACS Sustainable Chem. Eng., 2021, 9, 13033–13038 CrossRef CAS.
- U. S. Shenoy and D. K. Bhat, Towards achieving an ideal convergence of light and heavy electron conduction bands in SnTe: insights into copper doping, J. Alloys Compd., 2024, 1, 100001 CrossRef.
- U. S. Shenoy and D. K. Bhat, Tuning the Electronic Structure of Rhombohedral and Cubic GeTe for Thermoelectric Application: Influence of Molybdenum Doping, J. Phys. Chem. Solids, 2024, 188, 111943 CrossRef CAS.
- M. Hong, W. Lyu, Y. Wang, J. Zou and Z. G. Chen, Establishing the Golden Range of Seebeck Coefficient for Maximizing Thermoelectric Performance, J. Am. Chem. Soc., 2020, 142, 2672–2681 CrossRef CAS PubMed.
- U. S. Shenoy and D. K. Bhat, Probing of Bi doped GeTe thermoelectrics leads to revelation of resonant states, J. Alloys Compd., 2022, 921, 165965 CrossRef CAS.
- U. S. Shenoy and D. K. Bhat, Improving ZT of SnTe by Electronic Structure Engineering: Unusual Behaviour of Bi Dopant in the presence of Pb as a Co-dopant, Mater. Adv., 2021, 2, 6267–6271 RSC.
- U. S. Shenoy and D. K. Bhat, Selective Co-doping Improves the Thermoelectric Performance of SnTe: An Outcome of Electronic Structure Engineering, J. Alloys Compd., 2021, 892, 162221 CrossRef.
- H.-S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. Jeffrey Snyder, Characterization of Lorenz number with Seebeck coefficient measurement, APL Mater., 2015, 3, 041506 CrossRef.
- M. K. Jana, K. Pal, U. V. Waghmare and K. Biswas, The Origin of Ultralow Thermal Conductivity in InTe: Lone-Pair-Induced Anharmonic Rattling, Angew. Chem., Int. Ed., 2016, 55, 7792 CrossRef CAS PubMed.
- M. D. Nielsen, V. Ozolins and J. P. Heremans, Lone pair electrons minimize lattice thermal conductivity, Energy Environ. Sci., 2013, 6, 570–578 RSC.
- R. Basu, C. Nayak, R. Kumar, D. Bhattacharyya, S. N. Jha and A. Singh, Potency of Extended X-ray Absorption Fine Structure Spectroscopy toward the Determination of Individual Bond Grüneisen Parameter for High Thermoelectric Performance, ACS Appl. Energy Mater., 2023, 6, 2981–2988 CrossRef CAS.
- https://periodictable.com/Properties/A/AtomicRadius.v.html .
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00549j |
| This journal is © The Royal Society of Chemistry 2024 |