Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coal fly ash-ZIF composites for enhanced and stable carbon capture—an in-depth study†
Ramadurgam
Aniruddha
a,
Satyapaul A
Singh
 a,
Benjaram M
Reddy
a,
Benjaram M
Reddy
 b,
Akula
Venugopal
b,
Akula
Venugopal
 c and
Inkollu
Sreedhar
c and
Inkollu
Sreedhar
 *a
*a
aDepartment of Chemical Engineering, BITS Pilani Hyderabad Campus, Hyderabad, India. E-mail: isreedhar@hyderabad.bits-pilani.ac.in; Fax: +91 4066303998; Tel: +91 4066303512
bDepartment of Chemistry, BITS Pilani Hyderabad Campus, Hyderabad, India
cI&PC Division, IICT Tarnaka, Hyderabad, India
First published on 8th October 2024
Abstract
Composites possess significant potential to mitigate the shortcomings of their individual components, offering a measure of reinforcement. In this study, composites based on CFA based Na-A and ZIF-8 were synthesized and subjected to CO2 adsorption tests. The composites were identified as a class of ZIF-8@Na-A. These composites retained the physical attributes of their parent materials. Notably, the CO2 uptake performance of ZIF-8@Na-A (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
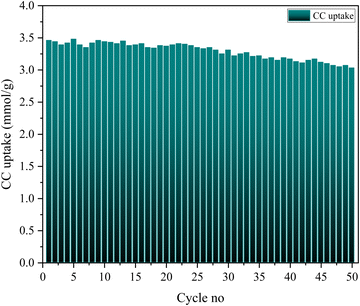
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) was particularly high, recording values around 3.48 mmol g−1 at 298 K and 1 bar. Hierarchical three step process optimization has been done to achieve the highest carbon capture and stability. Different synthesis protocols have been compared too. TGA studies have been used to validate the amine loading on the adsorbent. Among the factors influencing CO2 uptake, temperature and pressure emerged as the most influential, while the time of carbonation exhibited minimal impact. Kinetic analysis revealed that the optimized adsorbent adhered to Avrami kinetics, displaying high R2 values of 0.994. The Sips adsorption model demonstrated the best fit for explaining the adsorption behavior of the adsorbents. The average heat of adsorption for ZIF-8@Na-A was measured at −11 kJ mol−1. During a 50-cycle stability assessment, the adsorbent exhibited robust performance, retaining approximately 92% of its initial CO2 uptake. However, a subtle change in appearance was observed in the ZIF-8@Na-A adsorbent, which turned slightly pale yellowish after the completion of 50 cycles.
5) was particularly high, recording values around 3.48 mmol g−1 at 298 K and 1 bar. Hierarchical three step process optimization has been done to achieve the highest carbon capture and stability. Different synthesis protocols have been compared too. TGA studies have been used to validate the amine loading on the adsorbent. Among the factors influencing CO2 uptake, temperature and pressure emerged as the most influential, while the time of carbonation exhibited minimal impact. Kinetic analysis revealed that the optimized adsorbent adhered to Avrami kinetics, displaying high R2 values of 0.994. The Sips adsorption model demonstrated the best fit for explaining the adsorption behavior of the adsorbents. The average heat of adsorption for ZIF-8@Na-A was measured at −11 kJ mol−1. During a 50-cycle stability assessment, the adsorbent exhibited robust performance, retaining approximately 92% of its initial CO2 uptake. However, a subtle change in appearance was observed in the ZIF-8@Na-A adsorbent, which turned slightly pale yellowish after the completion of 50 cycles.
1. Introduction
Metal organic frameworks (MOFs) have emerged as a pivotal class of materials in the field of carbon capture over the past two decades. This surge in their significance could be attributed to their remarkable characteristics, including but not limited to their expansive surface area (500–2000 m2 g−1), versatile functionality, modifiable pore structure, exceptional pore volumes (0.3 cc g−1 to 1.5 cc g−1), presence of accessible metal sites, and the ability to tailor their morphology.1 In order to address certain limitations associated with metal–organic frameworks (MOFs), including thermal instability, structural degradation in the presence of moisture, and limited cyclic regeneration capability, zeolitic imidazolate frameworks (ZIFs), a specific subclass of MOFs, have emerged as a viable alternative. ZIFs2 have garnered significant attention in the scientific community due to their remarkable thermal stability, notable hydrophobicity, and exceptional physico-chemical characteristics.Composites have recently garnered significant attention within the realm of adsorption and catalysis. Composite materials are meticulously fabricated with the objective of synergistically amalgamating the inherent strengths of distinct classes, thereby effectively concealing any inherent weaknesses that may be present. The synthesis of a composite material consisting of metal–organic framework (MOF) and graphene oxide was done by Wang and group3 in their investigation on the adsorption of carbon dioxide (CO2). The composite material was designated as the Mg/DOBDC MOF@GO composite, with different ratios being investigated. The group of composites exhibited remarkable carbon capture (CC) efficiency by synergistically leveraging the substantial surface area of the metal–organic framework (MOF) and the strong affinity of graphene oxide towards CO2. The investigation conducted by Chang et al.4 focused on the examination of composites possessing a dual nature, consisting of magnesium oxide (MgO) and zinc oxide (ZnO), incorporated within zeolitic imidazolate framework-8 (ZIF-8). The composites exhibited remarkable carbon capture (CC) uptake values (1.3 mmol g−1) in comparison to ZIF-8 in its pure form (0.81 mmol g−1), while simultaneously preserving the favorable morphological characteristics of ZIF-8. In the study conducted by Tari and team,5 an innovative composite material named Cu-BDC/MCM-41 was synthesized, combining a stable metal–organic framework (MOF) with MCM-41. The composite material presented in this study exhibits a unique amalgamation of mesoporous and microporous structures, resulting in a significant enhancement of CO2 adsorption capabilities (7.00 mmol g−1) compared to its constituent materials. In our recent investigation,6 the focus was directed towards the exploration of coal fly ash as a potential resource for the production of value-added materials. Specifically, a composite material (CC uptake of 2.83 mmol g−1) comprising coal fly ash zeolite and ZIF-8 was synthesized and subsequently employed for the purpose of investigating its efficacy in CO2 adsorption. The corresponding investigation yielded noteworthy findings regarding the synergistic effect of combining zeolite and ZIF-8 on the uptake of carbon dioxide (CC). The current investigation represents a seamless extension of prior research endeavors, with a primary focus on elucidating the process of synthesizing and employing innovative composite materials.
Coal fly ash (CFA) is a widely encountered and potentially consequential byproduct arising from diverse industrial operations. The potential of this substance as a precursor in the advancement of commercial adsorbents tailored for the purification of gaseous pollutants has been extensively investigated by researchers.7 The appeal of CFA resides in its broad accessibility and cost-efficiency, both of which serve as crucial factors in facilitating comprehensive explorations of its extensive applicability in sorbent synthesis.8 A range of compositions are available for use as adsorbents made from coal fly ash.9 The diverse assortment of artificially produced adsorbents serves as a compelling testament to the multifaceted characteristics exhibited by coal fly ash.
The current investigation expands upon previous scholarly endeavors by exploring the synthesis and utilization of innovative composite materials. The present study encompasses the fabrication of composite structures, wherein ZIF-8 and Na-A are combined and subsequently subjected to tetraethylenepentaamine (TEPA) modification. Engineering dual-textured composites was the reasoning for the combination of Na-A and ZIF-8. Zeolitic imidazolate frameworks, in general, have been found to possess predominantly microporous properties, which make them highly effective in rapidly adsorbing CO2, as demonstrated by Pokhrel.10 Their high surface area and microporosity also make them potentially suitable candidates for amine modification. Materials with high specific surface area, such as ZIFs and MOFs, hold significant potential as hosts for amines due to their extensive porosity and structural diversity. However, the inherent microporous nature of these materials presents distinct challenges when it comes to amine loading. The narrow and confined pore structures typical of these materials can make it difficult to achieve uniform amine distribution throughout the porous network. This issue is exacerbated by the fact that, in many cases, the amine molecules must navigate through intricate pathways within the micropores, which can lead to incomplete or uneven loading. Moreover, the process of impregnating these materials with amines often requires prolonged interaction times. The slow diffusion of amines into the microporous structure means that achieving an optimal loading level is typically a time-intensive process. This extended duration is crucial, as insufficient interaction time can result in under-utilization of the available surface area, thereby diminishing the material's potential for CO2 capture. Despite these challenges, successful amine loading onto the extensive surface area of microporous materials can significantly enhance their performance in selective CO2 sorption. When adequately impregnated, the large surface area provided by materials like ZIFs and MOFs allows for a greater quantity of amine molecules to be anchored within the pores. This, in turn, increases the availability of active sites for CO2 adsorption, thereby improving the selectivity and capacity of the material for CO2 capture from mixed gas streams.
Primary amines, such as monoethanolamine and diethanolamine, have traditionally been utilized for the purpose of carbon dioxide absorption from feed streams owing to their convenient synthesis and comparatively lower activation energies. The present state of scientific investigation reveals that amines, such as diethanolamine (DEA) and TEPA, persist as preferred choices to be loaded onto neutral supports. Polymer-based fundamental compounds, exemplified by polyethylenimine (PEI)11–13 and 3-aminopropyltrimethoxysilane (APTMS), have recently surfaced in the realm of synthesizing composite materials. The exceptional affinity of these organic basic compounds towards acidic gaseous pollutants endows them with remarkable versatility and potential in the absorption processes of gaseous pollutants such as carbon dioxide (CO2) and sulfur dioxide (SO2).14 Moreover, the inherent characteristic of these substances renders them highly suitable for their impregnation onto high surface area sorbents such as activated carbons and porous organic frameworks, thereby significantly broadening their scope of potential applications. Significantly, aminopropyltrimethoxysilane (APTMS) was employed by Sara Ahsan and colleagues15 in their investigation on carbon dioxide (CO2) capture, specifically focusing on the application of zeolite-5 adsorbents. The experimental findings revealed an impressive carbon capture capacity of approximately 5.7 weight percent (wt%).
The outlet pressures of flue gases, typically maintained just above atmospheric levels (1 to 10 kPa above ambient pressure),16–18 are crucial for system efficiency, environmental compliance, and safe operation in industrial settings. Industrial flue gas, a byproduct of combustion processes in industries like power plants and cement production, typically contains a mix of gases and particles. Its main components include nitrogen (65–75%), carbon dioxide (10–20%), water vapor (5–15%), and oxygen (3–8%), along with smaller amounts of sulfur dioxide (SO2), nitrogen oxides (NOx), carbon monoxide (CO), particulate matter, and trace elements like heavy metals and volatile organic compounds (VOCs).19–21 The composition varies based on the fuel and process, impacting the design of pollution control systems and carbon capture technologies.
Typically, CO2 removal from flue gases via adsorption is conducted at or near atmospheric pressure (around 1 bar), as this corresponds to the typical exit pressure of flue gas streams in most industrial plants, with recovery of adsorbents done through temperature swing process.22 Operating at this pressure minimizes the need for additional energy input, making it a practical choice for many carbon capture processes. However, emerging capture technologies are increasingly exploring the use of higher process pressures, ranging from 4 bar to 10 bar.23 While maintaining an adsorber at such elevated pressures does require significantly more energy, this approach offers certain advantages. Notably, the recovery of CO2 from these high-pressure conditions is relatively straightforward, as the higher pressure can enhance the adsorption capacity and improve the efficiency of the capture process. An even more advanced and extreme approach involves the use of vacuum-assisted recovery following high-pressure CO2 adsorption.24–26 In this scenario, after CO2 is captured at pressures as high as 10 bar, a vacuum is applied to the system to facilitate the desorption of CO2 from the adsorbent material. This vacuum process helps to efficiently recover the CO2 by reducing the pressure, thereby driving the release of the gas from the adsorbent. Although this method requires sophisticated equipment and careful energy management, it can be highly effective in maximizing CO2 recovery, particularly in processes where high-pressure capture is used to enhance adsorption performance.
Proper pressure control ensures the effective performance of flue gas treatment systems, such as carbon capture units, while also optimizing the operation of downstream equipment like gas turbines and CHP systems. Maintaining appropriate outlet pressures helps to ensure that emission control devices function effectively, reducing pollutants like SOx, NOx, particulate matter, and CO2. Additionally, managing outlet pressures is a safety concern, as excessive pressure can lead to dangerous conditions, necessitating the use of pressure relief valves and other safety mechanisms. Optimized outlet pressures also contribute to energy efficiency by minimizing the operational costs of fans and blowers. Herein, the pressures of typical flue gases along with elevated pressures were considered to evaluate the heat of adsorption of the system.
The present study is focused on the examination of adsorption phenomena within the confines of a fixed bed reactor system. In order to optimize the precision and effectiveness of the conducted experiments, the present study utilized the response surface methodology (RSM) in tandem with a face-centered central composite design (CCD) as the chosen experimental design strategy. It is important to note that the carbon capture performance of an adsorbent is subject to the influence of various factors, including but not limited to the amine loading percentage, adsorbent weight, and temperature. It is noteworthy to acknowledge that traditional experimental designs frequently isolate these factors in order to investigate them individually, inadvertently neglecting the intricate interconnections that exist among them. Response surface methodology (RSM), however, surpasses these limitations by encompassing the simultaneous consideration of the combined effects of all aforementioned variables. Through the utilization of regression analysis, response surface methodology (RSM) facilitates the comprehensive evaluation of the combined impact of these factors on the adsorption process. This ultimately culminates in the identification of the most favourable process conditions. The implementation of this all-encompassing methodology not only amplifies accuracy but also diminishes the necessity for a substantial quantity of trials, thus preserving precious assets such as time, financial capital, chemical substances, and energy. The primary emphasis of our investigation is centred on three fundamental variables: temperature, carbonation duration, and system pressure. Upon implementing the methodological framework of response surface methodology (RSM), a comprehensive investigation into the intricate dynamics, adsorption modelling, and cyclic stability assessment of the synthesized adsorbents is conducted. The novelty of this study is that it employs a multifaceted approach to evaluate and optimize a novel adsorbent for carbon capture applications. It employs the usage of coal fly ash to synthesize value added sorbents. It begins with a comparison of various synthesis methods, followed by a first-level screening using BET data to assess adsorption characteristics. The adsorbent is then refined through a second-level screening, optimizing its composition by varying the Na-A and ZIF-8 ratio. Standardization of the response surface methodology (RSM) process is achieved through the CCD spherical experimental design. Subsequently, the RSM process is optimized to enhance carbon capture efficiency. The study explores the effect of TEPA loading on carbon capture uptake and analyzes the influence of temperature on TEPA loading. Cyclic stability tests assess the long-term performance over 50 cycles, while process kinetics modeling, breakthrough curve analysis, and adsorption isotherm modeling provide insights into the dynamic behavior and equilibrium relationships. Amine quantity determination through thermogravimetric analysis (TGA) and amine surface density calculations further contribute to a comprehensive understanding of the adsorbent's synthesis, performance, and key parameters.
2. Materials and methods
All the materials and synthesis methods are mentioned in detail in the ESI.†2.1. Characterization tools
Several analytical techniques were employed for in-depth material analysis. Fourier transform infrared (FTIR) analysis was conducted using the Jasco FTIR-4200, which offered a range spanning from 400 to 4000 nm with a remarkable resolution of ±0.5. High precision was ensured with a wavenumber accuracy of ±0.01 cm−1. The FTIR setup was equipped with a Ge/KBr beam splitter and a DLATGS detector along with DRA-81 accessory. Surface area analysis, using the Brunauer–Emmett–Teller (BET) method, was carried out with the Microtrac Bel SORP mini II instrument. This process was guided by the BEL SORP mini software. X-ray diffraction (XRD) analysis was conducted using the Rigaku ULTIMA-IV model, covering an angle range of 5–100° and employing a Cu X-ray source. Data collection was facilitated by both a scintillation counter and a dTex detector. Field emission scanning electron microscopy (FE-SEM) was performed with the FEI Apreo LoVac instrument. A versatile detector configuration, including the retractable STEM 3+ detector and DBS detector, was used. Furthermore, our FE-SEM was equipped with an energy dispersive X-ray spectroscopy (EDS) system, specifically the Aztec Standard EDS system, for comprehensive elemental analysis.2.2. Experimental set-up
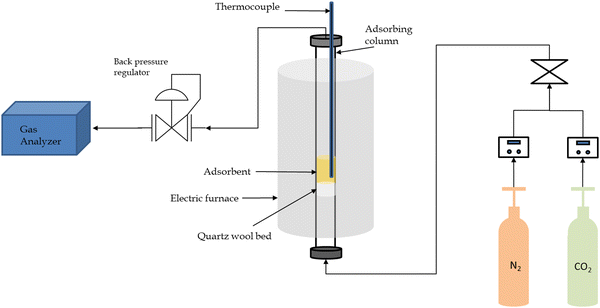
The experimental setup for this study was carefully designed to investigate the adsorption process. It consisted of several essential components and instruments to ensure precise and controlled conditions.The central component of the arrangement featured an adsorption column with a fixed bed, serving a critical function in the adsorption process. To maintain controlled and consistent temperatures throughout the experiment, an electric furnace was integrated into the system. Gas supply lines were thoughtfully connected to the setup, ensuring a steady and dependable source of gases for the adsorption procedure. For the fine-tuning of gas flow rates, mass flow controllers were effectively employed, guaranteeing precise gas flow regulation. The system's temperature conditions were diligently assessed and continually monitored using a thermocouple system, ensuring compliance with the desired range. The inlet of a quartz reactor tube was interconnected with the gas lines, functioning as the fixed bed adsorber. Quartz was deliberately chosen as the tube material due to its exceptional resistance to chemical reactions. Within the quartz tube, quartz wool served as a supportive medium for the adsorbent, effectively preventing the entrainment of adsorbent particles in the gas flow during the reaction. For additional security against the loss of adsorbent particles, a cyclone separator was affixed to the reactor tube's exit, proficiently separating solid particles from the exiting gas. Following cooling, the gas underwent analysis via a gas analyzer, enabling a comprehensive examination of its composition. This step was pivotal in assessing the efficiency of the adsorption process and determining the percentage of CO2 in the exit gas. To provide a visual overview of the setup, a schematic representation of the entire experimental system is presented in Fig. 1. The overall gas flow rate was consistently maintained at 150 mL min−1, while the CO2 flow rate was kept at 25 mL min−1. To optimize the gas analyzer's performance, a fixed 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio between nitrogen (N2) and CO2 was established. The operating pressure was fixed at 1 bar, with the use of a back pressure regulator to facilitate adsorption experiments at elevated pressures.
1 ratio between nitrogen (N2) and CO2 was established. The operating pressure was fixed at 1 bar, with the use of a back pressure regulator to facilitate adsorption experiments at elevated pressures.
3. Physico-chemical attributes
3.1. N2 adsorption isotherm analysis
The N2 adsorption isotherm experiments were conducted at 77 K and yielded information regarding the porosity and surface area characteristics of the various adsorbents under investigation. Notably from Table 1, ZIF-8 emerged as the frontrunner in this study, displaying the most remarkable BET surface area at 1580 m2 g−1, a clear indication of its exceptional capacity for gas adsorption at low temperatures. Moreover, ZIF-8 also boasted the largest pore volume among the materials, measuring a substantial 0.79 cm3 g−1, which further underscored its suitability for gas adsorption applications.| Adsorbent | BET surface area (m2 g−1) | Mesopore volume (cc g−1) | Micropore volume (cc g−1) |
|---|---|---|---|
| ZIF-8 | 1584 | 0.09 | 0.67 |
| Na-A | 231 | 0.04 | 0.10 |
| ZIF-8@Na-A SM | 72 | 0.001 | 0.04 |
| ZIF-8@Na-A IM | 476 | 0.04 | 0.28 |
| ZIF-8@Na-A via PM | 188 | 0.03 | 0.08 |
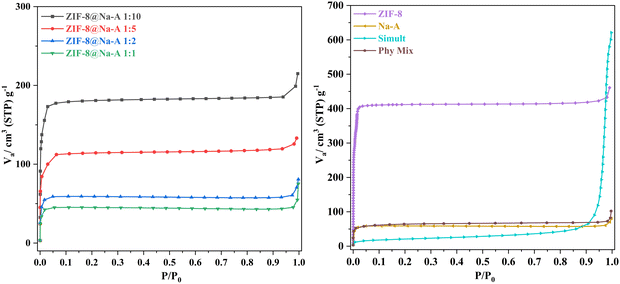
In contrast, ZIF-8 synthesized via the simultaneous method exhibited a significantly lower BET surface area, registering at only 78 m2 g−1. This discrepancy highlighted the impact of synthesis methods on the resultant materials, with the simultaneous synthesis method yielding a material with comparatively lower porosity. However, it is crucial to consider the presence of Na-A in both ZIF-8@Na-A via simultaneous synthesis and ZIF-8@Na-A via in situ synthesis. The descending order of surface area is clear: ZIF-8 leads with the highest surface area, followed by ZIF-8@Na-A via in situ synthesis, ZIF-8@Na-A via physical binding, and finally, ZIF-8@Na-A via simultaneous synthesis with the lowest surface area. It is noteworthy that the surface area of ZIF-8@Na-A was found to be lower than that of its parent material, ZIF-8, which can be attributed to the formation of ZIF-8 nanocrystals over the surface of Na-A, effectively reducing the accessible surface area. Overall, these findings provide valuable insights into the materials’ properties and their potential applications in gas adsorption and separation processes, highlighting the intricate relationship between synthesis methods and the resultant materials’ characteristics.
The BET surface area of the composite synthesized by physical blending was found to be less than that of either parent material because the components were simply mixed without achieving uniform distribution at the nano level. The BET method calculates specific surface area relative to the mass of the adsorbent, and the lack of evenness in the physical blend resulted in a lower overall surface area. For the composite synthesized via the simultaneous synthesis method, the chemical synthesis process itself was uneven and haphazard, preventing the formation of the ordered structures characteristic of the parent materials, leading to a decreased surface area. This is also evidenced by the SEM images (Fig. 2), which show the irregular and disordered morphology of the composite, further corroborating the reduced surface area findings.
3.2. Electron micrographs
Scanning electron micrographs show the topological and the morphological characteristics of ZIF-8, Na-A, ZIF-8@Na-A (in situ method) and ZIF-8@Na-A under simultaneous method, presented in Fig. 2. Pure ZIF-8 showed ordered particle structures. The structure of ZIFs is determined mostly by the ratio between the ligand and the metal. The Na-A synthesized exhibited well-defined cuboid-like structures with a relatively smooth morphology. Moreover, the internally produced Na-A displayed consistent particle sizes ranging from 100 nm to 150 nm.27 The morphology of the synthesized Na-A predominantly relied on the chemical ratio employed during synthesis. In contrast, the synthesized ZIF-8 exhibited dodecahedral structures. The successful synthesis of ZIFs also hinged on the crucial mole ratio between the metal ion and the organic linker. Notably, a Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hmim ratio of 1
Hmim ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 resulted in more disordered and interconnected ZIF-8 particles, while a Zn
8 resulted in more disordered and interconnected ZIF-8 particles, while a Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hmim ratio of 1
Hmim ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 yielded well-ordered nanocrystals. Interestingly, the simultaneous synthesis of ZIF-8@Na-A led to a distinct morphology that did not resemble either parent material's ordered structure. This departure from expected morphology might be attributed to the uneven crystal formation inherent in the simultaneous synthesis process. The resulting ZIF-8@Na-A composite showcased the characteristic cuboid particles associated with Na-A, yet it also contained meticulously ordered ZIF-8 nanocrystals forming over the surface of the Na-A particles, as depicted in the accompanying figure. Surprisingly, the geometry of these nanocrystals within the composite was more distinct compared to pure ZIF-8 nanocrystals.
70 yielded well-ordered nanocrystals. Interestingly, the simultaneous synthesis of ZIF-8@Na-A led to a distinct morphology that did not resemble either parent material's ordered structure. This departure from expected morphology might be attributed to the uneven crystal formation inherent in the simultaneous synthesis process. The resulting ZIF-8@Na-A composite showcased the characteristic cuboid particles associated with Na-A, yet it also contained meticulously ordered ZIF-8 nanocrystals forming over the surface of the Na-A particles, as depicted in the accompanying figure. Surprisingly, the geometry of these nanocrystals within the composite was more distinct compared to pure ZIF-8 nanocrystals.
The transmission electron micrographs (Fig. 3) also agreed with the scanning electron micrographs. The micrographs showed that the pure Na-A structures were largely not hollow, i.e., did not consist of structures with high BET surface area and porosity. This is also consistent with the BET surface area value obtained for the Na-A in Table 1. However, the morphologies obtained by both SEM and TEM are perfectly aligned for Na-A. This structural type is also similar to the Na-A, synthesized from halloysite minerals synthesized by Zhao and team28 for the purpose of NH4+ ion separation within feed water. Yuija et al.29 also synthesized similar Na-A structures using hydrothermal synthesis with pure chemicals and PEG. As for ZIF-8, it can be clearly observed that the in-house synthesized ZIF-8 was transparent indicating a high degree of porosity and high specific surface area, once again in agreement with the N2 adsorption isotherms presented in Fig. 3 and Table 1. These crystals were extremely similar to the ones obtained by Liyong Chen and group30 in their study of photocatalytic properties of Au@ZIF-8. Also, Luanwuthi et al.31 synthesized similar hollow and porous ZIF-8 structures for the separation of ferrocene methanol.
The ZIF-8@Na-A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
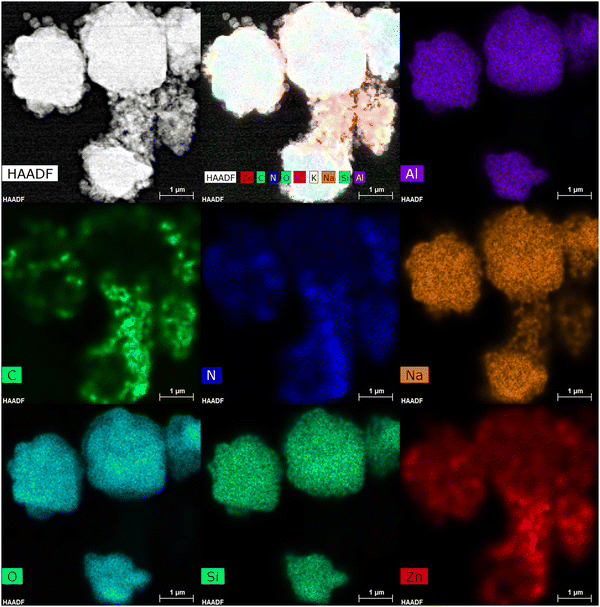
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 sorbent showed two distinct types of crystal structures. The opaque Na-A structures were clearly visible in the imaging. But on top of the Na-A, hollow and light ZIF-8 grains were also visible. This is a clear indication that ZIF-8 structures were formed over the surface of the bigger Na-A structures. The HAADF analysis also supported this observation. Fig. 4 shows the HAADF imaging of the various expected elements within the composite adsorbent. Elements expected within the Na-A structure, such as Na, Si, Al and O, were found to be clustered around clump areas of the composite image. This is a strong indication that these areas have Na-A structures within them. But surrounding these clusters are layers of Zn, C and N, elements found in the ZIF-8 structure. In fact, these elements even acted as a link between two Na-A clusters, hence proving that ZIF-8 formed over the surface of the existing Na-A crystals.
5 sorbent showed two distinct types of crystal structures. The opaque Na-A structures were clearly visible in the imaging. But on top of the Na-A, hollow and light ZIF-8 grains were also visible. This is a clear indication that ZIF-8 structures were formed over the surface of the bigger Na-A structures. The HAADF analysis also supported this observation. Fig. 4 shows the HAADF imaging of the various expected elements within the composite adsorbent. Elements expected within the Na-A structure, such as Na, Si, Al and O, were found to be clustered around clump areas of the composite image. This is a strong indication that these areas have Na-A structures within them. But surrounding these clusters are layers of Zn, C and N, elements found in the ZIF-8 structure. In fact, these elements even acted as a link between two Na-A clusters, hence proving that ZIF-8 formed over the surface of the existing Na-A crystals.
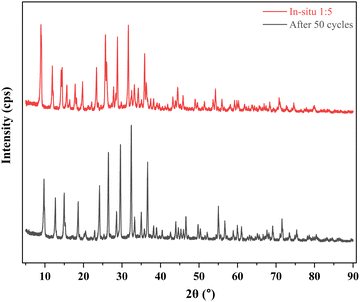
3.3. XRD diffractograms
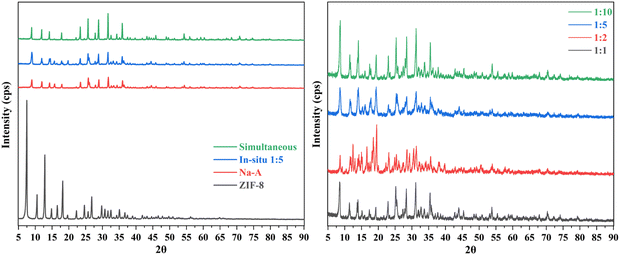
The diffractograms presented in Fig. 5 provide valuable insights into the crystalline structures of the materials under investigation. In particular, the diffractograms reveal distinctive peaks that are characteristic of each material, shedding light on their unique structural properties.In the case of ZIF-8, a series of well-defined peaks were observed at specific angles. Notably, these peaks were detected at 7.291°, 10.325°, 12.702°, 14.673°, 16.431°, 18.003°, 23.281°, and 28.654°. These peaks correspond to specific planes within the crystal lattice structure of ZIF-8. For instance, the peak at 7.291° is indicative of the (011) plane, while the peak at 10.325° corresponds to the (002) plane. Similarly, the peak at 12.702° is associated with the (112) plane, and the peak at 16.431° is attributed to the (013) plane. Furthermore, the peak at 18.003° signifies the presence of the (222) plane.32
However, when considering the ZIF-8@Na-A adsorbent, it was evident that these characteristic peaks shifted slightly. The diffractogram revealed peaks at angles 9.031°, 11.917°, 12.097°, 14.210°, 14.468°, 15.694°, 16.442°, 17.842°, 18.178°, 19.751°, 22.113°, 23.407°, 23.860°, 25.720°, 25.971°, 27.34°, 27.823°, 28.381°, 28.825°, 31.6674°, 32.544°, 33.201°, 34.232°, 35.08°, and 35.878°. These shifted peaks indicate changes in the crystallographic structure compared to pure ZIF-8. The presence of Na-A in the composite is believed to influence these shifts, possibly through interactions with the ZIF-8 structure.
In the case of the coal fly ash-based Na-A material, its diffractogram displayed prominent peaks at angles 8.968°, 11.949°, 14.253°, 15.736°, 17.888°, 21.520°, 22.200°, 23.480°, 24.620°, 25.789°, 26.083°, 27.904°, 28.920°, 31.746°, 32.641°, 33.336°, 34.350°, 35.110°, and 35.975°. These peaks align with established literature on the synthesis of Na-A from fly ash33 and Novembre et al.,34 reaffirming the material's crystallographic characteristics.
The dominance of characteristic Na-A peaks in the diffractogram of the ZIF-8@Na-A sorbent is an intriguing observation. This phenomenon can be attributed to the significant presence of Na-A within the composite material. Essentially, the abundance of Na-A appears to have played a pivotal role in shaping the diffractogram of the composite, effectively overshadowing the typical signature peaks of ZIF-8 during its synthesis process. This finding underscores the intricate interplay between the individual components in the composite. It suggests that the presence of Na-A exerts a profound influence on the structural characteristics and crystalline properties of the composite material. The unique interactions between ZIF-8 and Na-A within the composite are evidently reflected in the diffractogram, providing compelling evidence of these structural transformations. In essence, the dominance of Na-A peaks in the diffractogram serves as a clear indication of the composite's complex and interdependent crystalline properties.
4. Hierarchical optimization of the material and process
4.1. Adsorbent optimization
| Adsorbent | CC uptake (mmol g−1) | BET surface area (m2 g−1) | Mesopore volume (cc g−1) | Micropore volume (cc g−1) |
|---|---|---|---|---|
| ZIF-8 | 1.12 | 1584 | 0.09 | 0.67 |
| Na-A | 1.82 | 230 | 0.04 | 0.10 |
| ZIF-8@Na-A SM | 1.63 | 72 | 0.001 | 0.04 |
| ZIF-8@Na-A IM | 3.48 | 476 | 0.04 | 0.28 |
| ZIF-8@Na-A PB | 2.38 | 236 | 0.08 | 0.10 |
From Table 2, it is evident that pure ZIF-8 displayed high surface area and pore volume. Even when compared to the next best surface area shown by ZIF-8@Na-A synthesized via the in situ method, the difference is apparent. The ZIF-8@Na-A adsorbents synthesized via simultaneous and physical binding methods recorded values much lesser than that of the ZIF-8@Na-A via the in situ method. However, when the initial CC uptake values are brought into the picture, the differences are obvious. Pristine ZIF-8, despite having the highest surface area, recorded the lowest CC uptake value (1.12 mmol g−1) out of the four tested adsorbents. Furthermore, the ZIF-8@Na-A via the in situ method recorded the highest CC uptake of 3.48 mmol g−1. The key point to note here is that ZIF-8 in this method has been forced to crystallize on the surface of the resident Na-A. This could have contributed to an optimal combination of the physical properties of ZIF-8 and the high chemical affinity of Na-A towards CO2 in general. ZIF-8@Na-A synthesized via simultaneous synthesis recorded the lowest of the surface area and the second lowest CC uptake. This could be due to the incomplete crystallization of both Na-A and ZIF-8 during the synthesis. ZIF-8@Na-A IM demonstrated a lower specific surface area but a significantly higher CO2 uptake compared to pristine ZIF-8, indicating a superior performance despite the reduced surface area. When compared to the other synthesized composites, namely ZIF-8@Na-A SM and ZIF-8@Na-A PB, ZIF-8@Na-A IM not only showed the highest CC uptake but also possessed a greater specific surface area. This suggests that ZIF-8@Na-A IM is the most effective composite in terms of both CO2 adsorption capacity and surface area. Consequently, the overall trend is ZIF-8@Na-A IM > ZIF-8@Na-A PB > ZIF-8@Na-A SM in both CO2 uptake and BET surface area. This highlights the superior structural and adsorption properties of ZIF-8@Na-A IM among the tested materials.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, if the ratio of Zn2+ to Na-A was 1
10, if the ratio of Zn2+ to Na-A was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 during synthesis. Here, five such ratios were considered and were compared in terms of CC uptake. The results are tabulated in Table 3. The initial experimental conditions for the carbon capture uptake studies were as follows: temperature = 298 K, pressure = 1 bar, CO2% in the feed = 16.7% and gas feed flow rate = 150 mL min−1.
10 during synthesis. Here, five such ratios were considered and were compared in terms of CC uptake. The results are tabulated in Table 3. The initial experimental conditions for the carbon capture uptake studies were as follows: temperature = 298 K, pressure = 1 bar, CO2% in the feed = 16.7% and gas feed flow rate = 150 mL min−1.
| Adsorbent | CC uptake (mmol g−1) | BET surface area (m2 g−1) | Micropore volume (cc g−1) | Mesopore volume (cc g−1) |
|---|---|---|---|---|
ZIF-8@Na-A IM 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
3.61 | 711 | 0.31 | 0.19 |
ZIF-8@Na-A IM 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
3.48 | 476 | 0.28 | 0.04 |
ZIF-8@Na-A IM 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
2.57 | 242 | 0.09 | 0.03 |
ZIF-8@Na-A IM 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
2.31 | 188 | 0.07 | 0.03 |
From the results tabulated in Table 3 and from Fig. 6, the adsorbent with the ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 displayed the highest CC uptake. It would also be interesting to note that the 1
10 displayed the highest CC uptake. It would also be interesting to note that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 adsorbent was a close second, indicating that after a certain initial synthesis ratio, the increase in CC uptake was nominal. Here, the increase in the quantity of Zn2+ proved to be the deciding factor. The lower the Zn2+ content, the higher the CC uptake. The content of Na-A was constant in all these adsorbents, indicating that along with the highly basic nature of Na-A, the quantity of pores and the available surface area were also a key factor in determining the CC uptake. So, in line with this reasoning, the 1
5 adsorbent was a close second, indicating that after a certain initial synthesis ratio, the increase in CC uptake was nominal. Here, the increase in the quantity of Zn2+ proved to be the deciding factor. The lower the Zn2+ content, the higher the CC uptake. The content of Na-A was constant in all these adsorbents, indicating that along with the highly basic nature of Na-A, the quantity of pores and the available surface area were also a key factor in determining the CC uptake. So, in line with this reasoning, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adsorbent recorded the lowest CC uptake out of the four tested adsorbents. Higher quantities of Zn2+ may have deprived the CO2 molecules of additional sites to invade and thus get trapped. Fan Yang and group35 also synthesized a group of hybrids consisting of zeolite LiX and ZIF-8. In that study too, the amount of ZIF-8 controlled the CO2 uptake values. The highest uptake value amongst those hybrids was recorded by the LiX@ZIF-8 I sorbent (3.2 mmol g−1) whilst the least uptake was shown by the LiX@ZIF-8 III sorbent (1.6 mmol g−1). From here on, the adsorbent, in focus of this study, would be ZIF-8@Na-A IM 1
1 adsorbent recorded the lowest CC uptake out of the four tested adsorbents. Higher quantities of Zn2+ may have deprived the CO2 molecules of additional sites to invade and thus get trapped. Fan Yang and group35 also synthesized a group of hybrids consisting of zeolite LiX and ZIF-8. In that study too, the amount of ZIF-8 controlled the CO2 uptake values. The highest uptake value amongst those hybrids was recorded by the LiX@ZIF-8 I sorbent (3.2 mmol g−1) whilst the least uptake was shown by the LiX@ZIF-8 III sorbent (1.6 mmol g−1). From here on, the adsorbent, in focus of this study, would be ZIF-8@Na-A IM 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 for all further adsorption studies.
5 for all further adsorption studies.
4.2. CO2 uptake standardization
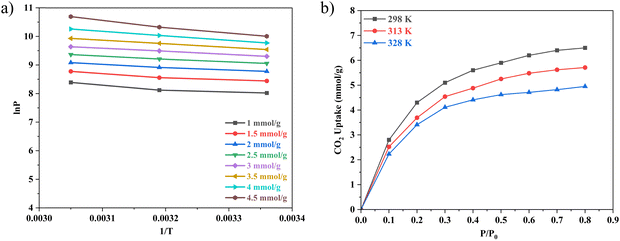
Within the ambit of temperature variation, a spectrum of temperatures was explored, encompassing the points of 25 °C, 40 °C, 62 °C, 80 °C, and 100 °C. Notably, as the temperature was manipulated and escalated, an interesting and significant trend emerged: there was a discernible decrease in the predicted CC uptake values when the ZIF-8@Na-A adsorbent was employed. This temperature-dependent phenomenon sheds light on the sensitivity of the adsorption process to thermal conditions. One of the noteworthy findings of this study pertains to the comparative performance of ZIF-8@Na-A against pure ZIF-8.36,37 It is worth emphasizing that one of the inherent challenges in employing MOFs in CC tests is the tendency for the CC values obtained at lower temperatures to exhibit poor cyclic retention. However, the results of this investigation highlighted the superiority of the ZIF-8@Na-A composite adsorbent in addressing this issue. In our previous research endeavor conducted under nearly identical conditions, pure ZIF-8 yielded a CC uptake value of 1.41 mmol g−1. In stark contrast, the composite adsorbent developed in the present study demonstrated a remarkable twofold enhancement in CC performance, thus manifesting its efficacy as an improved adsorbent in the context of carbon capture.
Furthermore, it is noteworthy that these findings are not isolated but resonate with analogous observations from other related studies. For instance, the study conducted by Zhang and co38 in 2014, which examined CO2 adsorption employing biochar at elevated temperatures, observed a similar temperature-sensitive behavior. In this investigation, both untreated and CO2-treated carbonaceous sorbents displayed sorption values of 0.89 mmol g−1 and 1.21 mmol g−1 at 20 °C, suggesting that temperature significantly influences the adsorption process. Similarly, another study,39 which delved into the use of zeolites for CO2 capture, observed similar trends. Both 13-X and WE-G 592 zeolites exhibited consistent CC uptake under varying conditions of CO2 concentration and total pressure. For instance, at 30 °C and 100 psi, the CC uptake values were approximately 5.0 mol kg−1 and 4.5 mol kg−1, respectively. Importantly, when subjected to the same process pressure but at an elevated temperature of 120 °C, these adsorbents retained a substantial portion of their CC uptake values, approximately 72% and 61%, respectively. This retention phenomenon was attributed to a high process pressure and the relatively high partial pressure of CO2 within the feed gas itself, highlighting the intricate interplay of multiple factors in CC processes.
The role of temperature in influencing adsorption capacity was found to be of paramount importance, rendering it a critical factor to consider. Upon examination of the data presented in Table S1 (ESI†), it became evident that the in-house synthesized adsorbent exhibited superior adsorption capabilities at lower temperatures. This observation aligned with the well-known exothermic nature inherent to physical adsorption processes. When delving further into this phenomenon, it became apparent that as the temperature increased, the interaction between solid and gas molecules at the interface intensified. This heightened interaction could be elucidated by the Boltzmann equation, which attributed it to the increased kinetic energy of the solid–gas molecules engaged in the adsorption process. Consequently, this heightened molecular interaction led to a reduction in the effective and accessible surface area available for adsorption. As a result, it could be reasonably concluded that lower sorption temperatures often yield higher sorption capacities. For adsorbents, optimal temperature for maximizing the adsorption capacity of each adsorbent was mostly the lowest temperature among the available options.
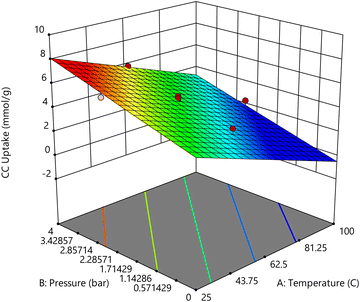
Process pressures were also of five parametric levels: 1.0 bar, 1.6 bar, 2.5 bar, 3.6 bar and 4 bar, as dictated by the RSM CCD spherical model. Indeed, the highest CC uptake of 7.1 mmol g−1 was observed at 3.4 bar and 40 °C. Furthermore, at 4 bar process pressure and 62.5 °C, the CC uptake was around 5.8 mmol g−1 indicating that process temperature also played an important role in determining the overall CC uptake. Wang et al.40 reported that for their own rice husk synthesized Na-A, the process pressure contributed to a higher CC value. K Yang et al.41 also observed that when the process pressures increased, the CC uptake values of their Y1302 adsorbent increased by 300%. Cheung and group42 also recorded that for the nano-NaKA adsorbent, an increase in pressure saw the enhancement of the CC uptake value by 100%. Returning to the adsorbents in the present study, as indicated by their N2 sorption patterns, they are all microporous in nature following the Type-I adsorption pattern (Fig. 6).43 This would mean that at high process pressures, the pressure difference between the process pressure and the pressure within the narrow micropores of the sorbents would promote high volume CO2 adsorption quickly. Fig. 7 presents the response surface of the effect of temperature and pressure on CO2 uptake.
In our investigation, the influence of various operational parameters on CC uptake values was meticulously examined. It was apparent that temperature and pressure played pivotal roles in shaping the outcomes of our study. An intriguing observation was made concerning carbonation time which appeared to exert a comparatively modest impact on CC uptake values. In particular, when the extension of carbonation time was undertaken, a slight increment in CC uptake was discerned. However, it is noteworthy that this increment did not amount to much. This is of a similar trend noted by Penchah and team in their research, which centered on the adsorption of CO2 onto a benzene-based hyper-cross-linked polymer.44 Further buttressing this trend, a study by Sreenivasulu et al. in 201845 reported a parallel trend. They found that longer feed times were linked with augmented CC uptake values for the adsorbents they investigated, thereby confirming the affirmative correlation between prolonged contact time and an amplified efficiency in carbon capture.
In summation, while temperature and pressure were identified as fundamental drivers in influencing CC uptake values in our study, the effect of carbonation time and the quantity of adsorbent used, although not negligible, displayed a more subtle influence. These findings resonate with the body of related research within the field, underscoring the pivotal role of contact time in the adsorption process and shedding light on the intricate interplay of diverse parameters in the realm of carbon capture.
A comparison of the performance of the adsorbents reported in the literature with that of the adsorbent developed in the present study is presented in Table 4 in terms of uptake capacity under varying conditions. ZIF-11@ZIF-8 exhibits the highest uptake capacity of 8.21 mmol g−1 at 25 °C and 4 bar, making it the most effective under these specific conditions.46 Conversely, 12.41% ZIF-8@LFNW shows the lowest uptake of 0.20 mmol g−1 at 25 °C and 1 bar, indicating limited efficiency. ZIF-8@3wt% g-C3N4 also stands out with a substantial uptake of 7.16 mmol g−1, but this is achieved under more extreme conditions of 45 °C and 15 bar. Other notable adsorbents include CS-ZX aerogel beads with an uptake of 4.23 mmol g−1 at 25 °C and 1 bar, and 13X-5CB, which has an uptake of 6.06 mmol g−1 at 25 °C and 2 bar. However, the adsorbents that showed higher CC uptake than the one studied in the present work either operated at high process pressures or low process temperatures. These comparisons highlight the significant variations in adsorption capacities and underline the importance of operational conditions in evaluating adsorbent performance.
| S. No. | Adsorbent | Uptake (mmol g−1) | Conditions | Ref. |
|---|---|---|---|---|
| 1 | LiX@ZIF-8 | 1.81 | 25 °C, 1 bar | 47 |
| 2 | ZIF-8@3wt% g-C3N4 | 7.16 | 45 °C, 15 bar | 48 |
| 3 | ZIF-11@ZIF-8 | 8.21 | 25 °C, 4 bar | 49 |
| 4 | CS/ZIF-8/MSNs-525 | 1.32 | 25 °C, 1 bar | 50 |
| 5 | 12.41% ZIF-8@LFNW | 0.20 | 25 °C, 1 bar | 51 |
| 6 | NaG1.2Z | 2.25 | 35 °C, 1 bar | 52 |
| 7 | CS-ZX aerogel beads | 4.23 | 25 °C, 1 bar | 53 |
| 8 | 13X-5CB | 6.06 | 25 °C, 2 bar | 54 |
| 9 | G-NaX | 4.32 | 25 °C, 14 bar | 55 |
| 10 | PC2-Z | 4.50 | 0 °C, 1 bar | 56 |
| 11 | K2CO3/FA aerogel | 2.02 | 20 °C, 1 bar | 57 |
| 12 | CFAZ@ZIF-8 | 2.83 | 25 °C, 1 bar | 58 |
| 13 | ZIF-8@MCM-41 | 3.03 | 25 °C, 1 bar | 59 |
| 14 | (Ce, Zn) ZIF-8 | 3.71 | 25 °C, 1 bar | 60 |
| 15 | ZIF-8@Na-A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
3.48 | 25 °C, 1 bar | This work |
Whilst examining the influence of temperature and pressure on CO2 uptake capacity individually, a clear pattern emerged: as the process temperature increases, the CO2 uptake capacity tends to decrease, while an increase in process pressure results in a corresponding increase in CO2 uptake. However, when these two factors are considered in tandem, the relationship becomes more nuanced. Studies indicate that the optimal conditions for maximizing CO2 uptake occur at a combination of high pressure and low process temperatures. For instance, at a pressure of 3.4 bar and a temperature of 40 °C (as reported in Table S1, Std 7, ESI†), the highest recorded CO2 uptake was 7.10 mmol g−1. This suggests that under these conditions, the material's affinity for CO2 is significantly enhanced, likely due to the lower temperature facilitating stronger physical adsorption forces and the higher pressure driving more CO2 molecules into the available adsorption sites. Interestingly, a similar set of conditions—3.4 bar pressure and 40 °C temperature—produced the second highest CO2 uptake of 6.63 mmol g−1 (Table S1, Std 3, ESI†). The only variable between these two experiments was the duration of feed flow. The small difference in uptake between these two conditions implies that while feed flow duration has some effect, its impact is relatively minor compared to the influence of temperature and pressure. Moreover, the data from Std 12 (Table S1, ESI†) provide additional insights. Despite operating at a higher process pressure, the CO2 uptake was observed to be lower, at 5.8 mmol g−1. This result suggests that the interaction between temperature and pressure is critical, and both must be optimized together to achieve maximum CO2 uptake. A higher pressure alone is insufficient if the temperature is not appropriately matched to enhance adsorption.
| CC uptake = 4.2935 − (1.4169 × A) + (0.856275 × B) − (0.0236645 × C) |
| Adsorbent | Temp. (°C) | Pressure (bar) | Time (min) | Predicted CC (mmol g−1) | Experimental CC (mmol g−1) |
|---|---|---|---|---|---|
| ZIF-8@Na-A | 55 | 3 | 120 | 5.12 | 4.88 |
The model F-value for ZIF-8@Na-A was recorded at 24.88, signifying the model's statistical significance. The high level of concordance observed between the predicted R2 value, which amounted to 0.953, and the adjusted R2 value, measuring at 0.945, provided strong evidence for a well-fitting model. A comparative analysis between these predicted values and the actual experimental results revealed reasonably favorable fit statistics. Notably, the standard deviation within the context of this experimental model for ZIF-8@Na-A was approximately 0.33. As depicted in Table 5, a noteworthy alignment was observed between the optimized and predicted values and their corresponding experimental counterparts. This alignment lent substantial credence to the efficacy of the RSM experimental design, underscoring its ability to accurately forecast adsorbent uptake levels within the predefined parameter ranges. The results, thus, affirm the successful application of the RSM approach in this study for precise predictions of adsorbent uptake levels within the specified parameter boundaries.
4.3. Enhancement of CC through amine loading
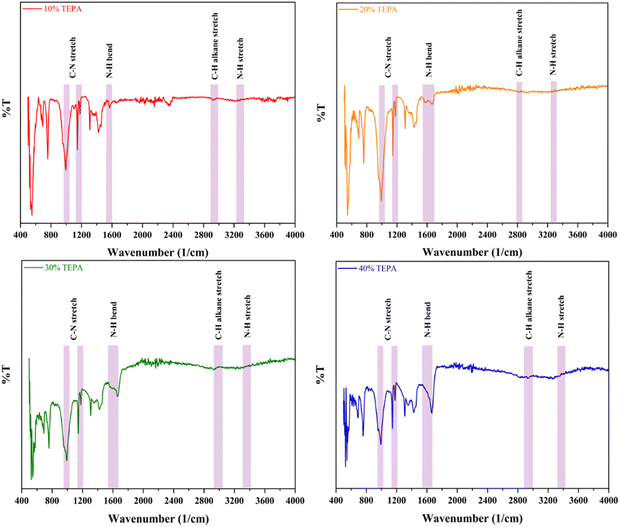
To enhance the CC uptake further, amine loading was done. Amines are well known to be great absorbents for acidic gases like CO2 and SO2. In particular, amines like TETA and TEPA are employed frequently to get rid of acidic gases and moisture from flue gas feed supply. To confirm the presence of amine loaded within the adsorbents, FTIR studies were conducted on all four adsorbents. The IR data corresponding to transmittance of all four adsorbents are presented in Fig. 8.As expected, all four TEPA loaded adsorbents displayed the strong presence of the secondary amine C–N stretch around 1200 cm−1.61 The 10%, 20%, 30% and 40% TEPA loaded adsorbents showed this stretch around 1179.07 cm−1, 1178.03 cm−1, 1178.02 cm−1 and 1178.03 cm−1 respectively (Fig. 8). The corresponding alkane stretch C–H for all these adsorbents was found at 2941.01 cm−1, 2932.86 cm−1, 2920.47 cm−1 and 2933.55 cm−1. Traditionally this stretch can be found around 2890 cm−1 to 3000 cm−1 and this aligns well with the peaks traditionally.62 The strong N–H bond representing the primary amine stretch is usually found between 1590 cm−1 and 1670 cm−1 and the secondary N–H stretch around 3200 cm−1 to 3450 cm−1.63 For the adsorbents studied here, the primary N–H bend peaks were observed at 1597.31 cm−1, 1665.70 cm−1, 1664.41 cm−1 and 1665.26 cm−1 and the secondary N–H stretch peaks were observed at 3267.00 cm−1, 3221.39 cm−1, 3219.08 cm−1 and 3265.35 cm−1 respectively.
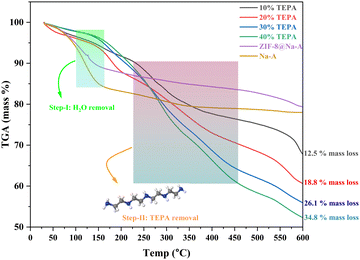
To properly evaluate the extent of amine loading and the decomposition stability of the TEPA loaded adsorbents, thermo-gravimetric analysis was performed. This analysis was done from room temperature to 600 °C with a 10° min−1 heating rate, and the data are given in Fig. 9. The samples were taken at various time intervals during the experimental CO2 analysis to determine the weight loss with the increase in temperature. The first step of decrease for these TEPA loaded adsorbents was recorded between 100 °C and 170 °C.64 This is mostly associated with the removal of water vapour and other volatile components. This loss was around 5 to 11% depending on the loading percentage. The 10% loaded adsorbent showed only around 5% at this step indicating the lower volume of H2O adsorbed. On the other hand, both 30% and 40% loaded adsorbents showed a high weight loss due to a higher volume of H2O adsorbed per unit mass. The second step of significant weight loss was observed between 200 °C and 400 °C. This is attributed to the amine loss from the adsorbent. The boiling point of TEPA is around 330 °C as per IUPAC, but the amine degradation would begin at much lower temperatures due to the instability of amines. This instability resulted in a huge weight loss with respect to the amount of adsorbent considered. For instance, the weight loss determined for the 40% TEPA loaded adsorbent demonstrated a decrease of 35%, which more or less aligned with the initial loading percentage. A similar alignment could be observed with both 20% and 30% TEPA loaded adsorbents as well. Only the 10% loaded adsorbent demonstrated a loss of around 13% within the temperature range mentioned. This could be due to the fact that ZIF-8 itself shows significant degradation at this temperature. In a study done by Harpreet Kaur et al.,65 ZIF-8 nanoparticles showed significant material degradation at temperatures greater than 200 °C. This coupled with amine degradation could have affected the weight loss. Another interesting observation was that, for both 30% and 40% TEPA loaded adsorbents, both Step-I and Step-II seemed to converge into a single step, while for the 10% and 20% TEPA loaded adsorbents both steps were distinct. This could be due to the fact that both 30% and 40% TEPA loaded adsorbents had larger volumes of CO2 adsorbed and consequently took longer to release the adsorbed CO2. Amine loading density was also computed to determine the amine loading throughout the adsorbent surface. The amine quantity was verified using the above TGA data. The surface amine density was computed to be around 0.0111 mmol of N m−2 for the 10% TEPA loaded adsorbent, 0.0129 mmol of N m−2 for the 20% TEPA loaded adsorbent, 0.0198 mmol of N m−2 for the 30% TEPA loaded adsorbent and 0.0317 mmol of N m−2 for the 40% TEPA loaded adsorbent.
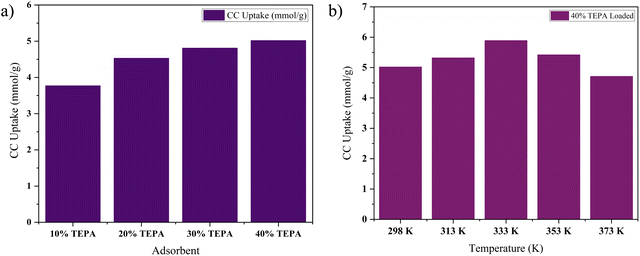
This trend finds support in the research conducted by Taheri and team involving TEPA-loaded mesoporous nanosilica tubes.66 They reported a remarkable upsurge in CC, particularly when the TEPA loading was increased from 10% to 30%. Specifically, a TEPA loading of 30% resulted in a calculated CC of approximately 9 mmol g−1. Similarly, Li and group observed a similar correlation when they investigated TEPA loading from 25% to 60%, which resulted in a 20% increase in CC values. In that study, the highest CC uptake, reaching 4.02 mmol g−1, was attained for Na-A loaded with 60% TEPA.67 An intriguing case emerged from the CC uptake study of TEPA loaded onto mesoporous silica gels, conducted by Zhao and his research team.68 They noted that as TEPA loading increased from 0% to 20%, CC uptake values experienced a notable increase of 27%. However, when the TEPA loading was further elevated from 20% to 50%, the CC uptake displayed a contrasting trend, decreasing by 28%. This decline was attributed to the consequences of excessive amine loading. While an increase in TEPA loading initially enhances CC uptake due to a higher content of basic amines, an excessive rise in amine loading can lead to pore blockage, reducing the available pore volume and active adsorption sites. Furthermore, an excessive amine loading can result in an uneven dispersion of amines across the surface and pores of the parent adsorbent.
Amines themselves are chemisorbents and thus actively absorb CO2 through a chemical reaction. ZIF-8 and Na-A, on the other hand, are both solid adsorbents, and their CO2 uptake is governed by physisorption, which relies on physical interactions rather than chemical bonds. Consequently, when amines are impregnated onto solid supports or physisorbents, the resulting sorption process is almost always a combination of both physisorption and chemisorption. In this context, TEPA plays a crucial role. TEPA is a strong chemisorbent, meaning it reacts chemically with CO2 to form stable compounds, thereby contributing significantly to the chemisorption aspect of the composite's sorption process. The incorporation of TEPA into a solid support like ZIF-8 or Na-A enhances the overall CO2 capture efficiency by leveraging the strengths of both sorption mechanisms. The solid support, being a physisorbent, provides a high surface area and porous structure that facilitates the initial capture of CO2 molecules through weaker, reversible physical interactions. Simultaneously, the impregnated amines (such as TEPA) chemically react with the CO2 molecules, forming stable carbamate or bicarbonate compounds. This chemisorption process is more robust and ensures a higher capacity for CO2 capture, as it involves the formation of chemical bonds, which are typically stronger and more stable than the physical interactions governing physisorption. Thus, the combination of physisorption and chemisorption in such a composite material allows for an efficient and effective CO2 capture system. The physisorbent component (ZIF-8 or Na-A) captures CO2 molecules through physical interactions, while the chemisorbent (TEPA) ensures a higher overall capture capacity through chemical reactions. This synergistic approach maximizes the advantages of both mechanisms, leading to improved performance in CO2 capture applications.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 adsorbent is shown in Fig. 10. The TEPA loaded version of ZIF-8@Na-A gave the highest CC uptake value at 60 °C. For example, the 40% TEPA loaded ZIF-8@Na-A showed an uptake value of 5.01 mmol g−1 at 25 °C. It then increased considerably to 5.89 mmol g−1 at 60 °C and decreased greatly to 4.71 mmol g−1 at 100 °C. Liu et al.69 conducted a thorough investigation of the CC uptake activity of the TEPA loaded Al-Fumarate MOF. In their study, the CC uptake for the 50% TEPA loaded Al-Fum MOF increased from 2.00 mmol g−1 at 45 °C to 3.40 mmol g−1 at 60 °C. But from 60 °C to 100 °C, the CC uptake decreased from 3.40 mmol g−1 to 1.50 mmol g−1. This is also in line with our own study. Similarly, Zhang et al.70 also conducted extensive studies on the CC behaviour of amine loaded porous silica. The TEPA loaded porous silica showed a considerable increase for the 60% TEPA loaded adsorbent from 3.75 mmol g−1 at 30 °C to 5.01 mmol g−1 at 75 °C. However, from there the CC uptake sharply decreased to 3.85 mmol g−1 at 105 °C. Modified carbon nanotubes impregnated with TEPA also displayed the same behaviour.71 A 75% TEPA loaded porous silica displayed an increase in CC from 25 °C to 60 °C and a decrease from there to 80 °C. In contrast to physisorption wherein an increase in process temperature is detrimental to CC uptake, in amine loaded sorption processes the trend is usually hard to predict. Since some degree of chemisorption is involved in amine loaded sorbents, a small increase in temperature could result in a better uptake. This is because at optimal temperatures, 60 °C in the present study, amine spreading across the surface of the parent sorbent would be even, thus promoting high CC uptakes. Furthermore, an increase from this optimal temperature would result in a higher kinetic energy in CO2 molecules, thus decreasing the adsorption uptake values.
5 adsorbent is shown in Fig. 10. The TEPA loaded version of ZIF-8@Na-A gave the highest CC uptake value at 60 °C. For example, the 40% TEPA loaded ZIF-8@Na-A showed an uptake value of 5.01 mmol g−1 at 25 °C. It then increased considerably to 5.89 mmol g−1 at 60 °C and decreased greatly to 4.71 mmol g−1 at 100 °C. Liu et al.69 conducted a thorough investigation of the CC uptake activity of the TEPA loaded Al-Fumarate MOF. In their study, the CC uptake for the 50% TEPA loaded Al-Fum MOF increased from 2.00 mmol g−1 at 45 °C to 3.40 mmol g−1 at 60 °C. But from 60 °C to 100 °C, the CC uptake decreased from 3.40 mmol g−1 to 1.50 mmol g−1. This is also in line with our own study. Similarly, Zhang et al.70 also conducted extensive studies on the CC behaviour of amine loaded porous silica. The TEPA loaded porous silica showed a considerable increase for the 60% TEPA loaded adsorbent from 3.75 mmol g−1 at 30 °C to 5.01 mmol g−1 at 75 °C. However, from there the CC uptake sharply decreased to 3.85 mmol g−1 at 105 °C. Modified carbon nanotubes impregnated with TEPA also displayed the same behaviour.71 A 75% TEPA loaded porous silica displayed an increase in CC from 25 °C to 60 °C and a decrease from there to 80 °C. In contrast to physisorption wherein an increase in process temperature is detrimental to CC uptake, in amine loaded sorption processes the trend is usually hard to predict. Since some degree of chemisorption is involved in amine loaded sorbents, a small increase in temperature could result in a better uptake. This is because at optimal temperatures, 60 °C in the present study, amine spreading across the surface of the parent sorbent would be even, thus promoting high CC uptakes. Furthermore, an increase from this optimal temperature would result in a higher kinetic energy in CO2 molecules, thus decreasing the adsorption uptake values.
5. Thermo-kinetics modelling and analysis
5.1. Adsorption kinetics modelling
To gain deeper insights into the adsorption process under consideration, it is imperative to delve into the realm of kinetic regimes, as they play a crucial role in elucidating the intricacies of adsorption behavior. The study of kinetics is instrumental in distinguishing between physical and chemical adsorption or even a blend of both. Within the framework of this investigation, kinetics modeling was carried out for the optimal conditions established in Section 4.2.2. Five kinetic models were applied, encompassing the pseudo first and second orders (PSO), Avrami kinetics, Elovich model, and the Weber–Morris model, which are mathematically expressed by eqn (1)–(5) respectively. These models bear considerable qualitative significance, as they offer valuable insights into the nature of adsorption processes. The PFO model, for instance, typically suggests a predominance of physisorption, which is generally a reversible process. Conversely, a strong concordance with the PSO model within the experimental data often signifies the prevalence of an irreversible chemisorption process governing the adsorption phenomenon. In essence, the employment of these kinetic models provides a comprehensive understanding of the adsorption mechanism at play, shedding light on the balance between physical and chemical interactions, and helping to discern the fundamental nature of the adsorption process.| Qt = Qe(1 − e−k1t) | (1) |
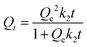 | (2) |
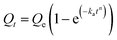 | (3) |
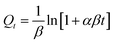 | (4) |
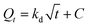 | (5) |
The parameters involved in the kinetic models are as follows:
- Qt: this represents the CC uptake in mmol g−1 at a given time ‘t’.
- Qe: this signifies the equilibrium CC uptake in mmol g−1, denoting the maximum uptake achievable under the given conditions.
- k1, k2, and ka: these are the rate constants associated with the pseudo first order, pseudo second order, and Avrami kinetics, respectively. They play a crucial role in determining the rate of adsorption or reaction occurring during the process.
- α and β: in the context of the Elovich model, ‘α’ represents the rate of initial adsorption, while ‘β’ corresponds to the rate of desorption. These parameters offer insights into the initial adsorption process and the subsequent desorption process.
- Kd: this parameter, known as the Weber–Morris intra-particle diffusion coefficient, pertains to the rate at which the adsorbate molecules or species diffuse within the porous structure of the adsorbent material. It characterizes the intra-particle diffusion process, which is a crucial step in the overall adsorption mechanism.
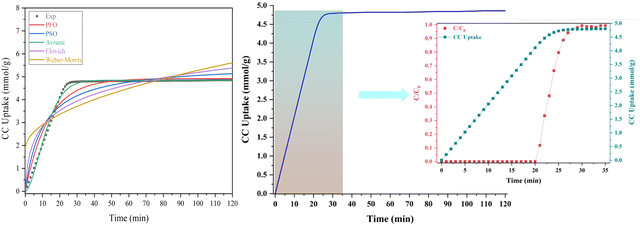
Fig. 11 and Table 6 offer valuable insights into the kinetics of the adsorption process for the adsorbent at hand. It is evident that the maximum CC capacity for the sorbent is rapidly achieved within just 25 minutes, after which the increase in CC uptake levels off. This behavior can be attributed to the limited retention of NaOH within the adsorbents in comparison to their overall volume. Notably, among the various kinetic models assessed, the Avrami model stands out for its superior fit to the experimental data for the process, as demonstrated in the figure. When comparing the determination coefficient (R2) of the PFO model to that of the pseudo second-order (PSO) model, both of which are presented in the table, it is evident that the PFO model provides a reasonably good fit for describing the adsorption kinetics. Surprisingly, the Avrami model emerges as the most appropriate model, with an impressively high R2 value of 0.994, indicating the dual nature of the adsorption process, encompassing both physisorption and chemisorption.
| Kinetic model | Temp. (K) | Q e exp. (mmol g−1) | Q e fit (mmol g−1) | k | n | C | α | β | R 2 |
|---|---|---|---|---|---|---|---|---|---|
| Pseudo first order | 328 | 4.88 | 4.92 | 0.0749 | 0.961 | ||||
| Pseudo second order | 328 | 4.88 | 5.56 | 0.0179 | 0.902 | ||||
| Avrami | 328 | 4.88 | 4.87 | 0.0125 | 1.66 | 0.994 | |||
| Elovich | 328 | 1.448 | 0.951 | 0.801 | |||||
| Weber–Morris | 328 | 0.3468 | 1.809 | 0.605 |
Supporting these findings, the study by Yang et al.72 in 2019, focusing on CO2 adsorption using carbonaceous sorbents pyrolyzed from tree leaves, also found that the PFO model accurately characterizes the adsorption kinetics. Similarly, a research work73 investigating CO2 adsorption onto activated carbons observed a close alignment with pseudo first-order kinetics, consistent with the findings of Yang et al. Additionally, in a subsequent study conducted by the same research group in 2020,74 examining CO2 adsorption onto yellow tuff, the PFO model was once again confirmed as a suitable descriptor. Furthermore, it is important to consider that the predominantly microporous nature of the adsorbent resulted in a swift initial adsorption rate, followed by a sharp deceleration as the micro-pores reached saturation. The Avrami model emerged as the most suitable option for describing the experimental data in comparison to the other models tested.
5.2. Adsorption isotherm modelling
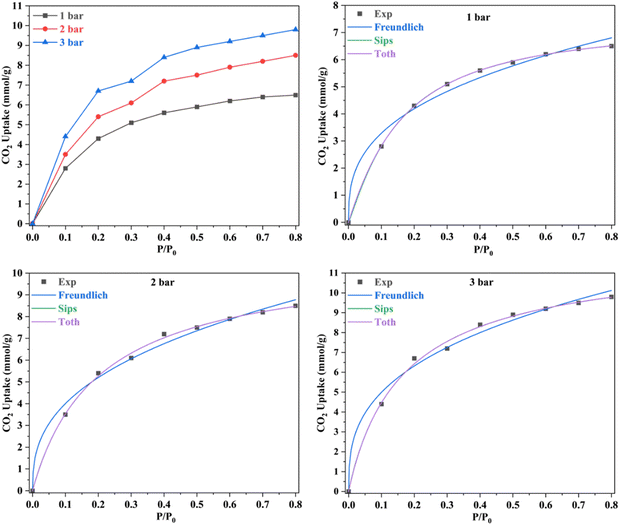
The concentration of CO2 is a crucial determinant in sorption uptake and plays a pivotal role in defining the point of adsorbent bed saturation. In Fig. 11, partial pressures of CO2 were adjusted in the range of 0 to 0.8 bar while maintaining a constant temperature of 298 K to investigate the influence of CO2 concentration on the adsorption process. Our observations revealed that an increase in the CO2 content in the feed corresponded to a higher quantity of CO2 being adsorbed. This trend was particularly noticeable as the CO2 feed percentage increased from 0 to 50, resulting in a nearly threefold increase in CC uptake within this range. However, beyond the 50% mark, the rate of increase became less pronounced, with only a 25% increase in CC uptake levels from 50% to 80%. This phenomenon may be attributed to the fact that, after a certain feed percentage, the adsorption capacity reaches a saturation point, beyond which further increases in CO2 concentration yield diminishing returns. In line with this observation, Li and group75 noted a similar trend in their study on the adsorption of CO2 over activated carbons produced within the temperature range of 540 °C to 800 °C. They found that the enhancement of CC uptake became increasingly marginal as the CO2 feed percentage increased. This behaviour aligns with materials boasting available surface areas exceeding 500 m2 g−1, as reported by Wilson and team.76 Ahmed and group77 also published findings showing a parallel trend in their investigations with TEPA loaded sorbents. They posited that at low CO2 partial pressures, the pores of Na-A quickly and readily become filled, while subsequent increases in CO2 partial pressure result in only marginal additional gains. A similar trend was observed in a study of CO2 adsorption over pure ZIF-8.78 Such behavior is typical for materials predominantly characterized by microporous nature, which is consistent with the nature of the ZIF-8@Na-A adsorbent, primarily exhibiting a microporous structure. Guan et al.79 also studied the adsorption isotherm trends of pure ZIF-8 in their published work. In that work, ZIF-8 was found to follow an increasing trend with an increase in CO2 partial pressure within the feed. The reasons again were attributed to the high microporosity of ZIF-8 itself.The amount of CO2 present is a critical factor in sorption uptake and determines when the adsorbent bed saturates. As seen in Fig. 12, partial pressures of CO2 were adjusted between 0 and 0.8 bar while maintaining a constant temperature of 298 K to examine the impact of CO2 concentration on the adsorption process. It was found that an increase in the feed's CO2 content was accompanied by an increase in the amount of CO2 adsorbed. This tendency was especially noticeable when CO2 feed percentages rose from 0 to 50, which caused the values of CC uptake within this range to nearly triple. But beyond 50%, the pace of rise became less significant. There was just a 25% rise in CC uptake levels from 50% to 80%. Guan et al.79 also worked on ZIF-8 based adsorbents and even there the uptake values increased with increasing CO2 concentration. Similarly, McEwen et al.80 also found the same trend. Four isotherm models, viz., the Langmuir model,81 Freundlich model,82 Sips model83 and Toth model,84 were considered. The Langmuir isotherm model assumes that adsorption occurs at specific sites on the adsorbent surface, and each site can accommodate only one adsorbate molecule. The Freundlich isotherm model is an empirical model that describes multilayer adsorption on heterogeneous surfaces. The Sips isotherm model, also known as the Langmuir-Freundlich or the Langmuir-like model, is a combination of Langmuir and Freundlich models. It allows for both monolayer and multilayer adsorption. The Toth isotherm model is an alternative to the Langmuir model, accommodating multilayer adsorption and heterogeneity.
The mathematical expressions for these isotherms are presented in eqn (6)–(9), respectively.
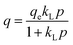 | (6) |
| q = kFp1/n | (7) |
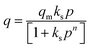 | (8) |
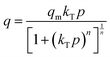 | (9) |
Within the context of these isotherms,
– ‘q’ denotes the quantity of CO2 adsorbed at a specific time ‘t’;
– ‘qm’ signifies the monolayer uptake, indicating the maximum capacity of the adsorbent for CO2 adsorption;
– ‘kL’, ‘kF’, ‘kS’, and ‘kT’ represent the adsorption constants associated with the Langmuir, Freundlich, Sips, and Toth isotherms, respectively. These constants play a pivotal role in determining the characteristics of the adsorption process and the affinity of the adsorbent for the adsorbate;
– 'n' is a parameter utilized to measure the heterogeneity in the Sips and Toth models. It provides insights into the non-uniformity of adsorption sites and the distribution of energies available for adsorption on the adsorbent surface.
The R2 values presented in Tables 7 and 8 indicate that the Langmuir isotherm model was not a good fit for the adsorbent across all three process pressures. For the ZIF-8@Na-A adsorbent, the Langmuir model did not fit at all for the considered pressures. In contrast, the Freundlich model achieved R2 values of 0.981, 0.988, and 0.987 at 1 bar, 2 bar, and 3 bar, respectively. Although the Sips model slightly outperformed the Toth model, as shown in Table 8, this suggests a mixed adsorption nature comprising both monolayer and multilayer characteristics. The compatibility of the Sips model with heterogeneous adsorbent surfaces aligns with the composite nature of the adsorbents. The nature of adsorption is heavily influenced by pore characteristics, as illustrated by the study on CO2 uptake over TEPA-modified TiO2 by Kapica-Kozar and colleagues.85 Similarly, in the studies by Azeem et al.86 on KOH activated porous carbons and by Melouki et al.87 on carbons derived from olive waste, the Sips model demonstrated an excellent fit to experimental data, with the Toth model being a close second. Yongha Park et al.'s comparative study88 involving activated carbon and zeolite-LiX for CO2 uptake also favored the Sips model for both adsorbents. However, Sun et al.'s89 investigation of CO2 adsorption on graphene with an average pore size of 3 nm highlighted Langmuir adsorption behavior, despite surface multilayer adsorption. Regarding the tested adsorbents, ZIF-8@Na-A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 exhibited a microporous nature indicating the presence of narrow, elongated pores within its structure. Adsorbents with such narrow micropores often exhibit heightened CO2 uptake rates under high process pressures. ZIF-8, being a framework with these narrow pores, capitalizes on the pressure differential, a pivotal factor for adsorption at elevated pressures. This inherent property makes MOFs and ZIFs well-suited for high-pressure adsorption processes. ZIF-8@Na-A also portrays a primarily microporous character. However, unlike pure ZIF-8, this composite showcases a significant decrease in microporosity. At lower process pressures, the micropores saturate rapidly, following a nearly linear trend. Subsequent increments are marginal, indicating gradual filling of existing mesopores.
5 exhibited a microporous nature indicating the presence of narrow, elongated pores within its structure. Adsorbents with such narrow micropores often exhibit heightened CO2 uptake rates under high process pressures. ZIF-8, being a framework with these narrow pores, capitalizes on the pressure differential, a pivotal factor for adsorption at elevated pressures. This inherent property makes MOFs and ZIFs well-suited for high-pressure adsorption processes. ZIF-8@Na-A also portrays a primarily microporous character. However, unlike pure ZIF-8, this composite showcases a significant decrease in microporosity. At lower process pressures, the micropores saturate rapidly, following a nearly linear trend. Subsequent increments are marginal, indicating gradual filling of existing mesopores.
| Adsorbent | Total pressure (bar) | Freundlich | ||
|---|---|---|---|---|
| k F | n | R 2 | ||
| ZIF-8@Na-A | 1 | 7.38 | 2.86 | 0.981 |
| 2 | 9.55 | 2.65 | 0.988 | |
| 3 | 10.64 | 2.94 | 0.987 | |
| Adsorbent | Total pressure (bar) | Sips | Toth | ||||||
|---|---|---|---|---|---|---|---|---|---|
| k S | Q m (mmol g−1) | n | R 2 | Q m (mmol g−1) | k T | n | R 2 | ||
| ZIF-8@Na-A | 1 | 8.4421 | 7.51 | 1.15 | 0.999 | 4.95 | 7.5638 | 1.25 | 0.998 |
| 2 | 4.6015 | 10.75 | 0.98 | 0.998 | 11.77 | 4.6891 | 0.95 | 0.994 | |
| 3 | 5.2541 | 12.08 | 0.96 | 0.998 | 14.34 | 5.4513 | 0.92 | 0.996 | |
5.3. Adsorption thermodynamics
The heat of adsorption was calculated using the Clausius–Clapeyron equation. Three temperatures, specifically 298 K, 313 K, and 328 K, were considered under a process pressure of 1 bar. The resulting plots, illustrating the relationship between 1/T (reciprocal temperature) and the natural logarithm of pressure (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P), are displayed in Fig. 13. These plots allowed valuable insights to be gained into the thermodynamics of the adsorption process and the energetics associated with CO2 uptake on the surfaces of the adsorbent at various temperatures.
P), are displayed in Fig. 13. These plots allowed valuable insights to be gained into the thermodynamics of the adsorption process and the energetics associated with CO2 uptake on the surfaces of the adsorbent at various temperatures.
In this investigation, eight distinct uptake values were scrutinized for ZIF-8@Na-A, encompassing a loading range from 1 mmol g−1 to 4.5 mmol g−1. The resulting analysis unveiled an average heat of adsorption for the ZIF-8@Na-A adsorbent at these loading levels, yielding a value of approximately −11.05 kJ kmol−1. Remarkably, this figure aligns closely with the typical range observed for pure ZIF-8. Fischer and Bell (2014) had previously reported heat of adsorption values for pure ZIF-8 that spanned from −12.0 to −19.5 kJ mol−1, while simulations consistently indicated heat of adsorption values ranging between −14.0 and −19.0 kJ mol−1.90 A parallel study by Russell and Migone91 disclosed that the heat of adsorption for modified ZIF-8 structures was around −18 kJ mol−1. Given the favorable fit of the Sips isotherm to our data, it was selected for the calculation of the isosteric heat of adsorption. This parameter serves as a fundamental indicator of the adsorbent's affinity for CO2 molecules and imparts critical insights into the thermodynamics governing the adsorption process.
6. Cyclic stability
Cyclic stability tests were carried out to thoroughly assess the durability and performance stability of the adsorbents over repeated usage. In each cycle, a standard sample weighing 5 grams was introduced into the reactor, and carbonation was conducted at a constant temperature of 298 K. The feed gas consisted of a mixture of N2 and CO2, with a total feed flow rate of 150 mL min−1, and CO2 constituted roughly one-sixth of the gaseous feed composition. Following each cycle of carbonation, the process of decarbonation or regeneration was executed at a temperature of 150 °C in an inert atmosphere. The selection of this temperature was deliberate, aimed at preserving the capacity of ZIF-8, as it is known to be sensitive to excessive heat exposure. The cyclic retention performance is graphically presented in Fig. 14. Remarkably, the adsorbent exhibited exceptional stability even after subjecting it to the rigors of 50 cycles of carbonation and regeneration. For the ZIF-8@Na-A adsorbent, which initially demonstrated a CC value of 3.45 mmol g−1 at 298 K, its CC uptake after 50 cycles remained impressively high at approximately 3.03 mmol g−1. This level of stability is particularly noteworthy considering the inclusion of ZIF-8 within the composite. Generally, zeolitic imidazolate frameworks (ZIFs) and metal–organic frameworks (MOFs) are known to be highly susceptible to degradation when repeatedly exposed to elevated temperatures. Notably, the ZIF-8@Na-A adsorbent exhibited a subtle change in colour, transitioning from its usual white appearance to a very pale tint of yellow after completing 50 cycles. A marginal loss of only nine percentage points over the course of 50 cyclic processes is indeed negligible. The cyclic performance of the adsorbent is visually depicted in Fig. 14, underscoring the remarkable stability achieved even under rigorous testing conditions.Fig. 15 clearly indicates the diminishing peaks between 7° and 24°, demonstrating the reduction in ZIF-8 intensity. This decrease in peak intensity suggests partial material degradation of ZIF-8 after 50 cycles. The BET surface area values further support this interpretation. Initially, the adsorbent had a specific surface area of 476 m2 g−1, which decreased to 424 m2 g−1 after 50 cycles. This decline in surface area corroborates the XRD data, indicating that ZIF-8 within the composite underwent partial degradation. The degradation of ZIF-8 can be attributed to the repeated cycling process, which likely causes structural breakdown and loss of crystallinity. This structural degradation is reflected in the XRD patterns, where the characteristic peaks of ZIF-8 become less pronounced. The diminishing intensity of these peaks between 7° and 24° signifies a loss of the ordered crystalline structure, which is essential for maintaining high surface area and porosity. The BET surface area analysis provides quantitative evidence of this structural degradation. The significant drop from 476 m2 g−1 to 424 m2 g−1 after 50 cycles indicates a reduction in the number of available adsorption sites, which is critical for the material's performance in CO2 capture. This reduction in surface area is directly linked to the loss of the ZIF-8 framework, further supporting the XRD findings. The partial degradation of ZIF-8 has a direct impact on the CO2 uptake capacity of the adsorbent. As the structural integrity of ZIF-8 diminishes, the material's ability to adsorb CO2 is compromised. This is because the high surface area and porosity of ZIF-8 are key factors in its efficiency as a CO2 adsorbent. The combined evidence from XRD and BET surface area analyses clearly indicates that the ZIF-8 within the composite undergoes partial degradation after 50 cycles.
Table 9 shows that the adsorbent synthesized in this study performs better than most other adsorbents. This includes both modified and unmodified adsorbents from the literature. Even after a period of 50 cycles, the adsorbent in the current study performed better than most of the reported sorbents in the table. The LiX@ZIF-8 adsorbent could retain around 71% of its initial CC uptake values after a period of 50 cycles. It is interesting to note from simulation studies that the Mg-MOF-74 adsorbent exhibited a good capture capacity of 5.77 mmol g−1 even upto 90 cycles. The rest of the adsorbents showed good retention capacities only for lower durations. Their efficiency for an increased duration time is yet to studied.
| S. No. | Adsorbent | Initial uptake (mmol g−1) | Number of cycles | Cyclic retention (%) | Ref. |
|---|---|---|---|---|---|
| 1 | SZX | 1.97 | 5 | 99 | 93 |
| 2 | Zeolite@carboHIPE | 1.35 | 15 | 70 | 94 |
| 3 | HZ2 | 4.00 | 5 | 99 | 95 |
| 4 | HZ4A-1-3 | 2.75 | 10 | 82 | 96 |
| 5 | ZIF-8@MCM-41 | 3.03 | 15 | 95 | 59 |
| 6 | (Ce, Zn) ZIF-8 | 3.71 | 15 | 94 | 60 |
| 7 | HZSM-5/AEEA | 4.44 | 10 | 75 | 97 |
| 8 | NaA-1.0 | 4.34 | 10 | 99 | 98 |
| 9 | Mg-MOF-74 | 5.77 | 90 | 95 | 92 |
| 10 | IBA-Z4A | 2.50 | 5 | 99 | 99 |
| 11 | PEI/MCS/PEG | 4.25 | 10 | 95 | 100 |
| 12 | 50 wt% MgO@ZIF-8 | 1.30 | 5 | 88 | 101 |
| 13 | 15TETA/ZIF-8 | 2.45 | 4 | 95 | 102 |
| 14 | LiX@ZIF-8-I | 1.75 | 50 | 71 | 35 |
| 15 | ZIF-8@Na-A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
3.48 | 50 | 92 | This work |
7. Conclusions
Through in situ synthesis techniques, novel composites were successfully synthesized. Systematic carbon capture (CC) uptake experiments were conducted on these adsorbents, employing RSM for process standardization.• BET analysis revealed that the ZIF-8@Na-A adsorbent demonstrated a diminished surface area compared to its parent materials. This decrease in surface area was further confirmed by scanning electron micrographs, which clearly depicted the presence of ZIF-8 formed upon the surface of Na-A.
• An increase in TEPA loading had a positive impact on CC uptake, with the maximum uptake achieved at a TEPA loading of 40%.
• Process pressure exhibited a favourable effect on CC uptake, with the highest recorded CC uptake values occurring at 3 bar pressure.
• The adsorption models derived through CCD modeling were found to align exceptionally well with the experimental data. Experiments conducted at the optimal values recommended by the CCD model closely matched the standard deviation values predicted by the model, affirming the reliability of the model's predictions.
• The Avrami model for kinetics provided a highly effective description of the adsorption kinetics, as indicated by an R2 value of 0.994.
• Sips adsorption modelling proved to be a robust method for explaining the experimental data, suggesting a combination of monolayer and multilayer adsorption mechanisms.
• The average heat of adsorption, calculated at −11.78 kJ mol−1, underscored the predominantly physical nature of the adsorption process, revealing that it was driven primarily by physisorption interactions.
• Impressively, the adsorbent exhibited exceptional cyclic performance, retaining over 92% of its initial adsorption capacities even after 50 cycles. Notably, ZIF-8@Na-A exhibited a subtle change in colour, shifting to a slightly pale-yellow hue after these repeated cycles, which may indicate the possibility of thermal alteration in response to the cyclic conditions.
In the realm of future research, there exists an exciting opportunity to delve deeper into the intricate relationship between synthesis parameters and the physicochemical attributes of composite materials. Specifically, key factors such as the metal-to-ligand ratio, the selection of synthesis temperature, and the choice of solvent are poised to take the centre stage. These parameters are known to exert a significant influence on the overall morphology and structural characteristics of the composites that have been the subject of this study. Understanding how these variables interact and impact the composite materials can provide valuable insights, not only in terms of optimizing synthesis processes but also in tailoring the properties of these materials for specific applications. This avenue of exploration holds great promise for advancing the field of composite materials and unlocking their full potential in various scientific and industrial domains.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this research work.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The authors extend their heartfelt gratitude to the Council of Scientific and Industrial Research (CSIR), Government of India, for sponsoring the project under the Scheme 22(0783)/19/EMR-II. They also wish to express their gratitude to BITS Pilani Hyderabad Campus for their invaluable support and facilitation of this project. Furthermore, the authors would like to acknowledge the Central Analytical Laboratory (CAL) at BITS Pilani HYD campus for their indispensable assistance, providing access to the essential analytical tools.References
- R. Aniruddha, I. Sreedhar and B. M. Reddy, J. CO2 Util., 2020, 42, 101297 CrossRef CAS.
- L. Valencia and H. N. Abdelhamid, Carbohydr. Polym., 2019, 213, 338–345 CrossRef CAS PubMed.
- J. Wang, S. Cui, Z. Li, S. Wen, P. Ning, S. Lu, P. Lu, L. Huang and Q. Wang, Chem. Eng. J., 2021, 415, 128859 CrossRef CAS.
- C. W. Chang, Y. H. Kao, P. H. Shen, P. C. Kang and C. Y. Wang, J. Hazard. Mater., 2020, 400, 122974 CrossRef PubMed.
- N. E. Tari, A. Tadjarodi, J. Tamnanloo and S. Fatemi, Microporous Mesoporous Mater., 2016, 231, 154–162 CrossRef CAS.
- R. Aniruddha and I. Sreedhar, Environ. Sci. Pollut. Res., 2021, 1, 1–10 Search PubMed.
- B. Sreenivasulu, I. Sreedhar, B. M. Reddy and K. V. Raghavan, Energy Fuels, 2017, 31, 785–794 CrossRef CAS.
- Z. Zhang, Y. Xiao, B. Wang, Q. Sun and H. Liu, Energy Procedia, 2017, 114, 2537–2544 CrossRef CAS.
- T. F. de Aquino, S. T. Estevam, V. O. Viola, C. R. M. Marques, F. L. Zancan, L. B. Vasconcelos, H. G. Riella, M. J. R. Pires, R. Morales-Ospino, A. E. B. Torres, M. Bastos-Neto and C. L. Cavalcante, Fuel, 2020, 276, 118143 CrossRef.
- J. Pokhrel, N. Bhoria, S. Anastasiou, T. Tsoufis, D. Gournis, G. Romanos and G. N. Karanikolos, Microporous Mesoporous Mater., 2018, 267, 53–67 CrossRef CAS.
- A. Huang and B. Feng, Int. J. Hydrogen Energy, 2018, 43, 2224–2231 CrossRef CAS.
- S. Xian, F. Xu, C. Ma, Y. Wu, Q. Xia, H. Wang and Z. Li, Chem. Eng. J., 2015, 280, 363–369 CrossRef CAS.
- S. Xian, F. Xu, C. Ma, Y. Wu, Q. Xia, H. Wang and Z. Li, Chem. Eng. J., 2015, 280, 363–369 CrossRef CAS.
- E. E. Unveren, B. O. Monkul, S. Sarioglan, N. Karademir and E. Alper, Petroleum, 2017, 3, 37–50 CrossRef.
- S. Ahsan, A. Ayub, D. Meeroff and M. Jahandar Lashaki, Chem. Eng. J., 2022, 437, 135139 CrossRef CAS.
- R. Thiruvenkatachari, S. Su, X. X. Yu and J. S. Bae, Int. J. Greenhouse Gas Control, 2013, 13, 191–200 CrossRef CAS.
- X. Zhao, Q. Cui, B. Wang, X. Yan, S. Singh, F. Zhang, X. Gao and Y. Li, Chin. J. Chem. Eng., 2018, 2292–2302 CrossRef CAS.
- N. Hedin, L. Chen and A. Laaksonen, Nanoscale, 2010, 2, 1819–1841 RSC.
- R. Habibi, F. Pourfayaz, M. Mehrpooya and H. Kamali, Sustainable Energy Technol. Assess., 2022, 52, 101984 CrossRef.
- M. Marczak-Grzesik, P. Piersa, M. Karczewski, S. Szufa, H. Ünyay, A. Kędzierska-Sar and P. Bochenek, Energies, 2021, 14, 7101 CrossRef CAS.
- J. Rosen, T. Geary, A. Hilmi, R. Blanco-Gutierrez, C.-Y. Yuh, C. S. Pereira, L. Han, R. A. Johnson, C. A. Willman, H. Ghezel-Ayagh and T. A. Barckholtz, J. Electrochem. Soc., 2020, 167, 64505 CrossRef CAS.
- D. Bahamon and L. F. Vega, Chem. Eng. J., 2016, 284, 438–447 CrossRef CAS.
- J. Schell, N. Casas, D. Marx, R. Blom and M. Mazzotti, Energy Procedia, 2013, 37, 167–174 CrossRef CAS.
- X. Zhu, T. Ge, F. Yang and R. Wang, Renewable Sustainable Energy Rev., 2021, 137, 110651 CrossRef CAS.
- R. T. Maruyama, K. N. Pai, S. G. Subraveti and A. Rajendran, Int. J. Greenhouse Gas Control, 2020, 102902 CrossRef CAS.
- K. N. Pai, J. D. Baboolal, D. A. Sharp and A. Rajendran, Sep. Purif. Technol., 2019, 211, 540–550 CrossRef CAS.
- E. Grabias-Blicharz, R. Panek, M. Franus and W. Franus, Materials, 2022, 15, 7174 CrossRef CAS PubMed.
- Y. Zhao, B. Zhang, X. Zhang, J. Wang, J. Liu and R. Chen, J. Hazard. Mater., 2010, 178, 658–664 CrossRef CAS PubMed.
- Y. Jiang, H. Qi, J. Wang, X. Sun, C. Lyu, P. Lu, R. Yang, A. Noreen, C. Xing and N. Tsubaki, Ind. Eng. Chem. Res., 2022, 61, 1725–1732 CrossRef CAS.
- L. Chen, Y. Peng, H. Wang, Z. Gu and C. Duan, Chem. Commun., 2014, 50, 8651–8654 RSC.
- S. Luanwuthi, A. Krittayavathananon, P. Srimuk and M. Sawangphruk, RSC Adv., 2015, 5, 46617–46623 RSC.
- Z. Zhang, S. Xian, H. Xi, H. Wang and Z. Li, Chem. Eng. Sci., 2011, 66, 4878–4888 CrossRef CAS.
- Z. Jiang, J. Yang, H. Ma, X. Ma and J. Yuan, Clean Technol. Environ. Policy, 2016, 18, 629–637 CrossRef CAS.
- D. Novembre, B. di Sabatino, D. Gimeno and C. Pace, Clay Miner., 2011, 46, 339–354 CrossRef CAS.
- F. Yang, J. Wu, X. Zhu, T. Ge and R. Wang, Chem. Eng. J., 2021, 410, 128322 CrossRef CAS.
- P. F. Liu, K. Tao, G. C. Li, M. K. Wu, S. R. Zhu, F. Y. Yi, W. N. Zhao and L. Han, Dalton Trans., 2016, 45, 12632–12635 RSC.
- T. Chokbunpiam, S. Fritzsche, C. Chmelik, J. Caro, W. Janke and S. Hannongbua, J. Phys. Chem. C, 2016, 120, 23458–23468 CrossRef CAS.
- X. Zhang, S. Zhang, H. Yang, Y. Feng, Y. Chen, X. Wang and H. Chen, Chem. Eng. J., 2014, 257, 20–27 CrossRef CAS.
- R. V. Siriwardane, M. S. Shen, E. P. Fisher and J. Losch, Energy Fuels, 2005, 19, 1153–1159 CrossRef CAS.
- Y. Wang, T. Du, H. Jia, Z. Qiu and Y. Song, Solid State Sci., 2018, 86, 24–33 CrossRef CAS.
- K. Yang, G. Yang and J. Wu, Chem. Eng. J., 2021, 404, 127056 CrossRef CAS.
- O. Cheung, Z. Bacsik, Q. Liu, A. Mace and N. Hedin, Appl. Energy, 2013, 112, 1326–1336 CrossRef CAS.
- S. Lowell and J. E. Shields, Powder Surface Area and Porosity, 1991, pp. 11–13 Search PubMed.
- H. Ramezanipour Penchah, A. Ghaemi and H. Ganadzadeh Gilani, Energy Fuels, 2019, 33, 12578–12586 CrossRef CAS.
- B. Sreenivasulu, I. Sreedhar, A. S. Singh and A. Venugopal, Energy Fuels, 2018, 32, 3716–3725 CrossRef CAS.
- S. R. Hosseini, M. Omidkhah, Z. Mehri Lighvan, S. Norouzbahari and A. Ghadimi, Sep. Purif. Technol., 2023, 307, 122679 CrossRef CAS.
- F. Yang, X. Zhu, J. Wu, R. Wang and T. Ge, Powder Technol., 2022, 399, 117090 CrossRef CAS.
- A. U. Khan, T. Noor, N. Iqbal, N. Zaman and Z. Hussain, J. Mater. Sci., 2023, 58, 3947–3959 CrossRef CAS.
- S. R. Hosseini, M. Omidkhah, Z. Mehri Lighvan, S. Norouzbahari and A. Ghadimi, Sep. Purif. Technol., 2023, 307, 122679 CrossRef CAS.
- L. Yin, D. Li, S. Li, F. Gai, T. Zhang, Y. Liu and X. Zhao, J. Dispers. Sci. Technol., 2023, 44, 2303–2310 CrossRef CAS.
- Y. Shi, G. Tian, R. Ni, L. Zhang, W. Hu and Y. Zhao, Sep. Purif. Technol., 2023, 322, 124356 CrossRef CAS.
- M. Boscherini, F. Miccio, E. Papa, V. Medri, E. Landi, F. Doghieri and M. Minelli, Chem. Eng. J., 2021, 408, 127315 CrossRef CAS.
- E. Luzzi, P. Aprea, M. S. De Luna, D. Caputo and G. Filippone, ACS Appl. Mater. Interfaces, 2021, 13, 20728–20734 CrossRef CAS PubMed.
- E. Khoramzadeh, M. Mofarahi, K. Chung and C. H. Lee, Sep. Purif. Technol., 2022, 280, 119917 CrossRef CAS.
- S. Candamano, A. Policicchio, G. Conte, R. Abarca, C. Algieri, S. Chakraborty, S. Curcio, V. Calabrò, F. Crea and R. G. Agostino, J. Cleaner Prod., 2022, 330, 129843 CrossRef CAS.
- F. Gan, B. Wang, Z. Jin, L. Xie, Z. Dai, T. Zhou and X. Jiang, Sci. Total Environ., 2021, 768, 144529 CrossRef CAS PubMed.
- B. Guo, J. Zhang, Y. Wang, X. Qiao, J. Xiang and Y. Jin, Energy, 2023, 263, 125764 CrossRef CAS.
- R. Aniruddha and I. Sreedhar, Environ. Sci. Pollut. Res., 2023, 30, 8393–8402 CrossRef CAS PubMed.
- R. Aniruddha, I. Sreedhar and B. M. Reddy, J. CO2 Util., 2022, 64, 102182 CrossRef CAS.
- R. Aniruddha, V. M. Shama, I. Sreedhar and C. M. Patel, J. Cleaner Prod., 2022, 350, 131478 CrossRef CAS.
- Y. Cao, F. Song, Y. Zhao and Q. Zhong, J. Environ. Sci., 2013, 25, 2081–2087 CrossRef CAS PubMed.
- K. M. Gilbert, E. N. Kirby, I. Escala, Z. Yuan, M. Du, M. S. R. M. Nasir, M. P. Khairunnisa, N. W. C. Jusoh and A. A. Jalil, IOP Conf. Ser.: Mater. Sci. Eng., 2020, 808, 012031 Search PubMed.
- A. Alkhouzaam, H. Abdelrazeq, M. Khraisheh, F. Almomani, B. H. Hameed, M. K. Hassan, M. A. Al-Ghouti and R. Selvaraj, Nanomaterials, 2022, 12, 1240 CrossRef CAS PubMed.
- Q. Ye, J. Jiang, C. Wang, Y. Liu, H. Pan and Y. Shi, Energy Fuels, 2012, 26, 2497–2504 CrossRef CAS.
- H. Kaur, G. C. Mohanta, V. Gupta, D. Kukkar and S. Tyagi, J. Drug Delivery Sci. Technol., 2017, 41, 106–112 CrossRef CAS.
- F. S. Taheri, A. Ghaemi and A. Maleki, Energy Fuels, 2019, 33, 11465–11476 CrossRef CAS.
- S. Li, S. Jia, T. Nagasaka, H. Bai and L. Yang, Sustainability, 2023, 15, 10144 CrossRef CAS.
- P. Zhao, G. Zhang, Y. Xu and Y. Lv, J. CO2 Util., 2019, 34, 543–557 CrossRef CAS.
- Q. Liu, Y. Ding, Q. Liao, X. Zhu, H. Wang and J. Yang, Colloids Surf., A, 2019, 579, 123645 CrossRef CAS.
- G. Zhang, P. Zhao and Y. Xu, J. Ind. Eng. Chem., 2017, 54, 59–68 CrossRef CAS.
- M. Irani, A. T. Jacobson, K. A. M. Gasem and M. Fan, Fuel, 2017, 206, 10–18 CrossRef CAS.
- G. Yang, S. Song, J. Li, Z. Tang, J. Ye and J. Yang, J. Mater. Sci. Technol., 2019, 35, 875–884 CrossRef CAS.
- P. Ammendola, F. Raganati and R. Chirone, Chem. Eng. J., 2017, 322, 302–313 CrossRef CAS.
- P. Ammendola, F. Raganati, R. Chirone and F. Miccio, Powder Technol., 2020, 373, 446–458 CrossRef CAS.
- D. Li, J. Zhou, Y. Wang, Y. Tian, L. Wei, Z. Zhang, Y. Qiao and J. Li, Fuel, 2019, 238, 232–239 CrossRef CAS.
- S. M. W. Wilson, F. Al-Enzi, V. A. Gabriel and F. H. Tezel, Microporous Mesoporous Mater., 2021, 322, 111089 CrossRef CAS.
- S. Ahmed, A. Ramli, S. Yusup and M. Farooq, Chem. Eng. Res. Des., 2017, 122, 33–42 CrossRef CAS.
- D. Liu, Y. Wu, Q. Xia, Z. Li and H. Xi, Adsorption, 2013, 19, 25–37 CrossRef CAS.
- Y. Guan, J. Shi, M. Xia, J. Zhang, Z. Pang, A. Marchetti, X. Wang, J. Cai and X. Kong, Appl. Surf. Sci., 2017, 423, 349–353 CrossRef CAS.
- J. McEwen, J. D. Hayman and A. Ozgur Yazaydin, Chem. Phys., 2013, 412, 72–76 CrossRef CAS.
- S. Alafnan, A. Awotunde, G. Glatz, S. Adjei, I. Alrumaih and A. Gowida, J. Pet. Sci. Eng., 2021, 207, 109172 CrossRef CAS.
- Gautam, R. P. Sah and S. Sahoo, Sādhanā, 2023, 48, 1–37 Search PubMed.
- L. Feng, Y. Shen, T. Wu, B. Liu, D. Zhang and Z. Tang, Adsorption, 2020, 26, 1101–1111 CrossRef CAS.
- C. Chilev, M. Dicko, P. Langlois and F. Lamari, Metals, 2022, 12, 1698 CrossRef CAS.
- J. Kapica-Kozar, B. Michalkiewicz, R. J. Wrobel, S. Mozia, E. Piróg, E. Kusiak-Nejman, J. Serafin, A. W. Morawski and U. Narkiewicz, New J. Chem., 2017, 41, 7870–7885 RSC.
- A. Sarwar, M. Ali, A. H. Khoja, A. Nawar, A. Waqas, R. Liaquat, S. R. Naqvi and M. Asjid, J. CO2 Util., 2021, 46, 101476 CrossRef CAS.
- R. Melouki, A. Ouadah and P. L. Llewellyn, J. CO2 Util., 2020, 42, 101292 CrossRef CAS.
- Y. Park, D. K. Moon, Y. H. Kim, H. Ahn and C. H. Lee, Adsorption, 2014, 20, 631–647 CrossRef CAS.
- J. Sun, C. Chen, Y. Zhang, W. Li and Y. Song, Chem. Eng. J., 2022, 430, 133172 CrossRef CAS.
- M. Fischer and R. G. Bell, CrystEngComm, 2014, 16, 1934–1949 RSC.
- B. Russell and A. Migone, Microporous Mesoporous Mater., 2017, 246, 178–185 CrossRef CAS.
- N. A. A. Qasem and R. Ben-Mansour, Appl. Energy, 2018, 230, 1093–1107 CrossRef CAS.
- T. F. de Aquino, S. T. Estevam, V. O. Viola, C. R. M. Marques, F. L. Zancan, L. B. Vasconcelos, H. G. Riella, M. J. R. Pires, R. Morales-Ospino, A. E. B. Torres, M. Bastos-Neto and C. L. Cavalcante, Fuel, 2020, 276, 118143 CrossRef.
- M. Mazaj, M. Bjelica, E. Žagar, N. Z. Logar and S. Kovačič, ChemSusChem, 2020, 13, 2089–2097 CrossRef CAS PubMed.
- M. Kim, J. W. Lee, S. Kim and Y. T. Kang, J. Cleaner Prod., 2022, 337, 130597 CrossRef CAS.
- D. Panda, E. A. Kumar and S. K. Singh, J. CO2 Util., 2020, 40, 101223 CrossRef CAS.
- H. Cheng, H. Song, S. Toan, B. Wang, K. A. M. Gasem, M. Fan and F. Cheng, Chem. Eng. J., 2021, 406, 126882 CrossRef CAS.
- X. Zhou, S. Shi, B. Ding, H. Jia, P. Chen, T. Du and Y. Wang, Environ. Sci. Pollut. Res., 2023, 30, 102803 CrossRef CAS PubMed.
- D. Panda, E. A. Kumar and S. K. Singh, Ind. Eng. Chem. Res., 2019, 58, 5301–5313 CrossRef CAS.
- M. Wang, L. Yao, J. Wang, Z. Zhang, W. Qiao, D. Long and L. Ling, Appl. Energy, 2016, 168, 282–290 CrossRef CAS.
- C. W. Chang, Y. H. Kao, P. H. Shen, P. C. Kang and C. Y. Wang, J. Hazard. Mater., 2020, 400, 122974 CrossRef PubMed.
- A. Mohammadi and A. Nakhaei Pour, J. CO2 Util., 2023, 69, 102424 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00597j |
| This journal is © The Royal Society of Chemistry 2024 |