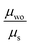Open Access Article
Open Access ArticleImpact of static and dynamic disorder effects on the charge transport properties of merocyanine single crystals†
Nora
Gildemeister‡
a,
Sven
Geller‡
 a,
Robert
Herzhoff
a,
Fabrizia
Negri
a,
Robert
Herzhoff
a,
Fabrizia
Negri
 b,
Klaus
Meerholz
*a and
Daniele
Fazzi
b,
Klaus
Meerholz
*a and
Daniele
Fazzi
 *ab
*ab
aInstitut für Licht und Materialien, Department für Chemie, Universität zu Köln, Greinstr. 4-6, 50939 Köln, Germany. E-mail: klaus.meerholz@uni-koeln.de
bUniversità di Bologna, Dipartimento di Chimica ‘Giacomo Ciamician’, Via P. Gobetti, 85, 40129 Bologna, Italy. E-mail: daniele.fazzi@unibo.it
First published on 20th September 2024
Abstract
Merocyanines are polar organic π-conjugated molecules consisting of electronic donor (D) and acceptor (A) subunits connected via a conjugated bridge. They have been investigated because of their unique self-assembly and optoelectronic properties, making them ideal active materials for organic electronic applications. The understanding of their charge transport properties at the nanoscale is very challenging and mostly an unexplored field. We report a theoretical study on modelling the hole transport parameters and mobility, together with the investigation of the structure–property relationships of seven merocyanine single crystals, consisting of different combinations of D–A units. We critically discuss the impact of both static (energetic) and dynamic (thermal) disorder effects on charge mobility and transport networks, by emphasizing the importance of including such contributions for an in-depth understanding of the charge transport properties of polar organic semiconductors.
Introduction
Merocyanines are polar organic π-conjugated molecules consisting of electron donor (D) and acceptor (A) subunits connected via a methine bridge. They have been studied for their self-assembly and optoelectronic properties, and they have been tested in the field of organic electronics (OE), namely nonlinear optical devices, photorefractivity,1,2 photodetectors, organic solar cells (OSCs),3 and organic field effect transistors (OFETs).4 Merocyanines are considered as ideal model systems to investigate the dipole–dipole interaction at the molecular scale, allowing the elucidation of both ground and excited state mechanisms governing the response functions in the solid state.5 Structure–property relationships were drawn by correlating the self-assembly characteristics with the charge and exciton transfer properties. Würthner et al. demonstrated how different D–A units, as well as the length, steric hindrance and flexibility of the lateral groups (e.g., solubilizing alkyl substituents) can remarkably influence the packing in the solid state and consequently the optical response of merocyanines, leading to sharp and well-defined J- or H-bands in the absorption spectrum.6Extensive experimental investigations were also carried out to rationalize the charge transport properties. Seminal contributions by Würthner and Meerholz7 highlighted the correlation between the merocyanine molecular packing in single crystals and the charge mobility. For crystals characterized by a hole mobility of μ > 0.05 cm2 V−1 s−1, merocyanines are organized in one-dimensional (1D) columns or 2D brickwork-type architectures.4 By optimizing the casting conditions to create extended single-crystalline domains, hole mobilities as high as 2.34 cm2 V−1 s−1 were measured in a single-crystal organic field effect transistor (SC-OFET), reaching similar performance levels as classical organic semiconductors, such as those based on acenes, naphthalenediimides or oligothiophenes.8
In contrast, few theoretical and computational investigations are present in the literature. Engels et al. first modelled the intra-molecular charge transport properties of a series of merocyanines, highlighting the impact of the cyanine-like structure in affecting both charge and exciton reorganization energy.9 Recently, we reported an extended computational study by modelling the intra- and inter-molecular charge transport (CT) properties of a library of merocyanines consisting of various donor and acceptor groups.9 For the CT intra-molecular properties (e.g., internal reorganization energy), we found that constrained density functional theory (C-DFT) is an effective method to describe the ground state bond length alternation (BLA) pattern of merocyanines in condensed phases, leading to hole reorganization energies (λ) of the order of 120–280 meV. Through the evaluation of electronic coupling integrals (J) and the use of a charge diffusion (hopping) kinetic-Monte Carlo algorithm, we computed the hole mobility for six merocyanine single-crystals belonging to the D1A1 species (D1 – 2-aminothiophene and A1 – 2-(4-alkylthiazol-2(3H)-ylidene)malonitrile, see the chemical structure in Fig. 1), and one crystal belonging to the D2A1 species (D2 – 1-butyl-3,3-dimethylindolin-2-ylidene (‘Fischer base’)). In agreement with experimental data, we found that the hole mobility maximizes when the merocyanines are packed in slipped, antiparallel, pairs arranged in 2D interconnected architectures.
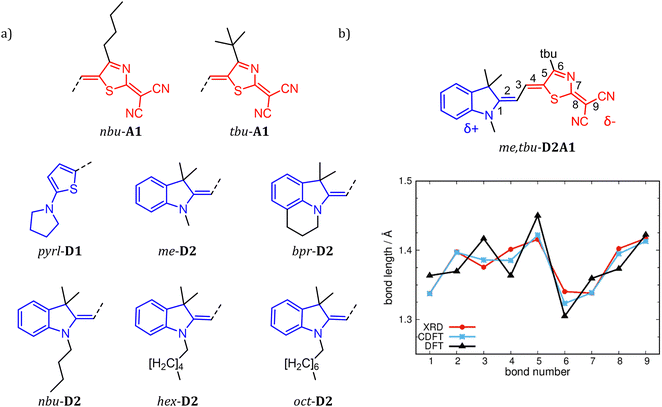 | ||
| Fig. 1 Chemical structures of R1-D1, R1-D2 and R2-A1 (a), with R1 = me-, bpr-, nbu-, hex-, oct- and pyrl- (blue sketches) and R2 = tbu- and nbu- (red sketches). (b) BLA path (see bond numbering) exemplary for me,tbu-D2A1. Bond lengths in Å are, respectively, from XRD data4 (red line), C-DFT (CAM-B3LYP-D3/6-311G**, gas phase, blue line, δD/A = ±0.6q) and DFT (ωB97X-D/6-311G**, gas phase, black line). | ||
The importance of including both static (electrostatic and polarization effects) and dynamic (thermal fluctuations) disorder in the simulations of the charge transport mechanisms of organic semiconductors has been largely documented.10–13 Electrostatic and induction effects shift the energy levels of the charge carriers14,15 affecting the site energy distribution (ΔEij) and ultimately the transfer rates (keTij) and the mobility.16 Dynamical effects can induce large fluctuations of the electronic transfer integrals, impacting as well on the transfer rate and charge mobility.17–20 The fine interplay between the electronic coupling and the reorganization energy, as quantified by the parameter ξ = 2|J|/λ, determines the charge transport regime, which can range from adiabatic (band-like, ξ ≥ 1) to intermediate (0.2 < ξ < 1) and non-adiabatic (hopping-like, ξ ≤ 0.2).21–23 Thermal disorder can either enhance the transfer rates opening new transport channels,24–26 for cases of highly localized charges (e.g., hopping regimes), or reduce the charge mobility, for cases of delocalized charge carriers (e.g., band or intermediate regimes).27,28 Generally, thermally induced fluctuations dynamically localize the charge carrier wave function over few molecular sites on the picosecond time scale, leading to complex (e.g., polaronic) transport mechanisms.17,18,22,29–31 While for classical (non-polar) organic semiconducting systems, such as acenes (e.g., naphthalene, tetracene, pentacene, and rubrene)26 and thioacenes,18 the impact of disorder effects on the charge transport properties has been well addressed theoretically and experimentally, for strong dipolar compounds such as merocyanines such effects are yet unexplored, and a fundamental understanding is still lacking.
In this investigation, we analyse how static and dynamic disorder effects impact on the charge transport properties of different merocyanines characterized by various D–A moieties and furbished with different lateral chains. The latter induce various solid-state packing motifs, ranging from columnar (1D) to brick-wall (2D and 3D) self-assembly. Our findings reveal a detrimental impact of static disorder on the charge mobility, regardless of the nature of the D–A groups. At the same time, our simulations show that thermal fluctuations lead to a broadening of the electronic coupling, independent of the D–A units and lateral chains. The thermal broadening, as well as the oscillations affecting the charge transfer integrals the most, parallels what was already observed for other organic semiconductors, like acenes10,25,32,33 perylene-bis-imide derivatives12 and thioacenes.34 Finally, we demonstrate how disorder effects change the hole mobility and the charge transport network by affecting its topology.
Methods
Materials
Two species of merocyanines were studied (Fig. 1a). The first (D1A1) is composed of a donor unit D1 (2-amino-thiophene) and an acceptor unit A1 (2-(4-alkylthiazol-2(3H)-ylidene)malonitrile).9 The second (D2A1) is made by a D2 (1-butyl-3,3-dimethylindolin-2-ylidene (‘Fischer base’)) group and an A1 unit (Fig. 1b). To reduce computational costs (as related to the evaluation of the static and dynamic disorder effects), we considered one prototypical species from D1A1, namely R1,R2-D1A1, with R1 pyrrolidine (pyrl-) attached at the donor moiety and R2tert-butyl attached at the acceptor (pyrl,tbu-D1A1). For the D2A1 species (Fig. 1b), a molecular library was generated by varying the lateral solubility groups attached on D2 (R1-), including methyl (me), propyl bridge (bpr), n-butyl (nbu), n-hexyl (hex) and n-octyl (oct) alkyl chains, as well as those attached on A1 (R2-), namely tert-butyl (tbu-) and n-butyl (nbu-) groups. The six resulting combinations (R1,R2-D2A1) are me,tbu-, bpr,tbu-, nbu,tbu-, nbu,nbu-, hex-tbu-, and oct,tbu-D2A1. All six combinations have been previously synthesised by Würthner et al. and the experimental data referring to the synthetic procedure and X-ray diffraction analyses can be found in ref. 4, 35 and 36.§Computational methods
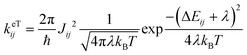 | (1) |
Charge carrier mobilities (μ), in the absence of static energetic disorder (ΔEij = 0), were computed for each single crystal of R1,R2-D2A1 (see the Materials section) via kinetic Monte-Carlo (kMC) simulations considering the Brownian diffusion scheme and calculating the diffusion coefficient D with a multiple set of kMC trajectories.19,20,51 An approximate linear dependence of the mean square displacement (MSD) of the charge [r(t) − r(0)]2 as a function of time t was obtained by averaging over the subsets of 1000 kMC trajectories. The diffusion coefficient D was obtained from the fitted linear dependence of the MSD:
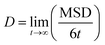 | (2) |
The charge mobility (μ) was finally computed by the Einstein–Smoluchowski equation:
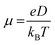 | (3) |
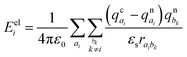 | (4) |
Results and discussion
Single molecule analysis: neutral equilibrium structures and intra-molecular reorganization energy
The coupling between the D–A units in merocyanines leads to intra-molecular charge transfer resulting in equilibrium molecular geometries that can be described by a linear combination of polyenic (neutral) and zwitterionic (charge transfer) structures.60 A correct description of both ground and excited state geometries challenges the majority of the standard quantum chemical approaches.9,61–64 In earlier work, we have shown that by tuning the ground state electronic partial charges, as localized on the donor (δD) and acceptor (δA) groups by applying the C-DFT methodology, optimized geometries (in a vacuum) reproduce the solid state experimental (XRD) bond length alternation (BLA) patterns. A best match between C-DFT and XRD molecular structures was found for a partial charge of δD/A = ±0.6q, which has been applied throughout this study as well.9 The experimental BLA pattern, as shown exemplary for me,tbu-D2A1 in Fig. 1b, is reproduced by our C-DFT calculations and in line with previous findings.9 The BLA patterns of all R1,R2-D2A1 are shown in the ESI,† Fig. S1. The BLA parameter, dBLA, defined as the difference between the average single- and double-bond lengths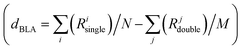 , ranges between −0.009 Å (me,tbu- and nbu,nbu-) and 0.001 Å (nbu,tbu-), indicating for all molecules a quasi-cyanine structure (dBLA = 0.000 Å) in the solid state. The computed C-DFT dBLA values range between 0.002 Å (nbu,tbu- and oct,tbu-) and 0.005 Å (nbu,nbu-), in good accordance with the experimental data (ESI,† Fig. S1 and Table S1). C-DFT calculations can best predict the single molecule bond length alternations in the solid state,9 as shown in Fig. 1b (blue lines), whereas the BLA pattern obtained by DFT gas phase calculations (black lines) cannot reproduce the XRD data (red lines). Indeed, the dBLA value as obtained by DFT for me,tbu- is with 0.049 Å significantly higher than the XRD (−0.009 Å) and C-DFT (0.004 Å) dBLA values.
, ranges between −0.009 Å (me,tbu- and nbu,nbu-) and 0.001 Å (nbu,tbu-), indicating for all molecules a quasi-cyanine structure (dBLA = 0.000 Å) in the solid state. The computed C-DFT dBLA values range between 0.002 Å (nbu,tbu- and oct,tbu-) and 0.005 Å (nbu,nbu-), in good accordance with the experimental data (ESI,† Fig. S1 and Table S1). C-DFT calculations can best predict the single molecule bond length alternations in the solid state,9 as shown in Fig. 1b (blue lines), whereas the BLA pattern obtained by DFT gas phase calculations (black lines) cannot reproduce the XRD data (red lines). Indeed, the dBLA value as obtained by DFT for me,tbu- is with 0.049 Å significantly higher than the XRD (−0.009 Å) and C-DFT (0.004 Å) dBLA values.
Upon charging the molecule (i.e., oxidation or formation of holes), the BLA changes (ESI,† Table S1). Such a structural variation impacts on the intra-molecular charge reorganization energy (λi) and, therefore, for a quantitative evaluation of λi, it is of utmost importance to correctly assess the BLA for both neutral and charged ground states. The computed (hole) reorganization energies range from 167 meV (me,tbu- and nbu,nbu-) to 179 meV (bpr,tbu-) (ESI,† Table S2) and are in agreement with previous findings.9
XRD structural analysis and electronic couplings of single crystals
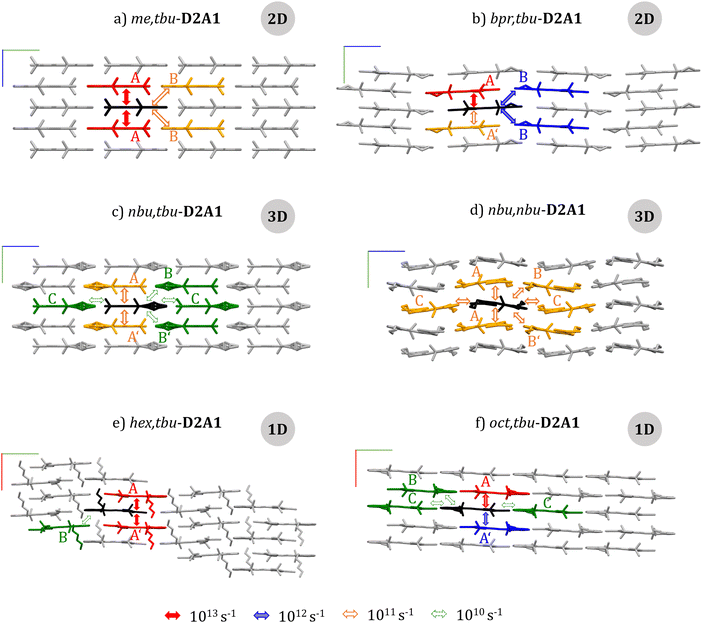 | ||
| Fig. 2 Side view (a – me,tbu-, b – bpr,tbu-, c – nbu,tbu-, d – nbu,nbu-, e – hex,tbu-, f – oct,tbu-D2A1) onto the long axis of the molecules. For each crystal, a schematic view of the charge transport pathways from the central molecule (black) to the nearest neighbour molecule (red, blue, orange, and green) is reported, with arrows showing the magnitude of the transfer rate (the colour code at the bottom). Cartesian axes of the unit cell: x (red), y (green) and z (blue). The topology of the charge transport network is indicated in grey circles (see the text and the ESI† for the network analysis). | ||
| Intra-columnar | Inter-columnar | |||||||
|---|---|---|---|---|---|---|---|---|
| R 1,R2- | Dimer | d COM (Å) | J ij (meV) | k eT (s−1) | Dimer | d COM (Å) | J ij (meV) | k eT (s−1) |
| me,tbu- | A | 6.164 | 59 | 1.5 × 1013 | B | 10.746 | 14 | 8.9 × 1011 |
| bpr,tbu- | A | 6.447 | 34 | 4.4 × 1013 | B | 12.635 | 16 | 1.0 × 1012 |
| A′ | 6.791 | 8 | 2.4 × 1011 | |||||
| nbu,tbu- | A | 6.264 | 16 | 1.0 × 1012 | B | 11.108 | 2 | 2.1 × 1010 |
| A′ | 6.255 | 11 | 4.9 × 1011 | B′ | 11.113 | 4 | 5.0 × 1010 | |
| C | 14.782 | 3 | 3.6 × 1010 | |||||
| nbu,nbu- | A | 6.293 | 6 | 1.5 × 1011 | B | 10.485 | 8 | 2.7 × 1011 |
| B′ | 9.955 | 6 | 1.3 × 1011 | |||||
| C | 13.499 | 6 | 1.3 × 1011 | |||||
| hex,tbu- | A | 6.322 | 46 | 1.5 × 1013 | B | 10.833 | 3 | 2.6 × 1010 |
| A′ | 6.650 | 64 | 2.9 × 1013 | |||||
| oct,tbu- | A | 6.676 | 80 | 2.6 × 1013 | B | 9.946 | 4 | 5.7 × 1010 |
| A′ | 6.919 | 31 | 3.8 × 1012 | C | 14.893 | 3 | 3.5 × 1010 | |
The highest Jij is along the intra-columnar direction with values ranging from 6 meV- (nbu,nbu-) up to 80 meV (oct,tbu-). For me,tbu- and nbu,nbu-, all intra-columnar transfer integrals are symmetric. For other cases, transfer integrals are asymmetric due to different distances between the ππ-planes as induced by longer alkyl chains (see couplings A and A′ in Table 1 and Fig. 2b, c, e and f).
By considering merocyanines displaced along the long molecular axis, the inter-columnar transfer integrals are small (<10 meV) for each species, except for me,tbu- and bpr,tbu-, showing values of 14 and 16 meV, respectively (dimer B, Table 1 and Fig. 2a and b). The same holds for inter-columnar couplings considering dimers displaced along the short axis, for which the coupling integrals are below 4 meV for all species (Fig. S2–S7 and Tables S3–S8, ESI†). Following the electronic coupling calculations, we classify the interactions as strong (Jij > 50 meV), medium (Jij = 10–40 meV) and weak (Jij < 10 meV) and analyse them with respect to different crystal directions. When couplings are non-equivalent (A and A′ in Table 1) for consecutive pathways along a specific direction (e.g., within a 1D column), we call these situations asymmetric. Furthermore, a network analysis of the transfer integrals for each crystal of R1,R2-D2A1 was performed and is reported in the ESI† (Fig. S9). Such analysis can anticipate the topology charge transport would assume in the absence of disorder: 1D transport network is predicted for hex,tbu- and oct,tbu-, 2D transport network for me,tbu- and bpr,tbu, and 3D transport network for nbu,nbu- and nbu,tbu-D2A1. The 3D transport networks for the latter species result from a balance between the intra-columnar hops and the large inter-columnar charge displacements, overall yielding an isotropic charge transport.
Kinetic Monte Carlo Brownian charge mobility: absence of disorder effects
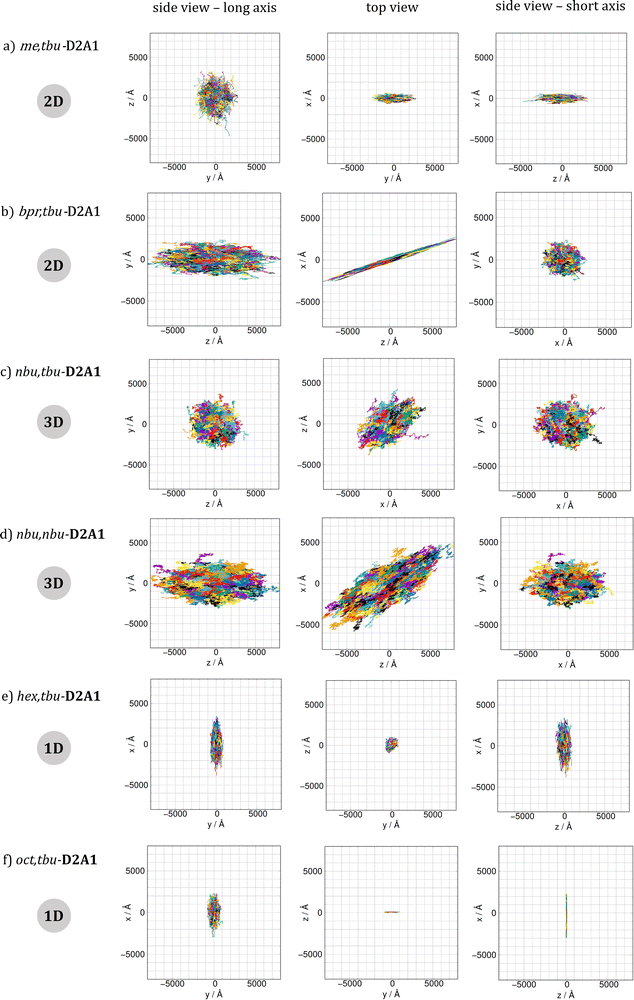
Brownian kMC simulations were performed to evaluate the hole diffusion trajectories of all six R1,R2-D2A1 merocyanine single crystals. Fig. 3 shows the hole spatial displacements resulting from the kMC simulations along with different Cartesian planes. For an easier comparison, the planes are ordered as the (i) side view onto the long axis of the molecules (corresponding to the view in Fig. 2), (ii) top view, and (iii) side view onto the short axis of the molecules. The kMC trajectories support the charge transport network picture reported previously, namely:– 1D for longer alkyl chains as hex,tbu- and oct,tbu-D2A1;
– 2D hole transport for molecules having short lateral alkyl chains, such as me,tbu- and bpr,tbu-D2A1;
– 3D for medium size lateral alkyl chains, like nbu,tbu- and nbu,nbu-D2A1.
Such classification defines the charge transport topologies as 1D, when the spatial displacement of the charge is larger by at least a factor of 2 for one direction over the two other directions. As 2D, when the spatial displacement is about the same in two directions, and at least a factor of 2 smaller in the third direction. Consequently, a 3D topology is defined as approximately similar displacements in all directions (see computed direction dependent mobilities in the ESI,† Table S13). The computed Brownian hole mobility, in the absence of disorder, is the highest for me,tbu- (0.206 cm2 V−1 s−1, 2D transport network) and bpr,tbu- (0.161 cm2 V−1 s−1, 2D transport), and it decreases up to a factor of 4 for hex,tbu- and oct,tbu- (0.067 and 0.065 cm2 V−1 s−1, respectively, both 1D transport), and up to an order of magnitude for nbu,tbu- and nbu,nbu- (0.020 and 0.030 cm2 V−1 s−1, both 3D transport), see values in Table 2.
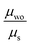 . The charge transport topology is reported in parenthesis for each case
. The charge transport topology is reported in parenthesis for each case
| R 1,R2-D2A1 | μ wo (cm2 V−1 s−1) without disorder | ΔEij (eV) | μ s (cm2 V−1 s−1) static disorder | |
|---|---|---|---|---|
| me,tbu- | 0.206 (2D) | ±0.125 | 0.105 (2D) | 2 |
| bpr,tbu- | 0.161 (2D) | ±0.358 | 0.007 (1D) | 23 |
| nbu,tbu- | 0.020 (3D) | ±0.683 | 0.002 (1D/2D) | 10 |
| nbu,nbu- | 0.030 (3D) | ±0.451 | 0.004 (1D/2D) | 8 |
| hex,tbu- | 0.067 (1D) | ±0.124 | 0.018 (1D/2D) | 4 |
| oct,tbu- | 0.065 (1D) | ±0.124 | 0.017 (1D) | 4 |
| pyrl,tbu-D1A1 | 0.160 (1D) | ±0.233 | 0.042 (1D) | 4 |
For me,tbu-D2A1, inter-columnar transfer rates are two orders of magnitude smaller than intra-columnar hops, leading to a sequence of fast (1.5 × 1013 s−1), short-range (6.164 Å) hops along the column and slow (8.9 × 1011 s−1), long-range (10.746 Å) hops between columns, resulting in 2D hole transport within the yz plane (Fig. 3a and ESI,† Fig. S2, Table S3).
The bpr,tbu-D2A1 has an intra-columnar asymmetry in the transfer rates (A and A′, Table 1), which could lead to charge trapping or delay phenomena. Inter-columnar transfer rates are one order of magnitude smaller than the highest intra-columnar hops, leading to an alternating sequence of fast (4.4 × 1013 s−1), short-range (6.447 Å) hops within the column and slow (1.0 × 1012 s−1), long-range (12.635 Å) hops between columns, showing a 2D transport path (Fig. 3b, and ESI,† Fig. S3 and Table S4). For nbu,tbu- and nbu,nbu-D2A1, the difference between intra- and inter-columnar transfer rates almost vanishes, leading to isotropic 3D transport pathways (Fig. 3c and d, also ESI,† Fig. S4 and S5, Tables S5 and S6). Finally, for merocyanines characterized by 1D transport (hex,tbu- and oct,tbu-D2A1), intra-columnar and inter-columnar transfer rates differ by three orders of magnitude (Table 1). For such reasons, hops occur almost exclusively along the direction of the higher transfer rates (intra-column), corresponding to the x axis (Fig. 3e and f, also ESI,† Fig. S6 and S7, Tables S7 and S8). Couplings along the column are asymmetric, resulting in asymmetric transfer rates differing by a factor of 2 for hex,tbu-D2A1, and by an order of magnitude for oct,tbu-D2A1 (Table 1). Such asymmetries can limit the final hole mobility, resulting in charge trapping for several hops within a dimer.
The computed hole mobilities of R1,R2-D2A1, in the absence of static and dynamic disorder effects, range from 2 × 10−1 to 2 × 10−2 cm2 V−1 s−1 (Table 2), with me,tbu- and bpr,tbu-D2A1 showing the highest values. Experimental charge mobilities, as taken from the literature, are measured on polycrystalline OFETs, showing high values for bpr,tbu- and nbu,tbu-D2A1 (0.18 and 0.14 cm2 V−1 s−1), followed by hex,tbu-D2A1 (0.050 cm2 V−1 s−1), nbu,nbu-D2A1 (0.026 cm2 V−1 s−1) and me,tbu-D2A1 (0.018 cm2 V−1 s−1).4 Despite being of the same order of magnitude, these data differ from the computed values. Reasons for such discrepancy are multiple, and they can be related to various factors, which can be traced back to both experimental (e.g., grain boundaries, impurities, and the size and orientation of the crystal domains) and theoretical (e.g., the absence of static and dynamic disorder effects, the validity of the hopping-regime, the absence of grain boundaries and semi-crystalline regions) aspects.
Table 2 compares the results discussed above with a prototypical merocyanine belonging to the D1A1 class, namely pyrl,tbu-D1A1 (see the chemical structure in Fig. 1a), and already studied by us.9 Such species, despite featuring a different donor unit (D1) and a 1D columnar packing in the solid state (see Fig. S8, ESI†), shows a computed Brownian hole mobility of 0.160 cm2 V−1 s−1 (semi-classical Marcus rates) that is of the same order of magnitude of both 1D and 2D charge transport cases predicted for the D2A1 species. As discussed in the next sections, the comparison between merocyanines belonging to these two classes (D1A1vs.D2A1) allows to draw more general structure–property relationships and to get insights into the role played by static and energetic disorder effects (see below) on this family of organic conjugated molecules.
Static (energetic) disorder
Electrostatic and polarization effects51,65–68 impact the site energy differences ΔEij, thereby influencing the transfer rates (see eqn (1)), the charge mobility, and the topology of the charge transport network.69,70 While one-dimensional charge transport is prone to structural defects, the prior effect of static disorder is to interconnect or disconnect certain pathways, thus determining a new topological connectivity.71 Such effects have never been modelled nor discussed in the literature of merocyanines, and we expect a strong impact of the polarization effects onto the charge transport properties of polar molecules in condensed phases.72The R1,R2-D2A1 library is an ideal platform to explore the impact of the energetic disorder over various charge transport networks, ranging from 1D, 2D up to 3D. Furthermore, the evaluation of ΔEij for pyr,tbu-D1A1 allows the comparison between different D–A classes, together with the definition of general design guidelines about merocyanines.
The computed ranges (i.e., min/max values) of the site energy differences (ΔEij) are reported in Table 2, while their standard deviation and distributions are included in the ESI,† Fig. S10 and Table S10. The smallest ΔEij are calculated for hex,tbu-, me,tbu- and oct,tbu-D2A1 (±0.125 eV), whereas it is largest for nbu,tbu-D2A1 (±0.683 eV). For comparison, for pyrl,tbu-D1A1, ΔEij is ±0.233 eV, being below bpr,tbu- (±0.358 eV) and nbu,nbu-D2A1 (±0.451 eV).
The ΔEij (±0.124–0.683 eV) are of the same order of magnitude or higher than the total (i.e., inner + outer sphere) reorganization energy of merocyanines (min. λ = 0.177 eV for pyrl,tbu-D1A1, max. λ = 0.229 eV for bpr,tbu-D2A1). Consequently, they will affect the final Marcus transfer rate constants via the (ΔEij + λ)2 term (eqn (1)). By definition, ΔEij are site-dependent properties. Therefore, certain directions within the crystal will be more affected than others by the inclusion of polarization effects.
By re-computing the Brownian kMC hole mobility in the presence of static disorder (μs), we observe a drop of μ (from a factor of two to more than an order of magnitude) for each R1,R2-D2A1 crystal (Table 2). The lowering of the charge mobility by turning on the polarizable effects is expected and it is in line with previous literature data on other organic semiconductors.15,72
Some interesting trends can be observed. For me,tbu-, hex,tbu- and oct,tbu-D2A1, which are characterised by high electronic couplings (Jij > 50 meV) and site energy differences (|ΔEij| = 0.124–0.125 eV) smaller than the total reorganization energy (0.217–0.227 eV), the charge transport pathways are almost not influenced by the presence of the energetic disorder, preserving the charge transport dimensionality as in the absence of static disorder. The reason for this behaviour is two-fold: (i) the site energy difference distribution is very narrow around zero, and (ii) the (ΔEij + λ)2 term in the semi-classical Marcus equation (eqn (1)) can be small or vanishing, thus leading to rate constants that are prevalently ruled by the electronic couplings.
Instead, bpr,tbu-, nbu,tbu- and nbu,nbu-D2A1 feature medium to small electronic couplings (Jij < 40 meV) and site energy differences (|ΔEij| = 0.358–0.683 eV) larger than the total reorganization energy (0.217–0.229 eV); therefore, the charge transport network changes notably by varying its topology. This is because the distribution of ΔEij is broader than the previous cases, and the (ΔEij + λ)2 term can be either small or large; therefore, the Marcus regime is highly affected, as well as the rate constants.
Notably, energetic disorder impacts the charge transport topology too. In detail, me,tbu-D2A1 has high intra-columnar couplings (56 meV) and medium/small inter-columnar electronic integrals (16 meV). Both pathways are preserved in the presence of static disorder, maintaining overall a 2D charge transport (ESI,† Fig. S11). Also, for hex,tbu- and oct,tbu-D2A1, characterized by high intra- and low inter-columnar couplings, the charge transport network is preserved as in the absence of static disorder (see transfer rates in the ESI,† Table S10 and Fig. S15 and S16). For the case of bpr,tbu-D2A1 instead, characterized by medium/small intra- and inter-columnar couplings and high ΔEij, the intra-column hops are strongly affected decreasing the transfer rates by orders of magnitude (see transfer rates in the ESI,† Tables S4, S10 and Fig. S12), therefore changing the charge transport network from 2D to a quasi 1D. Similarly, for nbu,tbu- and nbu,nbu-D2A1, characterized by medium/small couplings and high ΔEij, the charge transport network remarkably changes by localizing the hopping trajectories in few dimensions (ESI,† Table S10 and Fig. S13 and S14).
Considering the D1A1 class, namely pyrl,tbu-D1A1, the high intra-columnar couplings, together with the narrow site energy difference distribution and a ΔEij comparable with λ, lead to minor changes in the charge transport network (ESI,† Fig. S17) with respect to the absence of static disorder, paralleling the cases of me,tbu-, hex,tbu- and oct,tbu-D2A1.
Overall, in the presence of static disorder, large site energy distributions (max(|ΔEij|) ≫ λ) affect the transport network the most, for the case of bpr,tbu-, nbu,tbu- and nbu,nbu-D2A1 characterized by the highest decreases in μ (from a factor of 8 up to 23, see Table 2). For small site energy distributions (max(|ΔEij|) ≤ λ) and large couplings, for me,tbu-, hex,tbu- and oct,tbu-D2A1, the charge transport networks are preserved and the mobility value reduces by a factor of 2 up to 4 (Table 2).
Dynamic (thermal) disorder
Dynamic disorder effects, i.e. the variations of the coupling integrals as induced by thermal oscillations, including both intra- and inter-molecular vibrations (e.g., the centre of mass translations, librations and rotations), were computed through the evaluation of the Fourier Transform (FT) of the time-dependent auto-correlation function (ACF) of the coupling integrals 〈J(t + τ)J(t)〉/〈J(t)2〉 (see details in ref. 59, 73 and 74 and ESI,† Fig. S17 and S18). Couplings were computed by sampling the trajectories extracted from the MD simulations of three crystal structures, namely pylr,tbu-D1A1, me,tbu-D2A1 and nbu,tbu-D2A1. The three cases are considered as representative case studies for merocyanines featuring different D–A moieties and hole charge transport network topologies, respectively, 1D, 2D and 3D. The 1D and 2D cases (pyrl,tbu-D1A1 and me,tbu-D2A1) show strong anisotropy in the coupling network, featuring high intra-columnar transfer integrals (Jij > 50 meV) and low (Jij < 4 meV, 1D case) or medium (Jij = 16 meV, 2D case) electronic interactions across columns. The 3D case (nbu,tbu-D2A1) shows low transfer integrals (J ≤ 16 meV) in all directions.Fig. 4 reports the distribution and the time-dependent fluctuations for the highest Jij (ESI,† Fig. S20 for the coupling distributions of other dimers). For all merocyanines, broad distributions and large fluctuations of Jij are computed. The distribution of the transfer integrals (J) can be well fitted by a Gaussian function. The average value (〈J〉) increases for all merocyanines, as compared to the respective static (frozen crystal) value (Fig. 4 and ESI,† Table S11). Such an increase can be inferred to (intrinsic) thermal effects as well as to the quality (e.g., parameterization of bonded and non-bonded terms) of the force-field, impacting the relative positions and distributions of the molecules during the MD simulations. The thermal broadening of the transfer integrals, namely the standard deviation σ, is 52 meV for me,tbu-D2A1, 73 meV for nbu,tbu-D2A1 and 69 meV for pyrl,tbu-D1A1 (Fig. 4 and ESI,† Table S11). From the analysis of the FT of the coupling ACF (ESI,† Fig. S18), we observed that the active oscillations affecting the electronic couplings the most are those below 100 cm−1. Such frequencies, as documented in the literature for other conjugated compounds, can be associated with inter-molecular normal modes (e.g., translation, libration) involving the molecular backbone and the lateral chains of the molecules.12,19,20,27,75–77
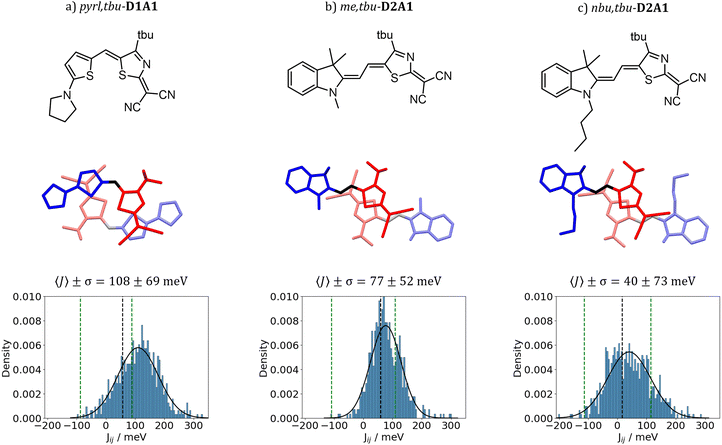 | ||
| Fig. 4 Dynamic disorder effects on dimer A of (a) pyrl,tbu-D1A1, (b) me,tbu- and (c) nbu,tbu-D2A1 (chemical structures and dimer geometries on top), showing the distribution of the coupling integrals Jij (Gaussian fit, black line) calculated at the ZINDO/S level, bottom panels. The mean value 〈J〉 and standard deviation σ are reported as well. Black dashed lines represent the value of the electronic coupling for the case of frozen crystals at the ZINDO/S level (i.e., XRD experimental structure), and the green lines mark the ±λ/2 energy range, remarking the validity of the non-adiabatic regime.21 | ||
The spread of the coupling integrals, as induced by thermal disorder, leads to the question, whether the non-adiabatic hopping mechanism is the suitable model to describe hole transport in merocyanines. In the absence of thermal oscillations (frozen crystal), the parameter ξ = 2|J|/λ ranges from 0.1 for nbu,tbu-D2A1 up to 0.6 for pyrl,tbu-D1A1 (ESI,† Table S11). Such values lie within the range of the hopping regime (i.e., validity of the non-adiabatic semi-classical Marcus approach),11,21,32,78 with only pyrl,tbu-D1A1 being relatively close to an intermediate regime. Inclusion of averaged coupling (〈J〉) in the evaluation of ξ (ξ = 2|〈J〉|/λ)79 leads to values of 0.4 for nbu,tbu-D2A1, 0.7 for me,tbu-D2A1 and up to 1.2 for pyrl,tbu-D1A1. This increase might suggest that different charge transport regimes than hopping should be considered. An in-depth investigation of such effects, together with the inclusion of charge transport schemes which go beyond the non-adiabatic Marcus approach,80 is currently under investigation in our group and they will be the subject for future works.
Albeit keeping a non-adiabatic regime (thermalized limit), we checked the impact of considering a second order (thermal) correction to the calculation of the non-adiabatic transfer rates, as suggested by Ratner and Troisi.73,79 The second order correction (ESI,† Section S10) to the non-adiabatic transfer rate is proportional to the factor 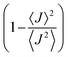 . When
. When 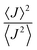 is close to unity, the impact of thermal oscillations is weak, and the thermal corrections to the transfer rates are negligible. In such cases, the use of eqn (1), by replacing the static J with the average of the coupling square 〈J2〉, is acceptable.79 However, when
is close to unity, the impact of thermal oscillations is weak, and the thermal corrections to the transfer rates are negligible. In such cases, the use of eqn (1), by replacing the static J with the average of the coupling square 〈J2〉, is acceptable.79 However, when 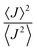 is smaller than unity, the thermal corrections become relevant.24 As also reported by Martinelli et al.,24 an equivalent description is given by introducing the parameter η, defined as
is smaller than unity, the thermal corrections become relevant.24 As also reported by Martinelli et al.,24 an equivalent description is given by introducing the parameter η, defined as 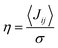 , with
, with 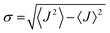 . Values of η ≥ 0.5 suggest the impact of lattice vibrations to be weak on the transfer rate equation, whereas values <0.5 imply a global increase of the transfer rates. For me,tbu-D2A1 and pyrl,tbu-D1A1, with η = 1.5 and 1.6, respectively, significantly larger than 0.5, consequently the non-adiabatic transfer rates are weakly affected by thermal corrections (see also
. Values of η ≥ 0.5 suggest the impact of lattice vibrations to be weak on the transfer rate equation, whereas values <0.5 imply a global increase of the transfer rates. For me,tbu-D2A1 and pyrl,tbu-D1A1, with η = 1.5 and 1.6, respectively, significantly larger than 0.5, consequently the non-adiabatic transfer rates are weakly affected by thermal corrections (see also 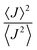 values in the ESI,† Table S11). For nbu,tbu-D2A1, with η = 0.5 and
values in the ESI,† Table S11). For nbu,tbu-D2A1, with η = 0.5 and 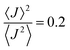 , thermal corrections can enhance significantly the non-adiabatic transfer rates.
, thermal corrections can enhance significantly the non-adiabatic transfer rates.
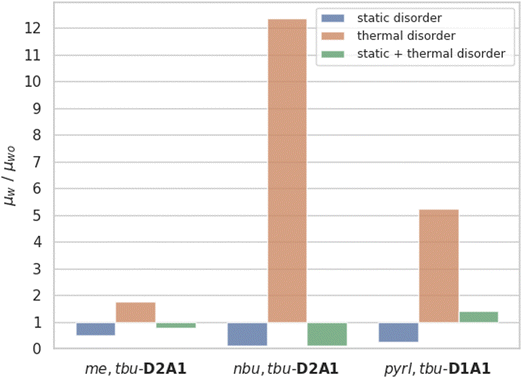
Given the above assumptions, in the frame of the non-adiabatic regime,79 we have re-computed the transfer rate constants and kMC mobilities by considering the thermalized value of the coupling integrals (〈J2〉) in the rate equation (eqn (1)), without taking into account the effect of static disorder (ESI,† Table S12). Thermalized Brownian hole mobilities (μt) overall increase, raising for me,tbu-D2A1 by a factor of 2, for nbu,tbu-D2A1 by a factor of 12 and for pyrl,tbu-D1A1 by a factor of 5 (Fig. 5 and ESI,† Table S12). The increase in charge mobility is remarkable for both nbu,tbu-D2A1 and pyrl,tbu-D1A1. For the first species, medium/small electronic couplings (J) and high thermal oscillations (〈J2〉) favour the opening of effective hole transfer channels, thus increasing the mobility. The computed thermal averaged charge mobility (0.247 cm2 V−1 s−1) is of the same order of magnitude to the average experimental device mobility (0.87 cm2 V−1 s−1), as measured on single crystal OFETs.8 For pyrl,tbu-D1A1, the largest increase in the charge mobility is mainly due of the increment of the electronic coupling values for the only-effective charge transport channel that is the intra-columnar one.
Static and dynamic disorder effects
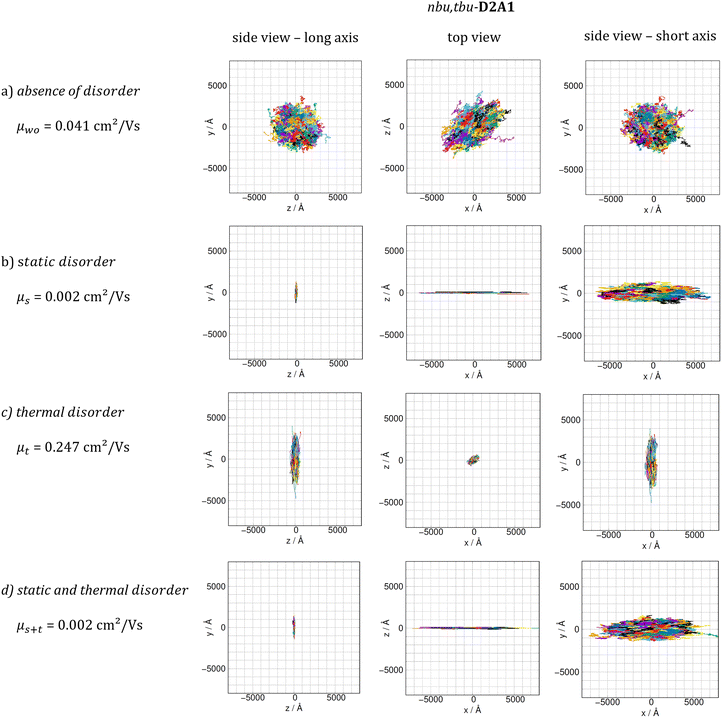
Lastly, we combined both static and dynamic disorder effects, thus evaluating the charge mobility by including the averaged square couplings (〈J2〉) as well as the site energy differences (the latter computed on the crystal structure) μs+t. When both effects are considered, the Brownian hole mobilities generally increase as compared to pure static disorder (except of nbu,tbu-D2A1, see below) and decrease as compared to the pure thermal disorder (ESI,† Table S12). The detrimental effects of static disorder are partially compensated by thermal motions. Such trends are summarized in Fig. 5, showing the ratio between the computed Brownian hole mobility in the presence of different kinds of disorder ((a) static – blue bars, (b) thermal – orange, and (c) static and thermal – green) with respect to those computed without any disorder. For nbu,tbu- and me,tbu-D2A1, the charge mobility computed in the presence of both types of disorder is dominated by the static one, which globally limits the charge diffusion. For pyrl,tbu-D1A1 instead, the static disorder is compensated by the thermal fluctuations and the final hole mobility in the presence of both disorder effects is larger than that without any disorder.For nbu,tbu-D2A1, in Fig. 6, the kMC hole trajectories are reported for all cases previously considered: (a) non-adiabatic transfer rates without disorder effects, (b) with static disorder effects, (c) with dynamic disorder effects, and (d) with both static and dynamic disorder effects. Without any disorder effects, the nbu,tbu-D2A1 charge transport pathways form an isotropic 3D transport network (Fig. 6a). In the presence of static disorder, the network is reduced to an anisotropic quasi-1D topology, leading to an overall decrease in mobility (Fig. 6b). With dynamic disorder, the charge transport is enhanced, and the transport topology is highly anisotropic along the columns (Fig. 6c). The inclusion of both, static and dynamic disorder, affords a similar quasi-1D topology (Fig. 6d) as in the presence of just the static effects (Fig. 6b), and the charge mobility is reduced by a factor of 10 compared to the case without any disorder effects (Table S12, ESI†). In ESI,† (Fig. S11 and S17) the results are reported for me,tbu-D2A1 and pyrl-D1A1, where the presence of static and dynamic disorder effects affects the computed charge mobility, however maintaining the charge transport topology (2D and 1D, respectively) as in the absence of disorder.
Generally, our data can parallel those already reported by Vehoff et al.71 for other organic single crystals constituted by apolar molecules (e.g., rubrene), that is the presence of (structural) disorder can reduce or increase the charge carrier mobility, depending also on the dimensionality of the charge transfer network. The one-dimensional transport is prone to structural defects, instead shifted anti-parallel alignments allow for 2D or 3D dimensional charge transport, reducing the influence of structural defects.
Conclusions
Merocyanines are D–A conjugated molecules considered as prototypical building blocks for studying the structure–property relationships of highly polar organic semiconductors. Tuning their D–A moieties and engineering their side groups are effective strategies to influence their supramolecular order in the solid state and their charge/exciton transport properties. Recently, experimental evidence reported the possibility for merocyanine single crystals to reach as high hole mobility (up to 2 cm2 V−1 s−1) as state-of-the-art small molecules (e.g., acenes and thioacenes). However, very few atomistic investigations aiming at modelling their charge transport properties are present in the literature, resulting in a general lack of fundamental understanding. We fill the gap, reporting here an in-depth computational investigation over a library of merocyanines, showing how static and dynamic disorder effects influence the charge transport parameters and mobility, by impacting both the transfer rates and the topology of the charge transport networks in single crystals. We considered seven merocyanines differing by their donor unit and side chains, showing different packing motifs in the solid state. All merocyanines pack in an antiparallel slipped fashion along the ππ-direction. Depending on the side groups, crystals form quasi 1D stacks that by interacting with neighbouring columns create interconnected 2D layers (mostly due to extended and flexible side chains). As the reorganization energies are similar for all species, the charge transfer rates and mobilities depend mainly on the coupling integrals and site energy differences.Our simulations show that for merocyanines characterized by high intra-column charge transfer integrals (>50 meV) and low inter-column couplings (<10 meV), a clear 1D transport network appears. For medium to small intra-columnar transfer integrals (10–40 meV), interactions across columns become relevant, leading to 2D or 3D transport. The computed mobilities are the highest for the 2D cases and the lowest for the 3D cases, reflecting the values of the coupling integrals.
When static disorder effects are included, a decrease in the charge mobility is computed for all species. Our simulations reveal that for those merocyanines characterized by small electronic couplings (<40 meV), when the site energy differences are larger than or similar to the reorganization energy, the charge transport network is affected the most, changing from 3D (without disorder) to 1D (with disorder), as the case of nbu,tbu-D2A1. Conversely, for those species featuring large charge transfer integrals (>50 meV) and site energy differences similar to the reorganization energy, the transport network is preserved, for pyrl,tbu-D1A1 and me,tbu-D2A1.
Dynamic disorder leads on average to an enhancement of the charge transport along these directions where the electronic couplings are the highest. The non-adiabatic hypothesis holds for most of the merocyanines investigated here, with only one case (pyrl,tbu-D1A1) being relatively close to an intermediate (i.e., small-polaron hopping) charge transport regime. Thermalized Brownian hole mobilities increase, raising up to a factor of 12 with respect to the absence of thermal effects. The increase in charge mobility is remarkable for both nbu,tbu-D2A1 and pyrl,tbu-D1A1.
When both static and dynamic disorder effects are considered, our simulations reveal that the former affects the charge mobility the most. We conclude that polarization effects are detrimental for the charge transport of polar dyes, and such a decrease cannot be compensated by thermal effects, even though the latter, for the case of merocyanines, leads to a general enhancement of the transfer rates.
Given the current investigation, and considering our previous computational study9 as well as the broad set of experimental data available in the literature,4 the best strategy to design merocyanines whose charge mobility is most resilient to static and dynamic disorder effects, can be to include strong donor–acceptor units, connected by a short, conjugated bridge (e.g., methylene, ethylene) and small lateral groups (e.g., methyl and n-butyl). These features would lead to polar dyes, characterised by low reorganisation energy and solid state anti-parallel brick-wall-like packing, which minimizes polarization effects and maximizes the enhancement of the charge mobility due to thermal oscillations.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. M., D. F., N. G., S. G. and R. H. acknowledge the DFG Research Training Group 2591 “Template-designed Organic Electronics (TIDE)” for supporting their research. They also acknowledge the Regional Computing Centre (RRZK) of the University of Cologne for providing computing time and resources on the HPC RRZK CHEOPS. D. F. and F. N. acknowledge the RFO funds from the University of Bologna. F. N. acknowledges the European Union—Next Generation EU under the Italian National Recovery and Resilience Plan (PNRR M4C2, Investiment 1.4—Call for tender no. 3138 dated 16/12/2021—CN00000013 National Centre for HPC, Big Data and Quantum Computing (HPC)—CUP J33C22001170001). D. F. acknowledges the Global Faculty Program of the University of Cologne within the focus area “Quantum Matter and Materials (QM2)”, the National Recovery and Resilience Plan (NRRP), Mission 04 Component 2 Investment 1.5 – NextGenerationEU, Call for tender no. 3277 dated 30/12/2021, Award Number: 0001052 dated 23/06/2022, and the National Project funded by the European Union – Next Generation EU, Project title “Modelling and design of organic conjugated redox materials for energy-saving applications: a bottom-up strategy”, code MUR 2022WKTH9E – CUP J53D23008810006.References
- F. Würthner, R. Wortmann, R. Matschiner, K. Lukaszuk, K. Meerholz, Y. DeNardin, R. Bittner, C. Bräuchle and R. Sens, Angew. Chem., Int. Ed. Engl., 1997, 36, 2765–2768 CrossRef.
- F. Würthner, R. Wortmann and K. Meerholz, ChemPhysChem, 2002, 3, 17–31 CrossRef.
- F. Würthner and K. Meerholz, Chem. – Eur. J., 2010, 16, 9366–9373 CrossRef PubMed.
- A. Liess, L. Huang, A. Arjona-Esteban, A. Lv, M. Gsänger, V. Stepanenko, M. Stolte and F. Würthner, Adv. Funct. Mater., 2015, 25, 44–57 CrossRef CAS.
- T. Kim, S. Kang, E. Kirchner, D. Bialas, W. Kim, F. Würthner and D. Kim, Chem, 2021, 7, 715–725 CAS.
- A. Liess, A. Arjona-Esteban, A. Kudzus, J. Albert, A.-M. Krause, A. Lv, M. Stolte, K. Meerholz and F. Würthner, Adv. Funct. Mater., 2019, 29, 1805058 CrossRef.
- H. Bürckstümmer, N. M. Kronenberg, M. Gsänger, M. Stolte, K. Meerholz and F. Würthner, J. Mater. Chem., 2010, 20, 240–243 RSC.
- A. Liess, M. Stolte, T. He and F. Würthner, Mater. Horiz., 2016, 3, 72–77 RSC.
- N. Gildemeister, G. Ricci, L. Böhner, J. M. Neudörfl, D. Hertel, F. Würthner, F. Negri, K. Meerholz and D. Fazzi, J. Mater. Chem. C, 2021, 9, 10851–10864 RSC.
- A. Landi and A. Troisi, J. Phys. Chem. C, 2018, 122, 18336–18345 CrossRef CAS.
- A. Troisi, Chem. Soc. Rev., 2011, 40, 2347–2358 RSC.
- S. Di Motta, M. Siracusa and F. Negri, J. Phys. Chem. C, 2011, 115, 20754–20764 CrossRef CAS.
- C. Poelking, E. Cho, A. Malafeev, V. Ivanov, K. Kremer, C. Risko, J.-L. Brédas and D. Andrienko, J. Phys. Chem. C, 2013, 117, 1633–1640 CrossRef CAS.
- J. Cornil, S. Verlaak, N. Martinelli, A. Mityashin, Y. Olivier, T. van Regemorter, G. D'Avino, L. Muccioli, C. Zannoni, F. Castet, D. Beljonne and P. Heremans, Acc. Chem. Res., 2013, 46, 434–443 CrossRef CAS PubMed.
- M. Schrader, C. Körner, C. Elschner and D. Andrienko, J. Mater. Chem., 2012, 22, 22258 RSC.
- V. Coropceanu, J. Cornil, D. A. Da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2016, 26, 2292–2315 CrossRef CAS.
- T. F. Harrelson, V. Dantanarayana, X. Xie, C. Koshnick, D. Nai, R. Fair, S. A. Nuñez, A. K. Thomas, T. L. Murrey, M. A. Hickner, J. K. Grey, J. E. Anthony, E. D. Gomez, A. Troisi, R. Faller and A. J. Moulé, Mater. Horiz., 2019, 6, 182–191 RSC.
- E. Di Donato, R. P. Fornari, S. Di Motta, Y. Li, Z. Wang and F. Negri, J. Phys. Chem. B, 2010, 114, 5327–5334 CrossRef CAS PubMed.
- S. Canola and F. Negri, Phys. Chem. Chem. Phys., 2014, 16, 21550–21558 RSC.
- H. Oberhofer, K. Reuter and J. Blumberger, Chem. Rev., 2017, 117, 10319–10357 CrossRef CAS PubMed.
- J. Blumberger, Chem. Rev., 2015, 115, 11191–11238 CrossRef CAS PubMed.
- S. Giannini, O. G. Ziogos, A. Carof, M. Ellis and J. Blumberger, Adv. Theory Simul., 2020, 3, 2000093 CrossRef CAS.
- N. G. Martinelli, Y. Olivier, S. Athanasopoulos, M.-C. Ruiz Delgado, K. R. Pigg, D. A. Da Silva Filho, R. S. Sánchez-Carrera, E. Venuti, R. G. Della Valle, J.-L. Brédas, D. Beljonne and J. Cornil, ChemPhysChem, 2009, 10, 2265–2273 CrossRef CAS PubMed.
- V. Coropceanu, R. S. Sánchez-Carrera, P. Paramonov, G. M. Day and J.-L. Brédas, J. Phys. Chem. C, 2009, 113, 4679–4686 CrossRef CAS.
- R. S. Sánchez-Carrera, P. Paramonov, G. M. Day, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2010, 132, 14437–14446 CrossRef PubMed.
- A. Troisi and G. Orlandi, J. Phys. Chem. A, 2006, 110, 4065–4070 CrossRef CAS PubMed.
- A. S. Eggeman, S. Illig, A. Troisi, H. Sirringhaus and P. A. Midgley, Nat. Mater., 2013, 12, 1045–1049 CrossRef CAS PubMed.
- T. Nematiaram and A. Troisi, Mater. Horiz., 2020, 7, 2922–2928 RSC.
- A. Girlando, L. Grisanti, M. Masino, A. Brillante, R. G. Della Valle and E. Venuti, J. Chem. Phys., 2011, 135, 84701 CrossRef PubMed.
- H. Yang, F. Gajdos and J. Blumberger, J. Phys. Chem. C, 2017, 121, 7689–7696 CrossRef CAS.
- S. Giannini, A. Carof, M. Ellis, H. Yang, O. G. Ziogos, S. Ghosh and J. Blumberger, Nat. Commun., 2019, 10, 3843 CrossRef PubMed.
- M. A. Dettmann, L. S. R. Cavalcante, C. Magdaleno, K. Masalkovaitė, D. Vong, J. T. Dull, B. P. Rand, L. L. Daemen, N. Goldman, R. Faller and A. J. Moulé, J. Chem. Theory Comput., 2021, 17, 7313–7320 CrossRef CAS PubMed.
- D. Vong, T. Nematiaram, M. A. Dettmann, T. L. Murrey, L. S. R. Cavalcante, S. M. Gurses, D. Radhakrishnan, L. L. Daemen, J. E. Anthony, K. J. Koski, C. X. Kronawitter, A. Troisi and A. J. Moulé, J. Phys. Chem. Lett., 2022, 13, 5530–5537 CrossRef CAS PubMed.
- A. Ojala, H. Bürckstümmer, J. Hwang, K. Graf, B. von Vacano, K. Meerholz, P. Erk and F. Würthner, J. Mater. Chem., 2012, 22, 4473–4482 RSC.
- T. L. Murrey, D. Hertel, J. Nowak, R. Bruker, T. Limböck, J. Neudörfl, S. Rüth, J. Schelter, S. Olthof, A. Radulescu, A. J. Moulé and K. Meerholz, J. Phys. Chem. C, 2020, 124, 19457–19466 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- E. Aprà, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Del Martin Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la-Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. van Voorhis, Á. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102 CrossRef PubMed.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef PubMed.
- S. F. Nelsen, S. C. Blackstock and Y. Kim, J. Am. Chem. Soc., 1987, 109, 677–682 CrossRef CAS.
- M. C. Zerner, in Reviews in computational chemistry, ed. K. B. Lipkowitz and D. B. Boyd, VCH, New York, NY, 2007, pp. 313–365 Search PubMed.
- B. Baumeier, J. Kirkpatrick and D. Andrienko, Phys. Chem. Chem. Phys., 2010, 12, 11103–11113 RSC.
- J. T. Kohn, N. Gildemeister, S. Grimme, D. Fazzi and A. Hansen, J. Chem. Phys., 2023, 159, 144106 CrossRef CAS PubMed.
- A. A. Hagberg, D. A. Schult and P. J. Swart, Exploring network structure, dynamics, and function using NetworkX, Pasadena, CA, USA, 2008 Search PubMed.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- Y. A. Berlin, G. R. Hutchison, P. Rempala, M. A. Ratner and J. Michl, J. Phys. Chem. A, 2003, 107, 3970–3980 CrossRef CAS.
- S. Di Motta, E. Di Donato, F. Negri, G. Orlandi, D. Fazzi and C. Castiglioni, J. Am. Chem. Soc., 2009, 131, 6591–6598 CrossRef CAS PubMed.
- D. P. McMahon and A. Troisi, J. Phys. Chem. Lett., 2010, 1, 941–946 CrossRef CAS.
- J. E. Norton and J.-L. Brédas, J. Am. Chem. Soc., 2008, 130, 12377–12384 CrossRef CAS PubMed.
- (a) D. L. Cheung and A. Troisi, Phys. Chem. Chem. Phys., 2008, 10, 5941 RSC; (b) T. Xu, W. Wang and S. Yin, J. Phys. Chem. A, 2018, 122, 8957–8964 CrossRef CAS PubMed.
- V. Rühle, A. Lukyanov, F. May, M. Schrader, T. Vehoff, J. Kirkpatrick, B. Baumeier and D. Andrienko, J. Chem. Theory Comput., 2011, 7, 3335–3345 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- (a) H. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS; (b) D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed; (c) B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed; (d) S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed; (e) M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- S. S. Skourtis, I. A. Balabin, T. Kawatsu and D. N. Beratan, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3552–3557 CrossRef CAS PubMed.
- S. R. Marder, C. B. Gorman, F. Meyers, J. W. Perry, G. Bourhill, J. L. Brédas and B. M. Pierce, Science, 1994, 265, 632–635 CrossRef CAS PubMed.
- R. Tomar, L. Bernasconi, D. Fazzi and T. Bredow, J. Phys. Chem. A, 2023, 127, 9661–9671 CrossRef CAS PubMed.
- B. Le Guennic and D. Jacquemin, Acc. Chem. Res., 2015, 48, 530–537 CrossRef CAS PubMed.
- H. Lischka, D. Nachtigallová, A. J. A. Aquino, P. G. Szalay, F. Plasser, F. B. C. Machado and M. Barbatti, Chem. Rev., 2018, 118, 7293–7361 CrossRef CAS PubMed.
- C. Brückner and B. Engels, Chem. Phys., 2017, 482, 319–338 CrossRef.
- T. Richards, M. Bird and H. Sirringhaus, J. Chem. Phys., 2008, 128, 234905 CrossRef PubMed.
- L. Stojanović, J. Coker, S. Giannini, G. Londi, A. S. Gertsen, J. Wenzel Andreasen, J. Yan, G. D’Avino, D. Beljonne, J. Nelson and J. Blumberger, Phys. Rev. X, 2024, 14, 021021 Search PubMed.
- P. Friederich, F. Symalla, V. Meded, T. Neumann and W. Wenzel, J. Chem. Theory Comput., 2014, 10, 3720–3725 CrossRef CAS PubMed.
- G. D'Avino, L. Muccioli, F. Castet, C. Poelking, D. Andrienko, Z. G. Soos, J. Cornil and D. Beljonne, J. Phys.: Condens.Matter, 2016, 28, 433002 CrossRef PubMed.
- N. E. Jackson, K. L. Kohlstedt, L. X. Chen and M. A. Ratner, J. Chem. Phys., 2016, 145, 204102 CrossRef PubMed.
- N. E. Jackson, L. X. Chen and M. A. Ratner, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8595–8600 CrossRef CAS PubMed.
- T. Vehoff, B. Baumeier, A. Troisi and D. Andrienko, J. Am. Chem. Soc., 2010, 132, 11702–11708 CrossRef CAS PubMed.
- P. Friederich, V. Meded, A. Poschlad, T. Neumann, V. Rodin, V. Stehr, F. Symalla, D. Danilov, G. Lüdemann, R. F. Fink, I. Kondov, F. von Wrochem and W. Wenzel, Adv. Funct. Mater., 2016, 26, 5757–5763 CrossRef CAS.
- A. Troisi, A. Nitzan and M. A. Ratner, J. Chem. Phys., 2003, 119, 5782–5788 CrossRef CAS.
- D. N. Beratan, S. S. Skourtis, I. A. Balabin, A. Balaeff, S. Keinan, R. Venkatramani and D. Xiao, Acc. Chem. Res., 2009, 42, 1669–1678 CrossRef CAS PubMed.
- G. Schweicher, G. D'Avino, M. T. Ruggiero, D. J. Harkin, K. Broch, D. Venkateshvaran, G. Liu, A. Richard, C. Ruzié, J. Armstrong, A. R. Kennedy, K. Shankland, K. Takimiya, Y. H. Geerts, J. A. Zeitler, S. Fratini and H. Sirringhaus, Adv. Mater., 2019, 31, 1902407 CrossRef CAS PubMed.
- A. Troisi, G. Orlandi and J. E. Anthony, Chem. Mater., 2005, 17, 5024–5031 CrossRef CAS.
- G. Ricci, S. Canola, Y. Dai, D. Fazzi and F. Negri, Molecules, 2021, 26, 4119 CrossRef CAS PubMed.
- J. Spencer, F. Gajdos and J. Blumberger, J. Chem. Phys., 2016, 145, 064102 CrossRef.
- A. Troisi, Mol. Simul., 2006, 32, 707–716 CrossRef CAS.
- S. Giannini, A. Carof and J. Blumberger, J. Phys. Chem. Lett., 2018, 9, 3116–3123 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00669k |
| ‡ These authors contributed equally to this work. |
| § CCDC 2004947 contains the supplementary crystallographic data of oct,tbu-D2A1 measured by Murrey et al.36 |
| This journal is © The Royal Society of Chemistry 2024 |