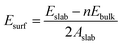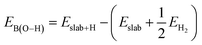Rutile-type metal dioxide (110) surfaces for the cyclic oxidation of methane to methanol

Abstract

The direct conversion of methane to methanol has attracted increasing interests, owing to the necessity for an abundant low-carbon source of energy. However, numerous challenges are encountered in attaining a high conversion rate and selectivity using the existing approach and catalysts. One of them is the need for a reaction halt and a reactivation of the catalyst using an oxidant at high temperature, which makes the whole process non-cyclic. In this study, we employ density functional theory calculations to evaluate rutile-type IrO₂(110), β-PtO₂(110), and β-MnO₂(110) surfaces not only for cleaving the H–CH₃ bond but also for forming methanol. We find that IrO₂(110) and β-PtO₂(110) thermodynamically and kinetically favor the C–H activation on the bridging μO-atom terminations via a heterolytic pathway. However, the formation of strong Ir–C and Pt–C bonds, which initially help the C–H bond scission, hinders the methanol formation. In the β-MnO₂(110) case, in contrast, the Mn–C interaction is quite weak, and the Mn(μ-O)Mn active site is electrophilic, thus allowing the formation of a stable ˙CH₃ radical intermediate state that becomes the driving force for a low-barrier homolytic C–H bond scission as well as a low-barrier and highly exothermic formation of methanol. This first cycle of methane oxidation results in a reduced β-MnO₂(110) surface, where no more μ-O active sites are available for the subsequent cycles of methane activation. Nonetheless, this reduced surface can also oxidize methane to methanol when the H₂O₂ oxidant is inserted in the mid-way reaction and forms new active sites of μ-OH. The second reaction is also highly exothermic although the C–H activation barrier is not as low as that for the fresh stoichiometric surface. This study suggests the β-MnO₂(110) surface as a potential catalyst for the cyclic oxidation of methane to methanol using the H₂O₂ oxidant without halting for reactivation.

---

1 Introduction

The utilization of earth-abundant low-carbon methane as a transition to renewable energy sources is highly desirable. However, methane, which is mainly present in natural gas, is difficult to store and transport. Therefore, developing an effective yet efficient means to convert methane to liquids such as methanol is considered essential. Unfortunately, the existing method to convert methane to methanol in industries involves a high-temperature formation of syngas (CO and H₂ mixture).^1,2 This approach, however, is not only costly but also inefficient as the resultant CO needs sequential quasi-catalytic treatments to produce methanol.^3,4 In the past decade, the development of heterogeneous catalysts (e.g., metal-exchanged zeolites) for the methane oxidation to methanol had significantly progressed.^5–8 In particular, Fe- and Cu-exchanged zeolites have enabled the reaction to proceed at room temperature,^9–12 which is crucial to reduce costs and more importantly to avoid an overoxidation to products more stable than methanol.^13–15 Accordingly, this has inspired broad development of new catalysts such as single-metal-modified surfaces such as graphene, CeO₂, TiO₂, ZnO, CuO, etc.^16–23

In these mono/diatomic-dispersed catalysts, however, the methane conversion undergoes the so-called stepwise reaction, where the catalyst must first be activated with O₂ or N₂O at high temperature to form the active metal–oxo sites prior to the main reaction of methane oxidation to methanol that takes place at a lower temperature.^24–27 After the first cycle of the reaction, the reaction must then be halted and the reduced catalyst must be reactivated using the same oxidant to continue the reaction to the second cycle and so on. This, consequently, makes the catalysts unpractical for industrial purposes. Attempts to make it more catalytic (i.e., cyclic/continuous reaction) have also been reported, but this approach is less preferred than the stepwise one due to the need for a higher temperature to decompose the oxidant, which accordingly increases the probability for overoxidation to occur and thus gives rise to selectivity issues.^28–31

In 2017, Liang et al.³² reported that the rutile-type IrO₂(110) surface is highly active for H–CH₃ bond scission at temperatures as low as 150 K with an extremely low activation barrier of 0.1 eV. Tsuji and Yoshizawa,³³ by means of density functional theory (DFT) calculations, then elucidated that the IrO₂(110) distorts the geometry of methane (C–H bond elongation and H–C–H angle widening) at the early stage of activation and cleaves the C–H bond in a heterolytic fashion that leads to the formation of a strong Ir–CH₃ bond, which explains the high activity of the catalyst. They also suggested β-PtO₂(110) as a catalyst that is more active than IrO₂(110) for the H–CH₃ bond scission owing to more geometrical distortions of the adsorbed methane and a stronger Pt–CH₃ bond.³³ Despite this, however, an excessively strong metal–CH₃ bond would lead to a new challenge when considering the energy required for the metal–CH₃ bond cleavage and the following HO–CH₃ recombination to form methanol. This is evident from the works by Yeh et al.³⁴ and Martin et al.,³⁵ showing that formaldehyde and CH_yO₂, instead of methanol, are two favorable products for methane oxidation on IrO₂(110) in the presence and absence of O₂, respectively. Also, Tsuji et al.³⁶ and Takagaki et al.³⁷ have shown that, only through engineering schemes such as nitrogen doping, oxygen defects, and applying supports, β-PtO₂(110) can convert methane to methanol.

In this study, we use DFT calculations to evaluate three rutile-type metal oxide surfaces, including IrO₂(110), β-PtO₂(110), and β-MnO₂(110), not only for catalyzing the methane activation but also for the methanol formation. Being the focus of this study, β-MnO₂(110) is found to easily cleave the H–CH₃ bond through a homolytic pathway, where a free ˙CH₃ radical, instead of a Mn–CH₃ ligand, is formed as the reaction intermediate, which contrasts the heterolytic mechanism favored by IrO₂(110) and β-PtO₂(110), and becomes the reason for an easy formation of methanol. This paper also discusses the origin of such different mechanisms and the possibility for the reduced β-MnO₂(110) to proceed the second cycle of the reaction by introducing H₂O₂ in the mid-way, which renders the catalyst potential for the cyclic (continuous) oxidation of methane to methanol without halting for reactivation.

2 Computational details

IrO₂, β-PtO₂, and β-MnO₂ are rutile-type crystals, where the latter two, in particular, have a distorted crystal structure. The optimized bulks were found to have lattice parameters of a = b = 4.522 Å and c = 3.184 Å for IrO₂; a = 3.089 Å, b = 4.519 Å, and c = 4.455 Å for β-PtO₂; and a = b = 4.474 Å and c = 2.972 Å for β-MnO₂. These optimized bulks were then used to construct 5 × 2 slab models with nine atomic layers of surface and 15 Å of vacuum for each, a large enough separation to minimize the effect of interactions between the periodically repeated adsorbates. The three topmost atomic layers were allowed to relax in all directions, while the rest were constrained to their optimized positions to represent the bulk.

Spin-polarized calculations were performed using the Kohn–Sham formulation^38,39 as implemented in the Vienna Ab initio Simulation Package (VASP) version 5.4.4.^40,41 The projector augmented wave (PAW) method was employed to describe the interaction between cores and electrons.^42,43 The electron exchange–correlation was treated using the Perdew–Burke–Ernzerhof (PBE)⁴⁴ functional based on the generalized gradient approximation (GGA). The plane-wave basis set with a sufficient cut-off energy of 500 eV (Fig. S1, ESI†) was used for all calculations. Considering the large slab models used here, we restricted the Brillouin zone sampling to the Γ point only except for PDOS calculations, in which a 3 × 3 × 1 k-point mesh was used. The zero-damping D3 method was utilized to account for the dispersion correction.⁴⁵ The GGA+U method of Dudarev's simplified rotationally invariant approach⁴⁶ was used with U_eff values of 7.5 and 5.1 eV, respectively, for the Pt 5d and Mn 3d orbitals, as optimized previously.^33,47,48 The use of different U_eff values was tested to insignificantly alter the relative energies (Fig. S2, ESI†). Unlike these two metal orbitals, the Ir 5d orbital exhibits a weak on-site Coulomb interaction of electrons, making the GGA+U treatment unnecessary, consistent with previous studies.^32,33 Due to a great number of metal atoms involved in the present slab surface models, as opposed to the mono/diatomic systems, the spin configuration was not set to a specific spin state. Instead, we let VASP optimize the spin state along with the geometry optimization. Therefore, when the calculations converged, both the geometry and the spin configuration were in the ground state. This is a standard well-accepted method used for many surface systems.^{16,33,47–49}

The conjugate gradient method was employed to optimize intermediate structures, while the climbing-image nudged elastic band (CI-NEB) method was used to locate transition states (TSs).⁵⁰ The image-dependent pair potential method was used to generate initial images for the CI-NEB calculations.⁵¹ The calculations were considered converged when the maximum forces on the unconstrained atoms are below 0.03 eV Å⁻¹. To confirm the presence of a saddle point, vibration frequency calculations were performed using the finite difference method with a small displacement of 0.015 Å. The Bader analysis algorithm⁵² was used to calculate atomic spin density, and optimized structures were visualized by using VESTA.⁵³ The bonding orbital analysis was performed using the projected crystal orbital Hamilton population (pCOHP) method, as implemented in the LOBSTER package.^54–58

The surface formation energy (E_surf) was calculated by using the following formula under the assumption that the surface was formed by cleaving the bulk structure.

where E_slab and E_bulk are the total energies of the slab surface and the bulk, respectively, while n is the ratio of the number of atoms in the slab model to the bulk, and A_slab is the surface area of the slab surface. The adsorption energy (E_ads) of an A molecule is defined as

E_ads = E_slab+A − (E_slab + E_A)

where E_slab+A is the total energy of the slab surface with an adsorbed A molecule and E_A is the total energy of an isolated A molecule. The M–C bond formation energy (M = Ir, Pt, Mn) was calculated by using the following equation, as also used in our previous study:⁵⁹

E_B(M−C) = E_slab+CH3 − (E_slab + E_CH3)

where E_slab+CH3 and E_CH3 are the total energies of a CH₃ ligand adsorbed on the surface M atom and an isolated ˙CH₃ radical, respectively. The O–H bond formation energy was calculated according to the following formula:
where E_slab+H and E_H2 are the total energies of a single H atom adsorbed on the surface O atom and an isolated H₂ molecule, respectively.

3 Results and discussion

3.1 Stability of the (110) surfaces

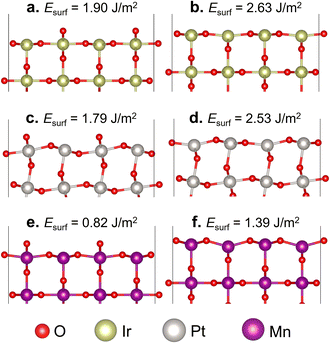
In the formation of the (110) surface from rutile-type metal oxides, there are two possible terminations on the topmost layer, namely the O- and M-terminated (110) surfaces (Fig. 1). In these two slab surface models, we have ensured that they consist of symmetrically arranged layers of positive and negative charges, thus exhibiting no net dipole moment perpendicular to the surface normal, which is aligned with the Tasker rules.⁶⁰ The calculated E_surf shows that the O-terminated surface model for all three studied oxides is easier to form than the M-terminated one. This suggests that the cleavage of IrO₂, β-PtO₂, and β-MnO₂ in a direction perpendicular to [110] tends to form layers covered with two-coordinated bridging O (μ-O) atoms, which is consistent with previous studies.^32,48,61 On the other hand, the M-terminated (110) surface involves one-coordinated dangling O atoms, which makes it less stable. Thus, in the next section, we consider only the O-terminated (110) surface (hereafter referred to as the stoichiometric surface) for evaluating the oxidation of methane to methanol.

Fig. 1 Optimized slab models of (a) and (b) IrO₂(110), (c) and (d) β-PtO₂(110), and (e) and (f) β-MnO₂(110) surfaces with O-termination (left side) and M-termination (right side). The corresponding E_surf (in J m⁻²) is indicated on each slab model.

3.2 Methane oxidation on the stoichiometric surface

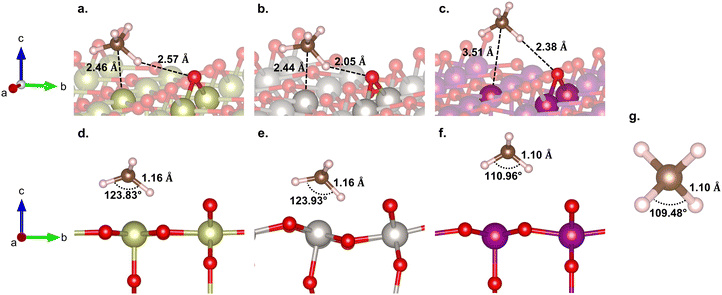
Here, we consider the bridging μO-atom terminations as the active sites abstracting the H atom of methane and being consumed to form methanol. Another reaction possibility of H₂O₂ being introduced together with methane to the surface was also considered. However, in this scenario, H₂O₂ decomposes into OOH + μOH (Fig. S3, ESI†), and the following methane reaction with the formed μOH proceeds according to the discussion in section 3.4. Therefore, we first focus our discussion of this section only on the former scenario.

Fig. 2 shows the reaction energy diagrams for all three studied surfaces, while the optimized structures for each reaction step are shown in Fig. S4 (ESI†). The reaction involves three elementary steps, namely methane adsorption, C–H bond activation, and methanol formation. In the first step, as expected, IrO₂(110) and β-PtO₂(110) strongly adsorb methane with adsorption energies (E_ads) of −0.75 and −0.65 eV, respectively, whereas β-MnO₂(110) weakly adsorbs methane (E_ads = −0.22 eV). Looking at the geometry of the adsorbed methane (Fig. 3), we find that only IrO₂(110) and β-PtO₂(110) are quite close to the adsorbed methane, which is a clear indication of a strong chemical adsorption. This chemisorption forms C–Ir and C–Pt interactions that distort the geometry of methane. As shown in Fig. 3d and e, a significant widening of the ∠H–C–H angle to about 124° and a C–H bond elongation to 1.16 Å are observed, consistent with the previous work of Tsuji and Yoshizawa.³³ In the β-MnO₂(110) case (Fig. 3c and f), on the other hand, the weakly adsorbed methane is quite far from the surface and no geometrical distortions are observed (see Fig. 3g for methane geometry in the gas phase), which indicate a physisorption.

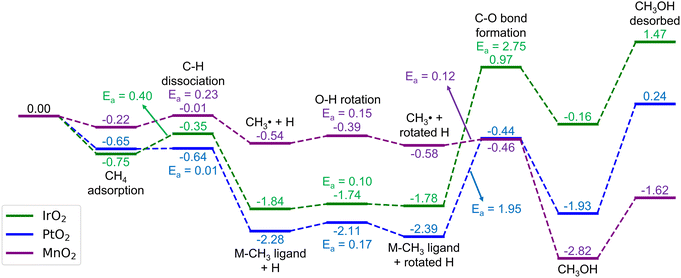Fig. 2 Energy diagrams (in eV) for the methane oxidation to methanol on the stoichiometric IrO₂(110), β-PtO₂(110), and β-MnO₂(110) surfaces. The corresponding optimized geometries are shown in Fig. S4 (ESI†).

Fig. 3 (top) Side and (bottom) isometric views of methane adsorption on (a) and (d) IrO₂(110), (b) and (e) β-PtO₂(110), and (c) and (f) β-MnO₂(110) surfaces, and (g) the structure of an isolated methane molecule.

In the subsequent C–H activation step, two well-studied pathways (i.e., the homolytic and heterolytic bond scissions that lead to the formation of a ˙CH₃ radical and an M–CH₃ ligand intermediate states, respectively) were considered, as many reports also focused on these.^62,63 However, the IrO₂(110) and β-PtO₂(110) surfaces disfavor the homolytic pathway as the calculations for the formation of the ˙CH₃ radical cannot converge to the minimum required accuracy and eventually forms Ir–CH₃ and Pt–CH₃ ligands. In contrast, as shown in Fig. 2, the formation of both the ˙CH₃ radical and Mn–CH₃ ligand on β-MnO₂(110) is favored, enabling us to calculate both the homolytic and heterolytic C–H bond scissions. However, interestingly, after the NEB calculations, we find that the TS structures found for both pathways are similar, which are radical-like TSs. Moreover, the Mn–CH₃ ligand formation (ΔE = −0.51 eV) is found to be slightly less stable than the ˙CH₃ radical formation (ΔE = −0.54 eV). These clearly indicate that the C–H activation on β-MnO₂(110) indeed favors the homolytic pathway.

In terms of energetics, among the studied catalysts, the C–H activation barrier is calculated as the lowest for β-PtO₂(110) (E_a = 0.01 eV), the middle for β-MnO₂(110) (E_a = 0.23 eV), and the highest for IrO₂(110) (E_a = 0.40 eV). It is worth noting that the TSs for β-PtO₂(110) and IrO₂(110) are more stable than the reference (i.e., methane in the gas phase), suggesting that the actual (apparent) activation barrier for IrO₂(110) and β-PtO₂(110) might be lower, as also reported by Liang et al.³² In terms of geometry (Fig. 4), the heterolytic C–H bond scission on IrO₂(110) and β-PtO₂(110) results in a four-centered TS, where the resultant CH₃⁻ fragment separates from the H⁺ fragment while interacting with the surface metal atom (M⋯C distance < 2.31 Å). In contrast, the bond scission on β-MnO₂(110) results in a ˙CH₃-like species (i.e., the geometry has not been fully planar yet, but somewhere in between tetrahedral and planar structures) that separates from both the Mn and H atoms and forms an almost planar geometry.

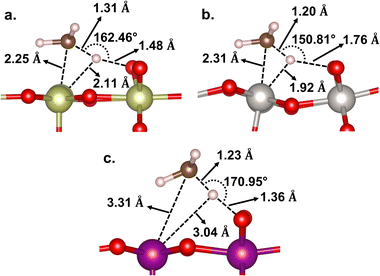Fig. 4 Geometries of the C–H transition state on (a) IrO₂(110), (b) β-PtO₂(110), and (c) β-MnO₂(110) surfaces.

In Fig. 5, the geometries of the M–CH₃ ligand and ˙CH₃ radical intermediate states are shown. The Ir–, Pt–, and Mn–CH₃ bond lengths are measured to be 2.07, 2.00, and 2.26 Å, respectively, which are consistent with their corresponding bond formation energies (E_B(M–C) = −2.90, −2.53, and −0.59 eV, respectively). This suggests that the Mn–C bond is so weak that it is not more stable than the ˙CH₃ formation that has a longer Mn⋯C distance (2.65 Å). Thus, we infer that the methane conversion to methanol on β-MnO₂(110) most probably proceeds through an intermediate state of the ˙CH₃ radical without being preceded or succeeded by the Mn–CH₃ formation. The formation of the ˙CH₃ radical is indicated by a planar sp² geometry of CH₃ (Fig. 5d) and the presence of a single unpaired electron on the C atom.

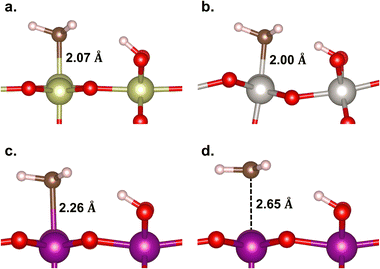Fig. 5 Geometries of the M–CH₃ ligand on (a) IrO₂(110), (b) β-PtO₂(110), and (c) β-MnO₂(110) surfaces, and (d) the ˙CH₃ radical on β-MnO₂(110).

The next elementary step is the methanol formation. Here, the CH₃ moiety or ˙CH₃ radical recombines with the OH moiety that resulted from the prior methane activation. Other possible pathways such as solvent-assisted methanol formation¹⁵ might also be possible but were excluded from the consideration for the sake of conciseness. To facilitate the HO–CH₃ recombination pathway, the OH fragment needs to rotate in a way that the H atom of the OH fragment points outward from the CH₃, while the O end of the OH fragment faces toward the CH₃, as also considered in our previous studies.^12,20,64 As shown in Fig. 2, this process is found to be low-barrier for all the studied catalysts (E_a = 0.1, 0.17, and 0.15 eV, respectively, for IrO₂(110), β-PtO₂(110), and β-MnO₂(110)).

The recombination between the CH₃⁻ and the rotated OH on the IrO₂(110) and β-PtO₂(110) surfaces requires a quite high activation barrier (E_a = 2.75 and 1.95 eV, respectively), the latter of which agrees well with the work of Tsuji et al. (2.07 eV).³⁶ Such a high E_a is as expected from the strong Ir–CH₃ and Pt–CH₃ bonds that need to be cleaved before the recombination. However, not to our expectation, the formation of methanol chemisorbed on these two surfaces is highly endothermic (ΔE = 1.62 and 0.46 eV, respectively, for IrO₂(110) and β-PtO₂(110)). These highly unfavored thermodynamic and kinetic aspects suggest that the methanol formation on these two oxide surfaces is unlikely to happen and, instead, stops at the formation of Ir–CH₃ and Pt–CH₃ bonds only.

In the β-MnO₂(110) case, in contrast, the methanol formation proceeds through a recombination between the ˙CH₃ and OH fragments with a low barrier (E_a = 0.12 eV) and high exothermicity (ΔE = −2.24 eV). Such a highly favored methanol formation may be attributed to the higher stability of Mn³⁺ (3d⁴) in the resultant Mn³⁺–CH₃OH–Mn³⁺ as compared to Mn⁴⁺ (3d³) in the CH₄ adsorption state. This is also evidenced from the −pCOHP calculations of the methanol formation (Fig. S5, ESI†) showing that the Mn–O antibonding orbital is located at a higher energy than the Ir–O and Pt–O antibonding orbitals, which again indicates that the Mn–O bonds are stronger and thus stabilize the system more significantly. On top of that, β-MnO₂(110) also desorbs methanol with a desorption energy (1.20 eV) being the lowest among the three studied catalysts (1.63 and 2.17 eV, respectively, for IrO₂(110) and β-PtO₂(110)) and comparable to that for the zeolites.^64,65 The geometrical parameters of the methanol adsorbed on the three catalysts are shown in Fig. S6 (ESI†). Fig. S7 (ESI†) shows a good Brønsted–Evans–Polanyi (BEP) relation^66,67 between E_a and ΔE for HO–CH₃ formation, suggesting that a more stable methanol formation requires a lower E_a. We have also tried to relate the E_a of HO–CH₃ formation to the O p-band center, as suggested by Ge and co-workers.^68,69 However, unfortunately, there seems no high dependency of the HO–CH₃ formation on the O p-band center (Fig. S8, ESI†).

We have also evaluated the stability of the formaldehyde (CH₂O) and dimethyl ether (C₆H₂O) formation as two possible side products of methanol overoxidation. As shown in Fig. S9 (ESI†), two alternative pathways (CH_4(g) → CH₂O* + H_2(g) and 2CH_4(g) → C₂H₆O* + H_2(g)) are considered, and it is found that the formation of CH₂O and C₆H₂O on all studied surface catalysts is much less stable than the methanol formation. This suggests that the overoxidation of methanol is unlikely to occur.

Overall, the reaction on β-MnO₂(110) is exothermic (ΔE = −1.62 eV) with a rate-determining barrier of only 0.23 eV and a highly favorable methanol formation as compared to the CH₂O and C₆H₂O formation. In contrast, the reaction on IrO₂(110) and β-PtO₂(110) surfaces initially proceeds with a low C–H barrier but then encounters difficulties in the formation and desorption of methanol with high endothermicity and a rate-determining barrier of >1.9 eV, making them unsuitable for catalyzing the direct conversion of methane to methanol.

3.3 Electronic structure analysis

From the discussion above, two questions arise: (1) why does β-MnO₂(110) favor the homolytic C–H scission, while IrO₂(110) and β-PtO₂(110) favor the heterolytic one and (2) why is the ˙CH₃ + OH formation on β-MnO₂(110) more stable than the methane adsorption? To answer the first question, we calculate the strength of M–C and O–H bonds formed in the M–CH₃ + O–H intermediate state to analyze which of the two contributes more to the stabilization of the intermediate state. As shown in Table 1, the Ir–CH₃ binding energy is two times higher than the O–H binding energy, suggesting that the Ir–C bond is extremely strong and thus contributes more to the state stabilization. On β-PtO₂(110), on the other hand, both the Pt–CH₃ and O–H bonds contribute equally to the stabilization, whereas for β-MnO₂(110), the O–H bond contributes predominantly to the formation of the Mn–CH₃ + O–H ligand state, indicating that the Mn–C bond is indeed weak. This table, thus, infers that the Ir–C and Pt–C interactions are strong enough to prevent the formation of ˙CH₃ as an intermediate state, making the homolytic C–H bond scission unfavorable for IrO₂(110) and β-PtO₂(110) surfaces. Also, this suggests that the C–H activation of methane on β-MnO₂(110) is driven more predominantly by the O–H bond formation, as also previously suggested by Liu et al. for methane activation on metal-zeolites.⁷⁰

Table 1 M–C and O–H binding energies on each studied metal oxide surface

Metal oxide surface	E B(M–C) (eV)	E B(O–H) (eV)
IrO2(110)	−2.90	−1.35
β-PtO2(110)	−2.53	−2.23
β-MnO2(110)	−0.59	−2.49

---

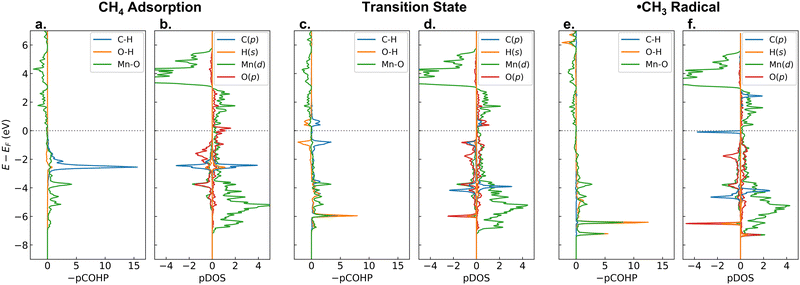
Now, to answer the second question, let us analyze the changes of −pCOHP and PDOS during the C–H activation on β-MnO₂(110). Fig. 6 shows the −pCOHP values of the dissociated C–H, the formed O–H, and the bridging Mn–O bonds as well as PDOS of the C-p, abstracted H-s, active Mn-d, and bridging O-p orbitals for the adsorption, transition, and intermediate states of methane activation. In Fig. 6a and b, we can see the degenerate σ_C–H bonding orbitals of methane as they are in the gas phase (see also Fig. S10 (ESI†), only the energy shifts due to the presence of the surface that alters the Fermi level (E_F)), indicating a weak adsorbate–surface interaction where the adsorbed methane is undistorted geometrically and electronically. During the homolytic C–H bond scission, the α-electron of the shared electrons in the C–H bond is taken by the H atom, while the β-electron is taken by the C atom. The α electron carried by the H atom is readily transferred to the antibonding Mn–O orbital, as indicated by the presence of a newly formed MnO–H bonding orbital at a low energy (green and orange lines at about −6 eV in Fig. 6c). The β electron, on the other hand, singly occupies the antibonding C-p orbital and forms a free ˙CH₃ radical, as indicated by the presence of an occupied C-p β-orbital and an unoccupied C-p α-orbital in the vicinity of the E_F (blue line in Fig. 6d). After the ˙CH₃ formation, the MnO–H bonding orbital becomes double due to the involvement of two Mn atoms bridging the OH moiety and shifts downward to slightly lower energies (Fig. 6e), indicating that the O–H bond becomes stronger. The unoccupied antibonding C-p α-orbital, on the other hand, shifts upward away from the E_F (Fig. 6f), indicating that the ˙CH₃ is stabilized. Such an electrophilic mechanism, where a transfer of the C–H α-electron leads to a stabilization of the radical intermediate state (˙CH₃ + O–H) and becomes the driving force for the C–H bond activation, is similar to the [FeO]²⁺-ZSM-5 case.⁷¹ It is worth noting that in the formation of the Mn–CH₃ + O–H intermediate state, no electron transfer and redox occur, thus explaining the low stability of the Mn–CH₃ and O–H bonds.

Fig. 6 −pCOHP and PDOS analyses of C–H activation on the β-MnO₂(110) surface: (a) and (b) CH₄ adsorption state, (c) and (d) transition state, and (e) and (f) ˙CH₃ radical state. Positive and negative −pCOHP values indicate bonding and antibonding interactions, respectively. Positive and negative PDOS values indicate states for the α and β electrons, respectively.

3.4 Methane oxidation on reduced β-MnO₂(110) using the H₂O₂ oxidant

Here, we can consider two possibilities of the H₂O₂ insertion: (1) being introduced together with methane to the stoichiometric surface, where the H₂O₂ decomposition to H + OOH proceeds earlier than the methane activation (Fig. S3, ESI†); or (2) being inserted in the mid-way reaction after a reduced surface is formed due to the consumption of all the μ-O terminations by the prior oxidation of methane (H₂O₂ decomposition to 2OH; Fig. S11, ESI†). Whichever the case, the μ-O terminations become μ-OH terminations that now abstract the H atom of methane. Thus, in this section, we focus our discussion on the reduced surface only. As shown in Fig. 7, the H₂O₂ decomposes favorably on the reduced β-MnO₂(110) surface into 2OH rather than H + OOH (Fig. S11, ESI†). This is possibly due to the absence of the bridging μO-atom terminations that may accommodate the dissociated H atom of H₂O₂. Fig. 7 shows that the H₂O₂ is first adsorbed on the reduced surface with a rather high E_ads of −0.80 eV. The HO–OH bond then dissociates into two OH fragments with a low activation barrier (E_a = 0.04 eV) to form two stable Mn–OH–Mn species with a quite high exothermicity (ΔE = −3.11 eV).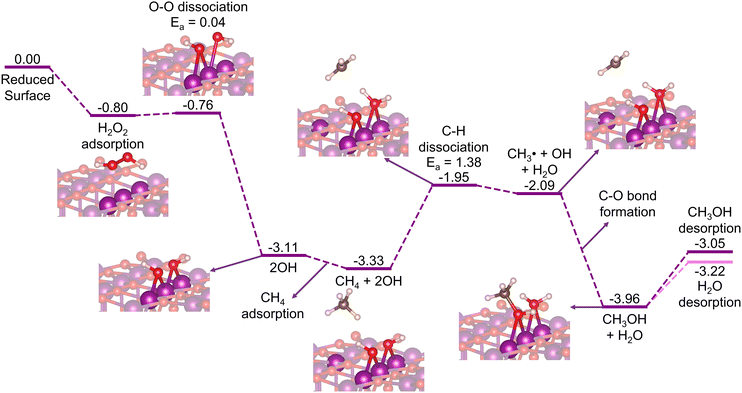

Fig. 7 Energy diagram (in eV) for CH₄ oxidation to CH₃OH on the reduced β-MnO₂(110) surface with H₂O₂ as the oxidation agent.

In the subsequent reaction steps, we consider methane adsorption on the OH-decorated surface, followed by a C–H bond activation via the homolytic pathway to directly form methanol. As shown in Fig. 7, the adsorption of methane is rather weak (E_ads = −0.22 eV), as also observed previously for the stoichiometric surface (Fig. 2). One H atom of methane is then abstracted in a homolytic fashion with E_a = 1.38 eV and accepted by one of the OH moieties forming a H₂O molecule adsorbed on the surface, while the remaining CH₃ fragment forms a free radical species as an intermediate state before the direct formation of methanol takes place. Comparing this to a mechanism where an Mn–CH₃ ligand is formed as an intermediate state, instead of ˙CH₃, we find a similar E_a and transition structure (Fig. S12, ESI†), indicating that the homolytic pathway is indeed favored. Moreover, the Mn–CH₃ formation (ΔE = −2.16 eV) is found to be significantly less stable than the methanol formation (ΔE = −3.96 eV), suggesting that the ˙CH₃ radical may directly form methanol without forming Mn–CH₃ as another intermediate state, as also indicated previously in Fig. 2. The desorption energy of methanol in this case (E_des = 0.91 eV) is found to be lower than that in the stoichiometric surface case (1.20 eV). Along with methanol, the formed H₂O molecule also desorbs facilely with an E_des of only 0.74 eV, which thus forms the reduced β-PtO₂(110) surface again. The subsequent cycles of the CH₄ + H₂O₂ → CH₃OH + H₂O reaction can then again proceed repeatedly.

Although the calculated C–H activation barrier for this reduced surface case is much higher than that for the stoichiometric surface case, the overall reaction is downhill and highly exothermic. Furthermore, using H₂O₂ as the oxidant allows the reaction to proceed in a cyclic fashion, where CH₄ and H₂O₂ are introduced together or mid-way continuously to the reactor without halting for reactivation treatments. These suggest that β-MnO₂(110), in the form of either an O- or an M-terminated surface, has the potential for oxidizing methane to methanol.

We have also considered O₂ as a possible oxidant to form the stoichiometric surface back. Unfortunately, as shown in Fig. S13 (ESI†), the activation energy for the O–O dissociation (E_a = 2.30 eV) is quite high, and the overall reaction is slightly endothermic (ΔE = 0.06 eV). This suggests that the reduced surface needs to be exposed to a high O₂ pressure at elevated temperature to regain the active surface, which is unfavorable for practical purposes of methane direct conversion to methanol.

4 Conclusions

By means of DFT calculations, we have investigated the possibility and mechanism of methane direct oxidation to methanol on three rutile-type metal oxide surfaces, namely IrO₂(110), β-PtO₂(110), and β-MnO₂(110). The three catalysts, through their bridging O-atom terminations on the topmost layer, are found to be highly active toward the C–H bond activation (E_a < 0.4 eV). However, only β-MnO₂(110) can oxidize the resultant CH₃ into methanol. Such an ability discrepancy is due to the formation of strong Ir–CH₃ and Pt–CH₃ bonds during the reaction via heterolytic C–H bond scission, consequently increasing the energy required to break the Ir–CH₃ and Pt–CH₃ bonds and to recombine with the OH ligand. In contrast, for the β-MnO₂(110) case, the formation of a free ˙CH₃ radical as the reaction intermediate instead of an Mn–CH₃ ligand facilitates a direct recombination of OH and CH₃ without the need for any prior bond breaking. The ability of β-MnO₂(110) to form a stable ˙CH₃ radical that drives the reaction to proceed with a low C–H activation barrier owes to the electrophilic nature of the surface.

We have also evaluated the possibility for the reduced β-MnO₂(110) surface to again oxidize methane to methanol by introducing the H₂O₂ oxidant in the mid-way reaction. We find that the H₂O₂ facilely decomposes to 2OH, which becomes the new active site for the methane activation. The overall reaction is found to be highly exothermic, and the calculated barrier for the rate-determining C–H activation (E_a = 1.38 eV) is moderate, much lower than the barrier calculated for the rate-determining methanol formation on IrO₂(110) and β-PtO₂(110). This renders β-MnO₂(110) potential for catalyzing the CH₄ + H₂O₂ → CH₃OH + H₂O reaction in a cyclic fashion.

Author contributions

F. D. N.: data curation, investigation, methodology, visualization, writing – original draft; H. A.: writing – review & editing; M. W.: writing – review & editing; M. K. A.: supervision, validation, writing – review & editing; A. G. S.: supervision, writing – review & editing; H. T. Y.: writing – review & editing; A. S.: formal analysis, writing – review & editing; K. Z.: writing – review & editing; M. H. M.: conceptualization, funding acquisition, formal analysis, writing – review & editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Indonesia Endowment Fund for Education (LPDP) and Indonesian Science Fund (DIPI) through the RISPRO International Collaboration research scheme (grant no. RISPRO/KI/B1/KOM/11/15539/1/2020). The computations were partly performed at the Research Institute for Information Technology of Kyushu University.

References

1. J. H. Lunsford, Catal. Today, 2000, 63, 165–174.
2. Z. Zakaria and S. K. Kamarudin, Renewable Sustainable Energy Rev., 2016, 65, 250–261.
3. H. D. Gesser, N. R. Hunter and C. B. Prakash, Chem. Rev., 1985, 85, 235–244.
4. H. Schulz, Appl. Catal., A, 1999, 186, 3–12.
5. M. H. Mahyuddin, Y. Shiota, A. Staykov and K. Yoshizawa, Acc. Chem. Res., 2018, 51, 2382–2390.
6. B. E. R. Snyder, M. L. Bols, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Chem. Rev., 2018, 118, 2718–2768.
7. N. F. Dummer, D. J. Willock, Q. He, M. J. Howard, R. J. Lewis, G. Qi, S. H. Taylor, J. Xu, D. Bethell, C. J. Kiely and G. J. Hutchings, Chem. Rev., 2022, 123, 6359–6411.
8. M. Ravi, M. Ranocchiari and J. A. van Bokhoven, Angew. Chem., Int. Ed., 2017, 56, 16464–16483.
9. J. S. Woertink, P. J. Smeets, M. H. Groothaert, M. A. Vance, B. F. Sels, R. A. Schoonheydt and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18908–18913.
10. P. Vanelderen, B. E. R. Snyder, M.-L. Tsai, R. G. Hadt, J. Vancauwenbergh, O. Coussens, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, J. Am. Chem. Soc., 2015, 137, 6383–6392.
11. M. L. Bols, S. D. Hallaert, B. E. R. Snyder, J. Devos, D. Plessers, H. M. Rhoda, M. Dusselier, R. A. Schoonheydt, K. Pierloot, E. I. Solomon and B. F. Sels, J. Am. Chem. Soc., 2018, 140, 12021–12032.
12. M. H. Mahyuddin, E. T. Lasiman, A. G. Saputro, S. V. Casuarina, N. Nugraha and H. K. Dipojono, Catal. Sci. Technol., 2023, 13, 5767–5775.
13. M. J. Wulfers, R. F. Lobo, B. Ipek and S. Teketel, Chem. Commun., 2015, 51, 4447–4450.
14. M. B. Park, S. H. Ahn, M. Ranocchiari and J. van Bokhoven, ChemCatChem, 2017, 9, 3705–3713.
15. M. H. Mahyuddin, S. Tanaka, R. Kitagawa, A. L. Maulana, A. G. Saputro, M. K. Agusta, H. T. Yudistira, H. K. Dipojono and K. Yoshizawa, J. Phys. Chem. C, 2021, 125, 19333–19344.
16. R. K. Singha, Y. Tsuji, M. H. Mahyuddin and K. Yoshizawa, J. Phys. Chem. C, 2019, 123, 9788–9798.
17. Z. Liu, E. Huang, I. Orozco, W. Liao, R. M. Palomino, N. Rui, T. Duchoň, S. Nemšák, D. C. Grinter, M. Mahapatra, P. Liu, J. A. Rodriguez and S. D. Senanayake, Science, 2020, 368, 513–517.
18. X. Cui, H. Li, Y. Wang, Y. Hu, L. Hua, H. Li, X. Han, Q. Liu, F. Yang, L. He, X. Chen, Q. Li, J. Xiao, D. Deng and X. Bao, Chem, 2018, 4, 1902–1910.
19. Y. Qin, H. Liu, L. Li, J. Han, H. Wang, X. Zhu and Q. Ge, J. Catal., 2023, 417, 323–333.
20. R. P. P. Sukanli, M. H. Mahyuddin, A. G. Saputro, M. K. Agusta, H. T. Yudistira, K. Yoshizawa and H. K. Dipojono, ACS Appl. Nano Mater., 2023, 6, 6559–6566.
21. Q. Shen, C. Cao, R. Huang, L. Zhu, X. Zhou, Q. Zhang, L. Gu and W. Song, Angew. Chem., Int. Ed., 2020, 59, 1216–1219.
22. E. Huang, I. Orozco, P. J. Ramírez, Z. Liu, F. Zhang, M. Mahapatra, S. Nemšák, S. D. Senanayake, J. A. Rodriguez and P. Liu, J. Am. Chem. Soc., 2021, 143, 19018–19032.
23. S. Bai, Y. Xu, P. Wang, Q. Shao and X. Huang, ACS Catal., 2019, 9, 6938–6944.
24. E. M. C. Alayon, M. Nachtegaal, A. Bodi and J. A. van Bokhoven, ACS Catal., 2014, 4, 16–22.
25. V. L. Sushkevich, D. Palagin and J. A. van Bokhoven, Angew. Chem., Int. Ed., 2018, 57, 8906–8910.
26. D. K. Pappas, A. Martini, M. Dyballa, K. Kvande, S. Teketel, K. A. Lomachenko, R. Baran, P. Glatzel, B. Arstad, G. Berlier, C. Lamberti, S. Bordiga, U. Olsbye, S. Svelle, P. Beato and E. Borfecchia, J. Am. Chem. Soc., 2018, 140, 15270–15278.
27. S. Grundner, M. A. C. Markovits, G. Li, M. Tromp, E. A. Pidko, E. J. M. Hensen, A. Jentys, M. Sanchez-Sanchez and J. A. Lercher, Nat. Commun., 2015, 6, 7546.
28. K. Narsimhan, K. Iyoki, K. Dinh and Y. Román-Leshkov, ACS Cent. Sci., 2016, 2, 424–429.
29. J. Xu, R. D. Armstrong, G. Shaw, N. F. Dummer, S. J. Freakley, S. H. Taylor and G. J. Hutchings, Catal. Today, 2016, 270, 93–100.
30. K. T. Dinh, M. M. Sullivan, K. Narsimhan, P. Serna, R. J. Meyer, M. Dincă and Y. Román-Leshkov, J. Am. Chem. Soc., 2019, 141, 11641–11650.
31. Y. K. Chow, N. F. Dummer, J. H. Carter, C. Williams, G. Shaw, D. J. Willock, S. H. Taylor, S. Yacob, R. J. Meyer, M. M. Bhasin and G. J. Hutchings, Catal. Sci. Technol., 2018, 8, 154–163.
32. Z. Liang, T. Li, M. Kim, A. Asthagiri and J. F. Weaver, Science, 2017, 356, 299–303.
33. Y. Tsuji and K. Yoshizawa, J. Phys. Chem. C, 2018, 122, 15359–15381.
34. C. H. Yeh, T. M. Le Pham, S. Nachimuthu and J. C. Jiang, ACS Catal., 2019, 9, 8230–8242.
35. R. Martin, C. J. Lee, V. Mehar, M. Kim, A. Asthagiri and J. F. Weaver, ACS Catal., 2022, 12, 2840–2853.
36. Y. Tsuji, K. Kurino and K. Yoshizawa, ACS Omega, 2021, 6, 13858–13869.
37. A. Takagaki, Y. Tsuji, T. Yamasaki, S. Kim, T. Shishido, T. Ishihara and K. Yoshizawa, Chem. Commun., 2023, 59, 286–289.
38. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
39. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
40. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
41. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
42. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
43. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
46. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
47. J. A. Dawson, H. Chen and I. Tanaka, ACS Appl. Mater. Interfaces, 2015, 7, 1726–1734.
48. D. A. Tompsett, S. C. Parker and M. S. Islam, J. Am. Chem. Soc., 2014, 136, 1418–1426.
49. M. H. Mahyuddin, R. V. Belosludov, M. Khazaei, H. Mizuseki and Y. Kawazoe, J. Phys. Chem. C, 2011, 115, 23893–23901.
50. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
51. S. Smidstrup, A. Pedersen, K. Stokbro and H. Jónsson, J. Chem. Phys., 2014, 140, 214106.
52. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
53. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
54. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 2002, 97, 8617–8624.
55. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
56. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567.
57. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
58. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940.
59. M. H. Mahyuddin, A. G. Saputro, R. P. P. Sukanli, F. Fathurrahman, J. Rizkiana, A. Nuruddin and H. K. Dipojono, Phys. Chem. Chem. Phys., 2022, 24, 4196–4203.
60. P. W. Tasker, J. Phys. C: Solid State Phys., 1979, 12, 4977.
61. H. Guan, G. Chen, J. Zhu and Y. Wang, J. Alloys Compd., 2010, 507, 126–132.
62. J. Xu, X. M. Cao and P. Hu, J. Phys. Chem. C, 2019, 123, 28802–28810.
63. A. A. Latimer, H. Aljama, A. Kakekhani, J. S. Yoo, A. Kulkarni, C. Tsai, M. Garcia-Melchor, F. Abild-Pedersen and J. K. Nørskov, Phys. Chem. Chem. Phys., 2017, 19, 3575–3581.
64. M. H. Mahyuddin, T. Tanaka, Y. Shiota, A. Staykov and K. Yoshizawa, ACS Catal., 2018, 8, 1500–1509.
65. M. H. Mahyuddin, Y. Shiota and K. Yoshizawa, Catal. Sci. Technol., 2019, 9, 1744–1768.
66. J. N. Brønsted, Chem. Rev., 1928, 5, 231–338.
67. M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24.
68. H. Liu, Y. Qin, L. Li, H. Wang, X. Zhu and Q. Ge, J. Catal., 2024, 431, 115388.
69. Y. Qin, L. Li, H. Liu, J. Han, H. Wang, X. Zhu and Q. Ge, J. Chem. Phys., 2024, 160, 134701.
70. C. Liu, G. Li and E. A. Pidko, Small Methods, 2018, 2, 1800266.
71. M. H. Mahyuddin, A. Staykov, A. G. Saputro, M. K. Agusta, H. K. Dipojono and K. Yoshizawa, J. Phys. Chem. C, 2020, 124, 18112–18125.

---

Footnote

† Electronic supplementary information (ESI) available: Geometrical structure of each reaction step on the stoichiometric surfaces; total DOS of CH₄ and ˙CH₃ in the gas phase; energy diagrams of H₂O₂ decomposition on the stoichiometric and reduced β-MnO₂(110); energy diagram of H–CH₃ bond scission on reduced β-MnO₂(110) via an alternative pathway; energy diagram of O₂ dissociation on reduced β-MnO₂(110); and CONTCAR files. See DOI: https://doi.org/10.1039/d4ma00827h

---