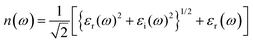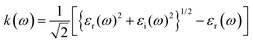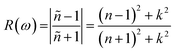Electric field and strain mediated zinc blende ZnSe: exploring its potential as a controlled stimulus responsive optical and optoelectronic material

Abstract

Herein, we reveal how stimuli precisely tune and tailor the optoelectronic response of zinc blende ZnSe, making it a candidate for advanced spintronic and optoelectronic technologies. Stimulus-driven bandgap engineering via electric fields and mechanical strain induces dynamic modulation: the bandgap narrows from 0.6 eV to 0.36 eV and widens from 0.67 eV to 1.45 eV under positive and negative electric fields, respectively, due to the Stark effect and phase transitions influenced by electron–electron interactions and the Mott transition. Compressive strain increases the bandgap from 1.6 eV to 2.45 eV, while tensile strain decreases it from 1.6 eV to 0.94 eV. We also investigate the effects of stimuli on the partial and total density of states, charge density, local density of states, and charge transfer, emphasizing the role of Zn (2s, 3d) and Se (2p) orbitals. The HOMO–LUMO gap analysis shows that electric fields enhance stability, while strain reduces it. Additionally, dynamic modulation of optical parameters—such as the dielectric function, refractive index, reflectivity, extinction coefficient, and conductivity—demonstrates controlled optoelectronics. Our findings highlight the potential of stimuli to significantly and dynamically modulate ZnSe electronic and optoelectronic properties, paving the way for innovative miniaturized optoelectronic technologies.

---

Introduction

II–VI semiconductors, well-known for their direct bandgaps, are recognized for their promising applications in optoelectronics and spintronics.^1–3 Unlike IIA–VI compounds, II–VI semiconductors have a metal d-band embedded within the primary valence band.^3–6 Among the diverse range of monovalent zinc blende chalcogenide phase II–VI materials, ZnSe stands out due to its favourable electronic, transport, and magnetic properties.^7–10 ZnSe crystallizes in a cubic lattice with a face-centred cubic (FCC) structure and tetrahedral coordination comprises of four zinc (Zn) and four selenium (Se) atoms and each zinc atom is covalently bonded to four equidistant selenium atoms, and each selenium atom is analogously bonded to four zinc atoms.^11–13 The atomic positions in ZnSe are (0 0 0), (0 ½ ½), (½ 0 ½), (½ ½ 0) for zinc, and (¼ ¼ ¼), (¼ ¾ ¾), (¾ ¼ ¾), (¾ ¾ ¾) for selenium, with lattice parameters of a = b = c = 5.67 Å, and bond angles α = β = γ = 90°. It belongs to the space group F4̄3m, space group number 216, and has a unit cell volume of 181.5 ų.^11,12 ZnSe is the subject of extensive experimental research due to its underlying optoelectronic properties,^2,7,13 which make it a paradigm for applications in the blue-green region of the electromagnetic spectrum, including blue lasers and optical waveguides.^14,15 Additionally, doping ZnSe with transition metals such as manganese (Mn), iron (Fe), nickel (Ni), chromium (Cr), and cobalt (Co) has further improved its properties, emphasizing its potential as a developing dilute magnetic semiconductor.^16–18 A variety of experimental methods, comprising molecular beam epitaxy (MBE),^19,20 electron beam evaporation (EBE),²¹ close space sublimation (CSS),²² metal–organic vapor phase epitaxy (MOVPE),^23,24 and magnetron sputtering, have been employed to grow and fabricate ZnSe thin films.^25,26 Recently, Fe and Ni single crystals have been successfully grown and deposited on ZnSe using MBE, establishing new possibilities for applications in microelectronics and magnetic switches.²⁷ Theoretically, numerous models and approximations within density functional theory (DFT) have been employed to examine the structural, electronic, optical, piezoelectric, mechanical, magnetic, phase stability, chemical reactivity, and photocatalytic properties of these materials. Notably, early research on ZnSe by Bernard and Zunger et al.²⁸ utilized the pseudopotential method to explain the electronic states using pseudo-atomic orbitals. The calculations employed a mixed basis all-electron method that integrates plane waves with localized orbitals, requiring the resolution of an atomic problem where the potential is presumed to be parallel to the crystal potential. Recently, the empirical pseudopotential method has been employed to determine the electronic band structure and density of states (DOS) for ZnSe and ZnTe.^29,30 Sukkabot et al.³⁰ explored the electronic, magnetic, and optical properties of Mn-doped ZnSe nanocrystals applying the tight-binding method. Huang Ching et al.³¹ and Karazhanov et al.³² used the linear combination of atomic orbitals (LCAO) method alongside density functional theory to compute the electronic band structures and DOS for a range of ZnX compounds. Rachidi et al.³³ explored the structural and electronic properties of ZnSe-based nanostructures applying the ab initio full potential linearized augmented plane waves (FP-LAPW) method. Christensen et al.³⁴ observed the influence of pressure on the electronic bandgap through the self-consistent linear muffin-tin orbital method. Gharamani et al.³⁵ examined the electronic band structures of ZnSe and ZnTe via the linear combination of Gaussian orbitals (LCGO) technique. Theoretical studies have first ever revealed that applying high external pressure substantially influences the structure, triggering phase transitions and distortions at elevated pressures. Lee et al.³⁶ explored the impact of d-state electrons on the band structures of ZnS, ZnTe, and ZnSe employing ab initio pseudopotential total energy calculations. Additionally, Merad et al.³⁷ utilized the tight-binding method to explore the electronic structures of ternary ZnSeTe and its binary components, ZnTe and ZnSe. Although there has been substantial research into the structural, electronic, mechanical, and optoelectronic properties of ZnSe and analogues II–VI semiconductors^1,2 including ZnO³¹ and CdS^1,2,31etc., however there is currently no available data on how stimuli can tailor and engineer the structural, microelectronic, and optoelectronic properties of these materials. The capability to tune, engineer and modulate the optoelectronic properties via electric fields and biaxial mechanical strain for the zinc blende ZnSe will makes valuable reference point for understanding and optimizing the potential of other wide-bandgap materials. Therefore, we have conducted systematically investigation on the effect of stimuli on structural, electronic, and optoelectronic properties of zinc blende ZnSe. We used the first-principles calculations within the framework of density functional theory (DFT) for ZnSe, conclusively demonstrating how stimulus-controlled modifications can enhance its optoelectronic properties.

Methodology

We performed theoretical calculations for the zinc blende (cubic) phase of ZnSe using the generalized gradient approximation (GGA) with the core plane-wave basis set and projected augmented waves (PAW) pseudopotential (pp) inside the Quantum Espresso simulation package,^38,39 adhering to density functional theory (DFT).^40–42 The exchange correlation potential was computed using the Perdew–Burke–Ernzerhof (PBE) non-linear core correction functional. The structure was optimized and assessed for the stimulus-responsive dynamics and engineering of the electronic bandgap, total density of states (TDOS), partial density of states (PDOS) and local density of states (LDOS). The plane wave expansion was set with an energy cutoff of 30 Ry and an 8 × 8 × 8 k-point grid in the first Brillouin zone. Convergence criteria for both self-consistent and non-self-consistent (NSC) calculations were set at 10⁻⁸ eV. Turbo time-dependent density functional theory (TTDFT) method^38,39 was employed to disclose the electron energy loss Spectrum (EELS) and the dielectric function. The real part of the dielectric function was obtained using the Kramers–Kronig relation, whereas the imaginary part was determined by summing the transitions from occupied valence states to unoccupied conduction states.^38–41 The DFT method has proven to be one of the most accurate methods for the computation of the electronic structure of solids.^42–46

Results and discussion

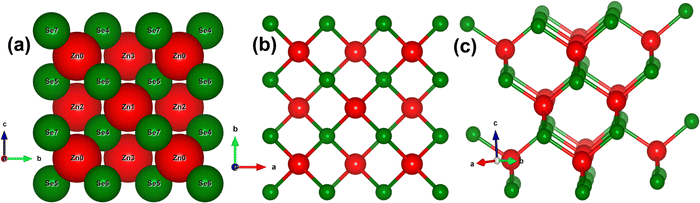
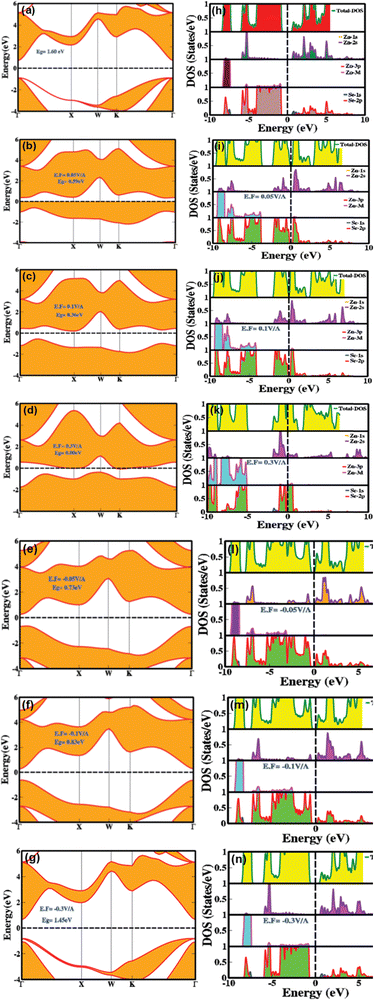
To ensure a highly accurate and systematic computational analysis, we conducted a series of unit cell optimization calculations, determining the equilibrium unit cell parameters to be a = b = c = 5.667 Å. These findings closely match previously reported experimental data.^7,9,11,18Fig. 1(a–c) depicts the stacking sequence and both the 2D and 3D structures of the zinc blende phase of ZnSe (ZB or B₃) at standard temperature and pressure (STP). ZnSe exhibits an interpenetrating face-centered cubic (FCC) lattice with tetrahedral coordination for both Zn and Se atoms, creating a continuous repeating pattern throughout the crystal with an ABCABC stacking sequence. This cubic structure of ZnSe is analogous to that of other binary semiconductors, such as GaAs.⁴⁷

Fig. 1 Crystal structure of zinc blende ZnS (a) stacking order (a) 2D view (b) 3D View.

The electronic bandgap provides crucial insight into the material's characteristics, whether it is a semiconductor, insulator, or conductor, by indicating the energy difference between the top of the valence band and the bottom of the conduction band. Fig. 2(a and h) illustrates the effect of an electric field (both with and without mediation/engineering) on the electronic bandgap, showing the total density of states (TDOS) and the partial density of states (PDOS) for zinc blende-phase ZnSe.

Fig. 2 Electric field engineered and modulated (a)–(g) electronic bandgap and (h)–(n) Partial and total density of states of zinc blende ZnSe using 0.00 V Å⁻¹, 0.01 V Å⁻¹, 0.05 V Å⁻¹, 0.1 V Å⁻¹, 0.3 V Å⁻¹, −0.01 V Å⁻¹, −0.05 V Å⁻¹, −0.1 V Å⁻¹ and −0.3 V Å⁻¹.

In the absence of an applied electric field, the zinc blende phase of ZnSe exhibits a direct bandgap of 1.6 eV at 0.0 V Å⁻¹, with both the valence band maximum and conduction band minimum located at the Γ point of the Brillouin zone. This bandgap profile is consistent with previously reported theoretical data.^8,11–13Fig. 2h illustrates the partial density of states (PDOS) and total density of states (TDOS) without an electric field, providing detailed information on the distribution of electronic states and their implications for electronic and optoelectronic properties. In the conduction band above the Fermi level, substantial contributions come from Zn(2s) and Se(2p) orbitals, with minor contributions from Se(1s) orbitals in the energy range of 0.5 eV to 5.5 eV. Conversely, the valence band predominantly features contributions from Zn (2s, 3d) and Se(2p) orbitals, with negligible contributions from Se(1s) within the energy ranges of −7.5 eV to −8.0 eV and −1.0 eV to −6.0 eV. The TDOS analysis reveals a broad peak centered around −7.5 eV in the valence band, primarily associated with Zn(3d) and Se(2p) orbitals. Additional peaks are observed around −4.0 eV to −7.0 eV and −0.5 eV to −3.5 eV, resulting from Zn (2s, 3d, 2p) and Se (2p) orbitals. In the conduction band, two broad peaks are present in the energy ranges of 0.1 eV to 3.5 eV and 3.6 eV to 5.5 eV, attributed to Zn (2s) and Se (2p) orbitals. The substantial overlap between Zn(2s) and Se(2p) orbitals indicates strong covalent and ionic interactions among the first nearest neighbor atoms or ions, with the Zn atoms in the zinc blende structure connected by the shortest lattice bonds. The significant overlap of p orbitals at the valence band maxima confirms sp³ hybridization. Upon applying an electric field, mechanisms such as the Stark effect, band bending, renormalization, intrinsic electric fields, electron–electron interactions, and crystal dipole interactions come into play, resulting in a narrowing, switching, and modulation of the electronic bandgap. Although the response of the orbital states in the PDOS and TDOS modulates, the overall trend remains consistent. Notably, the Stark effect and crystal dipole interactions play a crucial role in describing the electric field-induced responses of holes in the valence band and electrons in the conduction band, as well as the potential energy differences between electrons and holes. As the applied electric field increases systematically from 0.01 V Å⁻¹ to 0.1 V Å⁻¹, the electronic bandgap narrows from 0.6 eV to 0.36 eV. At a critical electric field strength of 0.21, the valence and conduction bands overlap at the Fermi level, resulting in a phase transition from semiconductor to conductor. A detailed examination of the electronic bandgap under varying electric fields is provided in Table 1. These electric field-induced modulation and engineering of the bandgap make these materials well-suited for applications in controlled photovoltaics, optical modulators, tunable lasers, switchable photodetectors, smart energy harvesters, and optoelectronic technologies.

Table 1 Detailed values of the electric field and strain mediated electronic bandgap and highest occupied molecular orbitals (HOMO) or bonding orbitals and lowest unoccupied molecular orbitals (LUMO) or anti-bonding orbital energy wave function properties of zinc blende ZnSe

E.F. (V Å^−1)	E g (eV)	Biaxial compressive strain (%)	E g (eV)	Biaxial compressive strain (%)	E HOMO	E LUMO	E LUMO–HUMO
0.01	0.66	0	1.60	0	7.741	8.3794	0.6378
0.03	0.64	2	1.86	2	8.579	9.5564	0.9769
0.05	0.59	4	2.16	4	9.475	10.755	1.2798
0.07	0.53	6	2.45	6	10.46	12.135	1.6708

---

0.08	0.47	Biaxial tensile strain (%)	E g (eV)	Biaxial tensile strain (%)	E HOMO	E LUMO	E LUMO–HUMO
0.09	0.41	0	1.60	0	7.741	8.3794	0.6378
0.1	0.36	2	1.34	2	7.017	7.365	0.348
0.2	00	4	1.13	4	6.342	6.401	0.0589
−0.01	0.67	6	0.94	6	5.723

---

−0.03	0.70	Uniaxial compressive strain (%)	E g (eV)	Uniaxial compressive strain (%)	E HOMO	E LUMO	E LUMO–HUMO
−0.05	0.73	0	1.60	0	7.741	8.379	0.6378
−0.07	0.76	2	1.60	2	7.741	8.379	0.6378
−0.08	0.79	4	1.60	4	7.741	8.379	0.6378
−0.09	0.80	6	1.60	6	6.236	7.843	1.6072

---

−0.1	0.83	Uniaxial tensile strain (%)	E g (eV)	Uniaxial tensile strain (%)	E HOMO	E LUMO	E LUMO–HUMO
−0.2	1.18	0	1.60	0	7.741	8.379	0.637
−0.3	1.45	2	1.60	2	7.741	8.379	0.6378
−0.4	0.64	4	1.60	4	7.741	8.379	0.6378
−0.5	00	6	1.60	6	7.752	8.423	0.6706

---

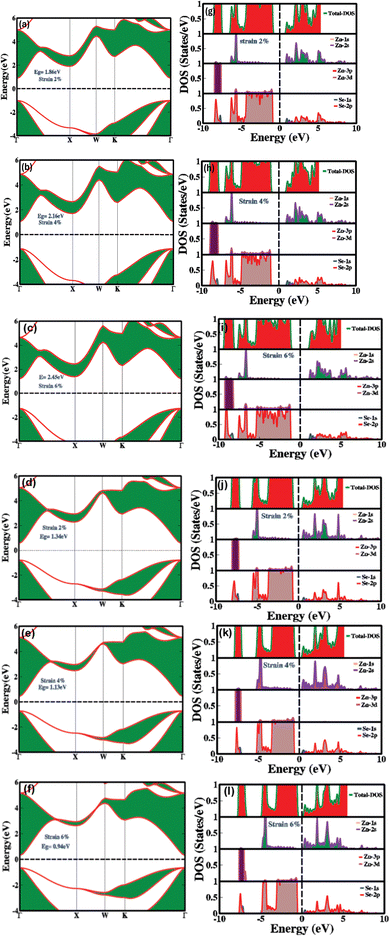
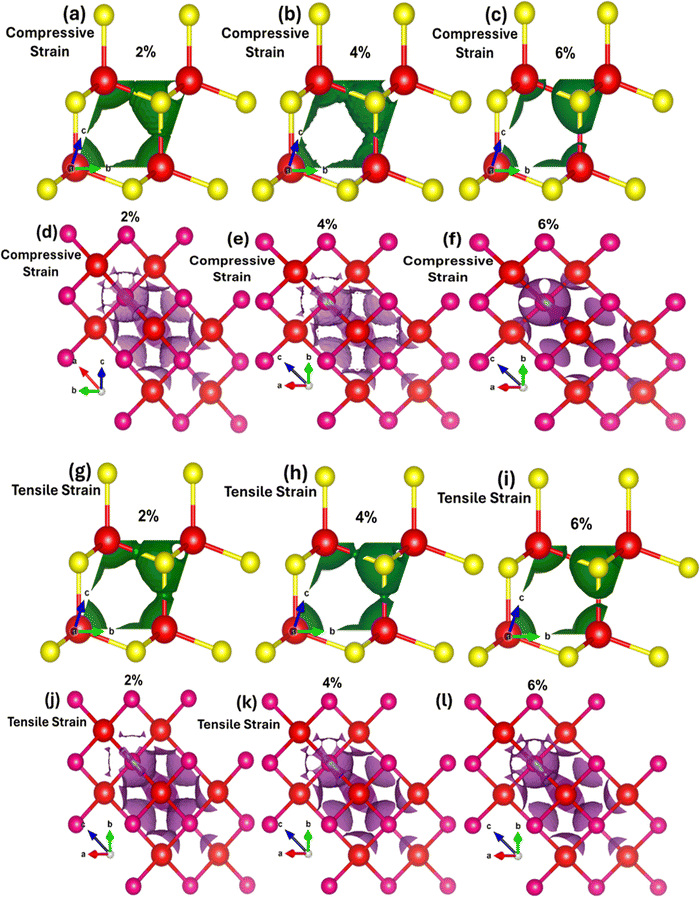
Fig. 3(a–f) demonstrates the impact of biaxial compressive and tensile strain on the electronic bandgap of zinc blende phase ZnSe. The data reveals substantial switching and modulation of the bandgap when biaxial strain is applied along the a and b axes. Conversely, uniaxial strain along the c-axis results in minimal or negligible changes (see Table 1 for detailed values). This insensitivity to uniaxial strain along the c-axis is due to the inherent symmetry of the cubic zinc blende crystal structure. This structure is isotropic within the [111] plane, ensuring uniform electronic properties across different axes. The lattice constants of ZnSe in the zinc blende structure are isotropic, leading to minimal anisotropy in the conduction and valence bands. Consequently, the uniform lattice parameters confirm that the conduction band minimum and valence band maximum remain nearly degenerate or exhibit similar characteristics in all directions. Thus, there is no significant strain-induced variation in the electronic bandgap along the c-axis in zinc blende ZnSe. Conversely, when biaxial strain is applied, we observed that the electronic bandgap increases with compressive strain (1.86 eV at 2%, 2.16 eV at 4%, and 2.45 eV at 6%) and decreases with tensile strain (1.34 eV at 2%, 1.13 eV at 4%, and 0.94 eV at 6%).

Fig. 3 Strain mediation and modulation of (a)–(c) electronic bandgap at 2%, 4% and 6% biaxial compressive strain (d)–(f) electronic bandgap at 2%, 4% and 6% biaxial tensile strain (g)–(i) partial (PDOS) and total density of states (TDOS) at 2%, 4% and 6% biaxial compressive strain (j)–(l) partial (PDOS) and total density of states (TDOS) at 2%, 4% and 6% biaxial tensile strain.

The variations in the electronic bandgap of zinc blende ZnSe under biaxial strain result from the interaction of the strain with the crystal lattice. Biaxial strain modifies the lattice parameters, bond lengths, bond angles, and band splitting within the crystal. This alteration in the lattice structure leads to distortions that affect the energies of the valence and conduction bands, thereby modifying the electronic bandgap. As shown in Fig. 3(a–c), compressive biaxial strain (at 2%, 4%, and 6%) significantly increases the electronic bandgap to 1.86 eV, 2.16 eV, and 2.45 eV, respectively. This increase is attributed to the effect of lattice compression on the electronic band structure. Compressive strain shortens bond lengths, reduces lattice parameters in the strained plane, enhances orbital overlap between neighboring atoms, and shifts the band edges (conduction band minimum (CBM) and valence band maximum (VBM)). These changes lead to an increase in the energy of the conduction band states, which results in a broader energy gap between the conduction and valence bands. In contrast, biaxial tensile strain (Fig. 3(d–f)) at 2%, 4%, and 6% leads to a decrease in the electronic bandgap, reducing it from 1.6 eV to 1.13 eV and then to 0.94 eV. The reduction in the bandgap under tensile strain is due to the expansion of the crystal lattice, which diminishes the overlap between atomic orbitals. This decreased overlap lowers the energy of the conduction band minimum more significantly than that of the valence band maximum, resulting in a smaller bandgap. Consequently, tensile strain effectively narrows the electronic bandgap, impacting the electronic, optoelectronic, and optical properties of zinc blende ZnSe.

The observed modulation and switching of the electronic bandgap under compressive and tensile biaxial strain highlights the potential for precise tuning of the bandgap in zinc blende ZnSe. This capability opens significant opportunities for designing advanced optoelectronic devices, such as lasers, photodetectors, and LEDs, where exact bandgap values are essential for achieving optimal performance. Mechanical strain exerts a substantial influence on both the partial density of states (PDOS) and the total density of states (TDOS) by modifying the electronic structure, affecting orbital contributions, and altering the positions and intensities of spectral peaks.

Fig. 3(g–l) explains how mechanical strain influences the PDOS and TDOS, presenting detailed insights into the variation and distribution of electronic states within the conduction and valence bands. This, in turn, affects the electronic and optoelectronic properties of zinc blende ZnSe. Under ambient conditions with no mechanical strain, Zn (2s) and Se (2p) orbitals are predominantly influential in the conduction band, while Zn (2s) and (3d) and Se (2p) orbitals dominate the valence band within the energy range of 0.5 eV to 5.5 eV. In contrast, biaxial compressive strain (2%, 4%, and 6%) alters orbital hybridization, leading to changes in the PDOS by redistributing orbital contributions. This results in increased localization and shifts the energy range to 1.0 eV to 6.0 eV for Zn (2s), (3d), and Se (2p) orbitals. Compressive strain decreases bond lengths, which enhances orbital overlap, leading to more pronounced and distinct peaks in the TDOS and PDOS within the bandgap energy ranges. Conversely, biaxial tensile strain produces the opposite effects.

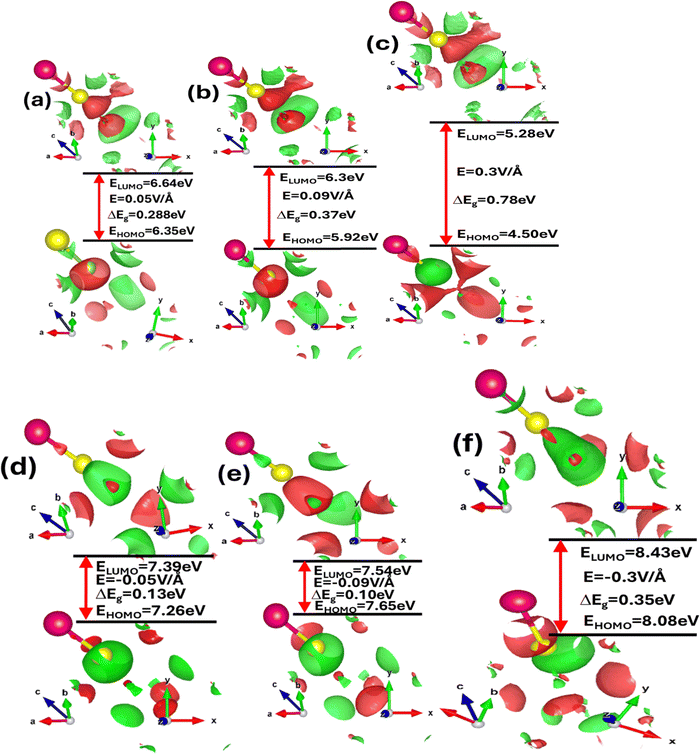
To comprehend the electronic and optoelectronic properties of zinc blende ZnSe, it is essential to analyze the effects of electric field and strain on the highest occupied molecular orbitals (HOMO) and lowest unoccupied molecular orbitals (LUMO). The HOMO orbitals are inherently lower in energy compared to the LUMO orbitals, which facilitates the bonding between Zn and Se atoms in ZnSe. The stable state of ZnSe is achieved through the interaction between Zn and Se electrons. In ZnSe, the HOMO orbitals are primarily composed of Zn(2s) and Se(2p) orbitals, which exhibit bonding characteristics, while the LUMO orbitals consist of Zn(3d) and Se(2p) orbitals, which exhibit antibonding characteristics. The energy difference between the HOMO and LUMO orbitals, known as the HOMO–LUMO gap, indicates the energy required for electrons to transition from the occupied HOMO state to the unoccupied LUMO state. This gap plays a crucial role in determining the material's chemical reactivity and electronic behavior. Fig. 4(a–f) illustrates the impact of the electric field, while Table 1 provide detailed values of the energy gap (ΔE = E_HOMO − E_LUMO) between the HOMO and LUMO orbitals under varying electric fields and strains.

Fig. 4 (a)–(f) Electric field mediated and engineered modulation of the highest occupied molecular orbitals (HOMO) or bonding orbitals and lowest unoccupied molecular orbitals (LUMO) or anti-bonding orbitals energy wave functions for zinc blende ZnSe calculated by means of the GGA approximation.

A larger HOMO–LUMO gap requires more energy for electron transitions, typically leading to reduced electrical conductivity. In contrast, a smaller HOMO–LUMO gap signifies increased chemical reactivity and enhanced electronic conductivity. The variations in this energy gap due to strain provide deeper insights into the chemical activity and electronic properties of zinc blende ZnSe. Thus, understanding how strain influences the HOMO–LUMO gap is crucial for elucidating the material's overall electronic behavior and reactivity. The detailed values of the energy gap between the HOMO and LUMO states are provided in Table 1. In the absence of external stimuli such as electric fields or mechanical strain, the HOMO–LUMO energy gap is 0.63 eV. However, this energy gap is tunable and varies with applied electric fields and mechanical strain, indicating the influence of both extrinsic and intrinsic factors on the chemical activity and electronic stability of ZnSe. When subjected to a positive electric field, the HOMO–LUMO energy gap increases, reflecting enhanced electronic stability and reduced chemical reactivity. Conversely, with a negative electric field, the energy gap slightly decreases, suggesting decreased electronic stability and increased chemical reactivity. Under compressive biaxial strain, the HOMO–LUMO energy gap increases from 0.97 eV to 1.67 eV for strain levels of 2%, 4%, and 6%. In contrast, tensile biaxial strain causes the HOMO–LUMO energy gap to decrease from 0.34 eV to 0.05 eV at the same strain levels. Additionally, both electric fields and mechanical strain affect the overall shape of the HOMO–LUMO energy states by altering interactions among various orbitals, such as Zn-1s, Zn-2s, Zn-3p, Zn-3d, Se-1s, and Se-2p.

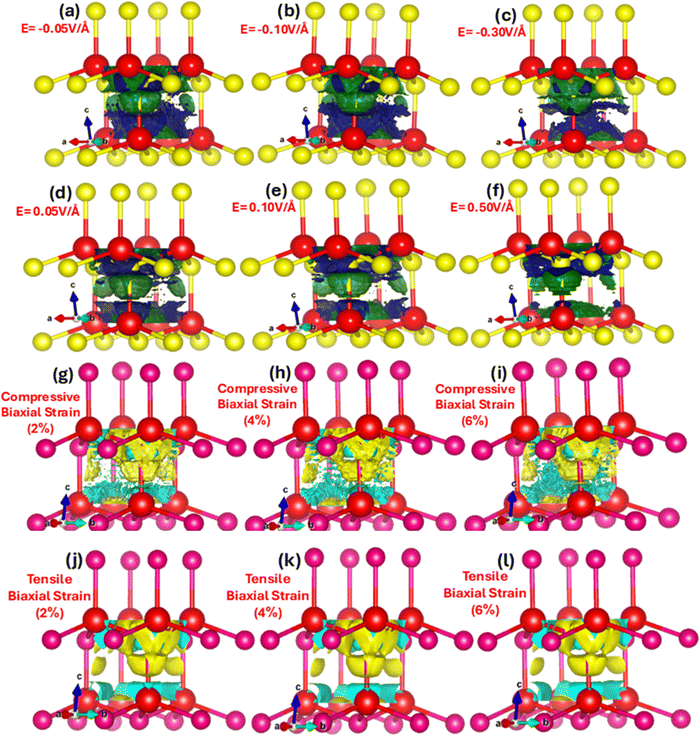
The charge transfer and hybridization between metallic Zn and chalcogen Se with electric field and strain is explored by charge density distribution provide insight into the spatial distribution of electrons throughout the unit cell. Fig. 5(a–l) represent electric field and strain mediated charge density distribution in ZnSe primitive unit cells. We witnessed that in the absence of applied electric field and strain the electron density is higher around the more electronegative Se atoms as compared to the Zn atoms. However, upon the electric field and mechanical strain (2%, 4% and 6%) the charge density significantly dynamically respond, modulates and tune. The electric field and strain on ZnSe induce polarization leading to a redistribution of charge density.

Fig. 5 Charge density distribution upon the application of stimulus (a)–(f) electric field (g)–(l) biaxial compressive and tensile strain in the primitive zinc blende ZnSe unit cell calculated using the GGA scheme.

In the presence of an electric field and strain (compressive or biaxial), positive Zn atoms and negative Se atoms shift relative to each other, producing a dipole moment, charge accumulation and sharing. The movement of the Zn cations and Se anions relative to applied electric field and strain show directional shared covalent bonding among the anion–anion (Se–Se) and anion–cation (Zn–Se) atoms and charge transfer approve ionic nature of ZnSe. Nevertheless, covalent bonding in zinc blende ZnSe is convincing in interactions with some ionic character develop due to the difference in electronegativity between zinc (cation) and selenium (anion). The charge density distribution modulates and triggers with electric field and strain validates the phase transition from the semiconductor to the metallic. The amount of charge (density) distribution and transfer of total and partial atoms with varying applied electric field (0.01 V Å⁻¹ to 0.1 V Å⁻¹) is listed in detail in Table 2. In the absence of applied electric field and strain it is obvious that the charge distribution is around the more electronegative Se anion and less around the Zn cations. However, the charge distribution and density trigger and shift with electric field, such as, at 0.01 V Å⁻¹ the amount of charge on Zn and Se is 18.7218 and 6.9879, which changes at 0.3 V Å⁻¹ and 0.5 V Å⁻¹ to 18.8933 and 6.3786, 18.8042 and 5.7790. Upon the application of the positive (+) applied electric field of 0.05 V Å⁻¹, 0.1 V Å⁻¹, 0.3 V Å⁻¹ and 0.5 V Å⁻¹ causes the charge transfer from Se (electronegative) to Zn (electropositive) and amounts of charges increase 0.1%, 0.321%, 0.916% and 0.44% on Zn, whereas 1%, 2.58%, 9.9562%, 17.3% decrease on Se. These results validate that with the application of electric field the charge density modulate and charges transfer from electronegative Se anions toward the Zn cations. Analogous is the case for the tensile biaxial strain, whereas converse is the case for the biaxial compressive strain. Such charge transfer causes change in the bonding characteristic due to modulation in the magnitude of charges on the Zn and Se. The detailed values of distribution and transfer of charges between Zn and Se using biaxial compressive and tensile strain is listed below in Table 3. It is apparent that biaxial compressive strain substantially fine-tunes and modulate the charges initiating the transfer from the electropositive Zn to the electronegative Se, such at 2%, 4% and 6% the amount of charge transfer between Zn and Se is 18.7015 and 7.0847, 18.6921 and 7.0913, 18.6831 and 7.0965.

Table 2 Electric field mediated detailed values of quantitative charge distribution and transfer of charges between orbital states (s, p and d) in the Zn and Se in zinc blende ZnSe system

No.	Electric field	Total charge	Zn				Se
		Zn	Se	s	p	d	s	p
1	0.01	18.7218	6.9879	2.7754	5.9986	9.9478	1.8928	5.0951
2	0.03	18.7304	6.9526	2.7874	5.9985	9.9445	1.8972	5.0555
3	0.05	18.7416	6.9146	2.8019	5.9985	9.9411	1.9013	5.0132
4	0.07	18.7557	6.8743	2.8195	5.9985	9.9377	1.9054	4.9689
5	0.09	18.7726	6.8328	2.8398	5.9985	9.9343	1.9093	4.9236
6	0.10	18.7819	6.8118	2.8508	5.9985	9.9327	1.9111	4.9007
7	0.30	18.8933	6.3786	2.9982	5.9981	9.8970	1.9266	4.4520
8	0.50	18.8042	5.7790	2.9776	5.9975	9.8291	1.9050	3.8740
9	−0.01	18.7149	7.0196	2.7654	5.9986	9.9509	1.8883	5.1313
10	−0.03	18.7090	7.0473	2.7565	5.9986	9.9539	1.8836	5.1637
11	−0.05	18.7038	7.0708	2.7486	5.9986	9.9566	1.8786	5.1921
12	−0.07	18.6992	7.0897	2.7415	5.9986	9.9590	1.8735	5.2162
13	−0.09	18.6950	7.1042	2.7352	5.9986	9.9611	1.8683	5.2359
14	−0.10	18.6931	7.1097	2.7324	5.9986	9.9621	1.8656	5.2441
15	−0.30	18.7162	7.0631	2.7521	5.9986	9.9656	1.8283	5.2348
16	−0.50	18.7932	6.6281	2.8407	5.9984	9.9542	1.8230	4.8051

---

Table 3 Biaxial and uniaxial compressive and tensile strain mediated detailed values of quantitative charge distribution and transfer of charges between orbital states (s, p and d) in the Zn and Se in zinc blende ZnSe system

Strain	Zn				Se
	Total	s	p	d	Total	s	p
0%	18.7103	2.7453	5.9986	9.9663	7.0767	1.8304	5.2463
Biaxial compressive
2%	18.7015	2.7357	5.9986	9.9672	7.0847	1.8145	5.2702
4%	18.6921	2.7276	5.9985	9.9660	7.0913	1.7983	5.2930
6%	18.6831	2.7207	5.9985	9.9639	7.0965	1.7818	5.3147
Uniaxial compressive
2%	18.7106	2.7456	5.9986	9.9663	7.0771	1.8306	5.2465
4%	18.7106	2.7456	5.9986	9.9663	7.0771	1.8306	5.2465
6%	18.7106	2.7456	5.9986	9.9663	7.0771	1.8306	5.2465
Biaxial tensile
2%	18.7388	2.7601	5.9987	9.9801	7.0737	1.8470	5.2267
4%	18.7551	2.7753	5.9987	9.9810	7.0642	1.8623	5.2019
6%	18.7751	2.7947	5.9987	9.9817	7.0532	1.8779	5.1753
Uniaxial tensile
2%	18.7106	2.7456	5.9986	9.9663	7.0771	1.8306	5.2465
4%	18.7106	2.7456	5.9986	9.9663	7.0771	1.8306	5.2465
6%	18.7106	2.7456	5.9986	9.9663	7.0771	1.8306	5.2465

---

However, converse is the case for biaxial tensile where charges transfer from Se to Zn such as, at 2%, 4% and 6% the amount of charge transfer between Zn and Se is 18.7388 and 7.0737, 18.7551 and 7.0642, 18.7751 and 7.0532. In case of uniaxial compressive and tensile strain insignificant charge transfer is observed, which is due to intrinsic structure of zinc blende ZnSe. We have calculated the influence of the strain and electric field-induced quantitative modulation and dynamics of charge transfer between s and p orbitals causing sp³ hybridization. The external electric field perturbs the energy levels and the spatial distribution of the electron wavefunctions causes a shift in the relative energies of the s and p orbitals, influencing charge transfer between these orbitals. The electric field starts a separation of charge or even induces a shift in the population of charge carriers between different bands (from the valence band to the conduction band or between different sub-bands). It is apparent that upon the application of positive electric field at 0.01 V Å⁻¹ the number of charges at s and p orbitals are 2.7754 and 5.0951 transfer to 2.8019 and 5.0132, 2.8508 and 4.9007, 2.9982 and 4.4520, 2.9776 and 3.8740 at 0.05 V Å⁻¹, 0.1 V Å⁻¹, 0.3 V Å⁻¹ and 0.5 V Å⁻¹. These results confirm that charges modulate and tune with applied electric field transfer from Zn(p) to Se(s) orbitals. Nevertheless, converse is case for negative applied electric field where the charges transfer from Se(s) to Zn(p) orbitals. Similarly, mechanical biaxial compressive and tensile strain changes (increase or decrease) the Zn–Se bond lengths and angles, substantially shift the charges between the s and p orbitals alter the nature of the bonding and antibonding states as revealed in detail in Table 3. However, in case uniaxial compressive and tensile strain no significant switching between s and p orbitals.

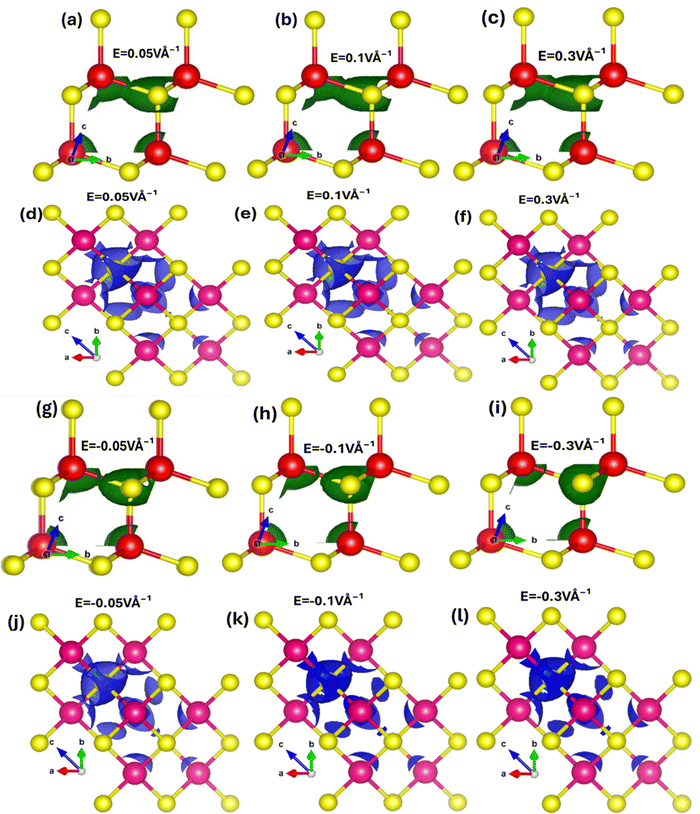
To explore how electric fields and mechanical strains (both compressive and tensile) affect local band patterns, band structure, and carrier redistribution in Zn and Se atoms, we performed local density of states (LDOS) calculations for zinc blende ZnSe. These calculations provide a detailed view of charge localization and transfer. Fig. 6(a–l) depicts the 2D and 3D modulations of the LDOS in ZnSe induced by an electric field. We observed that the electric field has a complex impact, altering the electronic band structure and causing a redistribution of carriers between Zn and Se atoms. LDOS is also connected to optical properties, influencing optical transitions and absorption spectra. Understanding how LDOS responds to external stimuli is crucial for the development and optimization of new electronic and optoelectronic devices using ZnSe. When an electric field is applied, charges, initially concentrated around the electronegative Se atoms, become polarized. These charges redistribute, with electrons and holes moving from Se to Zn atoms. This directional transfer of charge results in a shift in the absorption edge.

Fig. 6 Electric field mediated 2D and 3D view of local density states (LDOS) using (a)–(f) positive electric field 0.05 V Å⁻¹, 0.1 V Å⁻¹, 0.3 V Å⁻¹ and (g)–(l) negative electric field −0.05 V Å⁻¹, −0.1 V Å⁻¹, −0.3 V Å⁻¹.

However, converse is the case for the negative applied electric field where the charges shift from Zn atoms to Se atoms. These results confirm that electric field substantially manipulates the charge localization/transfer and band bending which provides a window of opportunity to design stimulus controlled optoelectronic technology. Similarly, mechanical strain (biaxial compressive and tensile) affects the local density of states (LDOS) in ZnSe. Tensile biaxial strain elongates the lattice structure, while compressive strain contracts it, both of which impact polarization, charge transfer, band structures, and the energy gap. Fig. 7(a–l) shows the 2D and 3D modulations of the local density of states (LDOS) in zinc blende ZnSe induced by biaxial compressive and tensile strains. Our observations reveal that both compressive and tensile strains significantly affect the LDOS of ZnSe, as they alter the electronic band structure. Compressive strain reduces the lattice constants, leading to changes in the electronic band structure, including shifts and modifications in band positions. This results in variations in the conduction band minimum and valence band maximum, influencing the available energy levels for electrons, band curvature, and causing localized modulations near the band edges.

Fig. 7 Strain mediated 2D and 3D view of local density states (LDOS) using (a)–(f) 2%, 4%, and 6% biaxial compressive strain and (g)–(l) 2%, 4%, and 6% biaxial tensile strain.

These effects are consistent with our findings on bandgap modulation under compressive strain. Fig. 7(a–f) illustrates that compressive strain alters the shape of the local charge distribution, indicating charge transfer and localization between Zn and Se atoms. Without compressive strain, the local charge density is higher around Se atoms, but this density shifts towards Zn atoms under compressive strain. Conversely, tensile strain affects the localized charge distribution and density in the opposite manner, as depicted in Fig. 7(g–l) for the LDOS of ZnSe under tensile strain.

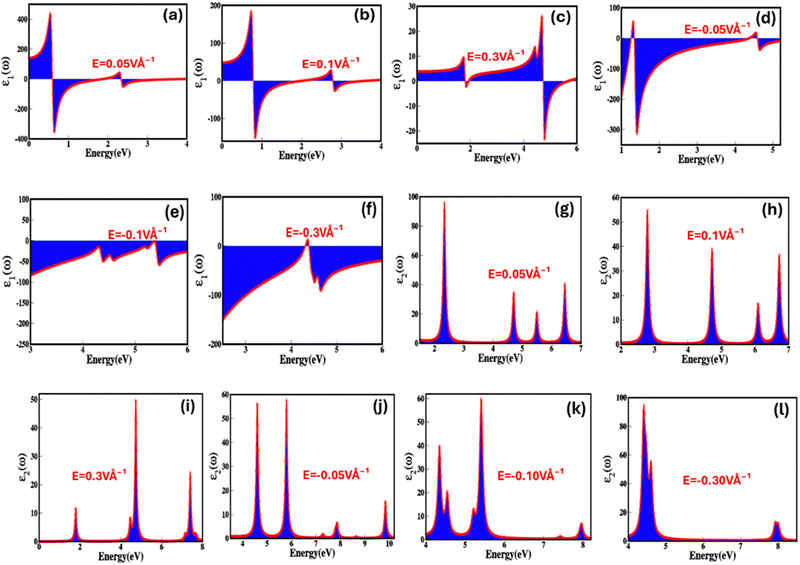
To reveal the potential of zinc blende ZnSe as stimulus responsive (electric field and strain) optoelectronic and photonic materials, we have step-by-step explored the optical parameters, which include real (ε₁(ω)) and imaginary (ε₂(ω)) part of dielectric, optical conductivity (σ(ω)), optical reflectivity (R(ω)), refractive index (n(ω)), extinction co-efficient (k(ω)) and energy loss function (ELS). The dielectric constant (relative permittivity) is a crucial parameter that reflects a material's capacity to store electric charge or energy offers insight into how the material interacts with an electric field and mechanical strain, enables us to derive various important optical properties. The dielectric function can be tailored, engineered, and controlled through intrinsic and extrinsic stimulus such as electric fields and strain. Fig. 8(a–l) represents electric field engineered real (ε₁(ω)) and imaginary (ε₂(ω)) part of dielectric function from 0.05 V Å⁻¹ to 0.3 V Å⁻¹ and −0.05 V Å⁻¹ to −0.3 V Å⁻¹ as a function of energy (eV) approve that zinc blende phase ZnSe is electric field sensitive/responsive dielectric material. The detailed values of real (ε₁(ω)) and imaginary (ε₂(ω)) part of dielectric function under the broad ranging applied electric field are listed in Table 4. Fig. 8(a–c) illustrate that the real part of dielectric function decreases with increase in the positive applied electric field as a function of energy (eV), such as the real part of dielectric constant changes into 17.74, 8.20, 7.57 at 0.05 V Å⁻¹, 0.1 V Å⁻¹, 0.3 V Å⁻¹. Such decrease in real (ε₁(ω)) dielectric function via applied electric field may be attributed due to the increase in absorption near the bandgap energy and interband transition. The decrease in the value of real (ε₁(ω)) dielectric function with positive electric field from 17.74 to 5.67 at 0.05 V Å⁻¹ to 0.3 V Å⁻¹ and increase from −68.97 to −53.89 with negative electric field between −0.05 V Å⁻¹ to −0.3 V Å⁻¹ agree with the bandgap shift with externally applied electric field.

Fig. 8 Electric-field mediated engineering and modulation of the (a)–(f) real (ε₁(ω)) part of dielectric (g)–(l) imaginary (ε₂(ω)) part of dielectric function of zinc blende ZnSe compounds calculated by GGA process.

Table 4 Comprehensive values of electric field and strain (biaxial compressive and biaxial) mediated real (ε₁(ω)) part of dielectric function, imaginary (ε₂(ω)) part of dielectric function, dielectric constant (ε(ω)), refractive index (n(ω)), extinction coefficient (k(ω)), optical conductivity (α(ω)) and reflectivity (R(ω)) of zinc blende phase ZnSe compound

E.F. (V Å)	ε 1(ω)	ε 2(ω)	ε(ω)	n(ω)	k(ω)	α(ω)	R(ω)
0.00	−52.59	45.16	−7.43	4.36	2.08	26.13	0.47
0.01	−7.70	26.29	18.59	5.11	5.16	64.84	0.68
0.03	25.90	24.74	50.64	5.56	4.16	52.27	0.63
0.05	17.74	48.06	65.80	4.21	2.08	26.13	0.46
0.07	12.08	42.82	54.90	6.56	3.46	43.47	0.62
0.09	8.64	38.52	47.16	6.84	4.07	51.14	0.64
0.1	8.20	36.66	44.86	6.81	3.85	48.38	0.64
0.3	7.57	18.04	25.61	12.34	0.79	9.92	0.72
−0.01	−13.62	27.94	14.32	4.82	4.77	59.94	0.65
−0.03	−25.17	29.92	4.75	4.83	4.79	60.19	0.66
−0.05	−68.97	30.57	−38.40	1.83	9.09	114.22	0.91
−0.07	−225.13	31.96	−193.17	2.23	8.51	106.93	0.89
−0.09	−194.37	30.15	−164.22	1.81	7.51	94.37	0.88
−0.1	−37.53	33.30	−4.23	2.45	7.38	92.73	0.85
−0.3	−53.89	44.00	−9.89	1.97	4.40	55.29	0.72

---

In Fig. 8(g–i) it is apparent that upon the application of positive electric field till the critical field the values of imaginary dielectric function are non-linear, modulate and increase in range from 26.29 to 42.28. However, these values continuously decreases and at critical applied electric field (E_c = 0.3 V Å⁻¹) there is sharp decrease due to the overlap between conduction and valence band establish the behavior transition from semiconductor to metallic. The rise in dielectric loss with increasing positive electric field can be ascribed to several physical factors that contribute to energy dissipation. These factors include increase in polarization loss, nonlinear higher polarization rate, increased conductive losses, dielectric breakdown, hysteresis effects, and alterations in relaxation processes. Furthermore, converse response is observed for the dielectric loss on negative applied electric field. The imaginary part of dielectric function represents four major absorption peaks present in the energy ranges 2–3 eV, 4.5–5.0 eV, 5.2–5.8 eV and 6.2–6.8 eV for the zinc blende ZnSe at 0.05 V Å⁻¹.

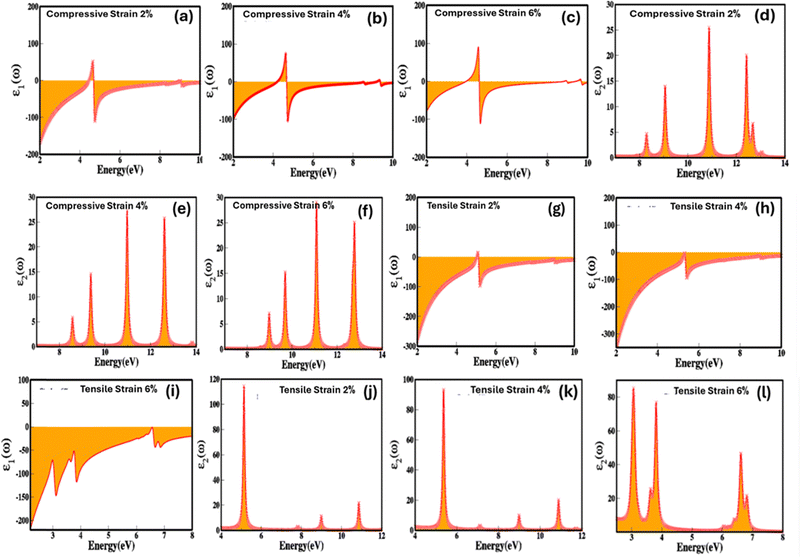
We have considered these four major absorption peaks and calculated average value of the imaginary part of dielectric function witnessed that the response is non-linear but overall values decreases as a function of applied electric field. The absorption peak dynamically responds to the electric field cause peaks shift from lower (peak 1, 2 and 3 as function energy 2.4 eV, 4.7 eV and 5.5 eV on the application of 0.05 V Å⁻¹) energy to higher (peak 1, 2 and 3 as function energy 2.8 eV, 4.9 eV, 6.2 eV and 6.9 eV on the application of 0.1 V Å⁻¹) energy upon the application of applied electric field. The shift in absorption peak validates the decrease in the electronic bandgap. It is apparent from Fig. 8(g–l) that the sharpness of the absorption peaks increases with applied electric field, which is initiated due to enhanced polarization, non-linear optical effect and quantum interference effect etc. We observed increase in width of few absorptions peak, which is initiated by the mixed optical transition at low electric field (0.01 V Å⁻¹, 0.03 V Å⁻¹, 0.03 V Å⁻¹etc.) have main influence from Zn-d and Se-p orbital shift with high electric field (0.1 V Å⁻¹, 0.3 V Å⁻¹etc.) to s–p–d orbitals. Similarly, converse is the case for the negative applied electric field because of the reverse in the polarization with applied field. These results confirm the electric field mediated dielectric response of ZnSe validate the potential in the controlled optoelectronics. Fig. 9(a–l) represents biaxial compressive and tensile strain mediated and engineered real (ε₁(ω)) and imaginary (ε₂(ω)) part of dielectric constant as a function of energy (eV).

Fig. 9 (a–l) Biaxial compressive and tensile strain mediated engineering and modulation of the real (ε₁(ω)) and imaginary (ε₂(ω)) part of dielectric function of zinc blende ZnSe compounds calculated by GGA process.

It is obvious from Fig. 9(a–c) that biaxial compressive strain is linked with the real part of the dielectric function and at 0%, 2%, 4% and 6% strain the real part of dielectric function increases and the values are −53.59, −19.45, −9.69 and 6.61. The biaxial compressive strain induces and alter the symmetry and lattice parameters which result is the arrangement of dipoles (polarization) in effective way causes the increase in the real part of the dielectric function. As evident from Fig. 9(a–c), that the real part of the dielectric function (ε_r(ω)) display a sharp increase within the energy range of 4 eV, reaching to its maximum at 4.5 eV. Beyond this point, it steadily decreases, exhibiting similar variations below zero and eventually reaching its minimum values. Furthermore, the intensity of peaks above and below the zero rises with the compressive strain 2%, 4% and 6% confirm increase in the real part of the dielectric function (ε_r(ω)). We also reveal that the increase in the biaxial compressive strain causes the non-linear decrease in modulation in the imaginary part of dielectric function (Fig. 9(d–f)). Such as in the absence of applied strain the value of imaginary part of dielectric function is 45.16 which abruptly decrease to 15.96 with increase in the compressive strain. The compressive strain causes the stabilization of polarization via reducing the dipole movement, impact on the carrier charge density, reduced domain wall motion, consequence in decrease in the energy loss lead in decline in the imaginary part of dielectric function. Upon the further increase 4% and 6% biaxial compressive strain there is slight but insignificant increase in values 18.38 and 19.14. This may be caused by slight destabilisation in polarization, charge density and domain wall motion upon further increase in the strain. However, converse is the case for the biaxial tensile strain (Fig. 9(g–l)). The values of 0%, 2%, 4% and 6% biaxial compressive and tensile strain are extracted by calculating the average value for four major absorption peaks. The four major absorption peaks at 2% of biaxial compressive and tensile strain are present in the energy ranges 8–8.5 eV, 8.7–9.5 eV, 10.5–11.2 eV, 12–13 eV and 4.5–5.5 eV, 8.5–9.5 eV, 10.3–11.3 eV for the zinc blende ZnSe. It calculated average values of 0%, 2%, 4% and 6% biaxial compressive and tensile strain for zinc blende ZnSe system are 45.16, 15.96, 18.38, 19.14 and 45.16, 37.57, 31.60, 47. 85.

These results conclude the ability to control, modulate and engineer the dielectric properties of zinc blende ZnSe using stimulus such as electric fields and strain empowers the development of novel advanced micro/nano and optoelectronic technologies with improved functionality, accuracy, and flexibility.

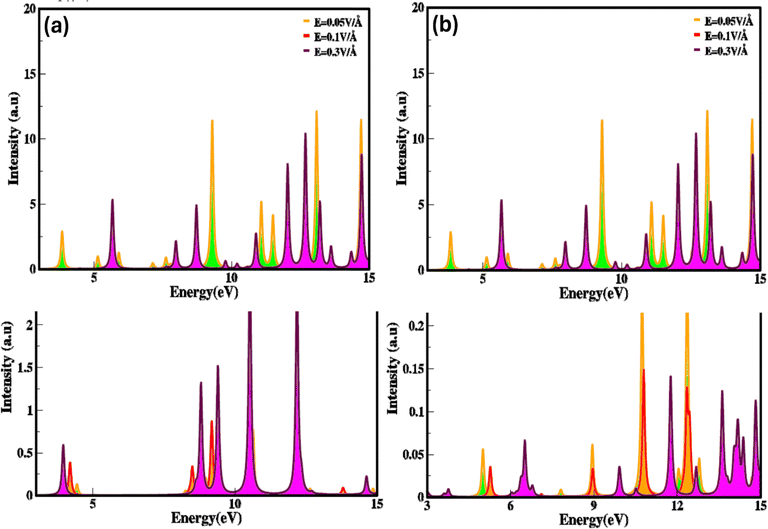
The electron energy loss (ELS) function gives information concerning how electrons lose energy as they interact with a material, are the reflection of the dielectric and collective excitations. It is a fundamental tool for characterizing materials at the local atomic and nanoscale, with applications covering from fundamental basic research to practical device engineering and designing. Electric field and strain modulated electron energy loss (ELS) function are represented in Fig. 10(a–d) These are confined to specific energy regions wherever the electrons are not hampered to their lattice site and oscillates with the exposure of light.

Fig. 10 Electric field and strain mediated electron energy loss function for zinc blende ZnSe compounds (a) and (b) positive and negative electric field (c) and (d) compressive and tensile strain calculated by GGA process.

It is evident that electron energy loss (ELS) function is related to the imaginary part of dielectric function. Such as the minimum value of electron energy loss correspond to the higher value of imaginary (ε_i(ω)) dielectric function and converse is for high value, modulate with switching and engineering of the electronic bandgap which is tailored and tune with stimulus (electric field and strain). The modulation in electron energy loss (ELS) function with strain and electric field arise due to shift in the excitation (plasmons, phonons) mechanisms and material response because they stimulate numerous collective modes and electronic transitions. At different levels of energy loss, various excitation modes are activated. Higher electron energy losses consequence in excitations that are less efficient in absorbing energy or show different spectral profiles, heading to a reduction in the imaginary (ε_i(ω)) part of the dielectric constant.

The refractive index (n(ω)) is fundamental physical property of the optoelectronic materials, is the measure of interactions and bending of light pass-through materials compared to its speed in the vacuum. It is a crucial physical parameter in designing and constructing optoelectronic systems. The values of refractive index ((n(ω)) are evaluated from the real ε_r(ω)) and imaginary (ε_i(ω)) part of dielectric function using formula.^40,48

The electric field and compressive and tensile strain mediated values of the refractive index, n(ω), and attenuation or extinction coefficient, k(ω), as a function of photon energy (eV) are presented in detail in Table 4. It is obvious that refractive index response to electric field is non-linear switch/modulate with applied electric field. The non-linear response is substantial at high electric field is attributed due to Kerr effect which involve a quadratic relationship between electric field and refractive index. In cases of 0%, 2%, 4% and 6% compressive biaxial strain the refractive index decreases from 7.79 to 4.72, 3.9, 3.66 (Table 5) with increase in strain. The decrease in refractive index is attributed due to collective physical factors involve increase in electronic bandgap, lattice distortion, photoelastic effect and electronic polarizability. The refractive index (n(ω)) decreases (7.79, 4.72, 3.90 and 3.66) linearly with increase in 0%, 2%, 4% and 6% biaxial compressive strain. The values of electric field engineered optical reflectivity are extracted using the fundamental relationship;^48,49

Table 5 Comprehensive values of biaxial compressive and tensile strain mediated refractive index (n(ω)), extinction coefficient (k(ω)), optical conductivity (α(ω)) and reflectivity (R(ω)) of zincblende phase ZnSe compound

Compressive strain (%)	n(ω)	k(ω)	α(ω)	R(ω)
0	7.79	2.91	36.56	0.63
2	4.72	1.68	21.11	0.46
4	3.90	2.35	29.53	0.47
6	3.66	2.61	32.79	0.48

---

Tensile strain (%)	n(ω)	k(ω)	α(ω)	R(ω)
0	7.79	2.91	36.56	0.63
2	6.24	3.00	37.69	0.59
4	6.28	2.51	31.54	0.57
6	9.81	2.63	33.04	0.68

---

We witnessed that optical reflectivity R(ω) respond non-linearly with positive applied electric field, while the values decrease with negative applied electric field. Optical reflectivity also responds to the biaxial compressive and tensile strain, such as it increases 0.63, 0.46, 0.47 and 0.48 with 0%, 2%, 4% and 6% strain, whereas for biaxial tensile strain where the values are non-linear 0.63, 0.59, 0.57, 068. The non-linear changes and increase in optical reflectivity in certain range of electric field point toward the selective optical reflection of materials lead to potential applications in filters and optical sensors.

Conclusions

In summary, we have effectively investigated the controlled engineering, dynamic modulation, and switchable tuning of the electronic bandgap of zinc blende ZnSe using stimuli such as electric fields and mechanical strain. This approach enables precise tailoring of ZnSe structural, electronic, and optoelectronic properties. Our findings reveal that electric fields and mechanical strain dynamically adjust the electronic bandgap. Specifically, an electric field ranging from 0.01 V Å⁻¹ to 0.1 V Å⁻¹ and −0.01 V Å⁻¹ to −0.1 V Å⁻¹ modulates the bandgap between 0.66 eV and 0.36 eV (∼44% decrease) and 0.67 eV to 0.83 eV (∼23% increase), respectively. Biaxial compressive and tensile strains ranging from 0% to 6% alter the bandgap from 1.60 eV to 2.45 eV (∼53% increase) and 1.60 eV to 0.94 eV (∼41% decrease), respectively. This dynamic modulation enhances ZnSe versatility for applications including infrared detectors and high-speed electronics (<1 eV), solar cells, LEDs, and laser diodes (1 eV to 2 eV), as well as blue-green LEDs, high-power electronics, and UV photodetectors (2 eV to 3 eV). Moreover, the modulation can induce a transition from semiconductor to metallic behavior. Our analysis of the total density of states, partial density of states, local density of states (LDOS), electron energy loss (ELS) function, charge density, and quantitative charge transfer confirms that stimulus-induced orbital modulations primarily involve Zn(2s) and Se(2p) orbitals in the conduction band, and Zn(2s) and(3d) and Se(2p) orbitals in the valence band, underscoring the impact of stimuli on optoelectronic properties. The stability and chemical reactivity of ZnSe are fine-tuned by systematically monitoring the energy gap shifts between HOMO and LUMO states under strain and applied electric fields. Furthermore, the electric field and strain-mediated dynamic modulation of optoelectronic parameters—such as the real and imaginary parts of the dielectric function, refractive index, optical reflectivity, extinction coefficient, and optical conductivity—demonstrates controlled optoelectronics with stimulus. Our comprehensive investigations conclude that stimulus controlled switchable dynamical modulation of the electronic and optoelectronic responses of zinc blende ZnSe, offering extensive prospects for utilization in the diverse multifunctional miniaturized novel optoelectronic technologies.

Data availability

The raw and processed data necessary to reproduce these findings cannot be shared at this moment, as it is part of an ongoing study. However, the data may be made available upon request.

Conflicts of interest

We hereby affirm that the work presented in this manuscript is novel and innovative, and we declare that there are no conflicts of interest.

Acknowledgements

We extend our sincere gratitude to our colleagues and researchers from the Material Modelling Lab, Department of Physics, Hazara University, Pakistan, for their valuable suggestions and insightful comments.

References

1. S. Adachi, Properties of semiconductor alloys: group-IV, III-V and II-VI semiconductors, John Wiley & Sons, 2009.
2. D. C. Reynolds, C. W. Litton and T. C. Collins, Some Optical Properties of Group II–VI Semiconductors (II). physica status solidi (b), Phys. Status Solidi B, 1965, 12(1), 3–55.
3. A. H. Reshak, Active photocatalytic water splitting solar-to-hydrogen energy conversion: Chalcogenide photocatalyst Ba2ZnSe3 under visible irradiation, Appl. Catal., B, 2018, 221, 17–26.
4. J. Fabian, A. Matos-Abiague, C. Ertler, P. Stano and I. Zutic, Semiconductor spintronics, arXiv, 2007, preprint, arXiv:0711.1461 DOI:10.48550/arXiv.0711.1461.
5. K. Sato and H. Katayama-Yoshida, First principles materials design for semiconductor spintronics, Semicond. Sci. Technol., 2002, 17(4), 367.
6. A. Chakrabarti, Role of NiAs phase in pressure-induced structural phase transitions in IIA-VI chalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(3), 1806.
7. M. Aven, D. T. Marple and B. Segall, Some electrical and optical properties of ZnSe, J. Appl. Phys., 1961, 32(10), 2261–2265.
8. B. I. Adetunji, P. O. Adebambo and G. A. Adebayo, First principles studies of band structure and electronic properties of ZnSe, J. Alloys Compd., 2012, 513, 294–299.
9. Q. Zhang, H. Li, Y. Ma and T. Zhai, ZnSe nanostructures: synthesis, properties and applications, Prog. Mater. Sci., 2016, 83, 472–535.
10. M. H. Zoubir, O. Cheref, M. Merabet, S. E. Benalia, L. Djoudi, D. Rached and M. Boucharef, First-principles study of structural, electronic and magnetic properties of diluted magnetic semiconductor and superlattices based on Cr-doped ZnS and ZnSe compounds in wurtzite-type crystal, Rev. Mex. Fis., 2024, 70, 020501.
11. R. Markowski, M. Piacentini, D. Debowska, M. Zimnal-Starnawska, F. Lama, N. Zema and A. Kisiel, Electronic structure of zinc blende ZnSe: theory and experiment, J. Phys.: Condens. Matter, 1994, 6(17), 3207.
12. F. Benkabou, H. Aourag and M. Certier, Atomistic study of zinc blende CdS, CdSe, ZnS, and ZnSe from molecular dynamics, Mater. Chem. Phys., 2000, 66(1), 10–16.
13. R. Khenata, A. Bouhemadou, M. Sahnoun, A. H. Reshak, H. Baltache and M. Rabah, Elastic, electronic and optical properties of ZnS, ZnSe and ZnTe under pressure, J. Comput. Mater. Sci. Eng., 2006, 38(1), 29–38.
14. D. B. Eason, Z. Yu, C. Boney, J. Ren, L. E. Churchill, J. W. Cook Jr, J. F. Schetzina and N. A. El-Masry, Quaternary II–VI alloys for blue and green light emitting diode applications, J. Cryst. Growth, 1994, 138(1–4), 709–713.
15. X. Huang, H. R. Heulings, J. Li, T. Yuen and C. L. Lin, Towards Dilute Magnetic Semiconductors: Fe and Co Substituted Inorganic–Organic Hybrid Materials Based on ZnSe, J. Nanosci. Nanotechnol., 2005, 5(9), 1487–1491.
16. A. Twardowski, Magnetic properties of Fe–based diluted magnetic semiconductors, J. Appl. Phys., 1990, 67(9), 5108–5113.
17. M. Boughrara, A. A. M'Hid and M. Kerouad, Diluted Magnetic Semiconductors, in Handbook of Semiconductors, CRC Press, 2024, pp. 12–25.
18. T. Yao, M. Ogura, S. Matsuoka and T. Morishita, High–quality ZnSe thin films grown by molecular beam epitaxy, Appl. Phys. Lett., 1983, 43(5), 499–501.
19. C. W. Huang, H. M. Weng, Y. L. Jiang and H. Y. Ueng, Optimum growth of ZnSe film by molecular beam deposition, Vacuum, 2008, 83(2), 313–318.
20. M. G. Syed Basheer Ahamed, V. S. Nagarethinam, A. R. Balu, A. Thayumanavan, K. R. Murali, C. Sanjeeviraja and M. Jayachandran, Influence of substrate temperature on the properties of electron beam evaporated ZnSe films, Cryst. Res. Technol., 2010, 45(4), 421–426.
21. M. Arslan, A. Maqsood, A. Mahmood and A. Iqbal, Structural and optical properties of copper enriched ZnSe thin films prepared by closed space sublimation technique, Mater. Sci. Semicond. Process., 2013, 16(6), 1797–1803.
22. T. Yokogawa, M. Ogura and T. Kajiwara, High quality ZnSe films grown by low pressure metalorganic vapor phase epitaxy using methylalkyls, Appl. Phys. Lett., 1987, 50(16), 1065–1067.
23. S. J. Irvine, Metal-organic vapour phase epitaxy. Narrow-gap II-VI Compounds for Optoelectronic and Electromagnetic Applications, Electronic Materials Series, Springer New York, NY, 1997, pp. 71–96.
24. H. H. Yudar, S. Pat, Ş. Korkmaz, S. Özen and V. Şenay, Zn/ZnSe thin films deposition by RF magnetron sputtering, J. Mater. Sci.: Mater. Electron., 2017, 28, 2833–2837.
25. Y. Zheng, Q. Liang, B. Li, G. G. Zeng, W. W. Wang, J. Q. Zhang, W. Li and L. H. Feng, The influence of sputtering power on the structural, morphological and optical properties of ZnSe thin films deposited by RF magnetron sputtering, Adv. Mater. Res., 2014, 1058, 240–243.
26. B. T. Jonker, J. J. Krebs and G. A. Prinz, Growth and magnetic characterization of single–crystal Ni films on ZnSe (001), J. Appl. Phys., 1988, 64(10), 5340–5342.
27. J. E. Bernard and A. Zunger, Optical bowing in zinc chalcogenide semiconductor alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34(8), 5992.
28. R. Khenata, A. Bouhemadou, M. Sahnoun, A. H. Reshak, H. Baltache and M. Rabah, Elastic, electronic and optical properties of ZnS, ZnSe and ZnTe under pressure, Comput. Mater. Sci., 2006, 38(1), 29–38.
29. W. Sukkabot, Tunable electronic, optical and magnetic characteristics in Mn-doped inverted type-I ZnSe/CdSe core/shell nanocrystals: Atomistic tight-binding model, Mater. Sci. Semicond. Process., 2022, 147, 106705.
30. M.-Z. Huang and W. Y. Ching, Calculation of Optical Excitations in Cubic Semiconductors. I. Electronic Structure and Linear Response, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 9446.
31. S. Zh Karazhanov, P. Ravindran, A. Kjekshus, H. Fjellvag and B. G. Svensson, Electronic Structure and Optical Properties of ZnX (X = O, S, Se, Te): A Density Functional Study, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 155104,  DOI:10.1103/PhysRevB.75.155104.
32. A. Rachidi, E. H. Atmani, N. Fazouan and M. Boujnah, A Study by Ab-Initio Calculation of Structural and Electronic Properties of Semiconductor Nanostructures Based on ZnSe, Mater. Sci. Appl., 2016, 7(9), 562–573.
33. N. E. Christensen and I. Gorczyca, Optical and structural properties of III-V nitrides under pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(7), 4397.
34. E. D. Ghahramani, D. J. Moss and J. E. Sipe, Full-band-structure calculation of first-, second-, and third-harmonic optical response coefficients of ZnSe, ZnTe, and CdTe, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43(12), 9700.
35. G. D. Lee, M. H. Lee and J. Ihm, Role of d electrons in the zinc blende semiconductors ZnS, ZnSe, and ZnTe, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 2, 1459.
36. D. Mourad and G. Czycholl, Theory of band gap bowing of disordered substitutional II–VI and III–V semiconductor alloys, Eur. Phys. J. B, 2012, 85, 1–3.
37. P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. De Gironcoli, P. Delugas, F. Ferrari Ruffino and A. Ferretti, Quantum ESPRESSO toward the exascale, J. Chem. Phys., 2020, 152(15), 154105.
38. S. Scandolo, P. Giannozzi, C. Cavazzoni, S. de Gironcoli, A. Pasquarello and S. Baroni, First-principles codes for computational crystallography in the Quantum-ESPRESSO package. Zeitschrift für Kristallographie-Crystalline, Materials, 2005, 220(5–6), 574–579.
39. W. Kohn and L. Sham, Density functional theory. InConference Proceedings-Italian Physical Society, 1996, vol. 49, pp. 561–572.
40. M. Orio, D. A. Pantazis and F. Neese, Density functional theory, Photosynth. Res., 2009, 102, 443–453.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
42. A. Hassan, M. Ismail, A. H. Reshak, Z. Zada, A. A. Khan, M. Arif, K. Siraj, S. Zada, G. Murtaza and M. M. Ramli, Effect of heteroatoms on structural, electronic and spectroscopic properties of polyfuran, polythiophene and polypyrrole: A hybrid DFT approach, J. Mol. Struct., 2023, 1274, 134484.
43. H. Yu, H. Huang, A. H. Reshak, S. Auluck, L. Liu, T. Ma and Y. Zhang, Coupling ferroelectric polarization and anisotropic charge migration for enhanced CO2 photoreduction, Appl. Catal., B, 2021, 284, 119709.
44. R. Ullah, A. H. Reshak, M. A. Ali, A. Khan, G. Murtaza, M. AL–Anazy, H. Althib and T. H. Flemban, Pressure–dependent elasto–mechanical stability and thermoelectric properties of MYbF3 (M= Rb, Cs) materials for renewable energy, Int. J. Energy Res., 2021, 45(6), 8711–8723.
45. S. Tabassam, A. H. Reshak, G. Murtaza, S. Muhammad, A. Laref, M. Yousaf, A. M. Al Bakri and J. Bila, Co2YZ (Y= Cr, Nb, Ta, V and Z= Al, Ga) Heusler alloys under the effect of pressure and strain, J. Mol. Graphics Modell., 2021, 104, 107841.
46. M. Husain, N. Rahman, A. H. Reshak, A. Habib, S. Ali, A. Laref, A. M. Al Bakri and J. Bila, Insight into the physical properties of the inter-metallic titanium-based binary compounds, Eur. Phys. J. Plus, 2021, 136(6), 624.
47. M. Arif, A. H. Reshak, S. U. Zaman, M. Husain, N. Rahman, S. A. Ahmad, M. Saqib, S. Khan, M. M. Ramli and A. Khan, Density functional theory-based study of the physical properties of cesium based cubic halide perovskites CsHgX3 (X = F and Cl), Int. J. Energy Res., 2022, 46(3), 2467–2476.
48. S. Arif, Electric field engineering and modulation of CuBr: a potential material for optoelectronic device applications, RSC Adv., 2023, 13, 7352–7365.
49. Y. Xue, D. Tian, D. Zhang, C. Zeng, Y. Fu, K. Li, H. Wang and Y. Tian, The mechanism of photocatalyst and the effects of co-doping CeO2 on refractive index and reflectivity from DFT calculation, Comput. Mater. Sci., 2019, 158, 197–208.

---