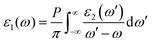A deep-ultraviolet nonlinear-optical material with a wide bandgap and large static dielectric polarizability coefficient: Na₆Si₃F₁₈

Abstract

A silicon-based noncentrosymmetric (NC) deep-ultraviolet (DUV) nonlinear optical material, Na₆Si₃F₁₈, has been synthesized through a hydrothermal method. Na₆Si₃F₁₈ possesses a [SiNa₉F₄₂] group, which is constructed by an isolated [SiF₆] octahedron and nine distorted [NaF₆] octahedra interconnected with one another to form a condensed 3D structure, which is beneficial to increase the static dielectric polarizability coefficient, which was calculated to be 4.3 times that of quartz. The first-principles calculations indicate that Na₆Si₃F₁₈ possesses a very large bandgap of 10.45 eV (∼118.76 nm), which originates from the [SiF₆] group and [NaF₆] group and is larger than that of SrB₄O₇. Na₆Si₃F₁₈ crystalizes in the P321 space group, and is a potential DUV nonlinear optical crystal with the addition of periodic phase match technology, which could break through the wall of 120 nm for all-solid-state lasers.

---

1. Introduction

Deep-ultraviolet (DUV) nonlinear optical (NLO) crystals have important applications in photolithography,¹ photoelectron spectroscopy,^2,3 micromachining, and photochemistry, among others.^4–10 Few NLO crystals can be used in the DUV region, and only KBe₂BO₃F₂ (KBBF) has achieved practical use.¹¹ With the development of DUV laser equipment and its new applications, DUV NLO crystals are badly needed for their irreplaceable role as the most mature method for extending the wavelength range into the DUV region. Limited by the birefringence phase-matching (PM) technology, researchers are searching for DUV NLO crystals that meet three key conditions: (1) the most important is a large bandgap of at least 6.2 eV (corresponding to an absorption edge of 200 nm); (2) moderate birefringence (between 0.06 and 0.9 at 1064 nm) to achieve the DUV PM; and (3) a large second harmonic generation (SHG) coefficient.^12–14 Thus, a great number of DUV NLO crystals have been discovered. Some examples include the borates β-BaB₂O₄ (BBO),¹⁵ LiB₃O₅ (LBO),¹⁶ CsB₃O₅,¹⁷ CsLiB₆O₁₀,¹⁸ K₂Al₂B₂O₇,¹⁹ BaAlBO₃F₂,²⁰ Rb₃Al₃B₃O₁₀F,²¹ Li₄Sr(BO₃)₂,²² Cs₂Al₂(B₃O₆)₂O,²³etc.; beryllium borates such as ABe₂BO₃F₂ (A = Na, Rb, Cs),^24–26 Sr₂Be₂B₂O₇,²⁷ NaBeB₃O₆, ABe₂B₃O₇,²⁸ Na₂CsBe₆B₅O₁₅,²⁹ NH₄Be₂BO₃F₂, γ-Be₂BO₃F,³⁰ BaMBe₂(BO₃)₂F₂ (M = Mg, Ca),³¹ BaBe₂BO₃F₃,³²etc.; and fluorooxoborates such as LiB₆O₉F,³³ Li₂B₆O₉F₂,³⁴ Li₂B₃O₄F₃,³⁵ AB₄O₆F (A = NH₄, Na, Rb, Cs),^36–39 K₃B₆O₉F₃,⁴⁰ Na₂B₆O₉F₂,⁴¹ M₂B₁₀O₁₄F₆ (M = Ca, Sr),⁴² CaBO₂F,⁴³etc.

Recently, some new methods for phase-matching without considering birefringence have been developed. SrB₄O₇ crystals with spontaneous domain structure have realized 121 nm tunable DUV coherent light using randomly quasi-phase-matched technology; this is the shortest wavelength achieved using NLO crystals, with about 0.04‰ SHG conversion efficiency.^44,45 Quartz with an artificial periodic grating structure showed unprecedented SHG conversion efficiency at 177.3 and 167.8 nm, which is comparable to that of KBBF crystals.⁴⁶

To date, none of these crystals has broken through the wall of 120 nm for all-solid-state lasers because their bandgaps are smaller than 10.33 eV (corresponding to an absorption edge at 120 nm). Based on existing theories and the recent development of PM technology, we summarize the 'anion–cation modulation strategies' (ACMS), which can provide an easy way to find DUV materials by combining the roles of anions and cations and considering the function of fluorine ions fully. The core ideas are as follows:

The first strategy is the cationic SP strategy. Cations of elements with s and p orbital electrons and empty d and f orbitals are selected. The best choice is an alkali metal or alkaline earth metal, as such cations contain s and p orbital electrons and no d and f orbital electron distribution, and thus do not exhibit d–d orbital or f–f orbital electron transitions. These cations show no absorption in the visible and ultraviolet regions and possess a short ultraviolet cutoff edge.

The second strategy is the complete fluorination strategy for anionic groups. Completely fluorinated groups without oxygen atoms are selected as the anion groups. Compared with anion groups with oxygen, these anions have stronger electronegativity, wider electronic transition bandgaps, and larger static dielectric polarizability coefficients. Moreover, this kind of anion group is usually in an isolated state, which could produce a large SHG coefficient through the asymmetric polyhedral distortion of the anion group. These anions include [SiF₆], [PF₆], [AlF₆], [BF₄], [NF₃], etc., or hybrid groups of these anionic groups. These structures are rich and diverse.

Herein, guided by the ACMS and many experiments, a DUV NLO crystal, Na₆Si₃F₁₈, was synthesized successfully. This crystal possesses a large bandgap, large static dielectric polarizability coefficient (4.3 times that of α-SiO₂), good physical properties (nondeliquescence, suitable hardness, and good stability), and good growth performance. More importantly, the raw materials are cheap and friendly to the environment. This crystal also proves the correctness of the ACMS.

In this work, the growth methods of millimeter-level Na₆Si₃F₁₈ crystals were investigated, including impurity crystallization and self-crystallization (Fig. S1, ESI†). The powder XRD patterns generated from the solved crystal structure fit well with the experimental one (Fig. S2, ESI†), which proves the accuracy of the crystal structure analysis. The SHG testing shows interesting outputs. The bandgap, partial density of states with spin polarization, birefringence, and dielectric polarizabilities matrix (Table S7, compared with those of quartz and Pmn2₁ phase SrB₄O₇, ESI†) were estimated using first-principles calculations. The results show that Na₆Si₃F₁₈ is a potential DUV NLO crystal with the addition of the periodic phase match technology introduced in ref. 46.

2. Experiments and first-principles calculations

The purities of all ingredients were confirmed using powder X-ray diffraction. NaF (AR, 98%), HIO₄·2(H₂O) (ACS reagent, 99%), HIO₃ (AR, 99.5%), and Na₂SiF₆ (AR,98%) were purchased from Macklin reagent. Ce(NO₃)₃·6H₂O (99.999%) was purchased from Beijing Hawk Science & Technology Co., Ltd.

2.1. Synthetic procedures

Na₆Si₃F₁₈ was grown using two methods, namely, impurity crystallization and self-crystallization. The impurity crystallization method used a hydrothermal method with the starting materials NaF (0.84 g, 0.02 mol), HIO₄·2(H₂O) (1.05 g, 0.05 mol), HIO₃ (3.1 g, 0.018 mol), Ce(NO₃)₃·6H₂O (0.5 g, 0.001 mol), and H₂O (5 mL, 0.278 mol). The starting materials were placed into a 25 mL Teflon liner equipped with a 304 stainless steel autoclave and heated at 513.15 K for three days, and then allowed to cool to room temperature naturally. The reaction products were washed with pure water and ethanol and then dried in an electric thermo-static-drying oven at 320.15 K for 5 hours. About 0.21 g of colorless block-shaped Na₆Si₃F₁₈ single crystals was obtained, and the largest one was nearly 3 mm in length (Fig. S1a and b, ESI†). This product was mainly crystallized from the small impurities of the starting materials. The element Si comes from the HIO₃, which contains the P2₁/c phase HI₃O₈ and P3₂21 phase SiO₂ (Fig. S1e, ESI†).

The self-crystallization method was also carried out using the same equipment and the same temperature control procedure with powder Na₂SiF₆ as the starting material (0.7 g, 0.0037 mol). About 0.46 g of millimeter-sized colorless block-shaped Na₆Si₃F₁₈ single crystals was obtained (Fig. S1c and d, ESI†). These crystals were mainly crystallized from the Na₂SiF₆ powder.

2.2. Single crystal X-ray diffraction

A colourless, block-shaped single crystal of Na₆Si₃F₁₈ was mounted on a MiTeGen micromount with perfluoroether oil. Data were collected from a shock-cooled single crystal at 150(2) K using a Bruker D8 VENTURE dual-wavelength Mo/Cu three-circle diffractometer with a microfocus sealed X-ray tube using mirror optics as the monochromator and a Bruker PHOTON III detector. The diffractometer was equipped with a low-temperature device and used MoK_α radiation (λ = 0.71073 Å). All data were integrated using SAINT, and a multi-scan absorption correction using SADABS was applied.^47,48 The structure was solved by direct methods using SHELXT and refined by full-matrix least-squares methods against F² using SHELXL-2019/1.^49,50 Crystallographic data for the structures reported in this paper have been deposited with the Cambridge Crystallographic Data Centre.⁵¹ CCDC 2304836† contains the supplementary crystallographic data for this paper. This report and the CIF file were generated using FinalCif.⁵² The crystallographic record and structural refinement information are listed in Table S1 (ESI†). Other crystal information, including fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters, atomic displacement parameters, selected geometric information, and torsion angles, are listed in Tables S2–S5 (ESI†).

2.3. Powder X-ray diffraction

Powder XRD was carried out using an automated Bruker D8 ADVANCE X-ray diffractometer with Cu Kα radiation (λ = 1.5418 Å) at indoor temperature in the 2θ range from 5° to 80° with a 0.2 s step time and a 0.02° scan step width (Fig. S2, ESI†).

2.4. Infrared (IR) spectroscopy

About 5 mg of Na₆Si₃F₁₈ crystal powder was ground with 500 mg dried KBr powder, and the mixed powder was pressed into a thin wafer under 15 MPa of pressure. Measurement was carried out using a NICOLET Is50 FT-IR Fourier transform infrared spectrometer at indoor temperature. The IR spectrum was recorded in the range from 400 to 4000 cm⁻¹ with a resolution of 4 cm⁻¹. 32 scans of the sample were acquired. Before testing the sample, the atmospheric influence was tested as the background.

2.5. Raman spectroscopy

The single-crystal Raman micro-spectroscopy of Na₆Si₃F₁₈ was carried out in the spectral range of −40.8 to 3772.4 cm⁻¹ (a range of 120–2600 cm⁻¹ was chosen for Fig. 2B) and a data resolution of about 0.083 cm⁻¹ using a WITec alpha300 Raman micro-spectrometer (Oxford Instruments, Oxford, England) coupled with a Peltier-cooled EMCCD detector at the Instrumental Analysis Center of Wuyi University. An all-solid-state Nd:YAG source laser with doubled frequency using a nonlinear optical crystal (λ = 532.22 nm) was used as the laser excitation source. Before the spectra were obtained, the laser excitation wavelength was calibrated using a standard Si crystal wafer at 520.7 cm⁻¹. The spectra were captured using a 50× objective lens (N.A. = 0.9) with a 50 μm diameter optical fiber. A grating of 600 g mm⁻¹ with spectral resolution of about 4 cm⁻¹ was used. In order to obtain a high enough signal-to-noise ratio, the EMCCD integration time was set as 30 s and the accumulation number as 5. The confocal depths were at least 1 μm below the crystal surface. All Raman spectra were processed using WITec Project Six 6.1.10.135 with a background subtraction polynomial fit.

2.6. UV-vis-NIR spectroscopy

The UV-vis-NIR transmittance spectra of Na₆Si₃F₁₈ were measured using a UH4150 UV-vis-NIR spectrophotometer with two Al₂O₃ plates as a reflectance material (100% reflectance) to cover the light hole of the integrating sphere. The pure Na₆Si₃F₁₈ crystal was ground into a powder and pressed into a thin wafer at 15 MPa for 10 minutes. The optical transmittance spectra show good transmittance from 200 nm to 2600 nm. There was an absorption valley around 340 nm in the spectra (Fig. S5, ESI†) for the spectrophotometer changing the light source from a xenon lamp to a tungsten lamp. The transmittance of powder wafers is usually weaker than that of single crystals, and the radius of the wafer is smaller than the radius of the aperture. The results show that Na₆Si₃F₁₈ has an absorption edge smaller than 200 nm, corresponding to a bandgap larger than 6.2 eV. This result is consistent with the experiments of the group of Chen Z. H.⁵³

2.7. First-principles calculations

The first-principles electronic structure calculations of Na₆Si₃F₁₈ were carried out using the plane-wave pseudopotential method⁵⁴ implemented by the CASTEP package⁵⁵ based on density functional theory.⁵⁶ The functionals developed by Perdew–Burke–Ernzerhof (PBE)⁵⁷ in generalized gradient approximation (GGA) form were adopted to describe the exchange–correlation terms in the Hamiltonian. The effective ion–electron interactions were modeled using the optimized normal-conserving pseudopotentials for all elements⁵⁸ (Na2s²2p⁶3s¹, Si3s²3p², F2s²2p⁵), which use a relatively small plane-wave basis set but possess high computational accuracy. To achieve energy convergence, the kinetic energy cutoff was 780 eV and intensive Monkhorst–Pack⁵⁹ k-point meshes of 2 × 2 × 2 Å⁻³ spanning less than 0.025 Å⁻³ in Brillouin zone were used.

The bandgaps calculated using the PBE functionals in the standard DFT framework are commonly smaller than the observed values for crystals with large bandgaps due to the discontinuity of exchange–correlation energy. The bandgap of Na₆Si₃F₁₈ was calculated using hybridized PBE0 functionals,⁶⁰ for which the relative error of the calculated bandgaps is less than 5%, as demonstrated in our previous study. This is consistent with the comparison of the result for the Pmn2₁ phase SrB₄O₇ crystal (the experimental bandgap is 120 nm, and the PBE0-functional-calculated result is 124 nm, a relative error of about 3.3%). In contrast, the HSE06 functionals show larger error for the calculated bandgap of SrB₄O₇ (135 nm, about 13% relative error). Thus, the PBE0 functionals have higher accuracy than the HSE06 functionals in these bandgap calculations.

Because of the discontinuity of the exchange–correlation energy used by the PBE functionals in the standard DFT framework, the calculated bandgap is smaller than experimental value. A scissor operator was chosen to correct the GGA method bandgap value. Based on the scissor-corrected band structure, the imaginary part of the dielectric function is calculated from the electron transition across the bandgap, and the real part, i.e., the refractive index, can be obtained using the Kramers–Kronig relations⁶¹:

Based on the calculated refractive index (n_x, n_y, n_z), the birefringence (Δn = n_z − n_y) could be obtained.

The dielectric polarizabilities matrices of Na₆Si₃F₁₈, α-SiO₂ and Pmn2₁ phase SrB₄O₇ were calculated using the PBE functional after crystal geometry optimization without changing the crystal cell. The crystal geometry optimized structures were used to calculate the polarizability, IR and Raman spectra. The corresponding optical and static dielectric polarizabilities matrices were obtained at both infinite frequency and zero frequency. The output of second harmonic generation has a positive correlation with the static dielectric polarizabilities coefficient.

3. Results and discussion

3.1. Crystal structure analysis

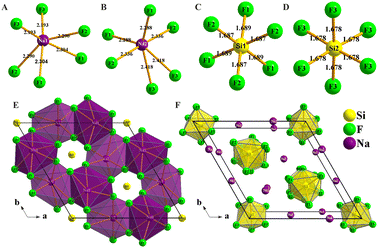
Na₆Si₃F₁₈ crystallizes in the noncentrosymmetric trigonal space group P321 (No. 150) with unit cell parameters of a = 8.8384(2) Å, b = 8.8384(2) Å, c = 5.0117(2) Å, α = 90°, β = 90°, γ = 120°, and Z = 3 (Table S1, ESI†). In the asymmetric unit, Na₆Si₃F₁₈ is comprised of two unique sodium atoms, two unique silicon atoms, and three unique fluorine atoms. As depicted in Fig. 1A–D, Na₆Si₃F₁₈ shows a 3D framework that contains two types of [NaF₆] octahedron coordination geometries and two types of [SiF₆] octahedron entities. All Na atoms are surrounded by six F atoms to form distorted [NaF₆] octahedra with Na–F distances ranging from 2.193 to 2.304 Å and 2.228 to 2.418 Å, and F–Na–F angles ranging from 62.23° to 160.18° and 57.23° to 178.46° for the Na1 and Na2 atoms, respectively. All Si atoms are connected by six F atoms to form [SiF₆] octahedra. The Si–F distances range from 1.687 to 1.689 Å and the F–Si–F angles range from 89.36° to 179.10° for the distorted [Si1F₆] octahedra, while the Si–F distances are only 1.678 Å and the F–Si–F angles range from 87.29° to 176.96° for the regular [Si2F₆] octahedra. All F atoms are connected by one silicon atom and two sodium atoms. This crystal is a polymorph of P3̄m1 phase Na₂SiF₆.⁶²

Fig. 1 Crystal structure of Na₆Si₃F₁₈. (A) Coordination of the Na1 atom; (B) coordination of the Na2 atom; (C) coordination of the Si1 atom; (D) coordination of the Si2 atom; (E) parallel projection of the corner-linked [NaF₆] octahedron structure viewed down [111]; (F) central projection of isolated [SiF₆] octahedron viewed down [111] in the primitive cell.

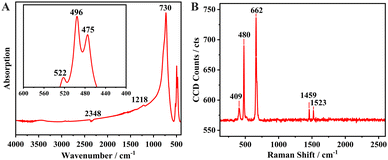Fig. 2 (A) Infrared spectrum of Na₆Si₃F₁₈. (B) Single-crystal Raman spectrum of P321 phase Na₆Si₃F₁₈ in the range of 120–2600 cm⁻¹.

As depicted in Fig. 1E and F, each primitive cell contains 27 atoms. There are eight Na1 atoms on the edge and two Na1 atoms at the face of the crystal cell, four Na2 atoms at the face and one Na2 atom in the cell, and four Si1 atoms at the face and four Si2 atoms at the edge center of the crystal cell. Each distorted [NaF₆] octahedron is corner-linked by F atoms to form a stereoscopic structure with four [NaF₆] octahedra and four [SiF₆] octahedra neighbours; the Si atoms are located in the center of the hexagon formed by the F atoms as viewed down the [001] direction. Every [SiF₆] octahedron is isolated from the others and connected by nine [NaF₆] octahedra to form a [SiNa₉F₄₂] group (Fig. S3 and S4, ESI†); the [SiNa₉F₄₂] groups are interconnected to each other to build a three-dimensional (3D) structure. Other crystal information, including the fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters, atomic displacement parameters, selected geometric information, and torsion angles, are listed in Tables S2–S5 (ESI†). The bond valence sums of all the elements of Na₆Si₃F₁₈ were calculated using the charge distribution in solids concept and the bond-length/bond-strength concept.^63–67 The original bond length data are from the CIF. The calculation results are listed in the Table S2 (ESI†), and fit well with the formal ionic charges.

3.2. Optical properties analysis

In order to investigate the component group vibration and rotation of Na₆Si₃F₁₈, the powder FT-IR spectrum and the single-crystal Raman micro-spectroscopy of Na₆Si₃F₁₈ were recorded and are presented in Fig. 2A and B, respectively. The site symmetry of the octahedral hexafluorosilicate [SiF₆] anion group is D_3d. Obvious Si–F strong IR bands are observed in the range of 400 to 800 cm⁻¹, as depicted in Fig. 2A. The highest peak at 730 cm⁻¹ has been assigned as the ν₃ (F_1u) band of the [SiF₆] anion group. The other three bands at 522, 496, 475 cm⁻¹ all correspond to the ν₄ band for the [SiF₆] group with two different environments.

In the single-crystal Raman spectrum range of 100 to 700 cm⁻¹, three strong bands are observed at 662, 480 and 409 cm⁻¹. The strongest peak at 662 cm⁻¹ belongs to the ν₁ (A_1g fundamental) Raman band of the [SiF₆] group. The other two Raman-active fundamental bands at 480 and 409 cm⁻¹ belong to ν₂ (E_g) and ν₅ (F_2g), respectively.⁶⁸ The UV-vis-NIR transmittance spectra shows that Na₆Si₃F₁₈ has an absorption edge smaller than 200 nm, corresponding to a bandgap larger than 6.2 eV (Fig. S5, ESI†).

3.3. First-principles calculations

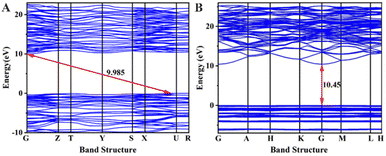
To investigate the origin of the physical properties of the Na₆Si₃F₁₈ crystal, the electronic band structures along the high-symmetry path in the first Brillouin zone were calculated using first-principles calculations with a comparison. In order to confirm the accuracy of the results, the Pmn2₁ phase SrB₄O₇ crystal was investigated using the same parameters. As depicted in Fig. 3A, the theoretical bandgap of SrB₄O₇ is 9.985 eV, which corresponds to 124 nm, which is very close to the experimental absorption edge (120 nm). In Fig. 3B, the theoretical band structure indicates that Na₆Si₃F₁₈ is a direct insulator with a valence band (VB) maximum and conduction band (CB) minimum at the same G point. Due to the discontinuity of the exchange–correlation energy used by the PBE functionals in the standard DFT framework, the calculated bandgap of P321 phase Na₆Si₃F₁₈ is 10.45 eV, which is smaller than its real bandgap. This result shows that the bandgap of Na₆Si₃F₁₈ is larger than that of the Pmn2₁ phase SrB₄O₇ crystal.

Fig. 3 (A) Band structures of Pmn2₁ phase SrB₄O₇ crystal (B) and P321 phase Na₆Si₃F₁₈ crystal.

The partial density of electronic states with spin polarization projected onto the constituent elements is shown in Fig. 4 and Fig. S5 (ESI†). Some characteristics could be concluded as follows: (1) the Na 2s orbitals are localized around −50 eV, making them very difficult to be stimulated by the disturbance of an external perturbation across the forbidden band, and they contribute almost nothing to the physical properties. (2) The energy levels between −25 eV and −15 eV are mainly constituted by Na 2p, Si 3s3p, and F 2s orbitals. These orbitals are hybridized with each other in this energy range to form the strong covalent interaction within the [SiF₆] ionic groups. Additionally, the Na 2p orbitals show a sharp peak at −20 eV and hardly hybridize with the other orbitals, demonstrating the strong ionicity of the Na atoms. (3) The top of the VB (−8 to 0 eV) is predominantly occupied by F2p and the bottom of the CB (10.5 to 20 eV) is predominantly occupied by Na2p3s and Si3s3p, which indicates that the stimulation of electrons across the bandgap mainly happens within the [SiF₆] and [NaF₆] groups. Finally, all the elements in this compound have a closed-shell electron configuration of [Ne]⁸ with paired electrons, which fits well with the calculation results that all spin-up states are symmetrically consistent with the spin-down states. Thus, Na₆Si₃F₁₈ is also a diamagnetic material.

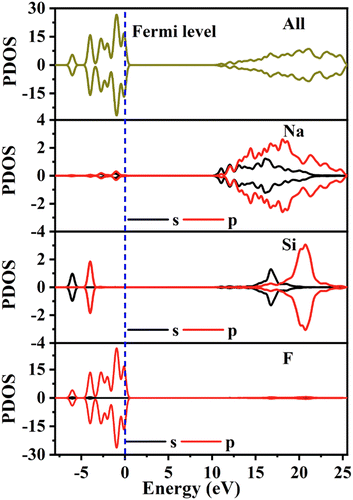Fig. 4 The partial density of states with spin polarization projected on the constituent elements of Na₆Si₃F₁₈.

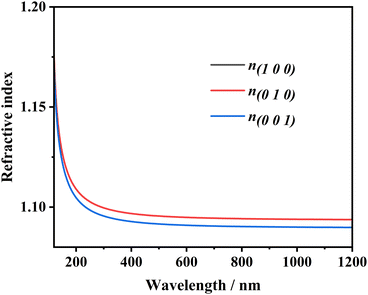
The refractive indices n and birefringence Δn of Na₆Si₃F₁₈ were calculated using first-principles theory. The P321 space group has two independent refractive indices, n₍₁₀₀₎ = n₍₀₁₀₎, and n₍₀₀₁₎. As depicted in Fig. 5, the refractive index curves show that n₍₁₀₀₎ is the maximum, which means that Na₆Si₃F₁₈ is a positive uni-axial crystal. The birefringence (Δn = n₍₁₀₀₎ − n₍₀₀₁₎) is 0.00396 at 532.36636 nm; other data are listed in Table S6 (ESI†). Based on the anionic group theory, the birefringence originates from the [SiF₆] and [NaF₆] octahedrons.

Fig. 5 The calculated refractive indices of the Na₆Si₃F₁₈ crystal.

The dielectric polarizabilities matrices of Na₆Si₃F₁₈, α-SiO₂ and Pmn2₁ phase SrB₄O₇ are shown in Table S7 (ESI†). Comparing the largest static dielectric polarizability coefficients, the coefficient d₃₃ of Na₆Si₃F₁₈ (about 4.3 times the d₃₃ of α-SiO₂) is very close to the coefficient d₂₂ of Pmn2₁ phase SrB₄O₇ (about 4.4 times the d₃₃ of α-SiO₂). SHG testing with a Q-switched Nd:YAG laser at 1064 nm showed that the output light of Na₆Si₃F₁₈ appears as white light (Fig. S7, ESI†), which might contain different wavelengths. The SHG tensors of Na₆Si₃F₁₈ compared with those of SiO₂ and SrB₄O₇ were also calculated and are listed in Table S8 (ESI†). Thus, to improve the SHG efficiency of the Na₆Si₃F₁₈ crystal, the addition of periodic phase match technology could be adopted.

4. Conclusions

In summary, a deep-ultraviolet silicon-based nonlinear optical crystal, Na₆Si₃F₁₈, was synthesized via a hydrothermal method. Na₆Si₃F₁₈ crystallizes in the noncentrosymmetric space group P321, with a unique [SiNa₉F₄₂] group. The [SiNa₉F₄₂] groups are interconnected with each other to construct a 3D structure, which possesses a very large bandgap of 10.45 eV (∼118.76 nm). Although the calculated birefringence of this compound is about 0.004 at 532 nm, the Na₆Si₃F₁₈ crystal could realize highly efficient deep-ultraviolet laser output with quasi-phase-matching techniques using added spatial periodic structures. Further research toward large-size and high-quality single crystals is on the way.

Author contributions

Tang C. C. designed and performed the experiments, calculations and wrote this paper; Jian X. X., Yang C., Huang Y. M. and Lin Z. S. performed the first-principles calculations of this paper; Wu X. Y., Gong Y. C., Zhou D. K. and Chen H. M. performed the experiments; Wang P. P. guided the optical testing; Guo R. X. performed the single crystal testing. All authors contributed to the general discussion.

Data availability

The data that support the results of this research are available from the corresponding author [CC.T], upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research was supported by the Natural Science Foundation of Fujian Province, China (Grant No. 2021J05426) and Wuyi University introduced talents research start-up fund (Grant No. YJ202010).

References

1. S. Ito, T. Onose and K. Kakizaki, et al., A sub-watt, line-narrowing, 193-nm solid state laser operating at 6 kHz with KBBF for injection-locking ArF excimer laser systems, Adv. Solid State Photonics, 2012 DOI:10.1364/ASSP.2012.AT4A.7.
2. T. Kiss, F. Kanetaka and T. Yokoya, et al., Photoemission spectroscopic evidence of gap anisotropy in an f-electron superconductor, Phys. Rev. Lett., 2005, 94(5), 057001.
3. T. Kiss, T. Shimojima and K. Ishizaka, et al., A versatile system for ultrahigh resolution, low temperature, and polarization dependent laser-angle-resolved photoemission spectroscopy, Rev. Sci. Instrum., 2008, 79(2), 023106.
4. I. K. Lednev, V. V. Ermolenkov, W. He and M. Xu, Deep-UV Raman spectrometer tunable between 193 and 205 nm for structural characterization of proteins, Anal. Bioanal. Chem., 2005, 381, 431–437.
5. G. D. Liu, G. Wang, Y. Zhu, H. Zhang, G. Zhang and X. Wang, et al., Development of a vacuum ultra-violet laser-based angle-resolved photoemission system with a superhigh energy resolution better than 1 meV, Rev. Sci. Instrum., 2008, 79, 023105.
6. W. T. Zhang, G. D. Liu and J. Q. Meng, et al., High energy dispersion relations for the high temperature Bi₂Sr₂CaCu₂O₈ superconductor from laser-based angle-resolved photoemission spectroscopy, Phys. Rev. Lett., 2008, 101, 017002.
7. J. Q. Meng, G. D. Liu and W. T. Zhang, et al., Coexistence of Fermi arcs and Fermi pockets in a high-T ccopper oxide superconductor, Nature, 2009, 462, 335–338.
8. Y. M. Xu, Y. B. Huang and X. Y. Cui, et al., Observation of a ubiquitous three-dimensional super-conducting gap function in optimally doped Ba0.6K0.4Fe2As2, Nat. Phys., 2011, 7, 198–202.
9. S. Q. Jin, M. L. Guo and J. X. Fan, et al., Deep UV resonance Raman spectroscopic study of C n F 2n + 2 molecules: the excitation of C–C σ bond, J. Raman Spectrosc., 2013, 44, 266–269.
10. T. A. Chen, C. P. Chuu and C. C. Tseng, et al., Wafer-scale single-crystal hexagonal boron nitride monolayers on Cu(111), Nature, 2005, 579, 219–223.
11. C. T. Chen, T. Kanai, X. Y. Wang, Y. Zhu and S. Watanabe, High-average-power light source below 200 nm from a KBe₂BO₃F₂ prism-coupled device, Opt. Lett., 2008, 33(3), 282–284.
12. Z. G. Hu, M. Yoshimura, Y. Mori and T. Sasaki, Design and growth of new NLO crystals for UV light, J. Cryst. Growth, 2005, 275, 232–239.
13. T. T. Tran, H. Yu and J. M. Rondinelli, et al., Deep ultraviolet nonlinear optical materials, Chem. Mater., 2016, 28, 5238–5258.
14. W. Zhang, H. Yu and H. Wu, et al., Phase-matching in nonlinear optical compounds: A materials perspective, Chem. Mater., 2017, 29, 2655–2668.
15. C. T. Chen, B. C. Wu, A. D. Jiang and G. M. You, A new-type ultraviolet SHG crystal-beta-BaB₂O₄, Sci. Sin., 1985, B18, 235–243.
16. C. Chen, Y. Wu, A. Jiang, B. Wu, G. You and S. Rand Lin, New nonlinear-optical crystal: LiB₃O₅, J. Opt. Soc. Am. B, 1989, 6, 616–621.
17. Y. C. Wu, T. Sasaki and S. Nakai, et al., CsB₃O₅: A new nonlinear optical crystal, Appl. Phys. Lett., 1993, 62(21), 2614–2615.
18. J. M. Tu and D. A. Keszler, CsLiB₆O₁₀: A noncentrosymmetric polyborate, Mater. Res. Bull., 1995, 30(2), 209–215.
19. Z. G. Hu, T. Higashiyama and M. Yoshimura, et al., A New Nonlinear Optical Borate Crystal K₂Al₂B₂O₇ (KAB), Jpn J. Appl. Phys., 1998, 37(10A), L1093–L1094.
20. Z. Hu, Y. Yue and X. Chen, et al., Growth and structure redetermination of a nonlinear BaAlBO₃F₂ crystal, Solid State Sci., 2011, 13, 875–878.
21. S. G. Zhao, P. F. Gong and S. Y. Luo, et al., Beryllium-free Rb₃Al₃B₃O₁₀F with reinforced interlayer bonding as a deep-ultraviolet nonlinear optical crystal, J. Am. Chem. Soc., 2015, 137, 2207–2210.
22. S. G. Zhao, P. F. Gong, L. Bai, X. Xu, S. Q. Zhang, Z. H. Sun, Z. S. Lin, M. C. Hong, C. T. Chen and J. H. Luo, Beryllium-free Li₄Sr(BO₃)₂ for deep-ultraviolet nonlinear optical applications, Nat. Commun., 2014, 5, 4019 -1-4019-7.
23. Z. Fang, X. X. Jiang and M. H. Duan, et al., Deep-ultraviolet nonlinear optical crystal Cs₂Al₂(B₃O₆)₂O: A benign member of the Sr₂Be₂(BO₃)₂O family with [Al₂(B₃O₆)₂O]²⁻ double layers, Chem. – Eur. J., 2018, 24, 7856–7860.
24. L. Mei, Y. Wang and C. Chen, et al., Crystal structure of sodium beryllium borate fluoride, Mater. Res. Bull., 1994, 29, 81–87.
25. C. D. McMillen, J. Hu, D. V. Derveer and J. W. Kolis, Trigonal structures of ABe₂BO₃F₂ (A = Rb, Cs, Tl) crystals, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 445–449.
26. A. Tressaud and K. Poeppelmeier, Electron and Photonic Properties of Fluorides Materials: Progress in Fluorine Science, Elsevier, Boston, 2016, vol. 6, pp. 113–137.
27. C. T. Chen, Y. B. Wang and B. C. Wu, et al., Design and synthesis of an ultraviolet transparent nonlinear optical crystal Sr₂Be₂B₂O₇, Nature, 1995, 373, 322–324.
28. S. Wang, N. Ye, W. Li and D. Zhao, Alkaline Beryllium Borate NaBeB₃O₆ and ABe₂B₃O₇ (A = K, Rb) as UV Nonlinear Optical Crystals, J. Am. Chem. Soc., 2010, 132, 8779–8786.
29. S. C. Wang and N. Ye, Na₂CsBe₆B₅O₁₅: An Alkaline Beryllium Borate as a Deep-UV Nonlinear Optical Crystal, J. Am. Chem. Soc., 2011, 133, 11458–11461.
30. G. Peng, N. Ye and Z. Lin, et al., NH₄Be₂BO₃F₂ and γ-Be₂BO₃F: Overcoming the layering habit in KBe₂BO₃F₂ for the next-generation deep-ultraviolet nonlinear optical materials, Angew. Chem., Int. Ed., 2018, 57, 8968–8972.
31. S. Guo, X. Jiang, M. Xia, L. Liu, Z. Fang, Q. Huang, R. Wu, X. Wang, Z. Lin and C. Chen, Structural Design of Two Fluorine–Beryllium Borates BaMBe₂(BO₃)₂F₂ (M = Mg, Ca) Containing Flexible Two-Dimensional [Be₃B₃O₆F₃]_∞ Single Laye without Structural Instability Problems, Inorg. Chem., 2017, 56, 11451–11454.
32. S. Guo, X. Jiang and L. Liu, et al., BaBe₂BO₃F₃: A KBBF-type deep-ultraviolet nonlinear optical material with reinforced [Be₂BO₃F₂]_∞ layers and short phase-matching wavelength, Chem. Mater., 2016, 28, 8871–8875.
33. G. Cakmak, J. Nuss and M. Jansen, LiB₆O₉F, the first lithium fluorooxoborate-crystal structure and Ionic conductivity, Z. Anorg. Allg. Chem., 2009, 635, 631–636.
34. T. Pilz and M. Jansen, Li₂B₆O₉F₂, a new acentric fluorooxoborate, Z. Anorg. Allg. Chem., 2011, 637, 2148–2152.
35. T. Pilz, H. Nuss and M. Jansen, Li₂B₃O₄F₃, a new lithium-rich fluorooxoborate, J. Solid State Chem., 2012, 186, 104–108.
36. G. Q. Shi, Y. Wang, F. F. Zhang, B. B. Zhang, Z. H. Yang, X. L. Hou, S. L. Pan and K. R. Poeppelmeier, Finding the next deep-ultraviolet nonlinear optical material: NH₄B₄O₆F, J. Am. Chem. Soc., 2017, 139, 10645–10648.
37. Z. Zhang, Y. Wang, B. Zhang, Z. Yang and S. L. Pan, Polar Fluorooxoborate, NaB₄O6F: A Promising Material for Ionic Conduction and Nonlinear Optics, Angew. Chem., Int. Ed., 2018, 57, 6577–6581.
38. B. B. Zhang, G. Q. Shi, Z. H. Yang, F. F. Zhang and S. L. Pan, Fluorooxoborates: beryllium-free deep-ultraviolet nonlinear optical materials without layered growth, Angew. Chem., Int. Ed., 2017, 56, 3916–3919.
39. X. F. Wang, Y. Wang, B. B. Zhang, F. F. Zhang, Z. H. Yang and S. L. Pan, CsB₄O₆F: A congruent-melting deep-ultraviolet nonlinear optical material with superior functional units recombination, Angew. Chem., Int. Ed., 2017, 56, 14119–14123.
40. G. Han, G. Shi, Y. Wang, B. Zhang, S. Han, F. Zhang, Z. Yang and S. L. Pan, K₃B₆O₉F₃: A New Fluorooxoborate with Four Different Anionic Units, Chem. – Eur. J., 2018, 24, 4497–4502.
41. G. Shi, F. Zhang, B. Zhang, D. Hou, X. Chen, Z. Yang and S. Pan, Na₂B₆O₉F₂: A Fluoroborate with Short Cutoff Edge and Deep-Ultraviolet Birefringent Property Prepared by an Open High-Temperature Solution Method, Inorg. Chem., 2017, 56, 344–350.
42. M. Luo, F. Liang, Y. X. Song, D. Zhao, F. Xu, N. Ye and Z. S. Lin, M₂B₁₀O₁₄F₆(M = Ca,Sr): Two Noncentrosymmetric Alkaline Earth Fluorooxoborates as Promising Next-Generation Deep-Ultraviolet Nonlinear Optical Materials, J. Am. Chem. Soc., 2018, 140, 3884–3887.
43. C. Tu, A. Tudi and W. Jin, et al., CaBO₂F: A novel deep-UV structural template with high nonlinear optical performance induced by electron delocalization, Sci. China Mater., 2023, 66(3), 1197–1204.
44. P. Trabs, F. Noack and A. S. Aleksandrovskvy, et al., Generation of coherent radiation in the vacuum ultraviolet using randomly quasi-phase-matched strontium tetraborate, Opt. Lett., 2016, 41(3), 618–621.
45. T. Pogosian and N. D. Lai, Theoretical investigation of three-dimensional quasi-phase-matching photonic structures, Phys. Rev. A, 2016, 94(6), 063821.
46. M. C. Shao, F. Liang, Z. M. Zhang, H. H. Yu and H. J. Zhang, Spatial Frequency Manipulation of a Quartz Crystal for Phase-Matched Second-Harmonic Vacuum Ultraviolet Generation, Laser Photonics Rev., 2023, 17(10), 2300244.
47. A. S. Bruker, SAINT, V8.40B, Bruker AXS Inc, Madison, Wisconsin, USA.
48. L. Krause, R. Herbst-Irmer, G. M. Sheldrick and D. Stalke, Comparison of silver and molybdenum microfocus X-ray sources for single-crystal structure determination, J. Appl. Cryst., 2015, 48, 3–10.
49. G. M. Sheldrick, SHELXT–Integrated space-group and crystal structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
50. G. M. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 3–8.
51. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
52. D. Kratzert, FinalCif, V118, https://dkratzert.de/finalcif.html.
53. W. Y. Zhang, Q. Jing, Y. Fang and Z. H. Chen, Synthesis, Structure and Properties of Nonlinear Optical Crystal Na₂SiF₆, Z. Anorg. Allg. Chem., 2017, 643, 1739–1743.
54. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients, Rev. Mod. Phys., 1992, 64, 1045–1097.
55. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Cryst. Mater., 2005, 220, 567–570.
56. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects*, Phys. Rev., 1965, 140, A1133–A1138.
57. J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
58. A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Optimized pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227–1230.
59. J. Hendrik and James D. Monkhorst, Special points for Brillouin-zone integrations—a reply. Pack, Phys. Rev. B: Solid State, 1977, 16, 1748–1749.
60. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170.
61. E. D. Palik and E. J. Prucha, Handbook of optical constants of solids, Academic Press, 1985.
62. C. Cipriani, Ricerche strutturistiche sul fluosilicato e sul fluogermanato di sodio, Rend. Soc. Mineral. Ital., 1955, 11, 58–77.
63. R. Hoppe, Effective coordination numbers (ECoN) and mean fictive ionic radii (MEFIR), Z. Kristallogr., 1979, 150, 23–52.
64. R. Hoppe, S. Voigt, H. Glaum, J. Kissel, H. P. Müller and K. J. Bernet, A new route to charge distributions in ionic solids, J. Less-Common Met., 1989, 156, 105–122.
65. I. D. Brown and D. Altermatt, Bond-Valence Parameters Obtained from a Systematic Analysis of the Inorganic Crystal Structure Database, Acta Crystallogr., 1985, B41, 244–247.
66. N. E. Brese and M. O’Keeffe, Bond-Valence Parameters for Solids, Acta Crystallogr., 1991, B47, 192–197.
67. M. O’Keeffe and N. E. Brese, Bond-Valence Parameters for Anion-Anion Bonds in Solids, Acta Crystallogr., 1992, B48, 152–154.
68. R. B. Badachhape, G. Hunter, L. D. McCory and J. L. Margrave, Infrared Absorption Spectra of Inorganic Solid. IV. Hexafluorosilicates. Raman Spectra of Aqueous SiF₆²⁻, Inorg. Chem., 1966, 5, 929–931.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2304836. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ma00973h

---