Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhanced HP1α homodimer interaction via force-induced salt bridge formation: implications for chromatin crosslinking and phase separation†
Shingo
Tsukamoto
 a,
Mohammad
Khavani
a,
Mohammad
Khavani
 a,
Nya
Domkam
a,
Nya
Domkam
 a and
Mohammad R. K.
Mofrad
a and
Mohammad R. K.
Mofrad
 *ab
*ab
aMolecular Cell Biomechanics Laboratory, Departments of Bioengineering and Mechanical Engineering, University of California, Berkeley, CA 94720, USA. E-mail: mofrad@berkeley.edu; Tel: (+1510) 643-8165
bMolecular Biophysics and Integrative Bioimaging Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 13th February 2024
Abstract
Recent studies have underscored the potential role of Heterochromatin Protein 1α (HP1α) in chromatin crosslinking, phase separation, and the orchestration of nuclear mechanics. One of the cornerstones of HP1α functionality lies in its homodimerization through the chromoshadow domain (CSD), which is crucial for these processes. Nevertheless, it has remained unknown how HP1α can foster condensations responding to mechanical force and induce phase separation in the mechanically unfavorable heterochromatin region. To elucidate the biophysical basis of HP1α, we used full atomistic molecular dynamics (MD) simulations, focusing on the CSD–CSD dimer of HP1α under a pulling force. Notably, force application resulted in a stronger, more stable interaction at the α-helix interface of the CSD–CSD. This enhanced interaction was attributed to a force-induced salt bridge formation on the α-helix interface, emerging from an angle alteration of a lysine residue that enables closer proximity to a glutamic acid residue on the paired CSD. This study reveals an intriguing facet of HP1α mechanics: its mechanical sensitivity, wherein dimerization strength is enhanced by mechanical force. The molecular dynamics of the CSD–CSD dimer under force provide novel insights into HP1α mechanics, contributing to our understanding of chromatin mechanics and phase separation.
Introduction
Mechanical forces, originating both inside and outside the cell, such as cell substrate stretching and actin contraction, are conveyed to the nucleus via the cytoskeleton and the LINC complex.1–3 The active and passive responses of the nucleus and chromatin to these mechanical forces impact gene transcription by modulating the accessibility of mechanosensitive transcription factors or by directly altering chromatin and DNA structures.4,5 Unlike the relatively stable structure of DNA, chromatin exhibits high mechanochemical dynamism, readily undergoing structural changes.6,7 Understanding the mechanical responses of chromatin is thus a challenging and crucial aspect of mechano-genomic regulation.Heterochromatin, characterized by its compact, transcriptionally silent, methylated, and mechanically rigid nature,8,9 plays a pivotal role in providing mechanical stability and shielding DNA from mechanical damage.10,11 Histone modifications can modulate chromatin condensation states, with histone methylation promoting increased heterochromatin content and nuclear stiffness.9,12–16 However, our previous study revealed that local strain distribution caused by cell substrate stretching remained unaffected by trichostatin A (TSA) treatment, a histone deacetylase inhibitor.17 Moreover, there is growing evidence that chromosomal proteins may exert distinct effects on nuclear and chromatin mechanics compared to histone methylation.18 These findings suggest that histone modification alone may not fully encompass the intricacies of intranuclear mechanics.
In recent years, Heterochromatin Protein 1α (HP1α), a chromosomal protein, has garnered increasing attention for its indispensable roles in maintaining nuclear and chromatin mechanics.18–21 HP1α accumulates within heterochromatin, where it compacts chromatin by bridging chromatin fibers, thereby contributing to the mechanical rigidity of the HP1α accumulates inside heterochromatin and compacts chromatin by bridging the chromatin fibers, contributing to the mechanical rigidity of the nucleus18,21–23 (Fig. 1B). Studies utilizing coarse-grained polymer models of chromatin have suggested that chromatin crosslinking can alter chromatin's mechanical response and properties.13,24 Additionally, HP1 has been shown to recruit proteins related to heterochromatin and facilitate liquid–liquid phase separation in vitro, a process that substantially influences nuclear stiffness.25–27 Importantly, the mechanical context in which phase separation occurs significantly affects the process.28,29 For instance, Shin et al. demonstrated the mechanical sensitivity of nuclear liquid condensation in regions characterized by lower mechanical energy, softer properties, and lower density, such as euchromatin.29 These findings contrast with the phase separation of HP1 in heterochromatin, which promotes chromatin compaction.26,27,29 Furthermore, optical trapping experiments applying external forces in stretch-relaxation cycles to HP1α-DNA condensation surprisingly revealed enhanced DNA compaction by HP1α following force application.20 However, several mechanochemical questions concerning how the mechanical properties and responses of HP1α enable its phase separation within heterochromatin and enhance the stability of HP1α-DNA condensation after force application remain unanswered. A detailed molecular analysis of HP1α mechanics can provide insights into these mechanochemical questions.
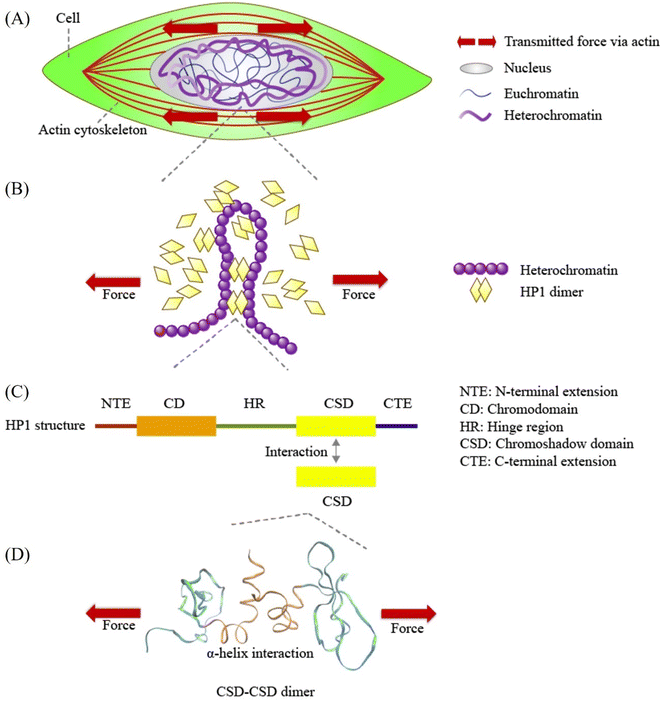 | ||
| Fig. 1 Schematic representation of force transmission at various scales, from cellular forces to Heterochromatin Protein 1α (HP1α). (A) Mechanical forces are transmitted from the cell through the cytoskeleton to the nucleus. (B) HP1α plays a pivotal role in binding and bridging chromatin fibers, contributing to phase separation and influencing chromatin structure and mechanics. (C) Human HP1α protein structure, highlighting its key domains: N-terminal extension (NTE), chromodomain (CD), hinge region (HR), chromoshadow domain (CSD), and C-terminal extension (CTE). CSD interacts with another CSD in the HP1α monomer, forming the HP1α homodimer. (D) A visual representation of the CSD–CSD dimer (PDB ID: 3I3C) in VMD software, indicating the application of schematic force. The orange and sky-blue regions represent the α-helix interface and other residue segments of the CSD–CSD dimer, respectively. | ||
At the molecular level, the formation of chromatin crosslinks and phase separation orchestrated by HP1 relies on HP1 dimerization.18,26,30–33 HP1 forms a homodimer through its chromoshadow domain (CSD)34 (Fig. 1C). The CSD monomer primarily interacts with another CSD through their α-helices to form this homodimer34 (Fig. 1D). Disruption of the CSD–CSD interactions leads to abnormal nuclear shape and inhibits DNA-driven phase separation.18,26 Despite the significance of CSD–CSD interactions in chromatin mechanics and phase separation demonstrated in previous studies, numerous questions remain unanswered. One key question is how the CSD–CSD α-helix-mediated interactions in the HP1 dimer maintain or alter their interactional strength in response to mechanical forces. Understanding the mechanical properties of CSD–CSD α-helix-mediated interactions in the HP1 dimer is crucial for unraveling the molecular and chromatin assemblies and the mechanical properties of chromatin and the nucleus.
To investigate the detailed molecular mechanisms underlying HP1α, we conducted molecular dynamics simulations to analyze the mechanical behavior and strength of CSD–CSD α-helix-mediated interactions under force application. Our simulations unveiled a remarkable sensitivity of the CSD–CSD interaction of HP1α to mechanical forces, resulting in the formation of force-induced salt bridge interactions. This newfound mechanical sensitivity provides fresh insights into HP1α′s mechanical resilience, phase separation, and mechano-genomic regulatory mechanisms.
Methods
Molecular dynamics simulation
GROMACS19.6 software package with the CHARMM36 force field was employed for the all-atom molecular dynamics (MD) simulation and corresponding analyses.35–38 The crystal structure of the CSD–CSD of the chromobox protein homolog 5 (CBX5), the human HP1 homolog alpha, is available on the protein database (PDB ID: 3I3C). Since there is a discrepancy in residue numbering between the PDB file and full-length sequences (UniProt ID: P45973), the residues were renumbered corresponding to the full-length sequence. The CSD–CSD structure was inserted into a long rectangular box (6 × 6 × 12 nm3) with periodic boundary conditions in all three directions, sufficiently large space in the direction of pulling to ensure an uninterrupted pulling process, free from interactions with the periodic images of the system. The system was solvated by using the CHARMM-modified TIP3P water model.39 The sodium and chloride counter ions were added to the system, representing the 150 mM concentration of NaCl where chromatin can be well aggregated.40,41 The energy minimization was performed for 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps with an energy tolerance of 1000 kJ mol−1 nm−1 to ensure the system has no steric clashes or inappropriate geometry. To increase the temperature and equilibrate the solvent and ions around the protein, the NVT (isothermal–isochoric) and NPT (isothermal–isobaric) ensembles with V-rescale thermostat at a constant temperature of 300 K were applied to the system for 5 ns for each with 1 fs time step. The Parrinello–Rahman barostat was employed for NPT ensembles to maintain the desired pressure at 1 atm. The damping parameters for the V-rescale thermostat and the Parrinello–Rahman barostat were set to 0.1 ps and 2 ps, respectively. The position of the heavy atoms of the protein was restrained during NVT and NPT equilibration to eliminate the additional variable of structural changes in the protein. Then, the protein relaxation was performed for 200 ns (with 2 fs time steps) as the product step without any position restrains in the equilibrated system. The particle mesh Ewald method was used for long-range electrostatic interactions with a short-range electrostatic cutoff distance of 1.0 nm. The cutoff for van der Waals interactions was 1.0 nm. The CSD–CSD dimer reached a very stable state after around 100 ns, even compared to a CSD monomer (ESI Fig. S1†). The obtained relaxed structures after 200 ns full atomistic simulations were used as the initial input for the next steered molecular dynamics (SMD) simulations.
000 steps with an energy tolerance of 1000 kJ mol−1 nm−1 to ensure the system has no steric clashes or inappropriate geometry. To increase the temperature and equilibrate the solvent and ions around the protein, the NVT (isothermal–isochoric) and NPT (isothermal–isobaric) ensembles with V-rescale thermostat at a constant temperature of 300 K were applied to the system for 5 ns for each with 1 fs time step. The Parrinello–Rahman barostat was employed for NPT ensembles to maintain the desired pressure at 1 atm. The damping parameters for the V-rescale thermostat and the Parrinello–Rahman barostat were set to 0.1 ps and 2 ps, respectively. The position of the heavy atoms of the protein was restrained during NVT and NPT equilibration to eliminate the additional variable of structural changes in the protein. Then, the protein relaxation was performed for 200 ns (with 2 fs time steps) as the product step without any position restrains in the equilibrated system. The particle mesh Ewald method was used for long-range electrostatic interactions with a short-range electrostatic cutoff distance of 1.0 nm. The cutoff for van der Waals interactions was 1.0 nm. The CSD–CSD dimer reached a very stable state after around 100 ns, even compared to a CSD monomer (ESI Fig. S1†). The obtained relaxed structures after 200 ns full atomistic simulations were used as the initial input for the next steered molecular dynamics (SMD) simulations.
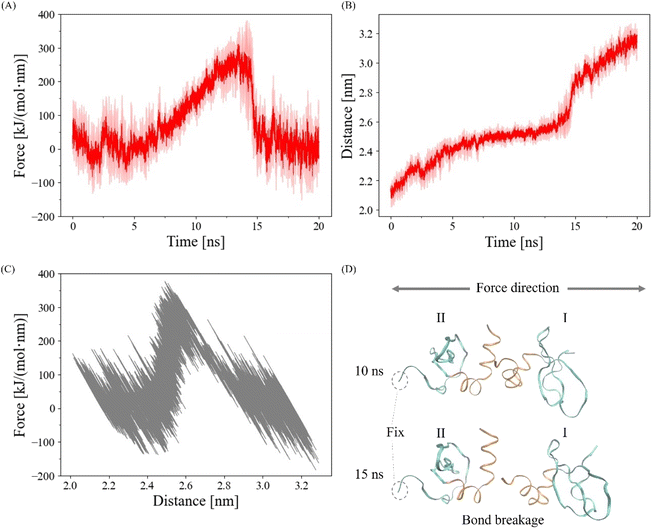
Center-of-mass pulling force was applied to the CSD–CSD dimer to obtain satisfied information of the α-helix binding interactional behaviors against force and simultaneously reduce computational costs.42 The harmonic potential was used for the pulling simulation, which enables the force to adjust based on the nature of the interactions of the CSD–CSD. Each monomer was pulled apart along the z-axis at a pull rate of 0.05 nm ns−1 while the edge residue of one monomer was fixed so that force was applied to the dimer in the same direction during the simulation (Fig. 2A). We defined the unconstrained, more natural state CSD monomer as ICSD and the position-constrained CSD monomer as IICSD. The deliberate application of a slow pulling rate serves to mitigate the potential disruption to the secondary structure of the protein, thereby facilitating the preservation of its conformational properties. The pulling simulation, the force-applied condition, was performed for 20 ns. The no-force condition, a control group, was defined as the further 20 ns relaxation with the edge residue constraint same as the force condition after the first 200 ns relaxation. The simulation was repeated three times (N = 3) for each force/no-force condition. The visualization of the simulation was performed by using VMD software.43
Trajectory file obtainment for analysis
The trajectory files saved every 10 ps were used for the analyses in force and no-force simulations. The α-helix interface of CSD–CSD was chosen for the analysis to obtain the important mechanical and chemical responses of HP1α dimer interaction. All analyzed results were plotted using Python.RMSD and RMSF
Root mean square deviation (RMSD) values of each α-helix of ICSD (unconstrained) and IICSD (constrained) throughout the simulation were computed by using GROMACS software (eqn (1)).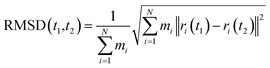 | (1) |
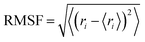 | (2) |
H-bond calculations
The number of inter-strand hydrogen bonds formed between the two α-helices of the CSD–CSD dimer and the H-bond lifetime were computed on GROMACS. H-bonds were counted when the distance between the possible acceptor (OH and NH groups) and donor (O and N atoms) pair was within 0.35 nm, and the angle between the hydrogen, oxygen, and nitrogen was below 30°. The histogram for the frequency of H-bond numbers between the α-helix interface before bond breakage was computed using Python. The histogram was also fitted by kernel density estimation (KDE) with a Gaussian kernel to visualize the distribution trend. The H-bond lifetime distribution was obtained by calculating the frequency of H-bond breakage within each lifetime interval divided by the total number of H-bonds that have broken over time. Lifetime intervals are every 10 ps, starting at 5 ps.Electrostatic energy, salt bridge pair distance, and salt bridge ratio calculations
The short-range inter-strand coulombic energy between the two α-helices of CSD–CSD with a 1.0 nm cutoff distance was calculated over simulation time on GROMACS and reported as the electrostatic interactions. Distances are measured between possible salt bridge pairs of Lys-NZ and Glu-CD (connected to both OE1 and OE2) in the α-helix interface (ESI Fig. S2†). The frequencies of the coulombic energy and salt bridge pair distance with kernel density estimation before the interaction breakage were plotted using Python. The salt bridge ratio was defined as the frequencies of salt bridge pairs within 0.4 nm divided by the total number of data over time before the interaction breakage.Force distribution analysis
The TRFDA GROMACS tool44 was used for the force distribution analysis for MD simulation. The coulombic energy was chosen for the force analysis to see the effect of salt bridge interactions. Assuming atom i is an atom in residue ri and j is in residue rj, the residue pairwise force acting on their center of mass was computed in eqn (3).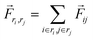 | (3) |
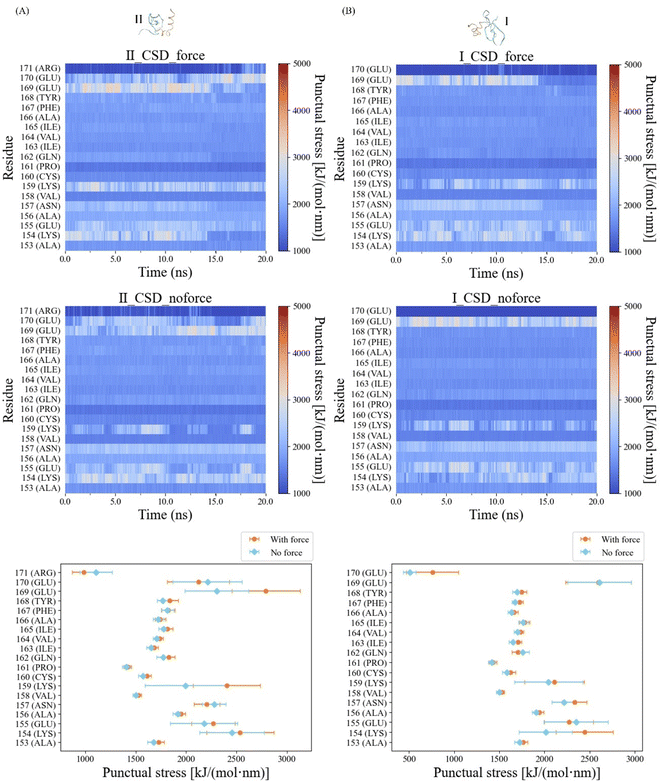
The punctual stress with units of force was defined as the sum of the absolute values of the magnitude of the vector pairwise force on a single atom or residue, enabling the identification of where pairwise forces accumulate and the detection of atomic-level hot-spots. We used the term “punctual stress” followed by the original paper of the TRFDA GROMACS tool.44 In the calculation of punctual stress, the force acting on a dimensionless point instead of an area was utilized due to the difficulty of defining geometrical properties. Punctual stress heatmaps and averages on the α-helix interface for each residue were made by using Python.
Structural analysis of residue pairs
The Lys-NZ or Glu-CD (ESI Fig. S2†) and α-carbon of a certain residue were chosen to define a vector. Angles before the interaction breakage cutoff were calculated between the two vectors of interest of the residues or between one vector and the z-axis in the pulling force direction on GROMACS. The angle frequencies with kernel density estimation before bond breakage were plotted using Python.Results
Previous experimental studies employing force application have underscored the significance of Heterochromatin Protein 1α (HP1α) in the mechanics of the nucleus and chromatin.18,20 Central to the mechanical roles of HP1 is its homodimerization through the chromoshadow domain (CSD), a process that underpins HP1's ability to establish chromatin crosslinks and drive phase separation.18,25,26,30–33 To delve deeper into the molecular intricacies governing the response of HP1α dimerization to applied force, our investigation was directed toward the CSD–CSD dimer. We utilized Root Mean Square Deviation (RMSD) and Root Mean Square Fluctuation (RMSF) analyses to gain insights into the specific residues and interactions that underpin the CSD–CSD dimer interaction. Subsequently, we investigated the detailed dynamics of the interplay between the CSD–CSD dimer interaction under conditions with and without applied force. We employed Force Distribution Analysis (FDA) to scrutinize how forces are distributed throughout the α-helix interfaces of the CSD–CSD dimer. This analysis aimed to provide a comprehensive understanding of the mechanical effects of pulling forces on individual residues within the dimer. Ultimately, our structural analysis elucidated the alterations in residue angles induced by the applied force, thus revealing the emergence of force-induced interactions within the CSD–CSD dimer.The disruption of CSD–CSD dimer interaction under pulling force
To validate the proper execution of our simulation, we applied a harmonic pulling force using GROMACS, as depicted in Fig. 2. In Fig. 2A and B, we present the averaged harmonic forces and distances between the centers of mass of each CSD monomer from three simulations along with the standard deviations indicated by the shaded areas. Notably, the CSD–CSD dimer interaction via the α-helix interface experienced a rupture within the 20 ns simulation period. The distance–force curve showed an increase in force between distances of 2.4 and 2.6 nm, followed by a sharp decrease upon reaching approximately 300 kJ mol−1 nm−1 at 2.6 nm (Fig. 2C). The maximum forces leading to interaction breakages were consistently observed between 13 and 15 ns, displaying notable fluctuations across all simulations. Consequently, to eliminate the influence of abnormal fluctuations resulting from the interaction breakage process and to effectively observe the impact of the pulling simulation on the α-helix interaction, we established a 12.5 ns cutoff for bond breakage.The role of amide groups and charged residues in interaction stability under force
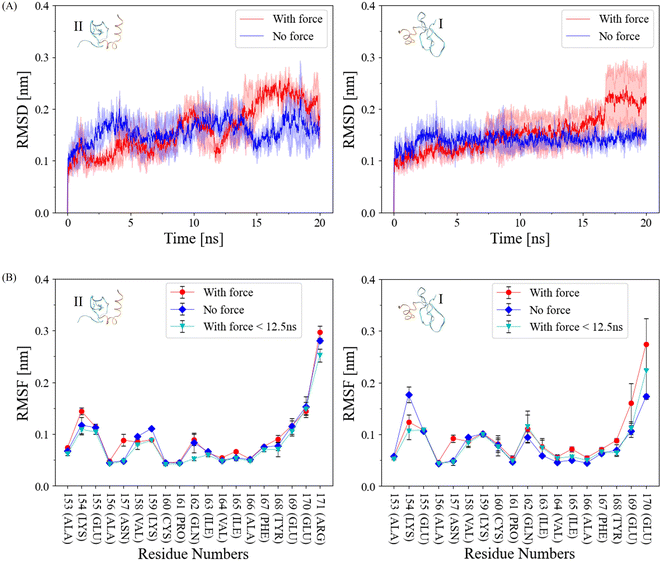
In our pursuit to comprehend the fluctuation dynamics at the α-helix interface of CSD–CSD induced by mechanical force, we calculated the Root Mean Square Deviation (RMSD) of this interface and compared the results between force-applied and no-force conditions (Fig. 3A). In the no-force condition, the RMSD remained relatively stable at around 0.15 nm throughout the simulation. In contrast, the RMSD under force exhibited a substantial increase after the interaction breakage, which occurred at the 12.5 ns cutoff. Curiously, RMSD values under force prior to this cutoff were relatively lower than those in the no-force condition. To explain this intriguing observation, we can postulate that certain regions within the proteins exhibit reduced flexibility when subjected to external forces. Consequently, these regions demonstrate reduced fluctuations during the simulation before reaching the breaking point, in contrast to systems devoid of applied forces.The Root Mean Square Fluctuation (RMSF) of each interacting α-helix within CSD–CSD was assessed based on individual residues (Fig. 3B). While most residues exhibited similar RMSF values between the force and no-force conditions, notable distinctions were observed in specific amide groups, such as residue Asn157, and certain charged residue groups, such as Lys154. Asn157 exhibited almost the same RMSF values in the no-force and the force-applied condition before the 12.5 ns bond breakage cutoff, but in the over 20 ns simulation, RMSF was higher in the force-applied condition. Interestingly, ILys154 presented a contrasting behavior, demonstrating a lower RMSF value under force-applied conditions than in the no-force condition, even before the bond breakage cutoff. The increased RMSF values under force throughout the simulation can be attributed to the significant bond breakages involving the corresponding residues, resulting in heightened fluctuations. Conversely, the lower RMSF values under force before the 12.5 ns cutoff may suggest the development or stabilization of bonds involving these specific residues.
Amide and charged residue groups play critical roles in the formation of hydrogen bonds and salt bridge interactions. To further elucidate the determinants behind the distinct fluctuation behaviors under force, we delved into the dynamics of hydrogen bonds (H-bonds) and salt bridge interactions in the subsequent sections.
Pulling force does not alter overall H-bond properties on the α-helix interface of the CSD–CSD dimer
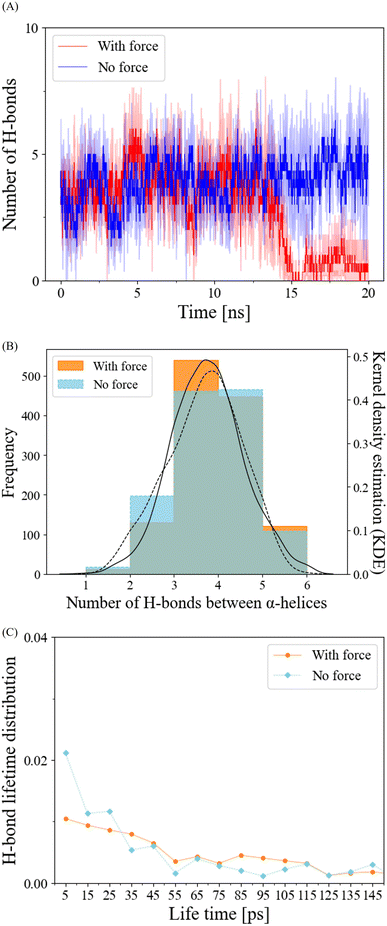
In our exploration of H-bond dynamics at the α-helix interface, we conducted an analysis of both the number and lifetime of H-bonds (Fig. 4). For the no-force condition and prior to the interaction breakage cutoff at 12.5 ns in the force condition, the number of H-bonds remained relatively constant, typically ranging from 3 to 5 (Fig. 4A and B). Following the cutoff, the force-applied condition exhibited a pronounced decrease in the number of H-bonds (Fig. 4A). When we examined the frequency distribution of the number of H-bonds using kernel density estimation (KDE) before the breakage cutoff, both the force and no-force conditions displayed similar trends, with peak frequencies observed at 3 to 5 H-bonds (Fig. 4B). The lifetime distribution of H-bonds before the breakage cutoff demonstrated that H-bond breakages occurred in a manner that was largely independent of the application of pulling force (Fig. 4C). These findings collectively suggest that the mechanical responses of H-bonds are not the primary factors contributing to the reduced RMSD and the stabilization of α-helix interface interactions in the dimerization of HP1.Discovery of a newly formed salt bridge under mechanical force enhancing the α-helix interface interaction in the CSD–CSD dimer
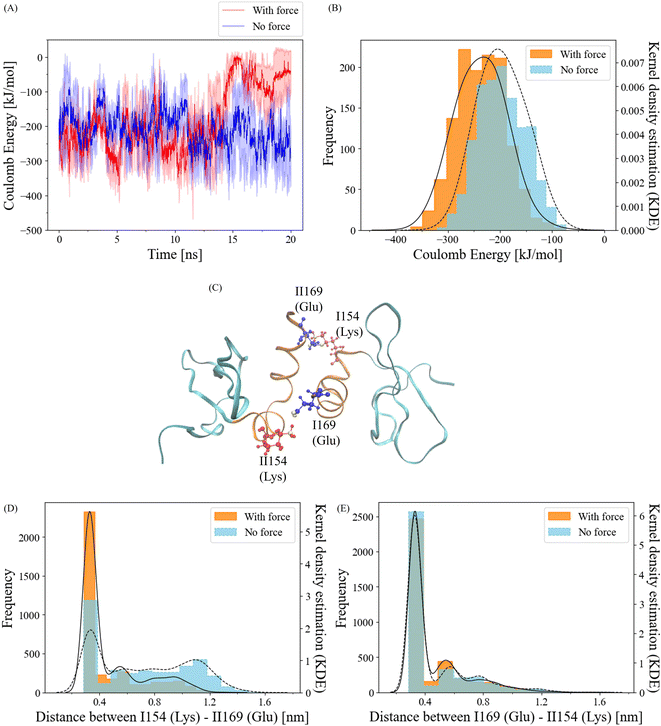
To gain insights into the behavior of salt bridge interactions between the α-helix interfaces under force, we initiated our investigation by calculating short-range coulombic energy changes within these interfaces over the course of the simulation (Fig. 5A). As expected, a significant decline in coulombic energy was observed after the 12.5 ns breakage cutoff. Interestingly, prior to this cutoff, attractive coulombic energy between the α-helix interfaces was more prominent when force was applied compared to the no-force condition. For a more quantitative analysis, we computed the distribution of coulombic energy before the breakage cutoff (Fig. 5B). In the absence of force, the coulombic energy displayed the highest frequency at approximately −200 kJ mol−1. In contrast, the peak of the Kernel Density Estimation (KDE) of the coulombic energy frequency with force was situated at about −240 kJ mol−1. The average coulombic energy values were −196 kJ mol−1 and −236 kJ mol−1 in the no-force and force conditions, respectively. These results clearly indicate that the application of a pulling force strengthens coulombic energy interactions at the α-helix interfaces of the CSD–CSD dimer.Salt bridge interactions are facilitated by coulombic attraction with water molecules.45 To validate the sequence data of the α-helix and visualize the residues, we identified potential residue pairs that could form salt bridge interactions (Fig. 5C). The residue ILys154 can interact with residue IIGlu169, and reciprocally, IGlu169 and IILys154 are capable of making salt bridges as well.
To quantitatively assess the dynamics of these salt bridge interactions, we calculated the distances between each residue pair. The positively charged atom involved is Lys NZ1, while the negatively charged atoms are Glu OE1 and OE2, contributing to the salt bridge. Since both Glu OE1 and OE2 atoms can participate in interactions with Lys NZ1, we selected Glu CD, which connects to both Glu OE1 and OE2, for distance calculations (ESI Fig. S2†).
Frequency distributions of the distance between Glu CD and Lys NZ1 for ILys154–IIGlu169 and IGlu169–IILys154 were determined (Fig. 5D and E). Prior to the 12.5 ns cutoff, the IGlu169–IILys154 residue pair exhibited similar frequencies within the salt bridge distance cutoff of 0.4 nm46 under both force and no-force conditions (Fig. 5E). The salt bridge ratios with and without force were approximately 66% and 69%. In contrast, the ILys154–IIGlu169 residue pair exhibited a notably higher frequency within 0.4 nm with force compared to the no-force condition (Fig. 5D). While the salt bridge ratio without force was only 32%, it increased to 66% when force was applied. These findings strongly suggest that the ILys154 and IIGlu169 residue pair is responsible for the salt bridge interaction, which responds to the application of pulling force.
Salt bridge residues exhibit elevated stress distribution
In our quest to elucidate the impact of pulling force on the mechanical characteristics of the α-helix interfaces within CSD–CSD, we conducted a comprehensive Force Distribution Analysis (FDA) across these interfaces. The color map representing the force-applied condition displayed notable punctual stress concentrations within the ILys154–IIGlu169 and IGlu169–IILys154 residue pairs prior to bond breakage. These punctual stresses on ILys154, IIGlu169, IGlu169, and IILys154 dramatically decreased due to the bond breakage between the α-helix (Fig. 6). In contrast, the color map for the no-force condition exhibited consistent high stress levels within the IGlu169–IILys154 residue pair throughout the entire simulation.To quantitatively evaluate the differences in punctual stress between the force and no-force conditions, we calculated the average punctual stress for each residue, accompanied by standard deviations, focusing on data prior to the bond breakage cutoff at 12.5 ns (Fig. 6). Notably, both the IGlu169 and IILys154 residues exhibited high punctual stresses in both force and no-force conditions. However, the stresses on ILys154 and IIGlu169 residues under force were approximately 500 kJ mol−1 nm−1 higher than those observed in the absence of force. These findings provide compelling support for the development of a salt bridge interaction between ILys154 and IIGlu169 under force conditions.
Furthermore, residue IILys159 displayed stress levels approximately 500 kJ mol−1 nm−1 higher when compared to the no-force condition (Fig. 6). Notably, IILys159 engaged in an internal salt bridge interaction with IIGlu118, a residue located near the opposite edge of the same CSD monomer (ESI Fig. S3A†). The frequencies of salt bridge interactions within a 0.4 nm range in the force condition were significantly higher compared to those in the no-force condition. The salt bridge ratios, considering the presence or absence of force, were 67% and 9%, respectively (ESI Fig. S3B†).
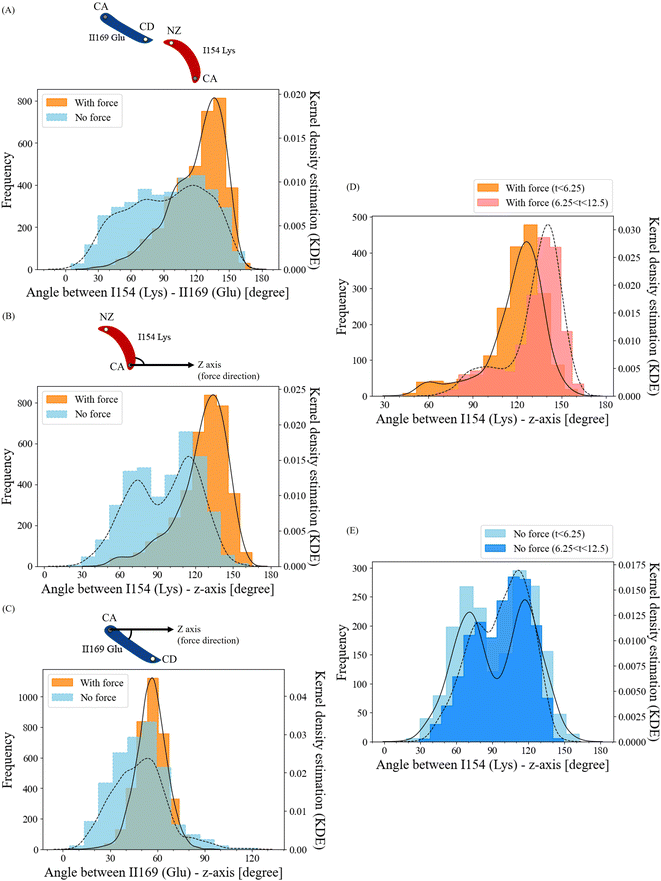
Force-induced angle change in residue ILys154 is the key to force-induced salt bridge interaction
To unravel how the application of force enables the ILys154 and IIGlu169 residue pair to form a salt bridge interaction, we conducted an in-depth analysis of the structural alterations in this residue pair. We compared the angle frequencies between ILys154 and IIGlu169 with and without force (Fig. 7A). In the absence of force, the angles between these residues appeared to be randomly distributed. However, when force was applied, the angles became concentrated within the range of 120° to 150°.To separately investigate the angle change behaviors of residues ILys154 and IIGlu169, we established the z-axis of the pulling direction as a reference and calculated the angles of ILys154 with respect to the z-axis and IIGlu169 with respect to the z-axis (Fig. 7B and C). The angles between residue IIGlu169 and the z-axis displayed relatively similar trends in both force and no-force conditions (Fig. 7C). However, the angle frequencies of residue ILys154 without force appeared to be relatively random, with two peaks around 70° and 110°. In contrast, when force was applied, the angles were highly concentrated in the range of 120° to 140° (Fig. 7B). Furthermore, this observation indicated that this particular residue exhibited greater flexibility over the course of the simulation, which aligns with the results obtained from the RMSF analysis. Collectively, these findings suggest that the angle change in residue ILys154 is the key factor in facilitating the formation of the force-induced salt bridge.
To understand the dissociation process of the developed salt bridge interaction, we divided the angle frequencies between residue ILys154 and the z-axis, considering the presence or absence of force. This division was carried out over two time intervals (0–6.25 ns vs. 6.25–12.5 ns) (Fig. 7D and E). The angles with high frequencies in the no-force condition exhibited similar patterns across both time intervals, with average angles of 93.8° for 0–6.25 ns and 96.8° for 6.25–12.5 ns (Fig. 7E). In contrast, for the force-applied condition, the peak of the angle distribution notably shifted towards higher angles over time (Fig. 7D), with the average angles being 118.7° during the 0–6.25 ns interval and increasing to 131.4° in the 6.25–12.5 ns interval. This shift towards higher angles over time indicates the disruption of the salt bridge interaction corresponded to an increase in the angle of residue ILys154.
Discussion
The role of Heterochromatin Protein 1α (HP1α) in nuclear and chromatin mechanics has been extensively studied in prior experiments involving force application.18,20 HP1 has been implicated in the formation of chromatin crosslinks and phase separation, mechanisms that are thought to provide structural rigidity to chromatin and the cell nucleus.18,25 A fundamental aspect of HP1's mechanical functionality is its homodimerization, primarily facilitated through the chromoshadow domain (CSD), which is crucial for establishing crosslinks between HP1 and chromatin, as well as for promoting phase separation.18,25,26,30–33 To gain a deeper understanding of the molecular intricacies of how HP1α dimerization responds to applied mechanical forces, this study focused on the CSD–CSD dimer of HP1α. Using full atomic molecular dynamics simulations, we applied a pulling force to this dimeric structure. While the overall state of hydrogen bonding across the α-helix interface of the CSD–CSD dimer remained relatively stable (Fig. 4), a novel salt bridge interaction emerged as a response to the applied force, leading to the reinforcement of the α-helix interface interactions (Fig. 5 and 6). This force-induced salt bridge formation was attributed to changes in the orientation of residue ILys154 on the α-helix interface (see Fig. 7). These findings emphasize the sensitivity of HP1α homodimerization to mechanical forces and offer insights into potential mechanisms underlying the strengthening of HP1α-DNA interactions, as previously observed in experimental studies.20The RMSD results reveal that the α-helix interface of CSD–CSD remains notably more stable under the influence of an applied force compared to the condition without force, particularly before the bond breakage occurs (Fig. 3A). This heightened stability can be attributed to the development of salt bridge interactions, specifically the ILys154–IIGlu169 and IILys159–IIGlu118 pairs, which fortify the α-helix interface when force is applied. In particular, the RMSF values for ILys154 in the force-applied scenario are significantly lower before the bond breakage, in comparison to the scenario without force (Fig. 3B). Furthermore, the residues IAsn157 and IIGln162 also exhibit reduced RMSF values under force when contrasted with the no-force condition. Although the overall properties of hydrogen bonds remain relatively unaffected by the applied force, it is noteworthy that the lifetime of the IIGln162–IAsn157 H-bond pair in the force scenario shows a prolonged trend as compared to the condition without force (ESI Fig. S4†). This trend may be attributed to the positioning of the IIGln162–IAsn157 residue pair in the force scenario, where it resides between the Lys154–Glu169 salt bridge interactions, thus contributing to the local stabilization of hydrogen bonds and bolstering the structural integrity of the α-helix interface within CSD–CSD in the presence of force.
Various types of interactions, including hydrogen bonds (H-bonds), van der Waals (vdW) forces, and salt bridge interactions, contribute to the intricate network of molecular interactions within proteins. Notably, salt bridge interactions are widely recognized as one of the most robust forms of residue–residue interactions.47 It is worth noting that the strength of salt bridge interactions can be influenced by a range of environmental factors, such as solvation, ion concentrations, and the spatial arrangement of charged residues on the protein's surface.47–49 Moreover, it has been suggested that certain MD simulation force fields, including CHARMM, may overestimate the strength of salt bridges compared to experimental data.50,51 The choice of force field can quantitatively influence the perceived strengths of these interactions.50 In our study, we scrutinized the coulombic energies of the α-helix interface, revealing an average value of approximately −236 kJ mol−1 when force was applied, in contrast to −196 kJ mol−1 in the absence of force. Quantum chemistry analyses have previously estimated that salt bridge interactions between a Glu and a Lys residue pair in an aqueous environment typically have an interaction energy of around −40 kJ mol−1.47 This analysis provides compelling evidence that the observed difference in energy between the force-applied and no-force conditions primarily arises from the development of Glu–Lys salt bridge interactions. These findings align with previous observations of force-induced Glu–Lys salt bridges in actin catch–slip bonds, shedding light on a potential mechanosensing mechanism governing force-dependent actin dynamics.52 Similarly, the identification of a force-induced Glu–Lys salt bridge in HP1α, as demonstrated in this study, suggests a plausible mechanosensing mechanism for governing force-dependent chromatin dynamics. These insights into the mechanical behaviors of salt bridges offer valuable clues as to how external forces may influence the structural and functional aspects of proteins, with potential implications for chromatin organization in response to mechanical cues.
The formation of the force-induced Glu–Lys salt bridge hinged on the dynamic shifts in the orientation of residue ILys154 (Fig. 7). Under the influence of the pulling force, residue ILys154 underwent a tilting motion towards its neighboring residue IIGlu169. This alteration in position brought the positively charged atom NZ1 in residue ILys154 within close proximity to the negatively charged atoms OE1 and OE2 in residue IIGlu169. As the force was consistently applied, the angle of residue ILys154 continued to increase in a direction opposing the applied force, ultimately leading to the disruption of the α-helix interface within the CSD–CSD dimer. It is worth noting that alterations in the angles and positions of lysine residues can have a significant impact on chemical interactions, a subject that has been explored in previous research.49,53 A more comprehensive understanding of the structural and chemical changes in lysine under external mechanical forces can offer a more nuanced interpretation of the development of lysine salt bridges from a chemical perspective. In addition to the detailed analysis of residue ILys154 and IIGlu169, we conducted an extensive structural assessment (ESI Fig. S5†). This evaluation encompassed the measurement of angles between the two α-helices, as well as the lengths of the inter-residue regions ILys154–IGlu169 and IILys154–IIGlu169 (ESI Fig. S5†). The outcomes of this structural analysis revealed that the trends in angles and lengths were similar between the force-applied and no-force conditions, underscoring the critical role of residue ILys154 in the mechanical response of the α-helix interface within the CSD–CSD dimer. Furthermore, we extended our analysis to encompass the angles of IGlu169–IILys154, the angles with respect to the z-axes of IGlu169 and IILys154, which were scrutinized in the same manner as residue ILys154 and IIGlu169 (ESI Fig. S6A†). The resulting data indicated that, while there were subtle variations in the height and location of the peaks in the angle distributions between the force-applied and no-force conditions, these distinctions were not substantial (ESI Fig. S6B and C†). Collectively, these results highlight the pivotal contribution of residue ILys154 to the mechanical response of the α-helix interface within the CSD–CSD dimer, shedding light on the underlying molecular mechanisms at play.
In our FDA analysis, punctual stress derived from coulombic interactions was obtained throughout the α-helix interface of the CSD–CSD to assess the mechanistic impacts of the ILys154–IIGlu169 salt bridge. We observed that while the punctual stress resulting from Lennard–Jones interactions was lower compared to that based on coulombic interactions, it exhibited similar trends (ESI Fig. S7†). Our FDA analysis of force distribution patterns revealed elevated stress levels not only in the residue ILys154–IIGlu169 under the force-applied condition but also in residue IILys159 when compared to their respective counterparts in the absence of force, as illustrated in Fig. 6. The heightened stress experienced by residue IILys159 was attributed to the development of a salt bridge with residue IIGlu118 within the same CSD monomer, as demonstrated in ESI Fig. S3.† This internal salt bridge may indeed serve as a significant contributing factor to the overall mechanical resilience of the CSD–CSD dimer when subjected to external pulling forces. It is important to note that this study primarily focused on the α-helix interface within the CSD–CSD dimer and, therefore, employed a center-of-mass pulling force approach. To gain deeper insights and to assess the realistic occurrence and mechanistic roles of the internal salt bridge, an edge–edge pulling force simulation is deemed necessary. Such an investigation would offer a comprehensive perspective on the entirety of structural changes within the CSD–CSD dimer and illuminate the functional significance of this internal salt bridge under varying mechanical conditions.
To provide a comprehensive analysis, positional constraints were employed in a manner similar to the conditions applied under force for a 20 ns relaxation simulation within the no-force scenario. The examination of angles involving ILys154–IIGlu169, ILys154-z-axis, and the assessment of punctual stress in these residues occasionally indicated that the salt bridge interaction could potentially occur even without the presence of an external force (see Fig. 5–7). This observation raises the possibility that these findings could be influenced by constraints imposed during the simulation. In molecular dynamics simulations, atoms inherently exhibit stochastic motion in response to the surrounding solvent. In the context of our constrained conditions, one CSD monomer was allowed to move freely, while the movement of the other CSD monomer was restricted. This inherent stochastic nature may occasionally result in the free CSD monomer drifting significantly apart from the constrained CSD monomer, thereby generating conditions akin to pseudo-force effects. To explore this further, we conducted a no-force condition simulation without any position constraints and measured the distance between ILys154 and IIGlu169 (ESI Fig. S8†). The frequency distribution of distances between ILys154 and IIGlu169 within the 0.4 nm range was notably lower compared to scenarios involving force application or constraints. This no-constraint data lends support to the notion that the natural occurrence of the ILys154–IIGlu169 salt bridge interaction is unlikely and underscores the sensitivity of this interaction to external forces.
Chromatin fibers within the nucleus exhibit dynamic and multidirectional movements, subjecting HP1 to forces originating from various orientations. However, when we explored the effects of alternative directional forces, we observed that the CSD–CSD dimer underwent rotation and separation, as presented in this study, or experienced significantly longer simulation times, although this specific data is not shown. This suggests that bond breakage induced by forces acting along different directions may be less likely to occur.
Additionally, it is worth noting that the time rate of the applied force can vary depending on the method of force application to the cellular system. The effects of different pulling rates of the applied force on the mechanosensitive salt bridge formation were investigated (ESI Fig. S9†). In addition to 0.05 nm ns−1 used in our simulation, 0.03 nm ns−1, 0.1 nm ns−1, and 0.5 nm ns−1 pulling rates were chosen. The slower pulling rate of 0.03 nm ns−1 showed a mechano-sensitivity comparable to that observed at the 0.05 nm ns−1. The salt bridge ratio of the 0.03 nm ns−1 simulation was 65%, almost the same as 66% of the salt bridge ratio in the 0.05 nm ns−1 simulation. Conversely, the salt bridge ratio decreased by 46% in the faster 0.1 nm ns−1 pulling rate simulation. The fastest rate of 0.5 nm ns−1 showed further reduction in the mechano-sensitivity for the ILys154–IIGlu169 salt bridge formation (ESI Fig. S9C†). The salt bridge ratio of the 0.5 nm ns−1 simulation was only 30%, closely mirroring the 32% observed in the no-force condition. However, such faster pulling rates would less likely occur in natural cellular system. For instance, in a prior experimental study, we endeavored to replicate conditions akin to vasoconstriction.17 Considering our results of around 0.02 intranuclear strain with 0.5 Hz and assuming 15 μm of the nucleus size,17,54 this calculation translates to a velocity of approximately 0.015 × 10−5 nm ns−1. Notably, this velocity is considerably slower than the rate employed in our simulation, which stands at 0.05 nm ns−1. Nonetheless, conducting simulations with the experimentally observed velocity remains a challenging endeavor due to computational constraints and limitations in calculation speed.
The dimerization of HP1α, which links chromatin fibers together, is a fundamental process crucial for bolstering the mechanical integrity of both chromatin and the cell nucleus.18 This mechanical fortification is further facilitated through the enhancement of the α-helix interface of the CSD–CSD dimer, achieved by the formation of salt bridges under force conditions. This salt bridge development represents the likely mechanism by which the HP1α dimer is reinforced, subsequently enhancing the resilience of chromatin against mechanical forces.
The development of force-induced salt bridges emerges as a determining factor in achieving stable HP1α-DNA condensations. This observation aligns with the findings of a prior experimental study that applied force to HP1α.20 Furthermore, in the context of HP1 and chromatin phase separation, a recent coarse-grained computational investigation examined the impact of HP1 dimer–dimer interactions on phase separation.55 By modulating the energy associated with these interactions, particularly in the hinge and NTE regions, with values ranging from 2kBT to 4kBT, 6kBT, and 10kBT (equivalent to approximately 5, 10, 15, and 25 kJ mol−1 at a standard temperature of 300 K), the coarse-grained model delineated four distinct phases: a mixed state with no phase separation, liquid-like droplets, droplets with incorporated polymer, and polymer-coated regimes.55 In this context, the energy derived from Lys–Glu salt bridge interactions, as indicated by quantum analysis, and the electrostatic energy difference between force and no-force conditions, which amounted to approximately 40 kJ mol−1,47 implies that the force-induced salt bridge formation may yield ample energy to influence the state of phase separation.
The enhanced interaction within CSD–CSD under force conditions offers valuable insights, shedding light on the counterexample of HP1 phase separation preference. Typically, phase separation occurs in regions characterized by lower mechanical energy, softness, and lower density, such as euchromatin.29 However, HP1-induced phase separation predominantly takes place in heterochromatin regions. The mechanical sensitivity exhibited by the CSD–CSD interaction, driven by force-induced salt bridge development, may enable HP1 to initiate phase separation in regions with higher mechanical energy, stiffness, and greater density, such as heterochromatin. The mechanical response of the CSD–CSD dimer, as elucidated in this study, implies that HP1α-chromatin phase separation is mechanosensitive, making the salt bridge development a likely mechanical switch governing chromatin condensation state. This underscores the significance of conducting molecular-scale analyses of HP1α mechanics.
Our simulation study has certain limitations, including the influence of positional constraints, the pulling rate, as discussed earlier, and an incomplete understanding of the significance of the force-induced salt bridge behavior in the overall HP1 structure. The mechanical force exerted by chromatin is expected to be transmitted from the chromodomain (CD) to the chromoshadow domain (CSD) through the disordered hinge region. The flexibility of the hinge region may, to some extent, dampen the transmission of force from CD to CSD. The application of homology modeling could enable the replication of CD-hinge-CSD protein regions and facilitate more precise simulations of force transmission from chromatin to CSD. Additionally, our study did not consider other protein interactions. Notably, proteins like Shugoshin (Sgo1) and the lamin B receptor (LBR) interact with the CSD dimer, exerting an influence on phase separation states.26 To gain deeper insights, simulating more complex and higher-order HP1 structures, related proteins, and DNA systems is necessary, providing a comprehensive understanding of HP1-driven chromatin mechanics.
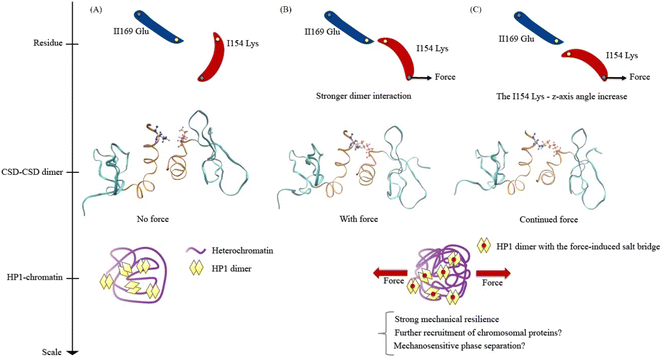
Lastly, we propose models for understanding the mechanical response of HP1α, encompassing the residue scale, the CSD–CSD dimer scale, and the HP1-chromatin interaction scale (Fig. 8). In a force-absent condition, the ILys154 angle is less likely to facilitate the formation of the ILys154–IIGlu169 salt bridge interaction (Fig. 8A). Consequently, the mechanical resilience of the HP1α is relatively low without force. However, in the presence of applied force, the pulling force induces an alteration in the ILys154 angle, leading to the development of the ILys154–IIGlu169 salt bridge interaction (Fig. 8B). As a result, the CSD–CSD dimer exhibits a stronger interaction and enhanced mechanical resilience against force, potentially allowing for the recruitment of more heterochromatin proteins and the promotion of phase separation. It is conceivable that the heterochromatin region, characterized by condensed chromatin, serves as a site for transmitting force to HP1α, which may prefer a mechanically robust environment found in heterochromatin. During the dissociation process under force, the interaction breaks as the ILys154 angle increases against the applied force direction (Fig. 8C). Continuous external pulling force disrupts the ILys154–IIGlu169 salt bridge interaction, ultimately leading to a high level of force-induced mechanical resilience.
Looking ahead, our future investigations will delve into the intricate dynamics of HP1-chromatin interactions, exploring their pivotal role in shaping HP1 and chromatin mechanics, as well as the state of phase separation.22,55 Moreover, it is worth noting that HP1 phase separation itself is suggested to hold key mechanical functions, which extend beyond its chromatin interaction or dimerization aspects.25 To comprehensively unravel the complex web of HP1 and chromatin mechanics, including the molecular-level mechanical behavior of the CSD–CSD dimer, we plan to conduct simulations involving the CD region interacting with H3K9me, the entire HP1 structure, and a comprehensive HP1-chromatin coarse-grained model. These efforts will provide a deeper understanding of how HP1 and chromatin's mechanical interplay is regulated and how it impacts intranuclear structure and mechanics.
Conclusions
In our investigation, we harnessed full atomistic molecular dynamics simulations to unravel the intricate molecular mechanics governing Heterochromatin Protein 1α (HP1α) when subjected to mechanical forces. Our primary focus was on the chromoshadow domain (CSD) within the HP1α dimer, given its pivotal role in facilitating chromatin crosslinks and phase separation. Employing a constant velocity force, we subjected the CSD–CSD dimer to a comparative analysis between force-applied and force-free conditions. Notably, we observed a heightened attractive coulombic energy between the α-helix interfaces under force, particularly before bond breakage, in comparison to the no-force scenario (Fig. 5A and B). This finding was further supported by the increased frequencies of distances between ILys154 and IIGlu169, potential salt bridge pairs, when force was applied (Fig. 5D). Additionally, force distribution analysis across the α-helix interfaces indicated greater stress on ILys154 and IIGlu169 in the presence of force (Fig. 6). Through an in-depth structural analysis of these α-helix interfaces, we unraveled the mechanism by which applied force induced a salt bridge formation between ILys154 and IIGlu169, driven by changes in the angle of ILys154 (Fig. 7A–C).Our molecular mechanistic analysis of the HP1α CSD–CSD dimer unveiled a remarkable response, with ILys154 altering its angle in reaction to mechanical force and fostering a salt bridge interaction with IIGlu169. This novel insight into the strengthening of HP1α CSD–CSD dimerization promises to enhance our understanding of HP1α phase separation within heterochromatin regions. Furthermore, it sheds light on the heightened resilience and condensation of HP1α-DNA in the presence of mechanical forces. In essence, this study underscores the potentially critical role of enhanced HP1α CSD–CSD dimer interactions when force is applied, offering valuable insights into the molecular foundation of HP1α dimerization, mechanosensitive phase separation, chromatin condensation and interactions, and ultimately, mechano-genomic regulation.
Author contributions
S. T., M. K., N. D., and M. R. K. M. designed research. S. T. performed all simulations and analyses and wrote the manuscript. M. K., N. D., and M. R. K. M. reviewed and modified the manuscript.Conflicts of interest
Shingo Tsukamoto, Mohammad Khavani, Nya Domkam, and Mohammad R. K. Mofrad declare that they have no conflicts of interest.Acknowledgements
Financial support by the National Science Foundation under Biomechanics and Mechanobiology Grant 1728407 is gratefully acknowledged. We thank the Japan Student Services Organization (JASSO) Student Exchange Support Program (Graduate Scholarship for Degree Seeking Students) and the SAITAMA GO GLOBAL STUDENT scholarship for supporting Shingo Tsukamoto's doctoral studies. This research used resources of the Extreme Science and Engineering Discovery Environment (XSEDE) super-computing facilities, supported by the National Science Foundation (NSF) Grant No. ACI-1053575.References
- K. N. Dahl, A. J. S. Ribeiro and J. Lammerding, Circ. Res., 2008, 102, 1307–1318 CrossRef CAS PubMed.
- Z. Jahed and M. R. Mofrad, Curr. Opin. Cell Biol., 2019, 58, 114–119 CrossRef CAS PubMed.
- S. Tsukamoto, K.-H. Chiam, T. Asakawa, K. Sawasaki, N. Takesue and N. Sakamoto, Biochem. Biophys. Res. Commun., 2022, 597, 37–43 CrossRef CAS PubMed.
- N. Wang, J. D. Tytell and D. E. Ingber, Nat. Rev. Mol. Cell Biol., 2009, 10, 75–82 CrossRef CAS PubMed.
- K. Wagh, M. Ishikawa, D. A. Garcia, D. A. Stavreva, A. Upadhyaya and G. L. Hager, Trends Cell Biol., 2021, 31, 457–472 CrossRef CAS PubMed.
- K. Maeshima, S. Iida and S. Tamura, Cold Spring Harbor Perspect. Biol., 2021, 13, a040675 CrossRef CAS PubMed.
- R. Raman, Reson, 2022, 27, 983–1002 CrossRef CAS.
- C. Uhler and G. V. Shivashankar, Trends Cancer, 2018, 4, 320–331 CrossRef CAS PubMed.
- A. D. Stephens, Mutat. Res., 2020, 821, 111712 CrossRef CAS PubMed.
- M. M. Nava, Y. A. Miroshnikova, L. C. Biggs, D. B. Whitefield, F. Metge, J. Boucas, H. Vihinen, E. Jokitalo, X. Li, J. M. García Arcos, B. Hoffmann, R. Merkel, C. M. Niessen, K. N. Dahl and S. A. Wickström, Cell, 2020, 181, 800–817 CrossRef CAS PubMed.
- A. D. Stephens, E. J. Banigan and J. F. Marko, Curr. Opin. Cell Biol., 2019, 58, 76–84 CrossRef CAS PubMed.
- J. C. Harr, A. Gonzalez-Sandoval and S. M. Gasser, EMBO Rep., 2016, 17, 139–155 CrossRef CAS PubMed.
- A. D. Stephens, E. J. Banigan, S. A. Adam, R. D. Goldman and J. F. Marko, Mol. Biol. Cell, 2017, 28, 1984–1996 CrossRef CAS PubMed.
- A. D. Stephens, P. Z. Liu, E. J. Banigan, L. M. Almassalha, V. Backman, S. A. Adam, R. D. Goldman and J. F. Marko, Mol. Biol. Cell, 2018, 29, 220–233 CrossRef CAS PubMed.
- L. Liu, Q. Luo, J. Sun, Y. Ju, Y. Morita and G. Song, Int. J. Biochem. Cell Biol., 2018, 96, 29–39 CrossRef CAS PubMed.
- A. D. Stephens, P. Z. Liu, V. Kandula, H. Chen, L. M. Almassalha, C. Herman, V. Backman, T. O'Halloran, S. A. Adam, R. D. Goldman, E. J. Banigan and J. F. Marko, Mol. Biol. Cell, 2019, 30, 2320–2330 CrossRef CAS PubMed.
- S. Tsukamoto, T. Asakawa, S. Kimura, N. Takesue, M. R. K. Mofrad and N. Sakamoto, J. Biomech., 2021, 119, 110292 CrossRef PubMed.
- A. R. Strom, R. J. Biggs, E. J. Banigan, X. Wang, K. Chiu, C. Herman, J. Collado, F. Yue, J. C. Ritland Politz, L. J. Tait, D. Scalzo, A. Telling, M. Groudine, C. P. Brangwynne, J. F. Marko and A. D. Stephens, eLife, 2021, 10, e63972 CrossRef CAS PubMed.
- T. Cheutin, A. J. McNairn, T. Jenuwein, D. M. Gilbert, P. B. Singh and T. Misteli, Science, 2003, 299, 721–725 CrossRef CAS PubMed.
- M. M. Keenen, D. Brown, L. D. Brennan, R. Renger, H. Khoo, C. R. Carlson, B. Huang, S. W. Grill, G. J. Narlikar and S. Redding, eLife, 2021, 10, e64563 CrossRef CAS PubMed.
- D. S. W. Lee, A. R. Strom and C. P. Brangwynne, APL Bioeng., 2022, 6, 021503 CrossRef CAS PubMed.
- D. Canzio, E. Y. Chang, S. Shankar, K. M. Kuchenbecker, M. D. Simon, H. D. Madhani, G. J. Narlikar and B. Al-Sady, Mol. Cell, 2011, 41, 67–81 CrossRef CAS PubMed.
- S. Machida, Y. Takizawa, M. Ishimaru, Y. Sugita, S. Sekine, J. Nakayama, M. Wolf and H. Kurumizaka, Mol. Cell, 2018, 69, 385–397 CrossRef CAS PubMed.
- E. J. Banigan, A. D. Stephens and J. F. Marko, Biophys. J., 2017, 113, 1654–1663 CrossRef CAS PubMed.
- J. F. Williams, I. V. Surovtsev, S. M. Schreiner, H. Nguyen, Y. Hu, S. G. J. Mochrie and M. C. King, bioRxiv, 2023, preprint, DOI:10.1101/2020.07.02.184127.
- A. G. Larson, D. Elnatan, M. M. Keenen, M. J. Trnka, J. B. Johnston, A. L. Burlingame, D. A. Agard, S. Redding and G. J. Narlikar, Nature, 2017, 547, 236–240 CrossRef CAS PubMed.
- A. R. Strom, A. V. Emelyanov, M. Mir, D. V. Fyodorov, X. Darzacq and G. H. Karpen, Nature, 2017, 547, 241–245 CrossRef CAS PubMed.
- R. W. Style, T. Sai, N. Fanelli, M. Ijavi, K. Smith-Mannschott, Q. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. X, 2018, 8, 011028 CAS.
- Y. Shin, Y.-C. Chang, D. S. W. Lee, J. Berry, D. W. Sanders, P. Ronceray, N. S. Wingreen, M. Haataja and C. P. Brangwynne, Cell, 2018, 175, 1481–1491 CrossRef CAS PubMed.
- S. V. Brasher, B. O. Smith, R. H. Fogh, D. Nietlispach, A. Thiru, P. R. Nielsen, R. W. Broadhurst, L. J. Ball, N. V. Murzina and E. D. Laue, EMBO J., 2000, 19, 1587–1597 CrossRef CAS PubMed.
- M. S. Lechner, D. C. Schultz, D. Negorev, G. G. Maul and F. J. Rauscher, Biochem. Biophys. Res. Commun., 2005, 331, 929–937 CrossRef CAS PubMed.
- M. S. Lechner, G. E. Begg, D. W. Speicher and F. J. Rauscher, Mol. Cell. Biol., 2000, 20, 6449–6465 CrossRef CAS PubMed.
- A. Thiru, D. Nietlispach, H. R. Mott, M. Okuwaki, D. Lyon, P. R. Nielsen, M. Hirshberg, A. Verreault, N. V. Murzina and E. D. Laue, EMBO J., 2004, 23, 489–499 CrossRef CAS PubMed.
- A. Kumar and H. Kono, Biophys. Rev., 2020, 12, 387–400 CrossRef PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- Computational Biochemistry and Biophysics, ed. O. M. Becker, M. Dekker, New York, 2001 Search PubMed.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O'Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell Jr. and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed.
- A. D. MacKerell Jr., D. Bashford, M. Bellott, R. L. Dunbrack Jr., J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed.
- H. C. Huang and R. D. Cole, J. Biol. Chem., 1984, 259, 14237–14242 CrossRef CAS PubMed.
- A. Shakya, S. Park, N. Rana and J. T. King, Biophys. J., 2020, 118, 753–764 CrossRef CAS PubMed.
- J. A. Lemkul and D. R. Bevan, J. Phys. Chem. B, 2010, 114, 1652–1660 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- B. I. Costescu and F. Gräter, BMC Biophys., 2013, 6, 5 CrossRef CAS PubMed.
- S. Pylaeva, M. Brehm and D. Sebastiani, Sci. Rep., 2018, 8, 13626 CrossRef PubMed.
- S. Kumar and R. Nussinov, ChemBioChem, 2002, 3, 604–617 CrossRef CAS PubMed.
- N.-Z. Xie, Q.-S. Du, J.-X. Li and R.-B. Huang, PLoS One, 2015, 10, e0137113 CrossRef PubMed.
- B. N. Dominy, H. Minoux and C. L. Brooks III, Proteins: Struct., Funct., Bioinf., 2004, 57, 128–141 CrossRef CAS PubMed.
- J. E. Donald, D. W. Kulp and W. F. DeGrado, Proteins: Struct., Funct., Bioinf., 2011, 79, 898–915 CrossRef CAS PubMed.
- K. T. Debiec, A. M. Gronenborn and L. T. Chong, J. Phys. Chem. B, 2014, 118, 6561–6569 CrossRef CAS PubMed.
- S. Kashefolgheta and A. V. Verde, Phys. Chem. Chem. Phys., 2017, 19, 20593–20607 RSC.
- C. Lee, J. Lou, K. Wen, M. McKane, S. G. Eskin, S. Ono, S. Chien, P. A. Rubenstein, C. Zhu and L. V. McIntire, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 5022–5027 CrossRef CAS PubMed.
- L. Zandarashvili, D.-W. Li, T. Wang, R. Brüschweiler and J. Iwahara, J. Am. Chem. Soc., 2011, 133, 9192–9195 CrossRef CAS PubMed.
- M. B. James and T. D. Giorgio, Mol. Ther., 2000, 1, 339–346 CrossRef CAS PubMed.
- M. Ancona and C. A. Brackley, Biophys. J., 2022, 121, 2600–2612 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The following analyses and data were conducted and obtained within this study: root mean square deviation (RMSD) profiles for the entire chromoshadow domain (CSD) dimer and individual monomers, as well as each α-helix within the CSD dimer and monomer, over the course of a 200 ns relaxation period. Visual representation of the CSD–CSD dimer, highlighting the salt bridge residue pairs ILys154–IIGlu169 and IIGlu118–IILys159. Frequency histograms depicting the distribution of distances between the salt bridge pair IIGlu118–IILys159. Analysis of hydrogen bond lifetime distribution for the IIGlu162–IAsn157 pair. Frequency histograms illustrating the distribution of angles between the two α-helices within the CSD–CSD dimer. Frequency histograms depicting the distribution of lengths for the residue pairs IGlu169–IILys154, IGlu169-z-axis, and IILys154-z-axis. Frequency histograms illustrating the distribution of distances between ILys154–IIGlu169, generated without applying any position constraints during a 20 ns duration. See DOI: https://doi.org/10.1039/d3mr00011g. |
| This journal is © The Royal Society of Chemistry 2024 |