Open Access Article
Open Access ArticleGreen-chemistry synthesis and optical properties of lead-free Cs2AgSbCl6 double perovskite by a mechanochemical method†
Karla Kariny F.
Barbosa
 *a,
Deisy
Aristizábal-Giraldo
b,
Jorge M.
Osorio-Guillén
*a,
Deisy
Aristizábal-Giraldo
b,
Jorge M.
Osorio-Guillén
 b,
José Javier S.
Acuña
a and
Fabio F.
Ferreira
b,
José Javier S.
Acuña
a and
Fabio F.
Ferreira
 a
a
aCenter for Natural and Human Sciences, Federal University of ABC, Santo André, SP 09210-580, Brazil. E-mail: fabio.furlan@ufabc.edu.br
bInstituto de Física, Universidad de Antioquia UdeA, Calle 70 No 52-21, Medellín, Colombia
First published on 20th February 2024
Abstract
Cs2AgSbCl6 double perovskite (DP) has been synthesized through many solid-state and solution routes. Still, using unsustainable solvents and complicated synthesis processes are unattractive for large-scale manufacturing. The synthesis of Cs2AgSbCl6 using a green approach, mechanosynthesis, offers a sustainable alternative to traditional methods, reducing the environmental impact of solvents and complex processes. X-ray diffraction confirms its double perovskite cubic structure with the space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225) and unit cell parameter a = 10.674(2) Å. Diffuse reflectance measurements indicate a slightly smaller indirect band gap (2.61 eV) than chemically synthesized perovskites. The compound demonstrates stability in air and under light. The electronic structure and optical properties of the host material are calculated using quasi-particle theory GW approximation and the Bethe–Salpeter equation (BSE), including the spin–orbit coupling (SOC); the latter is responsible for the emergence of an intermediate conduction band. These findings suggest that double halide perovskite semiconductors, exemplified by the Cs2AgSbCl6 DP, can be an eco-friendly alternative to lead halide perovskite semiconductors.
m (225) and unit cell parameter a = 10.674(2) Å. Diffuse reflectance measurements indicate a slightly smaller indirect band gap (2.61 eV) than chemically synthesized perovskites. The compound demonstrates stability in air and under light. The electronic structure and optical properties of the host material are calculated using quasi-particle theory GW approximation and the Bethe–Salpeter equation (BSE), including the spin–orbit coupling (SOC); the latter is responsible for the emergence of an intermediate conduction band. These findings suggest that double halide perovskite semiconductors, exemplified by the Cs2AgSbCl6 DP, can be an eco-friendly alternative to lead halide perovskite semiconductors.
Lead-based perovskites remain at the forefront of materials used in cutting-edge devices like light-emitting diodes (LEDs),1,2 solar cells,3 lasers,2 and photodetectors4 due to their exceptional efficiency.4–6 However, their commercial viability and widespread adoption face a significant challenge in the form of lead toxicity. To address this concern, researchers have developed an intriguing alternative: lead-free halide double perovskites, characterized by the general chemical formula A2M′M′′X6, where A represents a monovalent metal cation (typically Cs+), M′ stands for a monovalent cation (such as Ag+ or Cu+), M′′ represents a trivalent metal cation (e.g., Sb3+, In3+, and Bi3+), and X denotes a halide anion (like Cl−, Br−, or I−).4 Lead-free halide double perovskites present a diverse array of characteristics that position them as strong contenders against lead-based perovskites, boasting attributes such as extended recombination lifetimes at room temperature, enhanced resilience to heat and moisture, and more sustainability.7,8
The first Cs2AgSbCl6 (CASC) lead-free halide double perovskite was synthesized via a solution-state reaction aiming at promising photovoltaic absorber applications with an optical band gap of 2.6 eV.9 After that, colloidal Cs2AgInCl6 (CAIC) and Cs2AgSbCl6 nanocrystals were synthesized by injecting acyl halides into a metal acetate solution under atmospheric conditions and relatively mild temperatures. The Tauc analysis of concentrated nanocrystal absorption spectra results in band gaps with an indirect gap of 2.57 ± 0.05 eV for Cs2AgSbCl6 and a direct gap of 3.57 ± 0.03 eV for CAIC;10 Zhou et al. reported Cs2AgSbCl6 microcrystals synthesized by a hydrothermal method in a stainless steel Parr autoclave, which showed stability in air for several weeks.8 Nowadays, halide double perovskites can be synthesized in various ways, such as colloidal, mechanochemical, anti-solvent reprecipitation, hot injection, and solvothermal methods.4 However, as far as we are concerned, no green synthesis reports exist in the literature for Cs2AgSbCl6 compounds. In this context, we adopted a mechanochemical method to synthesize Cs2AgSbCl6 polycrystals as an alternative synthesis route to evaluate the structural changes promoted by milling times.
Mechanochemistry involves the initiation of chemical reactions through the application of mechanical energy, which can be generated by various forces and operating modes, including impact, compression, or shear.11 It has several advantages over the most commonly used solution-based processes, such as lower inherent toxicity, little or no solvent participation in the synthesis, and secondary phase suppression.3,11,12 Further advantages are the formation of high-purity phases with outstanding stability in lead-based perovskites, rapidity, simplicity, and reproducibility, coupled with significant potential for expanding the method to design diverse structures.11,13 Mechanochemical synthesis (MCS) has proven effective in producing a diverse range of quantum dots (QDs),14–16 encompassing all-inorganic and organohalide perovskites12,17,18 and double perovskite (DP) configurations.3,19,20 MCS proved to be a promising synthesis route for the production of halide double perovskites such as Cs2AgBiBr6 (CABB); such powders were successfully prepared by mechanochemical synthesis by Kubicki et al. They synthesized a wide range of mixed-halide Cs2AgBiX6 (X = Cl, Br, and I) double perovskites and employed solid-state 133Cs MAS NMR to identify the miscibility limits of the different halides.20 The work of Rodkey et al. demonstrated the estimated mass fractions of different phases formed in each milling stage until the formation of the pure Cs2AgBiBr6 phase (derived from Rietveld refinements using powder XRD data) and the band gap evolution as a function of grinding time.3
The Cs2AgSbCl6 double perovskite has a face-centered cubic structure (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), with a unit cell parameter a = 10.6682(1) Å.9,21 It exhibits a semiconducting behavior with an indirect band gap of 2.7 eV,21,22 which limits applications in some photovoltaic and optoelectronic devices due to moderate solar spectrum absorption.22,23
m), with a unit cell parameter a = 10.6682(1) Å.9,21 It exhibits a semiconducting behavior with an indirect band gap of 2.7 eV,21,22 which limits applications in some photovoltaic and optoelectronic devices due to moderate solar spectrum absorption.22,23
In this work, we demonstrate the synthesis of a lead-free inorganic double perovskite phase based on Cs2AgSbCl6 by mechanochemistry with different milling times. The structural characteristics showed that the milling time plays a fundamental role in forming the monophasic polycrystalline compound. We present a phase diagram formation derived from Rietveld refinements of powder XRD data. Also, we have calculated the electronic structure and the optical properties of Cs2AgSbCl6 using state-of-the-art quasi-particle methods such as GW and BSE.
1 Methods
1.1 Materials
CsCl (Inlab Confiança, 99.9%, 168.36 g mol−1), AgCl (Alfa Aesar, 99.5%, 143.32 g mol−1), SbCl3 (Alfa Aesar, 99%, 228.12 g mol−1), and HCl (Synth 38 wt% in water) were purchased and used as received without further purification.1.2 Synthesis of Cs2AgSbCl6 polycrystals
The inorganic Cs2AgSbCl6 double perovskite powder was first synthesized by mechanochemical grinding (i.e., ball milling) following previously reported methods for lead halide perovskites.11,20 The ball milling process used 1 μL HCl as solvent. CsCl, AgCl, and SbCl3 were mixed in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio. Ball milling was carried out at 30 Hz for different times (2, 5, 10, 15, and 60 minutes) to produce Cs2AgSbCl6 (for more details see the ESI†).
1 molar ratio. Ball milling was carried out at 30 Hz for different times (2, 5, 10, 15, and 60 minutes) to produce Cs2AgSbCl6 (for more details see the ESI†).
1.3 Characterization
Room-T powder X-ray diffraction (PXRD) data were collected on an STADI-P (STOE®, Darmstadt, Germany) diffractometer operating in transmission mode to confirm the phase purity and/or the mass fractions of the different phases formed at each stage. We used monochromatic Cu Kα1 (λ = 1.5406 Å) radiation selected using a curved Ge(111) monochromator, operating at a tube voltage of 40 kV and a current of 40 mA. Data were recorded with a Mythen 1K (Dectris®, Baden, Switzerland) from 10° to 90° (2θ), in steps of 0.015°, and a counting time of 100 s at each 1.05°. Data have been analyzed using the Rietveld method24,25 implemented in the program TOPAS-Academic v.7.26 Morphological studies and elemental analysis of materials were carried out by scanning electron microscopy (SEM) (JEOL JSM-6010LA, Pleasanton, CA, USA). The average SEM particle sizes were evaluated with ImageJ software.27 Crystallographic and structural investigations of the perovskite samples were also carried out using high-resolution transmission electron microscopy (HRTEM) (TEM-Thermo Fischer Talos F200X-G2) operating at 200 kV accelerating voltage using a field emission gun (X-FEG). The HRTEM image and electron diffraction patterns obtained from TEM analysis of the Cs2AgSbCl6 samples were indexed using Single Crystal Software (Java Electron Microscopy Software). The optical diffuse reflectance spectra were recorded on a UV-Vis-NIR spectrophotometer (Varian Cary 5000, Santa Clara, CA, USA) equipped with an integrating sphere; BaSO4 was used as a reference standard.1.4 Electronic structure and optical property computational setup
Spin-polarized first-principles density functional theory (DFT) calculations, including the spin–orbit coupling (SOC), were carried out using the Vienna Ab initio Simulation Package (VASP).28,29 For the exchange-correlation energy functional, we used the generalized gradient approximation (GGA) and its PBEsol parametrization.30 The projector augmented wave31 atomic reference configurations to describe the valence electrons were Cs: 5s25p66s1, Ag: 4d105s1, Sb: 5s25p3 and Cl: 3s23p5. During all calculations, we maintained an energy cut-off of 340 eV and 324 conduction bands, and a stopping criterion of 10−8 eV for the electronic minimization loop. The Brillouin zone (BZ) was sampled with a uniformly spaced 4 × 4 × 4 k-grid centered at Γ and a Gaussian smearing of 0.01 eV.To obtain the excited states, quasi-particle (QP) gap, and optical properties, we have used many-body perturbation theory within the G0W0 approximation32–34 and the Bethe–Salpeter equation (BSE) within the Tamm–Dancoff approximation.35–37 To perform the G0W0 calculations, we have kept the same input setup but with different projector augmented wave atomic reference configurations especially designed to produce accurate high-energy scattering properties above the vacuum level, and finally the number of frequency points used was 360. To record the absorption spectrum (the imaginary part of the frequency-dependent dielectric function) including the electron–hole (e–h) interaction (excitonic properties), the BSE Hamiltonian was set with 12 valence and 12 conduction bands, respectively.
2 Results
White to almost yellow-colored powders were obtained for different milling times and then subjected to heat treatment at 100 °C for 12 h (see Fig. 1(a)).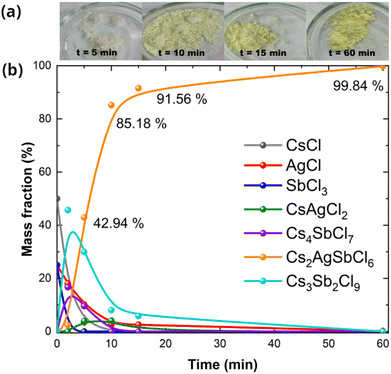 | ||
| Fig. 1 (a) Photographs and (b) the phase concentration for the Cs2AgSbCl6 double perovskite after varying ball-milling times, derived from Rietveld refinements using XRPD data. | ||
The crystal structure evolution of the samples as a function of the mixing time was studied by PXRD. The mass fractions of the different phases by increasing milling times are shown in Fig. 1(b), which were derived from Rietveld refinements using PXRD data, as illustrated in the ESI.†. It is possible to observe that the binary precursors react very quickly in the first few minutes, and their phases are suppressed after 10 minutes. After 2 minutes of milling, we observed a white powder related to the CsAgCl2 (ICSD 1509264) bimetallic halide phase.38 However, this phase is not observed with increasing milling times, suggesting that the reaction occurs preferentially for other phases. Below a milling time of 20 minutes, the samples contain a mixture of a cubic AgCl-phase (ICSD 56538), the 2D-Cs3Sb2Cl9 (ICSD 22075) perovskite, and the Cs2AgSbCl6 (ICSD 244674) double perovskite, a behavior similar to that reported by Rodkey et al.,3 which suggests that CsCl and SbCl3 precursors are the first to be incorporated into the Cs2AgSbCl6 phase and AgCl is the last one. Motivated by this observation, we propose a possible mechanochemical reaction for milling times above 20 minutes.
| CsCl + AgCl → CsAgCl2 | (1) |
| 3CsCl + 2SbCl3 → Cs3Sb2Cl9 | (2) |
| Cs3Sb2Cl9 + CsAgCl2 + AgCl → 2Cs2AgSbCl6 | (3) |
As shown in the powder X-ray diffractograms (Fig. 2), as the milling time increases, the AgCl (0.16 wt% after 60 minutes of milling) and the Cs3Sb2Cl9 concentrations decrease until the primary phase is formed. It can be seen that the Cs2AgCl6 phase is already formed in 2 minutes of milling, coexisting with other phases (see Fig. 1(b)). The various chemical reactions described in eqn (1)–(3) promoted by the mechanical energy of the mixer mill contribute significantly to the formation of the Cs2AgSbCl6 pure phase.
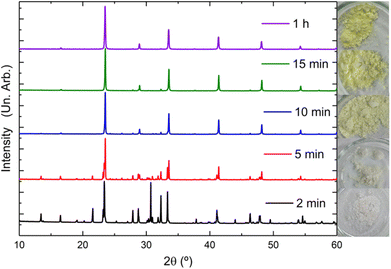 | ||
| Fig. 2 PXRD patterns of the Cs2AgSbCl6 double perovskite polycrystals obtained with different milling times. | ||
Our exhaustive grinding tests revealed that AgCl was always present in the final compound in amounts as high as 6 wt%. We then realized to add an HCl droplet (1 μL) close to 60 minutes of grinding, i.e., 5 minutes before finishing the grinding process, and we opened the microtube and pipetted 1 μL of HCl into the mechanosynthesized powders, closed the microtube, and continued grinding for another 5 minutes. We used this solvent, as it is widely used in hydrothermal synthesis, to obtain Cs2AgSbCl6. In the work of Zhou et al., the amount of solvent was varied to evaluate the band gap of Cs2AgSbCl6. They found that their samples had excellent stability, and the analysis of the X-ray diffractograms from samples measured after one month of storage (in the ambient atmosphere) showed no evidence of the material's decomposition, thus indicating stability.8
It is possible to observe different XRD patterns for samples with the same stoichiometry (main phase) and under the same experimental conditions: one with neat grinding and the other with liquid-assisted grinding (LAG); see Fig. S6 and S8 (ESI).† In Fig. S6,† one can observe the presence of the Cs2AgSbCl6, AgCl and Cs3Sb2Cl9 phases. Before finishing the grinding process (about 5 min before), 1 μL of HCl was added in an attempt to suppress the AgCl phase, and the rest of the grinding was completed. On the other hand, in Fig. S8,† after adding the HCl droplet, the 2D perovskite (Cs3Sb2Cl9) disappeared and the amount of AgCl decreased. We believe that the addition of HCl, by decreasing the AgCl amount, would interfere with the stoichiometry of the main phase, by decreasing the Ag content and also decreasing the Cl content of AgCl. However, additional work has to be performed, using synchrotron high-resolution powder X-ray diffraction, to obtain confident site occupancies and isotropic displacement parameters. We have provided magnified regions of the diffractograms obtained without (Fig. S7) and with (Fig. S9) (ESI)† the addition of the HCl droplet. One can notice that we can unequivocally identity the presence of the Cs3Sb2Cl9 phase in regard to the main Cs2AgSbCl6 phase.
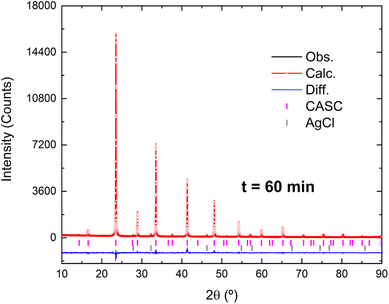
Fig. 3 displays the room-temperature Rietveld plot for the Cs2AgSbCl6 sample after 1 hour of milling. We found that all peaks of the pattern were successfully indexed to a cubic crystal system with the space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225); the unit cell parameter a = 10.674(2) Å, gof = 1.98, Rwp = 7.47%, and RBragg = 2.91% are in agreement with previous results.9,21
m (225); the unit cell parameter a = 10.674(2) Å, gof = 1.98, Rwp = 7.47%, and RBragg = 2.91% are in agreement with previous results.9,21
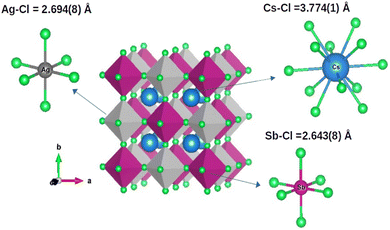
Fig. 4 shows the conventional unit cell of Cs2AgSbCl6 in the space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m; the fractional atomic coordinates are displayed in Table 1. Chlorine atoms (Cl) form a regular octahedron occupying the Wyckoff sites 24e. The Cs2AgSbCl6 cubic unit cell consists of a three-dimensional framework composed of corner-sharing alternating [AgCl6] and [SbCl6] octahedra. The Cs atoms are situated within the interstitial spaces created by these octahedra, leading to a doubled cell structure reminiscent of the elpasolite K2NaAlF6 arrangement.39 Silver (Ag) and antimony (Sb) atoms occupy their unique Wyckoff sites (4b and 4a, respectively) as indicated in Table 1. The Ag and Sb atoms are located in the center of the octahedron and are equidistant from the 6 Cl atoms. The Ag–Cl and Sb–Cl interatomic distances are ∼2.648(2) Å and ∼2.694(8) Å, respectively. The Cs atoms are located in the cavities formed between the octahedra with Cs–Cl interatomic distances of 3.774(1) Å.
m; the fractional atomic coordinates are displayed in Table 1. Chlorine atoms (Cl) form a regular octahedron occupying the Wyckoff sites 24e. The Cs2AgSbCl6 cubic unit cell consists of a three-dimensional framework composed of corner-sharing alternating [AgCl6] and [SbCl6] octahedra. The Cs atoms are situated within the interstitial spaces created by these octahedra, leading to a doubled cell structure reminiscent of the elpasolite K2NaAlF6 arrangement.39 Silver (Ag) and antimony (Sb) atoms occupy their unique Wyckoff sites (4b and 4a, respectively) as indicated in Table 1. The Ag and Sb atoms are located in the center of the octahedron and are equidistant from the 6 Cl atoms. The Ag–Cl and Sb–Cl interatomic distances are ∼2.648(2) Å and ∼2.694(8) Å, respectively. The Cs atoms are located in the cavities formed between the octahedra with Cs–Cl interatomic distances of 3.774(1) Å.
| Atom | Wyckoff site | x | y | z | B iso |
|---|---|---|---|---|---|
| Cs | 8c | 1/4 | 1/4 | 1/4 | 5.67 |
| Ag | 4b | 1/2 | 1/2 | 1/2 | 4.56 |
| Sb | 4a | 0 | 0 | 0 | 4.15 |
| Cl | 24e | 0.247(5) | 0 | 0 | 5.84 |
No decomposition of the Cs2AgSbCl6 powder was identified; after 365 days, the same structure was observed (see Fig. S3†), but the color changed from yellow to pale yellow.
2.1 SEM measurements
For polycrystalline Cs2SbAgCl6, the scanning electron microscopy (SEM) image (Fig. 5) reveals a heterogeneous morphology of massive particles with clusters (5–10 μm) of fragments of undefined shapes. However, on a higher magnification image (Fig. 5), it is possible to observe that each particle is, in fact, formed by an agglomeration of much smaller grains of typically 0.5–1 μm. As illustrated in Fig. S10 (ESI),† the occurrence of particles with diverse shapes and the formation of larger aggregated clusters are frequent outcomes during the application of this mechanosynthesis method. In MAP-EDS, it was observed that the homogeneity in the powders suggests the absence of secondary phases after 60 minutes of grinding. | ||
| Fig. 5 SEM image of the Cs2SbAgCl6 polycrystalline material. The scale bar at the lower right of the SEM image is between 5 μm on a 3.700× magnification scale. | ||
The elemental composition of the film determined by EDS, as shown in Table 2, was 19.68% Cs, 10.52% Ag, 10.94% Sb, and 61.8% Cl, the same as the expected composition of Cs2AgSbCl6 (20% Cs, 10% Ag, 10% Sb, and 60% Cl) within the EDS error.
| Atom | Mass% | mol% |
|---|---|---|
| Cl | 29.11 | 58.86 |
| Ag | 15.83 | 10.52 |
| Sb | 18.57 | 10.94 |
| Cs | 36.49 | 19.68 |
2.2 HRTEM measurements
Fig. 6(a and b) show, respectively, low-magnification and high-resolution TEM (HRTEM) images of spherical nanoparticles of uniform size of the Cs2AgSbCl6 double perovskite. | ||
| Fig. 6 (a) Low-magnification and SAED pattern (inset) and (b) high-resolution transmission electron microscope images of a Cs2AgSbCl6 nanoparticle. | ||
The FFT reveals the in-plane hexagonal atomic arrangement oriented along the 214 zone axis. The measured d spacings (see Table 3) for (242), (240), and (402) planes were observed from FFT presented as an inset in Fig. 6(b). The selected-area electron diffraction (SAED) pattern obtained over a large area (in the Fig. 6(a) inset) reveals the correspondence with the PXRD patterns in Fig. 3, indicating structural stability after treatment/synthesis.
| Spot | d (Å) | d* (1 Å−1) | Families of planes |
|---|---|---|---|
| 1 | 2.132(43) | 0.4690 | (242) |
| 2 | 2.318(46) | 0.4314 | (402) |
| 3 | 2.424(48) | 0.4126 | (240) |
2.3 UV-vis measurement
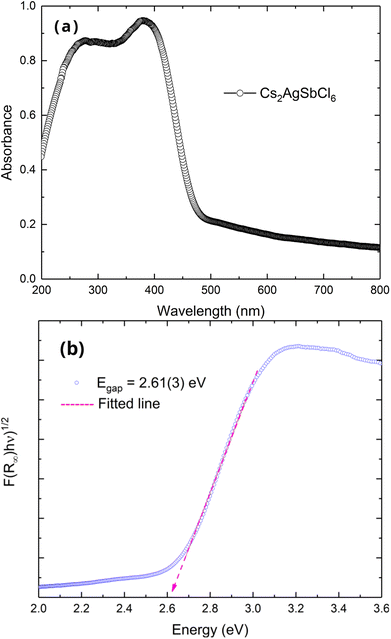
Fig. 7(a) depicts the optical absorption coefficient for the Cs2AgSbCl6 powdered sample related to the Kubelka–Munk function (F(R) = a = (1 − R)2/2R; R is the reflectance) versus energy (eV).The extrapolation of the linear region to the abscissa gives an indirect band gap; see the magenta line in Fig. 7(b). The value obtained for Cs2AgSbCl6 (∼2.61(3) eV) is in agreement with data reported in the literature for its band gap at room temperature8–10,21,40
2.4 Electronic structure and optical properties
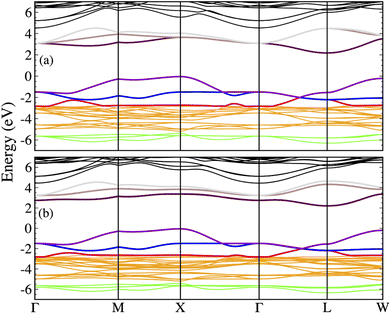
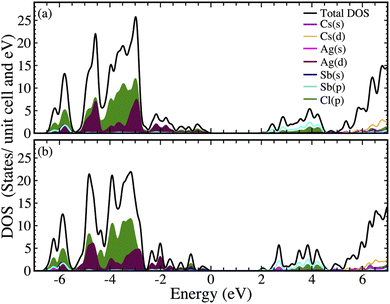
Fig. 8(a and b) show the QP dispersion relation for Cs2AgSbCl6 with and without SOC, respectively. The valence band maximum (VBM) and the conduction band minimum (CBM) are localized at the X and L points of the first-Brillouin zone (FBZ), respectively. The indirect calculated QP gaps are 2.22 eV and 2.26 eV with and without SOC, and the gaps at Γ are 4.59 and 4.23 eV. Furthermore, the calculated hole effective masses are −0.198 and −0.647 along the X–Γ and X–M directions without SOC, whereas they are −0.197 and −0.635, including SOC. On the other hand, the electron effective masses without SOC are 0.348 and 0.4 along the L–W and L–Γ directions, respectively, and with SOC, the obtained values are 0.355 and 0.413. Thus, the curvature of the dispersion relation in the neighborhood of the VBM and CBM is very similar with and without SOC. However, the main difference in the topology of the dispersion relation due to SOC is observed at the first bottom conduction bands (CBs), where the degeneracy is entirely left in the whole FBZ, except at Γ, where it is partially left. Furthermore, the SOC exposes an intermediate CB with a small width of 1.16 eV, then another two intermediate CBs that are degenerated at Γ with a width of 1.4 eV and then at higher energies are located the major contribution of the CBs. The presence of these intermediate bands can enhance the absorption of photons with lower energy by additional optical transitions, the first one from the valence band to the intermediate CBs and a second transition from the intermediate CBs to the main CBs, thus opening the prospect to improve thin-film solar cells efficiency exceeding the Shockley–Queisser limit.41The total and partial density of states (DOS) with and without SOC are shown in Fig. 9. The lower three valence bands (VBs) located between −6.5 to −5.4 eV are built up by the hybridization of Cl and Sb p-states with Ag d-states, and then the middle VBs situated across −5.2 eV to −2.6 eV are formed by the hybridization of Cl p and Ag d-states. The top three VBs placed between −2.8 to 0 eV show different orbital contributions, with the low band made up mainly of Ag d-states, and the two top VBs are the result of the hybridization of Cl p, Ag d, and Sb s-states. On the other hand, the bottom CBs are built up mainly by Sb p-states, and the next two intermediate CBs are formed by the hybridization of Sb p and Cl p-states with Ag s-states. Finally, the higher CBs are made from Cs s and Cl p-states.
Fig. 10 presents the imaginary part of the dielectric function (ε2) calculated at the level of the independent-particle approximation (IPA) and including the electron–hole (e–h) interaction (BSE). First, we discuss the obtained results without the SOC; it is observed that the onset of the IPA spectrum starts around 3.4 eV and then there are four well-defined peaks around 3.87, 4.47, 4.59, and 5.02 eV; these peaks are attributed mainly to the transition between Sb-p to Ag-d and Sb-p to Sb-states for the first two peaks, and Sb-p to Ag-d-states for the following two peaks. The inclusion of the e–h interaction causes the redistribution of the spectral weight and the oscillator strength. Now the onset and the main peaks are considerably moved toward lower energies (redshift), and the onset begins at 3.0 eV, and the first and second peaks are around 3.3 and 4.05 eV and show a considerable increment in their oscillator strength. Second, the calculated ε2 by IPA and including SOC shows some difference with the previous results; there is, in general, a redshift of the whole spectrum, with the onset starting at 3.0 eV and showing four well-defined peaks located around 3.5, 4.21, 4.69 and 4.99 eV. Moreover, there are two prominent shoulders around 3.8 and 3.9 eV caused by the splitting of the intermediate bands. Finally, the calculated ε2 using BSE and SOC shows more remarkable features. A redshift of the spectrum and an appreciable redistribution of the spectral weight are observed; the onset now starts around 2.6 eV, and the more prominent peaks are placed around 3.05, 3.81, 4.18, and 4.32 eV, and most significantly there is a continuous excitonic feature at 2.7 eV due to the inclusion of the e–h interaction.
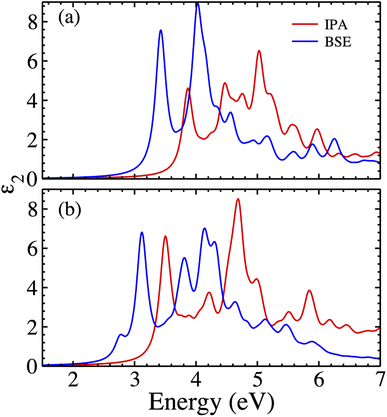 | ||
| Fig. 10 Cs2AgSbCl6 imaginary dielectric function calculated using the independent-particle approximation G0W0 – IPA (red dashed line) and BSE (blue line) (a) without and (b) including SOC. | ||
3 Discussion
This study introduces an innovative method for synthesizing Cs2AgSbCl6 powders, emphasizing its advantages in sustainability and scalability for industrial use. The new synthesis technique surpasses traditional methods during extended grinding periods exceeding 1 hour, resulting in Cs2AgSbCl6 powders that exhibit exceptional stability lasting at least 365 days.The characterization of the powders reveals a non-uniform distribution of particles with an average size of 10 μm, presenting characteristic clusters associated with mechanosynthesis. In order to check potential optoelectronic application, we dispersed the powders and prepared a solution that was used in the ancillary investigation using electron diffraction, demonstrating the presence of particles as small as 5–15 nm, exhibiting interplanar distances approaching 2.4 Å, which agrees with the (240) crystal plane as determined by powder X-ray diffraction (PXRD).
To manufacture films, we need to optimize the surface with homogeneous particle sizes, and the solution demonstrated that it is possible to separate the agglomerates while preserving the structural properties.
Furthermore, the synthesized powders exhibit optical properties akin to those found in polycrystalline samples in the literature, showcasing an indirect band gap of 2.8 eV (ref. 9 and 21) to 2.61(3) eV (this work). This remarkable consistency highlights the potential of mechanosynthesis as a promising avenue for producing perovskite halide powders with complex stoichiometries, offering possibilities for their application in advanced technologies such as thin-film technology and other cutting-edge applications.
Theoretical results agree with the existing literature,42 even though a larger value of the indirect gap was reported using the HSE06 hybrid functional,8,21 but none of them include explicitly quasi-particle corrections to obtain the electronic dispersion relation and the e–h interaction (excitonic effects) to calculate the optical spectrum. Here, taking into account the SOC, it does not affect significantly the calculated band gaps; however, the degeneracy of the intermediate CBs is left, and a full splitting of those bands is observed. On the other hand, the inclusion of the e–h interaction in the BSE Hamiltonian predicts that this effect leads to the redistribution of the spectral weight and the oscillator strength of ε2, showing a redshift of the spectrum with the onset of the absorption at 2.6 eV and a prominent continuous excitonic feature at 2.7 eV. These calculated values from the optical spectrum agrees exceptionally well with the value of the band-gap obtained experimentally.
A solar photon of energy equal to 2.7 eV is absorbed by an electron at the valence band (VB), which is promoted to the conduction band (CB), creating an electron–hole pair. Higher energy photons cause the VB → CB transition as well; however, the excess energy is given to the lattice in the form of heat when the carriers migrate to lower energy states, causing phonon emission. By the effect of the SOC, the degeneration of the CBM is left and intermediate bands appear, allowing the e–h pair to be generated by the simultaneous absorption of photons in the two sub-band gap transitions.41
Since the static dielectric constant of Cs2AgSbCl6 is small, the charge carrier recombination rate is high, thus affecting the overall performance of Cs2AgSbCl6-based devices43 for potential photovoltaic applications.
4 Conclusions
We have successfully synthesized Cs2AgSbCl6via an efficient mechanochemical route, making it highly appealing to industrial applications. Cs2AgSbCl6 exhibits superior stability compared to lead halide perovskites, with its structural and optical properties aligning closely with documented literature findings. Finally, it is established that the correct theoretical scheme to describe the optical properties of this material has to take into account the SOC and the continuous excitonic effects due to the e–h interaction, where an excellent agreement between the calculated and experimental gap is found.Author contributions
The manuscript was written through contributions of all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the São Paulo Research Foundation (proc. FAPESP 2021/03640-7 and 2023/01502-1), the Brazilian National Council for Scientific and Technological Development (CNPq proc. no. 305661/2019-9), the Coordination for the Improvement of Higher Education Personnel (CAPES finance code 001), Colombian MINCIENCIAS (Convocatoria doctorados nacionales No. 757 de 2016) and FCEN-Universidad de Antioquia (Colombia). The authors thank the Multiuser Experimental Center (UFABC) for the experimental support.Notes and references
- J. Luo, X. Wang, S. Li, J. Liu, Y. Guo, G. Niu, L. Yao, Y. Fu, L. Gao, Q. Dong, C. Zhao, M. Leng, F. Ma, W. Liang, L. Wang, S. Jin, J. Han, L. Zhang, J. Etheridge, J. Wang, Y. Yan, E. H. Sargent and J. Tang, Nature, 2018, 563, 541–545 CrossRef CAS PubMed.
- X.-G. Zhao, D. Yang, J.-C. Ren, Y. Sun, Z. Xiao and L. Zhang, Joule, 2018, 2, 1662–1673 CrossRef CAS.
- N. Rodkey, S. Kaal, P. Sebastia-Luna, Y. A. Birkhölzer, M. Ledinsky, F. Palazon, H. J. Bolink and M. Morales-Masis, Chem. Mater., 2021, 33, 7417–7422 CrossRef CAS PubMed.
- S. Ghosh, H. Shankar and P. Kar, Mater. Adv., 2022, 3, 3742–3765 RSC.
- T. Fang, T. Wang, X. Li, Y. Dong, S. Bai and J. Song, Sci. Bull., 2021, 66, 36–43 CrossRef CAS PubMed.
- W. S. Yang, B.-W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. I. Seok, Science, 2017, 356, 1376–1379 CrossRef CAS PubMed.
- A. H. Slavney, T. Hu, A. M. Lindenberg and H. I. Karunadasa, J. Am. Chem. Soc., 2016, 138, 2138–2141 CrossRef CAS PubMed.
- J. Zhou, X. Rong, M. S. Molokeev, X. Zhang and Z. Xia, J. Mater. Chem. A, 2018, 6, 2346–2352 RSC.
- W. Deng, Z.-Y. Deng, J. He, M. Wang, Z.-X. Chen, S.-H. Wei and H.-J. Feng, Appl. Phys. Lett., 2017, 111, 151602 CrossRef.
- J. C. Dahl, W. T. Osowiecki, Y. Cai, J. K. Swabeck, Y. Bekenstein, M. Asta, E. M. Chan and A. P. Alivisatos, Chem. Mater., 2019, 31, 3134–3143 CrossRef CAS.
- F. Palazon, Y. El Ajjouri and H. J. Bolink, Adv. Energy Mater., 2020, 10, 1902499 CrossRef CAS.
- D. Prochowicz, M. Saski, P. Yadav, M. Grätzel and J. Lewiński, Acc. Chem. Res., 2019, 52, 3233–3243 CrossRef CAS PubMed.
- A. D. Jodlowski, A. Yépez, R. Luque, L. Camacho and G. de Miguel, Angew. Chem., Int. Ed., 2016, 55, 14972–14977 CrossRef CAS PubMed.
- Z.-Y. Zhu, Q.-Q. Yang, L.-F. Gao, L. Zhang, A.-Y. Shi, C.-L. Sun, Q. Wang and H.-L. Zhang, J. Phys. Chem. Lett., 2017, 8, 1610–1614 CrossRef CAS PubMed.
- T. Tsuzuki and P. G. McCormick, Appl. Phys. A: Mater. Sci. Process., 1997, 65, 607–609 CrossRef CAS.
- D. Rambabu, S. Bhattacharyya, T. Singh, M. L. Chakravarthy and T. K. Maji, Inorg. Chem., 2020, 59, 1436–1443 CrossRef CAS PubMed.
- F. Palazon, Y. El Ajjouri, P. Sebastia-Luna, S. Lauciello, L. Manna and H. J. Bolink, J. Mater. Chem. C, 2019, 7, 11406–11410 RSC.
- M. Saski, D. Prochowicz, W. Marynowski and J. Lewiński, Eur. J. Inorg. Chem., 2019, 2019, 2680–2684 CrossRef CAS.
- G. García-Espejo, D. Rodríguez-Padrón, R. Luque, L. Camacho and G. de Miguel, Nanoscale, 2019, 11, 16650–16657 RSC.
- D. J. Kubicki, M. Saski, S. MacPherson, K. Galkowski, J. Lewiński, D. Prochowicz, J. J. Titman and S. D. Stranks, Chem. Mater., 2020, 32, 8129–8138 CrossRef CAS PubMed.
- J. E. F. S. Rodrigues, C. A. Escanhoela, B. Fragoso, G. Sombrio, M. M. Ferrer, C. Álvarez-Galván, M. T. Fernández-Díaz, J. A. Souza, F. F. Ferreira, C. Pecharromán and J. A. Alonso, Ind. Eng. Chem. Res., 2021, 60, 18918–18928 CrossRef CAS.
- A. Karmakar, M. S. Dodd, S. Agnihotri, E. Ravera and V. K. Michaelis, Chem. Mater., 2018, 30, 8280–8290 CrossRef CAS.
- Q. Liao, J. Chen, L. Zhou, T. Wei, L. Zhang, D. Chen, F. Huang, Q. Pang and J. Z. Zhang, J. Phys. Chem. Lett., 2020, 11, 8392–8398 CrossRef CAS PubMed.
- H. M. Rietveld, Acta Crystallogr., 1967, 22, 151–152 CrossRef CAS.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- A. Coelho, Coelho Software, Brisbane, 2012 Search PubMed.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- D. Hobbs, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 11556–11570 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- M. S. Hybertsen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390–5413 CrossRef CAS PubMed.
- L. Hedin, Phys. Rev., 1965, 139, A796–A823 CrossRef.
- M. Shishkin, M. Marsman and G. Kresse, Phys. Rev. Lett., 2007, 99, 246403 CrossRef CAS PubMed.
- M. Rohlfing and S. G. Louie, Phys. Rev. Lett., 1998, 81, 2312–2315 CrossRef CAS.
- S. Albrecht, L. Reining, R. Del Sole and G. Onida, Phys. Rev. Lett., 1998, 80, 4510–4513 CrossRef CAS.
- T. Sander, E. Maggio and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045209 CrossRef.
- Z. Zhang, R. Zhao, S. Teng, K. Huang, L. Zhang, D. Wang, W. Yang, R. Xie and N. Pradhan, Small, 2020, 16, 2004272 CrossRef CAS PubMed.
- L. R. Moras, J. Inorg. Nucl. Chem., 1974, 36, 3876–3878 CrossRef.
- T. T. Tran, J. R. Panella, J. R. Chamorro, J. R. Morey and T. M. McQueen, Mater. Horiz., 2017, 4, 688–693 RSC.
- A. Luque, A. Martí and C. Stanley, Nat. Photonics, 2012, 6, 146–152 CrossRef CAS.
- M. Babaei, V. Ahmadi and G. Darvish, J. Phys. Chem. Solids, 2022, 169, 110880 CrossRef CAS.
- X. Liu, B. Xie, C. Duan, Z. Wang, B. Fan, K. Zhang, B. Lin, F. J. Colberts, W. Ma and R. A. Janssen, et al. , J. Mater. Chem. A, 2018, 6, 395–403 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mr00024a |
| This journal is © The Royal Society of Chemistry 2024 |