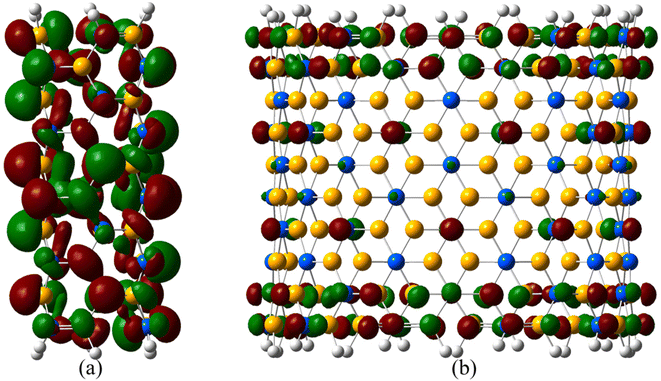Open Access Article
Open Access ArticleA hybrid density functional study on the mechanochemistry of silicon carbide nanotubes
Aabiskar
Bhusal
 *a,
Kapil
Adhikari
*a,
Kapil
Adhikari
 ab and
Qian
Sun
c
ab and
Qian
Sun
c
aPhysics Research Initiatives, Pokhara, Gandaki 33700, Nepal. E-mail: aabiskar@pri.org.np
bGandaki University, Pokhara, Gandaki 33700, Nepal
cCollege of Petroleum Engineering, Shandong Institute of Petroleum and Chemical Technology, Dongying, Shandong 257061, People's Republic of China
First published on 30th May 2024
Abstract
The constrained geometries simulate the external force (CoGEF) method mimics the application of external stress on molecules. Herein, we used the CoGEF method at the hybrid density functional theory level to investigate the behavior of silicon carbide nanotubes (SiCNTs) under longitudinal stress. When the SiCNTs are under longitudinal stress, we observe a gradual decrease in the binding energy and the frontier orbital gap with the applied strain until a critical threshold is reached. Beyond this threshold, a sudden increase in both parameters occurs, indicating the formation of some kind of stable structure. The higher binding energy of the larger SiCNTs makes them more resistant to rupture under strain, suggesting their increased mechanical strength. Additionally, we observed a rapid initial increase of Young's modulus of SiCNTs and convergence to a constant magnitude with further increase in their diameter. Therefore, CoGEF analysis provides invaluable insights into the changes occurring in the structural and electronic properties of SiCNTs when subjected to stress.
1 Introduction
The discovery of carbon nanotubes1 has attracted worldwide attention to such quasi-one-dimensional structures. Due to their exceptional mechanical and electrical properties, carbon nanotubes have become promising materials for various applications such as composite materials, coatings and films, electronics, energy storage, and biomedical engineering.2,3 In recent years, the scientific community has focused on silicon carbide nanotubes (SiCNTs) as an alternative to carbon nanotubes.SiCNTs are semiconducting materials composed of binary elements—silicon and carbon atoms—arranged in a tubular structure.4 There is a significant energy difference between sp2 and sp3 bond structures in silicon–carbon pairs.5 Consequently, fabricating SiC nanotubes and flat nanostructures like graphene is very challenging. Despite this, there have been successful attempts to synthesize silicon carbide nanotubes through various methods, including template-assisted growth,6 chemical vapour deposition,7 and, more recently, microwave heating techniques.8 SiCNTs offer additional advantages over their carbon counterparts, including improved reactivity, more biodegradability and biocompatibility, better stability against oxidation, and a higher adsorption energy platform for gas absorption and storage.9,10 Moreover, owing to the partially ionic nature of the silicon and carbon bond within SiCNTs, they possess a highly reactive exterior surface that facilitates sidewall decoration.11–13 Consequently, they find more suitability in gas sensors, drug delivery systems, hydrogen storage, and reinforced ceramics.14–18
Mechanochemistry is a relatively new field of study that examines how mechanical stress affects a molecule's physical and chemical properties. Studying the mechanochemical properties of SiCNTs is important for understanding their stability under stress and evaluating their suitability for mechanical applications, such as reinforcing nanocomposite materials. The mechanochemical behaviour of nanotubes can be explored by calculating their electronic structures and, hence, the chemical properties under mechanical stress. This study presents the mechanochemistry of SiCNTs under simulated external force.
There are two primary approaches to computational mechanochemistry, which differ based on how the force is considered. In the first approach, force is applied explicitly like in the ab initio steered molecular dynamics (AISMD),19 external force explicitly included (EFEI),20 force-modified potential energy surface (FMPES),19 and enforced geometry optimization (EGO)21 models. In contrast, the constrained geometries simulate external force (CoGEF)22 method applies force by constraining the geometry of the considered molecular system. Among these methods, the CoGEF model, developed by Beyer, has gained prominence for simulating molecular elongation through constrained geometry optimization.22–26
In the CoGEF method, the distance between the two reference atoms is increased stepwise. After each elongation, the distance between them is fixed. Subsequently, the structure is then relaxed along all the degrees of freedom except the constrained one. The CoGEF method has demonstrated its utility in the study of mechanochemical properties. For instance, Iozzi et al.23 used CoGEF to study the mechanochemical properties of disulfide bonds in three molecules of different sizes. Klein et al.24 used the CoGEF method to study the mechanochemical reactivity of many mechanophores and found an excellent match with the available experimental results. Using a combination of experimental and CoGEF ab initio simulations, Janpatompong et al.25 showed remarkable stability of conjugated olefins within phenylene vinylene polymer blocks towards cis–trans isomerization under significant elongation. Furthermore, our prior research utilized the CoGEF approach to investigate the alterations in electronic behavior induced by stress and determine the rupture force and Young's modulus of carbon nanotubes.26 To the best of our knowledge, no study has been conducted on the mechanochemistry of silicon carbide nanotubes using the CoGEF method.
This study delves into the mechanochemistry of silicon carbide nanotubes with different diameters. Firstly, we calculated the unconstrained nanotubes' binding energy per atom, representative bond lengths and bond angles, charge transfer, and frontier orbital gap. Subsequently, the nanotubes are subjected to stretching following the CoGEF model. The effects of strain exerted on the binding energy, frontier energy gap, bond lengths, bond angles and charge transfer are examined. The structural deformation of SiCNTs is also analyzed with strain. Furthermore, we computed the maximum threshold force and strain withstanding capacity of SiCNTs. Finally, we estimated the evolution of Young's modulus of SiCNTs with their diameter by linearly fitting the stress versus strain plot.
2 Methodology
SiCNTs can be constructed by rolling a SiC sheet similar to graphene to create a tube-like structure. The chiral vector (Ch) connecting the two crystallographically equivalent sites in two-dimensional SiC sheets can define this rolling process. The summation of two basis vectors (a1 and a2) defines the chiral vector and can be represented as Ch = na1 + ma2, where n and m are integers. The (n, m) index pair describes the geometry of the nanotube.27 SiCNTs are of three types based on the chiral vector indices (n, m): armchair, zigzag, and chiral.28 If n = m, it is an armchair nanotube, while m = 0 represents a zigzag nanotube. All other (n, m) chiral indices correspond to chiral nanotubes. Herein, we considered eight armchair SiCNTs with chiral indices ranging from (3, 3) to (10, 10). These SiCNTs are represented using the code Nnm. For example, (3, 3) is represented as N33, (4, 4) is represented as N44, and so forth. Because of the slight electronegativity difference between the carbon and silicon atoms within SiCNTs, they exhibit radial buckling behavior.29 Specifically, the more electronegative carbon atoms tend to radially move outward, while the silicon atoms move inward, resulting in the formation of two concentric cylinders. So, the diameters listed in Table 1 represent the average of the radii of these two cylinders for each SiCNT.| Chiral indices (n, m) | Symbol | No of atoms | Diameter (Å) |
|---|---|---|---|
| (3, 3) | N33 | 72 | 5.26 |
| (4, 4) | N44 | 96 | 6.99 |
| (5, 5) | N55 | 120 | 8.75 |
| (6, 6) | N66 | 144 | 10.49 |
| (7, 7) | N77 | 168 | 12.23 |
| (8, 8) | N88 | 192 | 13.97 |
| (9, 9) | N99 | 216 | 15.70 |
| (10, 10) | N1010 | 240 | 17.43 |
We considered a finite cluster approximation in which hydrogen atoms saturate the dangling bonds at the two ends of the nanotubes to simulate the effect of the infinite nanotube. Density functional theory (DFT) with the Becke-three-parameter-Lee–Yang–Parr (B3LYP) hybrid functional30,31 and 6-31G(d) basis set32 is used. At first, the optimized geometry of every nanotube is found. The equilibrium energy and the length are noted. The equilibrium length of the nanotube is defined as the distance between the two terminal silicon atoms of each nanotube. The electronic properties like binding energy per atom, calculated using eqn (1), and the HOMO–LUMO gap of nanotubes are compared.
 | (1) |
The CoGEF calculations of the nanotubes are carried out by stretching the constrained terminal silicon and carbon atoms at both ends (Fig. 1) in increments of 0.01 Å. The reaction coordinate is considered along the z-direction. Each successive constrained structure is optimized geometrically. The force experienced by the nanotube is computed by dividing the change in energy (ΔE) by the change in length (ΔL) along the z-direction of the nanotube relative to the unconstrained structure. This process is repeated until the magnitude of the force drops, indicating the formation of stable structures. The maximum force obtained is considered the rupture force, which brings about the mechanochemical transformation of the nanotube. Besides, the electronic properties of stretched and constrained nanotubes are compared. All the quantum mechanical calculations are done in the Gaussian 09 (ref. 33) suite of programs.
 | ||
| Fig. 1 Silicon carbide nanotube. The atoms inside the green band are constrained. White – hydrogen, blue – carbon and yellow – silicon. | ||
3 Results and discussion
3.1 Unconstrained nanotubes
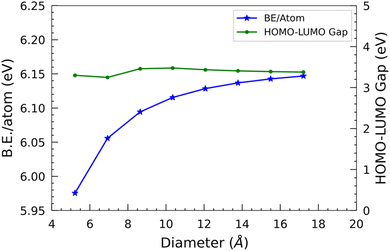
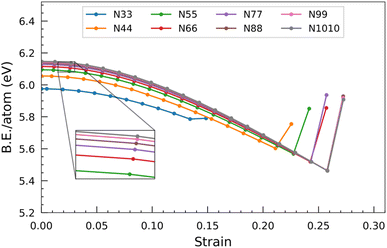
In the case of the smallest SiCNT considered, i.e. N33, each atom has a binding energy of 5.96 eV. We can observe a rapid increase in binding energy in N44, N55, and N66, which signifies a notable enhancement in the stability of these two nanotubes compared to N33. However, when the size of the nanotube surpasses that of N66, the binding energy gradually increases. It ultimately levels off at approximately 6.10 eV per atom.
The difference in the energies of the two frontier orbitals, i.e. HOMO–LUMO gap, determines the stability and conductivity of a molecular structure. It approximates the band gap of infinite nanotubes. In this study, we have used the finite cluster approximation, so this measure only gives the approximate value of the band gap of nanotubes. Also, the B3LYP functional used slightly overestimates the band gap.34 We are primarily interested in the qualitative comparison of the band gap of SiC nanotubes of different diameters, so it suffices for our discussion. Overall, the HOMO–LUMO gap first slightly decreases, and then increases, and finally decreases slightly with respect to the diameter of the nanotubes. The N44 SiCNT has the lowest HOMO–LUMO gap of 3.25 eV, whereas the N66 SiCNT has the maximum HOMO–LUMO gap of 3.48 eV. Interestingly, similar to B.E./atom, the HOMO–LUMO gap reaches a plateau as the nanotube diameter increases, i.e. beyond N66 SiCNT. The HOMO–LUMO gap of all the nanotubes is quite similar and approximately 3.3 eV, indicating their wide HOMO–LUMO gap semiconducting nature. This is in contrast to carbon nanotubes of armchair configuration, which exhibit metallic characteristics.35 Similar to the binding energy, the saturation point observed in the HOMO–LUMO gap signifies that the larger nanotubes approach the limiting value of the HOMO–LUMO gap of graphitic silicon carbide sheets.
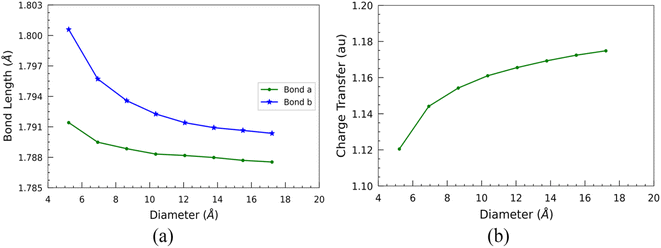
Furthermore, we examined the two types of optimized bond lengths of SiCNTs: the bond perpendicular to the axis of the nanotube, labeled “Bond a”, and the slanted bond, labeled “Bond b” (Fig. 1). The variation of these bond lengths with the SiCNT diameter is illustrated in Fig. 3(a). Overall, both of the bonds decrease monotonically with the size of nanotubes. Initially, both considered bond lengths exhibit a sharp decline before reaching a plateau. This decrease suggests heightened ionicity within the Si–C bonds of SiCNTs.36 To elucidate this, we performed a Mulliken charge analysis of the neighboring silicon and carbon atoms. For this, we considered the two adjacent carbon and silicon atoms in the nanotube central region to mitigate the influence of their ends on our change analysis. A charge transfer parameter is introduced as the difference in the Mulliken charges between these two atoms to quantify their charge displacement. The variation of charge transfer with the diameter is shown in Fig. 3(b). It's evident that as the nanotube size increases, the charge transfer—thus the ionicity of SiCNT bonds—also increases. This increase in the ionicity of Si–C bonds in larger nanotubes results in shorter and stronger bonds, consequently leading to an elevation in their binding energy.
Such electronic charge transfer from silicon to carbon atoms in SiCNTs leads to a highly reactive outer wall towards foreign adsorbate. This reactivity makes the SiCNTs attractive for various applications, including developing harmful gas detectors. By utilising pure SiCNTs or metal-functionalized SiCNTs, it might be possible to build highly sensitive gas sensors,14,18,37,38 thereby helping in industrial safety and environmental monitoring. In addition, due to the higher charge transfer (Fig. 3(b)) and the larger surface area in bigger nanotubes, they might be more suitable for constructing gas sensors.
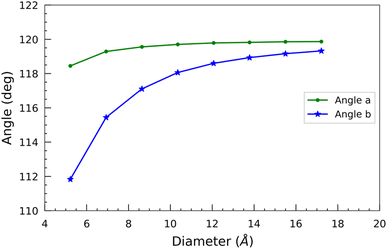
In addition, we measured two bond angles, “Angle a” and “Angle b”, at the opposite corners of the hexagon of each optimized nanotube (Fig. 1). “Angle a” features a silicon atom, while “Angle b” features a carbon atom at its vertex. The change of these angles with the diameter is shown in Fig. 4. In contrast to the bond lengths, both of these angles increase monotonically with the diameter of the SiCNTs. There isn't much variation observed in “Angle a” across different nanotube sizes. In contrast, “Angle b” exhibits a sharp initial increase followed by a gradual plateau in larger nanotubes. For instance, in the case of N33 SiCNT, its value is 111.83°, whereas it jumps to 119.32° in the case of N1010 SiCNT. The smaller angle of “Angle b” can be attributed to the higher radial buckling of smaller nanotubes. It pushes the carbon atoms out of the plane, forming a pyramidal shape with the carbon atom at its apex and three other silicon atoms forming its base.39 Both of these angles tend to converge around 120° for larger nanotubes due to the reduced curvature of the wall.
The frontier orbital electron density cloud of the smallest and biggest SiCNTs considered drawn at an isovalue of 0.02 e− Å−3 is shown in Fig. 5. In N33, molecular orbitals exhibit significant overlap between neighboring atoms due to the higher curvature, indicating higher sp3 hybridization. In contrast, the local structure is almost flat in the case of N1010 due to its small curvature. There is almost no orbital overlap due to reduced hybridization.
3.2 CoGEF analysis
Beyond a certain threshold strain, a noteworthy phenomenon occurs. The binding energy per atom abruptly increases, indicating the collapse of the nanotube and the formation of a new structure. This sudden increase in binding energy signifies transitioning from a strained and weakened state to a more favourable and energetically stable configuration.
To provide a specific example, consider the N55 SiCNT. The binding energy per atom of the unconstrained structure is calculated to be 6.09 eV. As the strain is applied, the binding energy per atom gradually decreases, reaching a minimum value of 5.57 eV when the strain magnitude reaches 0.23. However, further straining of the nanotube leads to its ultimate breakage and the subsequent formation of a new structure. This newly formed structure exhibits an increased binding energy per atom, measured to be 5.85 eV.
Fig. 7 illustrates the correlation between the HOMO–LUMO gap and applied strain across SiCNTs of varying diameters. The findings reveal a consistent pattern: as the nanotubes undergo elongation, the HOMO–LUMO gap decreases. Consequently, the energy required for electron transition decreases, resulting in enhanced conductivity and a shift towards more metallic behavior in the nanotubes. Notably, a significant change occurs at around 0.14 strain, manifesting as a remarkable shift in the slope of the HOMO–LUMO gap. It signifies that the gap experiences a substantial and rapid decrease, akin to the behaviour observed for binding energy. This point could mean the end of the elastic limit for the nanotubes, potentially prompting structural alterations that result in such a dramatic shift in electronic properties. Chen et al.39 also observed a similar significant change in the slope of the HOMO–LUMO curve when examining the N44 SiCNT under uniaxial tensile strain. Once a stable configuration is established beyond a certain strain threshold, the gap rapidly reverts almost to its unconstrained value. This implies that the escalation of the applied strain destabilizes the nanotubes, prompting them to exhibit increasingly metallic characteristics. Interestingly, the gap increments beyond the threshold strain in N33 and N44 nanotubes appear relatively minor compared to nanotubes with larger diameters.
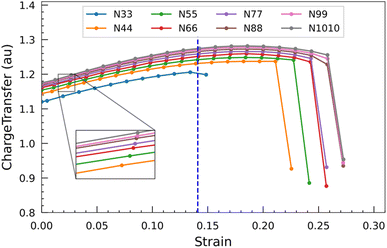
The graph presented in Fig. 8 shows the displacement of charge within the nanotubes subsequent to applying varying degrees of strain. The transfer of charge increases when the nanotube is progressively strained. This phenomenon indicates that the more electronegative carbon atom tends to accumulate a greater negative charge from the less electronegative silicon atom as the strain on the nanotube increases. Similar to the HOMO–LUMO gap, the charge transfer also starts to show a parabolic relationship at around 0.14 strain. Beyond this, when the strain approaches approximately 0.20, the charge transfer starts to decline. When the nanotubes ultimately yield and fracture, there is a pronounced and steep decline in the charge transfer. This remarkable drop indicates a loss of the previously enhanced charge transfer mechanism, likely due to the structural disruption caused by the nanotubes breaking under strain. From these observations, it can be inferred that the strength of the outer wall decoration of SiC nanotubes can be increased by subjecting them to an external force.
The frontier orbitals in N66 SiCNT drawn at an isovalue of 0.02 e− Å−3 under the influence of various strains are depicted in Fig. 9. In their unconstrained state, these molecular orbitals are primarily concentrated around the periphery of the nanotube. However, upon applying strain, these orbitals relocate towards the central region of the nanotube. So, we can conclude that straining lowers the frontier energy gap (Fig. 7) and causes a migration of the frontier orbitals towards the central area. This shift makes the central region more reactive compared to the rim region.
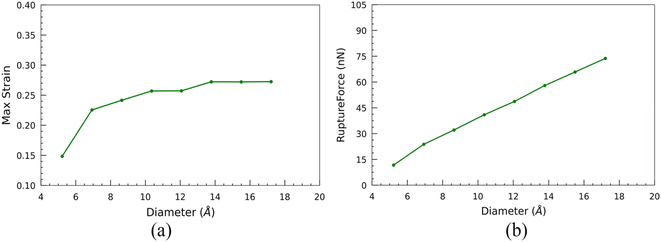
Additionally, the nanotubes exhibit a significant initial surge in their maximum strain-withstanding capacity at the breaking point. However, as the size of the nanotubes increases, this capability gradually diminishes until it ultimately levels off and remains constant (Fig. 11(a)). The maximum force experienced by the nanotube at this breaking point along the CoGEF path is referred to as the rupture force. The magnitude of the rupture force is influenced by the stability of the nanotube structure, which, in turn, depends on the nanotube's diameter. Nanotubes with larger diameters exhibit higher stability. Consequently, these larger-diameter nanotubes experience higher rupture forces than their smaller-diameter counterparts (Fig. 11(b)). For instance, the least stable SiCNT, N33, exhibits the lowest rupture force of 11.69 nN. In contrast, the most stable structure, N1010 SiCNT, experiences a significantly higher rupture force of 73.78 nN. This disparity in rupture forces highlights the impact of the nanotube diameter on their structural stability and resistance to mechanical strain.
In Fig. 13, we illustrate the structural evolution of the N66 SiCNT at strains of 0.16 and 0.24. As strain is applied, the honeycomb-like structure of the nanotube becomes distorted. At a strain of 0.26, the nanotube fractures near its midpoint, forming two stable clusters. Notably, bonds at the ends of fractured sections lose their characteristic hexagonal honeycomb pattern, adopting a square geometry instead. Therefore, the breaking strain brings about a significant change in the nanotube's structural integrity and geometry.
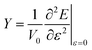 | (2) |
A nanotube can be considered a hollow cylinder, with V0 = 2πLRδR, where L, R, and δR are an unconstrained nanotube's length, radius, and thickness. To address the ambiguity surrounding the definition of δR, we decided to utilize an alternative approach proposed by Hernández et al.40 This approach considers Young's modulus independent of δR, and the new modulus so defined is termed effective Young's modulus (Ys) as shown in eqn (3).
 | (3) |
The evolution of effective Young's modulus with the diameter of SiCNTs is shown in Fig. 14. It can be observed that the effective Ys of SiCNTs increases with the increase in the diameter. Notably, for smaller SiCNTs, Ys has a pronounced and rapid increase. However, as the diameter of the nanotube increases, Ys becomes insensitive to further changes in the diameter. This trend can be attributed to the increase in the binding energy of the SiCNTs, due to a decrease in strain caused by the curvature effect. For instance, the smallest nanotube, N33, exhibits the minimum Ys value of 0.137 TPa m. As we move to slightly larger nanotubes, such as N55, Ys plateaus at around 0.16 TPa m. Our results are in excellent agreement with the magnitude of Ys obtained by Baumeier et al.41 employing DFT with self-interaction corrected pseudopotentials. The difference between our findings and theirs is minimal, amounting to a mere 3% at most. In contrast, Zhang et al.,42 using molecular dynamics simulation, reported a similar trend but slightly higher Ys values than our result. This might be because they used an empirical potential that didn't consider the curvature effect.
4 Conclusions
In this study, we studied the mechanochemistry of SiCNTs of different diameters using the CoGEF method. Initially, we investigated the influence of the size of unconstrained nanotubes on their stability and electronic properties. We observed that the binding energy and frontier orbital gap of unconstrained SiCNTs exhibit an increasing trend as the diameter increases. Furthermore, larger nanotubes exhibited smaller bond lengths and higher Mulliken charge transfer, suggesting an increased ionicity in the silicon and carbon bonds, highlighting their potential in gas sensing applications. When subjected to stretching, the binding energy and HOMO–LUMO gap of nanotubes decrease gradually until reaching a critical threshold strain, signifying their breakage. When the strain is further increased, they abruptly increase, indicating the formation of a stable structure. Both angles “a” and “b” decrease as strain is applied, while bond “a” remains nearly constant and bond “b” steadily increases. The honeycomb structure formed by the bonds of the nanotubes undergoes distortion under strain. Beyond the breaking point, the bonds at the fracture end form a square-shaped geometry. The higher binding energy in the case of larger nanotubes makes them capable of withstanding greater force; hence, they have a large rupture force. The increase in the ionicity of Si–C bonds within strained nanotubes makes them more conducive to outer wall decoration. Additionally, Young's modulus swiftly increases initially and then converges to a constant magnitude as the diameter increases.Conflicts of interest
There are no conflicts to declare.References
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS
.
- N. Jain, E. Gupta and N. J. Kanu, Smart Science, 2022, 10, 1–24 CrossRef
.
- M. F. L. De Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Science, 2013, 339, 535–539 CrossRef CAS PubMed
.
- C. Vatankhah and H. A. Badehian, Solid State Commun., 2022, 344, 114672 CrossRef CAS
.
- Y. Miyamoto and B. D. Yu, Appl. Phys. Lett., 2002, 80, 586–588 CrossRef CAS
.
- X.-H. Sun, C.-P. Li, W.-K. Wong, N.-B. Wong, C.-S. Lee, S.-T. Lee and B.-K. Teo, J. Am. Chem. Soc., 2002, 124, 14464–14471 CrossRef CAS PubMed
.
- Z. Xie, D. Tao and J. Wang, J. Nanosci. Nanotechnol., 2007, 7, 647–652 CrossRef CAS PubMed
.
- V. C. S. Tony, C. H. Voon, C. C. Lee, B. Y. Lim, S. C. B. Gopinath, K. L. Foo, M. K. M. Arshad, A. R. Ruslinda, U. Hashim, M. N. Nashaain and Y. Al-Douri, Mater. Res., 2017, 20(6), 1658–1668 CrossRef CAS
.
- R. S. Singh, Silicon, 2023, 15(10), 4501–4511 CrossRef CAS
.
- M. Eghbalian, R. Ansari and S. Haghighi, Diamond Relat. Mater., 2022, 121, 108764 CrossRef CAS
.
- M. Zhao, Y. Xia, F. Li, R. Q. Zhang and S. T. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 085312 CrossRef
.
- K. Adhikari and A. K. Ray, Phys. Lett. A, 2013, 377, 2147–2153 CrossRef CAS
.
- J.-x. Zhao and Y.-h. Ding, J. Phys. Chem. C, 2008, 112, 2558–2564 CrossRef CAS
.
- M. Doust Mohammadi, H. Y. Abdullah, S. Bhowmick and G. Biskos, Silicon, 2023, 15, 177–186 CrossRef CAS
.
- Z. Khatti, S. M. Hashemianzadeh and S. A. Shafiei, Adv. Pharm. Bull., 2018, 8, 163–167 CrossRef CAS
.
- R. S. Singh and A. Solanki, Chem. Phys. Lett., 2016, 660, 155–159 CrossRef CAS
.
- J.-x. Zhao and Y.-h. Ding, J. Chem. Theory Comput., 2009, 5, 1099–1105 CrossRef CAS PubMed
.
- P. Wu, W.-D. Duan, J.-X. Zhao, Q.-H. Cai, X.-G. Wang and X.-Z. Wang, J. Comput. Theor. Nanosci., 2011, 8, 2469–2473 CrossRef CAS
.
- M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martínez, J. Am. Chem. Soc., 2009, 131, 6377–6379 CrossRef CAS PubMed
.
- J. Ribas-Arino, M. Shiga and D. Marx, Angew. Chem., Int. Ed., 2009, 48, 4190–4193 CrossRef CAS PubMed
.
- K. Wolinski and J. Baker, Mol. Phys., 2009, 107, 2403–2417 CrossRef CAS
.
- M. K. Beyer, J. Chem. Phys., 2000, 112, 7307–7312 CrossRef CAS
.
- M. F. Iozzi, T. Helgaker and E. Uggerud, J. Phys. Chem. A, 2011, 115, 2308–2315 CrossRef CAS PubMed
.
- I. M. Klein, C. C. Husic, D. P. Kovács, N. J. Choquette and M. J. Robb, J. Am. Chem. Soc., 2020, 142, 16364–16381 CrossRef CAS PubMed
.
- Y. Janpatompong, K. Suwada, M. L. Turner and G. De Bo, Polym. Chem., 2023, 14, 1978–1982 RSC
.
- M. Tiwari, A. Bhusal and K. Adhikari, Himalayan Physics, 2019, 8, 39–46 CrossRef
.
-
H. Rafii-Tabar, Computational Physics of Carbon Nanotubes, Cambridge University Press, 2008 Search PubMed
.
- K. Adhikari and A. K. Ray, Phys. Lett. A, 2011, 375, 1817–1823 CrossRef CAS
.
- K. M. Alam and A. K. Ray, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 035436 CrossRef
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed
.
- J. Muscat, A. Wander and N. M. Harrison, Chem. Phys. Lett., 2001, 342, 397–401 CrossRef CAS
.
- Y. Matsuda, J. Tahir-Kheli and W. A. Goddard III, J. Phys. Chem. Lett., 2010, 1, 2946–2950 CrossRef CAS
.
- A. Zhang, X. Gu, F. Liu, Y. Xie, X. Ye and W. Shi, Phys. Lett. A, 2012, 376, 1631–1635 CrossRef CAS
.
- W.-q. Lin, F. Li, G.-h. Chen, S.-t. Xiao, L.-y. Wang and Q. Wang, Ceram. Int., 2020, 46, 25171–25188 CrossRef CAS
.
- R. Q. Wu, M. Yang, Y. H. Lu, Y. P. Feng, Z. G. Huang and Q. Y. Wu, J. Phys. Chem. C, 2008, 112, 15985–15988 CrossRef CAS
.
- H.-L. Chen, S.-P. Ju, J.-S. Lin, J. Zhao, H.-T. Chen, J.-G. Chang, M. H. Weng, S.-C. Lee and W.-J. Lee, J. Nanopart. Res., 2010, 12, 2919–2928 CrossRef CAS
.
- E. Hernández, C. Goze, P. Bernier and A. Rubio, Phys. Rev. Lett., 1998, 80, 4502–4505 CrossRef
.
- B. Baumeier, P. Krüger and J. Pollmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085407 CrossRef
.
- Y. Zhang and H. Huang, Comput. Mater. Sci., 2008, 43, 664–669 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2024 |