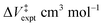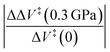Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modeling mechanochemistry: pressure dependence of Diels–Alder cycloaddition reaction kinetics†
Nicholas
Hopper
a,
François
Sidoroff
b,
Juliette
Cayer-Barrioz
 b,
Denis
Mazuyer
b,
Denis
Mazuyer
 b,
Bo
Chen
b,
Bo
Chen
 c and
Wilfred T.
Tysoe
c and
Wilfred T.
Tysoe
 *a
*a
aDepartment of Chemistry and Biochemistry, University of Wisconsin-Milwaukee, Milwaukee, WI 53211, USA. E-mail: wtt@uwm.edu
bLaboratoire de Tribologie et Dynamique des Systèmes, CNRS UMR5513, Ecole Centrale de Lyon, F-69134 Ecully cedex, France
cDonostia International Physics Center, IKERBASQUE, Basque Foundation for Science, 20018 Donostia-San Sebastián, Plaza Euskadi 5, 48009 Bilbao, Spain
First published on 1st August 2024
Abstract
We analyze the effect of pressure on the Diels–Alder (D–A) dimerization reactions using Evans–Polanyi (E–P) theory, a thermodynamic analysis of the way in which a perturbation, in this case a hydrostatic pressure, modifies a reaction rate. Because it is a thermodynamic analysis, the results depend only on the volumes of the initial- and transition-state structures and not on the pathways between them. The volumes are calculated by enclosing the initial- and transition-state structures in a van der Waals' cocoon. Pressure is exerted by multiplying the van der Waals' radii by some factor without allowing the initial- and transition-state structures to relax. The influence of the surrounding solvent is included by using the extreme-pressure, polarizable-continuum method (XP-PCM). The approach is illustrated in detail using cyclopentadiene dimerization for which the rates have been independently measured by two groups. The analysis provides results that are in good agreement with those found experimentally for measurements made up to ∼0.3 GPa. The activation volumes of other D–A reactions are calculated in the same way and lead to good agreement for non-polar reactants, but less good agreement for polar ones. The pressure can also distort the initial- and transition-state structures, which can be calculated from the initial- and transition-state Hessians. A pressure-dependent distortion requires knowing the area over which the hydrostatic pressure acts. This is obtained using the Stearn–Eyring postulate that the activation volume is the product of an activation length and the area over which the stress acts. The activation length is obtained from quantum calculations of the difference in the distances between the diene and dienophile in the initial- and transition states. This provides only minor corrections to the results for routinely accessible hydrostatic pressures.
Introduction
Arguably the most interesting and challenging problems in chemistry, physics and materials science are those that involve stimulating the transformation from one metastable state of the system to another. One method of modifying the rates of such transformations is by exerting forces on the system.1–11 While mechanochemically induced reactions have been known for millennia,12 and the grinding of food may have contributed to the development of early hominids,13 mechanochemistry is perhaps the least well-understood method of modulating chemical reaction rates. Despite this, a large number of mechanochemical reactions have been empirically discovered over the last few years, many of which can be performed with a minimum of solvent and are therefore environmentally friendly, or “green”.1–9,14–22 The large stresses required to induce mechanochemical reactions are often induced at solid–solid interfaces, such as in a ball mill,23 but it is difficult to study these interfacial processes so that it has been a challenge to rigorously test the validity of mechanochemical models. In addition to being used for chemical syntheses, mechanochemical processes appear to dominate the operation of lubricants24–26 in perhaps the most economically important subfield of mechanochemistry known as tribochemistry.The Born–Oppenheimer potential-energy surface (the BO-PES) is at the heart of physicochemical analyses of chemical-reaction rates. Molecules are the stable structures that form at local minima of the PES and calculating reaction kinetics requires measuring the transit rate from one metastable state to another. A challenge is to model the collective behavior of a large number of molecules. This can be accomplished either by using the fluctuation-dissipation theorem27 or by borrowing ideas from statistical thermodynamics by using transition-state theory.28 Transition-state theory proposes that, while there are an infinite number of possible trajectories from the reactants to the products, the most probable one proceeds via the lowest-energy pathway over an activation barrier. The unstable structure at the highest energy of this pathway is known as an “activated complex”. It can decompose with equal probabilities to either reform the reactant or form a product. The energy of the activated complex relative to the reactants (the initial state) is the activation energy, and the local PES around this point has one negative force constant (Hessian) due to the structure being unstable. This picture has the advantage of reducing a complex, multidimensional problem to a one-dimensional plot of potential energy as a function of the extent of the reaction, or the “reaction coordinate”. The problem is then to calculate the activated complex concentrations using statistical thermodynamics. When transition-state theory was developed, the nature of the activated complex was unclear, although now quantum-mechanical methods have been developed to compute its structure.29–33 An important consequence of this thermodynamic analysis is that the Gibbs free energy change between the transition- and the initial-states does not depend on the pathways between them. In transition-state theory, the reaction coordinate is merely defined as some value that increases as the reaction proceeds, but has been identified as the path of steepest decent from the transition state to the initial state.34 One of the most important benefits of transition-state theory is that it provides a formalism that enables chemists to correlate differences in chemical reactivity with molecular structure.35
The basic idea that underpins mechanochemistry is that a force or stress modifies the BO-PES to change the energies and locations of the initial- and transition-states of a reaction so as to change the rate constants.18,20 Judicious modification of the PES can selectively reduce the energy barriers of non-thermally accessible reaction pathways so that they become favorable.36 The reaction follows the force-displaced stationary points37 on this modified PES to lead to a so-called Newton trajectory.38 However, it would be advantageous to develop a theory that maintained the intuitive simplicity of transition-state theory while providing insights into the processes that control mechanochemical reactivity. A perturbation method of transition-state theory has been developed by Evans and Polanyi39,40 that fulfils these requirements that will be described in greater detail below.
Arguably an impediment to developing and testing theories of mechanochemical reaction rates has been the lack of precise measurements of the kinetics of well-characterized reactions. Fortunately, a large number of hydrostatic-pressure-modified reaction rate have been measured41–45 to allow mechanochemical theories to be tested.46–48
More recently, the rates of mechanochemical reactions have been measured using an atomic-force microscope (AFM) tip compressing or sliding on surfaces.24,45,49–51 In particular, the ability to characterize the nature of the surface reaction pathway52–54 has allowed the normal-stress dependence of the reaction rate to be measured and accurately modeled using Evans–Polanyi (E–P) perturbation theory.55,56 The goal of the work outlined in the following is to use E–P perturbation theory to calculate the activation volumes for the hydrostatic-pressure dependences of the rates of Diels–Alder cycloaddition reactions.
Evans–Polanyi perturbation theory
The Evans–Polanyi (E–P) analysis is based on the idea that the reaction rate depends on the equilibrium constant between the initial- and the transition state.39,40 The equilibrium constant for the overall reaction K depends on the standard, molar Gibbs free energy change for the process, ΔG°, as:ΔG° = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, K, | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, where ΔG° is now the Gibbs free energy change between the transition-state and initial-state.
K, where ΔG° is now the Gibbs free energy change between the transition-state and initial-state.
Depending on the reaction conditions, the Gibbs free energy G of a system can include perturbations described by some intensive variable, I (such as pressure or stress), by using the associated extensive conjugate variable, C, such that IdC equals the reversible work done on the system, so that G = U − TS + IC.58 In the case of a hydrostatic pressure, P, the conjugate variable is −V.59 Evans and Polanyi39,40 also used their perturbation theory to derive the Nernst and Tafel equations in electrochemistry.60 This approach is quite general and can be used for calculating the dependence of a chemical reaction rate on any perturbation as long as the corresponding conjugate variable is known. The conjugate variable, C, can itself depend on I,61 as was alluded to by Evans and Polanyi,39,40 so that the general equation for the standard Gibbs free energy change becomes:
| ΔG° = ΔU° − TΔS° + IΔC°(I). | (2) |
When the reaction rate is modified by a hydrostatic pressure, P, then k, the pressure-dependent rate constant is given by: 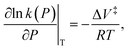 and integrating gives:
and integrating gives: 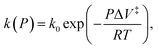 where P is the hydrostatic pressure, T the absolute temperature, k0 is the rate constant in the absence of an external pressure, and ΔV‡ is an activation volume. Assuming that the pre-exponential factor does not depend strongly on pressure and writing the rate constant in its Arrhenius form gives Eact(P) = Eact + PΔV‡. This commonly known as the Bell equation.62 This method is distinct from non-equilibrium thermodynamics63 and the Evans–Polanyi theory specifically applies to systems in which perturbations, such as a pressure or stress, modify the rate of a transition from one state to another over an activation barrier. This gives a linear dependence of the activation energy on pressure when the activation volume is a constant, but high-order dependences occur when the volume itself varies with pressure. There are several conceptual advantages to using such an Evans–Polanyi approach. As a consequence of Hess' law,57 as for transition-state theory, the rate depends only on the properties of the initial- and transition states, and is independent of the pathway between them.64,65
where P is the hydrostatic pressure, T the absolute temperature, k0 is the rate constant in the absence of an external pressure, and ΔV‡ is an activation volume. Assuming that the pre-exponential factor does not depend strongly on pressure and writing the rate constant in its Arrhenius form gives Eact(P) = Eact + PΔV‡. This commonly known as the Bell equation.62 This method is distinct from non-equilibrium thermodynamics63 and the Evans–Polanyi theory specifically applies to systems in which perturbations, such as a pressure or stress, modify the rate of a transition from one state to another over an activation barrier. This gives a linear dependence of the activation energy on pressure when the activation volume is a constant, but high-order dependences occur when the volume itself varies with pressure. There are several conceptual advantages to using such an Evans–Polanyi approach. As a consequence of Hess' law,57 as for transition-state theory, the rate depends only on the properties of the initial- and transition states, and is independent of the pathway between them.64,65
Second, the theory directly yields a formula for the pressure-dependent rate constant, the value that is experimentally measured, and does not involve the reaction activation energy, although it can be obtained from the rate constant using the Arrhenius relation if the pre-exponential factor is known. Third, it can be used to simultaneously analyze the influence of multiple perturbations on the Gibbs free energy and therefore on the reaction rate. Finally, it is more efficient than having to calculate the full energy profile and thus is useful for high-throughput analyses.
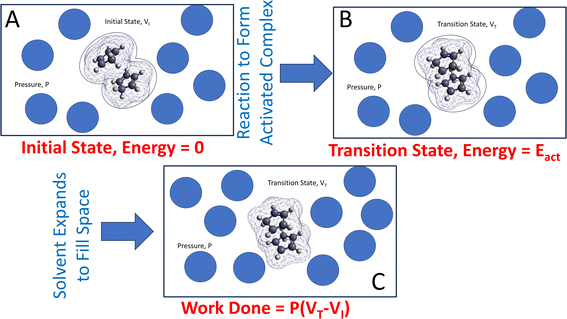
The approach is illustrated in Fig. 1. A reacting ensemble (in this case, two cyclopentadiene molecules in a van der Waals' bound initial-state configuration) with volume VI is surrounded by solvent molecules that collide with the reactants to exert a hydrostatic pressure P. During a reaction, the volume of the transition-state structure (the activated complex) changes to VT. Note that this volume change was not induced by the hydrostatic pressure but is a change that takes place naturally as the reaction occurs. This contribution to the Gibbs free energy is P(VT − VI) due to the surrounding solvent adjusting to maintain a constant pressure. This emphasizes the need to include the effect of the solvent on mechanochemical reactions that are carried out in solution. In the following analyses, the interaction is modeled using the polarizable continuum method (PCM).66
The same considerations apply in cases in which the reaction rate is modified by an AFM tip compressing or sliding on surfaces.24,45,49–51 The reaction results in a change of tip position when it contacts the initial- and transition-state structures so it undergoes additional work F(zT − zI), where F is the force and (zT − zI) is the height difference between the transition- and initial state structures. Here, (zT − zI) is known as the activation length.
However, as indicated by eqn (2), the perturbation can also change the value of conjugate variables, here the volumes, so that VT = VT(P) and VI = VI(P), so that the activation volume itself depends on pressure; ΔV‡ = ΔV‡(P). Methods for calculating this pressure dependence and for gauging its importance are also discussed.
Calculating linear-pressure-dependent reaction rates
Mechanochemical reaction rates are calculated using the perturbation method for transition-state theory developed by Evans and Polanyi39,40 by modeling the surrounding solvent using the extreme-pressure polarizable continuum (XP-PCM) method.46,47,66–68 This was not required for experiments carried out using an AFM tip in vacuo. An initial version of XP-PCM does not consider the distortion of the reacting ensemble inside the cavity and thus strictly measures an activation volume within the Bell approximation.We first analyze the Diels–Alder cycloaddition of cyclopentadiene because the pressure-dependent kinetics have been independently measured by two different laboratories to provide pressure-dependent activation volumes,41,42 which is then extended to analyzing other Diels–Alder reactions. The energy profiles were calculated using Gaussian 16 (ref. 69) to yield plots of the Gibbs free energy versus the intrinsic reaction coordinate (IRC). The Evans–Polanyi analysis only requires the effects on the initial- and transition-states to be calculated so that the influence of hydrostatic pressure and solvent on only these structures is calculated using the XP-PCM model.46,47,66–68 This calculates the energies of the initial- and transition-state structures embedded in a cavity of volume Vc that is constructed by enclosing them in van der Waals' spheres centered on the constituent atoms.67 The cavity uses spheres of radii Ri centered on each nucleus of the atoms, where Ri = fRvdW, and the RvdW are the van der Waals' radii of each atom. Additional spheres are added to create a solvent-excluded surface cavity. The volume of the cavity is varied by adjusting the scaling factor f so that smaller values of f decrease the volume and increase the hydrostatic pressure.
The XP-PCM method calculates an electronic free energy, Ger(P,R), where P is the pressure and R defines the nuclear positions. The cavity pressure is obtained from 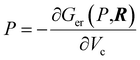 that also enables a so-called cavity free energy, Gcav(P,R), to be calculated66 to model the way in which the system interacts with a surrounding fluid. The method is described in greater detail elsewhere.46,67 The total energy is given by Gtot(P,R) = Ger(P,R) + Gcav(P,R). This method therefore differs from previous calculations of methyl thiolate mechanochemical reaction kinetics that were measured and modeled in vacuo.45,55 Only the Gibbs free energies of the initial- and transition-state structures are required as a function of the cavity volume, Vc, obtained by varying the parameter f over the suggested range from 1.2 to 0.9.46 As the cavity volume decreases, the energy of the system increases as the envelope interacts with the initial- or transition-state structures. The solvent is treated as a polarizable continuum with a uniform dielectric constant and the effect of solvent compressibility was taken into account using an η parameters, which was set to be 3. As such, the PCM methods is expected to work less well for polar reactants.
that also enables a so-called cavity free energy, Gcav(P,R), to be calculated66 to model the way in which the system interacts with a surrounding fluid. The method is described in greater detail elsewhere.46,67 The total energy is given by Gtot(P,R) = Ger(P,R) + Gcav(P,R). This method therefore differs from previous calculations of methyl thiolate mechanochemical reaction kinetics that were measured and modeled in vacuo.45,55 Only the Gibbs free energies of the initial- and transition-state structures are required as a function of the cavity volume, Vc, obtained by varying the parameter f over the suggested range from 1.2 to 0.9.46 As the cavity volume decreases, the energy of the system increases as the envelope interacts with the initial- or transition-state structures. The solvent is treated as a polarizable continuum with a uniform dielectric constant and the effect of solvent compressibility was taken into account using an η parameters, which was set to be 3. As such, the PCM methods is expected to work less well for polar reactants.
This Diels–Alder reaction has previously been analyzed by the XP-PCM method by performing energy calculations for structures throughout the whole reaction pathway,67 while here it is implemented within the framework of an Evans–Polanyi analysis and thus only requires the values for the initial- and transition-states, GIer(Vc) and GTer(Vc), to be calculated as a function of the cavity volume, Vc. This is analogous to the results obtained by compressing a methyl thiolate species on a copper surface except that, in that case, the structures of the adsorbed methyl thiolate species were allowed to relax.55 Since only the reactant molecules and the transition-state structures are analyzed, this allows energies to be calculated using small volume intervals allowing more precise fits to be made to plots of Gibbs free energy versus volume.
It has been found that the volume dependence of the Gibbs free energies can be reproduced quite well using a modification of the Murnaghan equation of state:
 | (3) |
 and using the constraint that Ger(Vc) − Ger(V0c) = 0 when x = 1 allows eqn (3) to be rewritten with the substitutions, aV0c = α, cV0c = γ and β = b − 1 to give:
and using the constraint that Ger(Vc) − Ger(V0c) = 0 when x = 1 allows eqn (3) to be rewritten with the substitutions, aV0c = α, cV0c = γ and β = b − 1 to give: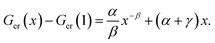 | (4) |
The pressures are calculated from  to give P as a function of Vc using the fitting parameters, α, β, and γ for the initial- and transition-state structures to yield:
to give P as a function of Vc using the fitting parameters, α, β, and γ for the initial- and transition-state structures to yield:
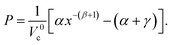 | (5) |
The pressure associated with each scaling factor f is then determined by averaging the pressure over all structures. This yields GRer(![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) ) and GTer(
) and GTer(![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) ). Gtot(
). Gtot(![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) ) for each structure is then computed by:
) for each structure is then computed by:
Gtot(![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) ) = Ger( ) = Ger(![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) ) + Gcav[P], ) + Gcav[P], | (6) |
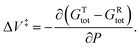 Note here that the initial-state structures used in the XP-PCM calculations are those of isolated reactant molecule, rather than the van der Waals' bound initial-state depicted in Fig. 1. That is, the initial-state energies and volumes represent the isolated reactant molecules in solution.
Note here that the initial-state structures used in the XP-PCM calculations are those of isolated reactant molecule, rather than the van der Waals' bound initial-state depicted in Fig. 1. That is, the initial-state energies and volumes represent the isolated reactant molecules in solution.
Evans–Polanyi theory indicates that a pressure-dependent rate constant k(P) is given by: 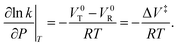 This equation can be integrated to give:
This equation can be integrated to give:
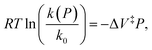 | (7) |
Note that this analysis includes the effect of the environment, but not distortions of the initial- and transition-state structures during compression. This approach therefore allows the importance of various contributions to the mechanochemical reaction rates to be gauged, in particular the influence of distortions at higher pressures. The way in which they are calculated is discussed below.
Calculating second-order pressure-dependences
As noted above, the activation volume can itself depend on pressure. It has been suggested that molecular distortions are key to modifying the rates of mechanochemical reactions,71,72 while the above analysis indicates that they do not to contribute the Bell-like, linear force or pressure dependences. However, they do contribute to second-order effects. In order to estimate the extent to which they contribute to mechanochemical activity, here we outline a method of calculating the stress dependence using the force constants (Hessians) of the initial- and transition-states. Hessians have previously been used to calculate force-dependent molecular distortions,73,74 but calculating stress-dependent distortions requires knowing the area over which the forces act. We note that, in the latest development of XP-PCM, geometry optimization under pressure is possible so that distortion of the reacting molecules could, in principle, be directly studied by XP-PCM.75 However, the current implementation of XP-PCM geometry optimization only works well for small molecules. For larger systems, such as the Diels–Alder reactions studied here, there tends to be convergence problems in the geometry optimization, which prompts us to use this alternative approach to study molecular distortion.Stress- (as opposed to force-) dependent distortions can be calculated from the values of the initial- and transition-state Hessians obtained from the quantum calculations by using the Stearn–Eyring approximation that relates the activation volume to the activation length.76 The shape of the potential energy surface as a function of the position vectors of the atoms, U(R), can be expanded up to second order about the turning points (the minimum (initial state) or a saddle point (transition state)). Since, by definition, their first derivatives are zero, the potential is:
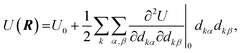 | (8) |
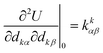 is the force constant (Hessian) matrix of the system. This can be written in matrix notation as
is the force constant (Hessian) matrix of the system. This can be written in matrix notation as 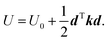
It is convenient to describe the potential energy using normal coordinates Q that involve the motion of all atoms of the reacting system. We introduce a 3N × 3N matrix L that transforms the coordinates from d to another system Q as Q = L−1d and d = LQ,77 so that eqn (8) becomes  Since the displacements are real and since L−1(L−1)T = I, where I is the identity matrix, then LTL = I. For a non-singular matrix L, then LT = L−1, so that L is an orthogonal matrix. We now choose a particular L matrix such that it diagonalizes the force-constant (Hessian) so that LTkL = Λ, where Λ is a diagonal 3N × 3N force-constant matrix with elements λ1, λ2, λ3,…λ3N, and kii = λi and kij = 0 for i ≠ j. Multiplying this equation by L yields the following eigenvalue equation:
Since the displacements are real and since L−1(L−1)T = I, where I is the identity matrix, then LTL = I. For a non-singular matrix L, then LT = L−1, so that L is an orthogonal matrix. We now choose a particular L matrix such that it diagonalizes the force-constant (Hessian) so that LTkL = Λ, where Λ is a diagonal 3N × 3N force-constant matrix with elements λ1, λ2, λ3,…λ3N, and kii = λi and kij = 0 for i ≠ j. Multiplying this equation by L yields the following eigenvalue equation:
| kL = LΛ, | (9) |
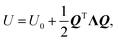 and, since Λ is a diagonalized Hessian, gives:
and, since Λ is a diagonalized Hessian, gives: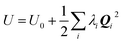 | (10) |
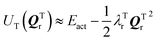 and
and 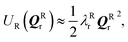 where Eact is the reaction activation energy and the negative sign in this equation reflects the fact that the transition-state potential is a saddle point. To calculate the effect of a force on the structures, since F = ∇U, then
where Eact is the reaction activation energy and the negative sign in this equation reflects the fact that the transition-state potential is a saddle point. To calculate the effect of a force on the structures, since F = ∇U, then  and
and 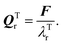 If the projected areas of the reactant molecules along directions parallel to QRr and QTr are AR and AT, then
If the projected areas of the reactant molecules along directions parallel to QRr and QTr are AR and AT, then 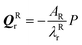 and
and  where P is the hydrostatic pressure. Substituting into the equations for the energy of the system gives a pressure-dependent energy change due to molecular distortion:
where P is the hydrostatic pressure. Substituting into the equations for the energy of the system gives a pressure-dependent energy change due to molecular distortion: | (11) |
Note that the positive initial-state and negative transition-state Hessians will generally lead to a reduction in activation volume at higher pressures. Evaluating this equation, however, requires knowing AT and AR, which can be determined from the activation volume calculated using XP-PCM when combined with an activation length obtained from the quantum calculations of the reaction as described in the following section. It should be noted that other, low-frequency modes of flexible functional groups attached to the reactants might also provide additional contributions to pressure-dependent changes to the activation volume.
Calculating values of AR and AT
Evans–Polanyi theory indicates that the activation length corresponds to a vector connecting the initial and transition states. Since the initial states for Diels–Alder reactions are more compliant than for the transition state,46 it will have a greater influence on the energy barrier than the much sharper transition state. This occurs because of the weak van der Waals' interactions between the initial-state reactants in this biomolecular process compared to the transition-state structure, which has shorter-range, bond-forming interactions. If we define the activation length relative to the initial state-location as Δx‡, then the Stearn–Eyring approximation gives ΔV‡ = ATΔx‡,76 so that we now need the correspond value of AR. However, microscopic reversibility requires that the activation length for the reverse reaction is −Δx‡, which defines an activation length relative to the transition-state. This is equivalent to a force acting in the reverse direction and will have an activation volume of −ΔV‡ so that the Stearn–Eyring approximation now gives −ΔV‡ = −ARΔx‡, so that AT = AR, so that eqn (11) becomes: where now AC is the area over which the stress acts and equals both AR and AT.
where now AC is the area over which the stress acts and equals both AR and AT.
This is first applied to the cyclopentadiene dimerization reaction with a view to establishing whether the XP-PCM method can be implemented within the framework of the Evans–Polanyi approach to reproduce the experimental mechanochemical reaction kinetics and secondly, to show how effects due to molecular distortions can be obtained using parameters that are directly available from DFT calculations and to establish how important they are over the range of pressures that are routinely available in mechanochemical processes. The Diels–Alder cycloaddition of cyclopentadiene41,42,46,48 was selected first because experimental results were obtained independently by two different groups, and the rates were also measured as function of pressure to allow the magnitude of second-order effects to be gauged.41,42 The method was then applied to other Diels–Alder reactions, methyl acrylate and isoprene,79 methyl acrylate and cyclopentadiene,42 isoprene dimerization,80 methyl vinyl ketone dimerization,80 and isoprene and methyl vinyl ketone,80 to further test the validity of the Evans–Polanyi approach and to gauge the relative importance of molecular distortion to the overall mechanochemical reactivity. Note that the results for polar reactants are likely to be less reliable that those for non-polar ones because of the limitations of the PCM method.
Results: hydrostatic-pressure induced Diels–Alder reactions: cyclopentadiene dimerization
We apply the Evans–Polanyi analysis to hydrostatic-pressure-modified mechanochemical reactions implemented using the XP-PCM method.43,44 We illustrate the approach for the Diels–Alder dimerization of cyclopentadiene via the endo reaction pathway. A polynomial fit, Gtot(P) − Gtot[f = 1.2] = a + bP + cP2 (see Fig. S2†) yields values of the parameters a, b, and c for the initial- and transition-states that are summarized in Table 1.| Initial state | Endo transition state | |
|---|---|---|
| a | −78947.468 | −139769.230 |
| b | 94.009 | 165.803 |
| c | 0.0006 | 0.0011 |
The resulting plots (see Fig. S2†) are quite linear indicating that, despite the reacting ensemble interacting with the surrounding solvent, the behavior is still Bell-like and the activation volume is pressure independent.
The experimental results are shown in Fig. 2 as a plot of 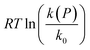 versus P, where eqn (7) indicates that the slope corresponds to −ΔV‡(P); the positive slope here corresponds to a decrease in volume in going from the initial to the transition state, i.e., a negative activation volume. Experiments were carried out independently by two groups.41,42 In particular, the rates were measured by Walling41 at several temperatures where all the data collapse onto a single plot when the temperature is taken into account (eqn (7)). The results are also in very good agreement with those obtained by Seguchi (
versus P, where eqn (7) indicates that the slope corresponds to −ΔV‡(P); the positive slope here corresponds to a decrease in volume in going from the initial to the transition state, i.e., a negative activation volume. Experiments were carried out independently by two groups.41,42 In particular, the rates were measured by Walling41 at several temperatures where all the data collapse onto a single plot when the temperature is taken into account (eqn (7)). The results are also in very good agreement with those obtained by Seguchi ( ).42 The solid black line shows the Bell-like results obtained from the XP-PCM theory as described above, and is in good agreement with experiment and yields an activation volume of −36.9 Å3 per molecule (−22.2 cm3 mol−1).
).42 The solid black line shows the Bell-like results obtained from the XP-PCM theory as described above, and is in good agreement with experiment and yields an activation volume of −36.9 Å3 per molecule (−22.2 cm3 mol−1).
 | ||
Fig. 2 Plot of 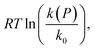 corresponding to the stress-dependence change in reaction activation energy in J mol−1, versus hydrostatic pressure in GPa, showing the experimental collected by Walling et al. ( corresponding to the stress-dependence change in reaction activation energy in J mol−1, versus hydrostatic pressure in GPa, showing the experimental collected by Walling et al. ( , ,  and and 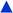 )41 and by Seguchi et al. ( )41 and by Seguchi et al. ( ).42 The theoretical prediction (black solid line) without pressure-induced distortion of the reaction ensemble (the Bell approximation) and including distortion by using the force constants (solid red line). ).42 The theoretical prediction (black solid line) without pressure-induced distortion of the reaction ensemble (the Bell approximation) and including distortion by using the force constants (solid red line). | ||
In order to investigate the influence of compliant initial and transition-states, and thus to gauge the extent of an extended-Bell-type contribution to the mechanochemical activity of cyclopentadiene dimerization,81 we compute the initial-state and transition-state force constants from Gaussian. We note that this could, in principle, have been estimated by allowing the structures of the reacting ensembles to relax for each compression step as was done for the normal-stress-induced decomposition of methyl thiolate species on copper.55
The activation volume obtained from the theoretical slope in Fig. 1 (−36.9 Å3 per molecule) and the locations of the reactants in the initial and transition states, Δx‡ = 1.51 Å per molecule (see Fig. S8R†), gives AC = 24.43 Å2 per molecule. The Gaussian calculation yields force constants of the initial- and transition-state energy profiles of  and
and  Note that the more compliant initial state will have a dominant influence on the P2 dependence. The potential energy surface used to calculate the value of the activation length also shows the shape of the potential about the initial- and transition-states. Harmonic fits are shown in Fig. S8R,† and reproduce the shape of the potential over quite a large range and yield the above values of kR and kT, in good agreement with the values for the transition state calculated directly from Gaussian (see ESI Section†). Similarly good agreement was obtained for the other Diels–Alder reactions. The results are plotted as a red solid line in Fig. 2 and show very little difference from those without the distortion (black line), suggesting that, under the pressures exerted in normal laboratory experiments of ∼0.3 GPa, the effect of molecular distortions is negligible.
Note that the more compliant initial state will have a dominant influence on the P2 dependence. The potential energy surface used to calculate the value of the activation length also shows the shape of the potential about the initial- and transition-states. Harmonic fits are shown in Fig. S8R,† and reproduce the shape of the potential over quite a large range and yield the above values of kR and kT, in good agreement with the values for the transition state calculated directly from Gaussian (see ESI Section†). Similarly good agreement was obtained for the other Diels–Alder reactions. The results are plotted as a red solid line in Fig. 2 and show very little difference from those without the distortion (black line), suggesting that, under the pressures exerted in normal laboratory experiments of ∼0.3 GPa, the effect of molecular distortions is negligible.
Results: other hydrostatic-pressure induced Diels–Alder reactions
The XP-PCM analysis using the Evans–Polanyi method was applied to calculating the activation volumes for other Diels–Alder cycloaddition reactions, which tend to be relatively insensitive to pressure82 and activation volumes measured for a Diels–Alder cycloaddition reactions in several different solvent yielded a standard variation of ∼0.7 cm3 mol−1.83 Note that the results, unlike the cyclopentadiene dimerization reaction, were from a single set of experiments so were not independently corroborated. The results are summarized in Table 2 and agree with experiment within a single standard deviation for non-polar reactants, cyclopentadiene and isoprene, as expected for the PCM method. As anticipated, the agreement for non-polar reactants is less good and tends to underestimate the value of the activation volume by ∼10 cm3 mol−1, possibly due to short-range interactions between the solvent and the reactant causing the force exerted on the reactants to be larger than it would have been. This idea can be tested by including a coordination sphere of solvent molecules around the reaction ensemble and embedding that in a polarizable continuum to explore whether this might be a method of enhancing mechanochemical reactivity.| System | ΔV‡(0)calc cm3 mol−1 | |
|---|---|---|
| CPD + CPD | ||
| Endo | −22.2* | −23.7 ± 2.0 |
| Exo | −21.4 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| CPD + MA | ||
| Endo | −21.6 | −30.1 ± 2.0 |
| Exo | −21.3* | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| IP + IP | ||
| Endo-1 | −21.6 | −24.3 ± 2.0 |
| Endo-2 | −22.6 | |
| Exo-1 | −21.5* | |
| Exo-2 | −19.4 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| IP + MA | ||
| Endo-1 | −23.5 | −30.7 ± 2.0 |
| Endo-2 | −24.0 | |
| Exo-1 | −22.5* | |
| Exo-2 | −21.9 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| IP + MVK | ||
| Endo-1 | −24.8 | −36.9 ± 2.0 |
| Endo-2 | −26.3 | |
| Exo-1 | −23.6* | |
| Exo-2 | −22.9 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| MVK + MVK | ||
| Endo | −26.9* | −36.0 ± 2.0 |
| Exo | −24.0 | |
The effect of molecular distortion on the activation volumes was calculated from the values of the force constants, activation lengths and areas over which the pressure acts using the method described above. The plots of energy as a function of the displacement of the diene and dienophile for these reactions are summarized in the ESI Section (Fig. S8†). The force constants were calculated for the initial- and transition-states with harmonic fits to the initial-and transition-state potentials plotted in Fig. S8.† The parabolic fits to the data cover quite a wide range and the resulting values are in good agreement with the force constants from Gaussian and the results are shown in Table 3. The last column shows the relative change in activation volume under the influence of a pressure of 0.3 GPa, where the corresponding change for cyclopentadiene dimerization, where the results are plotted in Fig. 2, is ∼5%. The results are within the errors limits of the measurements. However, since the change in activation volume scales as the square of the pressure, higher-pressure contacts such as in a ball mill will likely require second-order corrections. Note that the changes for the remainder of the reactions are of the order of a few percent.
| System | Δx‡ nm | A C nm2 | k I N m−1 | k T N m−1 | ΔΔV‡ (0.3 GPa)theory cm3 mol−1 | |
|---|---|---|---|---|---|---|
| CPD + CPD | ||||||
| Endo | 0.151 | 0.244 | 8.43 | −148.95 | 1.21 | 0.05 |
| Exo | 0.153 | 0.232 | 10.37 | −140.51 | 0.87 | 0.04 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| CPD + MA | ||||||
| Endo | 0.141 | 0.254 | 9.83 | −115.59 | 1.09 | 0.05 |
| Exo | 0.140 | 0.252 | 9.59 | −114.74 | 1.10 | 0.05 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| IP + IP | ||||||
| Endo-1 | 0.172 | 0.209 | 7.44 | −170.15 | 1.01 | 0.05 |
| Endo-2 | 0.182 | 0.206 | 5.87 | −170.04 | 1.26 | 0.05 |
| Exo-1 | 0.155 | 0.230 | 9.21 | −169.50 | 0.98 | 0.05 |
| Exo-2 | 0.167 | 0.193 | 6.16 | −175.50 | 1.06 | 0.05 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| IP + MA | ||||||
| Endo-1 | 0.147 | 0.266 | 8.07 | −140.17 | 1.49 | 0.06 |
| Endo-2 | 0.169 | 0.236 | 4.55 | −143.39 | 2.14 | 0.09 |
| Exo-1 | 0.193 | 0.193 | 3.13 | −136.75 | 2.11 | 0.09 |
| Exo-2 | 0.162 | 0.224 | 5.59 | −144.10 | 1.56 | 0.07 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| IP + MVK | ||||||
| Endo-1 | 0.143 | 0.288 | 7.86 | −133.33 | 1.80 | 0.07 |
| Endo-2 | 0.173 | 0.253 | 4.30 | −137.60 | 2.60 | 0.10 |
| Exo-1 | 0.155 | 0.252 | 5.33 | −132.89 | 2.07 | 0.09 |
| Exo-2 | 0.157 | 0.242 | 5.57 | −141.29 | 1.83 | 0.08 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| MVK + MVK | ||||||
| Endo | 0.150 | 0.297 | 7.95 | −136.43 | 1.89 | 0.07 |
| Exo | 0.141 | 0.283 | 12.80 | −157.72 | 1.04 | 0.04 |
Discussion
A perturbation method to transition-state theory first proposed by Evans and Polanyi has been applied to hydrostatic-pressure-modified Diels–Alder reactions. This general approach has previously been used to calculate pressure-dependent shear strengths of a sliding interface that yielded formulae that were in good agreement with those proposed on the basis of experiments.56 The same approach was used to predict the normal-stress-induced rates of the mechanochemical decomposition of ethyl thiolate species adsorbed on a Cu(100) surface measured in vacuum that was also in excellent agreement with experiments carried out on a well-characterized in UHV.55 Similar good agreement is found between experiment and theory for Diels–Alder cycloaddition reactions carried out in solution, where the interaction between the reactants and the solvent was modeled using the PCM method.In a similar way that transition-state theory has been advantageous for understanding thermal reaction rates and mechanisms, the perturbation method of transition-state theory preserves those advantages and additionally provides conceptual insights into the way static stresses modify the rates of chemical reactions and gives a physical meaning to the activation volume parameter that describe the phenomena.
We note that the E–P method is quite general and can include the effect of several simultaneous perturbations. Consequently, it can straightforwardly be extended to analyzing processes that include both normal and shear stresses.56 It could also investigate the combined effects of electric, magnetic or gravitational fields on mechanochemical reaction rates.
Like transition-state theory, the approach is fundamentally rooted in thermodynamics with all its associated advantages. Perhaps the most important is that the results depend only on the initial and final states of the system and is independent of the path taken between them.49 This accelerates the calculation and this approach can be viewed as a high-throughput method, but this is not the primary benefit.
We find that an Evans–Polanyi analysis implemented by the XP-PCM method gives good agreement with experiment within the Bell approximation in which the initial- and transition-state structures are assumed to be rigid for non-polar reactants. However, the reactant and transition-state structures can distort under the influence of applied forces/stresses, resulting in quadratic force/stress dependences of the activation energy, sometimes known as the extended-Bell model.81 This results in the activation volume/length depending on the stress/force as suggested in eqn (2). This causes the location of the transition-state structure to move closer to the reactants and the location of the reactants to move closer to the transition state,82 known as the Hammond effect11,64 by analogy to a similar effect found in organic chemistry.83 It should be noted that mechanochemical reactions are still thermally driven and only require a reduction is energy barrier to result in significant increases in reaction rates. Because measurements of the effect of hydrostatic pressure on reaction rates are made at pressures of 1 GPa or less,43,44 the influence of molecular distortion was gauged using the force constants for various Diels–Alder reactions adapted to stress-induced reactions. This required a knowledge of the area over which the stress acts, which was calculated from the activation volume and the value of the activation length using the Stearn–Eyring relation.76 This suggested that the influence of molecular distortion is not significant at a normal stress of ∼0.3 GPa, warranting the use of the Bell approximation for analyzing these systems.
These results suggest that the polarizable-continuum methods works well and gives quantitative agreement between experiment and theory for reactions that involve non-polar, hydrocarbon reactants. Thus, the weak solvent-reactant interaction allows the continuum approximation to work well. In addition, the small pressure increments (see Fig. S2–S7†) allow precise values of the pressure to be calculated. However, the systematic difference of ∼8 cm3 mol−1 between experiment and theory (Table 2) implies that effect of the solvent is due to local, short-range interactions. This suggests that the XP-PCM method could be applied to polar reactants by including a first coordination sphere of solvent molecules surrounding the reacting ensemble embedded in a polarizable continuum.
Conclusions
This paper shows how the Evans–Polanyi perturbation method can be applied to analyzing the pressure-dependent Diels–Alder cycloaddition of cyclopentadiene, for which there are independent and corroborative experimental results, using the extreme-pressure polarizable continuum (XP-PCM) model. This was extended to a series of other Diels–Alder reactions in which the results were in good agreement with experiment for non-polar reactants, while the result for non-polar reactants were ∼8 cm3 mol−1 larger than the calculated results. This effect was proposed to be due to the reactants appearing to be larger due to interactions with the solvent.The hydrostatic-pressure dependence is calculated just for the initial- and transition-state structures enclosed in a van der Waals' cocoon using XP-PCM model, where the reaction ensembles are not allowed to distort under the influence of the pressure. Note that only having to calculate the pressure dependence of the initial- and the transition-state structures allows the results to be obtained for a finer variation of cocoon volumes than would otherwise have been feasible. This allowed a full set of calculations to be rapidly carried out so that this approach is readily applicable to a wide range of pressure-modified mechanochemical reactions and will be useful for high-throughput calculations.
The effect of pressure-induced distortions on the initial- and transition-state structures could, in principle, have been computed by allowing them to relax during each compression cycle, but that would significantly lengthen the computation time. Instead, we used the force constants of the initial- and transition-state structures to estimate the energy change due to molecular distortions. This required knowledge of the area over which the pressures were exerted and was estimated using the Stearn–Eyring postulate from the calculated activation volume and activation length. The P2 dependence calculated in this way showed that it has a negligible effect on the activation volume suggesting that molecular distortion does not contribute to the mechanochemical response under stresses that can be routinely obtained in the laboratory for this type of high-pressure experiment.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
All authors contributed equally to the paper.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We gratefully acknowledge the Civil, Mechanical and Manufacturing Innovation (CMMI) Division of the National Science Foundation under grant number 2020525 for support of this work. This work was also supported by the French Agency for Ecological Transition (ADEME) through the IMOTEP project.References
- J. Sohma, Prog. Polym. Sci., 1989, 14, 451–596 CrossRef CAS.
- V. V. Boldyrev and K. Tkáčová, J. Mater. Synth. Process., 2000, 8, 121–132 CrossRef CAS.
- V. I. Levitas, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 184118 CrossRef.
- M. K. Beyer and H. Clausen-Schaumann, Chem. Rev., 2005, 105, 2921–2948 CrossRef CAS PubMed.
- Z. V. Todres, Organic Mechanochemistry and its Practical Applications, Taylor&Francis, Boca Raton, FL, 2006 Search PubMed.
- B. M. Rosen and V. Percec, Nature, 2007, 446, 381–382 CrossRef CAS PubMed.
- S. A. Mitchenko, Theor. Exp. Chem., 2007, 43, 211–228 CrossRef CAS.
- S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friscic, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447 RSC.
- S. L. Craig, Nature, 2012, 487, 176–177 CrossRef CAS PubMed.
- J.-L. Do and T. Friščić, ACS Cent. Sci., 2017, 3(1), 13–19 CrossRef CAS PubMed.
- D. E. Makarov, J. Chem. Phys., 2016, 144, 030901 CrossRef PubMed.
- H. J. Theophrastus, Theophrastus's History of Stones : with an English Version, and Critical and Philosophical Notes, Including the Modern History of the Gems, &C., Described by that Author, and of Many Other of the Native Fossils, London, 1774 Search PubMed.
- R. Planer, Curr. Anthropol., 2018, 59, 228 CrossRef.
- C. Suryanarayana, Prog. Mater. Sci., 2001, 46, 1–184 CrossRef CAS.
- S. Kipp, V. Šepelák and K. D. Becker, Chem. Unserer Zeit, 2005, 39, 384–392 CrossRef CAS.
- R. S. Varma, Green Chem. Lett. Rev., 2007, 1, 37–45 CrossRef CAS.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Nature, 2007, 446, 423–427 CrossRef CAS PubMed.
- J. Ribas-Arino, M. Shiga and D. Marx, Angew. Chem., Int. Ed., 2009, 48, 4190–4193 CrossRef CAS PubMed.
- S. M. Hick, C. Griebel, D. T. Restrepo, J. H. Truitt, E. J. Buker, C. Bylda and R. G. Blair, Green Chem., 2010, 12, 468–474 RSC.
- J. Ribas-Arino and D. Marx, Chem. Rev., 2012, 112, 5412–5487 CrossRef CAS PubMed.
- R. Boulatov, Nat. Chem., 2013, 5, 84–86 CrossRef CAS PubMed.
- G. A. Bowmaker, Chem. Commun., 2013, 49, 334–348 RSC.
- C. C. Piras, S. Fernández-Prieto and W. M. De Borggraeve, Nanoscale Adv., 2019, 1, 937–947 RSC.
- N. N. Gosvami, J. A. Bares, F. Mangolini, A. R. Konicek, D. G. Yablon and R. W. Carpick, Science, 2015, 348, 102–106 CrossRef CAS PubMed.
- J. Zhang and H. Spikes, Tribol. Lett., 2016, 63, 1–15 CrossRef CAS.
- R. P. Glovnea, A. K. Forrest, A. V. Olver and H. A. Spikes, Tribol. Lett., 2003, 15, 217–230 CrossRef CAS.
- E. Pollak and P. Talkner, Chaos, 2005, 15, 026116 CrossRef PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, G. Jóhannesson and H. Jónsson, in Theoretical Methods in Condensed Phase Chemistry, ed. S. D. Schwartz, Springer Netherlands, Dordrecht, 2002, pp. 269–302 Search PubMed.
- D. Sheppard and G. Henkelman, J. Comput. Chem., 2011, 32, 1769–1771 CrossRef CAS PubMed.
- B. Peters, in Reaction Rate Theory and Rare Events Simulations, ed. B. Peters, Elsevier, Amsterdam, 2017, pp. 183–208 Search PubMed.
- W. H. Miller, N. C. Handy and J. E. Adams, J. Chem. Phys., 1980, 72, 99–112 CrossRef CAS.
- T. H. Lowry and K. S. Richardson, Mechanism and Theory in Organic Chemistry, Harper & Row, 1987 Search PubMed.
- R. Rana, R. Bavisotto, N. Hopper and W. T. Tysoe, Tribol. Lett., 2021, 69, 32 CrossRef CAS.
- G. Subramanian, N. Mathew and J. Leiding, J. Chem. Phys., 2015, 143, 134109 CrossRef PubMed.
- W. Quapp and J. M. Bofill, Theor. Chem. Acc., 2016, 135, 113 Search PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1936, 32, 1333–1360 RSC.
- C. Walling and H. J. Schugar, J. Am. Chem. Soc., 1963, 85, 607–612 CrossRef CAS.
- K. Seguchi, A. Sera and K. Maruyama, Bull. Chem. Soc. Jpn., 1974, 47, 2242–2246 CrossRef.
- T. Asano and W. J. Le Noble, Chem. Rev., 1978, 78, 407–489 CrossRef CAS.
- A. Drljaca, C. D. Hubbard, R. van Eldik, T. Asano, M. V. Basilevsky and W. J. le Noble, Chem. Rev., 1998, 98, 2167–2290 CrossRef CAS PubMed.
- A. Boscoboinik, D. Olson, H. Adams, N. Hopper and W. T. Tysoe, Chem. Commun., 2020, 56, 7730–7733 RSC.
- B. Chen, R. Hoffmann and R. Cammi, Angew. Chem., Int. Ed., 2017, 56, 11126–11142 CrossRef CAS PubMed.
- T. Yang, R. Fukuda, R. Cammi and M. Ehara, J. Phys. Chem. A, 2017, 121, 4363–4371 CrossRef CAS PubMed.
- S. K. Jha, K. Brown, G. Todde and G. Subramanian, J. Chem. Phys., 2016, 145, 074307 CrossRef PubMed.
- R. Rana, G. Djuidje Kenmoe, F. Sidoroff, R. Bavisotto, N. Hopper and W. T. Tysoe, J. Phys. Chem. C, 2022, 126, 11585–11593 CrossRef CAS.
- R. Rana, N. Hopper, F. Sidoroff and W. T. Tysoe, Chem. Sci., 2022, 13, 12651–12658 RSC.
- J. R. Felts, A. J. Oyer, S. C. Hernández, K. E. Whitener Jr, J. T. Robinson, S. G. Walton and P. E. Sheehan, Nat. Commun., 2015, 6, 6467 CrossRef CAS PubMed.
- O. J. Furlong, B. P. Miller, P. Kotvis and W. T. Tysoe, ACS Appl. Mater. Interfaces, 2011, 3, 795–800 CrossRef CAS PubMed.
- O. Furlong, B. Miller and W. T. Tysoe, Wear, 2012, 274–275, 183–187 CrossRef CAS.
- H. Adams, B. P. Miller, P. V. Kotvis, O. J. Furlong, A. Martini and W. T. Tysoe, Tribol. Lett., 2016, 62, 1–9 CrossRef CAS.
- N. Hopper, F. Sidoroff, R. Rana, R. Bavisotto, J. Cayer-Barrioz, D. Mazuyer and W. T. Tysoe, Phys. Chem. Chem. Phys., 2023, 25, 15855–15861 RSC.
- N. Hopper, F. Sidoroff, J. Cayer-Barrioz, D. Mazuyer and W. T. Tysoe, Tribol. Lett., 2023, 71, 121 CrossRef.
- T. L. Hill, An Introduction to Statistical Thermodynamics, Dover Publications, 1986 Search PubMed.
- R. Hill, J. Mech. Phys. Solids, 1968, 16, 229–242 CrossRef.
- R. A. Alberty, Pure Appl. Chem., 2001, 73, 1349–1380 CrossRef CAS.
- J. O. M. Bockris, Electrochemistry, Butterworths, University Park Press, London, Baltimore, 1973 Search PubMed.
- J. Spooner and N. Weinberg, Can. J. Chem., 2016, 95, 149–161 CrossRef.
- G. Bell, Science, 1978, 200, 618–627 CrossRef CAS PubMed.
- I. Prigogine, Introduction to Thermodynamics of Irreversible Processes, Interscience Publishers, New York, 1968 Search PubMed.
- S. S. M. Konda, J. N. Brantley, B. T. Varghese, K. M. Wiggins, C. W. Bielawski and D. E. Makarov, J. Am. Chem. Soc., 2013, 135, 12722–12729 CrossRef CAS PubMed.
- S. M. Avdoshenko and D. E. Makarov, J. Phys. Chem. B, 2016, 120, 1537–1545 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- R. Cammi, J. Comput. Chem., 2015, 36, 2246–2259 CrossRef CAS PubMed.
- R. Cammi, in Annual Reports in Computational Chemistry, ed. D. A. Dixon, 2017, vol. 13, pp. 117–135 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian Inc., Wallingford, 2010 Search PubMed.
- R. Cammi, B. Chen and M. Rahm, J. Comput. Chem., 2018, 39, 2243–2250 CrossRef CAS PubMed.
- A. Khajeh, X. He, J. Yeon, S. H. Kim and A. Martini, Langmuir, 2018, 34, 5971–5977 CrossRef CAS PubMed.
- J. Yeon, X. He, A. Martini and S. H. Kim, ACS Appl. Mater. Interfaces, 2017, 9, 3142–3148 CrossRef CAS PubMed.
- K. Brandhorst and J. Grunenberg, Chem. Soc. Rev., 2008, 37, 1558–1567 RSC.
- T. Stauch and A. Dreuw, J. Chem. Phys., 2015, 143, 074118 CrossRef PubMed.
- R. Cammi and B. Chen, J. Chem. Phys., 2022, 157, 114101 CrossRef CAS PubMed.
- A. E. Stearn and H. Eyring, Chem. Rev., 1941, 29, 509–523 CrossRef CAS.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon Press, Oxford, 2002 Search PubMed.
- E. B. Wilson, J. C. Decius and P. C. Cross, Molecular Vibrations : the Theory of Infrared and Raman Vibrational Spectra, McGraw-Hill, New York, 1955 Search PubMed.
- C. Walling and J. Peisach, J. Am. Chem. Soc., 1958, 80, 5819–5824 CrossRef CAS.
- C. Brun and G. Jenner, Tetrahedron, 1972, 28, 3113–3121 CrossRef CAS.
- S. S. M. Konda, J. N. Brantley, C. W. Bielawski and D. E. Makarov, J. Chem. Phys., 2011, 135, 164103–164108 CrossRef PubMed.
- W. Tysoe, Tribol. Lett., 2017, 65, 48 CrossRef.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Computational methods, reaction pathways and structures, a description of the XP-PCM analysis, Fig. S1 to S8, Table S1, description of the curvature analysis, optimized gas-phase geometries and optimized gas-phase structural geometries. See DOI: https://doi.org/10.1039/d4mr00063c |
| This journal is © The Royal Society of Chemistry 2024 |