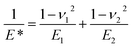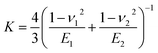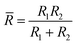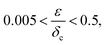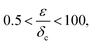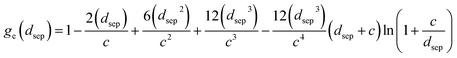Open Access Article
Open Access ArticleAn experimental and numerical study on adhesion force at the nanoscale†
Su-Hyun
Kim‡
ab,
Pan-Kyu
Choi‡
ab,
Yong-Bok
Lee
a,
Tae-Soo
Kim
a,
Min-Seung
Jo
a,
So-Young
Lee
a,
Hyun-Woo
Min
ab and
Jun-Bo
Yoon
 *a
*a
aSchool of Electrical Engineering, Korea Advanced Institute of Science and Technology (KAIST), 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea. E-mail: jbyoon@kaist.ac.kr
bSamsung Electronics Co., Ltd., 1, Samsungjeonja-ro, Hwaseong-si, Gyeonggi-do 18448, Republic of Korea
First published on 27th February 2024
Abstract
Adhesion has attracted great interest in science and engineering especially in the field pertaining to nano-science because every form of physical contact is fundamentally a macroscopic observation of interactions between nano-asperities under the adhesion phenomenon. Despite its importance, no practical adhesion prediction model has been developed due to the complexity of examining contact between nano-asperities. Here, we scrutinized the contact phenomenon and developed a contact model, reflecting the physical sequence in which adhesion develops. For the first time ever, our model analyzes the adhesion force and contact properties, such as separation distance, contact location, actual contact area, and the physical deformation of the asperities, between rough surfaces. Through experiments using atomic force microscopy, we demonstrated a low absolute percentage error of 2.8% and 6.55% between the experimental and derived data for Si–Si and Mo–Mo contacts, respectively, and proved the accuracy and practicality of our model in the analysis of the adhesion phenomenon.
Introduction
Adhesion has been of great research interest for a long time because it is a very fundamental, yet ubiquitous phenomenon observed in our everyday lives beyond our biologically discernible limits in nanotechnology. For instance, adhesion inadvertently exists in various forms in daily lives between contacts as simple as holding and lifting an object to taping a box. The phenomenon is more prominently observed at the nanoscale. Transitioning from the macro to nanoscale, the surface-to-volume ratio becomes significantly higher. As a result, surface forces including adhesion forces gain predominance and become more pronounced.1–4 Moreover, an extremely close separation distance between asperities on contact interfaces is achieved by the nanometre-scale surface roughness of materials, and the interfacial interaction between surfaces is amplified.As technological advancements gain tremendous momentum scaling down from the macro to nanoscale in recent years, the role of adhesion force in nanotechnology has become ever more important. Hence, the prediction of adhesion force between solid surfaces is critical not only for practical use in various fields of nanotechnology, including coatings,5 transfer printing,6,7 biomedical,8 and nanoelectromechanical systems9–13 but also in the analysis of physical phenomena such as conduction,14 friction15 or thermal transport16 between nano-asperities on material surfaces.
Historically, the importance of adhesion prediction has been acknowledged since Johnson, Kendall, and Roberts (JKR) adopted adhesion force in analysing contact between two spherical bodies in 1971.17 Afterwards, researchers focused on expanding the scope of the theoretical model from adhesion between a single pair of spheres to surfaces consisting of multi-asperities by applying Hertz,18 JKR,17 and Derjaguin–Muller–Toporov (DMT)19,20 theories. Numerous expanded models analyzed the influence of adhesion force on surface roughness, based on the Greenwood–Williamson model,21 which first examined contact properties between rough surfaces based on asperities. Fuller and Tabor22 developed a theory for the contact behavior of adhesive rough surfaces on elastic solids, while Roy Chowdhury and Pollock23 expanded it to include the influence of plastically deformed asperities. Furthermore, Chang24 conducted pioneering research on elastic–plastic adhesive contact between rough surfaces. Maugis25 then extended the DMT theory to elastic contacts of rough surfaces by incorporating the extra load from adhesion around contacts. Morrow26 provided a solution to make a transition between JKR17 and DMT19,20 in the analysis of adhesion in the elastic region. As described, an impressive number of studies have been conducted so far on the adhesion force between rough surfaces consisting of multi-asperities, but most are limited in predicting the accurate value of the adhesion force that could be reliably adopted for practical uses such as designing nanoscale devices.
The primary limitation lies in the predominant focus of many researchers on theoretically analyzing adhesion on idealized rough surfaces, with only a few studies incorporating experimental work.27–30 Additionally, a common approach in most studies involves assuming contact between flat and rough surfaces, modelled based on a large number of asperities with Gaussian height distribution. While this assumption may be effective for simple adhesion analysis, it falls short in accurately predicting adhesion between two rough surfaces in a realistic contact scenario. In contrast to most theoretical works, Prokopovich27,28 predicted interactions between real rough surfaces by utilizing surface morphology obtained from actual samples being tested and experimentally validated these predictions. However, it is important to note that this study is based on the analysis of contact between flat and rough surfaces within a restricted range of deformation. Consequently, its ability to capture the realistic contact situation is limited.
The second limitation observed in previous studies is insufficient consideration of adhesion forces between non-contacting asperities. Many models23,25,27,28,30 of rough surface adhesion assume that only areas in direct contact contribute to adhesion, primarily dealing with micrometer-scale roughness. However, in surfaces with nanometer-scale roughness, all non-contacting portions of the interface can be separated by less than 100 nm, and the van der Waals forces that come into play at this distance become non-negligible in the adhesion analysis. DelRio31 proposed a model to determine the adhesion force across non-contacting portions of the surfaces based on the calculated equilibrium separation distance between nano-asperities of the contact interface from measured roughness data of two rough surfaces, and experimentally verified the derived adhesion energy using micro-cantilevers. However, this approach disregards adhesion forces between contacting asperities, which could lead to significant errors, particularly in contacts between metals with high surface energy.
Finally, challenges arise when applying the previous models23–30 in real-life situations where accurate prediction of adhesion force is essential. This becomes particularly critical in the design and functionality of nanoscale devices that demand precise control of motion. The uniqueness of every nanoscale contact interface, stemming from the intricacies of nanoscale fabrication with a multitude of parameters, poses a significant challenge. Disparities between contact surfaces cannot be fully accounted for by previous models developed under fixed conditions. While previous research has successfully studied the very fundamental domains within the adhesion phenomena such as the relationship between surface roughness and the adhesion force, its applicability to real rough contact interfaces remains limited.
To overcome the limitations of existing models and propose a practical prediction model for adhesion, we firstly introduce a new approach to contact analysis in this paper. It stems from the nanoscale observation that the actual contact between interfaces occurs through a series of interactions between nano-asperities on solid surfaces. In the real contact process, nano-asperities on the contact interface deform sequentially. Because asperities vary in height, the tallest asperity pair on the surfaces contact first. The contacting asperities physically deform with applied external force, and more asperities come into contact. The separation distance between contact interfaces gets smaller until sufficient asperities contact and increased structural rigidity prevents further deformation. In other words, the adhesion force increases until the equilibrium separation distance between contact interfaces is reached. To reflect the dynamics in the natural contact process in our contact model, we calibrated the adhesion force based on the calculated value of the change in interfacial force, separation distance, and deformation of asperities every time a new contact asperity pair is created between interfaces during the contact process.
By employing an iterative and sequential contact analysis process, we present a practical predictive model designed to accurately forecast adhesion forces between contact interfaces across a broad spectrum of materials, including both metals and non-metals. Notably, our model introduces a new iterative contact analysis method by scrutinizing adhesion forces and key contact properties—such as separation distance, contact location, real contact area, and the deformation of contacting asperities—in each step of the contact process. In our approach, we specifically targeted addressing the previously mentioned second limitation, which involves insufficient consideration of adhesion forces between non-contacting asperities. To achieve this, we incorporated an analysis of both the adhesion force among contacting asperities and that of non-contacting ones. Our approach integrates well-established adhesion theories, such as JKR,17 DMT,19,20 Kogut & Etsion,32 and Johnson,33,34 within the contacting region of asperities, while employing the van der Waals force equation35 in the non-contacting region of asperities. Lastly, we conducted experimental adhesion measurements using force–distance (F–d) measurement utilizing an atomic force microscope (AFM).36 The result showed a mean absolute percentage error of 2.8% and 6.55% between the experimental and calculated adhesion forces for Si–Si and Mo–Mo contacts, respectively, demonstrating that our model truly reflects the actual contact between material interfaces.
Results and discussion
Nanoscale contact model between surfaces
To ensure the proposed nanoscale contact model accurately captures the realistic contact process between rough surfaces, it is essential to incorporate appropriate assumptions. These assumptions serve the purpose of simplifying the intricate process while minimizing the risk of significant errors. In our paper, the following assumptions are adopted:(a) The rough surfaces exhibit isotropic and homogeneous characteristics.
(b) The summits of all asperities take on a spherical shape.
(c) The summits of all asperities share a uniform radius, denoted as R, while the heights of the asperities vary.
(d) Deformation of the asperities on surfaces only occur during contact, with no bulk deformation of the mass body.
(e) Interactions between asperities can be neglected.
(f) All contact processes are quasi-static.
(g) The contact surfaces are contamination-free.
(h) Only dry adhesion is considered.
(i) The two contacting surfaces are of the same material with identical work functions.
(j) The two surfaces of contact are not hydrophilic.
The rationale behind the appropriateness of these assumptions, and their reflection of the contact conditions between surfaces, is detailed in ESI S1.†
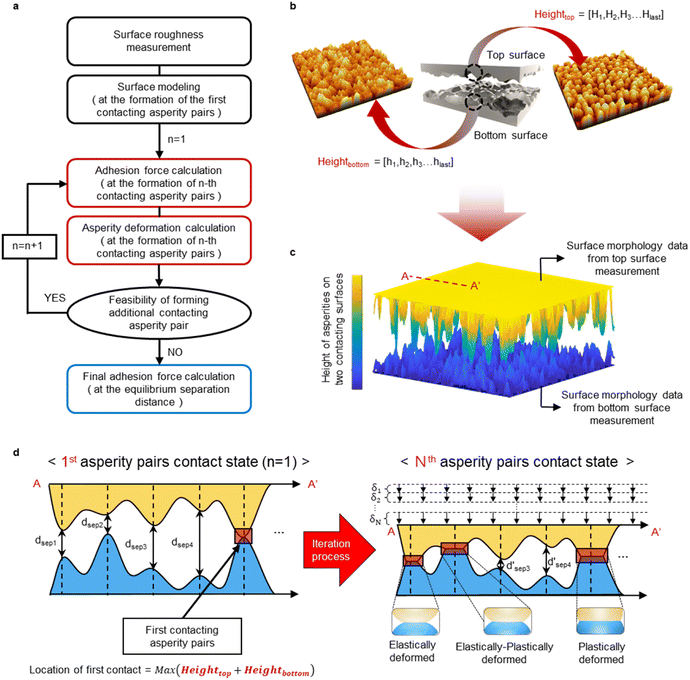
Fig. 1(a) presents the process flow of the proposed nanoscale contact model. In the first step, surfaces of interest are analyzed, and the surface model is created based on the obtained data (Fig. S1†) measured using the non-contact mode in AFM (Fig. 1(b)). Because surface morphology is a critical factor in determining the adhesion force, it is important that the nanoscale morphology and non-uniformities of the actual surface of the sample used in the analysis are reflected in collecting the surface roughness data. Fig. 1(c) shows the top and bottom surfaces that are expressed using the measured roughness data, and Fig. 1(d) demonstrates the cross-sectional view of the contact surfaces that we modelled based on the first contacting asperity pair which was obtained by determining the asperity pairs between the top and bottom contact surfaces having the largest combined height. Roughness data obtained by analyzing the top and bottom surfaces from Fig. 1(b) are heightbottom = [h1, h2, h3, …, hlast] and heighttop = [H1, H2, H3, …, Hlast]. From this data, the combined height of the first (initial) contacting asperity pair can be expressed as max (heighttop + heightbottom). Afterward, the separation distance (dsep) between the rest of the non-contacting asperity pairs is determined by
| dsep,n = max (heighttop + heightbottom) − (Hn + hn) | (1) |
After analysing the adhesion force between the contacting surfaces with the separation distance of the surfaces determined by the initial contact of the asperity pair, the magnitude of deformation experienced by the asperity pair can be calculated. This calculation is based on the compressive force between the surfaces, which is the sum of the external force and the adhesion force. As contacting asperities deform and the two surfaces draw closer, the next taller asperity pair comes into contact. Whenever new asperity pairs make contact, the separation distance between contact interfaces is updated. This updated distance is then utilized to re-calculate both the adhesion force and the extent of deformation between the asperities. The determination of whether additional asperity pairs can form is based on a comparison between the extent of deformation of the contacting asperity pairs and the separation distance between the next taller non-contacting asperity pair. Through this iterative process, illustrated in Fig. 1(d), when the Nth asperity pair makes contact, the contacting asperity pairs attain various contact states, spanning from elastic deformation to plastic deformation. This variation is contingent upon the extent of deformation. At the end, the asperity pairs between the surfaces that remain in non-contact experience a reduction in separation distance compared to their initial contact.
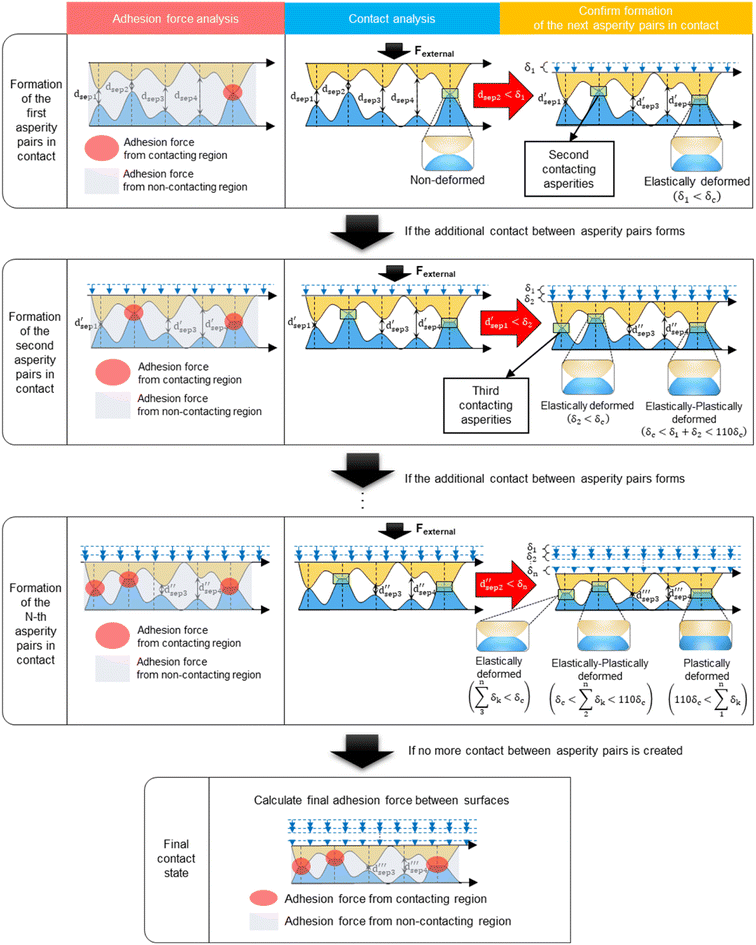
The detailed iteration process, starting from the contact state of the 1st asperity pair to reaching the contact state of the Nth asperity pair, is depicted in Fig. 2. The iteration initiates when the first pair of asperities makes contact and concludes when the asperity pairs cease to deform, and no further contacts occur due to densification. Upon the establishment of contact by a new asperity pair and determination of the corresponding separation distance, a sequential process unfolds, involving adhesion force analysis, contact analysis, and verification of whether the next asperity pairs make contact.
In the analysis of adhesion force, we considered the appropriate interfacial force, considering the material, contact state, and deformation of each asperity pair between contact interfaces. To ensure precision in adhesion force analysis, we performed separate calculations for the adhesion force between contacting asperities and non-contacting asperities.
To determine the adhesion force between contacting asperities, we used the early contact theory of spheres. In the examination of adhesion forces between contacting asperity pairs situated in the elastic region, either the JKR17 or DMT19,20 theory is employed depending on the material properties. The JKR theory is typically applicable to soft materials like rubber, while the DMT theory is suitable for hard materials such as metal. The determination of the appropriate theory for the material under analysis is facilitated by employing a Tabor parameter37 as follows:
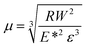 | (2) |
where μ is the Tabor parameter, R is the radius of curvature, W is the work of adhesion, ε is the intermolecular distance, E is the effective Young's modulus, and ν is Poisson's ratio. The DMT theory is used in the analysis when the tabor parameter is low (<1). In contrast, the JKR theory is applied when the Tabor parameter is significantly high (≫1). Eqn (3)–(5) below detail the formulas for determining the contact radius, deformation of nano-asperities, and adhesion force, employing the JKR theory.
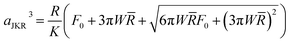 | (3) |
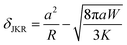 | (4) |
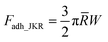 | (5) |
Likewise, eqn (6)–(8) outline the calculations for the contact radius, deformation of nano-asperities, and adhesion force using the DMT theory.
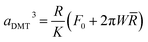 | (6) |
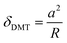 | (7) |
Fadh_DMT = 2π![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) W W | (8) |
where a is the contact radius, δ is the deformation of asperities, Fadh is the adhesion force, R is the radius of curvature, W is the work of adhesion, F0 is the applied pressure, E is the effective Young's modulus, and ν is Poisson's ratio.
The contacting asperities in the elastic–plastic deformation region are calculated by Kagot and Etsion's model,32 which are analyzed using finite element analysis and numerical fitting. The formulas are categorized into two ranges based on the degree of deformation (δ) and further subdivided into two additional ranges according to the magnitude of critical deformation (δc). Finally, four derived formulas in eqn (9)–(12) can be used to calculate the deformation of asperities and adhesion force in the intermediate regions of elasticity and plasticity. The four equations are described below:
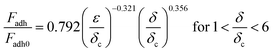 | (9) |
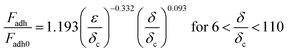 | (10) |
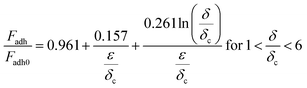 | (11) |
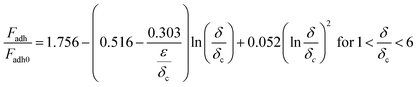 | (12) |
In the plastic deformation region, Johnson's theory33,34 is used, which delineates adhesion forces between small particles or asperities as relevant to both loading and unloading processes. These processes entail the application and removal of an external force on two contacting surfaces. During the loading process, hardness factors in as a key parameter to determine the contact radius, and the contact radius and deformation of asperities can be obtained as shown in eqn (13) and (14). In the unloading process, however, the behaviors of the spheres or asperities are more complex as their separation behaviors are either brittle or ductile depending on the contact radius at maximum compression, hardness, work of adhesion, and effective Young's modulus of the contacting body of mass. The brittle separation is marked by the elastic separation of spheres or asperities in contact, with the adhesion force during this process calculable using eqn (15). In contrast, ductile separation is characterized by inelastic separation of spheres, and the resulting adhesion force can be determined using eqn (16).
Hπa2 = 2π![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) W + F0 W + F0 | (13) |
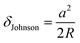 | (14) |
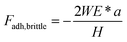 | (15) |
| Fadh,ductile = Hπa2 | (16) |
In contrast to analyzing the adhesion force between contacting asperities, the analysis of the non-contacting region between the two surfaces primarily focuses on attractive forces that manifest over long distances. While various forces may exist between surfaces with significant separation distances, our paper predominantly concentrates on the van der Waals force. This force, omnipresent between all substances, operates within the interatomic spacing range of approximately 0.2 nm to 10 nm and beyond.35 The exclusive consideration of the van der Waals force is attributed to our primary focus on the contact between identical substances under dry conditions. The van der Waals force can be obtained with eqn (17) below.
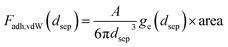 | (17) |
where A is the Hamarker constant, dsep is the separation distance between asperities, and c is a characteristic wavelength constant. As shown in the equation, the van der Waals force is influenced by separation distance and contact area and is inversely proportional to the third power of distance.
The comprehensive adhesion force between surfaces is derived by independently calculating the adhesion force in both the contacting and non-contacting regions of the surface. Summing up each individual calculation allows for a precise analysis of the adhesion force. More specifically, the adhesion force for each contacting asperity pair is computed based on its deformation state and subsequently aggregated. In the non-contacting region, the adhesion force is computed with a primary emphasis on the overlapping area characterized by a specific separation distance. Accordingly, the total adhesion force between the rough surfaces is calculated as follows:
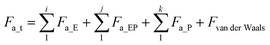 | (18) |
By accounting for the adhesion force between contacting and non-contacting asperities, the accuracy of the adhesion force analysis is substantially enhanced. During the analysis of adhesion force, the dominance of either the adhesion force in the contacting region or non-contacting asperities depends on the material in question. For instance, in metallic contacts with high surface energy,35,38 the prevailing force between contacting asperities is metallic bonding, which surpasses van der Waals forces. Therefore, the interfacial force between contacting asperities is given particular emphasis in metallic contact, where metallic bonding force prevails over van der Waals force. Conversely, in non-metallic contact, where van der Waals force dominates between interfaces, the attractive force between non-contacting asperities is accentuated.31,35 For these reasons, it is essential to analyze both contacting and non-contacting asperities to develop a model with a wide range of applicability to various types of materials. Our model comprehensively considers different types of contacts, thereby facilitating a precise and comprehensive analysis of various conditions in interfacial contacts.
In our contact analysis, the deformation of asperities is determined considering material properties and the sum of adhesion force and external force. The deformation regions are classified into three areas: elastic, elastic–plastic, and plastic. The criterion for delineating these ranges is established by the critical deformation value defined in eqn (19).39
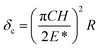 | (19) |
| C = 0.454 + 0.41ν |
The deformation of nano-asperities plays a critical role in determining the separation distance and adhesion force between two contacting rough surfaces. Therefore, when analyzing adhesion between two rough surfaces, the deformation of asperities must be considered in context. The deformation of asperities is calculated using the aforementioned early contact theories between spheres according to the deformation range.
After completion of the adhesion force and the contact analysis for the first contacting asperity pair, the possibility of the following contact is analyzed based on the magnitude of deformation in the preceding contact pairs. If the deformation in the first asperity pair in contact is sufficient to cover the separation distance between the asperities that are on the brink of contact, the next contact is established. As more asperities come into contact, the magnitude of deformation in the asperities subsides due to the increased repulsive force between contacting asperities and the incremented structural rigidity from densification of the contact pairs. Accordingly, the iterative analysis stops at the n-th pair of the asperities where the value of the separation distance required for the next asperity contact ((n + 1)-th) is greater than the value of the mechanical deformation of the existing asperity pairs in contact. At this point, the final separation distance can be calculated and the resulting adhesion force is determined by utilizing the separation distance and the contact and deformation states of the asperities in the final state.
Analysis of nanoscale contact properties between surfaces
To deeply understand the contact on the nanoscale, we analyzed adhesion force and various contact properties such as location, contact area, and deformation of contacting asperities. Using the proposed model, it is possible to examine contact phenomena that occur in every step of the iteration process. Fig. 3 visualizes the contact properties between two surfaces upon applying an external force. Fig. 3(a) shows that the proposed model can extract contact locations and real contact areas according to applied external forces ranging from 1 to 500 μN. The ratio of real contact area to the total apparent area (C/T) is found to be only 1.049% at the relatively high external force of 500 μN. The degree of deformation of the contacting asperities is demonstrated in Fig. 3(b). As the iteration process progresses, the deformation of the first contacting asperities increases, and new contact points are generated. Hence, the deformation of individual asperity pairs can be clearly analyzed using the proposed model. This contact process between interfaces that prolongs until the equilibrium separation distance is reached is visually demonstrated in Video S1.†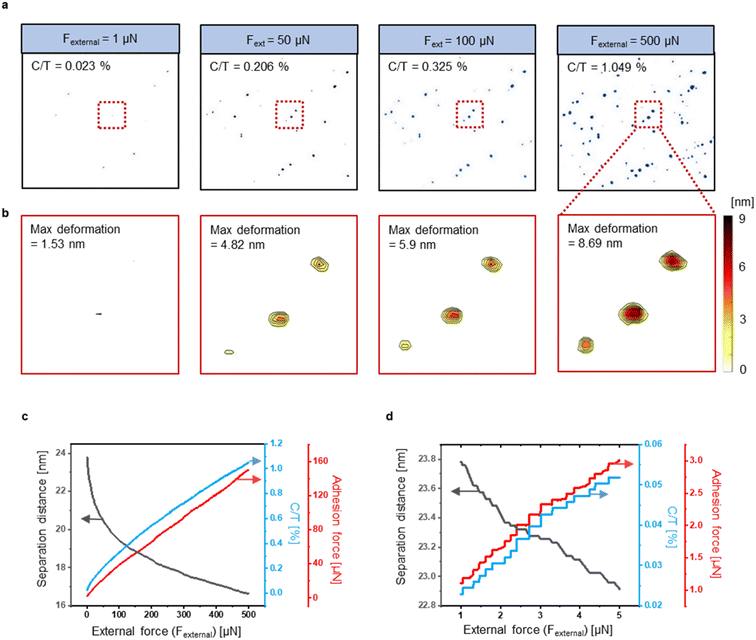 | ||
| Fig. 3 Analyzed contact phenomenon and properties using the proposed contact model. The proposed model can analyze the location, real contact area, and deformation of the contacting asperities in each step of the iteration process as shown in the visualization. The overall area of the contact between surfaces is 2 μm × 2 μm and the surface material is molybdenum. The RMS roughness are 10.46 nm and 5.07 nm for the sample and the AFM tip, respectively. (a) Graphics, from left to right, showing the location of the contact and the actual contact area between surfaces under the applied external force of 1 μN, 50 μN, 100 μN, and 500 μN. Each state can also be viewed as an intermediate process visualizing the mechanical changes in the real contacts as forces are applied incrementally up to 500 μN. This contact process between interfaces is visually demonstrated in Video S1.† (b) A magnified image showing the degree of deformation of the contacting asperities when the external forces of 1 μN, 50 μN, 100 μN, and 500 μN are applied. The color bar shows the deformation value at each point, and the max deformation value increases as a large force is applied. (c and d) Graph of separation distance (black; left axis), C/T (blue; right axis), and the adhesion force (red; right axis) according to the applied external forces. (c) Is a graph obtained by extracting data in units of 1 μN when the external force applied to the surface ranged from 1 μN to 500 μN, and (d) is a portion of the graph from Fig. 2(c) with a magnification factor of 100, obtained by extracting data in units of 10 nN when the external force applied to the surface is 1 μN to 5 μN. | ||
As shown in Fig. 3(c) and (d), the resultant separation distance, C/T, and adhesion force from the applied external force can be obtained through the iterative process using the model. Here, Fig. 3(c) demonstrates the direct relationship between the contact properties and the external forces and Fig. 3(d) shows the magnified image of Fig. 3(c). Demonstrating the resultant adhesion force from the microscopic applied forces, Fig. 3(c) exhibits a smooth linear curve. On the other hand, in Fig. 3(d), a step-wise change in the adhesion force between interfaces was shown when forces in the nanoscale were applied. Here, the abrupt increment in the adhesion force is due to the additional attractive force that occurs when contact between nano-asperities is newly formed. This trend in the adhesion forces is highly comparable to the experimental findings of the previous behavioral studies in nano-contacts in which quantized movement in physical phenomena such as friction, conduction, and thermal transport due to atomistic accounting14–16,40–42 was observed, suggesting that our proposed model can also be a powerful tool for studying non-continuum nano-contact behavior analysis. Moreover, our model can further extend its applicability to accurate analysis of nano-phenomena at the atomic level if atomic-scale surface morphology can be measured.43,44
Overall, Fig. 3(c) and (d) demonstrate that each contact between asperities, consisting of only a minute proportion of the entire surface, critically affects the total adhesion force between contacting interfaces when the applied compressive forces are in the range of nano-newton scale. The van der Waals force generally increases as the separation distance between surfaces decreases. However, in case of molybdenum, the metallic bonding forces between contacting asperities are much larger than the van der Waals force. Hence, as individual asperities come into contact with increasing external force at the nanoscale, adhesion force, dominated by metallic bonding force, increases in direct relation to the number of contacting asperities, forming a step-wise trend. The proposed model, therefore, can analyze in detail the adhesion force and contact properties between user-defined surfaces in the unit of desired forces.
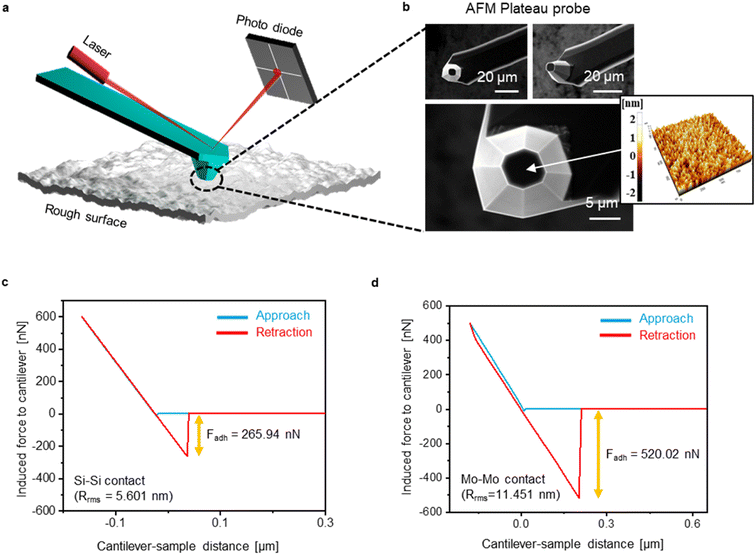
Verification of the proposed model with AFM experiments
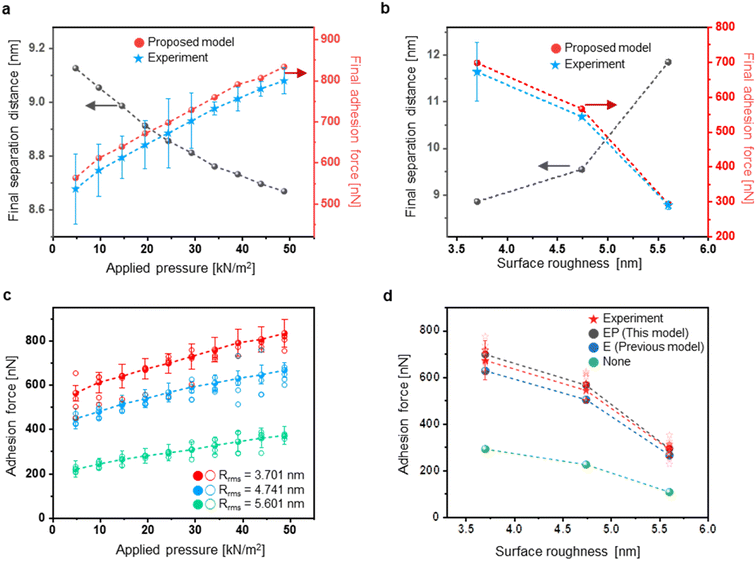
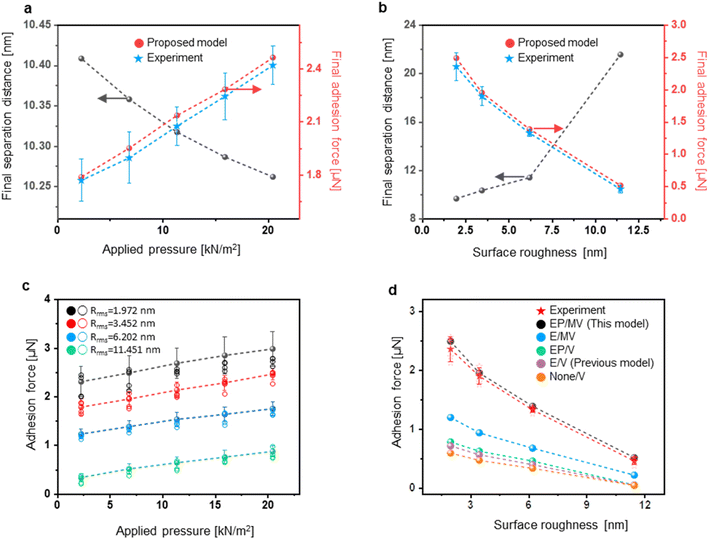
We conducted an AFM F–d experiment and implemented the proposed model for experimental verification. Fig. 4(a) shows an experimental setup of the F–d measurement in AFM. What is special in this experiment is that we introduced the plateau probe to our experiments for experimental measurement of adhesion force in surface-to-surface contact (Fig. 4(b)). Unlike the general AFM probe, the tip of the probe is plateaued out, allowing the measurement of the adhesion force between designated areas of contacting interfaces. The experimental value of the adhesion force was obtained from the resulting graph based on the F–d measurement conducted using the special AFM tips and the prepared samples with defined roughness spec. The measured adhesion force was obtained in the retraction process of the F–d measurement (Fig. S2†).Prior to the experiment, roughness of the sample and the AFM probe was measured (Fig. S3 and S4†). Following the experimental measurement, we compared the values of the adhesion forces obtained through the experiments and those predicted through the proposed contact model. We experimented using a non-metallic material of silicon (Si) and metallic material of molybdenum (Mo), which are widely used in CMOS and M/NEMS industries. Fig. 4(c) and (d) show the F–d curves obtained between an Si sample and Si probe, and Mo sample and Mo-coated probe, respectively. The interaction between the AFM probe and sample is demonstrated in the graph, and the experimental data was obtained from the retraction curve of the adhesion force. The experimental results of Si–Si and Mo–Mo contacts are shown and compared in the graphs in Fig. 5 and 6, respectively. Applied pressure and RMS roughness were compared to both the final separation distance and the adhesion force in Fig. 5(a) and (b), respectively, and demonstrated that a smaller final separation distance results in a larger adhesion force. Furthermore, the adhesion forces found based on the calculated final separation distances using our model were similar to those obtained from our experiment. Also, the graphs demonstrate that the change in the final separation distance according to surface roughness significantly impacts the final adhesion force. Moving forward, the Mo–Mo contact in Fig. 6(a) and (b) shows similar results to the Si–Si contact. However, it shows that a relatively small change in the separation distance results in a significant difference in the adhesion force due to the large metallic bonding force at the contacting region of the asperities. The graphs in Fig. 5(c) and 6(c) show a quantitative comparison and error analysis between the adhesion forces calculated using our model and those from the experiment under various applied pressures and surface roughness. The disparity between the predicted and experimentally obtained adhesion forces is quantified using the absolute percentage error. The absolute percentage error is a measure of the absolute difference between the predicted and actual values, expressed as a percentage. Accordingly, an average of 2.8% and a maximum of 5.41% in absolute percentage error of the Si–Si contact were observed. Also, an average of 6.55% and a maximum of 12.4% were found to be the absolute percentage error of the Mo–Mo contact. The results demonstrate that the proposed contact model is highly accurate as opposed to the previously reported contact models having error rates of at least 25%. Moreover, we found that the smaller the roughness value, the larger the applied pressure and the greater the adhesion force. Next, Fig. 5(d) and 6(d) compare the predicted values with the experimental values based on the material types and deformation region. In the case of the Si–Si contact, deformation of the asperities highly affects the magnitude of the adhesion force, but the effect of deformation regions, whether elastic or elastic–plastic, on the adhesion force is trivial because silicon has very small surface energy. Within the range of the applied pressure, elastic deformation predominantly occurs, so plastic deformation has no significant influence over the adhesion force. However, unlike Si–Si contacts, Mo–Mo contacts induce a considerable degree of plastic deformation due to the high surface energy of the metal. The values shown in the green and purple circles differed significantly from the experimental values because plastic deformation was not considered. Additionally, Fig. 6(d) shows that metallic bonding force comprises a significant portion of the overall adhesion force between surfaces. The green, purple, and orange circles were calculated based on van der Waals force without considering the metallic bonding force in the contacting region, and displayed significant errors against the experimental values. These results demonstrate the importance of considering appropriate adhesion forces and deformation ranges to develop an accurate adhesion force prediction model that could be practically utilized in various contact situations.
Overall, our proposed model displayed significantly improved accuracy compared to the previous models. Beyond its capability to accurately analyze adhesion force in nanoscale contacts, our model can become a foundation for analyzing various nano-physical phenomena such as electrical resistance, friction, or thermal transport. As an example, we demonstrated in ESI S5† the analysis of the contact process between two material interfaces and calculation of electrical resistance in parallel between nano-asperity pairs using our proposed model. Moreover, we compared the electrical contact resistance of our fabricated NEMS device between the calculated value using our model and the measured data from electrical testing (Fig. S6 and S7†). Hence, we demonstrated that our model successfully overcame previous limitations in calculating electrical contact resistance between nano-asperities due to the difficulties in analyzing the nanoscale contact phenomenon.
Conclusions
In our study, we introduce a practical nanoscale adhesion model capable of simulating both non-metallic and metallic contacts, taking into account the realistic contact process. This model employs an iterative analysis of contact and adhesion forces through a feedback loop, considering dynamic changes in the separation distance between surfaces. Through the sequential contact process of nano-asperities on contact interfaces, our model achieves a low absolute percentage error between experimental and predicted values. This suggests that our model serves as a valuable tool in unravelling the long-standing ambiguity surrounding the contact phenomenon. Furthermore, our analytical results on nanoscale contact properties using this model are comparable to the experimental verification of the quantized movement of physical phenomena such as friction, conduction, and thermal transport due to atomistic accounting on the nanoscale, which further confirms the model's accuracy. While certain assumptions were made to develop a practical predictive adhesion model, including the exclusive analysis of dry adhesion forces to simplify attractive forces between adjacent surfaces, our model exhibits limitations in analyzing adhesion forces under specific conditions, such as environments with high humidity or hydrophilic surfaces. Furthermore, our model is limited in analyzing materials with intermediate properties not covered by JKR and DMT theories. Despite these limitations, we believe our model establishes a practical and predictive tool that can be utilized with high accuracy for predicting the contact of materials across diverse surface energy ranges, spanning from metal to non-metal. Through the iterative analysis of the contact process, simulating a realistic contact scenario, we envision the potential for a comprehensive examination of various interfacial forces that come into play between surfaces. Furthermore, expanding experimental verifications of adhesion forces beyond our current tests involving Si and Mo surfaces to include other nano devices would contribute to the continual refinement of our model. As such, our model serves as a foundational tool for the analysis of adhesion forces across a diverse range of applications and the exploration of various physical phenomena at the nanoscale.Experimental
Surface roughness measurement
The surface roughness measurement was performed in the non-contact mode of the AFM system (Park, XE-100) with an AFM tip (NCHR, resonant frequency: 320 kHz, force constant: 42 N m−1). The scan size was 2 × 2 μm2 with 256 pixels, and data was measured through the line-fit of flattening routines and Z-drive mode.AFM F–d experiment
Adhesion force measurements were performed by the AFM system (Park, NX-10) in the ambient air conditions (at the measurement environment temperature of 19 °C and humidity of 18%). For the surface-to-surface contact examination, a special AFM tip (PL-FMR, resonant frequency: 75 kHz, force constant: 2.8 N m−1) was used. To analyze the adhesion forces for Mo–Mo contact, the silicon tip was coated with 40 nm of molybdenum. Before the experiment, sensitivity calibration for obtaining the correct F–d curve was performed in the AFM program (SmartScan RTM12d). Vertical contact and separation processes were executed using a piezo-electrically moved tip-mounted stage of the AFM (0.3 μm s−1). The AFM tips were used to measure each of the 4 silicon and molybdenum samples, and each tip was used 16 times.Author contributions
Conceptualization: S.-H. K., P.-K. C., Y.-B. L.; data analysis: S.-H. K., Y.-B. L.; methodology: S.-H. K., P.-K. C., Y.-B. L.; resources: T.-S. K., S.-Y. L.; supervision: J.-B. Y.; visualization: S.-H. K., P.-K. C.; writing – original draft: S.-H. K.; writing – review and editing: S.-H. K., P.-K. C., Y.-B. L., M.-S. J., H.-W. M., J.-B. Y.Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
This research was supported by the National R&D Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (RS-2023-00215430). This research was also supported by Samsung Electronics.References
- A. Tiwari, J. Wang and B. Persson, Phys. Rev. E, 2020, 102, 042803 CrossRef CAS PubMed.
- M. Ciavarella, J. Joe, A. Papangelo and J. Barber, J. R. Soc., Interface, 2019, 16, 20180738 CrossRef CAS PubMed.
- S. N. Ramakrishna, L. Y. Clasohm, A. Rao and N. D. Spencer, Langmuir, 2011, 27, 9972–9978 CrossRef CAS PubMed.
- K. Komvopoulos, J. Adhes. Sci. Technol., 2003, 17, 477–517 CrossRef CAS.
- A. Momber, S. Koller and H. Dittmers, J. Prot. Coat. Linings, 2004, 21, 44–50 Search PubMed.
- J. W. Jeong, S. R. Yang, Y. H. Hur, S. W. Kim, K. M. Baek, S. Yim, H.-I. Jang, J. H. Park, S. Y. Lee and C.-O. Park, Nat. Commun., 2014, 5, 5387 CrossRef CAS PubMed.
- M. A. Meitl, Z.-T. Zhu, V. Kumar, K. J. Lee, X. Feng, Y. Y. Huang, I. Adesida, R. G. Nuzzo and J. A. Rogers, Nat. Mater., 2006, 5, 33–38 CrossRef CAS.
- A. Braeutigam, A. N. Simsek, G. Gompper and B. Sabass, Nat. Commun., 2022, 13, 2197 CrossRef CAS PubMed.
- W. M. Van Spengen, R. Puers and I. De Wolf, J. Micromech. Microeng., 2002, 12, 702 CrossRef.
- K.-M. Hwang, J.-Y. Park, H. Bae, S.-W. Lee, C.-K. Kim, M. Seo, H. Im, D.-H. Kim, S.-Y. Kim and G.-B. Lee, ACS Nano, 2017, 11, 12547–12552 CrossRef CAS PubMed.
- P. K. Choi, Y.-B. Lee, S. Kim, T.-S. Kim and J.-B. Yoon, J. Microelectromech. Syst., 2021, 31, 87–96 Search PubMed.
- S. Rana, J. Mouro, S. J. Bleiker, J. D. Reynolds, H. M. Chong, F. Niklaus and D. Pamunuwa, Nat. Commun., 2020, 11, 1181 CrossRef CAS PubMed.
- Y.-B. Lee, M.-H. Kang, P.-K. Choi, S.-H. Kim, T.-S. Kim, S.-Y. Lee and J.-B. Yoon, Nat. Commun., 2023, 14, 460 CrossRef CAS PubMed.
- N. Agraıt, A. L. Yeyati and J. M. Van Ruitenbeek, Phys. Rep., 2003, 377, 81–279 CrossRef.
- Y. Mo, K. T. Turner and I. Szlufarska, Nature, 2009, 457, 1116–1119 CrossRef CAS PubMed.
- B. Gotsmann and M. Lantz, Nat. Mater., 2013, 12, 59–65 CrossRef CAS PubMed.
- K. L. Johnson, K. Kendall and A. Roberts, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1971, 324, 301–313 CAS.
- H. Hertz, Journal fur die Reine und Angewandte Mathematik, 1881, 92, 156 Search PubMed.
- B. V. Derjaguin, V. M. Muller and Y. P. Toporov, J. Colloid Interface Sci., 1975, 53, 314–326 CrossRef CAS.
- V. Muller, B. Derjaguin and Y. P. Toporov, Colloids Surf., 1983, 7, 251–259 CrossRef CAS.
- J. A. Greenwood and J. P. Williamson, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1966, 295, 300–319 CAS.
- K. Fuller and D. Tabor, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1975, 345, 327–342 Search PubMed.
- S. R. Chowdhury and H. Pollock, Wear, 1981, 66, 307–321 CrossRef CAS.
- W.-R. Chang, I. Etsion and D. Bogy, J. Tribol., 1988, 110, 50–56 CrossRef.
- D. Maugis, J. Adhes. Sci. Technol., 1996, 10, 161–175 CrossRef CAS.
- C. Morrow, M. Lovell and X. Ning, J. Phys. D: Appl. Phys., 2003, 36, 534 CrossRef CAS.
- P. Prokopovich and S. Perni, Langmuir, 2010, 26, 17028–17036 CrossRef CAS PubMed.
- P. Prokopovich and S. Perni, Colloids Surf., A, 2011, 383, 95–101 CrossRef CAS.
- H. Hu, S. Zhao, W. Wang, Y. Zhang, Y. Fu and Z. Zheng, Appl. Phys. Lett., 2021, 119, 071603 CrossRef CAS.
- C. A. Morrow and M. R. Lovell, International Joint Tribology Conference, 2004, vol. 41812, pp. 1245–1268 Search PubMed.
- F. W. DelRio, M. P. de Boer, J. A. Knapp, E. David Reedy Jr, P. J. Clews and M. L. Dunn, Nat. Mater., 2005, 4, 629–634 CrossRef CAS PubMed.
- L. Kogut and I. Etsion, J. Colloid Interface Sci., 2003, 261, 372–378 CrossRef CAS PubMed.
- K. L. Johnson and K. L. Johnson, Contact Mechanics, Cambridge University Press, 1987 Search PubMed.
- K. Johnson, Tribol. Int., 1998, 31, 413–418 CrossRef.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, 2011 Search PubMed.
- B. Cappella and G. Dietler, Surf. Sci. Rep., 1999, 34, 1–104 CrossRef CAS.
- D. Tabor, in Plenary and Invited Lectures, Elsevier, 1977, pp. 3–14 Search PubMed.
- A. Banerjea, J. Ferrante and J. R. Smith, in Fundamentals of Adhesion, Springer, 1991, pp. 325–348 Search PubMed.
- W. R. Chang, I. Etsion and D. B. Bogy, J. Tribol., 1987, 109, 257–263 CrossRef.
- T. D. Jacobs and A. Martini, Appl. Mech. Rev., 2017, 69, 060802 CrossRef.
- G. Rubio, N. Agrait and S. Vieira, Appl. Mech. Rev., 1996, 76, 2302 CAS.
- N. Mosso, U. Drechsler, F. Menges, P. Nirmalraj, S. Karg, H. Riel and B. Gotsmann, Nat. Nanotechnol., 2017, 12, 430 CrossRef CAS PubMed.
- G. R. Heath, E. Kots, J. L. Robertson, S. Lansky, G. Khelashvili, H. Weinstein and S. Scheuring, Nature, 2021, 594, 385–390 CrossRef CAS PubMed.
- N. Vogt, Nat. Methods, 2021, 18, 859 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary equations, figures, and videos. See DOI: https://doi.org/10.1039/d3na01044a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |