Blue phosphorene on Au(111): theoretical, spectroscopic and diffraction analysis reveal the role of single Au adatoms

Abstract

In investigating the monoatomic layers of P, several stable two-dimensional (2D) allotropes have been theoretically predicted. Among them, single-layer blue phosphorus (BlueP) appears to deliver promising properties. After initial success, where the structure of BlueP triangular patches on Au(111) was conceived on the basis of scanning tunneling microscopy (STM) and density functional theory (DFT), the surface structure model was revisited multiple times with increasing accuracy and insight of theoretical calculations and experimental datasets. Interestingly, the quest for a reliable atomic structure model of BlueP on Au(111) turned out to be very contentious and challenging, particularly considering the possible incorporation of Au atoms in the 2D sheet of P. This article proposes an extended report on theoretical findings that can be extracted from DFT calculations of the orbital projected band structure and employed for an efficient comparison protocol between the calculations and experimental datasets obtained from angle-resolved photoemission spectroscopy (ARPES). The findings, together with experimental and simulated data from STM imaging and surface X-ray diffraction (SXRD), show a clear way to verify the presence and characterize the stabilizing effect of foreign atoms in 2D materials.

---

Introduction

In the broad class of two-dimensional (2D) materials, phosphorus allotropes have drawn increasing attention owing to their attractive optoelectronic properties.^1–3 For example, 2D black phosphorus (BlackP) can be synthesized with a top-down approach, i.e. by exfoliation from its parent 3D material, and exhibits high carrier mobility^4–6 with a band gap that can be tuned by controlling the number of layers^7,8 and the external field.^9,10 Encouraged by these findings, other stable 2D phosphorus allotropes have been theoretically predicted.^11,12 Among them, single-layer blue phosphorus (BlueP) appears to be a promising material. Its buckled, quasi-planar atomic structure is reported to be almost as stable as BlackP¹³ with similar conducting properties¹³ and similarly tunable semiconducting band gap as a function of the number of layers¹⁴ and the applied external fields.¹⁵ Because of the lack of a parent 3D material, BlueP could be obtained only using a bottom-up approach, i.e. through the controlled deposition of P atoms on a suitable substrate.

The first experimental result reported in literature is the formation of BlueP triangular patches on Au(111) upon evaporation of BlackP,^16–18 arranged in a periodic rhombic unit cell corresponding to a (5 × 5)-Au(111) supercell. The first surface structure model proposed, made of two mirrored triangular islands of 16 P atoms each (P₁₆ × 2), was conceived on the basis of standard scanning tunneling microscopy (STM) topographic images.¹⁵ This model was then revised multiple times, with progressively increasing accuracy and insight, by means of complementary density functional theory (DFT) simulations and new, atomically resolved STM imaging. Oughaddou's group¹⁹ proposed a more complex unit cell, where the two islands have 19 P atoms each (P₁₉ × 2). Meanwhile, Zhao et al.²⁰ proposed a model with less P atoms in each island, but with the inclusion of single Au adatoms in the 2D unit cell. This latter model, built with 2 islands and 9 P atoms each and 9 Au atoms in each cell (P₉ × 2 + 9Au model), offered precise match with both STM images²¹ and dynamic LEED-I(V)²² measurements. Remarkably, the band structure of many proposed models showed common features that were in agreement with angle-resolved photoemission spectroscopy (ARPES) measurements, supporting a prevailing P-induced band dispersion between the Fermi level and the Au sp-band placed at ∼2 eV binding energy (BE). In the first case, Zhuang et al.¹⁷ claimed that the observed bandgap of the P states matched the calculated one, despite a very different band dispersion shape along k_//. For the same model, Golias et al.¹⁸ showed that the simulated P-related bands consistently fall between the Fermi level and the Au sp-band, although placed at a different BE with respect to the experimental results. Also, the P₉ × 2 + 9Au alloy model exhibits a dispersive band structure at low BE, partially resembling the experimental evidence of Zhao et al.²⁰

In summary, the quest for a reliable atomic structure model of BlueP on Au(111) turned out to be highly debated and challenging, particularly on the issue of the possible incorporation of substrate atoms in the 2D sheet. The comparison protocol between the DFT calculations and experimental evidence (mainly STM and ARPES) still appears to be a powerful tool available to researchers, although there is room for improvement. In this article, we propose an extended report on the theoretical findings that can be extracted from DFT calculations, and a more convincing and efficient comparison protocol between theory and experiment that can be used not only to validate and refine a single model, but also to discriminate between different atomic models. We employ STM imaging, surface X-ray diffraction (SXRD) and ARPES to create a comprehensive set of experimental data, and we apply an orbital projected unfolding procedure on the DFT calculated band structure to demonstrate the soundness of the atomic model presented and to provide accurate comparison tools. This proposal is fueled by the increasing need to understand the physical factors behind the bottom-up growth of complex 2D materials on ordered substrates. In this context, we will take into account the most prominent atomic model presented in the literature with Au (P₉ × 2 + 9Au) and will put particular attention on the possible presence of single Au atoms in the BlueP 2D mesh, to evaluate the driving force behind the incorporation of hetero-atoms, and to ease the future careful selection of proper substrates on which complex 2D materials such as BlueP can be grown in the form of single, pure phases. We compare this model with the one without the additional Au atoms (P₉ × 2). Other models with different numbers of P and Au atoms can be ruled out by considering the geometry displayed by experimental STM topography with atomic resolution available in literature.

Methods

Sample preparation

For each experiment, the Au(111) substrate was cleaned via iterated cycles of Ar⁺ ion sputtering (1.5 keV, 15′, 10 μA) at room temperature and annealing at 600 °C in ultra-high vacuum (UHV). Then, the BlueP–Au film was grown following the inexpensive recipe recently presented in ref. 23, i.e., by sublimation of red phosphorus (RedP) held in a Knudsen cell at 320 °C and deposition of the resulting P₄ and P₂ clusters on the sample kept at 250 °C, yielding a film identical to the one grown starting from the expensive BlackP precursor.

Scanning tunneling microscopy. STM investigations were carried out at 77 K in UHV conditions (base pressure < 8 × 10⁻¹¹ mbar) using a commercial Omicron Low-Temperature STM hosted at the CNR-IOM, Trieste, Italy. Images were acquired in constant-current mode and post-processed with drift correction and mild Gaussian smoothing.

Surface X-ray diffraction. SXRD measurements were performed at the SixS beamline at the SOLEIL Synchrotron radiation facility, Gif-Sur-Yvette, France. The experimental UHV chamber (base pressure < 3 × 10⁻¹⁰ mbar) is equipped with a z-axis diffractometer^24,25 and a two-dimensional hybrid pixel detector (XPAD S140)²⁶ to collect the scattered radiation intensities. Crystal (integer) truncation rods (CTRs) and (fractional) superstructure rods (SSRs) were obtained with a photon energy of 11.8 keV and an incident angle μ = 0.35°, processed by the software BINoculars²⁷ and analyzed with the ROD software suite.²⁸ To simulate the CTRs and SSRs, the structure factors were computed starting from the surface models developed by means of the DFT calculations. Thereafter, each model was refined by a multivariate optimization by least-square fitting the experimental data to yield best quantitative agreement on both χ² and R-factor measures. Miller indexes (H, K, L) are given in reciprocal lattice units (r.l.u.) with respect to the (5 × 5) superstructure.

Angle-resolved photoemission spectroscopy. ARPES k_// maps and electron momentum distribution curves (MDC) were collected in UHV (base p < 7 × 10⁻¹¹ mbar) using the spectroscopic photoemission and low-energy electron microscope (SPELEEM) instrument²⁹ that is located at the nanospectroscopy beamline of the Elettra synchrotron radiation facility, Trieste, Italy.³⁰ The photon beam (hν = 65 eV) was focused on the sample, and the area from which ARPES data is collected was further reduced by using a field-limiting aperture, yielding an effective probed region of 2 μm diameter. The overall photoelectron kinetic energy resolution was 0.33 eV.

Numerical simulations. DFT calculations were carried out using the QUANTUM ESPRESSO (QE) package³¹ empowered with the Perdew–Burke–Ernzerhof (PBE) functional³² within the generalized gradient approximation (GGA) to incorporate the exchange-correlation terms. In this case, the use of van der Waals corrections is essential: the Grimme-D3 scheme³³ was preferred to Grimme-D2, as the latter leads to a fictitious Au surface reconstruction upon structural optimization. The Au(111) surface was modeled with a 4-layer slab in a (5 × 5) in-plane unit cell (optimized lattice parameter 4.14 Å, slightly larger than the experimental value of 4.08 Å; slab spacing 12 Å) under periodic boundary conditions. 2 × 2 × 1 and 4 × 4 × 2 k-meshes were used to sample the first Brillouin zone for the self-consistent cycle and non-self-consistent cycle, respectively. The energy cutoffs for the plane wave expansion of the wavefunctions and the charge density were 40 and 300 Ry, respectively. Methfessel–Paxton smearing of the orbital occupation (energy broadening 0.01 Ry) improved the convergence of the self-consistent cycle.³⁴ The convergence thresholds were set to 10⁻⁶ Ry per atom for the total energy in self-consistent calculations, and to 10⁻³ Ry a₀⁻¹ for each component of all forces on the atoms in the structural optimization cycles. The error on the calculated equilibrium lattice parameter was 0.01 a₀. STM images were simulated employing the Tersoff–Hamann scheme.³⁵

A meaningful comparison of the ARPES maps and spectra with the calculated band structure requires a non-trivial orbital projected unfolding procedure recently implemented and interfaced with QE,³⁶ as the use of the (5 × 5) supercell reduces the First Brillouin Zone (FBZ) size with respect to the Au(111) primitive cell. Such procedure was applied along the Γ–K and Γ–M paths with a sampling of 200 different k points each. Its correctness was tested by simulating the clean Au(111) surface for both (5 × 5) and (1 × 1) cells and for slabs of different thickness (see Fig. S1 in ESI†). Remarkably, this analysis also shows that the Shockley surface state emerges only for simulations with thicker slabs. ARPES k_// maps were also obtained with the same package using a 2D equally spaced grid of 900 k-points.

Results

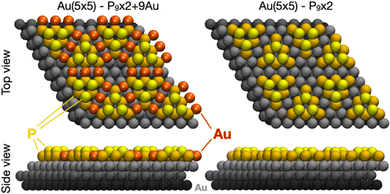
Our results discriminate between two structural models with different incorporations of substrate atoms, i.e., the one made of 18 P atoms and 9 Au atoms (P₉ × 2 + 9Au) most recently proposed by Zhao et al.²⁰ and one with the same pyramidal-shape twin islands of BlueP with 9 P atoms each, but without the Au bridging atoms (P₉ × 2). Both models are displayed in top and side views in Fig. 1.

Fig. 1 Top and side view of the ball rendering models of four (5 × 5) unit cells of BlueP–Au/Au(111). The Au(111) slab is displayed in grey, Au adatoms in red, and P atoms constituting the BlueP triangular islands in dark (lower) and light (higher) yellow. Only 3 Au slab layers are shown here for the best clarity, but the simulations have been performed with 4 slab layers.

We calculate the adsorption energy per P atom as follows:

E_ad = (E_tot − E_subs − N_PE_P)/N_P

where E_tot is the total energy of the whole structure in the simulation cell, E_subs is the energy of the Au substrate in the same simulation cell (with or without the additional 9 Au adatoms, depending on the model), E_P is the energy of the isolated P atom, and N_P is the number of P atoms included in the whole structure in the simulation cell.

This definition allows us to compare the stability of the P islands in the different structures, indicating that the P₉ × 2 + 9Au model (E_ad = −1.04 eV per P atom) is favored by about 20% over P₉ × 2 (E_ad = −0.81 eV per P atom) due to the presence of Au edge atoms that stabilize the BlueP flakes. Moreover, the structural parameters (Table 1) show that in the case of the P₉ × 2 + 9Au, both the buckling amplitude and the average distance between the coplanar P atoms are closer to the structural parameters of freestanding BlueP with respect to the P₉ × 2 phase.

Table 1 Geometric distances of the two investigated models and, for comparison, freestanding BlueP. Δz_P–P refers to the distance along the z-axis between the two P layers. Δr_P is the coplanar distance between the nearest-neighbor P atoms in the higher (top) and lower (bottom) P layers

	ΔzP–P (Å)	ΔrPtop (Å)	ΔrPbottom (Å)
P9 × 2	1.15	3.47	3.39
P9 × 2 + 9Au	1.18	3.33	3.22
BlueP free	1.26	3.29

---

STM

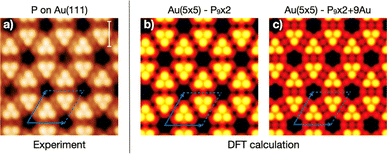
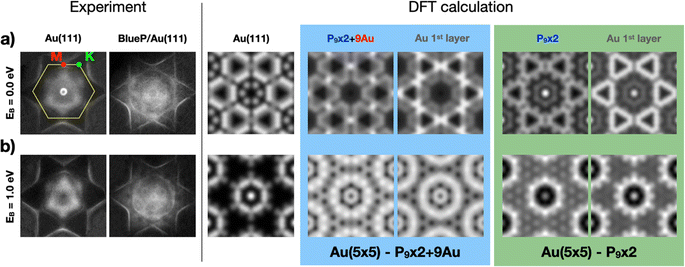
Fig. 2 contains a direct comparison between the experimental, atomically resolved STM topography and images simulated for both models. The surface consists of a rhombic unit cell containing two triangular, mirrored protrusions of three atoms each, separated by an intermediate atomic level. At the unit cell corners, hexagonal-shaped depressions appear with precise orientation, occasionally filled with additional P clusters.²⁰ Simulated images show similarities, such as the triangular, mirrored protrusions and hexagonal depression, but also some fine differences. Both intermediate levels in between the mirrored protrusions appear constituted by a triple intensity modulation aligned along the mirror axis, whose shape differs slightly between the two models considered. Moreover, the orientation of the hexagonal (black) depression differs between the models by 30°, correctly aligned with the experimental counterpart for the P₉ × 2 + 9Au. Thus, this model with 9 extra Au atoms seems to be in better agreement with the experimental STM data.

Fig. 2 (a) Experimental STM image of the BlueP–Au/Au(111) surface. The rhombic unit cell, depicted in blue, consists of two triangular protrusions and an intermediate level delimited by four hexagonal-shaped depressions at the cell corners. Bias −0.3 V, tunneling current 1.0 nA, white scale bar 1 nm. (b and c) Show the simulated appearance of the two models under STM inspection at the same lateral scale. Simulated bias −0.4 V, isosurface placed 3.0 Å above the highest P layer.

Nonetheless, it must be pointed out that some features can be distinguishable only in the experimental data obtained at low bias and high tunneling current with a perfect, rounded scanning tip. In fact, by looking carefully, one can notice that even our experimental STM image was produced by a very sharp, but slightly asymmetric tip. Such artifacts are very common and could easily bring the experiment-theory comparison to wrong conclusions when based on fine details, as it was the case for the atomic models initially proposed in the literature. In conclusion, the comparison between theory and experiment cannot be conclusive solely based on the STM data, even in the case of high quality, atomically resolved images, although such comparison can give relatively strong qualitative indications about the correct model.

Surface X-ray diffraction

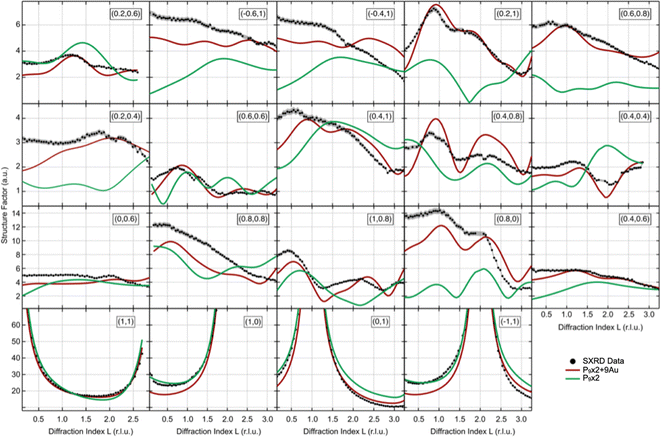
Independent information on this issue can be obtained from a fit of SXRD data acquired using a coherent, monochromatic X-ray beam diffracted at grazing angle by the BlueP–Au/Au(111) sample. An example of the diffraction pattern obtained can be found in Fig. S2 in ESI.† The experimental basis set consists of 1090 datapoints from 4 CTRs and 15 SSRs, i.e., all the symmetry-inequivalent crystal and superstructure rods included between zero- and first-order diffraction spots of the Au(111) substrate, covering an overall range of about 57 r.l.u. Fig. 3 shows the experimental intensity modulation of the rods as a function of the diffraction index L, superimposed to the optimized simulations for both P₉ × 2 + 9Au and P₉ × 2 structural models. Best fits are obtained by further relaxing the atomic positions in the unit cell with respect to the DFT-calculated structure, adopted as a starting point, and by allowing the distance between the superstructure atomic planes to vary with respect to the bulk termination (due to the limited thickness of the simulation slab, the interplanar distances are not accurately described – see Fig. S3 in ESI†). It should be noted that since the X-ray scattering cross-section for P atoms is much smaller than the one of Au, the iterative fit algorithm is not capable of discriminating effectively on the z-position of the P atoms, as their displacement does not contribute significantly to the simulated curves. Nevertheless, the enhanced signal from the Au atoms provides an advantage in trying to distinguish between the two model structures, which mainly differ by the restructuring of the substrate Au atoms. The atomic coordinates of the optimized model structures yielding the best agreement with the experimental diffraction data are listed in Table S1 in ESI.† The overall quantitative agreement between simulation and experiment for the SXRD data set is evaluated by both χ² and R-factor³⁷ for best solidity: the P₉ × 2 + 9Au and P₉ × 2 structure models yield R-factors (normalized chi-square values) of 0.146 (59) and 0.249 (224), respectively. This result provides solid evidence in favor of the P₉ × 2 + 9Au model.

Fig. 3 Measured CTRs (integer values of H and K) and SSRs (fractional values of H or K) of BlueP–Au/Au(111), and the calculated structure factors for P9 × 2 + 9Au and P9 × 2 optimized structural models.

ARPES

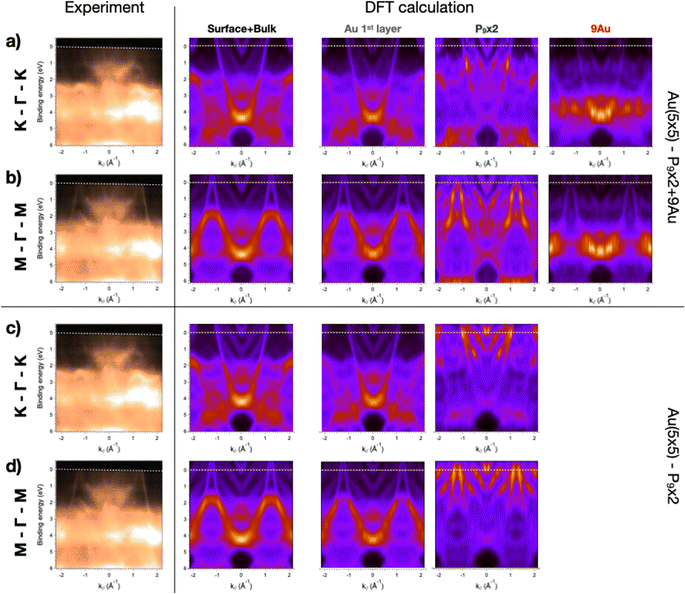
The SPELEEM microscope collects ARPES data as a stack of angle-resolved maps of the photoemitted electrons obtained by changing the probed electron kinetic energy (thus, the binding energy, BE) for a selected impinging photon energy. The measurement then delivers a 3D volume of data displayed along three axes, i.e., k_x, k_y (i.e., the electron momentum components parallel to the surface) and BE. By slicing along specific planes, one can obtain the electronic dispersion in reciprocal space (k_x, k_y) at a selected BE or the band structure along highly symmetrical crystallographic directions (k, BE). Both quantities can be simulated and displayed properly for a qualitative comparison between theory and experiment. The calculated band structure is extracted by integrating over the entire simulation cell, i.e., by summing the contributions of all the atoms in the slab calculation. Conversely, the photoelectrons that generate the ARPES spectra are emitted from just the topmost atomic layers because of the finite inelastic mean free path of the electrons. Therefore, a more reliable theory–experiment comparison can be obtained by firstly adding the contribution of the atoms lying on a single plane, and then performing an overall layer-by-layer weighted sum. Moreover, the calculated band structure needs to be unfolded properly, as described in the Methods section.

Fig. 4 displays the experimentally measured momentum distribution curves extracted along the high-symmetry directions in the reciprocal space (K–Γ–K and M–Γ–M), along with the calculated band structure of the two structural models considered. In particular, we show (from left to right) columns with simulated data extracted from the entire simulation cell (surface + bulk, second column), and then from the most significant homogeneous groups of atoms, i.e., the Au first layer (third column), the P adatoms (fourth column) and, for the first model only, the Au adatoms (right-most column). The experimental curves show a contribution ascribable to the BlueP–Au overlayer between 1 and 2 eV BE,²³ while the Au(111) substrate displays sp-bands across the Fermi energy and a strong d-band structure contribution below 2 eV BE. This BlueP–Au contribution in the occupied electronic states is also visible in the scanning tunneling spectroscopy dI/dV characteristics,¹⁶ but does not produce any relevant change of contrast in STM topography. Conversely, the calculated band structures obtained by averaging over the entire slab are dominated by the sp-bands of Au(111) between the Fermi energy and 2 eV. However, when disentangling the contribution of each atomic layer and displaying quantitatively the electronic density of states, one can clearly see the effect of BlueP–Au on the band structure. While the band structure of the top Au(111) layer is very similar to the bulk one, the P atoms yield a strong density of states at low BE. The P band structure differs greatly between the two models considered: the P₉ × 2 + 9Au model closely reproduces the experimental evidence, with a contribution to the density of states located between 1 and 2 eV BE and the proper position in the FBZ on both Γ–K and Γ–M profiles. Moreover, the 9 Au adatoms deploy an intense density of states around 4 eV BE. Conversely, the P₉ × 2 model predicts an intense density of states across the Fermi level in the band structure, a feature that is not observed experimentally.

Fig. 4 Experimental and theoretical band structures along K–Γ–K and M–Γ–M for the P₉ × 2 + 9Au model (a and b) and P₉ × 2 model (c and d). The color scales are black-yellow-white for the experimental data and black-purple-red-yellow for the theoretical representation. Theoretical results have been unfolded from (5 × 5) FBZ to (1 × 1) FBZ and are displayed after integration over the entire simulation cell (surface + bulk) and after projection on separate parts (Au 1st layer, P surface atoms and—in the first case—Au surface atoms). The Fermi level is highlighted with a dashed white line. Experimental data taken with a photon energy of 65 eV.

Similar indications are obtained by comparing the ARPES maps at selected BEs with the corresponding calculated momentum distribution of electrons in the (k_x, k_y) planes. Fig. 5 summarizes our experimental findings (on the left) and the results of the DFT calculations (on the right) for the two different models, right at the Fermi level (BE = 0) and at 1 eV, respectively. Experimental ARPES maps of the clean Au(111) termination and of BlueP–Au are presented to highlight the differences induced by the overlayer. At the Fermi energy, BlueP fades out the Au(111) surface state close to Γ. Furthermore, the triangle-shaped bands around K appear to be shrunk in size, and there is a higher density of states at M. At 1 eV BE, the band structure of BlueP–Au assumes the shape of two rings with radii of 0.80 Å⁻¹ and of 0.11 Å⁻¹ centered in proximity of the Γ–M direction and close to the Γ point, respectively. These and other main features are well reproduced by the P₉ × 2 + 9Au model: the triangle-shaped bands around K, originating from the first Au(111) atomic layer, and the P₉ × 2 + 9Au surface layer contribution, both display strong DOS also at M, while the distributed band structure calculated for the P₉ × 2 model shows low DOS at M. Moreover, this second model yields a strong density of states around Γ at the Fermi energy, a feature not present in the experimental data. At 1 eV BE, the P₉ × 2 + 9Au model resembles the two-ring structure around Γ. Meanwhile, for the P₉ × 2 model, just one ring of intermediate radius (0.65 Å⁻¹) and a localized DOS exactly at Γ are observed. The simulated ARPES maps of the clean Au(111) surface at both BEs are also reported in order to highlight the differences with the ones produced by the overlayers.

Fig. 5 Experimental and theoretical distribution of the photoemitted electrons in (k_x, k_y) (a) at the Fermi energy (i.e. Fermi surface mapping, 0 BE) and (b) at 1 eV BE. The FBZ hexagonal border (yellow) and the position of high-symmetry M (red) and K (green) points are highlighted. Experimental data taken with photon energy 65 eV. DFT calculations include the mapping of clean Au(111), and the contribution of P and Au surface atoms for both P₉ × 2 + 9Au (light blue) and P₉ × 2 (green) models. All pictures have the same lateral scale.

Discussion

The presented results support the P₉ × 2 + 9Au model as the best candidate to describe the BlueP–Au layer on Au(111). We find that only partial and qualitative discriminatory evidence between the two models under discussion can be obtained by comparing the STM experiments and simulations, since the presence of Au atoms can be inferred only indirectly on the basis of very fine morphological/DOS details in the topographic images. Such elements might easily lead to erroneous conclusions, as experimental STM images can be affected by poorly controllable tip-induced artifacts. More convincing and quantitative arguments are instead given by the intensity modulations of X-ray diffraction rods, which show that only the atomic model containing Au surface adatoms reproduces the experimental data. The 40% lower R-factor for the latter model (0.146 vs. 0.249) is statistically significant, and constitutes a much more conclusive statement than the STM comparison. We emphasize that this reduction is obtained by introducing atoms with high cross section (Au), so that their effect on the modulation of the diffraction rods overtakes the possible reduction induced by having more degrees of freedom in the calculation of the R-factor and normalized-chi-square. We also show that proper treatment and post-analysis of the DFT results on the electronic structure can express precise accounts on the correctness of the considered atomic models. We show that the band structure plots across both (k_x, k_y) and (k, BE) planes derived by integration on the entire unit cell are only partially comparable with the ARPES experimental data. Instead, the unfolding of separate contributions extracted from the co-planar surface atoms provides a more directly comparable set, and highlights the differences between the simulated atomic models. In our case, the enhanced sensitivity is essential to define the embedding of Au atoms in the BlueP film on Au(111). For this evaluation protocol, it is crucial to extract the band structure from single atomic planes, and to quantitatively display the density of states as a function of BE and k. Moreover, the density of states distribution on (k_x, k_y) projected on selected atoms can also give rise to different features that can be compared with experimental ARPES maps. Although this DFT-ARPES testing does not possess the same accuracy of SXRD, we believe that the proper comparison of experimental and simulated band structure achieves better precision in the diagnostic of foreign atoms in the 2D mesh with respect to STM topography, even with atomic resolution.

Conclusions

In conclusion, we show that a comprehensive approach based on a comparison of experiment and theory is on the right track to extrapolate complex atomic models of new 2D materials grown on selected substrates. While this is not a novel point, we instead pinpoint that for this quest, it is crucial to exploit tools capable of diagnosing the possible presence of host hetero-atoms in the 2D mesh. The matching between theory and experiment requires a solid foundation to validate the starting assumptions, and we believe that adequate elements of verification can be found, e.g., with angle-resolved diffraction and spectroscopy techniques discussed here, as well as other techniques, such as helium ion scattering. This result can be set in a more general context of smart design and realization of new 2D materials with attractive physical and chemical properties. Numerical simulations are fundamental to discovering which substrate is more promising for the defect-free bottom-up growth of 2D materials, such as BlueP. Parameters such as the adhesion energy per atom and the interatomic distance could be used as benchmarks to sense the substrate interaction, and establish if a complex atomic arrangement is favored over the ideal case. Regarding this aspect, temperature-dependent preparation schemes and the use of other techniques sensitive to the activation process of surface alloying would provide further insight. In general, the implementation of reliable and sensitive comparison protocols between experimental evidence and theoretical predictions can constitute the backbone for the engineering of next-generation materials.

Author contributions

Simone del Puppo: data curation, formal analysis, investigation, methodology, software, writing – review & editing. Pietro Biasin: data curation, formal analysis, investigation, software, writing – review & editing. Alessandro Sala: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, supervision, validation, visualization, writing – original draft. Paola Mantegazza: formal analysis, investigation, software, writing – review & editing. Ivan Pasqua: formal analysis, investigation, software, writing – review & editing. Elena Ghidorsi: formal analysis, investigation, writing – review & editing. Maria Caporali: funding acquisition, investigation, writing – review & editing. Andrea Resta: formal analysis, investigation, methodology, writing – review & editing. Alessandro Coati: investigation, methodology, writing – review & editing. Francesca Genuzio: investigation, methodology, writing – review & editing. T. Onur Menteş: investigation, methodology, writing – review & editing. Andrea Locatelli: investigation, methodology, writing – review & editing. Giovanni Comelli: funding acquisition, supervision, writing – review & editing. Cristina Africh: funding acquisition, supervision, writing – review & editing. Erik Vesselli: funding acquisition, investigation, methodology, supervision, writing – review & editing. Maria Peressi: conceptualization, funding acquisition, investigation, methodology, supervision, writing – review & editing. Alberto Verdini: conceptualization, funding acquisition, investigation, methodology, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. S., M. C., M. P., E. V. and A. V. acknowledge funding from the project “FERMAT – Fast ElectRon dynamics in novel hybrid organic-2D MATerials” funded by the MUR Progetti di ricerca di Rilevante Interesse Nazionale (PRIN) Bando 2017 – grant 2017KFY7XF. A. S. and M. P. acknowledge funding from the project “QUBOP” funded by the MUR Progetti di ricerca di Rilevante Interesse Nazionale (PRIN) Bando 2022 – grant 2022HAS7JY. M. P. acknowledges support from Fondazione ICSC – “Italian Research Center on High – Performance Computing, Big Data and Quantum Computing” – Spoke 7, Materials and Molecular Sciences – National Recovery and Resilience Plan (PNRR) – funded by MUR Missione 4 – Componente 2 – Investimento 1.4 – Next Generation EU (NGEU). Computational resources have been obtained from CINECA through the ISCRA initiative and the agreement with the University of Trieste. This work has been partially funded by the European Union – NextGenerationEU under the Italian Ministry of University and Research (MUR) National Innovation Ecosystem grant ECS00000041 – VITALITY. A. V. acknowledges Università degli Studi di Perugia and MUR for support within the project Vitality. A. V. acknowledges S. Cristiani for his great technical help.

Notes and references

1. X. Ling, H. Wang, S. Huang, F. Xia and M. S. Dresselhaus, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4523–4530.
2. F. Xia, H. Wang, J. C. M. Hwang, A. H. C. Neto and L. Yang, Nat. Rev. Phys., 2019, 1, 306–317.
3. M. Batmunkh, M. Bat-Erdene and J. G. Shapter, Adv. Energy Mater., 2018, 8, 1701832.
4. L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9(5), 372–377.
5. H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041.
6. L. Li, F. Yang, G. J. Ye, Z. Zhang, Z. Zhu, W. Lou, X. Zhou, L. Li, K. Watanabe, T. Taniguchi, K. Chang, Y. Wang, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2016, 11, 593–597.
7. V. Tran, R. Soklaski, Y. Liang and L. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 235319.
8. L. Li, J. Kim, C. Jin, G. J. Ye, D. Y. Qiu, F. H. Da Jornada, Z. Shi, L. Chen, Z. Zhang, F. Yang, K. Watanabe, T. Taniguchi, W. Ren, S. G. Louie, X. H. Chen, Y. Zhang and F. Wang, Nat. Nanotechnol., 2016, 12, 21–25.
9. Q. Liu, X. Zhang, L. B. Abdalla, A. Fazzio and A. Zunger, Nano Lett., 2015, 15, 1222–1228.
10. B. Deng, V. Tran, Y. Xie, H. Jiang, C. Li, Q. Guo, X. Wang, H. Tian, S. J. Koester, H. Wang, J. J. Cha, Q. Xia, L. Yang and F. Xia, Nat. Commun., 2017, 8, 1–7.
11. M. Wu, H. Fu, L. Zhou, K. Yao and X. C. Zeng, Nano Lett., 2015, 15, 3557–3562.
12. W. Zhang, X. Zhang, L. K. Ono, Y. Qi and H. Oughaddou, Small, 2024, 20, 2303115.
13. Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 112, 176802.
14. E. Montes, U. Schwingenschlögl, E. Montes and U. Schwingenschlögl, Adv. Mater., 2019, 31, 1807810.
15. B. Ghosh, S. Nahas, S. Bhowmick and A. Agarwal, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 115433.
16. J. L. Zhang, S. Zhao, C. Han, Z. Wang, S. Zhong, S. Sun, R. Guo, X. Zhou, C. D. Gu, K. D. Yuan, Z. Li and W. Chen, Nano Lett., 2016, 16, 4903–4908.
17. J. Zhuang, C. Liu, Q. Gao, Y. Liu, H. Feng, X. Xu, J. Wang, J. Zhao, S. X. Dou, Z. Hu and Y. Du, ACS Nano, 2018, 12, 5059–5065.
18. E. Golias, M. Krivenkov, A. Varykhalov, J. Sánchez-Barriga and O. Rader, Nano Lett., 2018, 18, 6672–6678.
19. W. Zhang, H. Enriquez, Y. Tong, A. Bendounan, A. Kara, A. P. Seitsonen, A. J. Mayne, G. Dujardin and H. Oughaddou, Small, 2018, 14, 1804066.
20. S. Zhao, J. L. Zhang, W. Chen and Z. Li, J. Phys. Chem. C, 2020, 124, 2024–2029.
21. J. L. Zhang, S. Zhao, M. Telychko, S. Sun, X. Lian, J. Su, A. Tadich, D. Qi, J. Zhuang, Y. Zheng, Z. Ma, C. Gu, Z. Hu, Y. Du, J. Lu, Z. Li and W. Chen, Nano Lett., 2019, 19, 5340–5346.
22. H. Tian, J.-Q. Zhang, W. Ho, J.-P. Xu, B. Xia, Y. Xia, J. Fan, H. Xu, M. Xie and S. Y. Tong, Matter, 2020, 2, 111–118.
23. A. Sala, M. Caporali, M. Serrano-Ruiz, F. Armillotta, E. Vesselli, F. Genuzio, T. O. Menteş, A. Locatelli, G. Comelli, C. Africh and A. Verdini, Nanoscale, 2022, 14, 16256–16261.
24. E. Vlieg, J. Appl. Crystallogr., 1997, 30, 532–543.
25. O. Robach, Y. Garreau, K. Aïd and M. B. Véron-Jolliot, J. Appl. Crystallogr., 2000, 33, 1006–1018.
26. J. Drnec, T. Zhou, S. Pintea, W. Onderwaater, E. Vlieg, G. Renaud and R. Felici, J. Appl. Crystallogr., 2014, 47, 365–377.
27. S. Roobol, W. Onderwaater, J. Drnec, R. Felici and J. Frenken, J. Appl. Crystallogr., 2015, 48, 1324–1329.
28. E. Vlieg, J. Appl. Crystallogr., 2000, 33, 401–405.
29. A. Sala, Imaging at the Mesoscale (LEEM, PEEM), in Springer Handbook of Surface Science, ed. M. Rocca, T. S. Rahman, L. Vattuone, Springer, Cham, 2020, pp. 387–425.
30. T. O. Menteş, G. Zamborlini, A. Sala and A. Locatelli, Beilstein J. Nanotechnol., 2014, 5, 1873–1886.
31. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
33. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
34. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621.
35. J. Tersoff and D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 805–813.
36. D. Pacilè, C. Cardoso, G. Avvisati, I. Vobornik, C. Mariani, D. A. Leon, P. Bonfà, D. Varsano, A. Ferretti and M. G. Betti, Appl. Phys. Lett., 2021, 118, 121602.
37. M. A. Van Hove, S. Y. Tong and M. H. Elconin, Surf. Sci., 1977, 64, 85–95.

---

Footnotes

† Electronic supplementary information (ESI) available: Simulated Au(111) band structure for different slab thickness, in-plane reciprocal space map of SXRD, simulated atomic plane distance for different slab thickness, atomic coordinates used for SXRD simulation. See DOI: https://doi.org/10.1039/d4na00192c

‡ Present address: SDG Group Italy, Via Vitruvio 1, 20124 Milan, Italy.

§ Present address: School of Chemistry, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK.

¶ Present address: Scuola Internazionale Superiore di Studi Avanzati, Via Bonomea 265, 34136 Trieste, Italy.

---