Designing N, P-doped graphene surface-supported Mo single-atom catalysts for efficient conversion of nitrogen into ammonia: a computational guideline

Abstract

Tuning the surroundings of single-atom catalysts (SACs) has been recognized as a successful approach to enhance their electrocatalytic efficiency. In this study, we utilized density functional theory (DFT) computations to systematically investigate how the coordination environment influences the catalytic performance of individual molybdenum atoms for the nitrogen reduction reaction (NRR) to NH₃. Upon comparing an extensive array of coordination combinations, Mo-based SACs were found to feature a distinctive N, P-dual coordination. Specifically, MoN₃P₁G demonstrates superior performance in the conversion of nitrogen into ammonia with an exceptionally low limiting potential (−0.64 V). This MoN₃P₁G catalyst preferably follows the distal pathway, with the initial hydrogenation step (*N₂ → *NNH) being the rate-determining step. Additionally, MoN₃P₁G exhibits the ability to suppress competing H₂ production, showcases high thermodynamic stability, and holds significant promise for experimental preparation. These findings not only contribute to diversifying the SAC family through localized coordination control but also present cost-effective strategies for enhancing sustainable NH₃ production.

---

Introduction

Hydrogen and ammonia gases are currently being adopted as alternatives to the currently depleting fossil fuels.^1,2 The forerunner includes hydrogen and the formation of a hydrogen economy. While hydrogen is noted for having the highest energy per unit mass among all fuels, its energy density per unit volume is limited due to its low density at ambient temperature. The hydrogen economy faces challenges associated with hydrogen transportation, storage, and safety.³ Hydrogen's low volumetric energy density necessitates the use of high-pressure gas cylinders or cryogenic tanks for transportation, which can be costly and require specialized infrastructure. Additionally, its flammability and propensity for leakage demand special safety measures^4,5 In contrast, ammonia offers a higher volumetric energy density and a wider flammability range but still requires careful handling. Overcoming these challenges would require significant investment in infrastructure and safety measures. Due to hydrogen's many challenges, ammonia may become a vital component for the world's future economic sectors, comprising energy, agriculture, transportation, and pharmaceuticals. As an alternative fuel source, ammonia offers several advantages to the current gasoline-driven energy sector and the foreshadowed hydrogen economy.^6,7 Like hydrogen, ammonia is an artificial substance that can be derived from biomass, fossil fuels, or alternative renewable sources. Notably, ammonia offers merits over hydrogen, including a higher volumetric energy density comparable to gasoline.⁸ Additionally, it boasts simpler production, treatment, and delivery, leveraging the existing framework as there is already an established infrastructure for producing and transporting ammonia, which could make it easier to scale up its use as a fuel, and better commercial viability.⁹ Ammonia can also be synthesized from sustainable energy like solar power and wind, positioning it as a potentially sustainable fuel.^10,11

The nitrogen reduction reaction (NRR) is a key focus in research due to its potential for sustainable ammonia synthesis. However, the current method requires high pressure (15–20 MPa) and temperature (400–500 °C), along with an iron catalyst, which can degrade over time, reducing reaction efficiency.^12,13 In this regard, researchers are working to develop more stable and efficient catalysts to overcome this challenge.^14,15 Various SACs were reported for their catalytic activity, which motivated us to focus on them in our study. Graphene was selected as a support for SACs.

Graphene has garnered significant interest because of its unique electronic, mechanical, and thermal properties.^16,17 Doping graphene with heteroatoms such as nitrogen, boron, and sulfur can further enhance its properties and make it suitable for various applications, including catalysis.^18–20 N-graphene has appeared as a favorable candidate for NRR catalysis.²¹ Moreover, the doping level and type of heteroatom can be controlled to optimize the catalytic performance.^22,23 It was proved that the local coordination atoms greatly affected the NRR catalytic activity.^24–27 Till now, there has been little work on tuning the coordination environment of SACs.²⁸ It was demonstrated that the asymmetrically dual-coordinated MN₂B₂ active site could enhance the reduction potential (U_L) of the NRR, particularly for metals with high spin states such as CrN₂B₂ (4 μB), VN₂B₂ (3 μB), and MoN₂B₂ (2 μB).²⁹ This phenomenon disrupted the scaling relations between the crucial nitrogen-containing intermediates, resulting in lower U_L values (−0.33 V < −0.53 V < −0.57 V). Also, it was proved that the MoB₃O active site, characterized by its distinctive coordination combination, showcased superior performance in the NRR, with U_L of −0.34 V.³⁰ It was discovered that the MoN₁C₂ active site facilitated the NRR via an enzymatic mechanism, demonstrating an exceptionally low overpotential of 0.24 V.³¹ The NRR was computationally investigated on (M2@B2-C2N), which revealed that the NRR could proceed with high efficiency for M₂ = Mo₂ and W₂, with U_L = −0.25 V and U_L = −0.27 V, respectively.²³

In this work, a singular molybdenum (Mo) center was chosen as a representative example to investigate the impact of local coordination, involving various types and quantities of dopants, on its catalytic activity in the nitrogen reduction reaction (NRR).^29,30,32,33 The four carbon atoms attached to the Mo center were replaced by N and P with different ratios to investigate the sensitivity of the NRR catalytic performance of Mo-G to the coordination environment. The performance of N_mP_n-Mo-graphene surfaces was investigated for the adsorption of N₂ for the NRR process. Furthermore, the potential mechanisms of the NRR on the Mo-graphene surface were investigated and discussed, including the adsorption and activation of nitrogen molecules, the reduction of nitrogen to ammonia, and the competing reactions that can lead to side products. The catalytic performance of Mo-graphene was compared to that of other tuned Mo-graphene catalysts with various coordination environments, containing nitrogen and phosphorus atoms. The advantages and limitations of using Mo-graphene for the NRR, such as the scalability, selectivity,³⁴ and stability of the catalyst for N₂ reduction for ammonia synthesis, were also studied. Finally, the prospects and challenges of using the Mo-graphene catalyst for the industrial-scale NRR are elaborated and future research directions are suggested.

Theoretical details

Density functional theory (DFT) simulations (spin-polarized) were accomplished via the projector augmented wave (PAW)³⁵ recommended pseudopotentials as executed in the Vienna Ab initio Simulation Package (VASP) code³⁶ on a supercell of size 14.92 Å × 12.27 Å to investigate the properties of the doped graphene surfaces and adsorbed species. The generalized gradient approximation Perdew–Burke–Ernzerhof functional (GGA-PBE)³⁷ was used, with the cut-off energy (E_cut) set to 400 eV to indicate the electronic exchange–correlation energies. Clusters of N₂, P₈, and Mo₂ were optimized in cubic cells with the length of 15, 20, and 25 Å respectively. Nitrogen and/or phosphorus-doped molybdenum-graphene models (N_mP_nMoG), where (m = 0–4, n = 0–4), are considered as supports. To avoid the interaction of two periodic structures, a vacuum slab of 25 Å was added in the Z direction and a 3 × 3 × 1 gamma-centered k-point grid was sampled for the Brillouin zone. The convergence criteria were set as follows: energy change of 5 × 10⁻⁶ eV with a maximum force of 0.02 eV Å⁻¹. Herein, eight catalysts were studied with doping N_mP_n (m = 0–4, n = 0–4) (P₄MoG, N₄MoG, N₃PMoG, N₂P₂MoGα, N₂P₂MoGβ, N₂P₂MoGγ, NP₃MoG and MoG) supported on molybdenum-doped graphene (MoG) sheets as models of calculation. The modulation provides ideal anchor sites for the N_m and P_n doping resulting in stable configurations. The total number of atoms was set to 4.

NRR reaction intermediates were computed via the computational hydrogen electrode (CHE) method for the Gibbs free energy (ΔG) calculations,^38,39 The chemical potential of the hydrogen atom was evaluated from the ground state energy of an H₂ molecule under standard conditions. At an arbitrary potential U vs. the standard hydrogen electrode (SHE), ΔG of each elementary step, including the proton–electron pair (H⁺ + e⁻), was shifted by −e·U. Harmonic approximation was employed to measure the ΔG of adsorbed species taking into account the entropy corrections and zero-point vibrational energy (ZPVE) at 298.15.⁴⁰ Solvent effect is not considered as in the case of NRR intermediates; its effect in the stabilization of water is estimated to be in the range of 0.1 eV.⁴¹ To investigate the thermal stability of the studied catalysts, ab initio molecular dynamics (AIMD) simulation was carried out in a canonical ensemble (NVT) with a time step of 2.0 fs. The simulations were run for a total of 10 ps, using the Nosé–Hoover chain thermostat to maintain a constant temperature.

Results and discussion

Nitrogen can be adsorbed on the surface of the catalyst in two different stable configurations; end-on (E) and side-on (S). Both were elucidated here for the different studied systems. The suffixes (E) and (S) are used to express the way of adsorption of nitrogen end-on and side-on, respectively. The bond length of N–N in a free nitrogen molecule was calculated to be 1.12 Å, while after adsorption it was elongated in all sixteen systems. The magnitude of elongation is higher in the side-on configuration than in the end-on counterpart, indicating better activation of N₂ in the side-on sites. The average N–N bond length in end-on systems is about 1.14 Å while for side-on systems it is about 1.20 Å. For MoN₃P₁G(S), MoN₂P₂Gγ(S) and MoN₂P₂Gβ(S), it increased to 1.27 Å, 1.25 Å and 1.24 Å, respectively, which makes these three catalysts have higher activity for protonation. In this work, sixteen systems were investigated for their NRR catalytic activity. Most of them are stable towards N₂ formation either by end-on or side-on configuration except MoP₄G(S) and MoN₁P₃G(S) as they required energy barriers of 0.77 and 1.8 eV, respectively.

The Bader charge analysis⁴² was performed, which indicated a charge transfer from molybdenum to the adsorbed nitrogen atoms. For the end-on adsorbed N₂, the charge accumulated on the nitrogen atom attached to Mo, which is denoted as N², while for side-on adsorbed N₂, the charge is distributed on both nitrogen atoms N¹ and N². The N₂ molecule adsorbed on the studied catalysts gained electrons, which made them have an affinity towards protonation especially MoN₃P₁G(S), MoN₂P₂Gγ(S) and MoN₂P₂Gβ(S). They gained −0.84 |e|, −0.75 |e| and −0.71 |e|, as shown in Fig. 1a–c respectively. It was noted that the Mo center acts as an electron transporter to both the graphene support and N₂-adsorbed intermediates. It transfers charge to both of them and carries a positive charge of 2.9 |e|, 1.4 |e| and 1.3 |e| for MoN₃P₁G(S), MoN₂P₂Gγ(S) and MoN₂P₂Gβ(S), respectively. The elongation of the N₂ length and enhancing Bader charge suggest these two systems as superior catalysts for N₂ conversion to ammonia.

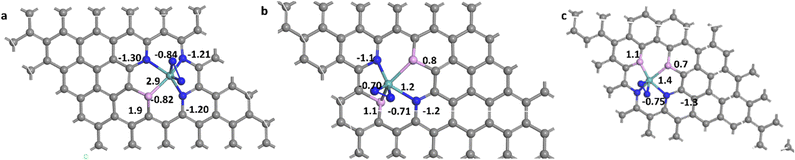Fig. 1 The Bader charge analysis for (a) MoN₃P₁G(S), (b) MoN₂P₂Gβ(S), and (c) MoN₂P₂Gγ(S); blue, light blue, purple and grey color for N, Mo, P and C atoms, respectively.

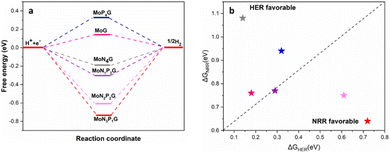
The NRR catalytic performance was surveyed for Mo-based graphene with different ratios of N and P atoms. All the possible mechanisms were considered. For each catalyst, the distal and the alternating routes were investigated. To ascertain the catalytic activity of the studied catalysts, Gibbs free energy (ΔG) was calculated for every step. From ΔG calculations, the rate determining step (RDS) was evaluated for each mechanism. At the beginning, adsorption of N₂(S) and N₂(E) probably occurred spontaneously on all the studied catalysts except MoP₄G(S) and MoN₁P₃G(S). All intermediates included in both pathways were calculated on MoG, MoP₄G, and MoN₄G, as shown in Fig. 2 and on MoN₁P₃G, MoN₂P₂Gβ and MoN₃P₁G catalysts, as shown in Fig. 3. Note that the rate-determining step seems to be the initial protonation NNH step for MoG(S), MoG(E), MoP₄G(E), MoN₄G(S), MoN₁P₃G(E) MoN₃P₁G(S), and MoN₃P₁G(E), while the rate determining step for MoN₄G(E), MoN₂P₂Gβ(E), and MoN₂P₂Gβ(S) is the formation of NH₃. Also, it was noted that the distal pathway is thermodynamically and kinetically more favorable than the alternating one for all the studied catalysts except MoN₂P₂Gβ(E).

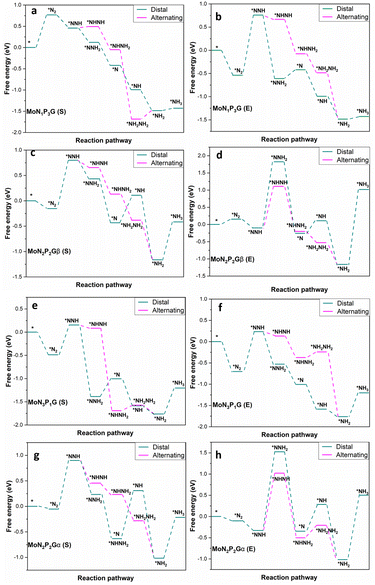Fig. 2 Distal and alternating routes for the NRR on MoN₁P₃G, MoN₂P₂Gβ, MoN₃P₁G and MoN₂P₂Gα catalysts with N₂ end-on (E) and side-on (S) adsorption.

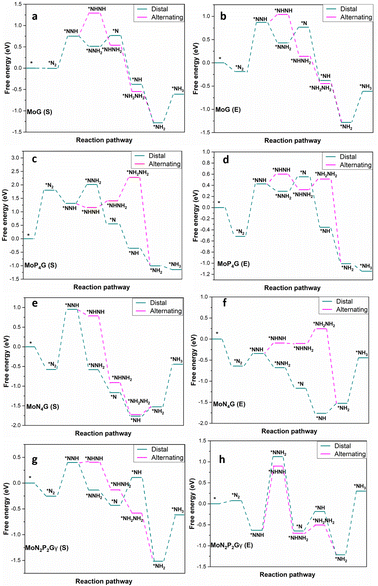Fig. 3 Distal and alternating routes for the NRR on MoG, MoP₄G, MoN₄G and MoN₂P₂Gγ catalysts with N₂ end-on (E) and side-on adsorption.

We summarized the ΔG of the rate determining step (RDS) of the distal pathway on all the studied catalysts for the two conformations end-on and side-on adsorption, as displayed in Fig. 4. It was noted that on MoG, MoN₁P₃G, MoN₁P₃G, and MoN₁P₃G catalysts, ΔG for the RDS in the side-on route was less than that on the end-on pathway (0.76, 0.77, 0.75 and 0.64 eV) versus (1.06, 1.3, 2.18 and 0.94 eV), respectively. However on MoP₄G and MoN₄G catalysts, ΔG for the RDS in the end-on route was less than that in the side-one (0.94 and 1.08 eV) versus (1.8 and 1.53 eV), respectively. Note that the MoN₃P₁G(S) catalyst has the lowest potential energy (−0.64 V versus SHE) among all studied conformations, making it a good candidate for the NRR. The optimized geometries of all intermediates on MoN₃P₁G(S) through the two pathways, distal and alternating, are shown in Fig. 5.

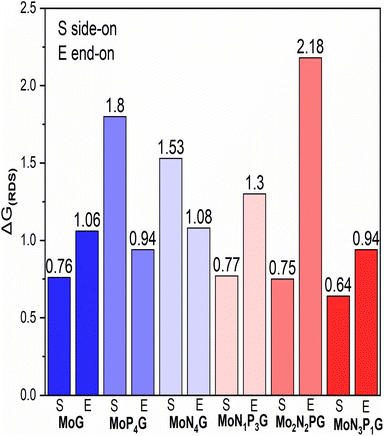Fig. 4 The change in Gibbs free energy for the RDS for the two configurations; end-on (E) and side-on (S) adsorption on the studied catalysts.

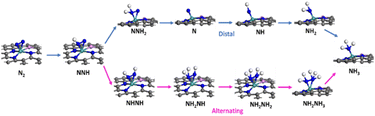Fig. 5 Relaxed structures of all the intermediates for the NRR through the two reaction routes on the MoN₃P₁G(S) catalyst.

It has been observed that N₂ tends to undergo “side-on” adsorption on the Mo atom, attached to three nitrogen atoms and one phosphorus atom bound to graphene. Following the protonation of one nitrogen atom, the formation of the NNH intermediate occurs, and NNH₂ or NHNH is generated through another proton transfer, either distally or in an alternating pathway. Ultimately, two ammonia molecules are generated and liberated following six protonation stages. It is evident that the MoN₁P₃G(S) keeps a consistent configuration throughout the nitrogen reduction reaction (NRR) process, owing to its robust binding energy. Therefore, it is evident that the presence of nitrogen and phosphorus atoms and the interaction between them and the molybdenum-supported graphene play a critical role in NRR activity. The N–N bond undergoes noticeable elongation through stepwise hydrogenation until it ultimately dissociates. Additionally, it is observed that the distal pathway leading to the formation of NNH₂ induces more pronounced N–N stretching compared to the alternative pathway, generating the second hydrogenation intermediate NHNH. The N–N bond dissociates at the NH₂NH₂ intermediate, forming NH₃.

It is well-established that the hydrogen evolution reaction (HER) is inherently associated with the NRR process, which is a crucial side reaction that competes with the intended NRR.^43–45 Consequently, suppressing the HER is imperative to enhance the selectivity of the NRR. The HER mechanisms on the various studied catalysts are depicted in Fig. 6a. With the exception of MoP₄G and MoG, hydrogen adsorption was found to be exothermic. In addition, the nitrogen adsorption energies are equal to or greater than the hydrogen adsorption energies on various Mo-supported graphene catalysts. In Fig. 6b, a comparison of the free energy changes for the Volmer step in the NRR and HER is presented. The better selectivity for the NRR over the HER can be revealed from the lower limiting potential (U_L) of the NRR than the HER counterpart. Consequently, both MoN₃P₁G(S) and MoN₂P₂Gβ(S) exhibit the capability to suppress the HER, achieving superior catalytic performance with better selectivity.

Fig. 6 (a) Free energy changes of H adsorption on the six studied catalysts. (b) The change in Gibbs free energy of the rate limiting step for the hydrogen evolution reaction (ΔG_HER) and the NRR (ΔG_NRR). The stars under the dashed line indicate that the NRR is more convenient than the HER.

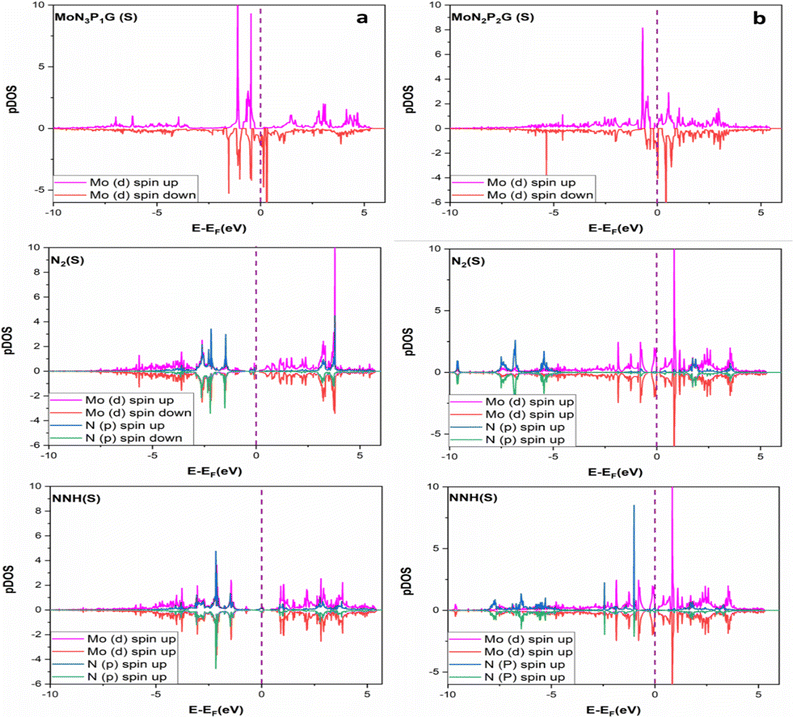
To get a better understanding of the superior catalytic NRR performance on MoN₃P₁G(S) and MoN₂P₂Gβ(S) catalysts, the projected density of states (PDOS) was investigated.⁴⁶ The interactions among N₂/NNH adsorbents and MoN₃P₁G(S) and MoN₂P₂Gβ(S) were analyzed as displayed in Fig. 7a and b, respectively. Strong hybridizations were observed among N 2p and Mo 3d orbitals. The presence of three nitrogen atoms with one phosphorus atom in the Mo-graphene support shifted the N 2p to a low energy region, resulting in higher nitrogen activity.

Fig. 7 The projected density of states (PDOS) Mo-d and of N_2p orbitals for N₂ and NNH intermediates on (a) MoN₃P₁G(S) and (b) MoN₂P_2βG(S). Magenta refers to the bonding portion, while the red colour is for the antibonding portion, and the purple dashed line is for the Fermi level.

To unveil the stability of the studied catalysts, ab initio molecular dynamics (AIMD) simulations were carried out. The thermal stability at 500 K for 10 ps was investigated. Fig. S1† illustrates the variations in temperature and energy over time during the simulations. Some oscillations in total energy and temperature were observed. However, after simulation, the skeleton and plenitude of the studied catalysts remained intact with the molybdenum atom staying fixed in the corresponding substrates, avoiding forming large particles during the simulations. The electrochemical stability of the studied catalysts was then assessed using the dissolution potential (U_diss)⁴⁷ with the results presented in Table S1.† Note that a material is deemed electrochemically stable if its U_diss is more than 0 eV. As outlined in Table S1,† the studied catalysts meet this criterion and are therefore electrochemically stable. The aforementioned results indicate that our catalysts exhibit favorable thermal and electrochemical stability, enabling their use as potential catalysts.

Conclusions

DFT calculations were utilized to survey the NRR catalytic performance of Mo-supported graphene with different ratios of N_m and P_n, where n, m = 0–4. The distal and alternating pathways were investigated for both side-on (S) and end-on (E) N₂ adsorption conformations. The calculations revealed that the sixteen studied systems had good NRR catalytic performance, especially MoN₃P₁G(S), which showed excellent catalytic activity with a small limiting potential of 0.64 eV vs. SHE. The superior NRR catalytic performance was interpreted based on N–N bond length elongation, which acquired nitrogen higher activity towards protonation and on the Bader charge analysis. The analysis revealed that the Mo center is an electron transporter for both moieties; the graphene substrate and the N₂-adsorbed intermediates. The adsorbed N₂ gains electrons from Mo-SACs, which increase its affinity for further protonation ending by NH₃ production. In addition, the MoN₃P₁G(S) and MoN₂P₂Gβ(S) systems suppressed the HER, which is a high competitor to the NRR. This study unveils how tuning the local environment of the metal center of SACs enhances the NRR catalytic activity.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Access to the BA-HPC supercomputing facilities provided by Bibliotheca Alexandria is warmly acknowledged.

References

1. S. M. Fawzy, G. E. Khedr and N. K. Allam, Int. J. Hydrogen Energy, 2023, 48(85), 33111–33118.
2. M. M. Abodouh, G. E. Khedr and N. K. Allam, Int. J. Hydrogen Energy, 2024, 61, 922–933.
3. M. Ball and M. Wietschel, The Hydrogen Economy: Opportunities and Challenges, Cambridge University Press, 2009.
4. B. C. Tashie-Lewis and S. G. Nnabuife, Chem. Eng. J. Adv., 2021, 8, 100172.
5. H. Brandhorst, M. Baltazar-Lopez, B. Tatarchuk, D. R. Cahela and T. Barron, 6th Int Energy Convers Eng Conf IECEC, Cleavlan, Ohio, 2008.
6. H. Li, X. Xu, X. Lin, J. Chen, K. Zhu and F. Peng, et al. , Nanoscale, 2023, 15(8), 4071–4079.
7. X. Liu, Y. Li, J. Zhang and J. Lu, Nano Res., 2021, 14(10), 3372–3378.
8. N. Li, Y. Tong, H. Li, L. Wang, F. Hou and S. X. Dou, et al. , Carbon, 2021, 182, 233–241.
9. C. Zamfirescu and I. Dincer, J. Power Sources, 2008, 185(1), 459–465.
10. K. Liu, J. Fu, L. Zhu, X. Zhang, H. Li and H. Liu, et al. , Nanoscale, 2020, 12(8), 4903–4908.
11. Z. Huang, M. Rafiq, A. R. Woldu, Q.-X. Tong, D. Astruc and L. Hu, Coord. Chem. Rev., 2023, 478, 214981.
12. A. M. Agour, E. Elkersh, G. E. Khedr, H. G. El-Aqapa and N. K. Allam, ACS Appl. Nano Mater., 2023, 6(17), 15980–15989.
13. H. Wang, S. Liu, H. Zhang, S. Yin, Y. Xu and X. Li, et al. , Nanoscale, 2020, 12(25), 13507–13512.
14. C. Li, Y. Fu, Z. Wu, J. Xia and X. Wang, Nanoscale, 2019, 11(27), 12997–13006.
15. C. Guo, J. Ran, A. Vasileff and S.-Z. Qiao, Energy Environ. Sci., 2018, 11(1), 45–56.
16. R. Leil, M. M. Abodouh, N. Javed and S. Sreekumar, et al. , Energy Adv., 2024, 3, 430–441.
17. S. A. Teama, G. E. Khedr and N. K. Allam, ACS Appl. Mater. Interfaces, 2024, 16(25), 32298–32310.
18. H. Liu, L. Wei, F. Liu, Z. Pei, J. Shi and Z. Wang, et al. , ACS Catal., 2019, 9(6), 5245–5267.
19. C. Liu, Q. Li, C. Wu, J. Zhang, Y. Jin and D. R. MacFarlane, et al. , J. Am. Chem. Soc., 2019, 141(7), 2884–2888.
20. S. Zhao, X. Lu, L. Wang, J. Gale and R. Amal, Adv. Mater., 2019, 31(13), 1805367.
21. S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton and S. D. Minteer, et al. , Nat. Catal., 2018, 1(7), 490–500.
22. B. Han and F. Li, J. Mater. Inf., 2023, 3(4), 24.
23. R. Guo, W. An, M. Liu, Y. Li, Y. Wang and S. Yang, et al. , Appl. Surf. Sci., 2024, 644, 158799.
24. D. Jiao, Y. Liu, Q. Cai and J. Zhao, J. Mater. Chem. A, 2021, 9(2), 1240–1251.
25. X. Li, Q. Zhou, S. Wang, Y. Li, Y. Liu and Q. Gao, et al. , J. Phys. Chem. C, 2021, 125(22), 11963–11974.
26. N. Sathishkumar and H.-T. Chen, ACS Appl. Mater. Interfaces, 2023, 15(12), 15545–15560.
27. Z. Guo, C. Liu, C. Sun, J. Xu, H. Li and T. Wang, ChemCatChem, 2023, 15(14), e202300669.
28. A. P. Hamsa, M. Arulprakasam and S. M. Unni, Chem. Commun., 2023, 59(72), 10689–10710.
29. L. Kong, S. Qiu, Q. Cai, J. Zhao and C. Sun, Sustainable Energy Fuels, 2021, 5(24), 6488–6497.
30. C. Ling, X. Bai, Y. Ouyang, A. Du and J. Wang, J. Phys. Chem. C, 2018, 122(29), 16842–16847.
31. X. Chen, W.-J. Ong, X. Zhao, P. Zhang and N. Li, J. Energy Chem., 2021, 58, 577–585.
32. X. Guo, X. Wan and J. Shui, Cell Rep. Phys. Sci., 2021, 2(6), 100447.
33. P. Hou, Y. Huang, F. Ma, G. Zhu, R. Du and X. Wei, et al. , Mol. Catal., 2023, 537, 112967.
34. G.-F. Chen, S. Ren, L. Zhang, H. Cheng, Y. Luo and K. Zhu, et al. , Small Methods, 2019, 3(6), 1800337.
35. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59(3), 1758–1775.
36. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54(16), 11169–11186.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
38. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin and T. Bligaard, et al. , J. Phys. Chem. B, 2004, 108(46), 17886–17892.
39. C. Cui, J. Han, X. Zhu, X. Liu, H. Wang and D. Mei, et al. , J. Catal., 2016, 343, 257–265.
40. G. Psofogiannakis, A. St-Amant and M. Ternan, J. Phys. Chem. B, 2006, 110(48), 24593–24605.
41. J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Nørskov, ChemSusChem, 2015, 8(13), 2180–2186.
42. G. Henkelman, Comput. Mater. Sci., 2006, 36, 354–360.
43. I. M. Badawy, G. E. Khedr, A. M. Hafez, E. A. Ashour and N. Allam, Chem. Commun., 2023, 59, 7974–7977.
44. G. E. Khedr, S. M. Fawzy and N. K. Allam, J. CO2 Util., 2023, 78, 102619.
45. C. Choi, S. Back, N.-Y. Kim, J. Lim, Y.-H. Kim and Y. S. Jung, ACS Catal., 2018, 8(8), 7517–7525.
46. Y.-C. Hao, Y. Guo, L.-W. Chen, M. Shu, X.-Y. Wang and T.-A. Bu, et al. , Nat. Catal., 2019, 2(5), 448–456.
47. J. Wu and Y. Yu, J. Colloid Interface Sci., 2022, 623, 432–444.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00298a

‡ Equal contribution.

---