Open Access Article
Open Access ArticlePredicting the mechanical properties of pristine and defective carbon nanotubes using a random forest model†
Ihtesham
Ibn Malek
,
Koushik
Sarkar
and
Ahmed
Zubair
 *
*
Department of Electrical and Electronic Engineering, Bangladesh University of Engineering and Technology, Dhaka 1205, Bangladesh. E-mail: ahmedzubair@eee.buet.ac.bd
First published on 2nd August 2024
Abstract
Data-driven models have lately emerged as a faster and less time-consuming method for computing material properties than computationally expensive conventional molecular dynamics and density functional theory-based simulations. Here, we developed a random forest (RF) model for comprehensively predicting mechanical properties such as stress and Poisson's ratio under varying strain and ultimate tensile strain of pristine and defective carbon nanotubes (CNTs). The variations in stress and Poisson's ratio with the strain of CNTs with a 0.4–2 nm diameter range were calculated by classical molecular dynamics simulations and characterized using parameters extracted from fitting polynomial equations. The fitting parameters and ultimate tensile strength showed distinct dependency on chiral indices, chiral angles, radii, and the presence of defects in CNTs, which constituted the target dataset. The dataset features were selected through principal component analysis, and the correlation with targets was scrutinized. We performed a comparative analysis of different machine learning algorithms for predicting mechanical properties, revealing the RF model as the best-performing algorithm. The RMSE for the stress–strain curve had a maximum value of 0.013 and 0.0143 for pristine and defective CNTs, respectively, while the correlation coefficients were ≫ 0.99 for all CNTs, showcasing the excellent predictive power of the model. The model made excellent predictions of properties for CNTs with diameters >2 nm, which is beyond the training dataset range, demonstrating the robustness of the model as a substitute for MD simulation. The insight gained from this study will benefit the research of nanocomposites, nanoelectronics, and nanomechanical systems incorporating CNTs.
1 Introduction
Carbon nanotubes (CNTs), hollow cylinders of graphite carbon atoms, gained prominence in nanotechnology due to their nano-size and unique properties.1 Their electronic, thermal, optical, and structural properties vary with length, diameter, alignment, and chiral indices (n, m).2–4 CNTs exhibit high thermal conductivity, a large surface area, ballistic transport on submicron scales, high electrical conductivity, and ultrahigh optical absorption.5–7 These attributes make CNTs versatile in applications such as energy harvesters,8 polarizers,9 thermoelectric nanogenerators,10 sensors, transparent electrodes, supercapacitors, and conducting composites.2 With an exceptional Young's modulus (∼1 TPa) and tensile strength (∼100 GPa), CNTs find extensive applications, serving as robust load-bearing reinforcements in composites and augmenting stiffness and strength through distinctive carbon–carbon bond structures.11 In polymer composites, the integration of CNTs enhances stiffness, strength, and toughness, especially when combined with resins.12 Efficient load transfer between CNTs and polymer matrices is evident. Furthermore, CNTs enhance the structural properties of polymer composites, elevating toughness through effective energy absorption.13 All these mechanical properties are interrelated,14 and atomic vacancy defects are crucial,15 which should be studied comprehensively.Computer-based numerical simulation has been an integral part of nanomaterials research due to its ability to rigorously study atomic dynamics under ideal conditions, which is extremely difficult, if not impossible, to achieve experimentally. Due to their nanometer level dimensions and unique thermal, mechanical, and electronic properties, CNTs are a promising subject for study with computational techniques. In the study of mechanical properties, MD simulation methodology has been predominately used in the case of CNTs.16 Computational studies have investigated various aspects of the mechanical properties of CNTs encompassing the effect of chirality,17,18 impact of hydrogen storage,19 elastic and plastic deformation,20,21 impact of temperature,22 and bending deformation.23 The fracture stress and strain calculated from the MD simulation of pristine CNTs were much higher than experimentally observed parameters, and simulations of CNTs with various vacancy defects revealed that their mechanical properties were influenced by defect orientation, position, and number.24,25 The simulation work by Jhon et al.26 reported excellent agreement with experimental data by introducing helical defects into SWCNTs. Several computational studies were carried out to develop a theoretical or finite element model.27 The studies mentioned here revealed intricate fracture formation and propagation details and the difference in stress distribution between pristine and defective CNTs. However, these studies only simulated a few CNTs that mostly belonged to the zigzag or armchair categories. Yazdani et al. pointed out the lack of comprehensive knowledge regarding the mechanical properties of CNTs with varying chirality, radius, and temperature.28 They carried out MD simulations of pristine CNTs at three different temperatures under compressive and tensile strain. The variations of buckling stress, fracture strain, and elastic modulus with diameter, temperature, and slenderness ratio were thoroughly investigated. Despite being more expansive than previous studies, only a qualitative picture of the variation of mechanical properties with CNT material data, such as radius and chiral angle, was achieved. The mechanical properties of nanotube membranes were studied theoretically;29 however, investigating such a system numerically would require multi-scale modeling techniques.30
Calculating the mechanical properties of different CNTs with varying chirality and radii to generate a complete database utilizing MD simulations is extremely time-consuming. Recently, data-driven computational methods were applied to predict material properties without resorting to time-consuming conventional computational methods.31,32 These new computation techniques can be used to calculate the time-efficient properties of unmodeled materials. Deep learning (DL), a cornerstone of machine learning (ML), has revolutionized various fields.33 Notably, DL has been successfully applied to determine chiral indices from electron microscopy images of CNTs,34 achieving a high accuracy of 90.5%. A further contribution to carbon materials, specifically carbon fibers, uses ML to predict the ultimate tensile strength and Young's modulus and achieves R2 values of 0.85 and 0.67 for the latter properties, respectively.35 In a different study, the dataset was generated by systematically varying the number of walls, chirality, crosslink density, and diameter of MWCNTs by MD simulation.36 The predicted ultimate tensile strengths exhibited errors of up to 5%. The benefits of dimensionality reduction in ML studies were demonstrated by Yadav et al.37 Their deep neural network (DNN) model accurately predicted the behavior of an unknown MWCNT configuration. Moreover, the physics-informed neural network (PINN) algorithm was proposed for solving brittle fracture problems by minimizing the variational energy of the system38 to minimize the residuals of the partial differential equations, where transfer learning can also be incorporated to enhance computational efficiency.39 However, developing a PINN model requires deep domain expertise in the specific physical laws governing CNTs, whereas data-driven approaches are simpler, focusing on leveraging existing datasets to make accurate predictions without the complexity of solving partial differential equations.
The applications of ML in carbon-related research include estimating the shear strength of carbon nanotube–polymer interfaces,40 and investigating the macroscopic delamination of carbon fiber-based composites.41 The interplay between geometrical and mechanical properties in CNTs, focusing on parameters such as diameter, number of walls, chirality, and crosslink density, was investigated by high-throughput molecular simulations.42 The study emphasized optimizing load transfer from outer to inner tubes, highlighting the enhanced performance observed in zigzag-type CNTs with 1.5–2.5% crosslink density and armchair-type CNTs with 3–4% crosslink density. A novel technique was devised for identifying point vacancies, the most common defects in SWCNTs, using vibrational analyses and ML.43 Utilizing a molecular-structural-mechanics approach, 240 SWCNT samples were modeled, and a polynomial support vector machine (SVM) achieved over 90% accuracy in classifying pristine and defective SWCNT samples.
Recently, a study regarding developing a DNN model capable of predicting the mechanical properties of SWCNTs was reported.44 The training dataset used in that work consisted of the tensile strength, stress, Young's modulus, and initial Poisson's ratio of all SWCNTs with a diameter under 4 nm, derived from MD simulation. Although the DNN model performed well in predicting most parameters, it showed a significant deviation in predicting the initial Poisson's ratio, indicated by the maximum deviation of −28.11% between predicted and calculated values. Moreover, this predictive model's performance was not tested on CNTs with a diameter beyond the dataset limit. The MD simulation results generated in the previous study were employed by Košmerl et al.45 in developing a convolutional neural network (CNN) model for predicting the stress–strain curve of SWCNTs. The dataset features consisted of chiral indices and strain variation for each CNT, and the target was stress variation. Though excellent predictions were obtained from the 1D CNN model, this model cannot predict the maximum tensile strain associated with a CNT. Consequently, such a model can only be used to predict stress if the maximum strain limit for a CNT is known from other sources. The dataset did not include the variation of Poisson's ratio with strain. A critical issue arose from randomly selecting data for testing, with no assurance that specific CNT data would be tested without prior training. Training each CNT individually would facilitate more accurate curve predictions. Hence, there is huge scope for developing techniques for CNT property prediction. Moreover, a comparative analysis between different ML models is required for better modeling performance.
Our work aimed to develop an ML-based model for predicting the ultimate strain, variation of stress, and Poisson's ratio with strain. The dataset consisted of the mechanical properties of all SWCNT configurations with 0.4 to 2 nm diameters, calculated from MD simulation. Both pristine and defective CNTs with one single vacancy defect are simulated using the MD methodology to generate the dataset and develop a more generalized model. Different ML algorithms belonging to classical, ensemble, and neural network classes were compared based on their performance metrics in predicting the stress–strain curve and ultimate tensile strain to find the algorithm best suited for predicting the mechanical properties of CNTs. The best model was the RF model, which was then employed to predict the variation of Poisson's ratio with strain. Excellent agreement between calculated and predicted values was observed. Finally, the RF model was utilized to predict the mechanical properties of nanotubes with a diameter of more than 2 nm, beyond the diameter limit of the training dataset.
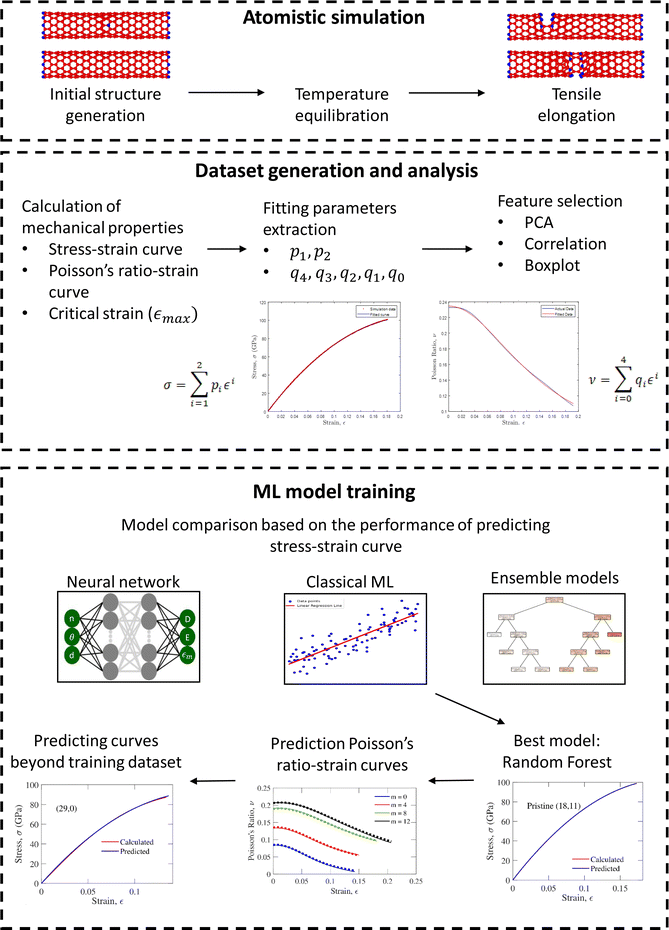
2 Computational details
The mechanical properties, such as the variation of true stress and Poisson's ratio under tensile strain for CNTs with various chiralities, are calculated by MD simulation. Several parameters are extracted from the stress–strain and Poisson's ratio–strain curves by fitting second- and fourth-order equations, respectively. The potential features consist of the chiral indices (n, m), chiral angle (θ), radius (r), and a binary indicator (d) denoting the presence of a defect. The binary indicator d = 0 signifies a pristine CNT and d = 1 indicates a defective CNT. The target value of this dataset consisted of the fitting parameters of the stress and Poisson's ratio curve and critical strain (εmax). The generated data were investigated using principal component analysis (PCA) and correlation analysis to extract dominant features for better ML training. Boxplot analysis provides valuable insight into data spread, variability, and the presence of outliers. A profound comprehension of the Random Forest (RF) method became imperative, given that the results derived from the RF model would be meticulously compared with outcomes from deep learning, classical machine learning, and ensemble models. The ML models are compared based on their performance metrics (R2, RMSE) in predicting parameters corresponding to the stress–strain curve and εmax. The model with the best performance, the RF method, was further employed in predicting the parameters of the Poisson's ratio–strain curve. The sequential workflow is concisely depicted in Fig. 1.The chirality of CNTs is defined by a pair of integers (n, m), where n ≥ m and for this work, n ∈ {5, 25} and m ∈ {0, 14}. The diameter (⊘) of the CNTs varies from 0.3910 nm to 1.9975 nm for the chiral index pairs (5, 0) and (25, 1), respectively. The nanotubes with smaller diameters were not included in this study because the stochastic nature of the calculated parameters becomes more pronounced for CNTs with smaller diameters due to fewer atoms. The diameter of the CNTs in this work was constrained below 2 nm as SWCNTs have a diameter of 1–2 nm, in general,.46
2.1 Initial structure generation
The atom coordinates of the initial structure of CNTs were generated by exploiting the helical and rotational symmetries of graphitic tubules.47 Firstly, a helical chain of carbon atoms was created by mapping atom coordinates on a cylinder with a radius calculated from chiral indices. Afterward, the helical chain was rotated to form the whole CNT and the atom coordinates of all the atoms of the CNT were produced. The radii of CNTs were calculated from the formula, , where R1 and R2 are the primitive lattice vectors of the hexagonal lattice. The theoretical chiral angle was defined by
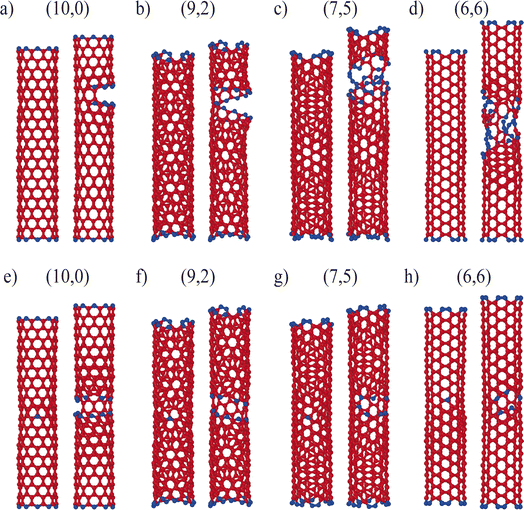
, where R1 and R2 are the primitive lattice vectors of the hexagonal lattice. The theoretical chiral angle was defined by  . The length of each CNT was kept at approximately five times its theoretical diameter. Both pristine and defective CNTs with single vacancy defects were generated and simulated to calculate mechanical properties. The CNTs with single vacancy defects were created by removing a single atom from approximately at the midpoint along the length of pristine CNTs. Thus, a single vacancy defect configuration with three dangling bonds was created, which is metastable and can only exist at very low temperatures.48 CNTs with such defect configurations were denoted as non-reconstructed structures. Energy calculation using tight-binding methodology and empirical potentials showed that the vacancy configuration with a pentagonal ring and only one dangling bond has the lowest energy among all the possible single vacancy defect configurations.49 Although a few simulation studies were carried out previously with non-reconstructed defect configurations,50,51 the tensile elongation in this work, carried out at room temperature, required the use of a stable reconstructed defect geometry in the MD simulations. The details of generating defective CNTs with reconstructed defects are in the ESI.† A total of 408 pristine and defective CNT structures were generated. The structures of pristine and defective CNTs of the zigzag, armchair, type-I, and type-II chiral classes are shown in Fig. 2.
. The length of each CNT was kept at approximately five times its theoretical diameter. Both pristine and defective CNTs with single vacancy defects were generated and simulated to calculate mechanical properties. The CNTs with single vacancy defects were created by removing a single atom from approximately at the midpoint along the length of pristine CNTs. Thus, a single vacancy defect configuration with three dangling bonds was created, which is metastable and can only exist at very low temperatures.48 CNTs with such defect configurations were denoted as non-reconstructed structures. Energy calculation using tight-binding methodology and empirical potentials showed that the vacancy configuration with a pentagonal ring and only one dangling bond has the lowest energy among all the possible single vacancy defect configurations.49 Although a few simulation studies were carried out previously with non-reconstructed defect configurations,50,51 the tensile elongation in this work, carried out at room temperature, required the use of a stable reconstructed defect geometry in the MD simulations. The details of generating defective CNTs with reconstructed defects are in the ESI.† A total of 408 pristine and defective CNT structures were generated. The structures of pristine and defective CNTs of the zigzag, armchair, type-I, and type-II chiral classes are shown in Fig. 2.
2.2 Molecular dynamics methodology
The CNTs were simulated using classical MD methodology with the LAMMPS open source software package.52 In a recent study, a machine learning interatomic potential was developed and showed better conformity to density functional theory (DFT) data for graphene/borophene heterostructures.53 However, this forcefield was not used in this work due to the lack of previous studies applying this potential to CNTs and information about the computational expense. Instead, the second generation Tersoff–Brenner potential, also known as the adaptive intermolecular reactive empirical bond order (AIREBO)54 forcefield, was used with the modification prescribed by Shendervo et al.55 to model the interaction between carbon atoms. Previous studies showed that simulating CNTs with the original AIREBO potential resulted in unphysically high stress and strain near the fracture point.18,20 This anomalous behavior was attributed to a lower cutoff distance of 1.7 Å of the switching function responsible for gradually turning off the nearest neighbor interaction. The way to circumvent this problem was to set the lower cutoff distance to 2 Å, as proposed by Shendervo et al.55 Simulated parameters agreed with the mechanical properties of CNTs reported in the literature by incorporating modified AIREBO potential.24,26The time integration was performed in the velocity-Verlet algorithm with a time step of 0.5 fs, as recommended in the literature.20 The shrink-wrapped boundary condition was applied in all three dimensions of simulation box because it enabled changes in the positions of the faces of the simulation box, ensuring that the simulation box encompassed all the atoms. The Noose–Hoover thermostat was applied to impose a constant temperature of 300 K on the simulated systems with a relaxation constant of 50 fs. In each simulation, the atoms of CNTs were divided into three groups along the z direction. Two groups of atoms were defined by a patch of 5 Å width located at the top and bottom edges of a CNT, and the rest of the atoms constituted the third and largest group in the middle. The atom groups at both ends were used to apply tensile strain to the atoms located in between them. The forces and velocities on all atoms in the top and bottom groups were set to zero except during initial energy minimization, and these atoms were not considered in the calculation of stress and radius in the post-processing.
The simulation process can be broadly divided into energy minimization, temperature equilibration, and tensile deformation. Firstly, energy minimization in the steepest descent algorithm with an energy and force tolerance of 10−10 and 10−10 eV Å−1 was carried out. Stringent minimization criteria were required to relax the CNTs before applying strain; otherwise, a significant non-zero stress value was observed without any strain. The diameter of CNTs was observed to increase slightly after energy minimization. Next, the system was equilibrated at 300 K for 25 ps, and the temperature was kept constant for the rest of the simulation. The tensile strain was applied by fixing the position of the bottom atom group while displacing the top atom group at a constant velocity such that the strain rate was 0.001 ps−1. This part of the simulation was run long enough for all the CNTs to reach their breaking points. Each CNT was simulated three times with different random number generator seeds. A few pristine CNTs were simulated to observe the effect of the strain rate and length of the CNTs. The strain rate, initial length, and calculated parameters, such as fracture strain, tensile strength, and Young's modulus, are mentioned in the ESI.†
2.3 Calculation of mechanical properties
The mechanical properties of CNTs, i.e., variation of true tensile stress (σ), Poisson's ratio (ν) with tensile strain (ε), and maximum tensile strain (εmax), were calculated. The value of these calculated parameters varied slightly from one run to another due to thermal influence. The fluctuation in fracture strain and tensile strength is represented in Fig. S3 and S4† with error bars in the ESI.† Hence, the data obtained from three seeds were averaged to produce the dataset. At first, the maximum strain was calculated for three different seeds of each CNT. If any of the maximum strains differed from the other two by more than 10%, it was considered as an outlier and disregarded from the calculation.44 The εmax is the average of the individual maximum strain calculated from three seeds for each CNT. Once the upper strain limit for each CNT was determined, the variation of σ, r, and ν with strain was calculated by averaging the data obtained from three MD simulations with different seeds.In calculating true stress, the stress induced by thermal energy was excluded, and only the virial stress due to pairwise interaction between atoms was considered. The summation of the product of virial stress and volume was calculated as the CNT was elongated under tensile strain. True stress can be determined by dividing the sum by the combined volume of all atoms. As the volume of a single atom is not well defined, the summation of the volume-stress product was divided by the total volume of the portion of the CNT under tensile strain. The volume was determined by considering the CNT as a hollow cylinder with a thickness of 3.4 Å with a radius calculated at each timestamp. The process of radius calculation is detailed in the ESI.† It is noteworthy that the incorporation of the varying radius ensured the determination of true stress. Poisson's ratio was calculated from the fundamental relationship between radial strain (εr) and tensile strain (εt) as shown in eqn (1).
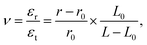 | (1) |
2.4 Target value extraction from simulated curves
Polynomial equations were fitted to the curve of variation of stress and Poisson's ratio with tensile strain, in MATLAB using the non-linear least squares method, to form the dataset of parameters, which was fed to the ML algorithm. The expression of symmetric second Piola Kirchhoff56 stress, as shown in eqn (2), was chosen as the functional form to be used in curve-fitting to the stress–strain data.| σ = Dε2 + Eε, 0 < ε < εmax | (2) |
Here, D and E are the third-order elastic and Young's modulus, respectively. Determining the functional form for the Poisson's ratio–strain curve was more challenging, as no functional form correlating these parameters was reported in the literature. A process of trial and error was employed to determine the best functional form such that the conditions of considerably low root mean squared error (RMSE) between the fitted curve and simulated data, good correlation factor between fitted and predicted parameters, and minimal RMSE between predicted and simulated Poisson ratio–stress curves were fulfilled. The following fourth-order equation provided the best fit among all the equations explored,
| ν = q4εnorm4 + q3εnorm3 + q2εnorm2 + q1εnorm + q0, 0 < ε < εmax, | (3) |
 . The dataset generated from this section contained the maximum strain (εmax), stress–strain fitting parameters (D and E), and Poisson's ratio–strain fitting parameters (q4, q3, q2, q1, and q0) as the target features. The goodness of fit of the polynomial equations to raw data is represented in Table 1.
. The dataset generated from this section contained the maximum strain (εmax), stress–strain fitting parameters (D and E), and Poisson's ratio–strain fitting parameters (q4, q3, q2, q1, and q0) as the target features. The goodness of fit of the polynomial equations to raw data is represented in Table 1.
| CNT type | Curve | R 2 | RMSE | ||||
|---|---|---|---|---|---|---|---|
| Maximum | Minimum | Mean | Maximum | Minimum | Mean | ||
| Pristine | Stress–strain | 1 | 0.9999 | 1 | 0.5591 | 0.092 | 0.2546 |
| Poisson's ratio–strain | 1 | 0.9992 | 1 | 6.906 × 10−4 | 6.1986 × 10−5 | 1.9912 × 10−4 | |
| Defective | Stress–strain | 1 | 0.9991 | 1 | 0.7902 | 0.0982 | 0.213 |
| Poisson's ratio–strain | 1 | 0.9981 | 1 | 4.9737 × 10—4 | 2.5225 × 10−5 | 1.2727 × 10−4 | |
2.5 Principal component analysis
PCA is a crucial dimensionality reduction tool in statistical and machine learning contexts. Its primary function is to transform the original variables into a set of principal components (PCs), thereby aiding in evaluating the feature's effectiveness for predicting data in regression tasks.57 To illustrate the process, consider a scenario involving two independent variables, denoted as X1 and X2. Variable X1 has three observations, namely X11, X12, and X13, and variable X2 has three observations, namely X21, X22, and X23, which are subsequently centralized before PCA is applied. The centralization involves subtracting the mean of each variable, leading to![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 1 and
1 and ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 2, respectively. Following centralization, the objective was to identify a line passing through the origin that maximizes the sum of squared distances between each point's projected position on the line and the origin. If the unit vector along this line, denoted as ϕ1, is calculated, and its perpendicular counterpart, ϕ2, is determined, both ϕ1 and ϕ2 will have two components, say ϕ11 and ϕ12 for ϕ1, and ϕ21 and ϕ22 for ϕ2. One is along X1, and another one will be along the X2 direction. The first principal component (PC1) was then computed for the 1st observation using the identified vectors,
2, respectively. Following centralization, the objective was to identify a line passing through the origin that maximizes the sum of squared distances between each point's projected position on the line and the origin. If the unit vector along this line, denoted as ϕ1, is calculated, and its perpendicular counterpart, ϕ2, is determined, both ϕ1 and ϕ2 will have two components, say ϕ11 and ϕ12 for ϕ1, and ϕ21 and ϕ22 for ϕ2. One is along X1, and another one will be along the X2 direction. The first principal component (PC1) was then computed for the 1st observation using the identified vectors,PC11 = ϕ11![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 11 + ϕ12 11 + ϕ12![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 21. 21. | (4) |
Generalizing the procedure for a dataset with ‘p’ observations and ‘q’ variables, the ‘i’-th principal component for the ‘m’-th observation is expressed as,
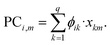 | (5) |
The coefficients ϕik are chosen to maximize the variance of each PC while ensuring orthogonality. Therefore, if x1, x2, …, xq represent the original variables, and X is the data matrix with q variables (rows) and p observations (columns), the i-th principal component for the m-th observation can be expressed as  , where coefficients ϕik are chosen to maximize the variance of PCi, subject to the constraint that
, where coefficients ϕik are chosen to maximize the variance of PCi, subject to the constraint that 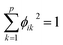 . Each PC should be orthogonal to the others. In general,
. Each PC should be orthogonal to the others. In general,
PC = ΦT![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) . . | (6) |
The principal components for all observations were obtained utilizing the process mentioned above in MATLAB. The resulting insights from the PCA were visualized, facilitating a more straightforward decision-making process. The variance ratio can be calculated for each PC, which is the ratio of the sum of squared values of those PC observations to the sum of squared values of all PCs for all observations. The variance ratio of each PC was calculated, which is the ratio of the sum of squared values of those PC observations to the sum of squared values of all PCs for all observations to assess its significance. The high variance in PC1 indicates its enriched information nature, potentially making it a powerful predictor compared to features where PC1 has lower variance ratios.
2.6 Correlation analysis
The correlation coefficient is a statistical measure quantifying the degree to which two variables are linearly related. The most commonly used correlation coefficient is Pearson's correlation coefficient (often denoted by corr). The correlation between two variables represents the cosine of the angle between the vectors formed by deviations from the means. If the angle is 0°, indicating a positive linear relationship, corr is 1; if it is 180°, indicating a negative linear relationship, corr is −1; and if the angle is 90°, indicating no linear relationship, corr is 0. For individual data points Xi and Yi corresponding to variables X and Y, with means![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) and Ȳ respectively, the formula for Pearson's correlation coefficient (corr) is given by the following equation and calculated in MATLAB,
and Ȳ respectively, the formula for Pearson's correlation coefficient (corr) is given by the following equation and calculated in MATLAB, | (7) |
2.7 Boxplot analysis
A boxplot succinctly illustrates a dataset's central tendency and variability. The box denotes the interquartile range (IQR), representing the span between the third quartile (Q3) and the first quartile (Q1), where the middle 50% of the data resides. Inside the box, the median is marked. The upper(lower) limit is defined by a value 1.5 times the IQR above(below) the Q3(Q1). Any data point beyond these limits is considered an outlier. Graphically, the box signifies the central region of data concentration, while the extension conveys the extent of variability. Outliers positioned beyond this range indicate extreme values. These analyses were carried out and the boxplot was plotted in MATLAB.2.8 Decision tree hierarchy in random forest regression
In an RF algorithm, regression combines predictions from multiple decision trees to provide a more robust and accurate outcome. Each decision tree in the forest independently predicts the target variable based on a subset of features. The final prediction is often an average or a weighted combination of these individual tree predictions. Focusing on a single decision tree within the RF, it utilizes recursive splitting of feature space to make decisions.In a dataset of four samples with features X and Y predicting Z, a decision tree may split the data based on conditions. These conditions can be determined based on the residual sum of squares (RSS) value, defined as  , where zi represents the actual values and
, where zi represents the actual values and 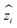 is the predicted value. If we want to predict Z based on the mean of the 2nd and 3rd samples of Y, then the predicted Z values for the first two samples would be the mean of the first two samples, and for the last two samples, it would be the mean of the last two samples, as the decision is made based on the average of the mid two values. This way, we can calculate the RSS for X and Y based on the average of two consecutive values. The decision is then made by choosing the value and variable for which the lowest RSS is obtained.
is the predicted value. If we want to predict Z based on the mean of the 2nd and 3rd samples of Y, then the predicted Z values for the first two samples would be the mean of the first two samples, and for the last two samples, it would be the mean of the last two samples, as the decision is made based on the average of the mid two values. This way, we can calculate the RSS for X and Y based on the average of two consecutive values. The decision is then made by choosing the value and variable for which the lowest RSS is obtained.
RF regression, a notable application of ensemble learning, operates by aggregating predictions from multiple decision trees. The training process involves bootstrapping, where subsets of the original dataset are randomly sampled with replacements for each tree, ensuring diversity. This process, known as bagging, enhances model generalization. The testing process leverages out-of-bag (OOB) scores, utilizing the samples not included in a tree's training set for evaluation.
Key features include the ability to handle non-linearity and outliers effectively. Hyperparameters, such as the number of trees, depth of trees, and minimum samples per leaf, are crucial in optimizing the model. Predictions are made by averaging or taking a majority vote of individual tree predictions. The advantages of RF regression include robustness against overfitting due to its ensemble nature, resilience in handling non-linear relationships in data, and effective management of outliers through the averaging effect. Collectively, these attributes make RF regression a powerful and versatile tool in the realm of ML regression tasks.
2.9 Random forest diversity and model architectures
An ensemble of trees was formed with a specified number of 100, allowing intricate relationships to be captured. The trees can potentially grow without bounds in depth and require at least a certain number of samples to form a leaf node. The splitting criterion was mean squared error (MSE). The hyperparameters are detailed in the ESI.† Additionally, this ensemble incorporated diverse base estimators, including a linear model, an extra tree model, a k-nearest neighbors (KNN) model, and an artificial neural network (ANN) model, which we integrated as prediction models in our study. The linear model introduces simplicity with an optional intercept term, while the extra tree model enhances diversity by considering random splits. The KNN model relies on the proximity of 5 neighbors with a uniform weighting scheme, while the ANN model utilizes a complex architecture with hidden layers and adjustable hyperparameters.In this study, we utilized several regression models, namely linear regression, support vector regression (SVR), decision tree regression, and KNN regression along with the RF model, to predict the target variables. Linear regression employed ordinary least squares (OLS) fitting, SVR utilized a radial basis function (RBF) kernel function, decision tree regression utilized the Gini impurity criterion, and KNN regression defaulted to 5 neighbors with the Euclidean distance metric.
In conjunction with the ensemble and classical ML models, we designed four deep learning architectures—CNN, residual network (ResNet), CNN ResNet, and multilayer perceptron (MLP)—to predict targets D, E, and εmax for predicting the stress vs. strain curve. Table 2 offers a comprehensive overview of these models. Each model entails unique architectural configurations, encompassing layer types, the number of layers, dense layer sizes, activation functions, output dense layer specifications, optimizers, loss functions, and training parameters mentioned in Table 2. Common parameters across all models include the Rectified Linear Unit (ReLU) activation function, an output dense layer with three nodes corresponding to D, E, and εmax the Adam optimizer with a learning rate of 0.001, the MSE loss function, and evaluation metrics based on R-squared. Training configurations encompass 2500 epochs, a batch size of 32, and early stopping. Additionally, features are standardized during data preprocessing.
| Parameters | CNN | ResNet | ResNet CNN | MLP |
|---|---|---|---|---|
| Layer type | Convolutional | Dense | Convolutional + residual blocks | Dense |
| Convolutional layers | 2 | 0 | 2 | 0 |
| Convolutional layers | 64, (1, 1), 64, (1, 1) | N/A | 64, (1, 1), 64, (1, 1) | N/A |
| Dense layers | 4 | — | 4 | — |
| Dense layers | 1024-512-256-128 | 1024-512-256-128 | 1024-512-256-128 | 256-128 × 2-64 × 4-32 × 4-16 × 2-8-3 |
3 Results and discussion
3.1 Molecular dynamics results
Atomistic models of representative pristine and defective CNTs belonging to the armchair, zigzag, and chiral classes are shown in Fig. 2. All the CNTs in this figure have similar diameters with different chiral angles. The initial structure and the structure right after the breakdown are given for each CNT. In the case of pristine nanotubes, no preferable position of fracture formation was observed. The fracture position was most likely to be determined by random thermal vibration. For defective CNTs, bond breaking starts in the vicinity of the defect and gradually propagates through the surface, bisecting the nanotube. Even though the CNT structure did not come apart as soon as the fracture occurred, the stress on the atoms was released; as a result, the tensile stress dropped significantly, if not to zero. The sudden drop in stress was considered as the breakdown. Videos showing the longitudinal stretching and breakdown of pristine and defective CNTs from Fig. 2 are provided in the ESI.†To ensure the validity of the simulation, the results obtained from MD simulations for various CNTs, both pristine and defective, were compared to previously reported simulation results. The calculated Young's modulus (E), tensile strength (σmax) and maximum strain (εmax) from this work and other studies employing various simulation methodologies such as MD, MM, and DFT are outlined in Table 3. Due to variability in the simulation methodology and subsequent post-processing methods, small deviations were observed from previously reported results. Nevertheless, a good agreement between our calculation and previous work was observed. All three calculated parameters for pristine CNTs agreed well with the data reported in ref. 44.
| Structure | Chiral indices (n, m) | E (GPa) | σ max (GPa) | ε max | Reference | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a The calculated data from this work are denoted by * symbol. Ref. 26, 28 and 44 are based on molecular dynamics simulations, ref. 58–60 are DFT studies, and the rest are molecular mechanics simulations. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pristine | (5, 5) | 780 | 105 | 0.297 | 61 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 916.9 | 100.7 | 0.209 | 44 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 123 | 0.216 | 62 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 820 | 135.3 | 0.34 | 58 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 904.46 | 105.15 | 0.213 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (6, 6) | 912 | 60 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 907.5 | 105.52 | 0.206 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (7, 7) | 930 | 59 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 908.12 | 107.03 | 0.21 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (9, 9) | 94 | 0.164 | 62 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 982.4 | 84.5 | 0.139 | 44 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 912.27 | 89.08 | 0.144 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (10, 0) | 1010 | 112.2 | 0.19 | 58 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1077 | 88.36 | 0.14 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (10, 10) | 958.3 | 119.85 | 0.195 | 28 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 909 | 105.5 | 0.207 | 44 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 903.65 | 208 | 0.2086 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (11, 9) | 918 | 104.1 | 0.196 | 44 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 921.03 | 105.96 | 0.194 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (12, 8) | 966.246 ± 4.736 | 117.098 ± 1.377 | 0.176 ± 0.004 | 26 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 921 | 98.8 | 0.177 | 44 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 940.04 | 101.7 | 0.1814 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (12, 12) | 112.1 | 0.188 | 17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 106.1 | 0.171 | 44 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 912.53 | 107.5 | 0.206 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (16, 4) | 106.1 | 0.171 | 17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1034.95 | 92.03 | 0.145 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (16, 8) | 97.01 | 0.167 | 17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 974.03 | 96.2 | 0.16 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (20, 0) | 93, 2 | 0.158 | 17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1070.91 | 90.65 | 0.138 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Defective | (5, 5) | 65 | 0.096 | 61 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89.1 | 0.103 | 27 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | 0.117 | 24 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 936.94 | 62.56 | 0.0969 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (10, 0) | 65 | 0.087 | 61 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69.6 | 0.0774 | 27 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64.8 | 0.086 | 63 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 | 0.089 | 24 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1047.18 | 68.08 | 0.088 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (12, 8) | 979.244 ± 3.821 | 79.885 ± 1.129 | 0.1 ± 0.002 | 26 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 933.73 | 69.8 | 0.0942 | * | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
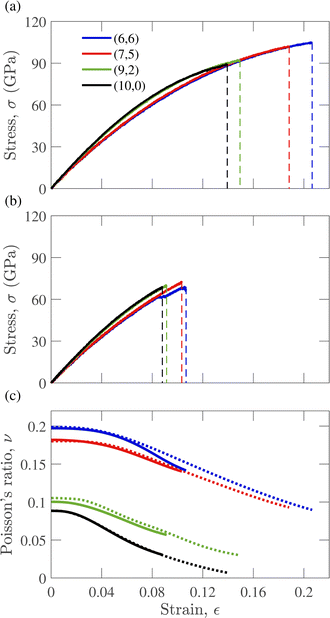
Fig. 3(a) and (b) show the stress–strain variation for pristine and defective CNTs. As observed from Fig. 3(a), critical stress and strain values increase with the increasing chiral angle of the pristine CNT structure. Hence, armchair (6, 6) and zigzag (10, 10) CNTs had the most and least critical tensile stress and strain, respectively. As evident from the figure, the chiral angle also played a major role in determining the shape of the stress–strain curve and, consequently, Young's modulus. The stress–strain curves of CNTs (6, 6) and (9, 2) almost overlapped up to the fracture point. Such similarity was attributed to the value of similar chiral angles, which are 30° and 24.5° for (6, 6) and (9, 2), respectively. Similarly, the curves of (9, 2) and (10, 0) almost overlapped due to their chiral angles of 9.83° and 0°, respectively. The Young's moduli for pristine CNTs (6, 6), (7, 5), (9, 2), and (10, 0) were 936.67, 927.974, 998.86, and 1022.2 GPa, respectively. Clearly, Young's modulus showed an increasing trend with the chiral angle. The same trend could be observed in defective CNTs, where the Young's moduli for (6, 6), (7, 5), (9, 2), and (10, 0) were 903.75, 907.44, 987.68, and 995.68 GPa, respectively. Introducing a single vacancy defect reduced the Young's modulus for all chiralities. The stress–strain curve for defective CNTs showed the same dependency on the chiral angle for the maximum strain and shape of curves. However, as observed from Fig. 3(b), a small decrease in stress for CNTs (6, 6) was observed before the fracture point. Such small decreases were observed for some defective CNTs with large chiral angles. The bond between a pair of pentagonal ring atoms broke down and produced three dangling bonds at high enough strain, which led to this small stress relaxation. Notably, such a relaxation process did not occur in all CNTs with large chiral angles. The exact mechanism of this phenomenon requires further investigation; however, for this work, the deviation introduced was trivial.
Poisson's ratios of defective and pristine CNTs are shown in Fig. 3(c). The influence of the chiral angle on the value of Poisson's ratio is apparent from the figure, showing an upward trend with increasing chiral angle. The value appeared almost constant at low strain and decreased to a minimum at the fracture point. The variation in Poisson's ratio was quite large, with the final value being less than half of the initial value for the pristine CNTs (6, 6), (9, 2), and (10, 0), as shown in Fig. 3(c). The curve of defective CNTs closely follows that of pristine CNTs, with an early fracture point compared to pristine CNTs. Due to the lower fracture point, the final and initial Poisson's ratio value variation for defective CNTs was not as large as that observed in pristine CNTs.
3.2 Extracted target values
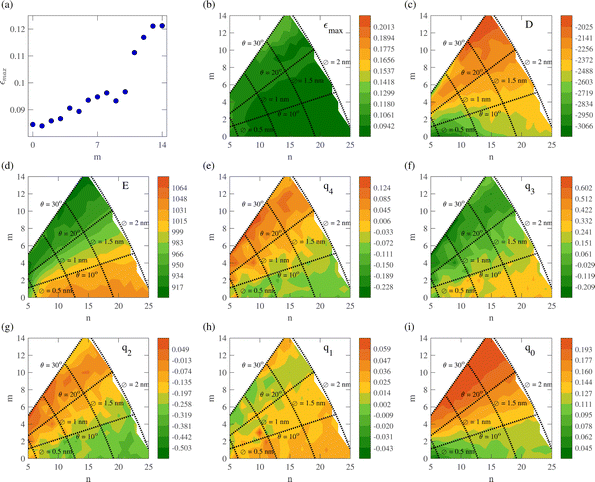
The overall influence of chiral indices (n, m), chiral angle, and CNT diameter on εmax and fitted parameters (D, E, q4, q3, q2, q1, and q0) can be garnered from the contour plots of Fig. 4 and 5 for pristine and defective CNTs, respectively. Fig. 4(a) shows the variation of εmax with m for pristine CNTs with n = 14. The increasing trend with θ, observed previously in Fig. 3, is clearly visible here. From Fig. 4, such an increasing trend with θ can be observed for all CNTs with various radii. The curves of εmax variation with m for pristine and defective CNTs are shown in Fig. 4(b) and 5(b), respectively. | ||
| Fig. 4 (a) Variation of maximum tensile strain (εmax) with the chiral index, m ∈ {0, 14} for n = 14 of pristine carbon nanotubes. Contour plots of (b) maximum tensile strain (εmax), (c and d) parameters obtained from fitting eqn (2) to the stress–strain data, and (e–i) parameters obtained from fitting eqn (3) to the Poisson's ratio–strain data extracted from the MD simulation of pristine carbon nanotubes. | ||
 | ||
| Fig. 5 (a) Variation of maximum tensile strain (εmax) with the chiral index, m ∈ {0, 14} for n = 14 in defective carbon nanotubes with single vacancy defects. Contour plots of (b) maximum tensile strain (εmax), (c and d) parameters obtained from fitting eqn (2) to the stress–strain data, and (e–i) parameters obtained from fitting eqn (3) to the Poisson's ratio–strain data extracted from the MD simulation of defective carbon nanotubes. | ||
Fig. 4(c)-(i) and 5(c)-(i) show fitting parameters corresponding to eqn (2) and (3) for pristine and defective CNTs respectively. The fitting parameters of stress–strain curves E and D strongly depended on θ for both pristine and defective CNTs. For defective CNTs in addition to θ, the diameter influenced the stress–strain fitting parameters significantly, whereas only a minor influence of the diameter was observed in the case of pristine CNTs. The variation of Poisson's ratio–strain fitting parameters appeared to have a more complex relationship with chiral indices. Although θ played a prominent role in their values, as observed in Fig. 4(e)-(i) and 5(e)-(i). The regions of the contour plot close to zigzag (θ = 0°) and armchair (θ = 30°) appear in contrasting colors. Fig. 4(i) and 5(i) represent the fitted initial Poisson's ratio for pristine and defective CNTs, respectively, since from eqn (3) setting ε ≈ 0 results in ν = q0. The initial Poisson's ratio strongly depended on the CNT diameter and θ. As seen in Fig. 3(c), the initial Poisson ratio did not change much from pristine to defective CNTs with the same chirality. As a result, the contour plots of this parameter for pristine and defective CNTs had similar color distributions.
3.3 Feature selection and target statistics
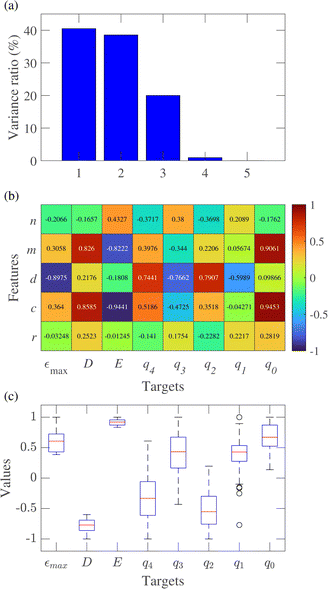
In the dataset, we had both features and targets for CNT mechanical property prediction. The set of potential features consists of n, m, d, r and θ. PCA revealed that three principal components captured almost 99% of the total variance, suggesting that only three features were sufficient for modeling. Choosing the three features for modeling became a crucial decision. Fig. 6(a) shows the impact of all five features using PCA. Since the binary indicator d is a critical factor, the exclusion of which will lead to data redundancy, d must be included in features. The remaining four features can be combined in six ways, and the variance ratios of these combinations are compared in Table 4.| Combination | PC1 | PC2 | PC3 |
|---|---|---|---|
| d, n, m | 34.483 | 33.333 | 32.194 |
| d, n, θ | 46.61 | 33.33 | 20.057 |
| d, n, r | 62.521 | 33.33 | 4.146 |
| d, m, θ | 62.668 | 33.33 | 3.999 |
| d, m, r | 48.364 | 33.33 | 18.303 |
| d, θ, r | 35.608 | 33.333 | 31.059 |
Among these six combinations, the sets (d, n, and m) and (d, θ, and r) demonstrated the minimal value of the variance ratio for PC1, 34.48 and 35.6, respectively. Hence, these sets were discarded for further consideration. Nevertheless, it is essential to emphasize that decisions cannot be solely derived from feature analysis. Examining how these features correlate with the target variables was imperative to making informed choices. Therefore, a holistic approach that considered feature analysis and their relationships with the targets was crucial for robust decision-making.
The correlation analysis unveiled intricate relationships among various structural parameters (n, m, d, θ, and r) and fitting parameters of stress–strain and Poisson's ratio–strain curves. The correlations between the potential features and εmax, D, and E are illustrated in the first three columns of Fig. 6(b). Specifically, the chiral angle exhibited a marked positive correlation of 0.8585 with parameter D and a robust negative correlation of −0.9441 with property E, indicating a systematic change in D and E as CNTs transition from armchair to zigzag configurations. The defect indicator (d) demonstrated a moderate positive correlation of 0.2176 with D, a negative correlation of −0.1808 with E, and a strong negative correlation with εmax. This implied that the presence of defects significantly reduced the ultimate strain of a CNT. Chiral indices (n, m) showed mixed correlations, with n positively correlated with E and negatively correlated with D and εmax. In contrast, m displayed a significant positive correlation with D and a noticeable negative correlation with E. Meanwhile, the radius r exhibited minimal correlation with the extracted parameters from the curve, suggesting a lower impact on these outcomes. This holistic understanding of correlations provides valuable insights into the intricate interdependencies governing the mechanical behavior of CNTs, guiding further exploration and optimization of their material properties.
The last five columns of Fig. 6(b) illustrate the correlation coefficients between different features (n, m, d, θ, and r) and their corresponding targets (q4, q3, q2, q1, and q0) that were extracted from the Poisson's ratio–strain curve. These coefficients signified the strength and direction of the linear relationships between each feature and target. These insights helped us understand how variations in each feature may influence changes in the target variables, providing valuable information for predictive modeling.
Indeed, while correlation analysis provided valuable insights into linear relationships between variables, it may not reliably capture complex nonlinear patterns in the data. Based on PCA analysis, the feature combinations (d, n, and θ), (d, n, and r), (d, m, and θ), and (d, m, and r) had the highest variance for PC1; however, r had the lowest correlation coefficient with most of the targets for the stress–strain curve. Therefore, considering these two data analyses, we prioritized (d, n, and θ) and (d, m, and θ) as the features. However, m and θ had almost the same correlation coefficients with all targets for the stress–strain curve, suggesting that these two features may be used interchangeably in machine learning. Thus, based on PCA and correlation analysis, the (n, d, and θ) combination was selected for the initial phase of training ML models to identify the best model.
The predictability of targets D, E and εmax can be inferred from their respective boxplots shown in Fig. 6(c), where normalization enables a unified representation. From Fig. 6(c), E exhibits a notably lower spread, a symmetric distribution, and fewer potential outliers, suggesting that it may be more amenable to prediction compared to D and εmax. The boxplot for εmax indicated a relatively higher spread, a right-skewed distribution, and the presence of potential outliers, implying that it might pose a greater challenge for prediction. Target D demonstrated a symmetric distribution with a moderate spread, and while reasonably predictable, the presence of outliers warranted careful consideration during modeling and evaluation.
Moreover, the boxplot illustrated the targets q4, q3, q2, q1, and q0 used in predicting the Poisson's ratio versus strain curve. Notably, five outliers are observed for the target q1. However, the most influential parameter q0 did not have any outliers, so it is expected that good curve prediction is possible, provided an accurate prediction of the q0 parameter. Since q0 had a lower spread and no outliers, this would not pose a problem. If the prediction turns out to be inadequate, fitting parameters can be extracted by applying constraints.
3.4 Comparative performance of various ML models
| Type | Models | R 2 | MSE | ||||
|---|---|---|---|---|---|---|---|
| ε max | D | E | ε max | D | E | ||
| Classical | Random forest | 0.99851 | 0.99809 | 0.99907 | 0.000017 | 0.0000043 | 0.000029 |
| Linear | 0.75839 | 0.93383 | 0.92643 | 0.00278 | 0.00016 | 0.00206 | |
| SVR | 0.39946 | −0.00722 | 0.74172 | 0.00690 | 0.00241 | 0.00724 | |
| Decision tree | 0.96956 | 0.95499 | 0.99014 | 0.00035 | 0.00011 | 0.00028 | |
| k-NN | 0.61709 | 0.68118 | 0.90792 | 0.00440 | 0.00076 | 0.00258 | |
| Deep learning | MLP | 0.99267 | 0.87892 | 0.99751 | 0.00008 | 0.00027 | 0.00008 |
| CNN | 0.97687 | 0.98128 | 0.99296 | 0.00025 | 0.00004 | 0.00021 | |
| ResNet | 0.97708 | 0.96094 | 0.98746 | 0.00027 | 0.00010 | 0.00039 | |
| CNN ResNet | 0.98498 | 0.97319 | 0.99048 | 0.00017 | 0.00007 | 0.00030 | |
| Ensemble | Linear | 0.80807 | 0.93807 | 0.93537 | 0.002229 | 0.000156 | 0.002011 |
| Extra tree | 0.95438 | 0.98011 | 0.98984 | 0.000529 | 0.018152 | 0.000316 | |
| k-NN | 0.56907 | 0.65901 | 0.90186 | 0.005005 | 0.000860 | 0.003053 | |
| ANN | 0.99402 | 0.99569 | 0.99773 | 0.000070 | 0.000010 | 0.000070 | |
In conclusion, RF consistently outperformed other models, underscoring its robustness in handling complex datasets. Neural network models were incorporated to enhance predictive performance with their capacity to capture intricate relationships. The RF emerged as the optimal model for predicting stress–strain curves owing to several key factors. Its ensemble of decision trees effectively captured intricate patterns and nonlinear relationships in the data, ensuring robust generalization to new samples and mitigating overfitting.
Notably, the RF required less hyperparameter tuning than neural networks, making it practical for datasets of moderate size. The model's interpretability, driven by its straightforward feature importance measure, enhanced insights into the impact of different features on predictions. The ability of RF to handle outliers and accommodate widespread data contributes to its superior performance. Aggregating predictions from multiple trees reduced sensitivity to noise, ensuring consistent results across estimators.
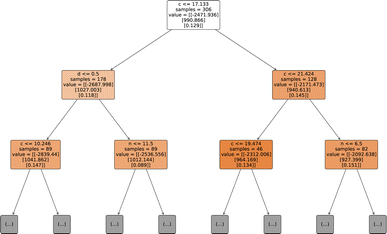
Compared to other ML and neural network alternatives, the model's versatility, computational efficiency, and feature space exploration further solidified it as the preferred choice for stress vs. strain curve prediction. Moreover, Fig. 7, which illustrates the decision-making process of RF, provided valuable insight into the internal workings of the model. This visual representation showcases how the RF made decisions based on the input features, offering a comprehensive view of its predictive capabilities. The parameters for the RF regressor included 100 trees, minimum samples to split set to 2, minimum samples per leaf set to 1, auto feature selection, and bootstrap sampling enabled.
3.5 Performance of the random forest model
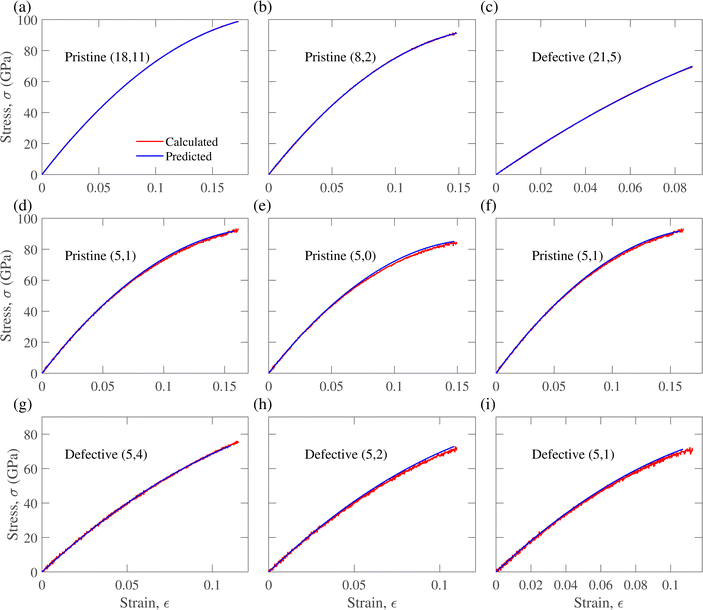
In illustrating the model's predictive performance, Fig. 8(a–c) provide visual comparisons between the actual and predicted data for parameters D, E1, and εmax, respectively. These figures vividly showcase the model's capability to closely align its predictions with the actual values. Furthermore, additional figures are presented to delve into the specific nuances of the model's accuracy. Fig. 9(a–c) specifically focus on percentage deviation errors for pristine CNTs, while Fig. 9(d–f) highlight the corresponding errors for defective CNTs. These visual representations offered a comprehensive view of the model's performance across distinct parameters, highlighting its efficacy in capturing deviations and trends in pristine and defective CNT scenarios.The stress–strain curve's prediction relied on predicting the parameters D, E, and εmax. Several plots illustrating the actual and predicted stress–strain curves of defective and pristine CNTs are provided in Fig. 10, to demonstrate the excellent prediction the RF model provides. Fig. 10(a–c) show the curves of CNTs for which the percentage deviations are minimum for the parameters εmax, D and E, respectively. The minimum percentage deviations for these three parameters are 1.41 × 10−3%, 3.8 × 10−3%, and 6.15 × 10−3%, corresponding to pristine CNT (18, 11), pristine CNT (8, 2) and defective CNT (21, 5), respectively. Interestingly, the other two parameters for these CNTs also had excellent agreement between actual and predicted parameters, resulting in the almost perfect superimposition of actual and predicted stress–strain curves, as seen in Fig. 10(a–c). Fig. 10(d–i) show the curves of pristine and defective CNTs, respectively, with maximum percentage deviations between the three parameters under discussion. The plots vividly illustrate the disparities between the predicted and true values, emphasizing the variations in the stress–strain curves for each scenario.
Regarding assessing the performance of the model in predicting stress–strain curves, Table 6 presents the normalized RMSE and R2 values calculated from predicted and actual curves for pristine and defective CNTs, belonging to the test split of the dataset, for which the percentage deviations are maximum between predicted and actual parameters D, E and εmax. Notably, defective CNTs exhibited more significant deviations. Furthermore, the RMSE for the predicted curves served as a comprehensive metric for assessing the model's overall performance. Although the maximum absolute error deviation for predicting parameters remained below 5 percent, noticeable RMSE arose when fitting the curve using these parameters. An important consideration was the imposition of zero stress beyond εmax, whether predicted or actual, contributing to the observed RMSE. This observation signified the model's inherent potential for accurate predictions and illuminated a trajectory for continual enhancements in its predictive capabilities.
| Parameters | Pristine | Defective | ||||
|---|---|---|---|---|---|---|
| D | E | ε max | D | E | ε max | |
| Deviation error (%) | −0.842 | 0.482 | 1.772 | −3.298 | −1.372 | 3.971 |
| Chiral indices | (5, 5) | (6, 0) | (5, 4) | (5, 4) | (5, 3) | (5, 4) |
| Normalized RMSE | 0.00524 | 0.00483 | 0.00545 | 0.00564 | 0.01314 | 0.00564 |
| R 2 | 0.99987 | 0.99994 | 0.99989 | 0.99981 | 0.99981 | 0.99981 |
Leveraging the RF model, we generate color plots depicting the RMSE and R2 values corresponding to various chiral indices (n, m) for stress–strain and Poisson’s ratio–strain curves. Fig. 11(a) and (b) illustrate R2 and RMSE values for stress–strain curves for pristine CNTs, while Fig. 11(c) and (d) present the corresponding plots for defective CNTs. These color plots visually represent the model's performance for most CNTs, with better results observed for pristine CNTs than their defective counterparts, although the deviation is not particularly pronounced. Fig. 12(a) and (b) illustrate R2 and RMSE values for Poisson's ratio–strain curves for pristine CNTs, while Fig. 12(c) and (d) present the corresponding plots for defective CNTs.
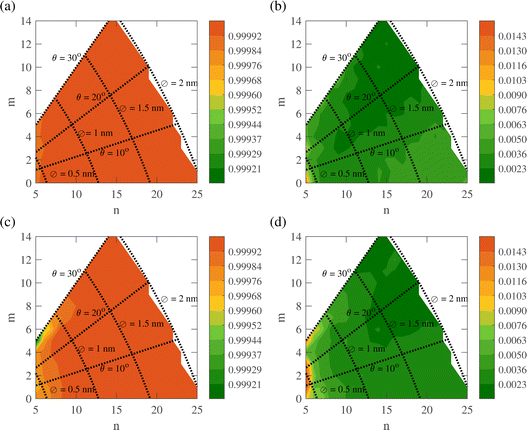 | ||
| Fig. 11 The variation of (a and c) R2 and (b and d) RMSE for stress–strain curves with chiral indices for (a and b) pristine and (c and d) defective carbon nanotubes. | ||
 | ||
| Fig. 12 The variation of (a and c) R2 and (b and d) RMSE for Poisson's ratio–strain curves with chiral indices for (a and b) pristine and (c and d) defective carbon nanotubes. | ||
Utilizing the successful RF model employed for stress–strain curve predictions, we extended its application to forecast the Poisson ratio vs. strain curve. The actual and predicted curves for the Poisson ratio are represented in Fig. 13. Fig. 13(a) corresponds to the pristine CNTs with chiral indices (12, 0), (12, 4), (12, 8), and (12, 12), while Fig. 13(b) illustrates the same for the defective CNTs with the same chiral indices. These plots directly compare the observed Poisson ratio behavior and the predictions generated by the model, offering insights into the model's accuracy and performance for specific chiral configurations.
Fig. 14(a) and (d) show the predicted values of q0, which represents the initial Poisson's ratio, for pristine and defective CNTs, respectively. A comparison with the actual values in Fig. 4(i) and 5(i) reveals a close match. The absolute percentage deviation error is depicted in Fig. 14(b) and (e) for pristine and defective CNTs, respectively. Notably, the deviation is generally low, especially for pristine CNTs. Actual vs. predicted values are plotted in Fig. 14(c) for pristine CNTs and Fig. 14(f) for defective CNTs, demonstrating the excellent accuracy of the predictions compared to the actual values, aligning closely with the ideal line of slope 1.
Finally, referring to Table 7, which presents a comparison between this work and previous studies, it is evident that all performance metrics in this study demonstrated superior performance compared to the compressive, fracture and tensile strength reported in ref. 4, 14, 15 and 44, despite having a smaller number of train data samples. As the ultimate tensile stress (σmax) was not a target, it was predicted from the predicted targets D, E, and εmax, following the equation σmax = Dεmax2 + Eεmax. The higher R-squared value for fracture strain than that in ref. 44 underscores the superiority of the RF model in predicting the fracture strain of SWCNTs. Notably, the MSE in percentage represents the mean of squared percentage deviation errors, yielding higher values due to its squared nature. Notably, the best and worst stress vs. strain curve predictions outperformed those in ref. 45 even with a significantly smaller dataset in comparison, clearly indicating the effectiveness of the methodology employed in this work.
| Parameters | Performance parameters | Model/material | Sample/split | References | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | R 2 | MAPE | MSE | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a The data calculated in this work are denoted by the * symbol. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Compressive strength | 0.939 | 5.4% | XGBoost/CNT in cementitious nanocomposites | 276/80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fracture strength !! | 0.92 | 5.8% | 261/80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tensile strength | 0.993 | 33.394% | GPR/polymer CNT composites | 198/80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
14 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tensile strength | 4.1% | HS-GNN/carbon nanostructure with defects | 1159/90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
15 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Young's modulus | 8.8% | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tensile strength | 0.986 | DNN/pristine SWCNT | 818/70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 15 |
44 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fracture strain | 0.989 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Young's modulus | 0.908 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Initial Poisson's ratio | 0.969 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Stress–strain curve (best prediction) | 1 | 9 × 10−6 | MLP/pristine SWCNT | 10, 48, 575/60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
45 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Stress–strain curve (worst prediction) | 0.987 | 0.0125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tensile strength | 0.996 | 0.988 | 0.521% | 0.468% | RF/SWCNT | 204 SWCNT + 204 SV-SWCNT = 408 samples/75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 25 |
* | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fracture strain | 0.998 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Young's modulus | 0.99953 | 0.0199% | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Initial Poisson's ratio | 0.9922 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Stress vs. strain curve best | 0.999993 | 1.64 × 10−6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Stress vs. strain curve worst | 0.99987 | 2.97 × 10−5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tensile strength | 0.98 | 0.9571 | 0.641% | 0.703% | RF/defective SWCNT | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fracture strain | 0.9905 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Young's modulus | 0.99769 | 0.0578% | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Initial Poisson's ratio | 0.9888 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Stress–strain curve (best prediction) | 0.999988 | 2.16 × 10−6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Stress–strain curve (worst prediction) | 0.99971 | 1.37 × 10−4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.6 Robustness of the proposed method
To assess the model's robustness and generalization capabilities, we conducted tests using the values of (n = 29), m, and ⊘ beyond the training range (⊘ ∈ {0.391, 1.9975} nm) for both pristine and defective CNTs. It must be mentioned that the MD simulation of this new set of CNTs took almost 54 hours to complete with the computational facilities available to the authors, whereas the predicted parameters from the RF model were practically generated instantaneously. The results are presented in Table 8. A few figures comparing the predicted and calculated stress–strain curves are provided in the ESI,† illustrating the prediction capability of our proposed model for CNTs beyond the dataset utilized. Notably, the model demonstrated remarkable accuracy in predicting the stress and Poisson's ratio variation, with strain curves providing very high R2 values and low RMSE, indicating its proficiency in replicating complex mechanical behaviors. Furthermore, the percentage deviation errors for critical mechanical properties such as εmax, σmax, Young's modulus, and initial Poisson's ratio are provided. These values unveiled the model's excellent predictive capabilities, even for CNTs falling outside the training dataset. The model's generalization performance underscores its ability to adapt and provide accurate predictions for diverse chiral indices and diameters of CNTs.| Type | m | ⊘ (nm) | R 2 | Normalized RMSE | Deviation error (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Stress | Poisson's ratio | Stress | Poisson's ratio | ε max | σ max | E | ν 0 | |||
| Pristine | 0 | 2.30 | 0.999941 | 0.999446 | 0.0045 | 0.0788 | −1.88 | 1.81 | −0.29 | −14.45 |
| 4 | 2.48 | 0.999944 | 0.998491 | 0.0044 | 0.0447 | −0.45 | 0.51 | −0.31 | −10.15 | |
| 8 | 2.68 | 0.999965 | 0.999643 | 0.0044 | 0.0446 | −1.61 | 0.04 | −0.63 | −8.74 | |
| 12 | 2.89 | 0.999984 | 0.999479 | 0.0023 | 0.0299 | 0.27 | 0.75 | −0.21 | −5.91 | |
| 16 | 3.14 | 0.999995 | 0.999733 | 0.0015 | 0.0260 | −1.64 | 0.81 | −0.08 | −4.74 | |
| 18 | 3.26 | 0.999996 | 0.999496 | 0.0012 | 0.0239 | −2.23 | 0.49 | −0.25 | −4.22 | |
| 20 | 3.39 | 0.999997 | 0.999827 | 0.0037 | 0.0362 | −0.44 | 0.89 | −0.58 | −6.24 | |
| 22 | 3.52 | 0.999994 | 0.998397 | 0.0019 | 0.0241 | −1.98 | 0.67 | −0.47 | −3.69 | |
| 24 | 3.65 | 0.999990 | 0.997896 | 0.0013 | 0.0416 | −1.19 | 1.17 | −0.28 | −5.40 | |
| 26 | 3.78 | 0.999996 | 0.999520 | 0.0051 | 0.0303 | −2.02 | −0.05 | −0.59 | −4.84 | |
| 29 | 3.99 | 0.999992 | 0.999475 | 0.0036 | 0.0284 | −2.01 | 0.68 | −0.61 | −4.39 | |
| Absolute mean | 0.999981 | 0.999218 | 0.0031 | 0.0371 | 1.43 | 0.72 | 0.39 | 6.62 | ||
| Defective | 0 | 2.3023 | 0.999959 | 0.999860 | 0.0036 | 0.0407 | −1.09 | −0.13 | −0.57 | 3.15 |
| 4 | 2.4765 | 0.999964 | 0.999546 | 0.0034 | 0.0093 | −0.36 | 0.23 | −0.52 | −0.89 | |
| 8 | 2.6770 | 0.999977 | 0.999647 | 0.0026 | 0.0409 | 3.21 | 2.89 | 0.11 | 5.11 | |
| 12 | 2.8986 | 0.999989 | 0.999681 | 0.0017 | 0.0232 | 1.43 | 2.10 | −0.08 | 3.30 | |
| 16 | 3.1367 | 0.999993 | 0.999833 | 0.0014 | 0.0142 | 1.48 | 2.39 | −0.26 | 2.40 | |
| 18 | 3.2608 | 0.999995 | 0.998317 | 0.0012 | 0.0401 | 12.59 | 10.49 | −0.38 | 0.16 | |
| 20 | 3.3879 | 0.999985 | 0.998138 | 0.0017 | 0.0294 | 12.21 | 10.37 | −0.72 | −1.46 | |
| 22 | 3.5175 | 0.999973 | 0.999898 | 0.0039 | 0.0181 | 5.07 | 5.65 | −0.48 | −2.25 | |
| 24 | 3.6494 | 0.999980 | 0.997501 | 0.0022 | 0.0313 | 6.70 | 6.40 | −0.48 | −2.34 | |
| 26 | 3.7834 | 0.999984 | 0.998506 | 0.0021 | 0.0196 | 1.92 | 2.92 | −0.27 | 2.42 | |
| 29 | 3.9878 | 0.999985 | 0.993771 | 0.0016 | 0.0127 | 0.29 | 2.05 | −0.37 | 0.04 | |
| Absolute mean | 0.999980 | 0.998609 | 0.0023 | 0.0254 | 4.21 | 4.15 | 0.39 | 2.14 | ||
4 Conclusion
MD simulations were conducted to analyze pristine and defective CNTs with single vacancies under uniaxial tensile strain at room temperature. Mechanical properties such as tensile stress and Poisson's ratio were computed for each CNT, and their variations with strain were determined. Such a comprehensive study on the mechanical properties of single vacancy defective CNTs is yet to be reported. To streamline the dataset, fitting parameters for the stress–strain curve, Poisson's ratio–strain curves, and critical strain were derived and utilized to train ML models. The low RMSE values indicated a high level of agreement between the fitted and calculated curves, enabling a reduction in the size of the ML dataset. Characterizing the curves with a set of parameters and critical strain resulted in a dataset that enables setting only the structural parameters of a CNT as features. The model trained on this dataset can predict the stress or Poisson's ratio curve of any CNT, provided only the chiral indices and defect information. A thorough investigation of different ML models was conducted, and their performances were compared to identify the most accurate model for predicting CNT stress–strain curves. The RF method emerged as the best-performing model, demonstrating excellent predictive capability with the highest percentage deviation of only 3.971% and a corresponding normalized RMSE of 0.00564. Subsequently, the RF method was applied to predict Poisson's ratio–strain curves. The average R2 for predicting the Poisson's ratio–strain curve was above 0.999, and the average RMSE was below 0.03 for both pristine and defective CNTs. The tensile strength, fracture strain, and Young's modulus were derived from the stress–strain curve, and the initial Poisson ratio was obtained from the Poisson's ratio–strain curve. The R2 for predicting all four parameters was above 0.95 for all the cases. This work is the first demonstration of an ML model capable of predicting both stress and Poisson's ratio at any given strain within the maximum strain limit specific to a CNT for both pristine and defective CNTs, given just structural information. Good agreement between predicted parameters from the RF model beyond the 2 nm diameter limit and MD simulated parameters implies that a great deal of computational resources are saved by employing our model. However, the predictions are subject to the predictive limit of the algorithm and the shortcomings of the empirical potential employed to generate the dataset. Our model delivered results quickly with reasonable accuracy. The inclusive dataset, encompassing both pristine and single vacancy defective CNTs, implies the potential extension of the RF method to model diverse defective structures, including di-vacancy, Stone-Wales defects, composites of CNTs, and nanoropes made of CNTs. Optical and electrical properties are expected to be predicted by applying our methodology.Data availability
Data for this article are available on GitHub at https://github.com/ra-ve-n/CNT-ML-29624.git.Author contributions
Ihtesham Ibn Malek: conceptualization, methodology, visualization, software, investigation, and writing – original draft. Koushik Sarkar: conceptualization, methodology, visualization, software, investigation, and writing – original draft. Ahmed Zubair: conceptualization, methodology, visualization, project administration, supervision, writing – original draft, and writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the facility and the support provided by the Department of Electrical and Electronic Engineering at the Bangladesh University of Engineering and Technology.Notes and references
- M. F. De Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Science, 2013, 339, 535–539 CrossRef CAS PubMed.
- R. Hirlekar, M. Yamagar, H. Garse, M. Vij and V. Kadam, Asian J. Pharm. Clin. Res., 2009, 2, 17–27 CAS.
- T. Imtiaz, J. Doumani, F. Tay, N. Komatsu, S. Marcon, M. Nakamura, S. Ghosh, A. Baydin, J. Kono and A. Zubair, Signal Process., 2023, 202, 108751 CrossRef.
- H. Adel, S. M. M. Palizban, S. S. Sharifi, M. I. Ghazaan and A. H. Korayem, Constr. Build. Mater., 2022, 354, 129209 CrossRef CAS.
- D. Tristant, A. Zubair, P. Puech, F. Neumayer, S. Moyano, R. J. Headrick, D. E. Tsentalovich, C. C. Young, I. C. Gerber, M. Pasquali, J. Kono and J. Leotin, Nanoscale, 2016, 8, 19668–19676 RSC.
- M. I. Tahmid, M. A. Z. Mamun and A. Zubair, Opt. Mater. Express, 2021, 11, 1267–1281 CrossRef.
- S. Vadukumpully, J. Paul, N. Mahanta and S. Valiyaveettil, Carbon, 2011, 49, 198–205 CrossRef CAS.
- A. Zubair, X. Wang, F. Mirri, D. E. Tsentalovich, N. Fujimura, D. Suzuki, K. P. Soundarapandian, Y. Kawano, M. Pasquali and J. Kono, Phys. Rev. Mater., 2018, 2, 015201 CrossRef CAS.
- A. Zubair, D. E. Tsentalovich, C. C. Young, M. S. Heimbeck, H. O. Everitt, M. Pasquali and J. Kono, Appl. Phys. Lett., 2016, 108, 141107 CrossRef.
- M. M. Islam and A. Zubair, Mater. Adv., 2023, 4, 6553–6567 RSC.
- M.-F. Yu, O. Lourie, M. J. Dyer, K. Moloni, T. F. Kelly and R. S. Ruoff, Science, 2000, 287, 637–640 CrossRef CAS PubMed.
- T.-W. Chou, L. Gao, E. T. Thostenson, Z. Zhang and J.-H. Byun, Compos. Sci. Technol., 2010, 70, 1–19 CrossRef CAS.
- G. Amaral-Labat, E. Gourdon, V. Fierro, A. Pizzi and A. Celzard, Carbon, 2013, 58, 76–86 CrossRef CAS.
- T.-T. Le, J. Compos. Mater., 2021, 55, 787–811 CrossRef CAS.
- Q. Zhao, J. J. Winetrout, Y. Xu, Y. Wang and H. Heinz, arXiv, 2021, preprint, arXiv:2110.00517, DOI:10.48550/arXiv.2110.00517.
- H. Rafii-Tabar, Phys. Rep., 2004, 390, 235–452 CrossRef CAS.
- T. Belytschko, S. Xiao, G. Schatz and R. Ruoff, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 235430 CrossRef.
- K. Mylvaganam and L. Zhang, Carbon, 2004, 42, 2025–2032 CrossRef CAS.
- L. Zhou and S.-Q. Shi, Comput. Mater. Sci., 2002, 23, 166–174 CrossRef CAS.
- C. Fu, Y. Chen and J. Jiao, Sci. China, Ser. E: Technol. Sci., 2007, 50, 7–17 CrossRef CAS.
- K. Liew, X. He and C. Wong, Acta Mater., 2004, 52, 2521–2527 CrossRef CAS.
- G. Dereli and B. Süngü, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 184104 CrossRef.
- Z. Kok and C. H. Wong, Mol. Simul., 2016, 42, 1274–1280 CrossRef CAS.
- R. Khare, S. L. Mielke, J. T. Paci, S. Zhang, R. Ballarini, G. C. Schatz and T. Belytschko, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 075412 CrossRef.
- E. G. Fefey, R. Mohan and A. Kelkar, Mater. Sci. Eng. B, 2011, 176, 693–700 CrossRef CAS.
- Y. I. Jhon, C. Kim, M. Seo, W. J. Cho, S. Lee and Y. M. Jhon, Sci. Rep., 2016, 6, 20324 CrossRef CAS PubMed.
- C. Baykasoglu, M. Kirca and A. Mugan, Composites, Part B, 2013, 50, 150–157 CrossRef CAS.
- H. Yazdani, K. Hatami and M. Eftekhari, Mater. Res. Express, 2017, 4, 055015 CrossRef.
- E. K. Hobbie, D. O. Simien, J. A. Fagan, J. Huh, J. Y. Chung, S. D. Hudson, J. Obrzut, f. J. Douglas and C. M. Stafford, Phys. Rev. Lett., 2010, 104, 125505 CrossRef CAS PubMed.
- H. Talebi, M. Silani, S. P. Bordas, P. Kerfriden and T. Rabczuk, Comput. Mech., 2014, 53, 1047–1071 CrossRef.
- T. Kirchdoerfer and M. Ortiz, Comput. Methods Appl. Mech. Eng., 2016, 304, 81–101 CrossRef.
- K. Karapiperis, L. Stainier, M. Ortiz and J. E. Andrade, J. Mech. Phys. Solids, 2021, 147, 104239 CrossRef.
- G. E. Hinton, S. Osindero and Y.-W. Teh, Neural Comput., 2006, 18, 1527–1554 CrossRef PubMed.
- G. D. Förster, A. Castan, A. Loiseau, J. Nelayah, D. Alloyeau, F. Fossard, C. Bichara and H. Amara, Carbon, 2020, 169, 465–474 CrossRef.
- N. Shirolkar, P. Patwardhan, A. Rahman, A. Spear and S. Kumar, Carbon, 2021, 174, 605–616 CrossRef CAS.
- Y. Xiang, K. Shimoyama, K. Shirasu and G. Yamamoto, Nanomaterials, 2020, 10, 2459 CrossRef CAS PubMed.
- U. Yadav, S. Pathrudkar and S. Ghosh, Phys. Rev. B, 2021, 103, 035407 CrossRef CAS.
- E. Samaniego, C. Anitescu, S. Goswami, V. M. Nguyen-Thanh, H. Guo, K. Hamdia, X. Zhuang and T. Rabczuk, Comput. Methods Appl. Mech. Eng., 2020, 362, 112790 CrossRef.
- S. Goswami, C. Anitescu, S. Chakraborty and T. Rabczuk, Theor. Appl. Fract. Mech., 2020, 106, 102447 CrossRef.
- A. Rahman, P. Deshpande, M. S. Radue, G. M. Odegard, S. Gowtham, S. Ghosh and A. D. Spear, Compos. Sci. Technol., 2021, 207, 108627 CrossRef CAS.
- Y. Zhang and X. Xu, J. Compos. Mater., 2021, 55, 2061–2068 CrossRef CAS.
- Y. Xiang and G. Yamamoto, Mater. Sci. Forum, 2021, 29–36 Search PubMed.
- J. Huang, J. Liew and K. Liew, Compos. Struct., 2021, 267, 113917 CrossRef CAS.
- M. Čanađija, Carbon, 2021, 184, 891–901 CrossRef.
- V. Košmerl, I. Štajduhar and M. Čanađija, Neural Comput. Appl., 2022, 34, 17821–17836 CrossRef.
- J. Ma, J.-N. Wang, C.-J. Tsai, R. Nussinov and B. Ma, Front. Mater. Sci. China, 2010, 4, 17–28 CrossRef.
- C. White, D. Robertson and J. Mintmire, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 5485 CrossRef CAS PubMed.
- A. Krasheninnikov and K. Nordlund, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.-Process., Meas., Phenom., 2002, 20, 728–733 CrossRef CAS.
- A. Krasheninnikov, K. Nordlund, M. Sirviö, E. Salonen and J. Keinonen, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245405 CrossRef.
- K. Tserpes, P. Papanikos and S. Tsirkas, Composites, Part B, 2006, 37, 662–669 CrossRef.
- M. Yang, V. Koutsos and M. Zaiser, Nanotechnology, 2007, 18, 155708 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- B. Mortazavi, M. Silani, E. V. Podryabinkin, T. Rabczuk, X. Zhuang and A. V. Shapeev, Adv. Mater., 2021, 33, 2102807 CrossRef CAS PubMed.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS.
- O. Shenderova, D. Brenner, A. Omeltchenko, X. Su and L. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 3877 CrossRef CAS.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- S. Wold, K. Esbensen and P. Geladi, Chemom. Intell. Lab. Syst., 1987, 2, 37–52 CrossRef CAS.
- C. Qian, B. McLean, D. Hedman and F. Ding, APL Mater., 2021, 9, 061102 CrossRef CAS.
- K. Gharbavi and H. Badehian, Comput. Mater. Sci., 2014, 82, 159–164 CrossRef CAS.
- A. Fereidoon, M. G. Ahangari, M. D. Ganji and M. Jahanshahi, Comput. Mater. Sci., 2012, 53, 377–381 CrossRef CAS.
- S. L. Mielke, D. Troya, S. Zhang, J.-L. Li, S. Xiao, R. Car, R. S. Ruoff, G. C. Schatz and T. Belytschko, Chem. Phys. Lett., 2004, 390, 413–420 CrossRef CAS.
- M. Meo and M. Rossi, Eng. Fract. Mech., 2006, 73, 2589–2599 CrossRef.
- S. Zhang, S. L. Mielke, R. Khare, D. Troya, R. S. Ruoff, G. C. Schatz and T. Belytschko, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 115403 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00405a |
| This journal is © The Royal Society of Chemistry 2024 |