Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum interference features and thermoelectric properties of macrocyclic-single molecules: theoretical and modelling investigation†
Sarah Hussein
Halboos
a,
Oday A.
Al-Owaedi
 *ab and
Enas M.
Al-Robayi
a
*ab and
Enas M.
Al-Robayi
a
aDepartment of Laser Physics, College of Science for Women, University of Babylon, Hilla 51001, Iraq. E-mail: oday.alowaedi@uobabylon.edu.iq
bAl-Zahrawi University College, Karbala, Najaf-Karbala Street, 56001, Iraq
First published on 2nd October 2024
Abstract
The quantum interference effect on the thermoelectric properties of cycloparaphenylacetylene-based molecular junctions was investigated theoretically using a combination of density functional theory (DFT) methods, a tight binding (Hückel) model (TBHM) and quantum transport theory (QTT). Manipulating the unique conjugation function of these molecules not only creates a quantum interference (QI) but it is also a robust strategy for improving the thermoelectric properties of these molecules. QI controls the transport behaviour and decreases the electrical conductance (G) from 0.14 × 10−7 to 0.67 × 10−11 S, as well as enhancing the Seebeck coefficient (S) from 14.4 to 294 μV K−1, and promoting the electronic figure of merit (ZelT) from 0.008 to 1.8, making these molecules promising candidates for thermoelectric applications.
Introduction
The tunneling transport process across the source|molecule|drain has attracted wide interest and is depicted as a coherent transport.1 Quantum interference (QI)2 is one of the most important phenomena that control3,4 the tunneling transport, and consequently impacts the properties of single-molecule junctions.5–12 The attractive functionality of π-conjugated molecules13 such as cycloparaphenylene (CPP)14 compounds makes them a target of a wide range of investigations.15–21 The efforts to form carbon nanotubes with precise structure have led to the development of CPP compounds, and these macrocyclic structures are composed of para-linked phenylene rings.22–26 Lambert et al.27 have demonstrated that cycloparaphenylene (CPP) macrocycles show a high electrical conductance due to the topological nature of the de Broglie wave created by electrons injected into the macrocycle from the source. The potential applications of CPP and its derivatives range from organic electronics28,29 to supramolecular sensing30–32 and bioimaging.33 Cycloparaphenylene and its derivatives could be perfect for exploring quantum interference (QI), since they provide a powerful strategy to investigate the propagation of de Broglie waves through the source|molecule|drain configuration. Oday A. Al-Owaedi34 proved that the multiple molecular templates of cycloparaphenylene molecules are an ideal host to inspect the quantum interference, and demonstrated that the destructive quantum interference (DQI) influenced the thermoelectric properties of these molecules and raised the Seebeck coefficient (S) from 3.13 to 37.24 μV K−1.In addition, there are many interesting phenomena have been found in cycloparaphenylene-based devices, such as a negative differential resistance (NDR),35 highly nonlinear I–V relationship,36 electrical switching37,38etc. Because of its wide applications, e.g., logic, memory, and amplification, NDR has attracted a lot of attention. The spectroscopic15–18 and optical19–21 properties of CPP molecules have been studied widely. Bryan M. Wong et al.39 found that the first electronic excitation in chiral nanorings is allowed because of a strong geometric symmetry breaking, which proves that cycloparaphenylene molecules possess extremely interesting optoelectronic properties with excitation energies increasing as a function of size, which is in contrast to typical quantum confinement effects. In this context, manipulating the transport paths of de Broglie waves through this kind of molecule will undoubtedly lead to the emergence of the quantum interference phenomenon.40–49 Herein, we explore the influence of QI on the electronic, thermoelectric and spectroscopic properties of CPP-based molecular junctions using a combination of density functional theory (DFT) methods,50,51 a tight binding (Hückel) model (TBHM)52 and quantum transport theory (QTT).53–62
Computational methods
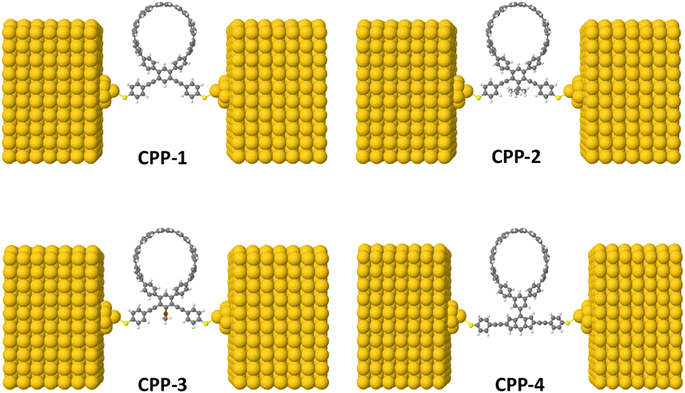
The initial optimization of gas phase molecules and isosurfaces calculations were carried out at the B3LYP level of theory63 with the 6-31G** basis set64,65 using density functional theory (DFT) and time-dependent DFT (TD-DFT)66 respectively. The geometrical optimization of all gold|CPP|gold configurations under investigation in this work was accomplished by the implementation of DFT67,68 in the SIESTA67 code, as shown in Fig. 4 and S2 (see the ESI†). The generalized gradient approximation (GGA) of the exchange and correlation functional is used with a double-ζ polarized (DZP) basis set, a real-space grid defined with an equivalent energy cut-off of 250 Ry. The geometry optimization for each structure is performed for forces smaller than 20 meV Å−1. The mean-field Hamiltonian obtained from the converged DFT calculations was combined with Gollum53 code. Quantum transport theory (QTT)54,69 implemented in Gollum has been used to calculate the electronic and thermoelectric properties of all molecular junctions. The optimized molecules have been attached to two (111)-directed pyramidal gold electrodes. Each electrode was constructed of seven layers of (111)-oriented bulk gold, with each layer consisting of 6 × 6 atoms and a layer spacing of 0.235 nm, which were used to create the molecular junctions. These layers were then further repeated to yield infinitely long gold electrodes carrying current, as shown in Fig. 4 (see the ESI for more details†).Results and discussion
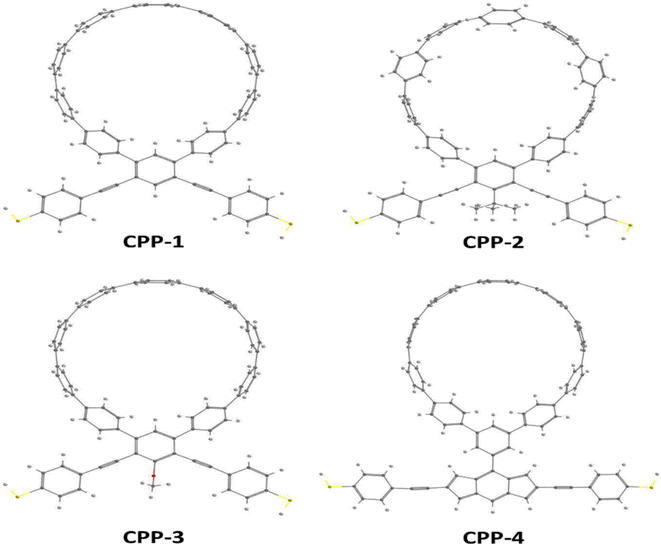
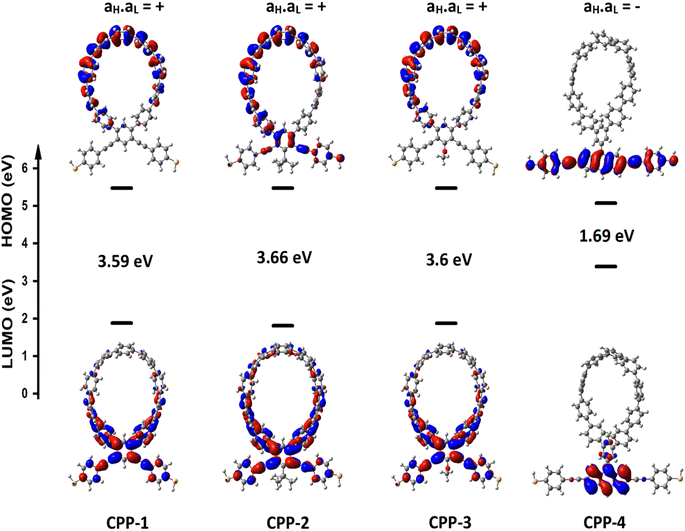
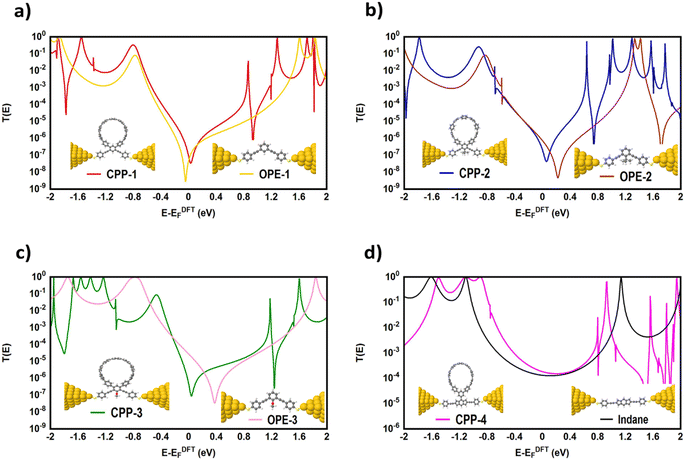
Fig. 1 shows that each molecule under investigation in this work is a necklace consisting of a mixture of two molecules. The first three molecules CPP-1, CPP-2 and CPP-3 consist of an oligo(phenylene ethylene) (OPE) molecule incorporated with a cycloparaphenylene (CPP) molecule, while molecule CPP-4 is a necklace consisting of a combination of a CPP molecule plus an indacene structure. All molecules are terminated by a thiol compound as an anchor group. In addition, molecules CPP-1, CPP-2 and CPP-3 possess meta-connectivity, while a connection of para is the distinguishing feature of molecule CPP-4. Furthermore, 2-methylpropane is the pendant structure of the molecule CPP-2, while the methoxy group represents the pendant group of the molecule CPP-3, and molecule CPP-4 contains an indacene compound as a pendant group.Obviously, the HOMOs of the first three molecules (CPP-1, CPP-2 and CPP-4) are localized on the circular part of each molecule, while they extend along the indacene structure for the fourth molecule (CPP-4). In contrast, LUMOs have a significant weight on the OPE part of the molecule for CPP-1, CPP-2 and CPP-3, while they have less weight on the indacene compound for the molecule CPP-4. In addition, the HOMOs and LUMO do not have a considerable weight on the circular part of CPP-4. The narrowest HOMO–LUMO gap (1.69 eV) is presented by the fourth molecule (CPP-4). To some extent, the other molecules exhibit gaps of similar values, as shown in Fig. 2 and Table 1.
| Molecule | HOMO (eV) | LUMO (eV) | H–L gap (eV) | A (a.u.) | A λ Max (nm) | E (a.u.) | E λ Max (nm) | f em | SS (nm) |
|---|---|---|---|---|---|---|---|---|---|
| CPP-1 | 5.47 | 1.88 | 3.59 | 1614.6 | 352 | 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 532 532 |
375 | 1.34 | 23 |
| CPP-2 | 5.47 | 1.81 | 3.66 | 1290.6 | 348 | 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 387.4 387.4 |
372 | 0.95 | 24 |
| CPP-3 | 5.47 | 1.87 | 3.6 | 1931.7 | 350 | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 303.1 303.1 |
374 | 1.3 | 24 |
| CPP-4 | 5.07 | 3.38 | 1.69 | 24.25 | 536 | 1871.2 | 592 | 0.04 | 56 |
In order to explore the impact of connectivity type and to prove the existence of QI66 in CPP molecules, as part of the current investigation an orbital analysis was performed, and it demonstrated that the destructive quantum interference (DQI) dominates the transport of most molecular junctions, as shown in Fig. 2. Lambert et al.70 have reported an orbital symmetry rule. Magic ratio theory67 is based on utilising the exact core Green's function, defined by:
| g(E) = (IE − H)−1 | (1) |
In the literature, various approximations to g(E) are discussed, one of which involves the approximation of including only the contributions to g(E) from the HOMO and LUMO. If the amplitudes of the HOMO on sites a and b are denoted 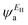 and
and 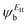 and the amplitudes of the LUMO are
and the amplitudes of the LUMO are 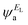 and
and 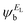 , then if the contributions from all other orbitals are ignored, then, a crude approximation to Green's function gba(E) is
, then if the contributions from all other orbitals are ignored, then, a crude approximation to Green's function gba(E) is
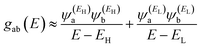 | (2) |
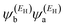 has the same sign as the LUMO product
has the same sign as the LUMO product 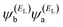 then the right-hand side of eqn (2) will vanish at some energy E in the range EH ≤ E ≤ EL. That is for some energy E within the HOMO–LUMO gap. In this case, one can say that the HOMO and the LUMO interfere destructively. On the other hand, if the HOMO and LUMO products have opposite signs then the right hand side of eqn (2) will not vanish within the HOMO–LUMO gap and one can say that the HOMO and LUMO interfere constructively within the gap (they could of course interfere destructively at some other energy E outside the gap). When the right-hand side of eqn (2) vanishes, the main contribution to gba(E) comes from all other orbitals, so in general eqn (2) could be a poor approximation. One exception to this occurs when the lattice is bipartite, because the Coulson–Rushbrooke (CR) theorem68 tells us that if a and b are both even or both odd, then the orbital products on opposite sides of eqn (3) and (4) have the same sign. Consequently, the HOMO and LUMO interfere destructively, while all other pairs of orbitals interfere destructively, leading to trivial zeros in the magic number table,70 for which gba(0) = 0.
then the right-hand side of eqn (2) will vanish at some energy E in the range EH ≤ E ≤ EL. That is for some energy E within the HOMO–LUMO gap. In this case, one can say that the HOMO and the LUMO interfere destructively. On the other hand, if the HOMO and LUMO products have opposite signs then the right hand side of eqn (2) will not vanish within the HOMO–LUMO gap and one can say that the HOMO and LUMO interfere constructively within the gap (they could of course interfere destructively at some other energy E outside the gap). When the right-hand side of eqn (2) vanishes, the main contribution to gba(E) comes from all other orbitals, so in general eqn (2) could be a poor approximation. One exception to this occurs when the lattice is bipartite, because the Coulson–Rushbrooke (CR) theorem68 tells us that if a and b are both even or both odd, then the orbital products on opposite sides of eqn (3) and (4) have the same sign. Consequently, the HOMO and LUMO interfere destructively, while all other pairs of orbitals interfere destructively, leading to trivial zeros in the magic number table,70 for which gba(0) = 0.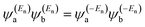 | (3) |
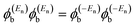 | (4) |
Obviously, this exact cancellation is a property of bipartite lattices only, but based on its success for bipartite lattices, one might suppose that eqn (2) is a reasonable approximation, for other lattices. Nevertheless, as pointed out by Yoshizawa et al.,71–74 since orbitals such as those in Fig. 2 are often available from DFT calculations, it can be helpful to examine the question of whether or not the HOMO and LUMO (or indeed any other pair of orbitals) interfere destructively or constructively, by examining the colours of orbitals. This is simplified by writing eqn (2) in the form
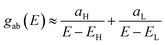 | (5) |
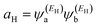 and
and 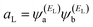 . If the HOMO product aH has the same sign as the LUMO product aL then the right-hand side of eqn (5) will vanish for some energy E in the range EH ≤ E ≤ EL. In other words, the HOMO and LUMO will interfere destructively at some energy within the HOMO–LUMO gap. However, this does not mean that the exact gba(E) will vanish. Indeed, if the right hand side of (5) vanishes, then the contributions from all other orbitals become the dominant terms.75 Nevertheless, this is an appealing method of identifying QI effects in molecules and describing their qualitative features.76
. If the HOMO product aH has the same sign as the LUMO product aL then the right-hand side of eqn (5) will vanish for some energy E in the range EH ≤ E ≤ EL. In other words, the HOMO and LUMO will interfere destructively at some energy within the HOMO–LUMO gap. However, this does not mean that the exact gba(E) will vanish. Indeed, if the right hand side of (5) vanishes, then the contributions from all other orbitals become the dominant terms.75 Nevertheless, this is an appealing method of identifying QI effects in molecules and describing their qualitative features.76
Studying the spectroscopic properties has become one of the necessary factors to complete an integrated investigation for any system in order to predicate the appropriate applications for that system. Therefore, the absorption and emission spectra of CPP molecules are topics of great interest for many investigations.15–21Fig. 3 and Table 1 show that the UV/visible absorption and emission spectra of the first three molecules (CPP-1, CPP-2 and CPP-4) exhibit a blueshift, since the range of the absorption spectrum extends from 350 to 352 nm, and the emission spectrum ranges from 372 to 375 nm. These results are consistent with the literature.15–21 On the other hand, molecule CPP-4 shows a visible light region, since its absorption and emission spectra are 536 and 592 nm respectively. Table 1 shows one of the most important parameters in optoelectronics applications, which is the emission oscillator strength (fem).77 Theoretically, for a given PL material, fem is directly proportional to the emission cross section (σem) and it is given by:78
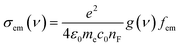 | (6) |
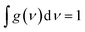 . Interestingly, the emission oscillator strengths (fem) of CPP-1, CPP-2 and CPP-3 are 1.34, 0.95 and 1.3 respectively, whereas molecule CPP-4 shows the lowest value of fem (0.04), as shown in Table 1. These results suggest that cycloparaphenylene-single molecules are promising candidates for optoelectronics applications.
. Interestingly, the emission oscillator strengths (fem) of CPP-1, CPP-2 and CPP-3 are 1.34, 0.95 and 1.3 respectively, whereas molecule CPP-4 shows the lowest value of fem (0.04), as shown in Table 1. These results suggest that cycloparaphenylene-single molecules are promising candidates for optoelectronics applications.
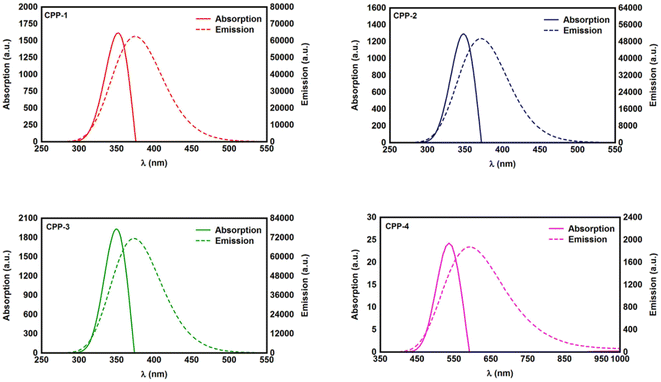 | ||
| Fig. 3 UV/Vis absorption spectra (solid curves) and emission spectra (dashed curves) for all molecules. | ||
In this work the transmission coefficient T(E) has been calculated by attaching the optimized molecules with two (111)-directed gold electrodes, as shown in Fig. 4. From these molecular junctions the electronic and thermoelectric properties were calculated using Gollum code.48,79 The transmission coefficient according to Landauer–Büttiker80 formalism is given by:
| T(E) = Tr{ΓR(E)GR(E)ΓL(E)GR†(E)} | (7) |
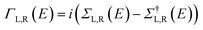 | (8) |
| GR = (EX − H − ΣL − ΣR)−1 | (9) |
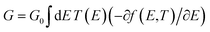 | (10) |
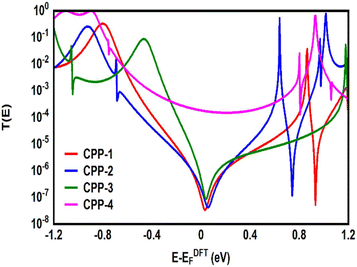
Many investigations83,84 have demonstrated that quantum interference (QI) arises from the tunneling of electrons through various molecular orbitals with different phases. Both of interfering and noninterfering effects are comprised in the transmission function, so the single interference between molecular orbitals cannot be diagnosed from the transmission function directly. Latha Venkataraman et al.84 have deconstructed the interferences of the molecular orbitals and established a powerful method to arrange these interferences in a matrix and display them pictorially as a QI map, which allows one to easily identify individual QI effects. The current study predicates that the HOMO–LUMO orbitals interfered destructively at the middle of the HOMO–LUMO gap, near the theoretical Fermi energy (0.0 eV) with transmission functions featuring antiresonances, as shown in Fig. 5. These results are in excellent agreement with various pen-and-paper methods85–87 that predicted the existence of antiresonances at the Fermi energy. The origin of the destructive quantum interference (DQI) is the node at the meta position in the HOMO which prevents electronic coupling between two meta substituents. Therefore, meta-linked wires show poor conductance and DQI for the same reason that electrophilic aromatic substitution reactions with electron-rich substituents, in general, do not occur at the meta-position.88,89
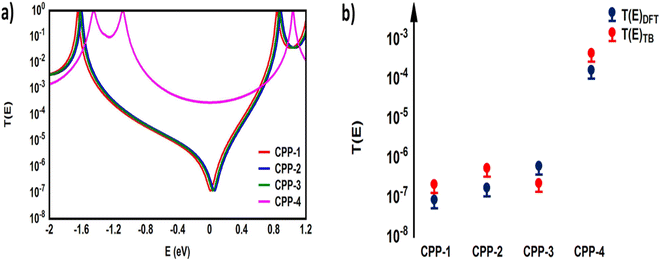
Fig. 5 shows the transmission coefficient T(E)90,91 of source|molecule|drain junctions. The transmission coefficient curves of the first three molecules (CPP-1, CPP-2 and CPP-3) show robust antiresonance features as a representation of the destructive quantum interference (DQI). These features are located at the middle of the HOMO–LUMO gap, toward the HOMO peak. In contrast, the antiresonance features disappeared in the transmission curve of the CPP-4 molecule, as well as presenting the highest value of T(E) along a wide range of energies, which refers to the constructive quantum interference (CQI). The order of T(E) is CPP-4 > CPP-3 > CPP-2 > CPP-1, as shown in Table 2. In addition, the theoretical Fermi energy (0.0 eV) lies within the HOMO–LUMO gap towards the HOMO resonance, which indicates the HOMO-dominated transport mechanism.92,93Fig. 5 reflects the fact that the destructive quantum interference (DQI) dominates the transport process through the first three molecules, and increases the values of Seebeck coefficient (S) and the electronic figure of merit (ZelT), and the transport behavior varies from one molecule to another, and this difference in turn will lead to a difference in the slope of the transmission coefficient T(E), which affects the values of the Seebeck coefficient.
| Molecule | T(E) | Γ | Ω a (eV) | Ω b (eV) |
|---|---|---|---|---|
| CPP-1 | 8.64 × 10−8 | 0.73 | 2.085 | 2.37 |
| CPP-2 | 1.82 × 10−7 | 0.8 | 1.937 | 2.24 |
| CPP-3 | 4.02 × 10−7 | 0.85 | 2.07 | 2.6 |
| CPP-4 | 1.8 × 10−4 | 2.3 | 1.8 | 2.25 |
The meta-linked structures have an extremely small number of transferred electrons (Γ), which leads to an impalpable T(E). In contrast, molecule CPP-4 with para connection exhibits a high value of T(E) due to the constructive quantum interference (CQI) (Fig. 6).
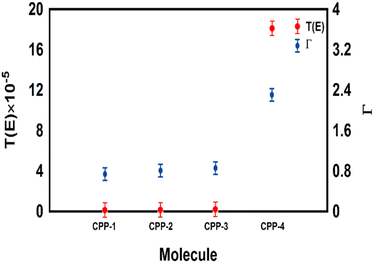 | ||
| Fig. 6 The number of electrons transferred from the molecule to electrodes (Γ) against the transmission coefficient T(E) for all molecules. | ||
The molecule length of all molecules is consistent with a dominant contribution from the coherent tunneling mechanism.94–98 The rectangular tunnel barrier model99 states that the electrical conductance through a single molecule (barrier) decreases exponentially with the length of the barrier, according to eqn (11).
| T(E) ∝ e−βl | (11) |
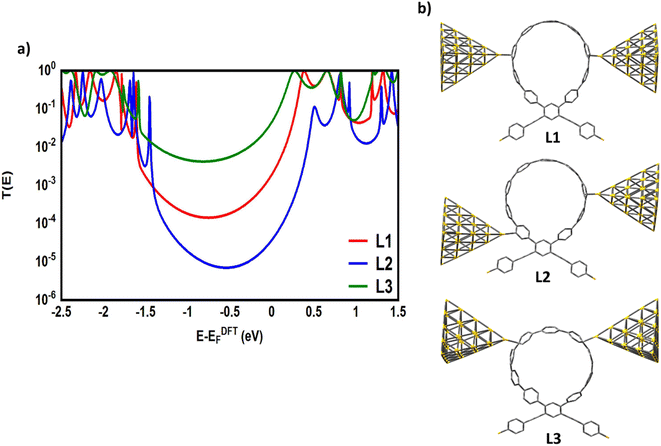
To gain a deeper understanding of the role of macrocyclic units and their effect on the properties of the molecular junctions under investigation in this work, we have calculated the transmission coefficient T(E) of molecular junctions that consist of only oligo(phenylene ethylene) (OPE) and indacene molecules and compared the results of both systems (with and without macrocyclic units), as shown in Fig. 7. Obviously, the absence of the macrocyclic unit has led to the widening of the HOMO–LUMO gap, as the value of this gap for molecular junctions that include a macrocyclic unit is smaller (on average) by 0.39 eV than that of the unit-free structures, as shown in Table 2. This result could be ascribed to the quantum size effect.100 On the other hand, the presence of the circular units impacts the slope of the transmission coefficient, which undoubtedly affects the Seebeck coefficient characteristics (see Fig. 11a). It is well known that the meta-connection leads to a destructive quantum interference (DQI) and an appearance of the antiresonance feature. Herein, the curve of the transmission coefficient of structures with a wheel shows two antiresonances, one at the middle of the HOMO–LUMO gap, near the theoretical Fermi energy (0.0 eV), and the second located between 0.8 and 1.2 eV, while the wheel-free compositions have just one antiresonance feature. Moreover, the CPP-4 molecule possesses a para connectivity, and the effect of the constructive quantum interference (CQI) is prominent via the highest transmission coefficient value, but there is also a small antiresonance feature in the transmission curve. In contrast, the transmission curve of the structure with the same backbone (indacene) and without a macrocyclic unit is completely free of antiresonance features. Based on these results, it can be concluded that the origin of the quantum interferences (QIs) is the connectivity type (meta or para) with an important contribution of the macrocyclic units. This contribution may be the result of a tilt or twist in the circular rings during the accommodation between electrodes. Indeed, these results and behaviour need more exploring and investigation. According to the rectangular tunnel barrier model99 and eqn (11), T(E) decreases exponentially with the length of the tunneling distance. The macrocyclic unit-based molecular junctions have the longest distance, but their transmission coefficient is the highest over a wide range of energies, as shown in Fig. 7. This could be explained in terms of the existence of more than one probability for the junction formation. The strong interactions between the extended π-system and gold electrodes create a good chance to form a molecular junction,27 and the high binding energy between sulfur (S) atoms and gold (Au) atoms101 represents another strong probability for the junction formation and molecule. This investigation took into account both of these probabilities, as shown in Fig. 7 and 8.
The theoretical models shown in Fig. 8 have simulated the probable contacts of gold electrodes to carbon atoms in the circular wheel of structure CPP-1 with various connections. The L1 model involves the formation of the molecular junction via a meta–meta connection. This kind of connectivity is well known to cause a difference in the phase of the traveling electronic waves, which in turn leads to a destructive quantum interference (DQI), that decreases the transmission coefficient as shown in Fig. 8a. In contrast, the L3 model shows the structure of the molecular junction with a para–para connection. This system shows the highest T(E) due to a constructive quantum interference (CQI). These results could be explained in terms of Mach–Zehnder interferometers.102 The de Broglie waves cross identical pathways of L3, which results in wave interference at the same phase, then CQI (T(E) = |eik3 + eik3|2 = |e|ik3 = |1 + 1|2 = 4), raising the T(E) of the whole system. In contrast, the different pathways of the L1 model lead to a low T(E), which could be attributed to DQI (T(E) = |eik4 + eik2|2 = |ei2π + eiπ| = |1 − 1|2 = 0). Model L2 exhibits a mixed connection consisting of meta and ortho positions. Interestingly, the transmission value of this structure is mediated between the lowest and highest values of T(E) of other systems, which could be understood by releasing a predication that the transmission coefficient of this structure is a result of the contributions of constructive (ortho) and destructive (meta) quantum interferences at the same time. These results open an important window to design new materials to control and utilize the quantum interference in different electronic applications. On the other hand, it could be observed that all T(E) curves are completely clear of any mark of the antiresonance feature, and so there is no dramatic difference between the slope of T(E) curves. Consequently, it is expected that the Seebeck coefficient of these models will not show promising results, as shown in Fig. S4 (see the ESI†).
In seeking to confirm the quantum interference effect and understand the transport behaviour of molecules and the relative effects of different pendant groups, a minimal tight-binding (Hückel) model (TBHM) has been constructed, as shown in Fig. 9. The simplest tight-binding Hamiltonian of the parents is obtained by assigning a site energy ε to each diagonal and a nearest neighbor hopping integral γ between neighbouring sites, i.e., Hii = ε and Hij = γ if i, j are the nearest neighbours.
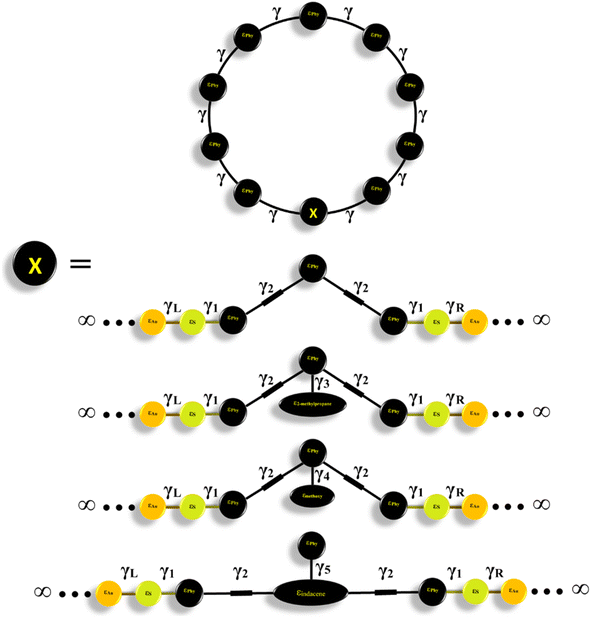 | ||
| Fig. 9 A minimal tight-binding (Hückel) representation of CPP molecules with different intramolecular coupling elements, γ, and different onsite energies ε. | ||
Fig. 9 shows a system connected to two one-dimension electrodes on both sides by weak nearest neighbor coupling of γR and γL. The tight-binding (Hückel) model (TBHM) neglects the interactions between electrons, which is considered a major defect, but it remains one of the widely used methods to visualize and understand the electronic properties of molecular junctions.103 In addition, the energy levels produced by this kind of computational method are diminished by a few electron voltages in comparison with the accurate values relative to those in a vacuum. However, the energy differences are appropriate to compare with DFT calculations and consequently this method is considered a powerful tool to obtain reasonable and precise results that could yield the fundamental physics and resolve the problems.104
Furthermore, TBHM not only takes into account all morphological aspects of molecular junctions, but also assumes that the electron transport is elastic and coherent.104Fig. 10 shows the transmission coefficient produced by TBHM as a function of electron energy of all models. If all sites are treated as the same and the on-site energies set to 0 eV and coupling integrals to −1 eV, the transmission values disagree with the DFT results (see the ESI†). However, by adjusting the coupling integrals (γ = γ1 = γL = γR = 0.5 and γ2 = 0.3 eV) for all models, as well as γ3 = 2.2, γ4 = 0.5 and γ5 = 0.3 eV, then by changing the on-site energies (εphy = 0.5, ε2-methylpropane = 0.7, εmethoxy = 0.7 and εindacene = 1.1 eV), the TBHM results are reproduced, as shown in Fig. 10a. The 2-methylpropane structure is joined by carbon–carbon sigma bonds allowing them to rotate about these bonds. In terms of Newman projection,105 the free rotation around single bonds results in various conformations. These conformations are classified as staggered and eclipsed conformations. Staggered conformations are the lower energy arrangements, whereas eclipsed conformations are higher in energy than staggered conformations due to bond straining. Herein, the tight-binding (TB) model depicts the molecular rotation by changing the value of γ3 to obtain the appropriate eclipsed conformation. For γ3 = 2, the TB model produces a DQI-dominated transport behaviour of model CPP-2. The rotation of the methoxy (OMe) pendant group for the CPP-3 molecule has been pictured as γ4. An excellent agreement between DFT and TB has been reached by adjusting γ4 to be 2. The results of TB agree with the results of DFT as shown in Fig. 10a, as well as confirming that there are two parameters controlling and switching the quantum interference from CQI to DQI, which are the connectivity type either para or meta, and the second parameter is the kind of pendant group.
 | ||
| Fig. 10 (a) Transmission coefficient as a function of electron energy for all models presented in Fig. 9. The coupling integrals γ = γ1 = γL = γR = 0.5 eV, γ2 = 0.3 eV, γ3 = 2.2, γ4 = 0.5, and γ5 = 0.9 eV are fixed for all models. The on-site energies are εphy = 0.5 eV for CPP-1, ε2-methylpropane = 0.7 eV for CPP-2, εmethoxy = 0.7 eV for CPP-3 and εindacene = 1.1 eV for CPP-4; (b) representation of the agreement between density functional theory (DFT) and tight-binding (TB) calculations. | ||
The slope of T(E) determines the Seebeck coefficient (S) and electronic figure of merit (ZelT), which are given by:
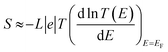 | (12) |
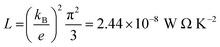 . In other words, S is proportional to the negative of the slope of ln
. In other words, S is proportional to the negative of the slope of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T(E), evaluated at the Fermi energy. Based on the Seebeck coefficient, the power factor was calculated by:
T(E), evaluated at the Fermi energy. Based on the Seebeck coefficient, the power factor was calculated by:| P = GS2T | (13) |
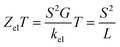 | (14) |
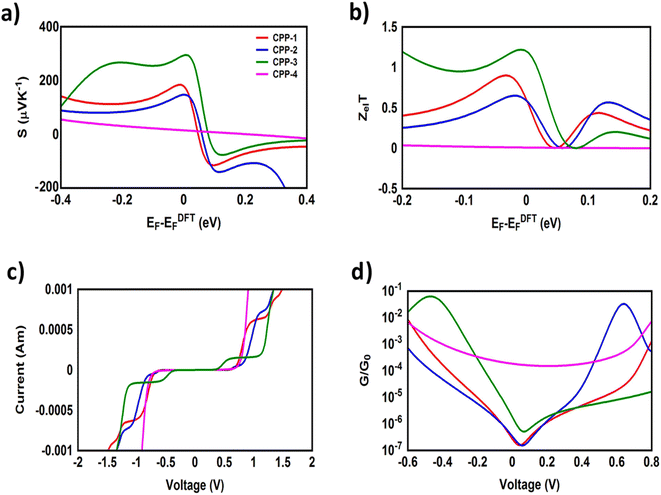
It is well known that the performance of thermoelectric materials is characterized by an efficient conversion of input heat to electricity.44,108 In this context, the enhancement of the power factor (P) and electronic figure of merit (ZelT), which depend on the Seebeck coefficient (S), is important. Fig. 11a, b and Table 3 show that the highest values of S and ZelT (294 μV K−1 and 1.12 respectively) have been exhibited by molecule CPP-3. In contrast, molecule CPP-4 presents the lowest values of these parameters (14.4 μV K−1 and 0.0081). In addition, molecules CPP-1 and CPP-2 introduce high S and ZelT values as shown in Table 3. These results not only established the important role of the existence of the destructive quantum interference in improvement of the S and ZelT characteristics but also show a crucial contribution of the pendant groups in promoting these properties. Furthermore, the competition between electrical conductance (G) and Seebeck coefficient (S) according to eqn (13) led to the power factor order of PCPP-4 > PCPP-3 > PCPP-2 > PCPP-1. In light of the aforementioned results, these molecules could be considered as promising candidates for thermoelectric applications. The values of transmission coefficient T(E), Seebeck coefficient (S) and electronic figure of merit (ZelT) are found to be higher when the contact Fermi energies are close to the middle of the HOMO–LUMO gap and increase as Fermi energies approach resonance with the highest occupied molecular orbitals (HOMO). To some extent, these results are consistent with an investigation of Milan et al.,109 since they reported that the electronic and electrical properties depend in a very sensitive manner on the position of the contact Fermi energies within the HOMO–LUMO gap.
| Molecule | S (μV K−1) | P (W K−1 × 10−23) | Z el T | V th (V) | G (S) |
|---|---|---|---|---|---|
| CPP-1 | 175 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 518 518 |
0.55 | 0.66 | 0.67 × 10−11 |
| CPP-2 | 147 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252.6 252.6 |
0.57 | 0.64 | 0.14 × 10−10 |
| CPP-3 | 294 | 267![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 951.6 951.6 |
1.12 | 0.43 | 0.31 × 10−10 |
| CPP-4 | 14.4 | 290![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 304 304 |
0.0081 | 0.69 | 0.14 × 10−7 |
Fig. 11c, d and Table 3 present the electrical conductance and current–voltage (I–V) characteristics of all molecular junctions, which are limited to the first and third quadrants of the I–V plane crossing the origin. Therefore, they are classified as components that consume electric power, and here the importance of the threshold voltage (Vth) value appears. The values of Vth range from 0.43 to 0.69 V, which makes these molecules promising candidates for electronic applications.
All molecules show a quantum staircase behaviour. Obviously, as the voltage increases, the density of electrons also increases, which leads to an increase in the number of occupied subbands. The dependence of conductance in this case is represented by a set of plateaus separated by steps of height 2e2/h: a stepwise change in the conductance of all molecule channels occurs each time the Fermi level coincides with one of the subbands. Hence, the quantum staircase behaviour could be attributed to the adiabatic transparency of the spin-nondegenerate subbands of these molecules.110,111 On the other hand, after the threshold bias voltage, the current increases obviously with the increasing bias voltage. When the bias voltage is further increased to a certain range [2, 2.5] V, the current decreases and the negative differential resistance (NDR) appears, as shown in Fig. 10c and S3.† These results are consistent with the results in the literature.35
Conclusions
Numerous methods and tools have been used to create the destructive quantum interference (DQI) phenomenon. From the current investigation it can be concluded that the cycloparaphenylene-single molecules and their derivatives represent a promising host for creating the quantum phenomena by manipulating the topological properties via crucial parameters, which are the connectivity or the pendant group. These parameters not only control the transport behaviour of CPP molecules, but also enhance the thermoelectric properties. Therefore, we believe that these findings will strongly help in developing fast and trustworthy design of molecular electronics and thermoelectric materials.‡Data availability
The data is available in the manuscript and ESI.†Author contributions
Sarah Hussein Halboosa: investigation, writing – original draft, visualization, calculations. Oday A. Al-Owaedi: supervision, investigation, writing – review & editing, conceptualization, validation, analysis, software, analysis, calculations. Enas M. Al-Robayia: supervision.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
S. H. H., O. A. A. and E. M. A. express their deep thanks and appreciation to the University of Babylon for the kind support. O. A. A. thanks Al-Zahrawi University College for the support.Notes and references
- T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002 CrossRef CAS.
- P. Sautet and C. Joachim, Chem. Phys. Lett., 1988, 153, 511–516 CrossRef CAS.
- M. Baghernejad, Y. Yang, O. A. Al-Owaedi, Y. Aeschi, B. Zeng, Z. M. Dawood, X. Li, J. Liu, J. Shi, D. Silvio, S. Liu, W. Hong and C. J. Lambert, Chem.–Eur. J., 2020, 26, 5264–5269 CrossRef CAS PubMed.
- D. Z. Manrique, C. Huang, M. Baghernejad, X. Zhao, O. A. Al-Owaedi, H. Sadeghi, V. Kaliginedi, W. Hong, M. Gulcur, T. Wandlowski, M. R. Bryce and C. J. Lambert, Nat. Commun., 2015, 6, 6389 CrossRef CAS PubMed.
- M. Mayor, H. B. Weber, J. Reichert, M. Elbing, C. von Hänisch, D. Beckmann and M. Fischer, Angew. Chem., Int. Ed., 2003, 42, 5834–5838 CrossRef CAS PubMed.
- M. Taniguchi, M. Tsutsui, R. Mogi, T. Sugawara, Y. Tsuji, K. Yoshizawa and T. Kawai, J. Am. Chem. Soc., 2011, 133, 11426–11429 CrossRef CAS PubMed.
- C. M. Guédon, H. Valkenier, T. Markussen, K. S. Thygesen, J. C. Hummelen and S. J. van der Molen, Nat. Nanotechnol., 2012, 7, 305 CrossRef PubMed.
- S. V. Aradhya, J. S. Meisner, M. Krikorian, S. Ahn, R. Parameswaran, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nano Lett., 2012, 12, 1643–1647 CrossRef CAS PubMed.
- C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. M. Woerde, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Angew. Chem., Int. Ed., 2013, 52, 3152–3155 CrossRef CAS PubMed.
- Y. Zhang, G. Ye, S. Soni, X. Qiu, T. L. Krijger, H. T. Jonkman, M. Carlotti, E. Sauter, M. Zharnikov and R. C. Chiechi, Chem. Sci., 2018, 9, 4414–4423 RSC.
- V. Rabache, J. Chaste, P. Petit, M. L. Della Rocca, P. Martin, J. C. Lacroix, R. L. McCreery and P. Lafarge, J. Am. Chem. Soc., 2013, 135, 10218–10221 CrossRef CAS PubMed.
- R. Frisenda, V. A. E. C. Janssen, F. C. Grozema, H. S. J. van der Zant and N. Renaud, Nat. Chem., 2016, 8, 1099 CrossRef CAS PubMed.
- Y. Shigeru and K. J. Eiichi, J. Synth. Org. Chem., Jpn., 2019, 77, 1147–1158 CrossRef.
- A. Yagi, Y. Segawa and K. Itami, J. Am. Chem. Soc., 2012, 134, 2962–2965 CrossRef CAS PubMed.
- H. Chen, M. R. Golder, F. Wang, R. Jasti and A. K. J. Swan, Carbon, 2014, 67, 203–213 CrossRef CAS.
- V. K. Patel, E. Kayahara and S. Yamago, Chem.–Eur. J., 2015, 21, 1–9 CrossRef PubMed.
- E. J. Leonhardt and R. Jasti, Nat. Rev. Chem, 2019, 3, 672–686 CrossRef CAS.
- R. Jasti, J. Bhattacharjee, J. B. Neaton and C. R. Bertozzi, J. Am. Chem. Soc., 2008, 130, 17646–17647 CrossRef CAS PubMed.
- Z. Liu and T. Lu, J. Phys. Chem. C, 2020, 124, 7353–7360 CrossRef CAS.
- X. Huang, X. Bai, P. Gan, W. Liu, H. Yan, F. Gao, H. Xu and Z. Su, New J. Chem., 2023, 47, 5390–5398 RSC.
- N. Li and M. Sun, ChemPhysChem, 2023, 24, e202200846 CrossRef CAS PubMed.
- R. Jasti, J. Bhattacharjee, J. B. Neaton and C. R. Bertozzi, J. Am. Chem. Soc., 2008, 130, 17646–17647 CrossRef CAS PubMed.
- S. Yamago, Y. Watanabe and T. Iwamoto, Angew. Chem., Int. Ed., 2010, 49, 757–759 CrossRef CAS PubMed.
- H. Omachi, S. Matsuura, Y. Segawa and K. Itami, Angew. Chem., Int. Ed., 2010, 49, 10202–10205 CrossRef CAS PubMed.
- V. K. Patel, E. Kayahara and S. Yamago, Chem.–Eur. J., 2015, 21, 5742–5749 CrossRef CAS PubMed.
- E. R. Darzi, B. M. White, L. K. Loventhal, L. N. Zakharov and R. Jasti, J. Am. Chem. Soc., 2017, 139, 3106–3114 CrossRef CAS PubMed.
- R. Almughathawi, S. Hou, Q. Wu and C. J. Lambert, Nano Lett., 2024, 24(16), 4972–4978 CAS.
- O. A. Al-Owaedi, D. C. Milan, M. Oerthel, S. Bock, D. S. Yufit, J. A. K. Howard, S. J. Higgins, R. J. Nichols, C. J. Lambert, M. R Bryce and P. J. Low, Organometallics, 2016, 35, 2944–2954 CrossRef CAS.
- E. Kayahara, L. Sun, H. Onishi, K. Suzuki, T. Fukushima, A. Sawada, H. Kaji and S. Yamago, J. Am. Chem. Soc., 2017, 139, 18480–18483 CrossRef CAS PubMed.
- T. Iwamoto, Y. Watanabe, T. Sadahiro, T. Haino and S. Yamago, Angew. Chem., Int. Ed., 2011, 50, 8342–8344 CrossRef CAS PubMed.
- P. Della Sala, C. Talotta, A. Capobianco, A. Soriente, M. De Rosa, P. Neri and C. Gaeta, Org. Lett., 2014, 16, 182–185 CrossRef PubMed.
- P. Della Sala, C. Talotta, T. Caruso, M. De Rosa, A. Soriente, P. Neri and C. Gaeta, J. Org. Chem., 2017, 82, 9885–9889 CrossRef CAS PubMed.
- B. M. White, Y. Zhao, T. E. Kawashima, B. P. Branchaud, M. D. Pluth and R. Jasti, ACS Cent. Sci., 2018, 4, 1173–1178 CrossRef CAS PubMed.
- O. A. Al-Owaedi, RSC Adv., 2024, 14, 14704–14715 RSC.
- H. Lizhi, G. Yandong, Y. Xiaohong, Z. Hongli and Z. Jie, Phys. Lett. A, 2017, 381, 2107–2111 CrossRef.
- Z. Crljen, A. Grigoriev, G. Wendin and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 165316 CrossRef.
- D. I. Gittins, D. Bethell, D. J. Schiffrin and R. J. Nichols, Nature, 2000, 408, 67–69 CrossRef CAS PubMed.
- I. C. Lekshmi, G. Berera, Y. Afsar, G. X. Miao, T. Nagahama, T. Santos and J. S. Mood-era, J. Appl. Phys., 2008, 103, 093719 CrossRef.
- B. M. Wong and J. W. Lee, J. Phys. Chem. Lett., 2011, 2, 2702–2706 CrossRef CAS PubMed.
- C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. M. Woerde, R. Eelkema, F. C. Grozema and H. S. van der Zant, Angew. Chem., Int. Ed., 2013, 52, 3152–3155 CrossRef CAS PubMed.
- L. A. Zotti and E. Leary, Phys. Chem. Chem. Phys., 2020, 22, 5638–5646 RSC.
- L. J. O'Driscoll and M. R. Bryce, Nanoscale, 2021, 13, 1103–1123 RSC.
- M. Schmidt, D. Wassy, M. Hermann, M. G. Teresa, N. Agräit, L. A. Zotti, B. Esser and E. Leary, Chem. Commun., 2021, 57, 745–748 RSC.
- A. Aggarwal, V. Kaliginedi and P. K. Maiti, Nano Lett., 2021, 21, 8532–8544 CrossRef CAS PubMed.
- R. M. Al-Utayjawee and O. A. Al-Owaedi, J. Phys.: Conf. Ser., 2021, 1818, 012208 CrossRef CAS.
- M. A. I. Obayes, E. M. Al-Robayi and O. A. Al-Owaedi, J. Phys.: Conf. Ser., 2021, 1973, 012147 CrossRef.
- S. Gunasekaran, J. E. Greenwald and L. Venkataraman, Nano Lett., 2020, 20, 2843–2848 CrossRef CAS PubMed.
- M. Camarasa-Gómez, D. Hernangómez-Pérez, S. M. Inkpen, G. Lovat, E. Fung, X. Roy, L. Venkataraman and F. Evers, Nano Lett., 2020, 20, 6381–6386 CrossRef PubMed.
- C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- E. Estrada, Proc. R. Soc. A, 2017, 474, 0721 Search PubMed.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef PubMed.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Zs Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi and L. A. Algharagholy, New J. Phys., 2014, 16, 93029 CrossRef.
- M. Jirásek, H. L. Anderson and M. D. Peeks, Acc. Chem. Res., 2021, 54, 3241–3251 CrossRef PubMed.
- C. J. Judd, A. S. Nizovtsev, R. Plougmann, D. V. Kondratuk, H. L. Anderson, E. Besley and A. Saywell, Rev. Lett., 2020, 125, 206803 CrossRef CAS PubMed.
- Z. Chen, J. Deng, S. Hou, X. Bian, J. L. Swett, Q. Wu, J. Baugh, L. Bogani, G. A. D. Briggs, J. A. Mol, C. J. Lambert, H. L. Anderson and J. O. Thomas, J. Am. Chem. Soc., 2023, 145, 15265–15274 CrossRef CAS PubMed.
- S. Richert, J. Cremers, I. Kuprov, M. D. Peeks, H. L. Anderson and C. R. Timmel, Nat. Commun., 2017, 8, 14842 CrossRef CAS PubMed.
- B. Limburg, J. O. Thomas, G. Holloway, H. Sadeghi, S. Sangtarash, J. Cremers, A. Narita, K. Müllen, C. J. Lambert, G. D. Andrew, B. J. Mol and H. L. Anderson, Adv. Funct. Mater., 2018, 28, 1803629 CrossRef.
- G. Sedghi, L. J. Esdaile, H. L. Anderson, V. M. García-Suárez, C. J. Lambert, S. Martin, D. Bethell, S. J. Higgins and R. J. Nichols, Nat. Nanotechnol., 2011, 6, 517–523 CrossRef CAS PubMed.
- N. Algethami, H. Sadeghi, S. Sangtarash and C. J. Lambert, Nano Lett., 2018, 18, 4482–4486 CrossRef CAS PubMed.
- E. Leary, B. Limburg, S. Sangtarash, A. Alanazy, I. Grace, K. Swada, L. J. Esdaile, M. M. Noori, T. González, G. Rubio-Bollinger, H. Sadeghi, N. Agrait, A. Hodgson, S. J. Higgins, C. J. Lambert, H. L. Anderson and R. Nichols, J. Am. Chem. Soc., 2018, 140, 12877–12883 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2198 CrossRef CAS.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef CAS.
- R. Erich and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- E. Leary, B. Limburg, S. Sangtarash, A. Alanazy, I. Grace, K. Swada, L. J. Esdaile, M. M. Noori, T. González, G. Rubio-Bollinger, H. Sadeghi, N. Agrait, A. Hodgson, S. J. Higgins, C. J. Lambert, H. L. Anderson and R. Nichols, J. Am. Chem. Soc., 2018, 140, 12877–12883 CrossRef CAS PubMed.
- C. J. Lambert and S.-X. Liu, Chem.–Eur. J., 2018, 24, 4193–4201 CrossRef CAS PubMed.
- K. Yoshizawa, Acc. Chem. Res., 2012, 45, 1612–1621 CrossRef CAS PubMed.
- T. Tada and K. Yoshizawa, Phys. Chem. Chem. Phys., 2015, 17, 32099–32110 RSC.
- Y. Tsuji and K. Yoshizawa, J. Phys. Chem. C, 2017, 121, 9621–9626 CrossRef CAS.
- K. Okazawa, Y. Y. Tsuji and K. Yoshizawa, J. Phys. Chem. C, 2020, 124, 3322–3331 CrossRef CAS.
- C. A. Coulson and G. S. Rushbrooke, Math. Proc. Cambridge Philos. Soc., 1940, 36, 193 CrossRef CAS.
- O. A. Al-Owaedi, ChemPhysChem, 2024, 25, e202300616 CrossRef CAS PubMed , 1–12..
- O. Qi, P. Qian and S. Zhigang, Nat. Commun., 2020, 11, 4485 CrossRef PubMed.
- A. V. Deshpande, A. Beidoun, A. Penzkofer and G. Wagenblast, Chem. Phys., 1990, 142, 123–131 CrossRef CAS.
- O. A. Al-Owaedi, S. Bock, D. C. Milan, M. Oerthel, M. S. Inkpen, D. S. Yufit, A. N. Sobolev, N. J. Long, T. Albrecht, S. J. Higgins, M. R. Bryce, R. J. Nichols, C. J. Lambert and P. J. Low, Nanoscale, 2017, 9, 9902–9912 RSC.
- M. Büttiker and R. Landauer, Phys. Rev. Lett., 1982, 49, 1739–1742 CrossRef.
- O. A. Al-Owaedi, ACS Omega, 2024, 9, 10610–10620 CrossRef CAS PubMed.
- R. J. Davidson, D. C. Milan, O. A. Al-Owaedi, A. K. Ismael, R. J. Nichols, S. J. Higgins, C. J. Lambert, D. S. Yufita and A. Beeby, RSC Adv., 2018, 8, 23585–23590 RSC.
- K. Yoshizawa, Acc. Chem. Res., 2012, 45, 1612–1621 CrossRef CAS PubMed.
- S. Gunasekaran, J. E. Greenwald and L. Venkataraman, Nano Lett., 2020, 20, 2843–2848 CrossRef CAS PubMed.
- T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002 CrossRef CAS.
- T. Markussen, R. Stadler and K. S. Thygesen, Nano Lett., 2010, 10, 4260–4265 CrossRef CAS PubMed.
- Y. Tsuji, R. Hoffmann, M. Strange and G. C. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E413–E419 CAS.
- M. Mayor, H. B. Weber, J. Reichert, M. Elbing, C. Hänisch, D. Beckmann and M. Fischer, Angew Chem. Int. Ed. Engl., 2003, 42, 5834–5838 CrossRef CAS PubMed.
- G. C. Solomon, C. Herrmann, T. Hansen, V. Mujica and M. A. Ratner, Nat. Chem., 2010, 2, 223–228 CrossRef CAS PubMed.
- H. Hakkinen, Nat. Chem., 2012, 4, 443–455 CrossRef PubMed.
- C. Herrmann, G. C. Solomon and M. A. Ratner, F, 2010, 114, 20813–20820 CAS.
- R. Davidson, O. A. Al-Owaedi, D. C. Milan, Q. Zeng, J. Tory, F. Hartl, S. J. Higgins, R. J. Nichols, C. J. Lambert and P. J. Low, Inorg. Chem., 2016, 55, 2691–2700 CrossRef CAS PubMed.
- M. Naher, D. C. Milan, O. A. Al-Owaedi, I. J. Planje, S. Bock, J. Hurtado-Gallego, P. Bastante, Z. M. Abd Dawood, L. RinconGarcia, G. Rubio-Bollinger, S. J. Higgins, N. Agrait, C. J. Lambert, R. J. Nichols and P. J. Low, J. Am. Chem. Soc., 2021, 143, 3817–3829 CrossRef CAS PubMed.
- F. Jiang, D. I. Trupp, N. Algethami, H. Zheng, W. He, A. Alqorashi, C. Zhu, C. Tang, R. Li, J. Liu, H. Sadeghi, J. Shi, R. Davidson, M. Korb, A. N. Sobolev, M. Naher, S. Sangtarash, P. J. Low, W. Hong and C. J. Lambert, Angew. Chem., Int. Ed., 2019, 58, 18987–18993 CrossRef CAS PubMed.
- M. H. Garner, H. X. Li, Y. Chen, T. A. Su, Z. Shangguan, D. W. Paley, T. F. Liu, F. Ng, H. X. Li, S. X. Xiao, C. Nuckolls, L. Venkataraman and G. C. Solomon, Nature, 2018, 558, 415–419 CrossRef CAS PubMed.
- B. Huang, X. Liu, Y. Yuan, Z. Hong, J. Zheng, L. Pei, Y. Shao, J. Li, X. Zhou, J. Chen, S. Jin and B. Mao, J. Am. Chem. Soc., 2018, 140, 17685–17690 CrossRef CAS PubMed; P. Moreno-Garcia, M. Gulcur, D. Z. Manrique, T. Pope, W. J. Hong, V. Kaliginedi, C. C. Huang, A. S. Batsanov, M. R. Bryce, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2013, 135, 12228–12240 CrossRef PubMed.
- B. Kim, J. M. Beebe, C. Olivier, S. Rigaut, D. Touchard, J. G. Kushmerick, X. Y. Zhu and C. D. Frisbie, J. Phys. Chem. C, 2007, 111, 7521–7526 CrossRef CAS.
- S. M. S. Al-Mohana, H. N. Najeeb, R. M. Al-Utayjawee, F. Babaeia and O. A. Al-Owaedi, RSC Adv., 2024, 14, 23699–23709 RSC.
- Q. Lu, K. Liu, H. M. Zhang, Z. B. Du, X. H. Wang and F. S. Wang, ACS Nano, 2009, 3, 3861–3868 CrossRef CAS PubMed.
- A. Rochefort and P. Avouris, Nano Lett., 2002, 2, 253–256 CrossRef CAS.
- M. Camarasa-Gómez, D. Hernangómez-Pérez, M. S. G. Inkpen, E. Lovat, E. Fung, X. Roy, L. Venkataraman and F. Evers, Nano Lett., 2020, 20, 6381–6386 CrossRef PubMed.
- L. Zehnder, Z. Instrumentenkd., 1891, 11, 275–285 Search PubMed.
- K. Walczak and L. S. Edward, Cent. Eur. J. Phys., 2005, 3, 555–563 CAS.
- K. Walczak and S. E. Lyshevski, Cent. Eur. J. Phys., 2005, 3, 555–563 CAS.
- M. S. Newman, J. Chem. Educ., 1955, 32, 344 CrossRef CAS.
- M. Burkle, T. J. Hellmuth, F. Pauly and Y. Asai, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165419 CrossRef.
- A. Putatunda and D. J. Singh, Mater. Today Phys., 2019, 8, 49–55 CrossRef.
- H. B. Schlegel, J. S. Binkley and J. A. Pople, J. Chem. Phys., 1984, 80, 1976–1981 CrossRef CAS.
- D. C. Milan, O. A. Al-Owaedi, M. Oerthel, S. Marqués-González, R. J. Brooke, M. R. Bryce, P. Cea, J. Ferrer, S. J. Higgins, C. J. Lambert, P. J. Low, D. Z. Manrique, S. Martin, R. J. Nichols, W. Schwarzache and V. M. García-Suárez, J. Phys. Chem. C, 2016, 120, 15666–15674 CrossRef CAS.
- I. A. Shelykh, N. T. Bagraev and L. E. Klyachkin, Semiconductors, 2003, 37, 1390–1399 CrossRef CAS.
- H. Ozawa, M. Baghernejad, O. A. Al-Owaedi, V. Kaliginedi, T. Nagashima, J. Ferrer, T. Wandlowski, V. M. García-Suárez, P. Broekmann, C. J. Lambert and M. Haga, Chem.–Eur. J., 2016, 22, 12732–12740 CrossRef CAS PubMed.
- S. Bock, O. A. Al-Owaedi, S. G. Eaves, D. C. Milan, M. Lemmer, B. W. Skelton, H. M. Osorio, R. J. Nichols, S. J. Higgins, P. Cea, N. J. Long, T. Albrecht, S. Martin, C. J. Lambert and P. J. Low, Chem.–Eur. J., 2017, 23, 2133–2143 CrossRef CAS PubMed.
- B. A. A. Al-Mammory, O. A. Al-Owaedi and E. M. Al-Robayi, J. Phys.: Conf. Ser., 2021, 1818, 012095 CrossRef CAS.
- O. A. Al-Owaedi, T. T. Khalil, S. A. Karim, M. H. Said, E. Al-Bermany and D. N. Taha, Syst. Rev. Pharm., 2020, 11, 110–115 CAS.
- H. Ozawa, M. Baghernejad, O. A. Al-Owaedi, V. Kaliginedi, T. Nagashima, J. Ferrer, T. Wandlowski, V. M. García-Suárez, P. Broekmann, C. J. Lambert and M. Haga, Chem.–Eur. J., 2016, 22, 12732–12740 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Theories and all details relevant to the computational methods, as well as the theoretical models of all source|molecule|drain configurations. See DOI: https://doi.org/10.1039/d4na00541d |
| ‡ The results of the current investigation were achieved based on theories and relevant computational methods, which are reported in the ESI.† It contains all details of the theoretical models of all source, molecule and drain configurations. In addition, the ESI† includes the results of the negative differential resistance (NDR) phenomenon for CPP molecules. Furthermore, the calculations and results of the Seebeck coefficient for different connections between the molecule and gold electrodes were mentioned, as well as all details and results of the tight-binding Hückel model (TBHM).112–115 |
| This journal is © The Royal Society of Chemistry 2024 |