Enriching 2D transition metal borides via MB XMenes (M = Fe, Co, Ir): Strong correlation and magnetism†
Jiawei
Tang‡
 a,
Shaohan
Li‡
bc,
Duo
Wang‡
d,
Qi
Zheng
bc,
Jing
Zhang
a,
Shaohan
Li‡
bc,
Duo
Wang‡
d,
Qi
Zheng
bc,
Jing
Zhang
 a,
Tao
Lu
a,
Tao
Lu
 bc,
Jin
Yu
bc,
Litao
Sun
bc,
Jin
Yu
bc,
Litao
Sun
 a,
Baisheng
Sa
a,
Baisheng
Sa
 e,
Bobby G.
Sumpter
e,
Bobby G.
Sumpter
 f,
Jingsong
Huang
f,
Jingsong
Huang
 f and
Weiwei
Sun
f and
Weiwei
Sun
 *g
*g
aSEU-FEI Nano-Pico Center, Key Laboratory of MEMS of Ministry of Education, School of Electronic Science and Engineering, Southeast University, Nanjing, 210096, China. E-mail: provels8467@gmail.com
bSchool of Materials Science and Engineering, Southeast University, Nanjing, 211189, China
cJiangsu Province Key Laboratory of Advanced Metallic Materials, Southeast University, Nanjing, 219210, China
dFaculty of Applied Sciences, Macao Polytechnic University, Macao, SAR, China
eMultiscale Computational Materials Facility, and Key Laboratory of Eco-Materials Advanced Technology, College of Materials Science and Engineering, Fuzhou University, Fuzhou 350100, China
fCenter for Nanophase Materials Sciences, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
gKey Laboratory of Quantum Materials and Devices of Ministry of Education, School of Physics, Southeast University, Nanjing, 211189, China
First published on 14th November 2023
Abstract
Recently, two-dimensional (2D) FeSe-like anti-MXenes (or XMenes), composed of late d-block transition metal M and p-block nonmetal X elements, have been both experimentally and theoretically investigated. Here, we select three 2D borides FeB, CoB and IrB for a deeper investigation by including strong correlation effects, as a fertile ground for understanding and applications. Using a combination of Hubbard corrected first-principles calculations and Monte Carlo simulations, FeB and CoB are found to be ferro- and anti-ferro magnetic, contrasting with the non-magnetic nature of IrB. The metallic FeB XMene monolayer, superior to most of the MXenes or MBenes, exhibits robust ferromagnetism, driven by intertwined direct-exchange and super-exchange interactions between adjacent Fe atoms. The predicted Curie temperature (TC) of the FeB monolayer via the Heisenberg model reaches an impressive 425 K, with the easy-axis oriented out-of-plane and high magnetic anisotropic energy (MAE). The asymmetry in the spin-resolved transmission spectrum induces a thermal spin current, providing an opportunity for spin filtration. This novel 2D FeB material is expected to hold great promise as an information storage medium and find applications in emerging spintronic devices.
New conceptsHere, we deliver a series of new 2D magnetic FeSe-like XMene (anti-MXene) borides, which were comprehensively studied by a combination of density functional theory (DFT) and Monte Carlo simulations. Compared with MXenes or MBenes, such mechanical buckled 2D layers hold advanced potential as user-friendly components in diverse electronic devices, enhancing versatility and promoting non-contamination. The novelties and metrics presented in this work can be summarized as follows: (i) the linear response theory was applied to provide a rational Hubbard strength to the d orbital, which is the right way of opening this series of 2D materials and shedding light on their potential applications. FeB, CoB and IrB fall into the ferro-, anti-ferro, and non-magnetic configurations, respectively. (ii) FeB is the most stable material, showing a substantial magnetic anisotropy energy of 416.6 μeV per Fe and remarkably high Curie temperatures of up to 425 K. A combination of the direct- and super-exchange interactions between adjacent Fe atoms plays a vital role in establishing long-range ferromagnetic ordering. (iii) The asymmetry of the transmission spectrum in FeB further confirms the absence of electron–hole symmetry, which could possibly lead to thermal spin-polarized current and potential spin filtration functionality. |
1. Introduction
Two-dimensional (2D) magnetic materials have garnered immense attention due to their potential in facilitating diverse applications ranging from nanoscale storage to transistor devices, owing to their super spin-dependent transport performances and ultra-light and ultra-thin characteristics.1–3 In particular, 2D spintronics offers excessive advantages towards high-speed, low-cost data storage as well as easily accessible logic devices for emerging electronic applications. A breakthrough in this field occurred in 2017 when long-range magnetic order was observed in ferromagnetic (FM) Cr2Ge2Te6 and CrI3 down to the limits of bilayer and monolayer structures, with Curie temperatures (TCs) of 28 and 45 K, respectively.4,5 Soon after, 2D Fe3GeTe2 was reported to be an itinerant ferromagnetic metal with a remarkably high TC value of ∼300 K, which could be strongly modulated by ionic gating.6 However, only a handful of such materials, including Cr2Ge2Te6,4 CrI3,5 VSe2,7 and Fe3GeTe2,8 are experimentally demonstrated to possess intrinsic 2D magnetism. As a result, the availability of mechanically robust 2D layers with long-range magnetic interactions and high transition temperatures remains limited. Under this backdrop, scientists are actively engaged in exploring and developing new materials along this line to unlock their pragmatic applications.Recently, a new family of FeSe-like 2D layers exhibiting excellent electronic and electrochemical properties was theoretically predicted. These 2D layers can be obtained via a top-down approach by removing the element A layer from the bulk structure of AM2X2 (I4/mmm) (A = alkali, alkaline earth, lanthanide, or actinide metals; M = transition metals; and X = nonmetal elements from IIIA–VIA groups).9 This process resulted in buckled 2D MX layers, with each having the inner layer of M sandwiched between two outer layers of tetra-coordinating X atoms.10–12 Since the 2D structures adopt the anti-stacking order of the known MXenes/MBenes, they were coined the name anti-MXene (or XMenes). The first member of the XMene family, 2D FeSe, was initially synthesized using bottom-up approaches such as molecular-beam epitaxy (MBE),10,13 chemical vapor deposition (CVD),14 and pulsed laser deposition (PLD).15 Subsequently, some of these 2D materials were further theoretically considered and even experimentally synthesized using both top-down and bottom-up approaches,16–18 making the further investigation of the 2D FeSe-like materials very intriguing. For instance, the FeB and CoB XMenes can be used as potential electrocatalysts for the hydrogen evolution reaction and anode materials for lithium- or sodium-ion batteries.9,19 In comparison, compositionally similar FeB and CoB MBenes have been reported as 2D magnets.20–22 The pristine FeB MBene exhibits Ising antiferromagnetism with a Néel temperature of 320 K and a robust magnetic anisotropy energy (MAE) up to 482.2 μeV per atom,21 while the functionalized FeBF, FeBO and FeBOH undergo a transition to exhibit FM behavior, with TC values of 250 K, 275 K and 300 K, respectively, and a MAE of ∼500 μeV per atom.22 Notably, the remarkable freedom in both the structure and composition of these metallic 2D layers offers exciting opportunities to achieve outperforming multifunctionalities and gain valuable insights into a unified understanding of these new 2D materials. With the recent advancements of MBenes, exploring the magnetic properties of metal boride XMenes could potentially offer new possibilities for utilizing these layers as active components in electronic devices, thereby exhibiting multifunctionalities.
The d and f electron-containing systems are often considered to fall into the strong correlation regime, where a wealth of entirely new states is often anticipated, pushing the frontiers of science much like the discovery of the fractional quantum effects. Strong correlation, to some extent, underpins many unique phases of quantum matter, including correlated insulators23–26 and magnetism.23,27 However, most of the d electron dominant XMenes have not been well addressed, particularly regarding their strong correlation induced magnetism. The delocalization error of d electrons often results in a qualitatively wrong metallic ground state. As a useful remedy, the DFT+U method28–32 has been widely employed to investigate the magnetic and electronic properties of 2D transition metal compounds and its results have often proven to be in line with experiments.33–36 It is plausible and mandatory to adopt the DFT+U method as a sophisticated treatment of the correlation strength of the d electron in the newly established XMenes. This approach would enable us to capture their ground states and unravel more and more peculiar performances.
Herein, we aimed to systematically investigate three stable transition metal borides, FeB, CoB, and IrB in the XMene phase. To rationally describe the strong correlation effects, the linear response approach will be utilized to estimate the Hubbard U parameters for partially filled d electron shells of transition metals. Several possible magnetic configurations were considered in order to capture the ground magnetic state. The 2D FeB monolayer is identified as a robust ferromagnetic (FM) metal, while the ground state for CoB and IrB corresponds to the weak anti-ferromagnetic (AF) and non-magnetic (NM) configurations, respectively. The ferromagnetic spin ordering in FeB is robustly maintained and capable of reaching a TC as high as 425 K, which is superior to the corresponding MBenes. As the first attempt to extend magnetic exploration from MXenes into XMene systems, our findings not only enrich the possible diversity of 2D transition metal borides but also pave the way for the application of novel multifunctional 2D XMene layers in realistic spin-electronic device applications.
2. Computational methods
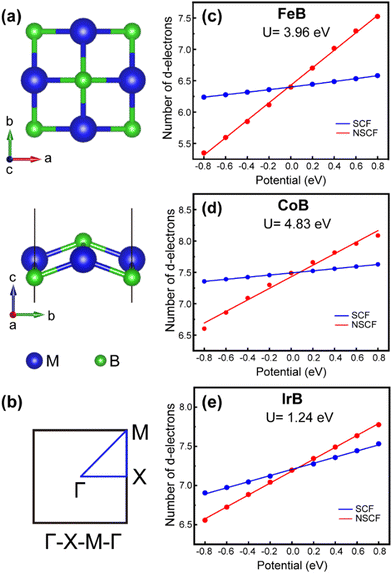
Density functional theory (DFT) calculations were performed using the Vienna Ab initio Simulation Package (VASP).37 To describe the ion–electron interactions, the Blöchl projector augmented wave method (PAW) was employed within the frozen-core approximation38 and the calculations utilized plane-wave basis sets. The generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE)39 was selected as the exchange–correlation functional. For the 2D layers examined in this work, the lattice vector along the z direction was fixed to 20 Å to avoid spurious interactions between periodic images. After a careful convergence test on the supercell, a high energy cutoff of 700 eV and a 12 × 12 × 1 Γ-centered Monkhorst–Pack k-mesh were found to be sufficient for converging the total energy within 1 meV per average atom. For all relaxations, the self-consistence convergence criterion for electron iterations was set to be 10−6 eV, and the ground-state structures were optimized by minimizing the Hellman–Feymann force until the norm of all the forces was less than 0.01 eV Å−1. A 3 × 3 × 1 supercell with a 4 × 4 × 1 k-mesh was adopted, which allowed us to explore different magnetic configurations, in the process of searching for the ground state. Spin–orbit coupling (SOC) was only considered in the MAE calculations. Crystal orbital Hamilton population (COHP) analysis was performed to investigate the bonding and antibonding states utilizing the local orbital basis suite for electronic-structure reconstruction (LOBSTER).40Dudarev's approach41 was employed to evaluate the strong correlation effect on the d orbital, with the correlation strength represented by the effective Hubbard Ueff = U − J on the d orbitals, where U and J are the on-site Coulomb and exchange parameters, respectively. The Ueff for each metal element was estimated using the linear-response approach formulated by Cococcioni et al.42 To achieve this, a linear fit of the number of d-electrons against the additional potential was performed to compute χ0 and χ, referring to the non-self-consistent interacting and self-consistent interacting density of the response functions of the correlated orbital with respect to additional localized perturbations. The parameter Ueff was then calculated according to the equation: Ueff = χ−1 − χ0−1. For a systematic comparison with DFT+U, we also performed calculations utilizing the Heyd–Scuseria–Ernzerhof hybrid functional (HSE06), which incorporates 75% of the PBE exchange, 25% of the Fock exchange, and 100% of the correlation energy from PBE.43 The validity of our main findings was reinforced through computations employing the HSE06 method. Therefore, in the subsequent discussion, our focus will be directed towards the PBE + U results.
The structure stabilities of the favorable magnetic state were investigated with the Hubbard correction applied. The phonon spectra calculations were carried out with the PHONOPY code44 in the framework of the density functional perturbation theory (DFPT)45 to assess the dynamical stability. For evaluating the thermal stability, the ab initio molecular dynamics (AIMD) simulations were additionally performed using a 3 × 3 × 1 supercell at 300 and 400 K for 5 ps with a time step of 1 fs. The algorithm of Nosé46 was employed to control the temperature during these simulations.
Monte Carlo (MC) simulations were conducted based on the Metropolis algorithm47 within the EspinS package,48 to identify the spin–spin correlation and to estimate the critical temperature. MC simulations were carried out on a supercell size of 50 × 50 × 1 with the periodic boundary conditions along the in-plane direction. The MC simulations with a total sampling of 2 × 106 steps began with a random initial spin configuration, and in each spin, 1 × 106 MC steps were performed. The specific heat CV was estimated under the equilibrium state of the system for a given temperature. The final electronic transport calculations were conducted using real space NEGF techniques implemented in the Atomistix Toolkit (ATK) code.49 Under a temperature gradient, the spin-dependent current is given by:50
 | (1) |
3. Results and discussion
3.1 Geometric structures and magnetic ground states
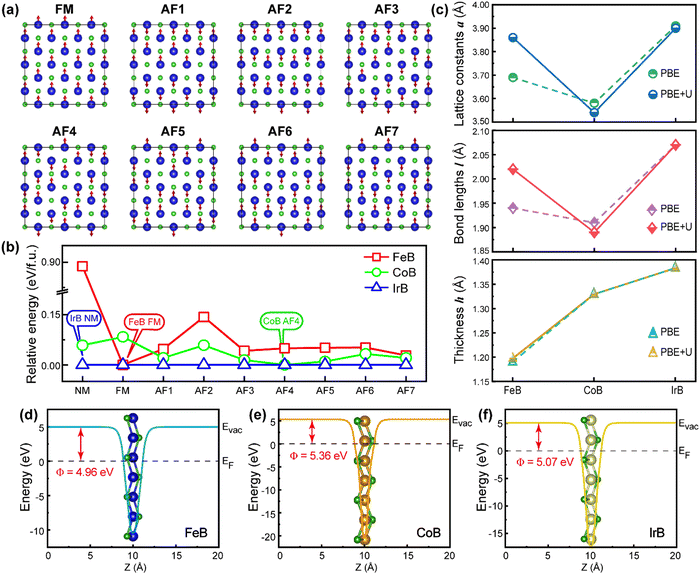
We begin with a structural characterization of 2D XMene (M = Fe, Co and Ir; X = B) monolayers, as illustrated in Fig. 1(a). The unit cell contains two M and two B atoms, all tetra-coordinated with their neighboring atoms. Interestingly, the MB monolayers exhibit a buckled configuration, with B atoms occupying the upmost surfaces giving a stacking sequence entirely opposite to MBenes,51–53 and hence being referred to as anti-MXenes or XMenes. The tetragonal 2D Brillouin zone in the reciprocal space is present in Fig. 1(b) with the high symmetry k-path along Γ (0, 0, 0) → X (0.5, 0, 0) → M (0.5, 0.5, 0) → Γ (0, 0, 0) for the expansion of the band structure and phonon dispersion curves in the following discussions. As depicted in Fig. 1(c)–(e), the Ueff values for FeB, CoB and IrB are found to be 3.96, 4.83, and 1.24 eV, respectively.Due to the carried d electrons, we considered the non-magnetic (NM), ferromagnetic (FM), and seven collinear anti-ferromagnetic (AF) configurations within a 3 × 3 × 1 supercell, as shown in Fig. 2(a). The relative energies of the non-magnetic and the other eight magnetic states in PBE+U are plotted in Fig. 2(b), indicating that IrB maintains the NM ground state, but FeB and CoB fall into the FM and AF4 magnetic configurations, respectively. For the FM FeB monolayer, the spin moment per Fe atom reaches about 2.42 μB, which is close to the value of the Fe atom in the bcc Fe (2.22–2.48 μB),54–56 but slightly lower than that of orthorhombic Pmma-FeB MBene (2.67–2.75 μB).21,22 For the AF CoB XMene, the spin moment per Co atom is 0.93 μB, approximately twice as high as that of CoB MBene (0.48 μB),22 but lower than the FM-state CoB6 monolayer with magnetic moments of 1.38 μB,57 and hcp Co (1.58–1.72 μB).56,58 It can be seen that compared to identically composed FeB/CoB MBenes, the spin moments are influenced by the geometry and the number of ligands, resulting in inherent orbital degeneracy or spin/electron occupation.
In Fig. 2(c), it is evident that IrB exhibits the largest equilibrium lattice constant, M–B bond length, and layer thickness, whereas CoB demonstrates the smallest equilibrium lattice constant and M–B bond length, and FeB possesses the smallest layer thickness among the three depicted 2D layers. Notably, the M–B bond lengths l of FeB, CoB and IrB XMenes are 2.02 Å, 1.89 Å and 2.07 Å, respectively, all shorter than those of the corresponding MBenes (FeB MBene: l1 = 2.15 Å, l2 = 2.05 Å; CoB MBene: l1 = 2.10 Å, l2 = 2.03 Å; and IrB MBene: l1 = 2.49 Å, l2 = 2.18 Å21). Furthermore, FeB XMene is more sensitive to strong correlation effects, displaying significant changes in the lattice parameter and M–B bond length, but limited changes in the layer thickness since the effects of a and l increase for FM-FeB cancel out each other. On the other hand, both CoB and IrB, whose metal components belong to group 9 of the periodic table, exhibit minimal changes. More importantly, each transition metal atom in MB XMenes is coordinated by only four B atoms, resulting in a different coordination geometry compared to MBenes (six B ligands). This reduced coordination number significantly impacts the crystal field splitting energy, leading to the splitting of the d orbitals into distinct energy levels (vide infra). Consequently, the electronic structure and magnetic properties of MB XMenes are altered compared to MBenes.
The work function is often considered as a pivotal parameter, providing essential insights on the novel field emitter cathodes and the Schottky barrier junctions and related applications, such as light-emitting diodes and field-effect transistors.59,60 Hence, we calculated the work functions of three distinct XMenes and the results are shown in Fig. 2(d)–(f). In the corresponding favorable magnetic ordering, the work functions Φ of FeB, CoB, and IrB are 4.96, 5.36 and 5.07 eV, which are slightly higher than those of bare MBenes (4.1–4.8 eV).61 Note that a pioneering investigation showcased the potential of utilizing Ti3C2Tx MXene, possessing a work function of 4.9 eV, as contact electrodes in organic thin-film transistors and complementary logic circuits, signifying a highly promising avenue.62 Another application of 2D conducting layers with a Φ ∼5.1 eV, is integrating into organic light-emitting diodes (OLEDs), which could approach the performance of modern state-of-the-art commercial OLEDs.63 All results pertaining to work functions not only confirm XMene's potential as a novel electrode candidate material but also suggest its viability for electronic applications.
3.2 The stabilities and electric properties
Since only FeB exhibits relatively large magnetic moments (>2 μB), we put our main focus on it. One of the intuitive but essential questions that arise is whether the magnetism induced by correlation effects could destabilize the structure or not. The calculated phonon spectra of FeB expanded along the path of Γ–X–M–Γ can be found in Fig. 3(a). As discussed above, the introduction of Hubbard U leads to a remarkable increase in both lattice and bond length, which could alter lattice vibrations. Nevertheless, it is noteworthy that no imaginary modes exist in the FeB monolayer, indicating that the FM ground configuration is dynamically stable. From the phonon partial density of states, one can observe that the B atoms mainly vibrate in the high-frequency region (>400 cm−1), while the vibrational states of Fe atoms correspond to the low-frequency region (<400 cm−1). Such a phenomenon agrees well with the general rule of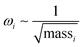 . Similarly, the NM-IrB monolayer also shows excellent stability (Fig. 3(b)), but due to the absence of magnetism, no further discussions will be pursued on this material. On the other hand, the AF-CoB does have some imaginary frequencies (∼−8.88 cm−1) at Γ (0, 0, 0), as shown in Fig. 3(c). Even though the dynamical stability recalculation has already been performed in a supercell as large as 6 × 6 × 1, the imaginary frequencies cannot be swiped out. We thus ruled out CoB for further discussions, as we probably go beyond the numerical truncation of the dynamical stability of magnetic 2D materials. We therefore only take FeB to deeper and wider analysis and discussion.
. Similarly, the NM-IrB monolayer also shows excellent stability (Fig. 3(b)), but due to the absence of magnetism, no further discussions will be pursued on this material. On the other hand, the AF-CoB does have some imaginary frequencies (∼−8.88 cm−1) at Γ (0, 0, 0), as shown in Fig. 3(c). Even though the dynamical stability recalculation has already been performed in a supercell as large as 6 × 6 × 1, the imaginary frequencies cannot be swiped out. We thus ruled out CoB for further discussions, as we probably go beyond the numerical truncation of the dynamical stability of magnetic 2D materials. We therefore only take FeB to deeper and wider analysis and discussion.
In addition to the dynamical stability, the thermal stability at room temperature is a critical factor in determining the practical viability of the material. One can see from the AIMD simulations at 300 K shown in Fig. 3(d) that the quenched structure of FeB after the AIMD simulations is robust and well-maintained without bond breaking or any evident phase transitions compared to the original structure. These clues clearly demonstrate that the FM-FeB monolayer is dynamically and thermally stable at room temperature, and therefore the following discussions are primarily based on the PBE+U results. All things considered, the 2D FM FeB and NM IrB monolayers show great promise for practical synthesis and offer ample opportunities for further exploration.
Next, we address the electronic structure of the FM FeB. Fig. 4(a) and (b) illustrates the spin-polarized band structure, total density of states (TDOS), and projected density of states (PDOS). The band structure displayed in Fig. 4(a) confirms the robust metallic character and spin splitting, with each spin channel crosses over the Fermi level. The magnetic ground states, magnetic moment, and metallic band structure have also been verified using the high-accuracy hybrid HSE06 functional, as depicted in Fig. S1 (ESI†), illustrating that our presented results are reliable. The total density of states (TDOS) in Fig. 4(b) reveals considerable asymmetric spin states, clearly validating the presence of a net magnetic moment. The Fe 3d states in the minority channel as well as the B 2p states in the majority channel are situated at the Fermi level. Moreover, the strong hybridization between the Fe-3d and the B-2p states in the minority channel appears around −3.5 to −1.0 eV, as indicated by the PDOS. This phenomenon is responsible for the asymmetric square planar crystal field, which will be discussed in the next section. Further analysis of the d orbital-projected density of states, as shown in Fig. 4(c), provides additional insights into the electronic structure of the FeB monolayer. Specifically, the spin up channel is primarily governed by the Fe-dx2−y2 states, with minimal involvement from other Fe d states. When it comes to the spin down channel, the Fe dxy, dyz and dx2−y2 states emerge as pivotal contributors. Note that the occupied state profiles of dyz and dxz orbitals bear striking coincidences, a phenomenon possibly attributed to orbital degeneracy. In addition, in the vicinity of the Fermi level, it is observed that the Fe-dxy and Fe-dyz orbitals exhibit hybridization in the spin-down channel. On the other hand, the dxy, dyz, dxz and dz2 orbitals show hybrid states in the spin-up channel within the energy range of approximately −3.8 to −4.6 eV. This anisotropic behavior of the d orbitals indicates a directional dependence of the bonding interactions within the FeB monolayer. Such anisotropy is expected to have significant implications for the material's magnetic and electronic properties, as well as its potential applications in spintronics and other fields. Finally, the Fermi surface of FeB is also observed as depicted in Fig. 4(d). For the spin-up Fermi surfaces, one of the two bands contributes to a pocket in the corner, pointing to a cross-shaped sheet, while the other band forms a planus “M”-shaped sheet centered at the X point. The spin-down Fermi surface is also composed of two bands passing through the Fermi energy, both forming distorted squares. This intricate Fermi surface topology underscores the intricate interplay of electronic states and band structures within these materials.
The electronic band structures, TDOS and PDOS of AF-CoB and NM-IrB XMenes are also depicted in Fig. S2 (ESI†). The Fig. S2(a) and (b), ESI† panel for the CoB monolayer displays a small indirect band gap of 0.04 eV, while the IrB monolayer in Fig. S2(c) and (d), ESI† lacks a band gap between the valence and conduction bands, featuring several partially occupied bands crossing the Fermi level in both spin channels. As shown in Fig. S2(b)–(d), ESI,† the computed TDOS for the spin-up and spin-down states in the 2D CoB and IrB monolayers are identical across the entire energy spectrum, which is understandable as the typical hallmark of an AF and NM configuration. In detail, the PDOS for 2D CoB and IrB reveal that the distributions around the Fermi level are primarily attributed to the 3d orbitals of the transition metal atoms, with the contribution from the B atoms being nearly negligible. However, considering the absence of noticeable magnetism in CoB and IrB monolayers, we refrain from redundant reporting on them hereafter.
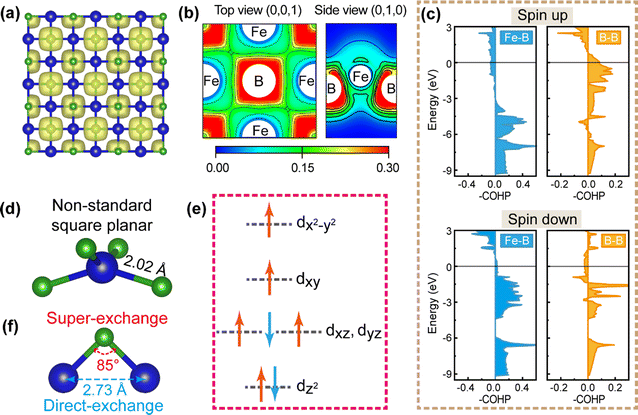
In Fig. 5(a), one can examine the electron localization functions (ELFs) to understand the bonding characteristics. The value of ELF is 0.0 for the region around Fe atoms, indicating their electron deficiency. Meanwhile, the B frameworks are fully encapsulated by homogeneous electron gas, which plays a pivotal role in constructing the B–B bonds. Notably, no local electron is seen between Fe atoms and B atoms, displaying the ionic bonding character. However, the bonding between Fe and B cannot be classified as purely ionic, as evidenced by the previous DOS analysis, which indicates an orbital coupling between Fe d and B p orbitals. To elucidate the distinct intra- and inter-layer bonding properties, we can project the ELF onto the (001) and (010) planes. The mappings on the (001) and (010) planes are shown in Fig. 5(b), illustrating that the in-plane interatomic ELF typically reaches about 0.15 and indicating a moderate degree of electron delocalization. The red/blue region on the color map signifies a high/low degree of electron localization, as indicated by the color bar. Conversely, the ELF along the out-of-plane is concentrated around the B atoms. In other words, covalent bonding is in the form of an intra-layer, in contrast to inter-layered ionic bonding. This interpretation is further substantiated by our COHP analysis (in Fig. 5(c)), revealing that the Fe–B and B–B bonds exhibit robust bonding states in both the spin-up and spin-down channels. Integrating the COHP curves up to the Fermi level yields the integral COHP (ICOHP) values, which qualitatively correlate with the strength of the corresponding bonds. The ICOHP strength of the Fe–B bonds for the spin-up and spin-down states are −0.98 and −1.36 eV per bond, respectively, higher than those of the B–B bonds (−0.47 eV per bond for the spin-up channel and −0.33 eV per bond for the spin-down channel), indicating that the stability of the entire FeB monolayer primarily arises from ionic bonds, with covalent bonds serving as a supplement. Furthermore, the electron cloud on the surface of the monolayer is notably extensive, which is indicative of its chemically active nature. In conclusion, through the analysis of ELF and COHP, we have revealed the bonding characteristics of the FeB monolayer, which consists of both ionic and covalent bonds that would help us gain a deep understanding of their chemical properties.
3.3 The magnetic properties
As can be seen from the electronic structure shown above, combined with the spin-density distributions presented in Fig. S3 (ESI†), the 3d electrons in Fe atoms are the origin of the magnetism. The magnetic properties of transition-metal compounds are closely related to the changes of valence states in transition metals, thus we first conducted Bader charge analysis64 for the FM FeB monolayer. The analysis demonstrates that each Fe atom transfers approximately 0.45 e− to each B atom within the FeB monolayer. In other 2D Fe–B materials, such as FeB3, the charge transfer is from Fe3+ to B1−, accounting for 0.87 e−.65 The valence states of Fe and P are regarded as +1 and −3, respectively, when the charge transfer from Fe1+ to P3− is 0.28 e− in 2D Fe3P.66 It was also claimed that Fe1+ cation in the recently predicted MBene-FeB donate 0.4 e− to B1−.21 Considering the electronegativity of P (2.1) atoms being close to that of B (2.0) atoms and the aforementioned results, we infer that the valence state of Fe in the FeB monolayer should be +1 by comparing the results of charge transfer. When the Fe atoms of FeB transfer one electron to neighboring B atoms, the seven remaining valence electrons of Fe atoms would fill into d-orbitals and hence the valence electronic configuration of Fe1+ cations are [Ar] [3d7]. It is shown that the FeB monolayer falls into the D4h point group, where the five d-orbitals can split into a1g (dz2), b1g (dx2−y2), b2g (dxy) and degenerated eg (dxz and dyz) orbitals. Furthermore, considering the B atoms mediated distorted-square-planar crystal field shown in Fig. 5(d) and the local 3d Hamiltonian in the Wannier basis, the energies of the orbitals in the ascend sequence fall into dz2, (dxz, dyz), dxy, dx2−y2, consistent with the high-spin state of Fe2+ ([Ar] [3d6]) state in an FeO4 square plane.67 Following Hund's rules and the Pauli exclusion principle, the Fe1+ ions should adopt the high-spin state. As shown in Fig. 5(e), the three unpaired d electrons correspond to a theoretical spin magnetic moment of 3 μB, extremely close to the ab initio calculated ∼2.42 μB. In summary, such an Fe–B polyhedral configuration forms weak crystal field splitting, resulting in a high-spin state of Fe1+ with a spin magnetic moment larger than 2 μB.Holding the crystal field splitting status and orbital alignment, we further move forward to the exchange mechanism behind the magnetic properties. It is found that the Fe–Fe bond length in FeB is 2.73 Å (shown in Fig. 5(f)), close to the length of Fe–Fe binding in FM α-Fe,54,55 so the direct magnetic exchange interaction by FM coupling might retain. In addition, the super-exchange interaction mediated via the B atom is likely to coexist. According to the Heitler–London model,68,69 the exchange integral J can be written as J ≃ 2k + 4βS, where the k denotes the exchange integral of electrons, β and S stand for the resonance coupling and the overlap integral of the interacting orbitals, respectively. If k has a dominant positive sign, it would result in an FM interaction, and vice versa. Based on the Goodenough–Kanamori rule,70–72 the bond angle of Fe–B–Fe is approximately 85°, close to 90° shown in Fig. 5(f), suggesting the overlap integral S is zero. Consequently, the 2k term acquires a large positive J, leaning towards the FM ground state, as we show above.
Having clarified the relationship between structural and magnetic configurations, we proceed to investigate the long-range behavior of the exchange interaction in the FeB XMene. To estimate the strength of magnetic coupling, we employ the Heisenberg model considering five neighbor interactions:
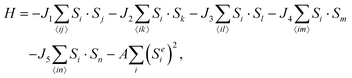 | (2) |
Next, through mapping the total energies of the FM and the five AF configurations (AF1, AF3, AF4, AF5 and AF7 in Fig. 2(a)) selected according to energy-increase order into the Hamiltonian, the corresponding energies can be further derived as follows:
| EFM = E0 − 36J1|S|2 − 36J2|S|2 − 36J3|S|2 − 72J4|S|2 − 36J5|S|2 −A|S|2, | (3) |
| EAFM1 = E0 − 12J1|S|2 − 18J2|S|2 + 12J3|S|2 + 24J4|S|2 + 36J5|S|2 − A|S|2, | (4) |
| EAFM3 = E0 − 4J1|S|2 − 4J2|S|2 + 4J3|S|2 + 24J4|S|2 + 8J5|S|2 − A|S|2, | (5) |
| EAFM4 = E0 + 4J1|S|2 + 12J2|S|2 − 4J3|S|2 − 8J4|S|2 − 4J5|S|2 − A|S|2, | (6) |
| EAFM5 = E0 + 4J1|S|2 + 12J2|S|2 − 4J3|S|2 − 24J4|S|2 + 36J5|S|2 − A|S|2, | (7) |
| EAFM7 = E0 − 12J1|S|2 − 4J2|S|2 + 12J3|S|2 + 16J4|S|2 + 20J5|S|2 − A|S|2, | (8) |
It was found that 2D FM metals should always offer superior advantages over 2D magnetic semiconductors in the view of applications, since a higher TC can be always expected driven by the surplus charge carriers in the FM metal.77 Monte Carlo (MC) simulations based on the Heisenberg models were performed to reach a rational value of TC. The temperature-dependent specific heat capacity CV for the FeB monolayers is plotted in Fig. 6(c). Based on the peak position of the specific heat curve, the Curie temperature of FeB monolayers is found to be 425 K. Using the same approach, our calculated TC for the monolayer CrI3, around 57 K (in Fig. S4, ESI†) falls within the theoretical range of 36–69 K78–80 and is very close to the experimental measurement of 45 K,5 suggesting the reliability of our calculations. Furthermore, magnetic moments of Fe atoms saturate at low temperatures and decrease continuously with increasing thermal fluctuations. Importantly, even when the temperature reaches 350 K, FeB retains a large magnetic moment of about 2 μB per Fe, and combined with the excellent thermal stability shown in Fig. 3(d) and Fig. S5 (ESI†), the FM FeB affords a huge advantage than many other 2D magnets.
Additionally, the spin–spin correlation was calculated by performing MC simulation at T = 5 K to achieve a deep understanding of the magnetic ordering. Fig. 6(d) shows the average value of the products of neighboring spins Sum(Si·Sj)/N and their absolute values Sum(|Si·Sj|)/N for the spin Hamiltonian given by the coupling constants. Here, N denotes the size of the lattice used in MC simulations. Interestingly, the Sum(Si·Sj)/N is 0 for the 1st and 4th nearest-neighbor spins, corresponding to the offset of FM and AF couplings. If Sum(Si·Sj)/N grounds to −1, like in the 2nd spins, an AF coupling is obtained, and vice versa for +1. Besides, for the 1st, 2nd, 3rd, and 4th spins, the values of the Sum(|Si·Sj|)/N are +1, which means that the spin direction is parallel or antiparallel to its neighbor. The net value of 1 reconfirms that the collinear FM of 2D FeB is stable at low temperatures, further suggesting that the 2D FeB monolayers are robust ferromagnets with relatively high Curie temperatures.
Finally, the calculated transmission spectrum of the device at zero bias without a gate voltage is shown in Fig. 6(e). The conductance is mainly contributed by the spin up channel, which is significantly higher compared to that of the spin down channel, thus leading to a high spin injection efficiency. The asymmetry of the transmission spectrum further confirms the absence of electron–hole symmetry. These characteristics can lead to the generation of thermal spin-polarized currents and potentially having the spin filtration functionality.81–83 We further conducted a detailed analysis of thermal spin-dependent currents concerning the left electrode temperature (TL) under various temperature gradient (ΔT) conditions between the left (TL) and right electrode (TR) junctions in the initial parallel configuration (PC), where ΔT = TR − TL. As illustrated in Fig. 6(f), a linear increase in both spin-up and spin-down current components for TL up to approximately 100 K can be observed. For TL between 100 K and 300 K, the spin-up current exhibits a quasi-linear trend, while the quasi-linear region for the spin-down current surpasses that of the up components of the current. This behavior is attributed to the greater mobility of carriers in the spin-up channel than its counterpart. The plot depicting temperature gradient-based spin-resolved current concerning ΔT (Fig. 6(g)) demonstrates a linear pattern for both spin-up and spin-down current components at varying cold electrode temperatures (TL). The spin-up dominant states in the electron conduction results in a notably higher spin-up electron current compared to the spin-down counterpart, underscoring a precise temperature-dependent spin filtration effect. Additionally, spin filtration efficiency (η) is evaluated by using the formula mentioned below:84
 | (9) |
4. Conclusions
In this report, we have utilized a multiscale modeling approach combining density functional theory and Monte Carlo simulations to investigate the electronic and magnetic properties of three novel 2D XMenes MB (M = Fe, Co, and Ir) monolayers. Through rational estimations of Hubbard U values, we have observed that both the FM FeB and the NM IrB exhibit dynamic stability at room temperature, while the AF CoB monolayer shows relatively less stability. Our findings highlight that FeB monolayers hold great promise as FM metals, characterized by a substantial MAE of 416.6 μeV per Fe and impressively high Curie temperatures of up to 425 K. The robust FM ground state above room temperatures can be attributed to the sizable MAE, strong Fe–B ionic bonds, and B–B bonding, resulting in a high-spin state with large magnetic moments. Furthermore, the direct-exchange and super-exchange interactions between adjacent Fe atoms play a vital role in establishing long-range ferromagnetic ordering, making these monolayers potentially suitable for room temperature spintronic device components. Additionally, the single-layered FeB XMene is a promising quantum 2D material in the field of spin caloritronics, as the spin transmission manifested. These feasible mechanically buckled 2D layers could be used as user-friendly components in many electronic devices, which facilitate uncontaminated and well-defined surfaces, advancing MXenes and MBenes. The new knowledge gained from this study opens up new avenues for exploring XMene monolayers and calls for further theoretical and experimental investigations into their electronic device applications.Author contributions
J. Tang: conceptualization, investigation, validation, data curation, and writing – original draft. S. Li: methodology, investigation, validation, and data curation. D. Wang: formal analysis, investigation, and writing – review & editing. J. Zhang: supervision, resources, and funding acquisition. Q. Zheng and B. Sa: software, investigation. T. Lu and J. Yu: supervision, validation, and resources. L. Sun: supervision, resources, and data curation. B. G. Sumpterf and J. Huang: resources, investigation, and writing – review & editing. W. Sun: conceptualization, project administration, resources, writing – review & editing, and funding acquisition.Conflicts of interest
The authors declare that they have no conflicts of interest.Acknowledgements
W. S. acknowledges the National Key Laboratory of Shock Wave and Detonation Physics (under Grant No. JCKYS2023212004) and Sinopec Key Research & Development Project (under Grant No. 223025). We also thank the Big Data Computing Center of Southeast University and a user project at the Center for Nanophase Materials Sciences (CNMS), which is a US Department of Energy, Office of Science User Facility at Oak Ridge National Laboratory for providing the facility support on the numerical calculations in this paper.References
- Y. W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349 CrossRef CAS PubMed.
- Y. Wang, Y. Huang, Y. Song, X. Zhang, Y. Ma, J. Liang and Y. Chen, Nano Lett., 2009, 9, 220–224 CrossRef CAS PubMed.
- Q. Hao, H. Dai, M. Cai, X. Chen, Y. Xing, H. Chen, T. Zhai, X. Wang and J.-B. Han, Adv. Electron. Mater., 2022, 8, 2200164 CrossRef CAS.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269 CrossRef CAS PubMed.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen and Y. Zhang, Nature, 2018, 563, 94–99 CrossRef CAS PubMed.
- M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M. H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289–293 CrossRef CAS PubMed.
- Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, W. Wu, D. H. Cobden, J. H. Chu and X. Xu, Nat. Mater., 2018, 17, 778–782 CrossRef CAS PubMed.
- J. Gu, Z. Zhao, J. Huang, B. G. Sumpter and Z. Chen, ACS Nano, 2021, 15, 6233–6242 CrossRef CAS PubMed.
- J. F. Ge, Z. L. Liu, C. Liu, C. L. Gao, D. Qian, Q. K. Xue, Y. Liu and J. F. Jia, Nat. Mater., 2015, 14, 285–289 CrossRef CAS PubMed.
- Y. Zhou, L. Miao, P. Wang, F. F. Zhu, W. X. Jiang, S. W. Jiang, Y. Zhang, B. Lei, X. H. Chen, H. F. Ding, H. Zheng, W. T. Zhang, J. F. Jia, D. Qian and D. Wu, Phys. Rev. Lett., 2018, 120, 097001 CrossRef CAS PubMed.
- C. W. Luo, I. H. Wu, P. C. Cheng, J. Y. Lin, K. H. Wu, T. M. Uen, J. Y. Juang, T. Kobayashi, D. A. Chareev, O. S. Volkova and A. N. Vasiliev, Phys. Rev. Lett., 2012, 108, 257006 CrossRef CAS PubMed.
- W. Li, H. Ding, Z. Li, P. Deng, K. Chang, K. He, S. Ji, L. Wang, X. Ma, J. P. Hu, X. Chen and Q. K. Xue, Phys. Rev. Lett., 2012, 109, 057003 CrossRef PubMed.
- J. Zhou, J. Lin, X. Huang, Y. Zhou, Y. Chen, J. Xia, H. Wang, Y. Xie, H. Yu, J. Lei, D. Wu, F. Liu, Q. Fu, Q. Zeng, C. H. Hsu, C. Yang, L. Lu, T. Yu, Z. Shen, H. Lin, B. I. Yakobson, Q. Liu, K. Suenaga, G. Liu and Z. Liu, Nature, 2018, 556, 355–359 CrossRef CAS.
- Z. Feng, J. Yuan, G. He, W. Hu, Z. Lin, D. Li, X. Jiang, Y. Huang, S. Ni, J. Li, B. Zhu, X. Dong, F. Zhou, H. Wang, Z. Zhao and K. Jin, Sci. Rep., 2018, 8, 4039 CrossRef PubMed.
- J. Zhou, L. Shen, M. D. Costa, K. A. Persson, S. P. Ong, P. Huck, Y. Lu, X. Ma, Y. Chen, H. Tang and Y. P. Feng, Sci. Data, 2019, 6, 86 CrossRef PubMed.
- X. Zhou, B. Wilfong, H. Vivanco, J. Paglione, C. M. Brown and E. E. Rodriguez, J. Am. Chem. Soc., 2016, 138, 16432–16442 CrossRef CAS PubMed.
- C. Ding, Y. Li, S. Ji, K. He, L. Wang and Q.-K. Xue, Nano Res., 2023, 16, 3040–3045 CrossRef CAS.
- S. Banerjee, K. Ghosh, S. K. Reddy and S. S. R. K. C. Yamijala, J. Phys. Chem. C, 2022, 126, 10298–10308 CrossRef CAS.
- Z. Jiang, P. Wang, X. Jiang and J. Zhao, Nanoscale Horiz., 2018, 3, 335–341 RSC.
- S. Wang, N. Miao, K. Su, V. A. Blatov and J. Wang, Nanoscale, 2021, 13, 8254–8263 RSC.
- M. Dou, H. Li, Q. Yao, J. Wang, Y. Liu and F. Wu, Phys. Chem. Chem. Phys., 2021, 23, 10615–10620 RSC.
- M. Imada, A. Fujimori and Y. Tokura, Rev. Mod. Phys., 1998, 70, 1039–1263 CrossRef CAS.
- R. Bistritzer and A. H. MacDonald, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 12233–12237 CrossRef CAS PubMed.
- Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori and P. Jarillo-Herrero, Nature, 2018, 556, 80–84 CrossRef CAS.
- Y. Xu, S. Liu, D. A. Rhodes, K. Watanabe, T. Taniguchi, J. Hone, V. Elser, K. F. Mak and J. Shan, Nature, 2020, 587, 214–218 CrossRef CAS PubMed.
- Y. Tang, L. Li, T. Li, Y. Xu, S. Liu, K. Barmak, K. Watanabe, T. Taniguchi, A. H. MacDonald, J. Shan and K. F. Mak, Nature, 2020, 579, 353–358 CrossRef CAS PubMed.
- S. Sarikurt, Y. Kadioglu, F. Ersan, E. Vatansever, O. U. Akturk, Y. Yuksel, U. Akinci and E. Akturk, Phys. Chem. Chem. Phys., 2018, 20, 997–1004 RSC.
- B. Zhang, G. Song, J. Sun, J. Leng, C. Zhang and J. Wang, Nanoscale, 2020, 12, 12490–12496 RSC.
- S. Wang, M. Khazaei, J. Wang and H. Hosono, J. Mater. Chem. C, 2021, 9, 9212–9221 RSC.
- X. Cheng, S. Xu, F. Jia, G. Zhao, M. Hu, W. Wu and W. Ren, Phys. Rev. B, 2021, 104, 104417 CrossRef CAS.
- C. Tang, K. Ostrikov, S. Sanvito and A. Du, Nanoscale Horiz., 2021, 6, 43–48 RSC.
- L. Zhou, F. Koermann, D. Holec, M. Bartosik, B. Grabowski, J. Neugebauer and P. H. Mayrhofer, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 184102 CrossRef.
- N. Sivadas, M. W. Daniels, R. H. Swendsen, S. Okamoto and D. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235425 CrossRef.
- M. Liu, J. Leveillee, S. Lu, J. Yu, H. Kim, C. Tian, Y. Shi, K. Lai, C. Zhang, F. Giustino and C.-K. Shih, Sci. Adv., 2021, 7, eabi6339 CrossRef CAS PubMed.
- C. Xu, J. Feng, H. Xiang and L. Bellaiche, npj Comput. Mater., 2018, 4, 57 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- N. Rezaei, M. Alaei and H. Akbarzadeh, Comput. Mater. Sci., 2022, 202, 110947 CrossRef CAS.
- M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- M. Büttiker, Y. Imry, R. Landauer and S. Pinhas, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6207–6215 CrossRef.
- L. T. Alameda, P. Moradifar, Z. P. Metzger, N. Alem and R. E. Schaak, J. Am. Chem. Soc., 2018, 140, 8833–8840 CrossRef CAS PubMed.
- H. Zhang, H. Xiang, F.-Z. Dai, Z. Zhang and Y. Zhou, J. Mater. Sci. Technol., 2018, 34, 2022–2026 CrossRef CAS.
- H. Zhang, F.-Z. Dai, H. Xiang, X. Wang, Z. Zhang and Y. Zhou, J. Mater. Sci. Technol., 2019, 35, 1593–1600 CrossRef CAS.
- Y. Tateyama and T. Ohno, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 174105 CrossRef.
- P. Olsson, T. P. C. Klaver and C. Domain, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 054102 CrossRef.
- C. Kittel, Introduction to Solid State Physics, Wiley, New York, 6th edn, 1986 Search PubMed.
- X. Tang, W. Sun, Y. Gu, C. Lu, L. Kou and C. Chen, Phys. Rev. B, 2019, 99, 045445 CrossRef.
- E. G. Moroni, G. Kresse, J. Hafner and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 15629–15646 CrossRef CAS.
- J. L. Freeouf and J. M. Woodall, Appl. Phys. Lett., 1981, 39, 727–729 CrossRef CAS.
- Y. Ando, Y. Gohda and S. Tsuneyuki, Surf. Sci., 2012, 606, 1501–1506 CrossRef CAS.
- R. Khaledialidusti, M. Khazaei, V. Wang, N. Miao, C. Si, J. Wang and J. Wang, J. Phys.: Condens. Matter, 2021, 33, 155503 CrossRef CAS PubMed.
- B. Lyu, M. Kim, H. Jing, J. Kang, C. Qian, S. Lee and J. H. Cho, ACS Nano, 2019, 13, 11392–11400 CrossRef CAS PubMed.
- S. Ahn, T.-H. Han, K. Maleski, J. Song, Y.-H. Kim, M.-H. Park, H. Zhou, S. Yoo, Y. Gogotsi and T.-W. Lee, Adv. Mater., 2020, 32, 2000919 CrossRef CAS PubMed.
- R. F. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- S. Chen, F. Wu, Q. Li, H. Sun, J. Ding, C. Huang and E. Kan, Nanoscale, 2020, 12, 15670–15676 RSC.
- S. Zheng, C. Huang, T. Yu, M. Xu, S. Zhang, H. Xu, Y. Liu, E. Kan, Y. Wang and G. Yang, J. Phys. Chem. Lett., 2019, 10, 2733–2738 CrossRef CAS PubMed.
- H. Xiang, C. Lee, H. J. Koo, X. Gong and M. H. Whangbo, Dalton Trans., 2013, 42, 823–853 RSC.
- W. Heitler and F. London, Z. Phys., 1927, 44, 455–472 CrossRef CAS.
- J.-P. Launay and M. Verdaguer, Electrons in Molecules: From Basic Principles to Molecular Electronics, Oxford University Press, Oxford, 2013 Search PubMed.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564–573 CrossRef CAS.
- J. Kanamori, J. Appl. Phys., 1960, 31, S14–S23 CrossRef.
- P. W. Anderson, Phys. Rev., 1959, 115, 2–13 CrossRef CAS.
- S. Bhatti, R. Sbiaa, A. Hirohata, H. Ohno, S. Fukami and S. N. Piramanayagam, Mater. Today, 2017, 20, 530–548 CrossRef.
- S. Wang, J. Wang and M. Khazaei, Phys. Chem. Chem. Phys., 2020, 22, 11731–11739 RSC.
- A. Lehnert, S. Dennler, P. Blonski, S. Rusponi, M. Etzkorn, G. Moulas, P. Bencok, P. Gambardella, H. Brune and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094409 CrossRef.
- G. H. Daalderop, P. J. Kelly and M. F. Schuurmans, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 11919–11937 CrossRef CAS PubMed.
- C. Zener, Phys. Rev., 1951, 82, 403–405 CrossRef CAS.
- S. Tiwari, J. Vanherck, M. L. Van de Put, W. G. Vandenberghe and B. Sorée, Phys. Rev. Res., 2021, 3, 043024 CrossRef CAS.
- W. Su, Z. Zhang, Q. Cao, D. Wang, H. Lu, W. Mi and Y. Du, Phys. Chem. Chem. Phys., 2021, 23, 22103–22109 RSC.
- S. Tiwari, M. L. Van de Put, B. Sorée and W. G. Vandenberghe, Phys. Rev. B, 2021, 103, 014432 CrossRef CAS.
- N. Pandey, A. Kumar and S. Chakrabarti, Appl. Surf. Sci., 2020, 504, 144411 CrossRef CAS.
- Y.-Z. Lv, P. Zhao and D.-S. Liu, Chin. Phys. Lett., 2017, 34, 107301 CrossRef.
- N. Pandey, A. Kumar and S. Chakrabarti, ACS Appl. Mater. Interfaces, 2019, 11, 39248–39253 CrossRef CAS PubMed.
- K. L. Yao, Y. Min, Z. L. Liu, H. G. Cheng, S. C. Zhu and G. Y. Gao, Phys. Lett. A, 2008, 372, 5609–5613 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nh00364g |
| ‡ J. T., S. L., and D. W. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |