Ultrahigh-quality graphene resonators by liquid-based strain-engineering†
Ding-Rui
Chen‡
 abc,
I-Fan
Hu‡
ad,
Hao-Ting
Chin
abc,
Yu-Chi
Yao
ad,
Radha
Raman
ce,
Mario
Hofmann
abc,
I-Fan
Hu‡
ad,
Hao-Ting
Chin
abc,
Yu-Chi
Yao
ad,
Radha
Raman
ce,
Mario
Hofmann
 d,
Chi-Te
Liang
d,
Chi-Te
Liang
 *d and
Ya-Ping
Hsieh
*d and
Ya-Ping
Hsieh
 *a
*a
aInstitute of Atomic and Molecular Sciences, Academia Sinica, Taipei, 10617, Taiwan. E-mail: yphsieh@gate.sinica.edu.tw
bInternational Graduate Program of Molecular Science and Technology, National Taiwan University, Taipei, 10617, Taiwan
cMolecular Science and Technology Program, Taiwan International Graduate Program, Academia Sinica, Taipei 10617, Taiwan
dDepartment of Physics, National Taiwan University, Taipei, 10617, Taiwan. E-mail: ctliang@phys.ntu.edu.tw
eDepartment of Physics, National Central University, Taoyuan 320, Taiwan
First published on 2nd November 2023
Abstract
Two-dimensional (2D) material-based nanoelectromechanical (NEM) resonators are expected to be enabling components in hybrid qubits that couple mechanical and electromagnetic degrees of freedom. However, challenges in their sensitivity and coherence time have to be overcome to realize such mechanohybrid quantum systems. We here demonstrate the potential of strain engineering to realize 2D material-based resonators with unprecedented performance. A liquid-based tension process was shown to enhance the resonance frequency and quality factor of graphene resonators six-fold. Spectroscopic and microscopic characterization reveals a surface-energy enhanced wall interaction as the origin of this effect. The response of our tensioned resonators is not limited by external loss factors and exhibits near-ideal internal losses, yielding superior resonance frequencies and quality factors to all previously reported 2D material devices. Our approach represents a powerful method of enhancing 2D NEM resonators for future quantum systems.
New conceptsMechanical oscillators are an age-old concept but scaling the size of the oscillator to the nanoscale opens up unexpected applications. Nanoelectromechanical oscillators are employed for ultraprecise molecular measurements and could open a route to produce hybrid electromechanical quantum systems for future computation and sensing. To realize these visions, however, breakthroughs in the realization and performance of nano-oscillators are required. We devised a new method to realizing drum-type resonators from 2D materials, an atom-thick crystal layer, in the form of large scale arrays with high robustness. Using a facile liquid-base method, we demonstrated a large tensioning of the resonators that decreased their energy loss significantly without compromising their fundamental operating mechanism. This modification could provide a general route to imparting nano-oscillators with the required performance to achieve exciting applications in molecular and quantum sensors. |
Introduction
Nanoelectromechanical (NEM) resonators have shown remarkable promise in a wide variety of fields ranging from sensing1–4 to energy harvesting.5 An exciting current route is the transfer of energy and information between NEM resonators and other sources. Recent work has demonstrated the coupling of mechanical resonators with a time-changing magnetic field leading to efficient energy transfer.6,7 Moreover, the coherent coupling between mechanical motion and other sources enables the entanglement of quanta for hybrid quantum information sources and quantum computers.8 Theoretical work has highlighted the potential of such hybrid qubits formed in mechanical resonators coupled to light,9 magnetic fields10 and electromagnetic fields.11To realize all these envisioned research directions, nanoelectromechanical resonators have to be optimized for minimal energy dissipation to sustain coherent vibrations for extended periods of time. The energy dissipation is represented by the inverse of the quality factor and is found to scale with resonator thickness.12,13 Consequently, two-dimensional (2D) materials enable resonators with ultimate sensitivity and coherence lifetime due to their atomic thickness.14,15
Despite this promise, 2D resonators have yet to outperform other resonators due to shortcomings in their integration. First, poor mechanical contact with the surroundings introduces spurious dissipation of energy and limits the quality factors.16,17 Moreover, surface adsorbates decrease their strength-to-mass ratio and cause variability in their mass density.18,19 Finally, slack in the resonators causes higher order modes and decreases their resonance frequency.20,21
We here demonstrate the potential of strain engineering to achieve 2D resonators with superior performance.22,23 Using a liquid-assisted tensioning method, controllable amounts of strain could be introduced through adjustment of the interaction between suspended graphene and its support. Through control of the surface energy, we were able to introduce unprecedented amounts of strain in graphene resonators as confirmed by Raman spectroscopy and atomic force microscopy. Our method increased the resonance frequency by six times without changing the fundamental transduction mechanism. The concurrent increase in quality factor with tensioning yielded unprecedented performance that approaches the theoretical limit.
Experimental section
Material preparation
We utilized chemical vapor deposition (CVD) to synthesize graphene with the aim of achieving large monolayer growth. We began by electrochemically polishing a copper foil at 1.5 V for 30 minutes, followed by annealing at 1020 °C for 70 minutes under 10 torr pressure and a hydrogen flow rate of 10 sccm in a 1′′ quartz tube heated by a clamshell furnace. Next, we introduced 10 sccm of methane to initiate graphene growth for 10 hours. Finally, the sample was cooled to room temperature with a continuous 10 sccm hydrogen flow.Device fabrication
We transferred the obtained samples using thermal release tape as a protective layer, followed by etching to remove the copper substrate, and then deposited them onto the target substrate. Following the dry transfer, the resonator was exposed to a liquid. Two silver paste contact electrodes were placed at opposite ends of the device to establish connections for the source and drain. Further details of the experimental setup and a schematic of the device structure can be found in the ESI† (Section S2).Characterization
Atomic force microscope (AFM) data was obtained on a Bruker Dimension Icon. Raman investigation was carried out in a home-built micro-Raman system with 532 nm excitation.Current–voltage characteristics were measured using a Keysight B2912A source meter. The resonant frequency measurement characterization utilized an electrostatic excitation scheme.24 A vector network analyzer (VNA) was used to manipulate and detect the graphene resonator array. A bias voltage from a DC power supply and an alternating voltage from the VNA were combined using a bias-tee and applied to the graphene resonator's gate. The bias voltage adjusted the conductance and tension of the resonator. Then, the output signal from the resonator was separated into AC and DC components using another bias-tee, with the AC signal directed to the VNA for further analysis (see ESI† for more details (Section S3)).
Results and discussion
Novel parallel-connected graphene resonator design
Although tensioning has been considered previously as an approach towards enhancing the performance of 2D resonators, the range of achievable strain has been limited below ∼0.2%.25 This constraint originates from a decrease in device yield when applying strain.18 Moreover, complex mechanical structures have to be produced to prevent slippage during straining.26,27We overcome these challenges by utilizing a novel design – an array composed of thousands of parallel-connected resonators. In such a system, breakage of a fraction of the resonators during tensioning would not render the whole device unusable, as the broken resonators do not contribute to the output signal. Moreover, slippage during tension would bring the resonators into contact with the substrate and they would not contribute to the resonator signal, either. (An estimate of the breakage from resonator data was added to the ESI† (Section S5.4).)
The concept for realizing such arrays is depicted in Fig. 1(a). In the first step, a dielectric film with micrometer-sized openings was created on a silicon substrate. To achieve high reliability and scalability, a nanosphere lithography approach was utilized.28 In this process, nanospheres (Si, Golden Innovation Business Co., Ltd, 1.5 μm) were deposited from an aqueous solution by an evaporation technique.29 Then, an aluminum oxide dielectric layer was deposited by e-beam evaporation. After sonication, the microspheres were removed, leaving 1.5-μm-diameter holes with 90 nm depth. A non-close-packed nanosphere pattern was selected to minimize the interaction between adjacent resonators and increase their mechanical robustness (inset, Fig. 1(a)).
In the second step, a graphene membrane was placed on top of the dielectric layer. The graphene acts as both an actuator and displacement sensor in a capacitive sensing technique.30 The drain current through the graphene is modulated by a back gate (inset, Fig. 1(b)) that also changes the distance of the suspended graphene to the gate terminal, resulting in an enhanced electrostatic control (Fig. 1(b)). In this scheme, the movement of the graphene membrane in response to an electric field between the substrate and graphene will cause a variable distance between the two electrodes resulting in a time-changing capacitance.31 The resulting change in gating efficiency can be detected in the drain current of graphene and correlated with the applied signal using a lock-in technique (Fig. 1(c)).30 Upon varying the frequency of the input signal, changes in amplitude and phase can be observed. The spectra of these parameters allow the identification of the resonance frequency and the quality factor of the system (Fig. 1(d)). The presence of a single peak suggests that individual holes are well separated and no hybridization between neighboring membranes occurs (see ESI† for more details (Section S5.1)).
Liquid-based strain-engineering for adjustable surface energy tension within the graphene resonators
In order to integrate graphene with the resonator, a dry transfer technique was utilized where a thermal release tape, which was used for supporting graphene, was removed in the forming gas at elevated temperatures.32 After removal, AFM was conducted, which indicates that graphene is suspended over the openings in the dielectric film. However, closer inspection reveals that graphene adhered to the sidewalls of the hole (Fig. 2(a)). This premise is supported by Raman spectroscopy that indicates a significant shift in Raman features when comparing supported and suspended graphene that could indicate the variation in strain between such regions (Fig. 2(b)).The observed morphology results from the competition of the elastic force within the suspended graphene and a decrease in surface energy through interaction with the walls.33–35 This mechanism is expected to provide a powerful method to adjust the tension within the graphene resonator through modification of the graphene/sidewall adhesion.
To adjust the surface energy at the wall, we devised a liquid assisted tensioning method. For this purpose, the resonator was exposed to a liquid after transfer. By choosing liquids with different surface tension parameters, a wide range of interactions can be achieved.36–38
Raman spectroscopy was employed to quantify the achievable strain after exposing the resonator to acetone or water. To distinguish the strain-induced Raman response from charge transfer-induced changes to the Raman spectra, we conduct a scaling analysis following Lee et al.39Fig. 2(c) shows the contribution of strain and charge transfer to the redshift of the G-band and 2D-band. It is evident that the data points from the three devices align with the strain-induced trends, confirming the dominance of built-in strain over charge transfer.
We demonstrate that acetone exposure results in a smaller strain than water, which agrees with the trend of their surface tension. Moreover, the highest observed strain is twice as large as previous tensioning methods40 and could be further enhanced by choosing a tensioning medium with an even higher surface tension, such as ethanol, NMP and DMF.41
Modifying mechanical properties and resonance characteristic by liquid tensioning
The presented strain engineering approach is expected to modify the fundamental mechanical properties of the suspended 2D material membrane.42 Indeed, we observe that the resonance frequency significantly changes under liquid tensioning following the trend of applied strain (Fig. 3(a)). This trend furthermore agrees with previous theoretical predictions (Fig. 3(b))42 (more details in the ESI† (Section S5.2)).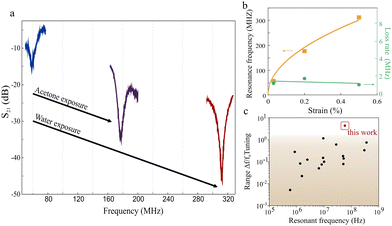 | ||
| Fig. 3 Strain engineering of resonator performance, (a) resonant frequency shift upon liquid immersion, (b) plot of strain dependence of resonance frequency and loss rate, (c) comparison of tunability with reported references (see ESI,† Table S1 for details). | ||
We extract an average strain sensitivity of 530 MHz %−1 over a strain range of 0.5% for our liquid tensioned resonators. The strain sensitivity and strain range represent the highest reported values (Fig. 3(c)).27,40,43,44
We conduct a scaling analysis of the strain-dependent changes in energy dissipation to identify the mechanism that limits the performance of the resonator.
Previous work established the clamping loss as the dominating external loss mechanism of resonators45 according to
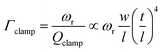 | (1) |
However, our experimental results demonstrate a constant dissipation rate throughout the whole frequency range (Fig. 3(b)), indicating that clamping loss is not the dominating factor in the loss mechanism of our resonators.
Instead, the scaling analysis hints at the importance of intrinsic dissipation mechanisms, such as viscous drag due to residual air47 or ohmic losses48 (more details on the scaling analysis and the potential loss mechanisms are supplied in the ESI† (Section S5.3)).
Investigation of the dissipation process and resonator performance
To elucidate the specific dissipation process responsible for the observed frequency-independent loss rates, we conduct resonator measurements under dynamic tension. For this purpose, a DC voltage is applied to the substrate that induces tension during the resonator operation (Fig. 4(a)). In the pristine device, we observe a parabolic dependence of resonator frequency on the applied force. This behavior indicates an elastic stiffening effect that is caused by the competition of elastic deformation and electric field.49 | ||
| Fig. 4 Investigation of dissipation mechanism, (a) electrostatically tuned resonance frequency for the three strain-engineered devices, and (b) quality factor as a function of the temperature for the strained device. (c) Comparison of the figure of merit (f × Q) for the devices used in this work to reported data.55–62 | ||
At higher values of strain, the stiffening is decreased. This behavior agrees with predictions for the effect of pre-strain on the bending process50 and highlights the dominance of internal dissipation over the investigated strain range.51
Interestingly, for 0.5% tensile strain a negative trend of resonance frequency with dynamic strain is observed. This effect is due to a capacitive softening effect brought about by a simultaneous changing of the carrier concentration in the electric field.52 This observation suggests that, at sufficiently high resonance frequencies, the internal loss is small enough to reveal secondary effects and those effects could eventually limit the achievable quality factor.
This picture is further investigated by temperature-dependent measurements of the quality factor (Fig. 4(b)). As the temperature increases, the quality factor decreases, which contradicts the predictions for viscous losses or surface bonds. Instead, the process agrees well with predictions of the electron dephasing in graphene during excitation by the gate16 (see ESI† (Section S5.3)). By analyzing the scaling relationship between the quality factor and the temperature (Q−1 ∼ Ts, with s denoting the scaling relation), one can ascertain the importance of this unavoidable mechanism compared to other loss processes.48 A theoretical limit for s is established at 1 and our device possesses a scaling relation of 0.94,16 approaching the theoretical limit and indicating the potential of our approach to produce near-ideal resonator devices.
Finally, we conduct a comparison of the resonator's figure of merit (f × Q, where f denotes the resonance frequency and Q signifies the quality factor).53,54 Our device demonstrates superior performance compared to literature reports featuring resonators with similar dimensions (Fig. 4(c)).55–62
Conclusions
Our work demonstrates the impact of strain-engineering on producing high-performance resonators. A robust fabrication approach permits the tensioning of 2D membranes to unprecedented values without compromising the device yield. A liquid-based process was utilized to adjust the tension of graphene devices through control of the graphene/support surface-energy. The resulting resonators exhibit superior resonance frequency and quality factor compared to all previous reports. This advance was ascribed to the suppression of external loss factors and near-ideal intrinsic losses. Our results open up new routes to utilizing mechanical degrees of freedom in hybrid quantum systems.Author contributions
Ding-Rui Chen – formal analysis, investigation, methodology, writing – review & editing; I-Fan Hu – methodology, validation, formal analysis, investigation, data curation; Hao-Ting Chin – material synthesis, methodology, validation, data curation; Yu-Chi Yao – material synthesis, data curation; Radha Raman – formal analysis, data curation; Mario Hofmann – formal analysis, investigation, methodology, software, writing (review & editing); Chi-Te Liang – methodology, resources, writing (review & editing); Ya-Ping Hsieh – conceptualization, writing (original draft), writing (review & editing), resources, supervision, funding acquisition. All authors reviewed and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Science and Technology Council in Taiwan (110-2628-M-002-005-MY3(MH), 110-2112-M-002-029-MY3 (CTL), 112-2112-M-001-051 (YH)) and Academia Sinica (AS-GCS-112-M04(YH)).References
- Y. T. Yang, C. Callegari, X. L. Feng, K. L. Ekinci and M. L. Roukes, Nano Lett., 2006, 6(4), 583–586 CrossRef CAS.
- K. Jensen, K. Kim and A. Zettl, Nat. Nanotechnol., 2008, 3(9), 533–537 CrossRef CAS PubMed.
- J. Moser, J. Güttinger, A. Eichler, M. J. Esplandiu, D. E. Liu, M. I. Dykman and A. Bachtold, Nat. Nanotechnol., 2013, 8(7), 493–496 CrossRef CAS.
- A. M. V. D. Zande, R. A. Barton, J. S. Alden, C. S. Ruiz-Vargas, W. S. Whitney, P. H. Pham, J. Park, J. M. Parpia, H. G. Craighead and P. L. McEuen, Nano Lett., 2010, 10(12), 4869–4873 CrossRef.
- V. Cimalla, F. Niebelschütz, K. Tonisch, C. Foerster, K. Brueckner, I. Cimalla, T. Friedrich, J. Pezoldt, R. Stephan, M. Hein and O. Ambacher, Sens. Actuators, B, 2007, 126(1), 24–34 CrossRef CAS.
- A. Noury, J. Vergara-Cruz, P. Morfin, B. Plaçais, M. C. Gordillo, J. Boronat, S. Balibar and A. Bachtold, Phys. Rev. Lett., 2019, 122(16), 165301 CrossRef CAS.
- A. A. Rendon-Hernandez, M. A. Halim, S. E. Smith and D. P. Arnold, Magnetically Coupled Microelectromechanical Resonators for Low-Frequency Wireless Power Transfer, 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS), IEEE, 2022, pp. 648–651.
- D. Garcia-Sanchez, A. San Paulo, M. J. Esplandiu, F. Perez-Murano, L. Forró, A. Aguasca and A. Bachtold, Phys. Rev. Lett., 2007, 99(8), 085501 CrossRef CAS PubMed.
- X. Gao, Z. Q. Yin and T. Li, Ann. Phys., 2020, 532(10), 2000233 CrossRef CAS.
- P. Rabl, S. J. Kolkowitz, F. Koppens, J. Harris, P. Zoller and M. D. Lukin, Nat. Phys., 2010, 6(8), 602–608 Search PubMed.
- M. Vafadar Yengejeh and B. Rameev, Appl. Magn. Reson., 2023, 54, 581–589 CrossRef CAS.
- L. Sementilli, E. Romero and W. P. Bowen, Adv. Funct. Mater., 2022, 32(3), 2105247 CrossRef CAS.
- A. K. Huttel, G. A. Steele, B. Witkamp, M. Poot, L. P. Kouwenhoven and H. S. van der Zant, Nano Lett., 2009, 9(7), 2547–2552 CrossRef CAS PubMed.
- H. Zhong, Z. Liu, X. Liu, G. Fu, G. Liu, J. Chen and C. Tang, Opt. Express, 2020, 28(25), 37294–37306 CrossRef CAS PubMed.
- M. Kumar and H. Bhaskaran, Nano Lett., 2015, 15(4), 2562–2567 CrossRef CAS PubMed.
- J.-W. Jiang and J.-S. Wang, J. Appl. Phys., 2012, 111(5), 054314 CrossRef.
- S. Y. Kim and H. S. Park, Appl. Phys. Lett., 2009, 94(10), 101918 CrossRef.
- S. Lee, C. Chen, V. V. Deshpande, G.-H. Lee, I. Lee, M. Lekas, A. Gondarenko, Y.-J. Yu, K. Shepard, P. Kim and J. Hone, Appl. Phys. Lett., 2013, 102(15), 153101 CrossRef.
- F. Ye, J. Lee and P. X. L. Feng, Nano Lett., 2018, 18(3), 1678–1685 CrossRef CAS.
- J. S. Bunch, A. M. van der Zande, S. S. Verbridge, I. W. Frank, D. M. Tanenbaum, J. M. Parpia, H. G. Craighead and P. L. McEuen, Science, 2007, 315(5811), 490–493 CrossRef CAS.
- J. Atalaya, A. Isacsson and J. M. Kinaret, Nano Lett., 2008, 8(12), 4196–4200 CrossRef CAS.
- M. M. Parmar, P. R. Y. Gangavarapu and A. K. Naik, Appl. Phys. Lett., 2015, 107(11), 113108 CrossRef.
- C. Chen, S. Rosenblatt, K. I. Bolotin, W. Kalb, P. Kim, I. Kymissis, H. L. Stormer, T. F. Heinz and J. Hone, Nat. Nanotechnol., 2009, 4(12), 861–867 CrossRef CAS.
- W. Y. Fung, E. N. Dattoli and W. Lu, Appl. Phys. Lett., 2009, 94, 20 CrossRef.
- X. Zhang, K. Makles, L. Colombier, D. Metten, H. Majjad, P. Verlot and S. Berciaud, Nat. Commun., 2020, 11(1), 5526 CrossRef CAS PubMed.
- F. Guan, P. Kumaravadivel, D. V. Averin and X. Du, Appl. Phys. Lett., 2015, 107(19), 193102 CrossRef.
- Y. Oshidari, T. Hatakeyama, R. Kometani, S. I. Warisawa and S. Ishihara, Appl. Phys. Exp., 2012, 5(11), 117201 CrossRef.
- J. C. Hulteen and R. P. Van Duyne, J. Vac. Sci. Technol., A, 1995, 13(3), 1553–1558 CrossRef.
- V. Dugas, J. Broutin and E. Souteyrand, Langmuir, 2005, 21(20), 9130–9136 CrossRef CAS PubMed.
- W. Y. Fung, E. N. Dattoli and W. Lu, Appl. Phys. Lett., 2009, 94(20), 203104 CrossRef.
- D. Weinstein and S. A. Bhave, Nano Lett., 2010, 10(4), 1234–1237 CrossRef CAS PubMed.
- J. Kang, D. Shin, S. Bae and B. H. Hong, Nanoscale, 2012, 4(18), 5527–5537 RSC.
- J. Wang, C. Teng, Y. Jiang, Y. Zhu and L. Jiang, Adv. Mater., 2019, 31(10), 1806742 CrossRef PubMed.
- J. S. Bunch and M. L. Dunn, Solid State Commun., 2012, 152(15), 1359–1364 CrossRef CAS.
- Y. He, W. F. Chen, W. B. Yu, G. Ouyang and G. W. Yang, Sci. Rep., 2013, 3(1), 2660 CrossRef CAS PubMed.
- W. Regan, N. Alem, B. Alemán, B. Geng, Ç. Girit, L. Maserati, F. Wang, M. Crommie and A. Zettl, Appl. Phys. Lett., 2010, 96(11), 113102 CrossRef.
- G. Zhao, X. Li, M. Huang, Z. Zhen, Y. Zhong, Q. Chen, X. Zhao, Y. He, R. Hu, T. Yang, R. Zhang, C. Li, J. Kong, J.-B. Xu, R. S. Ruoff and H. Zhu, Chem. Soc. Rev., 2017, 46(15), 4417–4449 RSC.
- B. J. Robinson, N. D. Kay and O. V. Kolosov, Langmuir, 2013, 29(25), 7735–7742 CrossRef CAS PubMed.
- J. E. Lee, G. Ahn, J. Shim, Y. S. Lee and S. Ryu, Nat. Commun., 2012, 3(1), 1024 CrossRef PubMed.
- S. Lee, C. Chen, V. V. Deshpande, G.-H. Lee, I. Lee, M. Lekas, A. Gondarenko, Y.-J. Yu, K. Shepard and P. Kim, Appl. Phys. Lett., 2013, 102, 15 Search PubMed.
- W. Chen, X. Gui, B. Liang, M. Liu, Z. Lin, Y. Zhu and Z. Tang, ACS Appl. Mater. Interfaces, 2016, 8(17), 10977–10984 CrossRef CAS.
- Y. Xu, O. Li and R. Xu, Graphene resonant channel transistor, 2013 IEEE International Wireless Symposium (IWS), IEEE, 2013 pp. 1–6.
- A. Okmi, X. Xiao, Y. Zhang, R. He, O. Olunloyo, S. B. Harris, T. Jabegu, N. Li, D. Maraba and Y. Sherif, Adv. Sci., 2022, 9(26), 2201336 CrossRef CAS.
- A. Okmi, Direct transfer techniques of graphene, PhD thesis, Georgia State University, 2022.
- J. H. Ko, J. Jeong, J. Choi and M. Cho, Appl. Phys. Lett., 2011, 98, 17 CrossRef.
- S. S. Verbridge, J. M. Parpia, R. B. Reichenbach, L. M. Bellan and H. G. Craighead, J. Appl. Phys., 2006, 99, 12 CrossRef.
- S. Schmid and C. Hierold, J. Appl. Phys., 2008, 104, 9 CrossRef.
- C. Seoánez, F. Guinea and A. H. Castro Neto, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(12), 125427 CrossRef.
- C. C. Wu and Z. Zhong, Nano Lett., 2011, 11(4), 1448–1451 CrossRef CAS PubMed.
- L. Sang, M. Liao, X. Yang, H. Sun, J. Zhang, M. Sumiya and B. Shen, Sci. Technol. Adv. Mater., 2020, 21(1), 515–523 CrossRef CAS PubMed.
- A. Kimball and D. Lovell, Phys. Rev., 1927, 30(6), 948 CrossRef CAS.
- P. F. Ferrari, S. Kim and A. M. van der Zande, Nano Lett., 2021, 21(19), 8058–8065 CrossRef CAS PubMed.
- K. Lynn, Performance parameters of micromechanical resonators, PhD thesis, National University of Singapore, 2010.
- A. Eichler, J. Moser, J. Chaste, M. Zdrojek, I. Wilson-Rae and A. Bachtold, Nat. Nanotechnol., 2011, 6(6), 339–342 CrossRef CAS PubMed.
- S. J. Cartamil-Bueno, M. Cavalieri, R. Wang, S. Houri, S. Hofmann and H. S. J. van der Zant, npj 2D Mater. Appl., 2017, 1(1), 16 CrossRef.
- C. Samanta, P. R. Yasasvi Gangavarapu and A. K. Naik, Appl. Phys. Lett., 2015, 107(17), 173110 CrossRef.
- N. Morell, A. Reserbat-Plantey, I. Tsioutsios, K. G. Schädler, F. Dubin, F. H. L. Koppens and A. Bachtold, Nano Lett., 2016, 16(8), 5102–5108 CrossRef CAS PubMed.
- F. Ye, J. Lee and P. X. L. Feng, Nanoscale, 2017, 9(46), 18208–18215 RSC.
- S. Sengupta, H. S. Solanki, V. Singh, S. Dhara and M. M. Deshmukh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(15), 155432 CrossRef.
- S. Kim, J. Yu and A. M. van der Zande, Nano Lett., 2018, 18(11), 6686–6695 CrossRef CAS PubMed.
- A. Castellanos-Gomez, R. van Leeuwen, M. Buscema, H. S. J. van der Zant, G. A. Steele and W. J. Venstra, Adv. Mater., 2013, 25(46), 6719–6723 CrossRef CAS PubMed.
- R. Yang; Z. Wang and P. X. L. Feng, All-electrical readout of atomically-thin MoS2nanoelectromechanical resonators in the VHF band, 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), 24–28 Jan. 2016, pp. 59–62.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nh00420a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |


