Open Access Article
Open Access ArticleCatalytic selectivity of nanorippled graphene†
Yu
Liu‡
 a,
Wenqi
Xiong‡
a,
Wenqi
Xiong‡
 b,
Achintya
Bera
b,
Achintya
Bera
 *c,
Yu
Ji
a,
Miao
Yu
a,
Shi
Chen
*c,
Yu
Ji
a,
Miao
Yu
a,
Shi
Chen
 a,
Li
Lin
a,
Li
Lin
 d,
Shengjun
Yuan
d,
Shengjun
Yuan
 *b and
Pengzhan
Sun
*b and
Pengzhan
Sun
 *a
*a
aInstitute of Applied Physics and Materials Engineering, University of Macau, Avenida da Universidade, Taipa, Macau SAR 999078, China. E-mail: pengzhansun@um.edu.mo
bKey Laboratory of Artificial Micro- and Nano-structures of the Ministry of Education and School of Physics and Technology, Wuhan University, Wuhan, 430072, China. E-mail: s.yuan@whu.edu.cn
cNational Graphene Institute, University of Manchester, Oxford Road, Manchester M13 9PL, UK. E-mail: achintya.bera@manchester.ac.uk
dSchool of Materials Science and Engineering, Peking University, Beijing, 100871, P. R. China
First published on 4th January 2024
Abstract
Experiments have shown that nanoscale ripples in a graphene membrane exhibit unexpectedly high catalytic activity with respect to hydrogen dissociation. Nonetheless, the catalytic selectivity of nanorippled graphene remains unknown, which is an equally important property for assessing a catalyst's potential and its fit-for-purpose applications. Herein, we examine the catalytic selectivity of nanorippled graphene using a model reaction of molecular hydrogen with another simple but double-bonded molecule, oxygen, and comparing the measurement results with those from splitting of hydrogen molecules. We show that although nanorippled graphene exhibits a high catalytic activity toward hydrogen dissociation, the activity for catalyzing the hydrogen–oxygen reaction is quite low, translating into a strong catalytic selectivity. The latter reaction involves the reduction of oxygen molecules by the dissociated hydrogen adatoms, which requires additional energy cost and practically determines the selectivity. In this sense, the well-established information about reactions in general of atomic hydrogen with many other species in the literature could potentially predict the selectivity of nanorippled graphene as a catalyst. Our work provides implications for the catalytic properties of nanorippled graphene, especially its selectivity. The results would be important for its extension to a wider range of reactions and for designer technologies involving hydrogen.
New conceptsGraphene is highly stable in air and is believed to inherit this extreme chemical inertness from graphite. To induce catalytic activity in the otherwise chemically inert graphene, structural modifications such as heteroatomic dopants, functional groups, edges or mechanical strain are generally required. Different from those well-established defect-type active sites, recent experiments have shown that nanoscale ripples that are ubiquitous and unavoidable in free-standing graphene membranes are highly reactive toward hydrogen dissociation. The catalytic activity of nanorippled graphene was mostly overlooked before, which could potentially provide another degree of freedom for tuning the catalytic properties of graphene-based materials. Despite the known information about the catalytic activity of nanorippled graphene, its selectivity remains unknown. Our present work provides experimental information on this aspect by showing that nanorippled graphene exhibits a high selectivity towards different reactions involving hydrogen and the well-documented information in the literature about the very general reactions of atomic hydrogen with many other species could provide potential prediction on the catalytic selectivity of nanorippled graphene, even if such information was from a different system and irrelevant to graphene. Our results would be important not only from a fundamental perspective on the catalytic properties of nanorippled graphene, but also for the development of new hydrogen technologies. |
Introduction
It is generally believed that graphene inherits chemical inertness from its parent material, graphite, and is highly stable in air. Nonetheless, this two-dimensional (2D) crystal is still widely considered for use in catalysis mainly due to the following reasons.1–11 First, graphene exhibits a huge surface area that can efficiently support catalytically active nanoparticles.1–5 Second, it is relatively easy to modify the defect-free 2D structure by introducing such as for example, heteroatomic dopants, functional groups and mechanical strain so that catalytic activity can be induced in the otherwise chemically inert graphene.1–7 Moreover, graphene and other 2D crystals can be used as atomically thin coatings to confine reactions to the interface formed with chemically reactive metals, allowing for precise control over the metals’ activity and selectivity.8–11On the other hand, it has also been observed in a few experiments that defect-free graphene can be more reactive than graphite.12–15 For example, monolayer graphene displays less resistance to thermal oxidation in air compared with few-layer graphene and graphite.12 Wrinkles and strained areas present in graphene are also reported to be more reactive than the flat regions and can promote surface functionalization by certain chemicals.13–15 These experiments imply that the described structural modifications are perhaps unnecessary in terms of inducing catalytic activity in graphene. Recent experiments16,17 have made it clear by showing that nanoscale ripples18–22 that are ubiquitous and unavoidable in monolayers of graphene exhibit strong catalytic activity with respect to splitting molecular hydrogen. These ripples/corrugations can be either dynamic (due to thermal fluctuations) or static (due to local strain caused by adsorbates or contaminants). Their presence has been predicted in theory18 and visualized in experiments using high-resolution tools such as electron and tunneling microscopy.19–21 Moreover, simulations22 have been employed to estimate the density distribution of different-size nanoripples in a freestanding graphene membrane. Using monocrystalline containers that were tightly sealed by such freestanding graphene monolayers, a slow but steady transport of molecular hydrogen through defect-free graphene membranes was detected under ambient conditions, whereas these membranes were found to be completely impermeable to the smaller and generally much more permeable helium atoms.16 The anomalous hydrogen transport was explained by a two-stage mechanism, which involved dissociation of molecular hydrogen on graphene's surface followed by cross-membrane flipping of adsorbed protons or hydrogen atoms by overcoming a 1-eV barrier.16 The flipping step is supported by proton transport measurements23–25 where the same 1-eV barrier was observed and, by the fact that a proton being adsorbed on graphene can easily capture one of the latter's electrons and becomes indistinguishable from a hydrogen adatom. However, the dissociation step is somewhat unexpected especially intuitively considering the fact that graphite is one of the most stable materials in nature and its elementary constituent, graphene, should inherit most of graphite's properties, including the chemical inertness. To rationalize this experimental observation from a theoretical viewpoint, simulations16,26–29 have suggested that the nanoripples present in graphene exhibit catalytic activity toward hydrogen dissociation and higher curvatures generally result in a lower dissociation barrier. More recently, experiments17 have proved this theoretical prediction. First, Raman measurements of monolayer graphene crystals that were exfoliated on an oxidized silicon wafer and conformal to its nanoscale roughness (inducing static nanoripples) showed the formation of C–H bonds in a hydrogen atmosphere. In contrast, these C–H bonds were absent from similar crystals but being placed over the atomically flat surface of graphite.17 Second, measurements using a hydrogen isotope exchange reaction, H2 + D2 ↔ 2HD, and a powder material containing mostly isolated and highly corrugated graphene monolayers, revealed that the activity of nanorippled graphene for catalyzing hydrogen dissociation was strong and even comparable to that of metals and other known catalysts.17 Furthermore, temperature dependence measurements yielded the same activation energy of about 0.4 eV in both experiments, suggesting the same mechanism (nanoripples) governing those observations in different setups.17 In spite of the known information about the catalytic activity of nanorippled graphene, its catalytic selectivity toward other hydrogen-related reactions remains unknown, which is an equally important property for evaluating the potential of a tested catalyst.
In the described hydrogen dissociation processes where nanorippled graphene was exposed to a pure hydrogen atmosphere and at an elevated temperature T, the split atomic hydrogen is known to be highly reductive. If we deliberately introduce a small amount of oxidizing species (for example, O2) into the reaction chamber, we would expect the reaction of hydrogen atoms with O2 (in addition to their recombination into H2) and hence, a pressure change on condition that the reactants (H2 and O2) and products constituting the gas phase are in different amounts. Detecting such pressure changes allows a careful analysis of the model hydrogen–oxygen reaction catalyzed by graphene and also, provides additional information about the latter's catalytic selectivity toward reactions and species other than hydrogen and its dissociation. Bearing these considerations in mind, we performed the following experiments.
Results and discussion
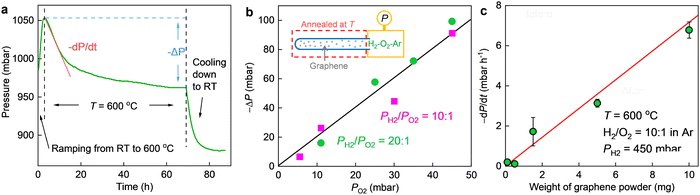
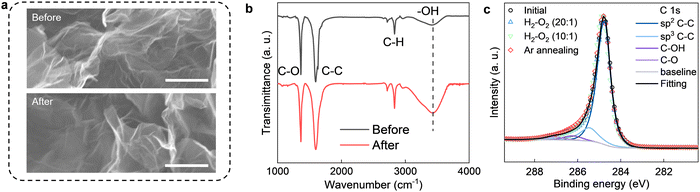
We used the same graphene powder as in the previous study,17 where the catalytic activity of the present nanoripples toward hydrogen dissociation was corroborated. It was commercially supplied (by ACS Material) and has been well-characterized before17,30 and also in the present study (Fig. 1 and ESI,† see below). Its constituent flakes were mostly isolated monolayers (Fig. S1, ESI†) and highly corrugated (Fig. 1a). By comparing the catalytic activity of this monolayer graphene powder with that of few-layer graphene (obtained by sonication)31 and charcoal in the reported hydrogen–deuterium exchange experiments,17 it was confirmed that nanoripples are more important in hydrogen dissociation than other suspicious active sites such as edges and functional groups. This powder was put into a quartz tube. The latter was sealed and connected (via a larger gas chamber) to a pressure gauge (Leybold). All connections were vacuum-tight. If elevated temperatures T were necessary to accelerate the reaction and measure T dependences, only the quartz tube (that is, the graphene powder) was slowly heated up, leaving the pressure gauge together with the gas chamber far from the heating zone and at room T (inset of Fig. 2b and Fig. S2, details and analyses see ESI†). Then we pumped the setup and put a gas mixture of H2, O2 and Ar into it. Changes in the total pressure P was recorded from the pressure gauge as a function of time t. The partial pressures of H2 and O2 (PH2, PO2) were carefully controlled. Ar was used as a carrier gas such that we could keep the total gas pressure at P ≈ 1 bar. To minimize the oxidization of graphene,12 the concentration of O2 was normally kept below 5%. This value was determined on the basis of the following test. We first mechanically exfoliated monolayer graphene crystals on an oxidized silicon wafer and then annealed them in a gas mixture containing O2 and H2 (or Ar). As shown in Fig. S3a and b (ESI†), we could hardly observe any oxidation induced defects after annealing the exfoliated crystals at 600 °C in either a H2–O2 or Ar–O2 mixture with the concentration of O2 being limited up to 10%. In contrast, similarly exfoliated graphene but annealed in an Ar–O2 mixture containing 20% of O2 was found to be severely oxidized (Fig. S3c, ESI†). The absence of graphene oxidation using the described O2 concentration was also confirmed by the following experimental and theoretical facts: (1) systematic characterizations of the graphene powder before and after the reaction using electron microscopy, Fourier-transform infrared spectroscopy (FTIR) and X-ray photoelectron spectroscopy (XPS) showed negligible changes in both morphological and chemical structures (in terms of the C–O bands in FTIR and XPS spectra, to be discussed in detail later); (2) our simulations found that the energy barrier for direct oxidation of graphene is much higher than its hydrogenation even in the presence of nanoripples (details see ESI,† Fig. S7).In the absence of graphene powder, no changes in P (better than a few mbar) could be detected over one day's time regardless of the partial pressures of H2 and O2 even if we heated the quartz tube to 600 °C (Fig. S4, ESI†). To initiate the reaction, we added a certain amount of graphene powder into the quartz tube as a catalyst and heated it to a higher T (at room T, P still remained the same). As exemplified in Fig. 2a, notable pressure changes were observed at 600 °C. The pressure first decayed and then gradually saturated as a function of time, resulting in a total pressure drop (−ΔP) about twice that of PO2. The same relation of −ΔP ≈ 2PO2 was also found for other PH2 and PO2 values, if PH2 was much higher than PO2 (for example, PH2/PO2 was set to 10 and 20, respectively, with the concentration of O2 varying from 0.5% to 5%, see Fig. 2b. For PO2 = 0, ΔP ≈ 0, as shown in Fig. S5, ESI†). This cannot be due to graphene oxidation because on the one hand, we did not observe any oxidation induced features either in the graphene powder (Fig. 1) or in the mechanically exfoliated graphene crystals (Fig. S3, ESI†) after the same annealing procedures and in the same gas atmosphere; on the other hand, the same powder but being annealed in a 95% Ar–5% O2 gas mixture yielded negligible changes in P (Fig. S6, ESI†). Instead, we attribute the observation to H2–O2 reaction catalyzed by graphene. At a constant T (e.g., 600 °C), the pressure in the initial reaction stage decreased approximately in a linear trend as a function of time (Fig. 2a) and the slop of P(t), −dP/dt, estimates the initial reaction rate. As shown in Fig. 2c, the reaction rate scales linearly with the amount of graphene powder. Taken together the absence of any morphological changes and sign of oxidation (Fig. 1 and Fig. S3, ESI†), it is concluded that the graphene powder was as a catalyst for speeding up the reaction.
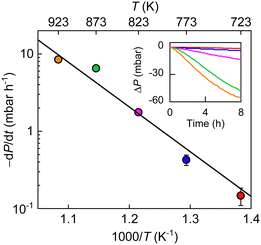
Trying to understand the mechanism of the observed H2–O2 reaction, we measured P(t) at different T (Fig. 3). The reaction progressed faster at a higher T and the T dependence of initial reaction rate followed the Arrhenius-type behavior. Its exponential fit allows us to estimate the reaction activation energy as 1.1 ± 0.1 eV, which is notably higher than that for hydrogen dissociation (∼0.4 eV).17 These results indicate that the monolayer graphene powder exhibits a higher catalytic activity and hence, a strong selectivity toward hydrogen dissociation over the tested reaction of hydrogen with oxygen. Because the latter reaction also involves hydrogen dissociation and, the dissociated hydrogen adatoms should have higher reducibility than hydrogen molecules, we believe it is the atomic hydrogen that results in the reduction of oxygen molecules. In this context, the active sites on graphene should be the same as that for hydrogen dissociation, that is, nanoripples, as previously corroborated,17 and the elementary step of O2 reduction by the hydrogen adatoms, which requires additional energy cost, should practically determine the selectivity. These experimental observations have been reproduced in simulations (details see ESI,† Fig. S7 and S8).
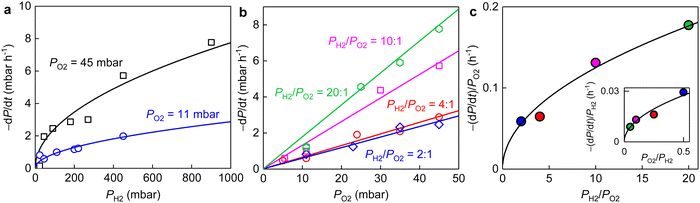
The overall reaction is described by xH2 + yO2 ↔ z (product), where x, y and z are stoichiometric coefficients and the product could be H2O2, H2O or other intermediates and/or their mixtures. Because we are only interested in the initial reaction rate (measured by the rate of total pressure change, −dP/dt), which is mostly determined by PH2 and PO2, the details regarding the nature of the product are less important at the moment. Nonetheless, FTIR and XPS were employed to examine the changes in graphene's chemical structure and the potential composition of the product (Fig. 1 and 5). If we define the forward and backward rate constants of this reaction as k1 and k−1, using the rate law for a chemical reaction,32 the reaction rate can be written as
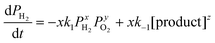 | (1) |
Or alternatively,
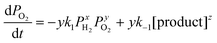 | (2) |
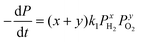 | (3) |
The same stoichiometric coefficients for H2 and O2 imply that the final product contained equivalent amount of hydrogen and oxygen atoms, presumably hydroxyl groups. The latter might either bond to graphene or with each other to form small molecules such as H2O2 (or H2O), reminiscent of the typical oxygen reduction reactions.33,34 These expectations from experimental measurements are fully supported by our simulations (details see ESI,† Fig. S8). To seek for any presence of hydroxyls, we carefully examined the FTIR and XPS spectra of the graphene powder before and after the reaction (Fig. 1b, c and 5).
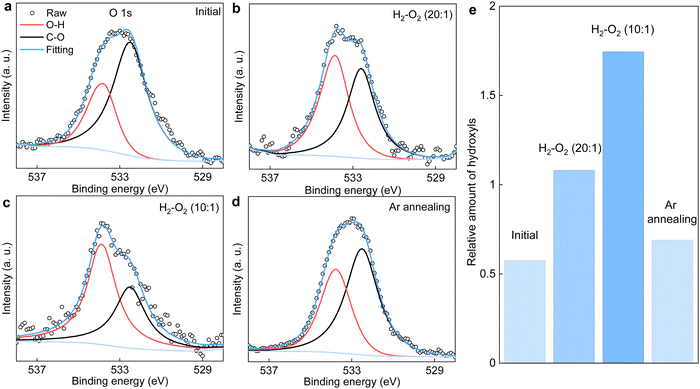
We notice several important features in the FTIR spectra (Fig. 1b). The intensity of the band located at ∼3430 cm−1 exhibits a pronounced increase (by a factor of ∼2) after the reaction. This band is typically assigned to hydroxyl groups and hence, proves our analysis for the pressure dependence measurements described above (Fig. 4). Furthermore, the intensity of the band assigned to C–O bonds (epoxy or ether) remains approximately the same, indicating the absence of graphene oxidation, whereas that of C–H bonds was increased by about 40% after the reaction. The formation of more C–H bonds is a direct proof for hydrogen dissociation on graphene's surface, which has also been well-documented in the previous work.17
In principle, the features observed in the FTIR spectra should also be present in the XPS spectra if the same samples are characterized. This is indeed the case for the evolution of C–O bonds, whereby changes in both FTIR and XPS C 1s spectra are negligibly small (Fig. 1c). Unfortunately, the formation of C–H bonds cannot be distinguished from the XPS C 1s spectra because its characteristic band (284.6–284.8 eV) overlaps with that of the C–C bonds (Fig. 1c). On the other hand, we note that the H2–O2 catalytic reaction leads to the formation of more hydroxyl groups, as clearly evidenced in the FTIR spectra shown in Fig. 1b. However, these hydroxyl groups do not bond to graphene's surface, otherwise this could be easily distinguished from the XPS C 1s spectra shown in Fig. 1c. Alternatively, the final product containing these hydroxyls would physically adsorb on graphene.
It is instructive to analyze the XPS O 1s spectra of the annealed graphene powder, which could provide additional information about the relative amount of hydroxyls being produced. Such analysis is shown in Fig. 5a–d. As per Fig. 1c, the C–O component remains unchanged after annealing the powder in various H2/O2 mixtures. Accordingly, the contribution of hydroxyls relative to that of C–O in the O 1s spectra serves as a measure for the amount of hydroxyls produced by the catalytic reaction. These results are summarized in Fig. 5e. It is evident that increasing the O2 concentration in the gas mixture generally produces more hydroxyls. Notably, the relative amount of hydroxyl groups after annealing the graphene powder in the gas mixture of PH2/PO2 = 20 is about twice that of the initial value before the reaction, in good agreement with the FTIR results in Fig. 1b. Moreover, the powder that was first annealed in the mixture of PH2/PO2 = 10 was then heated to the same T = 600 °C but in a pure argon atmosphere. We found the relative amount of hydroxyls decreased significantly and approached that before the reaction. This suggests the product of H2–O2 catalytic reaction can desorb from graphene's surface relatively easily (compared with covalent bonding) with the assistance of heating, which echoes the above characterizations inferring physisorption of the hydroxyl-containing product. This is also supported by our calculations revealing that further dissociation of the physisorbed product (presumably, H2O2, as suggested by simulations), resulting in the chemisorption of hydroxyls, requires overcoming another high energy barrier (Fig. S8, ESI†).
Conclusion
To conclude, our experiments using a powder material containing highly corrugated and mostly isolated graphene monolayers (Fig. 1 and Fig. S1, ESI†) show that it displays a much higher catalytic activity toward H2 dissociation over the H2–O2 reaction and therefore, a strong selectivity. The H2–O2 reaction was proceeded by the dissociation of H2 on graphene's surface followed by the reduction of O2. Hydrogen dissociation most probably occurred on the nanoripples ubiquitous in graphene, by overcoming a relatively low barrier of ∼0.4 eV, as well-documented before,17 whereas the resulting hydrogen adatoms further reduced molecular oxygen with the assistance of additional energy input, as supported by both experiments (Fig. 2–4) and simulations (Fig. S7 and S8, ESI†), which resulted in a much higher and overall barrier of >1 eV (Fig. 3). The latter step determines the catalytic selectivity of nanorippled graphene. In this context, the available information in the literature about the very general reactions of atomic hydrogen with other species could provide a potential prediction for the catalytic selectivity of nanorippled graphene, even if such information is gained from a different system and irrelevant to graphene. Our work provides insights in the catalytic properties of nanorippled graphene, especially its selectivity. The results can be important for the research and application of nanorippled graphene in a wider range of reactions involving hydrogen (e.g., water electrolysis and other electrochemical reactions). Furthermore, in addition to reacting with other species, the dissociated hydrogen by the nanorippled graphene might also be stored in confined systems, for example, the interior of nanotubes35 and nanoporous materials (e.g., metal–organic frameworks or covalent organic frameworks),36–38 which would promise new technologies for hydrogen storage and application using their dedicatedly designed combinations.Author contributions
P. Z. S. designed and directed the project with help from S. J. Y. and A. B. Y. L., A. B., Y. J. and M. Y. performed the measurements. W. Q. X. and S. J. Y. provided theoretical support. S. C. and L. L. contributed to interpretation of the experimental results and data analysis. P. Z. S. wrote the manuscript with input from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Science and Technology Development Fund (FDCT), Macao SAR (0063/2023/RIA1), the Natural Science Foundation of China (52322319), UM research grant (SRG2022-00053-IAPME), UM and UMDF research grant (MYRG-GRG2023-00014-IAPME-UMDF).Notes and references
- B. F. MacHado and P. Serp, Catal. Sci. Technol., 2012, 2, 54–75 RSC.
- S. Navalon, A. Dhakshinamoorthy, M. Alvaro and H. Garcia, Chem. Rev., 2014, 114, 6179–6212 CrossRef CAS PubMed.
- X. Fan, G. Zhang and F. Zhang, Chem. Soc. Rev., 2015, 44, 3023–3035 RSC.
- D. Deng, K. S. Novoselov, Q. Fu, N. Zheng, Z. Tian and X. Bao, Nat. Nanotechnol., 2016, 11, 218–230 CrossRef CAS PubMed.
- E. J. Askins, M. R. Zoric, M. Li, Z. Luo, K. Amine and K. D. Glusac, Nat. Commun., 2021, 12, 3288 CrossRef CAS PubMed.
- D. R. Dreyer, H. P. Jia and C. W. Bielawski, Angew. Chem., Int. Ed., 2010, 49, 6813–6816 CrossRef CAS PubMed.
- A. Primo, F. Neatu, M. Florea, V. Parvulescu and H. Garcia, Nat. Commun., 2014, 5, 5291 CrossRef CAS PubMed.
- Y. X. Yao, Q. Fu, Y. Y. Zhang, X. F. Weng, H. Li, M. S. Chen, L. Jin, A. Y. Dong, R. T. Mu, P. Jiang, L. Liu, H. Bluhm, Z. Liu, S. B. Zhang and X. H. Bao, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17023–17028 CrossRef CAS PubMed.
- S. F. L. Mertens, A. Hemmi, S. Muff, O. Gröning, S. De Feyter, J. Osterwalder and T. Greber, Nature, 2016, 534, 676–679 CrossRef CAS PubMed.
- T. Kosmala, A. Baby, M. Lunardon, D. Perilli, H. Liu, C. Durante, C. Di Valentin, S. Agnoli and G. Granozzi, Nat. Catal., 2021, 4, 850–859 CrossRef CAS.
- K. Hu, T. Ohto, Y. Nagata, M. Wakisaka, Y. Aoki, J. I. Fujita and Y. Ito, Nat. Commun., 2021, 12, 203 CrossRef CAS PubMed.
- L. Liu, S. Ryu, M. R. Tomasik, E. Stolyarova, N. Jung, M. S. Hybertsen, M. L. Steigerwald, L. E. Brus and G. W. Flynn, Nano Lett., 2008, 8, 1965–1970 CrossRef CAS PubMed.
- Q. Wu, Y. Wu, Y. Hao, J. Geng, M. Charlton, S. Chen, Y. Ren, H. Ji, H. Li, D. W. Boukhvalov, R. D. Piner, C. W. Bielawski and R. S. Ruoff, Chem. Commun., 2013, 49, 677–679 RSC.
- M. A. Bissett, S. Konabe, S. Okada, M. Tsuji and H. Ago, ACS Nano, 2013, 7, 10335–10343 CrossRef CAS PubMed.
- Y. H. Zhang, B. Wang, H. R. Zhang, Z. Y. Chen, Y. Q. Zhang, B. Wang, Y. P. Sui, X. L. Li, X. M. Xie, G. H. Yu, Z. Jin and X. Y. Liu, Carbon, 2014, 70, 81–86 CrossRef CAS.
- P. Z. Sun, Q. Yang, W. J. Kuang, Y. V. Stebunov, W. Q. Xiong, J. Yu, R. R. Nair, M. I. Katsnelson, S. J. Yuan, I. V. Grigorieva, M. Lozada-Hidalgo, F. C. Wang and A. K. Geim, Nature, 2020, 579, 229–232 CrossRef CAS PubMed.
- P. Z. Sun, W. Q. Xiong, A. Bera, I. Timokhin, Z. F. Wu, A. Mishchenko, M. C. Sellers, B. L. Liu, H. M. Cheng, E. Janzen, J. H. Edgar, I. V. Grigorieva, S. J. Yuan and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2022, 120, e2300481120 CrossRef PubMed.
- A. Fasolino, J. H. Los and M. I. Katsnelson, Nat. Mater., 2007, 6, 858–861 CrossRef CAS PubMed.
- J. C. Meyer, A. K. Geim, M. I. Katsnelson, K. S. Novoselov, D. Obergfell, S. Roth, C. Girit and A. Zettl, Solid State Commun., 2007, 143, 101–109 CrossRef CAS.
- R. Zan, C. Muryn, U. Bangert, P. Mattocks, P. Wincott, D. Vaughan, X. Li, L. Colombo, R. S. Ruoff, B. Hamilton and K. S. Novoselov, Nanoscale, 2012, 4, 3065–3068 RSC.
- P. Xu, M. Neek-Amal, S. D. Barber, J. K. Schoelz, M. L. Ackerman, P. M. Thibado, A. Sadeghi and F. M. Peeters, Nat. Commun., 2014, 5, 3720 CrossRef CAS PubMed.
- J. Yu, M. I. Katsnelson, T. Z. Zhang and S. J. Yuan, Phys. Rev. B, 2022, 106, 045418 CrossRef CAS.
- S. Hu, M. Lozada-Hidalgo, F. C. Wang, A. Mishchenko, F. Schedin, R. R. Nair, E. W. Hill, D. W. Boukhvalov, M. I. Katsnelson, R. A. W. Dryfe, I. V. Grigorieva, H. A. Wu and A. K. Geim, Nature, 2014, 516, 227–230 CrossRef CAS PubMed.
- M. Lozada-Hidalgo, S. Hu, O. Marshall, A. Mishchenko, A. N. Grigorenko, R. A. W. Dryfe, B. Radha, I. V. Grigorieva and A. K. Geim, Science, 2016, 351, 68–70 CrossRef CAS PubMed.
- O. J. Wahab, E. Daviddi, B. Xin, P. Z. Sun, E. Griffin, A. W. Colburn, D. Barry, M. Yagmurcukardes, F. M. Peeters, A. K. Geim, M. Lozada-Hidalgo and P. R. Unwin, Nature, 2023, 620, 782–786 CrossRef CAS PubMed.
- D. W. Boukhvalov and M. I. Katsnelson, J. Phys. Chem. C, 2009, 113, 14176–14178 CrossRef CAS.
- H. McKay, D. J. Wales, S. J. Jenkins, J. A. Verges and P. L. De Andres, Phys. Rev. B, 2010, 81, 075425 CrossRef.
- Q. Wan, H. Guo and S. Lin, ACS Catal., 2022, 12, 14601–14608 CrossRef CAS.
- W. Xiong, W. Zhou, P. Sun and S. Yuan, Phys. Rev. B, 2023, 108, 045408 CrossRef CAS.
- J. A. Hondred, L. R. Stromberg, C. L. Mosher and J. C. Claussen, ACS Nano, 2017, 11, 9836–9845 CrossRef CAS PubMed.
- Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. Gun'ko, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, Nat. Nanotechnol., 2008, 3, 563–568 CrossRef CAS PubMed.
- P. W. Atkins and J. De Paula, Physical Chemistry Thermodynamics and Kinetics, Oxford University Press, 8th edn, 2006, vol. 1 Search PubMed.
- D. W. Wang and D. S. Su, Energy Environ. Sci., 2014, 7, 576–591 RSC.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Norskov, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed.
- S. M. Lee, K. H. An, Y. H. Lee, G. Seifert and T. Frauenheim, J. Am. Chem. Soc., 2001, 123, 5059–5063 CrossRef CAS PubMed.
- M. P. Suh, H. J. Park, T. K. Prasad and D. W. Lim, Chem. Rev., 2012, 112, 782–835 CrossRef CAS PubMed.
- S. S. Han, H. Furukawa, O. M. Yaghi and W. A. Goddard, J. Am. Chem. Soc., 2008, 130, 11580–11581 CrossRef CAS PubMed.
- H. Furukawa and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 8875–8883 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental section, additional analyses, characterizations and measurement results. See DOI: https://doi.org/10.1039/d3nh00462g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O,
O,