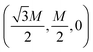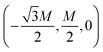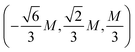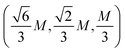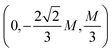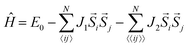CoX₂Y₄: a family of two-dimensional magnets with versatile magnetic order

Abstract

Two-dimensional (2D) magnetic materials offer a promising platform for nanoscale spintronics and for exploration of novel physical phenomena. Here, we predict a diverse range of magnetic orders in cobalt-based 2D single septuple layers CoX₂Y₄, namely, CoBi₂Te₄, CoBi₂Se₂Te₂, CoBi₂Se₄, and CoSb₂Te₄. Notably, CoBi₂Te₄ presents intrinsic non-collinear antiferromagnetism (AFM), while the others display collinear AFM. The emergence of AFM in all CoX₂Y₄ materials is attributed to the antiferromagnetic 90° Co–Te(Se)–Co superexchange coupling. The origin of non-collinear/collinear orders lies in competing Heisenberg exchange interactions within the Co triangular lattice. A pivotal factor governing the non-collinear order of CoBi₂Te₄ is the vanishingly small ratio of exchange coupling between next-nearest neighbour Co and the nearest neighbour Co (J₂/J₁ ∼ 0.01). Furthermore, our investigation into strain effects on CoX₂Y₄ lattices demonstrates the tunability of the magnetic state of CoSb₂Te₄ from collinear to non-collinear. Our prediction of the unique non-collinear AFM in 2D suggests the potential for observing extraordinary magnetic phenomena in 2D, including non-collinear scattering and magnetic domain walls.

---

New concepts

Since the ground-breaking discovery of intrinsically magnetic two-dimensional (2D) materials, there's been an intense race to spotlight new physical phenomena inherent to these materials and leverage them for cutting-edge spintronic applications. By harnessing the predictive power of first principles calculations along with Monte Carlo simulations, we introduce an innovative class of 2D magnetic materials CoX₂Y₄ exhibiting a diverse set of magnetic orders. This Co-based material family, which includes CoBi₂Te₄, CoBi₂Se₂Te₂, CoBi₂Se₄, and CoSb₂Te₄, represents a significant advance in our understanding of the intrinsically magnetic 2D materials: (i) in contrast to the typical collinear magnetic states prevalent in 2D materials, CoBi₂Te₄ exhibits an intrinsic non-collinear antiferromagnetic state. (ii) Antiferromagnetism in CoX₂Y₄ materials is induced by 90° superexchange interactions—historically correlated with ferromagnetism as in MnBi₂Te₄. This antiferromagnetism is attributed to the substantial π-bonding between Te(Se)-p_x and Co-d_xy orbitals. (iii) While the non-collinear magnetism has been typically associated with the Dzyaloshinskii–Moriya interaction, we illustrate that in the CoX₂Y₄ it originates from the competing Heisenberg exchange interaction. Our investigation not only widens the scope of 2D magnetic materials but also establishes a robust foundation for the exploration of new physical phenomena and the potential novel non-collinear spintronics applications.

Introduction

Intrinsically magnetic two-dimensional (2D) materials not only have attracted significant interest for their applications in nanoscale spintronics but also have become one of the most active fields in condensed matter research to study the fundamental physics of magnetism in reduced dimensions.^1–4 Since the discovery of few-layered van der Waals magnetism in Cr₂Ge₂Te₆⁵ and CrI₃,⁶ the family of 2D magnetic materials has developed rapidly.^6–12 Numerous demonstrations of new systems have been achieved in both ferromagnets (e.g., VSe₂,¹³ and Fe₃GeTe₂¹⁴) and antiferromagnets, such as MPX₃ materials (M  =  transition metal, X  =  S or Se).^15–17

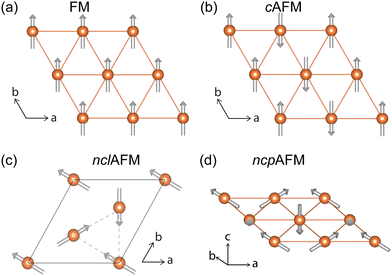
The majority of existing 2D magnetic materials have collinear spin orders, with all the spins being either parallel or antiparallel [see for example, Fig. 1(a) and (b)]. In contrast, non-collinear configurations represent situations in which spin direction varies across positions, devoid of a specific orientation as schematically depicted in Fig. 1(c). Unlike collinear spin orders, non-collinear configurations feature more complex arrangements such as spin spirals, helical structures, or random orientations. These configurations introduce additional degrees of freedom and tunability, leading to enhanced control over magnetic properties and novel emergent phenomena.^18–20 So far, non-collinear magnetism has mostly been observed in three-dimensional materials. For example, the kagome lattice in Mn₃Ir shows intrinsic non-collinear antiferromagnetism (nclAFM) and can exhibit a large anomalous Hall conductivity.^21,22 A recent work reported that the non-coplanar antiferromagnetism (ncpAFM) in triangular lattice compounds CoM₃S₆ (M = Nb, Ta) leads to a spontaneous topological Hall effect.²³ However, intrinsic non-collinear magnetism is rarely observed in 2D materials, imposing constraints on the development of spintronics based on low-dimensional non-collinear magnetism.

Fig. 1 Magnetic orders in CoX₂Y₄ SLs. (a) Ferromagnetic, (b) collinear antiferromagnetic, (c) non-collinear antiferromagnetic, and (d) non-coplanar antiferromagnetic order. Only Co atoms are shown for clarity. The on-site magnetic moment is specified by three components for each ion in the nclAFM and ncpAFM states. For the nclAFM state, the magnetic moments of three kinds of Co are , , and (0, −M, 0), respectively. The magnetic moments of four kinds of Co in the ncpAFM state are , , , and (0, 0, −M), respectively. M is the local magnetic moment per Co in CoX₂Y₄ SLs.

Numerous studies have been dedicated to achieving non-collinear magnetism in 2D materials, primarily through the application of external perturbations, including strain,^24,25 heterostructures,^26,27 and external magnetic or electric field.^28,29 For instance, 1T-CrTe₂ film exhibits ferromagnetic behavior with a high Curie temperature of 200 K, yet it can transition to a non-collinear spin texture under the influence of external magnetic field.²⁸ A recent theoretical study demonstrated that non-collinear magnetic states can be induced in various phases of 2D CrTe₂ through structural distortions.³⁰ Additionally, a 2D metal–organic framework can generate a non-collinear magnetic phase due to the dichotomy between frustrated local spins and conjugated electrons.³¹ Recent reports on non-collinear antiferromagnetism in vanadium-halide monolayers suggest they can serve as potential candidates for new multiferroic materials.^32,33 Despite these advancements, 2D materials with intrinsic non-collinear antiferromagnetism still remain largely unexplored.

One of the prominent mechanisms driving non-collinear magnetism is the Dzyaloshinskii–Moriya interaction (DMI), an antisymmetric exchange coupling resulting from spin–orbital coupling (SOC).^34,35 Crystal structures supporting DMI necessarily exhibit a broken inversion symmetry. In the realm of 2D magnetic materials, achieving intrinsically non-collinear magnetism through DMI without external perturbations poses a challenge, given that most 2D magnetic materials inherently maintain inversion symmetry. An alternative mechanism involves the competing Heisenberg interaction (J₁–J₂ model), which contains interactions not only between nearest neighbour spins (J₁) but also between next-nearest neighbours (J₂).^36–38 The decisive factor determining collinear or non-collinear magnetic orders is the ratio between J₂ and J₁, denoted as J₂/J₁. The application of J₁–J₂ model has been primarily focused on theoretical studies.^39–41 For instance, when examining a spin-½ state system on a triangular lattice, the nclAFM emerges as the magnetic ground state only when J₂/J₁ is less than 0.08. Within the range 0.08 ≲ J₂/J₁ ≲ 0.16, a quantum paramagnetic state prevails, and for larger values of J₂/J₁, a stripe collinear order is observed.⁴² Hence, small values of J₂/J₁ are pivotal in determining the non-collinear magnetic orders. However, the exploration of J₁–J₂ model within the realm of real materials has been relatively sparse. The competing Heisenberg interaction introduces an alternative strategy for investigating and discovering non-collinear magnetism in real 2D materials.

From the perspective of materials science, J₁ and J₂ originate from magnetic coupling between cations through superexchange and/or super–superexchange interactions.⁴³ The values of J₂/J₁ can vary depending on the composition of elements involved in these superexchange and/or super–superexchange interactions, leading to the emergence of different magnetic orders, including both collinear and non-collinear. Recently, the discovery of van der Waals MnBi₂Te₄-family materials has garnered significant interest in both 2D magnetism and topology.¹² This discovery provides a promising platform for exploring diverse magnetic orders arising from the exchange coupling between different transition metals. Here using a combination of first principles calculations and Monte Carlo simulations, we systematically investigated a series of cobalt-based 2D materials family CoX₂Y₄, specifically, CoBi₂Te₄, CoBi₂Se₂Te₂, CoBi₂Se₄ and CoSb₂Te₄. Our study reveals that CoBi₂Te₄ exhibits nclAFM with a Néel temperature of 10 K, which is associated with an antiferromagnetic J₁ and a tiny J₂/J₁ of approximately 0.01. Conversely, the exchange coupling strength between next-nearest neighbour Co is enhanced in CoBi₂Se₂Te₂, CoBi₂Se₄ and CoSb₂Te₄, resulting in a large J₂/J₁ and a collinear antiferromagnetism (cAFM) as the ground magnetic state rather than nclAFM configurations. Additionally, through our study of the impact of strains, we can conclude that applying tensile strains on the CoSb₂Te₄ lattice not only leads to a magnetic phase transition from cAFM to nclAFM but it also allows for a higher Néel temperature of 23 K. This work unveils a series of collinear and non-collinear antiferromagnetic 2D Co-based materials, shedding light on the intricate balance within the competing Heisenberg interaction and highlighting the role of mechanical strain as a control knob to induce magnetic phase transitions with higher Néel temperatures.

Computational methods

We performed structural optimization and magnetic property calculations for 2D CoX₂Y₄ family using plane-wave density functional theory⁴⁴ within the generalized gradient approximation (GGA)⁴⁵ as implemented in the VASP package.^46,47 A cut-off energy of 500 eV and a 12 × 12 × 1 Monkhorst–Pack mesh ensured a good convergence. We used an effective Hubbard U of 4 eV in Dudarev's scheme to adjust Co 3d-states,^48,49 consistent with literature for MnBi₂Te₄ and NiBi₂Te₄.¹² As magnetic properties of transition metal compounds rely on the U and J parameters, we assessed total energies of magnetic states of CoX₂Y₄ SLs under different schemes with varying U or J values. Through extensive testing, the ground magnetic states of CoX₂Y₄ SLs are robust under various effective U values ranging from 1 eV to 6 eV and J values ranging from 0 eV to 1 eV, see ESI† for more details. Crystal orbital Hamiltonian populations (COHPs) were calculated via the LOBSTER package to assess the orbital overlaps.^50,51 Néel temperatures were calculated by using Monte Carlo simulations. The hopping energies of super–superexchange interactions were calculated based on the tight-binding models of CoX₂Y₄ SLs as implemented in wannier90 code.⁵² Phonon dispersions were calculated using Phonopy code,⁵³ with force constants obtained from density functional theory calculations. See ESI† for further details on the computational methods.

Results and discussion

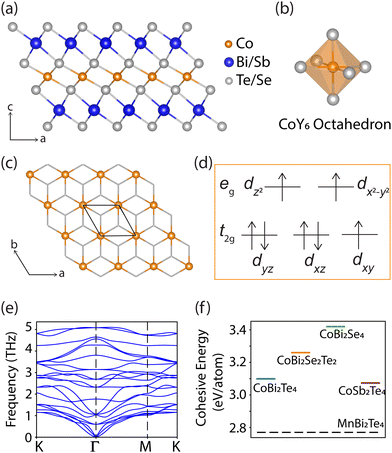
We systematically investigated a series of 2D CoX₂Y₄ materials CoBi₂Te₄, CoBi₂Se₂Te₂, CoBi₂Se₄ and CoSb₂Te₄. The fully relaxed single septuple layers (SL) of these materials stabilize in a trigonal crystal lattice with R3̄m space group, sharing a crystal structure similar with MnBi₂Te₄.^12,54 Taking CoBi₂Te₄ as an example, its septuple layer has Te–Bi–Te–Co–Te–Bi–Te stacking configuration, as shown in Fig. 2(a). In all 2D CoX₂Y₄ materials considered here, Co cations located in the middle atomic layer are on the same plane, forming a triangular lattice. These Co cations do not bond to each other directly; instead, they interact with each other via Co–Te(Se)–Co bonds [Fig. 2(a) and (c)]. Te(Se) acts as an intermediary between Co connections with every two nearest neighbouring Co atoms forming a Co–Te(Se)–Co bridge. Each Co cation has a six-fold coordination with the nearest Te(Se) anions forming a CoY₆ octahedron as shown in Fig. 2(b). Details of the crystal structures of all 2D CoX₂Y₄ materials are provided in Tables S1 and S2, ESI.†

Fig. 2 Crystal structure, electronic structure, and stability of 2D septuple layers of CoX₂Y₄ (CoBi₂Te₄, CoBi₂Se₂Te₂, CoBi₂Se₄, and CoSb₂Te₄). (a) and (b) Crystal structure of the CoX₂Y₄ SLs. (c) The top view of the arrangement of Co cations, the solid lines represent a unit cell. (d) Energy level diagram of Co²⁺ cation in CoX₂Y₄ SL. (e) Phonon dispersion of CoBi₂Te₄ SL (without magnetism) as an illustrative example; the absence of imaginary frequencies indicates its dynamic stability. (f) Cohesive energies of CoBi₂Te₄, CoBi₂Se₂Te₂, CoBi₂Se₄, and CoSb₂Te₄ SLs referred to that of MnBi₂Te₄ SL (dash line).

The magnetism of transition metals is dominated by d-electrons occupancy. According to the crystal field theory,⁵⁵ the d orbitals of the transition metal in octahedral coordination result in three triple-degenerate low energy t_2g (d_xz, d_yz, d_xy) orbitals and two double-degenerate high energy e_g (d_z², d_x²–y²) orbitals. Based on the chemical stoichiometry of all CoX₂Y₄ materials each Co has a valence of +2 by losing two s-electrons and remains seven electrons on d orbitals. The seven d-electrons can lead to a high-spin state of S = 3/2 or a low-spin state of S = 1/2 for Co in CoX₂Y₄. By comparing the total energies of high-spin and low-spin states, we found that high-spin states possess lower total energies in all cases (Table S3, ESI†), which is line with the high-spin state of Mn (i.e., S = 5/2) in MnBi₂Te₄. Hence, our focus for investigating the magnetism of the CoX₂Y₄ system lies on the ground spin state, specifically emphasizing the high-spin state of 3/2. In the high-spin state of Co, five d-electrons predominantly occupy the spin-up state of each d orbital, while the remaining two electrons occupy the spin-down state of the degenerate t_2g orbitals with lower energy [refer to Fig. 2(d)]. The projected density of states (PDOS) supports the high-spin state for the Co atom in CoX₂Y₄ systems, as depicted in Fig. S1, ESI.† The calculated local magnetic moment on Co in CoX₂Y₄ is ∼2.8 μ_B, providing a strong magnetism in the materials. This is further supported by the spatial spin charge density distribution (Fig. S2, ESI†).

To assess the dynamical stability and feasibility of experimental synthesis of CoX₂Y₄ single layers, we evaluated their phonon dispersions and cohesive energies. In all cases without considering magnetism, the absence of any imaginary phonon modes across the entire Brillouin zone suggests their dynamical stability [see Fig. 2(e) for example, and Fig. S3 in the ESI†]. Given the collinear or non-collinear antiferromagnetic nature of the ground magnetic states of CoX₂Y₄, as discussed below, we also evaluated the dynamical stability under their ground magnetic states, as illustrated in Fig. S3, ESI.† The phonon dispersions of CoBi₂Se₂Te₂, CoBi₂Se₄ and CoSb₂Te₄ SLs with collinear antiferromagnetic configuration showcase their robust dynamical stability. In the phonon dispersion of CoBi₂Te₄ SL under the consideration of non-collinear antiferromagnetic state, no significant imaginary mode was observed along the high-symmetry pathway, but with an increase in phonon softening of up to −0.19 THz around the Γ point. To mitigate these imaginary modes, larger supercells and enhanced computational precision are recommended. However, due to computational constraints related to non-collinear magnetism and the requirement of large supercells, achieving a more precise phonon dispersion for non-collinear antiferromagnetic CoBi₂Te₄ SL is beyond our current capability. To provide further information about this point, we also investigated the phonon dispersions of CoBi₂Te₄ SL in other magnetic orders including collinear ferromagnetic and antiferromagnetic states. Compared to non-magnetic phonon dispersion, neither magnetic state exhibits significant phonon softening. These results suggest that incorporating magnetism into the CoBi₂Te₄ lattice does not disturb its dynamical stability. Furthermore, we compared the cohesive energy of CoBi₂Te₄, CoBi₂Se₂Te₂, and CoBi₂Se₄ and CoSb₂Te₄ SLs with that of MnBi₂Te₄, a well-known material in the MnBi₂Te₄ family, which has been synthesized successfully and been the subject of intense recent research efforts.^56–58 The cohesive energies of CoBi₂Te₄, CoBi₂Se₂Te₂, CoBi₂Se₄, and CoSb₂Te₄ SLs are 3.10, 3.26, 3.43, and 3.07 eV per atom respectively, significantly higher than that of MnBi₂Te₄ (2.77 eV per atom), indicating strong feasibility of being synthesized in experiments [Fig. 2(f)]. We also assessed the formation energies of these CoX₂Y₄ SLs relative to elemental solids. The phases of the elemental solids considered to assess the formation energies are Fm3̄m Co, R3̄m Bi, R3̄m Sb, P3₁21 Te, and P3₁21 Se. Negative formation energies indicate thermodynamic stability of CoX₂Y₄ SLs, as summarized in Table S4 in ESI.†

We next investigated the ground state magnetic configuration of CoX₂Y₄ SLs by considering four distinct configurations as depicted in Fig. 1: (a) ferromagnetic (FM), (b) collinear antiferromagnetic (cAFM), (c) non-collinear antiferromagntic (nclAFM), and (d) non-coplanar antiferromagntic (ncpAFM). Upon comparing the total energies of all configurations, we found that cAFM [Fig. 1(b)] is the most stable magnetic state for CoBi₂Se₂Te₂, CoBi₂Se₄ and CoSb₂Te₄ SLs, whereas the intralayer nclAFM is the magnetic ground state for CoBi₂Te₄ SL [Fig. 1(c)]. The energy differences among different magnetic configurations without considering spin–orbital coupling (SOC) among different magnetic configurations are presented in Table 1. We noted that the magnetic ground states for CoX₂Y₄ SLs remain unchanged when SOC is considered, indicating the stability of the magnetic configurations (see Table S5, ESI†). Thus, we excluded SOC in the subsequent discussion.

Table 1 Magnetic properties of CoX₂Y₄ SLs. Local magnetic moments per Co (M), ΔE is the energy differences (without considering spin–orbital coupling) relative to the ferromagnetic configuration, exchange coupling parameters between nearest and next-nearest neighbouring Co atoms (J₁ and J₂), the magnetic anisotropy energy (MAE) considering spin–orbital coupling per Co (MAE = E_in-plane − E_out-of-plane), and Néel temperature (T_N)

	M (μB per atom)	ΔEcAFM (meV f.u.^−1)	ΔEnclAFM (meV f.u.^−1)	ΔEncpAFM (meV f.u.^−1)	J 1 (meV)	J 2 (meV)	J 2/J1	MAE (meV)	Easy axis	T N (K)
CoBi2Te4	2.76	−7.39	−8.21	−6.59	−0.82	−0.01	0.01	−0.18	In-plane	10
CoBi2Se2Te2	2.81	−10.37	−9.74	−9.82	−0.96	−0.19	0.20	0.04	Out-of-plane	22
CoBi2Se4	2.82	−6.25	−5.91	−5.64	−0.58	−0.11	0.19	0.08	Out-of-plane	13
CoSb2Te4	2.73	−8.03	−7.09	−7.20	−0.70	−0.19	0.27	−0.18	In-plane	19

---

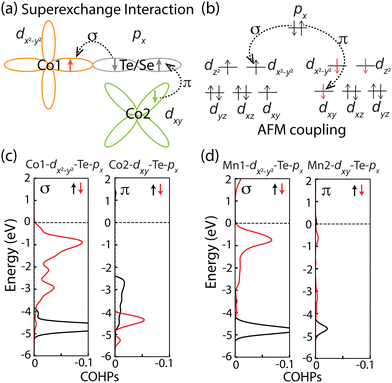
The antiferromagnetic ordering in CoX₂Y₄ SLs results from the antiferromagnetic exchange interaction between nearest neighbour Co cations. This interaction is dominated by the Co–Te(Se)–Co superexchange interaction, because the direct exchange coupling between Co is very weak due to a long distance between nearest neighbour Co ions (for example, the nearest Co–Co distance in CoBi₂Te₄ SL is 4.33 Å). The angles of the Co–Te(Se)–Co bridge in all CoX₂Y₄ SLs are close to the 90° (see Table S1 in the ESI†). According to Goodenough–Kanamori–Anderson rules,^59–61 the 90° superexchange coupling typically contributes to a FM state. Two common explanations exist: in one scenario, illustrated in Fig. S4, ESI,† the p_x and p_y orbitals of the central anion engage in σ bonds with the d orbital of neighbouring cations, resulting in FM coupling due to the orthogonality between p_x and p_y and lack of overlap. Alternatively, another explanation posits that the p_x/p_y orbital forms a σ bond with one cation while being orthogonal to the other cation, also leading to FM coupling (see Fig. S4b and c, ESI†). Both explanations underscore the FM nature of the 90° superexchange arising from orbital orthogonality without overlap in the superexchange channel. However, an AFM behaviour can be induced through the superexchange channel with continuous orbital overlapping.

In the Co–Te(Se)–Co superexchange coupling, one electron of the Te(Se)-p_x/p_y orbital can hop over to the Co-d_x²–y² orbital, referred to as a σ bond. Due to the Pauli principle, only the spin-down electron can hop to the d_x²–y²-orbital, because the d_x²–y²-orbital is occupied by a spin-up electron. The remaining spin-up electron of the p_x/p_y orbital will then enter into a direct exchange with the other Co of the Co–Te(Se)–Co bridge. Although the Te(Se)-p_x/p_y orbital is orthogonal to the d_x²–y²-orbital of the other Co, it can form a π bond with the d_xy-orbital, which shifts the electron to be spin-down. Thus, the entire Co–Te(Se)–Co presents an antiferromagnetic superexchange coupling, as illustrated in Fig. 3(a) and (b). The superexchange pathways via Te(Se)-p_x or Te(Se)-p_y are equivalent (Fig. S4d and f, ESI†), thus we take the Te(Se)-p_x channel as an example for the further discussion.

Fig. 3 The origin of the exchange coupling between nearest neighbour Co. (a) Superexchange coupling between the nearest neighbour Co 3d orbital via Te(Se) 5p orbital. (b) Schematics of antiferromagnetic superexchange interaction between Co1-d_x²–y²–Te(Se)-p_x and Co2-d_xy–Te(Se)-p_x. (c) The crystal orbital Hamiltonian populations (COHPs) of the overlap between Co1-d_x²–y²–Te-p_x orbitals and between Co2-d_xy–Te-p_x orbitals in CoBi₂Te₄ SL. (d) The COHPs of the overlap between Mn1-d_x²–y²–Te-p_x orbitals and between Mn2-d_xy–Te-p_x orbitals in MnBi₂Te₄ SL. The black and red solid lines represent spin-up and spin-down states of orbital overlap, respectively.

The p–d orbital overlap between Co and Te(Se) referred to as the σ and π bonds can be calculated through the crystal orbital Hamiltonian populations (COHPs) of the Co–Te(Se) bonds. See Fig. 3(c) for the COHPs for the overlap between the Te-p_x–Co1-d_x²–y² and Te-p_x–Co2-d_xy for the Co1–Te–Co2 bridge in CoBi₂Te₄ SL. Negative COHPs indicate the electrons at bonding energy level. The COHPs for the overlap between Te-p_x–Co1-d_x²–y² is relatively large, and the integrated bonding orbital is −0.22 eV, indicating a stronger σ bond. The COHPs for the overlap between Te-p_x–Co2-d_xy is relatively weak, with the integrated value of −0.06 eV, which indicates the π bond. The appearance of the σ and π bond of Te-p–Co-d leads to the antiferromagnetic coupling. The σ and π bonds of Te(Se)-p–Co-d in CoBi₂Se₂Te₂, CoBi₂Se₄, and CoSb₂Te₄ SLs are also confirmed by COHPs calculations as shown in Fig. S5 (ESI†), resulting in an antiferromagnetic coupling in all cases.

Other transition metals in MnBi₂Te₄-family materials, e.g., V, Mn, and Ni, have a similar structure with CoBi₂Te₄.^12,54,62 The angle of their superexchange bridge is also close to 90°, and they obey the same superexhange coupling rules; however, they present FM configuration as their ground state. To illustrate the role of superexchange interaction in determining the magnetic ground state in CoBi₂Te₄, we also calculated the COHPs of MnBi₂Te₄ to evaluate the strength of σ and π bonds. As illustrated in Fig. 3(d), the strength of the σ bond between Mn1-d_x²–y²–Te-p_x is comparable to Co. However, the π bond in MnBi₂Te₄ is very weak with the total bonding level of −0.005 eV, an order of magnitude smaller than in CoBi₂Te₄. Such a weak π bond cannot invert the d_xy-electron, thereby leading to a ferromagnetic superexchange coupling. In addition, the mechanism of the ferromagnetic superexchange coupling of V and Ni can be understood easily. The d_x²–y²-orbital of V is empty, and d_xy-orbital of Ni is fully filled, thus they cannot undergo the AFM coupling. Schematic diagrams for superexchange coupling for V and Ni are shown in Fig. S6 (ESI†).

Non-collinear magnetism can usually be explained by the Dzyaloshinskii–Moriya interaction (DMI)^34,63 or the double-exchange interaction (DE)^64,65 or the competing Heisenberg exchange interaction. The DMI is associated with inversion symmetry breaking, and DE arises between ions in different oxidation states. In CoBi₂Te₄, the R3̄m crystal symmetry preserves the inversion symmetry, and all Co ions have the same valence/oxidation states. Thus, it can be anticipated that nclAFM in CoBi₂Te₄ arises from the competing Heisenberg exchange interaction. On the other hand, CoBi₂Se₂Te₂, CoBi₂Se₄ and CoSb₂Te₄ SLs present cAFM as the ground magnetic state, which is expected to exhibit a different magnitude of J₂/J₁ from that of CoBi₂Te₄. Therefore, we next explored the Heisenberg exchange model of these CoX₂Y₄ SLs for a comparison.

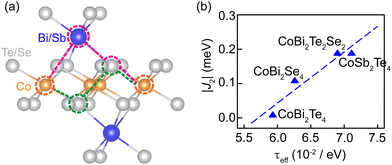
We calculated the exchange coupling parameters between nearest and next-nearest neighbour Co cations (J₁ and J₂) based on a Heisenberg model. In this model, the spin Hamiltonian is defined as

where E₀ is the reference energy, S_i is the spin of ith Co, the summation 〈ij〉 runs over all nearest neighbour Co sites, and the summation 〈〈ij〉〉 runs over all next-nearest neighbour Co sites. The exchange coupling parameters J₁ and J₂ are derived from the mapping analysis of the FM, cAFM and nclAFM configurations, see computational details in the ESI† for more details. As listed in Table 1, the calculated J₁ values of CoBi₂Te₄, CoBi₂Se₂Te₂, CoBi₂Se₄, and CoSb₂Te₄ SL are −0.82 meV, −0.96 meV, −0.58 meV and −0.70 meV, respectively. The negative J₁ in all cases indicates an antiferromagnetic exchange interaction, in line with the above analysis of antiferromagnetic superexchange coupling of Co–Te(Se)–Co. On the other hand, the J₂ values significantly vary among CoX₂Y₄. The J₂ of CoBi₂Se₂Te₂, CoBi₂Se₄, and CoSb₂Te₄ SLs is −0.19 meV, −0.11 meV, and −0.19 meV respectively, which results in relatively large J₂/J₁. In contrast, CoBi₂Te₄ has a J₂ value of −0.01 meV (J₂/J₁ ∼ 0.01), indicating a weak exchange coupling between next-nearest neighbour Co in CoBi₂Te₄. The large J₂/J₁ ratio in CoBi₂Se₂Te₂, CoBi₂Se₄, and CoSb₂Te₄ SLs lead to the formation of cAFM states, while a small J₂/J₁ in CoBi₂Te₄ SL results in a nclAFM configuration. Therefore, the formation of nclAFM in CoBi₂Te₄ SL is attributed to the small J₂/J₁, satisfying the competing Heisenberg interaction.

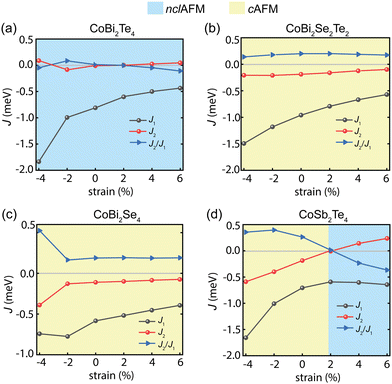
Looking at the structure of CoX₂Y₄ SLs, we observe that the exchange coupling between next-nearest neighbour Co can occur through multiple intermediate atoms, referred to as super–superexchange couplings. We analyzed two super–superexchange coupling channels: Co–Te(Se)–Bi(Sb)–Co and Co–Te(Se)–Te(Se)–Co, to compare the strength of exchange coupling between next-nearest neighbour Co within these CoX₂Y₄ SLs (Fig. 4(a)). Each super–superexchange coupling channel comprises three hopping fragments: Co–Te(Se), Te(Se)–Bi(Sb), and Bi(Sb)–Co in the Co–Te(Se)–Bi(Sb)–Co channel; and Co–Te(Se), Te(Se)–Te(Se), and Te(Se)–Co in the Co–Te(Se)–Te(Se)–Co channel. We calculated the hopping energies (τ) of each hopping fragment based on the tight-binding model (see Table S6, ESI†). The strength of the super–superexchange coupling can then be determined by the total hopping energy, which involves multiplying the energies of each fragment. The super–superexchange coupling emerges as the cumulative effect of these two channels (τ_eff).

τ_{Co–Te(Se)–Bi(Sb)–Co} = τ_Co–Te(Se)τ_{Te(Se)–Bi(Sb)}τ_Bi(Sb)–Co

τ_{Co–Te(Se)–Te(Se)–Co} = τ_Co–Te(Se)τ_{Te(Se)–Te(Se)}τ_Te(Se)–Co

τ_eff = τ_{Co–Te(Se)–Bi(Sb)–Co} + τ_{Co–Te(Se)–Te(Se)–Co}

As can be seen in Fig. 4(b), J₂ exhibits a strong correlation with τ_eff with an approximately linear relationship. Large J₂ values, i.e., 0.11 meV of CoBi₂Se₄, 0.19 meV of CoBi₂Se₂Te₂ and CoSb₂Te₄, are attributed to the strong super–superexchange coupling, while small J₂ of 0.01 meV for CoBi₂Te₄ aligns with a weak super–superexchange coupling. Besides, the weaker coupling in CoBi₂Te₄ compared to the others is associated with its larger bond lengths. Specifically, the smaller hopping energies along the Co–Te(Se)–Bi–Co pathway in CoBi₂Te₄ (i.e., 2.7 meV) explains this weaker coupling, in contrast to 7.3 meV for CoBi₂Se₄ and 9.6 meV for CoBi₂Se₂Te₂. This difference is further linked to the varying hopping energies between Bi–Co bonds: 0.04 eV for CoBi₂Te₄, 0.09 eV for CoBi₂Se₄, and 0.12 eV for CoBi₂Se₂Te₂. Notably, the hopping energy is inversely proportional to the bond length, which measures 4.38 Å for CoBi₂Te₄, 4.11 Å for CoBi₂Se₄, and 4.07 Å for CoBi₂Se₂Te₂ (see the information of bond lengths of CoX₂Y₄ in Table S2, ESI†). In comparison to CoSb₂Te₄, the weaker super–superexchange coupling in CoBi₂Te₄ is characterized by smaller hopping energies in the Co–Te–Te–Co channel: 0.057 eV for CoBi₂Te₄versus 0.068 eV for CoSb₂Te₄. This difference is due to the hopping fragment between Co–Te, i.e., 0.23 eV for CoBi₂Te₄, and 0.25 eV for CoSb₂Te₄, which is associated with bond lengths of 2.88 Å in CoBi₂Te₄ and 2.85 Å in CoSb₂Te₄. Consequently, CoBi₂Te₄ SL, which features the longest Co–Y, Y–Y, Y–X, and X–Co bonds among the CoX₂Y₄ SL family, shows the smallest J₂. This explains why nclAFM is exclusively observed in CoBi₂Te₄ SL according to the competing Heisenberg model.

Fig. 4 The origin of the exchange coupling between next-nearest neighbour Co. (a) The Co–Te(Se)–Bi(Sb)–Co (pink dash line) and Co–Te(Se)–Te(Se)–Co (green dash line) super–superexchange channels. The super–superexchange channels with orbital shapes are depicted in Fig. S7, ESI.† (b) The correlation between the τ_eff and |J₂| for CoX₂Y₄ SLs.

The Néel temperature represents the critical point at which antiferromagnetic materials lose their permanent magnetism. To calculate the Néel temperatures of CoX₂Y₄ SLs, in addition to exchange coupling parameters, we need to consider the magnetic anisotropy energy (MAE). MAE calculations were performed for all CoX₂Y₄ SLs along three high-symmetry directions, i.e., [100], [010], and [001], by considering spin–orbital coupling. The MAE of CoBi₂Te₄ and CoSb₂Te₄ is −0.18 meV, suggesting an in-plane easy axis. CoBi₂Se₂Te₂ and CoBi₂Se₄ exhibit an out-of-plane easy axis with positive MAE values of 0.04 and 0.08 meV, respectively. Using the MAE and exchange coupling parameters (J₁ and J₂), we estimated Néel temperatures through Monte Carlo simulations. The calculated Néel temperatures of CoBi₂Te₄, CoBi₂Se₂Te₂, CoBi₂Se₄ and CoSb₂Te₄ SLs are 10, 22, 13 and 19 K, respectively (see Fig. S8, ESI†), which are comparable to that of few-layered CrI₃ (17 K)^10,66 and MnBi₂Te₄ SL (12 K).⁵⁴

Since the MAE values in the CoX₂Y₄ SLs are of small magnitude, and are usually sensitive to the J parameters,⁶⁷ we tested the MAE under different J values (ranging from 0 to 1 eV) using the Liechtenstein approach. As shown in Fig. S9 (ESI†), with increasing J, the in-plane easy axis becomes energetically more favourable over out-of-plane axis. CoBi₂Te₄ and CoSb₂Te₄ retain an in-plane easy axis. CoBi₂Se₄ maintains an out-of-plane easy axis with reduced MAE, while the magnetic easy axis of CoBi₂Se₂Te₂ changes from out-of-plane to in-plane above 0.5 eV of J. Another factor that can influence magnetic anisotropy is the magnetic dipole–dipole interactions.^68–70 We examined the effect of dipole–dipole interactions on MAE. The dipole–dipole interaction energy is on the order of μeV; it does not alter the easy axes of CoX₂Y₄ SLs after dipole–dipole corrections. The MAE values with combined effects of SOC and dipole–dipole interactions of CoBi₂Te₄, CoSb₂Te₄, CoBi₂Se₂Te₂ and CoBi₂Se₄ are −0.17 meV, −0.17 meV, 0.05 meV, and 0.09 meV, respectively (see Table S7 in ESI† for more details).

Magnetic properties of 2D materials can often be tuned by applying strains.^71–73 Given that the formation of collinear or non-collinear states in CoX₂Y₄ is linked to the strength of the exchange coupling, it is worthwhile to investigate the effect of strain on the magnetic orders of all CoX₂Y₄ lattices studied here. We considered in-plane biaxial strains in CoX₂Y₄ lattices in the range of −4% to 6%, see Fig. 5. The J₁ values of CoBi₂Te₄, CoBi₂Se₂Te₂ and CoBi₂Se₄ undergo significant changes with strain, where compressing the lattice enhances the strength of exchange coupling and conversely, stretching the lattice weakens the coupling strength. The J₂ values of CoBi₂Te₄, CoBi₂Se₂Te₂ and CoBi₂Se₄ are not sensitive to strain, and J₂/J₁ ratio does not change significantly with strain [Fig. 5(a)–(c)]. Consequently, the nclAFM state of CoBi₂Te₄ and cAFM states of CoBi₂Se₂Te₂ and CoBi₂Se₄ remain robust. On the other hand, for CoSb₂Te₄, compressive lattice strain enhances the exchange coupling, while the coupling remains relatively robust under tensile strain. Notably, the J₂ parameter of CoSb₂Te₄ is sensitive to biaxial strain. As depicted in Fig. 5(d), positive tensile strain in the case where the lattice is stretched, it hugely weakens the AFM coupling between next-nearest neighbour Co atoms. Above 2% biaxial strain, J₂ in CoSb₂Te₄ transitions to positive values, indicating a transition from AFM to FM coupling between next-nearest neighbour Co atoms. Above this strain, the nclAFM state becomes the ground magnetic state of CoSb₂Te₄ SL. This result highlights that the nclAFM state can also arise from a negative J₂/J₁, attributed to the competition between AFM J₁ and FM J₂. Among the three cAFM materials, i.e., CoBi₂Se₂Te₂, CoBi₂Se₄ and CoSb₂Te₄, only CoSb₂Te₄ demonstrates a strain-tuned magnetic phase transition from collinear to non-collinear configurations. The transition is attributed to the significant alterations in the J₂ parameter of CoSb₂Te₄ under strain, distinguishing it from CoBi₂Se₂Te₂ and CoBi₂Se₄. A possible factor driving the transformation of J₂ from AFM to FM coupling in CoSb₂Te₄ is the domination of FM super–superexchange couplings between next-nearest neighbour Co under tensile strains. This coupling channel arises from the combination of two superexchange interactions: Co–Te(Se)–Co–Te(Se)–Co (Fig. S10, ESI†). In this channel, the FM super–superexchange coupling parameter J^FM₂ is proportional to J₁, i.e., J^FM₂ ∼ J₁. Examining the curvature of J₁ in CoBi₂Se₂Te₂, CoBi₂Se₄ and CoSb₂Te₄ reveals that CoSb₂Te₄ maintains large J₁ values under positive strains, in contrast to the declining J₁ observed in CoBi₂Se₂Te₂ and CoBi₂Se₄. This robust J₁ under strain can be attributed to the larger orbital radius of Te compared to Se, which fosters strong FM super–superexchange couplings in CoSb₂Te₄, hastening the transition of J₂ from AFM to FM coupling. Furthermore, we evaluated the Néel temperatures of the nclAFM state of CoSb₂Te₄ SL under strains of 2%, 4% and 6%, which can reach approximately 8, 18 and 23 K, respectively, as shown in Fig. S11 (ESI†). The increase of the Néel temperatures lies on the enhanced exchange coupling parameters under the strains. Therefore, applying strain can be considered as an effective means to tune the Néel temperatures.

Fig. 5 Magnetic state transitions in CoX₂Y₄ SLs with in-plane biaxial strain. The variation of J₁, J₂ and J₂/J₁ of CoBi₂Te₄ (a), CoBi₂Se₂Te₂ (b), CoBi₂Se₄ (c), and CoSb₂Te₄ (d) with in-plane biaxial strain. The blue and yellow zone represents the nclAFM and cAFM magnetic state, respectively.

Subsequently, we conducted band structure calculations of these systems: nclAFM CoBi₂Te₄, cAFM CoBi₂Se₂Te₂, cAFM CoBi₂Se₄, and cAFM CoSb₂Te₄ SLs. These analyses revealed that all of them exhibit characteristics of indirect insulators, displaying relatively large band gaps at the PBE level of theory (see Fig. S12, ESI†). Upon inclusion of SOC, noticeable changes occur in the band structures, resulting in a reduction of the band gap across all cases. Particularly noteworthy is a significant decrease observed in the band gap of CoBi₂Te₄, dropping from 0.96 eV without SOC to 0.31 eV with SOC. This drastic alteration is attributed to the pronounced effect of SOC on heavy atoms. In contrast to the cAFM configurations featuring doubly degenerate bands, the band structure of nclAFM CoBi₂Te₄ exhibits a more complex arrangement with non-degenerate bands.

Conclusions

In summary, we predicted a series of stable, Co-based intrinsically magnetic materials. Among them, CoBi₂Te₄ SL presents a nclAFM state, while CoBi₂Se₂Te₂, CoBi₂Se₄ and CoSb₂Te₄ SLs are cAFM. The antiferromagnetic states of CoX₂Y₄ SLs arise from the AFM 90° superexchange interaction between nearest neighbour Co atoms, which can be attributed to strong π bond of p_x–d_xy overlapping. The non-collinear configuration of CoBi₂Te₄ results from a small J₂/J₁ ratio of ∼0.01, associated by a very weak exchange coupling between next-nearest neighbour Co atoms (J₂ of −0.01 meV) induced by weak super–superexchange couplings. The collinear states of CoBi₂Se₂Te₂, CoBi₂Se₄, and CoSb₂Te₄ SLs are consistent with large J₂/J₁ ratios, which aligns with relatively strong super–superexchange couplings. Our investigation into the impact of strains on CoX₂Y₄ lattices reveals that the magnetic order of CoSb₂Te₄ can be tuned from collinear to non-collinear under strain, while the magnetic states of the other materials remain unchanged as their ground state. The CoSb₂Te₄ with nclAFM state can reach a higher Néel temperature of 23 K, which is attributed to the enhanced exchange coupling parameter under strains. Our predictions of these 2D CoX₂Y₄ materials not only broaden horizons for 2D magnets but also propose a potential strategy for searching for more novel non-collinear orders. Notably, the unique nclAFM state, characterized by non-collinear scattering patterns differing from collinear states, holds the promise of unveiling extraordinary magnetoelectric phenomena in 2D, such as the induction of anomalous Hall effect, thus motivating a further in-depth exploration.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare that they have no conflicts of interest.

Acknowledgements

The authors acknowledge support of the ARC Centre of Excellence FLEET (CE170100039) and the computational support from Australian National Computing Infrastructure (NCI) and the Pawsey Supercomputing Centre.

References

1. K. S. Burch, D. Mandrus and J.-G. Park, Nature, 2018, 563, 47–52.
2. M. Gibertini, M. Koperski, A. F. Morpurgo and K. S. Novoselov, Nat. Nanotechnol., 2019, 14, 408–419.
3. C. Gong and X. Zhang, Science, 2019, 363, eaav4450.
4. K. F. Mak, J. Shan and D. C. Ralph, Nat. Rev. Phys., 2019, 1, 646–661.
5. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269.
6. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273.
7. J. Tang, S. Li, D. Wang, Q. Zheng, J. Zhang, T. Lu, J. Yu, L. Sun, B. Sa, B. G. Sumpter, J. Huang and W. Sun, Nanoscale Horiz., 2024, 9, 162–173.
8. C. Tang, K. K. Ostrikov, S. Sanvito and A. Du, Nanoscale Horiz., 2021, 6, 43–48.
9. B. Li, Z. Wan, C. Wang, P. Chen, B. Huang, X. Cheng, Q. Qian, J. Li, Z. Zhang, G. Sun, B. Zhao, H. Ma, R. Wu, Z. Wei, Y. Liu, L. Liao, Y. Ye, Y. Huang, X. Xu, X. Duan, W. Ji and X. Duan, Nat. Mater., 2021, 20, 818–825.
10. M. Hossain, B. Qin, B. Li and X. Duan, Nano Today, 2022, 42, 101338.
11. Z. Liu, X. Li, W. Zhu, Z. F. Wang and J. Yang, Phys. Rev. B, 2023, 107, 014413.
12. J. Li, Y. Li, S. Du, Z. Wang, B.-L. Gu, S.-C. Zhang, K. He, W. Duan and Y. Xu, Sci. Adv., 2019, 5, eaaw5685.
13. M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289–293.
14. Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, W. Wu, D. H. Cobden, J.-H. Chu and X. Xu, Nat. Mater., 2018, 17, 778–782.
15. J.-U. Lee, S. Lee, J. H. Ryoo, S. Kang, T. Y. Kim, P. Kim, C.-H. Park, J.-G. Park and H. Cheong, Nano Lett., 2016, 16, 7433–7438.
16. C.-T. Kuo, M. Neumann, K. Balamurugan, H. J. Park, S. Kang, H. W. Shiu, J. H. Kang, B. H. Hong, M. Han, T. W. Noh and J.-G. Park, Sci. Rep., 2016, 6, 20904.
17. M. A. Susner, M. Chyasnavichyus, M. A. McGuire, P. Ganesh and P. Maksymovych, Adv. Mater., 2017, 29, 1602852.
18. S.-W. Cheong and F.-T. Huang, npj Quantum Mater., 2024, 9, 1–6.
19. A. Taga, L. Nordström, P. James, B. Johansson and O. Eriksson, Nature, 2000, 406, 280–282.
20. H. Ishizuka and N. Nagaosa, Sci. Adv., 2018, 4, eaap9962.
21. H. Chen, Q. Niu and A. H. MacDonald, Phys. Rev. Lett., 2014, 112, 017205.
22. Y. Zhang, Y. Sun, H. Yang, J. Železný, S. P. P. Parkin, C. Felser and B. Yan, Phys. Rev. B, 2017, 95, 075128.
23. H. Takagi, R. Takagi, S. Minami, T. Nomoto, K. Ohishi, M.-T. Suzuki, Y. Yanagi, M. Hirayama, N. D. Khanh, K. Karube, H. Saito, D. Hashizume, R. Kiyanagi, Y. Tokura, R. Arita, T. Nakajima and S. Seki, Nat. Phys., 2023, 1–8.
24. E. Simon, K. Palotás, L. Rózsa, L. Udvardi and L. Szunyogh, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 094410.
25. C. Deger, Sci. Rep., 2020, 10, 12314.
26. W. Sun, W. Wang, H. Li, G. Zhang, D. Chen, J. Wang and Z. Cheng, Nat. Commun., 2020, 11, 5930.
27. K. Huang, D.-F. Shao and E. Y. Tsymbal, Nano Lett., 2022, 22, 3349–3355.
28. J.-J. Xian, C. Wang, J.-H. Nie, R. Li, M. Han, J. Lin, W.-H. Zhang, Z.-Y. Liu, Z.-M. Zhang, M.-P. Miao, Y. Yi, S. Wu, X. Chen, J. Han, Z. Xia, W. Ji and Y.-S. Fu, Nat. Commun., 2022, 13, 257.
29. J. Liu, M. Shi, J. Lu and M. P. Anantram, Phys. Rev. B, 2018, 97, 054416.
30. N. Abuawwad, M. dos, S. Dias, H. Abusara and S. Lounis, J. Phys.: Condens. Matter, 2022, 34, 454001.
31. W. Jiang, Z. Liu, J.-W. Mei, B. Cui and F. Liu, Nanoscale, 2019, 11, 955–961.
32. C. Liu, W. Ren and S. Picozzi, Phys. Rev. Lett., 2024, 132, 086802.
33. S. Yu, Y. Xu, Y. Dai, D. Sun, B. Huang and W. Wei, Phys. Rev. B, 2024, 109, L100402.
34. H. Yang, J. Liang and Q. Cui, Nat. Rev. Phys., 2023, 5, 43–61.
35. R. E. Camley and K. L. Livesey, Surf. Sci. Rep., 2023, 100605.
36. E. Dagotto and A. Moreo, Phys. Rev. Lett., 1989, 63, 2148–2151.
37. H. A. Ceccatto, C. J. Gazza and A. E. Trumper, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 7832–7836.
38. J. Sirker, Z. Weihong, O. P. Sushkov and J. Oitmaa, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 184420.
39. M. Drescher, L. Vanderstraeten, R. Moessner and F. Pollmann, Phys. Rev. B, 2023, 108, L220401.
40. Y.-Z. Ren, N.-H. Tong and X.-C. Xie, J. Phys.: Condens. Matter, 2014, 26, 115601.
41. R. F. Bishop, P. H. Y. Li, D. J. J. Farnell and C. E. Campbell, J. Phys.: Condens. Matter, 2012, 24, 236002.
42. Y. Iqbal, W.-J. Hu, R. Thomale, D. Poilblanc and F. Becca, Phys. Rev. B, 2016, 93, 144411.
43. F. Zhang, Y.-C. Kong, R. Pang, L. Hu, P.-L. Gong, X.-Q. Shi and Z.-K. Tang, New J. Phys., 2019, 21, 053033.
44. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
47. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
48. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
49. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
50. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624.
51. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
52. A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699.
53. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
54. M. M. Otrokov, I. P. Rusinov, M. Blanco-Rey, M. Hoffmann, A. Yu Vyazovskaya, S. V. Eremeev, A. Ernst, P. M. Echenique, A. Arnau and E. V. Chulkov, Phys. Rev. Lett., 2019, 122, 107202.
55. J. H. Van Vleck, Phys. Rev., 1932, 41, 208–215.
56. P. Chen, Q. Yao, J. Xu, Q. Sun, A. J. Grutter, P. Quarterman, P. P. Balakrishnan, C. J. Kinane, A. J. Caruana, S. Langridge, A. Li, B. Achinuq, E. Heppell, Y. Ji, S. Liu, B. Cui, J. Liu, P. Huang, Z. Liu, G. Yu, F. Xiu, T. Hesjedal, J. Zou, X. Han, H. Zhang, Y. Yang and X. Kou, Nat. Electron., 2023, 6, 18–27.
57. W. Lin, Y. Feng, Y. Wang, J. Zhu, Z. Lian, H. Zhang, H. Li, Y. Wu, C. Liu, Y. Wang, J. Zhang, Y. Wang, C.-Z. Chen, X. Zhou and J. Shen, Nat. Commun., 2022, 13, 7714.
58. C. X. Trang, Q. Li, Y. Yin, J. Hwang, G. Akhgar, I. Di Bernardo, A. Grubišić-Čabo, A. Tadich, M. S. Fuhrer, S.-K. Mo, N. V. Medhekar and M. T. Edmonds, ACS Nano, 2021, 15, 13444–13452.
59. P. W. Anderson, Phys. Rev., 1950, 79, 350–356.
60. J. B. Goodenough, Phys. Rev., 1955, 100, 564–573.
61. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
62. E. K. Petrov, V. N. Men'shov, I. P. Rusinov, M. Hoffmann, A. Ernst, M. M. Otrokov, V. K. Dugaev, T. V. Menshchikova and E. V. Chulkov, Phys. Rev. B, 2021, 103, 235142.
63. Q. Zhang, J. Liang, K. Bi, L. Zhao, H. Bai, Q. Cui, H.-A. Zhou, H. Bai, H. Feng, W. Song, G. Chai, O. Gladii, H. Schultheiss, T. Zhu, J. Zhang, Y. Peng, H. Yang and W. Jiang, Phys. Rev. Lett., 2022, 128, 167202.
64. P. W. Anderson and H. Hasegawa, Phys. Rev., 1955, 100, 675–681.
65. P.-G. de Gennes, Phys. Rev., 1960, 118, 141–154.
66. Z. Wang, I. Gutiérrez-Lezama, N. Ubrig, M. Kroner, M. Gibertini, T. Taniguchi, K. Watanabe, A. Imamoğlu, E. Giannini and A. F. Morpurgo, Nat. Commun., 2018, 9, 2516.
67. E. Bousquet and N. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 220402.
68. B. Wang, Y. Wu, Y. Bai, P. Shi, G. Zhang, Y. Zhang and C. Liu, Nanoscale, 2023, 15, 13402–13410.
69. C. Jia, C. Jin, P. Shi, J. Su, Y. Zhang, X. Niu and B. Wang, Phys. Chem. Chem. Phys., 2024, 26, 2134–2139.
70. Y. Bai, Y. Wu, C. Jia, L. Hou and B. Wang, Appl. Phys. Lett., 2023, 123, 012401.
71. Y. Sun, Z. Zhuo, X. Wu and J. Yang, Nano Lett., 2017, 17, 2771–2777.
72. J. Cenker, S. Sivakumar, K. Xie, A. Miller, P. Thijssen, Z. Liu, A. Dismukes, J. Fonseca, E. Anderson, X. Zhu, X. Roy, D. Xiao, J.-H. Chu, T. Cao and X. Xu, Nat. Nanotechnol., 2022, 17, 256–261.
73. Y. Zhang, Z. Cui, B. Sa, N. Miao, J. Zhou and Z. Sun, Nanoscale Horiz., 2022, 7, 276–287.

---

Footnote

† Electronic supplementary information (ESI) available: Computational details; spin charge distribution of CoBi₂Te₄ SL; phonon spectra and COHPs of CoBi₂Te₂Se₂, CoBi₂Se₄, and CoSb₂Te₄ SLs; schematics and further analysis of ferromagnetic superexchange interaction in VBi₂Te₄ and NiBi₂Te₄; PDOS and band structures of CoX₂Y₄ SLs; magnetic capacities of CoX₂Y₄; the change of Néel temperatures in the nclAFM state of CoSb₂Te₄ under strains; structural information. See DOI: https://doi.org/10.1039/d4nh00103f

---