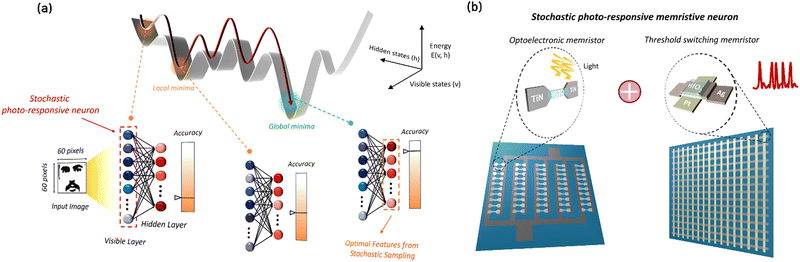
A stochastic photo-responsive memristive neuron for an in-sensor visual system based on a restricted Boltzmann machine†
Jin Hong
Kim‡
a,
Hyun Wook
Kim‡
a,
Min Jung
Chung
a,
Dong Hoon
Shin
a,
Yeong Rok
Kim
a,
Jaehyun
Kim
a,
Yoon Ho
Jang
a,
Sun Woo
Cheong
a,
Soo Hyung
Lee
a,
Janguk
Han
a,
Hyung Jun
Park
a,
Joon-Kyu
Han
*b and
Cheol Seong
Hwang
 *a
*a
aDepartment of Materials Science and Engineering and Inter-University Semiconductor Research Center, Seoul National University, Gwanak-ro 1, Gwanak-gu, Seoul 08826, Republic of Korea. E-mail: cheolsh@snu.ac.kr
bSystem Semiconductor Engineering and Department of Electronic Engineering, Sogang University, 35 Baekbeom-ro, Mapo-gu, Seoul 04107, Republic of Korea. E-mail: joonkyuhan@sogang.ac.kr
First published on 1st October 2024
Abstract
In-sensor computing has gained attention as a solution to overcome the von Neumann computing bottlenecks inherent in conventional sensory systems. This attention is due to the ability of sensor elements to directly extract meaningful information from external signals, thereby simplifying complex data. The advantage of in-sensor computing can be maximized with the sampling principle of a restricted Boltzmann machine (RBM) to extract significant features. In this study, a stochastic photo-responsive neuron is developed using a TiN/In–Ga–Zn–O/TiN optoelectronic memristor and an Ag/HfO2/Pt threshold-switching memristor, which can be configured as an input neuron in an in-sensor RBM. It demonstrates a sigmoidal switching probability depending on light intensity. The stochastic properties allow for the simultaneous exploration of various neuron states within the network, making identifying optimal features in complex images easier. Based on semi-empirical simulations, high recognition accuracies of 90.9% and 95.5% are achieved using handwritten digit and face image datasets, respectively. In addition, the in-sensor RBM effectively reconstructs abnormal face images, indicating that integrating in-sensor computing with probabilistic neural networks can lead to reliable and efficient image recognition under unpredictable real-world conditions.
New conceptsThis study proposes a stochastic photo-responsive memristive neuron composed of an Ag/HfO2/Pt (AHP) threshold-switching memristor and a TiN/In–Ga–Zn–O/TiN (TIT) optoelectronic memristor and an in-sensor restricted Boltzmann machine (RBM) architecture fabricated using this neuron. Unlike traditional neurons that exhibit regular and deterministic characteristics, the AHP memristor introduces a stochastic response originating from the random growth of Ag filaments. Furthermore, the TIT memristor converts light information into output current with a high ON/OFF current ratio. It has been confirmed that this stochastic neuron follows a sigmoidal switching probability depending on the light intensity. By applying the photo-responsive memristive neuron as an input neuron in the in-sensor RBM, the stochastic sampling is performed at the sensor stage, extracting optimal features for complex images without extra random number generators. Experimental simulations demonstrate a higher accuracy of 90.9% in handwritten digit classification compared to deterministic neurons. Additionally, a notable accuracy of 95.5% is achieved for complex face image recognition, showcasing its capability to handle real-world situations through face reconstruction under various lighting conditions. This research presents an improved method for developing an energy-efficient and reliable visual sensory system. |
Introduction
Conventional sensory systems based on von Neumann architecture encountered significant challenges due to the physical separation between sensing, computing, and memory units.1–4 This separation resulted in time delays and increased energy consumption, creating a bottleneck for implementing low-power sensors in mobile and the internet of things (IoT) devices. In-sensor computing emerged as an innovative approach to address these bottlenecks.5–7 The essence of this technology lies in that each sensor element not only collects data but also directly performs data preprocessing and basic analysis. This integration enables real-time data processing, significantly reducing the computing time and improving energy efficiency.8,9 Furthermore, in-sensor computing allows each sensor element to selectively transmit essential data, reducing data volume and enabling efficient delivery of necessary information.Meanwhile, the restricted Boltzmann machine (RBM) is a probabilistic neural network, considered promising for image recognition.10–12 Specifically, each neuron in an RBM responds stochastically to specific inputs, with switching probability following a sigmoidal form, in contrast to deterministic neurons. This stochastic nature allows the RBM to escape from local minima easily and explore multiple solutions on the error surface, making it less prone to overfitting and enabling it to quickly find the optimal features for complex images.13,14 Fig. S1 (ESI†) demonstrates the critical difference between stochastic and deterministic neurons when trapped in local minima. Stochastic neurons introduce randomness into the optimization process, allowing a higher chance of escaping from the local minima. In contrast, deterministic neurons are more likely to become stuck in local minima since they maintain a consistent neuron state. Therefore, the RBM can probabilistically explore various neuron states during learning and identify the optimal features for complex images. This characteristic is also helpful in reconstructing images to achieve a higher recognition rate even in situations of varying input images, making the RBM well-suited for use in visual sensory systems.
In recent years, memristive neuron devices have gained attention in neuromorphic computing.15–18 These devices offer increased integration density and reduced energy consumption compared to complementary-metal-oxide–semiconductor circuit-based approaches. Their minimalistic design suits low-power sensors for mobile and IoT devices, where energy efficiency is crucial.19–23 Moreover, memristive neuron devices exhibit stochastic properties that mimic the probabilistic behavior seen in biological neurons.24,25 This intrinsic stochasticity enables the application of memristive neuron devices as components in the RBM, where the probabilistic activation of neurons is essential for effective sampling.
This work proposes a stochastic photo-responsive memristive neuron and an in-sensor RBM architecture fabricated using this neuron, integrating the advantages of in-sensor computing with the RBM. Fig. 1a shows the proposed in-sensor RBM network structure, where the stochastic sampling in the sensor can replace the analog-to-digital converter (ADC). In general neuromorphic circuits, use of the ADC results in high area and energy costs, so replacing it with stochastic sampling will substantially enhance the system area efficiency and energy performance. The upper panel shows that the visible state (v) and hidden state (h) represent the vectorized combinations of possible neuron states. The z-axis corresponds to the energy for each (v, h) combination. It has stochastic photo-responsive input neurons, and their switching probability varies in response to light intensity. The real-time processing capability of in-sensor computing naturally aligns with the sampling principles of the RBM, where the hidden layer effectively captures the critical features of the input data.26 This synergy ensures that the in-sensor RBM efficiently processes large volumes of sensory data and extracts essential features, facilitating efficient image recognition processes. Fig. S2 (ESI†) shows three different visual systems: a conventional one with von Neumann architecture, an ex-sensor one based on a RBM, and an in-sensor visual system based on a RBM, respectively. The in-sensor RBM architecture demonstrates the reduced required data amount, significantly simplifying the circuit structure with minimum power consumption.
The stochastic photo-responsive neuron is composed of a serially connected TiN/In–Ga–Zn–O (IGZO)/TiN (TIT) optoelectronic memristor (optomemristor) and Ag/HfO2/Pt (AHP) threshold-switching memristor. The TIT optoelectronic memristor exhibits linear changes in current levels depending on light intensity. The AHP memristor exhibits probabilistic spiking depending on the applied voltage.27,28Fig. 1b shows the serially connected TIT optoelectronic memristor and the AHP threshold-switching memristor to construct the stochastic photo-responsive neuron. The TIT and AHP are serially connected, and a voltage is applied under controlled light illumination. Then, the applied voltage to the AHP threshold-switching memristor varies depending on the light intensity-controlled resistance of the TIT optoelectronic memristor. Therefore, the typical properties of stochastic photo-responsive neurons (sigmoidal activation function) can be achieved, in which switching probability varies in response to light intensity. Using the in-sensor RBM with the stochastic photo-responsive input neurons, handwritten digit recognition is demonstrated employing the Modified National Institute of Standards and Technology (MNIST) dataset, achieving a high accuracy of 90.9% in a relatively short iteration period compared to other neural networks with deterministic neurons. Moreover, face recognition and reconstruction are implemented using the Yale Face dataset, proving the effectiveness and reliability of the in-sensor RBM for complex image recognition in real-world environments.
Results and discussion
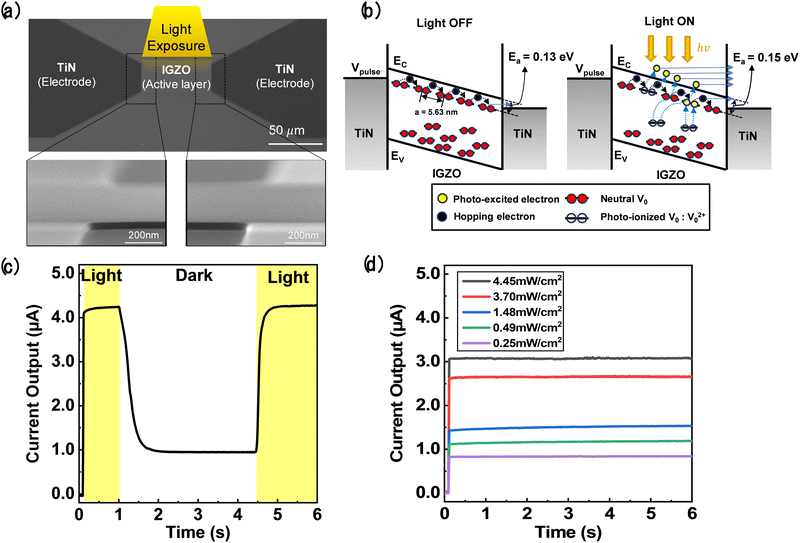
A. TiN/IGZO/TiN (TIT) optoelectronic memristor
Fig. 2a shows the scanning electron microscope (SEM) image of the TIT optoelectronic memristor, with the bottom panel images displaying a side SEM image of the overlapping area between the TiN electrode and the amorphous-IGZO active layer. The In![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ga
Ga![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn
Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratio is 1
O ratio is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. A line-cell structure, where the TiN electrodes were positioned on the sides of the IGZO active layer, was designed to maximize the light-receiving area. The fabrication process is explained in the Methods section.
4. A line-cell structure, where the TiN electrodes were positioned on the sides of the IGZO active layer, was designed to maximize the light-receiving area. The fabrication process is explained in the Methods section.
Fig. S3 (ESI†) shows temperature-dependent electrical conduction under the dark and light-illumination conditions. The experimental data fit well with the log (current density (J)) vs. electric field (E) relationship, indicating that hopping is the dominant conduction mechanism within the IGZO channel. The following equation describes the hopping conduction:
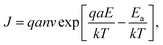 | (1) |
The activation energy was determined using the slopes of Arrhenius plots at low electric fields, with values calculated for the dark and light-illuminated states.31 The mean hopping distances in both states were almost identical (5.63 nm in the dark and 5.62 nm under illumination) in the temperature range of 303 K to 343 K, suggesting minimal change after exposure to light. Besides, the activation energy in the dark state was approximately 0.13 ± 0.01 eV, increasing to 0.15 ± 0.01 eV under illumination. It should be noted that the amorphous IGZO film has various energy states, such as donor levels (∼0.1 eV), localized states (∼0.2 eV), and deep levels.32,33 Under light-illumination conditions, many electrons in various energy states, including deep levels, are excited, increasing the number of electrons participating in conduction. Therefore, the remaining trap sites have deeper energy states, increasing activation energy.34 Conversely, under dark conditions, only shallow levels are involved in hopping, leading for fewer electrons with lower activation energies to contribute to the electrical conduction.
Based on the results of temperature dependency of the TIT device, Fig. 2b illustrates the band diagram to explain the working mechanism of the TIT optoelectronic memristor. The high Fermi level of IGZO increases the probability of overcoming local energy barriers near the mobility edge, allowing a higher chance of electron hopping conduction. Therefore, when illuminated, trapped electrons in oxygen vacancies (trap sites) are activated, leading to the ionization of oxygen vacancies (VO → V2+O + 2e−) and an increased photocurrent.35 Otherwise, V2+O neutralization occurs under dark conditions (V2+O + 2e− → VO), returning to the pristine states.33 Ionization and neutralization of the oxygen vacancies is a reversible reaction depending on the presence of light. Here, the VO, which cannot be rigorously defined in the amorphous structure, refers to the local oxygen deficiency. Under light illumination, electrons are excited and contribute to the higher output current. Therefore, the large number of photo-excited electrons due to increased light intensity can be attributed to the high output current.
Fig. 2c shows the white light response time of the TIT optoelectronic memristor at a read voltage of 2 V applied between the two TiN electrodes. The read voltage was applied for 6 seconds, during which the device was illuminated for 1 second, remained unilluminated for 3.5 seconds, and then illuminated again for 1.5 seconds to verify the output current's stability under the light ON or OFF conditions. The responsivity (R) representing this device's ON/OFF ratio is 4.51. When the device is exposed to light, the conductance increases due to the increased photo-excited electron density. The response time was approximately 0.5 seconds when exposed to a light intensity of 4.45 mW cm−2.
It should be noted that faster ionization of VO under light and neutralization of V2+O under dark conditions was achieved only after the electrical SET process because the excitation could be actively performed along the dominant conduction path between two electrodes.36 Fig. S4a and b (ESI†) demonstrate the I–V characteristics and the light response of the TIT device, respectively, before the electrical SET process at a constant read voltage of 5 V. The output current level was increased, and light response time was shortened with the assistance of the dominant conduction path formed by the electrical SET process. It should be noted that this phenomenon has also been observed in other optoelectronic memristors.36Fig. 2d shows the linear increase in current with increasing light intensity at the same reading voltage of 2 V, which displays a proportional output current level according to the light intensity. Additionally, Fig. S4c (ESI†) shows the electrical pulse test under various conditions. The conductance increases when a positive voltage pulse is applied, allowing precise control of conductance electrically and optically for integration with the AHP threshold-switching memristor.
B. Ag/HfO2/Pt (AHP) threshold-switching memristor
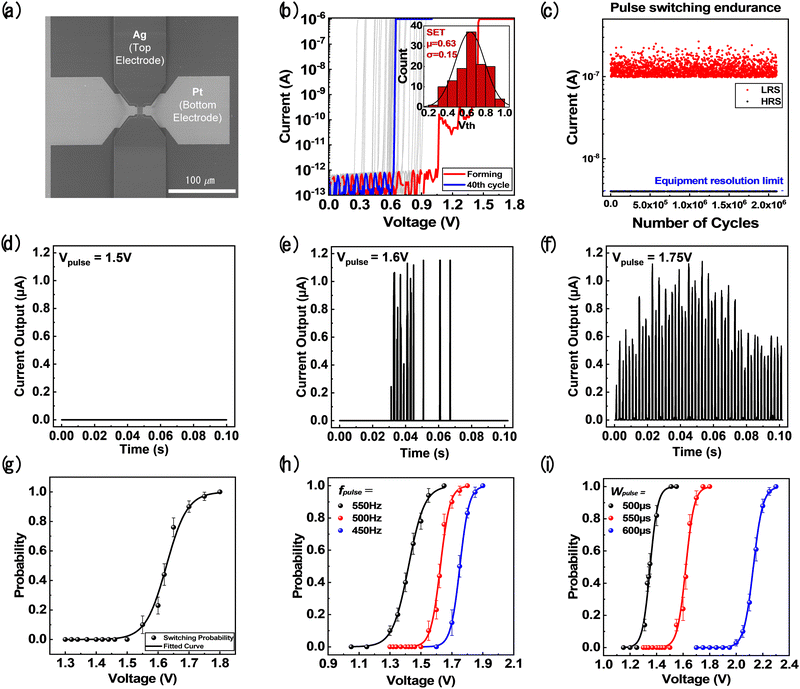
Fig. 3a shows the SEM image of the AHP threshold-switching memristor, and Fig. S5 (ESI†) shows a cross-sectional transmission electron microscope (TEM) image and energy dispersive spectroscopy (EDS) results. The detailed fabrication process is explained in the Experimental section. The threshold-switching behavior of the AHP memristor is attributed to weak filament formation and spontaneous rupture.37,38 In the pristine state, the Ag active electrode requires electroforming to facilitate the migration of Ag ions into the HfO2 layer under an electric field. This process forms a preferential metallic conducting path. After the electroforming process, when the voltage is above the threshold voltage (Vth) for the AHP memristor, oxidized Ag cations migrate and form weak Ag metal filaments in the HfO2 switching layer, leading to an abrupt transition to a low-resistance state (LRS).39It should be noted that volatile switching is crucial for neuron operations because nonvolatile switching requires additional reset circuits. The LRS to high-resistance state (HRS) transition in volatile switching occurs when the active electrode forms local clusters. Shukla et al. defined switching volatility as Δ = Ecluster − Efilament|E-field=0, where Δ, Ecluster, and Efilament refer to the restoring force for the device to return to the HRS, the energy of the cluster in the active electrode, and the energy of the filament in the active electrode, respectively.40,41 Among Ag, Cu, and Co electrodes, Ag exhibits the highest Δ value of 0.135 eV, showing the most active volatility. Fig. 3b shows the I–V characteristics of the fabricated device with volatile switching characteristics. The red graph shows the electroforming process, while the blue graph indicates the 40 cycles of threshold-switching behavior after forming. The inset graph represents the statistical distribution of Vth. Notably, Vth varies at each cycle due to the random injection of Ag cations.
The AHP devices with different HfO2 layer thicknesses were examined to determine the optimal configuration for stochastic neurons. Fig. S6a and b (ESI†) present the I–V characteristics and Vth distribution of the device with an HfO2 thickness of 3 nm, demonstrating a more uniform I–V curve with an average Vth of 0.26 V and a standard deviation of 0.01 V, which are inappropriate for the RBM implementation. As illustrated in Fig. S6c (ESI†), a thinner switching layer requires fewer Ag atoms for filament formation, leading to a lower threshold voltage. This results in limited injection paths and more uniform filament growth, which decreases stochasticity. Additionally, from the perspective of filament evolution dynamics, nucleation limits filament growth, leading to isotropic filament formation with low variation.42 Conversely, a thicker HfO2 layer increases the diffusion distance for Ag cations, ensuring sufficient random injection of Ag atoms during filament formation, as illustrated in Fig. S6d (ESI†). This property enhances the irregularity in the filament formation process, thereby increasing stochasticity. Therefore, the AHP device with an 8 nm HfO2 layer is optimal for stochastic neurons.
Fig. 3c demonstrates the reliability of the fabricated device by measuring pulse switching endurance using the house-built closed-loop pulse switching (CLPS) method. Stable resistance changes were achieved for more than 2 million cycles. The detailed methodology of CLPS is presented in Fig. S7 (ESI†). Fig. 3d–f show the current outputs of the AHP threshold-switching memristor under various voltage pulses as the inputs. The voltage amplitude (Vpulse) was varied while pulse frequency (fpulse), pulse width (Wpulse), and the number of applied pulses (Npulse) were fixed as 500 Hz, 550 μs, and 50 times, respectively. Fig. 3d shows no current response at a Vpulse of 1.5 V. However, spike responses by threshold switching were observed when Vpulse was increased to 1.6 V and 1.75 V, as shown in Fig. 3e and f. The variability in the threshold-switching behaviors was clearly illustrated by comparing the shapes and timings of the current output.43
Fig. 3g shows the switching probability (P) calculated from the spike responses mentioned above. It follows a sigmoidal activation function form when gradually increasing Vpulse from 1.3 V to 1.8 V, which is suitable for stochastic neurons in a RBM. This neuronal characteristic is known as strength-modulated spike frequency in biology, where the spiking frequency varies depending on the strength of the input signal.44,45 When the strength of the input signal increases, the neuron generates spikes at a higher frequency, while it produces spikes at a lower frequency when the strength decreases. The spiking probability, P, was calculated using the following equation:
| P = (Nspike × Wspike)/(Npulse × Wpulse), | (2) |
Fig. 3h and i show P variation depending on fpulse and Wpulse of the applied pulses. They all follow the sigmoidal form. However, an increase in fpulse from 450 Hz to 550 Hz induced a shift into the lower Vpulse direction because the increased fpulse enhanced the local migration of the Ag ions. Interestingly, increasing Wpulse from 500 μs to 600 μs resulted in a shift into the higher Vpulse direction. This trend is because increasing Wpulse caused a more global injection of Ag ions across the device area than the short Wpulse case, and the Ag filament tends to disperse and grow more homogeneously, which requires a higher voltage for switching.42 Therefore, fine-tuning the sigmoidal response of the device can be achieved by changing the Vpulse configuration, enhancing the functionality of the RBM.
C. Stochastic photo-responsive neuron
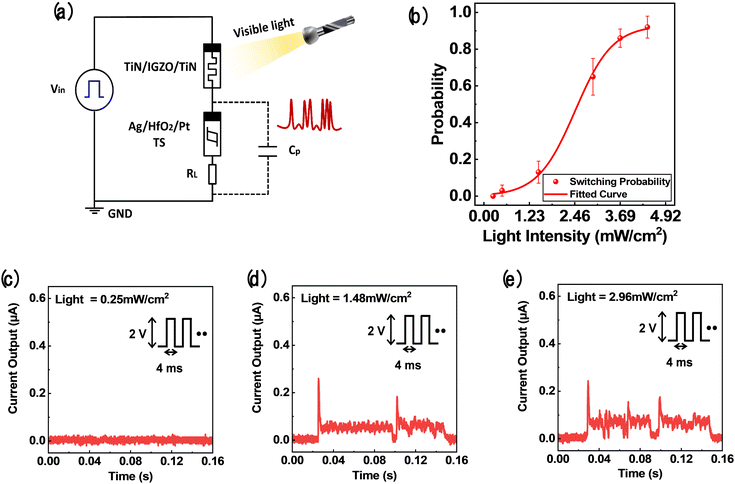
Fig. 4a shows the circuit diagram of a stochastic photo-responsive neuron that serves as an input neuron of an in-sensor RBM. The SET process of the TIT optoelectronic memristor and the electroforming process of the AHP threshold-switching memristor were performed separately beforehand. When the TIT optoelectronic memristor is serially connected to the AHP threshold-switching memristor and a voltage is applied, the applied voltage is divided according to the resistance of each device. As the resistance of the TIT optoelectronic memristor decreases upon exposure to light, the voltage distributed to the AHP threshold-switching memristor increases, thereby increasing the probability of generating spikes. The switching probability of the stochastic photo-responsive neuron follows the sigmoidal function according to the light intensity because the AHP memristor has a sigmoidal activation function, and the resistance of the TIT memristor is linearly proportional to light intensity.46 Conversely, a conventional photodetector with a high current output can cause excessive voltage application in the AHP memristor, potentially degrading the sigmoidal switching probability. Furthermore, IGZO's wide bandgap of ∼3.5 eV enables excitation with intermediate subgap sites, facilitating broadband light detection, including visible light.47 Therefore, the TIT optoelectronic memristor is essential to construct stochastic photo-responsive neurons. Since the resistance of the AHP memristor is much larger than that of the TIT memristor, a capacitor is connected in parallel to induce delay time for voltage application to the AHP threshold-switching memristor.The operation principle of the stochastic photo-responsive neuron circuit is as follows. The capacitor charges when the AHP memristor is initially in the high-resistance state (HRS). Once the voltage on the capacitor reaches Vth, the AHP memristor switches to the LRS, allowing for charge discharging, measured as a current flow through an oscilloscope with a load resistance (RL) of 1 MΩ. Subsequently, the AHP memristor returns to the HRS once the discharging completes.42 It should be noted that the background current was observed from the slow discharging behavior of the Ag filament. The output spikes generated by threshold-switching were identified when the current exceeding a specific value (0.067 μA) was observed. The switching probability was extracted at specific light intensities before and after the CLPS endurance test to evaluate the endurance of the photo-responsive neuron, as shown in Fig. S7 (ESI†). It was confirmed that the switching probability was not changed significantly even after 2 million cycles. Fig. 4b shows P as a function of light intensity of the stochastic photo-responsive neuron, following the sigmoidal activation function form. Therefore, the strength-modulated spike frequency behaviors were achieved by optical modulation. Fig. 4c–e display representative spike responses at different light intensities, while the pulse conditions were fixed with a pulse amplitude and width of 2 V and 4 ms, respectively. Fig. 4c shows no response at 0.25 mW cm−2 light intensity. However, Fig. 4d and e show the stochastic spiking responses at light intensities of 1.48 mW cm−2 and 2.96 mW cm−2, respectively. In these cases, the spikes represent the transition of the AHP memristor from the HRS to the LRS, with more frequent stochastic spiking observed at higher light intensities.25 Recent studies reported deterministic photo-responsive neurons based on metal-to-insulator transition (MIT) materials such as NbOx, VOx, or TaOx,23,48–51 which can hardly be adopted to the suggested energy-based algorithms. In contrast, this study achieved sigmoidal switching probability based on the random growth of the Ag filament, which provided the core ingredient for RBM implementation. The TIT optomemristor used in this study offers a proportional current response to light intensity, making it well-suited for photo-responsive neurons when combined with the AHP threshold-switching memristor. It is suitable for use as an input neuron in the visible layer of the in-sensor RBM architecture, where it can directly receive light and efficiently transmit signals to the hidden layer.
D. MNIST handwritten digit recognition
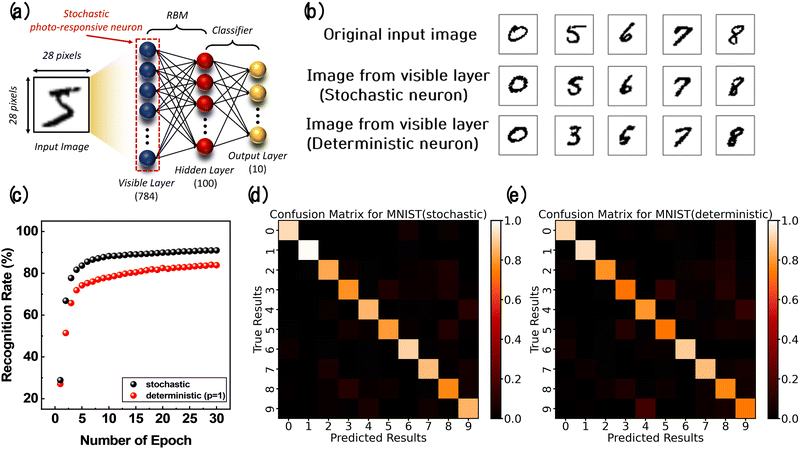
The in-sensor RBM was constructed with a Python software simulation to confirm the feasibility of the stochastic photo-responsive neuron for image recognition. Fig. 5a shows the in-sensor RBM network for the classification task of the MNIST dataset. It comprised 784 input neurons in the visible layer, 100 hidden neurons in the hidden layer, and 10 output neurons in the output layer. In the RBM, significant features are extracted at the hidden layer, followed by classification at the output layer.It should be noted that once the RBM has finished learning from the input image and the hidden layer states are determined, these states are then fed into a classification layer of the same size to confirm the final classification result. The measured sigmoidal switching probabilities according to the light intensity of stochastic photo-responsive neurons were incorporated into the visible neurons. At the same time, the cycle-to-cycle variation was also considered to reflect the experimental results precisely. Additionally, to reflect the sigmoidal switching probabilities of the hidden neurons, the switching probabilities obtained from AHP memristors under a pulse condition of 500 Hz (depicted in Fig. 3g) were utilized. The MNIST dataset consisted of handwritten digits from 0 to 9, each comprised of 28 × 28 pixels. A dataset of 6000 training images and 1000 test images were utilized. During the learning process, the switching probability of the hidden neurons was calculated using the input data in the visible layer. The state of the neuron was determined to be 0 or 1 through the switching probability, called the positive phase.26 The state of visible neurons was reconstructed based on the sigmoidal switching probabilities obtained from stochastic photo-responsive neurons. The reconstruction process, called the negative phase, was performed using symmetric weight values. The difference between actual and expected data was minimized by iterating these two phases. The synaptic weights of the RBM were updated through the contrastive divergence algorithm, followed by the sampling process. Fig. S8 (ESI†) shows the detailed learning process of the RBM.
The sampling results were carefully compared with the case using deterministic neurons in all layers to understand the impact of the stochastic neurons on the in-sensor RBM network. Fig. 5b shows the reconstructed images from the visible layer after performing 10 steps of Gibbs sampling, a method used to sample from the input data distribution. It is essential for estimating parameters by iteratively updating the states of visible and hidden neurons. The stochastic neurons almost reconstructed the shape of the handwritten digits of the original image, while the deterministic neurons reconstructed several digits into other digits of similar shape. The reason is that, unlike stochastic neurons, deterministic neurons undergo a non-probabilistic sampling process, leading to limited parameter updates and hindering the exploration of different error surfaces.52Fig. 5c shows that 90.9% and 82.8% recognition rates were achieved after 30 epochs for stochastic and deterministic neurons, respectively. The recognition rate achieved by stochastic neurons is sufficiently high compared to previous studies, as shown in Table S1 (ESI†). The confusion matrix using each type of neuron is shown in Fig. 5d and e, where a more obvious diagonal pattern was observed when the stochastic neurons were used.
In addition, a simulation was conducted to determine which layer, visible or hidden, contributes more significantly to the performance to better understand the benefits of the in-sensor RBM. As shown in Fig. S9 (ESI†), the recognition rate of the RBM with deterministic neurons as input neurons and stochastic neurons as hidden neurons has a lower recognition rate than the RBM with stochastic neurons as input neurons and deterministic neurons as hidden neurons. This result is because the input neurons directly influence feature extraction in the RBM network. Furthermore, a simulation was performed to compare the performance of the in-sensor RBM with conventional deep neural networks with no feature extraction process. Under identical conditions of network parameters, such as the number of layers and neurons, the recognition rate using the in-sensor RBM achieved a faster convergence. This performance is because the probabilistic activation of neurons in an RBM allows for exploring multiple features simultaneously, directly guiding toward the optimal feature extraction. Moreover, it was confirmed that using the hidden layer in the RBM, which is responsible for feature extraction, clearly improves the recognition rates compared to the neural networks without hidden layers. These results are presented in Fig. S10 (ESI†).
E. Yale face image recognition and face reconstruction
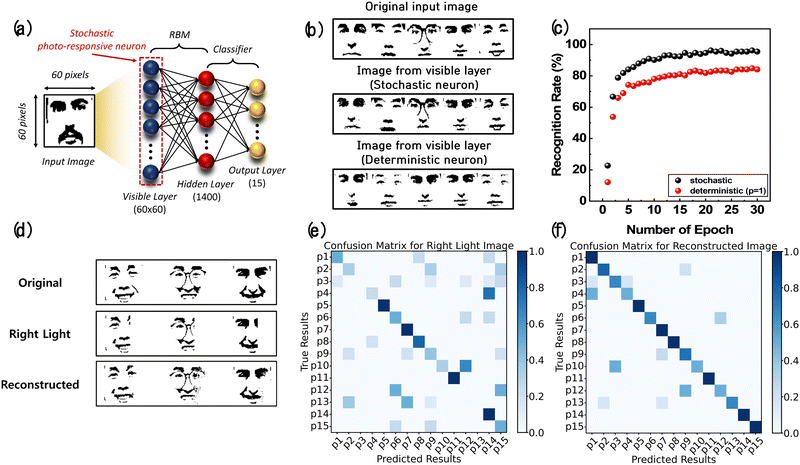
Face image recognition was conducted based on the Yale face dataset to demonstrate the effectiveness of the in-sensor RBM for complex image recognition. Even in environments where the face images were partially lost due to abnormal light intensity, it is possible to reconstruct images close to the original ones based on the images learned by the RBM. Fig. 6a illustrates the structure of the in-sensor RBM network used to classify 60 × 60 pixel face images of 15 people (p1–p15) based on the Yale face dataset. It comprised 60 × 60 stochastic photo-responsive neurons (input neurons) in the visible layer, 1400 hidden neurons in the hidden layer, and 15 output neurons in the output layer. The Yale face dataset consists of 165 datasets based on 15 people and 11 expressions. A dataset of 115 training images and 50 test images was utilized. The simulation was also conducted using the Python codes.Fig. 6b shows the results of Gibbs sampling conducted to reconstruct the original face images using stochastic and deterministic neurons. The sampling using stochastic neurons resulted in images almost identical to the original images, indicating that the RBM network was appropriately trained. In contrast, when using deterministic neurons, the sampling results appeared to be limited to certain people's faces. The hidden layer of the RBM should extract features that effectively reconstruct input data. However, since deterministic neurons do not activate probabilistically, several hidden neurons maintaining a consistent state across the sampling process lead to capturing only specific features of people. In other words, deterministic neurons are trapped in specific local minima in reconstructing faces, whereas stochastic neurons can explore various error surfaces, allowing them to escape local minima.26Fig. 6c displays the recognition rate for 15 people according to the number of training epochs. The recognition rates after 30 epochs were 95.5% and 84.1% when using stochastic and deterministic neurons, respectively. The confusion matrix of each case is shown in Fig. S11 (ESI†), where a clearer diagonal pattern was observed when the stochastic neurons were used.
Since the RBM can reconstruct images almost identical to the original images, it can help recognize abnormal face images, allowing reliable image recognition in real-world scenarios. Fig. 6d shows the result of reconstructing an abnormal face image when an intense right-side light was shone on a face. The confusion matrices based on the right-side light-shone face image and the reconstructed images are presented in Fig. 6e and f, respectively. The confusion matrix based on the reconstructed image showed a more evident diagonal pattern, representing a closer match between the predicted and the actual results. In addition to right-side light shone face images, abnormal images such as left-side light shone face images and center light shone face images could be reconstructed, as shown in Fig. S12 (ESI†). Therefore, the in-sensor RBM enhances reliability in recognizing images in the real world.
Conclusions
In conclusion, this work proposed a new in-sensor RBM architecture based on a stochastic photo-responsive memristive neuron composed of a serially connected TiN/IGZO/TiN optoelectronic memristor and Ag/HfO2/Pt threshold-switching memristor. The optomemristor demonstrated a short light response time of 0.5 seconds and an ON/OFF current ratio of 4.51, while the threshold-switching memristor exhibited stochastic spiking behavior, driven by the random growth of Ag filaments within the voltage range of 1.3 V to 1.8 V. These characteristics enabled the neuron to produce a spiking probability that followed a sigmoidal activation function in response to varying light intensities, making it suitable as an input neuron in an in-sensor RBM. Such inherent stochastic properties simultaneously explore various neuron states within the network, thereby extracting optimal features from complex image data. Two tasks were implemented using MNIST and Yale face datasets to confirm the feasibility of the stochastic photo-responsive neuron for image recognition, achieving high accuracies of 90.9% and 95.5%, respectively. It was also demonstrated that the in-sensor RBM could reconstruct abnormal face images close to the original images, even under unfavorable light illumination conditions. It is noteworthy that stochastic neurons can be integrated into existing deep neural networks and generative models, including the RBM. Therefore, this work provides a method to enhance the efficiency and reliability of various visual sensory systems.Methods
A. Device fabrication
First, the TiN/IGZO/TiN optomemristor fabrication process is described. As a starting substrate, SiO2 was thermally grown on the p-type (100) Si wafer. First, a 5 nm thick Ti adhesion layer and a 50 nm thick TiN electrode layer were deposited by sputtering and patterned by photolithography and dry etching. Next, an IGZO active layer was deposited by RF sputtering. The IGZO layer was also patterned by photolithography and dry etching. A line cell structure was designed to maximize the light- receiving area, where the TiN electrodes were positioned at the bottom of both sides of the IGZO active layer.Next, the Ag/HfO2/Pt threshold-switching memristor fabrication process is described. Using the same substrate, a 5 nm thick Ti adhesion layer and a 50 nm thick Pt bottom electrode layer were deposited by sputtering and patterned by photolithography and a lift-off process. Next, an 8 nm-thick HfO2 switching layer was deposited by atomic layer deposition (ALD) at a substrate temperature of 250 °C. The precursors for Hf and oxygen were tetrakis dimethylamido hafnium and O3, respectively. Next, a 70 nm thick Ag top electrode layer was deposited using the thermal evaporator and patterned by photolithography and a lift-off process. Finally, a 40 nm thick Pt passivation layer was deposited using an electron beam evaporator, followed by the lift-off process.
B. Electrical and optical measurements
The DC I–V characteristics were measured using the semiconductor parameter analyzer (4155A, Hewlett Packard). An Agilent 8110A pulse generator and oscilloscope (TDS 684C, Tektronix) were used for the pulse measurements. CLPS was conducted using an in-house field-programmable gate array board, applying pulses until the device reached the target resistance value. White light illumination was applied with a lamp power supply (FOK-100W, Fiber Optic).C. Software simulation
The image recognition simulations using the MNIST and Yale face datasets were performed using the PyTorch library in Python. In this work, the k-CD algorithm was employed that iterates Gibbs sampling k times to update the weights of the in-sensor RBM. The CD algorithm utilizes Gibbs sampling to calculate the joint probability of visible and hidden layer neurons to address the issue of exponential growth in computational complexity. This approach enables learning of the joint probability based on the distribution obtained from k iterations of Gibbs sampling, one of the Markov Chain Monte Carlo sampling methods. The learning rate for the k-CD algorithm was set to 0.01, with k chosen as 7. 6000 input images of MNIST datasets were sectored as 32 images per batch and 115 input images of Yale face datasets were sectored as 10 images per batch for the training process. In addition, to precisely reflect the cycle-to-cycle variation of the AHP threshold-switching memristor, a random value was generated from the coefficient of variance (CV) of the switching probability at a specific voltage. This value was multiplied by the mean value to follow the probability distribution obtained through measurements.Author contributions
Jin Hong Kim and Hyun Wook Kim designed, conducted and analyzed the experiments and wrote the main manuscript. Jin Hong Kim fabricated and characterized the electrical and optical properties of the devices. Hyun Wook Kim simulated the restricted Boltzmann machine and counterpart neural networks. Min Jung Chung validated and confirmed the methodology of the experiment. Dong Hoon Shin, Yeong Rok Kim, Jaehyun Kim, Yoon Ho Jang, Sun Woo Cheong and Hyung Jun Park developed experimental and analysis methodology. Sun Woo Cheong, Soo Hyung Lee, and Janguk Han provided software support. Joon-Kyu Han supervised the experiment and reviewed the writing of the manuscript. Cheol Seong Hwang guided the entire project and led the writing review and editing process.Data availability
This study was carried out using publicly available data from the Yale Face database at https://cvc.cs.yale.edu/cvc/projects/yalefaces/yalefaces.html and the MNIST handwritten digital database at https://yann.lecun.com/exdb/mnist/.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (Grant No. 2020R1A3B2079882). All facial images used in the Python software simulation were sourced from the Yale Face Database.Notes and references
- Y. Chen, X. Wu, J. Shen, Z. Huang, Z. Wang, L. Lyu, H. Bi, X. Wu and G. Shen, Adv. Sens. Res., 2023, 2, 2200034 CrossRef.
- J. K. Han, S. Y. Yun, S. W. Lee, J. M. Yu and Y. K. Choi, Adv. Funct. Mater., 2022, 32, 2204102 CrossRef.
- N. K. Upadhyay, H. Jiang, Z. Wang, S. Asapu, Q. Xia and J. Joshua Yang, Adv. Mater. Technol., 2019, 4, 1800589 CrossRef.
- G. Indiveri and S. C. Liu, Proc. IEEE, 2015, 103, 1379–1397 Search PubMed.
- F. Zhou and Y. Chai, Nat. Electron., 2020, 3, 664–671 CrossRef.
- T. Wan, B. Shao, S. Ma, Y. Zhou, Q. Li and Y. Chai, Adv. Mater., 2022, 35, 2203830 CrossRef PubMed.
- C. Dias, D. Castro, M. Aroso, J. Ventura and P. Aguiar, ACS Appl. Electron. Mater., 2022, 4, 2380–2387 CrossRef CAS PubMed.
- G. Feng, X. Zhang, B. Tian and C. Duan, InfoMat, 2023, 5, 12473 CrossRef.
- M. K. Song, J. H. Kang, X. Zhang, W. Ji, A. Ascoli, I. Messaris, A. S. Demirkol, B. Dong, S. Aggarwal, W. Wan, S. M. Hong, S. G. Cardwell, I. Boybat, J. S. Seo, J. S. Lee, M. Lanza, H. Yeon, M. Onen, J. Li, B. Yildiz, J. A. del Alamo, S. Kim, S. Choi, G. Milano, C. Ricciardi, L. Alff, Y. Chai, Z. Wang, H. Bhaskaran, M. C. Hersam, D. Strukov, H. S. P. Wong, I. Valov, B. Gao, H. Wu, R. Tetzlaff, A. Sebastian, W. Lu, L. Chua, J. J. Yang and J. Kim, ACS Nano, 2023, 17, 11994–12039 CrossRef CAS PubMed.
- M. W. Klein, C. Enkrich, M. Wegener and S. Linden, Science, 2006, 313, 502–504 CrossRef CAS.
- M. Ernoult, J. Grollier and D. Querlioz, Sci. Rep., 2019, 9, 1851 CrossRef.
- H. Manukian, Y. R. Pei, S. R. B. Bearden and M. Di Ventra, Commun. Phys., 2020, 3, 105 CrossRef.
- S. Patel, P. Canoza and S. Salahuddin, Nat. Electron., 2022, 5, 92–101 CrossRef.
- A. Fachechi, A. Barra, E. Agliari and F. Alemanno, IEEE Trans. Neural Networks Learn. Syst., 2024, 35, 1172–1181 Search PubMed.
- X. Duan, Z. Cao, K. Gao, W. Yan, S. Sun, G. Zhou, Z. Wu, F. Ren and B. Sun, Adv. Mater., 2024, 36, 2310704 CrossRef CAS.
- Y. Li and K.-W. Ang, Adv. Intell. Syst., 2021, 3, 2000137 CrossRef.
- T. Guo, K. Pan, Y. Jiao, B. Sun, C. Du, J. P. Mills, Z. Chen, X. Zhao, L. Wei, Y. N. Zhou and Y. A. Wu, Nanoscale Horiz., 2022, 7, 299–310 RSC.
- B. Dang, K. Liu, X. Wu, Z. Yang, L. Xu, Y. Yang and R. Huang, Adv. Mater., 2023, 35, 2204844 CrossRef CAS.
- S. Choi, J. Yang and G. Wang, Adv. Mater., 2020, 32, 2004659 CrossRef CAS.
- H. Abbas, Y. Abbas, G. Hassan, A. S. Sokolov, Y. R. Jeon, B. Ku, C. J. Kang and C. Choi, Nanoscale, 2020, 12, 14120–14134 RSC.
- M. Kim, M. A. Rehman, D. Lee, Y. Wang, D. H. Lim, M. F. Khan, H. Choi, Q. Y. Shao, J. Suh, H. S. Lee and H. H. Park, ACS Appl. Mater. Interfaces, 2022, 14, 44561–44571 CrossRef CAS.
- T. Wang, J. Meng, X. Zhou, Y. Liu, Z. He, Q. Han, Q. Li, J. Yu, Z. Li, Y. Liu, H. Zhu, Q. Sun, D. W. Zhang, P. Chen, H. Peng and L. Chen, Nat. Commun., 2022, 13, 7482 CrossRef.
- Q. R. A. Al-Taai, M. Hejda, W. Zhang, B. Romeira, J. M. L. Figueiredo, E. Wasige and A. Hurtado, Neuromorphic Comput. Eng., 2023, 3, 034012 CrossRef.
- W. Yi, K. K. Tsang, S. K. Lam, X. Bai, J. A. Crowell and E. A. Flores, Nat. Commun., 2018, 9, 4661 CrossRef PubMed.
- K. Wang, Q. Hu, B. Gao, Q. Lin, F. W. Zhuge, D. Y. Zhang, L. Wang, Y. H. He, R. H. Scheicher, H. Tong and X. S. Miao, Mater. Horiz., 2021, 8, 619–629 RSC.
- Y. Wang, F. Xu, J. Wang, X. Cui and T. Yi, J. Phys. Conf. Ser., 2022, 2347, 012014 CrossRef.
- D. Lee, M. Kwak, K. Moon, W. Choi, J. Park, J. Yoo, J. Song, S. Lim, C. Sung, W. Banerjee and H. Hwang, Adv. Electron. Mater., 2019, 5, 1800866 CrossRef.
- J. H. Cha, S. Y. Yang, J. Oh, S. Choi, S. Park, B. C. Jang, W. Ahn and S. Y. Choi, Nanoscale, 2020, 12, 14339–14368 RSC.
- F. C. Chiu, C. Y. Lee and T. M. Pan, J. Appl. Phys., 2019, 105, 074103 CrossRef.
- M. Estrada, Y. Hernandez-Barrios, A. Cerdeira, F. Ávila-Herrera, J. Tinoco, O. Moldovan, F. Lime and B. Iñiguez, Solid-State Electron., 2017, 135, 43–48 CrossRef CAS.
- M. D. Hossain Chowdhury, P. Migliorato and J. Jang, Appl. Phys. Lett., 2013, 102, 143506 CrossRef.
- T. Kamiya, K. Nomura and H. Hosono, Sci. Technol. Adv. Mater., 2010, 11 Search PubMed.
- G. R. Haripriya, H. Y. Noh, C. K. Lee, J. S. Kim, M. J. Lee and H. J. Lee, Nanoscale, 2023, 15, 14476–14487 RSC.
- J. Wang, J. Bi, G. Xu and M. Liu, Electronics, 2024, 13(8), 1427 CrossRef.
- M. G. Yun, Y. K. Kim, C. H. Ahn, S. W. Cho, W. J. Kang, H. K. Cho and Y. H. Kim, Sci. Rep., 2016, 6, 31991 CrossRef PubMed.
- S. Chen, Z. Lou, D. Chen and G. Shen, Adv. Mater., 2018, 30 Search PubMed.
- X. Zhang, W. Wang, Q. Liu, X. Zhao, J. Wei, R. Cao, Z. Yao, X. Zhu, F. Zhang, H. Lv, S. Long and M. Liu, IEEE Electron Device Lett., 2018, 39, 308–311 CAS.
- S. Chen, T. Zhang, S. Tappertzhofen, Y. Yang and I. Valov, Adv. Mater., 2023, 35, 2301924 CrossRef CAS.
- Z. Wang, M. Rao, R. Midya, S. Joshi, H. Jiang, P. Lin, W. Song, S. Asapu, Y. Zhuo, C. Li, H. Wu, Q. Xia and J. J. Yang, Adv. Funct. Mater., 2018, 28, 1704862 CrossRef.
- N. Shukla, R. K. Ghosh, B. Grisafe and S. Datta, 2017 IEEE International Electron. Devices Meeting (IEDM), IEEE, 2017, pp. 3–4 Search PubMed.
- S. Menzel, S. Tappertzhofen, R. Waser and I. Valov, Phys. Chem. Chem. Phys., 2013, 15, 6945–6952 RSC.
- S. A. Chekol, S. Menzel, R. W. Ahmad, R. Waser and S. Hoffmann-Eifert, Adv. Funct. Mater., 2022, 32, 2111242 CrossRef.
- K. Wang, Q. Hu, B. Gao, Q. Lin, F. W. Zhuge, D. Y. Zhang, L. Wang, Y. H. He, R. H. Scheicher, H. Tong and X. S. Miao, Mater. Horiz., 2021, 8, 619–629 RSC.
- Y. Zhou, J. Won, M. G. Karlsson, M. Zhou, T. Rogerson, J. Balaji, R. Neve, P. Poirazi and A. J. Silva, Nat. Neurosci., 2009, 12, 1438–1443 CrossRef PubMed.
- T. P. Carvalho and D. V. Buonomano, Neuron, 2009, 61, 774–785 CrossRef.
- H. Mao, Y. He, C. Chen, L. Zhu, Y. Zhu, Y. Zhu, S. Ke, X. Wang, C. Wan and Q. Wan, Adv. Electron. Mater., 2021, 8, 2100918 CrossRef.
- T. Kamiya, K. Nomura and H. Hosono, Phys. Status Solidi A, 2009, 206, 860–867 CrossRef CAS.
- C. Chen, Y. He, H. Mao, L. Zhu, X. Wang, Y. Zhu, Y. Zhu, Y. Shi, C. Wan and Q. Wan, Adv. Mater., 2022, 34, 2201895 CrossRef CAS.
- J. Wen, Z. Y. Zhu and X. Guo, Neuromorphol. Comput. Eng., 2023, 3, 014015 CrossRef.
- Q. Wu, B. Dang, C. Lu, G. Xu, G. Yang, J. Wang, X. Chuai, N. Lu, D. Geng, H. Wang and L. Li, Nano Lett., 2020, 20, 8015–8023 CrossRef CAS PubMed.
- S. K. Nath, S. K. Das, S. K. Nandi, C. Xi, C. V. Marquez, A. Rúa, M. Uenuma, Z. Wang, S. Zhang, R. J. Zhu, J. Eshraghian, X. Sun, T. Lu, Y. Bian, N. Syed, W. Pan, H. Wang, W. Lei, L. Fu, L. Faraone, Y. Liu and R. G. Elliman, Adv. Mater., 2024, 36, 2400904 CrossRef CAS.
- M. Zeng, Z. Li, J. W. Saw and B. Chen, Appl. Phys. Lett., 2024, 124, 032404 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nh00421c |
| ‡ J. H. Kim and H. W. Kim contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |