Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First-principles theory of the nitrogen interstitial in hBN: a plausible model for the blue emitter
Ádám
Ganyecz
 ab,
Rohit
Babar
ab,
Rohit
Babar
 ab,
Zsolt
Benedek
ab,
Zsolt
Benedek
 ab,
Igor
Aharonovich
ab,
Igor
Aharonovich
 cd,
Gergely
Barcza
cd,
Gergely
Barcza
 *ab and
Viktor
Ivády
*ab and
Viktor
Ivády
 *bef
*bef
aStrongly Correlated Systems Lendület Research Group, Wigner Research Centre for Physics, H-1525, Budapest, Hungary. E-mail: barcza.gergely@wigner.hu
bMTA-ELTE Lendület “Momentum” NewQubit Research Group, Pázmány Péter, Sétány 1/A, 1117 Budapest, Hungary. E-mail: ivady.viktor@ttk.elte.hu
cSchool of Mathematical and Physical Sciences, Faculty of Science, University of Technology Sydney, Ultimo, New South Wales 2007, Australia
dARC Centre of Excellence for Transformative meta-Optical Systems (TMOS), Faculty of Science, University of Technology Sydney, Ultimo, New South Wales 2007, Australia
eDepartment of Physics of Complex Systems, Eötvös Loránd University, Egyetem tér 1-3, H-1053 Budapest, Hungary
fDepartment of Physics, Chemistry and Biology, Linköping University, SE-581 83 Linköping, Sweden
First published on 24th January 2024
Abstract
Color centers in hexagonal boron nitride (hBN) have attracted considerable attention due to their remarkable optical properties enabling robust room temperature photonics and quantum optics applications in the visible spectral range. On the other hand, identification of the microscopic origin of color centers in hBN has turned out to be a great challenge that hinders the in-depth theoretical characterization, on-demand fabrication, and development of integrated photonic devices. This is also true for the blue emitter, which is a result of irradiation damage in hBN, emitting at 436 nm wavelength with desirable properties. Here, we propose the negatively charged nitrogen split interstitial defect in hBN as a plausible microscopic model for the blue emitter. To this end, we carried out a comprehensive first-principles theoretical study of the nitrogen interstitial. We carefully analyzed the accuracy of first-principles methods and showed that the commonly used HSE hybrid exchange–correlation functional fails to describe the electronic structure of this defect. Using the generalized Koopman's theorem, we fine-tuned the functional and obtained a zero-phonon photoluminescence (ZPL) energy in the blue spectral range. We showed that the defect exhibits a high emission rate in the ZPL line and features a characteristic phonon side band that resembles the blue emitter's spectrum. Furthermore, we studied the electric field dependence of the ZPL and numerically showed that the defect exhibits a quadratic Stark shift that is perpendicular to plane electric fields, making the emitter insensitive to electric field fluctuations in the first order. Our work emphasizes the need for assessing the accuracy of common first-principles methods in hBN and exemplifies a workaround methodology. Furthermore, our work is a step towards understanding the structure of the blue emitter and utilizing it in photonics applications.
1. Introduction
The development of quantum communication1–3 and quantum internet4,5 demands the preparation and processing of tailored photonic states to carry pieces of quantum information over long distances.6 Complex photonic technologies require on-demand emission of single photons from controllable single-photon emitters (SPEs). For real-life applications, SPEs need to produce high-purity single photons with a high emission rate, be robust against environmental disturbances, and offer solutions for chip-scale integration in photonic devices.Numerous materials platforms, ranging from silicon through diamond to polymers, have been proposed and tested for integrated quantum photonic applications.6 Each platform offers different advantages; however, so far no material has been found that can satisfy all the needs of large scale photonic applications. Therefore, currently the most viable approach is the optimization of different processing elements in various host materials offering cross-platform integration capabilities.6
At the forefront of the development of single-photon emitters, color centers in hexagonal boron nitride (hBN) have recently gained considerable attention.7 Numerous color centers have been reported that feature sharp ZPL lines at room temperature, on-demand single-photon emission rates in the MHz range, high spectral stability, and high quantum efficiency.8,9 These color centers can be engineered to realize SPEs emitting at various wavelengths in a wide spectral range.8,9 Due to its layered structure, hBN also offers versatile integration capabilities for photonic applications.7,10
Very recently, a color center emitting at ∼436 nm in hBN, named the blue emitter, has shown remarkable properties.7,11–13 In addition to the sharp room temperature emission line and high emission rate, the blue emitter is known for its outstanding spectral stability and robustness.12–16 The latter features are attributed to the quadratic electric field dependence of the Stark shift of the blue emitter, which makes the defect insensitive to weak electric field fluctuations in the first order.15
The blue emitter appears as a result of radiation damage in hBN and it is often observed in irradiated samples.11–13,17 In addition, the appearance of the blue emitter seems to show a close relationship to another emitter in the ultraviolet (UV) spectral range.17 The microscopic structure of the UV emitter is currently debated in the literature.18–20 This is also true for the blue emitter, as the identification of the blue emitter's microscopic structure remains elusive, hindering theoretical studies and slowing down the development of related photonic applications.13
From the analysis of the blue emitter's photophysics, several important properties of the underlying atomic and electronic structures have been deduced.15,16 From the quadratic Stark effect, one could infer a high D3h symmetry of the ground and excited state configurations.15 In addition, the stability of the center under continuous optical pumping suggests a closed shell ground state with fully occupied and completely empty defect state(s) in the lower half and the upper half of the band gap, respectively.16 Taking into account the conditions of fabrication, vacancies, interstitials, antisites, and complexes derived from the combination of these defects are the most plausible candidates of the microscopic structures that can be created by irradiation in hBN.13 Related structures, such as the nitrogen interstitial and the carbon split interstitial dimer, have already been suggested in ref. 15 as potential candidates that fulfill the abovementioned criteria. Furthermore, these defects were also discussed in several recent theoretical works.21–25 On the other hand, no comprehensive theoretical studies have been carried out for these candidates.
Here, we theoretically studied the negatively charged nitrogen interstitial defect and propose it as a microscopic model for the blue emitter in hBN. So far, no consensus has been achieved in the literature concerning the most favourable configuration of this defect. We show that the split interstitial configuration is the lowest energy form of the nitrogen interstitial. We carefully analyzed the accuracy of popular density functional theory (DFT) methods by testing the generalized Koopman's theorem26–28 for the defect states and carried out fractional occupation number weighted electron density (FOD)29,30 analysis on the system. We show that the excited state of the defect, exhibiting stretched nitrogen–boron bonds, cannot be described by the hybrid functional most often used for hBN. The fraction of the exact exchange contribution needs to be reduced to obtain a higher accuracy ZPL value. Furthermore, we calculated the photoluminescence (PL) spectra of the negatively charged nitrogen split interstitial and showed that they resemble the experimental spectra of the blue emitter. We also studied the electric field dependence of the ZPL energy and numerically demonstrated a quadratic Stark shift. We conclude that the nitrogen split interstitial defect is a promising model for the blue emitter, which may facilitate advances in the fabrication and utilization of the emitter.
2. Results: first-principles theory of the nitrogen interstitial in hBN
In this section, we carried out a focused theoretical study on the nitrogen split interstitial defect in hBN. Our goal is to achieve the highest possible accuracy for the Ni defect by utilizing a diverse set of state-of-the-art numerical methods. In particular, we studied the problem both with periodic DFT on supercells and with non-periodic DFT on cluster models. Relevant details of the methodology are provided in the discussions of the results in this section. The remaining technical details of the calculations are provided in the Methods section.2.1. The stable atomic configuration
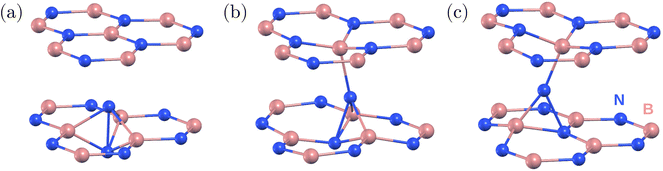
First, we studied the stable and metastable atomic configurations of an inter-layer nitrogen interstitial in hBN. We considered the negative charge state of the system, which is expected to be the most stable for Fermi energy values close to the middle of the band gap.22,24 Various related structures have been reported in the literature previously;21–24 however, no consensus has been achieved regarding the ground state configuration. Although multiple studies identified the [0001] split interstitial as the most favored configuration,21–23 a recent study found a tilted split interstitial configuration for the ground state.24 Furthermore, this tilted split interstitial configuration was proposed as a candidate for the 3.1 eV emitter.24In order to unambiguously identify the ground state configuration of the nitrogen interstitial in hBN, we investigated a series of potentially relevant defect configurations using periodic DFT in a multi-layered bulk system, see Fig. 1. We first placed the interstitial atom into a small orthorhombic 120-atom supercell of two-layer hBN with its AA′ stacking similar to that of the model used in ref. 24. Since the relaxation of the defect and over-mixing of the defect and host states can lead to different ground state structures,31 we considered both the semi-local PBE functional32 and hybrid HSE functional with a Fock exchange contribution of α = 0.30 and the screening parameter μ set to 0.4 Å−1 (also used in ref. 24) to identify the ground state. We found the [0001] split interstitial, Fig. 1(a), to be favorable by 0.59 eV (0.68 eV) than the lowest energy tilted split interstitial configuration calculated using the HSE(0.3) (PBE) functional. Therefore, we could not confirm the results of ref. 24, but our results are in line with earlier reports (ref. 21–23).
Before discussing our results for larger, convergent supercells, we point out shortcomings of the two-layer model. To study the stability of the model, we carried out molecular dynamics (MD) simulations at 500 K using the PBE functional. As a result of the atomic thermal motion, we observed the sliding of adjacent BN layers from stacking AA′ to AB1′, where the B atoms are aligned on top of each other, while N atoms slide to the hollow site.33 The fully relaxed [0001] split interstitial in the AB1′ stacked hBN was found to be 0.68 eV (0.95 eV), which is more favorable than in the AA′ stacked hBN calculated by using the HSE(0.3) (PBE) functional. This is due to reduction of the repulsive interaction between the N atoms in the AB1′ stacking. From the analysis of the atomic configurations proposed in ref. 24 and from our experiences with two-layer models, we conclude that the recently reported tilted ground state configuration24 is possibly a consequence of unphysical layer slippage. We note here that the sliding of the BN layers results in a metastable configuration in a four-layer model. To avoid slippage of the layers in the simulations, we included at least 4 layers in our bulk models hereinafter.
According to our findings, the hexagonal 512-atom supercell composed of four BN layers is sufficient to accurately describe the ground state configurations of the nitrogen interstitial in hBN. Using the HSE(0.3) functional and the 512-atom model, the [0001] split interstitial configuration was found to be the most favorable one, see Fig. 1(a), followed by a tilted interstitial configuration with a tilt angle of 17° from the [0001] axis along the hollow region and 0.51 eV higher in energy (16° and 0.50 eV with PBE), see Fig. 1(b). Another metastable interstitial configuration was obtained with a 0.50 eV higher energy and a pronounced tilt of 26° in the BN bond direction (25° and 0.59 eV with PBE). Unlike the previous configurations, the 26° tilted interstitial consists of a three-coordinated N atom, see Fig. 1(c). Additional calculations indicate that the energy difference between different configurations is more sensitive to the exchange fraction in comparison with the separation between hBN layers and the choice of van der Waals screening.
Using the HSE(0.3) functional, the distances between the split interstitial N atoms and the neighboring B atoms are d1 (interstitial nitrogen–nitrogen pair) 1.56 Å, d2 (interstitial nitrogen with the closest boron in the same layer) 1.57 Å, and d3 (interstitial nitrogen with boron from the top/bottom layer) 2.57 Å. The PBE distances are d1 = 1.60 Å, d2 = 1.58 Å, and d3 = 2.56 Å. The negatively charged split interstitial defect exhibits a high D3h symmetry in the ground state.
2.2. Electronic structure
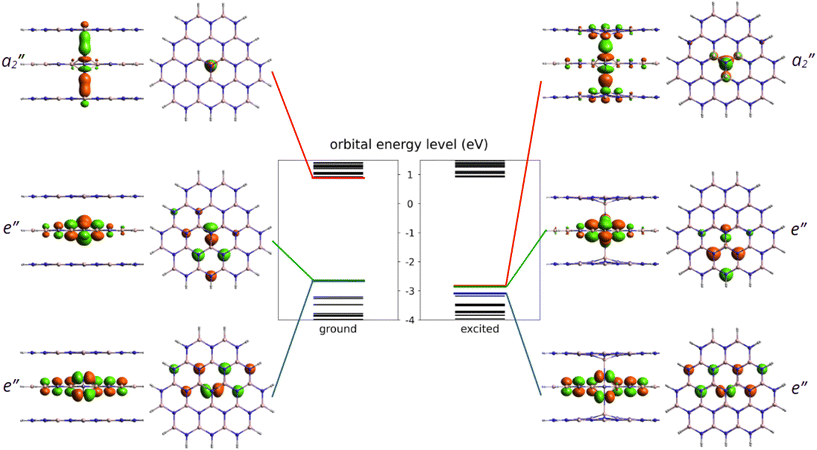
After identifying the most favourable configuration of the negatively charged nitrogen split interstitial defect in hBN, we continued our study with the analysis of the electronic structure of the defect. The two out-of-plane nitrogen atoms give rise to several defect states, some of which fall into the valence band. The ones that appear in the band gap are the fully occupied e′′ state and the empty a′′2 state, see Fig. 2. The ground state is a singlet and the defect possesses no spin.Optical transition between the occupied and the unoccupied defect states is allowed by perpendicular to c-polarized photons. In the excited state, the nitrogen atoms form long bonds with the closest boron atoms on the symmetry axis due to the occupation of the bonding a′′2 state. Consequently, the N–N distance d1 extends by about 26% (0.42 Å), while the B–N distance d3 on the symmetry axis contract by 33% (0.85 Å). We note that the excited state of the Ni(−) defect is slightly distorted due to the Jahn–Teller effect that reduces the symmetry to C2v. The three B–N distances in the middle plane (d2) change from 1.58 Å, 1.58 Å, and 1.58 Å to 1.67 Å, 1.67 Å, and 1.58 Å.
Accurate first-principles calculation of the optical properties of color centers in hBN has turned out to be a challenge. In order to draw reliable conclusions for the Ni(−) defect, we tested different methods, such as PBE and HSE(α) functionals in the periodic supercell models of the Ni(−) defect in hBN. For cluster models, we applied time-dependent DFT (TDDFT)34 with the PBE functional (PBE-TDDFT) and the n-electron valence state perturbation theory on top of the complete active space self-consistent field (CASSCF-NEVPT2) method. In periodic hexagonal 768-atom model, we used the constrained occupation method and Hellmann–Feynman forces to relax the excited state structure corresponding to the e′′ → a′′2 transition. The excited state geometry was first relaxed with the PBE functional and then continued with the HSE(α) functional. We note that relaxation of the excited state with HSE(α) (α ≈ 0.25–0.35) is cumbersome due to the change of ordering of the defect states and related structural instabilities. In our 261-atom cluster model of 5 adjacent hBN flakes, see Fig. 3, we initially optimized the ground state geometry at the PBE level of theory using the def2-SVP basis set. During the optimization, owing to its computational demands, only the middle 13 atoms are relaxed in each layer plus the additional interstitial nitrogen. From the obtained equilibrium geometry, we calculated the vertical excitation spectrum with PBE-TDDFT and CASSCF-NEVPT2 methods, requesting 3 roots (the ground state and 2 degenerate excited states in all cases). Then, we relaxed the structure of the excited state by PBE-TDDFT following the energy gradient of the corresponding root. The electronic energy of the excited state was calculated from a second vertical excitation spectrum calculated at the relaxed geometry. Using a larger basis set would have been too expensive; however, to obtain more accurate ZPL, the def2-TZVPD basis was applied to the middle 4 atoms of each layer plus the interstitial nitrogen while the def2-SVP basis set was applied to the remaining atoms. More details on the excited state calculations and the models can be found in the Methods section.
The adiabatic energy differences (EAD = EES − EGS) calculated for the various models are provided in Table 1. The true ZPL energy includes contribution from zero point energies of the phonon modes in the ground and excited states (EZPL = EES − EGS + ΔEZPE, where ΔEZPE = EESZPE − EGSZPE), see later. As can be seen, the adiabatic energy difference ranges in a wide energy interval starting at 2.38 eV up to 3.20 eV. The wave function-based NEVPT2 method predicts the highest energy difference of 3.20 eV.
| Model | Method | Adiabatic energy difference | ZPL |
|---|---|---|---|
| E AD | E ZPL = EAD + EZPE | ||
| 261-atom cluster | SA-CASSCF(4,3)-NEVPT2 | 3.20 | 3.10 |
| 261-atom cluster | Nonperiodic TDDFT and PBE | 2.38 | 2.28 |
| 768-atom supercell | Constrained periodic DFT and PBE | 2.40 | 2.30 |
| 768-atom supercell | Constrained periodic DFT and HSE(0.32) | 3.33 | 3.23 |
| 768-atom supercell | Constrained periodic DFT and HSE(0.208) | 3.06 | 2.96 |
| 768-atom supercell | Constrained periodic DFT and HSE(0.132) | 2.84 | 2.74 |
| Experiment | 2.844 (436)15 | ||
As demonstrated for other systems,35–37 the CASSCF-NEVPT2 method can provide accurate results when excited states of multi-reference character are considered. However, for the Ni(−) defect, both the ground state and the lowest energy singlet excited state possess a clear single-reference character. The leading electron configurations shown in Fig. 2 have 100.0% and 98.9% contributions in the ground and excited state wave functions, respectively, if 4 electrons and the 3 frontier orbitals form the active space. We note that similar wavefunction characters were obtained for systematically extended active spaces. Therefore, the accuracy of the NEVPT2 method in this case is comparable to the MP2 method,38 which is expected to be outperformed by a carefully chosen single-determinant DFT method.
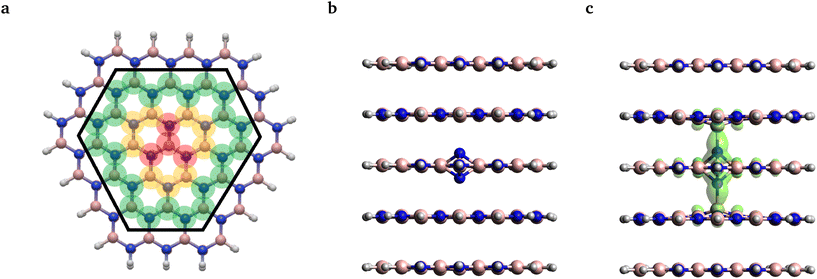
As an alternative investigation of the reliability of single-reference methods, we adopted the fractional occupation number weighted electron density (FOD) analysis method29 from quantum chemistry. Using this method one can identify potential static correlation features of the obtained DFT ground states, which might call for more sophisticated multi-reference methods. To this end, we carried out calculations on the same 261 atom cluster model, as shown in Fig. 3(a), using the PBE functional and the def2-SVP basis set.
The FOD analysis performed on the ground state geometry revealed no FOD density, see Fig. 3(b). For the excited state geometry, however, some FOD density was predicted, which was found to be localized around the defect center on the N–B bonds stretched along the symmetry axis, see Fig. 3(c). The shape of the FOD surface resembles the union of the two HOMOs and the LUMO with no detectable contribution from other orbitals. Thus, static correlation is only expected to be present in the aforementioned 4-electron 3-orbital (4,3) active space. As the CASSCF(4,3) calculation did not result in mixed states, it can be concluded that the obtained FOD plot indicates merely the quasi-degeneracy of the frontier orbitals and does not stem from the actual multireference character. Accordingly, we continued our analysis using TDDFT and constrained-DFT methods.
The PBE-TDDFT result obtained in a 261-atom cluster using the def2-SVP basis set and the PBE-constrained DFT result obtained in a 768-atom periodic model are provided in Table 1. As can be seen, the two methods agree very well with each other, indicating an appropriate basis set selection for the cluster model. On the other hand, the PBE-TDDFT and NEVPT2 results deviate by ≈0.8 eV. Since semi-local exchange–correlation functionals tend to underestimate and the NEVPT2 (∼MP2) method tends to overestimate excitation energies, we set our focus to hybrid DFT methods, which can be grasped as an interpolation between semi-local density functional theory and wavefunction theory.
In order to further narrow down the set of applicable methods, we selected the HSE0639 hybrid DFT functional for further investigations; nevertheless, we varied the mixing parameter (α, indicating the proportion of HF exchange in the functional formula) and thereby generated different HSE(α) methods. As the next step, we calculated the ZPL energy at the HSE(α) level of theory in a 768-atom periodic supercell model.
The most commonly used mixing parameter α ranges between 0.3 and 0.35 in hBN. These values are set by adjusting the theoretical band gap to the experimental one.22 While this method improves the description of the host states and localized orbitals of intrinsic defects, it may not work for all defects, especially when stretched bonds are observed, see Fig. 2(b).
In order to test the accuracy of the functional for the description of a given state, we used the generalized Koopman's theorem26–28 (ionization potential theory40–42 in other terminology). According to this theorem, the eigen energy of the highest occupied Kohn–Sham orbital and the ionization energy of the system should be equal when the exact exchange–correlation functional is used. Since the exact DFT functional is not known, approximate functionals may fail to fulfill this theorem. This failure manifests itself as a difference between the Kohn–Sham eigen energy and the ionization energy. The non-Koopman's energy ENK measures this as
| ENK = εHO − (EN+1 − EN), | (1) |
| ENK = E′NK(q,L⊥,L∥) + εcorr(q,L⊥,L∥), | (2) |
The non-Koopman's energy defined in eqn (1) and (2) is a good indicator of the accuracy of DFT functionals for localized defect states. When a functional with tunable parameters is used, such as the HSE(α) functional, adjustment of the free parameter may be utilized to decrease the non-Koopman's energy and thus to improve the description of the defect orbitals. This strategy has been successfully employed for several other point defect systems, see, for instance, ref. 28. On the other hand, we must first calculate the εcorr term, which may be comparable in absolute value with the non-Koopman's energy itself. To proceed with the analysis on the adiabatic excited state-ground state energy difference of the Ni(−) defect, we carefully investigated the value of the εcorr charge correction term.
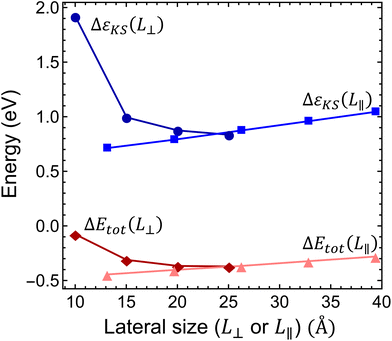
Interestingly, the scaling of the Kohn–Sham energy and the total energy shows an unexpected behavior, as depicted in Fig. 4. Considering the L⊥ perpendicular to c lateral size dependence of both the Kohn–Sham energy and the ionization energy, we observed converging curves that take finite values at the L⊥ → ∞ limit. This behaviour is typical of bulk models. On the other hand, for the L∥ parallel to the c lateral size of the supercell, we obtained a linear dependence, see Fig. 4, that diverges at the L∥ → ∞ limit. This odd behaviour is unexpected for the bulk model of several layers of hBN sheets under periodic boundary conditions. A similar linear dependence was, however, observed in a single-layer hBN sheet under vacuum in periodic boundary conditions,45,46 where the electrostatic interaction of the infinite charged layers diverges. Therefore, we conclude that the charge correction of the Kohn–Sham and total energy terms in the bulk hBN model cannot be described by the charge correction methods developed for conventional bulk semiconductors, such as diamond and silicon. The charge correction should account for the electrostatics of a localized charge in a 2D layer immersed in the media of relative permittivity other than 1 (due to the presence of other pristine hBN layers).
In order to circumvent this issue, one needs either to scale both perpendicular and parallel to plane lattice parameters simultaneously as suggested in ref. 47 or to use the correction method described in ref. 45. To model the systems, we expressed the finite-size and charge-dependent energy terms as45
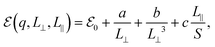 | (3) |
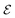 refers to either the Kohn–Sham energy or the total energy of the system,
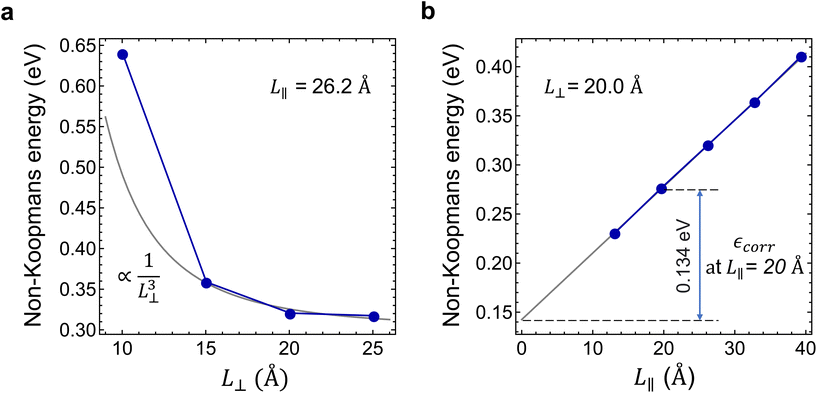
refers to either the Kohn–Sham energy or the total energy of the system, 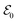 is the finite-size effect-free energy value that corresponds to the limit of a single-point defect in the material, and a, b, and c are the free parameters that we will use to fit eqn (3) to the calculated energy curves. S is the surface of the hBN layers in our finite periodic models. Note that for infinite layers, i.e. S → ∞, the last term on the right-hand side of eqn (3) vanishes. For finite supercells, however, the last term is of high relevance. Since we are interested in the non-Koopman's energy, we calculated the supercell size dependence of this energy term in the ground state and fitted eqn (3) directly to the obtained curve, see Fig. 5.
is the finite-size effect-free energy value that corresponds to the limit of a single-point defect in the material, and a, b, and c are the free parameters that we will use to fit eqn (3) to the calculated energy curves. S is the surface of the hBN layers in our finite periodic models. Note that for infinite layers, i.e. S → ∞, the last term on the right-hand side of eqn (3) vanishes. For finite supercells, however, the last term is of high relevance. Since we are interested in the non-Koopman's energy, we calculated the supercell size dependence of this energy term in the ground state and fitted eqn (3) directly to the obtained curve, see Fig. 5.
Considering the perpendicular to c lateral size dependence of the non-Koopman's energy at L∥ = 26.2 Å, we observed converging tendency, see Fig. 5(a), which is best fitted by a 1/L⊥3 function using points beyond 15 Å. The smallest supercell is apparently an outlier of the general trend expectedly due to the overlap of the defect states. We note here that the inclusion of higher than third order terms in eqn (3) may improve the fit,48 however, to avoid over-fitting of our data and to preserve the good fit at the dilute limit we limited our fit to the third order. As can be seen in Fig. 5(a), the non-Koopman's energy only slightly changes beyond L⊥ = 20 Å, thus we considered supercells of this later size to be convergent in the perpendicular to c direction. Therefore, for L⊥ ≥ 20 Å, we set parameters a and b to zero in eqn (3), which approximation causes an error no larger than 15 meV. Parallel to the c supercell size dependence of the non-Koopman's energy for L⊥ = 20.0 Å is depicted in Fig. 5(b). The points can be perfectly fitted with a linear curve, which intersects the energy axis at 0.145 eV for L∥ = 0. From the extrapolation to zero, we can obtain the finite-size effect-free non-Koopman's energy for the considered charged layered system, see ref. 45. For a 20 Å × 20 Å × 20 Å supercell consisting of 768 atoms, the spurious electrostatic energy correction to the non-Koopman's energy, see eqn (2), is εcorr = ENK − E′NK(−1, 20.0, 20.0) = 0.134 eV. The periodic model related to the electrostatic interaction between the negatively charged defect and the homogeneous positive background depends negligibly on the small variation of the defect states due to the choice of the functional. Therefore, we used the same correction for different HSE(α) functionals in the same supercell of 768 atoms.
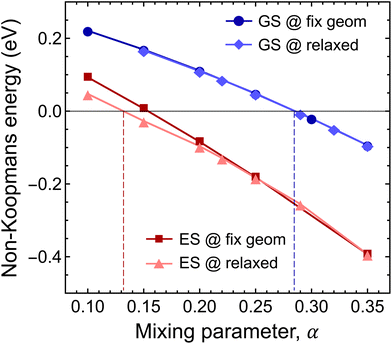
First, we studied the accuracy of the HSE(α) functional in the ground state of the negatively charged Ni defect. As can be seen in Fig. 6, ENK = 0 was achieved at α = 0.285. Note that geometry relaxation has only negligible effects on the non-Koopman's energy, see Fig. 6. The obtained optimal mixing parameter is close to α = 0.3 used in the analysis of the ground state properties, and thus our results presented for the stability of the Ni defect are valid. On the other hand, for the excited state, we observed a different behaviour. At α > 0.3, the finite-size effect-corrected non-Koopman's energy takes a significant negative value, indicating that the frequently used HSE({0.3, 0.32, 0.35}) functionals are not appropriate for the description of the excited state of the Ni(−) defect.
For the excited state, the non-Koopman's energy vanishes at α = 0.132 (α ≈ 0.154) when structural relaxation is taken (not taken) into account. Here, structural relaxation makes a difference in the non-Koopman's energy in contrast to the case of the ground state. These results clearly indicate the need for the reduction of the exact exchange contribution in the excited state. The mixing parameter α is connected to the degree of localization and to the long-range screening. In the present case, the charge localizations of the highest occupied e′′ and a′′2 orbitals of the ground and excited states are different, see Fig. 2. The former extends mostly in parallel to the plane direction, while the latter extends over 3 BN layers in perpendicular to the plane direction. We expect different degrees of screening for the in-plane and out-of-plane directions, which underpins the observation of different mixing parameters.
Since accurate description of the ground state and the excited state requires two different functionals, HSE(0.132) and HSE(0.285), the adiabatic energy differences of the states cannot be calculated with the highest accuracy. On the other hand, we can use our results to significantly narrow down the uncertainly of the theoretical predictions and provide the most likely value of the adiabatic energy difference and ZPL.
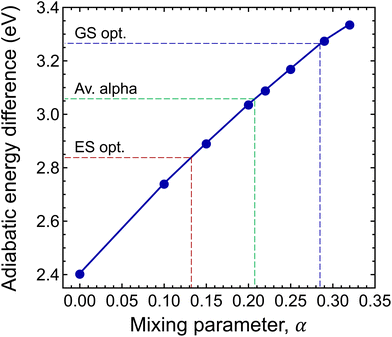
To this end, we calculated the mixing parameter dependence of the adiabatic energy difference of the ground and excited states, see Fig. 7 and Table 1. As can be seen, the energy difference decreases as the exact exchange contribution is reduced. At α = 0.285 and α = 0.132, the ground state and the excited state are described with high accuracy, respectively. The adiabatic energy differences corresponding to these mixing parameter values are 3.27 eV and 2.84 eV. We assume that the true value of the adiabatic energy difference could be found in this interval. On the other hand, due to the different behaviours of the ground and excited states, the accurate value of the adiabatic energy difference cannot be obtained with the HSE(α) functional using a single value of the mixing parameter. At the same time energy differences cannot be computed using two different functionals. Therefore, we defined the most plausible value of the adiabatic energy difference by the mean of the values obtained with the ground and excited state optimized functionals, which is EAD = 3.06 eV. Due to the approximately linear dependence of the adiabatic energy difference on the mixing parameter, the same value can be obtained using 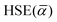 , where
, where 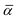 is the mean value of the optimized mixing parameters. The expected error margin of the adiabatic energy difference is approximately ±0.2 eV.
is the mean value of the optimized mixing parameters. The expected error margin of the adiabatic energy difference is approximately ±0.2 eV.
2.3. Electron–phonon coupling
Next, we investigated the local vibrations and the phonon side band of the photoluminescence spectrum of the negatively charged nitrogen split interstitial defect in hBN. For this purpose, we utilized cluster models of various sizes and non-periodic DFT. All DFT calculations on the cluster models were performed using the def2-SVP basis49 and PBE exchange–correlation functional.50 In order to preserve the distance of the van der Waals layers in line with experimental expectations, only the chemically most relevant atoms are considered in the geometry relaxation procedure. We demonstrate that the cluster model is capable of providing convergent predictions for the studied system by calculating the adiabatic energy difference of the ground and excited states with varying flake sizes, numbers of stacked layers, and geometrical optimization schemes. For further discussion, see Appendix A.For the PL spectrum calculations, three different cluster models were constructed from the bulk geometry relaxed using the VASP at the PBE level: (i) a 3-layer model with a relatively large layer size (L), (ii) a 3-layer model and (iii) a 5-layer model with a smaller layer size (S); see Fig. 3 and Appendix A. The atomic clusters were capped with hydrogen atoms at the edges, leading to B110N110H63, B56N56H46, and B92N94H75 clusters, respectively.
In order to preserve the well-defined layered structure of the standalone cluster, its geometry was only partially relaxed at the PBE level of theory using ORCA. In a minimalist case, besides the terminating hydrogen atoms, only the four atoms in the center of each layer and the interstitial N atom are considered in geometry optimization, see the atoms highlighted in translucent red in Fig. 3a. Since in this scheme we only optimized a small set of atoms, we refer to this relaxation strategy as S in the following discussion. In the other case, this subset was further expanded by the outer atoms of the 3 hexagonal rings around the center of each layer, see the atoms highlighted in red and yellow in Fig. 3a. In this case, the positions of 13 second-row atoms per layer near the center of the molecule plus the interstitial N were relaxed. By minimizing a medium set of atoms, we refer it to as strategy M. In the third case, denoted strategy L, the further shell of outer atoms were also optimized, highlighted in green in Fig. 3a, i.e., 37 atoms per layer plus the interstitial N were optimized. The various setups are labeled as A-B-C-D, where A is the number of layers in the cluster, B is the number of optimized layers, C is the size of the layers, and D refers to the region which was optimized in the layers. For example, 5-3-S-M means that a 5-layer model with the smaller layer was utilized and only 13 atoms per layer was optimized in the 3 middle layers plus the interstitial N.
Convergence of the photoluminescence spectra as a function of the cluster size and relaxation strategy is depicted in Fig. 8a. Due to the relatively large change of the position of the nitrogen atoms and the first neighbor atoms along the symmetry axis, see Fig. 2, the vertical gradient approximation51,52 was utilized. This means that the ground state geometry and Hessian were used, assuming that the excited state Hessian is the same, and the excited state geometry was estimated. In case of the smallest model of three layers (3-3-S-S), the intensity of the second peak is larger compared to the first peak associated with the ZPL. Similarly, the 3-layer model with the M region optimized (3-3-S-M) exhibits a large sideband. In contrast, the two spectra from the largest 5-layer model (5-3-S-M and 5-5-S-M) show a strong ZPL emission and much less pronounced sideband. The same can be achieved if the larger layer is used (L), which implies that convergence of the PL spectrum can be reached in the flake models. Due to the applied approximation, we expect higher uncertainty in the spectra, so instead of choosing from the five models which resemble the experimental spectrum, we used the largest 5-5-S-M model for further investigations. Note that in Fig. 8a, all transition lines, including the ZPL, were broadened by an empirical 300 cm−1 line width.
 | ||
| Fig. 8 (a) Calculated PL spectra with different geometry optimization setups. (b) The best calculated PL spectrum compared to the experimental results.16 Partial Huang–Rhys factors of each mode are also presented with bars. The line width is set to 300 cm−1. For better comparison of the theoretical and the experimental PL spectra, the theoretical spectrum was shifted to match the experimental ZPL. | ||
For the convergent model (5-5-S-M), we obtained a Huang–Rhys factor of 0.491 and radiative lifetime of 54 ns using a refractive index of 2.13. The corresponding transition dipole moment vector is (0.37574, −0.19576, −0.00215) in atomic unit, where the z direction is parallel to the c axis of hBN. It must be noted that due to the large difference between the ground and excited states, our investigation is limited to using the vertical gradient approximation that only uses the ground state geometry and Hessian. In this approximation, in the estimated excited state geometry, the N–N distance (d1) is not as large as we obtained with PBE-TDDFT; therefore, the transition dipole moment between the two states could differ considerably from what we obtain from PBE-TDDFT on the excited state geometry. In principle, we expect the lifetime to be overestimated in our calculations.
From the analysis of the partial Huang–Rhys factors, we deduce that the dominant local vibrations responsible for the phonon sideband are: (i) the movement of the atoms surrounding the defect causing the Jahn–Teller distortion, (ii) the stretching and contraction of the N–N bond in the defect, and (iii) the movement of the B atoms from the neighbouring layers towards the defect, see Fig. 9. These vibrations account for the geometry difference between the ground and excited states.
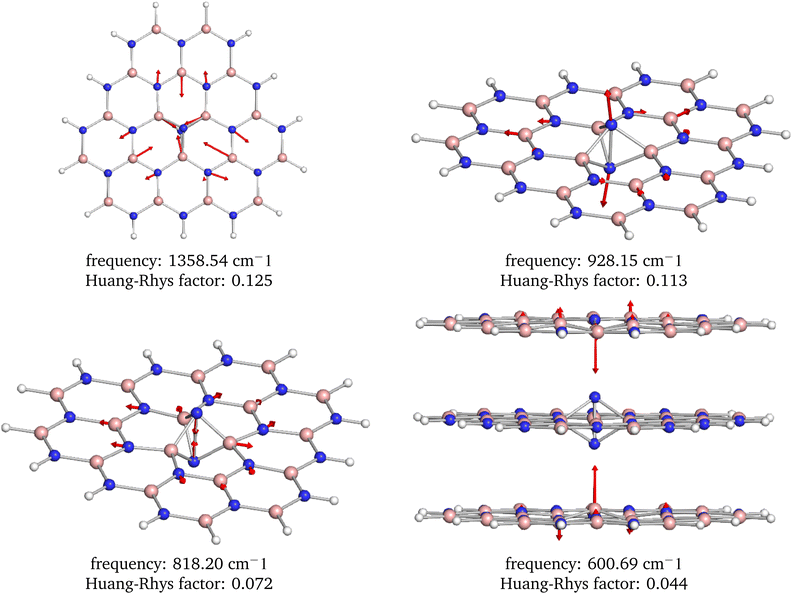 | ||
| Fig. 9 Visualization of the four most dominant phonon modes based on the Huang–Rhys factors. Note that these interesting modes are localized around the defect center. | ||
Lastly, we calculated the zero-point energy (ZPE) contribution to the adiabatic energy difference obtained in the previous section. From the sum of the two contributions, we computed the ZPL energy. The ZPE contribution was approximated by numerical frequency calculations where a 5-layer model with 261 atom were used and the middle 13 atoms were relaxed in each layer plus the interstitial nitrogen. For the ZPE contribution we obtained −0.10 eV, meaning that the zero point energy contribution of the local vibrational modes is larger in the ground state than in the excited state. This is understandable as stretched bonds are formed in the excited state configuration that give rise to softer potential and lower vibrational frequencies. We assume in this paper that the zero-point energy contribution does not significantly depend on the electronic structure calculation method used, thus we used the same zero point energy contribution in all ZPL value approximations. The third row in Table 1 provides the ZPE corrected adiabatic energy differences as obtained with different methods.
2.4. Electric field dependence of the ZPL energy
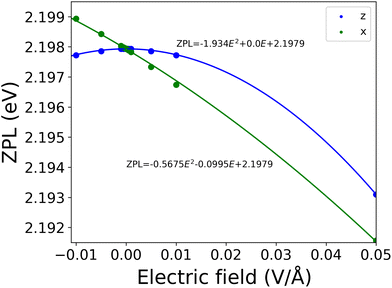
Finally, we numerically investigated the electric field dependence of the of the ZPL line of the negatively charged nitrogen split interstitial in hBN. As discussed in ref. 15 and 16, defects exhibiting high D3h symmetry in both the ground and excited states may be less sensitive to external electric fields and only the second or higher order electric field dependence is expected. The negatively charged Ni defect does exhibit D3h symmetry in the ground state, as also discussed in ref. 15; however, the excited state is Jahn–Teller unstable that lowers the symmetry to C2v. Therefore, it is a question whether the desirable quadratic dependence of the ZPL energy on the electric field is preserved even in such a low symmetry. Our preceding study15 suggests that the quadratic term dominates the electric field dependence of the ZPL; however, due to the applied large-scale model and consequent numerical uncertainties, the results need to be reconsidered using an improved independent model. Here, we used a cluster model, atomic basis functions, and the ORCA suit opposed to the slab model, plane wave basis set, and VASP package utilized previously.15To study the effect of the electric field on the zero-phonon line of the Ni(−) defect in hBN, a static field was applied perpendicular and parallel to the layers of the cluster model with varying strengths ranging from −0.05 to 0.05 V Å−1. For the calculations, we used the PBE-TDDFT method, which somewhat underestimates the ZPL energy, see Table 1; however, it can capture the polarization of the defect orbitals induced by the external electric field. We expect our results to be qualitatively accurate.
As can be seen in Fig. 10, perpendicular to the layers we found that the ZPL energy decreases quadratically with increasing strength of electric field. However, if the electric field is parallel to the layers, the ZPL energy depends almost linearly on the strength of the electric field. This behaviour was expected from the changes in dipole moment (Δμ = (−0.67, 0.42, −0.01) Debye) and polarizability (Δα) in both directions. In the parallel to the layer direction we obtained 55 Å3 for Δα, and 0.01 Debye for Δμ, while in perpendicular direction 17 Å3 and 0.67 Debye, respectively. We do not find a perfectly linear curve in the x direction due to the non-zero quadratic contribution to the Stark shift.
3. Discussion: a plausible model for the blue emitter in hBN
Finally, we compared our numerical results on the negatively charged nitrogen [0001] split interstitial to the experimental reports of the blue emitter in hBN.16 In summary, we proposed the Ni(−) defect as a working model for the blue emitter, although not all the experimental observations can be explained with the current model. Below, we list all the known pros and cons of this assignment.3.1. Pros
The blue emitter in hBN can be intentionally created by electron irradiation. As a result of primary damage caused by high energy electron bombarding, boron and nitrogen vacancies and interstitials can be created. Complex defect formation is expected as a result of the secondary processes, such as migration of the created defects and possible recombination with other defects in the lattice. The nitrogen split interstitial is a result of primary radiation damage and it is expected to be formed in substantial concentrations.Regarding the optical properties of the blue emitter, the underlying microscopic structure is expected to possess D3h symmetry, while the relevant electronic structure of the defect should consist of a fully occupied defect state in the lower half of the band gap and an unoccupied defect state in the upper half of the band gap. The latter conditions are deduced from the stability of the defect under continuous excitation. The negatively charged nitrogen split interstitial defect possesses a fully occupied e′′ state and an empty a′′2 state inside the band gap, giving rise to a singlet ground state. This electronic structure is in agreement with the expectations derived from the observed properties of the blue emitter.
The blue emitter is known to emit light mostly along out of plane directions with in-plane electric field polarization. Interestingly, if the perpendicular to c polarization of the blue emitter is not homogeneous, there is a preferential the in-plane polarization direction.15 This observation also implies that the three-fold rotation symmetry of the defect should be violated either in the ground state or the excited state, which has been overlooked previously. To explain this behaviour, we draw attention to the Jahn–Teller instability of the excited state of the Ni(−) defect. Since an electron is excited from the e′′ state to the a′′2 state, the symmetry is reduced to C2v in the excited state due to the Jahn–Teller distortion that gives rise to a clear single-axis polarization pattern in the calculated transition dipole moment. This is in agreement with the observations.
The blue emitter exhibits a well-resolved ZPL at 2.844 eV (436 nm).15 While it is challenging to accurately calculate the ZPL energy of the nitrogen interstitial, our prediction agrees within the error margin of our calculations with the ZPL energy of the blue emitter. We obtained 2.96 eV (419 nm), which is 12 meV (17 nm) blue shifted compared to the blue emitter's ZPL. This deviation is well within the estimated error bar of ±0.2 eV of our calculations.
Finally, we discuss the PL spectra of the blue emitter and the Ni(−) defect. As can be seen in Fig. 8, the experimental and convergent theoretical PL spectra agree very well with each other. Both spectra exhibit dominant emission in the ZPL and a vanishing sideband. For the Ni defect, we obtained a Huang–Rhys factor of 0.491 and a Debye–Waller factor of 0.61.
Due to the Jahn–Teller distorted excited state, the Ni(−) defect possesses a non-zero electric dipole in this state. The dipole is in the plane of the hosting hBN layer. Depending on angle δ of the in-plane electric field and the electric dipole of the defect, one may observe either linear (δ = 0°, 180°), or quadratic (δ = 90°, 270°), or mixed electric field dependence. This observation may explain the differences of the experimental results reported in ref. 15, 53 and 54.
3.2. Cons
For perpendicular to plane electric fields, we found a quadratic Stark shift, while the paper of Zhigulin et al. (ref. 15) reports a weak linear dependence. We attribute this difference to perpendicular to plane disturbances, for instance, due to bending of the hBN sample. Such a distortion can lift the in-plane reflection symmetry of the system, which in turn enhances the out-of-plane electric dipole component.The blue emitter possesses an excited state lifetime as short as ∼2.15 ns.16 Our computational results suggest a longer radiative lifetime in the range of 54 ns. We note that the calculations account only for radiative processes, thus the experimental excited state is expectedly shorter than the theoretical estimates. However, the deviation between the two values cannot be only explained by non-radiative processes. We anticipate that the deviation is due to the approximations used in the calculations.
Furthermore, according to recent studies on the fabrication of the blue emitter, there seems to be a correlation between the appearance of the blue emitter and the UV emitter in hBN.15–17 The latter has been assigned to the carbon dimer recently.18 Since the nitrogen interstitial and the carbon dimer structures have no common roots, the connection between the two defects is not obvious. We anticipate that the atomic structures are not related, but instead the stability of the optical bright state is affected in similar ways. For instance, due to their similar electronic structure, the position of the Fermi level may affect the two defects similarly. This may explain the presumed relationship of the appearance of the two defects.
4. Methods
4.1. Further details on the calculation of periodic models using the VASP
The density functional theory calculations for bulk models were performed using the Vienna Ab initio simulation package (VASP)55 within the projector-augmented wave (PAW) method56 with a plane-wave cutoff of 500 eV. The exchange–correlation functional is described by the generalized gradient approximation of Perdew, Burke, and Ernzerhof (PBE),50 and we also considered the screened hybrid functional of Heyd–Scuseria–Ernzerhof (HSE06)39 with a modified exact exchange fraction of 0.1–0.35 and a screening parameter of 0.4. The van der Waals interaction was included using the Grimme-D3 method with Becke–Johnson damping.57,58The unit cell of bulk hBN was optimized with a 15 × 15 × 5 k-point grid. We obtained lattice parameters of a = 2.50 Å and c = 6.56 Å, which are in agreement with the experimental values of a = 2.50 Å and c = 6.60 Å measured at 10 K.59 In the case of defect stability study, we considered an orthorhombic supercell of 120 atoms (5a, 3a + 6b, c) and a hexagonal supercell containing 512 or 768 atoms. The reciprocal space was sampled with the Γ-point. Atom relaxation was carried out until the forces are less than 0.01 eV Å−1 (0.025 eV Å−1) with the PBE (HSE(α)) functional. We also included the non-spherical contributions within the PAW spheres.
4.2. Further details on the numerical studies of cluster models using ORCA
The DFT calculations of the cluster models were performed using ORCA 5.0.3.60 Most of the calculations were performed with the PBE functional and the def2-SVP basis set49 if otherwise not noted. During all calculations with ORCA the resolution of identity (RI) approximation was used for the Coulomb term and the fitting basis was applied through the AutoAux feature. Geometry optimizations were performed with default settings. For excited states, different numbers of roots are required depending on the setups, and the corresponding root is chosen to be followed, which represents the correct excited state. FOD analysis was performed at 5000 K as suggested in the seminal article.29 Numerical frequency calculations were performed on only those atoms which were originally optimized at the particular model setup with steps of 0.005 Å3. The PL spectra were determined based on the Hessians obtained from the numerical frequency calculations using the vertical gradient approximation51,52 and a 300 cm−1 line width.Data availability
The data that support the findings of this study are available from the authors upon reasonable request.Author contributions
A. G., R. B., Z. B., and V. I. carried out the first-principles calculations. All authors contributed to the manuscript. The work was supervised by V. I. and G. B.Conflicts of interest
There are no conflicts to declare.Appendix A
In order to demonstrate that our cluster model is capable of providing convergent predictions for the studied system, we calculated the PBE-TDDFT ZPL energy with varying flake sizes, numbers of stacked layers, and geometrical optimization schemes. The corresponding numerical results are collected in Table 2. Note that ZPL energies in this study do not include ZPE contribution.| # Layers | # Relaxed layers | Layer size | Relaxation scheme | ZPL (eV) | |
|---|---|---|---|---|---|
| PBE | HSE(0.25) | ||||
| 3 | 3 | S | S | 2.005 | 3.030 |
| 3 | 3 | S | M | 2.398 | 3.359 |
| 3 | 3 | L | S | 2.051 | 3.112 |
| 3 | 3 | L | M | 2.491 | 3.499 |
| 3 | 3 | L | L | 2.388 | 3.572 |
| 5 | 3 | S | S | 1.953 | 3.001 |
| 5 | 3 | S | M | 2.168 | 3.390 |
| 5 | 5 | S | S | 1.954 | 3.000 |
| 5 | 5 | S | M | 2.198 | 3.389 |
Interestingly, we found that the ground state is relatively prone to the relaxation and the energy gap increases by granting more freedom for geometry relaxation than minimalist scheme S. By adding external layers to the minimal model of three stacked layers, the in-layer planarity of the excited state is preserved, yielding some 0.10–0.2 eV energy gain. This stabilization effect was found not to be sensitive to the relaxation of the additional covering layers. In conclusion, independently of the investigated cluster setups, the lowest singlet excitation was consistently found at around 2–2.5 eV. Based on the ZPL results in the following analysis, we studied the 5-layer model with smaller layers and optimized all of them with the M strategy.
The used def2-SVP is a minimal basis set, but using a larger basis set would be too expensive. To address this issue, we also studied how ZPL changes if larger basis sets are used on the center atoms. In our convergence test, def2-SVPD, def2-TZVP, and def2-TZVPD were applied only on: (i) the two N-s and two B-s in the center (4 atoms), (ii) 4 atoms at the center of the 3 middle layers plus the interstitial N (13 atoms) or (iii) 4 atoms of the 5 layer plus the interstitial N (21 atoms). The ZPLs are collected in Table 3. Using diffuse functions causes a less than 0.1 eV change in the ZPL; however, the application of the TZ quality basis set increases the ZPL from 2.20 eV to 2.28–2.38 eV. It can also be observed that including the outer layers has negligible impact. As a convergent PBE-TDDFT adiabatic ZPL value for the cluster model we obtained 2.38 eV, in good agreement with the results of constrained DFT calculations in a periodic model, see Table 1.
| Basis | 4 atoms | 13 atoms | 21 atoms |
|---|---|---|---|
| def2-SVPD | 2.215 | 2.230 | 2.239 |
| def2-TZVP | 2.339 | 2.357 | 2.352 |
| def2-TZVPD | 2.281 | 2.372 | 2.380 |
Acknowledgements
This research was supported by the National Research, Development, and Innovation Office of Hungary within the Quantum Information National Laboratory of Hungary (Grant No. 2022-2.1.1-NL-2022-00004) and within grants FK 135496 and FK 145395. I. A. acknowledges the Australian Research Council (CE200100010 and FT220100053) and the Office of Naval Research Global (N62909-22-1-2028) for the financial support. V. I. also appreciates the support from the Knut and Alice Wallenberg Foundation through the WBSQD2 project (Grant No. 2018.0071). The calculations were performed using resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC). We acknowledge KIFÜ for allowing us access to the computational resource based in Hungary.References
- N. Gisin and R. Thew, Nat. Photonics, 2007, 1, 165–171 CrossRef CAS.
- A. Orieux and E. Diamanti, J. Opt., 2016, 18, 083002 CrossRef.
- D. Cozzolino, B. Da Lio, D. Bacco and L. K. Oxenløwe, Adv. Quantum Technol., 2019, 2, 1900038 CrossRef.
- H. J. Kimble, Nature, 2008, 453, 1023–1030 CrossRef CAS PubMed.
- S. Wehner, D. Elkouss and R. Hanson, Science, 2018, 362, eaam9288 CrossRef PubMed.
- E. Pelucchi, G. Fagas, I. Aharonovich, D. Englund, E. Figueroa, Q. Gong, H. Hannes, J. Liu, C.-Y. Lu, N. Matsuda, J.-W. Pan, F. Schreck, F. Sciarrino, C. Silberhorn, J. Wang and K. D. Jöns, Nat. Rev. Phys., 2022, 4, 194–208 CrossRef.
- J. D. Caldwell, I. Aharonovich, G. Cassabois, J. H. Edgar, B. Gil and D. N. Basov, Nat. Rev. Mater., 2019, 4, 552–567 CrossRef CAS.
- I. Aharonovich, J.-P. Tetienne and M. Toth, Nano Lett., 2022, 22, 9227–9235 CrossRef CAS PubMed.
- A. Kubanek, Adv. Quantum Technol., 2022, 5, 2200009 CrossRef.
- A. Al-Juboori, H. Z. J. Zeng, M. A. P. Nguyen, X. Ai, A. Laucht, A. Solntsev, M. Toth, R. Malaney and I. Aharonovich, Adv. Quantum Technol., 2023, 6, 2300038, DOI:10.1002/qute.202300038.
- B. Shevitski, S. M. Gilbert, C. T. Chen, C. Kastl, E. S. Barnard, E. Wong, D. F. Ogletree, K. Watanabe, T. Taniguchi, A. Zettl and S. Aloni, Phys. Rev. B, 2019, 100, 155419 CrossRef CAS.
- C. Fournier, A. Plaud, S. Roux, A. Pierret, M. Rosticher, K. Watanabe, T. Taniguchi, S. Buil, X. Quálin, J. Barjon, J.-P. Hermier and A. Delteil, Nat. Commun., 2021, 12, 3779 CrossRef CAS PubMed.
- H. Liang, Y. Chen, L. Loh, N. L. Q. Cheng, Y. Chen, C. Yang, Z. Zhang, K. Watanabe, T. Taniguchi, S. Y. Quek, M. Bosman, G. Eda and A. Bettiol, Blue Quantum Emitters in hexagonal Boron Nitride, DOI:10.21203/rs.3.rs-2606377/v1.
- J. Horder, S. White, A. Gale, C. Li, K. Watanabe, T. Taniguchi, M. Kianinia, I. Aharonovich and M. Toth, Phys. Rev. Appl., 2022, 18, 064021 CrossRef CAS.
- I. Zhigulin, J. Horder, V. Ivady, S. J. U. White, A. Gale, C. Li, C. J. Lobo, M. Toth, I. Aharonovich and M. Kianinia, Phys. Rev. Appl., 2023, 19, 044011, DOI:10.1103/PhysRevApplied.19.044011.
- I. Zhigulin, K. Yamamura, V. Ivády, A. Gale, J. Horder, C. J. Lobo, M. Kianinia, M. Toth and I. Aharonovich, Mater. Quantum Technol., 2023, 3, 015002, DOI:10.1088/2633-4356/acb87f.
- A. Gale, C. Li, Y. Chen, K. Watanabe, T. Taniguchi, I. Aharonovich and M. Toth, ACS Photonics, 2022, 9, 2170–2177 CrossRef CAS.
- M. Mackoit-Sinkeviěienė, M. Maciaszek, C. G. Van de Walle and A. Alkauskas, Appl. Phys. Lett., 2019, 115, 212101 CrossRef.
- H. Hamdi, G. Thiering, Z. Bodrog, V. Ivády and A. Gali, npj Comput. Mater., 2020, 6, 1–7 CrossRef.
- S. Li, A. Pershin, G. Thiering, P. Udvarhelyi and A. Gali, J. Phys. Chem. Lett., 2022, 13, 3150–3157 CrossRef CAS PubMed.
- V. Wang, R.-J. Liu, H.-P. He, C.-M. Yang and L. Ma, Solid State Commun., 2014, 177, 74–79 CrossRef CAS.
- L. Weston, D. Wickramaratne, M. Mackoit, A. Alkauskas and C. G. Van de Walle, Phys. Rev. B, 2018, 97, 214104 CrossRef CAS.
- J. Strand, L. Larcher and A. L. Shluger, J. Phys.: Condens. Matter, 2019, 32, 055706 CrossRef PubMed.
- E. Khorasani, T. Frauenheim, B. Aradi and P. Deák, Phys. Status Solidi B, 2021, 258, 2100031 CrossRef CAS.
- J. Bhang, H. Ma, D. Yim, G. Galli and H. Seo, ACS Appl. Mater. Interfaces, 2021, 13, 45768–45777 CrossRef CAS PubMed.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 085202 CrossRef.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205209 CrossRef.
- V. Ivády, I. A. Abrikosov, E. Janzén and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205201 CrossRef.
- S. Grimme and A. Hansen, Angew. Chem., Int. Ed., 2015, 54, 12308–12313 CrossRef CAS PubMed.
- C. A. Bauer, A. Hansen and S. Grimme, Chem. – Eur. J., 2017, 23, 6150–6164 CrossRef CAS PubMed.
- J. D. Gouveia and J. Coutinho, Electron. Struct., 2019, 1, 015008 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. M. Gilbert, T. Pham, M. Dogan, S. Oh, B. Shevitski, G. Schumm, S. Liu, P. Ercius, S. Aloni, M. L. Cohen and A. Zettl, 2D Mater., 2019, 6, 021006 CrossRef CAS.
- E. Runge and E. K. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS.
- V. Ivady, G. Barcza, G. Thiering, S. Li, H. Hamdi, J.-P. Chou, O. Legeza and A. Gali, npj Comput. Mater., 2020, 6, 1–6 CrossRef.
- R. Babar, G. Barcza, A. Pershin, H. Park, O. B. Lindvall, G. Thiering, O. Legeza, J. H. Warner, I. A. Abrikosov, A. Gali and V. Ivády, Quantum sensor in a single layer van der Waals material, https://arxiv.org/abs/2111.09589.
- Z. Benedek, R. Babar, A. Ganyecz, T. Szilvasi, O. Legeza, G. Barcza and V. Ivady, npj Comput. Mater, 2023, 9, 187, DOI:10.1038/s41524-023-01135-z.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
- J. P. Perdew and M. Levy, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 16021–16028 CrossRef CAS.
- C.-O. Almbladh and U. von Barth, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 3231–3244 CrossRef CAS PubMed.
- C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Phys. Rev. Lett., 2009, 102, 016402 CrossRef PubMed.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef.
- D. Wang, D. Han, X.-B. Li, S.-Y. Xie, N.-K. Chen, W. Q. Tian, D. West, H.-B. Sun and S. Zhang, Phys. Rev. Lett., 2015, 114, 196801 CrossRef PubMed.
- H.-P. Komsa, N. Berseneva, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. X, 2014, 4, 031044 CAS.
- H.-P. Komsa and A. Pasquarello, Phys. Rev. Lett., 2013, 110, 095505 CrossRef PubMed.
- J.-Y. Noh, H. Kim and Y.-S. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205417 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- T. Petrenko and F. Neese, J. Chem. Phys., 2012, 137, 234107 CrossRef PubMed.
- F. J. A. Ferrer and F. Santoro, Phys. Chem. Chem. Phys., 2012, 14, 13549–13563 RSC.
- G. Noh, D. Choi, J.-H. Kim, D.-G. Im, Y.-H. Kim, H. Seo and J. Lee, Nano Lett., 2018, 18, 4710–4715 CrossRef CAS PubMed.
- N. Nikolay, N. Mendelson, N. Sadzak, F. Böhm, T. T. Tran, B. Sontheimer, I. Aharonovich and O. Benson, Phys. Rev. Appl., 2019, 11, 041001 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- W. Paszkowicz, J. Pelka, M. Knapp, T. Szyszko and S. Podsiadlo, Appl. Phys. A, 2002, 75, 431–435 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |