Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Selective ion transport in large-area graphene oxide membrane filters driven by the ionic radius and electrostatic interactions†
Lidia
Lancellotti
a,
Antonio
Bianchi
a,
Alessandro
Kovtun
 a,
Massimo
Gazzano
a,
Massimo
Gazzano
 a,
Tainah Dorina
Marforio
a,
Tainah Dorina
Marforio
 b,
Zhen Yuan
Xia
b,
Zhen Yuan
Xia
 c,
Matteo
Calvaresi
c,
Matteo
Calvaresi
 b,
Manuela
Melucci
b,
Manuela
Melucci
 *a,
Chiara
Zanardi
*a,
Chiara
Zanardi
 *ad and
Vincenzo
Palermo
*ad and
Vincenzo
Palermo
 *ad
*ad
aInstitute for Organic Synthesis and Photoreactivity, National Research Council (ISOF-CNR), via Piero Gobetti 101, 40129, Bologna, BO, Italy. E-mail: palermo@isof.cnr.it; manuela.melucci@isof.cnr.it; chiara.zanardi@unive.it
bDepartment of Chemistry ‘G. Ciamician’, Alma Mater Studiorum University of Bologna, via Selmi 2, 40126 Bologna, Italy
cDepartment of Industrial and Materials Science, Chalmers University of Technology, Gothenburg S-41296, Sweden
dDepartment of Molecular Sciences and Nanosystems, Ca’ Foscari University of Venice, via Torino 155, 30172 Venezia-Mestre, Italy
First published on 6th March 2024
Abstract
Filters made of graphene oxide (GO) are promising for purification of water and selective sieving of specific ions; while some results indicate the ionic radius as the discriminating factor in the sieving efficiency, the exact mechanism of sieving is still under debate. Furthermore, most of the reported GO filters are planar coatings with a simple geometry and an area much smaller than commercial water filters. Here, we show selective transport of different ions across GO coatings deposited on standard hollow fiber filters with an area >10 times larger than typical filters reported. Thanks to the fabrication procedure, we obtained a uniform coating on such complex geometry with no cracks or holes. Monovalent ions like Na+ and K+ can be transported through these filters by applying a low electric voltage, while divalent ions are blocked. By combining transport and adsorption measurements with molecular dynamics simulations and spectroscopic characterization, we unravel the ion sieving mechanism and demonstrate that it is mainly due to the interactions of the ions with the carboxylate groups present on the GO surface at neutral pH.
1. Introduction
Control of ion transport within membranes holds significant interest across various fields, including intracellular ion transport, healthcare, and water treatment.1–8The ability to induce selective ion transport in membranes could lead to valuable separations among multivalent (e.g. Ca2+, Mg2+, Pb2+, Cr3+) and monovalent (e.g. Na+, K+) metal ions, crucial for applications ranging from water desalination, softening, and purification to the extraction of rare elements.
In recent years, graphene oxide (GO) has emerged as one of the most promising materials for creating innovative membranes.9–15 These membranes can be fabricated through direct filtration of suspended GO nanosheets in water on porous substrates, resulting in highly ordered and uniform membranes with nanochannels formed between overlapped nanosheets.16–19 The application of an electric field has been found to induce selective migration of monovalent ions relative to divalent ones, offering new prospects for using GO membranes in ion separation applications.20–27 Several studies have demonstrated how ion migration can be modulated by the surface potential and influenced by an external electric field or changes in the polarity and field strength.20,28
While the mechanism behind the selective transport of ions within the nanochannels of membranes remains a subject of debate, it is generally accepted that it involves size exclusion and/or electrostatic interactions. The smaller diameters of monovalent cations (e.g. 3 and 4 Å for K+ and Na+, respectively) compared to those of multivalent cations (e.g. 6 and 8 Å for Ca2+ and Mg2+)29,30 explain the sieving mechanism based on steric effects. Various strategies have been developed to modify the interlayer spacing (d) of graphene-based structures, aiming to modulate their sieving activity. These strategies include physical confinement16 and alterations in the pH or ionic strength of the surrounding solution.31
Despite the advantages of GO-based membranes in inducing selective ion transport, their practical application has been limited to the laboratory scale due to constraints in producing compact and homogeneous filtering materials with surface areas larger than a few cm2, which are necessary for realistic water flows in real-world applications like water purification.
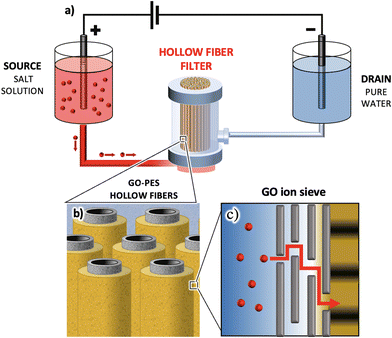
On the other hand, a well-established commercial filter type employs polymer hollow fiber modules, such as polyethersulfone (PES). These cost-effective modules are widely used for microfiltration. A typical filter consists of hundreds of hollow fibers (HF, Fig. 1a–c) of sub-millimeter diameter (300 μm in our case study) and nanometric lateral pores, determining the overall module cut-off (150 nm in our case study).
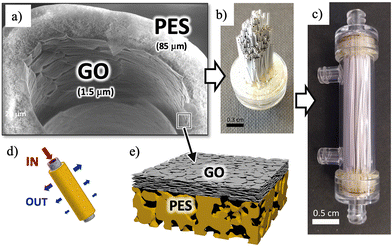 | ||
| Fig. 1 (a) SEM image of PES hollow fibers with an inner coating of GO. On the left part of the image, some cracks due to fiber cutting are used to show the layered structure of the coating. The thickness of each layer is reported. Additional SEM images of uniform coating are presented in the ESI.† (b) GO-PS hollow fibers mounted in a filter. (c) The whole filter assembled. (d) Cartoon showing the filtering mechanism of the hollow fibers with purified water coming out of the lateral surface pores. (e) Cartoon showing the water flux and filtering action across the GO-HF multilayer (not in scale). | ||
In the standard cross-flow filtration mode, the feed solution flows inside the fiber and the purified water crosses the fiber section, exiting from the lateral surface pores, as schematized in the cartoons of Fig. 1d and e.
Recently, we demonstrated the feasibility of coating PES fibers with GO, resulting in a composite bilayer membrane (HF-GO, Fig. 1d and e). This membrane retains the microfiltration properties of PES-HF while also enabling the adsorption of small organic molecules. The adsorption occurs through the intercalation of molecules between stacked GO layers, as confirmed by X-ray diffraction (XRD) analysis before and after adsorption.32
HF-GO fibers offer a unique opportunity to create GO membranes with a large area (approximately ≈250 cm2 instead of just a few cm2) and to study ion sieving in scalable and commercially available devices. The cut-off of these commercial filters is smaller than the average size of GO nanosheets, and this offers a unique opportunity to self-assemble uniform coatings of GO with a large area inside these hollow fibers by simple filtration. The process continues until a uniform coating is obtained on the whole surface of each of the >200 microfibers in the filter, as demonstrated by permeability experiments.32 Leveraging these multilayer fiber-like filters, we investigate here the transport of monovalent (i.e. Na+, Li+, and K+) and divalent ions (i.e. Ca2+ Mg2+, and Pb2+) induced by an applied potential difference in HF-GO filters. The goal is to demonstrate that the selective ion transport observed in planar membranes is preserved in these large-scale filters and to understand the mechanism controlling the transport.
We study the activated ion transport in GO-HF membranes and compare it with that in planar GO membranes, with adsorption studies on GO powders, and with molecular dynamics and quantum mechanics calculations. These analyses highlight the combined effect of the ionic radius and chemical interactions with GO nanosheets as driving forces behind selective ion transport.
2. Experimental
2.1 Reagents and solutions
GO powder (<35 mesh, >90% of sheets with a lateral size 300–3000 nm) was purchased from LayerOne and suspended in ultrapure water (18 MΩ cm resistivity). All solutions of cations under study were prepared by dissolving the corresponding chloride salts, purchased from Sigma Aldrich, in ultrapure water.2.2 Assembly of HF-GO filters
The structure of a typical HF-GO filter (VersatilePES, Plasmart, Medica SpA) is represented in Fig. 1a and b. Each filter contains 275 hollow fibers, 45 mm long, having an internal diameter of 300 μm, an external diameter of 470 μm and a cut-off of 150 nm. Each filter has a total filtering surface ≈250 cm2. Each filter possesses four inlets; head inlets have access to the inner side of the fibers, while lateral inlets have access to the outer side. It is possible to force a transmembrane flow by injecting water through one of the two head inlets, sealing the other head inlet (note as cross-flow filtration geometry).32HF internally coated with GO were obtained according to a previously reported procedure.32 Briefly, 2 mg mL−1 of GO suspension (obtained by sonication in ultrapure water for 4 h) was filtered in cross-flow mode. Being the average lateral dimension of GO nanosheets larger than the fibers cut-off,33 the GO nanosheets adhered to the inner surface of the hollow fibers; the process of coating is self-limiting, given that areas already coated with GO will see a reduction in flux, while holes and leaks will attract a higher flux until they get uniformly coated by GO, creating an ordered membrane (Fig. 1e), and then stabilized by annealing at 80 °C. The uniformity and adhesion of the GO films stabilized in this way on the fibers were excellent, similar to what already demonstrated in previous work. GO-PES-coated fibers showed no release even after extensive filtration tests performed following a procedure described in ref. 32.
Good uniformity was confirmed by static ion permeability tests: in absence of any driving force, no diffusion of ions across the filter was observed, which could exclude the presence of cracks or leaks even at nanometric size (see also more details in the “Results” section). SEM images taken on different cut fibers also showed a uniform stable coating, see Fig. 1a; additional SEM images of the fiber cross section, taken along the fiber long axis, can be found in the ESI.† The thickness of the GO coating was tuned by reiteration of the GO filtration process (i.e., by increasing the volume of GO suspension filtered) reaching a thickness of up to 1.5 μm. Table S1† shows the relationship between the amount of GO injected into the filter (% w/w) and the thickness of the GO membrane of the PES fiber finally obtained, together with the acronym of the filter used hereafter.
Before use, 1 L of 10−5 M aqueous solution of KCl was used to wash each filter in a dead-end configuration, i.e., in the same direction used later for ion transport. Each filter was then stored in this same electrolytic solution to tune the ionic conductivity when applying the electric field to activate ion migration. Some filters were treated and stored with HCl instead of KCl, as discussed below.
2.3 Ion migration setup for HF-GO filters
Ion migration was induced by connecting the setup reported in Fig. 2a to an Autolab PGSTAT12 potentiostat/galvanostat from Metrohm-Ecochemie. The commercial filters used for these tests possess four inlets, but only two of them were exploited for the ion transport throughout the HF-GO (see a photo of the real setup in Fig. S1 in the ESI†). Two Pt wire electrodes were set at the opposite sides of the filter, inside tanks containing 2 mL of water solution each.Tank 1 contained the electrolytic solution (0.1 M solution of the salt under investigation), while tank 2 contained ultrapure water (resistivity >18 MΩ cm). The two tanks were set at the same height to avoid any artefacts due to differences in pressure, which could influence transport behaviour. A constant potential of −1.0 V was applied to the electrode in tank 2, while the electrode in tank 1 was grounded. The variation of the conductivity of solution in tank 2 was tested every 10 min by performing measurements by electrochemical impedance spectroscopy (EIS), connecting interdigitated gold electrodes (DropSens-Metrohm) to the Frequency Response Analyzer (FRA) filter of the Autolab PGSTAT12 (Metrohm-Ecochemie). Frequency scans were performed over the range of 0.1–100 kHz with a signal amplitude of 50 mV. The DC bias was temporarily stopped during the collection of the EIS signal to avoid any interference; the impedance values were converted into conductivity values according to a methodology previously reported34 and, ultimately, to the total amount of ions transported to tank 2. The amount of ions transferred after 120 min was measured by atomic spectroscopy measurements (see Section 2.6). Three replicates were performed for each experiment. The linear correlation between the values of conductivity measured and the concentration of ions in solution was confirmed using a calibration curve (Fig. S2†).
2.4 Ion transport measurements in GO planar membranes
For comparison's sake, we also performed tests in a more classical geometry using planar membranes, as most of previously published paper reported. The ion transport of Na+ and Ca2+ through a planar GO membrane was studied following a previously reported method.35 GO membranes were prepared by vacuum filtration of 15 mL of a 2 mg mL−1 aqueous suspension of GO (obtained by 4 h sonication of GO in ultrapure water) on a flat alumina Whatman filter (pore size 0.2 μm). The dry membranes could be processed as self-standing films of pure GO. Two Pt electrodes were fixed on the opposite faces of the membrane and a potential difference of −1 V was applied between them. As a comparison experiment, filtration tests were also performed by applying pressure instead of an electric field; water was pumped throughout the membrane (2.5 mL min−1) using a Perimax 12 peristaltic pump (Spetec). The total amount of ions eventually passed through the planar membranes was quantified as previously described for the HF-GO filters.2.5 X-ray diffraction
The membranes were analysed by X-ray diffraction (XRD) and X-ray photoelectron spectroscopy (XPS). XRD patterns were obtained with a PANalytical X'Pert Pro X-ray diffractometer with nickel-filtered Cu Kα radiation and a fast X'Celerator detector; data were collected at 40 mA, 40 kV, collecting 25 s at each 0.05° 2-theta.2.6 X-ray photoelectron spectroscopy (XPS)
XPS patterns were obtained using a Phoibos 100 hemispherical energy analyser (Specs GmbH. Berlin. Germany) and Mg Kα radiation (photon energy 1253.6 eV; power = 125 W) in constant analyser energy (CAE) mode. More details on data analysis and acquisition are in the ESI† and in ref. 36.2.7 Batch adsorption experiments on GO nanosheets in suspension
To test the affinity of the different materials for target ions, we also performed a static adsorption test under batch conditions without any filtering or macroscopic flow. To this aim, 30 mg of GO were sonicated for 4 h in ultrapure water and exposed to 5 mL of solution of the cation under study. Experiments were performed in solutions containing 10−5 M KCl as well as in solutions containing HCl at various concentrations, namely 10−5, 10−3 and 10−1 M to highlight the interaction of the ions with GO at different protonation degrees. The suspensions were stirred for 120 min at room temperature to let the ions interact with the powder and the supernatant was then filtered to remove the GO powder. The setup used was similar to what we previously used to measure the affinity of GO for organic dyes.37 The concentration of ions remaining in the solution at the end of the treatment was analysed as described for the HF-GO filters.2.8 Ex situ analysis of the filtered solution and quantification of transported ions
After each test, analysis of transported ions was performed by atomic absorption spectroscopy (AAS) using a Varian SpectrAA220FS equipped with a Varian SPS-S auto-sampler. An air–acetylene flame was used and CsCl2 was utilized as an ionic suppressor. The samples were prepared in ultrapure water with Suprapur nitric acid. Standard solutions were prepared starting from 1000 mg L−1 stock solution. All solutions were stored in polythene bottles.The quantification of Li+, Ca2+, Mg2+, and Pb2+ was obtained by inductively coupled plasma optical emission spectroscopy (ICP-OES) performed with a PerkinElmer Optima 4200 DV simultaneous spectrometer. The sample introduction system used a pneumatic nebulizer coupled with a glass spray chamber. Four standard solutions for each cation were prepared starting from a 1000 mg L−1 standard solution to calculate the calibration plot of each element.
2.9 Molecular dynamics (MD) simulations
The model system representing GO was modelled on a 50 Å × 50 Å graphene sheet created with Visual Molecular Dynamics (VMD).38 The epoxy, hydroxyl and carboxyl groups were randomly positioned on graphene sheets using the GO-py program39 to reproduce the experimental O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio and the relative abundances of C–O functional groups obtained by XPS. Two GO sheets were initially placed at the interlayer distance experimentally determined by XRD analysis. The General Amber Force Field (GAFF) was used to describe GO. The atomic charges were obtained by AM1 calculations. The inter-layer zone was solvated with TIP3P waters and sodium and calcium ions were placed on 16 different initial positions to sample the interactions of the ions with the diverse regions of GO characterized by a distinct composition of functional groups.
C ratio and the relative abundances of C–O functional groups obtained by XPS. Two GO sheets were initially placed at the interlayer distance experimentally determined by XRD analysis. The General Amber Force Field (GAFF) was used to describe GO. The atomic charges were obtained by AM1 calculations. The inter-layer zone was solvated with TIP3P waters and sodium and calcium ions were placed on 16 different initial positions to sample the interactions of the ions with the diverse regions of GO characterized by a distinct composition of functional groups.
160 ns of MD simulations were carried out, fully sampling the behaviour of the cations in the inter-layer regions. Periodic boundary conditions (PBC) were employed to simulate infinite sheets. The analysis of MD simulations was performed with CPPTRAJ, a post-processing tool implemented in Amber18.40 The effect of the electric field was simulated using the “external electric field” implementation present in Amber18. An intensity of 1 V cm−1 was applied along the X-axis. The affinity of the ions for the GO sheets was computed using the MM-GBSA (Molecular Mechanics-Generalized Born Surface Area) algorithm.
2.10 Quantum mechanical (QM) calculations
The interaction energies between the different ions and carboxylates in GO were estimated by using Quantum Mechanics/Molecular Mechanics (QM/MM) calculations, employing the ONIOM method as implemented in Gaussian16.41 In these computations, the ion and a carboxylate group of GO were described at the DFT level (wB97XD/6-311++G** for all the atoms except for Pb described by the effective core potential (ECP) LanL2DZ).42–44 All the remaining atoms of GO were described with the Universal Force Field (UFF).45 The QEq formalism was used.463. Results and discussion
3.1 Ion transport of Na+ and Ca2+ in HF-GO filters induced by the electric field
Ion transport experiments in HF-GO filters were performed by connecting two plastic tanks to the filter as shown in Fig. 2. At rest, no changes in the water level of tank 1 and tank 2 were observed, indicating that the osmotic pressure did not play a significant role in the system. A platinum electrode was present in each tank to apply a potential difference across the entire system (Fig. S1 in the ESI†).In the absence of an applied potential, no spontaneous transport of ions was observed in the GO-coated filters and the ion concentration in tank 2 stayed null (Fig. S3 in the ESI†), demonstrating that even the thinnest GO coatings were uniform enough to block any ion transport in the absence of an external driving force. Even after long exposure, atomic spectroscopy analysis did not show the presence of Na+ and Ca2+ in tank 2, indicating that their concentration was under the limit of detection of the technique. Instead, we observed ions diffusing freely in the reference samples prepared without GO coating, the cut-off of the pristine fibers (150 nm) being much larger than the size of the ions, allowing tank 1 and tank 2 to reach an equal concentration (Fig. S3†). This evidence confirmed that the GO deposition approach used yielded a continuous coating on each fiber of the filter with no gaps or micro-cracks that would cause spontaneous leak of ions from tank 1 to tank 2.
After these initial checks, we activated ion transport by applying a potential of −1 V to electrode 2, while electrode 1 was grounded (Fig. 2a). The conductivity of the solution in tank 2 was monitored every 10 min by EIS, as described above. Fig. 3a shows, as an example, the variation of the conductivity due to the transport of Na+ in three different filters: after about 30 min, the conductivity of the solution increased, ultimately reaching a plateau after about 100 min. Besides the in situ measurements of ion concentration with EIS, the total number of ions ultimately present in tank 2 after 120 min was also quantified ex situ by atomic spectroscopy measurements to avoid possible artefacts due to other ions present in the solution influencing the total conductivity.
We compared the ion transport of monovalent and divalent cations which are relevant for water purification, namely Na+, Li+ and K+ with Ca2+, Pb2+, and Mg2+; these tests where repeated three times for each ion (see typical results in Fig. S4†) using GO coatings with 1.5 μm thickness (HF-GO-5).
Significant differences of transport were observed for different ions (Fig. 3b), suggesting that the transport in the GO membrane cannot be explained by a simple electric drift, but should depend on the chemical interaction of ions with the GO membrane.
Thanks to the 2D shape of the GO nanosheets, each ion should travel a tortuous path within the nanosheets (Fig. 2c), which have an interlayer distance of ca. 8–10 Å; while traveling in this space, ions will interact strongly with the numerous chemical moieties present on the surface of the GO nanosheets, so any difference in GO–ion interaction will be amplified by the tortuous path, leading to different diffusion rates. As an example, a rough estimate assuming an average GO sheet size of 1 μm, a layer thickness of 1.5 μm and an interlayer spacing of 8 Å gives a tortuous path of ≈0.94 mm for the ions to cross the filter.
Ca2+ has a larger hydrated radius than Na+ and, for its chemical nature, can be coordinated by the oxidized moieties present on the GO nanosheets. The ability of GO membranes to discriminate monovalent cations from bivalent cations has been demonstrated previously for planar GO membranes;35,47 this fundamental feature is observed also in the GO-HF studied here, which are more suitable for real applications.48–51
The differences observed could be due to (1) different sizes of the ions, expressed as the hydrated radius, (2) different charge, which will cause different ion mobilities in an electric field, or (3) different interactions with the charged moieties present on the GO surface.
Previous studies attributed the different permeation of ions in GO membranes to the different ionic radii of monovalent and divalent ions.18,19,52–54 To check if this hypothesis is true in our systems, Fig. 3b (black symbols) shows the concentrations of ions in tank 2 vs. the dimension of the hydrated radii of the relevant cation measured at neutral pH. An exponential correlation is observed for most ions (red dashed line in the semi-log plot of Fig. 3b), in agreement with previous reports on planar membranes35 with some interesting exceptions. Indeed, Pb2+ shows a lower permeation than Na+, despite having a similar hydrated radius. Moreover, the amount of Li+ is significantly lower with respect to Ca2+, despite their radii being similar. These results indicate that the transport properties of GO could not be explained by the ionic radius or charge alone, but rather by a combination of different parameters.
Besides the hydrated radius and charge, we also checked for a correlation of the number of ions transported across GO with other atomic parameters, such as the Stokes radius of the ions or their charge density (calculated as ionic charge/ion volume) but found no clear correlation with these additional parameters.
Indeed, the presence of charged groups protruding out of GO can foster the formation of coordination complexes with stability that does not follow the order of classical complexes in bulk solutions. Shibahara et al. demonstrated a strong chelating effect of GO functionalized with iminodiacetic acid, where the ability to capture heavy ions was depending on the synergic effect of the chelating acid groups and the GO surface.12 Sun et al. also demonstrated a synergic effect of aminobenzene groups to stabilize the Na+ ions on pristine (non-GO) graphene for energy storage applications.13
It is well known that negatively charged moieties on GO can be protonated; Terrones et al. demonstrated that there are three equilibria in GO, two relative to carboxylic acids exhibiting different acidity (pKa1 ≈ 4.0 and pKa2 ≈ 6.0) and one relative to alcohols (pKa4 ≈ 10.0).55 Titration experiments performed by adding KOH to the solutions of our GO confirmed that the most significant deprotonation took place at pH = 6.0 in agreement with previous results. Thus, to unravel the role played by the chemical interactions induced by oxidized moieties present on GO nanosheets in the ion transport, we pre-treated the filter with HCl at pH = 5 to partially protonate the carboxylate groups and remove the negative charge present on it according to: GO-COO− + H+ ⇄ GO-COO-H. We then tested again the transport of Ca2+ and Na+ (red symbols in Fig. 3b) as a representative example of ions possessing or not the tendency to be coordinated by Lewis organic donors. Quite interestingly, the amount of Ca2+ transported through GO increased 800 times when the filters were treated with HCl, going from 1.18 × 10−2 μmol to 9.78 μmol. We ascribe this effect to the fact that protonated oxygenated groups are not available to coordinate Ca2+. The amount of Na+ decreased slightly, going from 0.52 μmol to 0.1 μmol.
Thus, protonated groups are beneficial for Ca2+ transport, while hindering Na+ transport, due to the coordination effect previously mentioned.
To better explain the differences in the ion transport observed for GO-HF, we compared these results with atomistic simulations and with other tests performed in different simpler geometries using GO planar filters or measuring ion adsorption on GO with no ion transport, as detailed below.
3.2 Batch adsorption tests on GO nanosheets
Ion transport is a complex dynamic process, requiring a macroscopic flow of ions and significant varying gradients of concentration. We performed additional experiments in a simpler, more uniform system, i.e., under static batch conditions, where GO nanosheets were dispersed in suspension and exposed to known concentrations of the different ions at different pH values (Fig. 4a). It is well known that ions and small molecules can easily adsorb or intercalate into GO and can even partially exfoliate it.33 In this experiment, removal of ions from the batch solution was only due to the surface adsorption of such ions on GO caused by chemical affinity in the absence of any other driving forces like electric field and the pressure of concentration gradients. | ||
| Fig. 4 (a) Cartoon showing the adsorption of ions on GO under static conditions. (b) Percentage of ions adsorbed upon exposing 0.1 M solution to GO nanosheets at different pH values. | ||
The concentration of the solution was the same as that used in the HF-GO filtration tests; the protonation of GO was varied by varying the pH through addition of HCl to the solution. Fig. 4b and Table S2† show the results obtained. Each data point is an average of three separate tests.
The results showed that the uptake of Ca2+ decreased significantly at acidic pH, suggesting that the protonation of GO oxygenated groups at low pH hinders their coordination with Ca2+, thus lowering the adsorption efficiency toward Ca2+, in agreement with the ion transport results. Pb2+ and Mg2+ showed a strong interaction with GO, which became weaker at low pH as well, even if the change results only evident at a low pH value due to the strong interaction with GO oxidized moieties.
Instead, the uptake of Na+ and K+ in GO was poor with no significant differences at all pH values, confirming their weak chemical interaction with GO nanosheets, as expected based on the poor tendency of these ions to be coordinated by oxygenated groups. This agrees with what observed from experiments carried out in the filters. The uptake of Li+ was instead significantly stronger, due to its better interaction with GO, also this is in agreement with the transport measurements.
3.3 Computational analysis of ion interaction and diffusion in HF-GO membranes
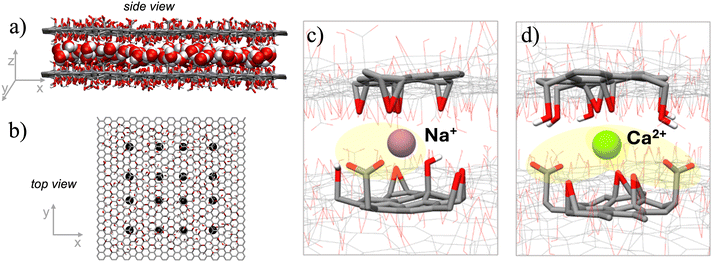
MD simulations were carried out to investigate the interaction and diffusion of Na+/Ca2+ in the HF-GO membrane at the atomic scale. These ions have been chosen as representatives of monovalent and bivalent ions even for the interest in their selective removal from water. To account for the intrinsic variability of GO surface chemistry, we modelled a realistic GO surface containing representative amounts of carboxyl, hydroxyl and epoxy functional groups based on the XPS data and tested each ion diffusion in 16 different areas of the nanosheets (Fig. 5a and b).We fully sampled the behaviour of the cations in the inter-layer regions (interactions with epoxides, hydroxyls, carboxylate and all the possible combinations). We evaluated the MM-GBSA binding energy for 5000 snapshots, sampling all the different positions that the cations can assume (Fig. S7 in ESI†). MD simulations demonstrated that both Na+ and Ca2+ interact significantly with the GO membrane. The adsorption energy of the divalent Ca2+ ion (−58.2 kcal mol−1) with the negatively charged membrane was higher than the monovalent Na+ ion (−39.3 kcal mol−1). The difference in the adsorption could be ascribed to the electrostatic interaction term (see Table S3†). In its favorite adsorption site (Fig. 5c), the monovalent Na+ ion interacts with a single carboxylate group, while the divalent Ca2+ ion can interact simultaneously with two carboxylates (Fig. 5d). This gives a much stronger electrostatic interaction for Ca2+ (−86.7 kcal mol−1) as compared to Na+ (−50.8 kcal mol−1). van der Waals interactions tend to destabilize the interaction for the larger Ca2+ ion (+28.9 kcal mol−1) more than for the smaller Na+ (+12.0 kcal mol−1), but this steric repulsion is not strong enough to counter the electrostatic attraction.
The spatial restriction between two GO sheets is crucial to entrap the ions, because in simulations with a single GO sheet, the ions were not stable on the nanosheet and could diffuse in the bulk water (see Table S4†). The average distance of the ion from the binding COO− groups (Fig. S5†) was roughly proportional to the ionic radius, but there was no clear correlation of such distance with the adsorption energy.
We quantitatively estimated the diffusion of Na+ and Ca2+: when the cations are in the inter-layer region, in the absence of an external electric field, the calculated diffusion constant for Na+ and Ca2+ was 2.6 and 1.8 × 10−11 m2 s−1, respectively. Such numbers are significantly smaller than what calculated in bulk water for Na+ and Ca2+ (6.63 and 1.28 × 10−9 m2 s−1, respectively).
When an external electric field with an intensity comparable to the experimental conditions (1 V cm−1) was applied in the simulation, the diffusion of Ca2+ was strongly reduced, going down to 0.42 × 10−11 m2 s−1 (4.5-fold reduction, see Table S4†), while the diffusion of the Na+ ion increased to 3.8 × 10−11 m2 s−1 (10-fold increase), in line with the experimental observations.
MD simulations suggest that, in the absence of an electric field, Ca2+ ions diffuse freely and can diffuse preferentially in areas with no blocking groups. When the electric field is applied, there is a preferential migration direction induced by the field and Ca2+ ions follow this direction, colliding with the functionalization, thus reducing their migration speed. As for Na+ ions, being smaller, this effect is less pronounced, and therefore an overall acceleration is observed in the presence of the electric field.
The model should be considered just indicative, given that the electric field is not always parallel to the nanosheets, and is partially shielded by the ions in solution. However, these results indicate that the external electric field could provide improved mobility for Na+ ions. On the opposite side, the diffusion of the Ca2+ ions is hindered.
The MD simulation and experimental results showed a crucial role of the carboxylate groups in the interaction between GO and ions. Thus, we decided to perform QM/MM calculation to evaluate quantitatively the binding energies between the carboxylate groups of GO nanosheets and the different ions (Fig. 5a).
Fig. 6 shows the correlation between the GO–ion dissociation energy (calculated by computation) and the amount of ions adsorbed by GO measured in the adsorption experiments.
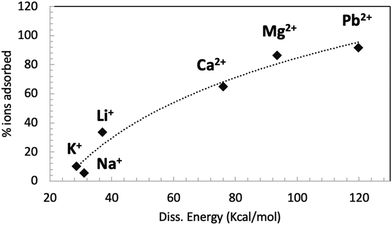 | ||
| Fig. 6 Relationship between the GO–ion dissociation energy calculated by simulations and the amount of ions adsorbed by GO measured in the batch adsorption experiment at neutral pH (also shown in Fig. 4). The dashed line is a guide for the eye. | ||
A good correlation between the computational and experimental data can be seen; ions with a weak interaction with GO, like Na+ and K+, can penetrate into GO and travel quite easily through the membrane. Ions with stronger interaction with GO, like Li+ and all divalent ions, can penetrate easily into GO but get stuck in specific adsorption sites of the membrane. This effect can be mainly ascribed to electrostatic interactions with the negatively charged groups of GO.
During their travel in the GO membrane, the ions will likely reside most of the time in correspondence of negatively charged groups (e.g. partially protonated COO− groups), eventually hopping from one group to the other and moving from tank 1 to tank 2.
Ca2+ ions have a strong interaction with such COO− groups, which will act as traps for the Ca, coordinating them in highly stable configurations. Upon protonation, such a trapping effect decreases, allowing the ions to better drift across the GO filter.
Na+ ions can also have weak interaction with GO, allowing them to pass in large quantities across GO jumping form one COO− to the other. Upon protonation, the amount of COO− available for such transport decreases, thus hindering slightly the Na transport. The different interactions of Ca2+ and Na+ would agree well with what observed in static batch adsorption tests (Fig. 4b) and with computational data (Fig. 5 and Table S3†).
3.4 Chemical and structural analysis of planar membranes after ion transport experiments
To further validate our model, we used XRD and XPS to detect the presence of the ions in the GO-HF membranes after electric tests of ion transport. The analysis was performed ex situ on the planar membranes prepared as described in Section 2.4, which could be measured by XPS and XRD.These planar membranes featured selective filtration as well, with Na+ being transported much better than Ca2+.
MD calculations suggested that Ca2+ is a better intercalant than Na+ in GO, even if showing worse transport properties. Indeed, XPS confirmed the presence of more Ca2+ than Na+ inside GO: we found about 0.18 at% of Ca2+ and 0.03 at% of Na+ in the membranes after transport experiment driven by the electric field. There is more calcium than sodium in the GO, even if more sodium is transported across GO. Thus, there is no correlation between the presence of ions in GO and the amount transported, confirming what already observed by MD, i.e., the ions which are more strongly interacting with GO do not show good transport performance.
We also used XPS to check if the ions transported damaged or modified the chemical structure of GO. The oxidation degree of the membranes was not affected by ion transport, the O/C ratio obtained from C 1s and O 1s XPS signals was within the narrow range between 0.38 and 0.40 in each membrane before and after the transport. The C 1s signals were almost identical in all samples. The analysis of C 1s signals showed only a small decrease of epoxy groups after the hydration of the membrane, while no difference in the composition was found between the hydrated GO membrane and the GO membrane after Na+ and Ca2+ passage. See the ESI† for more details.
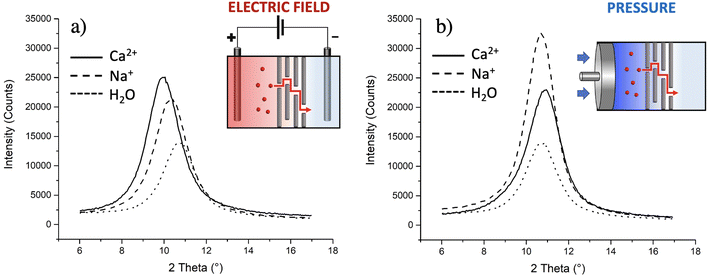
The presence of ions can vary the interlayer distance (d) between the GO nanosheets, so we used XRD to detect the eventual intercalation of ions in GO. Measurements were done on three membranes used for transport of Na+ and for Ca2+, respectively; the results were compared with the GO membranes exposed to pure water (d = 8.2 ± 0.2 Å). Fig. 7a shows clearly that the migration of ions within the membrane led to an increase of d, but with a different extent according to the different ions: d increased to (8.6 ± 0.1) Å for Na+ and to (9.0 ± 0.1) Å for Ca2+.
As a further test, we checked if similar results could be obtained without the electric field using instead brute force to achieve transport in the form of high hydraulic pressure, as typically done in reverse osmosis filters. Indeed, upon filtration of massive amounts of solution (>20 ml as compared to 2 ml used for electric field tests), some ions do indeed pass through and reach tank 2 with some preferential transport selectivity of Na+ over Ca2+ (+77% of Na+ ions passed with respect to Ca2+). However, no significant variations of d were observed by simply applying mechanical pressure using a pump (Fig. 7b). XRD is a bulk-responsive analytical method, so not sensitive to eventual ions blocked on the surface of the GO; analysing, instead, the treated membranes with a surface technique like XPS, a significant amount of Ca2+ was found on the membranes (0.42 ± 0.05 at%, more than double of what observed using the electric field, Table S5†), indicating that the membrane, in the absence of an electric field, acts as a sieve blocking most Ca2+ on its surface and that the electric field is needed to achieve transport of ions in GO, again highlighting the critical role of electrostatic interactions between the ions and GO.
4. Conclusions
We observed the transport of Na+, Ca2+ and other cations inside core–shell graphene oxide–polyethersulfone hollow fiber filters, demonstrating that even these commercial filters can retain the fundamental sieving characteristics of planar GO membranes, but with a significantly higher surface area. Cations may be transported across the filters through the application of a very low electric bias (−1 V) and be discriminated by the filters on the basis of their chemical affinity with the GO substrate as well as of their hydrated ionic radius.By combining experiments performed on ion transport and ion adsorption, together with molecular dynamics simulations, XPS and XRD characterization, we could demonstrate that the differences in ion transport can be ascribed only in part to the ionic hydrated radius; a significant effect is due to the strong interaction of the carboxylate groups present on GO with the travelling ions, enhanced by the confined geometry of the stacked GO nanosheets.
Ions which interact strongly with GO will easily penetrate in between the sheets, as in the case of Ca2+, but will not be able to diffuse rapidly through the GO coating. Protonation of the carboxylate groups will allow instead a faster diffusion of Ca2+. The adsorption of Pb2+ and Mg2+ is instead so efficient that it is not affected significantly by the partial protonation of oxygenated residues; the adsorptive efficiency of GO toward these cations decreases only at the lowest pH tested.56 GO could be used thus as an efficient scavenger of such ions for water purification, but not as a filter.
Monovalent ions can interact significantly with GO, but less than divalent ions. This difference is due mostly to electrostatic interactions with the charged carboxylate groups and only to a minor extent to steric effects due to the different ionic radii.
Na+ and K+ can travel easily within GO, interacting significantly but reversibly with the carboxylate groups. Li+ shows instead a stronger interaction with GO, which hinders its ion transport performance.
Besides providing fundamental insight into the transport mechanisms, this work provides new perspectives in the design of ion sieving devices based on commercially available building blocks (GO and PES filters), and scalable, low cost, and sustainable membrane fabrication procedures (water based, low energy demanding) to be applied in water softening and desalination, among the others.
Even if such filters still cannot be applied at the commercial level, this practical demonstration of performance and the better understanding of ion sieving mechanisms is, in our opinion, a significant step towards practical applications of GO-based membranes in water purification.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the support of this work by the project 881603-GrapheneCore3-H2020-SGA-FET-SH1 Graphil-GRAPHENE-FLAGSHIP and Medica SpA for providing free samples of Plasmart filter prototypes (Versatile PES®).References
- V. M. Volgin and A. D. Davydov, Ionic transport through ion-exchange and bipolar membranes, J. Membr. Sci., 2005, 259(1), 110–121 CrossRef CAS.
- B. Corry, Water and ion transport through functionalised carbon nanotubes: implications for desalination technology, Energy Environ. Sci., 2011, 4(3), 751–759 RSC.
- Y. Chen, Z. Zhu, Y. Tian and L. Jiang, Rational ion transport management mediated through membrane structures, Exploration, 2021, 1(2), 20210101 CrossRef PubMed.
- S. C. O'Hern, M. S. H. Boutilier, J.-C. Idrobo, Y. Song, J. Kong, T. Laoui, M. Atieh and R. Karnik, Selective Ionic Transport through Tunable Subnanometer Pores in Single-Layer Graphene Membranes, Nano Lett., 2014, 14(3), 1234–1241 CrossRef PubMed.
- C. Peter and G. Hummer, Ion Transport through Membrane-Spanning Nanopores Studied by Molecular Dynamics Simulations and Continuum Electrostatics Calculations, Biophys. J., 2005, 89(4), 2222–2234 CrossRef CAS PubMed.
- M. Jacek, G. Jan and M. Stanisław, Mathematical models of ion transport through cell membrane channels, Math. Appl., 2014, 42(1), 39 Search PubMed.
- L. Reuss, Ion Transport across Nonexcitable Membranes, in eLS, 2011 Search PubMed.
- D. S. Sholl and R. P. Lively, Seven chemical separations to change the world, Nature, 2016, 532(7600), 435–437 CrossRef PubMed.
- S. Dervin, D. D. Dionysiou and S. C. Pillai, 2D nanostructures for water purification: graphene and beyond, Nanoscale, 2016, 8(33), 15115–15131 RSC.
- Y. Lin, Y. Tian, H. Sun and T. Hagio, Progress in modifications of 3D graphene-based adsorbents for environmental applications, Chemosphere, 2021, 270, 129420 CrossRef CAS PubMed.
- G. Liu, W. Jin and N. Xu, Graphene-based membranes, Chem. Soc. Rev., 2015, 44(15), 5016–5030 RSC.
- R. Shibahara, K. Kamiya and Y. Nishina, Grafting chelating groups on 2D carbon for selective heavy metal adsorption, Nanoscale Adv., 2021, 3, 5823 RSC.
- J. Sun, M. Sadd, P. Edenborg, H. Grönbeck, P. H. Thiesen, Z. Xia, V. Quintano, R. Qiu, A. Matic and V. Palermo, Real-time imaging of Na+ reversible intercalation in “Janus” graphene stacks for battery applications, Sci. Adv., 2021, 7(22), eabf0812 CrossRef CAS PubMed.
- H. Huang, Y. Ying and X. Peng, Graphene oxide nanosheet: an emerging star material for novel separation membranes, J. Mater. Chem. A, 2014, 2(34), 13772–13782 RSC.
- L. Huang, M. Zhang, C. Li and G. Shi, Graphene-Based Membranes for Molecular Separation, J. Phys. Chem. Lett., 2015, 6(14), 2806–2815 CrossRef CAS PubMed.
- J. Abraham, K. S. Vasu, C. D. Williams, K. Gopinadhan, Y. Su, C. T. Cherian, J. Dix, E. Prestat, S. J. Haigh, I. V. Grigorieva, P. Carbone, A. K. Geim and R. R. Nair, Tunable sieving of ions using graphene oxide membranes, Nat. Nanotechnol., 2017, 12(6), 546–550 CrossRef CAS PubMed.
- R. R. Nair, H. A. Wu, P. N. Jayaram, I. V. Grigorieva and A. K. Geim, Unimpeded Permeation of Water Through Helium-Leak–Tight Graphene-Based Membranes, Science, 2012, 335(6067), 442–444 CrossRef CAS PubMed.
- R. K. Joshi, P. Carbone, F. C. Wang, V. G. Kravets, Y. Su, I. V. Grigorieva, H. A. Wu, A. K. Geim and R. R. Nair, Precise and Ultrafast Molecular Sieving Through Graphene Oxide Membranes, Science, 2014, 343(6172), 752–754 CrossRef CAS PubMed.
- Q. Yang, Y. Su, C. Chi, C. T. Cherian, K. Huang, V. G. Kravets, F. C. Wang, J. C. Zhang, A. Pratt, A. N. Grigorenko, F. Guinea, A. K. Geim and R. R. Nair, Ultrathin graphene-based membrane with precise molecular sieving and ultrafast solvent permeation, Nat. Mater., 2017, 16(12), 1198–1202 CrossRef CAS PubMed.
- Z. Y. Leong, Z. Han, G. Wang, D.-S. Li, S. A. Yang and H. Y. Yang, Electric field modulated ion-sieving effects of graphene oxide membranes, J. Mater. Chem. A, 2021, 9(1), 244–253 RSC.
- P. Sun, F. Zheng, K. Wang, M. Zhong, D. Wu and H. Zhu, Electro- and Magneto-Modulated Ion Transport through Graphene Oxide Membranes, Sci. Rep., 2014, 4(1), 6798 CrossRef CAS PubMed.
- X. Du, X. Ma, P. Zhang, J. Zheng, Z. Wang, F. Gao, X. Hao, S. Liu and G. Guan, A novel electric-field-accelerated ion-sieve membrane system coupling potential-oscillation for alkali metal ions separation, Electrochim. Acta, 2017, 258, 718–726 CrossRef CAS.
- X. Gong, J. Li, H. Lu, R. Wan, J. Li, J. Hu and H. Fang, A charge-driven molecular water pump, Nat. Nanotechnol., 2007, 2(11), 709–712 CrossRef CAS PubMed.
- A. Hassanvand, G. Q. Chen, P. A. Webley and S. E. Kentish, A comparison of multicomponent electrosorption in capacitive deionization and membrane capacitive deionization, Water Res., 2018, 131, 100–109 CrossRef CAS PubMed.
- J. Kou, J. Yao, H. Lu, B. Zhang, A. Li, Z. Sun, J. Zhang, Y. Fang, F. Wu and J. Fan, Electromanipulating Water Flow in Nanochannels, Angew. Chem., Int. Ed., 2015, 54(8), 2351–2355 CrossRef CAS PubMed.
- P. Sun, M. Zhu, K. Wang, M. Zhong, J. Wei, D. Wu, Z. Xu and H. Zhu, Selective Ion Penetration of Graphene Oxide Membranes, ACS Nano, 2013, 7(1), 428–437 CrossRef CAS PubMed.
- K. G. Zhou, K. S. Vasu, C. T. Cherian, M. Neek-Amal, J. C. Zhang, H. Ghorbanfekr-Kalashami, K. Huang, O. P. Marshall, V. G. Kravets, J. Abraham, Y. Su, A. N. Grigorenko, A. Pratt, A. K. Geim, F. M. Peeters, K. S. Novoselov and R. R. Nair, Electrically controlled water permeation through graphene oxide membranes, Nature, 2018, 559(7713), 236–240 CrossRef CAS PubMed.
- C. Cheng, G. Jiang, G. P. Simon, J. Z. Liu and D. Li, Low-voltage electrostatic modulation of ion diffusion through layered graphene-based nanoporous membranes, Nat. Nanotechnol., 2018, 13(8), 685–690 CrossRef CAS PubMed.
- J. Kielland, Individual Activity Coefficients of Ions in Aqueous Solutions, J. Am. Chem. Soc., 1937, 59(9), 1675–1678 CrossRef CAS.
- B. Tansel, J. Sager, T. Rector, J. Garland, R. F. Strayer, L. Levine, M. Roberts, M. Hummerick and J. Bauer, Significance of hydrated radius and hydration shells on ionic permeability during nanofiltration in dead end and cross flow modes, Sep. Purif. Technol., 2006, 51(1), 40–47 CrossRef CAS.
- H. Huang, Y. Mao, Y. Ying, Y. Liu, L. Sun and X. Peng, Salt concentration, pH and pressure controlled separation of small molecules through lamellar graphene oxide membranes, Chem. Commun., 2013, 49(53), 5963–5965 RSC.
- A. Kovtun, A. Bianchi, M. Zambianchi, C. Bettini, F. Corticelli, G. Ruani, L. Bocchi, F. Stante, M. Gazzano, T. D. Marforio, M. Calvaresi, M. Minelli, M. L. Navacchia, V. Palermo and M. Melucci, Core–shell graphene oxide–polymer hollow fibers as water filters with enhanced performance and selectivity, Faraday Discuss., 2021, 227(0), 274–290 RSC; A. Kovtun, M. Zambianchi, C. Bettini, A. Liscio, M. Gazzano, F. Corticelli, E. Treossi, M. L. Navacchia, V. Palermo and M. Melucci, Graphene oxide–polysulfone Filters for tap water purifcation, obtained by fast microwave oven treatment, Nanoscale, 2019, 11, 22780 RSC.
- Z. Y. Xia, S. Pezzini, E. Treossi, G. Giambastiani, F. Corticelli, V. Morandi, A. Zanelli, V. Bellani and V. Palermo, The Exfoliation of Graphene in Liquids by Electrochemical, Chemical, and Sonication-Assisted Techniques: A Nanoscale Study, Adv. Funct. Mater., 2013, 23(37), 4684–4693 CrossRef CAS.
- G. J. A. M. Brom-Verheijden, M. H. Goedbloed and M. A. G. Zevenbergen, A Microfabricated 4-Electrode Conductivity Sensor with Enhanced Range, Proceedings, 2018, 2(13), 797 Search PubMed.
- V. Quintano, A. Kovtun, F. Biscarini, F. Liscio, A. Liscio and V. Palermo, Long-range selective transport of anions and cations in graphene oxide membranes, causing selective crystallization on the macroscale, Nanoscale Adv., 2021, 3(2), 353–358 RSC.
- A. Kovtun, D. Jones, S. Dell'Elce, E. Treossi, A. Liscio and V. Palermo, Accurate chemical analysis of oxygenated graphene-based materials using X-ray photoelectron spectroscopy, Carbon, 2019, 143, 268–275 CrossRef CAS.
- A. Schlierf, H. F. Yang, E. Gebremedhn, E. Treossi, L. Ortolani, L. P. Chen, A. Minoia, V. Morandi, P. Samori, C. Casiraghi, D. Beljonne and V. Palermo, Nanoscale insight into the exfoliation mechanism of graphene with organic dyes: effect of charge, dipole and molecular structure, Nanoscale, 2013, 5(10), 4205–4216 RSC.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics Modell., 1996, 14(1), 33–38 CrossRef CAS PubMed.
- GO-py, Open source executable available in the GitHub repository at: https://github.com/go-python/gopy.
- D. A. Case, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, D. Ghoreishi, M. K. Gilson, H. Gohlke, A. W. Goetz, D. Greene, R. Harris, N. Homeyer, Y. Huang, S. Izadi, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, D. J. Mermelstein, K. M. Merz, Y. Miao, G. Monard, C. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, F. Pan, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, J. Smith, R. SalomonFerrer, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, L. Xiao, D. M. York and P. A. Kollman, AMBER 2018, University of California, San Francisco, 2018.
- T. Vreven, K. S. Byun, I. Komaromi, S. Dapprich, J. A. Montgomery, K. Morokuma and M. J. Frisch, Combining quantum mechanical methods with molecular mechanics methods in ONIOM, Abstr. Pap. Am. Chem. Soc., 2006, 232, 408–408 Search PubMed.
- P. J. Hay and W. R. Wadt, Abinitio effective core potentials for molecular calculations - potentials for the transition-metal atoms SC to HG, J. Chem. Phys., 1985, 82(1), 270–283 CrossRef CAS.
- P. J. Hay and W. R. Wadt, Abinitio effective core potentials for molecular calculations - potentials for K to Au including the outermost core orbitals, J. Chem. Phys., 1985, 82(1), 299–310 CrossRef CAS.
- W. R. Wadt and P. J. Hay, Abinitio effective core potentials for molecular calculations - potentials for main group elements NA to BI, J. Chem. Phys., 1985, 82(1), 284–298 CrossRef CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, UFF, a full periodic-table force-field for molecular mechanics and molecular-dynamics simulations, J. Am. Chem. Soc., 1992, 114(25), 10024–10035 CrossRef CAS.
- A. K. Rappe and W. A. Goddard, Charge equilibration for molecular-dynamics simulations, J. Phys. Chem., 1991, 95(8), 3358–3363 CrossRef CAS.
- L. Chen, G. Shi, J. Shen, B. Peng, B. Zhang, Y. Wang, F. Bian, J. Wang, D. Li, Z. Qian, G. Xu, G. Liu, J. Zeng, L. Zhang, Y. Yang, G. Zhou, M. Wu, W. Jin, J. Li and H. Fang, Ion sieving in graphene oxide membranes via cationic control of interlayer spacing, Nature, 2017, 550(7676), 380–383 Search PubMed.
- R. Mohd Firdaus, N. Berrada, A. Desforges, A. R. Mohamed and B. Vigolo, From 2D Graphene Nanosheets to 3D Graphene-based Macrostructures, Chem. – Asian J., 2020, 15(19), 2902–2924 CrossRef CAS PubMed.
- Y. Shen, Q. Fang and B. Chen, Environmental Applications of Three-Dimensional Graphene-Based Macrostructures: Adsorption, Transformation, and Detection, Environ. Sci. Technol., 2015, 49(1), 67–84 Search PubMed.
- Z. Sun, S. Fang and Y. H. Hu, 3D Graphene Materials: From Understanding to Design and Synthesis Control, Chem. Rev., 2020, 120(18), 10336–10453 CrossRef CAS PubMed.
- N. Yousefi, X. Lu, M. Elimelech and N. Tufenkji, Environmental performance of graphene-based 3D macrostructures, Nat. Nanotechnol., 2019, 14(2), 107–119 Search PubMed.
- L. Huang, Y. R. Li, Q. Q. Zhou, W. J. Yuan and G. Q. Shi, Graphene Oxide Membranes with Tunable Semipermeability in Organic Solvents, Adv. Mater., 2015, 27(25), 3797–3802 Search PubMed.
- H. W. Kim, H. W. Yoon, S. M. Yoon, B. M. Yoo, B. K. Ahn, Y. H. Cho, H. J. Shin, H. Yang, U. Paik, S. Kwon, J. Y. Choi and H. B. Park, Selective Gas Transport Through Few-Layered Graphene and Graphene Oxide Membranes, Science, 2013, 342(6154), 91–95 CrossRef CAS PubMed.
- H. Li, Z. N. Song, X. J. Zhang, Y. Huang, S. G. Li, Y. T. Mao, H. J. Ploehn, Y. Bao and M. Yu, Ultrathin, Molecular-Sieving Graphene Oxide Membranes for Selective Hydrogen Separation, Science, 2013, 342(6154), 95–98 CrossRef CAS PubMed.
- E. S. Orth, J. G. L. Ferreira, J. E. S. Fonsaca, S. F. Blaskievicz, S. H. Domingues, A. Dasgupta, M. Terrones and A. J. G. Zarbin, pK(a) determination of graphene-like materials: Validating chemical functionalization, J. Colloid Interface Sci., 2016, 467, 239–244 CrossRef CAS PubMed.
- M. Weller, T. Overton, J. Rourke and F. Armstrong, Inorganic Chemistry, Oxford University Press, Oxford, 7th edn, 2018 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr05874c |
| This journal is © The Royal Society of Chemistry 2024 |