Resolving the dynamic properties of entangled linear polymers in non-equilibrium coarse grain simulation with a priori scaling factors

Abstract

The molecular weight of polymers can influence the material properties, but the molecular weight at the experiment level sometimes can be a huge burden for property prediction with full-atomic simulations. The traditional bottom-up coarse grain (CG) simulation can reduce the computation cost. However, the dynamic properties predicted by the CG simulation can deviate from the full-atomic simulation result. Usually, in CG simulations, the diffusion is faster and the viscosity and modulus are much lower. The fast dynamics in CG are usually solved by a posteriori scaling on time, temperature, or potential modifications, which usually have poor transferability to other non-fitted physical properties because of a lack of fundamental physics. In this work, a priori scaling factors were calculated by the loss of degrees of freedom and implemented in the iterative Boltzmann inversion. According to the simulation results on 3 different CG levels at different temperatures and loading rates, such a priori scaling factors can help in reproducing some dynamic properties of polycaprolactone in CG simulation more accurately, such as heat capacity, Young's modulus, and viscosity, while maintaining the accuracy in the structural distribution prediction. The transferability of entropy–enthalpy compensation and a dissipative particle dynamics thermostat is also presented for comparison. The proposed method reveals the huge potential for developing customized CG thermostats and offers a simple way to rebuild multiphysics CG models for polymers with good transferability.

---

Haifei Zhan

Haifei Zhan is currently a Research Fellow at Zhejiang University, China. He received his Ph.D. degree in mechanical engineering from Queensland University of Technology (QUT, Australia). Prior to joining Zhejiang University, he held positions as a Postdoctoral Research Fellow, Lecturer, and Senior Lecturer in Australia. His research is centered on exploring the mechanical/thermal properties and deformation mechanism of advanced nanomaterials, spanning polymer nanocomposites, carbon nanomaterials, and alloys.

Introduction

The molecular weight of linear polymers can influence the transport and mechanical properties. However, for full-atomic simulations, the molecular weight at the experimental level can be a huge burden on the computational resources. For example, polycaprolactone (PCL) used in 3D printing usually has a molecular weight M_w of around 50 000 g mol⁻¹, corresponding to approximately 8000 atoms in one single chain.^1,2 For full-atomic simulations, building a model for the entangled PCL network at the same molecular weight requires a lot of computational resources. Meanwhile, the relaxation time τ required for the simulation of long-chain molecules increases with the molecular weight, i.e., τ ∝ M_w²,³ suggesting a significant increase of the computational resources. Because of such restrictions, most of the current MD simulations usually use short polymer chains. However, according to several recent research studies, the mechanical and rheological properties of polymer nanocomposites are influenced by the chain length dispersity⁴ and the relative size of the polymer chains and nanofillers.^5–7 Thus, investigating the material properties of a large system with molecular structures has its significance in polymer physics and materials science.

Coarse grain (CG) simulations map a group of atoms into one bead. By decreasing the total number of particles in the system, the computation efficiency can increase significantly. Thus, CG simulation has become a promising method to investigate the properties of large molecules, such as proteins,^8,9 DNA,¹⁰ and polymers,¹¹ or ensembled into large systems, such as virus¹² and nuclear pores.¹³ To maintain the prediction accuracy in CG models, many works have emphasized on the CG potentials developed by a top-down or bottom-up approach, i.e., the potentials are built by referencing the experimental data or full-atomic simulations, respectively. Both approaches can be adopted simultaneously, like the general-purpose potential Martini.^14,15 However, CG potentials usually have limitations on representability and transferability, and for general-purpose applications, expanding bead types and continuous reparameterization are required. As for the customized potential, the bottom-up approach is usually preferred but still faces the problem of transferability when expanding the temperature range¹⁶ or predicting non-fitted physical properties, especially for the dynamic properties.

The commonly used bottom-up method is the iterative Boltzmann inversion (IBI), which can reproduce identical probability distribution functions as the full-atomic simulation in each degree of freedom (DOF). However, as the distributions in the CG model are sampled from the mass centres of the atom groups, the distributions are wider and with larger variance compared with the atom-level distribution. Thus, the interactions from IBI are usually weaker than full-atomic simulations, leading to a mismatch in dynamic properties, such as diffusion rate,¹⁷ viscosity,¹⁸ and Young's modulus.¹⁹ On the other hand, the force matching (FM) method gives up the accuracy for structural distribution but targets to reproduce the same force profile as the full-atomic simulation.²⁰ With the FM potentials, the mechanical properties of the CG model for the bulk material can be reproduced accurately as the full-atomic results, and such a method has been applied to the polymer and its nanocomposites.²¹ However, the transferability to other thermodynamic properties requires further investigations. Recently, with the development of machine learning techniques, neural networks (NNs) have been applied to the reconstruction of the CG potential for force matching and beyond. The loss functions are built according to the force and energy difference between the prediction and ground truth.^22–25 Although the machine learning potential from NNs can rebuild the free energy surface, the prediction on diffusions and other dynamic properties and the transferability to other properties still need further investigation. Meanwhile, the machine learning potential can include more information into the loss function for optimization, and with NNs complex enough, the CG predictions can be tolerable for all fitted properties. However, the computation efficiency may be reduced, which can deviate from the original aim of CG simulation.

Simply building the CG potential from the bottom-up energy, force, or distribution profile can overlook the thermodynamic problems caused by the loss of entropy. The entropy loss is the intrinsic consequence of the loss of the DOF during the CG mapping process. However, as the calculation for the entropy by definition is too complex for macromolecules in the full-atomic simulation,²⁶ the loss of the entropy has not been quantified in most CG simulations. Some previous investigations use the estimations for the upper bound for configurational entropy to evaluate the loss in the CG system.^27,28 However, the influence of such entropy loss on other physical properties is still under investigation,²⁹ especially for the non-equilibrium state.³⁰ Some recent studies used excessive entropy scaling to predict the acceleration in the CG dynamics,^31,32 but the conclusions are not transferred to physical properties like heat capacity, modulus, and viscosity.

To rebuild the mismatched dynamic behaviour empirically, the simulation results can be rescaled or the potential parameters can be optimized according to the target thermodynamic properties while sacrificing the accuracy of structural properties, known as the a posteriori method. Several a posteriori scaling methods have been brought out to align the mean squared displacement (MSD) in CG simulation with the full-atomic simulation. The most direct way is to rescale the time, assuming that the time in the CG simulation corresponds to a longer time in the full-atomic simulation.³³ However, time rescaling conflicts with the traditional kinetic theory, where extending the time lowers the velocity of the molecules and decreases the temperature. Whether such time rescaling can be transferred to other dynamic properties, such as the strain rate effect on the modulus and viscosity, is not guaranteed. Moreover, the time rescaling factor does not have a monotonic relationship with the CG level¹⁷ and temperature.³⁴ Scaling down temperature can also suppress diffusion in CG simulation.³⁵ However, performing CG simulation at a lower temperature can lead to a mismatch in the structural distribution. With the sacrifice on the distribution accuracy, the energy renormalization (enthalpy compensation) method can also slow down the diffusion by increasing the non-bonding interaction.^36–38 However, the scaling factor has poor temperature transferability and needs to be temperature dependent by a posteriori fitting, suggesting that potential depends on the kinetic energy, which brings more processes when dealing with the local velocity gradient in non-equilibrium MD simulation.

Except for potential development and a posteriori scaling, some theoretical works focused on the thermostat by adding the friction force to slow down the diffusion, like the traditional thermostat in dissipative particle dynamics (DPD), the Lowe-Andersen thermostat,³⁹ or the Langevin equation.⁴⁰ The friction coefficient is determined a posteriori to match the diffusion coefficient or relaxation time, but with only one friction coefficient, the accuracy of other dynamic properties is not guaranteed. In dynamic force matching, the friction particles are added to introduce the friction force.⁴¹ The friction force can also be calculated according to the memory kernel in non-Markovian dynamics.⁴² The equation of motion is derived from the generalized Langevin equation (GLE) following the Mori–Zwanzig formalism^43,44 or machine learning techniques.⁴⁵ The velocity autocorrelation functions are usually presented to show that the CG dynamics can well fit the MD simulation results. Such methods are more reliable physically and have huge potential in future applications, as long as the computation efficiency is promising.

In this work, a novel a priori scaling method was attempted to resolve the multiple dynamic properties of PCL by bottom-up CG simulation. Both the thermostat and potentials were modified to resolve the dynamic problem caused by the loss of entropy in the CG model. The temperature scaling factor l was calculated from the loss of DOF in the CG model, which is applied to the IBI process when building the CG potentials. The proposed methods were tested on three different CG levels of PCL and compared with other common a posteriori scaling methods. With the scaling factors grounded in fundamental physics principles, the proposed method shows better transferability toward the heat capacity and Young's modulus at different strain rates while maintaining accuracy in structural distribution prediction. The transferability towards other material properties, such as MSD, thermal expansion, and viscosity, is also presented and compared with other a posteriori methods.

Methodology

CG mappings for PCL and the system setup

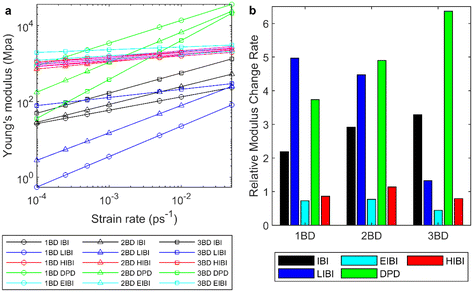
CG models were built at three different CG levels, where the repeat unit of the PCL was simplified to three beads, two beads, and one bead, named 3BD, 2BD, and 1BD models, respectively (Fig. 1a). The coordinates of the beads were sampled from the mass centre of the corresponding atom groups. The interactions include all the bond, angle, dihedral, and non-bonding interactions. Taking 3BD as an example, there are 6 types of non-bonding interactions (CM&CM, CM&M1, CM&M2, M1&M1, M1&M2, M2&M2), 3 types of bond interactions (CM–M1, M1–M2, M2–CM), 3 types of angle interactions (∠CM, ∠M1, ∠M2), and 3 types of dihedral interactions (²∠M1CM, ²∠CMM2, ²∠M2M1).

Fig. 1 (a) Different mapping strategies illustrated using a PCL tetramer. (b) Atomic configurations of the full-atomic model with each chain depicted in a different color. For clarity, only 20 out of the 40 chains are shown. The relaxed CG models of 3BD, 2BD, and 1BD mappings are presented in (c), (d) and (e), respectively.

The studied system comprises 40 polycaprolactone (PCL) chains, each consisting of 50 repeat units, resulting in an approximate molecular weight of 5700 g mol⁻¹ per chain. There are 36 120 atoms in total. Initially, a full-atomic model was constructed, where PCL chains were intricately mixed and entangled using the amorphous cell packaging feature in Material Studio 2018 (depicted in Fig. 1b). Following this initial packing, the system undergoes a relaxation process over 1 ns in the isothermal–isobaric ensemble to attain a stable density, maintaining a temperature of 300 K and a pressure of 1 bar. After relaxation, the side length of the box is around 7 nm. Subsequently, an additional 5 ns of relaxation in the canonical ensemble ensures equilibrium state attainment. MD simulations for PCL utilize the Optimized Potential for Liquid Simulation (OPLS) force field,⁴⁶ known for accurately reproducing PCL's mechanical and rheological properties compared to experimental data.^5,6 The initial configurations of CG models were directly mapped from the relaxed structures. Each CG model then undergoes relaxation using the same procedure as the full-atomic model, employing the corresponding potentials and thermostats, as detailed in the subsequent sections. The resulting post-relaxation CG configurations are depicted in Fig. 1c–e.

Iterative Boltzmann inversion

The target distribution functions of the interactions are acquired from the MD simulation. The initial guess of the potential can be acquired by Boltzmann inversion with the following equation:

U(q) = −k_BTln P(q)

where U is the potential, k_B is the Boltzmann constant, T is the temperature, and P is the probability distribution; q can be both bonding and non-bonding interactions. The potential can be determined according to the difference between current and target distribution: Uⁿ⁺¹ = Uⁿ + λΔUⁿ, where . λ is the damping factor to stabilize the system. Uⁿ and Pⁿ are the potential and distribution in the nth iteration, and P_tar is the target distribution. In this work, the IBI process was conducted by the Versatile Object-oriented Toolkit for Coarse-graining Application (VOTCA).⁴⁷ The MD and CG simulations were run using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).⁴⁸ A Nosé-Hoover thermostat and a barostat were used to control the temperature and pressure.

IBI at scaled temperature: a priori scaling

The a priori temperature scaling factor l was calculated according to the loss of the degrees of freedom (DOF). For the long-chain polymer, the loss of DOF is complex to calculate precisely, so l was estimated from the number of beads instead. In the repeating unit of the PCL, there are 18 atoms. Thus, the scaling factors l for 3BD, 2BD, and 1BD models are 6, 9, and 18, respectively. According to the definition of Gibbs free energy G = H − TS, for the CG model, when the entropy S decreases as the system DOF decreases by l, the temperature T should scale up by l to compensate for the entropy loss and keep the free energy the same. Meanwhile, scaling up the temperature can maintain the system's total kinetic energy the same, as l, and the number of particles N decreases by l. However, an increase in the temperature indicates that the kinetic energy of each bead increases. Thus, the interactions between the beads would be stronger to keep the distribution the same. For the modified IBI process, the temperature in the initial guess, update term, and sampling CG simulations are all scaled up by l, which is called high-temperature IBI (HIBI) in the following paragraphs. Theoretically, HIBI can produce the structural distribution accurately as the traditional IBI.

Since the kinetic energy of each bead increases in the HIBI, the diffusion could be even faster than the traditional IBI. The temperature in the CG simulation shows opposite rescaling requirements for the entropy compensation and the diffusion properties. Thus, to slow down the diffusion, the opposite scaling approach was attempted for comparison, i.e., the temperature is scaled down by l in the low-temperature IBI (LIBI). By scaling down the temperature, the kinetic energy of the CG beads decreases, which has the potential to align the dynamic properties in the CG simulation without losing the accuracy in the structural distribution. However, the interaction force would be weaker and the difference in entropy would be even larger than the traditional IBI. In the LIBI and HIBI, the Nosé-Hoover thermostat and barostat were adopted for consistency with the traditional IBI and full-atomic simulations.

Energy renormalization for IBI potential: a posteriori scaling

Inspired by previous work on the energy renormalization method for CG simulation,^36–38 the forces from the IBI for the non-bonding interactions are scaled up by α. Different from previous work, the tabulated potentials from the IBI were used as the base, instead of the Lennard-Jones (LJ) potential. In previous work, the scaling factors α are different at different temperatures, resulting in different potentials. For the equivalence in comparison with other methods for transferability and to avoid the conflict on the conservative of potentials, the energy renormalization potential was only developed at 300 K in the current work. Considering the difference with previous work, the method is called energy-renormalization IBI (EIBI) in the following paragraphs. As the system pressure will change after force rescaling, the simple pressure correction method was applied by adding a linear attractive potential.⁴⁹ A constant force was added Δf = −Δp × A × 0.1 × k_B × T/r_c, where Δp is the pressure difference, A is the scale factor, and r_c is the cut-off distance. The density for all models was controlled at 1.07 g cm⁻³ under 1.01 bar pressure, according to previous MD simulations with the OPLS potential for amorphous PCL.⁵ The pressure correction method may shift the position of the potential well slightly, which is similar to β in the previous energy renormalization method. The final potentials were acquired by numerical integration of the force. The force scaling factor α was set a posteriori so that the MSD of the mass centre of the PCL chains in the CG simulation matches with the full-atomic simulation results. Except for the non-bonding force, all other simulation settings are similar to the traditional IBI simulation.

Dissipative particle dynamics thermostat: a posteriori fitting

For the dissipative particle dynamics, additional dissipative force F^D and random force F^R were added to the equation of motion to slow down the diffusion. The dissipative force F_ij^D = −γω²(r_ij)(e_ij·v_ij) can add viscous force to the particles according to the relative velocity, while the random force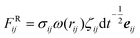 adds random force to each particle and maintains the Langevin thermostat with the dissipative force. In these equations, γ is the friction coefficient; ω is the weighting factor, depending on the relative position, ω(r_ij) = 1 − r_ij/r_c, r_ij < r_c; e_ij is the unit vector; v_ij is the relative velocity; σ_ij is the amplitude of the noise, 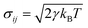; k_B is the Boltzmann constant and T is the temperature; ζ_ij is a uniformly distributed random number; dt is the time step. In the DPD simulations, the conservative forces are the traditional IBI results. The friction coefficient was set a posteriori to fit the viscosity from full-atomic simulation. Except for the thermostat, other settings are identical to the IBI simulations.

Results and discussion

Structural distribution functions

The target distributions were sampled from the full-atomic simulations every 1 ps during the relaxation simulation at 300 K in the canonical ensemble for 1 ns using the Nosé-Hoover thermostat. The structural distribution functions reflect the structural characteristics of the material, such as the neighbouring atom distances, bond length, angles, and the corresponding distributions. All the structural distribution functions can be reproduced accurately by the traditional IBI method (Fig. 2). Although the temperature is rescaled in the HIBI and LIBI for both CG simulations and potential development, the algorithm optimizes the potential to fit the distribution. Thus, the structural distribution predictions of both methods are as accurate as the traditional IBI (Fig. 2). The distribution predictions from the 3BD models are presented in Fig. 2, including all bonding interactions and the non-bonding interactions. The distributions for the 2BD and 1BD models can also match with the full-atomic results (ESI S1†). For the higher CG level, the bead number is smaller for the same system, thus more sampling frames are used in the IBI process to increase the dataset. The upscaling of the CG level does not have a significant influence on the distribution accuracy. Meanwhile, for the EIBI method, as the non-bonding forces are increased, the distributions cannot match the full-atomic result (ESI S2†). The distributions become more focused and the peak values have a slight shift because of pressure correction.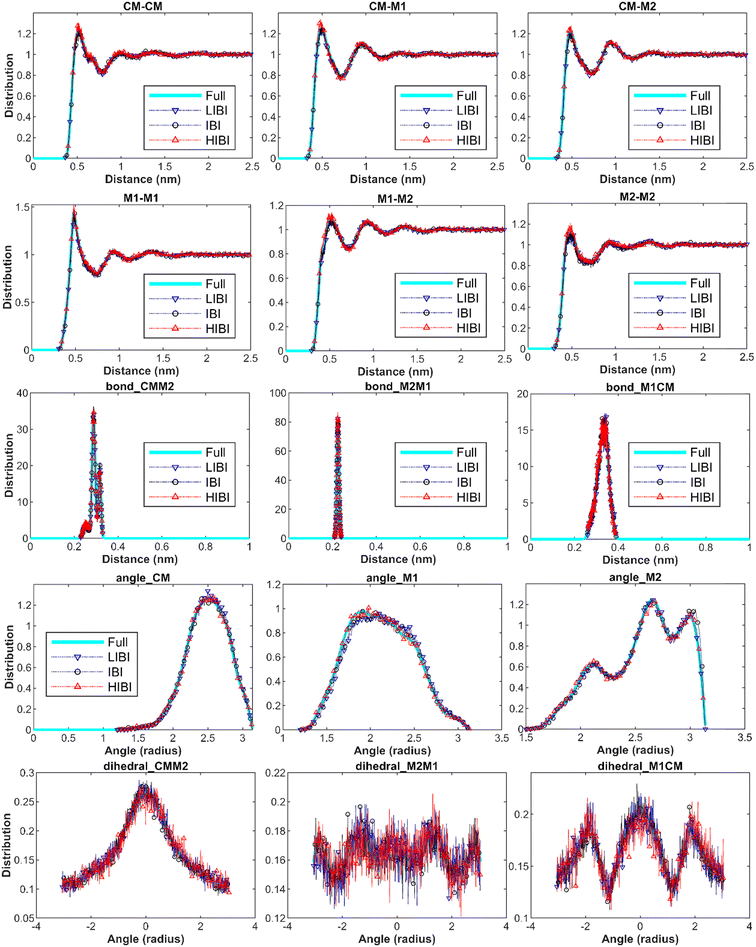

Fig. 2 Distributions of all the interactions in the 3BD model can match well with the target distributions from the full-atomic simulation with the traditional IBI, LIBI, and HIBI potentials.

Switching to the DPD thermostat, the distribution functions have a slight change but can match the full-atomic results in general for all 3BD (ESI S3†), 2BD, and 1BD models (ESI S4†). The slight mismatch is more likely to appear in angle and dihedral interactions. Since the conservative forces are from the IBI results, such alignment in the distribution is within expectation, showing that switching the thermostat algorithm has an ignorable influence on the distribution functions. As for the slight mismatch in the angular interactions, the frictional force in the DPD thermostat was calculated according to the relative linear velocity, and the angular velocity is not considered, which may underestimate the friction force for the rotational motion. Thus, the distributions for the angle interactions are slightly wider than the full-atomic results. Although the distribution mismatch could be eliminated by further potential update iteration in the IBI process, the updated potential requires resetting the friction coefficient to fit the viscosity a posteriori. Thus, another iteration loop needs to be built to update the potential and the friction coefficient, which seems not worthwhile as the distribution mismatch is not significant.

Mean squared displacement

The accuracy of the structural distribution cannot guarantee consistency in dynamic properties. The MSD curves can reflect the diffusion and relaxation properties. Thus, the MSD history was recorded during the relaxation simulation in the canonical ensemble at 300 K. As the particles in different CG models and full-atomic models are different, comparing the MSD of the particle can be inappropriate. Thus, the MSD of the mass centre of the PCL chains was compared. The outcomes for the initial 100 ps are depicted in Fig. 3. Detailed MSD curves for both atoms and CG beads throughout the entire relaxation process are available in ESI S5.† All interactions were not optimized according to the MSD, except for EIBI methods.

Fig. 3 Averaged MSD for the mass centre of PCL chains in different CG models compared with the full-atomic simulation (pink curve).

Compared with the full-atomic results, the traditional IBI method generates larger MSD, causing fast diffusion for all CG levels, especially for the 1BD model. Such fast dynamics are commonly observed in CG simulation with IBI potentials, which can be caused by the weak interactions generated from the mass centre distribution. As mentioned previously, the interactions in the HIBI are stronger to keep the same distribution. However, such an increment in interactions cannot suppress the diffusion, and the MSD for the HIBI is even higher than that for the IBI. The kinetic energy increment caused by temperature upscaling has a more significant impact on the diffusion characteristics than force increment when the distribution is kept the same. The difference between CG levels becomes more significant. In contrast, for the LIBI, the MSD decreases significantly and the difference between CG levels gets smaller.

The general shapes of the MSD curves from the IBI, HIBI, and LIBI are similar, but different from the full-atomic results. Although the LIBI method slows down the diffusion, compared with the full-atomic MSD curve, the MSD for the LIBI is lower in the first 1 ps, but exceeds the full-atomic MSD afterwards. The slope of the MSD for the LIBI is steeper at the sub-diffusion stage after 1 ps. Such results suggest that it is impossible to acquire the same diffusion curve by tuning the scaling factor for temperature, as the shape of the MSD cannot be altered by changing from l to l⁻¹ in the HIBI and LIBI. Moreover, as the slopes of the IBI MSD curves are different from the full-atomic results in different regions, it is impossible to use a single time-scaling factor to align the MSD curves for all diffusion stages.

The DPD thermostat can decrease the MSD with the friction force while using the IBI potential as the conservative potential field, but the shape is still different from the full-atomic result. The slope of the DPD MSD curve within the first picosecond is lower, but becomes higher in the sub-diffusion stage compared with the full-atomic MSD. Changing the friction coefficient cannot influence the shape of the MSD curve, thus it is impossible to fit the MSD by optimizing the friction coefficient. Thus, the friction coefficient γ was set a posteriori to fit the viscosity of the PCL in full-atomic simulation, which equals 0.025, 0.036, and 0.26 eV ps Å⁻² in the 3BD, 2BD, and 1BD models, respectively. As observed in Fig. 3, when the viscosities are the same, the MSD curves for all CG levels are identical in the DPD model.

Compared to the ratios of fiction coefficients (γ_3BD: γ_2BD: γ_1BD = 2 : 2.88 : 20.8) and the loss of DOF (l_3BD : l_2BD : l_1BD = 2 : 3 : 6), the ratio of γ is close to the ratio of l for the 3BD and 2BD models, while the γ of the 1BD model increases significantly. Recalling the results of MSD curves from other IBI methods, all the results show that the 1BD model may have different dynamic characteristics from the 2BD and 3BD models. For the 1BD model, the length of the bond is larger and the non-bonding interaction is weaker. Thus, the bonds are more likely to pass through each other when the time step is the same. Such bond passing can result in less entanglement of the chains and faster diffusion and requires additional friction force to slow down the diffusion properties. The segmental repulsive potential (SRP) can add repulsive force between the bonds to avoid the bonds passing through each other.⁵⁰ However, such modification can add extra repulsive force to the system and increase the pressure, which will lead to the density mismatch when running in the isothermal–isobaric (NPT) ensemble. Thus, the SRP is not used for the 1BD model in this work but should be considered for high CG levels where one bead presents more than 8 heavy atoms.

Compared with the other methods, the EIBI can reproduce the most accurate MSD compared with the full-atomic simulation for all CG levels. One apparent reason is that the scaling factor α was set a posteriori to fit the MSD curve. However, for the other CG methods, changing the scaling factor cannot change the shape of the MSD curves and is impossible to match the full-atomic MSD. Such results indicate that the non-bonding force is the dominant factor influencing the MSD curve. The force rescaling factor α is 6, 7.2, and 10.8 for the 3BD, 2BD, and 1BD models, respectively, which equals to l_3BD, 0.8l_2BD, and 0.6l_1BD. The force rescaling factor α increases with the CG level but slower than the increase of l by ratio.

Among all CG models, the EIBI can give the best estimation of MSD with the most sacrifice of the accuracy in the distribution predictions. For the IBI- and other IBI-derived methods, the shape of the MSD is not the same as the full-atomic simulation. Thus, it is impossible to reproduce the same MSD by simple temperature scaling or time scaling. Changing the thermostat to DPD can reduce the MSD, but it is still impossible to reproduce an accurate MSD curve by changing the friction coefficient.

Entropy, enthalpy, and heat capacity

In the previous energy renormalization method or current EIBI, the force rescaling factor was not set a priori according to the loss of entropy, but a posteriori according to the MSD. In the HIBI, the loss of entropy is compensated by the a priori temperature rescaling factor l, while the enthalpy is also altered in the CG potential. Thus, it is interesting to check the entropy and enthalpy values of all the CG models. All the CG models were relaxed in the canonical ensemble for 1 ns at temperatures ranging from 1 K to 450 K. The enthalpy H was calculated as H = U + pV, where U is the total energy of the system, p is the pressure, and V is the volume. The calculation of the absolute entropy according to the distribution can be extremely complex, especially for the full-atomic simulation where the number of atoms is large and the interaction types vary.²⁶ Thus, the change of the entropy was estimated as , where C_v is the heat capacity of the system and can be approximated by 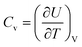.⁵¹

For all CG models, the total energies were recorded at different temperatures. Generally, the total energy U increases linearly when the temperature increases, indicating that the heat capacity C_v is almost a constant and does not change with temperature (Fig. 4a). Thus, the comparison between the entropy increment ΔS can be simplified to the comparison of heat capacity C_v. Compared to the full-atomic result, the C_v of most CG models are much smaller, except for the HIBI, which has a similar slope as the full-atomic simulation.

Fig. 4 (a) Total energy growth with temperature for each CG model compared with the full-atomic simulation results (pink curve). (b) Relative heat capacity for each CG model. (c) Scaled heat capacity of each CG model.

The total energy increment is the sum of the potential energy increment ΔS_p and the kinetic energy increment ΔE_k, ΔU = ΔE_p + ΔE_k, and . As the number of particles N is scaled down by l in the CG model, the ΔE_k is scaled down by the same scale. As for the potential energy increment ΔE_p, in the IBI process, the distribution is wider than that of each atom, and the force is generally weaker than in the full-atomic simulation. Thus, the potential increment will be smaller if the distribution prediction has good temperature transferability. Both factors result in a smaller ΔU and C_v for the traditional IBI method. As for the LIBI, the ΔE_k is scaled down by l two times, and the smaller kinetic energy also makes the interactions weaker to produce the same distribution. The ΔU of the LIBI is even smaller than the IBI. In contrast, by scaling up the temperature by l in the HIBI, the ΔE_k of the CG model is the same as the full-atomic simulation. As the kinetic energy is increased, the interactions need to be stronger to keep the same distribution, and thus ΔE_p also increases. The a priori scaling factor l not only compensates for the entropy loss but also increases the interaction strength. As a result, the prediction of C_v from the HIBI is closer to the full-atomic simulation.

As for the DPD simulation, as the conservative potential is the same as the IBI, the total energy U is the same as the IBI method. Such results show that adding non-conservative force does not influence the total energy of the system. For the EIBI method, by increasing the non-bonding interactions, the total energy is lower than the IBI results. The kinetic energy is the same as the IBI with the same thermostat, but the ΔE_p is smaller. As a result, the ΔU and C_v of the EIBI are a bit smaller than the IBI results.

The enthalpy of the CG model generally has a similar trend to the total energy (Fig. S6†). To acquire the similar Gibbs free energy (G = H − TS) in the CG simulation as the full-atomic simulation, as the entropy S is smaller in the CG simulation, the enthalpy H should be smaller to have the same free energy. However, as can be seen in Fig. S6,† most CG models can have a smaller H at 300 K compared to the full-atomic results, but because the ΔH is smaller, the H of the CG model gradually exceed the H of the full-atomic simulation when temperature decreases, except for the HIBI. Such results suggest that other CG models cannot reproduce the same free energy as the full-atomic simulation, when transferring to other temperature ranges, even for the EIBI method. It is important to mention that for the previous energy renormalization method, the force needs to be scaled with different factors at different temperatures to improve the transferability. However, having different potentials at different temperatures means that the potential is influenced by the kinetic energy, which brings a challenge to the traditional MD algorithm dealing with potential as a conservative quantity, especially for the velocity (or temperature) gradient in the non-equilibrium simulation.

As the heat capacity C_v is almost a constant in the studied temperature range, the relative entropy increment can be estimated from the relative heat capacity, 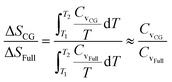. The HIBI can give the most accurate predictions on C_v and entropy increment (Fig. 4b). Generally, the relative C_v for the CG model decreases when the CG level upscales, even for the HIBI, where the entropy loss has been compensated by l. To see the relationship between the relative C_v and the loss of DOF more obviously, the relative C_v is scaled up by l for the IBI, EIBI, and DPD, and by l² for the LIBI. The scaled C_v can give better predictions (Fig. 4c). For the 1BD model, the error of scaled C_v is smaller than 5%. However, the error increases when the number of beads increases. The accuracy should increase with the number of beads by common sense. Such results indicate that the estimation of loss of DOF by l is not accurate at a lower CG level. For lower CG levels, the bonding interactions are stronger and more complex. Thus, simply estimating the loss of DOF by l may cause larger error.

Density and thermal expansion

To further investigate the temperature transferability of different CG methods, the entangled amorphous PCL models were relaxed in the isothermal–isobaric (NPT) ensemble, where the pressure was controlled at 1.01 bar. The Nosé-Hoover barostat was used for the IBI, HIBI, LIBI, and EIBI. For the DPD simulation, the Berendsen barostat was used to avoid double integration in LAMMPS. The density results for all the CG models are presented in Fig. 5. As the potentials were built from the full-atomic results at 300 K, all the methods can predict the density within ±2% error at 300 K. Extending the temperature range, for the 2BD and 3BD models, most density predictions fall in the region within ±2% error, except for the EIBI method. As the non-bonding forces are increased in the EIBI, the thermal expansion rate is generally lower, and thus the density prediction is less accurate when transferring to other temperatures. If different force scales and potentials are optimized at different temperatures, the density prediction from the EIBI could be better, which is the same logic as all other methods.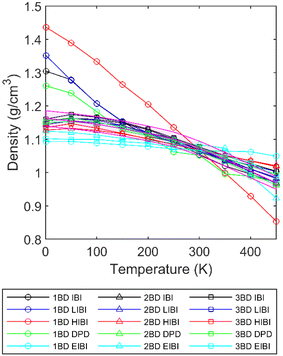

Fig. 5 Density of each CG model at the corresponding temperature. The pink area is the density from the full-atomic simulation with ±2% error.

For the 1BD model, the density predictions from the IBI, LIBI, HIBI, and DPD at a lower temperature are much higher than the full-atomic results. As the IBI-related CG method is based on the structural distribution, when the CG level scales up to 1BD, the information from the distribution is limited and could be insufficient for the transferability of temperature. Recalling the MSD result of the IBI, the difference in the diffusion characteristics and possible bond crossing could be other reasons, causing disentanglement and poor temperature transferability. Adding the repulsive force between the bonds could be helpful for the 1BD model to improve such transferability. For the EIBI, as the non-bonding force is increased, especially for the 1BD model, density prediction is less influenced by the CG level.

Young's modulus

In the presented CG methods, the dynamic properties are improved compared to the traditional IBI method at the equilibrium state. It is interesting to check how these methods perform in the non-equilibrium simulations and influence the mechanical response of the amorphous entangled polymer chains. Tensile tests were conducted for each PCL model at 300 K with different strain rates. The initial state is the equilibrium result after isothermal–isobaric relaxation. While bulk PCL exhibits isotropy, the polymer model at the nanoscale introduces local anisotropy due to different entanglement states in each direction. Thus, the moduli were averaged across all three dimensions to accommodate this intrinsic anisotropy. The modulus was determined using a dynamic approach involving stretching at a constant rate, rather than employing the quasi-static method,⁵² which is better suited for polymers in a glassy state. Meanwhile, as there are fewer atoms in the CG model, the pressure fluctuation is larger, which leads to a larger fluctuation in the modulus predictions. The relationship between moduli and strain rates was fitted to the exponential functions, and the fitted results are presented in Fig. 6. The original data in different tensile directions can be found in ESI S7 and S8.† Generally, for all the tested models, the modulus increases with the strain rate. As the strain rates are much higher than the experiment, the fitted results need extrapolation to compare with the experiments.

Fig. 6 (a) Fitted curves for the Young's modulus acquired from different CG models at different strain rates compared with the full-atomic simulation results. The pink belt is the modulus from the full-atomic simulation with ±10% error. (b) Relative slope of each CG model compared with the full-atomic simulation.

For the traditional IBI method, the modulus is lower than the full-atomic results at the same strain rate for all CG levels. Because the interactions acquired from the IBI are generally weaker than the full-atomic interaction, for the homogeneous deformation without diffusion, the stress increment will be lower. Thus, when the CG level increases, the modulus decreases in the IBI CG model. At the same time, the diffusion can influence the modulus, as the sliding of the polymer chains can cause strain and relaxation of stress. For the IBI CG model, the diffusion is faster than the full-atomic model (Fig. 3). Thus, for the same strain rate, more diffusion happens in the CG model, which can reduce the modulus further.

As for the LIBI, although the diffusion is slower, the modulus is generally lower than the traditional IBI caused by the weaker interactions from the LIBI potential. The modulus decreases when the CG level increases for the LIBI model. Such results suggest that for the amorphous entangled polymer system, the modulus is dominated by the interaction strength and the influence from the diffusion is weaker. However, for the 3BD LIBI model, the modulus at a slower strain rate is higher than the IBI results, indicating that at a slower strain rate, the diffusion rate could have a more significant impact on the modulus than the interaction strength. However, such a phenomenon is not observed in the 2BD and 1BD models, suggesting that their diffusion may be not slow enough to enhance the system modulus.

The modulus predicted by the HIBI is close to the full-atomic results for all CG levels. The interaction in the HIBI is much stronger than in the IBI so that the distribution is the same with larger thermal noise. As a result, the modulus is much higher than the traditional IBI. As the thermal noise scales up with the CG level in the HIBI, the force also scales up to keep the distribution, which compensates for the weak interactions caused by the wider distribution at the higher CG level. With such compensation, the modulus predictions from all CG levels are similar and close to the full-atomic results. Meanwhile, the fast diffusion results in an earlier yielding during the tensile deformation.

The EIBI method gives the second closest modulus prediction. By increasing the non-bonding force, the interaction strength is increased and the diffusion is slowed down. Thus, the modulus is higher than the traditional IBI method. The force scale factors were set to fit the MSD curve, which was not optimized for the Young's modulus. Generally, the moduli of the 1BD and 2BD models are close to the modulus in the full-atomic simulation. The moduli of the 3BD model are higher than the full-atomic simulation. Such results suggest that the EIBI has the potential to fit the diffusion properties and the mechanical properties at the same time. The overestimation of the 3BD model may be caused by the large force scale factor. A smaller force scaling factor could give a lower modulus prediction while sacrificing a bit on the accuracy of the MSD prediction. Meanwhile, the MSD curves have slight fluctuations (Fig. 3), which brings some room to adjust the force scaling factor α.

As for the DPD results, as the extra dissipative force is added to increase the friction, the modulus is significantly higher than the Nosé-Hoover thermostat, although the potentials are from the IBI. When the strain rate increases, the relative velocity between the particles increases and the dissipative force increases. Thus, the Young's modulus shows stronger connections with the strain rate and the slope for the Young's modulus versus the strain rate is larger than the IBI method. Compared with the full-atomic results, the dynamic response of Young's modulus is more significant in the DPD simulation than the full-atomic results. As the friction coefficient was fitted according to the viscosity only at the strain rate of 0.003 ps⁻¹, such a coefficient cannot guarantee the modulus prediction accuracy at various strain rates. For the 3BD model, the closest modulus estimation is around 0.003 ps⁻¹ strain rate, but the strain rate for the closest estimation decreases when the CG level increases. The modulus predictions increase when the CG level is upscale, suggesting that the modulus is influenced by the friction coefficient significantly. However, the modulus of the 3BD model is the most sensitive to the strain rate change. Thus, applying the DPD thermostat to the non-equilibrium tensile test requires further modifications in the algorithm for the entangled polymer chains in the future.

Viscosity

The shear viscosity was also acquired for each model by the non-equilibrium simulation. The simulation box has shear deformation with a constant shear strain rate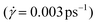 . The shear viscosity η was calculated as 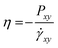, where P_xy is the element of the pressure tensor in the shearing direction. The temperature was kept at 400 K with the SLLOD equation of motion.⁵³ As the thermal expansion rates are different for different CG models, the densities of the CG models were kept the same as the full-atomic simulation at 400 K by deforming the simulation box for comparison. The pressure history was recorded after 1 ns of shearing simulation when the steady velocity gradient is formed. The viscosity was calculated as the average value sampled from pressure history for 1 ns. For each model, the shear deformation was conducted in three directions (xy, yz, and xz). The result is the average value from the simulations in these three directions. The relative viscosity values from each CG model compared to the full-atomic result are presented in Fig. 7. As the friction coefficient in the DPD is adapted according to the viscosity value, DPD can give the most accurate prediction of the viscosity.

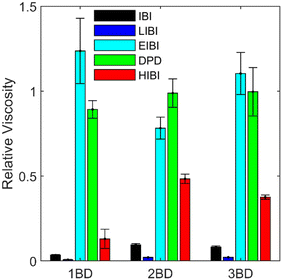Fig. 7 Relative viscosity of each CG model compared with the full-atomic model. The error bars are the relative standard deviation sampled from the shear simulation in the three directions.

For the traditional IBI method, the viscosity is 10 times smaller than the full-atomic results, as the diffusion is faster and the interaction is weaker in the CG models. The results from the 2BD and 3BD models are similar, but the 1BD model has a much lower viscosity. In the LIBI, the diffusion is slowed down, but the viscosity is even lower than that of the IBI. Such results indicate that the interaction strength has a larger influence on the viscosity compared to the diffusion when the distributions are kept the same. For the HIBI, as the interaction strength is increased, the viscosity increases about five times compared to the IBI results. However, the viscosity is still lower than the full-atomic prediction, which may be caused by the fast diffusion in the HIBI model. For the EIBI, the viscosity is higher than the HIBI and close to the full-atomic value. The predicted viscosity has an error of 25% compared to the full-atomic model. The accuracy increases when the number of beads increases in the CG model. As the MSD curves of the EIBI are close to the full-atomic model, it is not surprising that the EIBI can provide the most accurate prediction of the viscosity with the cost of the accuracy of the structural distribution.

Conclusions and outlooks

In this study, three levels of coarse-graining were employed. Given that the coarse-grained potentials entail two-body interactions, similar to full-atomic simulations, the computational expense increases linearly with the number of particles in the simulation box. As a result, simulations using the 3BD, 2BD, and 1BD models are 6, 9, and 18 times faster than those using the full-atomic model, respectively. Different rescaling methods were adopted to resolve the dynamic properties of entangled PCL chains by CG simulation. A novel a priori temperature rescaling method is proposed, which compensates for the entropy loss by rescaling the temperature. The HIBI proposed can give an accurate prediction for the heat capacity and Young's modulus while maintaining the accuracy of structural distribution and thermal expansion. The viscosity predicted by the HIBI is better than that by the traditional IBI but still lower than the full-atomic results, which can be caused by the fast diffusion. Switching the thermostat to DPD gives an extra friction coefficient to fit the viscosity a posteriori, without influencing the conservative force. However, the predictions on other properties, such as MSD and modulus, require further improvement. As for the modified energy renormalization method (EIBI), multiple dynamic properties can be reproduced at the same time, such as MSD, modulus, and viscosity. However, the EIBI has poor temperature transferability on density and cannot present the structural distribution accurately. Based on the current findings, the HIBI emerges as a superior approach capable of simultaneously replicating multiple physical properties, encompassing structural, thermal, mechanical, and rheological aspects, showing the strength for integrating CG thermostat scaling with CG potential development. With its solid physical foundation and ease of acquisition, the a priori scaling method can be extended to other polymer systems or even more complex systems such as nanocomposites. Looking ahead to the future of CG modelling, using machine learning techniques has the potential to reproduce more physical properties at the same time with a higher computational cost. On the other hand, building a modified thermostat for CG simulation, which can produce the same averaged kinetic energy but with larger fluctuations according to the loss of entropy, could be useful to improve the transferability towards the dynamic properties for the potentials acquired from the IBI process. Such an approach holds promise for investigating fracture-related properties, where the influence of diffusion is paramount.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Author contributions

YN designed the models and carried out the simulations. All authors contribute to the analysis, discussion, and writing.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

H.Z. would like to acknowledge the financial support from the National Natural Science Foundation of China (12172325) and the Zhejiang Provincial Natural Science Foundation (LR22A020006). C.L. would like to acknowledge the financial support from the National Natural Science Foundation of China (11925206, U22A20254). Y.G. would like to acknowledge the financial support from the ARC Discovery Project (DP200102546). The High-Performance Computing (HPC) resources provided by the Queensland University of Technology (QUT) are gratefully acknowledged (Y.G.). This research was undertaken with the assistance of resources and services from Intersect Australia Ltd and the National Computational Infrastructure (NCI), which is supported by the Australian Government.

References

1. P. Mieszczanek, T. M. Robinson, P. D. Dalton and D. W. Hutmacher, Convergence of Machine Vision and Melt Electrowriting, Adv. Mater., 2021, 33(29), e2100519.
2. J. Kwon, C. DelRe, P. Kang, A. Hall, D. Arnold, I. Jayapurna, L. Ma, M. Michalek, R. O. Ritchie and T. Xu, Conductive Ink with Circular Life Cycle for Printed Electronics, Adv. Mater., 2022, 34(30), e2202177.
3. C. M. Roland, L. A. Archer, P. H. Mott and J. Sanchez-Reyes, Determining Rouse relaxation times from the dynamic modulus of entangled polymers, J. Rheol., 2004, 48(2), 395–403.
4. B. L. Peters, K. M. Salerno, T. Ge, D. Perahia and G. S. Grest, Effect of Chain Length Dispersity on the Mobility of Entangled Polymers, Phys. Rev. Lett., 2018, 121(5), 057802.
5. Y. Nie, C. Li, H. Zhan, L. Kou and Y. Gu, Effect of nonaffine displacement on the mechanical performance of degraded PCL and its graphene composites: an atomistic investigation, Nanoscale, 2022, 14(38), 14082–14096.
6. Y. Nie, H. Zhan, L. Kou and Y. Gu, Atomistic Insights on the Rheological Property of Polycaprolactone Composites with the Addition of Graphene, Adv. Mater. Technol., 2021, 7(4), 2100507.
7. J. L. Suter, M. Vassaux and P. V. Coveney, Large-Scale Molecular Dynamics Elucidates the Mechanics of Reinforcement in Graphene-Based Composites, Adv. Mater., 2023, 23, 2302237.
8. P. C. T. Souza, S. Thallmair, P. Conflitti, C. Ramírez-Palacios, R. Alessandri, S. Raniolo, V. Limongelli and S. J. Marrink, Protein–ligand binding with the coarse-grained Martini model, Nat. Commun., 2020, 11(1), 3714.
9. M. Majewski, A. Pérez, P. Thölke, S. Doerr, N. E. Charron, T. Giorgino, B. E. Husic, C. Clementi, F. Noé and G. De Fabritiis, Machine learning coarse-grained potentials of protein thermodynamics, Nat. Commun., 2023, 14(1), 5739.
10. S. E. Farr, E. J. Woods, J. A. Joseph, A. Garaizar and R. Collepardo-Guevara, Nucleosome plasticity is a critical element of chromatin liquid-liquid phase separation and multivalent nucleosome interactions, Nat. Commun., 2021, 12(1), 2883.
11. B. Zhang, X. Chen, W. Lu, Q. M. Zhang and J. Bernholc, Morphology-induced dielectric enhancement in polymer nanocomposites, Nanoscale, 2021, 13(24), 10933–10942.
12. A. Yu, A. J. Pak, P. He, V. Monje-Galvan, L. Casalino, Z. Gaieb, A. C. Dommer, R. E. Amaro and G. A. Voth, A multiscale coarse-grained model of the SARS-CoV-2 virion, Biophys. J., 2021, 120(6), 1097–1104.
13. S. Mosalaganti, A. Obarska-Kosinska, M. Siggel, R. Taniguchi, B. Turoňová, C. E. Zimmerli, K. Buczak, F. H. Schmidt, E. Margiotta, M.-T. Mackmull, W. J. H. Hagen, G. Hummer, J. Kosinski and M. Beck, AI-based structure prediction empowers integrative structural analysis of human nuclear pores, Science, 2022, 376(6598), eabm9506.
14. P. C. T. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grunewald, I. Patmanidis, H. Abdizadeh, B. M. H. Bruininks, T. A. Wassenaar, P. C. Kroon, J. Melcr, V. Nieto, V. Corradi, H. M. Khan, J. Domanski, M. Javanainen, H. Martinez-Seara, N. Reuter, R. B. Best, I. Vattulainen, L. Monticelli, X. Periole, D. P. Tieleman, A. H. de Vries and S. J. Marrink, Martini 3: a general purpose force field for coarse-grained molecular dynamics, Nat. Methods, 2021, 18(4), 382–388.
15. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. d. Vries, The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations, J. Phys. Chem. B, 2007, 111, 7812.
16. T. D. Potter, J. Tasche and M. R. Wilson, Assessing the transferability of common top-down and bottom-up coarse-grained molecular models for molecular mixtures, Phys. Chem. Chem. Phys., 2019, 21(4), 1912–1927.
17. K. M. Salerno, A. Agrawal, D. Perahia and G. S. Grest, Resolving Dynamic Properties of Polymers through Coarse-Grained Computational Studies, Phys. Rev. Lett., 2016, 116(5), 058302.
18. A. F. Behbahani, L. Schneider, A. Rissanou, A. Chazirakis, P. Bačová, P. K. Jana, W. Li, M. Doxastakis, P. Polińska, C. Burkhart, M. Müller and V. A. Harmandaris, Dynamics and Rheology of Polymer Melts via Hierarchical Atomistic, Coarse-Grained, and Slip-Spring Simulations, Macromolecules, 2021, 54(6), 2740–2762.
19. K. C. Lai, Y. Han, P. Spurgeon, W. Huang, P. A. Thiel, D. J. Liu and J. W. Evans, Reshaping, Intermixing, and Coarsening for Metallic Nanocrystals: Nonequilibrium Statistical Mechanical and Coarse-Grained Modeling, Chem. Rev., 2019, 119(11), 6670–6768.
20. S. Izvekov and G. A. Voth, A Multiscale Coarse-Graining Method for Biomolecular Systems, J. Phys. Chem. B, 2005, 109, 2469.
21. B. Arash, H. S. Park and T. Rabczuk, Mechanical properties of carbon nanotube reinforced polymer nanocomposites: A coarse-grained model, Composites, Part B, 2015, 80, 92–100.
22. J. Wang, S. Olsson, C. Wehmeyer, A. Perez, N. E. Charron, G. de Fabritiis, F. Noe and C. Clementi, Machine Learning of Coarse-Grained Molecular Dynamics Force Fields, ACS Cent. Sci., 2019, 5(5), 755–767.
23. L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, DeePCG: Constructing coarse-grained models via deep neural networks, J. Chem. Phys., 2018, 149(3), 034101.
24. A. Moradzadeh and N. R. Aluru, Transfer-Learning-Based Coarse-Graining Method for Simple Fluids: Toward Deep Inverse Liquid-State Theory, J. Phys. Chem. Lett., 2019, 10(6), 1242–1250.
25. H. Chan, M. J. Cherukara, B. Narayanan, T. D. Loeffler, C. Benmore, S. K. Gray and S. Sankaranarayanan, Machine learning coarse grained models for water, Nat. Commun., 2019, 10(1), 379.
26. P. M. Piaggi and M. Parrinello, Entropy based fingerprint for local crystalline order, J. Chem. Phys., 2017, 147(11), 114112.
27. R. Baron, A. H. d. Vries, P. H. Hunenberger and W. F. v. Gunsteren, Comparison of Atomic-Level and Coarse-Grained Models for Liquid Hydrocarbons from Molecular Dynamics Configurational Entropy Estimates, J. Phys. Chem. B, 2006, 110, 8464.
28. R. Baron, A. H. d. Vries, P. H. Hu1nenberger and W. F. v. Gunsteren, Configurational Entropies of Lipids in Pure and Mixed Bilayers from Atomic-Level and Coarse-Grained Molecular Dynamics Simulations, J. Phys. Chem. B, 2006, 110, 15602.
29. G. G. Rondina, M. C. Böhm and F. Müller-Plathe, Predicting the Mobility Increase of Coarse-Grained Polymer Models from Excess Entropy Differences, J. Chem. Theory Comput., 2020, 16(3), 1431–1447.
30. P. Bilotto, L. Caprini and A. Vulpiani, Excess and loss of entropy production for different levels of coarse graining, Phys. Rev. E, 2021, 104(2), 024140.
31. J. Jin, K. S. Schweizer and G. A. Voth, Understanding dynamics in coarse-grained models. I. Universal excess entropy scaling relationship, J. Chem. Phys., 2023, 158(3), 034103.
32. J. Jin, K. S. Schweizer and G. A. Voth, Understanding dynamics in coarse-grained models. II. Coarse-grained diffusion modeled using hard sphere theory, J. Chem. Phys., 2023, 158(3), 034104.
33. K. M. Salerno, A. Agrawal, B. L. Peters, D. Perahia and G. S. Grest, Dynamics in entangled polyethylene melts, Eur. Phys. J.: Spec. Top., 2016, 225(8–9), 1707–1722.
34. B. L. Peters, K. M. Salerno, A. Agrawal, D. Perahia and G. S. Grest, Coarse-Grained Modeling of Polyethylene Melts: Effect on Dynamics, J. Chem. Theory Comput., 2017, 13(6), 2890–2896.
35. J. B. Accary and V. Teboul, Time versus temperature rescaling for coarse grain molecular dynamics simulations, J. Chem. Phys., 2012, 136(9), 094502.
36. W. Xia, N. K. Hansoge, W.-S. Xu, F. R. Phelan Jr., S. Keten and J. F. Douglas, Energy renormalization for coarse-graining polymers having different segmental structures, Sci. Adv., 2019, 5, eaav4683.
37. J. Song, D. D. Hsu, K. R. Shull, F. R. Phelan, J. F. Douglas, W. Xia and S. Keten, Energy Renormalization Method for the Coarse-Graining of Polymer Viscoelasticity, Macromolecules, 2018, 51(10), 3818–3827.
38. W. Xia, J. Song, C. Jeong, D. D. Hsu, F. R. Phelan, J. F. Douglas and S. Keten, Energy-Renormalization for Achieving Temperature Transferable Coarse-Graining of Polymer Dynamics, Macromolecules, 2017, 50(21), 8787–8796.
39. H.-J. Qian, C. C. Liew and F. Muller-Plathe, Effective control of the transport coefficients of a coarse-grained liquid and polymer models using the dissipative particle dynamics and Lowe–Andersen equations of motion, Phys. Chem. Chem. Phys., 2009, 11(12), 1962.
40. T. Ohkuma and K. Kremer, A composition transferable and time-scale consistent coarse-grained model for cis-polyisoprene and vinyl-polybutadiene oligomeric blends, J. Phys. Mater., 2020, 3(3), 034007.
41. A. Davtyan, G. A. Voth and H. C. Andersen, Dynamic force matching: Construction of dynamic coarse-grained models with realistic short time dynamics and accurate long time dynamics, J. Chem. Phys., 2016, 145(22), 224107.
42. C. Ayaz, L. Scalfi, B. A. Dalton and R. R. Netz, Generalized Langevin equation with a nonlinear potential of mean force and nonlinear memory friction from a hybrid projection scheme, Phys. Rev. E, 2022, 105(5–1), 054138.
43. Z. Li, H. S. Lee, E. Darve and G. E. Karniadakis, Computing the non-Markovian coarse-grained interactions derived from the Mori-Zwanzig formalism in molecular systems: Application to polymer melts, J. Chem. Phys., 2017, 146(1), 014104.
44. S. Wang, Z. Li and W. Pan, Implicit-solvent coarse-grained modeling for polymer solutions via Mori-Zwanzig formalism, Soft Matter, 2019, 15(38), 7567–7582.
45. S. Wang, Z. Ma and W. Pan, Data-driven coarse-grained modeling of polymers in solution with structural and dynamic properties conserved, Soft Matter, 2020, 16(36), 8330–8344.
46. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236.
47. D. Fritz, K. Koschke, V. A. Harmandaris, N. F. van der Vegt and K. Kremer, Multiscale modeling of soft matter: scaling of dynamics, Phys. Chem. Chem. Phys., 2011, 13(22), 10412–10420.
48. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ‘t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171.
49. D. Reith, M. Pütz and F. Müller-Plathe, Deriving effective mesoscale potentials from atomistic simulations, J. Comput. Chem., 2003, 24(13), 1624–1636.
50. T. W. Sirk, Y. R. Slizoberg, J. K. Brennan, M. Lisal and J. W. Andzelm, An enhanced entangled polymer model for dissipative particle dynamics, J. Chem. Phys., 2012, 136, 134903.
51. M. Forsblom and G. Grimvall, Heat capacity of liquid Al: Molecular dynamics simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(13), 132204.
52. N. Vu-Bac, M. A. Bessa, T. Rabczuk and W. K. Liu, A Multiscale Model for the Quasi-Static Thermo-Plastic Behavior of Highly Cross-Linked Glassy Polymers, Macromolecules, 2015, 48(18), 6713–6723.
53. D. J. Evans and G. P. Morriss, Nonlinear-response theory for steady planar Couette flow, Phys. Rev. A, 1984, 30(3), 1528–1530.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr06185j

---