Open Access Article
Open Access ArticleMultivariate regression analysis of factors regulating the formation of synthetic aluminosilicate nanoparticles†
Faisal T.
Adams
 *a,
McNeill
Bauer
a,
Clément
Levard
*a,
McNeill
Bauer
a,
Clément
Levard
 b and
F. Marc
Michel
a
b and
F. Marc
Michel
a
aDepartment of Geosciences, Virginia Polytechnic Institute and State University, Blacksburg, VA 24061, USA. E-mail: fadams@vt.edu
bAix Marseille Univ, CNRS, IRD, INRAE, Coll France, CEREGE, Aix-en-Provence, France
First published on 21st February 2024
Abstract
Interest is growing in nanoparticles made of earth abundant materials, like alumino(silicate) minerals. Their applications are expanding to include catalysis, carbon sequestration reactions, and medical applications. It remains unclear, however, what factors control their formation and abundance during laboratory synthesis or on a larger industrial scale. This work investigates the complex system of physicochemical conditions that influence the formation of nanosized alumino(silicate) minerals. Samples were synthesized and analyzed by powder X-ray diffraction, in situ and ex situ small angle X-ray scattering, and transmission electron microscopy. Regression analyses combined with linear combination fitting of powder diffraction patterns was used to model the influence of different synthesis conditions including concentration, hydrolysis ratio and rate, and Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si elemental ratio on the particle size of the initial precipitate and on the phase abundances of the final products. These models show that hydrolysis ratio has the strongest control on the overall phase composition, while the starting reagent concentration also plays a vital role. For imogolite nanotubes, we determine that increasing concentration, and relatively high or low hydrolysis limit nanotube production. A strong relationship is also observed between the distribution of nanostructured phases and the size of precursor particles. The confidences were >99% for all linear regression models and explained up to 85% of the data variance in the case of imogolite. Additionally, the models consistently predict resulting data from other experimental studies. These results demonstrate the use of an approach to understand complex chemical systems with competing influences and provide insight into the formation of several nanosized alumino(silicate) phases.
Si elemental ratio on the particle size of the initial precipitate and on the phase abundances of the final products. These models show that hydrolysis ratio has the strongest control on the overall phase composition, while the starting reagent concentration also plays a vital role. For imogolite nanotubes, we determine that increasing concentration, and relatively high or low hydrolysis limit nanotube production. A strong relationship is also observed between the distribution of nanostructured phases and the size of precursor particles. The confidences were >99% for all linear regression models and explained up to 85% of the data variance in the case of imogolite. Additionally, the models consistently predict resulting data from other experimental studies. These results demonstrate the use of an approach to understand complex chemical systems with competing influences and provide insight into the formation of several nanosized alumino(silicate) phases.
1. Introduction
Nanosized alumino(silicate) minerals attract great interest due to their unique morphologies (1D, 2D or nanospheres), high surface availability, and relative ease of production via sol–gel or hydrolysis reactions. Aluminum-based nanowires, nanoplatelets, aluminosilicate nanotubes, and amorphous silica nanospheres are some of the particles commonly researched. They are also favored for use due to the abundant availability of their constituent elements, which contributes to their environmental sustainability.Synthetic imogolite has been researched for use in catalysis, gas adsorption, and polymer nanocomposites among other applications due to its tunable size, hydrophilicity, high surface area and aspect ratio, and functionalized surface.1–5 Both imogolite (Al2SiO3(OH)4) and proto-imogolite are aluminosilicate nanominerals that typically occur together in varying proportions, and although the primary distinguishing factor between them is their morphologies, they are both suggested to possess the same “imogolite-like local structure” (ILS).6 These aluminosilicates are composed of gibbsite-like sheets of aluminum hydroxide (Al(OH3)) with isolated silica (SiO4) tetrahedra occupying the center position of the six-membered rings formed by the Al octahedra.7
Imogolite forms high aspect ratio nanotubes that are 2–3 nm in diameter and can extend up to several μm in length,8,9 while proto-imogolite is said to possess a “rooftile” shape,10 eventually transforming into imogolite nanotubes in solution. The curvature observed in the particles is believed to be due to strain resulting from the size disparity between the silica tetrahedra and the lacunar sites of the gibbsite-like sheets. This discrepancy causes different types of curvature, resulting in the formation of tubes and spheres in one and two dimensions, respectively.6 The exact transformation method is still under discussion although an oriented aggregation-based growth is the foremost conclusion.6,11 Other secondary phases have been observed during the synthesis of these nanoparticles, specifically Al-(oxy)hydroxides and amorphous silica.12–14
Pseudo-boehmite is a poorly crystalline and hydrated aluminum oxyhydroxide (γ-AlOOH), studied for its influences spanning from radiolysis in nuclear material storage and waste sites15,16 to health applications, where it is one of the oldest and most commonly used adjuvants in vaccines.17 It is formed under similar conditions to its more crystalline counterpart, boehmite, from aluminum ion precursors hydrothermally aged at alkaline conditions, and has a double-sheet structure of aluminum octahedra forming nanosized wires, platelets or rafts.18,19 Alternatively, amorphous silica nanoparticles (SiO2) possess localized structures of 2-membered to 8-membered siloxane rings, and are arguably the most commonly produced of all synthetic nanosized materials.20 This nanoparticle has found widespread industrial use in food and cosmetics, as well as biotechnological applications in cancer therapy and enzyme immobilization.21,22
Several synthesis investigations have reported a mixture of 2 or more of these nanoparticles occuring12,13 and others have discussed isolated conditions impacting their formation,23,24 yet there has been no holistic study of the influence synthesis conditions have on the resulting phase distribution of these materials. Experimental studies of imogolite and proto-imogolite, or allophane ((Al2O3)(SiO2)1.3–2·2.5–3H2O), formation have tested separately the effects of starting concentration, pH, and elemental ratios on the various morphologies.25–28 Others have suggested that excess silica to aluminum in the starting solution will suppress imogolite formation due to the limited capacity for silica polymers in the inner tube. Excess silica may be accommodated by silica polymers residing in the larger interiors of spherical allophane and/or by the increased number of reactive surface sites on proto-imogolite fragments.7 Another study suggested that imogolite is not favored at hydrolysis ratios less than 1.5 due to differences in imogolite and proto-imogolite stabilities at different pH and OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ranges.24 Taken together these prior studies suggest that alumino(silicate) nanoparticle formation may be influenced by two or more competing factors. The presence of various mixtures of nanosized and/or nanostructured phases provides an additional challenge for quantifying them into separate phases, especially using relatively accessible scattering-based approaches like X-ray diffraction.
Al ranges.24 Taken together these prior studies suggest that alumino(silicate) nanoparticle formation may be influenced by two or more competing factors. The presence of various mixtures of nanosized and/or nanostructured phases provides an additional challenge for quantifying them into separate phases, especially using relatively accessible scattering-based approaches like X-ray diffraction.
This paper attempts to describe which key variables including concentration, elemental Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio, hydrolysis ratio and speed of base addition impact the formation of these different nanosized minerals. The influence of these conditions on some precursor particle sizes and their compounding effect on nanotube formation is also described. Systematic synthesis experiments were combined with in situ and ex situ analytical characterization and multivariate linear regression analysis to determine the quantitative influence each factor had on final phase abundance. This is the first study designed to unravel the competing effects of these different synthesis variables, as well as to probe the role of precursor particle size on imogolite formation using experimental data. This study also employs a unique approach29 to quantify the distribution of nanoparticle mineral phases via linear combination fitting of laboratory powder X-ray diffraction data. The results are important for greater understanding of alumino(silicate) synthesis, where individual variables can be isolated and understood for their effect on the system. The framework of the study can be adapted and utilized for other chemical processes where competing effects complicate the products of a system.
Si ratio, hydrolysis ratio and speed of base addition impact the formation of these different nanosized minerals. The influence of these conditions on some precursor particle sizes and their compounding effect on nanotube formation is also described. Systematic synthesis experiments were combined with in situ and ex situ analytical characterization and multivariate linear regression analysis to determine the quantitative influence each factor had on final phase abundance. This is the first study designed to unravel the competing effects of these different synthesis variables, as well as to probe the role of precursor particle size on imogolite formation using experimental data. This study also employs a unique approach29 to quantify the distribution of nanoparticle mineral phases via linear combination fitting of laboratory powder X-ray diffraction data. The results are important for greater understanding of alumino(silicate) synthesis, where individual variables can be isolated and understood for their effect on the system. The framework of the study can be adapted and utilized for other chemical processes where competing effects complicate the products of a system.
2. Results
2.1 Syntheses of nanosized alumino(silicates)
Analysis of the pH during various syntheses suggested various formation stages based on localized trends, and these stages were supported by visual cues. NaOH addition during the initial minutes of the experiment resulted in a rapid pH rise. The pH began to decrease as soon as NaOH addition finished, during which a translucent gel-like phase appeared in the solution. The subsequent stage was marked by a period of rapid pH decrease where the solution, depending on starting conditions, either turned clear or developed a white cloudy precipitate. The precipitate persisted for the rest of the synthesis without any noticeable change for those conditions where it formed. Finally, the pH would become relatively stable after 60 minutes.2.2 Phase identification
The final solids of each synthesis were characterized by high-resolution transmission electron microscopy (HR-TEM) imaging and/or pXRD analysis. Four distinct phases were identified. Fig. 1 presents pXRD profiles for samples consisting of what we presume to be high purity imogolite and proto-imogolite, as well as for an amorphous silica and pseudo-boehmite reference. All four pXRD profiles show a series of one or more broad, weak peaks consistent with materials lacking long-range periodicity (i.e., short-range ordered). The pXRD patterns of each agree with previously reported data.7,30–32 HR-TEM images of the pseudo-boehmite and proto-imogolite endmembers generally showed highly aggregated nanoparticles with different morphologies (Fig. S1†). The endmember that has been reported to be allophane based on its pXRD characteristics in older studies25 showed no evidence of well-formed spherical nanoparticles. In agreement with more recent studies, we assumed that the morphological characteristics of this sample were consistent with proto-imogolite and have referred to it as such throughout this study. Amorphous silica consisted of globular aggregates with varying particle sizes in the range of 10 s to 100 s of nm (Fig. S1†). This was confirmed through EDS analysis which showed the sample contained only silicon. Overall, the sizes and morphologies observed in HR-TEM were generally consistent with what has been reported previously for synthetic pseudo-boehmite, imogolite, proto-imogolite, and amorphous silica.The majority of the other products of the different synthesis experiments did not result in a single pure phase but contained a mixture of the different endmembers instead. Qualitative evidence for these mixtures was provided by pXRD, which showed combinations of distinct pXRD peaks for imogolite, proto-imogolite, pseudo-boehmite and/or amorphous silica all present in a single sample (Table 1).
| Concentration (M) | NaOH addition (mL min−1) | Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio Si ratio |
Hydrolysis ratio | Imogolite (%) | Proto-imogolite (%) | Am. silica (%) | Ps. boehmite (%) |
|---|---|---|---|---|---|---|---|
| 0.005 | 10 | 1 | 2 | 100.0 | 0.0 | 0.0 | 0.0 |
| 0.005 | 5 | 1 | 2 | 90.9 | 0.0 | 0.0 | 9.1 |
| 0.005 | 10 | 2 | 2 | 19.7 | 0.0 | 3.8 | 76.5 |
| 0.005 | 2 | 2 | 3 | 9.7 | 16.9 | 8.6 | 64.8 |
| 0.005 | 2 | 1 | 3 | 8.4 | 0 | 2.7 | 88.9 |
| 0.005 | 2 | 2 | 2 | 100 | 0 | 0 | 0 |
| 0.005 | 5 | 1.5 | 2 | 100 | 0 | 0 | 0 |
| 0.005 | 5 | 2 | 3 | 0 | 27 | 3 | 70 |
| 0.005 | 10 | 1.5 | 3 | 0 | 59.8 | 2.8 | 37.4 |
| 0.005 | 10 | 1 | 3 | 0 | 74 | 10.3 | 15.7 |
| 0.005 | 5 | 1 | 0.5 | 6.6 | 87.5 | 5.9 | 0 |
| 0.005 | 2 | 2 | 0.5 | 33.8 | 52.4 | 6.6 | 7.2 |
| 0.005 | 10 | 2 | 1 | 89 | 5 | 0 | 6 |
| 0.005 | 10 | 2 | 0.5 | 50.6 | 38.9 | 0 | 10.5 |
| 0.005 | 2 | 1 | 1 | 15.6 | 73.9 | 0 | 10.5 |
| 0.01 | 5 | 1 | 2 | 32.4 | 67.6 | 0.0 | 0.0 |
| 0.01 | 2 | 1.5 | 2 | 20.2 | 79.8 | 0.0 | 0.0 |
| 0.01 | 2 | 1.5 | 3 | 0 | 29.2 | 9.8 | 61 |
| 0.02 | 10 | 1.5 | 1 | 9.6 | 48.9 | 29.4 | 12.1 |
| 0.05 | 5 | 2 | 2 | 23.7 | 76.3 | 0.0 | 0.0 |
| 0.05 | 5 | 2 | 3 | 6 | 0 | 1.4 | 92.6 |
| 0.05 | 10 | 1.5 | 0.5 | 0 | 78.8 | 21.2 | 0 |
| 0.05 | 10 | 1 | 0.5 | 0 | 77.3 | 22.7 | 0 |
| 0.05 | 5 | 1 | 3 | 0 | 90 | 10 | 0 |
| 0.1 | 5 | 2 | 3 | 10.5 | 0 | 0 | 89.5 |
| 0.1 | 10 | 1 | 0.5 | 0 | 36.4 | 63.6 | 0 |
| 0.1 | 10 | 2 | 0.5 | 0 | 70.1 | 29.9 | 0 |
| 0.1 | 10 | 2 | 2 | 0.0 | 96.0 | 4.0 | 0.0 |
| 0.1 | 2 | 1 | 1 | 0 | 92.6 | 7.4 | 0 |
| 0.1 | 10 | 1 | 2 | 0.0 | 96.4 | 3.6 | 0.0 |
| 0.1 | 5 | 1 | 1 | 0 | 82.2 | 17.8 | 0 |
| 0.1 | 0.5 | 2 | 1 | 0 | 84.1 | 15.9 | 0 |
| 0.1 | 10 | 1.5 | 3 | 0 | 32.5 | 0 | 67.5 |
| 0.125 | 10 | 2 | 1 | 0 | 56.5 | 43.5 | 0 |
| 0.125 | 2 | 1.5 | 1 | 0 | 72 | 28 | 0 |
| 0.125 | 5 | 2 | 1 | 0 | 77.5 | 22.5 | 0 |
| 0.125 | 1 | 2 | 1 | 0 | 85 | 15 | 0 |
| 0.125 | 2 | 1 | 1 | 0 | 58.3 | 41.7 | 0 |
| 0.125 | 2 | 2 | 1 | 0 | 79.9 | 20.1 | 0 |
| 0.125 | 5 | 1.5 | 3 | 0 | 86.2 | 13.8 | 0 |
| 0.125 | 2 | 2 | 2 | 0.0 | 90.4 | 9.6 | 0.0 |
| 0.125 | 10 | 1.5 | 3 | 0 | 50.5 | 7.3 | 42.2 |
| 0.125 | 10 | 1 | 3 | 0 | 93 | 7 | 0 |
| 0.125 | 5 | 1 | 3 | 0 | 94 | 6 | 0 |
| 0.15 | 2 | 2 | 3 | 5.8 | 0.1 | 3 | 91.1 |
| 0.15 | 5 | 2 | 1 | 0 | 91.6 | 8.4 | 0 |
| 0.15 | 5 | 1 | 1 | 0 | 60.7 | 39.3 | 0 |
| 0.15 | 2 | 2 | 1 | 0 | 85.4 | 14.6 | 0 |
| 0.15 | 0.5 | 2 | 1 | 0 | 84.7 | 15.3 | 0 |
| 0.15 | 5 | 1.5 | 2 | 0.0 | 85.3 | 14.7 | 0.0 |
| 0.15 | 1 | 2 | 1 | 0 | 91.2 | 8.8 | 0 |
| 0.15 | 10 | 1.5 | 3 | 0 | 76.5 | 0 | 23.5 |
| 0.16 | 10 | 1 | 1 | 0 | 54.9 | 45.1 | 0 |
| 0.16 | 10 | 1.5 | 1 | 0 | 74.1 | 25.9 | 0 |
| 0.16 | 2 | 2 | 1 | 0 | 75.6 | 16.4 | 8 |
| 0.175 | 0.5 | 2 | 1 | 0 | 65.1 | 34.9 | 0 |
| 0.175 | 0.5 | 1 | 1 | 0 | 61.1 | 38.9 | 0 |
| 0.175 | 2 | 1 | 1 | 0 | 36.6 | 63.4 | 0 |
| 0.175 | 5 | 1 | 1 | 0 | 53.7 | 46.3 | 0 |
| 0.175 | 10 | 1.5 | 3 | 0 | 45.7 | 27.1 | 27.2 |
| 0.175 | 2 | 1.5 | 1 | 0 | 72.3 | 27.7 | 0 |
| 0.175 | 5 | 2 | 1 | 0 | 83.8 | 16.2 | 0 |
| 0.175 | 2 | 2 | 1 | 0 | 87.6 | 12.4 | 0 |
| 0.175 | 10 | 2 | 3 | 0 | 79.1 | 0 | 20.9 |
| 0.185 | 2 | 2 | 1 | 0 | 38.4 | 61.6 | 0 |
| 0.185 | 2 | 1 | 1 | 0 | 48 | 52 | 0 |
| 0.185 | 5 | 1.5 | 3 | 0 | 100 | 0 | 0 |
| 0.2 | 2 | 2 | 1 | 0 | 79.6 | 20.4 | 0 |
| 0.2 | 2 | 2 | 3 | 0 | 25.7 | 2.6 | 71.7 |
| 0.2 | 10 | 1 | 0.5 | 0 | 26.3 | 73.7 | 0 |
| 0.2 | 10 | 1.5 | 0.5 | 0 | 39 | 61 | 0 |
| 0.2 | 10 | 1.5 | 1 | 0 | 72.8 | 27.2 | 0 |
| 0.2 | 10 | 1 | 3 | 0 | 93 | 7 | 0 |
| 0.2 | 10 | 1 | 2 | 0.0 | 100.0 | 0.0 | 0.0 |
2.3 Linear combination fitting
Linear combination fitting of pXRD was used to quantify the abundances of imogolite, proto-imogolite, pseudo-boehmite and amorphous silica in a set of 74 synthesis products. An example of the LCF fit of a pXRD pattern from a synthesized product is shown in Fig. 1. Table 1 shows the results of LCF analysis and summarizes the starting conditions used for each synthesis. LCF results show that the abundances of proto-imogolite and imogolite varied from 0 up to 100% for the different synthesis conditions. The abundance of amorphous silica, varied between 0 to ∼74%, while pseudo-boehmite ranged from 0 to 93%. Based on the distinct peak positions presented for each phase, a linear combination of two phases would only work on samples lacking the distinct peaks for the other reported phases. For example, significant quantities of amorphous SiO2 commonly occurred with proto-imogolite, and the diffraction patterns for those samples lacked the distinct peaks for imogolite at ∼8 degrees, and pseudo-boehmite at ∼50 degrees. A linear combination of those conditions using all 4 phases would usually result in 0 weights or extremely low values for the absent phases. Conversely, using 2 phases for a sample that possessed more peaks than could be accounted for resulted in very poor or failed fits, based on the visual inspection of the difference patterns or complete inability to fit any peaks present. The data illustrate how variations in the abundances of proto-imogolite, imogolite, and amorphous silica occur with differences in synthesis conditions.2.4 Regression modeling of imogolite, pseudo-boehmite, proto-imogolite and amorphous silica
Due to the relatively high number of conditions (Table 1) that did not result in a detectable amount of imogolite, any standard multivariate regression performed would be skewed by those zero values. A binary logistic regression coupled with a likelihood ratio test of all parameters was used to identify the most significant condition dictating the presence of imogolite. Concentration was found to be, by far, the most statistically significant parameter determining the presence of imogolite nanotubes (Fig. 2).This binary regression was used to determine the concentration at which imogolite nanotubes are likely to occur. A subset of the data in Table 1 obtained using that concentration cutoff was then analyzed with a multivariate regression to determine factors affecting the proportion. The proportion of imogolite is modeled with the following relationship:
 | (1) |
In eqn (1), IM represents the resulting proportion of imogolite as a percentage, conc refers to the initial Al solution concentration (M), H corresponds to the hydrolysis ratio (mol mol−1), rate is the rate of base addition (ml min−1) and cat is the cation ratio (mol mol−1). The negative coefficient for concentration implies increased imogolite proportion with lower concentrations, while the quadratic relationship for the amount of base added implies decreased proportion at relatively low and high OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratios. We also observe a complex relationship between the hydrolysis ratio, rate at which the base is added, and the cation ratio as indicated here by the interaction terms and visualized in the ESI (Fig. S2†). The overall model was found to be significant, with a p-value less than 0.0001, and an adjusted R2 of 0.85, meaning it explains 85% of the variance in the data. The starting concentration and hydrolysis ratio were both considered statistically significant factors, with confidence >99.99%. Cation ratio was significant, by virtue of its interaction with the rate at which base is added, at >95% confidence. The imogolite proportions predicted in the model were compared to the experimentally measured counterparts based on the initial synthesis conditions, and the resulting plot is shown in Fig. 4a.
Al ratios. We also observe a complex relationship between the hydrolysis ratio, rate at which the base is added, and the cation ratio as indicated here by the interaction terms and visualized in the ESI (Fig. S2†). The overall model was found to be significant, with a p-value less than 0.0001, and an adjusted R2 of 0.85, meaning it explains 85% of the variance in the data. The starting concentration and hydrolysis ratio were both considered statistically significant factors, with confidence >99.99%. Cation ratio was significant, by virtue of its interaction with the rate at which base is added, at >95% confidence. The imogolite proportions predicted in the model were compared to the experimentally measured counterparts based on the initial synthesis conditions, and the resulting plot is shown in Fig. 4a.
The Root Mean Square Error (RMSE) is 0.65, meaning the model can predict the imogolite proportion to within ±0.3%, after correcting for the cube root transformation. The Durbin–Watson (DW) statistic for the residuals of this model is 2.95, and we therefore fail to reject the null hypothesis that the residuals are independent at a p-value of 0.05. A plot of the model predicted values and their corresponding residuals as observed in Fig. 4 was used to check for adherence of the results to modeling assumptions.
The residuals were assessed using the Shapiro–Wilks test, and we failed to reject the null hypothesis that the residuals are normally distributed at a p-value of 0.05. Normality of residuals was further confirmed, visually, using a Q–Q plot (not shown). For subsequent models, these checks are summarized in the ESI (Table S1†).
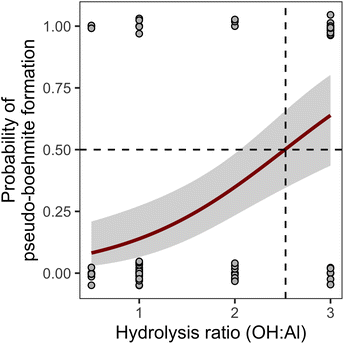
A similar approach was employed for the pseudo-boehmite model, which also exhibited a prevalence of zero values. The logistic regression for this phase showed that hydrolysis is the dominant factor determining the presence of pseudo-boehmite.
From the model for Fig. 3, we determine that hydrolysis ratios higher than 2.53 have >50% probability of producing pseudo-boehmite. Using that cutoff and performing the multivariate regression analysis on the resulting subset of data, the following model for the pseudo-boehmite proportion is obtained:
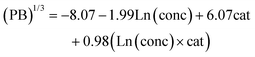 | (2) |
In eqn (2), PB represents the resulting proportion of pseudo-boehmite as a percentage, conc refers to the initial solution concentration (M), and cat corresponds with the Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si cation ratio (mol mol−1). The overall model is statistically significant with p-value = 0.0002. The statistically significant synthesis parameters are concentration (>99%) and cation ratio (>99.9%). Although the negative coefficient for concentration implies an inverse relationship with pseudo-boehmite proportion, and the positive value for cation ratio indicates increased proportion with increasing cation ratio, the presence of an interaction term implies there may be slight variations in the trends. These variations are visualized in the ESI (Fig. S3†). This model passes all feasibility tests of normality, autocorrelation, and residual trends. The fits and residual plots are shown in Fig. 4.
Si cation ratio (mol mol−1). The overall model is statistically significant with p-value = 0.0002. The statistically significant synthesis parameters are concentration (>99%) and cation ratio (>99.9%). Although the negative coefficient for concentration implies an inverse relationship with pseudo-boehmite proportion, and the positive value for cation ratio indicates increased proportion with increasing cation ratio, the presence of an interaction term implies there may be slight variations in the trends. These variations are visualized in the ESI (Fig. S3†). This model passes all feasibility tests of normality, autocorrelation, and residual trends. The fits and residual plots are shown in Fig. 4.
Proto-imogolite showed up in various quantities for most conditions used in Table 1. A multivariate regression was carried out on the entire dataset, producing the following model:
 | (3) |
Here, the percentage proportion of proto-imogolite is expressed as PI, while rate refers to the rate of base addition (mL s−1). The ubiquitous nature with which this particle occurs means there are complex trends even with individual synthesis parameters. Modeling the data requires the use of additional variables as observed in eqn (3). This model implies that slower base addition, and higher cation ratio promote proto-imogolite formation, however, the inclusion of interaction terms indicates variations in those trends (Fig. S4†). Both variables were found to be statistically significant, while the overall model was also significant with a p-value less than 0.0001. The model passes all feasibility tests while the resulting fit and residual trend are shown in Fig. 4.
Finally, the model developed for amorphous silica synthesis is described as:
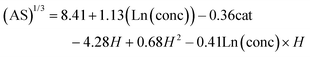 | (4) |
Eqn (4) implies that a relative increase in the concentration of starting reagents, as well as a relative decrease in the hydrolysis ratio are the key factors promoting proto-imogolite (PI) formation. Intuitively, lower Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratios (expressed as cat in eqn (4)) suggest that as Si increases relative to Al, excess Si further contributes to the total amorphous silica proportion. The interaction term in this model indicates that higher initial concentrations significantly increase amorphous silica proportion at a hydrolysis ratio of 2 or less (Fig. S5†). Al concentration and hydrolysis ratio were the most important factors with >99.999% significance. The model passes all feasibility tests while the resulting fit and residual trend are shown in Fig. 4.
Si ratios (expressed as cat in eqn (4)) suggest that as Si increases relative to Al, excess Si further contributes to the total amorphous silica proportion. The interaction term in this model indicates that higher initial concentrations significantly increase amorphous silica proportion at a hydrolysis ratio of 2 or less (Fig. S5†). Al concentration and hydrolysis ratio were the most important factors with >99.999% significance. The model passes all feasibility tests while the resulting fit and residual trend are shown in Fig. 4.
2.5 In situ D v(R) particle size analysis and regression modeling
In situ SAXS studies were performed on a subset of synthesis conditions from Table 1, and the average and median particle sizes obtained via Dv(R) analysis are shown in Table 2. For consistency in the determination of mean particle size, all particles were assumed to be spherical in shape, which leads to a valid size distribution with the caveat that sizes derived for more anisotropically shaped particles, like proto-imogolite, are slightly larger than the real dimensions possessed.33| Concentration (M) | NaOH addition (mL min−1) | Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio Si ratio |
Hydrolysis ratio | Mean diameter (nm) | Median diameter (nm) |
|---|---|---|---|---|---|
| 0.005 | 2 | 1 | 3 | 8.2 | 2.8 |
| 0.005 | 2 | 2 | 3 | 8.6 | 3.2 |
| 0.005 | 10 | 1 | 2 | 1.16 | 1.2 |
| 0.005 | 10 | 2 | 2 | 1.2 | 1.2 |
| 0.005 | 2 | 2 | 2 | 1.1 | 1 |
| 0.005 | 10 | 2 | 2 | 1.2 | 1.2 |
| 0.005 | 5 | 1.5 | 2 | 1.04 | 1 |
| 0.01 | 2 | 2 | 3 | 7.3 | 2.8 |
| 0.05 | 5 | 2 | 3 | 3.8 | 1.6 |
| 0.05 | 10 | 1.5 | 0.5 | 1.0 | 1.0 |
| 0.05 | 10 | 1 | 0.5 | 1.6 | 1.6 |
| 0.1 | 0.5 | 2 | 1 | 1.5 | 1.4 |
| 0.1 | 2 | 1 | 1 | 1.6 | 1.5 |
| 0.1 | 5 | 1 | 1 | 1.8 | 1.8 |
| 0.1 | 5 | 2 | 3 | 4.0 | 1.6 |
| 0.1 | 10 | 1 | 0.5 | 1.0 | 1.0 |
| 0.1 | 10 | 2 | 0.5 | 1.2 | 1.2 |
| 0.125 | 1 | 2 | 1 | 1.8 | 1.8 |
| 0.125 | 2 | 2 | 1 | 1.5 | 1.4 |
| 0.125 | 5 | 2 | 1 | 1.7 | 1.6 |
| 0.15 | 0.5 | 2 | 1 | 1.9 | 1.4 |
| 0.15 | 1 | 2 | 1 | 1.1 | 1.1 |
| 0.15 | 2 | 2 | 1 | 1.7 | 1.8 |
| 0.15 | 2 | 2 | 3 | 1.6 | 1.6 |
| 0.15 | 5 | 1 | 1 | 1.6 | 1.5 |
| 0.15 | 5 | 2 | 1 | 3.6 | 1.6 |
| 0.175 | 0.5 | 1 | 1 | 1.5 | 1.6 |
| 0.175 | 0.5 | 2 | 1 | 1.6 | 1.6 |
| 0.175 | 2 | 2 | 1 | 1.3 | 1.2 |
| 0.175 | 5 | 1 | 1 | 1.6 | 1.6 |
| 0.175 | 5 | 2 | 1 | 1.7 | 1.5 |
| 0.175 | 10 | 2 | 3 | 1.8 | 1.2 |
| 0.185 | 5 | 1.5 | 3 | 2.0 | 1.2 |
| 0.2 | 10 | 1 | 3 | 2.4 | 1.2 |
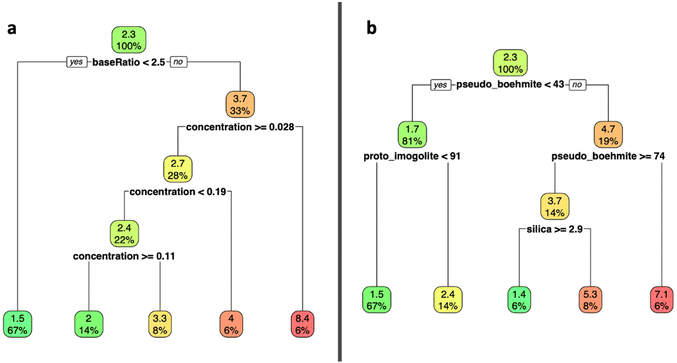
A regression tree analysis was used to model the impact of input conditions on precursor particle size (Fig. 5a), and the subsequent role of that precursor size on the phase distribution of nanoparticles (Fig. 5b). To prevent overfitting, a minsplit of 5 was chosen during modeling, which corresponds to the minimum number of observations each terminal node must contain before a split is attempted.
We observed that the most significant input condition that determines precursor particle size is the amount of base added, followed by the initial Al concentration. At a hydrolysis ratio above 2.5, particles were mostly larger than ∼2 nm, and generally increased in size with decreasing concentration. From the second decision tree, we observe that the ∼2 nm cut-off indicates whether the system becomes predominantly Al-based (pseudo-boehmite) or aluminosilicate-based (proto-imogolite). Larger precursors (∼5 nm and bigger) correspond to a predominant pseudo-boehmite product at over 74%, while smaller (∼2 nm and smaller) particles resulted in proto-imogolite dominant products.
Tracking Dv(R) results in situ through the first hour of synthesis show the effect of pH during and after base addition on particle size. Throughout the pre-oven synthesis process, the size of precursor particles hovers around the same size, and there is no obvious increase in particle size with time. The mean distribution of particle sizes with time (Fig. S6†) confirms there is little to no particle growth until oven treatment.
3. Discussion
3.1 Growth stages of ILS nanoparticles
Studies in the literature conducted at similar conditions have suggested that the first stage of particle formation during base addition involves the formation of soluble Al and Si complexes, followed by the spontaneous formation and growth of gibbsite-like Al(OH)3 nanoparticles.14,25 At low hydrolysis ratios, the rapid uptake of OH− by Al3+ is apparent when the addition of NaOH ceases, after which the pH is observed to decrease. This effect presents itself at higher hydrolysis ratios, as a pseudo-plateau around pH 4. In the following step, tetrahedrally coordinated silica attach to the gibbsite-like sheets, a process which displaces –OH groups, releases H3O+ (ref. 30) and results in the condensation of what we suggest to be the proto-imogolite precursors. With supporting in situ SAXS data (Fig. S6†), we conclude that the processes facilitating the condensation of particles occurs immediately as the base is being introduced, and all resulting particles are of similar sizes. Further stabilization in precursor particle formation and particle density over time results in decreasing pH that eventually stabilizes by the final stage. During oven treatment, additional condensation occurs and causes a drop in pH. Comparisons of sample pH pre and post oven treatment show a drop in all cases, which was 0.6 units at the least and 2 units at most. For syntheses carried out at a hydrolysis ratio of 5, post-synthesis pH was >11.7 and no drop in pH was observed during synthesis and after oven treatment. Using pXRD, we concluded that the relatively high pH at a hydrolysis ratio of 5 resulted in the co-precipitation of amorphous Al (hydr)oxides and amorphous silica only. As such, those data are not included in our models, but the diffraction pattern and corresponding pH data for one sample can be found in the ESI (Fig. S7†).3.2 Evidence of allophane versus proto-imogolite production in the literature
Extensive syntheses of nanosized aluminosilicates have been carried out by a variety of researchers at differing starting conditions. Many of these starting conditions overlap directly with those chosen for this study. Although the authors of the current study did not produce any well-formed nanospheres with the expected sizes of 3–5 nm, as previously described for allophane, multiple other studies have reported the production of allophane using similar methods and conditions. The pXRD patterns of allophane and proto-imogolite are indistinguishable, and so cannot be used as evidence towards the production of allophane.7,28 HRTEM images are the strongest evidence for allophane as a direct measure of morphology, but it is not a ubiquitous technique used, when distinguishing between imogolite and allophane. Recent models of allophane-like products have cast doubt on the idealized 3–5 nm spherical structures due to the variable Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio and the less well-defined structure.34 Owing to its variable composition, it has been proposed that allophane should be thought of as a series of nanominerals rather than a single species.35 It is the opinion of the authors that often what is called allophane in the literature, unless clearly demonstrated through TEM imaging, is actually proto-imogolite11 in a variety of morphologies.
Si ratio and the less well-defined structure.34 Owing to its variable composition, it has been proposed that allophane should be thought of as a series of nanominerals rather than a single species.35 It is the opinion of the authors that often what is called allophane in the literature, unless clearly demonstrated through TEM imaging, is actually proto-imogolite11 in a variety of morphologies.
3.3 Influence of synthesis conditions on formation of alumino(silicates)
Hydrolysis ratio and the initial Al concentration during synthesis were the most relevant condition in all models and their corresponding equations as reported. As a consequence of modifying hydrolysis ratio across different syntheses, the pH of pre-oven samples increases with values ranging from 3 at a hydrolysis ratio of 0.5 to 10 at the hydrolysis ratio of 3. Wang et al.26 observed a structural breakdown in so-called allophanes at pH > 11 and obtained amorphous products they attributed to the desilication and dealumination of the ILS. At lower hydrolysis ratios below 1, proto-imogolite is the overwhelmingly dominant product, with some amorphous silica contribution and little to no imogolite.Synthesis studies of an imogolite analogue discovered that at hydrolysis ratio values below 1.5, extensive tubular structures were unable to form, and significant structural defects were observed at values below 2.0.24 Our imogolite regression model supports that experimental result with imogolite proportion maximized close to OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al of 2 and dropping off on either side of that value.
Al of 2 and dropping off on either side of that value.
Additionally, increasing the initial concentration of reagents, specifically Al, leads to a lower proportion of imogolite. It has been suggested that an increase in concentration hinders imogolite proportion,36 and this effect has been attributed to the presence of Cl− ions commonly used in imogolite synthesis.37 Despite using electron microscopy with complementary XRD data, the authors of that study could not detect imogolite fibers when Cl− concentrations were above 50 mM. They also noticed that the use of diprotic bases, such as Ca(OH)2 that resulted in salts like CaCl2, returned relatively lower imogolite contents compared to monoprotic bases at similar cation concentrations. According to other studies, producing high concentrations of nucleated particles impede imogolite growth kinetics, especially the growth of longer tube structures.3,10 Our model agrees with the already established effects of concentration on imogolite proportion.
The Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio was a significant factor in modeling all phases except pseudo-boehmite. At lower pH values and in the presence of excess Si associated with lower Al
Si ratio was a significant factor in modeling all phases except pseudo-boehmite. At lower pH values and in the presence of excess Si associated with lower Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratios, we suspect the Si complexes in solution polymerize since there are fewer gibbsite-like-sheets with which to bond. Further, amorphous Si has been shown to inhibit imogolite growth, while polymerizing Si chains originating on tetrahedral sites and creating Si-rich local structure are known to occur for proto-imogolite.7 We observe these effects as the prevalent co-existence of appreciable amounts of amorphous silica and proto-imogolite in our pXRD patterns, while the reverse holds true for imogolite predominant versions of our samples.
Si ratios, we suspect the Si complexes in solution polymerize since there are fewer gibbsite-like-sheets with which to bond. Further, amorphous Si has been shown to inhibit imogolite growth, while polymerizing Si chains originating on tetrahedral sites and creating Si-rich local structure are known to occur for proto-imogolite.7 We observe these effects as the prevalent co-existence of appreciable amounts of amorphous silica and proto-imogolite in our pXRD patterns, while the reverse holds true for imogolite predominant versions of our samples.
None of the products containing pseudo-boehmite exhibited the sharp diffraction peaks associated with its crystalline phase, despite being aged for 7 days. Compared to other similarly aged products, this finding hints at the presence of alumino(silicates) as a method for controlling or inhibiting the crystallization of pseudo-boehmite nanoparticles.
Using the models derived for each nanoparticle phase, we produce phase maps as a function of input Al, H+ and Si concentrations (Fig. 6). These maps confirm that there are localized areas in the chemical space where the proportion of any particle is maximized, with overlapping regions elsewhere that produce mixed phase products. Imogolite is observed to occur within a relatively narrow region of synthesis space, consistent with commonly reported conditions in the literature. Proto-imogolite occurs over a wider range, which could be explained by the suggestion that it has variations in composition, and this agrees with the more varied examples from the literature. Pseudo-boehmite occurs at relatively higher Al concentrations and lower acidity, while amorphous silica predominates at high Si concentrations except at very low acidity.
 | ||
| Fig. 6 Phase maps of imogolite, proto-imogolite, pseudo-boehmite and amorphous silica. Contours are derived from model predicted values, and the base addition rate was optimized for the formation of imogolite and pseudo-boehmite in each case. Hollow circles represent the experimental data obtained in this study, and the size of each circle correlates to the percent proportion of that nanoparticle. The colored “x” shows the position of reported input conditions from the literature.7,25,38,39 These studies reported single phase products, so we assume 100% proportion of that particle in the respective phase map. | ||
3.4 Regression approaches in geochemical systems
Alongside the use of in situ data, a multivariate regression approach has allowed for a holistic description of the system. Using this systematic methodology creates the opportunity to explore unaddressed questions. Modeling predicts that proto-imogolite is energetically favored to persist when precursor particles are less than 4 nm in size.6 Using this multivariate approach, and assuming the accurate quantification and explanation of factors influencing the system, we can probe the relationships between synthesis conditions, particle size and phase distribution. Our models, specifically the decision tree visualized in Fig. 5, imply that particle size is directly linked to synthesis conditions, but larger particles mostly form in conditions that favor the formation of pseudo-boehmite.The first split in our decision tree, corresponding to the greatest difference in resulting phase occurs at threshold of 2.3 nm – below this mean particle size, proto-imogolite becomes the dominant phase in the system. We are unable to detect the proposed critical size for imogolite formation at this stage of the synthesis process, as both imogolite and proto-imogolite precursors have similar sizes. It is also possible that the growth needed to achieve this critical size occurs very early on in the aging step, but after the hydrolysis stage. Our Dv(R) plots show that a range of particle sizes occur after hydrolysis (Fig. S8†), and the distribution of particle sizes are expected to directly correlate with the distribution of phases.6 Simulated fits of proto-imogolite SAXS data using a mixture of proto-imogolite sizes has been shown to adequately fit the corresponding SAXS data, further highlighting the polydispersity in precursor particle sizes.40
Past studies suggested that the mechanism of growth involves the thermodynamic self-assembly of precursor particles,41 while others proposed a kinetic growth process where “seeds” of pre-existing nanotubes grow to longer lengths in the presence of precursor particles.42 More recent studies seem to agree with the notion of kinetically driven growth via aggregation of pre-formed sections, although it is less certain why particle growth slows down drastically after approximately 3 days of aging.
4. Conclusions
The present study uses a systematic synthesis procedure combined with a suite of complementary analytical techniques, assessed using linear combination fitting and analyzed with multivariate regression techniques, to determine the influence of starting physical and chemical conditions on the final phase composition of nanosized alumino(silicate) products. Although synthesis methods previously reported to have formed allophane were used, the only definite products produced were imogolite and proto-imogolite. Using a systems approach allowed us to examine how concentration of starting reagents, elemental ratios, hydrolysis ratios, and precursor particle sizes all simultaneously and independently influenced the proportion of each endmember. We produced linear models with statistically significant high predictive power that quantitatively described the effect each factor had on the phase abundance of each endmember. The models accurately represented what was found experimentally in several literature studies.These models can help answer questions about nanoparticle formation, and address factors in a uniquely systems-based approach not yet employed in this field. This approach can be applied to a multitude of geochemical systems to produce predictive models about crystallization. Using these models, we can probe questions about what chemical and physical properties are most important during mineral or precursor formation, which can lead to insights about mechanisms and reactions.
5. Experimental
5.1 Synthesis
Nanosized aluminosilicates were synthesized at room temperature using a method adapted from the literature.7,14,27,43 Solutions of aluminum chloride hexahydrate (AlCl3·6H2O, Sigma-Aldrich, 99%) were prepared in a standard borosilicate glass reactor to obtain concentrations ranging from 0.005 M to 0.2 M. Tetraethyl orthosilicate (TEOS, Sigma-Aldrich, 99.9%) was immediately added to reach Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si molar ratios ranging from 1 to 2. TEOS was added prior to inducing hydrolysis to minimize silica polymerization. Hydrolysis was achieved by pumping a 0.1 M sodium hydroxide solution (NaOH, Fisher Scientific, 99%) at rates ranging from 0.5 to 10 mL min−1, using a peristaltic pump (Ismatec IPC8) fitting with Tygon 2-stop tubing (Ismatec SC0824) to achieve [OH]
Si molar ratios ranging from 1 to 2. TEOS was added prior to inducing hydrolysis to minimize silica polymerization. Hydrolysis was achieved by pumping a 0.1 M sodium hydroxide solution (NaOH, Fisher Scientific, 99%) at rates ranging from 0.5 to 10 mL min−1, using a peristaltic pump (Ismatec IPC8) fitting with Tygon 2-stop tubing (Ismatec SC0824) to achieve [OH]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Al] hydrolysis ratios of 0.5 to 3. The resulting solution was stirred at 400 RPM for 1 hour, while monitoring pH at 5-second intervals (Oakton PC 2700). The solutions were then transferred to 125 mL anaerobic glass serum bottles sealed with butyl rubber stoppers and aluminum seals (DWK Life Sciences 223748), and then heated constantly at 95 °C for 7 days (Fisher Isotemp 215G). The resulting solution or gel was then dialyzed against 18.2 MΩ cm ultrapure water using a 12–14
[Al] hydrolysis ratios of 0.5 to 3. The resulting solution was stirred at 400 RPM for 1 hour, while monitoring pH at 5-second intervals (Oakton PC 2700). The solutions were then transferred to 125 mL anaerobic glass serum bottles sealed with butyl rubber stoppers and aluminum seals (DWK Life Sciences 223748), and then heated constantly at 95 °C for 7 days (Fisher Isotemp 215G). The resulting solution or gel was then dialyzed against 18.2 MΩ cm ultrapure water using a 12–14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da, 25 mm diameter standard grade membrane (Spectra Por) until the conductivity of the solution reached below 2 μS m−1. The dialyzed solution was then dried at 40 °C to obtain a film and/or coarse powder, subsequently ground up for consistency into a fine white powder for further analysis. The imogolite endmember was synthesized at an Al concentration of 0.002 M, Al
000 Da, 25 mm diameter standard grade membrane (Spectra Por) until the conductivity of the solution reached below 2 μS m−1. The dialyzed solution was then dried at 40 °C to obtain a film and/or coarse powder, subsequently ground up for consistency into a fine white powder for further analysis. The imogolite endmember was synthesized at an Al concentration of 0.002 M, Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio of 2 and OH
Si ratio of 2 and OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio of 2. Proto-imogolite conditions were similar except for an Al concentration of 0.2 M. For pseudo-boehmite, Al concentration was 0.1 M, the OH
Al ratio of 2. Proto-imogolite conditions were similar except for an Al concentration of 0.2 M. For pseudo-boehmite, Al concentration was 0.1 M, the OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al hydrolysis ratio was 3, 0.2 M ethanol (Fisher Scientific), and the suspension was aged for 24 hours. Synthesis of an amorphous silica sample used as a reference was reported previously.44
Al hydrolysis ratio was 3, 0.2 M ethanol (Fisher Scientific), and the suspension was aged for 24 hours. Synthesis of an amorphous silica sample used as a reference was reported previously.44
5.2 Powder X-ray diffraction analysis
Powder X-ray diffraction (pXRD) data were collected using a Rigaku MiniFlex II Desktop X-ray diffractometer equipped with a CuKα source (30 kV to 15 mA). Dried samples were homogenized using an agate mortar and pestle and the powders were pack mounted into a well in a zero-background single crystal silicon holder. Diffracted intensities from the samples were collected from 5° to 80° 2θ in 0.01° increments. Exposure time was 2 seconds per step and the sample holder was rotated continuously during data collection. pXRD patterns of imogolite, proto-imogolite, and amorphous silica were selected as endmember components based on maximum purity assessed by pXRD comparisons, SAXS, and TEM data. Diffraction patterns obtained for all endmembers were cross-referenced with the studies cited in the literature on the synthesis of high-purity particles. It is worth noting in the case of imogolite, that even high-purity products have been found to contain minor amounts of proto-imogolite.23,40 Background subtraction was performed for all pXRD patterns using the Fityk program45 to improve peak visibility and uniformity in fitting. Linear combination fitting (LCF, WinXAS 3.0) was used to estimate the proportions of pseudo-boehmite, imogolite, proto-imogolite, and amorphous silica in each synthesized product. Quaternary combinations of the endmember pXRD patterns were fitted to each sample pattern, from 7.5° to 80° 2θ, and weight fractions for each component were determined using a least-squares minimization procedure. The sum of the weight fractions was normalized to 100%. Residuals were visually assessed.5.3 Small angle X-ray scattering
Small angle X-ray scattering (SAXS) data were collected using a Panalytical Empyrean Nano Edition multi-purpose X-ray scattering platform equipped with a Cu anode (λCuKα = 1.5406 Å) and elliptic beam focusing optic with a 1/32° fixed slit. Diffracted intensities from the samples and backgrounds were collected from −0.15 to 6° 2θ in approximately 0.014° increments using a GaliPIX3D area detector or proportional detector. Exposure times ranged from 60–320 s per point. Dry samples were flat mounted between Mylar films and measured in a ScatterX78 evacuated sample holder and beam path. In situ experiments were performed using a custom liquid flow cell designed for use with the ScatterX78 vacuum stage. In brief, the synthesis solution was pumped continuously from the reactor into the flow cell and then returned to the reactor using a peristaltic pump. Scans were collected continuously during each experiment to monitor for changes in particle size distribution during initial hydrolysis and subsequent mixing. Once the solution began to show stable results, usually up to 90 minutes into the experiment, the final 5 scans were averaged, and the background subtracted. Volume-weighted size distribution (Dv(R)) analysis33 was performed using EasySAXS (Panalytical).5.4 Transmission electron microscopy
HR-TEM imaging was performed on a JEOL 2100 operating at 200 keV and a JEOL EDS equipped with a Silicon Drift Detector at ∼127 eV energy resolution (NCFL, ICTAS, Virginia Tech). Samples were diluted to 10 ppm, and then dialyzed against methanol using a 12–14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da, 25 mm diameter standard grade membrane (Spectra Por). Before imaging, samples were placed in a sonicating bath for 1 minute to disperse aggregates. The samples were mounted on Lacey-carbon, 300 mesh, copper-backed grids from Ted Pella. The grids were dried in air and stored in a benchtop vacuum chamber.
000 Da, 25 mm diameter standard grade membrane (Spectra Por). Before imaging, samples were placed in a sonicating bath for 1 minute to disperse aggregates. The samples were mounted on Lacey-carbon, 300 mesh, copper-backed grids from Ted Pella. The grids were dried in air and stored in a benchtop vacuum chamber.
5.5 Multivariate linear regression analysis
Multivariate(multiple) linear regression analysis was applied to LCF data that estimated each endmember proportion of imogolite, proto-imogolite, and amorphous silica. The starting physical and chemical conditions were input as continuous explanatory variables, with separate regression models developed for each endmember as the response variable. All independent variables were analyzed to confirm a lack of correlation between them for each model. Models were correctly specified, and residuals were checked to confirm adherence to regression modeling assumptions including normality, stochasticity, homogeneity of variance, and lack of autocorrelation. All regression analyses were performed using R on RStudio.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge financial support provided by the National Science Foundation through CAREER 1652237. This work used shared facilities at the Nanoscale Characterization and Fabrication Laboratory, which is funded and managed by Virginia Tech's Institute for Critical Technology and Applied Science. Additional support was provided by the Virginia Tech National Center for Earth and Environmental Nanotechnology Infrastructure (NanoEarth), a member of the National Nanotechnology Coordinated Infrastructure (NNCI), supported by NSF (ECCS 1542100 and ECCS 2025151).References
- I. Bottero, B. Bonelli, S. E. Ashbrook, P. A. Wright, W. Zhou, M. Tagliabue, M. Armandi and E. Garrone, Phys. Chem. Chem. Phys., 2011, 13, 744–750 RSC.
- E. Paineau, Appl. Sci., 2018, 8, 1921 CrossRef.
- P. Maillet, C. Levard, O. Spalla, A. Masion, J. Rose and A. Thill, Phys. Chem. Chem. Phys., 2011, 13, 2682–2689 RSC.
- E. Garrone and B. Bonelli, in Developments in Clay Science, ed. P. Yuan, A. Thill and F. Bergaya, Elsevier, 2016, vol. 7, pp. 672–707 Search PubMed.
- R. Gelli, S. Del Buffa, P. Tempesti, M. Bonini, F. Ridi and P. Baglioni, J. Colloid Interface Sci., 2018, 511, 145–154 CrossRef CAS PubMed.
- A. Thill, P. Picot and L. Belloni, Appl. Clay Sci., 2017, 141, 308–315 CrossRef CAS.
- C. Levard, E. Doelsch, I. Basile-Doelsch, Z. Abidin, H. Miche, A. Masion, J. Rose, D. Borschneck and J. Y. Bottero, Geoderma, 2012, 183–184, 100–108 CrossRef CAS.
- F. Ohashi, S. Tomura, K. Akaku, S. Hayashi and S. I. Wada, J. Mater. Sci., 2004, 39, 1799–1801 CrossRef CAS.
- J. P. Gustafsson, Clays Clay Miner., 2001, 49, 73–80 CrossRef CAS.
- C. Levard, A. Masion, J. Rose, E. Doelsch, D. Borschneck, C. Dominici, F. Ziarelli and J.-Y. Bottero, J. Am. Chem. Soc., 2009, 131, 17080–17081 CrossRef CAS PubMed.
- C. Levard, J. Rose, A. Thill, A. Masion, E. Doelsch, P. Maillet, O. Spalla, L. Olivi, A. Cognigni, F. Ziarelli and J. Y. Bottero, Chem. Mater., 2010, 22, 2466–2473 CrossRef CAS.
- S. M. Barrett, P. M. Budd and C. Price, Eur. Polym. J., 1991, 27, 609–612 CrossRef CAS.
- T. Henmi and K. Wada, Am. Mineral., 1976, 61, 379–390 CAS.
- S. I. Wada, A. Eto and K. Wada, J. Soil Sci., 1979, 30, 347–355 CrossRef CAS.
- M. L. Westbrook, R. L. Sindelar and D. L. Fisher, J. Radioanal. Nucl. Chem., 2015, 303, 81–86 CrossRef CAS.
- L. Liu, J. Chun, X. Zhang, M. Sassi, A. G. Stack, C. I. Pearce, S. B. Clark, K. M. Rosso, J. J. De Yoreo and G. A. Kimmel, Environ. Sci. Technol., 2022, 56, 5029–5036 CrossRef CAS PubMed.
- E. B. Lindblad, Immunol. Cell Biol., 2004, 82, 497–505 CrossRef CAS PubMed.
- P. d. S. Santos, A. C. V. Coelho, H. d. S. Santos and P. K. Kiyohara, Mater. Res., 2009, 12, 437–445 CrossRef CAS.
- S. Iijima, T. Yumura and Z. Liu, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 11759–11764 CrossRef CAS PubMed.
- J. G. Croissant, K. S. Butler, J. I. Zink and C. J. Brinker, Nat. Rev. Mater., 2020, 5, 886–909 CrossRef CAS.
- F. Rancan, Q. Gao, C. Graf, S. Troppens, S. Hadam, S. Hackbarth, C. Kembuan, U. Blume-Peytavi, E. Rühl, J. Lademann and A. Vogt, ACS Nano, 2012, 6, 6829–6842 CrossRef CAS PubMed.
- D. Napierska, L. C. J. Thomassen, D. Lison, J. A. Martens and P. H. Hoet, Part. Fibre Toxicol., 2010, 7, 39 CrossRef CAS PubMed.
- P. Picot, Y. Liao, E. Barruet, F. Gobeaux, T. Coradin and A. Thill, Langmuir, 2018, 34, 13225–13234 CrossRef CAS PubMed.
- C. Levard, A. Masion, J. Rose, E. Doelsch, D. Borschneck, L. Olivi, P. Chaurand, C. Dominici, F. Ziarelli, A. Thill, P. Maillet and J. Y. Bottero, Phys. Chem. Chem. Phys., 2011, 13, 14516–14522 RSC.
- F. Ohashi, S. I. Wada, M. Suzuki, M. Maeda and S. Tomura, Clay Miner., 2002, 37, 451–456 CrossRef CAS.
- S. Wang, P. Du, P. Yuan, X. Zhong, Y. Liu, D. Liu and L. Deng, Appl. Clay Sci., 2018, 166, 242–249 CrossRef CAS.
- E. Montarges-Pelletier, S. Bogenez, M. Pelletier, A. Razafitianamaharavo, J. Ghanbaja, B. Lartiges and L. Michot, Colloids Surf., A, 2005, 255, 1–10 CrossRef CAS.
- P. Du, P. Yuan, D. Liu, S. Wang, H. Song and H. Guo, Appl. Clay Sci., 2018, 158, 211–218 CrossRef CAS.
- A. Namayandeh, O. J. Borkiewicz, N. M. Bompoti, M. Chrysochoou and F. M. Michel, Environ. Sci. Technol., 2022, 56, 15672–15684 CrossRef CAS PubMed.
- N. Arancibia-Miranda, M. Escudey, M. Molina and M. T. García-González, Nanomaterials, 2013, 3, 126–140 CrossRef CAS PubMed.
- S. Musić, N. Filipović-Vinceković and L. Sekovanić, Braz. J. Chem. Eng., 2011, 28, 89–94 CrossRef.
- Z. Zhang and T. J. Pinnavaia, Langmuir, 2010, 26, 10063–10067 CrossRef CAS PubMed.
- O. Glatter, J. Appl. Crystallogr., 1980, 13, 7–11 CrossRef CAS.
- C. Levard and I. Basile-Doelsch, in Developments in Clay Science, ed. P. Yuan, A. Thill and F. Bergaya, Elsevier, 2016, vol. 7, pp. 49–65 Search PubMed.
- R. L. Parfitt and J. M. Kimble, Soil Sci. Soc. Am. J., 1989, 53, 971–977 CrossRef CAS.
- V. C. Farmer, A. R. Fraser and J. M. Tait, Geochim. Cosmochim. Acta, 1979, 43, 1417–1420 CrossRef CAS.
- S.-I. Wada and C. Sakimura, Clay Sci., 2000, 11, 115–123 CAS.
- Y.-H. Pan, Q.-Y. Zhao, L. Gu and Q.-Y. Wu, Desalination, 2017, 421, 160–168 CrossRef CAS.
- L. Denaix, I. Lamy and J. Y. Bottero, Colloids Surf., A, 1999, 158, 315–325 CrossRef CAS.
- P. Picot, T. Lange, F. Testard, F. Gobeaux and A. Thill, Appl. Clay Sci., 2023, 241, 107013 CrossRef CAS.
- S. Mukherjee, V. M. Bartlow and S. Nair, Chem. Mater., 2005, 17, 4900–4909 CrossRef CAS.
- H. Yang, C. Wang and Z. Su, Chem. Mater., 2008, 20, 4484–4488 CrossRef CAS.
- Y.-T. Huang, D. J. Lowe, G. J. Churchman, L. A. Schipper, R. Cursons, H. Zhang, T.-Y. Chen and A. Cooper, Appl. Clay Sci., 2016, 120, 40–50 CrossRef CAS.
- A. C. Cismasu, F. M. Michel, A. P. Tcaciuc and G. E. Brown, Geochim. Cosmochim. Acta, 2014, 133, 168–185 CrossRef CAS.
- M. Wojdyr, J. Appl. Crystallogr., 2010, 43, 1126–1128 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional experimental results and modeling details, including TEM images, interaction plots, pH data, model checks and their descriptions (PDF). See DOI: https://doi.org/10.1039/d4nr00473f |
| This journal is © The Royal Society of Chemistry 2024 |