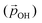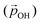Tuning electronic levels in photoactive hydroxylated titania nanosystems: combining the ligand dipole effect and quantum confinement

Abstract

Reducing the size of titania (TiO₂) to the nanoscale promotes the photoactive anatase phase for use in a range of applications from industrial catalysis to environment remediation. The nanoscale dimensions of these systems affect the magnitude of the electronic energy gap by quantum confinement. Upon interaction with aqueous environments or water vapour, the surfaces of these systems will also be hydroxylated to some degree. In turn, this affects the electronic energy levels due to the cumulative electrostatic effect of the dipolar hydroxyl (–OH) ligands (i.e. the ligand dipole effect). Using accurate density functional calculations, we investigate the combined effects of quantum confinement and the hydration-induced ligand dipole effect on a set of realistic titania nanosystems over a wide range of hydroxylation. Our detailed investigation reveals that, contrary to previous models, the ligand dipole effect does not-linearly depend on the ligand coverage due to the formation of inter-ligand OH⋯OH hydrogen bonds. To account for the resulting effects, we propose a refined model, which describes the ligand dipole effect more accurately in our systems. We show that both hydroxylation (by the ligand dipole effect) and size (by quantum confinement) have significant but distinct impacts on the electronic energy levels in nanotitania. As an example, we discuss how variations in these effects can be used to tune the highest unoccupied energy level in nanotitania for enhancing the efficiency of the hydrogen evolution reaction. Overall, we show that any specific energy shift can be achieved by a range of different combinations of nanosystem size and degree of hydroxylation, thus providing options for energy-level tuning while also allowing consideration of practical constraints (e.g. synthetic limitations, operating conditions) for photochemical applications.

---

Introduction

Nanoparticles (NPs) of the photoactive anatase polymorph of titania (TiO₂) are widely studied and used for a range of photochemical uses such as photocatalytic H₂ production,¹ or remediation of polluted water.² In such applications, titania NPs are expected to be significantly hydroxylated due to interaction with their aqueous working environment.³ The photochemical importance of surface OH groups in these systems due to their role in hydroxyl radical formation (˙OH) is well established.^4–6 Surface hydroxyls and adsorbed water can also help to stabilise surface hole centres in photocatalytic processes.⁷ Herein, we show that hydroxylation can have a surprisingly significant further effect on the energetic positions of the frontier orbital energy levels that eventually define the band edges in sufficiently large titania NPs. Band edge positions play an essential role in determining the utility and performance of semiconducting materials for photocatalytic applications.^8,9 Generally, the degree and type of alignment of a material's band edge energies with the energy levels of species interacting with its surfaces can strongly influence the transfer of photo-generated charge carriers for reduction/oxidation reactions. For photocatalytic water splitting, for example, the band edges of the system in question should lie above and below the redox potentials for H₂ and O₂ respectively.¹⁰ Understanding and controlling factors that significantly affect band edge positions are thus critical for developing and advancing photoelectrochemical technologies.

The band edge positions of the bulk anatase phase have been widely studied with respect to those of the less photoactive rutile polymorph due to a proposed staggered alignment having a synergistic role in photocatalytic water splitting.¹¹ The energy gap in titania NPs is highly affected by size-dependent quantum confinement (QC),¹² which, in turn, can thus affect the rutile-anatase energy edge alignment.¹³ The main effect of QC upon decreasing NP size is to increase the spacing between those discrete energy levels that define the band gap in the corresponding extended system. Attempts to more finely tune band edge positions in titania NPs without varying their size have followed a number of different strategies such as: engineering morphology and/or crystallinity,^14–17 chemical doping,^18,19 and creation of heterostructures with other materials.^20–22 These approaches require significant control of the detailed chemical structure of the NPs and, once employed, cannot be easily and/or dynamically changed by external means. In this work we examine the influence on band edge positions in nanotitania by ever-present surface hydroxyls, whose surface coverage can be controlled by external conditions (e.g. water vapour partial pressure).^3,23

For small anhydrous titania nanoclusters, hydration leads to progressive increasing the coverage of surface –OH species which in turn leads to a gradual fluctuating increase in the electronic gap magnitude.²³ This gap increase is ascribed to the stabilisation of the electronic structure of the nanoparticle as a result of hydroxylation-induced healing of local undercoordinated atoms/defects. For the relatively large titania NPs considered herein, we also find a similar hydroxylation-induced moderate energy gap increase. However, we find that the main effect of hydroxylation is to significantly shift both band edge positions in a similar parallel manner. This phenomenon can be ascribed to the ligand-induced Stark effect in which the cumulative electric field from the dipoles of surface ligands act to uniformly shift all the electronic energy levels of the NP with a linear dependence on ligand coverage. This effect was first observed, and has been subsequently mainly explored, for controlling the band edge positions of quantum dots by organic ligands for increasing solar cell efficiencies.^24–26 In the field of photocatalysis, there have also been a few studies using dipolar fields of organic ligands to improve catalytic performance,^27,28 where the effect is usually referred to as the ligand-induced dipole effect (LIDE).²⁹ In the following, we will use the acronym LIDE to be consistent with the practice in the photocatalytic literature.

Herein, we focus on LIDE in hydroxylated anatase titania NPs using realistic models developed in previous works^16,30 which have been used to rationalise experimental results on hydroxylated anatase NPs.³ As far as we are aware, hydroxylation induced LIDE for titania has only been previously studied using periodic slab models of ideal surfaces with small numbers of hydrogen atoms placed on oxygen atoms (i.e. hydrogenation) on regular surface sites.^31,32 In contrast, our NP based approach allows for a highly detailed examination of hydroxylation from dissociated water at various different sites such as corners, edges and facets. In addition, with the absence of periodic boundary constraints in our NP models, we can follow a gradual and progressive hydroxylation over a wide range of –OH coverages. Thereby, we show that LIDE in our systems has an unexpected non-linear –OH ligand coverage dependence that detailed analysis of the results shows to be due to effects of OH⋯OH interactions. Using our versatile NP models, we are also able to examine the additional effect of QC by considering hydroxylated NPs with different sizes. We note that as our models are discrete, they also allow us to use the true vacuum level as a natural unambiguous reference for all band edge energies for all NP systems considered.¹³ To provide further context for our work, we compare our results for anatase NPs with analogous calculations on a non-crystalline anatase-mimicking NP,³⁰ and on an extended anatase surface slab model.

Overall, our study provides a highly detailed and systematic description of the combined effects of hydroxylation (through LIDE, electronic stabilisation and inter-ligand interactions) and system size (governing QC) on the electronic band edge positions in titania nanosystems. Due to the versatility of our modelling approach, we can accurately assess the relative influence of each effect and thereby provide guidance on how to combine these factors to optimise band edge positions for photocatalytic applications. Specifically, we show how the band edges in our considered systems vary relative to the standard potentials for the hydrogen evolution reaction (HER) and the oxygen evolution reaction (OER) involved in water splitting. The valence band maximum (VBM) is always found to be lower than the potential for the OER. In contrast, by following level-alignment with respect to hydroxylation and system size, we show that the conduction band minimum (CBM) can be sensitively tuned to be above or below the potential for the HER. We highlight that any particular level alignment can be achieved using a range of different choices of size and hydroxylation degree. Unlike many other level-tuning approaches such as chemical doping or interfacing with other materials, these system variables are not dependent on chemically detailed interventions. As such, varying size and hydroxylation degree provides a top-down approach to tuning electronic energy levels, whose versatility means that it can accommodate different practical constraints when designing and/or operating photochemical nanosystems.

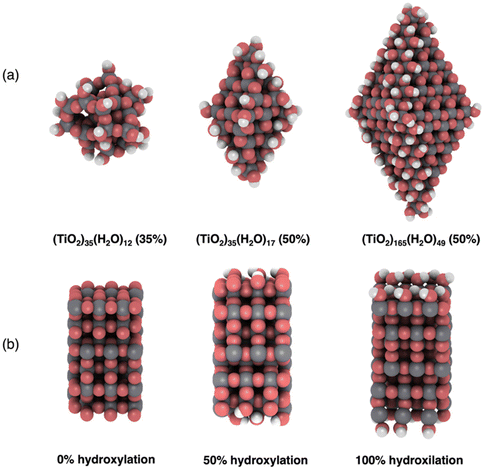
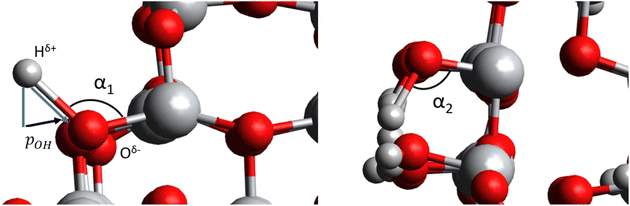
Models and computational strategy

We employ three previously reported realistic titania NP models with different sizes and crystalinities.^3,16,30 Two of these (TiO₂)_n NPs, with sizes n = 35, 165, possess the anatase crystal structure with bipyramidal faceted morphologies. We also consider one amorphous (TiO₂)₃₅ NP with a roughly spherical morphology. All NP structures are shown in Fig. 1a. The anatase titania NPs were designed following a top-down strategy in which the bulk anatase crystal is cut to generate bipyramids with the most stable (101) surface on all exposed facets.^12,16 The bare anatase titania NPs were progressively hydroxylated considering the relative reactivity of different surface sites (e.g., apical, edge, facet).³ The amorphous (TiO₂)₃₅ NP was generated by a simulated annealing process³³ in which the faceted (TiO₂)₃₅ NP was heated up to 3000 K, followed by sequential cooling steps.³⁰ The simulated annealing was performed using the NanoTiO interatomic potential (IP)³⁴ and the GULP code.³⁵ The structures of the hydroxylated amorphous (TiO₂)₃₅ NPs were generated by separate simulated annealing runs for each degree of hydroxylation.³⁰

Fig. 1 (a) Examples of hydroxylated NP structures. From left to right: an annealed amorphous (TiO₂)₃₅(H₂O)₁₂ NP, and faceted anatase crystalline (TiO₂)₃₅(H₂O)₁₇ and (TiO₂)₁₆₅(H₂O)₄₉ NPs. The percentages in parentheses indicate the degree of hydroxylation. (b) Supercell of an extended (101) surface model of anatase with 0 (left), 50% (middle) and 100% (right) degrees of hydroxylation. Atom key: O – red, Ti – grey, H – white.

To compare with our NP based results we also considered a periodic slab model of the (101) anatase surface (see Fig. 1b). This model consists of six layers of a (3 × 1) anatase supercell in which the (101) surface is symmetrically exposed on either side of slab. Periodically repeated slabs in the out-of-plane direction were separated by approximately 20 Å of vacuum space to avoid artificial inter-slab interactions. For each degree of hydroxylation considered we symmetrically hydroxylated both top and bottom surfaces of the slab to avoid the build-up of anisotropic electric fields. In these models, the averaged electrostatic potential over the mid-plane in the vacuum space was used to define a zero reference for evaluating the changes in band edge positions with respect to hydroxylation. Note that in the discrete NP systems the real vacuum level could be used as an absolute energy reference. In both the slab and NP systems we define the degree of hydroxylation with respect to the maximum hydroxylation we could achieve (i.e., defined to be 100%).

All the anhydrous (TiO₂)_n and hydrated (TiO₂)_n(H₂O)_m nanostructures and surface models were relaxed using all-electron DFT-based calculations as implemented in the FHI-aims code.³⁶ The Perdew–Burke–Ernzerhof (PBE) exchange–correlation density functional³⁷ was selected to perform the structural optimizations. A light tier-1 numerical atom-centred orbital basis set was employed. Such a basis set is comparable in accuracy to a TZVP Gaussian-type orbital basis set for TiO₂.¹² The convergence thresholds for atomic forces and total energy during the optimization were set to 10⁻⁵ eV Å⁻¹ and 10⁻⁶ eV, respectively. A 1 × 1 × 1 k-point grid (i.e. Γ-point) was used in the (101) surface model. We verified that Γ-point calculations provide sufficiently converged energies for the relatively large periodic supercell employed (see ESI†).

DFT calculations employing the PBE functional are generally reliable in providing a good structural description of materials. However, generalised gradient approximation (GGA) functionals such as PBE tend to be relatively poor when describing electronic properties such as the energy gap and band edge positions.³⁸ Hybrid density functionals which mix in a percentage of Hartree–Fock exchange into GGA functionals can help to overcome this systematic drawback.³⁹ A hybrid PBEx (12.5% Hartree-Fock exchange) functional has previously been shown to significantly improve the description of the electronic structure of titania systems.^40,41 A systematic PBEx-inspired correction of our computed PBE-based energy gaps and band edge positions was employed throughout.⁴¹

Results and discussion

We divide the discussion of our results into three parts. We first discuss the evolution of the electronic energy gap (E_g) values and how they are influenced by system size and hydroxylation. Afterwards, we focus on the effect of hydroxylation-induced LIDE on the band edges in our considered systems. Finally, we relate our results to water splitting though comparison of band edge energies with the potentials for the HER and OER and suggest how hydroxylation, and system size could be used to optimise photocatalytic performance. As our NP models are discrete systems, the VBM and CBM are formally associated with the highest occupied molecular orbital (HOMO) energy and the lowest unoccupied molecular orbital (LUMO) energy, respectively. As such we will tend to refer to HOMO and LUMO values when discussing our NP-based results.

Electronic energy gaps

We first consider the E_g values of the (101) anatase surface slab and the faceted titania NPs with respect to degree of hydroxylation (see Fig. 2). For the anhydrous anatase slab, we obtain an E_g value of 3.58 eV, which is 0.25 eV larger than the experimental band gap of bulk anatase (3.23 eV).⁴² As our approach provides an accurate E_g value for bulk anatase,⁴⁰ this is likely due to the finite thickness of our slab model and the associated band-opening effect of QC. Upon reducing the size and dimension of the anatase slab to anatase NPs of progressively decreasing size (i.e., (TiO₂)₁₆₅ > (TiO₂)₃₅) both the HOMO and LUMO are shifted up in energy, but with the LUMO upshift being more pronounced. In the smallest anhydrous anatase (TiO₂)₃₅ NP considered, this QC-induced effect raises the value of E_g to 3.84 eV, which is 0.26 eV higher than for the anhydrous slab. With hydroxylation, the main influence of QC is maintained with the E_g values being smaller in the hydroxylated slabs with respect to those in the correspondingly hydroxylated NPs. However, increasing hydroxylation also leads to a differential small increase in E_g values for different system sizes. For the anatase slab, the magnitude of E_g increases by 0.05 eV from 0%–100% hydroxylation. In contrast, for the corresponding increase in hydroxylation, the increase in E_g is of 0.18 and 0.31 eV for (TiO₂)₁₆₅ and for (TiO₂)₃₅, respectively. This increase in E_g is likely due to hydroxylation-induced healing of local undercoordinated atoms/defects and a concomitant stabilisation of the electronic structure, as noted in previous work on hydroxylated titania nanoclusters.²³ The relative increase in the magnitude of this effect with reducing system size is probably due to the increasing proportion of low-coordinated surface sites (especially at corners and edges) going from the planar surface slab to progressively smaller discrete NPs. For the smallest NP, this overall increase in E_g with hydroxylation is also accompanied by relatively large energy fluctuations with respect to small changes in hydroxylation as also observed in small titania nanoclusters.²³ However, this effect seems to diminish with increasing system size, where the hydroxylation-induced E_g increase becomes smaller and more gradual.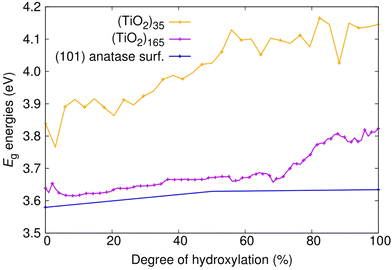

Fig. 2 Evolution of E_g energies with degree of hydroxylation of the (TiO₂)_n (n = 35, and 165) anatase NPs and the extended (101) anatase surface as depicted in Fig. 1.

Band edge positions

For the anhydrous anatase slab, the VBM energy is found to be −8.4 eV and the CBM energy to be −4.9 eV. These values correspond well to other calculated band edge energies reported for bulk anatase (−8.3 eV and −4.9 eV).⁴³ We note that these latter values were obtained by a method which, similar to our approach, uses an absolute vacuum reference and hybrid functionals, and which has been confirmed to be quite reliable as compared with experiment.¹¹ As noted above, both the corresponding HOMO and LUMO of the anhydrous NPs are higher in energy due to QC. The resultant HOMOs of both the largest (TiO₂)₁₆₅ and smallest (TiO₂)₃₅ NPs are upshifted by approximately 0.3 eV. In the case of the LUMOs, the upshift is also about 0.3 eV for (TiO₂)₁₆₅, but almost 0.5 eV for (TiO₂)₃₅. Upon hydroxylation, all initial band edge/orbital energies appear to initially increase in a fairly parallel linear manner with respect to the degree of hydroxylation. With increasing hydroxylation, the rate of increase in these energies slows down gradually. Overall, the total upshift in the edge/orbital energies is >1 eV in all cases from 0–100% hydroxylation. These data are summarised in Fig. 3. We note that this hydroxylation-induced orbital energy up-shift is not only observed for the HOMO and LUMO in our systems but is a general effect that effects all orbital energies. In Fig. S1 and S2 of the ESI† we show, for example, the hydroxylation dependent energies of ten energy levels ranged between LUMO+5 and HOMO−5 and for a significantly deeper lying energy level.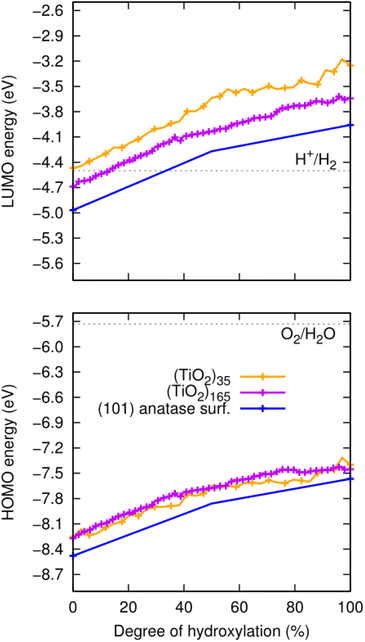

Fig. 3 Evolution of the energies of the HOMO (lower) and LUMO (upper) with degree of hydroxylation of the (TiO₂)_n (n = 35, and 165) anatase NPs and the extended (101) anatase surface as depicted in Fig. 1. Dotted grey lines represent the redox potentials for the HER (upper) and the OER (lower), which have the approximate values of −4.5 and −5.7 eV, respectively.^44,45

We also note that the magnitude of this effect does not strongly depend on the underlying anatase crystal structure. To show this, we compare the hydroxylation dependence of the HOMO and LUMO of the faceted anatase (TiO₂)₃₅ NP with that of an amorphous (TiO₂)₃₅ NP where the structure of the titania core of the NP and the positions of all hydroxyls are optimised for each degree of hydroxylation via simulated annealing³⁰ (see Fig. 4). The annealed NP clearly shows relatively larger fluctuations in the energies of the frontier orbitals. These variations are related to both the structure of the titania NP core structure and the hydroxylation configuration, which are re-calculated for each degree of hydroxylation through the annealing process. However, generally, we see that the average values of both the HOMO and LUMO in both NP types increase systematically in a similar way and over very similar energy ranges.

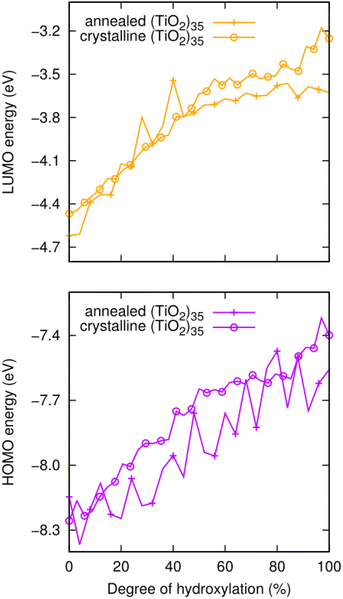Fig. 4 Evolution of the HOMO (lower) and LUMO (upper) energies with respect to the degree of hydroxylation for annealed amorphous and faceted anatase (TiO₂)₃₅ NPs as depicted in Fig. 1.

From the above, we propose that the general hydroxylation-dependent upshift in all orbital energies in all our systems is most likely due to the LIDE coming from the cumulative electrostatic field of the surrounding dipolar –OH groups. To quantify the total –OH-induced dipole moment acting on the NP, the sum of the components of each –OH dipole vector in the direction of the centre of the NP should be calculated. To obtain the effective radial O–H distances, we use the angle α between Ti–O–H atoms and project the O–H bond distance (d_OH) along Ti–O bond direction, which taken to be approximately in-line with the radial direction to the NP centre (see Fig. 5). Rather than assuming that the charge separation in each –OH group is constant, we also measure possible H^δ+ and O^δ− variations. Taking the above considerations into account, we use the following expression for the total magnitude of the –OH dipole contribution 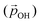for each degree of hydroxylation:

where N is the number of OH groups on a NP, and Q_H is the positive charge on the H atoms in every OH ligand. We obtain the Q_H charges using the Hirshfeld atomic charge partitioning scheme.⁴⁶ Unlike dipoles, atomically partitioned charges are not observables, and their accuracy cannot be directly assessed. Here, we scale the magnitude of all partitioned charges by a constant factor of ∼0.7, such that the scaled atomic charges in a calculation of the water molecule reproduces the experimental H₂O dipole moment. We note that this constant scaling does not affect any of our reported trends, but just provides OH dipole magnitudes that are more reasonably in line with the OH bond moment in the water molecule.⁴⁷ In the context of dissociative water adsorption, H and OH constituents interact, respectively, with under-coordinated O and Ti surface atoms. In this way, the hydration process leads to two kinds of hydroxyls which both can lead to an added dipole. We estimate the total dipole using the calculated charge on the H atoms and assuming that the deficit of electrons is only taken by the neighbouring O atom in each case. Lastly, for each –OH group, the factor cos(α_i) projects out the component of the dipole vector along the Ti–O bond direction(i.e. approximately the radial direction leading towards the centre of the NP).

Fig. 5 Left: Radial component of the dipole moment vector acting towards the centre of a titania NP associated with a single hydroxyl group. Right: A relatively higher hydroxylation regime in which OH⋯OH H-bonding leads to α₂ < α₁, and a reduced value of . Large grey, red, and small grey spheres correspond to Ti, O and H atoms, respectively.

We note that LIDE is usually modelled as being linearly proportional to ligand coverage with a fixed dipole per ligand.^26,29,31,32 This dipole is typically assumed to arise from the intrinsic dipole of the ligand and from the induced polarisation due to the ligand-surface interaction. In our expression, the dipole of the –OH group and how it is affected by structural change (via d_OH and α) and polarisation (via Q_H) due to the interaction with the surface is taken into account. We note that the contributions to the overall dipole through polarisation of the TiO₂ surface due to interaction with the –OH groups has been reported to be very small and largely independent of OH coverage on rutile surfaces.³¹ The small variation in the partial charges of the surface Ti (and O) atoms with respect to hydroxylation in our systems also confirms this conclusion.

Here, we use eqn (1) to estimate how the total hydroxylation-induced polarisation varies with –OH coverage. In all studied systems, we find that d_OH has an almost constant value, and thus has a linear effect on the total dipole with respect to changes in degree of hydroxylation. In contrast, with varying hydroxylation we find non-linear contributions to the total dipole for α and Q_H. Specifically, we find that both α and Q_H decrease with increasing hydroxylation, which tends to moderate the overall dipole increase. The reason for the decrease in both α and Q_H is the formation of OH⋯OH inter-hydroxyl H-bonds which becomes more and more prevalent with higher –OH coverages. These H-bond interactions trigger an increased bending of the Ti–O–H bond angles, making α increasingly closer to 90° and thus causing a 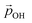decrease. Fig. 5 shows this ligand bending effect by comparing α for low and high hydroxylation. Similarly, with increasing H-bonding, we find that the OH⋯OH, H-bonded network promotes a partial delocalisation/polarisation leading to a reduction in the absolute values of the atomically partitioned charges on the hydroxyl groups, and a dipole reduction. The change in both the average value of α and Q_H with respect to the degree of hydroxylation for the (TiO₂)_n (n = 35, 165) anatase NPs is provided in the ESI (Fig. S3†). In Fig. 6 we show evolution of given by eqn (1) with respect to hydroxylation for our n = 35 and n = 165 (TiO₂)_n anatase NPs. For reference we also show the typically assumed model in which the total dipole is linearly dependent on ligand coverage.

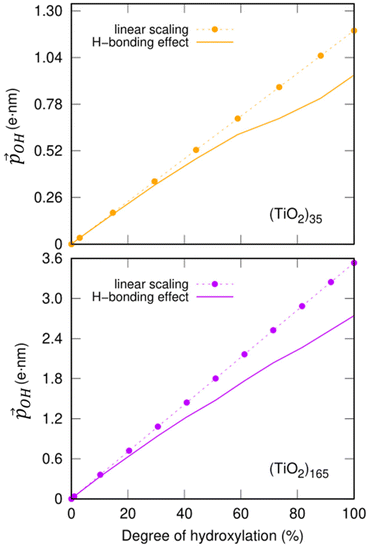Fig. 6 Total –OH dipole moment 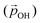versus degree of hydroxylation for the faceted (TiO₂)₃₅ (TiO₂)₃₅ (upper) and (TiO₂)₁₆₅ (lower) NPs. The dashed line shows the case in which all –OH dipoles contribute equally irrespective of hydroxylation, while the solid line incorporates the variability of α and Q_H following eqn (1).

Clearly, the H-bonding induced α variation and charge delocalisation tends to increasingly moderate the increase in 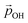with increasing hydroxylation. For 50–100% hydroxylation for the (TiO₂)₁₆₅ NP, for example, the magnitude of 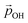varies from −15% to −22% with respect to a linear model. This tendency is very similar to that we report for the variation of energy levels with respect to degree of hydroxylation (see Fig. 2 and 3). The link between these two phenomena is likely to be LIDE whose effect on energy levels can be estimated using our calculated values of 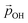for each degree of hydroxylation for each of our systems using eqn (2):²⁶

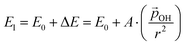where the energy of a level, E_l is given by the energy of the level in the anhydrous TiO₂ 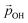system (E₀) plus the LIDE shift (ΔE) which depends mainly on (where we use the dipole moment evaluated using eqn (1)), and r, an effective radius of the system in question (which, for NPs, is taken to be the radius of a spherical NP with the same volume as the corresponding NP). Finally, A is a system dependent fitting constant.

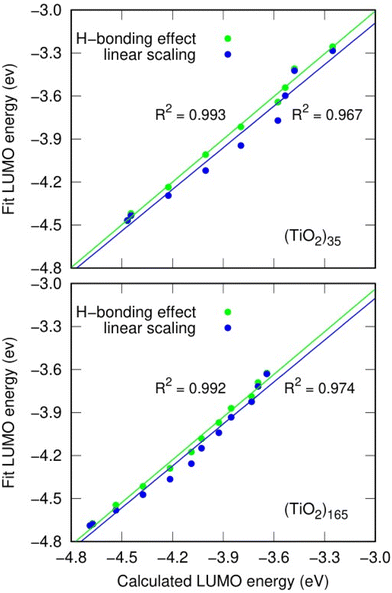
As an example, we use the LIDE dependent shifting in the LUMO with respect to hydroxylation in the (TiO₂)_n (n = 35, 165) NPs. In Fig. 7 we compare the DFT-calculated hydroxylation dependent variation in the LUMO energy levels of these two systems with predictions using eqn (2) from using: (i) constant dipoles for each hydroxyl, (ii) OH dipoles calculated using eqn (1). In both systems both models (i) and (ii) provide a good fit to the variation in LUMO energies indicating that the main effect on the energy change is due to LIDE. Comparing the models, we can also see that in both systems, using the dipoles from eqn (1) provides a non-negligible improvement over the linear dipole model.

Fig. 7 Correlation between DFT-calculated LUMO energy values and model-estimated-values for different degrees of hydroxylation for the (TiO₂)₃₅ and (TiO₂)₁₆₅ NPs incorporating effects of inter-OH H-bonding (green), and by using a simple linear model (blue).

We can further justify the use of our new detailed model for fitting the variation in energy levels with respect to the total dipole moment from surface –OH groups. In Fig. 8 we show the evolution in the HOMO and LUMO energies of our faceted NPs directly from DFT calculations with respect to 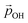calculated using eqn (1). In all cases we observe a very good correlation, which again supports the link between energy level shifting and hydroxylation-induced LIDE. The correlation between total dipole and energy shift is slightly less strong for the HOMO in the larger NP (R² = 0.95) than in the other cases examined (R² = 0.99). This lower correlation is related to a levelling of the (TiO₂)₁₆₅ HOMO level for high hydroxylation (>70%) which also results in an abrupt upshift in the E_g value (see Fig. 2). This may be related to specific surface sites being stabilised through chemical bonding and thus not purely a dipolar effect.

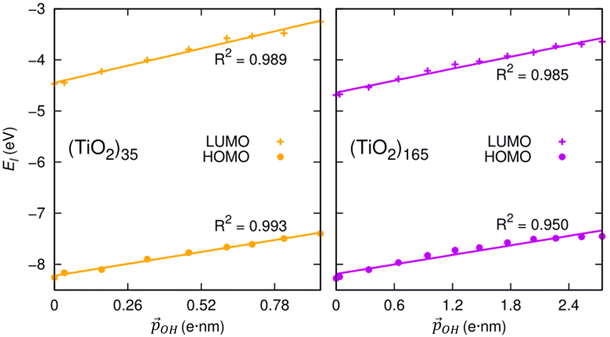Fig. 8 Correlation between calculated HOMO (LUMO) energies and projected total –OH dipole moment for the anatase (TiO₂)₃₅ and (TiO₂)₁₆₅ NPs calculated using eqn (1).

Relevance to water splitting and extrapolation to larger NP sizes

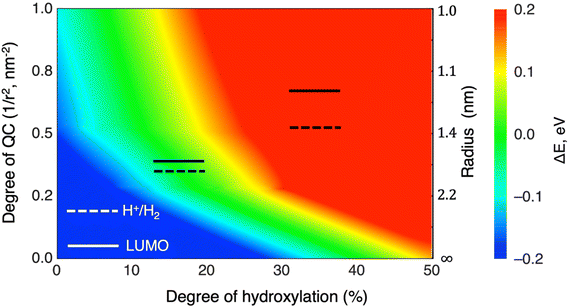
The position of the absolute redox potential for the OER is always significantly higher than the HOMO energies in our considered systems (see Fig. 3). As such, photo-generated holes in the HOMO would easily drive the OER for all systems for all degrees of hydroxylation. However, for solar-induced water splitting, the low HOMO energy would entail a relatively large E_g. With respect to capturing the maximum amount of useful energy from available sunlight, this would be detrimental. Minimising E_g under the conditions that: (i) the HOMO lies just below the redox potential for the OER, and (ii) the LUMO lies just above the redox potential for the HER, would help maximise the solar efficiency of water splitting photocatalysts. In the following, we focus on tuning the LUMO for the HER, assuming that the OER potential could be matched by employing other strategies (e.g., alternative materials,⁴⁸ doping⁴⁹).

For low hydroxylation degrees, the high QC of the smallest (TiO₂)₃₅ anatase NP causes it to have a LUMO which is optimally placed just above the HER redox potential. We note, however, that the anatase NPs of this size are metastable with respect to amorphous NPs^16,30 which tend to have lower lying LUMO levels for the lowest hydroxylation (see Fig. 3). We also note that it would be practically very difficult to prepare populations of NPs that are confined to such a small size range while also restricting their natural tendency to be hydroxylated through reaction with water. In larger NPs, the lower QC leads to a decrease in the LUMO. However, this effect can be compensated by increased hydroxylation and thus higher LIDE which causes a LUMO energy increase. Moving to higher hydroxylation in larger anatase NPs thus allows for more practically viable NPs to have an optimally tuned LUMO energy. As such an approach is linked only to the controllable working conditions of as-synthesised NPs, it also avoids the use of extra level-tuning measures (e.g. doping, interfacing with other materials). We note that very recently reported experiments have indicated that the induced dipole effect of deliberately grafted –OH ligands can enhance of photocatalytic activity of BiPO₄.⁵⁰

More generally, the combination of LIDE and QC allows one to tune the energy levels for a particular application. Our results show how orbital energies vary with the degree of hydroxylation for three sizes of NPs and for the infinite-sized limiting case of the extended anatase (101) surface. By interpolating between these results, we can provide approximate maps of how hydroxylation affects any chosen orbital level(s) for arbitrary system sizes. As an example, in Fig. 9 we show how the LUMO in anatase NPs can be tuned by combinations of hydroxylation and size to be either above or below the HER redox potential. For LUMO energies well above the HER (red region in Fig. 9) the reducing power of hydroxylated titania NPs is relatively enhanced. We specifically highlight the hydroxylation/size-tuning of the LUMO for efficient E_g matching (i.e. to be just above the HER redox potential – see green region in Fig. 9). Overall, Fig. 9 shows that many titania systems of different sizes and degree of hydroxylation can achieve specified electronic level alignments.

Fig. 9 LUMO versus HER potential energy level alignment plot with respect to varying the degree of hydroxylation (x-axis), degree of QC (left y-axis) and anatase system size (right y-axis). The colours indicate the regions where the LUMO is below/above the HER potential (blue/red) and where the LUMO is between 0–0.1 eV above the redox potential of the HER (green).

We note that in Fig. 9 we assume that only –OH groups from dissociated water causes the LIDE effect at all sizes. This scenario is most probable for non-crystalline NPs for which the surfaces tend to be more irregular and reactive. For more crystalline bipyramidal anatase NPs, a low-to-moderate degree of hydroxylation will readily occur through dissociative water adsorption on lower-coordinated edges and corner sites.³ Larger anatase bipyramidal NPs will have a higher proportion of their surfaces terminated by regular (101) facets. For the extended (101) surface, it is likely that there is a competition between molecular and dissociative water adsorption and that the balance between these two is temperature dependent.⁵¹ Recent work using a combination of surface X-ray spectroscopy and DFT calculations has reported a 3 : 1 ratio of dissociative versus molecular water on the (101) anatase surface at room temperature.⁵² For suitably high water coverages, having such a mixture of molecular H₂O (25%) and –OH (75%) bound to (101) NP facets would be more than sufficient to reach the higher degrees of hydroxylation considered in Fig. 9.

In future work it would also be interesting to consider influence of the accompanying molecularly adsorbed water on the (101) facets of larger bipyramidal NPs at higher water coverages. Molecularly adsorbed water has a high dipole (similar in magnitude to that of –OH) and is thus also expected produce a dipolar Stark effect in titania NPs. However, for the effect to be cumulative and vary systematically with changes in coverage, the dipoles should be radially aligned. For low temperatures a coherent ordering of molecularly adsorbed water may indeed be possible and could induce a very similar effect to that we describe for –OH groups. However, we would expect molecular adsorption to be more susceptible to disordering (e.g. via H-bond network rearrangements) at higher temperatures, thus diminishing any effect.

Conclusions

Employing accurate DFT based calculations, we have carefully analysed the influence of system size and hydroxylation on the electronic energy levels in a set of titania nanosystems, including realistic NP models and an extended anatase surface slab. Reducing system size increases the spacings between energy levels in a non-linear manner due to QC. Conversely, the cumulative electrostatic dipole of surface –OH ligands shifts all the energy levels by a uniform amount due to the LIDE. The magnitude of this latter shift is found not to be linearly dependent on the degree of ligand coverage, as is usually assumed in LIDE models. Instead, we show that inter-ligand interactions, in this case OH⋯OH H-bonds, can lead to a non-negligible coverage-dependent dipole reduction, due to ligand bending and charge delocalisation.

We show that size-induced QC and hydroxylation-driven LIDE can have significant, but distinct impacts on the electronic energy levels in nanotitania systems. As a highlighted example, we show how combined variations in QC and LIDE can be used to tune the highest unoccupied energy level in anatase NPs with respect to the HER redox potential. Here, we show that any specific energy shift can be achieved by a range of different combinations of system size and degree of hydroxylation. This flexibility means that one can achieve level-tuning (e.g., to enhance the HER) while taking into account different practical constraints (e.g., synthetic NP size limitations, degrees of hydroxylation due to operating conditions). We also note that, unlike many other proposed level-tuning approaches (e.g., chemical doping, interfacing with other materials), LIDE and QC do not require chemically detailed interventions. In summary, we show that combining QC and LIDE provides a highly versatile top-down approach to tuning electronic energy levels in photoactive nanomaterials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the financial support from MCIN/AEI/10.13039/501100011033 through projects PID2020-115293RJ-I00, PID2021-126076NB-I00, PID2021-127957NB-100, TED2021-129506B-C22, TED2021-132550B-C22 and the María de Maeztu CEX2021-001202-M project and from the Generalitat de Catalunya through the projects 2021-SGR-00079 and 2021-SGR-00354. Red de investigación RED2022-134295-T (FOTOFUEL) is also partly acknowledged. The reported research is also involved in the European Cooperation in Science and Technology (COST) Actions: CA18234 (CompNanoEnergy) and CA21101 (COSY). M. R.-P. acknowledges the Ministerio de Ciencia e Innovación (MICIN) for a Formación Personal Investigador (FPI) fellowship (PRE2019-087627). We also thank the Red Española de Supercomputación (RES) for the provision of supercomputing time.

References

1. H. Idriss, Curr. Opin. Chem. Eng., 2020, 29, 74–82.
2. J. Ryu and W. Choi, Environ. Sci. Technol., 2008, 42, 294–300.
3. L. Mino, Á. Morales-García, S. T. Bromley and F. Illas, Nanoscale, 2021, 13, 6577–6585.
4. K. Kobayakawa, Y. Nakazawa, M. Ikeda, Y. Sato and A. Fujishima, Ber. Bunsenges Phys. Chem., 1990, 94, 1439–1443.
5. J. Wang, X. Liu, R. Li, P. Qiao, L. Xiao and J. Fan, Catal. Commun., 2012, 19, 96–99.
6. A. Di Paola, M. Bellardita, L. Palmisanoa, Z. Barbierikovác and V. Brezovác, J. Photochem. Photobiol., A, 2014, 273, 59–67.
7. E. G. Panarelli, S. Livraghi, S. Maurelli, V. Polliotto, M. Chiesa and E. Giamello, J. Photochem. Photobiol., A, 2016, 322, 27–34.
8. E. A. Abdullah, Eur. J. Chem., 2019, 10, 82–94.
9. H. L. Tan, F. F. Abdi and Y. H. Ng, Chem. Soc. Rev., 2019, 48, 1255–1271.
10. M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473.
11. D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. Sokol, Nat. Mater., 2013, 12, 798–801.
12. O. Lamiel-Garcia, K. C. Ko, J. Y. Lee, S. T. Bromley and F. Illas, J. Chem. Theory Comput., 2017, 13, 1785–1793.
13. K. C. Ko, S. T. Bromley, J. Y. Lee and F. Illas, J. Phys. Chem. Lett., 2017, 8, 5593–5598.
14. X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891–2959.
15. M. Maeda and T. Watanabe, Surf. Coat. Technol., 2007, 201(22–23), 9309–9312.
16. Á. Morales-García, A. M. Escatllar, F. Illas and S. T. Bromley, Nanoscale, 2019, 11, 9032–9041.
17. Y.-H. Wang, K. H. Rahman, C.-C. Wu and K.-C. Chen, Catalysts, 2020, 10(6), 598.
18. A. Fuerte, M. D. Hernández-Alonso, A. J. Maira, A. Martinez-Arias, M. Fernandez-Garcia, J. C. Conesa and J. Soria, Chem. Commun., 2001, 24, 2718–2719.
19. E. R. Remesal and Á. Morales-García, Phys. Chem. Chem. Phys., 2022, 24, 21381–21387.
20. O. Fontelles-Carceller, M. J. Muñoz-Batista, E. Rodríguez-Castellón, J. C. Conesa, M. Fernández-García and A. Kubacka, J. Catal., 2007, 347, 157–169.
21. H. I. Elsaeedy, A. Qasem, H. A. Yakout and M. Mahmoud, J. Alloys Compd., 2021, 867, 159150.
22. M. Allès, E. R. Remesal, F. Illas and Á. Morales-García, Adv. Theory Simul., 2022, 6(10), 2200670.
23. A. Cuko, A. M. Escatllar, M. Calatayud and S. T. Bromley, Nanoscale, 2018, 10, 21518–21532.
24. N. Yaacobi-Gross, M. Soreni-Harari, M. Zimin, S. Kababya, A. Schmidt and N. Tessler, Nat. Mater., 2011, 10, 974.
25. P. R. Brown, D. Kim, R. R. Lunt, N. Zhao, M. G. Bawendi, J. C. Grossman and V. Bulovic, ACS Nano, 2014, 8, 5863–5872.
26. D. M. Kroupa, M. Vörös, N. P. Brawand, B. W. McNichols, E. M. Miller, J. Gu, A. J. Nozik, A. Sellinger, G. Galli and M. C. Beard, Nat. Commun., 2017, 8, 15257.
27. R. Wick-Joliat, T. Musso, R. R. Prabhakar, J. Löckinger, S. Siol, W. Cui, L. Sévery, T. Moehl, J. Suh, J. Hutter, M. Iannuzzi and S. D. Tilley, Energy Environ. Sci., 2019, 12, 1901.
28. F.-Y. Fu, I. Shown, C.-S. Li, P. Raghunath, T.-Y. Lin, T. Billo, H.-L. Wu, C.-I. Wu, P.-W. Chung, M.-C. Lin, L.-C. Chen and K.-H. Chen, ACS Appl. Mater. Interfaces, 2019, 11, 25186.
29. S. Yang, D. Prendergast and J. B. Neaton, Nano Lett., 2012, 12, 383–388.
30. M. Recio-Poo, Á. Morales-García, F. Illas and S. T. Bromley, Nanoscale, 2023, 15, 4809–4820.
31. D. Zhang, M. Yang and S. Dong, J. Phys. Chem. C, 2015, 119, 1451.
32. D. Zhang, M. Yang and S. Dong, Phys. Chem. Chem. Phys., 2015, 17, 29079–29084.
33. S. Kirkpatrick, C. D. Gelatt Jr. and M. P. Vecchi, Science, 1983, 220, 671–680.
34. A. Macià Escatllar, Á. Morales-García, F. Illas and S. T. Bromley, J. Chem. Phys., 2019, 150, 214305.
35. J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341.
36. V. Blum, R. Gehre, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
37. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. Á. Morales-García, R. Valero and F. Illas, J. Phys. Chem. C, 2017, 121, 18862–18866.
39. I. de P. R. Moreira, F. Illas and R. L. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155102.
40. K. C. Ko, O. Lamiel-García, J. Y. Lee and F. Illas, Phys. Chem. Chem. Phys., 2016, 18, 12357–12367.
41. Á. Morales-García, R. Valero and F. Illas, Phys. Chem. Chem. Phys., 2018, 20, 18907.
42. B. Kraeutler and A. J. Bard, J. Am. Chem. Soc., 1978, 100, 5985–5992.
43. J. Buckeridge, K. T. Butler, C. R. A. Catlow, A. J. Logsdail, D. O. Scanlon, S. A. Shevlin, S. M. Woodley, A. A. Sokol and A. Walsh, Chem. Mater., 2015, 27(11), 3844–3851.
44. D. Cho, K. C. Ko, O. Lamiel-Garcia, S. T. Bromley, J. Y. Lee and F. Illas, J. Chem. Theory Comput., 2016, 12(8), 3751–3763.
45. S. Trasatti, Pure Appl. Chem., 1986, 58, 955.
46. F. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138.
47. L. Burnelle and C. A. Coulson, Trans. Faraday Soc., 1957, 53, 403–405.
48. L. Zhao, Q. Cao, A. Wang, J. Duan, W. Zhou, Y. Sang and H. Liu, Nano Energy, 2018, 45, 118.
49. M. Abbas, T. ul Haq, S. N. Arshad and M. Zaheer, Mol. Catal., 2020, 488, 110894.
50. Z. Yang, Z. Qiang, J. Wang, Y. Wang and W. Yao, Small Struct., 2024, 5, 2300339.
51. L. E. Walle, A. Borg, E. M. J. Johansson, S. Plogmaker, H. Rensmo, P. Uvdal and A. Sandell, J. Phys. Chem. C, 2011, 115(19), 9545–9550.
52. I. M. Nadeem, J. P. Treacy, S. Selcuk, X. Torrelles, H. Hussain, A. Wilson, D. C. Grinter, G. Cabailh, O. Bikondoa, C. Nicklin, A. Selloni, J. Zegenhagen, R. Lindsay and G. Thornton, J. Phys. Chem. Lett., 2018, 9(11), 3131–3136.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr06189b

---