Photocatalytic activity of dual defect modified graphitic carbon nitride is robust to tautomerism: machine learning assisted ab initio quantum dynamics

Abstract

Two-dimensional graphitic carbon nitride (GCN) is a popular metal-free polymer for sustainable energy applications due to its unique structure and semiconductor properties. Dopants and defects are used to tune GCN, and dual defect modified GCN exhibits superior properties and enhanced photocatalytic efficiency in comparison to pristine or single defect GCN. We employ a multistep approach combining time-dependent density functional theory and nonadiabatic molecular dynamics (NAMD) with machine learning (ML) to investigate coupled structural and electronic dynamics in GCN over a nanosecond timescale, comparable to and exceeding the lifetimes of photo-generated charge carriers and photocatalytic events. Although frequent hydrogen hopping transitions occur among four tautomeric structures, the electron–hole separation and recombination processes are only weakly sensitive to the tautomerism. The charge separated state survives for about 10 ps, sufficiently long to enable photocatalysis. The employed ML-NAMD methodology provides insights into rare events that can influence excited state dynamics in the condensed phase and nanoscale materials and extends NAMD simulations from pico- to nanoseconds. The ab initio quantum dynamics simulation provides a detailed atomistic mechanism of photoinduced evolution of charge carriers in GCN and rationalizes how GCN remains photo-catalytically active despite its multiple isomeric and tautomeric forms.

---

1. Introduction

Graphitic carbon nitride (GCN) is a metal-free polymeric semiconductor that has emerged as a promising photocatalyst for solar-driven energy conversion and environmental remediation applications.^1–4 The high stability, facile synthesis, low cost and visible light absorption capacity of GCN contribute significantly to a plethora of reactions including water splitting and CO₂ reduction.^5–11 Its polymeric nature allows for structural flexibility as well and can serve as a compatible host substrate to other inorganic nanoparticles. Despite these impressive characteristics, the photocatalytic performance of pristine GCN has been limited due to its intrinsic issues, including recombination of photo-generated charge carriers, inefficient charge separation, and poor conductivity.^12,13 Modification strategies, such as engineering surface vacancies, introducing dopants or heteroatoms, and building hybrid structures, can tackle these drawbacks to a great extent by effectively tuning the physicochemical properties of carbon nitride, thereby increasing the efficiency of conversion of the energy of light into photocatalytic chemical reactions.^14–16 Nitrogen defects in GCN can create mid-gap bands that can be used for excitation and extraction of charge carriers, act as reactive sites, facilitate charge separation, prevent charge recombination, and expand the optical response of the photocatalyst material overall.^17,18 On the other hand, O doping enhances the photocatalytic performance due to improvements in material's electronic band structure.^19–21 Through synergistic enhancement, dual-defect-modified GCN (ON-GCN) exhibits superior properties, including a pronounced shift in light absorption towards longer wavelengths and a modulated energy band structure, combined with more-effective charge carrier separation, surpassing that of undoped GCN.^22–24 ON-GCN is advantageous over N-defect GCN because it exhibits a longer carrier lifetime and has a higher oxidation potential. GCN exhibits polymorphism^25,26 in which structural changes²⁷ can lead to modification in the electronic properties and charge carrier dynamics of the dual defect system. Tautomeric events occur over long times and are not captured by ab initio simulations, since ab initio molecular dynamics (MD) trajectories are limited to a few picoseconds. Modeling quantum dynamics of charge carriers using nonadiabatic (NA) MD further adds to the computational cost, while NAMD simulations provide the most direct route to understanding excited state processes in molecules and materials.^2,28–32

Recently, machine learning (ML) has emerged as a powerful tool to overcome the computational cost of first principles methods. It is developing rapidly and has already been applied to a wide range of systems and processes.^33–39 ML methods are paving the way to uncover complex reaction paths and to correlate and predict material structure and properties, providing a balance between accuracy and efficiency. Generation of long MD trajectories with ab initio quality results is now feasible with the aid of ML force fields (MLFFs).^37–39 An MLFF modeling of dual defect GCN can effectively sample a diverse set of structural conformations that impact electronic properties and charge carrier dynamics. ML also provides a means to accelerate the calculation of the electronic properties needed as the input for NAMD simulations of excited state dynamics. To mimic time-resolved experiments, NAMD requires electronic state energies and NA couplings (NACs) between states. Our group has recently demonstrated that the computational cost of NAMD can be reduced by interpolating the NAMD Hamiltonian along an MLFF trajectory.^40–43

In this work, we report a multiscale methodology and study the coupled structural evolution and quantum dynamics of charge carriers in dual defect ON-GCN over a nanosecond timescale by combining NAMD and real-time time-dependent density functional theory (RT-TDDFT) with supervised ML learning. We train an MLFF to investigate structural changes in dual defect ON-GCN over nanosecond MD trajectories, revealing hydrogen hopping involving four tautomeric structures. Higher energy structures remain metastable for significant periods of time, indicating that they should be taken into account when interpreting experiments. We sample the NAMD Hamiltonian along the trajectories and interpolate it to femtosecond resolution, needed to perform robust time-domain DFT and NAMD simulations. Despite the pronounced hydrogen atom hopping, the electronic dynamics is only weakly sensitive to tautomerism, because the dominant tautomers have similar electronic properties, and the most electronically distinct structure rarely appears. We show that catalytically active states are populated for 5–10 ps, which should be sufficient to perform elementary photochemical reactions, such as bond breaking, since bond oscillation periods are 100 times shorter. The ML-NAMD methodology used here allows us to sample rare events that can influence excited state dynamics in modern materials and to perform quantum dynamics simulations over nanosecond timescales. Our simulations provide atomistic insights into the photoinduced excited state dynamics of GCN and illustrate how GCN can remain photo-catalytically active in its multiple structural forms.

2. Computational details

Geometry optimization, ground state MD, and electronic structure calculations are performed with the Vienna ab initio simulation package.^44,45 The Perdew–Burke–Ernzerhof⁴⁶ exchange–correlation functional and the projected-augmented wave method (PAW)⁴⁷ describing the interactions between electrons and ion cores are employed. A 2 × 2 × 1 simulation cell consisting of 60 atoms is used to model the dual defect ON-GCN. The plane-wave basis energy cutoff is set to 530 eV for all DFT calculations. van der Waals interactions are described via the optB86b-vdW method.⁴⁸ A 20 Å vacuum layer is introduced in the z direction to eliminate interactions between layers. A 3 × 3 × 1 Γ-centered k-point Monkhorst–Pack mesh is used for geometry optimizations and electronic property characterization. Structures and charge densities are visualized using VESTA software.⁴⁹

An MLFF is built using the DeepPOT-SE⁵⁰ approach, as implemented in the DeepMD-Kit package,⁵¹ utilizing a deep learning neural network to describe interatomic interactions in the ON-GCN systems based on just a small amount of ab initio training data. The geometry is first optimized at 0 K. Then, the system is heated to temperatures from 100 K to 1600 K with a 100 K step, by velocity rescaling in the NVT ensemble to generate a training set for the MLFF. A total of ∼20 000 configurations of training data are generated. Specifically, the training dataset consists of 3000 structures at 300 K, 1500 structures at 200 K and 400 K, and 1000 structures each at the rest of the temperatures. More ab initio data points are obtained at 200–400 K than other temperatures to represent better the subsequent room temperature MLFF simulation. High temperature structures are needed to gather a diverse set of structure patterns, including transition paths between different tautomers. A cutoff radius of 9 Å is used for neighbor searching with 0.5 Å as the smoothing distance. The dimensions of the embedding and fitting nets are set to 25 × 50 × 100 and 240 × 240 × 240, respectively. The neural network is trained using the Adam stochastic gradient descent method⁵² with a learning rate that decreased exponentially starting from the value of 0.001. The input data are split into 80% training and 20% testing sets. Thereafter, the system is heated to 300 K and a Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)⁵³ is used to generate 1 ns MD trajectories with the trained MLFF model using a 1 fs timestep. Single point ab initio calculations are carried out at every 10 ps along the ML generated 1 ns trajectories at the Γ-point only for computational efficiency, since the direct bandgap of 2 × 2 pristine GCN lies at the Γ-point.⁵⁴ The potential energies from DFT and ML calculations are compared to validate the MLFF used, Fig. S2.† The root-mean-square deviation in the energy is within 10 meV per atom, and the root-mean-square difference for the ab initio and ML forces is 0.16 eV Å⁻¹, as per the recommended acceptable error.³⁸

The 1 ns long NVE trajectories generated using an MLFF are used to perform NAMD calculations. Structures are chosen at every 64 fs of each trajectory to calculate ab initio electronic energy levels and NACs by computing the overlap of adjacent wavefunctions using the CA-NAC package.^55,56 This information is used as input by the inverse fast Fourier transform (iFFT) code⁴² to interpolate the energy levels and NACs for the entire 1 ns trajectories with a 1 fs timestep. The 64 fs sampling interval represents a power of 2, i.e., 2⁶, that is needed for iFFT. The interpolation of the NA Hamiltonian greatly reduces the computational cost required to calculate all NACs and energy levels using only ab initio methods. A total of 100 atomic initial conditions and 100 stochastic realizations for each initial condition are used for each NAMD simulation. NAMD calculations are carried out using the decoherence induced surface hopping (DISH)⁵⁷ method under the classical path approximation, as implemented in the PYXAID^58,59 package. A more detailed description of the NAMD/TDDFT method can be found in our previous papers.^60,61

3. Results and discussion

The multiple defect system considered here is constructed by creating a nitrogen vacancy that leads to the formation of a C–C bond. The other defects involve formation of the CN group along with the NH and NH₂ groups, and replacement of a nitrogen atom by an oxygen atom. Fig. 1 shows the optimized structures of the modified dual defect ON-GCN. The four structures differ in the position of one of the hydrogens in the ring. These tautomeric structures are obtained from the temperature sampled training set. Ab initio total energies, reported in Table 1, indicate that the structure shown in Fig. 1a is the most stable, while that in Fig. 1d is the least stable.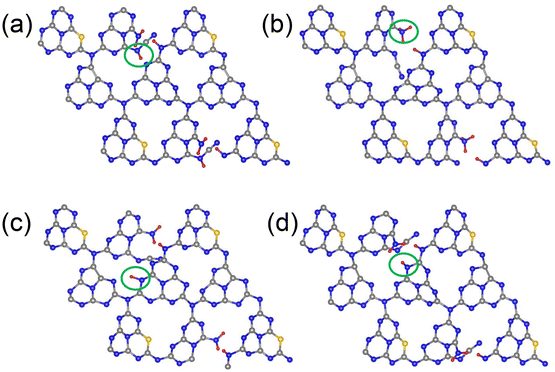

Fig. 1 Optimized structures of dual defect ON-GCN tautomers. The structures are labeled based on the position of the circled hydrogen atoms as (a) NH–CN (most stable structure), (b) NH₃, (c) N_Hβ and (d) N_Hα (least stable structure), Table 1. C: grey, N: blue, O: golden and H: red.

Table 1 Total energies of the four tautomer structures shown in Fig. 1. NH–CN is the most stable, and N_Hα is the least stable

Structure	Total energy (eV)
NH-CN	−460.38
NH3	−459.62
N_Hβ	−448.69
N_Hα	−447.42

---

The projected densities of states (PDOS) of the optimized structure of the four tautomers, Fig. 2, demonstrate that even a small modification in the ON-GCN structure by a shift of the H atom can lead to notable changes in the electronic properties of the material. For instance, changing the position of hydrogen from NH–CN to N_Hβ alters the energy and degeneracy of the deep hole trap state and the valence band maximum (VBM). The degeneracy of the spin up and down components of the d1 trap is lifted, and the VBM separates from the rest of the band. The corresponding orbital charge densities for NH–CN are shown in Fig. S1.† CBM, VBM and trap states energy level alignments are of prime importance to photocatalytic applications, including a multitude of oxidation and reduction reactions initiated by energetic charge carriers. A variety of tautomeric structures exist in the training set, allowing one to use MLFFs to study whether various structures appear on the timescales of carrier trapping and recombination, and whether these structures influence charge carrier properties and dynamics.

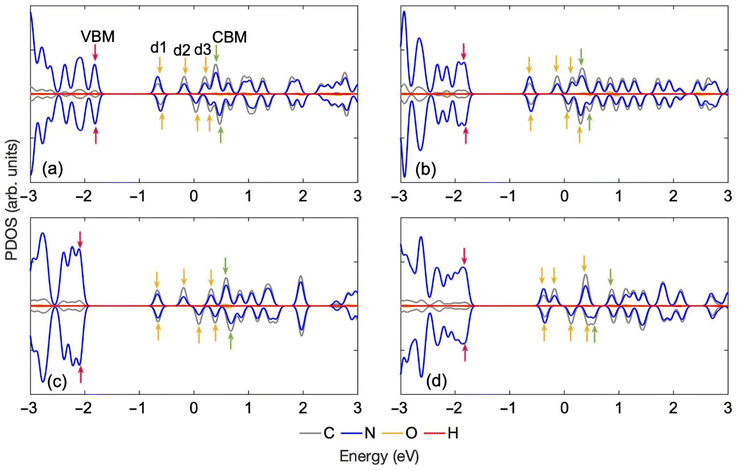Fig. 2 Partial density of states (PDOS) for the optimized structures of the ON-GCN tautomers shown in Fig. 1: (a) NH–CN, (b) NH₃, (c) N_Hβ and (d) N_Hα. Hopping of just one hydrogen leads to substantial changes in the electronic properties. The Fermi level is set to 0 eV. Band edges and defect states are marked with colored arrows: VBM: pink, CBM: green, defects (d1–d3): yellow.

We generate 1 ns long MD trajectories using an MLFF starting from the most stable and least stable structure, Table 1, at 300 K and 400 K. 300 K corresponds to ambient conditions, while 400 K represents photovoltaic or photocatalytic operating conditions, during which significant local heating can occur as charges relax nonradiatively through manifold trap states. Fig. S2† shows a comparison of the potential energies of the system predicted by MLFF with DFT energies calculated for the same geometries along the 1 ns trajectory generated starting from the most stable structure at 300 K. Deviations between ML and DFT results are around 10 meV per atom, providing a satisfactory agreement³⁸ for this complex system with multiple defects. Furthermore, ab initio electronic energy levels calculated for both trajectories at 300 K remain stable and only fluctuate around average values, as shown in Fig. 3a–d. The relative positions of the energy levels remain the same as those in the PDOS of the optimized structures, Fig. 2.

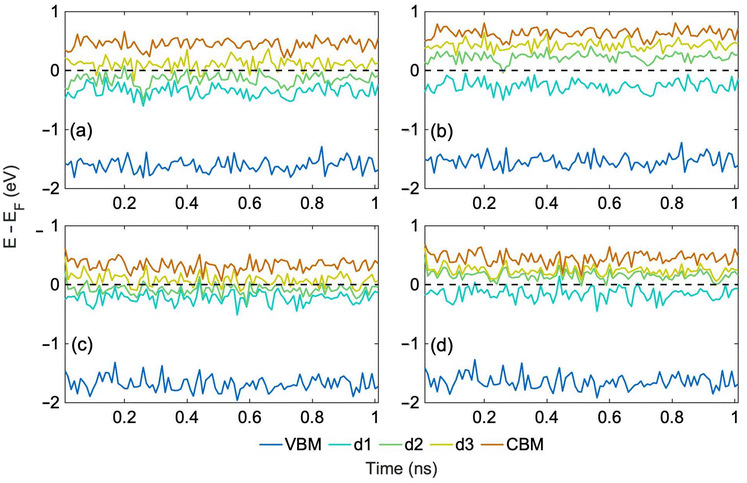Fig. 3 (a) Spin up and (b) spin down ab initio energy levels calculated every 10 ps along the 1 ns ML trajectory at 300 K starting from the most stable NH–CN structure, Fig. 1a, and (c) spin up, (d) spin down levels for the trajectory starting from the least stable N_Hα structure (Fig. 1d). The corresponding hydrogen hopping trajectories are shown in Fig. 4a and b, respectively. The Fermi energy has been subtracted from the KS state energies to set the Fermi level to 0.

Fig. 4 demonstrates the hydrogen hopping dynamics in ON-GCN. Fig. 4a and c show the results for the ML MD trajectories starting from the most stable structure at 300 K and 400 K, respectively. Conformational hopping between NH–CN and NH₃ tautomers occurs multiple times at both temperatures. Hydrogen is considered to be bonded to the particular labelled nitrogen atom when the N–H bond length is less than 1.2 Å. On the other hand, for the MD trajectories starting from the least stable structure, Fig. 4b and d, hydrogen hopping only takes place between NHα and NH–CN tautomers. In this case, the system does not reach the most stable form even after 1 ns. This implies that metastable, higher energy structures can survive for long times. Therefore, the existence of long-lived structures should be considered when interpreting experimental data, and a careful characterization of multiple structures seems mandatory. The trajectories corresponding to the higher temperature show more frequent hydrogen hops between two structures, as expected due to higher thermal energy. Trajectory snapshots during ten random hydrogen hopping events show that it takes on an average 7 fs for the hydrogen to hop from one position to the other. Fig. S3† illustrates one such instance, in which hopping from NH₃ to NH-CN structures takes 9 fs.

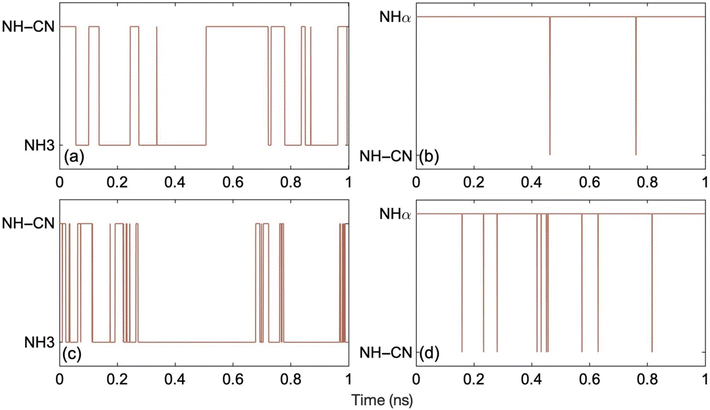Fig. 4 Hydrogen hopping dynamics over 1 ns ML trajectories generated starting from (a) the most stable structure (NH–CN) at 300 K, (b) the least stable structure (N_Hα) at 300 K, (c) the most stable structure (NH–CN) at 400 K, and (d) the least stable structure (N_Hα) at 400 K. The y-axis presents the position of the hydrogen circled in the corresponding structures (a)–(d) of Fig. 1. The frequency of hydrogen hopping increases at higher temperatures. The N–H bond length ranges from 0.98– to 1.26 Å. Hydrogen hopping occurs when the N–H bond length exceeds 1.26 Å.

Correlating the evolution of the electronic energy levels, Fig. 3, with the hydrogen hopping dynamics, Fig. 4, we can rationalize why the electronic energy levels do not undergo substantial changes as a result of the hops, even though the electronic properties of the four tautomers exhibit differences at 0 K, Fig. 2. The hopping dynamics shown in Fig. 4a corresponds to the spin up and down electronic levels in Fig. 3a and b. Despite multiple hydrogen hops seen in Fig. 4a, the electronic energy levels seen in Fig. 3a and b do not undergo any jumps, because the PDOS of NH-CN and NH₃ are similar, Fig. 2a and b. On the other hand, for the trajectory in Fig. 4b, with the evolution of the spin up and down electronic levels shown in Fig. 3c and d, we again do not observe significant changes in the electronic levels, because the hops are rare, and the system rapidly returns to the initial structure through hydrogen rearrangement. The analysis suggests that the structural changes should have little influence on the charge carrier dynamics.

Nonradiative charge recombination is the dominant undesired mechanism that limits the availability of free charge carriers, an important factor for photocatalytic activity. NAMD models excited state dynamics of photo-generated charge carriers coupled to vibrational motions, directly mimicking the non-equilibrium ultrafast processes. Fig. 5 shows the results of the NAMD simulations, in which the electron and hole are initiated in the CBM and VBM, respectively. Although the solar spectrum and other light sources used in photocatalysis and photovoltaics cover a wide energy range, charge carriers generated away from the edges of the fundamental bandgap relax rapidly to the CBM and VBM through the dense manifolds of band states,^62,63Fig. 2. The electronic configurations forming the NAMD active space are shown in Fig. S4.† The populations shown in Fig. 5 are summed up over all electron and hole traps, and the corresponding timescales obtained by exponential fitting of the rise and decay of the relevant curves are summarized in Table 2. The evolution of the populations of the individual multi-electron states are presented in Fig. S5† and respective timescales are given in Table S1.† Photo-generated electrons and holes are required for desired oxidation and reduction reactions. Localized midgap states facilitate charge separation, promote photo-catalytic activity and extend light absorption into longer wavelengths. At the same time, midgap traps act as recombination centers and reduce carrier lifetimes.^64–68

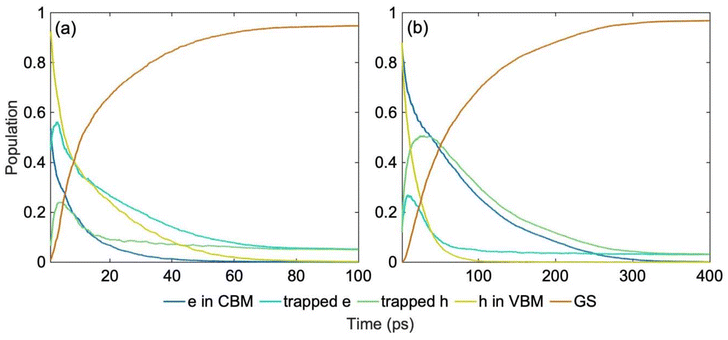Fig. 5 Nonradiative charge trapping and recombination dynamics in (a) spin up (b) spin down channels at 300 K starting from the most stable ON-GCN tautomer (NH–CN), Fig. 1a. The energy level fluctuations and hydrogen hopping trajectory are shown in Fig. 3a, b and 4a, respectively. More detailed information is provided in Fig. S4,† and the timescales are reported in Table 2. Electron and hole separation and trapping occur within picoseconds, and charge recombination takes place within tens to hundreds of picoseconds.

Table 2 Electron and hole trapping and recombination timescales (in ps) obtained from the rise and decay of the populations shown in Fig. 5. State-resolved data are shown in Fig. S4, S5 and Table S1.† Charge separation and trapping takes picoseconds, while charge recombination occurs within tens of picoseconds

ON-GCN	Electron in CBM Decay	Trapped electron rise	Trapped hole rise	Hole in VBM decay
Spin up	7.8	4.03	1.57	15.58
Spin down	15.03	20.12	8.82	76.28

---

The NAMD simulations demonstrate that the separation of the charge carriers, facilitated by trapping of electrons and holes, occurs within a few picoseconds. The two spin channels exhibit different dynamics, because of the differences in the spin up and down electronic structure, Fig. 2. This suggests that spin selection techniques can be used to control charge separation and recombination.^69–71 The populations of the electron and hole trap states reach over 50% in approximately 10 ps. This timescale should be sufficient to perform an elementary photochemical reaction, such as bond breaking, provided the chemical species is already present at the charge trapping site. For comparison, a period of oscillation of typical chemical bonds, such as C–C or C=O is about 50 fs. Thus, the photo-generated charge exists in a catalytic site for around a hundred bond oscillation periods. The NAMD results obtained here by sampling the system atomic dynamics over 1 ns are consistent with and slightly longer than those obtained previously⁷² for the most stable isomer using a short ab initio MD trajectory.⁷³

4. Conclusion

To summarize, we have reported a multistep simulation methodology combining time-domain DFT, NAMD and ML and have applied it to capture rare structural and electronic events in dual defect modified graphitic carbon nitride that is actively investigated for photocatalytic applications. We observe tautomerism between four different structures induced by hydrogen hopping that occurs on the timescales of tens to hundreds of picoseconds, comparable to charge carrier trapping and recombination times. The charge carrier dynamics is found to be robust to the tautomerism because the electronic properties of the dominant tautomers are similar, and the most different tautomer is accessed rarely. Our simulations indicate that photo-generated charges are separated on a picosecond timescale and the catalytically active states remain populated for 10 ps. This is sufficient to perform elementary photochemical reactions, such as bond breaking, since bond oscillations are two orders of magnitude faster. The ML-NAMD methodology reported here allows one to sample infrequent processes that influence excited state dynamics in modern materials and to perform quantum dynamics simulations over times comparable to the timescales of structural rearrangements and photocatalytic reactions. Proper sampling of structural dynamics on the same timescale as the electronic evolution, assisted by ML techniques, can uncover important rare events^74–77 that influence or even control material's photocatalytic activity and other properties. The reported simulation generates a detailed atomistic picture of excited state dynamics in the dual defect modified GCN and rationalizes how GCN remains active in the presence of multiple isomeric and tautomeric forms.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by funding from the USA National Science Foundation, grant CHE-2154367. D. C. thanks the Spanish Ministry of Science and Innovation, projects MICIN/FEDER PID2022-136231NB-I00 and RED2022-134939-T.

References

1. Z. Zhao, Y. Sun and F. Dong, Graphitic Carbon Nitride Based Nanocomposites: A Review, Nanoscale, 2015, 7, 15–37.
2. X. Niu, Y. Yi, X. Bai, J. Zhang, Z. Zhou, L. Chu, J. Yang and X. Li, Photocatalytic Performance of Few-Layer Graphitic C₃N₄: Enhanced by Interlayer Coupling, Nanoscale, 2019, 11, 4101–4107.
3. N. Rono, J. K. Kibet, B. S. Martincigh and V. O. Nyamori, A Review of the Current Status of Graphitic Carbon Nitride, Crit. Rev. Solid State Mater. Sci., 2020, 1–29.
4. Q. Li and J. L. Wang, Facing the Key Challenges of Two-Dimensional Electronics, Matter, 2023, 6, 2496–2498.
5. X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, A Metal-Free Polymeric Photocatalyst for Hydrogen Production from Water under Visible light, Nat. Mater., 2009, 8, 76–80.
6. J. Tian, Q. Liu, C. Ge, Z. Xing, A. M. Asiri, A. O. Al-Youbi and X. Sun, Ultrathin Graphitic Carbon Nitride Nanosheets: A Low-Cost, Green, and Highly Efficient Electrocatalyst toward the Reduction of Hydrogen Peroxide and Its Glucose Biosensing Application, Nanoscale, 2013, 5, 8921–8924.
7. J. Qin, J. Huo, P. Zhang, J. Zeng, T. Wang and H. Zeng, Improving the Photocatalytic Hydrogen Production of Ag/g-C₃N₄ Nanocomposites by Dye-Sensitization under Visible Light Irradiation, Nanoscale, 2016, 8, 2249–2259.
8. A. Wang, C. Wang, L. Fu, W. Wong-Ng and Y. Lan, Recent Advances of Graphitic Carbon Nitride-Based Structures and Applications in Catalyst, Sensing, Imaging, and Leds, Nano-Micro Lett., 2017, 9, 47.
9. S. Sun and S. Liang, Recent Advances in Functional Mesoporous Graphitic Carbon Nitride (mpg-C₃N₄) Polymers, Nanoscale, 2017, 9, 10544–10578.
10. J. Safaei, N. A. Mohamed, M. F. Mohamad Noh, M. F. Soh, N. A. Ludin, M. A. Ibrahim, W. N. Roslam Wan Isahak and M. A. Mat Teridi, Graphitic Carbon Nitride (g-C₃N₄) Electrodes for Energy Conversion and Storage: A Review on Photoelectrochemical Water Splitting, Solar Cells and Supercapacitors, J. Mater. Chem. A, 2018, 6, 22346–22380.
11. S.-F. Ng, J. J. Foo and W.-J. Ong, Solar-Powered Chemistry: Engineering Low-Dimensional Carbon Nitride-Based Nanostructures for Selective CO₂ Conversion to C₁–C₂ Products, InfoMat, 2022, 4, e12279.
12. S. Cao, J. Low, J. Yu and M. Jaroniec, Polymeric Photocatalysts Based on Graphitic Carbon Nitride, Adv. Mater., 2015, 27, 2150–2176.
13. S. Yin, J. Han, T. Zhou and R. Xu, Recent Progress in g-C₃N₄ Based Low Cost Photocatalytic System: Activity Enhancement and Emerging Applications, Catal. Sci. Technol., 2015, 5, 5048–5061.
14. L. Zhou, H. Zhang, H. Sun, S. Liu, M. O. Tade, S. Wang and W. Jin, Recent Advances in Non-Metal Modification of Graphitic Carbon Nitride for Photocatalysis: A Historic Review, Catal. Sci. Technol., 2016, 6, 7002–7023.
15. Z. Mo, H. Xu, Z. Chen, X. She, Y. Song, J. Wu, P. Yan, L. Xu, Y. Lei, S. Yuan and H. Li, Self-Assembled Synthesis of Defect-Engineered Graphitic Carbon Nitride Nanotubes for Efficient Conversion of Solar Energy, Appl. Catal., B, 2018, 225, 154–161.
16. M. Makaremi, S. Grixti, K. T. Butler, G. A. Ozin and C. V. Singh, Band Engineering of Carbon Nitride Monolayers by N-Type, P-Type, and Isoelectronic Doping for Photocatalytic Applications, ACS Appl. Mater. Interfaces, 2018, 10, 11143–11151.
17. W. Tu, Y. Xu, J. Wang, B. Zhang, T. Zhou, S. Yin, S. Wu, C. Li, Y. Huang, Y. Zhou, Z. Zou, J. Robertson, M. Kraft and R. Xu, Investigating the Role of Tunable Nitrogen Vacancies in Graphitic Carbon Nitride Nanosheets for Efficient Visible-Light-Driven H₂ Evolution and CO₂ Reduction, ACS Sustainable Chem. Eng., 2017, 5, 7260–7268.
18. J.-Y. Tang, X. Y. Kong, B.-J. Ng, Y.-H. Chew, A. R. Mohamed and S.-P. Chai, Midgap-State-Mediated Two-Step Photoexcitation in Nitrogen Defect-Modified g-C₃N₄ Atomic Layers for Superior Photocatalytic CO₂ Reduction, Catal. Sci. Technol., 2019, 9, 2335–2343.
19. F. Wei, Y. Liu, H. Zhao, X. Ren, J. Liu, T. Hasan, L. Chen, Y. Li and B.-L. Su, Oxygen Self-Doped g-C₃N₄ with Tunable Electronic Band Structure for Unprecedentedly Enhanced Photocatalytic Performance, Nanoscale, 2018, 10, 4515–4522.
20. D. A. Tran, C. T. Nguyen Pham, T. Nguyen Ngoc, H. Nguyen Phi, Q. T. Hoai Ta, D. H. Truong, V. T. Nguyen, H. H. Luc, L. T. Nguyen, N. N. Dao, S. J. Kim and V. Vo, One-Step Synthesis of Oxygen Doped g-C₃N₄ for Enhanced Visible-Light Photodegradation of Rhodamine B, J. Phys. Chem. Solids, 2021, 151, 109900.
21. J. Li, B. Shen, Z. Hong, B. Lin, B. Gao and Y. Chen, A Facile Approach to Synthesize Novel Oxygen-Doped g-C₃N₄ with Superior Visible-Light Photoreactivity, Chem. Commun., 2012, 48, 12017–12019.
22. H. Katsumata, F. Higashi, Y. Kobayashi, I. Tateishi, M. Furukawa and S. Kaneco, Dual-Defect-Modified Graphitic Carbon Nitride with Boosted Photocatalytic Activity under Visible Light, Sci. Rep., 2019, 9, 14873.
23. P. Babu, S. Mohanty, B. Naik and K. Parida, Synergistic Effects of Boron and Sulfur Co-Doping into Graphitic Carbon Nitride Framework for Enhanced Photocatalytic Activity in Visible Light Driven Hydrogen Generation, ACS Appl. Energy Mater., 2018, 1, 5936–5947.
24. X. Zhang, P. Ma, C. Wang, L. Gan, X. Chen, P. Zhang, Y. Wang, H. Li, L. Wang, X. Zhou and K. Zheng, Unraveling the Dual Defect Sites in Graphite Carbon Nitride for Ultra-High Photocatalytic H₂O₂ Evolution, Energy Environ. Sci., 2022, 15, 830–842.
25. A. Thomas, A. Fischer, F. Goettmann, M. Antonietti, J. O. Müller, R. Schlögl and J. M. Carlsson, Graphitic Carbon Nitride Materials: Variation of Structure and Morphology and Their Use as Metal-Free Catalysts, J. Mater. Chem., 2008, 18, 4893–4908.
26. W. J. Ong, L. L. Tan, Y. H. Ng, S. T. Yong and S. P. Chai, Graphitic Carbon Nitride (g-C₃N₄)-Based Photocatalysts for Artificial Photosynthesis and Environmental Remediation: Are We a Step Closer to Achieving Sustainability?, Chem. Rev., 2016, 116, 7159–7329.
27. H. Wang, X. D. Zhang, J. F. Xie, J. J. Zhang, P. A. Ma, B. C. Pan and Y. Xie, Structural Distortion in Graphitic-C₃N₄ Realizing an Efficient Photoreactivity, Nanoscale, 2015, 7, 5152–5156.
28. R. Sarkar, M. Habib, S. Pal and O. V. Prezhdo, Ultrafast, Asymmetric Charge Transfer and Slow Charge Recombination in Porphyrin/Cnt Composites Demonstrated by Time-Domain Atomistic Simulation, Nanoscale, 2018, 10, 12683–12694.
29. P. Zereshki, Y. Q. Wei, F. Ceballos, M. Z. Bellus, S. D. Lane, S. Pan, R. Long and H. Zhao, Photocarrier Dynamics in Monolayer Phosphorene and Bulk Black Phosphorus, Nanoscale, 2018, 10, 11307–11313.
30. X. Niu, G. Wu, X. Zhang and J. Wang, Interlayer Coupling Prolonged the Photogenerated Carrier Lifetime of Few Layered Bi₂OS₂ Semiconductors, Nanoscale, 2020, 12, 6057–6063.
31. W. Li, Y. L. She, A. S. Vasenko and O. V. Prezhdo, Ab Initio Nonadiabatic Molecular Dynamics of Charge Carriers in Metal Halide Perovskites, Nanoscale, 2021, 13, 10239–10265.
32. X. Zhao, H. Lu, W.-H. Fang and R. Long, Correlated Organic-Inorganic Motion Enhances Stability and Charge Carrier Lifetime in Mixed Halide Perovskites, Nanoscale, 2022, 14, 4644–4653.
33. Z. Song, X. Wang, F. Liu, Q. Zhou, W.-J. Yin, H. Wu, W. Deng and J. Wang, Distilling Universal Activity Descriptors for Perovskite Catalysts from Multiple Data Sources Via Multi-Task Symbolic Regression, Mater. Horiz., 2023, 10, 1651–1660.
34. X. Chen, S. Lu, X. Wan, Q. Chen, Q. Zhou and J. Wang, Accurate Property Prediction with Interpretable Machine Learning Model for Small Datasets Via Transformed Atom Vector, Phys. Rev. Mater., 2022, 6, 123803.
35. Y. Zhou, Y. Ouyang, Y. Zhang, Q. Li and J. Wang, Machine Learning Assisted Simulations of Electrochemical Interfaces: Recent Progress and Challenges, J. Phys. Chem. Lett., 2023, 14, 2308–2316.
36. P. O. Dral, Quantum Chemistry in the Age of Machine Learning, J. Phys. Chem. Lett., 2020, 11, 2336–2347.
37. K. Hansen, F. Biegler, R. Ramakrishnan, W. Pronobis, O. A. von Lilienfeld, K. R. Müller and A. Tkatchenko, Machine Learning Predictions of Molecular Properties: Accurate Many-Body Potentials and Nonlocality in Chemical Space, J. Phys. Chem. Lett., 2015, 6, 2326–2331.
38. T. Wen, L. Zhang, H. Wang, W. E and D. J. Srolovitz, Deep Potentials for Materials Science, Mater. Futures, 2022, 1, 022601.
39. J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Mueller and A. Tkatchenko, Combining Machine Learning and Computational Chemistry for Predictive Insights into Chemical Systems, Chem. Rev., 2021, 121, 9816–9872.
40. B. Wang, W. Chu, A. Tkatchenko and O. V. Prezhdo, Interpolating Nonadiabatic Molecular Dynamics Hamiltonian with Artificial Neural Networks, J. Phys. Chem. Lett., 2021, 12, 6070–6077.
41. Y. Wu, N. Prezhdo and W. Chu, Increasing Efficiency of Nonadiabatic Molecular Dynamics by Hamiltonian Interpolation with Kernel Ridge Regression, J. Phys. Chem. A, 2021, 125, 9191–9200.
42. B. Wang, W. Chu and O. V. Prezhdo, Interpolating Nonadiabatic Molecular Dynamics Hamiltonian with Inverse Fast Fourier Transform, J. Phys. Chem. Lett., 2022, 13, 331–338.
43. B. Wang, L. Winkler, Y. Wu, K.-R. Muller, H. E. Sauceda and O. V. Prezhdo, Interpolating Nonadiabatic Molecular Dynamics Hamiltonian with Bidirectional Long Short-Term Memory Networks, J. Phys. Chem. Lett., 2023, 14, 7092–7099.
44. G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal–Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
45. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
47. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
48. J. Klimeš, D. R. Bowler and A. Michaelides, van der Waals Density Functionals Applied to Solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
49. K. Momma and F. Izumi, Vesta 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data, J. Appl. Crystallogr., 2011, 44, 1272–1276.
50. L. Zhang, J. Han, H. Wang, W. A. Saidi, R. Car and W. E, End-to-End Symmetry Preserving Inter-Atomic Potential Energy Model for Finite and Extended Systems, Advances in Neural Information Processing Systems, 2018, 2018, 4436–4446.
51. H. Wang, L. Zhang, J. Han and W. E, Deepmd-Kit: A Deep Learning Package for Many-Body Potential Energy Representation and Molecular Dynamics, Comput. Phys. Commun., 2018, 228, 178–184.
52. D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, arXiv, 2014, preprint, arXiv:1412.6980,  DOI:10.48550/arXiv.1412.6980.
53. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. I. Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Lammps-a Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales, Comput. Phys. Commun., 2022, 271, 108171.
54. Q. Gao, X. Zhuang, S. Hu and Z. Hu, Corrugation Matters: Structure Models of Single Layer Heptazine-Based Graphitic Carbon Nitride from First-Principles Studies, J. Phys. Chem. C, 2020, 124, 4644–4651.
55. W. Chu and O. V. Prezhdo, Concentric Approximation for Fast and Accurate Numerical Evaluation of Nonadiabatic Coupling with Projector Augmented-Wave Pseudopotentials, J. Phys. Chem. Lett., 2021, 12, 3082–3089.
56. W. Chu, Q. Zheng, A. V. Akimov, J. Zhao, W. A. Saidi and O. V. Prezhdo, Accurate Computation of Nonadiabatic Coupling with Projector Augmented-Wave Pseudopotentials, J. Phys. Chem. Lett., 2020, 11, 10073–10080.
57. H. M. Jaeger, S. Fischer and O. V. Prezhdo, Decoherence-Induced Surface Hopping, J. Chem. Phys., 2012, 137, 22A545.
58. A. V. Akimov and O. V. Prezhdo, The Pyxaid Program for Non-Adiabatic Molecular Dynamics in Condensed Matter Systems, J. Chem. Theory Comput., 2013, 9, 4959–4972.
59. A. V. Akimov and O. V. Prezhdo, Advanced Capabilities of the Pyxaid Program: Integration Schemes, Decoherence Effects, Multiexcitonic States, and Field-Matter Interaction, J. Chem. Theory Comput., 2014, 10, 789–804.
60. S. Agrawal, W. Lin, O. V. Prezhdo and D. J. Trivedi, Ab Initio Quantum Dynamics of Charge Carriers in Graphitic Carbon Nitride Nanosheets, J. Chem. Phys., 2020, 153, 054701.
61. S. Agrawal, A. S. Vasenko, D. J. Trivedi and O. V. Prezhdo, Charge Carrier Nonadiabatic Dynamics in Non-Metal Doped Graphitic Carbon Nitride, J. Chem. Phys., 2022, 156, 094702.
62. C. Xu, G. Q. Zhou, E. M. Alexeev, A. R. Cadore, I. Paradisanos, A. K. Ott, G. Soavi, S. Tongay, G. Cerullo, A. C. Ferrari, O. V. Prezhdo and Z. H. Loh, Ultrafast Electronic Relaxation Dynamics of Atomically Thin Mos₂ Is Accelerated by Wrinkling, ACS Nano, 2023, 17, 16682–16694.
63. T. Wang, L. Jin, J. Hidalgo, W. Chu, J. M. Snaider, S. Deng, T. Zhu, B. Lai, O. Prezhdo, J. P. Correa-Baena and L. Huang, Protecting Hot Carriers by Tuning Hybrid Perovskite Structures with Alkali Cations, Sci. Adv., 2020, 6, eabb1336.
64. D. Liu, C. M. Perez, A. S. Vasenko and O. V. Prezhdo, Ag-Bi Charge Redistribution Creates Deep Traps in Defective Cs₂AgBiBr₆: Machine Learning Analysis of Density Functional Theory, J. Phys. Chem. Lett., 2022, 13, 3645–3651.
65. J. Ran, B. Wang, Y. Wu, D. Liu, C. M. Perez, A. S. Vasenko and O. V. Prezhdo, Halide Vacancies Create No Charge Traps on Lead Halide Perovskite Surfaces but Can Generate Deep Traps in the Bulk, J. Phys. Chem. Lett., 2023, 14, 6028–6036.
66. L. Li, R. Long and O. V. Prezhdo, Why Chemical Vapor Deposition Grown MoS₂ Samples Outperform Physical Vapor Deposition Samples: Time-Domain Ab Initio Analysis, Nano Lett., 2018, 18, 4008–4014.
67. L. Qiao, W. H. Fang, R. Long and O. V. Prezhdo, Extending Carrier Lifetimes in Lead Halide Perovskites with Alkali Metals by Passivating and Eliminating Halide Interstitial Defects, Angew. Chem., Int. Ed., 2020, 59, 4684–4690.
68. C. J. Tong, L. Li, L.-M. Liu and O. V. Prezhdo, Synergy between Ion Migration and Charge Carrier Recombination in Metal-Halide Perovskites, J. Am. Chem. Soc., 2020, 142, 3060–3068.
69. C. Cheng, W. H. Fang, R. Long and O. V. Prezhdo, Water Splitting with a Single-Atom Cu/TiO₂ Photocatalyst: Atomistic Origin of High Efficiency and Proposed Enhancement by Spin Selection, JACS Au, 2021, 1, 550–559.
70. M. Ai, L. Pan, C. Shi, Z.-F. Huang, X. Zhang, W. Mi and J.-J. Zou, Spin Selection in Atomic-Level Chiral Metal Oxide for Photocatalysis, Nat. Commun., 2023, 14, 4562.
71. K. Saini, A. N. Nair, A. Yadav, L. G. Enriquez, C. J. Pollock, S. D. House, S. Yang, X. Guo and S. T. Sreenivasan, Nickel-Based Single-Molecule Catalysts with Synergistic Geometric Transition and Magnetic Field-Assisted Spin Selection Outperform RuO₂ for Oxygen Evolution, Adv. Energy Mater., 2023, 13, 2302170.
72. S. Gumber, S. Agrawal and O. V. Prezhdo, Excited State Dynamics in Dual-Defects Modified Graphitic Carbon Nitride, J. Phys. Chem. Lett., 2022, 13, 1033–1041.
73. B. Wang, Y. Wu, D. Liu, A. S. Vasenko, D. Casanova and O. V. Prezhdo, Efficient Modeling of Quantum Dynamics of Charge Carriers in Materials Using Short Nonequilibrium Molecular Dynamics, J. Phys. Chem. Lett., 2023, 14, 8289–8295.
74. W. Chu, W. A. Saidi and O. V. Prezhdo, Long-Lived Hot Electron in a Metallic Particle for Plasmonics and Catalysis: Ab Initio Nonadiabatic Molecular Dynamics with Machine Learning, ACS Nano, 2020, 14, 10608–10615.
75. B. Wang, W. Chu, Y. Wu, D. Casanova, W. A. Saidi and O. V. Prezhdo, Electron-Volt Fluctuation of Defect Levels in Metal Halide Perovskites on a 100 ps Time Scale, J. Phys. Chem. Lett., 2022, 13, 5946–5952.
76. Y. Wu, D. Liu, W. Chu, B. Wang, A. S. Vasenko and O. V. Prezhdo, Fluctuations at Metal Halide Perovskite Grain Boundaries Create Transient Trap States: Machine Learning Assisted Ab Initio Analysis, ACS Appl. Mater. Interfaces, 2022, 14, 55753–55761.
77. D. Liu, Y. Wu, A. S. Vasenko and O. V. Prezhdo, Grain Boundary Sliding and Distortion on a Nanosecond Timescale Induce Trap States in CsPbBr₃: Ab Initio Investigation with Machine Learning Force Field, Nanoscale, 2022, 15, 285–293.

---

Footnote

† Electronic supplementary information (ESI) available: Charge densities of key orbitals, comparison of machine learning and ab initio energies, trajectory snapshots for hydrogen hopping dynamics, a schematic of electronic configurations in the active space, detailed analysis of nonradiative relaxation dynamics and the corresponding timescales, and coordinates of the optimized structures. See DOI: https://doi.org/10.1039/d4nr00606b

---