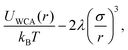Open Access Article
Open Access ArticleStructure and dynamics in suspensions of magnetic platelets†
Margaret
Rosenberg
 *ab,
Sofia S.
Kantorovich
*ab,
Sofia S.
Kantorovich
 ab,
Alexey O.
Ivanov
ab,
Alexey O.
Ivanov
 c and
Philip J.
Camp
c and
Philip J.
Camp
 d
d
aFaculty of Physics, University of Vienna, Kolingasse 14-16, Vienna 1090, Austria. E-mail: margaret.rosenberg@univie.ac.at
bResearch Platform MMM, University of Vienna, Oskar-Morgenstern-Platz 1, Vienna, Austria
cUral Federal University, Lenin Avenue 51, Ekaterinburg, 620000, Russia
dSchool of Chemistry, University of Edinburgh, David Brewster Road, Edinburgh EH9 3FJ, Scotland, UK
First published on 1st May 2024
Abstract
In this research, we employ Brownian dynamics simulations, density functional theory, and mean-field theory to explore the profound influence of shape anisotropy of magnetic nanoplatelets on suspension magnetic response. Each platelet is modelled as an oblate cylinder with a longitudinal point dipole, with an emphasis on strong dipolar interactions conducive to self-assembly. We investigate static structural and magnetic properties, characterising the system through pair distribution function, static structure factor, and cluster-size distribution. The findings demonstrate that shape-specific interactions and clustering lead to significant changes in reorientational relaxation times. Under zero field, distinctive modes in the dynamic magnetic susceptibility identify individual particles and particle clusters. In the presence of an applied field, the characteristic relaxation time of clusters increases, while that of single particles decreases. This research provides insights into the intricate interplay between shape anisotropy, clustering, and magnetic response in platelet suspensions, offering valuable perspectives for recent experimental observations.
1 Introduction
Colloidal suspensions with well-defined, strong responses to external magnetic fields are of interest for both biomedical applications, such as drug delivery or magnetic hyperthermia,1–4 and for industrial applications such as seals, dampers and microfluidic magnetic pumping.5,6 The degree of control with magnetic fields, and magnetic-field gradients, means that such suspensions really are functional materials. Ferrofluids are important examples of such materials, and they have been studied extensively over the last half-century.7–9 They consist of magnetic particles suspended in a non-magnetic, carrier liquid. Conventionally, the particles are quasi-spherical, single-domain, and homogeneously magnetised, which means that the interactions between the particles are approximately equal to those between point dipoles.10 One approach to tailoring the desired properties and responses of the magnetic colloidal suspension for desired applications is to use colloidal particles with an anisotropic shape and/or magnetised core.11 Examples include magnetic nanoplatelets, where the magnetisation is aligned perpendicular to the plane of the platelet. The shape of the platelet confers steric anisotropy, and in the simplest case, there is a single point dipole at the center. Significantly, such particles have been shown in experiments to exhibit a macroscopic ferromagnetic phase.12In order to assess the usefulness of such colloids for applications, all of the magnetic properties need to be characterised. Such work has begun using simulations,13,14 in which the static magnetic properties, such as the magnetisation curve and the static susceptibility, have been determined, and correlated with the microscopic structure. Recent experimental findings suggest pronounced shape-induced differences in the dynamic magnetic susceptibility, χ(ω), of magnetic platelet suspensions15 as compared to that of spherical particles.16,17 The function χ(ω) defines the response of the magnetisation to an AC magnetic field, and there are in-phase and out-of-phase components to the response. The power dissipation, and hence heating rate, is proportional to the out-of-phase component, χ′′(ω).18 This property, in particular, is important for magnetic hyperthermia applications. In the experiments by Küster et al.,15 the out-of-phase component χ′′(ω) for magnetic platelet dispersions in the isotropic phase was shown to exhibit three modes at low concentrations, with the lowest and highest frequency peaks separated by three orders of magnitude. The authors attribute the low-frequency modes to collective relaxation, and point out that some of the longer relaxation times could be attributed to the effects of polydispersity. In a subsequent study,19 it was shown that varying the surfactant concentration and/or the magnetic nanoparticle concentration can shift or suppress the low- and medium-frequency modes, reinforcing the idea of a link between these modes and platelet aggregation.
In the case of ferrofluids with spherical colloidal nanoparticles, the dynamic magnetic susceptibility can be described theoretically using the well-established modified mean-field theory for weakly interacting particles. In simulations, it can be computed most conveniently using the equilibrium, zero-field magnetisation time-correlation function, which is linked to χ(ω) via linear-response theory.17,20,21 With weak to moderate interactions, χ(ω) is characterised by a single timescale corresponding to the Brownian rotation time of the particles, and χ′′(ω) shows a peak at the corresponding frequency. Generally speaking, interactions increase this rotation time, and decrease the peak frequency, due to correlated motions of the particles. In ferrofluids with strong magnetic intraparticle interactions, the changes in microstructure induced by the self-assembly of the particles have been shown to affect the dynamic susceptibility very strongly, and in particular, new features appear in χ(ω) corresponding to whole-cluster dynamics, and intracluster single-particle motions.17 The inclusion of a static uniform magnetic field, as in the experimental setup in ref. 15, can also shift the peak of the dynamic susceptibility to higher frequencies, because it provides an extra restoring force (torque) on the orientations of the particles, and hence accelerates the rate of relaxation.22
A more complex behaviour can be observed if the particles are not ferromagnetic but have finite magnetic anisotropy. In this case, the dynamics also depends on the internal properties of the magnetic nanoparticles.23–26 For the platelets addressed in our work, however, the internal magnetic anisotropy is so high, that they can safely be considered ferromagnetic.
The aim of this work is to explore the microscopic origins of the observations made in the experiments by Küster et al.15 In particular, computer simulations are used to assess the effects of the platelet shape on the structural properties, static magnetic properties, and the dynamic magnetic susceptibility, and hence provide a microscopic explanation for the unusually broad features in the dynamic susceptibility measured in recent experiments. Based on experimental observations, the magnetic moments on the platelets are chosen so that there is a coexistence of both single particles and self-assembled clusters, which means that there will be several distinct features present in χ(ω). The microstructure is then tuned by varying the concentration, which is analogous to the experimental procedure of varying the surfactant concentration, and the changes in χ(ω) are determined. This experimental procedure of surfactant tuning is based on the electrostatic stabilisation of the colloids. Due to screening, these are predominantly short-range effects, and therefore can be considered as part of the effective shape of the particles in coarse-grained simulation models. This is of course a simplification, which may lead to discrepancies between experimental and simulation outcomes. However, the objective of this study is to find the underlying mechanism of the aforementioned experimental observations, which should not be affected.
The rest of this article is organised as follows. The simulation model and methods are summarised in Section 2. The results are presented in Section 3, beginning with a characterisation of the static magnetic properties and microstructure with and without external fields (Section 3.1), moving on to the dynamic magnetic susceptibility in zero field (Section 3.2), and finishing with a brief study of the effects of an external field on the dynamics (Section 3.3). The conclusions, and a discussion of the relevance of the results to experiments, are presented in Section 4.
2 Simulation model and methods
2.1 Model
The platelets were constructed using a raspberry model, where an anisotropic shape constructed out of a central interaction site surrounded by massless virtual interaction sites at fixed relative distances. For platelets, this has been described in detail in ref. 14. At the chosen aspect ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 8 virtual sites were equally spaced on a circle at a radial distance of σ = 1 from the ninth, central interaction site of the platelet. The central interaction site carries a fixed point dipole oriented perpendicular to the plane of the platelet. This can also been seen in the simulation snapshots in Fig. 2 and 4. The virtual interaction sites represent the steric anisotropy of the platelet,27 but the dynamical trajectory of the platelet is based on the mass and inertia tensor of the central site. The inertia tensor was set to that of a cylindrical platelet with radius R = 3σ/2 and height h = σ, and so the elements were Ix = Iy = m(3R2 + h2)/12, and Iz = mR2/2, where m is the platelet mass.
3, 8 virtual sites were equally spaced on a circle at a radial distance of σ = 1 from the ninth, central interaction site of the platelet. The central interaction site carries a fixed point dipole oriented perpendicular to the plane of the platelet. This can also been seen in the simulation snapshots in Fig. 2 and 4. The virtual interaction sites represent the steric anisotropy of the platelet,27 but the dynamical trajectory of the platelet is based on the mass and inertia tensor of the central site. The inertia tensor was set to that of a cylindrical platelet with radius R = 3σ/2 and height h = σ, and so the elements were Ix = Iy = m(3R2 + h2)/12, and Iz = mR2/2, where m is the platelet mass.
The steric interactions between all constituent sites were described by the Weeks–Chandler–Andersen (WCA) potential,28
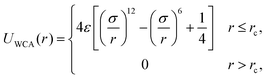 | (1) |
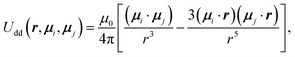 | (2) |
| UH(μi) = −μ0(μi·H). | (3) |
2.2 Brownian dynamics simulations
Brownian dynamics (BD) simulations were performed using the simulation package ESPResSo, versions 4.1.4 and 4.2.0.27 BD was achieved with overdamped Langevin dynamics simulations in the NVT ensemble, with N platelets in a simulation box of volume V at temperature T. The Langevin equations of motion are given by (4):| mẍ(t) = F(t) − γẋ(t) + XT(t) | (4) |
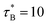 in Lennard-Jones units. The strength of the dipolar interactions is usually characterised by the dipolar coupling constant,
in Lennard-Jones units. The strength of the dipolar interactions is usually characterised by the dipolar coupling constant,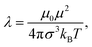 | (5) |
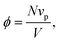 | (6) |
Unless otherwise specified, the static properties presented in Section 3.1 were calculated using the same methodology as described in ref. 14. This is mostly relevant for the clustering, where an adjusted distance cutoff was used to account for the anisotropy of the platelets.
The static (initial) susceptibility of an isotropic system is given by
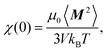 | (7) |
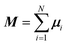 is the instantaneous magnetisation. The dynamic susceptibility was calculated as in ref. 20 by taking the Fourier transform of the magnetisation autocorrelation function C(t), which is defined by
is the instantaneous magnetisation. The dynamic susceptibility was calculated as in ref. 20 by taking the Fourier transform of the magnetisation autocorrelation function C(t), which is defined by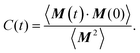 | (8) |
The dynamic susceptibility is given by
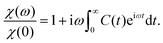 | (9) |
In the case of a static external magnetic field, 〈M〉 ≠ 0, and M(t) is replaced by δM(t) = M(t) − 〈M〉. The autocorrelation function and dynamic susceptibility are then resolved into components parallel and perpendicular to the applied field.22 This situation is discussed further in Section 3.3.
When there was not much structuring in the system, such as at low concentration, C(t) and χ(ω) were characterised by a single, rather short time scale, and it was found that direct numerical transforms of C(t) (using SciPy31) were adequate. Numerical transforms were found to be inadequate as the concentration ϕ, and degree of self-assembly, increased, and in these cases, C(t) was fitted with a sum of exponentials,
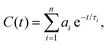 | (10) |
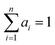 , and n ≤ 4. The value of n was chosen to be as low as possible while maintaining accuracy and realistic fitting errors. Given this representation of C(t), the dynamic magnetic susceptibility χ(ω) = χ′(ω) + iχ′′(ω) is simply a sum of Debye susceptibilities:
, and n ≤ 4. The value of n was chosen to be as low as possible while maintaining accuracy and realistic fitting errors. Given this representation of C(t), the dynamic magnetic susceptibility χ(ω) = χ′(ω) + iχ′′(ω) is simply a sum of Debye susceptibilities: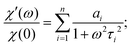 | (11a) |
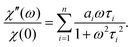 | (11b) |
3 Results and discussion
3.1 Static properties
The centre-to-centre radial distribution functions30g(r) of magnetic nanoplatelet suspensions at various concentrations ϕ are shown in Fig. 1(a). Even at the lowest concentration studied, ϕ = 0.050, some self-assembly is shown by the pronounced nearest-neighbour peak. While the zero of the WCA interaction is located at r ≃ 1.12σ, the lowest-energy separation with head-to-tail dipolar interactions minimisesand with λ = 7, this is r ≃ 0.96σ. The height of the primary peak increases with increasing concentration, with an emerging second peak indicating the formation of columns. The distance at which the radial distribution function levels out is initially r ≃ 3σ at ϕ = 0.050, which is approximately equal to one platelet diameter. As the concentration is increased, g(r) begins to show features beyond this point, which hints at an eventual third peak. All of these processes are monotonic with increasing volume fraction. This is consistent with previous simulation results on platelets,14 and confirms that there is a coexistence of single particles and clusters for the chosen parameter range.
The corresponding static structure factors30S(q) are also shown in Fig. 1(b). The values of S(q) at low q indicate that with increased concentration, the isothermal compressibility (due to magnetic and steric interactions) decreases, as expected. Otherwise, it indicates growing structural inhomogeneity arising from cluster formation. The primary peak at qσ ≃ 2 indicates structuring on the length scale of r ≃ 2π/q = 3σ, which is basically the range over which g(r) deviates significantly from 1. This corresponds to a ‘pre-peak’, indicating intermediate-range order over that length scale. The next peak at qσ ≃ 6 corresponds to the nearest-neighbour separation around r ≃ σ. Note that the second and third peaks show a pronounced asymmetry, which is characteristic of chain-like correlations between dipoles,32,33 or in this case, columnar correlations between platelets. The shape of the platelets also affects the local minima in S(q), as these are flatter and broader than those for highly clustered dipolar-sphere fluids, and this arises because the distance of closest approach depends on the mutual orientations of the platelets.
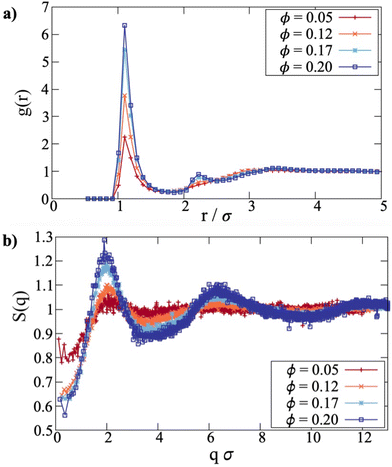
Details on the clustering of the platelets are presented in Fig. 2(a). The cluster-size distribution is shown as the fraction p(n) of particles in clusters of size n. As ϕ is increased from 0.010 to 0.200, the fraction of unclustered particles, p(1), decreases from 0.967 to 0.354, or alternatively, the fraction of particles in clusters, 1 − p(1), increases from 0.033 to 0.646. Interestingly, in the concentration range ϕ ≥ 0.050, the dimer fraction (shown in red) stays within the range 0.17 ≤ p(2) ≤ 0.20, but reaches a maximum at ϕ = 0.130. In fact, similar behaviour is seen for other small-cluster fractions, like trimers and tetramers. Essentially, as the concentration is increased, the fraction of monomers decreases, the fractions of particles in medium-sized clusters remain roughly constant, and the fractions of particles in large clusters increase. It should be noted, though, that the clustering is predominantly based on a distance criterion,‡ and hence the distinction between clusters becomes blurred at high concentrations, but p(n) gives some idea of how the particles are associated.
Simulation snapshots in Fig. 2(b and c) give a direct impression of the aggregation state. The platelets are coloured depending on whether they are monomers, in dimers, in trimers, etc., using the same scheme as p(n). At ϕ = 0.070, most of the platelets are monomers. The average separation between neighbouring particles is 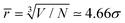 , which is larger than the platelet diameter, and the particles are not oriented in suitable ways to form clusters. At ϕ = 0.195,
, which is larger than the platelet diameter, and the particles are not oriented in suitable ways to form clusters. At ϕ = 0.195, ![[r with combining overline]](https://www.rsc.org/images/entities/i_char_0072_0305.gif) ≃ 3.31σ, the majority of the platelets are aggregated to form mostly ferromagnetically aligned, defect-free columns, although a few clusters also feature defects. This can be seen by comparing (for instance) the light green column in the lower right corner to the yellow structure in the lower left, where most of the platelets are aligned in a column, but an additional platelet at the lower left corner of the aggregate is attached at an angle. As discussed in detail in previous work,14 when two spheres form an energetically stable bond, their dipoles are oriented head-to-tail. This energy minimum is rather deep and wide, so that even relatively large thermal-noise induced angular fluctuations cannot break such a bond. In contrast, if two platelets come close enough to form a head-to-tail bond, even a slight rotation of one of them leads to a significant growth in the interdipolar distance and leads to bond breakage. Moreover, while for touching spheres the antiparallel orientation of dipoles can also lead to the formation of an energetic bond, for anisotropic platelets side-by-side, the distance between the dipoles turns out to be too large for the bond to form. As an outcome, not only do platelets aggregate less for the same values of dipole moment, but they also mostly exclusively form columns. Hence, the clusters are quite rigid, in that the platelets are in contact face-to-face, and with the dipoles aligned head-to-tail. This means that there are no significant intracluster fluctuations, which is important to remember when interpreting the dynamic magnetic susceptibility in Sections 3.2 and 3.3. It should also be noted that while ϕ = 0.200 is around the largest feasible concentration where there are distinct columns, simulations of monodisperse steric platelets do not exhibit a nematic phase at this aspect ratio,34 and no signs of nematic ordering were observed in the present case.
≃ 3.31σ, the majority of the platelets are aggregated to form mostly ferromagnetically aligned, defect-free columns, although a few clusters also feature defects. This can be seen by comparing (for instance) the light green column in the lower right corner to the yellow structure in the lower left, where most of the platelets are aligned in a column, but an additional platelet at the lower left corner of the aggregate is attached at an angle. As discussed in detail in previous work,14 when two spheres form an energetically stable bond, their dipoles are oriented head-to-tail. This energy minimum is rather deep and wide, so that even relatively large thermal-noise induced angular fluctuations cannot break such a bond. In contrast, if two platelets come close enough to form a head-to-tail bond, even a slight rotation of one of them leads to a significant growth in the interdipolar distance and leads to bond breakage. Moreover, while for touching spheres the antiparallel orientation of dipoles can also lead to the formation of an energetic bond, for anisotropic platelets side-by-side, the distance between the dipoles turns out to be too large for the bond to form. As an outcome, not only do platelets aggregate less for the same values of dipole moment, but they also mostly exclusively form columns. Hence, the clusters are quite rigid, in that the platelets are in contact face-to-face, and with the dipoles aligned head-to-tail. This means that there are no significant intracluster fluctuations, which is important to remember when interpreting the dynamic magnetic susceptibility in Sections 3.2 and 3.3. It should also be noted that while ϕ = 0.200 is around the largest feasible concentration where there are distinct columns, simulations of monodisperse steric platelets do not exhibit a nematic phase at this aspect ratio,34 and no signs of nematic ordering were observed in the present case.
The initial static magnetic susceptibility is shown as a function of concentration in Fig. 3. Before delving into more intricate theories, we begin by recomputing the Langevin susceptibility for platelets, where the standard expression is rewritten in terms of λ and ϕ (of platelets):
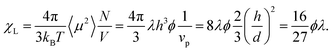 | (12) |
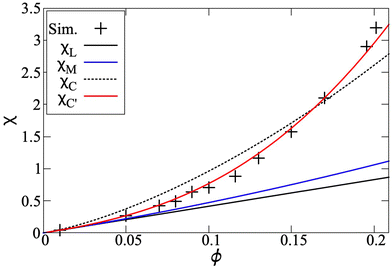 | ||
| Fig. 3 The initial static magnetic susceptibility as a function of the platelet volume fraction. The data from simulation (black crosses) is compared to the Langevin susceptibility χL (black), first-order modified mean-field theory χM (blue), the original reformulation of the chain model χC (black, dashed) and the chain model with a modified correlation coefficient χC′ (red). These latter two curves are based on (14) – see text. | ||
In Fig. 3, χL is shown with the solid black line, and it is clearly below the simulation data, shown by the symbols. The blue curve is obtained by using the Langevin susceptibility in the well-established first-order modified mean-field (MMF1) theory expression,35
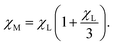 | (13) |
The expression in eqn (13) for spherical particles was extended in order to take into account self-assembly in chain-like aggregates:36
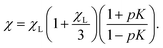 | (14) |
Here, p is the probability of two platelets forming a dimer, and it depends on both the platelet concentration and the platelet-dimer partition function q2, which was rigorously derived for platelets as a function of λ in ref. 19. The coefficient K shows how strongly two neighbours in a dimer are correlated, and for the case of spheres, it depends on the dipolar coupling constant as K ∼ coth(λ/2) − 2/λ. If one uses this expression for platelets, then it does not give good agreement with the simulation data, as evidenced by the black dashed line in Fig. 3. However, this result is not very surprising, because the correlations between platelets are very different from those between spheres, as detailed previously in ref. 14. Locally, the correlations between two platelets are determined by their steric anisotropy, and can be better characterised by a normalised orientational order parameter, Q ∼ tanh(κϕ), where κ is a system specific constant.37,38 The solid red line in Fig. 3 was obtained by fitting to the simulation data, giving κ ≃ 5.5. The qualitative gap between the initial susceptibility of platelets and spheres is the consequence of not only the quantitative difference in the cluster-size distributions, but also their dependence on the magnetic material concentration and local intercluster correlations.
The application of an external magnetic field is expected to enhance even further the correlations between platelets, and hence the aggregation due to the alignment of the dipoles. The strength of the particle–field interaction is characterised by the Langevin parameter
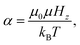 | (15) |
Magnetisation curves, normalised by the value of the saturation magnetisation, Ms, for systems with ϕ ≤ 0.050 are shown in Fig. 5. The simulation results are compared to both the Langevin magnetisation curve for non-interacting particles, and the MMF1 theory.35 The Langevin magnetisation curve is
| ML = MsL(α), | (16) |
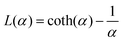 . The MMF1 expression for platelets is given by
. The MMF1 expression for platelets is given by| MM = MsL(αeff), | (17) |
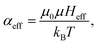 | (18a) |
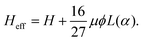 | (18b) |
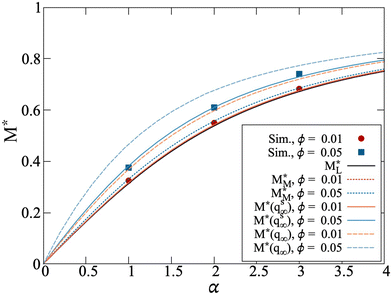 | ||
Fig. 5 Normalized magnetisation curves for systems with ϕ = 0.010 (red/orange) and ϕ = 0.050 (blue). The abbreviation M* = M/Ms is used as an abbreviation to denote division by the saturation magnetization, which allows for direct comparison between simulation and analytical theory. Simulation data is denoted by red circles (ϕ = 0.010) or blue squares (ϕ = 0.050). Lines correspond to the theoretical models discussed in text, comparing Langevin theory  (solid black, eqn (16)), first-order modified mean-field theory (solid black, eqn (16)), first-order modified mean-field theory  (MMF1, dotted lines, eqn (17)), the chain model for spheres M*(qs∞) (solid lines), and the chain model adjusted for platelets M*(q∞) (dashed lines). (MMF1, dotted lines, eqn (17)), the chain model for spheres M*(qs∞) (solid lines), and the chain model adjusted for platelets M*(q∞) (dashed lines). | ||
The effective field is the sum of the external field and a term that takes into account the interplatelet dipolar interactions; the latter term is analogous to that for dipolar spheres.35 For the lower values of ϕ, the magnetisation (red circles) deviates only slightly from the Langevin curve (black line), suggesting that the particles in these systems are only weakly interacting. For ϕ = 0.050 (blue squares), where clustering starts to occur, the magnetisation curve is clearly larger than both the Langevin and MMF1 predictions (black line, blue dotted line), reflecting the fact that there are significant positional and orientational correlations between the dipole moments.
As with the initial susceptibility, the direct application of the chain model36 does not describe the simulation data very well. Fig. 5 shows simulation data for ϕ = 0.010 and ϕ = 0.050, along with the theoretical prediction for magnetisation M*(qs∞) (solid lines). In the chain-model approach for spheres, the role of interparticle correlations is captured by the ratio between the partition functions of a two-particle chain in zero and infinitely strong magnetic fields, and this depends on the dipolar coupling constant λ. For details, see the ESI.† But it is clear that, as compared to spheres, platelets are not only less magnetically correlated, but also their correlations are concentration dependent. Therefore, we adjust the ratio between the zero-field and infinite-field partition functions with the same orientational order parameter Q, as for the initial susceptibility. This means that only for highly concentrated platelet suspensions will there be a field-induced correlation enhancement as for spheres. This assumption results in the orange and blue dashed lines for ϕ = 0.010 and ϕ = 0.050, respectively, shown in Fig. 5 and denoted as M*(q∞). Note that such a modification of the platelet dimer partition function in an infinite magnetic field represents structural properties very similar to those discussed in Fig. 4. If the spherical approximation is used, then the degree of aggregation is found to be more than twice as high as that seen in simulations. See the ESI† for more details.
In applied field, the platelets form columns or stacks aligned along the field direction, and hence the system becomes structurally anisotropic. A convenient way of characterising the ordering in such cases is to split the static structure factor into two components for wave vectors that are parallel (q‖) and perpendicular (q⊥) to the field H.39–42 There have been many calculations of these functions for magnetised ferrofluids containing spherical particles.43–48 Results for the platelets system with ϕ = 0.050 are shown in Fig. 6. Perpendicular to the field, in Fig. 6(a), there is a single peak, and it shifts to lower q⊥ with increasing field strength. This is consistent with alignment of the platelets in the field direction, and that any side-by-side correlations occur over distances comparable to the platelet diameter r ≃ 3σ, giving rise to the peak at q⊥σ ≃ 2. With increasing field strength, the columns repel each other more due to the side-by-side parallel alignment of the dipoles, and this explains the shift to smaller values of q⊥. No longer-range ordering is signaled in S(q⊥). Parallel to the field, in Fig. 6(b), there are peaks at multiples of q‖ ≃ 2π, signaling nearest-neighbour distances r ≃ σ. This confirms stacking of the platelets into columns oriented in the field direction. The peak heights grow with increasing field strength, indicating an increase in clustering.
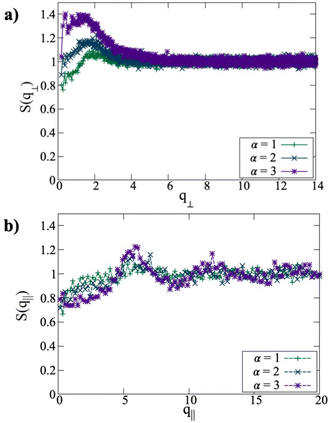 | ||
| Fig. 6 Structure factors perpendicular to the field S(q⊥) (a) and parallel to the field S(q‖) (b) at ϕ = 0.050 and with α = 1, 2, 3. | ||
To summarise the main findings from this section, the zero-field results indicate the absence of orientational and spatial ordering, and show that the extent of self-assembly is consistent with previous work. An interesting observation is that the clustering in zero field occurs with an almost constant dimer fraction. The initial static magnetic susceptibility agrees with the MMF1 theory prediction at low ϕ, but deviates significantly from it at higher concentrations. By assuming that the dependence of the local correlations between platelets depends on the concentration, and by taking the platelet anisotropy into account when calculating the dimer partition function, one can extend an existing chain model for the initial susceptibility of dipolar hard spheres36 and achieve very good agreement with simulation data.
The formation of clusters is favoured even by low to moderate applied fields. At sufficiently low concentrations, the magnetisation curve follows the Langevin law, but as the concentration is increased, the results tend towards the MMF1 theory. But as soon as clustering sets in, the MMF1 theory is no longer accurate. The direct application of the chain model developed for the magnetic response of dipolar spheres36 overestimates both the magnetisation and the cluster size, confirming that platelets are less spatially and orientationally correlated than spheres. The aforementioned extension, to take account of concentration and anisotropy effects, brings the theory into agreement with simulations. The structure factors are consistent with field-induced aggregation of the platelets into columns aligned along the field direction.
3.2 Dynamic magnetic susceptibility: H = 0
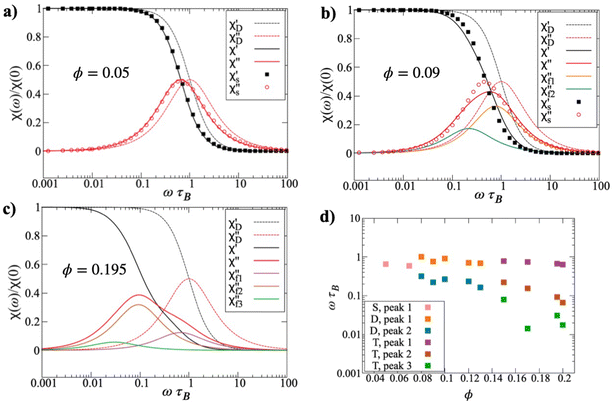
The dynamic magnetic susceptibility χ(ω) in zero field has been calculated for systems over the concentration range 0.010 ≤ ϕ ≤ 0.200. In each case, C(t) was fitted with a sum of exponentials as described in Section 2.2, and χ(ω) was calculated as a sum of Debye-like functions. Fig. 7(a)–(c) shows the frequency spectra for systems with ϕ = 0.050, 0.090, and 0.195. In each case, both the real and imaginary parts of χ(ω) are shown, but the imaginary part χ′′(ω) most clearly indicates the relevant time scales. At ϕ = 0.050, the peak in χ′′(ω) is slightly shifted to lower frequencies than ωτB = 1. For non-interacting particles, the peak would be at precisely ωτB = 1, where τB is the Brownian rotation time for the relevant particle shape. That the peak is at slightly lower frequency indicates the effects of interparticle interactions, which generally lead to a slowing down of the rotational dynamics due to correlated, collective motions of the particles.20,21,49 For ϕ = 0.050, an attempt to apply a modified-Weiss (MW) approach that works well for spherical particles,21 does not result in a good agreement. The platelets exhibit significantly slower dynamics as compared to spheres with the same number density. In the static limit, χ(0) is the initial magnetic susceptibility, shown in Fig. 3. At ϕ = 0.050, the MW model is practically the same as the MMF1 theory. Hence, the presence of interparticle correlations at equilibrium are only apparent in the frequency spectra. At intermediate and higher concentrations, interparticle interactions strongly affect the microstructure, χ′′(ω) is considerably broader than a Debye-like function, which is also shown in Fig. 7(a) for reference. The fact that the system contains some clusters, as well as unclustered particles, suggests that there could be a superposition of dynamical features in χ(ω). Separating out features due to different clusters, and the interactions between them, is a tricky business because accurate models are required for each. In lieu of such models, C(t) and χ(ω) have been analysed as described in Section 2.2, and Fig. 7(b) shows two Debye-like components that when summed provide a sufficiently good fit to the simulation data. One component has its peak near ωτB ≃ 1, and the other near ωτB ≃ 0.2. A tempting interpretation of this is that these peaks correspond to monomers and clusters (predominantly dimers), respectively.Turning to a higher concentration, ϕ = 0.195 in Fig. 7(c), it is clear that χ′′(ω) broadens substantially. In this case, three Debye-like functions were required to provide an adequate fit. This shows that even lower frequency reorientational dynamics have appeared, which presumably arise from clusters that are much larger than dimers. This is consistent with the evolution of the cluster-size distribution discussed in Section 3.1. The low-frequency features in χ′′(ω) are dominant, and there is a clear high-frequency shoulder. The three required components are centered on frequencies of ωτB ≃ 1, 0.08, and 0.03.
It must be stressed that fitting a discrete sum of exponentials to C(t) is only a means to an end, and the business of fitting a distribution of time scales is complicated.50,51 It cannot be inferred from fits of two or three exponentials that there are only two or three characteristic timescales. But broadly speaking, it does indicate that there are motions spanning, in some cases, a couple of orders of magnitude. With this caveat in mind, Fig. 7(d) shows the peak positions in χ′′(ω) as functions of the concentration ϕ. The data are not particularly smooth, especially at low frequencies, because the peak positions are inferred from fitting a slowly decaying autocorrelation function, which is noisy at long times. For concentrations ϕ ≤ 0.070, a single characteristic time scale is sufficient to describe χ(ω), and the corresponding frequency is a bit less than ωτB due to a combination of weak interactions between monomers, and the presence of some small clusters, as explained above. In the concentration range 0.080 ≤ ϕ ≤ 0.130, two time scales are sufficient, and they differ by up to one order of magnitude. Referring to the results of Section 3.1, this concentration range is where a substantial number of dimers are formed, and some larger clusters begin to appear. For concentrations ϕ ≥ 0.15, three time scales are required, and the lowest-frequency motions are almost two orders of magnitude slower than the single-particle ones. So, the combination of the cluster-size distributions and the spectra indicates that there are distinct features arising from single particles (with peak frequencies ωτB ∼ 1), small clusters like dimers and trimers (ωτB ∼ 0.1), and larger clusters (ωτB ∼ 0.01). Note that cluster formation does not give rise to any high-frequency features, meaning ωτB > 1. Some intracluster motions might occur on sufficiently short time scales, but these will not be visible in χ(ω) because it is dominated by the contributions from single particles, and clusters with large net dipole moments.17
3.3 Dynamic magnetic susceptibility: H > 0
In a static applied field H, there are two dynamic magnetic susceptibilities, parallel and perpendicular to the field direction. The physical meaning is that when a weak AC probing field h(t) = h0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−iωt is applied parallel and perpendicular to H, it causes different AC responses in the magnetisation. In the parallel case, the average magnetisation is 〈M〉 ≠ 0, and δM(t) = M(t) − 〈M〉 = χ‖(ω)h(t). In the perpendicular case, 〈M〉 = 0, and M(t) = χ⊥(ω)h(t). For ferrofluids containing spherical particles with weak to moderate interactions, it is known that the peaks in each χ′′(ω) increase with increasing field due primarily to the additional torque from the field, and to a lesser extent, an increase in chain-like correlations between the particles.22,52,53 The effects are not very pronounced, though, and with typical values of λ = 1 and ϕs = 0.1, the peak frequencies may change from about ωτB ≃ 0.8 at α = 0 (due to interactions) to ωτB ≃ 1.1 at α = 5 (due to the field).22 They key point is that there may not be huge effects on the peak frequencies with increasing field, unless there is extensive structuring in the system.
e−iωt is applied parallel and perpendicular to H, it causes different AC responses in the magnetisation. In the parallel case, the average magnetisation is 〈M〉 ≠ 0, and δM(t) = M(t) − 〈M〉 = χ‖(ω)h(t). In the perpendicular case, 〈M〉 = 0, and M(t) = χ⊥(ω)h(t). For ferrofluids containing spherical particles with weak to moderate interactions, it is known that the peaks in each χ′′(ω) increase with increasing field due primarily to the additional torque from the field, and to a lesser extent, an increase in chain-like correlations between the particles.22,52,53 The effects are not very pronounced, though, and with typical values of λ = 1 and ϕs = 0.1, the peak frequencies may change from about ωτB ≃ 0.8 at α = 0 (due to interactions) to ωτB ≃ 1.1 at α = 5 (due to the field).22 They key point is that there may not be huge effects on the peak frequencies with increasing field, unless there is extensive structuring in the system.
The peak frequencies for low-concentration suspensions are shown in Fig. 8. Fig. 8(a) shows the effects of increasing (low) concentration and increasing (low) fields. The lines are guides to the eye, based on the following formulas for the relaxation times of non-interacting spherical particles parallel and perpendicular to the field:
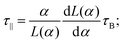 | (19) |
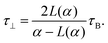 | (20) |
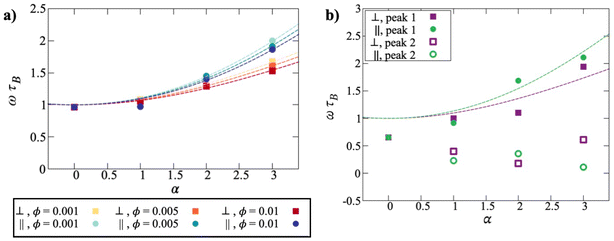 | ||
| Fig. 8 Peak frequencies for low-concentration suspensions, with simulation data denoted by points. (a) Fits of eqn (19) and (20) to the data (dotted lines). We see an increase in frequency both parallel and perpendicular to the field. (b) Peak frequency at the fixed concentration of 0.050, with increasing field. While the single-particle peak frequency increases with field (filled symbols), due to scatter, the secondary peak (open symbols) does not show a clear trend. | ||
These formulas were put forward in ref. 52 and 53 as the longest relaxation times parallel and perpendicular to the field, respectively, and were shown to agree well with simulation data.22 A limitation of these formulas is that the relaxation times apply only to isolated or very weakly interacting particles. To take account of some kind of effective field experienced by the particles, the Langevin parameter was replaced by a scaled value, αeff = fα, where the fitted scaling factors were f‖ = 0.90 and f⊥ = 0.95 for ϕ = 0.001. At these concentrations, the degree of clustering is low despite the presence of the field, and this results in a single characteristic decay time for both the parallel and perpendicular field components. At the lowest field strength, α = 1, the results effectively correspond to the Debye prediction, and there is no significant difference between the relaxation parallel and perpendicular to the field. With increasing field strength, the single particle frequency increases. This effect takes place both parallel and perpendicular to the field, although it is stronger parallel to the field. Both the frequencies, and the difference between them, increase with increasing field strength. These trends are apparent for all three, low concentrations studied, with very little difference. This is to be expected, as these three systems show effectively the same microstructure.
At the highest concentration studied in a field, ϕ = 0.050, there are significant increases in clustering, and this results in the appearance of two peaks in χ′′(ω). The results are shown in Fig. 8(b), with the peak frequencies shown as a function of the Langevin parameter. As in the zero-field case, the higher-frequency peak can be identified with single-particle relaxation, and the lower-frequency peak with the relaxation of clusters. The numerical values do not vary smoothly with α due to poor statistics, but the general trends appear to be as follows. With α = 0, τ‖ and τ⊥ are the same, by definition, and longer than τB due to weak interactions. Moreover, at this volume fraction, there is no zero-field clustering, and so a single exponential is sufficient to fit C(t). This explains the single peak frequency ωτB < 1.
Clustering is promoted even at α = 1, and so this leads to two characteristic timescales for each of the parallel and perpendicular susceptibilities. The higher peak frequencies correspond to single particles, and these are above the zero-field frequencies because of the effects of the field, as shown in Fig. 8(a). The lower peak frequencies can be attributed to particle aggregation: more specifically, as shown in Fig. 4, the formation of dimers. With increasing α, the single-particle frequencies increases, as expected, and the cluster frequencies decreases. As in the field-free case, this frequency decrease can be linked to an increase in cluster size from dimers to larger aggregates. The ordering of the parallel and perpendicular frequencies is not regular, due to the difficulty in resolving the peak positions in χ′′(ω) accurately. But for the single particles, it looks like the parallel frequency is generally higher than the perpendicular one, as shown in Fig. 8(a). The situation is not so clear for the clusters, and all that can be said is that the characteristic frequencies decreases with increasing α, and that this is a clear signal of cluster growth.
4 Conclusions
4.1 Key findings
This simulation study was focused on suspensions of dipolar magnetic nanoplatelets under conditions where there is a coexistence of single particles and clusters. The complex cluster size distribution is reflected in both the static magnetic response, and in the dynamic magnetic susceptibility, with time scales spanning almost two orders of magnitude. A theory describing chain formation in suspensions of spherical magnetic particles can be adapted successfully to account for platelet anisotropy, and the dependence of interparticle correlations on concentration. Depending on the concentration, χ(ω) can be described by a superposition of up to three functions defined by distinct characteristic time scales. The highest-frequency feature corresponds to single-particle rotations, which are only weakly affected by the long-range dipole–dipole interactions. Small clusters and large clusters give rise to features at frequencies about one and two orders of magnitude smaller, respectively. When a static external field is applied, the aggregation in the system increases strongly. At low concentrations, there is a small increase in the single-particle frequency characterising the parallel response, due to the additional torque arising from the field. New features appear at lower frequencies due to the field-induce clustering. Similar but weaker changes appear in the dynamic magnetic susceptibility perpendicular to the field.4.2 Relevance to experiments
Experimental systems of barium hexaferrite nanoplatelets have a polydisperse size distribution, with particle diameters (meaning the platelet major axes) in the range d = 20–80 nm.15 The Brownian relaxation times τB are proportional to d2, and hence the range of relaxation times should vary by a factor of around (80/20)2 = 16. If the system is divided into ‘small’ and ‘large’ fractions, using some criterion, then in the absence of clustering or significant interparticle interactions, the respective peak frequencies would correspond to ω ≃ τB,small−1 and ω ≃ τB,large−1. But a factor of 16 is far less than the ratio of the high-frequency (HF) and low-frequency (LF) peak positions measured in experiments,15 which approaches 103.The current simulation study suggests one possible explanation of the experimental observations. The results show that interactions, and particularly clustering, lead to dramatic increases in the relaxation times, approaching two orders of magnitude. If the large particles self-assembled into clusters, then the corresponding features in the dynamic magnetic susceptibility would appear at ω ≪ τB,large−1. The preferential clustering of the large particles would be driven by the larger dipolar coupling constant (∝μ2/σ3). Therefore, if the small particles did not self-assemble (giving a HF feature at ω ≃ τB,small−1), and the large particles did self-assemble (giving a LF feature at ω ≃ 0.02τB,large−1 as per the simulations), then the ratio of the HF and LF peak positions would be around 0.02/16 = 1.25 × 10−3 as observed in experiments.
More recent experimental studies54 including bias fields have explored two distinct concentration ranges. At very low concentrations, the singular high-frequency peak shifts to higher values with increasing bias field, in agreement with established models,52 with the same qualitative behavior as Fig. 8(a). At higher concentrations, where two distinct peaks are observed, the relation between the Brownian relaxation time and the bias field becomes non-monotonous and is not well-described by existing theory. This mirrors the issue found in this paper, shown in Fig. 8(b), with resolving the underlying effects in intermediate and higher-concentration suspensions under the influence of bias fields.
The essential point is that interparticle interactions and clustering cause much larger changes in the dynamics than what would be expected on the basis of platelet size alone. Dipole–dipole interactions, and the concomitant structure formation, lead to changes in the relevant rotational time scales by up to two orders of magnitude. Small changes in particle size translate into large changes in dipole moment, interaction strength, and the tendency to cluster. Incorporating these effects into simple particle-based models is complicated, especially when other types of (non-magnetic and steric) interactions are present. Nonetheless, the principal conclusion from this work is that particle interactions and clustering have large effects on the dynamic magnetic susceptibility, and that these must be taken into account when inferring anything about the structural and magnetic properties of the system.
Author contributions
M. R.: data curation; formal analysis; visualisation; writing – original draft. S. S. K.: conceptualisation; data curation; formal analysis; visualisation; writing – original draft. A. O. I.: calculation of the partition function for platelets; formal analysis; conceptualisation. P. J. C.: conceptualisation; data curation; formal analysis; visualisation; writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. R. acknowledges funding from the Austrian Academy of Science (OeAW) and the Vienna Doctoral School of Physics (VDS-P). We thank Dr R. Weeber and Dr E. Pyanzina for fruitful discussions. Partial research funding from UrFU Program of Development within the Priority-2030 Program is gratefully acknowledged.Notes and references
- J. F. Liu, B. Jang, D. Issadore and A. Tsourkas, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2019, 11, 1571 Search PubMed.
- G. G. Flores-Rojas, F. López-Saucedo, R. Vera-Graziano, E. Mendizabal and E. Bucio, Macromol, 2022, 2, 374–390 CAS.
- O. Cervantes, Z. del Rocio Lopez, N. Casillas, P. Knauth, N. Checa, F. A. Cholico, R. Hernandez-Gutiérrez, L. H. Quintero, J. A. Paz and M. E. Cano, Molecules, 2022, 27, 544 CrossRef CAS PubMed.
- V. Socoliuc, M. Avdeev, V. Kuncser, R. Turcu, E. Tombácz and L. Vekas, Nanoscale, 2022, 14, 4786–4886 RSC.
- X. Zhang, L. Sun, Y. Yu and Y. Zhao, Adv. Mater., 2019, 31, 1903497 CrossRef CAS PubMed.
- D. Wang, S. Zheng, H. Liu, J. Tang, W. Miao, H. Wang, Y. Tian, H. Yang and L. Jiang, Adv. Mater., 2019, 31, 1805953 CrossRef PubMed.
- R. E. Rosensweig, Ferrohydrodynamics, Dover Publications, Inc., New York, 1998 Search PubMed.
- S. Odenbach, Ferrofluids: magnetically controllable fluids and their applications, Springer Verlag, Berlin, 2002 Search PubMed.
- E. Blums, A. Cebers and M. Maiorov, Magnetic Fluids, Walter de Gruyter, Berlin, 1997 Search PubMed.
- B. F. Edwards, D. M. Riffe, J.-Y. Ji and W. A. Booth, Am. J. Phys., 2017, 85, 130–134 CrossRef.
- P. Tierno, Phys. Chem. Chem. Phys., 2014, 16, 23515–23528 RSC.
- M. Shuai, A. Klittnick, Y. Shen, G. P. Smith, M. R. Tuchband, C. Zhu, R. G. Petschek, A. Mertelj, D. Lisjak, M. Copic, J. E. Maclennan, M. A. Glaser and N. A. Clark, Nat. Commun., 2016, 7, 10394 CrossRef CAS PubMed.
- M. Rosenberg, Ž. Gregorin, P. H. Boštjančič, N. Sebastián, D. Lisjak, S. S. Kantorovich, A. Mertelj and P. A. Sánchez, J. Mol. Liq., 2020, 312, 113293 CrossRef CAS.
- M. Rosenberg and S. S. Kantorovich, Phys. Chem. Chem. Phys., 2023, 25, 2781–2792 RSC.
- M. Küster, F. Ludwig, A. Eremin, P. H. Boštjančič, D. Lisjak, N. Sebastián, A. Mertelj and H. Nádasi, J. Mol. Liq., 2022, 360, 119484 CrossRef.
- A. Lebedev, S. Kantorovich, A. Ivanov, I. Arefyev and A. Pshenichnikov, J. Mol. Liq., 2019, 277, 762–768 CrossRef CAS.
- P. J. Camp, A. O. Ivanov and J. O. Sindt, Phys. Rev. E, 2021, 103, 062611 CrossRef CAS PubMed.
- R. E. Rosensweig, J. Magn. Magn. Mater., 2002, 252, 370–374 CrossRef CAS.
- H. Nádasi, M. Küster, A. Mertelj, N. Sebastián, P. H. Boštjančič, D. Lisjak, T. Viereck, M. Rosenberg, A. O. Ivanov, S. S. Kantorovich, A. Eremin and F. Ludwig, J. Mol. Liq., 2023, 382, 121900 CrossRef.
- J. O. Sindt, P. J. Camp, S. S. Kantorovich, E. A. Elfimova and A. O. Ivanov, Phys. Rev. E, 2016, 93, 063117 CrossRef PubMed.
- A. O. Ivanov and P. J. Camp, Phys. Rev. E, 2018, 98, 050602(R) CrossRef.
- T. M. Batrudinov, Yu. E. Nekhoroshkova, E. I. Paramonov, V. S. Zverev, E. A. Elfimova, A. O. Ivanov and P. J. Camp, Phys. Rev. E, 2018, 98, 052602 CrossRef CAS.
- K. Simeonidis, M. P. Morales, M. Marciello, M. Angelakeris, P. de la Presa, A. Lazaro-Carrillo, A. Tabero, A. Villanueva, O. Chubykalo-Fesenko and D. Serantes, Sci. Rep., 2016, 6, 38382 CrossRef CAS PubMed.
- T. Yoshida, Y. Matsugi, N. Tsujimura, T. Sasayama, K. Enpuku, T. Viereck, M. Schilling and F. Ludwig, J. Magn. Magn. Mater., 2017, 427, 162–167 CrossRef CAS.
- R. Takeda, S. Ota, T. Yamada and Y. Takemura, J. Magn. Soc. Jpn., 2018, 42, 55–61 CrossRef CAS.
- S. Ranoo, B. B. Lahiri, T. Muthukumaran and J. Philip, Appl. Phys. Lett., 2019, 115, 043102 CrossRef.
- F. Weik, R. Weeber, K. Szuttor, K. Breitsprecher, J. de Graaf, M. Kuron, J. Landsgesell, H. Menke, D. Sean and C. Holm, Eur. Phys. J.: Spec. Top., 2019, 227, 1789–1816 Search PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237 CrossRef CAS.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, Oxford, 4th edn, 2013, pp. 13–59 Search PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, San Diego, 2nd edn, 2002, pp. 40–42 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- D. Levesque and J. J. Weis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5131–5140 CrossRef CAS PubMed.
- P. J. Camp and G. N. Patey, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5403–5408 CrossRef CAS PubMed.
- J. A. C. Veerman and D. Frenkel, Phys. Rev. A, 1992, 45, 5632–5648 CrossRef PubMed.
- A. O. Ivanov and O. B. Kuznetsova, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 041405 CrossRef CAS PubMed.
- V. S. Mendelev and A. O. Ivanov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051502 CrossRef PubMed.
- K. R. Purdy, Z. Dogic, S. Fraden, A. Rühm, L. Lurio and S. G. J. Mochrie, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 031708 CrossRef PubMed.
- J. J. Binney, N. J. Dowrick, A. J. Fischer and M. E. J. Newman, The Theory of Critical Phenomena, Oxford University Press, 2002 Search PubMed.
- D. J. Cebula, S. W. Charles and J. Popplewell, Colloid Polym. Sci., 1981, 259, 395–397 CrossRef CAS.
- F. Gazeau, E. Dubois, J.-C. Bacri, F. Boué, A. Cebers and R. Perzynski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031403 CrossRef CAS PubMed.
- G. Mériguet, F. Cousin, E. Dubois, F. Boué, A. Cebers, B. Farago and R. Perzynski, J. Phys. Chem. B, 2006, 110, 4378–4386 CrossRef PubMed.
- A. Wiedenmann, U. Keiderling, M. Meissner, D. Wallacher, R. Gähler, R. P. May, S. Preévost, M. Klokkenburg, B. H. Erné and J. Kohlbrecher, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 184417 CrossRef.
- P. C. Jordan, Mol. Phys., 1973, 25, 961–973 CrossRef CAS.
- J. B. Hayter and R. Pynn, Phys. Rev. Lett., 1982, 49, 1103–1106 CrossRef.
- S. Hess, J. B. Hayter and R. Pynn, Mol. Phys., 1984, 53, 1527–1533 CrossRef CAS.
- J. P. Huang, Z. W. Wang and C. Holm, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061203 CrossRef CAS PubMed.
- J. J. Cerdà, E. Elfimova, V. Ballenegger, E. Krutikova, A. Ivanov and C. Holm, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 011501 CrossRef PubMed.
- E. A. Elfimova, A. O. Ivanov and P. J. Camp, J. Chem. Phys., 2012, 136, 194502 CrossRef PubMed.
- A. O. Ivanov, V. S. Zverev and S. S. Kantorovich, Soft Matter, 2016, 12, 3507–3513 RSC.
- A. C. Fogarty, A. C. Jones and P. J. Camp, Phys. Chem. Chem. Phys., 2011, 13, 3819–3830 RSC.
- A. O. Ivanov and V. S. Zverev, Mathematics, 2021, 9, 2450 CrossRef.
- M. A. Martsenyuk, Yu. L. Raikher and M. I. Shliomis, Sov. Phys. JETP, 1974, 38, 413–416 Search PubMed.
- M. I. Shliomis and Yu. L. Raikher, IEEE Trans. Magn., 1980, 16, 237–250 Search PubMed.
- M. Küster, H. Nádasi, A. Eremin, P. H. Boštjančič and F. Ludwig, J. Magn. Magn. Mater., 2023, 588, 171368 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of partition function calculations. See DOI: https://doi.org/10.1039/d4nr01120a |
| ‡ As in ref. 14 there were additional checks on the dipole alignment and negative interaction energy to reduce false positives in weakly interacting systems. However, since clusters at high concentrations will interact, this is not sufficient to differentiate them. |
| This journal is © The Royal Society of Chemistry 2024 |