Open Access Article
Open Access ArticleElectrostatic interactions and structural transformations in viral shells†
Ivan Yu.
Golushko
 a,
Daria S.
Roshal
a,
Daria S.
Roshal
 a,
Olga V.
Konevtsova
a,
Olga V.
Konevtsova
 a,
Sergei B.
Rochal
a,
Sergei B.
Rochal
 *a and
Rudolf
Podgornik
*a and
Rudolf
Podgornik
 *bcde
*bcde
aFaculty of Physics, Southern Federal University, Rostov-on-Don, Russia. E-mail: rochal_s@yahoo.fr
bSchool of Physical Sciences and Kavli Institute for Theoretical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
cCAS Key Laboratory of Soft Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
dWenzhou Institute of the University of Chinese Academy of Sciences, Wenzhou, Zhejiang 325000, China
eDepartment of Theoretical Physics, Jozef Stefan Institute, Ljubljana, Slovenia. E-mail: rudolf.podgornik@ijs.si
First published on 1st October 2024
Abstract
Structural transformations occurring in proteinaceous viral shells (capsids) can be induced by changing the pH of bathing solution, thus modifying the dissociation equilibrium of ionizable amino acids in proteins. To analyze the effects of electrostatic interactions on viral capsids, we construct a model of 2D isotropic elastic shells with embedded point charges located in the centers of mass of individual proteins. We find that modification of the electrostatic interactions between proteins affects not only the size and shape of capsids, but in addition induces substantial deformations of hexamers in capsid structures. Using bacteriophage P22 and Nudarelia capensis omega virus (NωV) as examples, we analyze the capsid faceting and propose an explanation as to why the hexamers in spherical procapsid are skewed, while they acquire a regular shape in the faceted state. Also, we examine the electrostatic and elastic effects that can explain different shapes of coronavirus shells decorated with spikes, which are often localized in compact areas over the shell surface. The proposed mechanism of local curvature generation is supported by the remarkable correspondence between the shell shape and the distribution of spikes in model and observed shells.
Introduction
By modifying the charging state of viral proteins, changes in the pH level of the bathing solution often control processes occurring during the life cycle of viruses. For example, Coronaviruses,1 Alphainfluenzaviruses,2 Vesiculoviruses3 and some other enveloped viruses require acidic pH in order to infect the cells. A decrease in pH induces conformational changes in glycoproteins (spikes), randomly located on the surface of the polymorphic shells of these viruses, which causes fusion with the cell membrane at initial stages of infection.4,5 A similar process also enables the infection with Alphaviruses and Flaviviruses, where surface glycoproteins form an additional protein layer, covering the membrane shell.6 Flaviviruses are structurally similar to Alphaviruses, but a change in the bathing solution pH induces not only a conformational change in the surface glycoproteins, but also their repacking,7 occurring during another key stage of the viral life cycle – its maturation.Maturation, often induced by the virus migrating through regions of a cell with different pH levels, is typical of almost all well-studied animal and bacterial viruses exhibiting icosahedral symmetry,8 resulting in a stable infectious virion.7,8 The details of these maturation mechanisms differ among virus families. In the case of bacteriophages, at the initial stages of maturation, the genome is packaged into a pre-assembled protein shell (procapsid). During this process, while the immature spherical procapsid often acquires an icosahedral faceting,9–11 other structural symmetries are also possible. For example, mature shells of bacteriophages from the Cystoviridae family have a dodecahedral faceting, while immature shells before genome packaging resemble a dodecahedron with inward buckled faces.12,13 In contrast, pH-related maturation of tetraviruses, which include Nudaurelia capensis omega virus (NωV) that infects insects, transforms the spherical procapsid into a shell with a geometry reminiscent of a rhombic triacontahedron.14,15 It is interesting to note that even when morphological changes of the capsid are triggered by the genome packaging, similar changes can be induced also in vitro, by modifying the acidity of the environment.8,9 In fact, when subjected to the acidic pH conditions, the HK97 procapsid increases its volume and degree of faceting, just as it does in vivo during the genome packaging.9
The first model describing morphological changes associated with virus maturation16 was based on the theory of thin elastic shells applied to one of the most common capsid transformations: from a nearly spherical to a faceted icosahedral shape. The model considered the capsid as a shell with vanishing wall thickness, whose shape is controlled by a single dimensionless parameter, the Föppl–von Kármán (FvK) number, inducing icosahedral faceting when it is sufficiently large. A further generalization of the thin elastic shell model was based on a consistent inclusion of electrostatic interactions, combining elasticity of thin icosahedral shells with the pH dependence of capsid charge distribution,17 which was shown to induce the inflation of the shell as well as changes in its faceting even at a constant FvK value. The unifying feature of these various models16–19 is the form of the elastic energy based on the model of a triangular net of identical springs, implying the equality of the two 2D Lamé coefficients λ and μ, that characterize the in-plane elasticity. In what follows, we propose a non-degenerate electro-elastic shell model, parameterized by an effective charge of the shell together with two independent elastic dimensionless constants, the FvK number and the Poisson ratio. This generalized thin elastic shell model is rich enough to fully explain the experimentally observed distortions of the local protein order during the maturation of icosahedral viruses.
The outline of the paper is as follows. In the first part of the paper, we propose the generalized electro-elastic model and use it to study structural transformations in icosahedral viral shells consisting of capsomeres. The latter are structural units, usually possessing 5- or 6-fold symmetry and consisting of 5 or 6 proteins. However, under some conditions the shell hexamers can become deformed,10,11,14,20 as is the case when the immature capsid exhibits a spherical shell composed of skewed hexamers, while the mature capsid is faceted with regular hexamers.8 By considering the model shells with low FvK number and specific well-defined values of the Poisson ratio, we show that at appropriate environment conditions, giving rise to sufficiently large charges of the proteins, the hexamers become skewed. Elaborating on this observation, we further refine the model so that it is able to describe this type of procapsid-to-capsid structural transformation. In the second part of the paper, we apply the same kind of reasoning to explain the shape genesis in polymorphic lipid–protein shells of coronaviruses. As is known, the shapes of these viruses correlate with the distribution of protein spikes on their surfaces: regions with higher spike concentration exhibit a higher Gaussian curvature.21 We examine possible reasons for the local increase in curvature and make an attempt to explain this effect by the electrostatic repulsion between the protruding spikes as well as their binding with the curved M-proteins immersed in lipid bilayer. Our model allows us to obtain shells that are indeed remarkably similar in shape with the polymorphic virus particles of coronaviruses.
Electro-elastic model of icosahedral viral shell
In the continuum approximation, the elastic energy Eel of a strained thin shell with zero spontaneous curvature can be written as: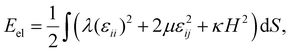 | (1) |
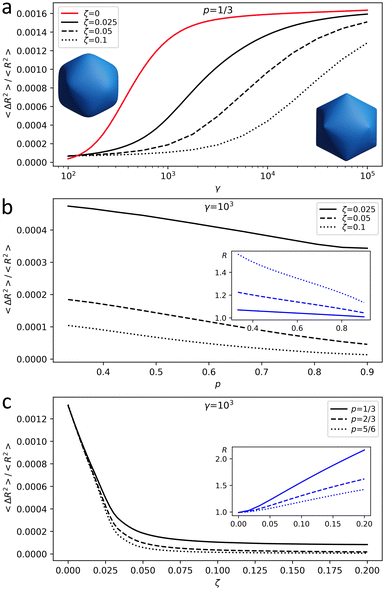
About 20 years ago, Nelson et al.16 studied virus capsid faceting in the framework of the energy eqn (1). They considered capsids as discrete shells with spherical topology consisting of identical finite elements with a shape of a regular triangle. To model the shells, they used an icosahedron net cut from a plane trigonal lattice so that all 12 vertices of the icosahedron coincided with lattice vertices. The shell shape was then shown to be fully characterized by a single dimensionless parameter, the FvK number γ = YR2/κ, where R is the average shell radius. The degree of shell faceting was characterized by asphericity, defined as As = 〈ΔR2〉/R2, where the averaging takes place over all the triangulation nodes and ΔR is the difference between the value of R and the shell radius directed to the node. For small FvK numbers, γ ≲ 102, shells with more than 180 triangles were found to exhibit essentially a spherical shape, whereas for large FvK numbers, γ ≳ 103, they became icosahedrally faceted. Within this model,16 the asphericity does not depend on Poisson ratio and the limit with λ = μ (p = 1/3) was often used to reproduce shapes of icosahedral viral capsids.13,17,19
Here, we consider a more general elastic model corresponding to λ ≠ μ, that consistently includes the contribution of electrostatic interaction between capsid proteins, modelled as point charges in the total energy of the shell. Within the linearized Debye–Huckel screened electrostatics (see Methods), the electrostatic interaction energy between identical point charges is approximated as:
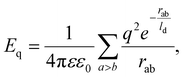 | (2) |
We assume that the coordinates of the charges coincide with the nodes of the shell triangulation or are uniquely expressed through them. The equilibrium shape of the shell can then be deduced by minimizing its total (free) energy Eel + Eq with respect to coordinates of the triangulation nodes. In order to make the expression for the electro-elastic energy scale invariant, we normalize it by the value of bending rigidity κ and express all lengths in units of the average shell radius R of uncharged shell. For the uncharged shell the value of R does not change during the shell faceting.16 Thus, in our model, there are three independent dimensionless parameters: FvK number γ, Poisson ratio p and effective electrostatic coupling strength ζ = q2/(4πεε0κR) (for more details see Methods).
Before considering the structural features of real capsids, we analyze the model behavior in the simplest case of a homogeneously charged shell: each node of the triangulation is occupied by a point charge. To further simplify the analysis, we ignore the screening (ld ≫ R), which obviously increases effect of electrostatic interactions on the shell shape.
Fig. 1 is obtained for the shell (18,0), which has 3242 vertices; see notation of triangulation indices (h,k) in ref. 22 and 23. According to ref. 16 and 19 and our own results, shells of this and larger sizes reach the continuum limit. Fig. 1 shows how shell asphericity As depends on the control parameters of the model. Ranges for γ and ζ are chosen so that the resulting shell asphericity values are of the same order as the ones observed in real capsids16,19 and the radius variation agrees with the relative change in their size during maturation.9,10,12,14 When Poisson ratio is fixed, asphericity increases with γ and decreases with ζ, i.e. the larger the total charge of the shell, the closer its shape is to a sphere (see Fig. 1a for the case of p = 1/3). Fig. 1b shows that the shape of a charged shell depends on the Poisson ratio: with an increase of p, both equilibrium radius and asphericity of the shell decrease. When p → 1 shear modulus of the shell μ tends to zero, and small μ values provide a more homogeneous charge distribution making the shell more spherical and slightly decreasing its radius.
Finally, Fig. 1c demonstrates that the increase of the electrostatic interaction energy predictably leads to the expansion of the shell and simultaneous decrease of its asphericity.
Note that the standard approach16 is based on the fact that the 2D Young modulus of the membrane is proportional to its thickness Y ∝ h, while the membrane bending rigidity κ ∝ h3.24 Since the total volume of the proteins comprising the shell wall is approximately proportional to hR2, FvK depends on the capsid wall thickness as γ ∝ h−3. Thus, the inflation of the shell due to protein rearrangement should simultaneously decrease its wall thickness and increase its faceting, an argument usually invoked in the context of capsid maturation.8 However, according to our results, if the shell is inflated by the electrostatic repulsion between its proteins, the degree of the capsid faceting should actually decrease. Such a decrease of faceting with a simultaneous increase of the shell volume is observed, for example, during the transitions between the EI-II and EI-IV states of the bacteriophage HK97 capsid8,9 or during the maturation of NωV,14 which we discuss in more detail later. Importantly, morphological changes in the capsid are often more complex and not limited to the changes in the degree of faceting and the average shell radius. Actually, in some viruses, during the transformation from the procapsid to the capsid state, the initially deformed hexamers become much more regular. In the following section, we develop our model further to rationalize such transformations by assigning a point charge to each protein in the viral shell and placing the charges only in those triangulation vertices that correspond to positions of the protein centers of mass.
Structural transformations associated with faceting and electrostatic mechanism of hexamer deformation
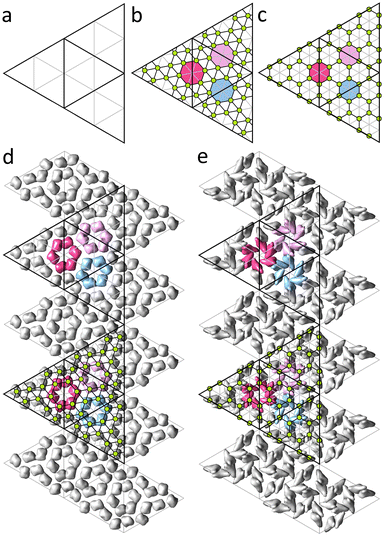
In this Section we consider shells that are described by the Caspar and Klug (CK) model25 and based on icosahedral triangulations of a sphere, or spherical lattices (SLs).22 Each SL is described by a pair of integers (h,k) which correspond to a translation of the trigonal lattice, that is an edge of the spherical icosahedron. The number of nodes in SL equals 10T + 2 where T = h2 + k2 + hk is the triangulation factor. In the CK model nodes of the SL are decorated with capsomeres: 12 vertices of the spherical icosahedron are occupied by pentamers, the rest of the nodes of the triangulation are occupied by hexamers. Thus, capsids satisfying the CK model consist of 60T proteins.In order to construct model shells, reflecting protein order in real capsids, it is reasonable to use triangulations that are commensurate with capsomer organization in the CK model. Only in this case proteins, and their associated electrostatic charges, occupy equivalent positions relative to the triangulation nodes. Both the CK geometrical model and the icosahedral triangulation of a sphere are based on unwrapping icosahedron surface into a net of 20 identical equilateral triangles and superimposing it onto the corresponding plane trigonal lattice. Thus, for CK and spherical triangulations to be commensurate, elementary triangle (see Fig. 2a) of the plane lattice underlying the CK structure should be Q times larger than that of the triangulation of the model shell, where Q is an integer. To maintain hexagonal symmetry characteristic of both structures, the value of Q should satisfy the condition Q = l2 + m2 + lm, where l,m are also integers, i.e. Q = 3, 4, 7, 9, 13… If Q ≥ 7, the multiplied trigonal lattice of the model shell can be decorated with non-overlapping regular hexagons (representing hexamers) with their vertices coinciding with some of the vertices of the shell triangulation. These coinciding vertices correspond to positions of proteins. For Q = 7 and Q = 9, such decorated triangulations match trihexagonal and honeycomb lattices, respectively, excluding the nodes in the centers of the hexagons (see Fig. 2b and c). Let us note that in many capsids, positions of centers of mass (CMs) of proteins are close to the centers of the trihexagonal or honeycomb spherical lattices,23 which is also the case for other proteinaceous shells considered further in this section.
Electro-elastic model of P22 capsid maturation
The procapsid of bacteriophage P22 consists of an outer protein shell formed by 420 proteins (T = 7) that are organized in honeycomb order23 and an inner core formed by so-called scaffold proteins, which serves as a substrate for the outer shell. The procapsid has almost perfectly spherical shape but its hexamers are highly deformed (Fig. 3a). At the DNA packaging stage, scaffold proteins are eliminated from the shell and its average radius increases. In addition, the resulting capsid adopts a faceted shape and hexamers become more symmetrical (see Fig. 3a and b).Previously,23 we analyzed the shear strain field corresponding to the observed hexamer transformation. Our approach was based on symmetry analysis of the irreducible modes possible in the isotropic spherical shell and we associated changes in the shape of hexamers with the irreducible shear mode with wave number l = 6. Only for specific values of l (including l = 6), does the shear strain preserve the icosahedral symmetry and is fully defined by a single parameter, its amplitude. By applying the irreducible spherical shear field with l = 6 to the honeycomb lattice, we demonstrated that the resulting displacements of its nodes are strikingly similar to the displacements of proteins observed in the P22 capsid during maturation. Nonetheless, the phenomenological theory23 leaves the following important questions unanswered. Why does this particular strain emerge in the shell? Why is the honeycomb lattice deformed in the procapsid and undeformed in the mature capsid and not vice versa? And finally, how does this process relate to the faceting of the capsid observed during maturation? As we show in what follows, the answers to these questions can be obtained with a relatively simple discrete microscopic model derived within the theoretical framework discussed in the previous section.
The negatively charged coat-binding domains of scaffold proteins are electrostatically attracted to the positively charged domains of the capsid proteins.26–28 Therefore, it seems reasonable to assume that the imbalance of electrostatic forces, occurring after the detachment of the scaffold proteins, is the main driving force for morphological changes in the shell during maturation of the bacteriophage. For the sake of simplicity, we consider a model shell, in which electro-elastic parameters remain unchanged and the only role of the scaffold proteins is to serve as a substrate that enforces the shell to be in the procapsid state. In addition, we position 420 point charges, corresponding to individual proteins of the outer shell, in the nodes of the model shell that corresponds to SL (3,6); see Fig. 3d. Some nodes are thus not occupied by charges and correspond to the capsomere centers, forming SL (4,1), whereas the occupied nodes form a spherical honeycomb lattice. In the procapsid state, the radial displacements of the shell vertices are prohibited due to the presence of the substrate, so all of them are confined to the spherical surface with radius being equal to the average radius of the uncharged shell.
Since the displacements of the protein mass centers in the procapsid are described by a shear strain,23 it is reasonable to assume that in the considered case the shear modulus is small and the value of μ is substantially smaller than that of λ. In this case, the shear strain can then arise due to electrostatic repulsion between charged proteins. Spherical trigonal lattice with electrostatic charges occupying vertices of approximately equilateral triangles has the lowest electrostatic energy and the tendency of point charges to equalize distances to their nearest neighbors can destabilize the honeycomb SL at a sufficiently large value of ζ. This scenario is reminiscent of the classic Euler instability occurring in plates and rods under mechanical load. While in the considered case, the emerging deformation increases the distances between neighboring charges, the bending of the rod compensates the positive strain generated by the load.
Shells with deformed hexamers occupy a large region of the parameter space. However, if we follow our assumption that electro-elastic parameters remain unchanged in both immature and mature states, the observed morphologies are reproduced only in a much smaller region. Fig. 3 shows constrained (panel (c)) and unconstrained (panel (d)) states of the same charged shell with parameters: γ = 421, ζ = 5, p = 0.75 (λR2/κ = 729, μR2/κ = 120). One can see that upon the transformation from the procapsid (Fig. 3a and c) to the capsid (Fig. 3b and d), distortion of hexamers disappears. The model also reproduces the experimentally observed increase by 11% of the shell average radius.
Electrostatic deformation of hexamers in the encapsulin compartment
Another example of a shell with honeycomb protein order and deformed hexamers is the encapsulin compartment (6NJ8). This icosahedral capsid-like organelle (see Fig. 4a) consists of 240 proteins and is used by bacterium Quasibacilllus thermotolerans to store iron.20 The organelle assembles directly in the solution in its final conformation and thus, unlike the P22 capsid, does not undergo any maturation.20 Nonetheless, its proteins undoubtedly interact with each other electrostatically. We estimate (see Methods) that the proteins have a negative charge of the order of ∼−15e0 at neutral pH, which agrees with the fact that iron ions stored in the organelle are positively charged.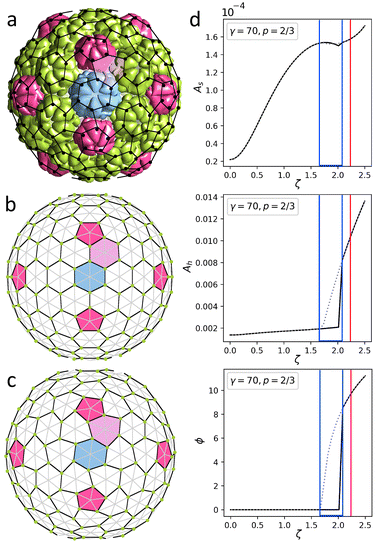 | ||
| Fig. 4 Structures of encapsulin iron storage compartment of Quasibacilllus thermotolerans and deformed honeycomb spherical lattice. (a) Protein shell 6NJ8. Black dots show positions of protein centers of mass. (b and c) Uncharged and charged model shells based on trigonal spherical lattice (6,0) (grey and black lines). Green dots show positions of point electrostatic charges. The honeycomb lattice (3,3) is outlined with black lines. Honeycomb lattices in panels (a) and (c) are identical. (d) Geometric features of the model shell vs. effective electrostatic coupling strength ζ. The dependence of asphericity As, degree of hexamer deformation Ah, and pentamer rotation angle ϕ on the electrostatic coupling parameter ζ are shown. Solid/dotted lines correspond to increase/decrease of ζ. Blue lines outline a region with hysteresis. Red line corresponds to the state shown in panel (c). See Movie 1† visualizing transformation from (b) to (c). | ||
As in the case of P22, we construct the model shell using the honeycomb lattice (Fig. 4b) and this simple example helps us to analyze in more detail the effect of electrostatic interactions on the asphericity as well as hexamer deformation. We consider a shell with parameters γ = 70, p = 2/3, ld = 0.13R (≈25 Å), and ζ = 2.22 since this choice provides the best correspondence between experimental and model structures. Calculating the geometric parameters of the real structure using protein CMs (shown by black dots in Fig. 4a) gives: As ≈ 1.4 × 10−4, Ah ≈ 1.1 × 10−2, ϕ = 9.4°, which is in excellent agreement with parameters of the model shell shown in Fig. 4c: As ≈ 1.6 × 10−4, Ah ≈ 1.0 × 10−2, ϕ = 9.6°. Here Ah describes the degree of deformation of the hexamers, which is defined as Ah = (〈ΔRh2〉)/(Rh2), where Rh is the average hexamer radius and ΔRh is the deviation of the radius in each vertex from the average; ϕ is the rotation angle of the pentamers.
In order to examine the model behavior in more detail, we start by varying the value of electrostatic coupling strength ζ. In Fig. 4d we show how a gradual increase in the charge of the shell, quantified by ζ, eventually leads to a spontaneous loss of stability of the spherical honeycomb lattice, accompanied by a jump in ϕ and Ah. As the symmetry of the shell decreases Ih → I, two enantiomorphic structures with opposite capsomer twists can appear (the one corresponding to the real structure is shown in Fig. 4). During the reverse transformation (shown by the grey dotted line), both Ah and ϕ values demonstrate a pronounced hysteresis, which is also noticeable for As. Interestingly, similar first-order phase transition can be observed in the shell by a gradual increase of the Poisson ratio p at constant charge ζ = 2.22. Also, if the model shell is based on a chiral lattice (as in the case of P22), then the state with deformed hexamers can be achieved without undergoing the first-order phase transition.
Deformation of the trihexagonal protein lattice during the NωV maturation
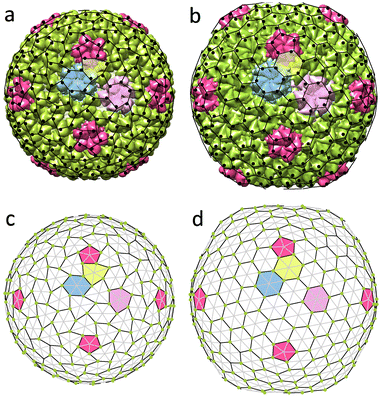
We now turn our attention to NωV of the Teteravirus family, which, unlike two previous assemblies, has trihexagonal protein arrangement. Maturation of this virus relies on the changes of pH in the bathing environment29 and is accompanied by substantial morphological changes in the capsid (compare Fig. 5a and b). Expression of a single capsid protein of NωV is sufficient for self-assembly of virus-like particles with structures identical to the authentic virions.30 Similar to virions, particles assembled at pH = 7.6 (see Fig. 5a) undergo fast (less than 100 ms) structural transition when exposed to acidic pH ≈ 5.0.14,31 Importantly, provided that the exposure to acidic pH was short-termed,14,31 this transition is reversible in both the mutant virus-like particles as well as the wild-type capsids. During this reversible step the average radius of the shell decreases by 16% (from 196 Å to 169 Å), the shell in addition becomes more faceted (As increases from 4.6 × 10−5 to 1.7 × 10−3, see Fig. 5a and b correspondingly), while its hexamers become more symmetric (Ah changes from 2.9 × 10−3 to 1.1 × 10−3). Note that just as before, the geometrical features of the shell are calculated using the coordinates of protein CMs.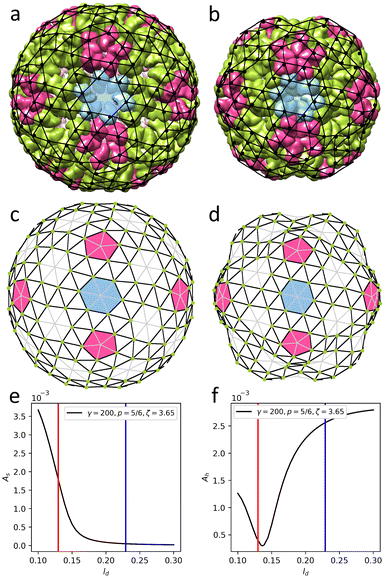 | ||
| Fig. 5 Structures changes in the morphology of the Nudarelia capensis omega virus (NωV) upon maturation. (a) Procapsid 8A41 with deformed hexamers. (b) Capsid 8AAY with regular hexamers. Black dots in panels (a), (b) show protein centers of mass. (c and d) Model shells corresponding to the procapsid and mature capsid based on trigonal spherical lattice (4,2) (outlined with grey and black lines). Green dots on the nodes of the trihexagonal lattice (outlined with black lines) show positions of point electrostatic charges. Deformed and undeformed hexagonal lattices are superimposed onto protein shells in panels (a), (b). (e and f) Geometric features of the model shell vs. screening length ld. As is asphericity, while Ah is degree of hexamer deformation. Blue line corresponds to panel (c); red line corresponds to panel (d). See Movie 2† for the visualization of transformation from (c) to (d). | ||
To construct a model shell, we superimpose the trihexagonal lattice, formed by protein CMs, onto the trigonal SL (4,2). In this way the positions at 2-fold and 5-fold symmetry axes correspond to the centers of capsomers and remain devoid of charges (see Fig. 5c). Since the maturation transition is activated by the pH variation, it is reasonable to assume that the change in electrostatic interactions between proteins plays a key role in the process. Our estimates show that the decrease in pH from 7.6 to 5.0 (discussed in ref. 14 and 31) leads to an approximately two-fold decrease in protein net charge, from ∼11e0 to ∼5e0 (see Methods). In view of this, we tried to find a set of mechanical parameters that would allow us to reproduce the morphological changes of the capsid by varying the effective electrostatic interaction strength, but it became clear that in such a model the observed shape transition cannot be achieved solely by changing ζ. However, when in addition to decreasing electrostatic interaction strength we allow for variation of elastic properties of the shell, both morphologies can be reproduced in a sufficiently wide parameter range. For example, the procapsid shape can be reproduced at ζ = 12, γ = 1600, p = 5/6, and ld = 0.23R. Then, in order to transform it into the shape corresponding to the mature capsid a lower electrostatic interaction strength, one can use the following model parameters: γ = 150, p = 5/6, ζ = 3, and ld = 0.11R.
Surprisingly, it nevertheless turned out that both states can be accurately reproduced in the model shell, with elastic parameters γ = 200, p = 5/6 and constant electrostatic coupling strength ζ = 3.65, on varying the screening length ld only, as shown in Fig. 5. Panels (c) and (d) show two model states with ld = 0.23R (≈38.9 Å) and ld = 0.13R (≈21.3 Å), corresponding to immature and mature capsids, respectively. Note that on the figure scale, these model shells are practically indistinguishable from the ones discussed in the previous paragraph. Upon transition from (c) to (d), the average radius of the model shell decreases by 14% and both the initial and final shapes coincide almost perfectly with real structures (see Fig. 5a and b). Hexamers also follow the experimentally observed trend and symmetrize from Ah = 2.6 × 10−3 to 4 × 10−4 (see Fig. 5e and f). Also note that unlike in the shell shown in Fig. 4, no hysteresis is observed, since mirror symmetry is absent from the start (see Fig. 5e and f).
This unusual transformation mechanism can be explained by the fact that the above-mentioned decrease in pH level not only reduces the net charges of the proteins but also affects their distribution, which in our simplified model, can be described as an effective reduction in the effective screening length. In this context, we note that in the mature state the screening length ld appears to be about half of the triangulation edge, meaning that only the nearest proteins interact with each other. Such an interaction could be associated not only with electrostatics but possibly also with short-range steric repulsion. To clarify this point, let us note that the morphology of the mature capsid can be reproduced for an uncharged shell, in which the equilibrium lengths (see eqn (M2)) of the edges belonging to the trihexagonal lattice (i.e. edges connecting the centers of nearest proteins) are reduced. Another possible explanation could be related to the details of the protein charge dissociation that can in some cases lead to effective attraction or at least diminished repulsion between identical proteins. In fact, under certain solution conditions32–34 competition between amino acid dissociation and electrostatic interaction can cause spontaneous symmetry breaking, resulting in electrostatically generated attraction and thus fundamentally modifying the energetics of the capsid shell.
Shape genesis of coronavirus shells
Coronaviruses, unlike most other viruses, possess a polymorphic shell which can be spherical, ellipsoidal, cylindrical, and even conical.21 The shell consists of a lipid membrane with a large number of embedded structural proteins, M proteins being the most abundant.21,35,36 It protects a helical nucleocapsid formed by genomic RNA complexed with nucleoproteins. To infect cells, the virus uses protruding elongated spikes, which are formed by three S-proteins and embedded into its lipid membrane.37 The spike distribution in the coronavirus shell correlates broadly with its shape.21 In spherical shells, the spikes are uniformly distributed; in conical and tubular ones, they are grouped at one and two ends of the shell, accordingly. Thus, spikes are located at those regions of the coronavirus surface where its Gaussian curvature is maximal. In this section, we utilize the developed electro-elastic model to explain the observed relationship between localization of the spikes and the shape of coronavirus shells.In the environment of the endoplasmic reticulum–Golgi intermediate compartment (pH ≈ 7.0), where assembly of the virions takes place,38,39 S-proteins constituting coronavirus spikes are charged.37,40,41 For example, according to our estimates, the net charge of the SARS-CoV-2 spike should be around ∼−14.5e0, consistent with ref. 42. In coronaviruses, the spike density can be relatively high: a shell can have up to 100 spikes.21 Thus, sufficient repulsive electrostatic forces between similarly charged spike heads might locally bend the shell. Below we first examine the effect of electrostatic spike repulsion on the membrane shape and then analyze another possible mechanism of the membrane bending that is associated with the curvature generation by M proteins that readily bind to the spikes.
Taking into account the morphology of virus particles,42 we model spikes as point charges located at normals to the centers of the faces of the shell triangulation at a uniform height h = 0.3R and limit the minimal distance between spike attachment sites to h.
Since a lipid membrane provides a structural basis for the shells of coronaviruses, their elastic properties therefore differ essentially from those of icosahedral protein capsids analyzed in the previous sections. Recall that lipid membranes are often considered as incompressible 2D liquids with zero shear rigidity μ = 0 and nonzero bending rigidity.43,44 Nevertheless, high concentration of M proteins, interacting with one another,21 reinforces coronavirus shell and can make it much more rigid than the ordinary pure lipid vesicles. It thus seems reasonable to model the lipid–protein coronavirus membrane as a shell with nonzero shear rigidity and describe it by the same set of elastic parameters as the previously considered protein shells. Taking into account the ability of M proteins to form locally organized clusters and bind to S-proteins, we assume that membrane regions with high concentration of spikes have a higher in-plane rigidity.
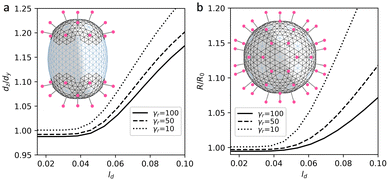
In the proposed curvature-inducing electrostatic mechanism, an initially spherical membrane is deformed by interaction between charged spikes. We use the model shells based on the achiral SL (8,0) with ζ = 5 and “base” elastic parameters γ ≈ 10 and p = 11/12 to properly encode its quasi-lipid nature. In more rigid region, for each triangular finite element with a charge corresponding to a spike and twelve of its nearest neighbors, we set the elastic parameters to γr ≈ 100 and p = 2/3. This increases both λ and μ coefficients since bending rigidity associated with all shell edges is assumed to be constant. Let us note that for the considered shells with inhomogeneous elastic properties, at ζ = 0 the ground state remains to be a sphere for any distribution of regions with higher rigidity (see more detail in Methods). Fig. 6a explains the electrostatic mechanism and demonstrates how localization of the spikes at the opposite poles of the spherical membrane elongates it. Importantly, by varying spike distribution one can also obtain other characteristic shapes of coronavirus shells, which are shown in insert of Fig. 7.
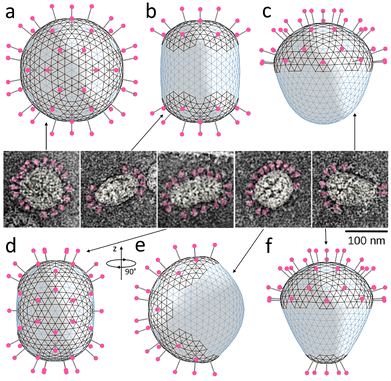 | ||
| Fig. 7 Relation between spike distribution and shape of SARS-CoV particles. (a–d and f) Model shells with different numbers and distributions of spikes located in more rigid lipid–protein regions with positive spontaneous curvature (the corresponding edges are shown in black). The shells contain 80, 40, 20, 42, and 25 spikes, respectively. (e) The same shell as in panel (d) turned by 90° around the vertical axis. Insert in the center contains microscopic images adopted from ref. 21 and shows typically observed morphologies of virus particles. Spikes are highlighted in magenta. | ||
Let us examine this electrostatic curvature generating mechanism in more detail. Fig. 6a shows that in order to elongate the spherical shell by 17% (at the considered value of ζ and elastic parameters), the screening length should be of the order of 0.1R. A more elongated morphologies, which are typical of coronaviruses, can be obtained by decreasing γr. However, naturally, at lower values of γr, repulsion between neighboring spikes stretches regions of their localization more and overall increases the size of the shell (see Fig. 6b). In contrast, however, according to ref. 21, virus particles with higher density of spikes have on average lower radii.
Also, we note that since the average radius of coronavirus shell is around 50 nm (see insert of Fig. 7), the value ld ≈ 0.1R corresponds to the screening length of 5 nm, which is 5 times higher than physiological value λ0; see Methods. If we consider finite size of the coronavirus spike heads, we can estimate an average distance between surfaces of the neighboring spikes as 4–6 nm, which is also substantially larger than λ0. Thus, the influence of electrostatic repulsion between the spikes most likely cannot be the key factor determining the shapes of the polymorphic envelopes of coronaviruses: in fact, the observed shapes of the shells can be reproduced only by assuming an anomalously small value of electrostatic screening.
The second well-known mechanism we consider here is associated with presumed ability of M proteins to locally increase spontaneous curvature of the lipid membrane.21,54,55 Following ref. 21, more recent papers54,55 assume that by binding with the spikes, M proteins change their conformation and become able to increase spontaneous curvature of the membrane, which consequently decreases the average radius of the virus particle. This effect can be reproduced also in the framework of our model by introducing a nonzero spontaneous curvature to the system energy. In the continuum approximation described by eqn (1), this can be achieved by substituting H with H-2/R0, where R0 is a radius of spontaneous curvature arising due to M-proteins co-localization with protein spikes. Modification of the discrete model is described in Methods.
Fig. 7 shows that all the characteristic morphologies can be reproduced by simply placing the spikes on the surface of the spherical shell, with their distribution roughly matching the experimentally observed one, and minimizing the free energy of the system. We follow our assumption that the regions containing the spikes are more rigid; therefore, we use the same material constants as in the previously considered mechanism. Additionally, we introduce the positive spontaneous curvature (α0 = 0.3) associated with the edges located in more rigid regions; see more details in Methods. Since, as we have previously discussed, electrostatic repulsion between spikes should be relatively weak, we neglect it in further simulations (ζ = 0).
As expected, homogeneous spike distribution preserves the initial spherical shape of the shell (panel (a)) making it smaller. Placing groups of 20 spikes surrounded by regions with positive spontaneous curvature at two opposite ends of the shell, induces an axisymmetric cylindrical shape (panel (b)), while placing spikes exclusively (panel (c)) or mostly (panel (f)) at one end induces a conical shape. Finally, panels (d) and (e) show the same shell, which depending on the orientation, is similar in shape either to the third or the fourth coronavirus particle in the insert.
Let us note that in this purely mechanical limit, Poisson ratio has negligible effect on the resulting shapes. Moreover, the variety of coronavirus shapes can be obtained without increasing rigidity of the regions of the spike localization. Nonetheless, we kept the rigidity inhomogeneous to stay consistent with our initial assumption based on experimental facts.
Conclusion
We analyzed changes in the local structure and overall shape of proteinaceous shells, occurring as a consequence of electrostatic interactions between the shell proteins. These morphological changes are typical of many capsids since maturing viruses usually migrate through various cell regions with different pH levels, in the process modifying partial charges of ionizable amino acids in proteins and thus changing the electrostatic interactions between them.45 Moreover, multiple experimental studies show that the same modifications of capsids, analogous to those observed in vivo, can be reproduced also in vitro by modifying pH or salinity of the buffer solution. Note that during the virus maturation other mechanisms, not necessarily related to electrostatics, are also possible and have indeed been proposed,13,23,46,47 the most notable is the capsid faceting due to the thinning of the shell walls.16To study structural transformations in icosahedral protein shells, we first constructed their symmetrized models. Being based on the icosahedral spherical lattices, these model shells consist of identical triangular finite elements, characterized by two independent 2D Lamé coefficients, in distinction from the previous approaches13,16,17,19 based upon their equality. The third material characteristic of the model is the bending rigidity, which controls the resistance of the shell assembly to the variation of angles between neighboring finite elements. The electrostatic interactions are modeled in the standard Debye–Huckel limit as screened Coulomb interactions between point charges, characterized by effective electrostatic coupling strength parameter. We assume that these model charges correspond to total protein charges, located at the centers of mass of individual proteins. In the shells considered, these centers of mass then form an approximately honeycomb or trihexagonal spherical lattice, commensurate with the triangular spherical lattice used to accommodate the triangular finite elements. Our approach thus combines the quasi-continuum description of elastic properties with the discrete charge distribution, reflecting the structure of real protein shells. Importantly, the use of triangulations with a relatively low number of vertices not only reduces the computational resources required for energy minimization, but also avoids any possible problems associated with the application of point forces and moments to an elastic shell considered as a continuum.16
Despite its relative simplicity, the proposed approach allowed us to reproduce structural features of the virus shells that are impossible to model using homogeneous charge distribution. One of such features is the hexamer deformation that occurs due to the repulsion between protein charges. This effect is observed, for example, in the spherical procapsid of the P22 bacteriophage and disappears in a larger mature faceted capsid, with centers of protein charges being located further away from each other. We were also able to describe a similar transition in the shell of Nudarelia capensis omega virus (NωV), which in its mature form contains more regular hexamers and has a smaller radius than the immature state. We reproduced the maturation transformation of this shell by fitting the parameters of the electrostatic interactions in our model.
The approach that we developed also allowed us to extend the analysis of shape generation and obtain model shells that exhibit morphologies remarkably similar to polymorphic lipid–protein shells of coronaviruses. First, for that purpose, we have modeled the elongated protein spikes, covering coronavirus particles, as point charges residing on the local surface normals at a finite distance away from the membrane surface. We demonstrated that weakly-screened repulsion between protruding spikes curves the shell, and in principle could explain the experimentally observed correlation between spike distribution and shapes of coronavirus particles, but is most likely not a key factor determining shell morphology. The second investigated mechanism of the shell shaping is more probable and relies on the ability of M-proteins, residing in specific conformation, to generate spontaneous curvature in lipid–protein membranes of coronaviruses.
To assess the possible applications of our findings, let us stress that both, the integration of spikes into the shells of coronaviruses, as well as the maturation of the virus capsids, are pivotal for the formation of infection capable virions. The electro-elastic model that we proposed adds some rationalizing principles underlying these processes and should be useful in searching for new antiviral strategies targeted at their disruption. Another promising area of application and development of this model could be in the context of bioinspired protein nanocontainers for targeted delivery and sustained drug release, since nanocontainers are often designed to operate based on the same principles as pH induced maturation of viral capsids.
Methods
Calculating net charges of proteins
Following our previous works,48–50 in order to estimate the net charges of proteins at different pH levels, we first calculated charges of their ionizable amino acid residues, using the Henderson–Hasselbalch equation: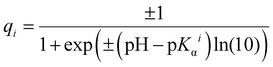 | (M1) |
Screening length and Debye–Huckel approximation
To estimate screening length λ0, the following equation48–50 is used: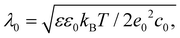 | (M2) |
We based our approach on an approximate theory of electrostatic interactions, disregarding the many possibly important mechanisms modifying its nature and spatial dependence. Its parameters should therefore be understood as effective ones, being dependent on the details of all the mechanisms that are not included explicitly in the interaction: short range repulsion, charge regulation effects, dielectric constant variation etc.52
Electro-elastic energy of the discrete shell
Elastic energy of the shell considered in continuum approximation (1) for the discretized shell reads: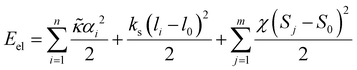 | (M3) |
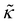 is the microscopic bending rigidity and αi is the angle between normal vectors of two triangles (triangular finite elements) sharing i-th edge, ks is the stretching rigidity of the edges/bonds, li is i-th edge length and l0 its equilibrium value. The second sum in eqn (M3) runs over all m triangles of the shell, χ is the second material coefficient characterizing in plane rigidity of the shell, Sj is j-th triangle area and
is the microscopic bending rigidity and αi is the angle between normal vectors of two triangles (triangular finite elements) sharing i-th edge, ks is the stretching rigidity of the edges/bonds, li is i-th edge length and l0 its equilibrium value. The second sum in eqn (M3) runs over all m triangles of the shell, χ is the second material coefficient characterizing in plane rigidity of the shell, Sj is j-th triangle area and 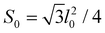 is its equilibrium value. If m → ∞, one can establish the relationship between the parameters in the discrete and continuous models by comparing expressions for the energy area density. Namely, two-dimensional Lamé parameters and bending rigidity can be expressed in terms of microscopic parameters χ, ks, κ as:
is its equilibrium value. If m → ∞, one can establish the relationship between the parameters in the discrete and continuous models by comparing expressions for the energy area density. Namely, two-dimensional Lamé parameters and bending rigidity can be expressed in terms of microscopic parameters χ, ks, κ as: 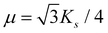 ,
, 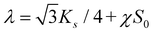 ,
, 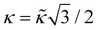 . For the spherical shell the total area of the triangulation mS0 is approximately equal to 4πR2 and thus m = 16πR2/l02.
. For the spherical shell the total area of the triangulation mS0 is approximately equal to 4πR2 and thus m = 16πR2/l02.
Dimensionless electro-elastic coupling energy (see eqn (1) and (2)) of the discrete shell takes the following form:
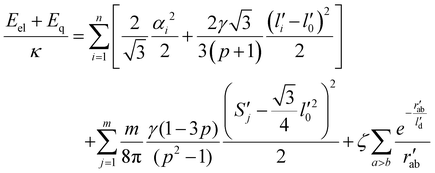 | (M4) |
When calculating shapes of coronavirus shells, the equilibrium sizes of triangular finite elements were assumed to coincide with their sizes in a spherical shell of a unit radius. Such a redefinition of the equilibrium lengths and areas of finite elements allows us to exclude the effect of shell faceting. However, we note that for small values of γ and γr, that were used for shell modelling, this redefinition of the equilibrium values has only minor influence on the resulting shapes.
In the approach assuming that regions of spike localization have nonzero spontaneous curvature, we substitute αi2 in eqn (M4) with (αi − αi0), where αi0 equals zero for all the edges except for the ones residing in the more rigid regions, where it equals α0. Following the work55 we approximated (αi − αi0)2 as −2cos(αi − αi0) + 2. Further, considering that 2cos(αi − αi0) = cos(αi)cos(αi0) + sin(αi)sin(αi0), we calculated cos(αi) as dot product of normal vectors corresponding to two nearest triangles. We recommend to calculate the value of sin(αi) as the mixed product of the same two normal vectors with a unit vector that is parallel to the common edge of these triangles. The proper sign of sin(αi) is ensured by the correct choice of the unit vector director. This method of calculation allows for faster minimization process since it does not require taking root of values that are close to zero.
Author contributions
R. P. conceived of the idea that the capsid morphology is strongly dependent on the charge distribution in the shell. S. R. proposed the mathematical model of the hexamer deformation. I. G. with the help of D. R. composed programs and performed most calculations. O. K. contributed to the interpretation of results and carried out their visualization. All the authors participated in discussion and writing the article.Data availability
This study was carried out using publicly available structural data from RCSB Protein Data Bank (RCSB PDB)53 at https://www.rcsb.org with structure ID's mentioned throughout the text.Conflicts of interest
There are no conflicts to declare.Acknowledgements
I. G., D. S., O. K. and S. R. acknowledge financial support from the Russian Science Foundation, grant No. 22-12-00105. R. P. acknowledges funding from the Key Project No. 12034019 of the Natural Science Foundation of China.References
- A. J. B. Kreutzberger, A. Sanyal, A. Saminathan, L. M. Bloyet, S. Stumpf, Z. Liu, R. Ojha, M. T. Patjas, A. Geneid, G. Scanavachi, C. A. Doyle, E. Somerville, R. B. Da Cunha Correia, G. Di Caprio, S. Toppila-Salmi, A. Mäkitie, V. Kiessling, O. Vapalahti, S. P. J. Whelan, G. Balistreri and T. Kirchhausen, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2209514119 CrossRef CAS PubMed.
- J. J. Skehel and D. C. Wiley, Annu. Rev. Biochem., 2000, 69, 531–569 CrossRef CAS PubMed.
- A. Helenius, M. Marsh and J. White, J. Gen. Virol., 1982, 58, 47–61 CrossRef CAS PubMed.
- T. Zhou, Y. Tsybovsky, J. Gorman, M. Rapp, G. Cerutti, G. Y. Chuang, P. S. Katsamba, J. M. Sampson, A. Schön, J. Bimela, J. C. Boyington, A. Nazzari, A. S. Olia, W. Shi, M. Sastry, T. Stephens, J. Stuckey, I. T. Teng, P. Wang, S. Wang, B. Zhang, R. A. Friesner, D. D. Ho, J. R. Mascola, L. Shapiro and P. D. Kwong, Cell Host Microbe, 2020, 28, 867–879 CrossRef CAS.
- L. Li, J. Jose, Y. Xiang, R. J. Kuhn and M. G. Rossmann, Nature, 2010, 468, 705–708 CrossRef CAS.
- J. White, J. Kartenbeck and A. Helenius, J. Cell Biol., 1980, 87, 264–272 CrossRef CAS PubMed.
- T. Y. Tan, G. Fibriansah and S. M. Lok, PLoS Pathog., 2020, 16, e1008542 CrossRef.
- D. Veesler and J. E. Johnson, Annu. Rev. Biophys., 2012, 41, 473–496 CrossRef PubMed.
- L. Gan, J. A. Speir, J. F. Conway, G. Lander, N. Cheng, B. A. Firek, R. W. Hendrix, R. L. Duda, L. Liljas and J. E. Johnson, Structure, 2006, 14, 1655–1665 CrossRef.
- D. H. Chen, M. L. Baker, C. F. Hryc, F. DiMaio, J. Jakana, W. Wu, M. Dougherty, C. Haase-Pettingell, M. F. Schmid, W. Jiang, D. Baker, J. A. King and W. Chiu, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1355–1360 CrossRef PubMed.
- I. Gertsman, L. Gan, M. Guttman, K. Lee, J. A. Speir, R. L. Duda, R. W. Hendrix, E. A. Komives and J. E. Johnson, Nature, 2009, 458, 646–650 CrossRef PubMed.
- D. Nemecek, N. Cheng, J. Qiao, L. Mindich, A. C. Steven and J. B. Heymann, J. Mol. Biol., 2011, 414, 260–271 CrossRef PubMed.
- O. V. Konevtsova, D. S. Roshal, R. Podgornik and S. B. Rochal, Soft Matter, 2020, 16, 9383–9392 RSC.
- R. Castells-Graells, J. R. S. Ribeiro, T. Domitrovic, E. L. Hesketh, C. A. Scarff, J. E. Johnson, N. A. Ranson, D. M. Lawson and G. P. Lomonossoff, Commun. Biol., 2021, 4, 1–12 CrossRef.
- V. V. Pimonov, O. V. Konevtsova and S. B. Rochal, Acta Crystallogr., Sect. A: Found. Adv., 2019, 75, 135–141 CrossRef.
- J. Lidmar, L. Mirny and D. R. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 1–11 CrossRef PubMed.
- D. Roshal, O. Konevtsova, A. Lošdorfer Božič, R. Podgornik and S. Rochal, Sci. Rep., 2019, 9, 5341 CrossRef PubMed.
- A. Šiber and R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 1–5 CrossRef.
- M. Widom, J. Lidmar and D. R. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 1–11 CrossRef PubMed.
- T. W. Giessen, B. J. Orlando, A. A. Verdegaal, M. G. Chambers, J. Gardener, D. C. Bell, G. Birrane, M. Liao and P. A. Silver, eLife, 2019, 8, e46070 CrossRef PubMed.
- B. W. Neuman, G. Kiss, A. H. Kunding, D. Bhella, M. F. Baksh, S. Connelly, B. Droese, J. P. Klaus, S. Makino, S. G. Sawicki, S. G. Siddell, D. G. Stamou, I. A. Wilson, P. Kuhn and M. J. Buchmeier, J. Struct. Biol., 2011, 174, 11–22 CrossRef.
- S. B. Rochal, O. V. Konevtsova, A. E. Myasnikova and V. L. Lorman, Nanoscale, 2016, 8, 16976–16988 RSC.
- S. B. Rochal, O. V. Konevtsova and V. L. Lorman, Nanoscale, 2017, 9, 12449–12460 RSC.
- L. Landau and E. Lifshitz, Theory of Elasticity Vol. 7, Pergamon Press Ltd, Bristol, 1970 Search PubMed.
- D. L. Caspar and A. Klug, Cold Spring Harbor Symp. Quant. Biol., 1962, 27, 1–24 CrossRef.
- M. H. Parker and P. E. Prevelige, Virology, 1998, 250, 337–349 CrossRef.
- V. A. Essus, G. S. E. Souza Júnior, G. H. P. Nunes, J. dos S. Oliveira, B. M. de Faria, L. F. Romão and J. R. Cortines, Viruses, 2023, 15, 516 CrossRef PubMed.
- G. P. Padilla-Meier and C. M. Teschke, J. Mol. Biol., 2011, 410, 226 CrossRef.
- M. Tomasicchio, P. A. Venter, K. H. J. Gordon, T. N. Hanzlik and R. A. Dorrington, J. Gen. Virol., 2007, 88, 1576–1582 CrossRef PubMed.
- D. K. Agrawal and J. E. Johnson, Virology, 1995, 207, 89–97 CrossRef.
- D. J. Taylor, N. K. Krishna, M. A. Canady, A. Schneemann and J. E. Johnson, J. Virol., 2002, 76, 9972–9980 CrossRef PubMed.
- A. Majee, M. Bier and R. Podgornik, Soft Matter, 2018, 14, 985–991 RSC.
- A. Majee, M. Bier, R. Blossey and R. Podgornik, Phys. Rev. Res., 2020, 2, 043417 CrossRef.
- A. Majee, M. Bier, R. Blossey and R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2019, 100, 050601 CrossRef PubMed.
- E. A. J. Alsaadi and I. M. Jones, Future Virol., 2019, 14, 275–286 CrossRef PubMed.
- Z. Zhang, N. Nomura, Y. Muramoto, T. Ekimoto, T. Uemura, K. Liu, M. Yui, N. Kono, J. Aoki, M. Ikeguchi, T. Noda, S. Iwata, U. Ohto and T. Shimizu, Nat. Commun., 2022, 13, 1–12 Search PubMed.
- D. Lauster, K. Osterrieder, R. Haag, M. Ballauff and A. Herrmann, Front. Microbiol., 2023, 14, 1169547 CrossRef.
- J. Saraste and K. Prydz, Cells, 2021, 10, 503 CrossRef PubMed.
- W. A. Wang, A. Carreras-Sureda and N. Demaurex, J. Cell Sci., 2023, 136, jcs260685 CrossRef.
- B. Jawad, P. Adhikari, R. Podgornik and W.-Y. Ching, J. Phys. Chem. Lett., 2022, 13, 3915–3921 CrossRef PubMed.
- P. Adhikari, et al. , Phys. Chem. Chem. Phys., 2020, 22, 18272–18283 RSC.
- L. Javidpour, A. Božič, A. Naji and R. Podgornik, Soft Matter, 2021, 17, 4296–4303 RSC.
- I. Y. Golushko, S. B. Rochal and V. L. Lorman, Eur. Phys. J. E, 2015, 38, 1–7 CrossRef PubMed.
- I. Y. Golushko and S. B. Rochal, J. Exp. Theor. Phys., 2016, 122, 169–175 CrossRef.
- R. Zandi, B. Dragnea, A. Travesset and R. Podgornik, Phys. Rep., 2020, 847, 1–102 CrossRef.
- O. V. Konevtsova, V. L. Lorman and S. B. Rochal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2016, 93, 1–11 CrossRef PubMed.
- R. F. Bruinsma and W. S. Klug, Annu. Rev. Condens. Matter Phys., 2015, 6, 245–268 CrossRef.
- S. B. Rochal, O. V. Konevtsova, D. S. Roshal, A. Božič, I. Y. Golushko and R. Podgornik, Nanoscale Adv., 2022, 4, 4677–4688 RSC.
- O. V. Konevtsova, I. Y. Golushko, R. Podgornik and S. B. Rochal, Nanoscale Adv., 2023, 5, 4140–4148 RSC.
- O. V. Konevtsova, I. Y. Golushko, R. Podgornik and S. B. Rochal, Biomater. Sci., 2022, 11, 225–234 RSC.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Press, 2016 Search PubMed.
- R. Podgornik and D. Andelman, J. Club Condens. Matter Phys., 2020 DOI:10.36471/JCCM_September_2020_02.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef PubMed.
- S. Li and R. Zandi, Viruses, 2022, 14, 2089 CrossRef PubMed.
- Y. Zhang, S. Anbir, J. McTiernan, S. Li, M. Worcester, P. Mishra, M. E. Colvin, A. Gopinathan, U. Mohideen, R. Zandi and T. E. Kuhlman, Sci. Adv., 2024, 10, 7030 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Movie 1: deformation of hexamers in a shell modelling encapsulin iron storage compartment; Movie 2: model of structural changes in the Nudarelia capensis omega virus upon maturation. See DOI: https://doi.org/10.1039/d4nr02612h |
| This journal is © The Royal Society of Chemistry 2024 |