Open Access Article
Open Access ArticleExploring nitrogen-mediated effects on Fe and Cu cluster development in graphene: a DFT study†
L. A.
Alvarado-Leal
*a,
J. I.
Paez-Ornelas
 *b,
M. A.
Ruiz-Robles
a,
J.
Guerrero-Sánchez
*b,
M. A.
Ruiz-Robles
a,
J.
Guerrero-Sánchez
 b,
J. M.
Romo-Herrera
b,
J. M.
Romo-Herrera
 *b,
H. N.
Fernández-Escamilla
a,
Noboru
Takeuchi
b and
E. G.
Perez-Tijerina
a
*b,
H. N.
Fernández-Escamilla
a,
Noboru
Takeuchi
b and
E. G.
Perez-Tijerina
a
aCICFIM Facultad de Ciencias Físico Matemáticas, Universidad Autónoma de Nuevo León, San Nicolás de los Garza, Nuevo León, Código Postal 66450, Mexico. E-mail: luis.alvaradoll@uanl.edu.mx; jmromo.at.ens.cnyn.unam.mx
bCentro de Nanociencias y Nanotecnología, Universidad Nacional Autónoma de México, Apartado Postal 14, Ensenada Baja California, Código Postal 22800, Mexico
First published on 3rd October 2024
Abstract
The controlled growth and stability of transition metal clusters on N-doped materials have become the subject of intense investigation for unveiling comprehension on the cluster growth evolution. In this study, we investigated the growth mechanisms of non-magnetic (copper) and magnetic (iron) clusters on graphene with two atomic vacancies, with and without pyridinic nitrogen (N). Our results determine the role of pyridinic N in the growth and physicochemical properties of the mentioned metal clusters. In an N environment, Cu grows perpendicularly, whereas under N-deficient conditions, the clusters agglomerate. Fe cumulate-type clusters are formed regardless of the presence of N. However, N causes the Fe clusters to rise over one side of the surface without deforming the monolayer; meanwhile, in the absence of N, the Fe clusters protrude from both sides of the monolayer. Remarkably, the presence of N makes it feasible to induce magnetization in the Cun–N4V2 systems and aid in focalizing the magnetic properties on the Fe clusters for the Fen–N4V2 case. These findings offer insights into the role of N in cluster growth, with potential implications for diverse applications, including magnetic and electrocatalytic materials.
1. Introduction
In recent years, the integration of graphene and transition metals has emerged as a promising route in materials science, offering unique opportunities for tailoring electronic, magnetic, and catalytic properties at the nanoscale.1,2 In particular, the controlled growth and stability of transition metal clusters on graphene surfaces have become the subject of intense investigation.3,4Recent studies have demonstrated that when small groups of Ni, Pd, and Pt atoms are adsorbed on a graphene layer, they generally retain the structural characteristics of gas-phase atomic groups.5,6 However, the strength of their interaction weakens as the size of the metal groups increases.5–8 Moreover, researchers have explored the adsorption of transition metal atoms on graphene to modify their electronic, magnetic, and surface reactivity properties. This exploration holds significant implications in diverse fields, including spintronics, nanomagnetism, data storage, and catalysis.9–12
Parallel investigations have scrutinized the interactions between metal clusters and graphene sheets, revealing that interfacial energy substantially influences the stability of these metal/graphene systems.13 Similar interaction energies are observed for specific cluster sizes, even when oriented differently upon contact with the graphene material.13 Another research strand is the potential of employing diverse defective graphene sheets to support transition metals.14 It was observed that metals form stronger bonds with defective graphene, thereby contributing to their stabilization without significantly compromising the magnetic properties. Notably, magnetic anisotropy is boosted substantially when certain metals are deposited on defective graphene despite the intrinsic non-magnetic nature of carbon.15,16
Recent density functional theory studies have advanced our understanding of the structural, electronic, and magnetic properties of small transition metal clusters. For iron clusters (Fen, n ≤ 17), significant findings include “magic numbers” at specific sizes (n = 6, 8, 10, 13, and 15) and noncollinear magnetic structures influenced by the Jahn–Teller effect, revealing high magnetic moments across varying configurations. The chemical reactivity of these clusters is primarily influenced by the coordination of individual atoms, and the addition of cobalt (Co) has been shown to enhance magnetic properties through structural rearrangements, providing insights into potential catalytic and magnetic applications.17–20 Additionally, studies on small copper clusters (Cun, n ≤ 15) have demonstrated a preference for compact structures and identified unique growth pathways such as triangular and pentagonal bipyramidal arrangements. Furthermore, copper clusters on graphene quantum dots (GQDs) exhibit enhanced binding energy and conductivity, particularly when vacancies are present in graphene, highlighting new strategies for catalytic applications.21,22
Multiple variables, including the chemical environment, can impact the incorporation or growth of metals on the graphene network. These variables must be carefully analyzed to determine the factors that could favor or disfavor the process to obtain the desired metal/graphene system. Whether by cluster aggregation or growth, from the design of a single-atom catalyst (SAC) to a specific (few atoms) cluster, the process must be controllable and reproducible.
The performance of metallic SACs can be adversely affected by a considerable increase in the size of metal clusters and increased surface roughness, leading to a decrease in efficiency.23–25 The primary objectives when trying to synthesize metallic SACs are high dispersion of individual atoms on suitable supports, i.e., graphitic surfaces,26–29 and reduction of contamination due to byproducts during synthesis. The most reasonable option to conduct experimental investigations on metallic SACs is the vacuum deposition method due to its good control over cluster size30,31 and non-byproduct formation during synthesis. Therefore, this is a great opportunity for synthesis methods employing mass-selected and soft-landing techniques32–35 in combination with magnetron sputtering36 or inert gas condensation37–39 due to their high atomic dispersion on substrates,40 highly controlled cluster size,41,42 and exceptionally low contamination compared with chemical methods that utilize molecules as stabilizers and chemical reactants as precursors of metallic atoms,43 such as iron (Fe) single atoms and clusters.44–48
The incorporation of nitrogen into the carbon lattice has been widely explored for many reasons, such as modifying graphene's electronic properties and enabling fine-tuning of its electrical conductivity.49,50 It is reported that nitrogen stabilizes carbon lattices with atomic vacancies or structural deformations. N-doped systems, such as N-doped nanotubes, are also widely applied in catalytic reactions.51,52 Furthermore, nitrogen can facilitate strong interactions with transition metal atoms, potentially influencing cluster nucleation and growth.53,54 Recent studies have shown that N-doped graphene-supported clusters, such as Fe3@N4C16, exhibit enhanced electrocatalytic performance in the electrochemical nitrogen reduction reaction (eNRR) due to the modulation of the local electronic environment by nitrogen coordination.55
Transition metal single-atom catalysts (SACs) and clusters supported on graphene have demonstrated exceptional catalytic activity in various chemical reactions, and the ability to control their formation and stability through nitrogen doping can open new avenues for designing efficient catalysts.56–58 In this study, we employed density functional theory (DFT) calculations to explore the effects of nitrogen on the formation and stability of magnetic and non-magnetic clusters (Fe and Cu, respectively) on graphene substrates. Specifically, we investigated the cluster aggregation and growth mechanisms from one- to six-atom clusters at carbon vacancies with and without pyridinic nitrogen, shedding light on the underlying mechanisms and potential applications of these composite systems. The outcomes of this research could drive innovations in various fields, from catalysis to advanced electronic devices.
2. Methods
Spin-polarized DFT calculations were conducted using the Quantum ESPRESSO package.59–61 We employed ultrasoft pseudopotentials with the GGA–PBE approach (Perdew, Burke, and Ernzerhof) for the exchange–correlation (XC) potential.62 Additionally, we accounted for long-range dispersion-corrected van der Waals interactions utilizing the Grimme-D3 scheme.63 Kinetic energy cutoffs were set at 30 Ry and 240 Ry for the wave function and charge density, respectively. In geometric optimization, a Γ-centered Monkhorst–Pack mesh with k-point grids of 3 × 3 × 1 was applied for Brillouin zone integrations and 9 × 9 × 1 for electronic analysis.64 We included an empty space of 20 Å perpendicular to the monolayer to prevent self-interaction due to periodic boundary conditions. The investigation of cluster growth was carried out in a 5 × 5 periodicity supercell.3. Results and discussion
3.1. Substrates models TM0–NxV2
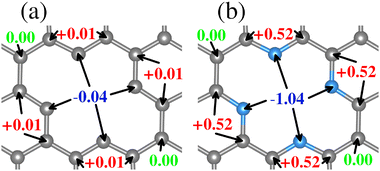
Structural deformations in the carbon lattice tend to favor the coalition between the carbon substrate and the metallic adatoms. It is reported in the literature that the graphene lattice with two continuous carbon vacancies induces a hole that traps a metal adatom and incorporates it into the graphene lattice, generating a single-atom catalyst (SAC) model.52 Therefore, for the initial phase of this study, we optimized the unit cell of the graphene structure to construct two carbon substrates where the cluster would interact. The optimized lattice parameter is a0 = 2.46 Å, in good agreement with the experimental value.65 Next, two graphene (5 × 5) models were built. The first one contains only a double vacancy (see Fig. 1(a)), whereas for the second model, we employed a graphene monolayer with two carbon vacancies that contain four pyridinic nitrogen atoms substituting four carbon atoms surrounding the double vacancy (see Fig. 1(b)).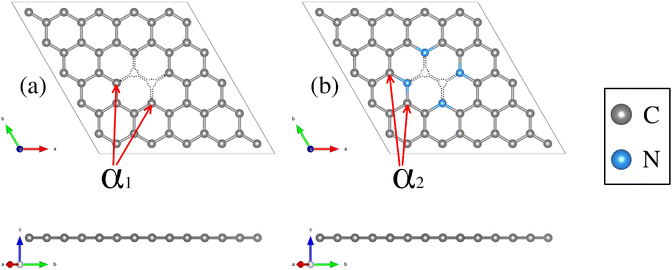 | ||
| Fig. 1 Structural top and side views of (a) TM–N0V2 and (b) TM–N4V2. The C and N atoms are depicted as gray and blue spheres. | ||
These configurations are denoted as TMn–N4V2 and TMn–N0V2, where TM = {Fe, Cu}, the index n in TMn represents the number of transition metal (TM) atoms incorporated into the model (where n varies from 0 to 6), Nx denotes the number of incorporated pyridinic nitrogen atoms in the monolayer (in this case, four or zero), and V2 stands for the count of vacancies within the graphene original lattice. We designate carbon atoms bonded to the TM as Cα1 and to N as Cα2, as illustrated in Fig. 1. Despite the disparity in nitrogen doping between both models, their structural resemblance is noteworthy, as both exhibit a planar structure, with C–C bond lengths of 1.42 Å and C–N bond lengths of 1.34 Å for the nitrogenated lattice.
Since both models contain different species around the vacancies where the TM atom is captured and incorporated into the lattice, we have characterized the charge distribution of the atoms around the vacancies of the clean substrates. To this end, we have employed the Bader charge (BC) formalism, which allows us to quantify the charge values associated with each atom.66,67 The values obtained allow us to measure changes in the charge distribution (ΔQ = evalence − Bader) and provide vital information on the substrate–adsorbate interaction.
Regarding the charge distribution of the substrate models, an RGB color code has been employed to differentiate between charge loss, unchanged, and gain, respectively, depending on the ΔQ values. The charge redistribution is practically negligible when the system lacks N (see Fig. 2(a)). The slight variation of ΔQ in the TM0–N0V2 model is around the carbon atoms of the vacancies due to the missing bonds. In contrast, for the TM0–N4V2 model (see Fig. 2(b)), it is evident that the ΔQ values for the pyridinic nitrogen atoms indicate their role in inducing a redistribution of charge within the system due to the difference in electronegativity between the C and N atoms. The N atoms become charge acceptors, gaining an average of −1.04e. In contrast, the Cα2 atoms donate charge with an average value of +0.52e, while the remaining carbon atoms in the graphene lattice remain neutral.
3.2. Cluster formation in TMn–NxV2 models
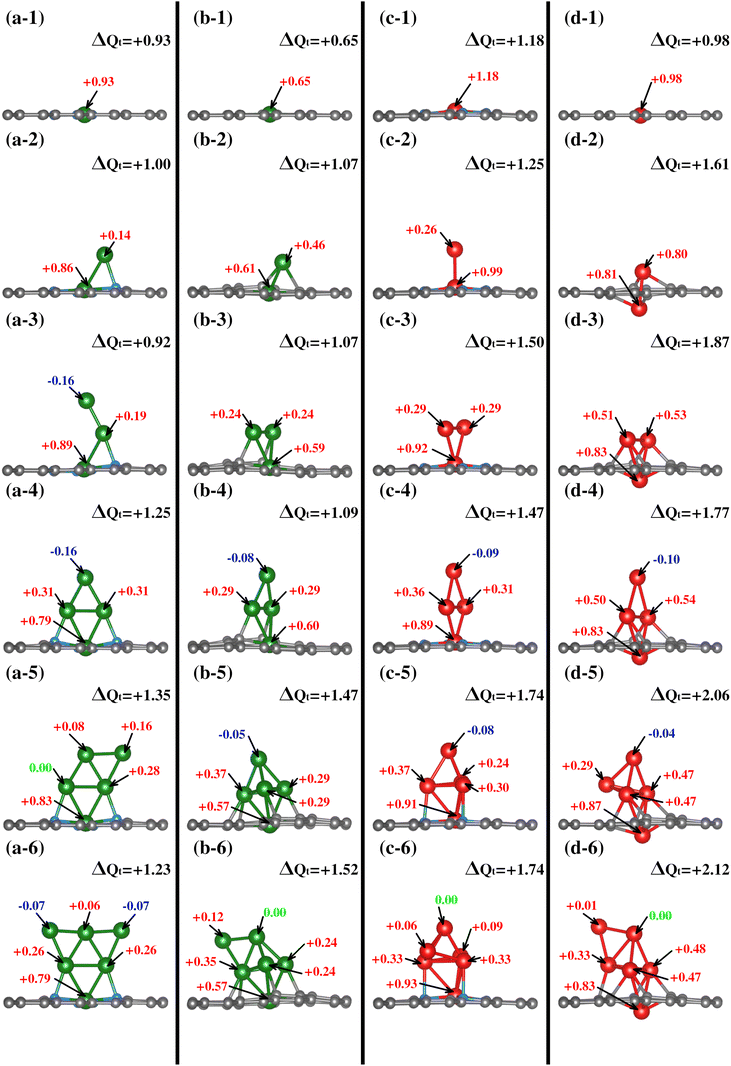
Once the TM0–NxV2 substrates were structurally characterized, the systematic incorporation of Fe or Cu atoms, from one to six, in both monolayers was studied to delve into how the chemical environment of the substrate N or Cα atoms influences the TMn adsorption states. This section thoroughly explores the one-by-one incorporation of TMn atoms to form a cluster geometric shape. It describes their structural evolution during the growth stages, charge distribution, and magnetic and electronic properties as the TMn cluster size increases. Furthermore, we do not combine TM species into the cluster. Fe and Cu elements were chosen due to their magnetic and non-magnetic characters in their corresponding bulk phases. However, the magnetic dipole moments in both TMn clusters were explored due to their small cluster size.The first incorporation of the TM atom (TM#1) into both substrates (TM1–NxV2) was favored at the C vacancies. These are the most favorable structural models for the initial TM adsorption, as depicted in Fig. 3(a-1), (b-1), (c-1), and (d-1) for Cu1–N4V2, Cu1–N0V2, Fe1–N4V2, and Fe1–N0V2, respectively, leading to a planar model with the formation of two pentagonal rings and two hexagonal rings (additional views of the adsorption states are shown in Fig. S1-1†).
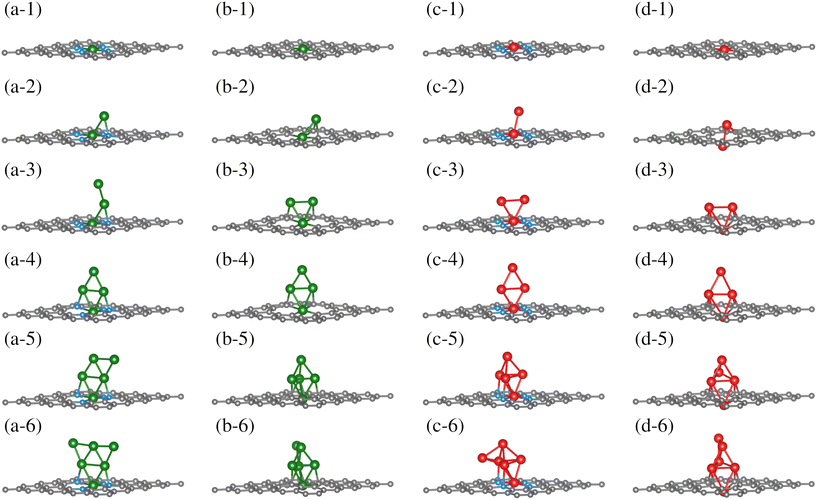 | ||
| Fig. 3 Growth mechanism of clusters in the TMn–NxV2 systems. The growth within the same system is observed horizontally, and the same growth stage is presented vertically for different systems. The C, N, Cu, and Fe atoms are depicted as dark, blue, green, and red spheres. For additional views of these configurations, refer to Fig. SI1.† | ||
For the next TM incorporation, the TM2–NxV2 minimum energy models are illustrated in Fig. 3(a-2, b-2, c-2 and d-2). In the case of Cu2–N4V2, the second Cu atom (Cu#2) achieves a two-fold coordination with bonds to the first Cu atom (Cu#1) and to a neighboring N atom in a bridge-type position, as shown in Fig. 3(a-2). Meanwhile, in the Cu2–N0V2 structure, Cu#2 is located over a hexagonal ring, reaching a three-fold coordination with Cu#1 and two Cα1 atoms, as depicted in Fig. 3(b-2). In contrast, the Fe2–N4V2 model's second Fe atom (Fe#2) does not form bonds with the lattice and remains in a top position above Fe#1, as shown in Fig. 3(c-2). Finally, in the Fe2–N0V2 structure, a subtle deformation in the carbon system emerges; Fe#2 binds to two Cα1 atoms, forming a hexagonal ring with the lattice and laying over the substrate. As a result, this model is no longer planar. Fe#2 bonds to Fe#1, driving it down the lattice and creating a symmetrical model. In this configuration, Fe#1 is now bonded to only two Cα1 atoms, instead of four Cα1 as in the TM1–N0V2 model, as shown in Fig. 3(d-2). The Fe2–N0V2 model does not present pentagonal rings since the Fe–Fe bond turns them into hexagonal non-planar rings (see Fig. S1-1†). Accordingly, there are already evident geometrical differences between the four TM2–NxV2 models. The differences are influenced by a combination of factors. For example, in the case of the copper models (Cu2–N4V2 and Cu2–N0V2), the second copper atom can form different types of bonds depending on its local environment. This is because copper can have different oxidation states and coordination geometries, which influence how it bonds with neighboring nitrogen and carbon atoms. In contrast, in the iron models (Fe2–N4V2 and Fe2–N0V2), the second iron atom tends to maintain a higher position above the carbon substrate. This may be due to the unique magnetic and electronic properties of iron, which can influence its interaction with the carbon network and affect its ability to form bonds with other atoms. Additionally, differences in the structure of the models may be related to the availability of binding sites and the stability of the formed bonds. For instance, in the case of the Fe2–N0V2 model, subtle deformation in the carbon network may be influenced by the interaction between the iron atoms and nearby carbon atoms, resulting in a more complex and non-planar structure.
The subsequent incorporation of TMs is related to the TMn–NxV2 models. An open structure constitutes the most stable model for Cu#3 on TM3–N4V2. Cu#3 only bonds with Cu#2, whereas the rest of the model remains unchanged, extending the Cu-cluster shape upward, as depicted in Fig. 3(a-3). On the other hand, Cu#3 in Cu3–N0V2 forms three chemical bonds, binding with the pair of Cu atoms (Cu#1 and Cu#2) and a Cα1. Moreover, the Cu#2 atom also reaches three-fold coordination. However, instead of being bound with two Cα1 as in Cu2–N0V2, it bounds to one Cα1 and the other two Cu atoms, forming a triangular shape, as shown in Fig. 3(b-3). The Cα1 atoms bonded to Cu atoms are in the same pentagonal ring. The Fe3–NxV2 model holds a triangular shape for the Fe atoms on both substrates. However, only Fe#1 is bonded to the four N atoms along the monolayer plane, while neither Fe#2 nor Fe#3 bonds to any substrate atom. In this configuration, the Fe3 triangle cluster lies perpendicular to the substrate plane, positioning Fe#2 and Fe#3 over opposite hexagonal rings (Fig. 3(c-3)). On the other hand, in Fe3–N0V2, since Fe#1 has crossed the substrate lattice, Fe#2 and Fe#3 bond to two Cα1 each. Fe3–N0V2 presents a more significant number of chemical bonds, as shown in Fig. 3(d-3). Furthermore, in Cu3–N0V2, Fe3–N4V2, and Fe3–N0V2, the TM cluster shape induces a similar chemical environment for TM#2 and TM#3; that is to say, these are atoms with equivalent bond symmetries.
The fourth TM incorporation generates the TM4–NxV2 models shown in Fig. 3(a-4, b-4, c-4 and d-4). Note that in the Cu4–NxV2 model, three Cu atoms are chemically bonded to the substrate. On the nitrogenated substrate, Cu#1 bonds to all N atoms; Cu#2 and Cu#4 bond to an opposite N atom in Cu4–N4V2 (Fig. 3(a-4)). Meanwhile, in Cu4–N0V2, Cu#4 is the Cu atom that does not bind to the substrate (Fig. 3(b-4)), and as described in the Cu3–N0V2 model, Cu#2 and Cu#3 bond to adjacent Cα1 in a pentagonal ring. For Fe4–N4V2, Fe#1 is still the only Fe atom of the Fe4 cluster that is chemically bonded to the substrate; the other three Fe atoms bond only to Fe atoms, adopting a perpendicular planar configuration (Fig. 3(c-4)). On the other hand, in Fe4–N0V2, Fe#4 is the only Fe atom that doesn't bond to the substrate, and the rest of the Fe atoms remain unchanged compared with the Fe3–N0V2 model (Fig. 3(c-4)). The TM4–NxV2 model form rhomboidal cluster shapes across the substrates except for Cu4–N0V2, where the rhombohedral cluster shape is planar and perpendicular to the monolayer (see Fig. S1(a–d)4†). Additionally, the TM4 cluster induces an identical adsorption position for TM#2 and TM#3, generating a triangular configuration with TM#1.
The subsequent incorporation generates the TM5–NxV2 models. For Cu#5 on the nitrogenated substrate (TM5–N4V2), a semi-triangular cluster shape is generated where Cu#5 is two-fold coordinated with the Cu#4 atom and a Cu atom that interacts with an N atom from the substrate (Fig. 3(a-5)). For the TM5–N0V2 substrate, the Cu#5 atom reaches a three-fold coordination with three Cu atoms, completing a rhombohedral shape (Fig. 3(b-5)). For the addition of Fe atoms, the Fe#5 atom also achieves a similar configuration to the previously described Cu#5 over the TM5–N4V2 substrate, while on TM5–N0V2 the same cluster shapes emerge. In this configurations, a pair of Fe atoms supporting the top Fe#5 atom of the rhombohedral cluster establishes an interaction with the surface.
Finally, we present the TM6–NxV2 models. In the Cu6–N4V2 model, the Cu6 cluster maintains its planar arrangement, forming a planar triangular cluster. In the Cu6–N0V2 model, Cu#6 bonds with two Cu atoms (Cu#4 and Cu#5) in a bridge position, as shown in Fig. 3(b-6). For the Fe6–N4V2 model, Fe#6 bonds to three Fe atoms without interacting with the surface atoms, as shown in Fig. 3(c-6). Meanwhile, in the Fe6–N0V2 model, Fe#6 similarly binds to the Fe cluster as Cu#6 does in forming the Cu6 cluster. In addition, the optimized structures of free-standing Cu/Fe clusters, independent of the substrate, are provided in the ESI (S1).†
All TMs display charge loss upon joining the substrate for the first TM incorporation. Notably, a discernible trend exists where TM#1 tends to lose more electronic charge in a nitrogen-rich environment. This trend is primarily attributed to nitrogen's role as a charge acceptor, as shown in the first row of Fig. 4. On the nitrogenated substrates, Cu loses +0.93e while Fe loses +1.18e; on the TM1–N0V2 substrate the values are +0.65e and +0.98e for Cu and Fe.
In contrast to TM1–NxV2, in the TM2–NxV2 models, TM#1 reduces its charge donation value to the substrate, and in all cases, TM#2 also shows an electronic donor charge character. As described in the structural characterization of the cluster shape in TMn–NxV2 section, since the TM#2 chemical environment is distinct in each TM2–NxV2 model, TM#2 yields different amounts of charge. In Cu2–N4V2, Cu#2 (bonded to Cu#1 and a N atom) gives +0.14e, in addition to the +0.86e provided by Cu#1, resulting in the entire Cu2 cluster giving +1.00e to the substrate (see Fig. 4(a-2)). Meanwhile, in Cu2–N0V2, Cu#2 (bonded to Cu#1 and two Cα1) yields +0.46e and Cu#1 yields +0.61e. Hence, the Cu2 cluster gives a total of +1.07e to the substrate (see Fig. 4(b-2)). In Fe2–N4V2, Fe#1 and Fe#2 provide +0.99e and +0.26e, respectively, as shown in Fig. 4(c-2); therefore, the Fe2 cluster yields +1.25e to the substrate. In Fe2–N0V2, the Fe2 cluster yields +1.61e; since both Fe atoms have a similar chemical environment, the calculated ΔQ for each Fe atom is almost identical (see Fig. 4(d-2)). All the calculated ΔQ values per TM atom and the clusters’ ΔQ values are shown in Fig. 4.
The clusters composed by a third TM atom (TM3–NxV2) present a donor charge character except for the Cu3–N4V2 model where the third adatom presents an electron gain value of −0.16e, and the previous adatoms had values +0.19e and +0.89e. Note that the coordination of this atom is single-bonded with the previous Cu atom. In contrast, for the other TM3–NxV2 models, the incorporated atoms are two-fold coordinated with the previous TM atoms, and interaction with the substrate for the second and third TM is also evident for the substrates without N. The total cluster charge values are +0.92, +1.07, +1.50, and +1.87 for Cu3–N4V2, Cu3–N0V2, Fe3–N4V2, and Fe3–N0V2, respectively (see Fig. 4(a-d3)).
With the fourth TM incorporation and the formation of a planar cluster for the studied models, the TM#4 atom does not interact with the substrate. It is only two-fold coordinated with the contiguous TM atoms, presenting a charge acceptor character. For Cu4–N4V2 (Fig. 4(a-4)), the charge values are −0.16e, +0.31e, +0.31e, and +0.79e, providing a total cluster charge of +1.25e. In Cu4–N0V2, the same trend appears with charge values of −0.08e, +0.29e, +0.29e, and +0.60e for a total of +1.1e for the complete cluster. The same trend is observed for the Fe cluster, where the Fe atoms had charge values of −0.09e and −0.10e for Fe4–N4V2 and Fe4–N0V2. Accordingly, the cluster charge values are +1.25, +1.09, +1.47, and +1.77. In this case, although the TM#4 atom accepts a minimal charge, its role as an acceptor suggests a unique dynamic in the system. This is due to its position and interactions with neighboring atoms, where factors like low electron density and electrostatic forces may have an influence. Such behavior underscores the complexity of these systems, where slight variations have significant impacts on their behavior and properties.
The subsequent incorporation of atoms generates the TM#5 models, except for the semi triangular Cu5–N4V2 cluster, where the added Cu atom acts as a charge donor with a value of +0.16e, the rhombohedral clusters with the TM at the tip present a ΔQ gain of −0.05e, −0.08e and −0.04e for Cu5–N0V2, Fe5–N4V2, and Fe5–N0V2, respectively. The cluster charge values are +1.35, +1.47, +1.74, and +2.06.
Finally, for the clusters formed by six atoms, it is observed that the triangular planar cluster has a charge acceptor character at the edges, two-fold coordinated Cu atoms, with values of −0.07e. The remaining systems, which form rhombohedral clusters, show a TM with unchanged charge ΔQ = 0. The total charge migration values are +1.23, +1.52, +1.74, and +2.21 for Cu6–N4V2, Cu6–N0V2, Fe6–N4V2, and Fe6–N0V2, respectively.
Overall, throughout the growth process, the TMn cluster donates electronic charge to the substrates. Additionally, atoms within each TMn cluster with equivalent chemical environments exhibit the same ΔQ value.
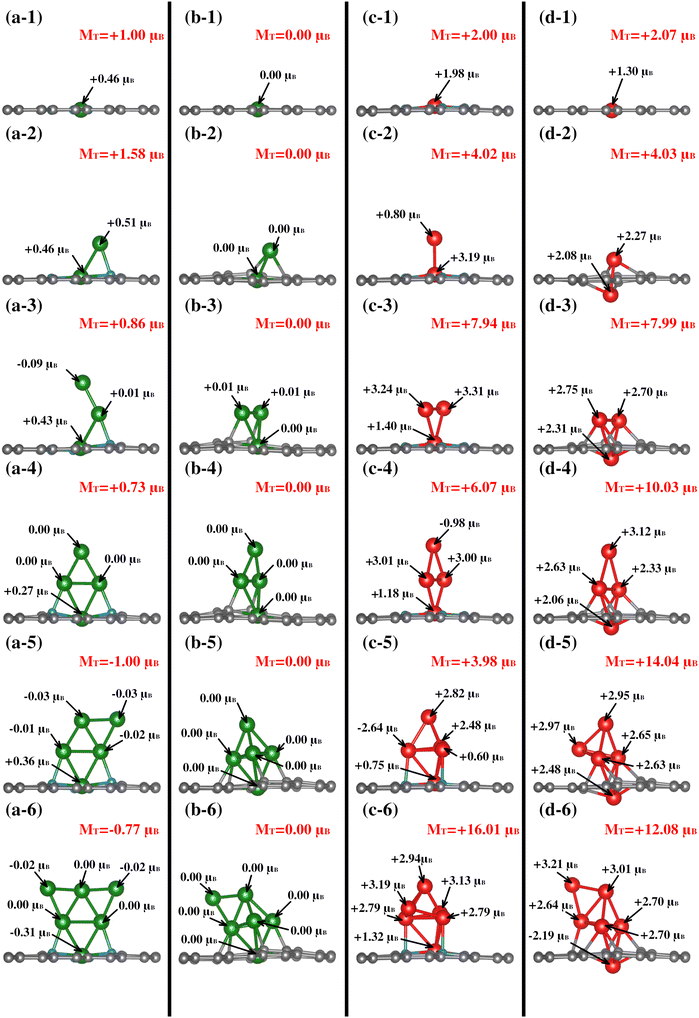
| System | Cu–N4V2 (μB) | Cu–N0V2 (μB) | Fe–N4V2 (μB) | Fe–N0V2 (μB) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M T | M Cl | M subs | M T | M Cl | M subs | M T | M Cl | M subs | M T | M Cl | M subs | |
| TM1 | 1.00 | 0.46 | 0.54 | 0.00 | 0.00 | 0.00 | 2.00 | 1.98 | 0.02 | 2.07 | 1.30 | 0.77 |
| TM2 | 1.58 | 0.98 | 0.60 | 0.00 | 0.00 | 0.00 | 4.02 | 4.00 | 0.02 | 4.03 | 4.36 | −0.33 |
| TM3 | 0.86 | 0.34 | 0.52 | 0.00 | 0.00 | 0.00 | 7.94 | 7.97 | −0.03 | 7.99 | 7.78 | 0.21 |
| TM4 | 0.73 | 0.28 | 0.45 | 0.00 | 0.00 | 0.00 | 6.07 | 6.22 | 0.14 | 10.03 | 10.16 | −0.13 |
| TM5 | −1.00 | −0.48 | −0.52 | 0.00 | 0.00 | 0.00 | 3.98 | 4.01 | −0.03 | 14.04 | 13.71 | 0.34 |
| TM6 | −0.77 | −0.38 | −0.38 | 0.00 | 0.00 | 0.00 | 16.01 | 16.19 | −0.18 | 12.08 | 12.09 | −0.01 |
Between the Cu–N4V2 and Cu–N0V2 systems, the main distinction lies in the total magnetization of the structure. In Cu–N4V2, there is consistently intrinsic magnetization in the system. In contrast, the Cu–N0V2 structures exhibit negligible magnetization throughout the cluster growth, as depicted in columns a and b of Fig. 5. This suggests that Cu in a nitrogen-free environment does not induce polarization in the substrate, unlike in an environment with nitrogen (refer to Table 1). Additionally, it is noteworthy that as the cluster grows in Cu–N4V2, the Cu atoms in the monolayer exhibits significant magnetic characteristics. This point is attributed to forming bonds with nitrogen, inducing a magnetic moment in Cu. This can be observed in Fig. 5(a-3), (a-4), (a-5), and (a-6), where the copper in the monolayer displays the highest magnetic moments of +0.43μB, +0.27μB, +0.36μB, and −0.31μB, respectively.
In the case of the Fe–NxV2 structures, Table 1 shows that in structures with N, the primary contribution to the total magnetization comes from the cluster, with minimal contribution from the substrate. This is attributed to Fe being inherently magnetic, and the presence of N does not significantly affect its polarization throughout the cluster growth. On the other hand, in the Fe–N0V2 structures, Table 1 suggests a more substantial contribution from the substrate, as observed in Fig. 5(d-1). In this case, the substrate contributes +0.77μB, adding to the +1.30μB from Fe, resulting in a total magnetization of +2.07μB. It is noteworthy that, unlike iron, the presence of nitrogen is crucial for inducing polarization in the Cu species. This observation can be elucidated by considering the electronic and chemical interactions within the Cu–N systems. Cu is a transition metal with partially filled d-orbitals, making it inherently susceptible to magnetic moments. However, in the absence of specific external influences, the magnetic behavior of copper might remain relatively subdued. The introduction of nitrogen into the system creates a dynamic environment where the Cu atoms interact with the nitrogen atoms, forming Cu–N bonds. These bonds can introduce unpaired electrons and alter the electronic configuration of the Cu atoms. The interaction with nitrogen induces a magnetic polarization in the Cu species, enhancing its magnetic characteristics. In contrast, Fe is already a well-known magnetic species due to its intrinsic magnetic moments arising from its electron configuration. Therefore, in the Fe–N systems, the impact of nitrogen on iron magnetic behavior may be comparatively less pronounced. Fe's inherent magnetism is less influenced by nitrogen, resulting in a more consistent magnetic behavior throughout the cluster growth.
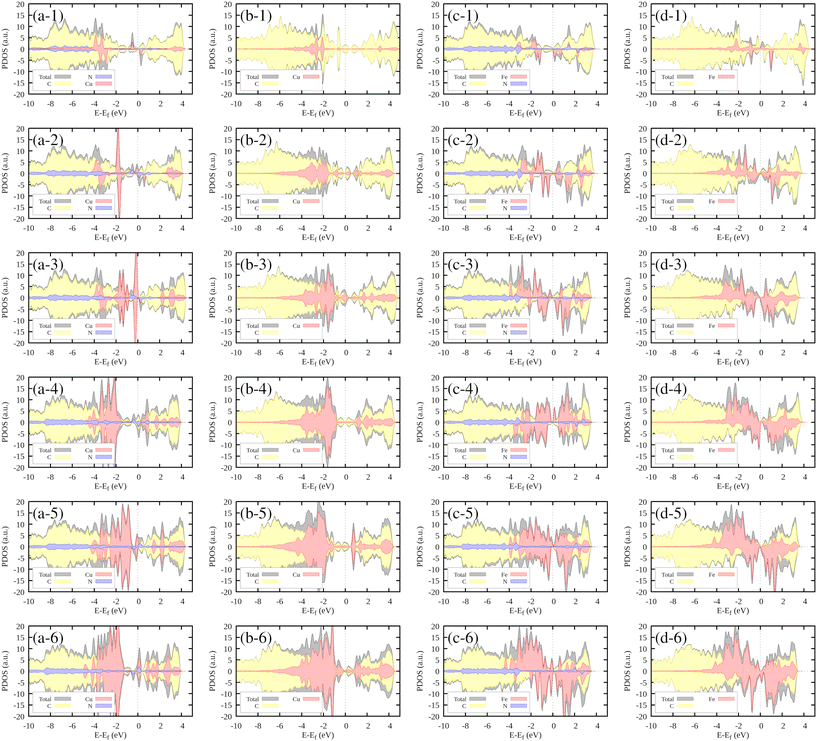
In the case of Cu–N0V2, where nitrogen is absent, copper (Cu) exhibits contributions at the same energy level and slightly to the right (Fig. 6(b-1)). This observation indicates the stability that copper gains when it incorporates embedded nitrogen within the monolayer. As the cluster grows, the Cu contributions increase in intensity, consistently remaining at around −2 eV.
In the context of the Fe–N4V2 system, which is presented in Fig. 6(c-1), it is worth highlighting the position of the contributions in relation to the formation of N–Fe bonds. These contributions are observed at approximately 2 eV, which is slightly to the right compared to their counterparts in the case of copper (Cu). This difference in positioning suggests distinct energy requirements and behaviors for bond formation between nitrogen and iron as opposed to nitrogen and copper. Furthermore, as the cluster size increases, we notice an intriguing phenomenon. The intensity of the iron (Fe) contributions intensifies, indicating an enhanced presence of iron atoms in the system. However, this observation is particularly intriguing because these contributions do not maintain a uniform energy level. Instead, they are distributed at various energy levels, indicating a diverse range of bonding configurations or states within the growing cluster.
Finally, in the case of the Fe–N0V2 system (Fig. 6(d-1)), we can observe a similar trend to the previous scenario. The behavior of the Fe contributions manifests at varying energy levels, displaying significant asymmetry between the spin-up and spin-down states. This asymmetry in the energy distribution further underscores the intricate electronic properties of the growing cluster, shedding light on the complexity of the Fe–C interactions in the absence of nitrogen.
In Fig. S3-1 of the ESI,† the DOS contribution from the most exposed transition metal in the system is highlighted in green. Notably, the contributions closest to the Fermi level, indicative of electronic states readily available for interaction, predominantly originated by the most exposed TMs. This observation hints at the unique electronic influence exerted by the most exposed TM within the cluster. Its distinct positioning or bonding characteristics likely facilitate localized electronic interactions, resulting in the emergence of prominent electronic states near the Fermi level. These states, in turn, play a pivotal role in shaping the electronic properties of the entire system, particularly in the vicinity of the Fermi energy.
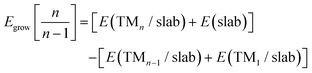 | (1) |
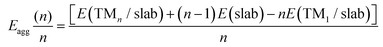 | (2) |
The Egrow and Eagg values denote the growth and aggregation energies, respectively. Egrow compares the TMn cluster against TMn−1 with a dispersed TM to analyze the one-atom growth mechanism. Meanwhile, Eagg compares the TMn clusters with the n-TM dispersed. As the equations are expressed, negative Egrow or Eagg values indicate a thermodynamically more favorable configuration. This means that growth or aggregations are viable, respectively. E(TMn/slab) is the TMn–NxV2 total energy and E(slab) is the substrate energy.
We will first discuss the Egrow results. Regarding the growth energies, as depicted in Fig. 7(a), it is evident that in the initial step, all the TM2–NxV2 systems exhibit positive growth energies. Physically, considering eqn (1), this means a greater likelihood of adatoms arriving at vacancies rather than cluster growth. In this case, the positive energy values indicate that the influx of adatoms favors the saturation of vacancies before cluster growth, a trend observed across all systems. If controllable incorporation of TMs into carbon substrates could be achieved through high vacuum synthesis methods like magnetron sputtering, inert gas condensation, and soft-landing techniques (as clarified in the Introduction section), then highly dispersed SACs could be obtained, provided that two carbon vacancies are present in the substrate. It is noteworthy that the Fe2–N0V2 system has the lowest Egrow value of 0.21 eV. Meanwhile, the N-doped substrates present the highest Egrow values.
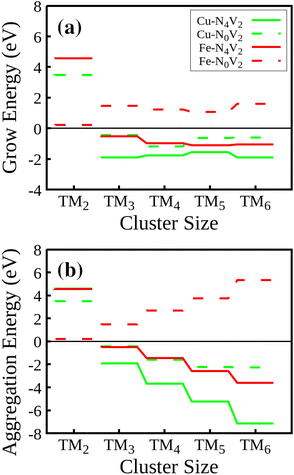 | ||
| Fig. 7 (a) Growth energies and (b) aggregation energies for the TM–NxV2 structures during cluster formation. | ||
The cluster growth will only occur once the vacancies are filled with the first TM. From now on, we will consider TM1–NxV2 as E(slab) in eqn (1). Once the vacancies are saturated and more TMs are incorporated into the system, one-atom cluster growth becomes feasible for Cu regardless of the presence of nitrogen, as evidenced by the negative Egrow value. Meanwhile, Fe cluster growth is only viable in the nitrogenate substrate, since the Egrow value of Fe–N0V2 is positive.
In terms of the aggregation energies, as described by eqn (2) and illustrated in Fig. 7(b), we can observe that the Eagg values for clusters made of two atoms are positive. This observation confirms that it is imperative to first saturate the vacancies with a TM before cluster growth or aggregation in any system. Once this step is accomplished, the TM cluster aggregation becomes feasible for the Cu clusters on both substrates and the Fe cluster on the N-doped monolayer due to the negative value of Eagg.
These findings on aggregation and growth energies suggest that once all vacancies are saturated by a TM, a nitrogen-rich environment promotes the cluster growth mechanism, enabling systems to achieve increased stability as the growth process goes on. This observation aligns with findings in published studies that have highlighted the role of nitrogen in modulating the properties and chemical reactivity of materials.51,55 Specifically, these studies have emphasized the influence of nitrogen on the selectivity of specific reactions, such as the oxygen reduction reaction (ORR), where the presence of nitrogen in nitrogen-doped graphitic carbon materials has been shown to affect the preferred reaction pathway.51 This consistency among findings underscores the significance of nitrogen in materials engineering for specific applications in fields like energy and the environment.
4. Conclusions
In this study, we investigated the growth mechanism of Cu and Fe clusters on a graphene monolayer, particularly examining scenarios with and without nitrogen doping (TMn–NxV2). Our analysis reveals intriguing growth patterns, especially within Cu-based systems. The presence of pyridine nitrogen induces a more structured and orderly growth of Cu clusters, forming a stable plane perpendicular to the monolayer. In contrast, in nitrogen-deficient environments, Cu clusters exhibit less organized, more clumped formations.Pyridine nitrogen also plays a crucial role in improving the structural stability of Fe clusters, reducing the deformations often observed in its absence. Additionally, nitrogen facilitates magnetization in Cun–N4V2 systems and focuses the magnetic properties in Fe clusters.
Using the formalism of aggregation and growth energies, we explored system stability, highlighting nitrogen as a key factor in enhancing stability, particularly favoring Cu cluster growth. Notably, as the cluster size increases, this stabilizing effect diminishes, suggesting a transition towards bulk-like behavior similar to Fe. These findings provide a deeper understanding on how pyridine nitrogen affects growth dynamics and catalytic properties, offering valuable insights for designing electrocatalysts. Understanding the minimum cluster size before transitioning to metallic behavior, similar to bulk iron, is crucial for influencing material reactivity and catalytic properties. These insights are essential for tailoring materials for improved electrocatalytic performance, with applications ranging from renewable energy generation to environmental cleanup.
Data availability
The data supporting this article have been included as part of the ESI.† For any further details please do not hesitate contacting us (E-mail: jmromo@ens.cnyn.unam.mx; or luis.alvaradoll@uanl.edu.mx).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support provided through DGAPA-UNAM with projects IN102725, IN111223, IG101124, and IN105722. Calculations were performed in the DGTIC-UNAM Supercomputing Center projects LANCAD-UNAM-DGTIC-051, LANCAD-UNAM-DGTIC-382, and LANCAD-UNAM-DGTIC-368. J. I. P. O. thanks DGAPA-UNAM for a postdoctoral position.References
- Y. Tang, Z. Yang and X. Dai, Trapping of metal atoms in the defects on graphene, J. Chem. Phys., 2011, 135, 224704 CrossRef PubMed
.
- B. Chai, T. Peng, J. Mao, K. Li and L. Zan, Graphitic carbon nitride (g-C3N4)-Pt-TiO2 nanocomposite as an efficient photocatalyst for hydrogen production under visible light irradiation, Phys. Chem. Chem. Phys., 2012, 14, 16745–16752 RSC
.
- Y.-H. Zhang,
et al., Tuning the magnetic and transport property of graphene with Ti atom and cluster, Comput. Mater. Sci., 2012, 56, 95–99 CrossRef CAS
.
- O. Üzengi Aktürk and M. Tomak, AunPtn clusters adsorbed on graphene studied by first-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 085417 CrossRef
.
- C. R. C. Rêgo, P. Tereshchuk, L. N. Oliveira and J. L. F. Da Silva, Graphene-supported small transition-metal clusters: A density functional theory investigation within van der Waals corrections, Phys. Rev. B, 2017, 95, 235422 CrossRef
.
- E. Yoo,
et al., Enhanced Electrocatalytic Activity of Pt Subnanoclusters on Graphene Nanosheet Surface, Nano Lett., 2009, 9, 2255–2259 CrossRef CAS PubMed
.
- H. Yan,
et al., Single-Atom Pd1/Graphene Catalyst Achieved by Atomic Layer Deposition: Remarkable Performance in Selective Hydrogenation of 1, 3–1Butadiene, J. Am. Chem. Soc., 2015, 137, 10484–10487 CrossRef CAS PubMed
.
- R. Hussain,
et al., Density functional theory study of palladium cluster adsorption on a graphene support, RSC Adv., 2020, 10, 20595–20607 RSC
.
- M. Manadé, F. Viñes and F. Illas, Transition metal adatoms on graphene: A systematic density functional study, Carbon, 2015, 95, 525–534 CrossRef
.
- M. P. Lima, A. J. R. da Silva and A. Fazzio, Adatoms in graphene as a source of current polarization: Role of the local magnetic moment, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245411 CrossRef
.
- C. M. Acosta, M. P. Lima, R. H. Miwa, A. J. R. da Silva and A. Fazzio, Topological phases in triangular lattices of Ru adsorbed on graphene: Ab initio calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155438 CrossRef
.
- X.-Q. Dai, Y.-N. Tang, J.-H. Zhao and Y.-W. Dai, Absorption of Pt clusters and the induced magnetic properties of graphene, J. Phys.: Condens. Matter, 2010, 22, 316005 CrossRef PubMed
.
- K. Okazaki-Maeda, Y. Morikawa, S. Tanaka and M. Kohyama, Structures of Pt clusters on graphene by first-principles calculations, Surf. Sci., 2010, 604, 144–154 CrossRef CAS
.
- S. Sahoo, M. E. Gruner, S. N. Khanna and P. Entel, First-principles studies on graphene-supported transition metal clusters, J. Chem. Phys., 2014, 141(7), 074707 CrossRef PubMed
.
- H. Johll, J. Wu, S. W. Ong, H. C. Kang and E. S. Tok, Graphene-adsorbed Fe, Co, and Ni trimers and tetramers: Structure, stability, and magnetic moment, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(20), 205408 CrossRef
.
- R. C. Longo, J. Carrete, J. Ferrer and L. J. Gallego, Structural, magnetic, and electronic properties of Nin and Fen nanostructures (n=1–4) adsorbed on zigzag graphene nanoribbons, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 115418 CrossRef
.
- O. Diéguez, M. M. G. Alemany, C. Rey, P. Ordejón and L. J. Gallego, Density-functional calculations of the structures, binding energies, and magnetic moments of Fe clusters with 2 to 17 atoms, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63(20), 205407 CrossRef
.
- J. Berwanger, S. Polesya, S. Mankovsky, H. Ebert and F. J. Giessibl, Atomically Resolved Chemical Reactivity of Small Fe Clusters, Phys. Rev. Lett., 2020, 124(9), 096001 CrossRef CAS PubMed
.
- Q.-M. Ma, Z. Xie, J. Wang, Y. Liu and Y.-C. Li, Structures, binding energies and magnetic moments of small iron clusters: A study based on all-electron DFT, Solid State Commun., 2007, 142, 114–119 CrossRef CAS
.
- G. Mpourmpakis, G. E. Froudakis, A. N. Andriotis and M. Menon, Role of Co in enhancing the magnetism of small Fe clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(10), 104417 CrossRef
.
- G. H. Guvelioglu, P. Ma, X. He, R. C. Forrey and H. Cheng, First principles studies on the growth of small Cu clusters and the dissociative chemisorption of H2, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(15), 155436 CrossRef
.
- F. Montejo-Alvaro,
et al., Icosahedral transition metal clusters (M13, M = Fe, Ni, and Cu) adsorbed on graphene quantum dots, a DFT study, Phys. E, 2019, 110, 52–58 CrossRef CAS
.
- Y. Chen, Z. Huang, P. Hu, J. Chen and X. Tang, Improved performance of supported single-atom catalysts via increased surface active sites, Catal. Commun., 2016, 75, 74–77 CrossRef CAS
.
- S. Wang,
et al., Dopants adsorbed as single atoms prevent degradation of catalysts, Nat. Mater., 2004, 3, 143–146 CrossRef CAS PubMed
.
- J. M. Thomas, Z. Saghi and P. L. Gai, Can a Single Atom Serve as the Active Site in Some Heterogeneous Catalysts?, Top. Catal., 2011, 54, 588–594 CrossRef CAS
.
- Y. Zhu,
et al., Single-Atom Iron-Nitrogen Catalytic Site with Graphitic Nitrogen for Efficient Electroreduction of CO2, ChemistrySelect, 2020, 5, 1282–1287 CrossRef CAS
.
- D. Lyu,
et al., Ultra-high surface area graphitic Fe-N-C nanospheres with single-atom iron sites as highly efficient non-precious metal bifunctional catalysts towards oxygen redox reactions, J. Catal., 2018, 368, 279–290 CrossRef CAS
.
- S. An,
et al., High-Density Ultra-small Clusters and Single-Atom Fe Sites Embedded in Graphitic Carbon Nitride (g-C3N4) for Highly Efficient Catalytic Advanced Oxidation Processes, ACS Nano, 2018, 12, 9441–9450 CrossRef CAS PubMed
.
- H. Zhang,
et al., A Graphene-Supported Single-Atom FeN5 Catalytic Site for Efficient Electrochemical CO2 Reduction, Angew. Chem., Int. Ed., 2019, 58, 14871–14876 CrossRef CAS PubMed
.
- X.-F. Yang,
et al., Single-Atom Catalysts: A New Frontier in Heterogeneous Catalysis, Acc. Chem. Res., 2013, 46, 1740–1748 CrossRef CAS PubMed
.
- Y. Chen, Z. Huang, Z. Ma, J. Chen and X. Tang, Fabrication, characterization, and stability of supported single-atom catalysts, Catal. Sci. Technol., 2017, 7, 4250–4258 RSC
.
- U. Heiz, A. Sanchez, S. Abbet and W.-D. Schneider, Catalytic Oxidation of Carbon Monoxide on Monodispersed Platinum Clusters: Each Atom Counts, J. Am. Chem. Soc., 1999, 121, 3214–3217 CrossRef CAS
.
- W. E. Kaden, T. Wu, W. A. Kunkel and S. L. Anderson, Electronic Structure Controls Reactivity of Size-Selected Pd Clusters Adsorbed on TiO2 Surfaces, Science, 2009, 326, 826–829 CrossRef CAS PubMed
.
- Y. Lei,
et al., Increased Silver Activity for Direct Propylene Epoxidation via Subnanometer Size Effects, Science, 2010, 328, 224–228 CrossRef CAS PubMed
.
- S. Abbet,
et al., Acetylene Cyclotrimerization on Supported Size-Selected Pdn Clusters (1 < n < 30): One Atom Is Enough!, J. Am. Chem. Soc., 2000, 122, 3453–3457 CrossRef CAS
.
- H. Haberland, M. Karrais, M. Mall and Y. Thurner, Thin films from energetic cluster impact: A feasibility study, J. Vac. Sci. Technol., 1992, 10, 3266–3271 CrossRef CAS
.
- M. Gracia-Pinilla, E. Martínez, G. S. Vidaurri and E. Pérez-Tijerina, Deposition of Size-Selected Cu Nanoparticles by Inert Gas Condensation, Nanoscale Res. Lett., 2009, 5(1), 180 CrossRef CAS PubMed
.
- M. J. Martínez-Carreón,
et al., Synthesis and structural analysis of gold-palladium alloy nanoparticles using co-sputtering of independent sources, Mater. Res. Express, 2019, 6, 046515 CrossRef
.
- L. G. Silva,
et al., Synthesis of Fe Nanoparticles Functionalized with Oleic Acid Synthesized by Inert Gas Condensation, J. Nanomater., 2014, 2014, 1–6 Search PubMed
.
- M. Gracia-Pinilla, D. Ferrer, S. Mejía-Rosales and E. Pérez-Tijerina, Size-Selected Ag Nanoparticles with Five-Fold Symmetry, Nanoscale Res. Lett., 2009, 4(8), 896 CrossRef CAS PubMed
.
- E. Pérez-Tijerina,
et al., Highly size-controlled synthesis of Au/Pd nanoparticles by inert-gas condensation, Faraday Discuss., 2008, 138, 353–362 RSC
.
- Y. Chen, Z. Huang, Z. Ma, J. Chen and X. Tang, Fabrication, characterization, and stability of supported single-atom catalysts, Catal.: Sci. Technol., 2017, 7, 4250–4258 RSC
.
- B. Singh,
et al., Single-Atom (Iron-Based) Catalysts: Synthesis and Applications, Chem. Rev., 2021, 121, 13620–13697 CrossRef CAS PubMed
.
- L. Takele Menisa,
et al., Single atomic Fe-N4 active sites and neighboring graphitic nitrogen for efficient and stable electrochemical CO2 reduction, Nanoscale Horiz., 2022, 7, 916–923 RSC
.
- Y. Zhu,
et al., Single-Atom Iron-Nitrogen Catalytic Site with Graphitic Nitrogen for Efficient Electroreduction of CO2, ChemistrySelect, 2020, 5, 1282–1287 CrossRef CAS
.
- D. Lyu,
et al., Ultra-high surface area graphitic Fe-N-C nanospheres with single-atom iron sites as highly efficient non-precious metal bifunctional catalysts towards oxygen redox reactions, J. Catal., 2018, 368, 279–290 CrossRef CAS
.
- S. An,
et al., High-Density Ultra-small Clusters and Single-Atom Fe Sites Embedded in Graphitic Carbon Nitride (g-C3N4) for Highly Efficient Catalytic Advanced Oxidation Processes, ACS Nano, 2018, 12, 9441–9450 CrossRef CAS PubMed
.
- H. Zhang,
et al., A Graphene-Supported Single-Atom FeN5 Catalytic Site for Efficient Electrochemical CO2 Reduction, Angew. Chem., Int. Ed., 2019, 58, 14871–14876 CrossRef CAS PubMed
.
- H.-J. Shin,
et al., Control of Electronic Structure of Graphene by Various Dopants and Their Effects on a Nanogenerator, J. Am. Chem. Soc., 2010, 132, 15603–15609 CrossRef CAS PubMed
.
- B. Kumar,
et al., Controlled Growth of Semiconducting Nanowire, Nanowall, and Hybrid Nanostructures on Graphene for Piezoelectric Nanogenerators, ACS Nano, 2011, 5, 4197–4204 CrossRef CAS PubMed
.
- H. N. Fernandez-Escamilla,
et al., Understanding the Selectivity of the Oxygen Reduction Reaction at the Atomistic Level on Nitrogen-Doped Graphitic Carbon Materials, Adv. Energy Mater., 2021, 11, 2002459 CrossRef CAS
.
- L. A. Alvarado-Leal,
et al., Density Functional Theory Study of Single-Atom Transition Metal Catalysts Supported on Pyridine-Substituted Graphene Nanosheets for Oxygen Reduction Reaction, ACS Appl. Nano Mater., 2023, 7, 338–347 CrossRef
.
- B. F. Habenicht, D. Teng, L. Semidey-Flecha, D. S. Sholl and Y. Xu, Adsorption and Diffusion of 4d and 5d Transition Metal Adatoms on Graphene/Ru(0001) and the Implications for Cluster Nucleation, Top. Catal., 2013, 57, 69–79 CrossRef
.
- J. Barth, Transport of adsorbates at metal surfaces: from thermal migration to hot precursors, Surf. Sci. Rep., 2000, 40, 75–149 CrossRef CAS
.
- B. Han and F. Li, Regulating the electrocatalytic performance for nitrogen reduction reaction by tuning the N contents in Fe3@NxC20-x (x = 0 4): a DFT exploration, J. Mater. Inf., 2023, 3(4), 24 Search PubMed
.
- M. E. Geusic, M. D. Morse and R. E. Smalley, Hydrogen chemisorption on transition metal clusters, J. Chem. Phys., 1985, 82, 590–591 CrossRef CAS
.
- K. Yam, N. Guo, Z. Jiang, S. Li and C. Zhang, Graphene-Based Heterogeneous Catalysis: Role of Graphene, Catalysts, 2020, 10, 53 CrossRef CAS
.
- L. Zhang, Q. Xu, J. Niu and Z. Xia, Role of lattice defects in catalytic activities of graphene clusters for fuel cells, Phys. Chem. Chem. Phys., 2015, 17, 16733–16743 RSC
.
- P. Giannozzi,
et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed
.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864–B871 CrossRef
.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
- K. S. Novoselov,
et al., Electric Field Effect in Atomically Thin Carbon Films, Science, 2004, 306, 666–669 CrossRef CAS PubMed
.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef
.
- M. Yu and D. R. Trinkle, Accurate and efficient algorithm for Bader charge integration, J. Chem. Phys., 2011, 134(6), 064111 CrossRef PubMed
.
- C. Jin,
et al., Adsorption of Transition-Metal Clusters on Graphene and N-Doped Graphene: A DFT Study, Langmuir, 2022, 38, 3694–3710 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr02713b |
| This journal is © The Royal Society of Chemistry 2024 |