α-Graphyne with ultra-low diffusion barriers as a promising sodium-ion battery anode and a computational scheme for accurate estimation of theoretical specific capacity†
Babuji
Dandigunta
abc,
Abhijitha
V G
ac,
Sharma S. R. K. C.
Yamijala
 bc and
B. R. K.
Nanda
bc and
B. R. K.
Nanda
 *ac
*ac
aCondensed Matter Theory and Computational Lab, Department of Physics, IIT Madras, Chennai-600036, India. E-mail: nandab@iitm.ac.in
bComputational Chemistry and Materials Science Lab, Department of Chemistry, IIT Madras, Chennai-600036, India
cCenter for Atomistic Modelling and Materials Design, IIT Madras, Chennai-600036, India
First published on 19th August 2024
Abstract
Sodium-ion batteries are considered as potential alternatives to conventional lithium-ion batteries. To realize their large-scale practical applications, it is essential to identify suitable anode candidates exhibiting promising electrochemical properties such as high specific capacity, low diffusion energy barrier, and excellent cyclic stability. In this work, using density functional theory (DFT) calculations and ab initio molecular dynamics simulations, we examine α-graphyne – a carbon-based 2D material – as a potential anode candidate. Our results show that AGY exhibits an ultra-low diffusion barrier of 0.23 eV along both the horizontal and vertical directions and a low average anodic voltage of 0.36 V. Our AIMD studies at 300 K show excellent thermodynamical stability with the loading of four sodium atoms, resulting in a theoretical specific capacity (TSC) of 279 mA h g−1. Doping studies show that varying the nature of acetylenic links of AGY with electron-rich (nitrogen) or electron-deficient (boron) elements, the adsorption strength and diffusion barriers for Na atoms on AGY can be tuned. Furthermore, treating AGY as a case study, we find that conventional DFT studies are expected to overestimate the TSC by a huge margin. Specific to AGY, this overestimation can be up to ∼300%. We identify that ignoring the probable formation of temperature-driven metal clusters is the main reason behind such overestimations. Furthermore, we develop a scheme to calculate TSC with higher accuracy. The scheme, which can be easily generalized to the universal class of electrodes, is evolved by concurrently employing AIMD simulations, DFT calculations and cluster analysis.
1 Introduction
To meet the growing global energy demand, renewable energy harvesting is essential. Rechargeable batteries are leading the way in this regard among the available energy storage technologies1 due to their design flexibility and portability. Though lithium-ion batteries2,3 (LIBs) are the front runners in the battery technology for energy storage, factors such as fewer and unevenly distributed lithium reserves, toxicity,4 and lack of a robust recycling technology5 have become the main obstacles for their sustainable use. Given the uniform geographical distribution of sodium, sodium-ion batteries6,7 (NIBs) are increasingly gaining attention as promising alternatives for LIBs. Besides their impressive energy density, NIBs can be manufactured from nonflammable, harmless, and widely available materials. Sodium has a theoretical gravimetric capacity8 of 1166 mA h g−1 and an impressive reduction potential (−2.71 V vs. SHE), not far from the lithium (−3.04 V vs. SHE). As lithium and sodium belong to the same group in the periodic table, NIBs show similar working principles as that of LIBs. Another benefit is the use of a cost-effective and lightweight current collector, such as aluminum, in NIBs, as opposed to LIBs, where there is a risk of Li–Al alloy formation.9Despite all these benefits, issues with NIBs must be resolved before realizing their practical application. During fast cycling of NIBs, the bigger size of Na+ ion can irreversibly10 expand the anode material composite and lead to the electrode disintegration. Being more than three times heavier than Li+ ion, Na+ can consume a significant amount of the stored energy during NIB cycling.9 Low coulombic efficiency and cycle life are other major drawbacks for NIB. These limitations can be addressed by incorporating better anode materials into NIBs.11 Given their porosity, hard and soft carbon12 were explored as suitable anode materials for NIBs but at the cost of low initial coulombic efficiency and poor rate performance. The rate and cyclability of NIBs can be further enhanced with high-performance two-dimensional anode materials. Several 2D materials, such as graphene and its derivatives, transition metal dichalcogenides (TMD), and MXenes, were investigated for their potential application as NIB anodes. However, these materials suffer from irreversible phase transitions and high electrolyte reactivity due to functionalization.13 Pure elemental 2D materials14 known as Xenes (e.g., graphene, phosphorene, silicene) are gaining interest in energy research and are well-suited as anode materials for NIBs. These materials offer versatile properties, including large active surface area, more exposure of internal atoms, improved charge transfer kinetics, structural stability, lower effective mass, high theoretical capacity, and two-way adsorption. In particular, carbon-based 2D materials stand out due to carbon's structural and hybridization flexibility, as evident by its long list of allotropes.15 Xenes of carbon with electronic properties comparable to that of graphene, having large cavities in their structure, need to be explored to realize a potential 2D carbonaceous NIB anode.
α-Graphyne (AGY), a 2D non-natural allotrope of carbon, belongs to the category of carbon-based Xenes known as graphynes, theoretically first predicted by Baughman et al.16 Composed of sp2 and sp hybridized carbons, large in-plane cavities, and a high Poisson's ratio17 of 0.87, AGY can be a potential anode for NIBs. Though graphdiyne and γ-graphyne, two members of the graphyne family, have been experimentally synthesized,18,19 AGY is yet to be synthesized. However, recent experimental progress shows the successful synthesis20 of the monomer unit required for the extended production of the AGY layer. In addition, several theoretical studies elucidate the dynamic stability of AGY using phonon frequency studies. For example, Yang et al.21 reported the phonon studies of AGY in which no imaginary frequencies were observed, indicating its excellent dynamical stability. Owing to its promising material properties, AGY has been investigated as an emerging electrode for metal ion batteries via first-principles methods. In a comprehensive investigation, Hwang et al.22 explored the applicability of AGY as a potential anode material for lithium-ion batteries (LIBs), while Li et al.23 explored on AGY nanotubes as LIB anodes. In a separate study, Singh and et al.24 studied the applicability of AGY as an anode material for sodium-ion batteries (NIBs), taking into account its unit cell structure, which leads to unreasonably high theoretical specific capacity (the TSC). Yuan et al.25 studied AGY nanotubes as potential anode materials for NIBs. These studies report two different TSC values for NIBs using AGY as an anode. To resolve this discrepancy, in our study, we proposed a mechanism for accurate prediction of the TSC of an electrode, which is discussed in the next sections.
The present work proposes α-graphyne (AGY) as a potential anode for sodium-ion batteries based on a comprehensive set of computational studies that include density functional theory calculations, ab initio molecular dynamics simulations, and transition state theory based nudged elastic band (NEB) methods. In this work, we demonstrate that AGY has a desirable adsorption strength of −0.9 eV per atom, an open circuit voltage of 0.36 V vs. Na/Na+, followed by an impressive TSC of 279 mA h g−1, the possibility of both inplane and out-of-plane diffusion with minimal barriers of 0.19 eV and 0.23 eV respectively. We showcase the AGY's structural resilience through its cyclical ability to revert to its original state. Furthermore, we demonstrated the high thermal stability of AGY at room temperature. Our detailed studies reveal that conventionally applied first principles workflow (through adsorption energy calculations) overestimates the TSC in general. Specific to AGY, this overestimation can be up to ∼300%. We identify that ignoring the probable formation of temperature-driven metal clusters is the main reason behind such overestimations. Here, we propose a scheme involving temperature-dependent AIMD simulation to substantially improve the accuracy of the TSC calculation using first-principles methods.
2 Computational details
The first principles calculations are performed using a plane wave-based pseudopotential approach, as implemented in the Quantum ESPRESSO.26,27 A monolayer of AGY is prepared with a vacuum of 20 Å in the z-direction. Perdew–Burke–Ernzerhof functional under the generalized gradient approximation is used to account for exchange–correlation effects. Vanderbilt ultrasoft pseudopotentials are used to consider the ion-electron interactions. We performed both cell and ionic relaxation for pristine AGY, and all other adsorption calculations, we performed ionic relaxation. Adsorption energy is calculated using the formula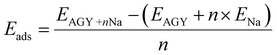 | (1) |
3 Structure of AGY
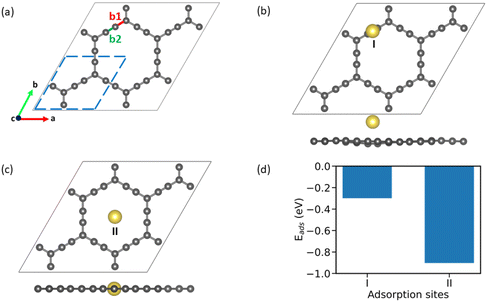
AGY is a 2D non-natural allotrope of carbon with hexagonal rings similar to graphene. However, unlike graphene, which has six-membered hexagonal rings, AGY has 18-atom hexagonal rings with two different types of bonds between the C atoms, namely, C(sp2)–C(sp) {b1} and C(sp)–C(sp) {b2}. The optimized geometry of 2 × 2 supercell of AGY is presented in Fig. 1a with bonds b1 and b2 highlighted in red and green color, respectively (unit cell is highlighted with blue dashed lines). The optimized lattice parameter and bond lengths of AGY are a = b = 6.95 Å, 1.23 Å (b1) and 1.39 Å (b2), respectively. These parameters are in good agreement with the reported results.16,31–354 Results and discussion
4.1 Adsorption study of Na on AGY
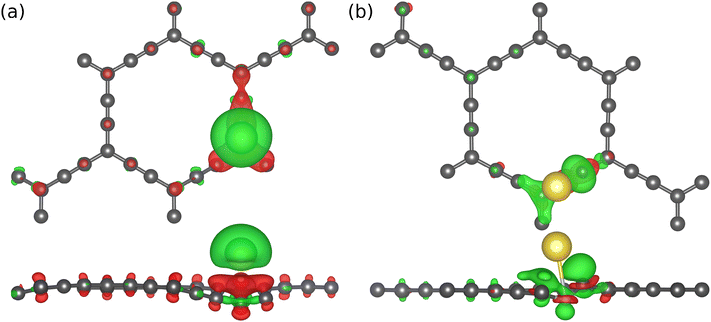
To begin with, we examined the appropriateness of the supercell size by performing adsorption energy calculations on 1 × 1, 2 × 2, and 3 × 3 AGY. Our results reveal that unit cell calculations are inaccurate due to the increased density of adatoms (Na atoms). However, the results show that 2 × 2 supercell is sufficient to calculate adsorption energies accurately. In addition, the 2 × 2 supercell of AGY gives a symbolic representation of the AGY structure since it captures at least one hexagonal carbon atom ring. Hence, in all our further calculations, we have used the 2 × 2 supercell of AGY. The optimized geometry of AGY, as shown in Fig. 1(a), exhibits five adsorption sites for the Na atom (see Fig. S1 of the ESI†). We systematically analyzed all possible adsorption configurations, and after the geometry optimization, we obtained only two distinct adsorption sites, as shown in Fig. 1(b & c). These adsorption configurations are named as site-I and site-II to simplify the discussion in the text. At site-I (Fig. 1(b)), the sodium atom is placed 3 Å above the b2 bond of the acetyl chain. As these carbon atoms are partially positive in charge, the Na atom optimizes at a height of ∼2.47 Å from the plane of AGY with an adsorption strength of −0.3 eV (Fig. 1(d)). However, at site-II (Fig. 1(c)), the Na atom is placed in the plane of AGY (center of the hexagonal ring). In this site, the Na atom maintains an equal distance from both sp and sp2 carbon atoms of the AGY and as a result, it shows a higher adsorption strength of −0.9 eV. The optimized structures corresponding to the site-3 and 4 are presented in Fig. S2 of the ESI.†The preferential adsorption of Na atoms at site II can be explained as follows. Due to the higher s character, sp hybridized C atoms are electron-rich, compared to the sp2 hybridized C atoms. Considering the electron-donating nature of the Na atom, it is subjected to weaker and stronger repulsion by sp2 and sp hybridized C atoms, respectively, when placed within the central hexagonal ring of AGY. Due to the symmetric nature of the ring, the Na atom at site II is equidistant from the surrounding C atoms compared to the Na atom at site I. Hence, the repulsive forces on the Na atom are more balanced at site II than at site I. This is the reason for higher adsorption strength at site II, and it is also supported by Bader charge analysis (see Table S1 of the ESI†).
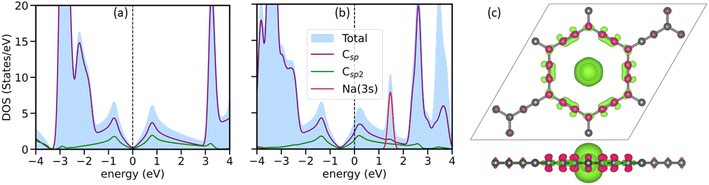
Analyzing the AGY's electronic structure before and after Na atoms’ adsorption reveals valuable information about the nature of the interaction between AGY and Na atoms. Further, it is also important to decide the rate performance of the battery. Here, we plotted the total and partial density of states for pristine and Na-adsorbed AGY. Fig. 2(a) shows that pristine AGY has Dirac cone-like behavior at the Fermi level, similar to the graphene.36 After the adsorption of a single Na atom, due to the charge transfer from the Na atom to the C atoms of AGY, the Dirac cone shifts to the lower energy values, Fig. 2(b). Further, to confirm the direction of charge transfer, we have plotted the charge density difference using the following expression:
| Δρ(r) = ρAGY+Na(r) − ρAGY(r) − ρNa(r) | (2) |
4.2 Thermodynamical stability
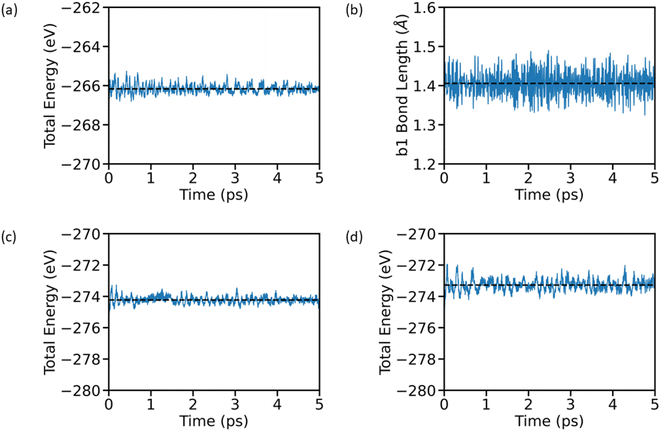
As we perform adsorption energy analysis at 0 K and the battery operating temperature lies in the range of 300–500 K, it is important to consider thermal effects for the reliable prediction of various battery related matrices of an electrode. Hence, it is important to analyze the thermodynamic stability and suitability of AGY at room temperature for its application as a potential anode for NIB. Here, we have considered the optimized structure Fig. 1(a) and performed AIMD simulation for 5 ps with a timestep of 0.5 fs. To elucidate the thermodynamical stability of AGY, we have considered two parameters, namely, the dynamical evolution of the total energy of the system and the bond length b1, which are presented in Fig. 3(a and b). The minimal fluctuation of total energy and b1 about their equilibrium values of −266.17 eV and 1.41 Å, respectively, indicates the excellent structural and thermodynamical stability of AGY at room temperature. To see the temperature effects on the system with the concentration of Na, AGY is loaded with 4 sodium atoms and subjected to AIMD at 300 K and 500 K as thermal runaway reactions occur in batteries in the 300 K–500 K temperature range.37 The results shown in Fig. 3(c and d) indicate no significant structural breakdown or phase transformation or any rare events even after the loading of four Na atoms, indicating excellent thermodynamical stability of AGY with Na concentration.4.3 Migration energy barrier
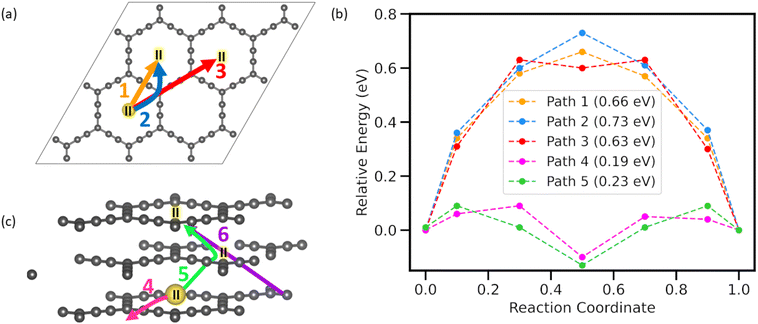
Adsorption energy, electronic structure, and thermodynamical stability studies elucidate the potential of AGY to act as anode material for NIBs. However, in any anode material with a high diffusion barrier, a significant portion of the free energy stored during charging is required to overcome this barrier. Hence, another important property of a good anode material is to have a minimum diffusion energy barrier for adatoms. To quantify the diffusion barriers, we used the nudged elastic band (NEB)38 method with seven images to estimate the barrier for the sodium atom. As AGY has large hexagonal rings in its structure, we have considered both in-plane and out-of-plane diffusion paths for Na atoms, and diffusion between the most stable sites (II) is considered in all the NEB calculations. Since site II has the highest adsorption energy, calculating the barrier between site II in adjacent C18 rings will give the upper limit of the diffusion barrier. A total of 6 paths were chosen for the NEB study. As depicted in Fig. 4(a and c), paths-1, -2, and -3 are considered in monolayer AGY, and paths-4, -5, and -6 are considered between ABA-stacked trilayer AGY. Here, we have considered the ABA stacked trilayer, owing to its relatively higher stability (Fig. S3 of the ESI†), and it is in accordance with earlier reported39 results.Path 1 is the shortest diffusion path connecting the most preferred adsorption site II of two adjacent hexagonal rings. Along path-1, the Na atom moves across the sp hybridized C atom chain and shows a transition state exactly above the bond between sp hybridized carbon atoms. Path-2 connects the same sites as path-1 with the intermediate of the reaction coordinate above the corner C atom. Path-3 connects site II, located in the second nearest hexagonal ring, in which the Na atom moves along the full length of the acetylenic chain to reach the other site. The energy profile, Fig. 4(b) for all three inplane paths shows a nearly equal energy barrier of ∼0.7 eV as all the paths involve the movement of Na atom on the sp and sp2 hybridized C atoms. As C atoms in the sp chain of the AGY are electron-rich in nature and the Na atom has a positive charge, there exists a coulombic attraction between them, which is responsible for the increased energy barrier.
In the case of vertical diffusion, we have considered three distinct paths, namely, path-4, -5, and -6, as shown in Fig. 4(c). Paths 5 and 6 correspond to two possible pathways for the out-of-plane diffusion of Na atoms in AGY. The Na atom migrates through the central cavity in a zigzag manner for path 5 and along a diagonal for path 6. The symmetric nature of the energy profile for paths 4 and 5 about the center of C18 ring (site II) of the middle AGY layer further confirms the stable adsorption of Na at site II on AGY. It is to be noted that in the trilayered AGY, the stable adsorption site for the Na atom is in the center of the hexagonal cavity of the middle AGY layer compared to the initial and final configurations of NEB calculations (see Fig. S3 of the ESI†). This is due to the synergistic effect of the top and bottom layer carbon atoms. Hence, the corresponding energy profiles show a dip at the stable adsorption site: the center of the hexagonal cavity of the middle AGY. A low energy barrier of 0.19 eV is observed for path 4, despite being similar to path 1; along path 4, the Na atom follows a curved line as in path 2 for migration. In the monolayer study, though path-1 is energetically more favorable than path-2, in stacked AGY, the Na atom diffused through path-2 owing to the effect of stacking (see Fig. S4 of the ESI†). A large energy barrier of 4.38 eV is observed for path-6; in this case, the sodium atom travels at an angle to the acetyl link of the bottom AGY layer and middle AGY layer, where it experiences attraction from the C atoms of both layers. As the Na atom lies near the corner sp2 C atoms in the initial stage of diffusion and they mainly receive charges in the process of adsorption, there exists a significant interaction between Na and C atoms and, hence, responsible for increased energy barrier along path-6. The vertical diffusion in a zigzag manner along path-5 shows a negligible diffusion energy barrier of 0.23 eV. As Na ion moves through the center of hexagonal rings of the AGY layers for path-5 and the size of these rings is large compared to the ionic diameter of the Na+ (2.04 Å (ref. 40)), diffusion along path 5 shows a very low energy barrier. Hence, AGY can be the most suitable anode candidate for the NIBs with high power densities. In high-power density applications like electric vehicles, the battery undergoes frequent dis/charging at high rates. In such cases, traditional anode materials, such as graphite and other 2D materials without in-plane cavities, can experience the accumulation of ions in some parts of the anode, leading to permanent volume expansion. This expansion compromises the anode's connection with the current collector, resulting in decreased efficiency and cycling life. However, along with planar diffusion, AGY facilitates vertical diffusion via its large central cavities, which effectively prevents anode expansion even under high dis/charge rates, thereby maintaining the high cycle life of NIB and, hence, can act as a potential anode candidate for NIBs.
4.4 Doping studies
While diffusing between the stable adsorption sites in AGY, the sodium atom needs to migrate across or along the acetylenic links, i.e., edges of the C18 ring. Therefore, acetylenic connections form an essential component of the diffusion pathways, and by varying the nature of these acetylenic connections, we can tune the adsorption strength and diffusion energy barriers for Na atoms on AGY. To study the effect of electron-rich or electron-deficient acetylenic links, we have considered the substitution doping of B/N atom onto AGY at sp and sp2 carbon atom locations. This doping acts as hole/electron doping as B and N atoms are one electron deficient and rich, respectively, compared to carbon atoms. To study the feasibility of doping, we first examined the stability of the B/N-doped AGY by calculating their formation energies by using eqn (3). | (3) |
The results presented in Table 1 reveal that doping B at the sp2 site and N at the sp site is energetically favorable. Hence, these configurations are considered for Na atom adsorption energy and further electronic structure analysis of the doped AGY. The adsorption energies of Na atom on B/N-doped AGY are mentioned in Table 2. In the case of B doping at sp2 site (see Fig. 5(b)), B is one electron deficient compared to C, and in the process of adsorption, the Na atom donates the electron to the substrate. This results in a strong interaction between B and C atoms. Hence, it is responsible for the improved adsorption strength compared to pristine AGY. In contrast, N doping at sp site shows positive adsorption strength. The positive adsorption strength indicates the repulsive nature of the interaction between N and C atoms. The adsorption energy trend in B/N-doped AGY is as follows.
| Eads, N-sp < Eads, AGY without doping < Eads, B-sp2 |
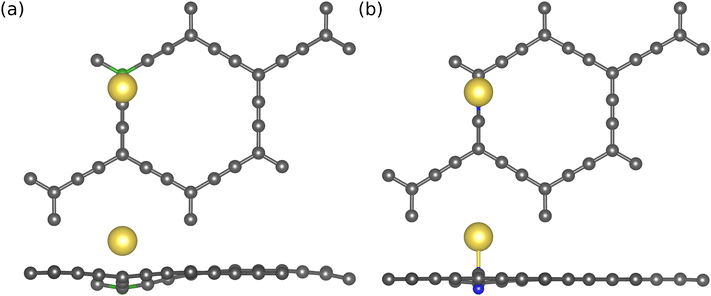 | ||
| Fig. 5 Top and side views of Na adsorption on (a) boron (green) atom doped at sp2 site, and (b) nitrogen (blue) atom doped on sp site of AGY. | ||
| Doping configuration | E Formation (eV) |
|---|---|
| B-sp2 | −0.32 |
| B-sp | 0.90 |
| N-sp2 | 1.40 |
| N-sp | −0.26 |
| Doping configuration | E ads (eV) |
|---|---|
| B-sp2 | −1.26 |
| AGY without doping | −0.30 |
| N-sp | 0.09 |
These results elucidate that by doping the B or N atom at sp2/sp site of AGY, we can significantly alter the adsorption energy of the AGY anode. According to our adsorption energy studies, a B-AGY can lead to an anode of higher specific capacity, and N-AGY can lead to an anode with low diffusion barriers. Thus, B/N atom doping can significantly alter the adsorption energy of the Na atom on the AGY. We further studied the feasibility of increasing doping concentration and its effect on Na atom adsorption. But the battery-related matrices of AGY at higher B/N-doping concentrations did not improve significantly (see section S2 of the ESI†).
Density of states. As shown in Fig. 6, the total and partial density of states (PDOS) for AGY significantly changes after doping with B/N atoms. Fig. 6(a and b) represent the total and PDOS of the pristine and Na-adsorbed AGY, respectively. The total and partial density of states of B-AGY are shown in Fig. 6(c). For B doping, the Dirac cone of the material shifts towards the higher energy, resulting in the availability of a large number of allowed states at the Fermi level of the system due to hole doping. Upon the addition of the Na atom to this system, previously available states were observed to be occupied due to the charge-donating nature of the Na atom. This heavy occupancy of the available states after the Na atom adsorption explains the significantly higher adsorption energy observed for this configuration. The fewer states available even after the adsorption of the Na atom indicate the metallic nature of the system, as shown in Fig. 6(d).
An opposite trend is observed in the case of N-doping in comparison to the B-doping. Here, the Dirac cone of the N-doped AGY shifts towards the lower energy, as shown in Fig. 6(e). The nitrogen 2p orbital contributes insignificantly to the allowed states at the Fermi level. Unlike the case of Na adsorption on pristine and B-doped AGY, the N-doped AGY has a minute but observable contribution of Na 3s orbital to the states at the Fermi level, as shown in Fig. 6(f). This indicates weaker and more of a van der Waal's interaction between Na and N-doped AGY as reflected in the low adsorption energy strength for this configuration.
Charge density difference. Using the following expression as an estimate, we studied the direction of charge transfer of B/N-doped AGY upon Na adsorption.
| Δρ(r) = ρdoped-AGY+Na(r) − ρdoped-AGY(r) − ρNa(r) | (4) |
Fig. 7 shows the charge density difference (CDD) in the B/N-doped systems upon the adsorption of Na atom. Here, Fig. 7(a) represents the top and the side view of the CDD plot for B-doped AGY. Here, the boron atom bonded to the sp carbon atom gains a significant amount of charge from the sodium atom, represented by the larger red lobe. This strong accumulation of charge at the Csp–B bond is due to the hole-doping nature of the B atom. In addition, some of the sp atoms gain charge from the Na atom via inductive effect, as evident by the tiny red lobes on them. In the case of Na atom adsorption on N-doped AGY, the Csp–N bond undergoes significant charge redistribution as evident from the similar sizes of red and green lobes at the Csp–N bond. In this case, sp2 carbon atoms gained a small amount of charge, as evidenced by the tiny green lobes on the corner C atoms. Bader charge analysis shows that compared to the B-doping, the Na atom donates less charge to the N-doped AGY system, which explains the weaker adsorption strength of Na on N-AGY. Doped AGY's structural and thermodynamical stability is discussed in section S1 of the ESI.†
4.5 Theoretical specific capacity
The above discussions on the electrochemical properties of AGY show that it can act as a potential anode material for NIBs. In addition, the theoretical specific capacity (TSC) of an electrode is another important parameter that decides the suitability of the electrode for practical applications. By definition, the TSC of an anode represents the amount of charge that can be stored per unit mass of the anode material. In general, the TSC of any electrode material is given by the formula: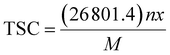 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 801.4 is the Faraday's constant (in mA h mol−1), ‘n’ is the number of Na atoms loaded, ‘x’ is the valency of the Na atom (x = 1), and M is the molecular weight of the AGY. The TSC of any electrode can be evaluated by conventional method41–49 of performing concentration dependent adsorption study. In general, metal ion batteries involve the rocking chair mechanism50 of the active metal ion in the battery operation, i.e., the metal ions are either stored or released from the electrode material.
801.4 is the Faraday's constant (in mA h mol−1), ‘n’ is the number of Na atoms loaded, ‘x’ is the valency of the Na atom (x = 1), and M is the molecular weight of the AGY. The TSC of any electrode can be evaluated by conventional method41–49 of performing concentration dependent adsorption study. In general, metal ion batteries involve the rocking chair mechanism50 of the active metal ion in the battery operation, i.e., the metal ions are either stored or released from the electrode material.
To mimic this rocking chair mechanism, the concentration of Na atoms is increased in a stepwise manner by maintaining a minimum distance between any two adjacent Na atoms and the structures are fully relaxed. We performed a convex hull calculation where multiple structural conformations of 2 × 2 AGY supercell for a given value of n are optimized. We have considered up to 10 distinct configurations for each value of n and computed Eads referring to eqn (1) and the results are shown in Fig. 8(a). According to eqn (1), a negative value of Eads represents the stability of the structure with n loaded Na atoms, and the same structure is considered for (n + 1)th loading. An example of structural conformations of AGY loaded with 13 Na atoms is shown in Fig. S5 of the ESI.† In addition, the optimized structures are shown in Fig. S6 and S7 of the ESI.† Our results show that for the case of n = 13, Eads reduces to the lowest negative value, and for all other cases, it becomes positive. Hence, we considered n = 13 as the upper limit of n, implying a capacity of ∼906 mA h g−1 using this conventional method. In Fig. 8(a), deviation observed in Eads values for the same n value is attributed to different structural conformations optimizing to different local minima on the potential energy surface. This is the reason for the variation in reported TSC values for AGY24,25 as anode material for NIBs. As shown in the Table 3, the TSC value estimated for AGY using the conventional method is comparable to that of other carbon-based 2D anode materials reported in the literature.
| Carbon-based anode | Specific capacity (mA h g−1) |
|---|---|
| Pristine graphene51 | 308 |
| Graphene (with maximum divacancy content)52 | 1450 |
| X-graphene53 | 1302 |
| Graphdiyne54 | 553 |
| Biphenylene55 | 1075 |
| Pentagraphene56 | 1489 |
| PAI-graphene57 | 1674 |
| Haeckelite58 | 1116 |
| C456759 | 1116 |
| Graphenylene60 | 641 |
| 14,14,14-Graphyne61 | 1788 |
| α-Graphyne24 | 1396 |
| α-Graphyne (our work) | 906 |
Further, we also calculated the open circuit voltage (OCV) of the AGY as a function of the concentration of Na atoms. OCV is another important parameter of any electrode material, which represents the theoretical upper limit of the operating voltage of an anode material. OCV is calculated using the formula:
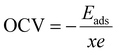 | (6) |
Though the conventional method is suitable, it has a major drawback of dealing with a huge combinatorial space of configurations. Compared to single Na adsorption, all other adsorption cases with multiple numbers of Na atoms show a vast configurational space. The ways to load n number of sodium atoms on AGY increase exponentially with n. In such cases, it is difficult to identify the most stable configuration for each loading. For example, in the convex hull calculations, we showed that conformations with the same number of sodium atoms exhibit both positive and negative Eads values despite satisfying the energy and force convergence constraints. Hence, depending on the final optimized structure of AGY loaded with n number of sodium atoms it is difficult to decide the possibility of further loading of Na atoms. In addition, it gets more and more meticulous in handcrafting the structural conformations for multiple values of n. Another important limitation of this conventional method is the lack of temperature effects in the DFT calculations. As we performed DFT calculations at 0 K, the proposed TSC is not accurate. For accurate prediction of the TSC, both adsorption energy analysis and AIMD simulations are required. For instance, in the case of aluminum ion battery62 using graphdiyne cathode the adsorption study predicts that the achievable TSC is ∼154 mA h g−1 (5 AlCl4) on one side of the graphdiyne, in contrast to that the AIMD simulations predict that only 3 AlCl4 can be loaded on one side of the graphdiyne, reducing the TSC to ∼90 mA h g−1. Hence, there is a need for a method that does quick and diverse sampling of the PES of AGY loaded with Na atoms, accounting for the temperature effects as well.
4.6 Estimating the TSC from AIMD studies
If one goes strictly by the adsorption energy calculations, as discussed above, the TSC of AGY is ∼906 mA h g−1. A recent ab initio study24 reports a TSC of 1396 mA h g−1 for NIBs using AGY. However, in this study, a single unit cell is considered which constrains the freedom of relaxation of the host AGY structure after loading. Here, we pursue AIMD simulations at 300 K to get an alternate estimate of the TSC by incorporating the structural dynamics. In AIMD, the PES is quickly sampled on the fly which is much faster compared to the meticulous design of configurations and their geometry optimizations. We performed AIMD simulations for AGY 2 × 2 supercell loaded with varying numbers of sodium atoms at 300 K, with Nóse–Hoover thermostat. In this method, we plan to estimate the TSC based on the adsorption energy of the AGY loaded with Na atoms. Unlike the static expression for Etotal in eqn (1), we consider the total energy of the system at each time step during the AIMD simulation, as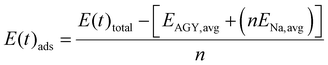 | (7) |
To maintain the parity, instead of taking the static energy values EAGY and ENa as one would obtain from DFT, we carried out AIMD calculations at 300 K for these independent systems and averaged their energies (EAGY, avg and ENa, avg) over a time period of 5 ps. In eqn (7), E(t)total refers to the total energy of the loaded anode structure at time t on a 2 × 2 AGY supercell. n refers to the number of Na atoms loaded on AGY. The ensemble average of Eads (t) is synonymous with the expected value of Eads. Hence, for AGY loaded with n sodium atoms, as long as the mean value of E(t)ads is negative, i.e., Eads, mean < 0, we consider the loading is energetically favorable. To determine the upper limit of loading (n), we performed AIMD runs for n varying from 1 to 13. As illustrated in Fig. 9(e–i), Eads > 0 is observed for n ≥ 5. The maximum possible value of n observed in the AIMD method was far below the maximum value of n observed in the conventional method i.e., n = 13. From Fig. 9(a–d), we observe n = 4 is the upper limit till the condition that the average value of Eads is negative, is satisfied. In addition, the structure obtained at the end of the AIMD simulation with four Na loading was selected and then we removed the loaded Na atoms, considering this structure as our initial configuration. Then we relaxed the structure and it reverted back (see Fig. S8 of the ESI†) to its pristine structure without any buckling, indicating its structural reversibility upon de/intercalation. This upper limit of n = 4, translates to the TSC of Na4C32 or ∼279 mA h g−1.
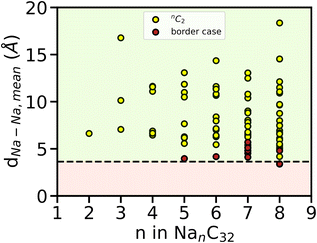
To further validate the TSC value obtained above and to understand why Eads, mean becomes positive from n = 5, we computed the mean interatomic distances dNa–Na, mean (Å) of all possible pairs of Na atoms, throughout the AIMD simulation of Na intercalated AGY. Independent AIMD calculation was performed for pristine Na metal (BCC) at 300 K and a mean value of 3.64 Å was observed. This value is in good agreement with the experimentally observed value of 3.71 Å. With this value as reference, dNa–Na, Ref, the dNa–Na, mean for each pair of Na atoms is evaluated for all loading configurations (NanC32, where 2 ≤ n ≤ 8). Here, we consider the maximum value of n at which the condition dNa–Na, mean > dNa–Na, Ref is strictly satisfied for all Na–Na combinations throughout the AIMD simulation. The results are shown in Fig. 10, and in that black dashed line indicates the dNa–Na,Ref.
In Fig. 10, yellow circles represent the interatomic distance between each pair of Na atoms for a given value of n i.e., nC2. The red circles above the black dashed line indicate the cases with dNa–Na < dNa–Na, Ref at least for a short period of time but dNa–Na, mean > dNa–Na, Ref (see Fig. S9 of the ESI†). In general, during dis/charging of a battery, the clustering of metal atoms in the anode leads to the formation of dendrite resulting in a short-circuit. Hence, we considered each red circle as the nucleation center for dendrite growth. From Fig. 10, it is evident that for n ≤ 4, each pair of Na atoms strictly satisfies the condition dNa–Na, mean > dNa–Na, Ref without a single event of clustering. However, the red circle starts to appear from n = 5 and the same continues for n = 6, 7, 8. In particular, for one instance of n = 8, showed strict clustering where dNa–Na, mean < dNa–Na, Ref, throughout the simulation. This approach estimates a maximum possible loading of AGY with n = 4, complementing the TSC estimate from adsorption energy studies using AIMD simulation as mentioned in the above discussion. Both approaches result in a TSC of ∼279 mA h g−1 for AGY as an anode for NIB. When AGY is paired with a high energy density NIB cathode such as P2-Na0.66Ni0.26Zn0.07Mn0.67O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63 with a specific capacity 143 mA h g−1 and an OCV of 3.5 V Vs. Na/Na+, it can show an impressive negative to positive material capacity of 1.95 (N/P ratio64) for the same mass of anode and cathode, followed by a remarkable cell voltage of 3.14 V.
63 with a specific capacity 143 mA h g−1 and an OCV of 3.5 V Vs. Na/Na+, it can show an impressive negative to positive material capacity of 1.95 (N/P ratio64) for the same mass of anode and cathode, followed by a remarkable cell voltage of 3.14 V.
5 Summary and outlook
To summarise, with the aid of density functional theory calculations and ab initio molecular dynamics simulations we examined α-graphyne (AGY) as a potential anode for sodium-ion battery. With large hexagonal rings, AGY exhibits both in-plane and out-of-plane diffusion for Na atoms with negligible energy barriers of 0.19 eV and 0.23 eV, respectively. AGY shows a low open circuit voltage value of 0.36 V (vs. Na/Na+) as well as excellent thermodynamical stability with four Na atoms adsorbed in its structure and results in a theoretical specific capacity of 279 mA h g−1 at 300 K.As a byproduct of the present study, we find that a conventional DFT calculation is overestimating the TSC for AGY by ∼300% as it gives a value of 906 mA h g−1. This brings our attention to the well-known problem of discrepancy between the specific capacities reported from theory and experiments. We find that, while estimating the adsorption energy using DFT, ignoring the probable formation of temperature-driven metal clusters is the main reason behind such overestimations. To reduce the mismatch, alternate approaches need to be explored. Here, we propose a scheme involving temperature-dependent AIMD simulation, which substantially improves the accuracy of the TSC estimation. To demonstrate it, we show that adsorption energy for loading of five (TSC of 348 mA h g−1) and thirteen (TSC of 906 mA h g−1) Na atoms on a 2 × 2 supercell of AGY using DFT are −0.319 eV/Na and −0.001 eV/Na, respectively. However, a 300 K AIMD simulation shows that as we increase the loading from four to five Na atoms, the adsorption energy becomes positive (+0.14 eV/Na). Therefore, the predicted TSC is around 279 mA h g−1.
To conclude, we believe that the present study will open up new avenues to carry out further theoretical and experimental studies on AGY as a potential anode for sodium-ion batteries. In addition, we anticipate that our analysis will lead to the formulation of efficient computational approaches to calculate the TSC.
Author contributions
Babuji Dandigunta: conceptualization, investigation, data curation, formal analysis, writing – original draft, visualization. Abhijitha V G: conceptualization, investigation, formal analysis, writing – review & editing. Sharma S.R.K.C. Yamijala: formal analysis, writing – review & editing. B. R. K. Nanda: conceptualization, formal analysis, supervision, investigation, writing – review & editing, project administration, funding acquisition and resources.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. R. K. Nanda acknowledges the funding of the present work by the Department of Science and Technology, India, through Grant No. CRG/2020/004330. Sharma S. R. K. C Yamijala acknowledges the financial support of IIT Madras through its new faculty support grant DST-SERB (SRG/2021/001455). All authors highly acknowledge the computational resources provided by the High-Performance Computing Environment (HPCE) at IIT Madras.References
- M. Troldborg, S. Heslop and R. L. Hough, Renewable Sustainable Energy Rev., 2014, 39, 1173–1184 CrossRef.
- J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- S. Khammuang, A. Pratumma, A. Sakulkalavek, T. Kaewmaraya, T. Hussain and K. Kotmool, Phys. Chem. Chem. Phys., 2023, 25, 19612–19619 RSC.
- F. Larsson, P. Andersson, P. Blomqvist and B.-E. Mellander, Sci. Rep., 2017, 7, 1–13 CrossRef CAS PubMed.
- T. C. Wanger, Conserv. Lett., 2011, 4, 202–206 CrossRef.
- A. N. Singh, M. Islam, A. Meena, M. Faizan, D. Han, C. Bathula, A. Hajibabaei, R. Anand and K.-W. Nam, Adv. Funct. Mater., 2023, 2304617 CrossRef CAS.
- N. Tapia-Ruiz, A. R. Armstrong, H. Alptekin, M. A. Amores, H. Au, J. Barker, R. Boston, W. R. Brant, J. M. Brittain and Y. Chen, et al. , J. Phys.: Energy, 2021, 3, 031503 CAS.
- Z. Wang, X. Zhang, S. Zhou, K. Edström, M. Strømme and L. Nyholm, Adv. Funct. Mater., 2018, 28, 1804038 CrossRef.
- L. Zhao, T. Zhang, W. Li, T. Li, L. Zhang, X. Zhang and Z. Wang, Engineering, 2023, 24, 172–183 CrossRef CAS.
- T. Perveen, M. Siddiq, N. Shahzad, R. Ihsan, A. Ahmad and M. I. Shahzad, Renewable Sustainable Energy Rev., 2020, 119, 109549 CrossRef CAS.
- Z. Hu, M. Tebyetekerwa, A. E. Elkholy, Q. Xia, T. Hussain, H. Liu and X. S. Zhao, Electrochim. Acta, 2022, 423, 140611 CrossRef CAS.
- X. Chen and Y. Zhang, Int. J. Energy Res., 2021, 45, 9753–9779 CrossRef CAS.
- Y.-M. Chang, H.-W. Lin, L.-J. Li and H.-Y. Chen, Mater. Today Adv., 2020, 6, 100054 CrossRef.
- Z. Xie, B. Zhang, Y. Ge, Y. Zhu, G. Nie, Y. Song, C.-K. Lim, H. Zhang and P. N. Prasad, Chem. Rev., 2021, 122, 1127–1207 CrossRef PubMed.
- E. H. Falcao and F. Wudl, J. Chem. Technol. Biotechnol., 2007, 82, 524–531 CrossRef CAS.
- R. Baughman, H. Eckhardt and M. Kertesz, J. Chem. Phys., 1987, 87, 6687–6699 CrossRef CAS.
- Z. Jia, Y. Li, Z. Zuo, H. Liu, C. Huang and Y. Li, Acc. Chem. Res., 2017, 50, 2470–2478 CrossRef CAS PubMed.
- G. Li, Y. Li, H. Liu, Y. Guo, Y. Li and D. Zhu, Chem. Commun., 2010, 46, 3256–3258 RSC.
- Q. Li, Y. Li, Y. Chen, L. Wu, C. Yang and X. Cui, Carbon, 2018, 136, 248–254 CrossRef CAS.
- Z. Li, M. Smeu, A. Rives, V. Maraval, R. Chauvin, M. A. Ratner and E. Borguet, Nat. Commun., 2015, 6, 6321 CrossRef CAS PubMed.
- X. Yang, Z. Dai, Y. Zhao and S. Meng, Phys. Chem. Chem. Phys., 2018, 20, 15980–15985 RSC.
- H. J. Hwang, J. Koo, M. Park, N. Park, Y. Kwon and H. Lee, J. Phys. Chem. C, 2013, 117, 6919–6923 CrossRef CAS.
- C. Li, J. Ma, B. Kang, G. Zhang, F.-F. Wang, L. Zhai and J. Lee, Mater. Today Chem., 2022, 26, 101254 CrossRef CAS.
- T. Singh, J. R. Choudhuri and M. K. Rana, Nanotechnology, 2022, 34, 045404 CrossRef PubMed.
- Y. Yuan, X. Song, J. Ma, Y. Chen, F. Wang, B. Kang and J. Y. Lee, Catalysts, 2022, 12, 670 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al. , J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- J. Moellmann and S. Grimme, J. Phys. Chem. C, 2014, 118, 7615–7621 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078 CrossRef CAS PubMed.
- W. Wu, W. Guo and X. C. Zeng, Nanoscale, 2013, 5, 9264–9276 RSC.
- J.-M. Ducere, C. Lepetit and R. Chauvin, J. Phys. Chem. C, 2013, 117, 21671–21681 CrossRef CAS.
- N. Narita, S. Nagai, S. Suzuki and K. Nakao, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 11009 CrossRef CAS.
- L. Pan, L. Zhang, B. Song, S. Du and H.-J. Gao, Appl. Phys. Lett., 2011, 98, 173102 CrossRef.
- S. B. Mishra, S. Ramaprabhu and B. Nanda, et al. , Nanoscale Adv., 2022, 4, 3870–3882 RSC.
- A. C. Neto, F. Guinea, N. M. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109 CrossRef.
- Q. Wang, P. Ping, X. Zhao, G. Chu, J. Sun and C. Chen, J. Power Sources, 2012, 208, 210–224 CrossRef CAS.
- H. Jónsson, G. Mills and K. W. Jacobsen, Classical and quantum dynamics in condensed phase simulations, World Scientific, 1998, pp. 385–404 Search PubMed.
- V. G. Abhijitha, S. B. Mishra, S. Ramaprabhu and B. R. K. Nanda, Nanoscale Adv., 2022, 4, 3870–3882 RSC.
- Y. Zhang, S. Liu, Y. Ji, J. Ma and H. Yu, Adv. Mater., 2018, 30, 1706310 CrossRef PubMed.
- J. Liu, C. Zhang, L. Xu and S. Ju, RSC Adv., 2018, 8, 17773–17785 RSC.
- J. Zhang, Y.-F. Zhang, Y. Li, Y.-R. Ren, S. Huang, W. Lin and W.-K. Chen, Phys. Chem. Chem. Phys., 2021, 23, 5143–5151 RSC.
- X. Lv, F. Li, J. Gong, J. Gu, S. Lin and Z. Chen, Phys. Chem. Chem. Phys., 2020, 22, 8902–8912 RSC.
- J. Liu, M. Qiao, X. Zhu, Y. Jing and Y. Li, RSC Adv., 2019, 9, 15536–15541 RSC.
- N. Khossossi, D. Singh, A. Banerjee, W. Luo, I. Essaoudi, A. Ainane and R. Ahuja, ACS Appl. Energy Mater., 2021, 4, 7900–7910 CrossRef CAS.
- H. Xie, Y. Qie, I. Muhammad and Q. Sun, J. Phys. Chem. Lett., 2021, 12, 1548–1553 CrossRef CAS PubMed.
- T. D. Pham, H. D. Luong, K. Sato, Y. Shibutani and V. A. Dinh, Phys. Chem. Chem. Phys., 2019, 21, 24326–24332 RSC.
- N. K. Jena, R. B. Araujo, V. Shukla and R. Ahuja, ACS Appl. Mater. Interfaces, 2017, 9, 16148–16158 CrossRef CAS PubMed.
- V. Vishnubhotla, A. Kabiraj, A. J. Bhattacharyya and S. Mahapatra, J. Phys. Chem. C, 2022, 126, 8605–8614 CrossRef CAS.
- S. Choi, J. Kang, J. Ryu and S. Park, Macromol. Res., 2020, 28, 1175–1191 CrossRef CAS.
- K. C. Wasalathilake, G. A. Ayoko and C. Yan, Carbon, 2018, 140, 276–285 CrossRef CAS.
- D. Datta, J. Li and V. B. Shenoy, ACS Appl. Mater. Interfaces, 2014, 6, 1788–1795 CrossRef CAS PubMed.
- S. Wang, Y. Si, B. Yang, E. Ruckenstein and H. Chen, J. Phys. Chem. Lett., 2019, 10, 3269–3275 CrossRef CAS PubMed.
- Z. Xu, X. Lv, J. Li, J. Chen and Q. Liu, RSC Adv., 2016, 6, 25594–25600 RSC.
- T. Han, Y. Liu, X. Lv and F. Li, Phys. Chem. Chem. Phys., 2022, 24, 10712–10716 RSC.
- B. Xiao, Y.-c. Li, X.-f. Yu and J.-b. Cheng, ACS Appl. Mater. Interfaces, 2016, 8, 35342–35352 CrossRef CAS PubMed.
- Z. Cheng, X. Zhang, H. Zhang, J. Gao, H. Liu, X. Yu, X. Dai, G. Liu and G. Chen, Phys. Chem. Chem. Phys., 2021, 23, 18770–18776 RSC.
- M. Zhou, Y. Shen, J. Liu, L. Lv, X. Gao, X. Wang, X. Meng, X. Yang, Y. Zheng and Z. Zhou, Solid State Ionics, 2022, 378, 115898 CrossRef CAS.
- Y. Gao, D. Li and T. Cui, ACS Appl. Electron. Mater., 2021, 3, 5147–5154 CrossRef CAS.
- G. d. S. L. Fabris, A. dos Reis Albuquerque, R. Dovesi and J. R. Sambrano, Mater. Sci. Eng., B, 2021, 268, 115121 CrossRef.
- M. Makaremi, B. Mortazavi and C. V. Singh, Appl. Mater. Today, 2018, 10, 115–121 CrossRef.
- S. B. Mishra, A. V. Gopala, S. Ramaprabhu and B. Nanda, ACS Appl. Energy Mater., 2021, 4, 7786–7799 CrossRef CAS.
- Q. Liu, Z. Hu, M. Chen, C. Zou, H. Jin, S. Wang, S.-L. Chou, Y. Liu and S.-X. Dou, Adv. Funct. Mater., 2020, 30, 1909530 CrossRef CAS.
- J. Betz, G. Bieker, P. Meister, T. Placke, M. Winter and R. Schmuch, Adv. Energy Mater., 2019, 9, 1803170 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Other possible adsorption sites and their adsorption energies, relative energies of AA and AB stacked AGY, reaction coordinates for the six diffusion paths considered in NEB calculations, distinct configurations for the loading of 13 Na atoms on the AGY, optimized structures for AGY loaded with 2 to 13 Na atoms, interatomic distance for each pair of Na atoms during AIMD simulations, cyclic durability of α-graphyne, final structures of three example Na atom loading for all 10 combinations, trilayer AGY energetics, thermodynamical stability, and formation energy analysis of doped AGY system. See DOI: https://doi.org/10.1039/d4nr02797c |
| This journal is © The Royal Society of Chemistry 2024 |