Conductive filament distribution in nano-scale electrochemical metallization cells

Abstract

We report a combined experimental and theoretical study of the spatial distributions and sizes of conductive filaments in nano-scale electrochemical metallization (ECM) cells. Each cell comprises a silver nanocube as active electrode, a titanium dioxide (TiO₂) or aluminum oxide (Al₂O₃) layer as dielectric, and a highly-doped silicon substrate as passive counter electrode. Following electroforming of the ECM cell and subsequent mechanical delamination of the silver nanocubes, current maps at previous particle locations reveal an intriguing metal distribution in the TiO₂, with preferential accumulation close to the original locations of the nanocube edges. We assign this behavior to electric field enhancements close to the cube edge positions. In contrast, filaments in Al₂O₃ layers show a comparatively homogenous distribution, which may be assigned to its lower dielectric permittivity. By increasing the oxide thickness, the total area of conductive spots in the current maps increases monotonically for both materials. Kinetic Monte-Carlo simulations of ion migration dynamics in TiO₂ confirm the experimental observations, describing both the preferred locations and oxide thickness-dependent metal loadings associated with filament formation. Overall, our findings are highly valuable for the design of future electrochemical metallization cells, especially in the sub-100 nm regime, where optimal filament control is of major importance for achieving lowest device-to-device variability.

---

Introduction

Recently, there has been a tremendous increase of interest in novel concepts for memory and computing that extend beyond von Neumann architectures, with resistive switching materials emerging as powerful components for a novel class of functional devices.^1–5 Among the variety of different systems and associated physical mechanisms of resistive switching, electrochemical metallization (ECM) cells are one of the most promising candidates for neuromorphic computation and non-volatile data storage.^6–8 In one common ECM device concept, a solid dielectric layer is sandwiched between an active and a passive electrode (AE and PE, respectively). While the PE is commonly fabricated from a noble metal such as Pt, the AE typically consists of a metal such as Ag or Cu, which is easily oxidized under the application of a positive electrical potential, thereby providing highly mobile ions to the dielectric, which then serves as solid electrolyte. Popular dielectrics include various types of oxides such as TiO₂, SiO₂, Al₂O₃ or Ta₂O₅, 2D dichalcogenides or layered combinations thereof, as well as novel nanoscale materials and systems.^4,9–11 Under the application of an external electrical driving force, metal ions migrate through the oxide towards the PE. Depending on the mobility of ions and the concentration of quasi-free electrons in the oxide, ions are reduced either at the PE or on their way towards it, within the bulk of the oxide. Once metal accumulation reaches from AE to PE, a conductive filament (CF) is formed, leading to strongly enhanced conductance of the device, i.e., a transition from a high resistance state (HRS) to a low resistance state (LRS) occurs.

Much understanding of the filament formation and rupturing processes has been gained in recent years,^12–14 also thanks to thorough characterization of the formed filament locations, including their structures and compositions, using transmission electron microscopy (TEM), scanning electron microscopy (SEM), scanning tunneling microscopy (STM), and conductive-probe atomic force microscopy (CP-AFM),^4,13,15–20 which in particular includes the 3D-tomography work of Celano et al.¹⁶ Nevertheless, details of filament formation still remain under debate, as this process critically depends on several interdependent, non-equilibrium processes (ion migration, electronic and thermal transport), as well as on various material and interface properties (e.g., oxide crystallinity and dielectric permittivity, defects, chemical redox potentials, electrode work functions). These factors, as well as the actual electrode geometries and oxide thicknesses, and the electrical parameters used for the initial electroforming step, eventually all determine the functional characteristics and performance of the device. Important figures of merit for the latter are the conductance ON/OFF ratio, the memristive switching endurance and retention.

Controlling the (initial) filament formation becomes especially important when large arrays of ECM cells are fabricated, with a targeted lowest device-to-device variability. In this context, much effort has already been devoted to pre-define or spatially confine the position of the forming filaments,²¹ including nanoparticle- or nanopore-based architectures, or involving different electric field concentrators.^22–30 However, to the best of our knowledge, filament formation below nanoscale electrodes of flat shape, and in particular investigations of their spatial distribution with respect to the electrode geometry, has not been studied in detail. Here, electric field-enhancement effects at the sharply defined electrode edges may well be anticipated to play a significant role, depending on the dielectric permittivity of the oxide. Such a study would enhance the detailed understanding and the ability to predict/control filament formation, providing crucial knowledge that may become especially relevant for future memory architectures involving large numbers of sub-100 nm wide electrodes in 3D-stacked cross-bar geometries.³¹

In the present work, we report such a spatially-resolved investigation of silver (Ag) conductive filaments in TiO₂ and Al₂O₃ layers that have formed below silver nanocubes (AgNCs) possessing edge lengths of 100 nm. Using CP-AFM, we observe a clear accumulation of CF material close to cube edges for thin TiO₂ layers, which can be directly assigned to the impact of locally enhanced electric fields. In contrast, this effect was not observed for Al₂O₃, a material with lower dielectric constant. For thicker oxides of both kinds, however, the filaments comprise larger amounts of accumulated material, most likely due to the enhanced time required for filament formation to reach the LRS. Complementary kinetic Monte-Carlo (kMC) simulations of ion migration and accumulation into CFs support our experimental results and mechanistic interpretation regarding the electric field-enhanced filament formation process. As an analytical technique complementary to important alternative, microscopy methods mentioned above, CP-AFM following delamination of the top electrode may provide a direct spatial mapping of the conducting filament paths – a key information for ECM cell architectures and operation. We are convinced that our findings are highly relevant for the understanding and design of future nanoscale electrochemical metallization cells, where optimal filament control will be of major importance for achieving highest device-to-device reproducibility.

Results and discussion

Sample preparation and pre-characterization

For characterization of filament growth in nano-scale ECM cells, AgNCs with a side-length of 100 nm were used as AE. Regular arrays of such AgNCs were first deposited on a thin layer of TiO₂ on top of a highly p-type doped Si substrate, using a site-selective immobilization scheme, as we have previously reported.³² Following immobilization, the space between the AgNCs was filled (planarized) by an insulating polymer to enable CP-AFM measurements.

Initially, individual AgNCs were located by scanning the surface of the AgNC sample by AFM, as illustrated in Fig. 1a. Next, identified single AgNCs were electroformed by increasing the voltage applied to the p-Si substrate with respect to the AFM tip, ramping from 0 V to −10 V (sweep rate 0.5 V s⁻¹). As shown in Fig. 1b, at approximately −8 V bias an abrupt change of the current was measured, indicating the successful formation of the ECM CF. The LRS current was limited by a compliance current I_CC of 120 mA to prevent hard-breakdown of the device. Subsequently, the AgNC area was scanned again with a read-out voltage in the range of 2–4 V. Typical height and current maps of an electro-formed AgNC on 10 nm TiO₂ are shown in Fig. 1c and d, respectively. The shown AgNC protrudes from the surrounding planarizing polymer by ∼15 nm (denoted as “height AgNC”), making contact formation to the conductive probe tip possible. As expected, a solid spot of enhanced conductance (denoted as “current AgNC”) indicates successful electroforming.

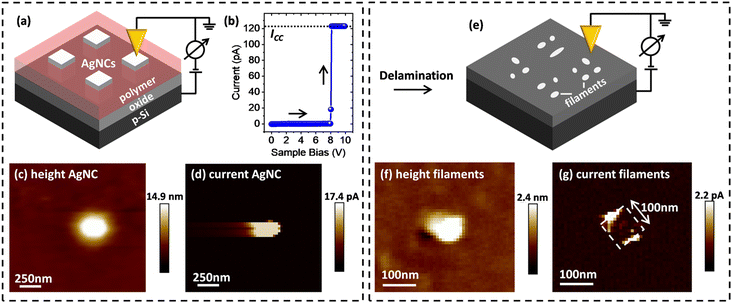Fig. 1 Schematic of conductive filament localization via ex situ CP-AFM. (a) Schematic illustration of NC localization and associated measurement setup. (b) Absolute current–voltage (I–V) characteristics during the electro-forming of single AgNCs (I_CC: compliance current). (For cyclic I–V characteristics data showing pronounced threshold switching behavior, refer to ref. 32.) (c) Height and (d) current maps prior to AgNC delamination, in which a continuous area of high conductance at the AgNC position is observed (note that the streaking in the horizontal direction is a scanning artifact). (e) Schematic illustration of the CP-AFM mapping of the exposed 10 nm thick TiO₂ layer after removing the planarizing polymer and the AgNCs via mechanical/chemical delamination. (f) Height and (g) current maps acquired after delamination, in which small and locally defined spots of enhanced conductance along the previous AgNC edge positions (dashed white box) are observed.

CP-AFM study of conductive filament distribution

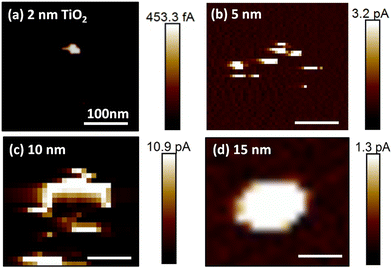
After single AgNCs had been located and electroformed, the AgNCs were carefully removed from the surface by chemical/mechanical delamination, as described in the Experimental section. Following the delamination process, the original AgNC locations were re-investigated by CP-AFM, as illustrated in Fig. 1e. The resulting topographic profile (Fig. 1f) shows a significant decrease in the feature height, consistent with removal of the AgNCs. The observation of an ∼2 nm high protrusion at the original NC location indicates the presence of minor material residues that were not completely removed during delamination. Importantly, significant differences are also present in the corresponding conductance map: as can be seen in Fig. 1g, several bright features of enhanced conductance can now be observed, distributed along the sides of a square-shaped area, as depicted by the white dashed line. This square-shaped area has a side-length of 100 nm and reflects the dimensions of the AgNC that was previously located at this position. These fine features in the conductance map represent localized regions of low resistance through the underlying oxide and can thus be attributed to the locations of filaments generated during electroforming.

To study the dependence of this localized filament formation as a function of oxide thickness, we carried out the same experiment for four different TiO₂ layer thicknesses (from 2 nm to 15 nm). For each thickness, at least five samples were investigated with one or more AgNC(s). Representative current maps collected at the positions of individual electroformed AgNCs after the delamination process were recorded at a positive sample bias of 2 V to 4 V and are shown in Fig. 2a–d. For a small oxide thickness of 2 nm, only a single defined current spot with a diameter of ∼25 nm is typically observed. Increasing the oxide thickness to 5 nm and 10 nm, a distinct increase of the total area of conductive features is measured, presumably originating from more conductive material being deposited below the AgNC during electroforming. This can be understood by considering that, for larger oxide thicknesses, more time is required for a complete CF to form since ions must travel a larger distance before they arrive at the oxide/p-Si interface, where they are reduced. During this extended formation time in thicker oxides, ions may also be injected at other positions, leading to additional metal deposition, in parallel with the initially forming filament. While for small oxide thicknesses, the areas of high conductance are preferentially located at the previous AgNC edge locations (as described above), we instead observe large and continuous areas of enhanced conductance without fine-structure for the case of TiO₂ layer thicknesses above 10 nm (see current map for a 15 nm oxide sample in Fig. 2d).

Fig. 2 Evolution of local conductance with increasing TiO₂ layer thickness, measured at 2 V bias. Current maps (a) to (d) show areas below electroformed AgNCs after delamination for oxide thicknesses of 2 nm, 5 nm, 10 nm, and 15 nm, respectively. With increasing oxide thickness, the total area of conductive features increases, resulting in the lack of an observable fine-structure for the case of the 15 nm thick oxide.

We assign all conductive spots and areas, irrespective of oxide thickness, to partly or completely formed conductive Ag filaments. Here, partly formed CFs may also contribute to the local conductance if the gap between the end of the filament and the p-Si is small enough to support significant tunneling currents. Cross-sectional scanning electron microscopy (SEM) studies of electroformed AgNCs on 20 nm TiO₂, prepared by focused-ion beam milling (FIB), confirmed metal accumulation at the particle edges (cf. ESI Fig. S1†). While such edge accumulation was already less evident in the current map for 15 nm thick oxide (Fig. 2d), the additional metal enrichment within the TiO₂ in the central region below the cube may not have been resolvable in the (tilted) cross-sectional SEM image. We note that, in some cross-sectional images, spherical bright features in the TiO₂ layer below AgNC edges were observed. Such features are indicative of contracted CFs due to Rayleigh instability effects typically observed in ECM cells featuring threshold switching.³³

Comparison to Al₂O₃ as dielectric

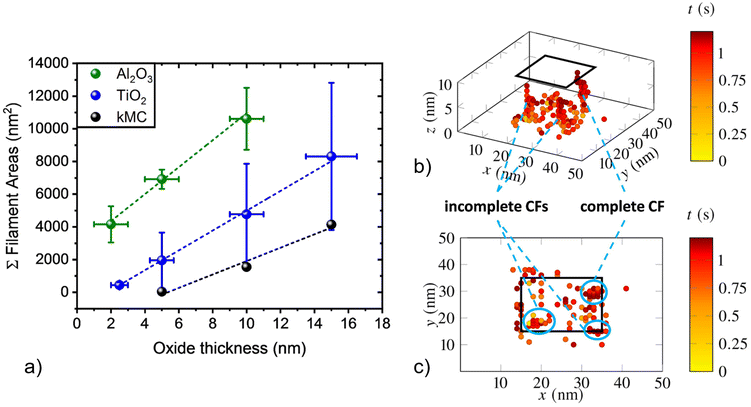
To gain insight into the role of the chosen dielectric material on the observed CF distribution below the AgNCs during electro-forming, additional experiments were carried out with aluminum oxide. Al₂O₃ thin films were grown by atomic layer deposition (ALD) on highly p-type doped Si wafer pieces following native SiO₂ removal in diluted HF(aq) [caution: hydrofluoric acid (HF(aq)) is very hazardous to health; special care/training is mandatory]. Similar to the experiments described above using TiO₂, ECM cells comprising AgNCs on Al₂O₃ layers with thicknesses of 2, 5, and 10 nm were electroformed by application of a forming voltage of up to −10 V. Subsequently, AgNCs were removed by mechanical delamination and the underlying oxide areas were evaluated by CP-AFM by applying a read-out voltage of 2 V to 4 V. While conductive regions in the location of the original AgNC were also present for the case of Al₂O₃, two distinct differences were observed: (i) in contrast to AgNCs on TiO₂, where threshold switching prevailed,³² AgNCs on Al₂O₃ featured bipolar non-volatile memory switching (cf. ESI, Fig. S2a†), and (ii) current maps of areas below AgNCs on Al₂O₃ did not show the pronounced distribution along particle edges as they do for TiO₂, but rather a solid and dense geometry (cf. ESI, Fig. S2b†). We assign this observation to mainly originate from a different electric field distribution inside the aluminum oxide. As directly visualized by electrostatic finite element simulations (cf. ESI, Fig. S3†), the smaller relative permittivity of Al₂O₃ results in a more homogeneous electric field distribution, resulting in less field concentration at the NC edges compared to TiO₂. Furthermore, we note that a different structural quality of the conformal ALD-grown Al₂O₃ compared to the TiO₂ layer (obtained by Ti sputtering and oxidation) may additionally contribute to the observed differences in CF distribution and electrical characteristics.

Despite the differences described above, the general trend of increasing conductive area with increasing oxide thickness is also observed for the case of Al₂O₃. This behavior can be seen in Fig. 3a, in which the integrated conductive areas obtained from CP-AFM are plotted as a function of oxide thickness for both Al₂O₃ (green points) and TiO₂ (blue points) dielectric layers. As for TiO₂, an approximately linear correlation is obtained for Al₂O₃, though with larger conductive areas for a given oxide thickness. As discussed above for the case of TiO₂, we attribute the increasing areas to the longer times needed for CF formation when a larger oxide thickness is to be bridged, thereby resulting in more conductive material being deposited within the oxide layer. At the same time, a more homogeneous field distribution is likely to lead to enhanced parallel nucleation and growth of multiple filaments.

Fig. 3 Experimental CP-AFM data and kinetic Monte-Carlo simulations of conductive filament growth. (a) Comparison of the integrated filament areas per AgNC as a function of oxide layer thickness obtained by ex situ CP-AFM for the case of Al₂O₃ (green) and TiO₂ (blue), along with the results from kMC simulations of TiO₂ (black). Dashed lines represent linear fits to the data. For the experimental data, at least five different TiO₂ and Al₂O₃ samples (delaminated AgNCs) per oxide thickness were evaluated. Error bars are the standard deviations of the data. Simulated absolute values are smaller than the experimental data, though an approximately linear increase of integrated CF area with increasing oxide thickness is confirmed; (b) and (c) show the outcomes of a kMC simulation that includes the local electric field distribution, yielding filament structures in TiO₂, presented in side- and top-view, respectively. Each dot represents a Ag cluster with the color scale ranging from yellow to red, indicating the filament formation time. A simulation volume of 20 nm × 20 nm × 10 nm was used. The kMC simulation confirms Ag-cluster formation preferentially at AgNC edges (as marked by blue colored ellipses), consistent with the experimental observation.

Model calculations

In order to further investigate the anticipated influence of local electric field inhomogeneities and oxide thickness on CF growth, complementary three-dimensional kinetic Monte-Carlo (kMC) simulations of ion migration were carried out. Simulations using kMC setups have proven to be well suited for theoretical investigation of CF growth and dissolution at the nano-scale.^34–36 We used our previously reported kMC simulation tool and parametrization.³² The kMC model was extended by adding a local electric field component. We implemented a Poisson-solver, which runs every time a Ag-ion is immobilized and update the local electric field at each lattice point. In this way, the local electric field distribution inside the oxide layer below the AgNC is updated, leading to a modulation of the injection and oxidation barrier height for ions at the Ag/oxide interface. In addition, the locally enhanced field at positions where Ag-ions have already been reduced and immobilized at the p-Si/oxide interface influences ion migration, leading to preferred ion trajectories towards these positions and, therefore, more guided CF growth. This can be observed in detail in Fig. 3b and c, where a resulting CF structure, here exemplarily investigated for TiO₂ as dielectric, is shown in side- and top-view, respectively. The color scale, ranging from yellow to red, indicates the elapsed simulation time. Each dot shown in the simulation area represents one immobilized Ag-cluster. The simulation was executed for three different TiO₂ layer thicknesses of 5 nm, 10 nm (in Fig. 3b and c), and 15 nm, within a sample area of 20 nm × 20 nm. Importantly, taking the locally enhanced electric field at AgNC edges into account results in a clear preference for ion injection at these positions, with Ag clusters preferentially occurring at AgNC sides (enclosed by blue colored ellipses in the figure). Filament formation times are in the range of a few 100 ms, which is in line with our previous findings.³² Overall, the results from our model calculations are in good agreement with the current maps obtained by ex situ AFM for 10 nm TiO₂ layers, such as those given in Fig. 1g and 2c, where preferred material deposition at AgNC edges was also observed.

To further compare results obtained by ex situ CP-AFM and kMC, i.e., to compare the estimated amount of Ag deposited in the oxide as a function of oxide thickness until complete CF formation, simulated two-dimensional cross-sections such as that presented in Fig. 3c were analyzed for TiO₂ layer thicknesses of 5 nm, 10 nm, and 15 nm. In detail, areas of formed clusters projected into the x–y plane that were larger than 2 nm × 2 nm (such as the features highlighted by blue ellipses), were integrated and then multiplied by a scaling factor 25 for comparison with the CP-AFM results (100 nm × 100 nm AgNC/oxide interface area). Fig. 3a shows the resulting simulated integrated CF areas as a function of oxide thickness for TiO₂, as obtained by kMC simulations (black), compared to the experimental data obtained by CP-AFM discussed above. Clearly, the experimental observation of an approximately linear increase in integrated CF area with increased thickness for both oxide materials is qualitatively confirmed by the kMC simulations. However, integrated kMC areas appear systematically smaller compared to the areas obtained by CP-AFM. This deviation can partially be assigned to underestimated ionic hopping rates, overestimated energy barriers for injection and oxidation of metal atoms, and to the inherent limitations of comparing three-dimensional kMC simulation results to measured 2D data, as obtained by CP-AFM. Also, significantly, experimentally obtained conductive areas might appear larger than their true physical dimensions due to restrictions in experimental spatial resolution. Indeed, this is a common artifact and it is especially apparent in the direction of AFM trace and re-trace for moderate scan-rates and biases, as observed in Fig. 1d. Here, the measured side-length of the AgNC in the horizontal direction appears to be 200 nm rather than the expected value of 100 nm. For a better quantitative comparison of experiment and simulation, an improved determination of the conductive areas obtained in CP-AFM will have to be developed in the future. Nevertheless, the qualitative agreement between experiment and simulation lends support to the conclusion that thicker oxide layers lead to increased Ag deposition within the oxide due to longer filament formation times.

Conclusions

In summary, our findings highlight the importance of active electrode geometry, as well as oxide thickness and composition, for small ECM devices in the range of ∼100 nm. These parameters are found to have a major impact on filament growth position and stability, and are therefore expected to significantly impact device performance. In particular, our ex situ studies have shown that for a rectangular (square) AE geometry and for oxides with a high dielectric permittivity ε_r, ion injection tends to occur preferentially at positions close to the AE edges. This effect becomes especially relevant for thin oxides. By contrast, oxides with lower ε_r yield a more homogeneous electric field distribution in the oxide and, therefore, less influence of AE geometry on CF growth is obtained. Future studies shall focus on an improved absolute size determination of the conductive areas as measured by CP-AFM and on a better understanding of the microscopic correlation between CF growth and oxide material parameters, while also taking possible interfacial effects (electrode/material) into account. Further, our kMC simulations shall also be extended to Al₂O₃ and other, different oxide materials, to cover a broader range of dielectric constants. Overall, our findings may become particularly important for the future down-scaling of ECM cells with highest device-to-device reproducibility. In this context, a thin, high-dielectric constant oxide combined with cone-shape electrodes lends itself as the optimal choice.

Experimental section

Sample chip preparation, functionalization and assembly

The process sequence for preparing TiO₂ coated silicon, of molecular functionalization and NC assembly was carried out as previously described.³²

Atomic layer deposition

ALD of Al₂O₃ layers was carried out using a custom-built system at a substrate temperature of 200 °C. One ALD cycle consisted of a 200 ms pulse of H₂O vapor, followed by 15 s purging with N₂ at a flow rate of 400 sccm, which was succeeded by a 200 ms pulse of trimethyl aluminum, followed again by 15 s of N₂ purging. The number of cycles was adjusted to achieve the desired layer thicknesses of 2, 5, and 10 nm by considering the growth per cycle (GPC) of 1.15 Å per cycle.

(Conductive-probe) atomic force microscopy

CP-AFM characterization following planarization was carried as previously described, with electroforming of single AgNC achieved by applying up to −10 V to the p-Si substrate with respect to the AFM tip (sweep rate 0.5 V s⁻¹). A compliance current of I_CC = 120 mA was set.

AgNC delamination

AgNCs were carefully removed from the surface by a combined chemical/mechanical delamination procedure: the surface of the samples was first immersed in acetone for a few minutes, which dissolved the planarizing layer. Subsequently, the formed mixed solution layer was removed via careful mechanical application of a cotton swap, which was laterally dragged across the surface without pressing it into the substrate. In this way, the underlying oxide layer was exposed without introducing significant physical damage. Afterwards, the surface was rinsed in isopropanol for ∼30 s to remove residues of acetone, and the sample was finally blown dry with a N₂ gun. The described delamination process was carried out directly on the AFM stage, with samples still mounted on the chuck, thereby allowing the respective area of interest to be located by re-engaging the tip after delamination.

Simulations

Kinetic Monte Carlo simulations were carried out on workstations equipped with Intel cores using a self-written program code (C++).

Author contributions

MS and MT designed the experiments; MS fabricated all samples, carried out all I–V and related experiments and analyzed the results for all junctions. MS also characterized the samples using AFM, etc. OB carried out the ALD depositions under the supervision of IS. MR carried out the kMC simulations under the supervision of AG. MS, MT, MR, AG and IS wrote the manuscript. All the authors discussed the results and edited the manuscript.

Data availability

The source code of our kMC simulation tool together with the input files and output data is available on https://zenodo.org/doi/10.5281/zenodo.13776081.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors thank R. Mittermeier and P. Weiser for technical support and useful discussions. M.T. and M.S. thank the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for funding (project number 245845833) within the International Research Training Group IRTG 2022 – Alberta Technical University of Munich School for Functional Hybrid Materials (ATUMS). Support within TUM IGSSE is greatly appreciated.

References

1. S. H. Lee, X. Zhu and W. D. Lu, Nanoscale resistive switching devices for memory and computing applications, Nano Res., 2020, 13(5), 1228–1243,  DOI:10.1007/s12274-020-2616-0.
2. J. Zhu, T. Zhang, Y. Yang and R. Huang, A comprehensive review on emerging artificial neuromorphic devices, Appl. Phys. Rev., 2020, 7(1), 011312,  DOI:10.1063/1.5118217.
3. Z. Wang, et al., Resistive switching materials for information processing, Nat. Rev. Mater., 2020, 5(3), 173–195,  DOI:10.1038/s41578-019-0159-3.
4. K. Sun, J. Chen and X. Yan, The Future of Memristors: Materials Engineering and Neural Networks, Adv. Funct. Mater., 2021, 31(8), 2006773,  DOI:10.1002/adfm.202006773.
5. J. J. Yang, D. B. Strukov and D. R. Stewart, Memristive devices for computing, Nat. Nanotechnol., 2013, 8(1), 13–24,  DOI:10.1038/nnano.2012.240.
6. I. Valov, R. Waser, J. R. Jameson and M. N. Kozicki, Electrochemical metallization memories - Fundamentals, applications, prospects, Nanotechnology, 2011, 22(25), 254003,  DOI:10.1088/0957-4484/22/25/254003.
7. R. Waser, R. Dittmann, C. Staikov and K. Szot, Redox-based resistive switching memories nanoionic mechanisms, prospects, and challenges, Adv. Mater., 2009, 21(25–26), 2632–2663,  DOI:10.1002/adma.200900375.
8. S. Chen, T. Zhang, S. Tappertzhofen, Y. Yang and I. Valov, Electrochemical-Memristor-Based Artificial Neurons and Synapses—Fundamentals, Applications, and Challenges, Adv. Mater., 2023, 35(37), 2301924,  DOI:10.1002/adma.202301924.
9. F. Pan, S. Gao, C. Chen, C. Song and F. Zeng, Recent progress in resistive random access memories: Materials, switching mechanisms, and performance, Mater. Sci. Eng., R, 2014, 83(1), 1–59,  DOI:10.1016/j.mser.2014.06.002.
10. M. Lanza, F. Hui, C. Wen and A. C. Ferrari, Resistive Switching Crossbar Arrays Based on Layered Materials, Adv. Mater., 2023, 35(9), 2205402,  DOI:10.1002/adma.202205402.
11. V. K. Sangwan and M. C. Hersam, Neuromorphic nanoelectronic materials, Nat. Nanotechnol., 2020, 15(7), 517–528,  DOI:10.1038/s41565-020-0647-z.
12. D. Ielmini, Resistive switching memories based on metal oxides: Mechanisms, reliability and scaling, Semicond. Sci. Technol., 2016, 31(6), 063002,  DOI:10.1088/0268-1242/31/6/063002.
13. Y. Yang, P. Gao, S. Gaba, T. Chang, X. Pan and W. Lu, Observation of conducting filament growth in nanoscale resistive memories, Nat. Commun., 2012, 3, 732,  DOI:10.1038/ncomms1737.
14. S. Menzel, U. Böttger, M. Wimmer and M. Salinga, Physics of the Switching Kinetics in Resistive Memories, Adv. Funct. Mater., 2015, 25(40), 6306–6325,  DOI:10.1002/adfm.201500825.
15. M. Lanza, A review on resistive switching in high-k dielectrics: A nanoscale point of view using conductive atomic force microscope, Materials, 2014, 7(3), 2155–2182,  DOI:10.3390/ma7032155.
16. U. Celano, et al., Three-dimensional observation of the conductive filament in nanoscaled resistive memory devices, Nano Lett., 2014, 14(5), 2401–2406,  DOI:10.1021/nl500049g.
17. Y. Yang, et al., Probing electrochemistry at the nanoscale: in situ TEM and STM characterizations of conducting filaments in memristive devices, J. Electroceram., 2017, 39(1–4), 73–93,  DOI:10.1007/s10832-017-0069-y.
18. M. Speckbacher, et al., Nonvolatile Memristive Switching in Self-assembled Nanoparticle Dimers, ACS Appl. Electron. Mater., 2020, 2(4), 1099–1105,  DOI:10.1021/acsaelm.0c00099.
19. Y. M. Kim, J. Lee, D. J. Jeon, S. E. Oh and J. S. Yeo, Advanced atomic force microscopy-based techniques for nanoscale characterization of switching devices for emerging neuromorphic applications, Appl. Microsc., 2021, 51(1), 7,  DOI:10.1186/s42649-021-00056-9.
20. J. Song, Y. Zhou and B. D. Huey, 3D structure-property correlations of electronic and energy materials by tomographic atomic force microscopy, Appl. Phys. Lett., 2021, 118(8), 080501,  DOI:10.1063/5.0040984.
21. T. Li, H. Yu, S. H. Y. Chen, Y. Zhou and S. T. Han, The strategies of filament control for improving the resistive switching performance, J. Mater. Chem. C, 2020, 8(46), 16295–16317,  10.1039/d0tc03639k.
22. B. K. You, et al., Reliable Memristive Switching Memory Devices Enabled by Densely Packed Silver Nanocone Arrays as Electric-Field Concentrators, ACS Nano, 2016, 10(10), 9478–9488,  DOI:10.1021/acsnano.6b04578.
23. K. Y. Shin, Y. Kim, F. V. Antolinez, J. S. Ha, S. S. Lee and J. H. Park, Controllable Formation of Nanofilaments in Resistive Memories via Tip-Enhanced Electric Fields, Adv. Electron. Mater., 2016, 2(10), 1600233,  DOI:10.1002/aelm.201600233.
24. J. Spring, et al., Toward Controlling Filament Size and Location for Resistive Switches via Nanoparticle Exsolution at Oxide Interfaces, Small, 2020, 16(41), 2003224,  DOI:10.1002/smll.202003224.
25. B. Cheng, et al., Ultra compact electrochemical metallization cells offering reproducible atomic scale memristive switching, Commun. Phys., 2019, 2(1), 28,  DOI:10.1038/s42005-019-0125-9.
26. J. Li, C. Yao, W. Huang, N. Qin and D. Bao, Highly uniform resistive switching properties of NiFe2O4 films by embedding well-ordered pyramid-shaped Pt/Au nanostructures, J. Alloys Compd., 2022, 890, 161814,  DOI:10.1016/j.jallcom.2021.161814.
27. H. Liu, et al., Controlled Formation of Conduction Channels in Memristive Devices Observed by X-ray Multimodal Imaging, Adv. Mater., 2022, 34(35), 2203209,  DOI:10.1002/adma.202203209.
28. Y. Sun, et al., Guiding the growth of a conductive filament by nanoindentation to improve resistive switching, ACS Appl. Mater. Interfaces, 2017, 9(39), 34064–34070,  DOI:10.1021/acsami.7b09710.
29. D. W. Tao, Z. J. Jiang, J. B. Chen, B. J. Qi, K. Zhang and C. W. Wang, Stable resistive switching characteristics from highly ordered Cu/TiO2/Ti nanopore array membrane memristors, Appl. Surf. Sci., 2021, 539, 148161,  DOI:10.1016/j.apsusc.2020.148161.
30. K. Zhang, P. Ganesh and Y. Cao, Deterministic Conductive Filament Formation and Evolution for Improved Switching Uniformity in Embedded Metal-Oxide-Based Memristors—A Phase-Field Study, ACS Appl. Mater. Interfaces, 2023, 15(17), 21219–21227,  DOI:10.1021/acsami.3c00371.
31. J. Y. Seok, et al., A review of three-dimensional resistive switching cross-bar array memories from the integration and materials property points of view, Adv. Funct. Mater., 2014, 24(34), 5316–5339,  DOI:10.1002/adfm.201303520.
32. M. Speckbacher, et al., Directed Assembly of Nanoparticle Threshold-Selector Arrays, Adv. Electron. Mater., 2019, 5(7), 1900098,  DOI:10.1002/aelm.201900098.
33. Z. Wang, et al., Threshold Switching of Ag or Cu in Dielectrics: Materials, Mechanism, and Applications, Adv. Funct. Mater., 2018, 28(6), 1704862,  DOI:10.1002/adfm.201704862.
34. D. Ielmini and V. Milo, Physics-based modeling approaches of resistive switching devices for memory and in-memory computing applications, J. Comput. Electron., 2017, 16(4), 1121–1143,  DOI:10.1007/s10825-017-1101-9.
35. W. Sun, et al., Understanding memristive switching via in situ characterization and device modeling, Nat. Commun., 2019, 10(1), 3453,  DOI:10.1038/s41467-019-11411-6.
36. N. Liu, et al., Realization of synapse behaviors based on memristor and simulation study with kmc method, IEEE J. Electron Devices Soc., 2020, 8, 981–985,  DOI:10.1109/JEDS.2020.3023015.

---

Footnote

† Electronic supplementary information (ESI) available: Cross-sectional SEM images of AgNCs on TiO₂ after electrical operation, DC IV-data of AgNCs on Al₂O₃, current map after delamination of AgNCs from Al₂O₃, finite element simulations of electric field distribution in TiO₂ and Al₂O₃. See DOI: https://doi.org/10.1039/d4nr02870h

---