Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dehydration of alcohols catalyzed by copper(II) sulfate: type II dyotropic reactions and stepwise mechanisms†
Jorge
Sánchez-Quesada
 a,
Carlos
López-Cruz
a,
Carlos
López-Cruz
 a,
Abel
de Cózar
a,
Abel
de Cózar
 bcd,
Ana
Arrieta
bcd,
Ana
Arrieta
 b,
Iosune
Arrastia
b,
Iosune
Arrastia
 bc and
Fernando P.
Cossío
bc and
Fernando P.
Cossío
 *bc
*bc
aInternational Flavours & Fragrances IFF Inc., Avda. Felipe Klein 2, Benicarló 12580, Castellón, Spain
bDepartment of Organic Chemistry I, Facultad de Química, Kimika Fakultatea, Universidad del País Vasco, Euskal Herriko Unibertsitatea (UPV/EHU), Manuel de Lardizabal 3, 20018, San Sebastián, Donostia, Spain. E-mail: fp.cossío@ehu.es
cDonostia International Physics Center (DIPC), Manuel de Lardizabal 4, 20018 Donostia, San Sebastián, Spain
dIKERBASQUE, Basque Foundation for Science, Plaza Euskadi 5, 48009, Bilbao, Spain
First published on 31st January 2024
Abstract
Dehydration of alcohols in the presence of copper(II) sulfate has been analyzed computationally. Density functional theory (DFT) calculations on selected alcohols indicate that this reaction can take place via two possible mechanisms: (a) concerted – although asynchronous – type II dyotropic reactions, or (b) stepwise E1-like processes, in which cleavage of the C–O bond occurs in the first step, followed by syn proton elimination. Our calculations show the relationship between the initial alcohol structure and the preferred mechanism, which is a type II dyotropic reaction for primary alcohols, whereas a stepwise process is the favored one when stable carbocation intermediates are energetically accessible. The dehydration of dehydrolinalool (2,7-dimethyl-6-en-1-yn-3-ol, DHL) to yield different alkenes of interest in the fragrance industry is discussed as a case study of its regiochemistry.
1. Introduction
Alkenes are essential compounds in the chemical industry due to their versatility associated with the existence of the reactive carbon–carbon double bond. In fact, they are starting materials or key intermediates in the synthetic routes of many valuable compounds such as drugs, pesticides, plastics and fragrances. Therefore, knowledge of the mechanism of alkene synthesis is very important for the development and optimization of industrial processes.Among all the alkene synthetic methods reported in the literature, one of the most used protocols involves the dehydration of readily accessible alcohols by heating in the presence of an acid catalyst. This method is denoted as hydro-hydroxy-β-elimination and it is usually carried out using concentrated sulfuric or phosphoric acid.1
According to the accepted mechanism of the hydro-hydroxy-β-elimination of alcohols in an acidic environment,2 the first step corresponds to the protonation of a hydroxy moiety to generate an alkyloxonium cation intermediate, which is a better nucleofuge than a hydroxyl anion. This rate-limiting step releases water and the resulting carbenium ion deprotonates to generate a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond. Generally, three different mechanisms are considered depending on whether water loss and deprotonation occur simultaneously (E2) or sequentially (E1 if the first step is water release or E1cB if deprotonation occurs initially).3
C double bond. Generally, three different mechanisms are considered depending on whether water loss and deprotonation occur simultaneously (E2) or sequentially (E1 if the first step is water release or E1cB if deprotonation occurs initially).3
The E1 mechanism involves the formation of a carbocation in the rate-determining step; therefore, it is prone to different migration processes. Noteworthily, if more than one β-hydrogen is available, the most substituted trans-alkene is preferentially produced, in line with Saytzeff's rule. The general preference order of the substitution degree of the final alkene is tertiary > secondary > primary, which correlates with the relative stabilities of the corresponding carbenium intermediates.
Another protocol reported in the literature is the pyrolytic syn-elimination of alcohol derivatives. These latter compounds include esters, xanthates (Chugaev's elimination), amine N-oxides (Cope's elimination) or sulfamate ester intermediates (the Burgess dehydration). In these cases, the accepted mechanism involves a cyclic transition state where the two groups (a hydroxyl derivative or an N-oxide and a β-hydrogen atom) leave in a concerted (but not necessarily synchronous) manner. As in the previous cases, this 1,2-elimination reaction usually follows Saytzeff's rule.
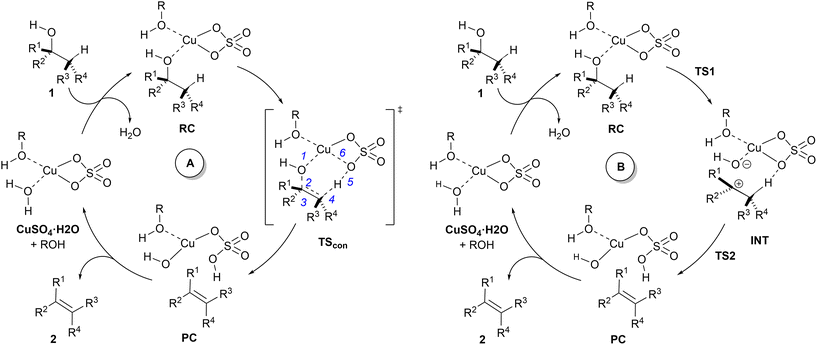
A related mechanism that can yield alkenes 2 from alcohols 1via a catalytic type II dyotropic reaction4–7 can be envisaged. This reaction consists of a double group transfer (in our case, a hydrogen atom and a hydroxy group) from the alcohol to a bifunctional catalyst that can be regenerated via a subsequent dehydration (Scheme 1). Given the nature of this catalyst, an alternative E2 mechanism via an antiperiplanar transition structure would be of higher energy. This reaction would be syn-1,2-elimination that does not require the formation of an alcohol derivative. This concerted reaction can evolve in a continuous manner by losing synchronicity towards a stepwise E1-like dehydroxy-dehydro elimination reaction, in which a carbenium hydroxy ionic pair is the key intermediate (Scheme 1).
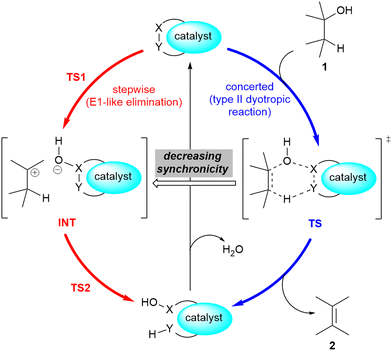 | ||
| Scheme 1 Possible 1,2-dehydration of alcohols 1via type II dyotropic and E1-like elimination reactions. The possible substituents in alcohol 1 and alkene 2 are not specified. | ||
The catalytic dehydration of alcohols in the presence of CuSO4, both in solution8–12 and adsorbed on silica gel,13,14 to yield alkenes is a useful method for the chemical synthesis of alkenes via a formal 1,2-elimination reaction that can be envisaged within the conceptual framework presented in Scheme 1. This procedure requires relatively high temperatures and avoids undesired rearrangements or the preparation of more reactive ester intermediates. Despite its practical and conceptual interest, this reaction has been scarcely described in the literature and no details about the nature of its mechanism have been reported so far.
In 1980, Hoffman and co-workers10 published an outline of the species involved in the catalytic activity of this reaction. The authors explored the reactivity of several alcohols and reported the tertiary ≈ benzylic > allylic > secondary reactivity trend. In view of these results, the authors hypothesized that carbenium ion formation is the key step of the reaction. This proposal was supported by the observation that Saytzeff-type regiochemistry is favoured and trans-olefins are obtained as major stereoisomers. Another remarkable experimental finding is that the addition of small amounts of pyridine to the reaction mixture inhibits the catalytic activity. However, no explanation about the role of copper in the dehydration reaction was provided. Within this context and taking into account our previous studies on dyotropic reactions,15–22 we considered the occurrence of a type II dyotropic reaction in this catalytic dehydration reaction as a starting hypothesis. Of course, depending upon the evolution of synchronicity in these reactions induced by different substituents, a transition from concerted to stepwise mechanisms could be envisaged.
Based on these antecedents and our starting hypothesis, in this paper, we report our results on the mechanism of the dehydration reaction of alcohols catalyzed by monomeric CuSO4. We selected several significant examples in order to gain a better understanding of the regio- and stereochemistry of this reaction. In addition, a relevant case of industrial interest was also studied.
2. Computational details
Optimization of geometries and thermochemical calculations were carried out using the Minnesota M0623,24 meta-GGA functional. Energies were computed by means of the Tao–Perdew–Staroverov–Scuseria TPSS25,26 correlation-exchange functional in order to get more accurate energy barriers. In calculations with this latter functional, Grimme D3 with the Becke–Jones damping potential27 (D3BJ) was included to improve the description of dispersion energies. All the calculations were carried out using the Gaussian 1628 suite of programs. Solvent effects were estimated by the polarization continuum model (PCM) method using the self-consistent reaction field (SCRF) approach.29 All SCRF-PCM calculations were performed using methanol (ε = 32.613) as the model solvent. For the calculation of Gibbs energies, standard conditions at different temperatures (298.15 or 423.15 K, 1 M) were assumed. The standard 6-31G(d,p) basis set was used for C, O, S and H atoms. The Hay–Wadt30 small core effective potential (ECP) including a double-ξ valence basis set (invoked by the LanL2dz keyword) was used for Cu atoms. Gibbs activation barriers were computed within the DFT31 framework at the M06(PCM)/6-31G(d,p)&LanL2dz level of theory using TPSS-D3BJ(PCM)/6-31G(d)&LanL2dz//M06(PCM)/6-31G(d,p)&LanL2dz total energies.The unrestricted spin approximation (UM06) was used because of the formal doublet character of Cu(II), with a correction of spin contamination to keep 〈S2〉 ≈ 0.75 a.u.
All the stationary points were characterized by harmonic vibrational analysis.32 Local minima showed positive definite Hessians. Fully optimized transition structures (TSs) showed one and only one imaginary frequency associated with nuclear motion along the chemical transformation under study. Reaction paths were checked using Intrinsic Reaction Coordinate (IRC) calculations.33,34
Wiberg bond indexes and Natural Bond Orbital atomic charges were computed within the NBO35 method implemented in Gaussian16. NBO charges on carbon atoms were computed including the charge of hydrogen atoms attached to them. Bond indices36BAB between atoms A and B in the NBO basis were computed according to the Wiberg definition:
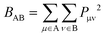 | (1) |
Synchronicites37,38 Sy were computed as defined in eqn (2):
 | (2) |
 | (3) |
In eqn (2), δBav is the average value of δBi for the n chemical bonds being modified along the reaction coordinate, as indicated in eqn (4):
 | (4) |
Eqn (2)–(4) provide an intuitive estimate of the synchronicity of the reaction, since for a perfectly synchronous process, δBi = δBav for any i = 1, 2…, n and therefore Sy = 1. According to the reaction mechanisms considered in the dehydration reaction catalysed by CuSO4, we considered n = 6 in eqn (2)–(4), as indicated in Scheme 2A, since the remaining bond orders did not vary significantly along the reaction coordinate.
Selectivities were computed using the previously computed Gibbs free activation energies by means of the Eyring equations for the respective elementary steps:
 | (5) |
Given the complex kinetic profiles (vide infra) of the dehydration reactions studied, both the Curtin–Hammett kinetics,39,40 and numerical integration41 of the respective differential equations were performed, normalizing the concentrations of the different elimination products to 100.
3. Results and discussion
General considerations
In view of the above-mentioned precedents, two possible mechanisms for the dehydration of alcohols in the presence of copper(II) sulfate were envisaged (Scheme 2). In order to obtain a computationally accessible structure, an isolated unit of CuSO4 was considered. In our calculations, we added an additional explicit molecule of alcohol in order to complete the tetra-coordinated environment of the copper(II) centre,42 thus avoiding spurious interactions between the copper atom and C–H or C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds. Since this additional alcohol molecule does not participate in the reaction coordinate, we selected methanol (R = Me in Scheme 2) as the model alcohol. The introduction of explicit additional solvent molecules indirectly attached to the Cu atom did not significantly affect the geometry of the stationary points and increased the computed activation barriers (see the ESI†). Therefore, in successive calculations we considered only one explicit molecule of solvent and tackled the bulk medium by means of the continuum dielectric model. Both mechanisms start with a reactive complex RC, in which two equivalents of alcohol 1 interact with CuSO4.
C double bonds. Since this additional alcohol molecule does not participate in the reaction coordinate, we selected methanol (R = Me in Scheme 2) as the model alcohol. The introduction of explicit additional solvent molecules indirectly attached to the Cu atom did not significantly affect the geometry of the stationary points and increased the computed activation barriers (see the ESI†). Therefore, in successive calculations we considered only one explicit molecule of solvent and tackled the bulk medium by means of the continuum dielectric model. Both mechanisms start with a reactive complex RC, in which two equivalents of alcohol 1 interact with CuSO4.
The mechanism denoted as A in Scheme 2 corresponds to the application of the present process of the general type II dyotropic reaction mechanism depicted in Scheme 1. According to this mechanism, the reaction would be concerted with a sole transition structure, denoted as TScon, which connects the reactive complex RC with product-like complex PC. The copper moiety of this latter complex would evolve towards the formation of the corresponding monohydrate complex, with the concomitant release of alkene 2. In subsequent catalytic cycles, the Cu(II) centre could coordinate to one or two molecules of alcohol, depending upon the release of one equivalent of water, which should not affect the nature of the mechanism.
Another possible mechanism, denoted as B in Scheme 2, could consist of a stepwise process in which the complete asynchronicity of mechanism A results in the formation of an ionic pair denoted as INT. This mechanism requires two transition structures, denoted as TS1 and TS2 in Scheme 2. In the first one, the hydroxy group of the starting alcohol 1 is transferred to the metallic centre, thus leaving a carbocationic centre at the former alcohol moiety. The second saddle point TS2 involves the cleavage of the C–H bond contiguous to the cationic centre to yield complex PC, similar to that postulated for mechanism A. In principle, a continuous transition between mechanisms A and B can be expected, depending upon the asynchronicity associated with the saddle point TScon (mechanism A) and the stability of the carbonium part of ionic pair INT (mechanism B).
Computational elucidation of the different mechanisms can be determined by numerical integration of the kinetic equations obtained using the kinetic constants associated with the respective elementary steps as indicated in eqn (5). Assuming a downhill and irreversible evolution of product complexes PC to alkenes 2, the reaction rates can be approximated as
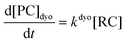 | (6) |
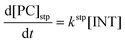 | (7) |
In both cases, the evolution of the starting reaction complexes corresponding to the different mechanisms is described by the kinetics of matrix Y that includes the reaction intermediates and reactive complexes:
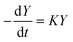 | (8) |
In eqn (8), matrix K contains the appropriate kinetic constants, calculated by means of eqn (5).
The concentration [Pi] of product Pi with respect to the total ensemble of products was calculated according to eqn (9):
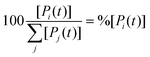 | (9) |
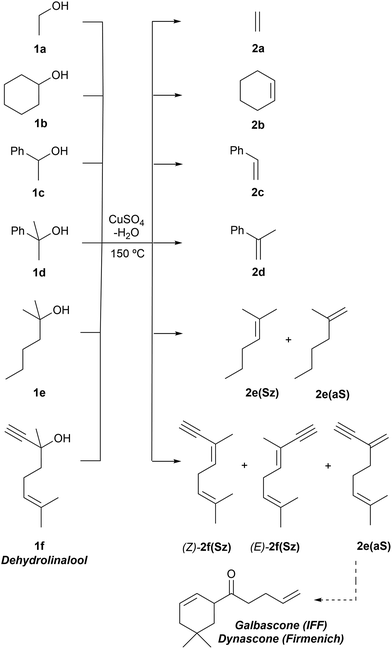
We carried out our computational study by analyzing a set of alcohols with different degrees of substitution, which are gathered in Scheme 3. Ethanol (1a), cyclohexanol (1b), 1-phenylethan-1-ol (1c) and 2-phenylpropan-2-ol (1d) do not pose regiochemical issues, since these alcohols can only yield ethene (2a), cyclohexene (2b), styrene (2c) and 1-methyl styrene (2d) as unsubstituted, monosubstituted and disubstituted alkenes. Instead, 2-hexanol (1e) can yield two regioisomers that can be classified as Saytzeff 2e(Sz) and anti-Saytzeff 2e(aS) trisubstituted and disubstituted alkenes, respectively. Finally, the dehydration of dehydrolinalool (1f) was studied. This alcohol is of great interest in the flavour and fragrance industry43 and can yield two Saytzeff stereoisomers, denoted as (E)-2f(Sz) and (Z)-2f(Sz) in Scheme 3, and one anti-Saytzeff alkene, denoted as 2f(aS). This latter compound is a key intermediate in the synthesis of Galbascone or Dynascone (1-(5,5-dimethylcyclohexen-1-yl)pent-4-en-1-one), a synthetic fragrance of great industrial interest.44 The computed Gibbs free energy reaction profiles and the main geometrical features of the transition structures for the dehydration of 1a–f were collected and are shown in Fig. 1–10. Free energies were computed at 25 °C (298.15 K) and 150 °C (423.15 K), since the reported experimental studies were conducted at temperatures ranging from 120 °C to 150 °C.
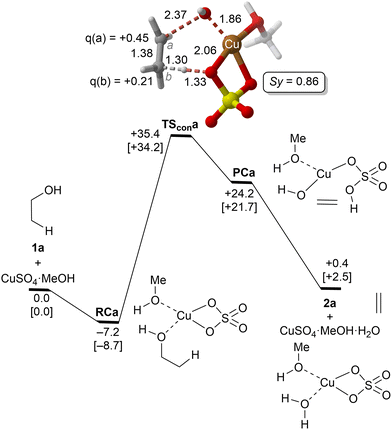 | ||
| Fig. 1 Reaction profile and the main geometrical features of the transition structure associated with the elimination reaction of alcohol 1a catalyzed by CuSO4 computed at the UTPSS-D3BJ/(PCM)/6-31G(d,p)&LanL2dz//UM06(PCM)/6-31G(d,p)&LanL2dz level of theory. Relative Gibbs energies, in kcal mol−1, were computed at 298.15 K and 423.15 K (values between brackets). Synchronicities were calculated using eqn 2. Distances are in Å. Relevant NBO charges are also included. | ||
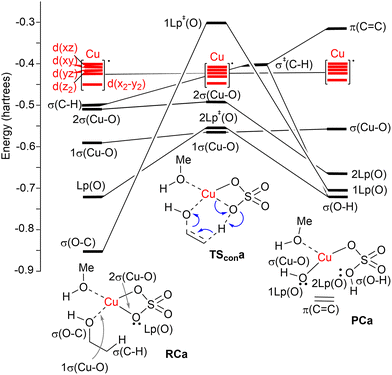 | ||
| Fig. 2 Correlation NBO diagram for the transformation of reactive complex RCa into PCaviaTScona. The blue curved arrows show the electronic motion along the reaction coordinate. | ||
 | ||
| Fig. 3 Reaction profile and the main geometrical features of the transition structure associated with the elimination reaction of alcohol 1b catalyzed by CuSO4. See the caption of Fig. 1 for more details. | ||
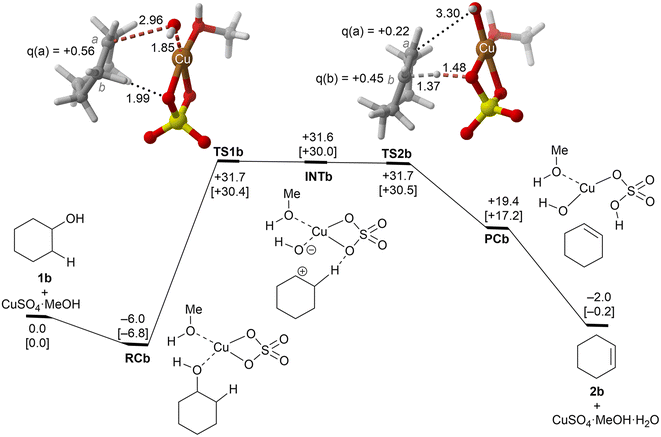
 | ||
| Fig. 4 Reaction profile and the main geometrical features of the transition structure associated with the elimination reaction of alcohol 1c catalyzed by CuSO4. The kinetic constants associated with each elementary step are also indicated. See the caption of Fig. 1 for more details. | ||
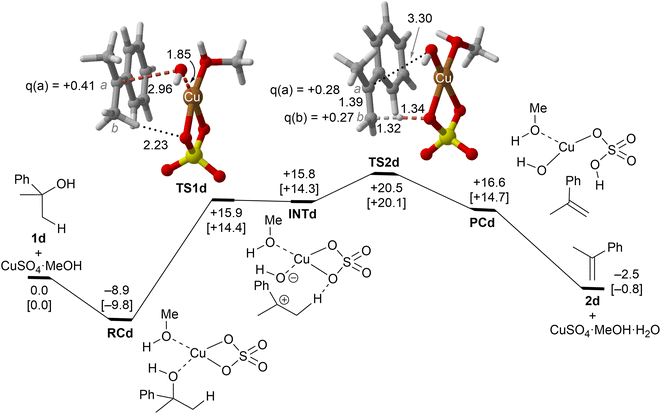 | ||
| Fig. 5 Reaction profile and the main geometrical features of the transition structure associated with the elimination reaction of alcohol 1d catalyzed by CuSO4. See the caption of Fig. 1 for more details. | ||
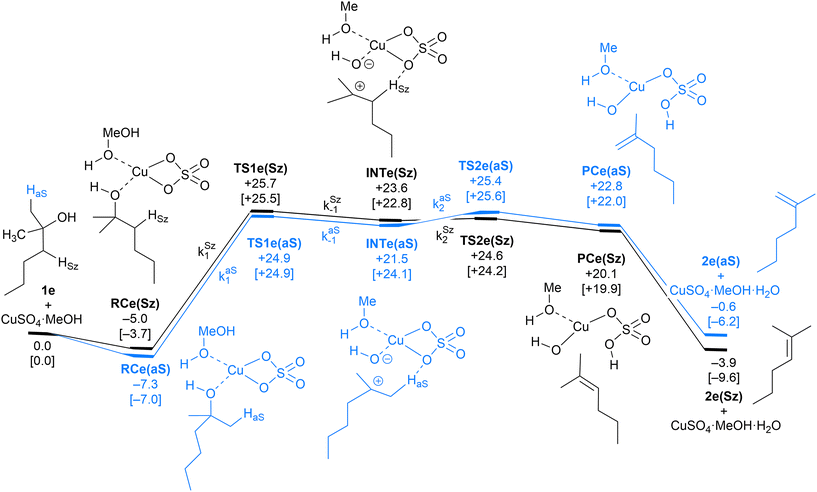 | ||
| Fig. 6 Computed Saytzeff (Sz) and anti-Saytzeff (aS) reaction profiles associated with possible elimination reactions of hexan-2-ol (1e) catalyzed by CuSO4. See the caption of Fig. 1 for further details. Selected kinetic constants for elementary steps are also given (see eqn (12)–(15)). | ||
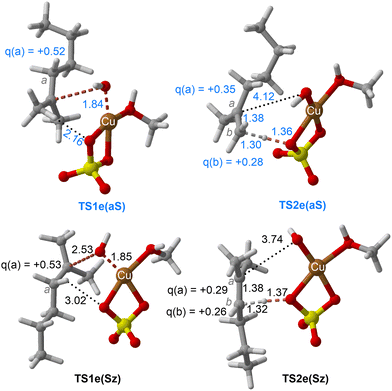 | ||
| Fig. 7 Chief geometrical features of Saytzeff (Sz) and anti-Saytzeff (aS) transition structures associated with possible elimination reactions of hexan-2-ol (1e) catalyzed by CuSO4. See the caption of Fig. 1 for more details. | ||
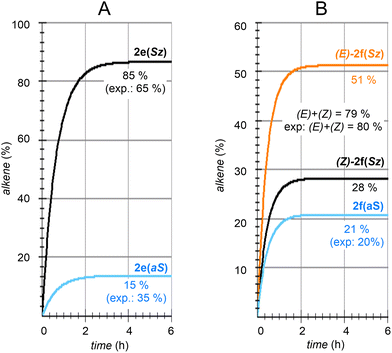 | ||
| Fig. 8 Numerical simulation of the calculated regio- and stereochemistry associated with the dehydration reaction of hexan-2-ol (1e) and dehydrolinalool (1f) catalyzed by CuSO4. | ||
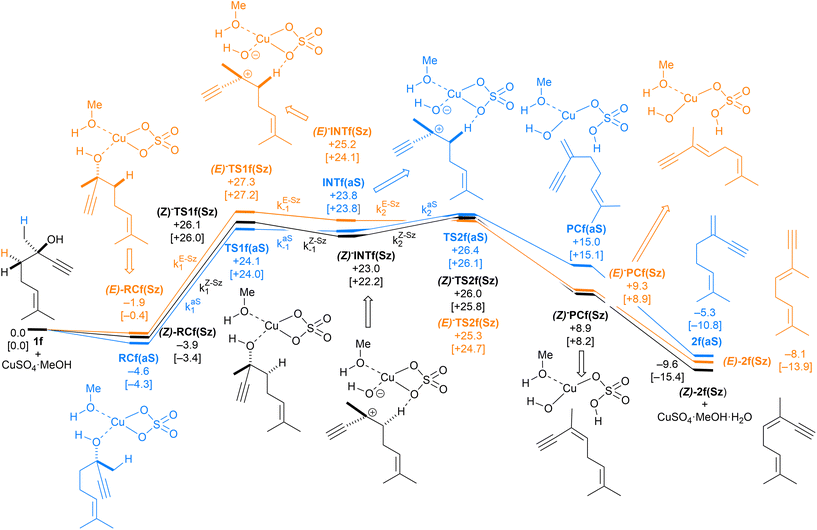 | ||
| Fig. 9 Computed reaction profile and the main geometrical features of the transition structure associated with all possible elimination reactions of dehydrolinalool (1f) catalyzed by CuSO4. See the caption of Fig. 1 for more details. | ||
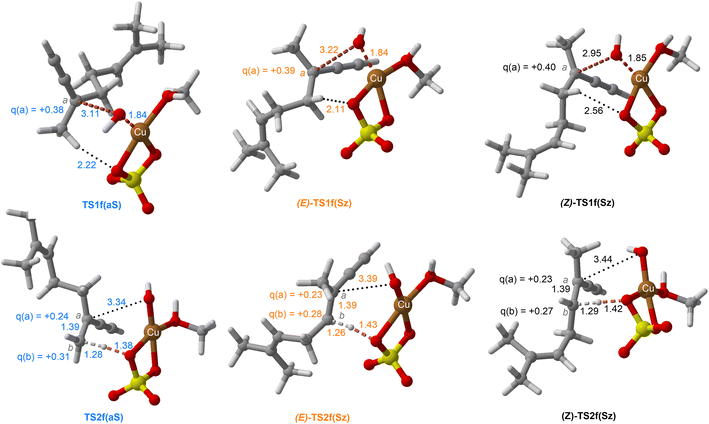 | ||
| Fig. 10 Chief geometrical features of Saytzeff (Sz) and anti-Saytzeff (aS) transition structures associated with possible elimination reactions of hexan-2-ol (1e) catalyzed by CuSO4. See the caption of Fig. 1 for more details. | ||
Dehydration of ethanol
The parent reaction 1a→2a was computed first. The corresponding reaction profile is shown in Fig. 1. According to our results, copper(II) sulfate forms a stable complex RCa with 1a due to the initial interaction between the oxygen atom of the alcohol and the metallic centre. From this reactive complex, alkene 2a is formed viaTScona in a single step, with an activation barrier of ca. 35 kcal mol−1 to generate the product complex PCa in which the double C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is generated with the concomitant breaking of one of the Cu–O bonds of Cu(II) sulphate. This high-energy barrier is in full agreement with the fact that CuSO4 is not used as a catalyst in the industrial dehydration reaction of ethylene45 and with the poor reactivity of primary alcohols. Geometric inspection of TScona shows that it corresponds to a slightly asynchronous type II dyotropic reaction (Sy = 0.86), in which the reagent C–O bond breaking process is more developed than the cleavage of the C–H bond. This is reflected in the long C–O critical bond distance in TScona and the higher positive NBO charge computed for C(a), which shows a partial primary carbocation character. Noteworthily, transformation of the product complex into hydrated copper(II) sulfate is required to make the reaction slightly exergonic with respect to the isolated reagents. Once hydrated copper(II) sulfate is formed, reactive complex RCa is regenerated via an exergonic water–alcohol exchange, thus closing the catalytic cycle (see the ESI†).
C bond is generated with the concomitant breaking of one of the Cu–O bonds of Cu(II) sulphate. This high-energy barrier is in full agreement with the fact that CuSO4 is not used as a catalyst in the industrial dehydration reaction of ethylene45 and with the poor reactivity of primary alcohols. Geometric inspection of TScona shows that it corresponds to a slightly asynchronous type II dyotropic reaction (Sy = 0.86), in which the reagent C–O bond breaking process is more developed than the cleavage of the C–H bond. This is reflected in the long C–O critical bond distance in TScona and the higher positive NBO charge computed for C(a), which shows a partial primary carbocation character. Noteworthily, transformation of the product complex into hydrated copper(II) sulfate is required to make the reaction slightly exergonic with respect to the isolated reagents. Once hydrated copper(II) sulfate is formed, reactive complex RCa is regenerated via an exergonic water–alcohol exchange, thus closing the catalytic cycle (see the ESI†).
Alternative reaction mechanisms, in which copper(II) complexes act as Brønsted acids, i.e., ethanol (1a) protonation as the initial step of the elimination process, were also evaluated. Our results show that this latter process is endergonic (see the ESI†). Therefore, this mechanistic hypothesis was not further investigated.
A correlation diagram of the localized NBOs of RCa, TScona and PCa permitted us to analyze this parent reaction, thus gaining a better understanding of the nature of the electronic changes along the reaction coordinate associated with this type II dyotropic transfer reaction. Firstly, we observed that the d-AOs of Cu(II) are not involved in the reaction, since they remain essentially unaffected. Secondly, it was concluded that the C(b)–H bond is transformed into a σ(O–H) localized MO and the π(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) double bond, whereas one σ(CuO) localized MO becomes a lone pair centered at one oxygen atom. Instead, the initial σ(C–O) bond evolves towards a localized lone pair centered on the oxygen of the new hydroxyl group bound to copper(II). The whole ensemble of NBOs shows electronic circulation along the cyclic transition structure. This analysis also shows a strong destabilization in TScona and the endergonic character of this elementary step, fully compatible with the high activation energy associated with this reaction, which precludes its use in practical transformations. A lesser contribution of the term associated with the highly energetic cleavage of the localized σ(C–H) orbital should result in a stepwise process with a lower activation energy. Likewise, a more substituted carbon atom linked to the hydroxy group would result in a lower NBO σ(C–O) → Lp‡(O) transition, associated with a lower activation energy and a stepwise mechanism.
C) double bond, whereas one σ(CuO) localized MO becomes a lone pair centered at one oxygen atom. Instead, the initial σ(C–O) bond evolves towards a localized lone pair centered on the oxygen of the new hydroxyl group bound to copper(II). The whole ensemble of NBOs shows electronic circulation along the cyclic transition structure. This analysis also shows a strong destabilization in TScona and the endergonic character of this elementary step, fully compatible with the high activation energy associated with this reaction, which precludes its use in practical transformations. A lesser contribution of the term associated with the highly energetic cleavage of the localized σ(C–H) orbital should result in a stepwise process with a lower activation energy. Likewise, a more substituted carbon atom linked to the hydroxy group would result in a lower NBO σ(C–O) → Lp‡(O) transition, associated with a lower activation energy and a stepwise mechanism.
Dehydration of cyclohexanol, 1-phenylethan-1-ol and 2-phenylpropan-2ol
These alcohols were selected because of their different structural and electronic features and lack of regiochemical issues.In the case of cyclohexanol (1b), our calculations show that the dehydration process corresponds to a stepwise mechanism, in which the initial C–O bond breaking process (TS1b) leads to the formation of a highly unstable ionic pair INTb, and the alcohol moiety is transformed into a secondary carbocation intermediate. Evaluation of the ion pair dissociation energy shows that INTb is a stable enough intermediate, whose dissociation energy is of ca. 15 kcal mol−1 (see the ESI†). Therefore, E1 elimination without the participation of Cu(II) sulphate in the C–H dehydro step was not considered. In this case, the secondary carbenium centre is stable enough to favor the dehydroxy-dehydro stepwise elimination instead of the dyotropic process. Once the development of the positive charge on the carbon atom proceeds, the potential energy surface is almost flat, and INTb evolves into cyclohexene through saddle point TS2bvia an essentially barrierless process. Noteworthily, in this latter transition structure, the C(b) charge is higher than the one of C(a) due to the electron density transfer from the C–H breaking bond. The computed activation barrier corresponding to the rate-limiting step is ca. 4 kcal mol−1 lower than the one computed for ethanol 1a, a result in line with the reactivity trend described experimentally. In addition, as in the previous case, the transformation of the product complex onto hydrated copper(II) sulfate is also required to make the reaction exergonic.
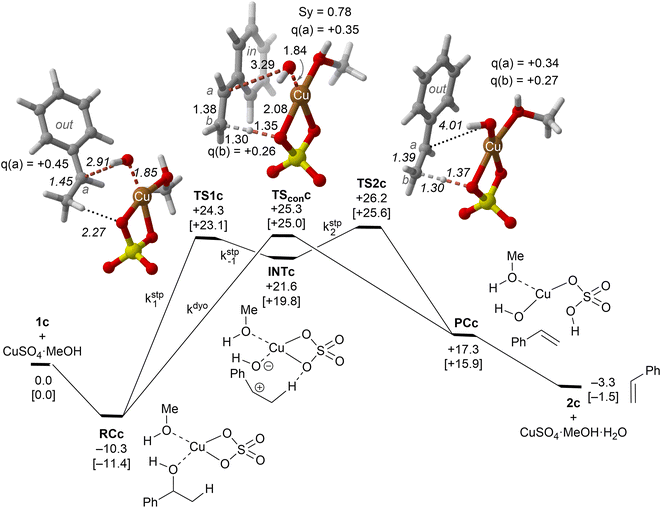
Our calculations show that the dehydration reaction obtained for 1-phenylethan-1ol (1c) is compatible with both mechanisms (Fig. 4). This result was surprising because it is known that benzylic carbocations are more stable than other secondary carbocations (such as INTb) due to the charge delocalization (resonance) of the benzylic moiety. Therefore, a priori, a stepwise mechanism analogous to cyclohexanol (1b) would be expected. However, careful inspection of TSconc shows the existence of a stabilizing interaction between the inner (denoted as in in Fig. 4) phenyl group and the copper(II) atom that favors the existence of the concerted dyotropic transition structure. In TSconc, the breaking of the C–O bond is more developed than that of the C–H one as reflected by the C–O bond distance of 3.29 Å, where the charge on C(a) is also delocalized in the phenyl ring. This concerted saddle point is less synchronous than the parent congener TScona (Sy = 0.78, see Fig. 4). However, when the phenyl group is in an outer orientation with respect to the Cu(II) centre, the stabilizing interaction observed in TSconc is not present and the mechanism turns out to be stepwise (Fig. 4). In this latter case, the rate-limiting step takes place viaTS1c and leads to the ionic pair INTc. From this intermediate, the product complex PCc is formed viaTS2c, with an activation energy of ca. 6 kcal mol−1 at 150 °C. The energies of TSconc and TS1c are quite similar, with the concerted saddle point being ca. 2 kcal mol−1 more energetic than its first stepwise congener. However, the stepwise mechanism requires an additional energy barrier to yield alkene 2c. In order to quantify the relative participation of both mechanisms, we applied eqn (6)–(8), in which the matrix of intermediates Yc is:
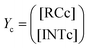 | (10) |
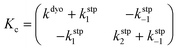 | (11) |
In eqn (11), the kinetic constants are defined in Fig. 4. Using the values obtained from the respective activation energies, we obtained a dyotropic![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) stepwise ratio of 70
stepwise ratio of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30. Therefore, in the 1c→2c dehydration reaction, the type II dyotropic reaction is the major contributor to the two-component mechanism shown in Fig. 4.
30. Therefore, in the 1c→2c dehydration reaction, the type II dyotropic reaction is the major contributor to the two-component mechanism shown in Fig. 4.
Copper(II) sulfate-catalyzed dehydration of 2-phenylpropan-2-ol (1d) follows a stepwise mechanism, in which resonance-stabilized carbocation intermediate INT1d is formed after the C–O bond breaking step. In the rate-limiting step, the long C–O critical distance of TS1d is compatible with the late character of this saddle point, in which the C–O bond breaking process is quite advanced and associated with an activation barrier of 24 kcal mol−1 with respect to RCd. In addition, the positive charge in C(a) is clearly developed. In contrast to the 1b case, the activation barrier associated with the second step is not negligible (5–6 kcal mol−1). Remarkably, the energy required for this process is lower than the activation barriers associated with the dehydration of 1a or 1b and 1c, in agreement with the tertiary > secondary > primary alcohol reactivity trend reported experimentally.
Regiochemistry
The dehydration reaction of 2-hexanol (1e) offers a more complicated scenario than the above discussed alcohols since two alkenes can be formed: highly substituted (Saytzeff) 2e(Sz) and less substituted (anti-Saytzeff) 2e(aS) (Scheme 3). The computed energetic profiles collected in Fig. 6 correspond to a stepwise elimination in both cases, as expected for a tertiary alcohol that would generate a stable carbocation intermediate after the initial transfer of the hydroxyl moiety to the metallic centre. We computed two different reaction profiles associated with the C–O bond breaking process anticipating the structure of the final alkenes through C–HSz/aS⋯Cu interactions via saddle points TS1e(Sz) and TS1e(aS). The activation barriers associated with these initial steps are slightly different. However, the carbocations INTe(Sz) and INTe(aS) are close in energy. Therefore, the selectivity towards Saytzeff or anti-Saytzeff cannot be related directly to this initial step, since the subsequent hydrogen elimination must play a significant role. Evaluation of the NBO charges (Fig. 7) shows more developed charges on TS2a(aS) than on TS2e(Sz). The positive charge on C(b) of TS2e(aS) indicates a significant character of a highly unstable primary carbocation, which makes the C–HaS bond breaking more energetic compared to TS2e(Sz), in which the charge is stabilized by the alkyl substituent, thus making a higher barrier for the formation of 2e(aS). Based on the obtained reaction profiles, we computed the Saytzeff/anti-Saytzeff ratio of alkenes 2e assuming their irreversible formation via the downhill release of the alkene moiety in product complexes PCe(Sz) and PCe(aS), respectively: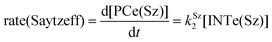 | (12) |
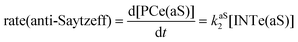 | (13) |
Now, the corresponding matrix Ye is:
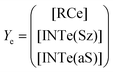 | (14) |
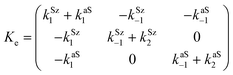 | (15) |
The solution of eqn (8) and (12)–(15) by numerical integration yields the kinetic profiles gathered in Fig. 8A. According to our results, the Saytzeff![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anti-Saytzeff ratio is 85
anti-Saytzeff ratio is 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15, in qualitative agreement with the experimentally observed 65
15, in qualitative agreement with the experimentally observed 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 and in line with the observations of Hofmann about the Saytzeff regioselectivity.10
35 and in line with the observations of Hofmann about the Saytzeff regioselectivity.10
All our attempts to locate a transition structure connecting INTe(Sz) and INTe(aS) met with no success. This result suggests that the potential energy surface is very complex in this region of the reaction coordinate or that both intermediates can equilibrate before the second transition structures TS2e(Sz) and TS2e(aS) despite the fact that our IRC analysis connected these saddle points with the corresponding intermediates. In any case, when we performed Curtin–Hammett simulations that eliminated the effect of these intermediates, we obtained a 2e(Sz)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2e(aS) ratio of 84
2e(aS) ratio of 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16, which is virtually identical to the value obtained after numerical simulation.
16, which is virtually identical to the value obtained after numerical simulation.
Finally, the dehydration of dehydrolinalool (1f) was analyzed. The reaction profiles and the main geometrical features of the respective transition structures are shown in Fig. 9 and 10, respectively. In this reaction, there are three C–H bonds at the alpha position with respect to the OH group. Therefore, we analyzed the energetic profiles associated with the generation of two highly substituted (Saytzeff) alkenes (Z)-2f(Sz) and (Z)-2f(Sz) and one less substituted (anti-Saytzeff) alkene 2f(aS). As expected, in all cases, the reaction is a stepwise elimination, in which a stable propargyl–tertiary carbocation intermediate is generated after the initial C–O bond cleavage. The computed activation barriers associated with the step are in the range of 27–29 kcal mol−1, with small energy variations between the transition structures depending on the C–H⋯Cu interaction considered. As indicated above, those differences cannot be directly related to the final regioselectivity, since ionic pairs INTf and transition structures TS2f, associated with the H-elimination, play a significant role. As in the preceding case, we estimated the formation of alkenes 3f in terms of the respective product complexes PCf:
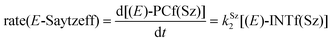 | (16) |
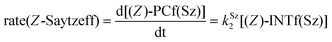 | (17) |
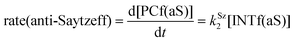 | (18) |
The corresponding intermediate matrix Yf includes the equilibrated reactive complexes RCf and the ionic intermediates INTf:
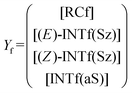 | (19) |
Matrix Kf, which includes the kinetic constants indicated in Fig. 9, is as follows:
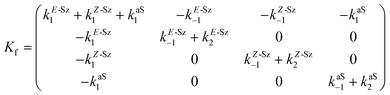 | (20) |
Following the above-described procedure and using eqn (16)–(20), we obtained the kinetic profile shown in Fig. 8B. According to our results, the calculated (E)-2f(Sz)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Z)-2f(Sz)
(Z)-2f(Sz)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2f(aS) ratio is 51
2f(aS) ratio is 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21, which corresponds to a Saytzeff
21, which corresponds to a Saytzeff![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anti-Saytzeff ratio of 79
anti-Saytzeff ratio of 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21, which is in excellent agreement with the 80
21, which is in excellent agreement with the 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ratio reported by Hoffman et al.10 Also in this case, we did not find transition structures among (E)-INf(Sz), INTf(aS) and (Z)-INTf(Sz). Following the same considerations indicated for the previous transformation, we tested the distribution of isomers applying the Curtin–Hammett kinetics and found a ratio of 68
20 ratio reported by Hoffman et al.10 Also in this case, we did not find transition structures among (E)-INf(Sz), INTf(aS) and (Z)-INTf(Sz). Following the same considerations indicated for the previous transformation, we tested the distribution of isomers applying the Curtin–Hammett kinetics and found a ratio of 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14, which is in lower agreement with the experimental data (see Fig. 8B).10
14, which is in lower agreement with the experimental data (see Fig. 8B).10
4. Conclusions
In this work, we have presented a DFT study on the reaction mechanisms associated with the dehydration of alcohols catalyzed by CuSO4. Our calculations show that the process corresponds to a concerted but asynchronous type II dyotropic reaction for primary alcohols, in which the C–O bond breaking event develops earlier than the C–H cleavage event. In the cyclic transition structure, the copper(II) atom plays a crucial role by assisting the hydroxyl moiety release. As far as secondary or tertiary alcohols are concerned, the reaction profile evolves towards a stepwise mechanism in which the initial C–O bond breaking process generates a carbenium–hydroxyl ionic pair intermediate, which gives rise to the final alkene through an H-abstraction step assisted by an oxygen atom of the sulfate moiety. Analyses of the energy profiles show that the activation barrier associated with the first step is the highest one, but the second transition structure lays above in energy and plays a significant role in the selectivity of the process through which different products can be obtained. This complex kinetic situation can be analyzed within a Curtin–Hammett framework. However, numerical integration of the respective ensembles of differential equations provides computed selectivities corresponding to the dehydration reactions of 2-methyl-2-hexanol (1e) and dehydrolinalool (1f) that agree reasonably well with the experimental reports. The computed reactivity trend for the dehydration of alcohols following the proposed mechanisms is tertiary > secondary > primary, which is in perfect agreement with the experimental results. Therefore, in general, anti-Saytzeff alkenes will be obtained as major dehydration products. This situation poses an important challenge for the regioselective synthesis of anti-Saytzeff alkenes of interest in the fragrance industry, such as the precursor of Galbascone (Dynascone).Author contributions
J. S.-Q.: conceptualization, funding acquisition, project administration, supervision, and validation. C. L.-C.: conceptualization, project administration, supervision, and validation. A. de C.: data curation, formal analysis, investigation, methodology, validation, visualization, writing – original draft, and software. A. A. and I. A.: data curation, formal analysis, investigation, methodology, and validation. F. P. C: conceptualization, funding acquisition, project administration, supervision, formal analysis, methodology, validation, resources, and writing – review & editing. All the authors revised and contributed to the final version of the manuscript.Conflicts of interest
The authors declare that they have no known competing financial interests that could have influenced the work reported in this article.Acknowledgements
Financial support for this work was provided by the Spanish Ministerio de Ciencia, Innovación y Universidades (MICIN/AEI/ PID2019-104772GB-I00 and MCIN/AEI/RED2022-134287-T) and the Gobierno Vasco/Eusko Jaurlaritza (GV/EJ, Grant IT-1553-22). The authors thank SGI/IZO-SGIker of the UPV/EHU and the DIPC for the generous allocation of computational resources.References
- W. H. Brown, C. S. Foote, B. L. Iverson, E. V. Anslyn and B. M. Novak, Aldehydes and Ketones. Organic Chemistry, Brooks/Cole Belmont, CA, 2012 Search PubMed.
- M. B. Smith and A. J. March, March's Advanced Organic Chemistry: Reactions, Mechanisms and Structure, Wiley Interscience, New York, 2007 Search PubMed.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, Sausalito, CA, 2005 Search PubMed.
- M. T. Reetz, Angew. Chem., Int. Ed. Engl., 1972, 11, 129–130 CrossRef CAS.
- M. T. Reetz, Tetrahedron, 1973, 29, 2189–2194 CrossRef CAS.
- M. T. Reetz, in Advances in Organometallic Chemistry, ed. F. G. A. Stone and R. West, Academic Press, 1977, vol. 16, pp. 33–65 Search PubMed.
- I. Fernández, F. P. Cossío and M. A. Sierra, Chem. Rev., 2009, 109, 6687–6711 CrossRef PubMed.
- F. C. Whitmore and E. Rohrmann, J. Am. Chem. Soc., 1941, 63, 2033–2035 CrossRef CAS.
- G. W. Francis and J. F. Berg, Acta Chem. Scand., Ser. B, 1977, 31, 721–722 CrossRef.
- R. V. Hoffman, R. D. Bishop, P. M. Fitch and R. Hardenstein, J. Org. Chem., 1980, 45, 917–919 CrossRef CAS.
- T. Pieterse, C. Marais and B. C. B. Bezuidenhoudt, ARKIVOC, 2022, 2022, 217–231 Search PubMed.
- E. J. Eisenbraun, K. W. Payne and J. S. Bymaster, Org. Prep. Proced. Int., 2006, 32, 557–561 CrossRef.
- T. Nishiguchi, N. Machida and E. Yamamoto, Tetrahedron Lett., 1987, 28, 4565–4568 CrossRef CAS.
- T. Nishiguchi and C. Kamio, J. Chem. Soc., Perkin Trans. 1, 1989, 707–710, 10.1039/P19890000707.
- I. Fernández, F. M. Bickelhaupt and F. P. Cossío, Chem. – Eur. J., 2012, 18, 12395–12403 CrossRef PubMed.
- I. Fernández, F. P. Cossío and M. A. Sierra, Acc. Chem. Res., 2011, 44, 479–490 CrossRef PubMed.
- I. Fernández and F. P. Cossío, J. Comput. Chem., 2016, 37, 1265–1273 CrossRef PubMed.
- F. Cervantes-Navarro, A. de Cózar, F. P. Cossío, M. A. Fernández-Herrera, G. Merino and I. Fernández, Chem. Commun., 2015, 51, 5302–5305 RSC.
- G. Frenking, F. P. Cossío, M. A. Sierra and I. Fernández, Eur. J. Org. Chem., 2007, 2007, 5410–5415 CrossRef.
- I. Fernández, M. A. Sierra and F. P. Cossío, J. Org. Chem., 2007, 72, 1488–1491 CrossRef PubMed.
- I. Fernández, M. A. Sierra and F. P. Cossío, Chem. – Eur. J., 2006, 12, 6323–6330 CrossRef PubMed.
- M. A. Sierra, I. Fernández, M. J. Mancheño, M. Gómez-Gallego, M. R. Torres, F. P. Cossío, A. Arrieta, B. Lecea, A. Poveda and J. Jiménez-Barbero, J. Am. Chem. Soc., 2003, 125, 9572–9573 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. Sun, Phys. Rev. Lett., 2009, 103, 026403 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian 16, Revision C.01, Gaussian, Inc, Wallingford, CT, 2016 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, Oxford, New York, 1989 Search PubMed.
- J. W. McIver Jr. and A. Komornicki, J. Am. Chem. Soc., 1972, 94, 2625–2633 CrossRef.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- H. P. Hratchian and H. B. Schlegel, in Theory and Applications of Computational Chemistry: The First 40 Years, ed. E. Dykstra, G. Frenking, K. S. Kim and G. Scuseria, Elsevier, Amsterdam, 2005, pp. 195–249 Search PubMed.
- F. Weinhold and C. R. Landis, Valency and Bonding –A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, Cambridge CB2 2RU, UK, 2005 Search PubMed.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- M. Agirre, S. Henrion, I. Rivilla, J. I. Miranda, F. P. Cossío, B. Carboni, J. M. Villalgordo and F. Carreaux, J. Org. Chem., 2018, 83, 14861–14881 CrossRef CAS PubMed.
- A. Moyano, M. A. Pericas and E. Valenti, J. Org. Chem., 1989, 54, 573–582 CrossRef CAS.
- J. I. Seeman, J. Chem. Educ., 1986, 63, 42 CrossRef CAS.
- J. I. Seeman, Chem. Rev., 1983, 83, 83–134 CrossRef CAS.
- B. K. Carpenter, Determination of Organic Reaction Mechanisms, JohnWiley & Sons, New York, 1984 Search PubMed.
- J. Lin, D.-W. Guo and Y.-Q. Tian, Cryst. Growth Des., 2008, 8, 4571–4575 CrossRef CAS.
- A. Lapczynski, S. P. Bhatia, C. S. Letizia and A. M. Api, Food Chem. Toxicol., 2008, 46, S117–S120 CrossRef CAS PubMed.
- J. Scognamiglio, C. S. Letizia and A. M. Api, Food Chem. Toxicol., 2013, 62, S74–S82 CrossRef CAS PubMed.
- D. Fan, D.-J. Dai and H.-S. Wu, Materials, 2013, 6, 101–115 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ob02052e |
| This journal is © The Royal Society of Chemistry 2024 |