Pyramidal inversion in the solid state

Abstract

Pyramidal inversion is a stereochemical phenomenon that describes the interconversion between two equivalent pyramidal configurations of the same chemical species. Using the IO₃ molecule as a prototypical trigonal pyramidal unit, pyramidal inversion has been observed in the solid state by applying hydrostatic pressure to crystals of barium di-iodate monohydrate, Ba(IO₃)₂·H₂O, without chemical reaction or the introduction/elimination of guest molecules. The pyramidal inversion was identified by high-pressure single-crystal synchrotron X-ray diffraction from the appearance of charge density on the unoccupied side of the IO₃ pyramid at pressures above 5 GPa. The percentage of inverted pyramids increases with pressure, from 2.5% at 5.10(5) GPa to 17.5% at 14.84(5) GPa. The energetic competition between the original and inverted IO₃ pyramids as a function of pressure is investigated by density functional theory calculations, finding the two configurations to be very close in energy. Factors contributing to the observation of pyramidal inversion in barium iodate monohydrate are discussed and it is suggested that hydrogen bonding due to the presence of water may play a significant role.

---

1. Introduction

A tri-coordinated atom can be positioned outside of the plane defined by its three bonded atoms, and it may exist on either side of the plane, thereby making a trigonal pyramid. Pyramidal inversion, as described in ref. 1–3, is the phenomenon of interconversion between these configurations, and is observable in many molecules, including the well-known example of ammonia (NH₃)⁴ and its analogs.⁵ Pyramidal inversion has traditionally been observed in the fluid state (gas/liquid/solvent). To the best of the authors’ knowledge, this study represents the first observation of pyramidal inversion in a system composed of a single chemical species in the solid state. Here, the inversion of IO₃ pyramids in barium iodate monohydrate, Ba(IO₃)₂·H₂O, is driven solely by an increase in the thermodynamic variable of pressure. No other chemical species are involved. Recently, the inversion of a VO₅ square pyramidal unit, which forms a constituent of a larger dodecavanadate shell, was observed in the solid state, however, differing from the current work, the VO₅ inversion was driven by the capture/elimination of guest gas molecules.⁶ In the current work we observe that the statistical distribution of original and inverted IO₃ pyramids shifts towards inverted pyramids with increasing pressure, with the percentage of inverted pyramids increasing from 2.5% at 5.10(5) GPa to 17.5% at 14.84(5) GPa. Below 5.1 GPa the inversion is not observed, suggesting the possible existence of a critical pressure.

The properties of metal iodate materials under high-pressure conditions have been increasingly attracting attention over recent years due to their piezoelectric and nonlinear optical properties⁷ which originate from the relative orientations of the IO₃ pyramids in the crystal structure, in particular the relative orientations of the iodine lone electron pairs.⁸ However, previous studies have solely focused on anhydrous metal iodate structures (with the exception of ref. 9), disregarding the fact that the IO₃ ion is strongly hydratable¹⁰ and that naturally occurring iodates can be hydrated.¹¹ The inclusion of H₂O may play an important role in facilitating the inversion of the IO₃ pyramids in Ba(IO₃)₂·H₂O which was not observed in the only other previously studied hydrated metal iodate, Ca(IO₃)₂·H₂O,⁹ although it should be noted that, in contrast to the present work, Ca(IO₃)₂·H₂O was not studied by single-crystal X-ray diffraction. The crystal structures of barium and calcium bi-iodate monohydrate are also different, suggesting that the specific crystal structure of Ba(IO₃)₂·H₂O facilitates the pyramidal inversion.

The iodate ion, IO₃, is the main building block of the Ba(IO₃)₂·H₂O crystal structure and is the focus of this work. It was first observed to have a pyramidal structure in 1937 via the observation of 4 Raman active bands in iodate-containing solutions, rather than 3 bands expected of trigonal planar geometry.¹² In the IO₃ molecule, the iodine atom has a 5+ oxidation state. Therefore, in addition to the three covalent I–O bonds, the I atom also has a lone electron pair which repels the 3 oxygen atoms out of the planar configuration. The lone pair leads to many of the useful anisotropic phenomena associated with iodate materials, such as nonlinear optical properties, like second-harmonic generation, or ferroelectric and piezoelectric properties, making them attractive for technological applications.⁷

2. Experiment and calculation methods

2.1. Sample preparation

Single crystals of Ba(IO₃)₂·H₂O were synthesised at room temperature using a single diffusion gel growth mechanism. Barium meta silicate (Ba₂SiO₃·9H₂O) was dissolved in double distilled water, creating a gel with a density of 1.03 g cc⁻¹. 0.5 M molarity potassium iodate was then added to the gel. Glacial acetic acid was then added to the gel raise the pH to 4.2. To prevent air bubbles in the gel medium, this acidified gel solution was poured into a test tube 20 cm long and 2.5 cm in diameter. For four days, the gel solution was left in the test tube undisturbed. 10 ml of a 0.25 M barium chloride solution was added to the gel once it had set. Sealing the test tubes helped prevent contamination. For the duration of the growth phase the tubes were not disturbed. Within a week, white, needle-shaped, transparent, high-quality single crystals of Ba(IO₃)₂·H₂O were obtained. A single crystal of Ba(IO₃)₂·H₂O is shown in situ in a diamond anvil cell in ESI Fig. S1.†

2.2. High-pressure single-crystal X-ray diffraction

In this work three different single-crystal X-ray diffraction (SCXRD) experiments were carried out: two at the University of La Laguna (ULL); and one at the European Synchrotron Radiation Facility (ESRF). The data from the two experiments at the ULL have been combined into a single data set in all subsequent discussion and figures. All measurements were acquired at room temperature.

At the ULL, SCXRD measurements were conducted using a molybdenum radiation source (λ = 0.71073 Å) with a beam diameter of 150 μm, utilizing a Rigaku SuperNOVA diffractometer equipped with an EOS charge-coupled device (CCD). High-pressure (HP) measurements involved the utilization of a Mini-Bragg diamond anvil cell featuring an 85° opening angle and anvil culets with a diameter of 500 μm, thus creating the required high-pressure environment. A stainless-steel gasket, with a central hole measuring 200 μm in diameter and 75 μm in depth, was used to contain the sample. A methanol–ethanol (4 : 1) mixture was used as the pressure-transmitting medium (PTM). Positioned on the diffracting side of one of the diamond anvils, the sample was accompanied by a ruby sphere for use as the pressure sensor. The sample size was: 150 × 100 × 60 μm (Experiment 1)/80 × 50 × 40 μm (Experiment 2).

At the ESRF, SCXRD measurements were conducted at beamline ID15B using an Eiger2 X CdTe 9M (DECTRIS) detector with an X-ray wavelength of 0.41 Å and beam size of 1 × 1 μm. The sample (50 μm × 50 μm × 50 μm) was loaded into a membrane-style diamond anvil cell with an opening angle of 60°. A 200 μm stainless steel gasket was indented to a thickness of 90 μm and a chamber of 300 μm diameter was drilled in the centre. The culet size of the diamonds was 600 μm. A ruby sphere was included in the chamber to measure the sample pressure. Helium was used as the PTM.

CrysAlisPro software was used to process all measurements. The ABSORB7 program was used for numerical absorption correction based on Gaussian integration over a multifaceted crystal model. The crystal structure was refined for each pressure, using previous results as starting points. As starting point, we solved the structure at ambient conditions, applying the novel dual-space algorithm implemented in SHELXT program.¹³ Fourier recycling and least-squares refinement were used for the model completion with SHELXL-2018.¹⁴ All non-hydrogen atoms were refined anisotropically, and all hydrogen atoms were placed in geometrically suitable positions and refined with isotropic thermal parameters related to the equivalent isotropic thermal parameter of the parent atom. Due to limitations of the opening angle of our diamond anvil cell, it was only possible to collect about 30–60% of the reflections present in a full dataset. Consequently, and due to the ratio between reflections and parameters to be refined, only the heaviest atoms were refined anisotropically, with the rest being refined isotropically, while the positions of the hydrogens were always calculated in the last step of the refinement procedure.

Around 3.5 GPa we observed the presence of a residual peak compatible with a positional splitting for the iodine atom, with that peak becoming more relevant as the pressure was increased. Therefore, this positional splitting was accounted for in the subsequent refinements above 4 GPa, in which the occupancy factor between both positions for the iodine atom were also refined, restricting the thermal factors of the I1 and I2 atoms to the same value. It should be noted that, given the limitation of experimental data acquired on high pressure samples, we cannot precisely determine the occupation factor of the iodine atom, however the increase in the occupation of the I2 site on sample compression is clear.

2.3. Density functional theory calculations

In this work simulations were performed with the well-known plane wave pseudopotential method in the framework of density-functional theory (DFT, ref. 15) implemented in the Vienna Ab initio Simulation Package, VASP.^16,17 We used the projector augmented wave (PAW) pseudopotentials (ref. 18 and 19) provided in the VASP pseudopotentials database, and the exchange correlation term was described using the generalized gradient approximation (GGA), using the AM05^20,21 functional. Brillouin zone k-point sampling was performed using a dense Monkhorst-Pack²² with a grid of 6 × 6 × 6. A plane-wave basis set with an energy cutoff of 600 eV was used to ensure accurate and highly converged results. For the different analyzed structures, all degrees of freedom, lattice parameters, and internal atomic parameters were fully relaxed with self-consistent convergence criteria of 0.003 eV Å⁻¹, 10⁻⁶ eV and below 0.1 GPa for the atomic forces, the self-consistent total energy convergence, and the diagonal terms of the stress tensor, respectively. From our simulations we obtain a set of volume, energy, and pressure data that can be fitted using an equation of state, EOS.

The major, intermediate and minor principal compression axes (κ₂, κ₃ and κ₁) respectively, were determined using the PASCaL web tool for principal axis strain calculations,²³ with magnitudes of 10.1(1), 5.88(5) and 2.50(7) × 10⁻³ GPa⁻¹. The compressibility is highly anisotropic, with κ₂ being four times more compressible than κ₁, for example. The anisotropic compressibility can be explained in terms of the crystal structure. The respective directions of the major, intermediate and minor compression axes are: [010], [409] and [301]. Therefore, the major compression axis, κ₂, is exactly parallel to the crystallographic b axis, which also corresponds to the Ba–O bond direction. It is also perpendicular to the chains of BaO₁₁ units which go through the crystal structure (Fig. S3†). Therefore, the BaO₁₁ chains are pushed into the space occupied by the H₂O molecule, rather than into each other. The intermediate compression axis, κ₃, is in the direction between the c axis and the ac face diagonal, therefore it points roughly along the BaO₁₁ chains. The minor compression axis, κ₁, is roughly parallel to the a axis, and therefore pushes the edge sharing BaO₁₁ units (which link the chains together), pushing one BaO₁₁ chain into the adjacent chain.

3. Results and discussion

3.1. Ambient pressure crystal structure of Ba(IO₃)₂·H₂O

The crystal structure of barium di-iodate monohydrate, Ba(IO₃)₂·H₂O, as determined by room-temperature single-crystal X-ray diffraction (SCXRD), was first reported in ref. 24, where it was found to have a monoclinic lattice (space group I2/c, Z = 4) isostructural to the di-bromate and di-chlorate analogs Ba(BrO₃)₂·H₂O and Ba(ClO₃)₂·H₂O.^25–27 Subsequent room-temperature and low-temperature single-crystal neutron diffraction studies, combined with Raman and infrared vibrational studies, confirmed an earlier hypothesis that the H₂O molecule in Ba(IO₃)₂·H₂O exhibits dynamical disorder at ambient temperature.^28,29 The water H atom positions exhibit less disorder than the water O atoms to which they are bonded.

The ambient pressure structure of Ba(IO₃)₂·H₂O as determined by SCXRD in this work is shown in Fig. 1a. The starting atomic positions and lattice parameters used in the refinement were all taken from ref. 28. In the present work, the unit cell parameters of Ba(IO₃)₂·H₂O at ambient conditions were determined to be: a = 9.0494(2) Å, b = 7.9814(2) Å, c = 9.9187(3) Å and β = 92.147(2)°. The optimized unit cell parameters determined from the density functional theory calculations at ambient pressure are in excellent agreement: a = 8.96826 Å, b = 8.11657 Å, c = 10.00231 Å and β = 90.865°. CIF files from the present work are available free of charge from the Cambridge Crystallographic Data Centre (CCDC) under deposition numbers 2341132–2341134.† SCXRD refinement details for selected pressure are included in Table S1 in the ESI† and example two-dimensional SCXRD precession images are available in Fig. S4.†

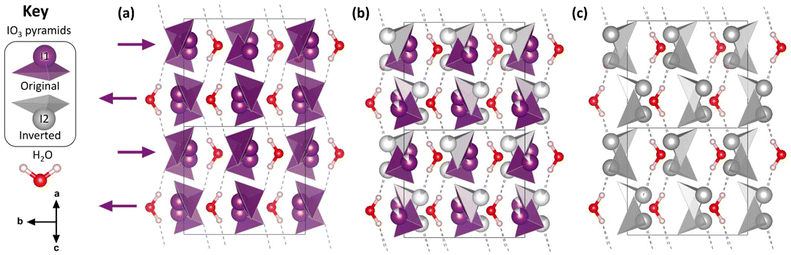Fig. 1 The crystal structure of Ba(IO₃)₂·H₂O. The Ba atoms have been omitted for clarity. See Fig. S2† for a version of Fig. 1 which includes the Ba atoms. (a) The structure at ambient pressure. (b) The structure at high pressure (9.59(5) GPa) where the occupation of the I(2) site is 12.5%. (c) The hypothetical fully-inverted structure. The crystal structure is viewed along the ac body diagonal, perpendicular to the b axis: uvw projection vector (101), hkl upwards vector (100), space group I2/a (no. 15, setting 3). Hydrogen bonds are shown as dashed lines. The key shows the essential molecular units of the structure. The black arrows below the key indicate the crystal axes.

The essential building blocks of the Ba(IO₃)₂·H₂O crystal structure (IO₃ and H₂O) are shown in the key in Fig. 1. In the crystal structure there is one crystallographically unique iodine atom I1 and it occupies the 8e Wyckoff position. The iodine atom is coordinated by three oxygen atoms (O1, O2, and O3) each forming single I–O covalent bonds, thereby forming the previously described IO₃ pyramids. It is important to note for later discussion that all of the IO₃ pyramids in the crystal structure are identical in terms of their chemical environment. In total, the structure contains four crystallographically distinct oxygen atoms, with the fourth one (O4) belonging to the H₂O molecule. The water molecule has an ideal trigonal planar coordination, as shown in Fig. 2a. It forms two equivalent H1⋯O2 hydrogen bonds, each to the O2 vertex of an IO₃ pyramid, and a Ba1–O4 metal–oxygen bond which points exactly parallel to the crystallographic b-axis. This description of the trigonal coordination of the water molecule (Fig. 2a) constitutes the chemical formula, Ba(IO₃)₂·H₂O, and crystal motif which shall be used later to discuss the high-pressure evolution of the crystal structure. The ‘V-shaped’ IO₃⋯HOH⋯O₃I motifs are related by a 2₁ screw axis in the a direction. Consequently, they are arranged into layers along the (101) body diagonal, pointing in alternating directions along the b-axis according to the layer which they are in, as shown by the purple arrows in Fig. 1a. The crystallographically unique Ba atom (Ba1) is located within the layers and it is coordinated by oxygen atoms forming octadecahedral BaO₁₁ units (see Fig. S2a†). Of these 11 oxygen atoms, six come from corner-sharing with six IO₃ pyramids, four come from edge-sharing with two IO₃ pyramids, and one comes from H₂O, which forms the shortest Ba–O distance. The BaO₁₁ units share edges to form two parallel chains that run along the crystallographic c-axis (see Fig. S2b and S2c†).

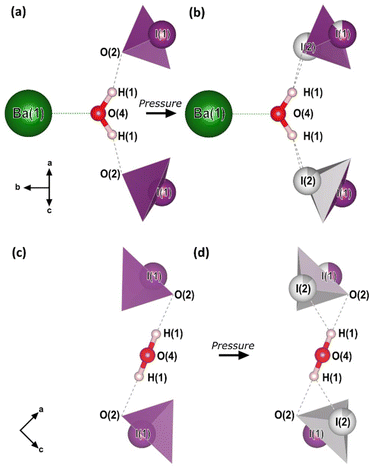Fig. 2 The crystal motif and chemical formula, Ba(IO₃)₂·H₂O. (a and c) The crystal motif of the low-pressure (0–5 GPa) crystal structure, before pyramidal inversion is observed. (b and d) The crystal motif of the high-pressure (5–15 GPa) crystal structure, showing the partial occupation of both I1 and I2 sites. All of the atomic positions shown were determined from SCXRD in this work with the exception of the H atom positions which are taken from the ambient-pressure single-crystal neutron diffraction study of ref. 28. The H atom positions from our optimized DFT calculations agree with those of ref. 28. The black arrows indicate the crystal axes.

3.2. High-pressure evolution of the crystal structure of Ba(IO₃)₂·H₂O

To explore the mechanism driving the inversion of the IO₃ pyramids, here we examine the geometric evolution of the IO₃ pyramids based on Rietveld refinement of SCXRD measurements. The numerical quantities given in this section are based on the ESRF data only, although the data from all experiments agree and are shown in the figures. The description of the pressure evolution of the crystal structure begins at ambient pressure and follows the compression of the crystal. Below, the description is separated into two subsections: (1) before pyramidal inversion is observed (0 to 5.10(5) GPa), and, (2) pressure-induced pyramidal inversion (5.10(5) to 14.84(5) GPa).

3.2.a. Before pyramidal inversion is observed. Beginning from ambient pressure, the atomic positions in the crystal structure were determined at increasing pressure increments via SCXRD. From these values, it is possible to calculate various parameters, such as bond lengths, unit-cell volume, and compressibility (discussed later). Another parameter, the height of the IO₃ pyramid, is defined as the distance at which the iodine atom is displaced from the triangular base, d(I–O₃). The pyramid height is used as a key indicator of the pyramidal geometry since it depends on both the inter-oxygen distance, d(O–O), and the I–O bond lengths, d(I–O). At pressures below 5.10(5) GPa, the height of the original IO₃ pyramid increases with pressure, as shown in Fig. 3a, beginning at 0.842(5) Å at 0 GPa and increasing up to 0.878(5) Å at 5.10(5) GPa. The SCXRD results from the ULL and the ESRF show the same trend. At the same time, the I–O bond lengths stay relatively constant (Fig. S5†), which means that the increasing height is the result of a decreasing O–I–O bond angle (Fig. S6†), or in other words, a ‘stretching’ of the IO₃ pyramid in the direction perpendicular to the triangular base with increasing pressure. The increase in pyramid height also directly correlates with an increase in pyramidal volume (see Fig. 3b) with increasing pressure. The overall IO₃ volume increase between 0 and 5.10(5) GPa is approximately 4%. Although this result may seem counterintuitive, the total crystal unit cell volume decreases over the whole pressure range studied (see Fig. 3c) due to the decreasing volume of the compressible BaO₁₁ octadecahedra (see Fig. 3b) which, between 0 and 5.10(5) GPa, decreases by approximately 9%. A second-order Birch–Murnaghan equation of state (B′₀ = 4) was fitted to the unit cell volume over the whole pressure range studied using Eosfit7c³⁰ resulting in a zero pressure unit cell volume of V₀ = 710.3(8) Å and a bulk modulus of B₀ = 37.2(3) GPa, which is consistent with the literature value of B₀ = 39.0(7) GPa for Ca(IO₃)₂·H₂O.⁸ The Ba(IO₃)₂·H₂O bulk modulus determined here from the experimental SCXRD data is also in agreement with the bulk modulus determined from our DFT calculation results, (see Fig. 3c) which find the bulk modulus to be, B₀ = 32.0(5) GPa. The unit cell lattice parameters from the experiment and DFT calculations up to 15 GPa are shown in Fig. S7.† The text to create CIF files for the Ba(IO₃)₂·H₂O crystal structure at 0, 11.59(5), and 14.84(5) GPa are included in the ESI.† They are also available free of charge from the Cambridge Crystallographic Data Centre (CCDC) under deposition numbers 2341132–2341134.† XRD refinement details for these pressures are also included in Table S1 in the ESI.†

Fig. 3 The pressure evolution of the polyhedral geometry and volume determined from SCXRD. (a) The IO₃ pyramid height, d(I–O₃). (b) The volume of the original and inverted IO₃ pyramid (right y-axis), and the volume of the BaO₁₁ unit (left y-axis). (c) The volume-pressure equation of state (EOS) of Ba(IO₃)₂·H₂O according to SCXRD (black) and DFT calculations (red). The experimental values determined from SCXRD at the ULL and the ESRF for the BaO₁₁ unit in part (b) and for the unit cell in part (c) were fitted with single Birch–Murnaghan equations of state. In (c) the error in unit cell volume is smaller than the symbols. The insets show schematic representations of the IO₃ pyramids to assist the reader with the description of the IO₃ evolution. The error on all experimental pressure measurements is ±0.05 GPa.

One possible explanation for the increase in height of IO₃ pyramids below 5 GPa is the growing electrostatic interaction between the electron-dense I1 iodine atom lone electron pairs (LEPs) and the electrophilic (δ+) hydrogen atom of the water molecule. To better visualize this interaction, the reader is referred to Fig. 4a, which shows the repeating pattern of the crystal motif which was shown in detail in Fig. 2a. As previously described, the H₂O molecule forms two equivalent hydrogen bonds, each to the O2 vertex of an IO₃ pyramid, shown by the solid red lines. Although the H₂O molecule is hydrogen bonded to these two IO₃ pyramids, it is actually coordinated by four IO₃ pyramids in total, where the two extra IO₃ pyramids come from neighboring motifs, as shown in Fig. 4b and more detail in Fig. 4c and d. The two IO₃ pyramids of the original motif (shown in purple) are related by a 180° rotation about the Ba1–O4 bond (parallel to the b-axis). Therefore, their orientations relative to the H₂O molecule are identical. In that orientation, the LEP of the I1 atom points away from the H₂O molecule. In other words, the water molecule can “see” only the triangular bases of the IO₃ pyramids to which it is hydrogen bonded (see Fig. 2a and c). In contrast, the IO₃ pyramids which come from the neighboring motifs (shown in yellow) are oriented so that their LEPs point toward the H₂O molecule of the original motif (see Fig. 4d). It should be reiterated here that the purple and yellow IO₃⁻ pyramids are crystallographically identical, therefore, if the ‘yellow’ pyramids get taller, so do the ‘purple’ pyramids. Apart from the H atoms, the nearest atom to the O4 atom of the H₂O molecule is the O2 vertex of the IO₃ pyramid to which it is hydrogen bonded. The d(O4–O2) distance varies very little over the entire pressure range studied, varying between 2.75 and 2.65 Å, as shown by the red data in Fig. 5. (The data in Fig. 5 are color-coded to match the interatomic distances of interest shown in Fig. 4.) The next nearest atom to the O4 atom of the H₂O molecule is the iodine I1 atom from the neighboring motifs. The d(O4–I1) distance decreases from 3.5 Å to 3.3 Å as pressure is increased from 0 to 5.10(5) GPa, as shown by the yellow data in Fig. 5. In other words, as pressure is increased, the I1 atom approaches LEP-first towards the water molecule (see Fig. 4d), thereby increasing interaction between the I1 LEP and the H^δ+ of the water molecule and increasing the IO₃ pyramid height. Following the convention of Jeffrey et al.^31,32 a hydrogen bond in the range 3.5 to 3.3 Å is compatible with ‘weak’ hydrogen bonding, whereas a hydrogen bond in the range 2.6 to 2.8 Å is compatible with ‘moderate’ bonding. Therefore, the hypothesis is that below 5.10(5) GPa there is a competition between the O2 vertex of IO₃, and the LEP of the I1 atom from the neighboring motif, to form hydrogen bonds with the water molecule. The hydrogen bond to the O2 vertex of the IO₃ pyramid is dominant since it is shorter (2.7 Å vs. 3.3 Å), however between 0 and 5.10(5) GPa the I1 approaches the water molecule more quickly, indicating that the I^LEP becomes more competitive with increasing pressure. Looking at Fig. 4c and d, it is clear that a slight rotation of the H₂O molecule about the Ba–O4 bond (crystallographic b-axis) would favor the I^LEP–H^δ+ electrostatic attraction because the position of the I(1) atoms fulfills the strict directionality requirements of hydrogen bonding. At 5.10(5) GPa, the angle subtended by the O2 vertex and Ba1 atom about the water molecule is φ(O2–O4–Ba1) = 109.6(4)° (see Fig. 4d). The angle subtended by the I1 and Ba atom about the water molecule, φ(I1–O4–Ba1) = 123.3(2)°, which is closer to the angle defined by the hydrogen atoms according to ref. 28, φ(H–O4–Ba1) = 122.0(4)°, which would favor the hydrogen bond interaction with the I1 atoms. Since the H atom positions cannot be determined from SCXRD, the H positions shown throughout this article are taken from the neutron diffraction study of ref. 28, although it is plausible that the H₂O molecule may rotate to a new equilibrium position, forming bifurcated H-bonds with both the O2 vertex and the I1 LEP. From these results it is clear is that between 0–5.10(5) GPa it appears to be energetically favourable for the IO₃ pyramids to increase in height and volume, possibly due to the strengthening electrostatic interaction between the I1 LEP and the H^δ+ atoms of the H₂O molecule. However, the trend of increasing IO₃ pyramid volume with increasing pressure cannot physically continue indefinitely and, as described in the next section, the trend is broken at higher pressures.

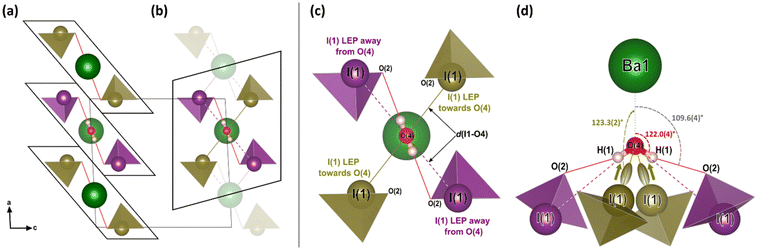Fig. 4 The low-pressure crystal structure of Ba(IO₃)₂·H₂O. (a) The repeating motif corresponding to the chemical formula of barium di-iodate monohydrate including the hydrogen bonds (solid red lines) to the O2 vertex of the IO₃ pyramids. (b) An alternative motif that emphasizes the importance of the neighbouring IO₃ pyramids (yellow) whose I atoms are closer to the water O4 atom. (c) A detailed expanded view of part (b) which shows atom labels and the important interatomic distances (which are plotted as a function of pressure in Fig. 3b). (d) A rotated view of part (c) to clarify the interaction of the I1 electron pair with the water molecule. The black arrows indicate the crystal axes. The Ba1–O4–H1 angle of 122.0° (red) is taken from the ambient pressure neutron diffraction measurements of ref. 28.

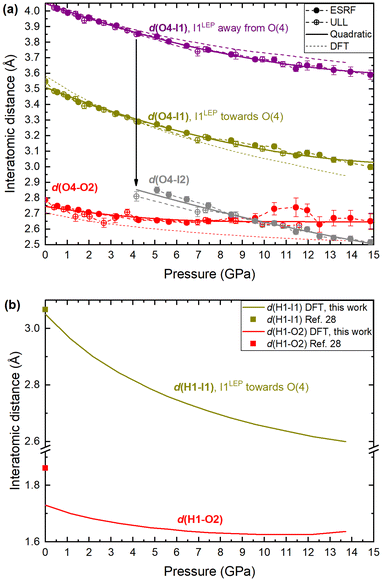Fig. 5 Interatomic distances in Ba(IO₃)₂·H₂O with increasing pressure according to SCXRD and DFT calculations. (a) The interatomic distance between the iodine atom and the O4 oxygen atom of the H₂O molecule, d(I–O4). d(O4–O2), which corresponds to the hydrogen bond between the O4 vertex of the IO₃ pyramid and the oxygen atom of the H₂O molecule at ambient pressure, is included for comparison (red). (b) The hydrogen bond distances, d(H1–I1) and d(H1–O2), according to DFT calculations. The symbols at ambient pressure are taken from the neutron diffraction study of ref. 28. The error on all experimental pressure measurements is ±0.05 GPa.

3.2.b. Pressure-induced pyramidal inversion. Above 5 GPa, a peak in the electron density is observed on the opposite side of the triangular base of the IO₃ pyramid, as shown in Fig. S8.† This electron density corresponds to the iodine atom, I2, which is displaced to the opposite side of the triangular base of the IO₃ pyramid, forming an inverted IO₃ pyramid. Regarding the nomenclature used in the remainder of this work, the two types of IO₃ units shall be referred to as the ‘original (I1) pyramid’ and the ‘inverted (I2) pyramid’ which is shown in grey in Fig. 1–3. There are several salient remarks about the appearance of the inverted I2 pyramid and the behavior of the IO₃ pyramids in the pressure range from 5.10(5) to 14.84(5) GPa, in particular relating to: the I1/I2 iodine site occupation; the IO₃ pyramid height/volume; and changes in intermolecular hydrogen bonding, all of which are discussed below. The role of the H₂O molecule in the crystal structure, and the resulting hydrogen bonding, appears to be significant in the high-pressure evolution of the crystal structure in this relatively low pressure range.

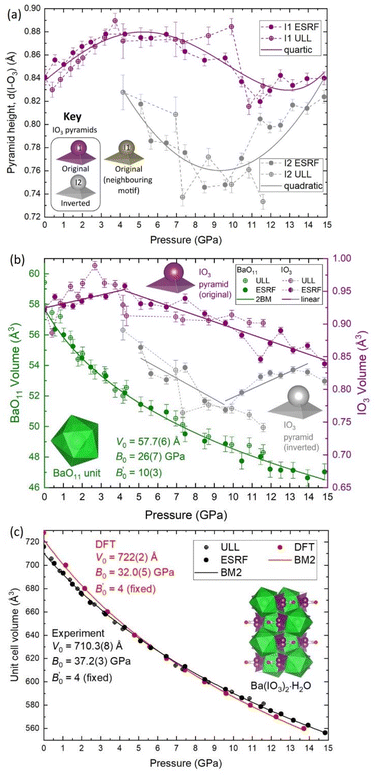
Firstly, regarding the I1/I2 site occupation, at 5.10(5) GPa, the lowest pressure at which the I2 atom was observed, the occupation of the I2 site is only 2.6%, meaning that most of the iodine atoms remain in the original I1 position. The occupation of the I2 site increases with pressure up to 17.5% at 14.84(5) GPa (see Fig. S9†). Therefore, within the pressure range 5.10(5) to 14.84(5) GPa, the distribution of original I1 pyramids and inverted I2 pyramids shifts towards the inverted I2 pyramid with increasing pressure, although the equilibrium is always biased towards the original I1 pyramid. This suggests that the two configurations must be increasingly energetically similar with increasing pressure. This hypothesis is supported by DFT calculations discussed later in this section. The Ba(IO₃)₂·H₂O structure with a distribution of original/inverted IO₃ pyramids is shown with an I2 site occupancy of 12.5% in Fig. 1b.

Secondly, regarding the IO₃ pyramid height and volume, strictly speaking pyramidal inversion, as defined in ref. 1–3, refers to conversion between two equivalent isomers, however in this case the two pyramids are not equal. The inverted I2 pyramid is always shorter than the original I1 pyramid (see Fig. 3a) and it always has a lower volume (see Fig. 3b). For example, at 5.10(5) GPa the original I1 pyramid has a volume of 0.9318 ų, and the inverted I2 pyramidal volume of 0.8641 ų, which constitutes a volume decrease upon inversion of approximately 7%, thereby making the original I1 pyramid more favourable than the inverted I2 pyramid from a purely thermodynamic perspective since the total internal energy (U) can be referred to U = Q − PV under the assumption that there is no heat (Q) transfer during the pyramidal inversion. That agrees with the fact that the majority remains in the original I1 configuration as observed in SCXRD. The appearance of the I2 pyramid also coincides with a change in the pressure evolution of the I1 pyramid height and volume as observed by the change in gradients in Fig. 2a and b. Between 5–10 GPa, both the I1 and I2 pyramids decrease in height and volume with increasing pressure, which is the expected result for a crystal under compression. Above 10 GPa the behaviour changes again, with I1 volume continuing to decrease under compression, albeit with a relatively constant pyramid height remaining with pressure, and the I2 height and volume beginning to increase again with increasing pressure. This observation is consistent with the explanation offered in the previous section for the increasing height of the I1 pyramid below 5 GPa. Specifically, as the I2 atom approaches the H₂O molecule more closely than the water O2 atom, the I^LEP–H^δ+ interaction becomes stronger, causing the height of the pyramid to increase.

Thirdly, regarding the distance between the I atom and the O4 atom of the H₂O molecule, at 5.1 GPa the I–O distance in the original I1 pyramid is d(I1–O4) = 3.30 Å, whereas the I–O distance in inverted I2 pyramid the distance is d(I2–O4) = 2.80 Å (see yellow vs. grey data in Fig. 5a), making the I2 atom much more competitive than the I1 atom with the hydrogen-bonded O2 vertex in terms of distance from the H₂O molecule (see red vs. grey data in Fig. 5a). The I2 atom even becomes the closest atom to the H₂O molecule above 10 GPa. The shortening of the I–O4 distance upon pyramidal inversion also is shown in Fig. 2 by the appearance of the grey I2 atoms. This decrease in the I–OH₂ distance constitutes a change from ‘weak’ to ‘moderate’ hydrogen bonding according to the aforementioned convention of Jeffrey et al.^31,32 The H atom may form bifurcated hydrogen bonds with the I2 atom and the O4 atom, as shown in Fig. 2b and d. Therefore, the inverted I2 pyramid is competitive with the original I1 pyramid due to two main factors: the formation of shorter hydrogen bonds due to its proximity to the H₂O molecule; and the decrease in pyramidal volume. The hydrogen bond distances (H–O and H–I) based on the geometrically optimised structures from DFT calculations are shown in Fig. 5b, supporting the hypothesis that the H–I bond distance (yellow) becomes increasingly competitive with the H–O distance (red) with increasing pressure. The interatomic distances determined from DFT shown in Fig. 5a (dashed lines) show excellent agreement with the distances determined via SCXRD. From these results it is clear is that between 5.10(5)–14.84(5) GPa the SCXRD measurements unambiguously reveal pressure-induced pyramidal inversion in the IO₃ pyramids.

It is worth mentioning that one potential contribution to the kinetic barreier between the original and inverted iodine site is the I1–I2 distance. For example, in the low-pressure crystal structure (Fig. 1a), the shortest I–I distance is d(I1–I1) = 3.580(2) Å. In a hypothetical fully inverted structure (Fig. 1c) the shortest I–I distance is d(I2–I2) = 3.11(4) Å. However, in the real high-pressure crystal structure (Fig. 1b), which contains a distribution of I1 and I2 pyramids, the shortest I–I distance is d(I1–I2) = 2.692 Å, which is similar to the I–I covalent bond length in gaseous I₂ molecules (2.665 A, ref. 33) and shorter than the I–I distance in solid crystalline iodine (2.728(1) Å, ref. 34). The proximity of neighboring I1 and I2 atoms may contribute to the potential barrier to pyramidal inversion.

In order to quantify the competition between the I1 and I2 sites we performed additional DFT calculations where the occupation of the I1 and I2 sites was approximated in the following way. The experimentally determined Ba(IO₃)₂·H₂O structures, which were refined against the SCXRD patterns, had partial I1 and I2 site occupations, where the total occupation (I1 + I2) is equal to 1. DFT calculations cannot be performed for partially occupied atomic sites. Therefore, to approximate, for example, an I2 site with a partial occupation of 0.25, one quarter of the I1 atoms in the crystal structure were replaced with their analogue I2 atoms. The Ba(IO₃)₂·H₂O until cell contains eight I atoms, therefore in the example case of 25% IO₃ inversion, there would be six original I1 atoms and two inverted I2 atoms. In order to treat the atoms individually in this way it was necessary to remove the monoclinic crystal symmetry (C2/c) and treat the structure as triclinic (P1), except in the cases of 0% and 100% I2, in which cases it was treated as monoclinic. This approach constitutes an approximation because the real site occupation, derived from SCXRD, is the time-average site occupation, i.e. at any random instant the I2 site may or may not be occupied with a statistical probability proportional to the observed occupation. In the DFT calculations, the I2 site is either always or never occupied. Therefore, the DFT calculations do not account for any kinetic effects.

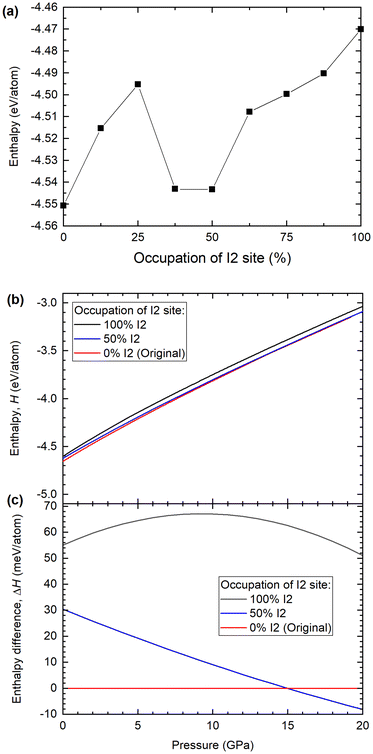
Fig. 6a shows the calculated enthalpy for the Ba(IO₃)₂·H₂O structure as a function of the percentage of inverted I2 pyramids, from 0% to 100%, in increments of 12.5%. All nine structures were calculated using the DFT optimized lattice parameters from the case of 0% I2 at 12.2 GPa: a = 12.2910 Å, b = 7.1088 Å, c = 8.7465 Å and β = 131.77°. According to the SCXRD data, at 12.2 GPa the occupation of the I2 site is approximately 17%. According to the DFT data in Fig. 6a, there is a local minimum in the enthalpy between 37.5 and 50% I2. The energy difference between 0% and 50% configurations is ∼30 meV at ambient pressure. For comparison, the thermal energy at room temperature is k_BT = 25 meV. Therefore, the 0% and 50% states they are almost equally probable according to thermodynamics. This implies that, experimentally, a 25% pyramidal inversion is to be the expected observation at 12.2 GPa barring any kinetic barriers. In order to approximate the kinetic barrier we can use the enthalpy data of Fig. 6a. To move from the initial (0%) to the final state (50%), the system must transition through a higher enthalpy intermediate state (25%), therefore the transition rate is influenced by an activation energy, which is the magnitude of the potential barrier (commonly referred to as the kinetic barrier) separating the enthalpy minima. In Fig. 6a the greatest difference between the local enthalpy maximum (25%) and the two enthalpy minima (0% and 50%) gives an activation energy of E_a = 54 meV. The minimum proportion of pyramidal inversion is therefore given by the exponential function e^−E_a/K_BT, where at 300 K, K_BT = 25 meV. This leads to e^−55/25 = 0.11, which is which is equivalent to 11% inversion. It is therefore reasonable to posit that the 17.5% pyramidal inversion which we observe experimentally is a plausible outcome, since it is situated between the minimum (11%) and maximum (25%) values predicted by our model.

Fig. 6 Enthalpy of competing Ba(IO₃)₂·H₂O configurations according to density functional theory calculations. (a) Calculated enthalpy for the Ba(IO₃)₂·H₂O structure at 12.2 GPa with 0, 12.5, 25, 37.5, 50, 62.5, 75, 87.5 and 100% IO₃ inversion. (b) The enthalpy and (c) enthalpy of the 50 and 100% configurations relative to the 0% configuration.

According to the SCXRD experiments, the percentage of I2 inversion increases with pressure. Therefore, the enthalpies of the 0, 50% and 100% I2 configurations were calculated as a function of pressure, as shown in Fig. 6b and c. The enthalpy difference between the 0% and 50% I2 configurations decreases monotonically with increasing pressure, which is consistent with the experimental observation that the I2 occupation increases monotonically with increasing pressure. At pressures higher than 15 GPa, the 50% I2 configuration becomes the most energetically favorable (Fig. 6c). Therefore, according to DFT calculations and experimental SCXRD measurements, increasing pressure shifts the distribution of I1/I2 iodine atoms towards the I2 site.

4. Conclusion

In this work, inversion of the pyramidal IO₃ molecule has been observed in the solid state in crystals of barium di-iodate mono-hydrate, Ba(IO₃)₂·H₂O, under hydrostatic compression via single-crystal synchrotron X-ray diffraction up to 15 GPa. The percentage of inverted pyramids increases with pressure, from 2.5% at 5.10(5) GPa to 17.5% at 14.84(5) GPa. The geometric evolution of the IO₃ pyramids has been investigated based on the atomic positions determined from the SCXRD data, finding that the distance between the O4 atom of the water molecule and the iodine atom may play a key role in the stabilization of the inverted IO₃ pyramids. The energetic competition between the original and inverted IO₃ pyramids as a function of pressure was investigated by density functional theory calculations, finding that the original and inverted IO₃ pyramids are energetically competitive.

This work opens clear directions for future work. For example, does pyramidal inversion occur in the anhydrous version of barium di-iodate? α-Ba(IO₃)₂ exhibits a similar monoclinic structure (C2/c) wherein the Ba²⁺ and IO₃⁻ ions have the same site symmetry as they do in the hydrated version studied here.³⁵ A similar high-pressure study of α-Ba(IO₃)₂ would unequivocally answer the question of whether the presence of the water molecule plays a role in the pyramidal inversion observed in this work. Similarly, does pyramidal inversion occur in the isostructural di-bromate and di-chlorate analogs Ba(BrO₃)₂·H₂O and Ba(ClO₃)₂·H₂O?^25–27 Can the IO₃ pyramidal inversion be encouraged by heating, rather than by hydrostatic compression? According to the DFT calculation results this is theoretically plausible, but it has not been tested experimentally. Finally, there remains the unanswered question about what happens at pressures above 15 GPa. According to the SCXRD results the volume of the inverted IO₃ pyramid may be increasing with compression, similar to what occurs with the original IO₃ pyramid at lower pressures. The trend of increasing volume/atom cannot continue indefinitely and may lead to a phase transition.

Author contributions

The manuscript was written through the contribution of all authors. All author have given approval to the final version of the manuscript.

Data availability

Crystallographic data for Ba(IO₃)₂·H₂O at ambient pressure, 11.59 GPa and 14.84 GPa have been deposited at the CCDC under deposition numbers 2341132–2341134 and can be obtained from https://www.ccdc.cam.ac.uk.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Spanish Research Agency (AEI) and Spanish Ministry of Science, Innovation, and Universities (MCIN) under grant PID2022-138076NB-C41/C44, and MALTA Consolider Team Network (RED2022-134388-T), co-financed by EU FEDER funds (https://doi.org/10.13039/501100011033). This work was also supported by the Generalitat Valenciana under Grant No. PROMETEO CIPROM/2021/075-GREENMAT and MFA/2022/007. R.T. acknowledges funding from the Generalitat Valenciana for the postdoctoral Fellowship No. CIAPOS/2021/20. J.S.-M. acknowledges the Spanish Ministry of Science, Innovation and Universities for the PRE2020-092198 fellowship. The authors are grateful to Samuel Gallego-Parra for assistance in performing measurements at the ESRF. This study forms part of the Advanced Materials program and is supported by MCIU with funding from European Union Next Generation EU (PRTR-C17.I1) and by the Generalitat Valenciana.

References

1. L. Ayarde-Henriquez, C. Guerra, M. Duque-Norena and E. Chamorro, Revisiting the bonding evolution theory: a fresh perspective on the ammonia pyramidal inversion and bond dissociations in ethane and borazane, Phys. Chem. Chem. Phys., 2023, 25, 27394–27408.
2. P. International Union of and C. Applied, 2006, 10.1351/goldbook.P04956.
3. A. Rauk, L. C. Allen and K. Mislow, Pyramidal Inversion, Angew. Chem., Int. Ed. Engl., 1970, 9, 400–414.
4. A. Rauk, L. C. Allen and E. Clementi, Electronic Structure and Inversion Barrier of Ammonia, J. Chem. Phys., 1970, 52, 4133–4144.
5. G. W. Koeppl, D. S. Sagatys, G. S. Krishnamurthy and S. I. Miller, Inversion barriers of pyramidal (XY3) and related planar (=XY) species, J. Am. Chem. Soc., 1967, 89, 3396–3405.
6. Y. Kikukawa, K. Seto, S. Uchida, S. Kuwajima and Y. Hayashi, Solid-State Umbrella-type Inversion of a VO₅ Square-Pyramidal Unit in a Bowl-type Dodecavanadate Induced by Insertion and Elimination of a Guest Molecule, Angew. Chem., Int. Ed., 2018, 57, 16051–16055.
7. A. Liang, R. Turnbull and D. Errandonea, A review on the advancements in the characterization of the high-pressure properties of iodates, Prog. Mater. Sci., 2023, 136, 101092.
8. V. R. Kalinin, V. V. llyukhin and N. V. Belov, Crystal structure of triclinic modification of potassium iodate, Dokl. Akad. Nauk SSSR, 1978, 239(3), 590–593.
9. A. Liang, L.-T. Shi, R. Turnbull, F. J. Manjón, J. Ibáñez, C. Popescu, M. Jasmin, J. Singh, K. Venkatakrishnan, G. Vaitheeswaran and D. Errandonea, Pressure-induced band-gap energy increase in a metal iodate, Phys. Rev. B, 2022, 106, 235203.
10. M. D. Baer, V.-T. Pham, J. L. Fulton, G. K. Schenter, M. Balasubramanian and C. J. Mundy, Is Iodate a Strongly Hydrated Cation?, J. Phys. Chem. Lett., 2011, 2, 2650–2654.
11. G. E. Ericksen, M. E. Mrose and J. W. Marinenko, J. Res. U.S. Geol. Surv., 1974, 471–478.
12. S. T. Shen, Y. T. Yao and T.-Y. Wu, Depolarization of Raman Lines and Structure of Chlorate, Bromate and Iodate Ions, Phys. Rev., 1937, 51, 235–238.
13. G. M. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
14. G. Sheldrick, SHELXT - Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
15. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138.
16. J. Hafner, Ab initio simulations of materials using VASP: Density-functional theory and beyond, J. Comput. Chem., 2008, 29, 2044–2078.
17. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
18. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
19. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
20. A. E. Mattsson, R. Armiento, J. Paier, G. Kresse, J. M. Wills and T. R. Mattsson, The AM05 density functional applied to solids, J. Chem. Phys., 2008, 128, 084714.
21. R. Armiento and A. E. Mattsson, Functional designed to include surface effects in self-consistent density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085108.
22. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
23. M. Lertkiattrakul, M. L. Evans and M. J. Cliffe, PASCal Python: A Principal Axis Strain Calculator, J. Open Source Softw., 2023, 8, 5556.
24. H. D. Lutz, E. Alici and W. Buchmeier, Kristallstrukturen des Sr(BrO₃)₂·H₂O, Ba(BrO₃)₂·H₂O, Ba(IO₃)₂·H₂O, Pb(CIO₃)₂·H₂O und Pb(BrO₃)₂·H₂O, Z. Anorg. Allg. Chem., 1986, 535, 31–38.
25. S. K. Sikka, S. N. Momin, H. Rajagopal and R. Chidambaram, Neutron–Diffraction Refinement of the Crystal Structure of Barium Chlorate Monohydrate Ba(ClO₃)₂·H₂O, J. Chem. Phys., 1968, 48, 1883–1889.
26. G. Kartha, Structure of halogenates of the type A (BO₃)₂·H₂O, Proc. Natl. Acad. Sci., India, Sect. A, 1953, 38, 1–12.
27. G. Kartha, Structure of barium chlorate monohydrate Ba(ClO₃)₂·H₂O, Acta Crystallogr., 1952, 5, 845–846.
28. T. Kellersohn, H. D. Lutz, T. Vogt, R. G. Delaplane and I. Olovsson, Structural instabilities of the trigonally coordinated water molecules in Ba(IO₃)₂·H₂O and Pb(ClO₃)₂·H₂O studied by X-ray and neutron diffraction at 25 and 295 K, Acta Crystallogr., Sect. B: Struct. Sci., 1992, 48, 166–172.
29. H. D. Lutz and N. Lange, Dynamic behaviour of water molecules with trigonal coordination in solid hydrates, J. Mol. Liq., 1990, 46, 255–261.
30. R. J. Angel, M. Alvaro and J. Gonzalez-Platas, EosFit7c and a Fortran module (library) for equation of state calculations, Z. Kristallogr. - Cryst. Mater., 2014, 229, 405–419.
31. T. Steiner, The Hydrogen Bond in the Solid State, Angew. Chem., Int. Ed., 2002, 41, 48–76.
32. G. A. Jeffrey, An introduction to Hydrogen Bonding, Oxford University Press, Oxford, 1997.
33. L. V. Gurvich, I. V. Veyts and C. B. Alcock, Thermodynamic Properties of Individual Substances, Hemisphere Pub. Co., New York, 1989.
34. F. Bertolotti, A. V. Shishkina, A. Forni, G. Gervasio, A. I. Stash and V. G. Tsirelson, Intermolecular Bonding Features in Solid Iodine, Cryst. Growth Des., 2014, 14, 3587–3595.
35. V. Petricek, K. Maly, B. Kratochvil, J. Podlahova and J. Loub, Barium diiodate, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2130–2132.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2341132–2341134. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4qi01021c

---