Open Access Article
Open Access ArticleExploring HCl–HCl interactions: QZVPP calculations, improved Lennard-Jones potential, and second virial coefficient analysis for thermodynamics and industrial applications
Waqas Amber Gill a,
Muhammad Tariq Azizb,
Hany W. Darwishc and
Muhammad Ramzan Saeed Ashraf Janjua
a,
Muhammad Tariq Azizb,
Hany W. Darwishc and
Muhammad Ramzan Saeed Ashraf Janjua *b
*b
aDepartamento de Química Física, Universidad de Valencia, Avda Dr Moliner, 50, Burjassot, E-46100, Valencia, Spain
bDepartment of Chemistry, Government College University Faisalabad, Faisalabad 38000, Pakistan. E-mail: Janjua@gcuf.edu.pk; Dr_Janjua2010@yahoo.com
cDepartment of Pharmaceutical Chemistry, College of Pharmacy, King Saud University, P.O. Box 2457, Riyadh 11451, Saudi Arabia
First published on 8th January 2024
Abstract
In this paper, we present a comprehensive analysis of HCl–HCl interactions, including QZVPP calculations, energy fitting, conformation validation, and the determination of the second virial coefficient B using improved Lennard-Jones (ILJ) potential parameters. To acquire accurate interaction energies, initial QZVPP calculations are performed on approximately 1851 randomly generated HCl–HCl conformations. Then, these energies are used to fit an improved Lennard-Jones potential energy surface, allowing for a robust description of HCl–HCl interactions. The ILJ potential parameters are then used to validate particular HCl dimer conformations, ensuring their stability and consistency with experimental observations. The correlation between calculated and experimental conformations strengthens the validity of the ILJ potential parameters. In addition, the second viral coefficient B is calculated at various temperatures using the ILJ potential. The obtained B values are compared to experimental data, demonstrating close agreement, and validating the ILJ potential's ability to accurately capture the intermolecular interactions and gas-phase behavior of the HCl–HCl system. The results of this study demonstrate the effective implementation of QZVPP calculations, energy fitting, and ILJ potential parameters in validating HCl–HCl conformations and accurately determining the second virial coefficient B. The high degree of concordance between calculated B values and experimental data demonstrates the validity of the ILJ potential and its suitability for modeling HCl–HCl interactions. This research contributes to a greater comprehension of HCl–HCl interactions and their implications for numerous chemical and atmospheric processes. The validated conformations, energy fitting method, and calculated second virial coefficients provide valuable instruments for future research and pave the way for more accurate modeling and simulations of HCl–HCl systems.
1. Introduction
In the field of molecular interactions, the interaction potential between hydrogen chloride (HCl) molecules is a topic of considerable fascination and significance.1–3 Understanding the nature and extent of the HCl–HCl interaction is essential for elucidating4 the behavior of HCl in diverse chemical and physical processes. We present a comprehensive analysis of the HCl–HCl interaction potential to shed light on the forces that govern this essential molecular interaction. The interaction potential between HCl and HCl has been the subject of numerous theoretical and experimental studies.5,6 Theoretical techniques, such as ab initio calculations and molecular dynamics simulations,7 have been instrumental in elucidating the electronic structure and energetics of HCl dimers.8 These computational methods provide important insights into the potential energy surface and intermolecular forces that regulate the HCl–HCl interaction. Alternatively, experimental techniques, such as spectroscopy and scattering investigations, provide complementary information regarding the interaction potential and intermolecular forces.9,10Initial research centered on establishing the equilibrium distance, minimum potential energy, and binding energy of the HCl dimer.11,12 These studies demonstrated the importance of dipole–dipole interactions and dispersion forces in the stabilization of the HCl–HCl complex.12 Using theoretical calculations, a thorough exploration of the HCl–HCl interaction potential was conducted, revealing the significant impact of electrostatic forces and the contribution of van der Waals interactions in the HCl dimer.13,14 The contribution of dipole–dipole and van der Waals forces to the HCl dimer was empirically supported by dispersion experiments that determined the interaction potential.15–18 The nature of the HCl–HCl interaction potential has been studied in greater detail thanks to the development of computational methodologies and experimental techniques. These studies have investigated higher-order interactions19 and anisotropic effects,20 resulting in a deeper comprehension of the forces at work in the HCl dimer. The results demonstrated the importance of three-body interactions and orientation-dependent forces in determining the interaction potential between HCl dimers.21 Insightful experimental techniques, such as infrared spectroscopy, have also contributed to the potential HCl–HCl interaction.9,22,23 Using infrared spectroscopy, the interaction potential, and vibrational properties of the HCl dimer were investigated, providing experimental evidence that supported the theoretical predictions of the potential energy surface.14 This study also shed light on the vibrational modes underlying the HCl–HCl interaction.
Simulations of molecular dynamics7 have been demonstrated to be an efficient method for investigating the HCl–HCl interaction potential and its role in a variety of processes. Simulations of molecular dynamics were used to investigate the intermolecular forces and dynamics of the HCl dimer,24 casting light on the importance of hydrogen bonding and dipole-induced polarization in determining the behavior of HCl molecules.
The Lennard-Jones (LJ) potential is commonly utilized to get potential from interaction energies.25,26 However, the short- and long-range shortcomings of the LJ scheme are widely documented.27–29 In addition to this model, Pirani et al. suggested an improved Lennard-Jones (ILJ) potential,27,28 which is straightforward and precise and provides greater flexibility by introducing an additional parameter in a way that substantially all the LJ model's drawbacks are addressed. In noble gas systems, as well as under conditions of great angular precision and energy, it has been demonstrated that this potential performs well for dispersion interactions, accurately recreating vibrational springs.28,29 It appears to be particularly helpful for molecular dynamics simulations of, notably, non-covalent interactions through the careful selection of the proper parameters. When giving the system partial charges, electrostatic contributions to the interaction are frequently considered by a coulombic expression.30,31 We employed multicenter techniques for electrostatic contribution (3-centers). The ILJ functional is used in this work to create a set of force fields that can assess van der Waals interactions like those seen in the HCl–HCl system. We suggest various forms of force fields and consider how the electrostatic component affects the parameters using various charge schemes, whose effectiveness will be assessed.
These models are sufficient to capture the interactions while also enabling high-level CCSD(T) calculations. At the B3LYP/6-31G**32,33 level, the first fixed HCl monomer was optimized. Then we fixed the H–Cl distance (0.000, 0.000, −1.215028) Å and (0.000, 0.000, 0.071472) Å respectively. Following this optimization, the structure was considered in all subsequent computations of interaction energy. We estimated the appropriate interaction energies at the CCSD(T)/QZVPP basis using Dalton30 level to benchmark the interaction energies. The Dalton program was used to calculate the CCSD(T) interaction energies, and it was verified that adding more vectors had no impact on the target system. 80 random orientations were created for the hydrogen chloride dimer, and each conformation of the dimer was scanned along the intermolecular distance between 3.3 and 12.0 (with substantially more sampling near the equilibrium distance). As a result, all 80 relative orientations were considered over a total of 22 distances. The interaction energy was computed at CCSD(T)/QZVPP around 1851. To produce 3-center force fields, suitable potentials were fitted to the energies acquired CCSD(T) level. The energies were all considered throughout the fitting process rather than being averaged across the orientations.
In summary, the goal of this work is to offer analytical HCl–HCl interaction potentials based on various potentials and charge schemes. To achieve this, we employed CCSD(T)/QZVPP calculations. The specifics of the theoretical methods will be described in Section 2. The force field will be covered in Section 3. In Section 4, the second virial coefficient will be discussed while the conclusion will be discussed in Section 5.
2. Theoretical methods
To construct a potential energy surface, it is common to break it down into distinct contributions, such as electrostatic and non-electrostatic forces. For the (HCl)2 potential energy surface, the coulombic interactions between the charged particles in the molecules contribute to the electrostatic forces, while van der Waals forces between the neutral particles contribute to the non-electrostatic forces. By assuming separability, these two contributions can be treated independently of each other, and the total potential energy can be expressed as the sum of the electrostatic and non-electrostatic contributions. This assumption simplifies the construction of the potential energy surface and enables easier handling of the separate contributions. Additionally, assuming that both parts of the potential energy surface can be represented as sums over centers in the A and B molecules allows for the calculation of potential energy contributions by summing the contributions from each atom or center in both molecules. This approach provides a relatively straightforward and computationally efficient description of the interactions between the two molecules. However, it is important to acknowledge that these assumptions may not apply to all molecular systems, and more advanced methods may be necessary in certain scenarios.
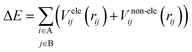 | (1) |
There are different ways to describe the resulting interactions between molecules, which can include coulombic sums over assigned atomic charges, as well as interactions between dipoles, quadrupoles, and higher-order multipoles.
The coulombic34 sum is given by
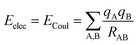 | (2) |
The potential energy surface can be divided into distinct contributions, such as electrostatic and non-electrostatic forces. Electrostatic forces arise from coulombic interactions between charged particles in the molecules, while non-electrostatic forces arise from van der Waals forces between neutral particles.
| Vtot(R) = Vnelec(R) + Velec(R) = VILJ(R) + VCoul(R) | (3) |
The ILJ27,28 potential is a model to describe the non-electrostatic portion of the potential energy surface in molecular simulations. Typically, the non-electrostatic interactions in molecular simulations are attributed to van der Waals forces resulting from fluctuations in the electron cloud surrounding the atoms and molecules.
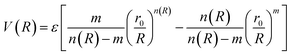 | (4) |
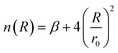 | (5) |
We have also a second virial coefficient (B2) from the Gauss–Legendre quadrature (using Gaussian 09)35 equation which is given by
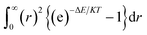 | (6) |
The integration interval (0 to infinity) is transformed into a finite interval, using the substitution 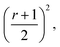 which maps the interval [0, ∞] to the interval [−1, 1]. The integral then becomes:
which maps the interval [0, ∞] to the interval [−1, 1]. The integral then becomes:
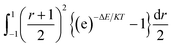 | (7) |
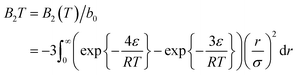
The second virial coefficient is given by substituting Lennard-Jones parameters to the second virial coefficient function potential,
 | (8) |
This equation relates the second virial coefficient to the temperature and the parameters of the Lennard-Jones potential (ε and σ). It is often used in the study of intermolecular interactions in gases and liquids.
The CUHRE (CUBA Library) algorithm37 was utilized to approximate the definite integral of a function over a specified interval. It is a numerical integration method that excels in handling high-dimensional integrals, which can be computationally expensive and inefficient for traditional numerical integration methods. The name “CUHRE” stands for “Cubature on Highly Uniform Random Evaluations”.
3. Force field
The HCl–HCl force field describes the interactions between hydrogen chloride (HCl) molecules, which play a crucial role in understanding their behavior in various environments.7,38 The improved Lennard-Jones (ILJ)27,28 potential is a mathematical model used to represent the intermolecular forces between molecules. It is an enhanced version of the classical Lennard-Jones potential, incorporating additional flexibility39 through a dimensionless parameter β. In the case of HCl–HCl interactions, the ILJ potential accounts for the size and shape of the HCl molecule. The size and shape determine how closely two HCl molecules can approach each other. The ILJ potential consists of two main components: the attractive component and the repulsive component. The attractive component arises from temporary fluctuations in the electron distribution of the HCl molecule,40 leading to the formation of induced dipoles. These induced dipoles generate attractive forces between HCl molecules,41 allowing them to come closer together. On the other hand, the repulsive component42 of the ILJ potential is due to the overlapping electron clouds of the two HCl molecules. As the molecules get too close, the repulsive forces become dominant, preventing them from approaching further. The ILJ potential introduces an additional dimensionless parameter β to add flexibility to the model. This parameter allows for adjustments to the shape of the potential energy curve, providing a more accurate representation of the HCl–HCl interactions. By varying the value of β, we can explore different scenarios and tailor the potential to reproduce experimental observations. The value of β influences the overall shape of the potential energy curve, affecting the balance between the attractive and repulsive forces.43 Higher values of β result in a steeper repulsive region and a narrower attractive well,44,45 while lower values of β lead to a shallower repulsive region and a wider attractive well.46,47 This flexibility in adjusting β helps fine-tune the potential to match experimental data. The HCl–HCl force field utilizing the ILJ potential, including the dimensionless parameter β, allows for the exploration of structural arrangements, dynamic processes, and thermodynamic properties of HCl molecules in diverse systems. By comparing the predictions of the force field with experimental observations, the accuracy of the model can be assessed and refined.Several methods, including Hirshfeld,49,50 CHELPG,51–53 Minimal Basis Set (MBS),52–54 Merz–Kollman,52,53,55 and Natural Bonding Orbital (NBO),56,57 which are commonly used to calculate atomic charges in molecular simulations, were employed during the optimization process.
In Table 1, βClCl the fitted value is 7.628, while the Hirshfeld value is 7.618. The fitted εClCl value is 0.381 kJ mol−1, slightly higher than the Hirshfeld value of 0.375 kJ mol−1. For the rClCl parameter, the fitted value is 3.215 Å, whereas the Hirshfeld value is slightly higher at 3.225 Å. Moving on to βHCl, the fitted value is 8.379, and the Hirshfeld value is 8.369. As for εHCl, the fitted value is 0.617 kJ mol−1, slightly surpassing the Hirshfeld value of 0.611 kJ mol−1. In terms of rHCl, the fitted value is 3.525 Å, while the Hirshfeld value is slightly lower at 3.515 Å. For βHH, the fitted value is 7.264, whereas the Hirshfeld value is 7.254. The fitted εHH value is 0.427 kJ mol−1, slightly higher than the Hirshfeld value of 0.421 kJ mol−1. Lastly, the fitted rHH value is 3.955 Å, while the Hirshfeld value is 3.961 Å.
| Parameters | Fitted | Hirshfeld | CHelpG | MBS | MK | NBO |
|---|---|---|---|---|---|---|
| qH (e−) | 0.424 | 0.190 | 0.212 | 0.332 | 0.209 | 0.243 |
| βClCl | 7.628 | 7.618 | 7.651 | 7.645 | 7.681 | 7.756 |
| εClCl (kJ mol−1) | 0.381 | 0.375 | 0.378 | 0.368 | 0.394 | 0.399 |
| rClCl (Å) | 3.215 | 3.225 | 3.231 | 3.247 | 3.235 | 3.265 |
| βHCl | 8.379 | 8.369 | 8.347 | 8.354 | 8.391 | 8.384 |
| εHCl (kJ mol−1) | 0.617 | 0.611 | 0.644 | 0.622 | 0.631 | 0.647 |
| rHCl (Å) | 3.525 | 3.515 | 3.575 | 3.569 | 3.545 | 3.583 |
| βHH | 7.264 | 7.254 | 7.249 | 7.271 | 7.221 | 7.235 |
| εHH (kJ mol−1) | 0.427 | 0.421 | 0.435 | 0.409 | 0.442 | 0.475 |
| rHH (Å) | 3.955 | 3.961 | 3.979 | 3.941 | 3.982 | 3.967 |
| r2 | 0.999 | 0.996 | 0.993 | 0.998 | 0.994 | 0.998 |
| MAE (kJ mol−1) | 0.372 | 0.891 | 0.299 | 0.582 | 0.852 | 0.876 |
Comparing the fitted values with the corresponding Hirshfeld or other charge values provides insight into the agreement between the values obtained from the fitting procedure and the Hirshfeld or other charges, which are derived from an ILJ method for calculating atomic charges.
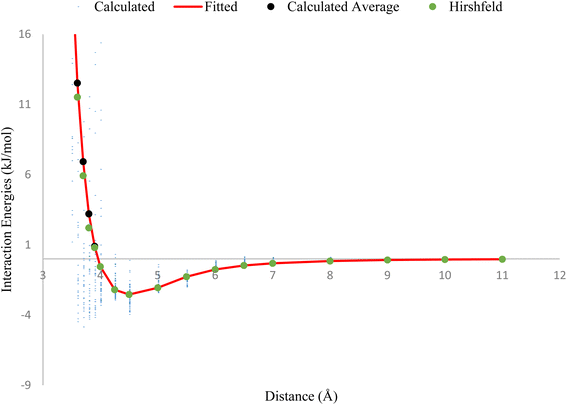
The plot in Fig. 1, compares the interaction energies of two HCl–HCl dimers at varying separation distances. The tiny blue points on the plot represent the interaction energies calculated using the CCSD(T)/QZVPP level of theory. The black points correspond to the average interaction energies utilizing the QZVPP method, while the green points represent the Hirshfeld method using the ILJ potential. The red line on the plot was fitted using the ILJ potential, meaning that the parameters in the ILJ potential were adjusted to closely match the calculated interaction energies from the QZVPP of theory. The plot shows that the optimized ILJ potential (red line) closely matches the calculated average interaction energies (black points), indicating that the ILJ potential is a reasonable model for describing the non-electrostatic interactions between HCl molecules.
During the fitting process, various properties of the HCl–HCl system are evaluated. These properties include interaction energies, and the Mean Absolute Error (MAE) represented in Fig. 2. The MAE is a statistical metric used to quantify the average absolute difference between the fitted values and the reference data. In the context of fitting the ILJ potential to the HCl–HCl system, the MAE is calculated by comparing various properties, such as interaction energies, obtained from the fitted potential to the reference values. A lower MAE indicates a better fit, as it reflects a smaller overall deviation between the fitted potential and the reference data. The process of fitting the ILJ potential to the HCl–HCl system involves evaluating the interaction energies, determining the charges using different methods, and quantifying the accuracy of the fitted potential using the Mean Absolute Error (MAE). These steps ensure that the fitted ILJ potential accurately captures the behavior of the HCl–HCl interaction and provides reliable predictions for various properties of the system.
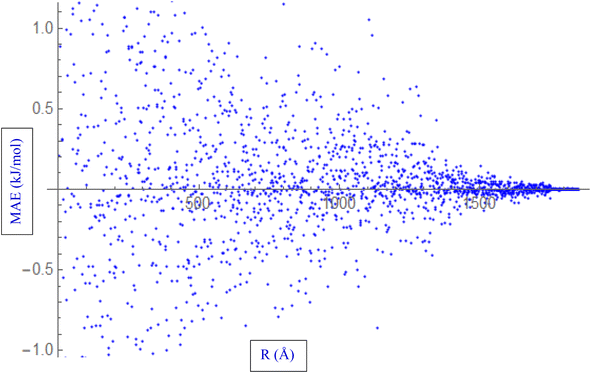 | ||
| Fig. 2 Fitting ILJ potential to the HCl–HCl system, including evaluation of interaction energies, distances, and MAE. | ||
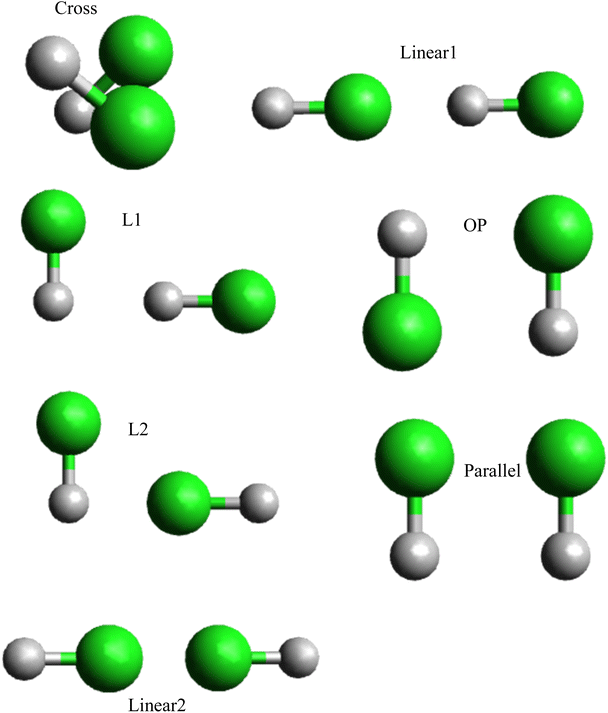
Various methods can be utilized to validate the properties of the hydrogen chloride–hydrogen chloride dimer, such as calculated structures, Morse fitting,48 and ILJ graphs, which offer valuable insights into its stability and behavior. In the previous section, analytical interaction potentials were developed for the interaction between two hydrogen chloride dimers. To assess the accuracy of the fitted potentials obtained from calculations, we employed relevant geometries of the HCl dimer molecule, which corresponded to seven distinct interaction conformations: L1, L2, Linear1, Linear2, P, OP, and Cross shape (Fig. 3). Energy profiles were calculated at the CCSD(T) level, which is a high-level ab initio method renowned for its precision in energy calculations, for each selected conformation. The CCSD(T)-optimized geometries were employed to compare the interaction energies obtained from the fitted potentials to the CCSD(T) energies for these same geometries. By comparing the predicted outcomes from the fitted potentials to the highly accurate results obtained from high-level ab initio calculations, we can evaluate the performance of the potential and refine its parameters, if needed. This method of benchmarking fitted potentials with high-level ab initio calculations is a prevalent approach in computational chemistry that enables the assessment of the accuracy and reliability of developed potentials.
In Table 2 among the different shapes of HCl–HCl, the most stable shape is L2,58 in both CCSD(T) and ILJ potential calculations, L2 exhibits the highest dissociation energy (De) values, reaching 6.253 kJ mol−1 for CCSD(T) and 6.245 kJ mol−1 for ILJ potential. Additionally, L2 also has the longest equilibrium distance (re) with values of 0.317 Å for CCSD(T) and 0.316 Å for ILJ potential. The combination of the highest De values and the relatively longer re indicates that L2 possesses stronger bonding between the HCl molecules, making it the most stable configuration among the considered shapes. OP shows moderate dissociation energy (De) values, measuring at 5.815 kJ mol−1 for CCSD(T) and 5.805 kJ mol−1 for ILJ potential. Its equilibrium distance (re) is also moderate, with values of 3.667 Å for CCSD(T) and 3.662 Å for ILJ potential. The combination of moderate De values and equilibrium distance places OP in a stable position between the most and least stable shapes. The least stable shape is Linear2, which exhibits the lowest dissociation energy (De) values among all shapes, measuring at 1.296 kJ mol−1 for CCSD(T) and 1.291 kJ mol−1 for ILJ potential. Additionally, Linear2 has the shortest equilibrium distance (re) with values of 5.124 Å for CCSD(T) and 5.115 Å for ILJ potential. The low De values and the relatively shorter re indicate that Linear2 experiences weaker bonding between the HCl molecules, leading to its position as the least stable shape.
| Shapes | Parameters | CCSD(T) | ILJ potential |
|---|---|---|---|
| Linear1 | De (kJ mol−1) | 0.531 | 0.525 |
| re (Å) | 4.391 | 4.382 | |
| Linear2 | De (kJ mol−1) | 1.296 | 1.291 |
| re (Å) | 5.124 | 5.115 | |
| OP | De (kJ mol−1) | 5.815 | 5.805 |
| re (Å) | 3.667 | 3.662 | |
| Cross | De (kJ mol−1) | 0.426 | 0.423 |
| re (Å) | 4.436 | 4.425 | |
| Parallel | De (kJ mol−1) | 0.867 | 0.864 |
| re (Å) | 3.128 | 3.125 | |
| L2 | De (kJ mol−1) | 6.253 | 6.245 |
| re (Å) | 0.317 | 0.316 | |
| L1 | De (kJ mol−1) | 5.941 | 5.937 |
| re (Å) | 0.375 | 0.368 |
There are two primary methods to establish the parameters for the ILJ potential function. The first involves fitting the function to ab initio calculations, while the second involves using semi-empirical expressions that relate the parameters to experimentally measurable quantities such as polarizabilities and C6 coefficients.59
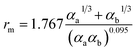 | (9) |
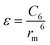 | (10) |
The significance of higher-order terms, such as C8 and C10 coefficients,60 increases as the distance between particles decreases, and they can substantially impact the shape of the intermolecular potential energy surface. Nevertheless, in traditional expansion, the C6 coefficient is the most critical term, as it represents the strength of the long-range dispersion forces. The equation can be expressed as:
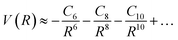 | (11) |
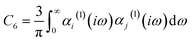 | (12) |
The C6 coefficient can be expressed in terms of the dynamic polarizability of the individual atoms or molecules and the separation distance between them, as outlined by the Casimir–Polder integral.61 The calculated polarizabilities are dependent on the accuracy of the data utilized to determine the Cauchy-like dispersion coefficients,62 as well as the validity of the assumptions underlying the Lorentz–Lorenz equation.63
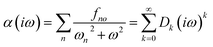 | (13) |
The accuracy of the estimated polarizability depends on the accuracy of the static polarizability calculation and the order of the Padé approximants [n,m]αc64 used.
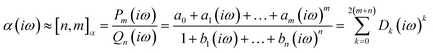 | (14) |
It can be proven that
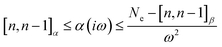 | (15) |
The auxiliary function β65 plays a crucial role in producing Padé approximants, which are valuable for approximating complex functions and lowering the computational cost of function evaluations.
| β(iω) = Ne − ω2α(iω) ≥ [n,n − 1]β | (16) |
A different approach, known as the single-center (one-center) approach, has also been utilized. In this method, the electrostatic portion is described by the interaction between two linear quadrupoles.66
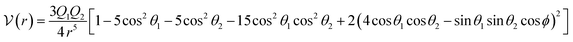 | (17) |
In Table 3, the experimental value of the polarizability (α0) for HCl is 2.515 Å3.67 Among the calculated values, CC3 yields a polarizability value of 2.517 Å3. The percentage difference between the experimental and calculated values for CC3 is only −0.08%. This small difference indicates that the calculated value using CC3 is very close to the experimental value, suggesting good agreement. The experimental value of the quadrupole moment (Q) for HCl is 3.843 DÅ.68 The calculated value using CC3 is 3.842 DÅ, resulting in a percentage difference of −0.89%. Again, this small difference indicates good agreement between the experimental and calculated values obtained using CC3. The agreement obtained with CC3 calculations is sufficient for modeling the single center potential of HCl. This implies that the CC3 method captures the essential features and accurately represents the behavior of HCl based on the provided parameters, making it a suitable approach for studying HCl's properties and potential interactions in theoretical and computational investigations.
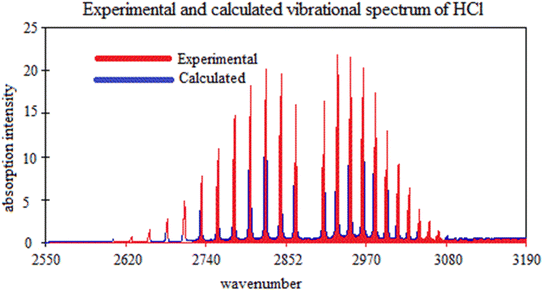
In Table 4, the calculated fundamental frequency at the def2-qzvpp level is slightly lower (by 2 cm−1) compared to the experimental value.69 This small difference indicates a relatively good agreement between the experimental and calculated values. It suggests that the def2-qzvpp level of calculation captures the fundamental frequency of the molecule with reasonable accuracy as shown in Fig. 4. The close agreement between the experimental and calculated fundamental frequencies indicates that the def2-qzvpp level of calculation provides a reasonably accurate estimation of the vibrational behavior of the HCl molecule.
| Experimental fundamental79 | 2886 cm−1 |
| Calculated (def2-qzvpp) | 2884 cm−1 |
4. Second virial coefficient B
The second virial coefficient (B) represents the average pairwise interactions between HCl molecules.70,71 It captures the effects of both the attractive forces, which are typically dominated by the dipole–dipole interactions, and the repulsive forces arising from the overlapping electron clouds of the molecules.72 The value of the second virial coefficient (B) provides information about the strength and nature of intermolecular interactions in HCl gas.73 If the value of B is positive, it suggests that the attractive forces dominate over the repulsive forces, leading to an increased likelihood of molecular association and a gas with a larger effective volume.74 On the other hand, a negative value of B indicates that the repulsive forces are dominant, resulting in a compressed gas with a smaller effective volume.75The second virial coefficient (B) is often temperature-dependent, with its value decreasing as temperature increases.76 This is due to the weakening of intermolecular interactions at higher temperatures. Experimental measurements and theoretical calculations can be used to determine the second virial coefficient for HCl gas across a range of temperatures.77 These values are valuable for characterizing the behavior of HCl gas and can be utilized in equations of state and thermodynamic models to predict properties such as vapor–liquid equilibria and mixture behavior. Selected data from the literature have been fitted by least squares to the equation,
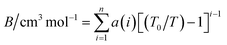 | (18) |
| T/K | Experimentala (B, cm3 mol−1) | Fitted (B, cm3 mol−1) | CHelpG (B, cm3 mol−1) | Hirshfeld (B, cm3 mol−1) | MBS (B, cm3 mol−1) | MK (B, cm3 mol−1) | NBO (B, cm3 mol−1) |
|---|---|---|---|---|---|---|---|
| a Ref. 78 and 79. | |||||||
| 190 | −450.094 | −453.254 | −427.589 | −445.893 | −461.571 | −446.093 | −455.145 |
| 210 | −341.804 | −344.865 | −324.713 | −336.603 | −353.281 | −338.803 | −346.915 |
| 230 | −269.041 | −272.652 | −255.588 | −263.841 | −280.517 | −266.041 | −274.329 |
| 270 | −181.088 | −184.047 | −172.033 | −175.887 | −192.564 | −178.087 | −186.071 |
| 310 | −131.972 | −134.271 | −125.373 | −126.772 | −143.449 | −129.971 | −136.158 |
| 350 | −101.38 | −104.659 | −96.311 | −96.179 | −112.857 | −98.379 | −106.652 |
| 390 | −80.6018 | −83.674 | −76.5716 | −75.401 | −92.079 | −77.601 | −85.679 |
| 430 | −65.4887 | −68.017 | −62.2142 | −60.288 | −76.966 | −62.4886 | −70.462 |
| 470 | −53.89 | −56.264 | −51.195 | −48.691 | −65.367 | −50.8921 | −58.368 |
At T = 190 K, the experimental value of the second virial coefficient (B) is −450.094 cm3 mol−1, while the fitted value is −453.254 cm3 mol−1. For T = 210 K, the experimental value of B is −341.804 cm3 mol−1, and the fitted value is −344.865 cm3 mol−1. At T = 230 K, the experimental value of B is −269.041 cm3 mol−1, and the fitted value is −272.652 cm3 mol−1. For T = 270 K, the experimental value of B is −181.088 cm3 mol−1, while the fitted value is −184.047 cm3 mol−1. At T = 310 K, the experimental value of B is −131.972 cm3 mol−1, and the fitted value is −134.271 cm3 mol−1. For T = 350 K, the experimental value of B is −101.38 cm3 mol−1, while the fitted value is −104.659 cm3 mol−1. At T = 390 K, the experimental value of B is −80.6018 cm3 mol−1, and the fitted value is −83.674 cm3 mol−1. For T = 430 K, the experimental value of B is −65.4887 cm3 mol−1, and the fitted value is −68.017 cm3 mol−1. At T = 470 K, the experimental value of B is −53.89 cm3 mol−1, while the fitted value is −56.264 cm3 mol−1.
Comparing the experimental values of the second virial coefficient (B) with the corresponding fitted values at each temperature provides insight into the accuracy of the fitting procedure. It allows for an assessment of how well the fitted values capture the experimental observations and indicates the degree of agreement between the two sets of values for the charges.
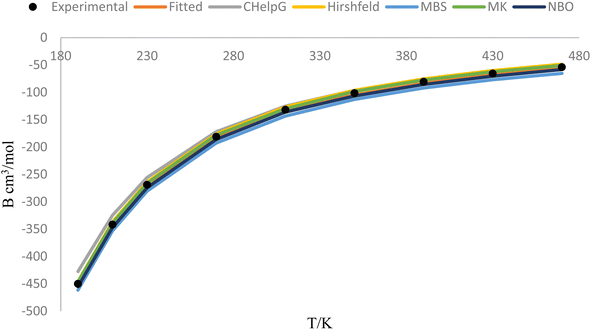
Fig. 5 represents the behavior of the second virial coefficient (B) for hydrogen chloride gas at different temperatures (ranging from 190 K to 470 K). The solid lines in the figure show the behavior of B as a function of temperature, considering the adjusted improved Lennard-Jones (ILJ) parameters and different charge schemes. The fitted line represents the values of B obtained through the fitting procedure, where the ILJ parameters have been adjusted to best match the experimental data. This line represents the model's prediction for the behavior of B across the temperature range. The lines corresponding to different charge schemes, such as CHelpG, Hirshfeld, MBS, MK, and NBO, represent the behavior of B using those specific charge distribution methods. These lines show how the choice of charge scheme affects the predicted behavior of B. The black dots on the figure represent the experimental values of B at each temperature point. These experimental values serve as reference points and are obtained through measurements or calculations based on experimental data. The closeness of the fitted line and the charge scheme lines to the black dots indicates the degree of agreement between the model's predictions and the experimental observations. By comparing the fitted line and the different charge scheme lines with the experimental data represented by the black dots, we can assess the accuracy of the model and the effectiveness of the different charge schemes in reproducing the experimental behavior of B.
Fig. 5 provides a visual representation of the comparison between the calculated and experimental values of B for hydrogen chloride gas. It demonstrates the behavior of B with temperature, showing how the ILJ parameters and different charge schemes impact the predicted values.
In Table 6, the calculated entropy value of 186.736 J K−1 mol−1 obtained using the def2-qzvpp calculations is compared to the experimental entropy value of 186.902 J K−1 mol−1 at a temperature of 298.15 K. The small difference between the experimental and calculated values suggests that the def2-qzvpp calculations provide a reasonable estimation of the entropy at the given temperature of HCl.
| Temperature | Experimental80 | Calculated | |
|---|---|---|---|
| Entropy | 298.15 K | 186.902 (J K−1 mol−1) | 186.736 (J K−1 mol−1) |
5. Conclusion
Using QZVPP calculations, energy fitting, conformation validation, and the determination of the second virial coefficient B utilizing improved Lennard-Jones (ILJ) potential parameters, this research concludes with a comprehensive analysis of HCl–HCl interactions. Initial QZVPP calculations on a vast number of arbitrarily generated HCl–HCl conformations allowed for the acquisition of precise interaction energies. Then, these energies were used to fit an improved Lennard-Jones potential energy surface, resulting in an accurate description of HCl–HCl interactions. The substantiation of particular HCl dimer conformations using the ILJ potential parameters further ensured their stability and concordance with experimental findings. The observed correlation between calculated and experimental conformations further validates the ILJ potential parameters. In addition, the calculation of the second virial coefficient B at different temperatures using the ILJ potential was in close agreement with experimental data. This result validates the ability of the ILJ potential to precisely represent the intermolecular interactions and gas-phase behavior of the HCl–HCl system. The results of this study demonstrate the efficient application of QZVPP calculations, energy fitting, and ILJ potential parameters for validating HCl–HCl conformations and accurately determining the second virial coefficient B. The high degree of agreement between calculated B values and experimental data validates the ILJ potential and demonstrates its suitability for modeling HCl–HCl interactions. This investigation contributes to a greater comprehension of HCl–HCl interactions and their significance in a variety of chemical and atmospheric processes. The validated conformations, energy fitting method, and calculated second virial coefficients serve as valuable research instruments and pave the way for more accurate modeling and simulations of HCl–HCl systems. These developments have the potential to enhance our comprehension of HCl–HCl interactions and their effect on related phenomena.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Researchers Supporting Project number (RSPD2024R812), King Saud University, Riyadh, Saudi Arabia for funding this work.References
- Y. Ma, J. Zhang, K. Huang and L. Jiang, Highly efficient and selective separation of ammonia by deep eutectic solvents through cooperative acid-base and strong hydrogen-bond interaction, J. Mol. Liq., 2021, 337, 116463 CrossRef CAS.
- N. Balakrishnan, On the role of van der Waals interaction in chemical reactions at low temperatures, J. Chem. Phys., 2004, 121(12), 5563–5566 CrossRef CAS PubMed.
- I. Khan, P. Panini, S. U.-D. Khan, U. A. Rana, H. Andleeb, D. Chopra, S. Hameed and J. Simpson, Exploiting the role of molecular electrostatic potential, deformation density, topology, and energetics in the characterization of S··· N and Cl··· N supramolecular motifs in crystalline triazolothiadiazoles, Cryst. Growth Des., 2016, 16(3), 1371–1386 CrossRef CAS.
- H. Yamamoto and K. Futatsugi, “Designer Acids” Combined Acid Catalysis for Asymmetric Synthesis, Angew. Chem., Int. Ed., 2005, 44(13), 1924–1942 CrossRef CAS.
- N. O. Eddy, H. Momoh-Yahaya and E. E. Oguzie, Theoretical and experimental studies on the corrosion inhibition potentials of some purines for aluminum in 0.1 M HCl, J. Adv. Res., 2015, 6(2), 203–217 CrossRef CAS PubMed.
- M. Oubaaqa, M. Ouakki, M. Rbaa, A. S. Abousalem, M. Maatallah, F. Benhiba, A. Jarid, M. E. Touhami and A. Zarrouk, Insight into the corrosion inhibition of new amino-acids as efficient inhibitors for mild steel in HCl solution: experimental studies and theoretical calculations, J. Mol. Liq., 2021, 334, 116520 CrossRef CAS.
- M. Svanberg, J. B. C. Pettersson and K. Bolton, Coupled QM/MM molecular dynamics simulations of HCl interacting with ice surfaces and water clusters− Evidence of rapid ionization, J. Phys. Chem. A, 2000, 104(24), 5787–5798 CrossRef CAS.
- C. Toubin, S. Picaud, P. N. M. Hoang, C. Girardet, B. Demirdjian, D. Ferry and J. Suzanne, Structure and dynamics of ice Ih films upon HCl adsorption between 190 and 270 K. II. Molecular dynamics simulations, J. Chem. Phys., 2002, 116(12), 5150 CrossRef CAS.
- M. J. Elrod and R. J. Saykally, Determination of the intermolecular potential energy surface for (HCl)2 from vibration–rotation–tunneling spectra, J. Chem. Phys., 1995, 103(3), 933–949 CrossRef CAS PubMed.
- V. Buch, J. Sadlej, N. Aytemiz-Uras and J. P. Devlin, Solvation and Ionization Stages of HCl on Ice Nanocrystals, J. Phys. Chem. A, 2002, 106(41), 9374–9389 CrossRef.
- Y. Liu, J. Li, P. M. Felker and Z. Bačić, HCl–H 2 O dimer: an accurate full-dimensional potential energy surface and fully coupled quantum calculations of intra-and intermolecular vibrational states and frequency shifts, Phys. Chem. Chem. Phys., 2021, 23(12), 7101–7114 RSC.
- F. Tao and W. Klemperer, Ab initio potential energy surface for the HCl dimer, J. Chem. Phys., 1995, 103(3), 950–956 CrossRef CAS.
- Q. Zeng, S. Yu, D. Li, A. R. Oganov and G. Frapper, Emergence of novel hydrogen chlorides under high pressure, Phys. Chem. Chem. Phys., 2017, 19(12), 8236–8242 RSC.
- J. S. Mancini, A. K. Samanta, J. M. Bowman and H. Reisler, Experiment and Theory Elucidate the Multichannel Predissociation Dynamics of the HCl Trimer: Breaking Up Is Hard to Do, J. Phys. Chem. A, 2014, 118(37), 8402–8410 CrossRef CAS.
- A. D. Buckingham, P. W. Fowler and J. M. Hutson, Theoretical studies of van der Waals molecules and intermolecular forces, Chem. Rev., 1988, 88(6), 963–988 CrossRef CAS.
- M. A. Spackman, A simple quantitative model of hydrogen bonding, J. Chem. Phys., 1986, 85(11), 6587–6601 CrossRef CAS.
- F. O. Kannemann and A. D. Becke, van der Waals Interactions in Density-Functional Theory: Intermolecular Complexes, J. Chem. Theory Comput., 2010, 6(4), 1081–1088 CrossRef CAS.
- J. P. Wagner and P. R. Schreiner, London Dispersion in Molecular Chemistry-Reconsidering Steric Effects, Angew. Chem., Int. Ed., 2015, 54(42), 12274–12296 CrossRef CAS PubMed.
- K. Pernal, R. Podeszwa, K. Patkowski and K. Szalewicz, Dispersionless Density Functional Theory, Phys. Rev. Lett., 2009, 103(26), 263201 CrossRef PubMed.
- J. Bae, Formation of ZnO Nanocones Using Wet Chemical Etching of ZnO Nanorods in an Aqueous Solution of HCl, J. Nanosci. Nanotechnol., 2009, 9(12), 7398–7401 CrossRef CAS PubMed.
- M. W. Cole, D. Velegol, H.-Y. Kim and A. A. Lucas, Nanoscale van der Waals interactions, Mol. Simul., 2009, 35(10–11), 849–866 CrossRef CAS.
- A. K. Samanta, G. Czakó, Y. Wang, J. S. Mancini, J. M. Bowman and H. Reisler, Experimental and Theoretical Investigations of Energy Transfer and Hydrogen-Bond Breaking in Small Water and HCl Clusters, Acc. Chem. Res., 2014, 47(8), 2700–2709 CrossRef CAS PubMed.
- M. Fárník and D. J. Nesbitt, Intramolecular energy transfer between oriented chromophores: high-resolution infrared spectroscopy of HCl trimer, J. Chem. Phys., 2004, 121(24), 12386 CrossRef PubMed.
- A. K. Samanta, Y. Wang, J. S. Mancini, J. M. Bowman and H. Reisler, Energetics and Predissociation Dynamics of Small Water, HCl, and Mixed HCl–Water Clusters, Chem. Rev., 2016, 116(9), 4913–4936 CrossRef CAS PubMed.
- C.-D. Wu, T.-H. Fang, J.-Y. Lo and Y.-L. Feng, Molecular dynamics simulations of hydrogen storage capacity of few-layer graphene, J. Mol. Model., 2013, 19(9), 3813–3819 CrossRef CAS PubMed.
- E. Dundar, P. Boulet, C. Wexler, L. Firlej, P. Llewellyn and B. Kuchta, Heterogeneous melting of methane confined in nano-pores, J. Chem. Phys., 2016, 145(14), 144704 CrossRef CAS PubMed.
- F. Pirani, M. Albertí, A. Castro, M. Moix Teixidor and D. Cappelletti, Atom–bond pairwise additive representation for intermolecular potential energy surfaces, Chem. Phys. Lett., 2004, 394(1–3), 37–44 CrossRef CAS.
- F. Pirani, S. Brizi, L. F. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Beyond the Lennard-Jones model: a simple and accurate potential function probed by high resolution scattering data useful for molecular dynamics simulations, Phys. Chem. Chem. Phys., 2008, 10(36), 5489 RSC.
- A. Lombardi and F. Palazzetti, A comparison of interatomic potentials for rare gas nanoaggregates, J. Mol. Struct.: THEOCHEM, 2008, 852(1–3), 22–29 CrossRef CAS.
- M. Albertí, A. Aguilar, J. M. Lucas and F. Pirani, Competitive Role of CH4–CH4 and CH− π Interactions in C6H6–(CH4) n Aggregates: The Transition from Dimer to Cluster Features, J. Phys. Chem. A, 2012, 116(22), 5480–5490 CrossRef PubMed.
- M. K. Rana, H. S. Koh, H. Zuberi and D. J. Siegel, Methane Storage in Metal-Substituted Metal–Organic Frameworks: Thermodynamics, Useable Capacity, and the Impact of Enhanced Binding Sites, J. Phys. Chem. C, 2014, 118(6), 2929–2942 CrossRef CAS.
- A. D. Becke, Perspective: fifty years of density-functional theory in chemical physics, J. Chem. Phys., 2014, 140(18), 18A301 CrossRef PubMed.
- W. J. Hehre, R. Ditchfield and J. A. Pople, Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56(5), 2257–2261 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396 CrossRef CAS PubMed.
- S. Gagui, H. Bendjeddou, H. Meradji, B. Chouial, B. Hadjoudja, S. Ghemid, R. Khenata, A. K. Kushwaha, D. P. Rai and S. B. Omran, Phase stability and optoelectronic characteristics of Ba 1− x Be x S: a DFT-based simulation, J. Mol. Model., 2020, 26, 1–21 CrossRef.
- V. J. Menon and D. C. Agrawal, Comment on ‘The Stefan-Boltzmann constant in n-dimensional space’, J. Phys. A: Math. Gen., 1998, 31(3), 1109–1110 CrossRef.
- T. Hahn, Cuba—a library for multidimensional numerical integration, Comput. Phys. Commun., 2005, 168(2), 78–95 CrossRef CAS.
- C. Girardet and C. Toubin, Molecular atmospheric pollutant adsorption on ice: a theoretical survey, Surf. Sci. Rep., 2001, 44(7–8), 159–238 CrossRef CAS.
- E. Garcia, A. Laganà, F. Pirani, M. Bartolomei, M. Cacciatore and A. Kurnosov, Enhanced flexibility of the O2+ N2 interaction and its effect on collisional vibrational energy exchange, J. Phys. Chem. A, 2016, 120(27), 5208–5219 CrossRef CAS PubMed.
- R. Huber, S. Spörlein, J. E. Moser, M. Grätzel and J. Wachtveitl, The Role of Surface States in the Ultrafast Photoinduced Electron Transfer from Sensitizing Dye Molecules to Semiconductor Colloids, J. Phys. Chem. B, 2000, 104(38), 8995–9003 CrossRef CAS.
- D. T. Anderson, R. J. Hinde, S. Tam and M. E. Fajardo, High-resolution spectroscopy of HCl and DCl isolated in solid parahydrogen: direct, induced, and cooperative infrared transitions in a molecular quantum solid, J. Chem. Phys., 2002, 116(2), 594–607 CrossRef CAS.
- S. Falcinelli, F. Pirani, P. Candori, B. G. Brunetti, J. M. Farrar and F. Vecchiocattivi, A New Insight on Stereo-Dynamics of Penning Ionization Reactions, Front. Chem., 2019, 7, 445 CrossRef CAS PubMed.
- M. Reguzzoni, A. Fasolino, E. Molinari and M. C. Righi, Potential energy surface for graphene on graphene: Ab initio derivation, analytical description, and microscopic interpretation, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(24), 245434 CrossRef.
- A. L. Frischknecht, Forces between nanorods with end-adsorbed chains in a homopolymer melt, J. Chem. Phys., 2008, 128(22), 224902 CrossRef PubMed.
- W. Chen, S. Tan, Z. Huang, T.-K. Ng, W. T. Ford and P. Tong, Measured long-ranged attractive interaction between charged polystyrene latex spheres at a water-air interface, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74(2), 021406 CrossRef PubMed.
- A. Kirchner and A. Schadschneider, Simulation of evacuation processes using a bionics-inspired cellular automaton model for pedestrian dynamics, Phys. A, 2002, 312(1–2), 260–276 CrossRef.
- T. D. Kühner, S. R. White and H. Monien, One-dimensional Bose-Hubbard model with nearest-neighbor interaction, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61(18), 12474–12489 CrossRef.
- D. W. Jacobson and G. B. Thompson, Revisting Lennard Jones, Morse, and NM potentials for metals, Comput. Mater. Sci., 2022, 205, 111206 CrossRef CAS.
- T. Lu and F. Chen, Atomic Dipole Moment Corrected Hirshfeld Population Method, J. Theor. Comput. Chem., 2012, 11(1), 163–183 CrossRef CAS.
- S. Van Damme, P. Bultinck and S. Fias, Electrostatic Potentials from Self-Consistent Hirshfeld Atomic Charges, J. Chem. Theory Comput., 2009, 5(2), 334–340 CrossRef CAS PubMed.
- K. B. Wiberg and P. R. Rablen, Comparison of atomic charges derived via different procedures, J. Comput. Chem., 1993, 14(12), 1504–1518 CrossRef CAS.
- K. B. Wiberg and P. R. Rablen, Atomic charges, J. Org. Chem., 2018, 83(24), 15463–15469 CrossRef CAS PubMed.
- D. Jacquemin, T. L. Bahers, C. Adamo and I. Ciofini, What is the “best” atomic charge model to describe through-space charge-transfer excitations?, Phys. Chem. Chem. Phys., 2012, 14(16), 5383 RSC.
- B. Wang, S. L. Li and D. G. Truhlar, Modeling the Partial Atomic Charges in Inorganometallic Molecules and Solids and Charge Redistribution in Lithium-Ion Cathodes, J. Chem. Theory Comput., 2014, 10(12), 5640–5650 CrossRef CAS PubMed.
- Z. Jiroušková, R. S. Vařeková, J. Vaněk and J. Koča, Software news and updates electronegativity equalization method: parameterization and validation for organic molecules using the Merz-Kollman-Singh charge distribution scheme, J. Comput. Chem., 2009, 30(7), 1174–1178 CrossRef PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, NBO 6.0: natural bond orbital analysis program, J. Comput. Chem., 2013, 34(16), 1429–1437 CrossRef CAS PubMed.
- F. Weinhold, Natural bond orbital analysis: a critical overview of relationships to alternative bonding perspectives, J. Comput. Chem., 2012, 33(30), 2363–2379 CrossRef CAS PubMed.
- Q. Zeng, S. Yu, D. Li, A. R. Oganov and G. Frapper, Emergence of novel hydrogen chlorides under high pressure, Phys. Chem. Chem. Phys., 2017, 19(12), 8236–8242 RSC.
- F. Ortmann, F. Bechstedt and W. G. Schmidt, Semiempirical van der Waals correction to the density functional description of solids and molecular structures, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(20), 205101 CrossRef.
- G. Starkschall and R. G. Gordon, Calculation of Coefficients in the Power Series Expansion of the Long-Range Dispersion Force between Atoms, J. Chem. Phys., 1972, 56(6), 2801–2806 CrossRef CAS.
- E. A. Power and T. Thirunamachandran, Casimir-Polder potential as an interaction between induced dipoles, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 48(6), 4761 CrossRef CAS PubMed.
- J.-K. Krüger, J. Baller, T. Britz, A. Le Coutre, R. Peter, R. Bactavatchalou and J. Schreiber, Cauchy-like relation between elastic constants in amorphous materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(1), 12206 CrossRef.
- K. E. Oughstun and N. A. Cartwright, On the Lorentz-Lorenz formula and the Lorentz model of dielectric dispersion, Opt. Express, 2003, 11(13), 1541–1546 CrossRef PubMed.
- G. A. Baker Jr and J. L. Gammel, The padé approximant, J. Math. Anal. Appl., 1961, 2(1), 21–30 CrossRef.
- C. Byrne, Auxiliary-function minimization algorithms, Appl. Anal. Optim., 2018, 2(2), 171–198 Search PubMed.
- P. A. Kralchevsky, N. D. Denkov and K. D. Danov, Particles with an undulated contact line at a fluid interface: interaction between capillary quadrupoles and rheology of particulate monolayers, Langmuir, 2001, 17(24), 7694–7705 CrossRef CAS.
- K. J. Miller, Additivity methods in molecular polarizability, J. Am. Chem. Soc., 1990, 112(23), 8533–8542 CrossRef CAS.
- F. H. De Leluw and A. Dymanus, Magnetic properties and molecular quadrupole moment of HF and HCl by molecular-beam electric-resonance spectroscopy, J. Mol. Spectrosc., 1973, 48(3), 427–445 CrossRef.
- K. P. Huber, Molecular Spectra and Molecular Structure: IV. Constants of Diatomic Molecules, Springer Science & Business Media, 2013 Search PubMed.
- H. A. Larsen, W. M. Atkins and A. Nath, Probing interactions of therapeutic antibodies with serum via second virial coefficient measurements, Biophys. J., 2021, 120(18), 4067–4078 CrossRef CAS PubMed.
- A. Quigley and D. R. Williams, Similar interaction chromatography of proteins: a cross interaction chromatographic approach to estimate the osmotic second virial coefficient, J. Chromatogr. A, 2016, 1459, 47–56 CrossRef CAS PubMed.
- K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Nanoscale Forces and Their Uses in Self-Assembly, Small, 2009, 5(14), 1600–1630 CrossRef CAS PubMed.
- J. A. Pathak, S. Nugent, M. F. Bender, C. J. Roberts, R. J. Curtis and J. F. Douglas, Comparison of Huggins coefficients and osmotic second virial coefficients of buffered solutions of monoclonal antibodies, Polymers, 2021, 13(4), 601 CrossRef CAS PubMed.
- S. Saito, J. Hasegawa, N. Kobayashi, N. Kishi, S. Uchiyama and K. Fukui, Behavior of monoclonal antibodies: relation between the second virial coefficient (B 2) at low concentrations and aggregation propensity and viscosity at high concentrations, Pharm. Res., 2012, 29, 397–410 CrossRef CAS PubMed.
- C. L. Cheung, A. I. Rubinstein, E. J. Peterson, A. Chatterji, R. F. Sabirianov, W.-N. Mei and J. J. DeYoreo, Steric and Electrostatic Complementarity in the Assembly of Two-Dimensional Virus Arrays, Langmuir, 2010, 26(5), 3498–3505 CrossRef CAS PubMed.
- R. Hellmann, Reference Values for the Second Virial Coefficient and Three Dilute Gas Transport Properties of Ethane from a State-of-the-Art Intermolecular Potential Energy Surface, J. Chem. Eng. Data, 2018, 63(2), 470–481 CrossRef CAS.
- C. Wormald, Water–hydrogen chloride association. Second virial cross coefficients for water–hydrogen chloride from gas phase excess enthalpy measurements, J. Chem. Therm., 2003, 35(3), 417–431 CrossRef CAS.
- J. H. Dymond and E. B. Smith, The virial coefficients of pure gases and mixtures: a critical compilation, Oxford University Press, Oxford, 1980 Search PubMed.
- J. P. O'Connell, The virial coefficients of pure gases and mixtures. A critical compilation (Dymond, J.H.; Smith, E.B.), J. Chem. Educ., 1981, 58(8), A246 CrossRef.
- J. D. Cox, D. D. Wagman and V. A. Medvedev, CODATA Key Values for Thermodynamics, Hemisphere, New York, 1989 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |