Open Access Article
Open Access ArticleEnhancement in the dielectric and magnetic properties of Ni2+–Cu2+ co-doped BaFe11Cu1−xNixO19 hexaferrites (0.0 ≤ x ≤ 1.0)
M. Atif *a,
H. Ul Husnaina,
Atta Ur Rehman
*a,
H. Ul Husnaina,
Atta Ur Rehman ab,
U. Younasa,
T. Rafiquea,
W. Khalida,
Z. Ali
ab,
U. Younasa,
T. Rafiquea,
W. Khalida,
Z. Ali a and
M. Nadeemc
a and
M. Nadeemc
aFunctional Materials Lab, Department of Physics, Air University, PAF Complex E-9, Islamabad, Pakistan. E-mail: matif@mail.au.edu.pk
bDepartment of Physics, The University of Hong Kong, Pokfulam, Hong Kong
cPolymer Composite Group, Physics Division, Directorate of Science, PINSTECH, P.O. Nilore, Islamabad, Pakistan
First published on 26th February 2024
Abstract
Herein, Ni2+–Cu2+ co-doped barium hexaferrites (BaFe11Cu1−xNixO19, 0.0 ≤ x≤ 1.0 with an interval of 0.25) were successfully synthesized using a co-precipitation method. The formation of a magnetoplumbite structure with the P63/mmc space group was confirmed by Rietveld refinement of the obtained X-ray diffraction patterns. Microstructural investigations revealed grains in the shape of hexagonal plates, while co-doping resulted in a variation in the grain sizes of the prepared samples. X-ray photoelectron spectroscopy was performed to determine the valence state of iron in the prepared hexaferrites. Impedance spectroscopy analysis revealed that dielectric permittivity initially decreased with an increase in the co-dopant content up to x = 0.5 and then increased by two orders of magnitude for x = 1.0. Alternatively, resistive properties showed microstructural resistance values in the range 105–108 Ω, with the highest value obtained for the sample with x = 0.5. Furthermore, magnetic measurements indicated that all the prepared samples exhibited ferrimagnetic behaviour. Saturation magnetization and magnetic anisotropy values were found to be the highest for the sample with x = 1.0, which also had the lowest coercivity among the prepared samples. Herein, the observed variations in the obtained results can be explained by the variations in grain sizes and the Fe2+/Fe3+ ratio associated with the preferential occupation of co-dopants at octahedral sites. Based on our findings, the BaFe11Ni1O19 (x = 1.0) composition appears to be the most promising choice as a microwave absorption material among the prepared samples owing to the coexistence of high dielectric permittivity (>103 at 107 Hz) and saturation magnetization (73 emu g−1).
1. Introduction
Presently, hexaferrites are one of the most extensively investigated materials because of their wide range of practical application in fields such as magnetic shielding, mobile communication, electronic devices, magnetic biosensors, magnetic recording devices, and stealth technologies.1,2 Generally, hexaferrites have a more complicated structure compared to spinel ferrites and orthoferrites and are a very important class of permanent magnets. Based on the chemical composition and crystalline structure of hexaferrites, they can be divided into six different types.3 Among them, M-type hexaferrites (MeO·6Fe2O3, where Me is Ba, Sr, or Pb) are the most significant type of hexaferrites owing to their remarkable properties, which include high coercivity, high permittivity, high permeability, and high values of isotropic constants as well as its chemical stability and high corrosion resistance.4 The crystal structure of an M-type hexaferrite is composed of a combination of R = Me2+Fe63+O112−, S = Fe63+O82−, R*, and S* blocks, where R* and S* are 180° inversion of the R and S block, respectively, along the hexagonal c-axis.3 One unit cell of M-type hexaferrites is made up of two molecules, and each molecule contains five layers of oxygen atoms. There is a total of 64 ions in each unit cell, including two heavy metal divalent cations, 38 oxygen ions, and 24 ferric ions. The presence of ferric (Fe3+) ions imparts magnetism to this type of hexaferrite. In each sub-lattice of M-type hexaferrites, there are a total of 12 ferric ions occupying five distinct interstitial sites, namely 12k, 4f2, 4f1, 2a, and 2b. Six of these 12 ferric ions occupy a 12k (octahedral) site with a positive spin. On 4f2 (octahedral) and 4f1 (tetrahedral) sites, there are two ferric ions with spin-down. On 2a (octahedral) and 2b (trigonal bipyramidal) sites with spin-up, there is one ferric ion.3 In total, eight of the twelve ferric ions have spin-up, while four have spin-down. This indicates that after balancing with four spin-down ferric ions, there are still four spin-up ferric ions.5 These four spin-up ferric ions contribute to the total magnetic moment of M-type hexaferrite. Iron (Fe) is a d-block element with five unpaired electrons in its outermost orbit, resulting in a magnetic moment of 5 µB for each ferric ion. Due to the presence of four spin-up ferric ions in each unit cell of hexaferrite, the net magnetic moment of each cell is 20 µB.6Among the M-type hexaferrite materials, barium hexaferrite (BaFe12O19) has attracted considerable interest from researchers due to its outstanding dielectric and magnetic properties, which make it useful as an electromagnetic wave absorber.7,8 When electromagnetic waves interact with microwave absorbers, the energy of the incident wave is absorbed by the absorbers. At the ferromagnetic resonance frequency, this energy absorption is at its maximum. The ideal choice for a microwave absorber is a material that can both absorb high-energy waves and respond quickly to incident radiation. Typically, the absorption of an incident waves by a material depends on its dielectric permittivity (ε′), saturation magnetization (Ms), and the magnitude of its response to an incident wave, which is defined by its coercivity (Hc). Thus, if a material has a high ε′ and Ms with a low Hc, it may act as a microwave absorber. Given that BaFe12O19 has a high values of ε′ and Ms but an equally strong Hc, it is inappropriate for use in microwave absorber applications. This problem can be solved by substituting transition metal cations for Ba2+ or Fe3+ ions in BaFe12O19, which reduces the Hc value of the material and improves its magnetic and microwave-absorbing properties.9 Manglam et al. explored the magnetic properties of Zn2+-doped BaFe12−xZnxO19 hexaferrites.10 They found that the maximum Ms and minimum Hc values were obtained for x = 0.2, which were described in terms of the lattice strain and super-exchange interaction, respectively. Behera et al. investigated the impact of Ni2+ doping on the magnetic and dielectric characteristics of BaFe12−xNixO19.11 According to them, the dielectric constant was found to increase with an increase in the Ni2+ doping content, while the values of Ms and Hc decreased with Ni2+ doping. Wang et al. reported the coexistence of remarkable improvements in the dielectric and magnetic characteristics of Ni2+-doped BaFe12−xNixO19 hexaferrites due to the presence of more Fe2+/Fe3+ pair dipoles and the preferential occupancy of Ni2+ ions at the 4f2 sites.12 Kumar et al. explored the effect on Cu2+ doping on the properties of BaFe12−xCuxO19 hexaferrites.13 According to them, a correlation was established between the structural parameters and magnetic/dielectric properties, and they found the maximum Ms, minimum Hc, and high dielectric constant for the x = 1.0 sample. To further improve the magnetic and microwave-absorbing properties of barium hexaferrites, co-doping of Ni2+ with a combination of some other divalent metal ions has been reported in the literature. Widyastuti et al. reported that the magnetic properties of barium hexaferrite can be significantly improved by doping Ni2+ and Zn2+ ions in place of Fe3+.14 They found that the highest Ms (95 emu g−1) and the lowest Hc (0.12 T) were obtained for x = 0.6 among the BaFe12−2xNixZnxO19 hexaferrites prepared at pH = 11 and sintered at 1050 °C. Moreover, Susilawati et al. found that the values of Ms and ε′ increased, while the Hc value decreased with an increase in the co-dopant contents in BaFe12−2xNixCoxO19 hexaferrites.15 However, the maximum reflection loss of −14.47 dB together with an absorption coefficient of 96.43% was achieved for the x = 1.0 sample. Hence, based on the above-mentioned literature, we found that the coexistence of high dielectric and magnetic characteristics in co-doped barium hexaferrites makes these materials potential candidates as high-performance microwave absorbers.
In this work, divalent transition metals such as Ni2+ and Cu2+ were utilized as a replacement for Fe3+ in M-type barium hexaferrites to alter their magnetic and dielectric characteristics because of their close ionic radii and electronic configuration. Moreover, the replacement of Fe3+ by the lower valence of Ni2+–Cu2+ ion pair may generate extra charge carriers for conduction, leading to high dielectric permittivity in barium hexaferrites. Further, it is anticipated that the magnetic nature of this ion pair will maintain the magnetic interactions, which may enhance the magnetization and reduce the coercivity depending on their preferential occupation of the octahedral sites in M-type hexaferrites.13,16 Therefore, different compositions of BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.50, 0.75, and 1.0 were prepared using the co-precipitation method, and then investigated for their microstructural, magnetic, and dielectric characteristics. Based on the obtained results, we found the coexistence of considerable high saturation magnetization (50–73 emu g−1) and dielectric permittivity (∼103–105@10 Hz) in the prepared samples.
2. Experimental details
The co-precipitation method was used to synthesize Ni2+-doped BaFe11Cu1−xNixO19 with x = 0.0, 0.25, 0.50, 0.75, and 1.0. The precursors used for the synthesis of the above-mentioned samples were barium nitrate [Ba(NO3)2, Sigma-Aldrich, 99%], ferric nitrate [Fe(NO3)3·9H2O, Alfa-Aesar, 99%], copper nitrate [Cu(NO3)2·2.5H2O, Sigma-Aldrich, ≥98%], nickel nitrate [Ni(NO3)2·6H2O, Sigma-Aldrich, ≥98%], potassium hydroxide [KOH, Sigma-Aldrich, 90%], and deionized water. Initially, stoichiometric quantities of nitrates were mixed in 100 mL deionized water and stirred for 15 min on a hot plate under magnetic stirring. The mixed solution of nitrates was incorporated dropwise into 100 mL solution of KOH. Subsequently, the mixture was stirred for 2 h at 80 °C on the hotplate, and then precipitates were formed. After multiple washings with deionized water, the samples were dried in an oven for 8 h at 100 °C. These dried samples were manually crushed into a fine powder using a mortar and pestle, and then annealed for 12 h at 1000 °C. The annealed powders were compressed under a compaction pressure of 5 tons per cm2 using a hydraulic press to produce pellets. Finally, the pelletized samples were sintered for 6 h at 1200 °C in a furnace.X-ray diffraction (ARL EQUINOX 3000) was performed to determine the structural phase of the prepared samples using Cu-Kα radiation with a wavelength of λ = 1.5418 Å. The machine was operated at a voltage of 40 kV/30 mA to observe the peaks in the 2θ range of 10° to 70°. Scanning electron microscopy (Hitachi S4800, FE-SEM) was used to study the surface morphology of the prepared samples. Energy dispersive X-ray spectroscopy (Oxford Instruments X-Max 80) was utilized to study the elemental compositional analysis of the prepared samples. To characterize the valence state of iron in the prepared hexaferrites, X-ray photoelectron spectroscopy was performed using a SPECS PHOIBOS 100 instrument working at 1486.6 eV (Al Kα). An Alpha-N Analyzer (Novocontrol, Germany) was used to investigate the dielectric properties at room temperature. The magnetic properties were measured at room temperature using a magnetic measurement system (MPMS XL-7, Quantum Design Corporation, USA).
3. Results and discussion
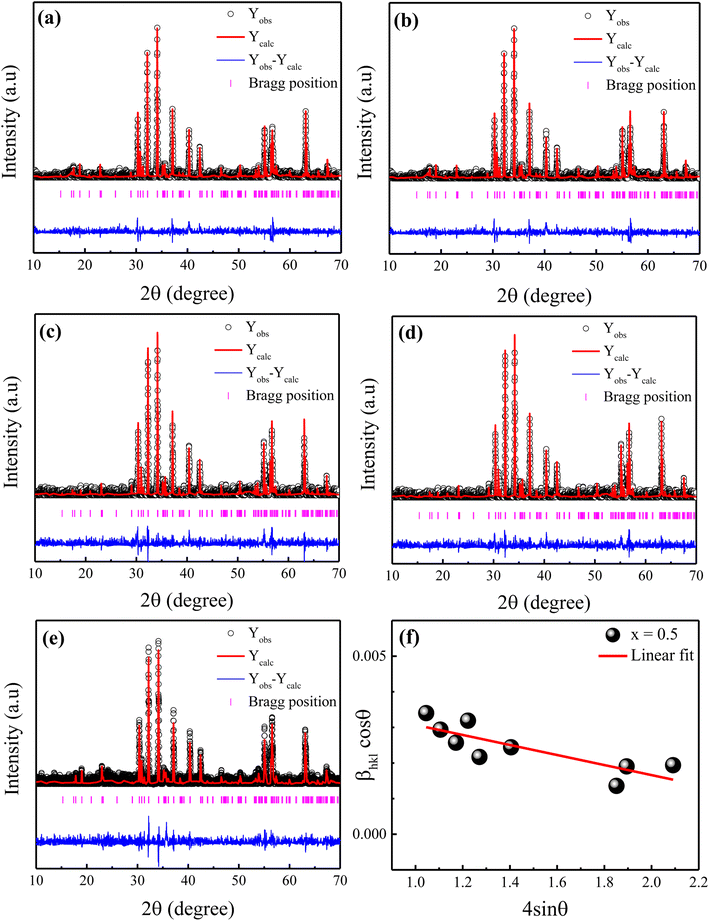
The X-ray diffraction patterns of the Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.50, 0.75, and 1.0 are displayed in Fig. 1(a–e), respectively. As can be seen, all the produced samples exhibit XRD patterns corresponding with the standard JCPDS File No. 00-039-1433 for the M-type hexagonal structure with the P63/mmc space group.17 Moreover, the XRD patterns demonstrate the absence of typical impurity peaks for all the samples, confirming the phase purity of the produced samples. The FullProf software was used to perform Rietveld structural refinements on the XRD patterns of the produced samples. The peak profiles were refined using the pseudo-Voigt function and the background was fitted using a polynomial with six coefficients. The structural parameters were refined until they approached a goodness of fit (χ2) value of close to 1.0. Here, the small goodness of fit values (χ2 = 1.30–1.63) confirm that the structural parameters are accurate. The estimated refined values of the lattice constants (a,c), unit-cell volume (V), and goodness of fit (χ2) are listed in Table 1. It can be seen that the estimated values of lattice parameters for the BaFe11Cu1O19 hexaferrites (x = 0.0) are a = 5.9058 Å and c = 23.270 Å, which are consistent with the reported work.13 However, these values are found to be higher than the respective values of a = 5.887 Å and c = 23.203 Å for the pure BaFe12O19 sample prepared under similar conditions (not shown here).18 The possible reason for the observed increase in the lattice parameters of x = 0.0 is due to the replacement of Fe3+ with a smaller ionic radius (0.645 Å) by Cu2+ ions with a larger ionic radius (0.73 Å).19 Moreover, with an increase in the Ni2+ doping content (x) in the BaFe11Cu1−xNixO19 hexaferrites, the values of the lattice parameters (a,c) were found to decrease up to x = 0.5, and then increase with a further increase in the content of Ni2+ ions (i.e., x > 0.5). This variation in the lattice constants can be ascribed to the difference in the ionic radii of the dopant Ni2+ (0.69 Å) ions compared to Fe3+ (0.645 Å) and Cu2+ (0.73 Å), valence change of Fe3+ to Fe2+, and the site occupancy of Cu2+/Ni2+ ions in the hexagonal unit-cell. Here, the initial decrease in the lattice parameters of the BaFe11Cu1−xNixO19 samples up to x = 0.5 can be attributed to the replacement of the Cu2+ ions from their preferable 4f2 site20 by the Ni2+ ions at the 12k and 4f2 sites.12 This is because in an octahedral field, the ionic radius of Ni2+ (0.69 Å) is smaller than that of Cu2+ (0.73 Å), resulting in a decrease in the lattice parameters. However, for x > 0.5, the effect of forming oxygen vacancies to balance the charge neutrality has a greater effect on the lattice parameters than the effect of replacing Fe3+ ions in the lattice with Cu2+ and Ni2+, resulting in an increase in the Fe2+ ions (will be discussed later in detail). The ionic radius of Fe2+ at the octahedral site is 0.78 Å, which is found to be larger than that of the Cu2+/Ni2+/Fe3+ ions, resulting in an increase in the lattice constant values. Further, the observed variation in the unit-cell volume (V) is consistent with the changes in the lattice parameters of the produced samples, as can be seen in Table 1. Alternatively, the c/a ratio of the prepared hexaferrite samples was found to be less than 3.98, indicating the presence of an M-type hexagonal structure.21 Further, the Williamson–Hall method was employed to estimate the average crystallite size (d) and lattice strain (ε) of the Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.50, 0.75, and 1.0, which is defined as follows:22
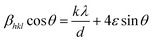 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ vs. 4
θ vs. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ for the prepared sample with x = 0.5. According to this representative plot, the slope of the straight line provides the lattice strain (ε) in the prepared hexaferrites, while the y-intercept provides the average crystallite size (d). A similar procedure was also followed for the other samples (not shown here). The calculated values of ε and d for the produced samples are presented in Table 1. It was found that with an increase in the Ni2+ doping content, the value of d decreased from 61 nm (x = 0.0) to 40 nm (x = 0.5), and then increased to 56 nm (x = 1.0). In contrast, the value of ε initially increased with an increase in the Ni2+ doping content up to x = 0.5, which can be attributed to the replacement of Cu2+ by Ni2+ ions with a smaller ionic radius. However, for a higher Ni2+ content (x > 0.5), the observed decrease in the value of ε can be attributed to the creation of defects (oxygen vacancies) at the octahedral sites, which caused the unit-cell volume to expand slightly, and then reduced the distortion in the hexaferrite structure.
θ for the prepared sample with x = 0.5. According to this representative plot, the slope of the straight line provides the lattice strain (ε) in the prepared hexaferrites, while the y-intercept provides the average crystallite size (d). A similar procedure was also followed for the other samples (not shown here). The calculated values of ε and d for the produced samples are presented in Table 1. It was found that with an increase in the Ni2+ doping content, the value of d decreased from 61 nm (x = 0.0) to 40 nm (x = 0.5), and then increased to 56 nm (x = 1.0). In contrast, the value of ε initially increased with an increase in the Ni2+ doping content up to x = 0.5, which can be attributed to the replacement of Cu2+ by Ni2+ ions with a smaller ionic radius. However, for a higher Ni2+ content (x > 0.5), the observed decrease in the value of ε can be attributed to the creation of defects (oxygen vacancies) at the octahedral sites, which caused the unit-cell volume to expand slightly, and then reduced the distortion in the hexaferrite structure.
| Sample (x) | a (Å) | c (Å) | c/a | V (Å)3 | χ2 | d (nm) | ε (×10−3) | G (µm) |
|---|---|---|---|---|---|---|---|---|
| 0.0 | 5.907 | 23.250 | 3.936 | 702.54 | 1.35 | 61 | 0.76 | 2.14 |
| 0.25 | 5.902 | 23.240 | 3.937 | 701.05 | 1.34 | 55 | 1.11 | 1.53 |
| 0.5 | 5.891 | 23.207 | 3.939 | 697.45 | 1.63 | 40 | 1.69 | 1.09 |
| 0.75 | 5.895 | 23.241 | 3.942 | 699.42 | 1.55 | 48 | 0.99 | 1.81 |
| 1.0 | 5.899 | 23.270 | 3.944 | 701.24 | 1.35 | 56 | 0.93 | 2.03 |
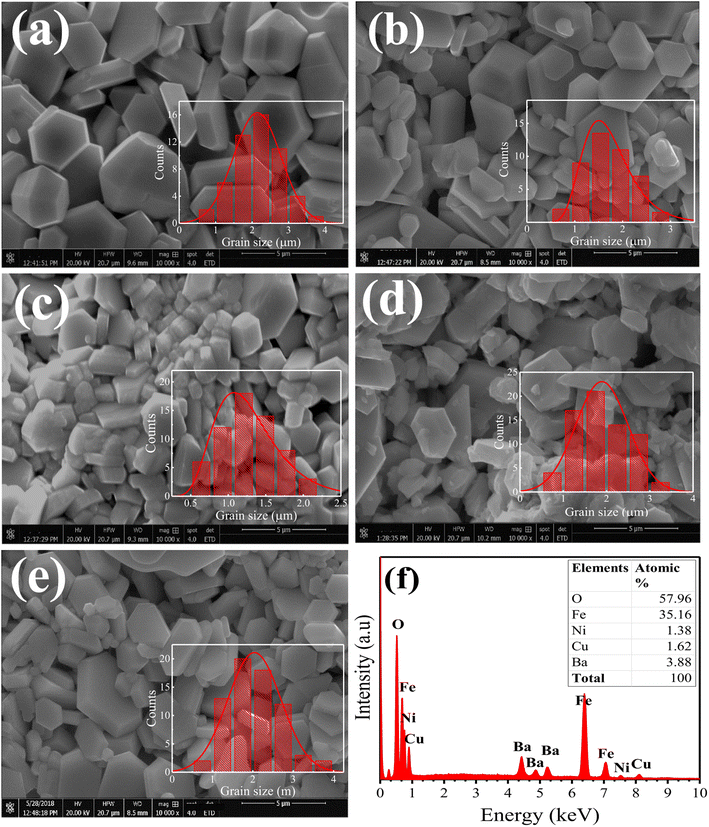
The surface morphological analysis of the Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.50, 0.75, and 1.0 was studied using scanning electron microscopy (FE-SEM). Fig. 2(a–e) demonstrate the SEM micrographs of the prepared hexaferrites, respectively, which were taken from the fractured surfaces of the pelletized samples sintered for 6 h at 1200 °C. The FE-SEM images show that all samples exhibit a heterogeneous distribution of grain sizes, with the majority of grains possessing a hexagonal shape and different sizes. The ImageJ software was used to determine the average grain size (G) and the results are listed in Table 1. The grain size was found to decrease with an increase in Ni2+ doping concentration up to x = 0.5, and then it increased. Here, the variation in grain size with Ni2+ doping in the BaFe11Cu1−xNixO19 hexaferrites can be attributed to several factors, such as the difference in the ionic radius, strain, porosity, and microstructural features, which can interact and influence each other. The initial decrease in grain size with an increase in the Ni2+ concentration can be due to the increase in the lattice strain caused by the mismatch in ionic radius, which hinders the grain growth.10 However, at higher doping concentrations (x > 0.5), the grain size may increase due to the agglomeration of grains, relaxation of strain, and lattice expansion. Fig. 2(f) displays the result of energy dispersive X-ray spectroscopy (EDX) performed on a representative BaFe11Cu0.5Ni0.5O19 (x = 0.5) sample. The EDX spectrum only shows the spectral lines of Ba, Fe, Cu, Ni and O, indicating the phase purity of the material. The inset of the figure shows the atomic proportions of each element, indicating that the prepared sample has a stoichiometric ratio for each ion, which is identical to the BaFe11Cu0.5Ni0.5O19 sample.
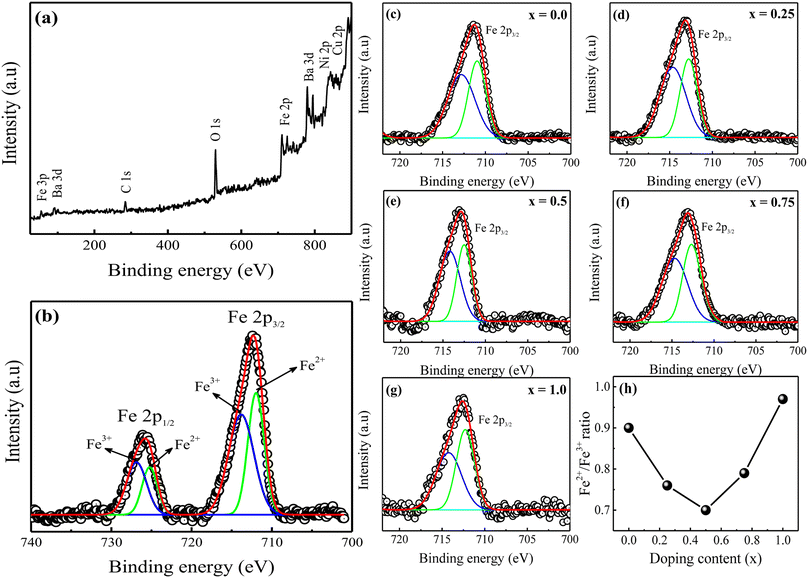
Fig. 3(a) displays a representative X-ray photoelectron spectroscopy (XPS) survey spectrum for the prepared BaFe11Cu1−xNixO19 hexaferrites with x = 0.75. The spectrum exclusively reveals peaks associated with the C, Ba, Fe, Cu, Ni, and O elements.23 The C 1s peak at 284.8 eV can be attributed to contaminating carbon. The location of this peak was utilized to calibrate the binding energies of all of the other elements. All other samples exhibited comparable survey spectra (not shown here). The binding energy of each element proves that the prepared hexaferrites have a single-phase, without any additional impurity phases. Fig. 3(b) shows the high-resolution XPS spectrum of Fe 2p for the sample with x = 0.75, which was obtained with a small energy step size. Here, the two peaks with binding energies of 712.2 eV and 725.6 eV correspond to Fe 2p3/2 and Fe 2p1/2 of the Fe species, respectively.16 These peaks were deconvoluted into two peaks, with the first peak representing the valence state of Fe2+ and the subsequent peak representing the Fe3+ state. Each fitting peak in the spectrum of Fe 2p was considered to have the form of a Lorentzian–Gaussian distribution. Moreover, the relative area of the corresponding peaks can be used to determine the ratio of Fe ions with the Fe2+ valence state to that with Fe3+. Fig. 3(c–g) illustrate the comparative Fe 2p3/2 XPS spectra of the prepared BaFe11Cu1−xNixO19 hexaferrites with x = 0.0–1.0. Based on the analysis, it was observed that the Fe2+/Fe3+ ratio decreased as the concentration of Ni2+ doping increased until x = 0.5, after which it increased significantly (see Fig. 3(h)). This behavior can be attributed to the fact that hexaferrites sintered in air often possess intrinsic oxygen vacancies and Fe2+ ions,12 which can be altered upon Ni2+ doping. The subsequent section will provide a comprehensive analysis of the impact of Ni2+ doping on the predicted Fe2+/Fe3+ ratio, which is a crucial factor in determining the conduction mechanism of hexaferrites, and may consequently alter the electrical properties of the prepared samples.
Fig. 4(a) shows the behaviour of the real part of dielectric permittivity (ε′) versus applied frequency for the produced Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.50, 0.75, and 1.0 measured at room temperature. Typically, the dielectric polarization in pure BaFe12O19 is determined by the exchange of charges between the Fe2+ ↔ Fe3+ ions at the octahedral site, while the Fe2+/Fe3+ ratio is determined by the conversion of dominant Fe3+ to Fe2+ via doping, sintering, and environmental conditions.24,25 As can be seen in the graph, the ε′ values rapidly decrease in the low-frequency region, while in the high-frequency region, they become nearly frequency independent. The Maxwell–Wagner polarisation model precisely explains this phenomenon, which is consistent with Koop's theory.26 It was proposed that ferrites are composed of conducting grains (Gs) separated by resistive grain-boundaries (GBs). At low frequencies, the charge carrier moves from Gs to GBs, causing local lattice distortion due to the asymmetric charge distribution that travels along the applied field. This polarisation is referred to as space charge polarisation. However, as the frequency of the applied field increases, this slowly moving lattice distortion (space charge polarisation) cannot keep up and falls behind, resulting in a decrease in the ε′ values with an increase in frequency.27 Moreover, the figure demonstrates that the obtained value of ε′ for the BaFe11Cu1O19 sample (i.e., x = 0.0) is comparably high compared to the pure BaFe12O19 sample prepared under similar conditions (not shown here) within the available frequency domain.27 Here, the observed enhancement in ε′ value can be attributed to the increase in electron transfer between the Fe2+ ↔ Fe3+ ions to maintain the charge neutrality at the octahedral sites. However, with the incorporation of Ni2+ doping content up to x = 0.5, the initial decreasing trend of ε′ may be due to the increase in the lattice strain (ε), which causes a distortion in the hexaferrite structure. This distortion may lead to a reduction in the concentration of intrinsic oxygen vacancies, which reduces the number of sites available for oxygen vacancies.12 Consequently, the concentration of Fe2+ ions decreases with an increase in the Ni2+ doping content due to the fact that the intrinsic Fe2+ ions in BaFe11Cu1O19 may transform into Fe3+ ions to achieve charge balance at the octahedral sites, which weakens the exchange of charges between the Fe2+ ↔ Fe3+ ions, resulting in reduced values of ε′ up to x = 0.5. Hence, the possible reason for this lower value of ε′ is that at x = 0.5, the ratio of Cu2+ and Ni2+ ions reaches an optimum balance, where the concentration of oxygen vacancies and Fe2+ ions may be at their minimum in the system, resulting in a more stable lattice configuration and reduced polarization. However, a further increase in the Ni2+ doping content (x > 0.5) may cause a reversal in this trend and decrease the lattice strain. This decrease in lattice strain facilitates the formation of defects, including the creation of oxygen vacancies and the reduction of Fe3+ to Fe2+. Therefore, the formation of Fe2+/Fe3+ pair dipoles with an increase in the Ni2+ doping content begins to contribute to the permittivity of the prepared samples, resulting in an increase in ε′ value for the x > 0.5 samples. Moreover, the permittivity may also be affected by the transition of some of the Ni2+ ions to Ni3+ with an increase in the Ni2+ doping content.16 Here, the ε′ value was found to be highest for the BaFe11Ni1O19 (x = 1.0) sample, which is ascribed to its highest dipole density (i.e., Fe2+/Fe3+ and Ni2+/Ni3+) among the prepared samples. This results in a colossal permittivity (∼105) for the BaFe11Ni1O19 sample, which is two orders of magnitude higher than the permittivity of the pure BaFe12O19 sample and also among the highest reported values to date.11,12,28
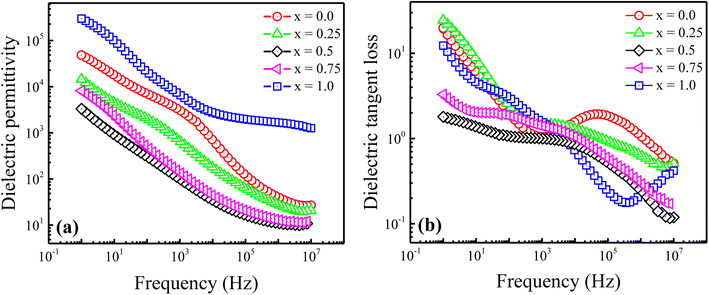 | ||
Fig. 4 Variation in (a) dielectric permittivity (ε′) and (b) dielectric tangent loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) versus frequency for the Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.5, 0.75, and 1.0. δ) versus frequency for the Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.5, 0.75, and 1.0. | ||
The frequency dependence of the dielectric tangent loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for the Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.50, 0.75, and 1.0 measured at room temperature is displayed in Fig. 4(b). As seen in the graph, the tan
δ) for the Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.50, 0.75, and 1.0 measured at room temperature is displayed in Fig. 4(b). As seen in the graph, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values exhibit similar behaviour to that of dielectric permittivity. At lower frequencies, tan
δ values exhibit similar behaviour to that of dielectric permittivity. At lower frequencies, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ has a higher magnitude because of the dominance of GBs, which inhibits the charge carrier hopping mechanism. Therefore, there is increased absorption, leading to greater loss. However, Gs are more conductive at higher frequencies because of the charge carrier hopping between the Fe2+/Fe3+ and Ni2+/Ni3+ ions at the octahedral site. Consequently, tan
δ has a higher magnitude because of the dominance of GBs, which inhibits the charge carrier hopping mechanism. Therefore, there is increased absorption, leading to greater loss. However, Gs are more conductive at higher frequencies because of the charge carrier hopping between the Fe2+/Fe3+ and Ni2+/Ni3+ ions at the octahedral site. Consequently, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is reduced given that there is less absorption at higher frequencies. Moreover, a dielectric relaxation peak was observed for all the samples, which indicates that the frequency at which electrons/holes hop between different ionic states is synchronized with the frequency of the applied alternating current.29 However, as the Ni2+ doping concentration increases, the observed peaks shifted to a lower frequency, and the peak intensity decreased slightly. This peak shifting is due to the increased relaxation time of the polarizable entities in the prepared samples, which is influenced by the presence of additional dipoles introduced by the Ni2+ doping content. The obtained results suggest values of tan
δ is reduced given that there is less absorption at higher frequencies. Moreover, a dielectric relaxation peak was observed for all the samples, which indicates that the frequency at which electrons/holes hop between different ionic states is synchronized with the frequency of the applied alternating current.29 However, as the Ni2+ doping concentration increases, the observed peaks shifted to a lower frequency, and the peak intensity decreased slightly. This peak shifting is due to the increased relaxation time of the polarizable entities in the prepared samples, which is influenced by the presence of additional dipoles introduced by the Ni2+ doping content. The obtained results suggest values of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ <1.0 at higher frequencies (105–107 Hz). Among the prepared samples, the reduced tan
δ <1.0 at higher frequencies (105–107 Hz). Among the prepared samples, the reduced tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value for the x = 1.0 sample together with the colossal ε′ value makes this composition attractive for high-frequency applications.
δ value for the x = 1.0 sample together with the colossal ε′ value makes this composition attractive for high-frequency applications.
Fig. 5 displays the variation in AC conductivity (σac) with applied frequency for the prepared Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.50, 0.75, and 1.0 measured at room temperature. Typically, the microscopic motion of charge carriers within the hexagonal ferrites can be inferred from the frequency (f) vs. AC conductivity (σac) plot. As seen in the figure, the behaviour of σac shows the opposite dependence on frequency as that of ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. Here, the conductivity increases with an increase in frequency for all the samples. The values of σac are small at lower frequencies and high at higher frequencies. It is well known that electron hopping between Fe2+ and Fe3+ ions is the key factor that determines the conductivity of hexaferrites and this electron hopping is strongly dependent on the concentration of Fe2+ and Fe3+ ions at the octahedral site.24 This hopping process increases with an increase in frequency, making conductive Gs more dominant, and hence the conductivity increases. Thus, to understand the observed dispersive behaviour of the conductivity graphs, the obtained data was fitted with Jonscher's power law, as follows:30
δ. Here, the conductivity increases with an increase in frequency for all the samples. The values of σac are small at lower frequencies and high at higher frequencies. It is well known that electron hopping between Fe2+ and Fe3+ ions is the key factor that determines the conductivity of hexaferrites and this electron hopping is strongly dependent on the concentration of Fe2+ and Fe3+ ions at the octahedral site.24 This hopping process increases with an increase in frequency, making conductive Gs more dominant, and hence the conductivity increases. Thus, to understand the observed dispersive behaviour of the conductivity graphs, the obtained data was fitted with Jonscher's power law, as follows:30
| σac(ω) = σo + Aωn | (2) |
 | ||
| Fig. 5 Frequency-dependent AC conductivity (σac) for Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.5, 0.75, and 1.0. | ||
| Samples (x) | Jonscher power law | Equivalent circuit model | ||||||
|---|---|---|---|---|---|---|---|---|
| σo | n | R1 (Ω) | C1 (F) | R2 (Ω) | C2 (F) | C3 (F) | RT (Ω) | |
| 0.0 | 3.55 × 10−6 | 0.66 | 2.75 × 104 | 4.50 × 10−12 | 4.37 × 105 | 2.93 × 10−9 | 6.25 × 10−11 | 4.65 × 105 |
| 0.25 | 5.24 × 10−8 | 0.52 | 7.05 × 105 | 3.14 × 10−11 | 3.19 × 107 | 9.41 × 10−9 | 5.82 × 10−12 | 3.26 × 107 |
| 0.5 | 8.10 × 10−9 | 0.50 | 1.75 × 107 | 1.17 × 10−11 | 4.19 × 108 | 4.12 × 10−8 | 3.95 × 10−12 | 4.36 × 108 |
| 0.75 | 2.37 × 10−7 | 0.48 | 1.46 × 105 | 7.17 × 10−12 | 1.09 × 106 | 1.07 × 10−9 | 1.79 × 10−11 | 1.23 × 106 |
| 1.0 | 1.78 × 10−6 | 0.26 | 1.74 × 104 | 3.97 × 10−11 | 1.36 × 105 | 5.21 × 10−8 | 7.68 × 10−11 | 1.53 × 105 |
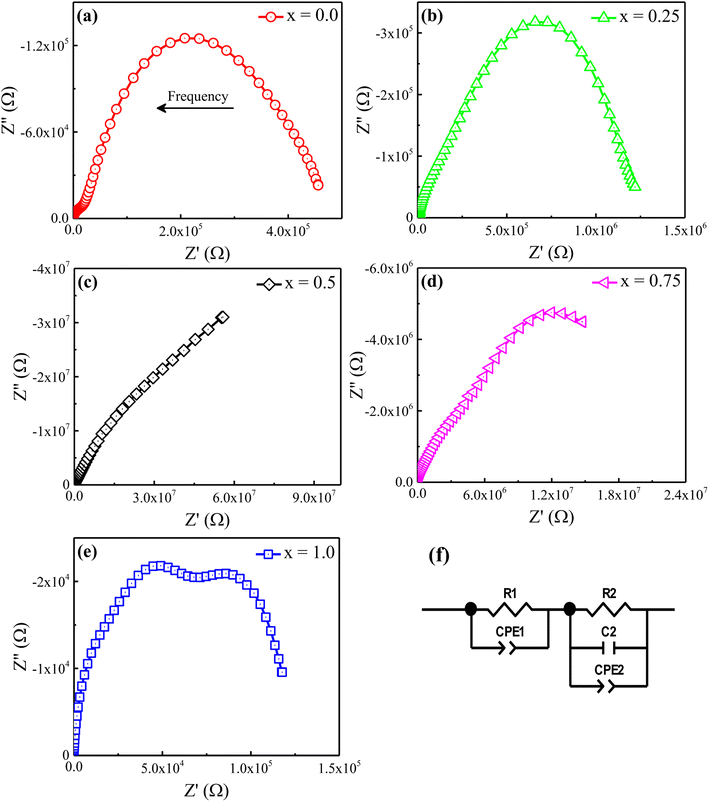
The Nyquist plane plots of the prepared Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.50, 0.75, and 1.0 measured at room temperature are shown in Fig. 6. Typically, the Nyquist plane plot consists of one or more completely resolved or poorly resolved semi-circles, depending on the number of dielectric relaxation processes or crystallographic phases present in the produced samples. In our single-phase produced samples, we observed two poorly resolved semi-circles with dissimilar widths. These semi-circles correspond to separate dielectric relaxation processes, namely Gs and GBs. We used the ZView software to fit our experimental data with an equivalent circuit model to further analyze the Nyquist plane plots. The components of the applied circuit were (R1Q1) and (R2Q2C3) linked in series, where R1 and R2 are the resistance, C1 and C3 are the capacitance, and Q1 and Q2 are the constant phase elements reflecting the capacitance variation from the optimal dielectric behavior. The following formulas were used to calculate the capacitance of each constant-phase element:31
| C = Q1/nR(1−n/n) | (3) |
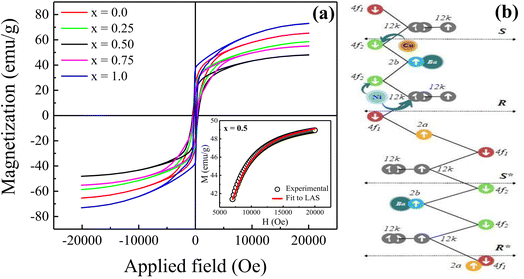
Fig. 7(a) displays the magnetic hysteresis loops of the Ni2+-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.50, 0.75, and 1.0 measured at room temperature under an applied magnetic field of ±20 kOe. The saturation magnetization (Ms), remanence magnetization (Mr), and coercivity (Hc) values of all the prepared samples were obtained using these hysteresis loops. The obtained values for these parameters are listed in Table 3. As can be observed, the magnetic characteristics changed significantly with the dopant concentration in the BaFe11Cu1−xNixO19 hexaferrites due to the preferential occupancy of the Cu2+ and Ni2+ ions at different crystellographic sites. As shown in Fig. 7(b), the magnetic moment of BaFe12O19, which is typically deduced by analyzing the difference in magnetic moments between the crystallographic sites, was measured to be 20 µB (i.e., M = M(12k + 2a + 2b)↑ − M(4f1 + 4f2)↓).18,33 Here, the Ms value for the prepared BaFe11Cu1O19 sample (x = 0.0) was found to be 65 emu g−1, which is comparatively higher than that of the pure BaFe12O19 sample (i.e., 55 emu g−1) prepared under similar conditions. This observed improvement in Ms value for the x = 0.0 sample can be understood based on the fact that the comparatively less magnetic Cu2+ (1 µB) ions replace the Fe3+ (5 µB) ions at their preferential 4f2 spin-down site and convert more Fe3+ into Fe2+ ions at the octahedral sites due to charge compensation. Therefore, the magnetic moment on the spin-down site decreases, leading to an increase in the Ms value for the BaFe11Cu1O19 compared to the BaFe12O19 sample.34 However, upon the incorporation of Ni2+ (2 µB) ions in place of Cu2+ (1 µB) ions in the BaFe11Cu1−xNixO19 hexaferrites, we found that the value of Ms initially decreased with an increase in the Ni2+ doping content up to x = 0.5, and thereafter it increased. Here, the observed initial decrease in the Ms value with an increase in Ni2+ content may be related to the decrease of the net magnetic moment per formula unit, indicating the preferential occupation of Ni2+ at the 12k spin-up and 4f2 spin-down sites, while the Cu2+ ions occupy the 4f2 spin-down site in the place of the Fe3+ ions (see Fig. 7(b)). Thus, the difference in magnetic moments across the sites decreases, leading to a decline in the Ms value from 65 emu g−1 (x = 0.0) to 50 emu g−1 (x = 0.5). However, when the Ni2+ doping content exceeded x = 0.5, the Ni2+ ions gradually occupied the 4f2 spin-down sites, while the Cu2+ ions take up the 4f2 site together with reducing more Fe3+ ions to Fe2+ ions. This leads to an increase in the difference between the sites, and thus the value of Ms increases from 50 emu g−1 (x = 0.5) to 73 emu g−1 (x = 1.0). Among the produced samples, the highest value of Ms was obtained for the BaFe11Ni1O19 sample (x = 1.0), which is found to be higher than the reported values,12 where the respective value of Ms decreases at a higher Ni2+ content due to the formation of a secondary phase having comparatively weak magnetic nature. Furthermore, the magnetic anisotropy (K1) of the prepared samples was estimated by employing the law of approach to magnetic saturation (LAS), which can be expressed as follows:35,36
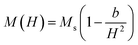 | (4) |
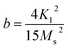 | (5) |
| Sample (x) | Ms (emu g−1) | Mr (emu g−1) | Hc (Oe) | K1 × 105 (erg g−1) |
|---|---|---|---|---|
| 0.0 | 65 | 24 | 238 | 3.87 |
| 0.25 | 58 | 22 | 430 | 3.44 |
| 0.5 | 49 | 16 | 500 | 2.71 |
| 0.75 | 55 | 20 | 387 | 3.10 |
| 1.0 | 73 | 35 | 222 | 4.53 |
The inset of the figure shows the fitting of the high-field region (i.e., H ≫ Hc) of the representative hysteresis loop of the x = 0.5 sample. According to the values of the fitting parameters (Ms and b), the values of K1 for the prepared samples were calculated. As shown in Table 3, the value of K1 initially decreased, and then increased with an increase in the Ni2+ doping content, reaching a minimal value at x = 0.5. In M-type hexaferrites, the 12k, 4f2, and 2b sites are known as major contributors to the magnetic anisotropy.37 Therefore, the initial decrease observed in the K1 value is attributed to the competition between the Ni2+ and Cu2+ ions to occupy the 12k, 4f2 and 4f2 sites in place of Fe3+ ions, respectively, thereby weakening the magnetic anisotropy. However, the observed increase in K1 for x > 0.5 can be explained by the probable occupation of the Ni2+ and Cu2+ ions at the 4f2 site, which transfer more Fe3+ ions from the octahedral to tetrahedral sites, thus increasing the magnetic anisotropy. Moreover, the variation in coercivity (Hc) with an increase in the Ni2+ doping content can be related to the changes in magnetic anisotropy (K1) and grain size (G) of the prepared hexaferrites (see Table 1). Here, we found that Hc has a positive relationship with K1 and inverse dependance on G.38,39
Table 4 shows a comparison of the magnetic and dielectric characteristics of the prepared BaFe11Cu1−xNixO19 hexaferrites (x = 0.0 and 1.0) with the reported relevant compositions measured at room temperature. The comparison reveals that the fabricated sample BaFe11Ni1O19 (x = 1.0) exhibits comparatively high values of saturation magnetization (Ms) and dielectric permittivity (ε′) together with a low dielectric tangent loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ). This is probably because of the influence of the Ni2+ ions occupying the 4f2 sites and the increased dipole density (Fe2+/Fe3+). Therefore, the coexistence of high magnetic saturation and dielectric permittivity in the BaFe11Ni1O19 material presents potential for its utilization in microwave-absorbing devices. This highlights its application in new technologies and helps advance materials that are designed to effectively attenuate electromagnetic waves.
δ). This is probably because of the influence of the Ni2+ ions occupying the 4f2 sites and the increased dipole density (Fe2+/Fe3+). Therefore, the coexistence of high magnetic saturation and dielectric permittivity in the BaFe11Ni1O19 material presents potential for its utilization in microwave-absorbing devices. This highlights its application in new technologies and helps advance materials that are designed to effectively attenuate electromagnetic waves.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) at a representative frequency (f) from other studies compared to our results measured at room temperature
δ) at a representative frequency (f) from other studies compared to our results measured at room temperature
| Composition | Ms (emu g−1) | Dielectric parameters | Reference | ||
|---|---|---|---|---|---|
| f (Hz) | ε′ | tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ δ |
|||
| BaFe12O19 (18–65 nm) | 18–51 | 10 MHz | <50 | <0.2 | 40 |
| BaFe12−xCoxO19 (x = 0.0, 0.05, 0.1, 0.2) | 75.36–56.08 | 10 MHz | 400–300 | <0.2 | 41 |
| BaFe12−2xCoxSmxO19 (x = 0.0, 0.2, 0.4, 0.6) | 51.17–80.20 | 3 MHz | 7.42–5.06 | <0.05 | 42 |
| Ba1–xCexFe12–xCoxO19 (x = 0.0–0.2) | 46–37 | 1 GHz | 3.8–2.2 | <0.5 | 43 |
| BaFe12−xNixO19 (x = 0, 0.1, 0.2, 0.3, 0.4, 0.5) | 68–59 | 10 MHz | ∼100 | <1.0 | 11 |
| BaFe12−2xNixO19 (x = 0, 0.3, 0.5) | 55.35–57.57 | 1 MHz | 90–150 | <0.1 | 28 |
| Ba1−xNdxFe12−yCuyO19 (x,y = 0.0, 0.15, 0.30, 0.45, 0.60) | 68.4–42.3 | 10 MHz | 150–300 | <1.0 | 44 |
| BaCuxCrxFe12−2xO19 (0.0 ≤ x ≤ 0.5) | 50.84–68.99 | 1 MHz | 8–16 | <0.2 | 45 |
| BaFe12−2xNixZrxO19 (0.0 ≤ x ≤ 1.0) | 71.5–20.5 | 1 MHz | 300–930 | <1.0 | 16 |
| BaFe11Ni1O19 | 73 | 10 MHz | 1300 | 0.4 | This work |
| BaFe11Cu1O19 | 65 | 30 | 0.45 | ||
4. Conclusions
In this study, we investigated the effect of Ni2+–Cu2+ co-doping on the structural, dielectric, and magnetic characteristics of barium hexaferrites. The co-precipitation technique was employed to prepare Ni2+–Cu2+ co-doped BaFe11Cu1−xNixO19 hexaferrites with x = 0.0, 0.25, 0.50, 0.75, and 1.0. All the prepared samples showed the development of a single-phase hexagonal structure, according to the Rietveld refinement of their XRD patterns. The structural analysis revealed that doping of Ni2+ and Cu2+ changed the values of the lattice parameters (a,c), unit-cell volume, lattice strain, and crystallite size, which were explained in terms of the difference in the ionic radii and occupation at the different crystallographic sites. The FE-SEM analysis showed that the grains are hexagonal in shape, while EDX confirmed the stoichiometry of the produced samples. The XPS analysis confirmed the formation of Fe2+ ions; however, the ratio of Fe2+/Fe3+ changed with an increase in the Ni2+ doping content. Dielectric measurements displayed a decreasing trend in the frequency-dependent dielectric behavior, in accordance with Maxwell–Wagner interfacial polarization. Alternatively, the impedance analysis showed a considerable variation in the resistive properties of the prepared samples with an increase in the Ni2+–Cu2+ doping content. The observed variation in the dielectric and resistive properties were attributed to the changes in the grain size and electron–hole transfer between the charge carriers. The magnetic measurements showed that the Ni2+–Cu2+ co-doping caused a noticeable variation in the values of Ms and Hc measured at room temperature. This was attributed to the preferential occupation of the Ni2+ ions at the different crystallographic sites, which may have a more significant impact on the overall magnetic moment. Based on the obtained results, we found that the sample with x = 1.0 had the highest dielectric permittivity (>103 at 107 Hz) and magnetization (73 emu g−1) together with a lowest dielectric tangent loss (0.2) and material resistance (1.5 × 105 Ω). This makes the BaFe11Ni1O19 composition a promising choice as a microwave absorption material, which requires high dielectric permittivity and magnetization together with a reduced dielectric tangent loss. Currently, experiments are being conducted to measure the electromagnetic interference (EMI) shielding efficacy of this material. In the future, we are planning to disperse BaFe11Ni1O19 in a conductive matrix to develop a light-weight, flexible, and efficient composite material for microwave absorbing applications.Author statement
M. Atif: conceptualization, supervision, writing – review & editing. H. Ul Husnain: investigation, data curation, writing – original draft. Atta Ur Rehman: investigation, visualization, formal analysis. U. Younas: investigation, formal analysis. T. Rafique: investigation, formal analysis. W. Khalid: software, validation. Z. Ali: writing – review & editing. M. Nadeem: conceptualization, resources.Conflicts of interest
There are no conflicts to declare.References
- L. A. Dobrzański, M. Drak and B. Ziębowicz, Materials with specific magnetic properties, J. Achiev. Mater. Manuf. Eng., 2006, 17, 37–40 Search PubMed.
- L. Deng, Y. Zhao, Z. Xie, Z. Liu, C. Tao and R. Deng, Magnetic and microwave absorbing properties of low-temperature sintered BaZrxFe12-xO19, RSC Adv., 2018, 8, 42009–42016 RSC.
- R. C. Pullar, Hexagonal ferrites: a review of the synthesis, properties and applications of hexaferrite ceramics, Prog. Mater. Sci., 2012, 57, 1191–1334 CrossRef CAS.
- P. Campbell, Permanent Magnet Materials and Their Application, Cambridge University Press, Cambridge, 1994 Search PubMed.
- B. J. Evans, F. Grandjean, A. P. Lilot, R. H. Vogel and A. Gérard, 57Fe hyperfine interaction parameters and selected magnetic properties of high purity MFe12O19 (M = Sr, Ba), J. Magn. Magn. Mater., 1987, 67, 123–129 CrossRef CAS.
- R. A. McCurrie, Ferromagnetic Materials: Structure and Properties, Academic Press Limited, London, 1994 Search PubMed.
- R. Valenzuela, Novel Applications of Ferrites, Phys. Res. Int., 2012, 2012, 591839 Search PubMed.
- A. V. Trukhanov, V. G. Kostishyn, L. V. Panina, V. V. Korovushkin, V. A. Turchenko, P. Thakur, A. Thakur, Y. Yang, D. A. Vinnik, E. S. Yakovenko, L. Yu. Matzui, E. L. Trukhanova and S. V. Trukhanov, Control of electromagnetic properties in substituted M-type hexagonal ferrites, J. Alloys Compd., 2018, 754, 247–256 CrossRef CAS.
- H. Kojima, Fundamental properties of hexagonal ferrites with magnetoplumbite structure, Handbook of Ferromagnetic Materials, Elsevier, 1982, vol. 3, pp. 305–391 Search PubMed.
- M. K. Manglam, S. Kumari, L. K. Pradhan, S. Kumar and M. Kar, Lattice strain caused magnetism and magnetocrystalline anisotropy in Zn modified barium hexaferrite, Phys. B, 2020, 588, 412200 CrossRef CAS.
- P. Behera and S. Ravi, Effect of Ni doping on structural, magnetic and dielectric properties of M-type barium hexaferrite, Solid State Sci., 2019, 89, 139–149 CrossRef CAS.
- M. Wang, Q. Xu, S. Wang, Z. Wang, N. Ma and P. Du, Formation of BaFe12-xNixO19 ceramics with considerably high dielectric and magnetic property coexistence, J. Alloys Compd., 2018, 765, 951–960 CrossRef CAS.
- S. Kumar, S. Guha, S. Supriya, L. K. Pradhan and M. Kar, Correlation between crystal structure parameters with magnetic and dielectric parameters of Cu-doped barium hexaferrite, J. Magn. Magn. Mater., 2020, 499, 166213 CrossRef CAS.
- Widyastuti, N. Sasria, A. M. Alviani, M. D. Febri R. and V. Mitha P., Ni and Zn Substituted M-type Barium Hexaferrite Processed by Sol–Gel Auto Combustion Method, J. Phys.: Conf. Ser., 2017, 877, 012015 CrossRef.
- Susilawati, A. Doyan, H. Khair, M. Taufik and Wahyudi, Electrical, Magnetic and Microwave Absorption Properties of M-type Barium Hexaferrites (BaFe12-2xCoxNixO19), J. Phys.: Conf. Ser., 2018, 1011, 012009 CrossRef.
- Y. Zou, J. Lin, W. Zhou, M. Yu, J. Deng, Z. Chen, G. Luo and D. Wang, Coexistence of high magnetic and dielectric properties in Ni-Zr co-doped barium hexaferrites, J. Alloys Compd., 2022, 907, 164516 CrossRef CAS.
- M. Amini and A. Gholizadeh, Shape control and associated magnetic and dielectric properties of MFe12O19 (M = Ba, Pb, Sr) hexaferrites, J. Phys. Chem. Solids., 2020, 147, 109660 CrossRef CAS.
- M. Atif, S. Ullah, A. Ur Rehman, K. Shahzad, W. Khalid, Z. Ali, Y. Chen, H. Guo and M. Nadeem, Structural, magnetic, and dielectric properties of Ti4+−M2+ co-doped BaFe11Ti0.5M0.5O19 hexaferrites (M = Co2+, Ni2+, Zn2+), Ceram. Int., 2021, 47, 15245–15252 CrossRef CAS.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr. A, 1976, 32, 751–767 CrossRef.
- M. J. Iqbal, M. Naeem Ashiq and P. Hernandez-Gomez, Effect of annealing temperature and substitution of Zr-Cu onmagnetic properties of strontium hexaferrite nanoparticles, J. Phys.: Conf. Ser., 2009, 153, 012053 CrossRef.
- M. A. Almessiere, Y. Slimani, N. A. Tashkandi, A. Baykal, M. F. Saraç, A. V. Trukhanov, I. Ercan, I. Belenli and B. Ozçelik, The effect of Nb substitution on magnetic properties of BaFe12O19 nanohexaferrites, Ceram. Int., 2019, 45, 1691–1697 CrossRef CAS.
- G. K. Williamson and W. H. Hall, X-ray line broadening from filed aluminium and wolfram, Acta Mater., 1953, 1, 22–31 CrossRef CAS.
- S. Vadivelan and N. Victor Jaya, Investigation of magnetic and structural properties of copper substituted barium ferrite powder particles via co-precipitation method, Results Phys., 2016, 6, 843–850 CrossRef.
- M. Atif, M. H. Alvi, S. Ullah, A. Ur Rehman, M. Nadeem, W. Khalid, Z. Ali and H. Guo, Impact of strontium substitution on the structural, magnetic, dielectric and ferroelectric properties of Ba1-xSrxFe11Cr1O19 (x = 0.0–0.8) hexaferrites, J. Magn. Magn. Mater., 2020, 500, 166414 CrossRef.
- B. Unal, M. A. Almessiere, A. V. Trukhanov, A. Baykal, Y. Slimani, M. V. Silibin, A. Ul-Hamid and A. Manikandan, A study on the conductivity, dielectric, and microwave properties of SrNbxYxFe12-2xO19 (0.00≤x≤0.05) nanohexaferrites, J. Mater. Res. Technol., 2022, 17, 2975–2986 CrossRef CAS.
- K. W. Wagner, The distribution of relaxation times in typical dielectrics, Ann. Phys., 1993, 40, 817–819 Search PubMed.
- N. Raghuram, T. Subba Rao and K. Chandra Babu Naidu, Electrical and impedance spectroscopy properties of hydrothermally synthesized Ba0.2Sr0.8-yLayFe12O19 (y = 0.2 – 0.8) nanorods, Ceram. Int., 2020, 46, 5894–5906 CrossRef CAS.
- M. A. Rafiq, M. Waqar, T. A. Mitza, A. Farooq and A. Zulfiqar, Effect of Ni2+ Substitution on the Structural, Magnetic, and Dielectric Properties of Barium Hexagonal Ferrites (BaFe12O19), J. Electron. Mater., 2017, 46, 241–246 CrossRef CAS.
- T. Rafique, M. Atif, A. Ur Rehman, H. Wahab, W. Khalid, Z. Ali and M. Nadeem, Colossal permittivity, resistive and magnetic properties of zinc substituted manganese ferrites, J. Alloys Compd., 2022, 923, 166454 CrossRef CAS.
- A. K. Jonscher, Dielectric Relaxations in Solids, Chelsea Dielectrics, London, 1983 Search PubMed.
- E. Barsoukov and J. R. Macdonald, Impedance Spectroscopy Theory, Experiments and Applications, Wiley, New York, 2005 Search PubMed.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Electroceramics: characterization by impedance spectroscopy, Adv. Mater., 1990, 2, 132 CrossRef CAS.
- S. Caliskan, M. A. Almessiere, A. Baykal, Y. Slimani, H. Gungunes, A. Demir Korkmaz, A. Ul-Hamid and I. A. Auwal, Magnetic properties of Sr0.5Ba0.5HoxFe12-xO19 (x ≤ 0.10) nanohexaferrites, Appl. Phys. A, 2023, 129, 616 CrossRef CAS.
- M. A. Rafiq, M. Waqar, Q. K. Muhammad, M. Waleed, M. Saleem and M. S. Anwar, Conduction mechanism and magnetic behavior of Cu doped barium hexaferrite ceramics, J. Mater. Sci.: Mater. Electron., 2018, 29, 5134–5142 CrossRef CAS.
- M. A. Almessiere, Y. Slimani, H. S. El Sayed, A. Baykal and I. Ercan, Microstructural and magnetic investigation of vanadium-substituted Sr-nanohexaferrite, J. Magn. Magn. Mater., 2019, 471, 124–132 CrossRef CAS.
- O. Ramanjaneyulu, N. Suresh Kumar, D. Baba Basha and K. Chandra Babu Naidu, Structural, thermal, magnetic, and electrical properties of Ba1-xCuxFe12O19 (x = 0.2–0.8) nanoparticles, J. Mater. Sci.: Mater. Electron., 2023, 34, 449 CrossRef CAS.
- Z. Yang, C. S. Wang, X. H. Li and H. X. Zeng, (Zn, Ni, Ti) substituted barium ferrite particles with improved temperature coefficient of coercivity, Mater. Sci. Eng. B., 2002, 90, 142–145 CrossRef.
- J. Chen, Z. Wang, Z. Cheng, Z. Shi, X. Deng, Y. Chen, Y. Zou, G. Luo and W. Zhou, Investigation on the structural, magnetic, and dielectric properties of Ni2+–Zr4+ co-doped Y-type hexaferrite Ba2Ni2Fe12O22, J. Mater. Sci.: Mater. Electron., 2022, 33, 16889–16898 CrossRef CAS.
- A. Gholizadeh and V. Banihashemi, Effects of Ca–Gd co-substitutionon the structural, magnetic, and dielectricproperties of M-type strontium hexaferrite, J. Am. Ceram. Soc., 2023, 106, 5351–5363 CrossRef CAS.
- S. Kumar, S. Supriya, L. K. Pradhan, R. Pandey and M. Kar, Grain size effect on magnetic and dielectric properties of barium hexaferrite (BHF), Phys. B, 2020, 579, 411908 CrossRef CAS.
- A. Kumar, M. K. Verma, S. Singh, T. Das, L. Singh and K. D. Mandal, Electrical, Magnetic and Dielectric Properties of Cobalt-Doped Barium Hexaferrite BaFe12−xCoxO19 (x = 0.0, 0.05, 0.1, and 0.2) Ceramic Prepared via a Chemical Route, J. Electron. Mater., 2020, 49, 6436–6447 CrossRef CAS.
- G. Asghar, S. Asri, S. N. Khusro, G. H. Tariq, M. S. Awan, M. Irshad, A. Safeen, Z. Iqbal, W. H. Shah and M. Anis-ur-Rehman, Enhanced Magnetic Properties of Barium Hexaferrite, J. Electron. Mater., 2020, 49, 4318–4323 CrossRef CAS.
- Z. Lalegani and A. Nemati, Effects of Ce–Co substitution on structural, magnetic and dielectric properties of M-type barium hexaferrite nanoparticles synthetized by sol–gel auto-combustion route, J. Mater. Sci.: Mater. Electron., 2015, 26, 2134–2144 CrossRef CAS.
- F. Bibi, S. Iqbal, H. Sabeeh, T. Saleem, B. Ahmad, M. Nadeem, I. Shakir, M. Aadil and A. Kalsoom, Evaluation of structural, dielectric, magnetic and photocatalytic properties of Nd and Cu co-doped barium hexaferrite, Ceram. Int., 2021, 47, 30911–30921 CrossRef CAS.
- A. A. Gor, N. M. Devashrayee, T. Gupta, C. C. Chauhan and R. B. Jotania, A study of the effect of the Cu and Cr co-doping on structural, magnetic and dielectric properties of barium hexaferrites synthesized in presence of mentha leaves extract, Mater. Today Commun., 2023, 37, 107214 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |