Open Access Article
Open Access ArticleImproving the magnetic moment of Ca2Ge and promoting the conversion of semiconductors to diluted magnetic semiconductors using Mn-doping
Weifu Cen ab and
Zean Tian
ab and
Zean Tian *ac
*ac
aCollege of Big Data and Information Engineering, Guizhou University, Guiyang, 550025, China. E-mail: tianzean@hnu.edu.cn
bSchool of Material Science and Engineering, Guizhou Minzu University, Guiyang, 550025, China
cCollege of Computer Science and Electronic Engineering, Hunan University, 410082, China
First published on 26th February 2024
Abstract
The dilute magnetic properties of materials have important potential applications in the field of electronic science and technology. Intrinsic Ca2Ge is a new environmentally friendly semiconductor material, and exhibits cubic and orthorhombic phases. The crystal structure characteristics of Ca2Ge indicate that the modulation of its dilute magnetic properties can theoretically be achieved by doping with magnetic elements. The study of band structures shows that Ca2Ge is a semiconductor, while Mn doped Ca2Ge is a semi-metal. The results of density of states and atomic population analysis show that Mn doped Ca2Ge exhibits ferrimagnetism with a magnetic moment of 5 μB, and the orbital splitting energy of the Mn atom is 1.0 eV. Mn-doping changes the cubic crystal field of Ca2Ge, and the charge transfer and electron polarization of Ca d and Ge p orbitals are affected by Mn atoms. The Ca d orbital is split into dzz, dzy, dzx, dxx–yy and dxy orbitals, and the contribution of spin of each d split orbital to the magnetic moment of the Ca d orbital is in the order dxy > dyz > dxz > dxx–yy > dzz. The Ge p orbital is split into px, py and pz orbitals, and the spin contribution of each p orbital to the magnetic moment of the Ge p orbital is in the order py > pz > px. The analysis of atom populations shows that the charge transfer and spin of Ca and Ge change with Mn doping, and the difference between spin up and spin down increases, improving the magnetism of Ca2Ge and forming a dilute magnetic semiconductor.
1. Introduction
Diluted magnetic semiconductor materials (DMS) have semiconductor and electromagnetic properties, as a result of regulation of the charge freedom and spin freedom. Electronic devices using these properties have a wide range of potential applications in information processing, storage, transmission and other fields, and are of great significance to the development of electronic information technology.1–3 Semi-metallic materials are a particular type of DMS with a particular band structure, high electron polarization at the Fermi level, a total magnetic moment that is a multiple of the Bohr magneton, and a high Curie temperature TC. Therefore, semi-metallic materials are preferred materials for manufacturing magnetic ion-implanted DMS electronic devices.4–8 Recently, investigations of DMS have mainly focused on III–V, IV, II–VI, oxide and sulfide semiconductors, such as GaAs, GaN, Si, Ge, ZnO, MoS2, etc.9–13 The preparation of DMS mainly uses transition metal atoms or rare earth ions, which have spin magnetic moment, doped to substitute some atoms in the semiconductor material.14–16 The magnetic moment of DMS is produced by the exchange of p state electrons of the anions and d state electrons of the magnetic ions, which are changed by the external temperature and doping concentration, so they may be ferromagnetic, sub ferromagnetic and antimagnetic.17,18As a new type of II–VI narrow band gap semiconductor, Ca2Ge has high TC, high carrier mobility, low dielectric constant, and excellent optical and other properties.19 Furthermore, it is compatible with conventional silicon processes and overcomes the physical quantum limitations of Si (conventional Si integrated circuit IC in the range of 2–20 nm), and has higher intrinsic hole mobility than GaAs and Si, so has potential application value in sensors and optoelectronic devices.20,21 The band structure and photoelectric characteristics of Ca2Ge have been studied using the first principles method.22 It is found that cubic phase Ca2Ge is a direct band-gap semiconductor with a band gap of 0.56 eV, and the lattice constant is 0.719 nm.23 The stability of Ca–Ge alloys is affected by pressure and temperature, while the vibrational free energy depends only on temperature.24,25 Study of the structure, phonon spectrum, and lattice dynamics of Ca2Ge found that the phonon correlation of Ca2Ge is higher than that of Ca2Si, which provides a theoretical basis for the use of Ca2Ge in low power devices.26
Recently, theoretical research has shown that the valence electron of Ca 3p64s2 is unstable in the Ca2Ge electron system. In order to form a stable state, the electron is transferred from the 4s orbital to the 3d orbital, forming a stable structure, 3d14s1.27 Due to the particularity of Ca 3d state electrons, it is speculated that there is a correlation between Ca 3d state electrons and Ge 3p state electrons in Ca2Ge compounds. The outer electron configuration of the central Ca ion is 3d1, and its unfilled d state electrons provide the valence bonding for the doped magnetic ions, forming a new electronic state, resulting in changes in the original electronic orbitals, electronic state, local structure, etc. Theoretically, this material has the possibility to become a DMS with excellent performance. Therefore, it is meaningful to develop Ca2Ge as a new DMS material.
In order to clarify the magnetization mechanism and the influence of the physical field on the magnetism, the electronic structure and magnetic mechanism of intrinsic Ca2Ge and Mn-doped Ca2Ge are studied using a first principles method. The influence of the mechanism of Mn doping on the electronic structure and magnetic properties of Ca2Ge is investigated extensively, and the regulatory mechanism for the electronic structure and magnetic properties is analyzed. It is found that the electronic orbitals of Ca and Ge form spin magnetic moments upon Mn-doping.
2. Modelling and crystalline field theory
2.1 Modelling
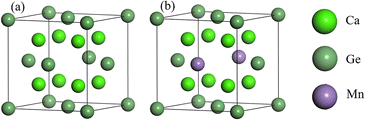
Cubic phase Ca2Ge belongs to the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group with lattice constants a = b = c = 0.719 nm, and α = β = γ = 90°.22,23,26–28 Each cell contains 8 Ca atoms and 4 Ge atoms. The doping model of Ca8Mn1Ge3 is established by replacing a Ge with a Mn atom. The structural model is shown in Fig. 1. The same method is used to construct the Ca7Mn1Ge4 doping model by replacing a Ca with a Mn atom. Since Ca is in two unequal positions in the Ca2Ge system, there are two structures of Ca7Mn1Ge4. The band structure of Ca8Mn1Ge3 shows that it is a semi-metal, while Ca7Mn1Ge4 is a metal, so this work just discusses the Ca8Mn1Ge3 DMS.
m space group with lattice constants a = b = c = 0.719 nm, and α = β = γ = 90°.22,23,26–28 Each cell contains 8 Ca atoms and 4 Ge atoms. The doping model of Ca8Mn1Ge3 is established by replacing a Ge with a Mn atom. The structural model is shown in Fig. 1. The same method is used to construct the Ca7Mn1Ge4 doping model by replacing a Ca with a Mn atom. Since Ca is in two unequal positions in the Ca2Ge system, there are two structures of Ca7Mn1Ge4. The band structure of Ca8Mn1Ge3 shows that it is a semi-metal, while Ca7Mn1Ge4 is a metal, so this work just discusses the Ca8Mn1Ge3 DMS.
The pseudopotential plane wave method based on first principles is used for calculation, and the calculation is completed using the Cambridge Serial Total Energy Package (CASTEP).29,30 The Broyden, Fletcher, Goldfarb and Shanno (BFGS) algorithm is used to optimize the geometrical structure of Ca2Ge, and then six different approximation methods for generalized gradient approximations in the scheme of Perdew, Burke and Ernzerhof (GGA-PBE), revised Perdew–Burke–Ernzerhof (GGA-RPBE), Perdew–Wang 91 (GGA-PW91), Wu and Cohen (GGA-WC), Perdew et al. (GGA-PBEsol), and local density approximation (LDA) are used for the exchange correlation energy for finding the most stable structure and the most suitable approximate calculation method. All the calculations below are performed on the basis of this structure terminally. On this basis, the electronic structure and electromagnetic properties of intrinsic Ca2Ge and Mn-doped Ca2Ge are investigated. The ultra soft pseudo-potential (USPP) method is used to deal with the interaction between ions and electrons. The convergence threshold of interatomic force is 0.001 eV nm−1, the internal stress is not more than 0.02 GPa, the convergence threshold of atomic displacement is 5 × 10−5 nm, the convergence standard of energy between two iterations is 5.0 × 10−7 eV per atom, and the convergence standard of self-consistent field is 2 × 10−6 eV per atom. The truncation energy is selected as 380 eV, and the K point in the Brillouin region using the Monkhorst–Pack method is selected as 4 × 4 × 4. The valence electrons involved in the calculation are Ca 3s23p64s2, Ge 4s24p2 and Mn 3d54s2. Due to Mn being a transition metal, the Mn 3d orbit is not filled, and the enhanced electron delocalization leads to inaccurate calculation results. In order to improve the accuracy of the result, the GGA + Ueff (Hubbard U) method is used to correct the Mn 3d orbital, where the effective Hubbard parameter, Ueff, of the Mn atom is set to 3.0 eV. The electronic structure and magnetic properties of Mn doped Ca2Ge are studied with U set to 3.0 eV.
2.2 Crystalline field theory
The bonding of metallic complexes is analogous to the action of positive and negative ions in ionic crystals. The metal–ligand interaction is of electrostatic character, and the ligand is treated as a point charge. The role of ligands is to establish a negative charge potential field, and the field is referred to as a crystalline field. Under the perturbation of the crystalline field, the d orbital of the metal undergoes energy level splitting, and the electrons fill the split d orbit from low to high, resulting in a decrease of the total energy after splitting. The splitting energy is called the crystal field stabilization energy.31When the central ion with d electrons is considered, the Hamiltonian of the d electrons is written as:
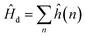 | (1) |
Under the single-electron approximation, the electron–electron interaction term is not considered, and the Hamiltonian operator is defined as:
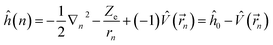 | (2) |
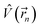 is the electrostatic field of the ligand.
is the electrostatic field of the ligand.
Under the point charge model, the charge of a ligand is defined as −q, and the metal–ligand distance is a. Using results of classical electrostatics, the following equation can be obtained:
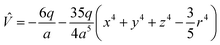 | (3) |
In a spherical coordinate system:
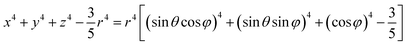 | (4) |
The single electron Schrodinger's equation is:
| (ĥ0 + ĥ′) = εiΨi | (5) |
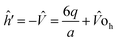 | (6) |
Using the perturbation method to approximately solve the single-electron Schrodinger's equation, the total electron wave function is obtained:
| Ψd = IΨ1…Ψn | (7) |
The total electron energy is written as:
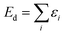 | (8) |
According to crystalline field theory, the symmetry of the crystalline field determines the mode of d orbital splitting, and the perturbation of the energy level splitting is defined as:
| ĥ0Ψi(0) = εi(0)Ψi(0) | (9) |
| εi = εi(0) + Δεi | (10) |
The first order perturbation correction is written as:
| Δεi = Δεi(1) = 〈Ψi(0)|ĥ′|Ψi(0)〉 | (11) |
The zero-order wave function is written as:
| Ψi(0) = Ψnlm = NnlRnl(r,θ)Ylm(θ,φ) | (12) |
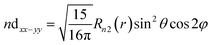 | (13) |
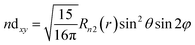 | (14) |
The first order perturbation correction is written as:
| Δεeg = 〈ndxx–yy|ĥ′|ndxx–yy〈 | (15) |
Similarly:
| Δεt2g = 〈ndxy|ĥ′|ndxy | (16) |
3. Results and discussion
3.1 Structure optimization
The crystal structure of Ca2Ge is optimized by GGA-PBE, GGA-RPBE, GGA-PW91, GGA-WC, GGA-PBEsol and LDA approximation methods. The system energy optimized by different approximation methods is shown in Table 1. It can be seen from Table 1 that the lattice constant obtained by the GGA-RPBE method is in good agreement with the experimental value and the energy value calculated is −8454.32 eV, lower than the energy obtained under other approximation methods, indicating that the structure of Ca2Ge obtained using the GGA-RPBE method is the most stable.16 Therefore, the band structure, electron density of states, atomic population and orbital population are calculated using the GGA-RPBE method.| Method | PBE | RPBE | PW91 | WC | PBEsol | LDA |
|---|---|---|---|---|---|---|
| Energy/eV | −8448.27 | −8454.32 | −8453.83 | −8538.13 | −8431.4 | −8452.17 |
| a/Å | 7.201 | 7.182 | 7.20 | 7.148 | 7.148 | 7.00 |
3.2 Band structure
The integral path of cubic phase Ca2Ge is W-L-G-X-W-K along the direction of highly symmetric points in the Brillouin region under the plane wave basis set group. Fig. 2(a)–(d) show the band structure of the intrinsic Ca2Ge and Mn-doped Ca2Ge with spin up and spin down. It can be seen from Fig. 2(a) and (b) that the top and bottom of the spin up and spin down valence bands are both located at point X, forming a direct band gap Eg = 0.57 eV. The band structures of the spin up and spin down states are exactly the same. That is, the intrinsic Ca2Ge has no magnetism, which is consistent with the results in reference.2 Fig. 2(c) and (d) show the band structure diagram of Mn doped Ca2Ge. It can be seen from the figure that the band structure of Mn doped Ca2Ge with spin up forms a direct band gap of 0.32 eV at point X, while the band structure with spin down presents metallic characteristics with a band gap of 0 eV, indicating that Ca2Ge with Mn doping forms a semi-metal. Comparing Fig. 2(a–d), it can be observed that the impurity bands exist for spin up and spin down when Mn is doped. In the spin up band structure, the influence of impurity bands is relatively small, and the band distribution is similar to that of intrinsic Ca2Ge, while in the spin down band structure, the distribution of impurity bands has a greater impact. As a result, the distribution in the spin-down band structure is significantly different from that of the spin-up band structure, indicating that magnetism appears in Ca2Ge after Mn doping. In order to explore the mechanism of magnetism and its source, the density of states is analyzed.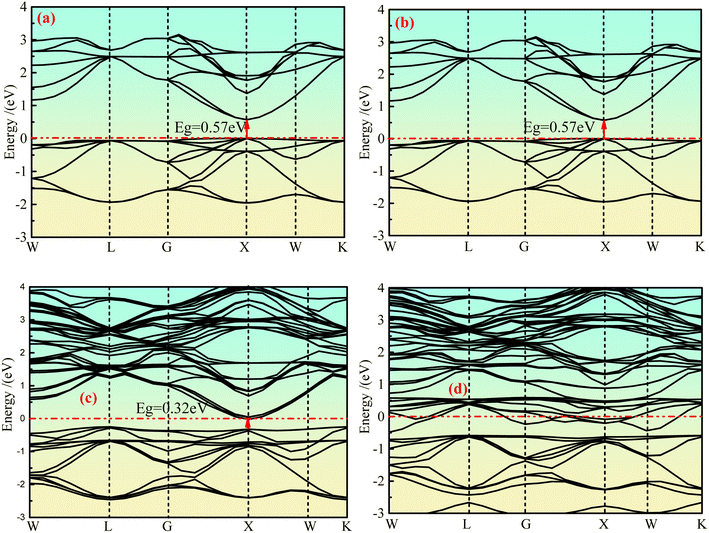 | ||
| Fig. 2 The band structure of Ca2Ge: (a) intrinsic with spin up, (b) intrinsic with spin down, (c) Mn-doping with spin up, (d) Mn-doping with spin down. | ||
3.3 Electron state density
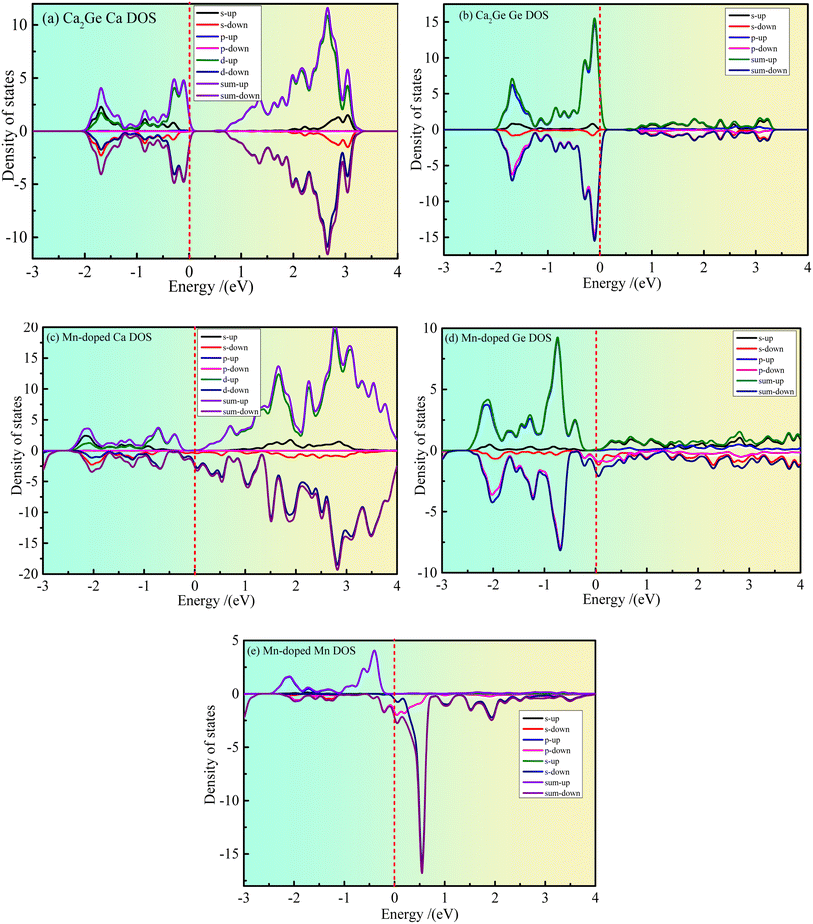
Fig. 3(a–e) show the partial density states (PDOS) of intrinsic Ca2Ge and Mn doped Ca2Ge. Fig. 3(a and b) show the PDOS of Ca and Ge in the intrinsic Ca2Ge system, respectively. It can be seen from Fig. 3(a) that in the energy range of −2–0 eV and 0.6–3.1 eV, contribution is mainly of Ca 3d state electrons. The contribution of Ca 3s state electrons is smaller, and the contribution of Ca 3p state electrons is zero. It can be seen from Fig. 3(b) that the valence band of intrinsic Ca2Ge is mainly contributed to by Ge 2p state electrons in the energy range of −2–0 eV and by Ge 2s state electrons in the energy range of 0.6–3.5 eV. Therefore, the valence band of intrinsic Ca2Ge is mainly contributed to by electrons of Ca 3d and Ge 2p states, and the conduction band is mainly contributed to by Ca 3d state electrons. In the valence band, the density of Ca 3d and Ge 2p states with spin up and down form symmetrical distributions, and in the conduction band, the density of Ca 3d states with spin up and spin down also form symmetrical distributions. Therefore, Ca and Ge do not exhibit magnetism in the intrinsic Ca2Ge system. These results are consistent with the analysis results of the band structure of the intrinsic Ca2Ge.Fig. 3(c–e) show the PDOS of Ca, Ge and Mn in the Mn-doped Ca2Ge system. It can be seen from Fig. 3 that in the energy range of −2–0 eV, the spin up PDOS is mainly contributed to by Ca 3d, Ge 2p and Mn 3d state electrons, while the spin down PDOS is mainly contributed to by Ca 3d and Ge 2p state electrons. In the energy range of 0–4 eV, the spin up PDOS is mainly contributed to by Ca 3d, Ge 2p, and Mn 3d state electrons, while the spin down PDOS is mainly contributed to by Ca 3d, Ge 2p, and Mn 3d electrons. It can be seen from Fig. 3(e) that the density of spin-up and spin-down states presents an asymmetric distribution. In particular, a large spin-up density peak appears near −0.4 eV, and a strong spin-down density peak appears near 0.6 eV. The energy interval between the peaks of the two states is about 1.0 eV. This shows that Mn 3d is magnetic and the orbital splitting energy of Mn is 1.0 eV. At the same time, it is worth noting that when Mn is doped in Ca2Ge, the distribution of the Ca and Ge state densities is affected by Mn, and the densities of the Ca and Ge states are asymmetric. Therefore, it can be inferred that the magnetism of the Mn-doped Ca2Ge system is not only derived from Mn atoms. In order to further clarify the influence of Mn atom doping on the density of Ca and Ge states and the influence on the magnetic properties of the Ca2Ge system, it is necessary to analyze the electron orbitals of each atom in the system. The atomic population and orbital population are discussed below.
3.4 Atomic population
The atom population results show that the magnetic moment of the Mn atom is 5.09 μB, that of the Ge atom is 0.03 μB, and that of the Ca atom is −0.12 μB. The results indicate that the main source of magnetism is the spin polarization of Mn atoms. However, the polarization of Ge and Ca atoms is affected by the polarization of the Mn atom. The Ca atom exhibits antiferromagnetism, the Ge atom exhibits ferromagnetism, and Mn doped Ca2Ge exhibits ferromagnetism. Fig. 4 shows the charge distribution of the electron orbital of Ca2Ge. Fig. 4(a) and (c) show that the distribution of the electron orbital of Ca in the Ca2Ge system changes from the original 3s23p64s2 to the more stable 3s23p63d14s1. In the intrinsic Ca2Ge, the spin up charges of the s, p and d orbitals are equal to those of spin down, for Ca and Ge. In the Mn doped Ca2Ge system, the charges of the s, p and d electron orbitals with spin up and down Mn atoms are quite different. In particular, the Mn 3d orbital has the most significant difference of charge between spin up and spin down. In the doped Ca2Ge system, the spin up and spin down charges of the s and p electron orbitals of the Ge atom are affected by the Mn atom, so that the charge of the s and p electron orbitals of each Ca atom is redistributed. For Ca 3d, the spin up charge increases from 0.25e to 0.34e, and the spin down charge increases from 0.25e to 0.33e, but the charges in the Ca 4s and Ca 3p orbitals are almost unaffected. However, Mn doping has different effects on each Ge atom, and the discussion of the change of the charge of the Ge atom is based on the average effect. For the Ge 3s orbital, the spin up charge decreases from 0.99e to 0.9e, and the spin down charge decreases from 0.99e to 0.86e. For the Ge 3p orbital, the spin up charge decreases from 2.04e to 1.91e, and the spin down charge decreases from 2.04e to 1.84e. The results show that the charge of Ca 3d is increased, and the charge of Ge 3s and Ge 3p decrease with Mn doping. Simultaneously, the charge revolutions of Ca and Ge are changed by Mn doping. In the intrinsic Ca2Ge system, each Ca atom transfers and gains 1.02e, and each Ge loses 2.05e. However, each Ca atom gains 0.85e, the Mn atom loses 2.07e, and the three Ge atoms lose 1.64e, 1.57e, and 1.58e with Mn doping.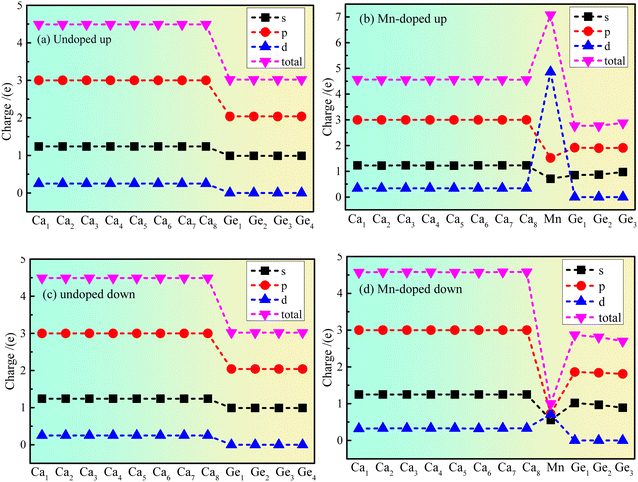 | ||
| Fig. 4 The charge distribution of electron orbitals of Ca2Ge: (a) spin up of intrinsic Ca2Ge, (b) spin up of Mn doped Ca2Ge, (c) spin down of intrinsic Ca2Ge, (d) spin down of Mn doped Ca2Ge. | ||
3.5 Orbital populations
Fig. 5 shows the orbital energy level spin of Ca2Ge. Fig. 5(a) shows that the Ca d orbital is split into dxy, dyz, dxz, dxx–yy and dzz orbitals by the force of the crystal field in the intrinsic Ca2Ge system. The maximum angle of the dxy, dyz and dxz orbitals is between the axes, forming a plane-symmetric orbital and forming a t2g orbital level with the same polarization. The maximum values of dzz and dxx–yy along the axial direction form an axially symmetric orbital and form an eg orbital with the same polarization. t2g and eg have equal magnetic moments of spin up and spin down, so the d orbital does not exhibit magnetism. When Mn is doped, the spin up state of t2g is split into dyz, dyz and dxz orbitals, and dyz is lower spin, while dyz and dxz are high spin. The spin up state of the eg orbital is split into dzz and dxx–yy orbitals. The order of polarization of each orbital is as follows: dxy, dxz > dyz > dzz > dxx–yy. The spin down states of the t2g and eg orbitals are split into dxy, dyz, dxz, dxx–yy and dzz orbitals with different polarization. The order of polarization of each orbital is as follows: dyz > dxz > dxy > dxx–yy > dzz. Thus, when Mn is doped, the contribution of spin splitting to the magnetic moment of the d orbital is in the following order: dxy > dyz > dxz > dxx–yy > dzz. Fig. 5(b) shows the orbital level spin of Ge p. In the intrinsic Ca2Ge system, the spin polarizations of the px, py and pz orbitals are the same. When Mn is doped, the polarization of the spin up and spin down states decreases, the spin polarizations of the px, py and pz orbitals are different, and the contributions of spin splitting to the magnetic moment of the p orbital are in the order py > pz > px.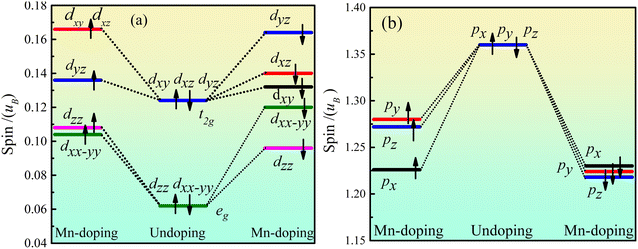 | ||
| Fig. 5 Ca2Ge orbital level spin of Ca2Ge: (a) the orbital energy level spin of Ca d, (b) the orbital energy level spin of Ge p. | ||
4. Conclusions
In this work, the electronic structure and electromagnetic properties of Mn doped Ca2Ge were studied by the first principles method based on density functional theory, and its magnetization mechanism was analyzed. The mechanism of Mn doped Ca2Ge forming a dilute magnetic semiconductor was explained. The conclusions are as follows:(1) Mn doped Ca2Ge has two modes, one of which is Mn replacing Ca atoms, and Ca2Ge forming a metal; the other is Mn replacing Ge atoms, and Ca2Ge forming a semi-metal. The spin up band structure forms a direct band gap of 0.32 eV, and the spin down band structure presents metallic characteristics.
(2) Electron state density and atomic population analysis shows that one of the electrons in the 4s orbital of Ca is transferred to the 3d orbital, forming a 3s23p63d14s1 configuration that is more stable than the 3s23p64s2 configuration. The orbital splitting energy as a result of the Mn doping is 1.0 eV, which has a weak polarizing effect on Ca 3d and Ge 3p electrons. The result leads to an increase in the orbital electrons of Ca 3d, a decrease in the orbital electrons of Ge 3p, the charge transfer of the Ca atom decreasing, the charge transfer of the Ge atom increasing, and the formation of a ferromagnet with a molecular magnetic moment of 5.0 μB.
(3) The doping of Mn atoms changes the crystal field of Ca2Ge, so the charge, orbital and spin of each atom are redistributed. The degenerate energy levels of t2g and eg of Ca are relieved and split into dzz, dzy, dzx, dxy and dzz−yy orbitals, while the degenerate energy levels of Ge p are relieved and split into px, py, pz orbitals. Under the action of the crystal field, the spin up and spin down polarization magnetic moment increases, and the magnetism of Ca2Ge is improved, forming a dilute magnetic semiconductor.
Data availability
The data that support the findings of this study are available on request from the corresponding author.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the National Natural Science Foundation of China (Grant No. 51661005 and U1612442), the Science and Technology Foundation of Guizhou Province, China (No. 1Y[2020]200, 1Y[2020]205), the Youth Science and Technology Talents Growth Fund Program of the Ministry of Education Province, China (No. KY[2021]103, KY[2022]155), the teaching reform project of Guizhou Minzu University, China.References
- J. M. K. Al-zyadi, A. H. Ati and K.-L. Yao, Bulk and surfaces half-metallicity of RbSe with zinc-blende structure: first-principles study, Appl. Phys. A., 2020, 126, 612 CrossRef CAS.
- D. Wu, H. Lv, Z. Zhou, X. Li, X. Wu and J. Yang, Orbital design of two-dimensional transition-metal peroxide Kagome crystals with antioncogenic Dirac half metallicity, J. Phys. Chem. Lett., 2021, 12, 3528–3534 CrossRef CAS PubMed.
- R. Dhakal, S. Nepal, I. Galankis, R. P. Adhikan and G. C. Kaphle, Prediction of half-metallicity and spin-gapless semiconducting behavior in the new series of FeCr-based quaternary Heusler alloys: An ab initio study, J. Alloys Compd., 2021, 852, 160500 CrossRef.
- M. Mushtaq, I. Muhammad, A. Ali, M. Atiff Sattar and S. Muhammad, First-principles search for half-metallic ferromagnetism in CsCrZ2 (Z=O, S, Se or Te) Heusler alloys, J. Mol. Graphics Modell., 2020, 98, 107620 CrossRef CAS PubMed.
- S. Idrissi, S. Ziti, H. Labrim and L. Bahmad, Half-metallicity and magnetism in the full Heusler alloy Fe2MnSn with L21 and XA stability ordering phases, J. Low Temp. Phys., 2021, 202, 343–359 CrossRef CAS.
- Y. Li, J. Zhu, P. Ramesh, J. Huang and F. Zhou, Screen the half-metallic X2Y (Al/Si) full-Heusler alloys based on the first-principles calculations, Comput. Mater. Sci., 2021, 193, 110391 CrossRef CAS.
- A. N. Andriotis and M. Menon, Magnetism versus band-gap relationship in diluted magnetic semiconductors: megadome impurity behavior of the magnetic dopant complexes, J. Phys.: Condens.Matter, 2022, 34(1–8), 195801 CrossRef CAS PubMed.
- A. Kuman, M. Kumar, P. Chandra Sati, M. K. Srivastava, S. Ghosh and S. Kumar, Structural, magnetic and optical properties of diluted magnetic semiconductor (DMS) phase of Ni modified CuO nanoparticles, Curr. Appl. Phys., 2021, 32, 24–35 CrossRef.
- M. Kaminska and A. Twardowski, Mn and other magnetic impurities in GaN and other III-V semiconductors-perspective for spintronic applications, J. Mater. Sci., 2008, 19, 828–834 CAS.
- Y. Zhang, Z. Liu, Z. Wu, X. Ma and G. Wu, Influence of order on the magnetic and electronic properties of quaternary half-metallic Heusler CoFeTiSn alloy, J. Alloys Compd., 2020, 842, 155977 CrossRef CAS.
- D. N. Papadimitriou, Structural, optical, electrical properties, and strain/stress of electrochemically deposited highly doped ZnO layers and nanostructured ZnO antireflective coatings for cost-effective photovoltaic device technology, Thin Solid Films, 2016, 605, 215–231 CrossRef CAS.
- L. Testseris, Novel Au- and Ge-based two-dimensional materials formed through topotactic transitions of AB2-like structures, Nonascale, 2016, 8(28), 13558–13561 RSC.
- L. Tsetseris, Ca- and Sc-based ternary AlB2-like crystals: a first-principles study, J. Phys.: Condens.Matter, 2017, 29(1–7), 045701 CrossRef PubMed.
- N. Mamouni, F. Goumrhar, E. Salmani, A. Benyoussef and H. Ez-Zahraouy, Spin-orbit interaction in SnO2 based diluted magnetic semiconductor: Ab-initio calculations, J. Magn. Magn. Mater., 2021, 535, 168084 CrossRef CAS.
- I. Jabbar, Y. Zaman, K. Althubeiti, S. Al Otaibi, M. Zahid Ishaque, N. Rahman, M. Sohai, A. Khan, A. Ullah, T. Del Rosso, Q. Zaman, R. Khan and A. Khan, Diluted magnetic semiconductor properties in TM doped ZnO nanoparticles, RSC Adv, 2022, 12, 13456 RSC.
- C. Autieri, C. Sliwa, R. Islam, G. Cuono and T. Dietl, Momentum-resolved spin splitting in Mn-doped trivial CdTe and topological HgTe semiconductors, Phys. Rev. B, 2021, 103, 115209 CrossRef CAS.
- G. Ding, J. Wang, H. Chen, X. Zhang and X. Wang, Investigation of nodal line spin-gapless semiconductors using first-principles calculations, J. Mater. Chem. C, 2022, 10, 6530–6545 RSC.
- F. Ungar, M. Cygorek and V. M. Axt, Trend reversal in the magnetic-field dependence of exciton spin-transfer rates in diluted magnetic semiconductors due to non-Markovian dynamics, Phys. Rev. B, 2018, 97, 045210 CrossRef CAS.
- D. B. Migas, L. Miglio, V. L. Shaposhnikov and V. E. Borisenko, Comparative study of structural, electronic and optical properties of Ca2Si, Ca2Ge, Ca2Sn, and Ca2Pb, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(20), 1–7 CrossRef.
- S. A. Dotsenko, D. V. Fomin, K. N. Galjin, D. D. Goroshko and N. G. G. Growth, optical and electrical properties of Ca2Si film grown on Si(111) and Mg2Si/Si(111) substrates, Phys. Procedia, 2011, 11, 95–98 CrossRef CAS.
- M. G. Brik, Comparative first-principles calculations of electronic, optical and elastic anisotropy properties of CsXBr3 (X=Ca, Ge, Sn) crystals, Solid State Commun., 2011, 151(23), 1733–1738 CrossRef CAS.
- J. Tani and H. Kido, Investigation of structural, elastic, and lattice-dynamical properties of Ca2Si, Ca2Ge and Ca2Sn based on first-principles density functional theory, Comput. Mater. Sci., 2015, 97, 36–41 CrossRef CAS.
- L. Lin, Y. Yang, W. Cen, B. Yao and J. Ou, Effect of As and Ga doping on the electronic structure and photoelectric properties of cubic Ca2Ge, Mater. Res. Express, 2020, 7(12), 126304 CrossRef CAS.
- H. Okamoto, CaGe (Calcium-Germanium), J. Phase Equilib., 2003, 24(6), 581 CrossRef CAS.
- Y. Djaballah, A. Pasturel and A. Belgacem-Bouzida, Thermodynamic assessment of the calcium-germanium system, J. Alloys Compd., 2010, 497, 74–79 CrossRef CAS.
- H. Bouderba, Y. Djaballah, A. Belgacem-Bouzida and R. Beddiaf, Temperature and pressure effects on phase stabilities in the Ca-Ge system from first-principles calculations and Debye-Gruneisen model, Intermetallics, 2012, 28, 108–119 CrossRef CAS.
- R. Wang, Z. Tian, Q. Xiao, W. Cen and Q. Zheng, The effect of Ni/Co-doping on electronic structure and optical properties of cubic Ca2Ge, Optik (Stuttg.), 2021, 243, 167422 CrossRef CAS.
- M. O. Shevchenko, M. I. Ivanov, V. V. Berezutski, M. L. Ivanov and V. S. Sudavtsova, Thermodynamic Properties of Alloys in the Binary Ca-Ge System, J. Phase Equilib. Diffus., 2015, 36(6), 554–572 CrossRef CAS.
- V. Milman, K. Refson, S. J. Clark, C. J. Pickard, J. R. Yates, S.-P. Gao, P. J. Hasnip, M. I. J. Probert, A. Perlov and M. D. Segall, Electron and bibrational spectroscopies using DFT, plane waves and pseudopotentials: CASTEP implementation, J. Mol. Struct.: THEOCHEM, 2010, 954, 22–35 CrossRef CAS.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, First-principles simulation: ideas, illustrations and the CASTEP code, J. Condens. Matter Phys., 2002, 14, 2717–2744 CrossRef CAS.
- M. D. Waton, L. J. Collins-Mclntyre, L. R. Shelford, A. I. Coldea, D. Prabhakaran, S. C. Speller, T. Mousavl, C. R. M. Grovenor, Z. Salman, S. R. Giblin, G. van der Laan and T. Hesjedal, Study of the structural, electric and magnetic properties of Mn-doped Bi2Te3 single crystals, New J. Phys., 2013, 14, 103016 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |