Open Access Article
Open Access ArticlePhase transitions and spectral shifts: a quantum mechanical exploration of vibrational frequency in magnesium ferrite†
Tahani Saad Almutairi *
*
Department of Chemistry, Section of Physical Chemistry, Taibah University, Madinah, 42353, Saudi Arabia. E-mail: talmutairi@taibahu.edu.sa
First published on 16th January 2024
Abstract
Spinel ferrites represent an integral subset of magnetic materials, with their inherent properties largely influenced by cation occupancy and spin interaction. In this study, we present an in-depth theoretical exploration of the phase transition landscape of pure magnesium-ferrite, deploying hybrid functionals and a local Gaussian basis set to scrutinize the relaxed lattice structure, relative energy, magnetic properties, electronic characteristics, and vibrational frequencies. Our investigation reveals that the ground state of magnesium-ferrite is an open-shell system with an inverse structure. This is characterized by the complete occupancy of octahedral sites by magnesium atoms, with Iron atoms dispersed between both tetrahedral and octahedral sites. We found a relative energy difference of 0.41 eV between the antiferromagnetic ground configuration and the ferro arrangement within the inverse structure. Furthermore, our research also delved into the impact of spin rearrangement and inversion (X = 0.0, 0.5 and 1) on Raman and infrared spectra. Notably, the lattice distortion from the cubic form, apparent in the optimized structure, resonates in the IR and Raman spectra, resulting in significant splitting. The frequencies calculated in this study align well with experimental values, suggesting that the literature's current assignments warrant reevaluation in light of this new data. The results presented herein can be instrumental in detecting the phase of Mg ferrites from experimental spectra, thereby paving the way for a more profound comprehension of their properties and possible uses.
1. Introduction
Ferrite materials (MFe2O4) (M = Ni, Co, Mn, Mg or Zn) have gained prominence as multifaceted materials in recent years, offering a myriad of applications in cutting-edge technology. These spinel-structured oxide materials demonstrate exceptional physical, chemical, and magnetic properties, making them an essential component in diverse areas, such as electronics, communications, energy, and environmental sectors.1–3 As a versatile material, Mg ferrite possesses unique magnetic and physical properties that render it useful across a wide array of applications.4–7 Its high magnetic permeability, minimal magnetic losses, and remarkable magnetic stability make it ideal for magnetic cores,8 while its high electrical resistivity and low thermal conductivity render it a promising material for energy conversion applications.9Mg ferrite can adopt spinel structures in which divalent metal ions and trivalent metal distributed over the octahedral and tetrahedral sites.10–12 Various techniques are in place to manipulate Mg ferrite's crystal structure and composition, which subsequently influences its magnetic and electrical properties. These include synthesis methods, doping, processing conditions, post-processing treatments, and ligand functionalization.6,11,13–17 Adjusting the crystal structure and composition of Mg ferrite requires a deep understanding of its inherent properties and the invention of innovative synthesis and processing methods to customize its properties for specific utilities.18,19 Numerous studies have highlighted the profound influence of thermal treatment on Mg ferrite's magnetic properties, attributing it to the distribution and magnetic ordering of cations over tetrahedral and octahedral sites.20–22
The captivating world of vibrational spectra of ferrites is a field that has seen considerable attention in scientific literature, thanks to the theoretical foundations laid by Waldron.23,24 Waldron's model interprets the vibrations of this system using the point group Td's irreducible representations. In principle, four IR active normal vibrations can be identified. The v1, the highest frequency, is associated with vibrations along the tetrahedral bonds. Meanwhile, the v2 frequency relates to vibrations along the octahedral bonds. The v3 and v4, on the other hand, represent the metal ion vibrations within their respective tetrahedral and octahedral environments. However, every model has its limitations. Waldron's model, as well as those proposed by White and De Angelis, have shown some challenges in interpreting certain characteristics observed in experimentally obtained spectra.25 For instance, variations and splitting in the v1 and v2 bands reported by different researchers for distinct ferrites are perplexing phenomena yet to be fully explained. Moreover, inverse spinals add another layer of complexity. In these instances, each degenerate vibration may undergo splitting, leading to three separate frequency vibrations. This splitting primarily happens due to symmetry reduction. Numerous factors have been proposed to explain the splitting observed in the main bands, such as the Jahn–Teller distortions, the presence of a divalent metal in the octahedral complex, and the varying synthesis conditions.25,26 The assignment of Raman modes further complicates the scenario as there are discrepancies between different studies.10,27,28 Interestingly, the splitting of the five modes predicted by group theory for the cubic structure has also been observed.16,29 A particularly elusive area is the phase transformation between various Mg ferrite configurations and their impact on frequencies, a topic rarely explored in literature using density functional theory (DFT).7,30–33 This study aims to bridge this gap by examining the influence of cation distribution and magnetic ordering on the infrared (IR) and Raman spectra through DFT and using a hybrid functional. The ultimate goal is to provide theoretical insight into the phase change landscape of Mg ferrite, shedding light on the complexities of this fascinating field.
2. Computational methods
Theoretical investigations were performed within the framework of density functional theory (DFT) using the CRYSTAL17 software.34 The functionals utilized in the calculations include the global hybrid functional B3LYP (20% of HF exchange),35 PBE0 (25% of HF exchange),36 and range-separated HSE06 (the fraction of HF exchange varies based on the distance between electrons),37 which largely rectify the self-interaction error of pure DFT functionals. The choice of functionals is essential in DFT, as they significantly affect the predicted relative energies and thereby influence the interpretation of system stability and vibrational properties. B3LYP, in particular, has garnered widespread acceptance for its consistent performance in modeling a diverse array of chemical systems.34,38,39 It merges the Becke three-parameter exchange with the Lee–Yang–Parr correlation functional, offering an extensively benchmarked and experimentally validated balance of accuracy and computational tractability. This has cemented its status as a preferred choice for computational studies, particularly when a reliable depiction of crystal behavior is paramount. Furthermore, B3LYP's ability to predict vibrational frequencies and other electronic properties is well-documented in comparative literature, underscoring its reliability and the rationale for its selection in this study. Gaussian-type functions were utilized for the all-electron basis set for all atoms involved.40–42 The optimized structure enabled us to derive the IR and Raman active frequencies and intensities. We employed spin-polarized computations to investigate the effect of spin ordering on electronic and structural properties. In the ferromagnetic (FM) configuration, all magnetic moments were initially oriented in one direction. Conversely, in the antiferromagnetic (AFM) configuration, the magnetic moments between two Fe atoms in the unit cell were set to be antiparallel. The five thresholds, denoted as Ti, which govern the truncation criteria for the Coulomb and exchange infinite series, were set to 8 (T1–T4) and 16 (T5). The self-consistent-field cycle used 10−8 and 10−10 Hartree energy convergence thresholds for optimization and vibration frequency calculations, respectively. The comprehensive optimization process, which involved lattice parameters and all atomic bases in the cell, used a root mean square (r.m.s.) displacement of 10−5 Å. The shrinking factors dictating the count of independent k-points employed in the sampling of the Monkhorst–Pack grid were configured to 88. The frequencies (wavenumber) ωp were computed from second energy derivatives relative to atomic displacements u at the Γ point,43,44 according to the following equations.
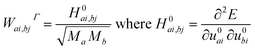 | (1) |
In these equations, u denotes the atomic displacements of atom a, and b in the system, with the atomic mass, respectively. The i-th and j-th denote atomic coordinates. We were then able to determine the shift in frequencies due to isotopic substitutions at no additional computational cost by replacing the masses in eqn (1). The study used a coupled Perturbed–Hartree–Fock/Kohn–Sham method (CPHF/KS)45,46 to calculate the integrated intensity for IR absorption and evaluated Raman intensities analytically.
3. Results and discussion
3.1 Bond lengths, charge and spin distribution, energy, and band structure
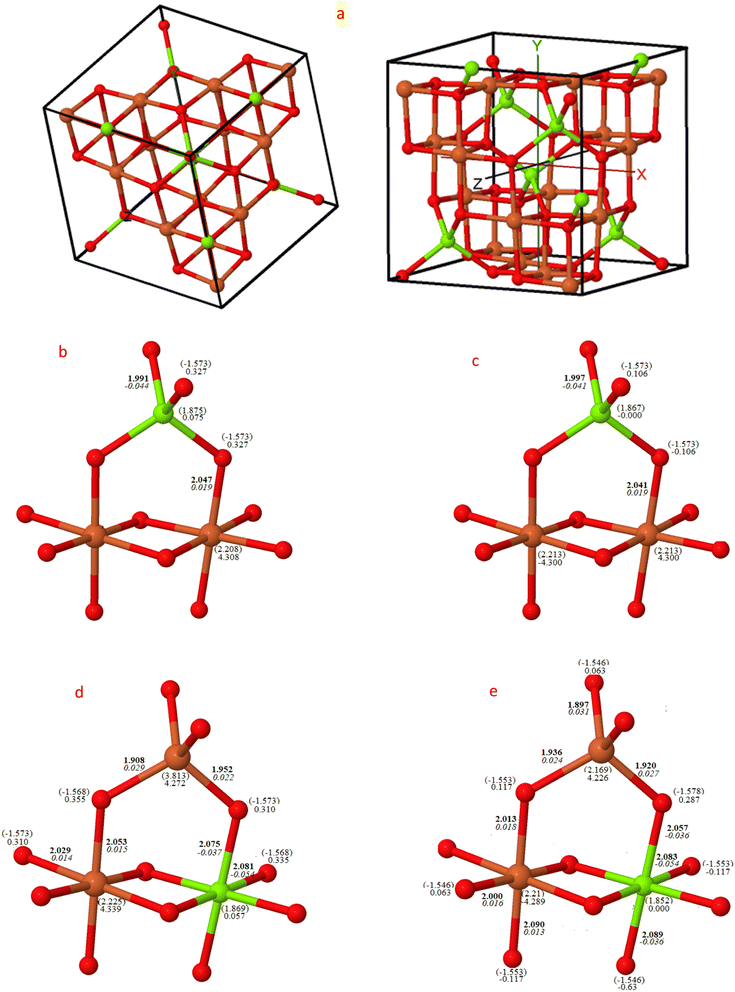
The consolidated visualizations of the converged structures of both normal and inverse magnesium ferrite in their two spin configurations, ferromagnetic (FM) and antiferromagnetic (AFM), are depicted in Fig. 1. Under both FM and AFM conditions, the cubic symmetry is preserved when X = 0, as demonstrated by the Mg–O and Fe–O bond lengths of approximately 4 × 1.99 Å and 6 × 2.04 Å. These measurements align closely with the recorded values of 1.99 Å and 2.02 Å, respectively.19 The charge and spin distribution data highlight the ionic properties of the system, with the oxygen atom gaining a charge of −1.57|e|, while magnesium and iron atoms lose charges of 1.87|e| and 2.21|e| respectively. Bond populations are reported as −0.04 and 0.02 respectively. In the AFM configuration, there is a distinct alternating distribution of spin densities over the iron atoms in B-sites (4.3|e| α, −4.3|e| β), thereby maintaining a net zero spin per cell. However, in the FM configuration, all spins align parallel (4.3 α).With the complete transformation to inverse structure, there is a clear distortion from the cubic form, resulting in two and three non-equivalent Fe–O and Mg–O bond lengths for FM (X = 1) and AFM (X = 1) respectively. This alters both the charge and spin distributions, as indicated in Fig. 1. The magnetic moment of iron in the A-site is smaller than in the B-site by approximately 0.06|e|, and inversely, the magnetic moment of Mg in the B-site is lower than in the A-site by 0.02|e| in the FM configuration, but this becomes zero in both AFM structures. The FM lattice parameter when X = 0 is 8.51 Å, which decreases to 8.46 Å when inverted to FM (X = 1), closely matching the measured value of 8.44 Å.47
The relative energy difference among the six optimized structures was analyzed using three functionals and is presented in Table 1. The most stable configuration was determined to be the inverse structure with AFM arrangements.27,48 MFO is an antiferromagnetic material, with magnetic moments aligned in an antiparallel orientation, resulting in a net magnetic moment of zero. This is consistent with experimental observations of zero magnetization at a Curie temperature of 738 K.49 This antiferromagnetic behavior is attributed to its inverse spinel structure, where the magnetic moments of iron ions on tetrahedral sites are compensated by the magnetic moments of iron ions on octahedral sites due to the nonmagnetic nature of magnesium atoms. The energy difference between FM and AFM in the (X = 1) arrangement was found to be notably high at 0.41 eV (B3LYP), even considering the free energy inclusive of zero-point energy (Table 2).
| Functionals | (X = 0) | (X = 0.5) | (X = 1) | ||||
|---|---|---|---|---|---|---|---|
| FM | AFM | FM | AFM | FM | AFM | ||
| B3LYP | E | −6057.0980 | −6057.0950 | −6057.0882 | −6057.0988 | −6057.0905 | −6057.1059 |
| ER | 0.21 | 0.29 | 0.48 | 0.19 | 0.41 | 0.00 | |
| HSE06 | E | −6055.9801 | −6055.9767 | −6055.9687 | −6055.9784 | −6055.9704 | −6055.9845 |
| ER | 0.12 | 0.21 | 0.43 | 0.16 | 0.38 | 0.00 | |
| PBE0 | E | −6055.9858 | −6055.9823 | −6055.9747 | −6055.9841 | −6055.9764 | −6055.9901 |
| ER | 0.12 | 0.21 | 0.42 | 0.16 | 0.37 | 0.00 | |
| Energy | X = 0 | X = 0.5 | X = 1 | |||
|---|---|---|---|---|---|---|
| FM | AFM | FM | AFM | FM | AFM | |
| EL | −164822.0184 | −164821.9344 | −164821.7512 | −164822.0390 | −164821.8142 | −164822.2312 |
| E0 | 0.9533 | 0.9406 | 0.9544 | 0.9510 | 0.9580 | 0.9602 |
| ET | 0.3613 | 0.3668 | 0.3608 | 0.3624 | 0.3589 | 0.35819 |
| S (meV per (cell K)) | 1.9515 | 1.9954 | 1.9414 | 1.9549 | 1.9208 | 1.9171 |
| PV | 0.0000975 | 0.0000974 | 0.0000968 | 0.0000961 | 0.0000958 | 0.0000957 |
| TS | 0.5818 | 0.5949 | 0.5788 | 0.5828 | 0.5727 | 0.5715 |
| ET + PV − TS | −0.2203 | −0.2279 | −0.2178 | −0.2203 | −0.2136 | −0.2133 |
| EL + E0 + ET + PV − TS | −164821.2855 (0.20) | −164821.2218 (0.26) | −164821.0147 (0.47) | −164821.3083 (0.18) | −164821.0698 (0.41) | −164821.4843 (0.00) |
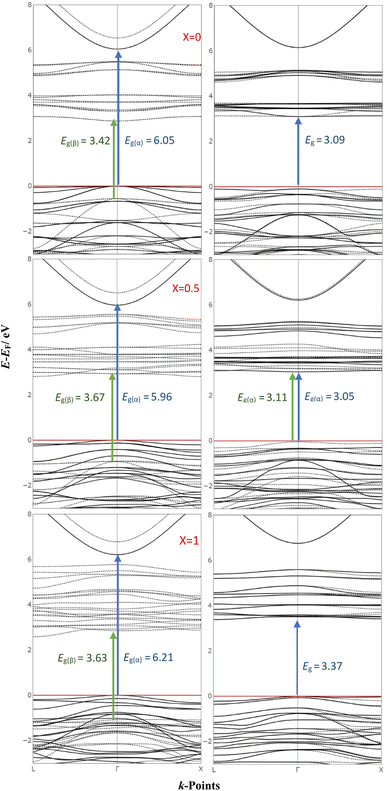
The band structures of MFO in their FM configurations were compared to their corresponding AFM configurations, as illustrated in Fig. 2. The influence of inversion on the electronic structure was minimal, with the band gap increasing by 0.16 eV for α bands and 0.21 eV for β bands in FM and by 0.28 eV in AFM upon transitioning from the normal to inverse structure. The band gaps of the AFM structures in this study closely match the measured value of 2.48 eV for samples calcinated at 700 °C,50 and 2.38 eV (ref. 51) for those calcinated at 550 °C. The variations in band gaps with changing temperatures may be related to cation disorder within the crystal or existing defects such as oxygen vacancies.30,52 In the FM configuration (X = 0 and 1), the band gaps along the α and β spins are open at the gamma point (direct band gap), while only the α gap is direct for X = 0.5. In the AFM configuration, the shift between the α and β bands is minor, resulting in virtually identical band gaps.
3.2 Spectroscopic characterization: investigating crystal structures via Raman and infrared spectroscopy
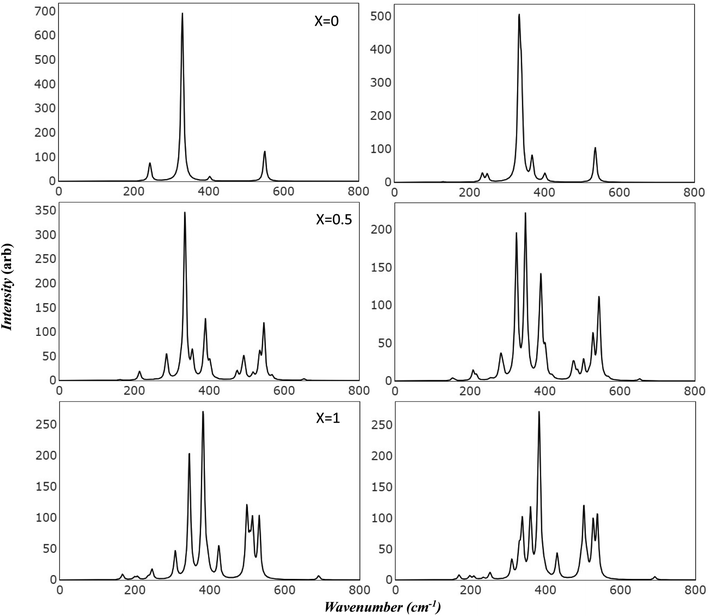
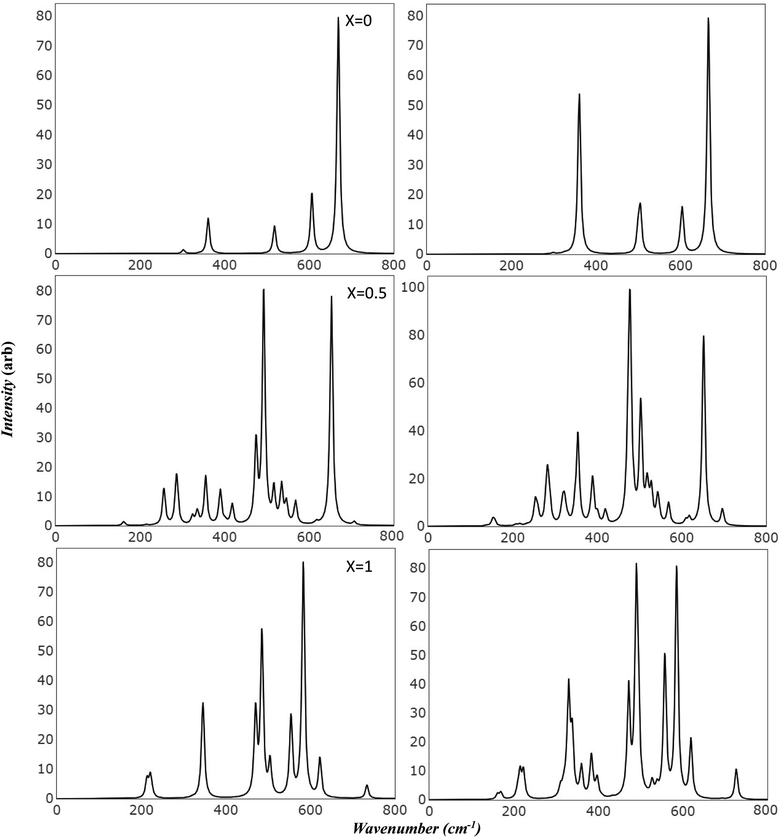
Raman and Infrared spectroscopy serve as robust methodologies for comprehensively probing vibrational properties in various materials. These techniques provide invaluable perspectives on the crystal structure, chemical composition, and defective characteristics by scrutinizing the frequency and intensity of the scattered light. Additionally, they can be employed to investigate the impact of extrinsic factors, such as temperature and pressure, on the vibrational characteristics of the material under study. Through meticulous observation of spectral changes under diverse conditions, researchers can achieve a more profound comprehension of the physical principles that govern the magnetic and electrical attributes of Mg ferrite. Importantly, the simulated spectra has introduced a powerful tool in scientific resources. This facilitates precise characterization of spectral features, effectively avoiding numerous confounding factors such as preparation methods, temperature variations, defects, and intrinsic structural disorder, which may otherwise make the analysis unclear.Fig. 3 presents the simulated vibrational frequencies and intensities of Mg ferrite geometries (X = 0.0, 0.5, 1.0) within two spin configurations: ferromagnetic (FM) and antiferromagnetic (AFM). All spectra are computed at the B3LYP level and visualized using a pseudo-Voigt function, a linear combination of Lorentzian and Gaussian functions, with a full width at half maximum of 8 cm−1. For the FM configuration (X = 0.0), four triply degenerate T1u modes, predicted by group theory analysis for the Fd3m space group structure, are discerned. These four peaks are observed at 243, 330, 403, and 550 cm−1, with the peak at 330 cm−1 showcasing an exceptionally high intensity compared with the others. The two lowest frequency peaks are subject to disagreement across different papers regarding their detection and precise location.10 In its AFM counterpart, the intense peak is slightly affected by the new configuration (332 cm−1), with a small peak appearing at 338 cm−1. Additional minor peaks emerge at 129 and 367 cm−1, and the low-frequency peak (243) splits into two peaks at 234 and 247 cm−1. At higher frequencies, peaks are observed at 400 and 403 cm−1, and one at 536 cm−1, marking a shift of 14 cm−1 compared to 550 cm−1 in FM. The FM spectra analysis reveals that the peak at 243 cm−1 is associated with the bending mode of the Fe–O–Mg bond, and the subsequent two peaks at 330 and 403 cm−1 are connected to the bending bond of O–Mg–O and Fe–O–Mg. The highest frequency band at 550 cm−1 signifies a combination of the stretching mode of the Mg–O bond and the bending mode of the Fe–O–Mg bond.
In the AFM configuration, the peak at 129 cm−1 involves the bending modes of Fe–O–Mg and Fe–O–Fe, and the subsequent two peaks at 234 and 247 cm−1 entail the bending mode of Fe–O–Mg, sustaining the same modes as the 243 cm−1 in FM. The peak at 332 cm−1 and its shoulder at 338 cm−1 are more correlated than other modes, as they comprise the stretching mode of Fe–O–Fe and bending modes of O–Mg–O, Fe–O–Fe, and Fe–O–Mg. The final modes (400, 403, 536 cm−1) involve the bending and stretching of O–Mg–O and Fe–O–Mg bonds.
The IR spectra reflect splitting upon transitioning from normal to complete inverse structure. For FM (X = 1.0), low frequency region reveals a small peak at 167 cm−1, followed by peaks at 199, 207, and 246 cm−1, which correspond to the 243 cm−1 peak in FM (X = 0). These peaks are associated with the bending mode of both cations, except for the modes at 207 and 246 cm−1, which relate to the iron cation, O–Fe–O. The peak at 246 cm−1 appears with small shoulders at 236 cm−1, signifying a combination of bending modes of O–Fe–O, FeO–Mg– and Fe–O–Fe. At moderate frequencies, high-intensity peaks appear at 308 cm−1, encompassing the bending of all cations, and 346 cm−1, marking the stretching mode of O–Fe–O. A peak at 383 cm−1 has the highest intensity and involves a complex mode of Mg–O stretching and Fe–O–Mg bending. The peak at 424 cm−1 exhibits stretching modes for Fe–O and Fe–O–Mg. In the high-frequency region, a group of split peaks are observed (499, 507, 514, and 532 cm−1), corresponding to the unsplit peak at 550 cm−1 in FM (X = 0). The mode at 499 cm−1 is linked to the stretching of Fe–O and Mg–O bonds and the bending of Fe–O–Fe. The peaks at 507 and 514 cm−1 relate to the stretching of Mg–O and the bending of O–Mg–O, respectively, and the one at 532 cm−1 involves the stretching of Fe–O bonds.
The highest frequency peak at 690 cm−1 appears in an otherwise flat area in the normal spectra, making it a potential marker for identifying the inverted structure. This mode involves the stretching of Fe–O and the bending of Fe–O–Mg and Fe–O–Fe. Baraton et al. detected this high frequency peak for Mg ferrite at 700 cm−1, alongside the two main peaks (v1, v2) at 581 and 424 cm−1, and found that it becomes more pronounced as the Mg content increases.10
Table 3 presents a comparison of the frequencies observed in FM and AFM orderings within an inverted structure. A marked shift is observed for AFM (where X = 1) when compared to its FM counterpart. Specifically, the peaks observed at 252, 431, 527, and 539 cm−1 in AFM display an upward shift by 6, 7, 13, and 7 cm−1, respectively, when compared to the corresponding FM frequencies (246, 424, 514 and 532 cm−1). In the FM spectrum, the peak at 346 cm−1 diminishes to half its original intensity when it shifts to 338 cm−1 in the AFM spectrum. This shift is accompanied by the emergence of a new peak at 360 cm−1. The group of FM peaks at 499, 507, 514, 532 cm−1 exhibit a significant shift in the AFM spectrum, appearing at 494, 511, 527 and 539 cm−1, respectively. Their intensities also decrease by half. A dominant peak emerges at 503 cm−1 in the AFM spectrum, displaying a high intensity. This peak is associated with the stretching mode of both Fe–O and Mg–O bonds. The two modes at 494 and 511 cm−1 blend with the 503 cm−1 peak, resulting in a broad, dominant peak.
| Sy | Frequencies (cm−1) FM (X = 1) | Frequencies (cm−1) AFM (X = 1) | Shifts (cm−1) |
|---|---|---|---|
| B2u | 167 | 169 | +2 |
| B3u | 199 | 198 | −1 |
| B2u | 207 | 209 | +2 |
| B1u | 236 | 234 | −2 |
| B3u | 246 | 252 | +6 |
| B1u | 308 | 310 | +2 |
| B2u | 346 | 338 | −8 |
| 360 | |||
| B3u | 381 | 382 | −1 |
| B1u | 383 | 384 | −1 |
| B3u | 394 | 394 | 0 |
| B2u | 395 | 397 | +2 |
| B1u | 408 | 408 | 0 |
| B3u | 424 | 431 | +7 |
| B3u | 499 | 494 | −5 |
| B1u | 507 | 503 | +4 |
| 511 | |||
| B1u | 514 | 527 | +13 |
| B1u | 529 | 529 | 0 |
| B2u | 532 | 539 | +7 |
| B1u | 690 | 692 | +2 |
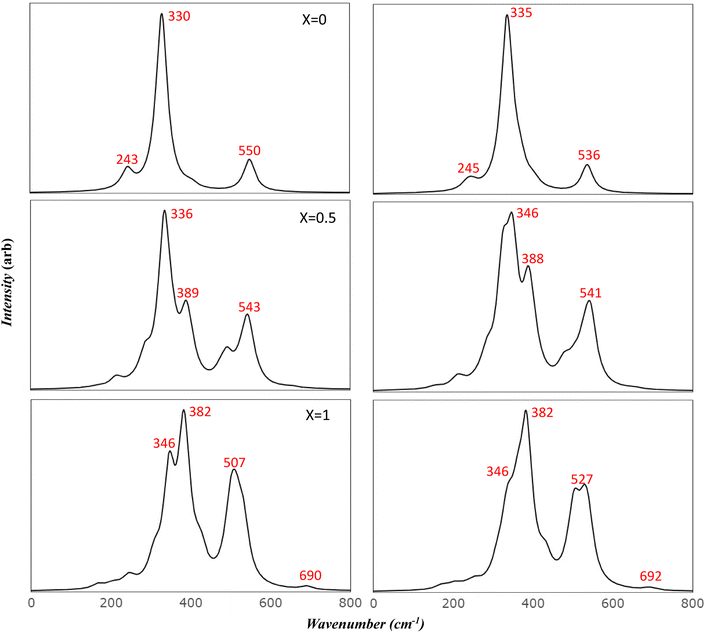
To more accurately mimic the experimental broadening of peaks and create a more representative image, we adjusted the full width half maximum value from 8 to 35 cm−1. This was done using a linear combination of Lorentzian curves to derive the pseudo-Voigt functional form, as depicted in Fig. 4. The results we obtained showed a satisfactory agreement with the most commonly reported values for v1 and v2, as listed in Table 4. These results also provided an explanation for the fewer features observed in the experimental data.
Previous studies have reported the splitting of IR peaks in MFO due to deformation from a cubic to a non-cubic structure. For instance, Waldron reported v1 and v2 at 565 and 406 cm−1, respectively, along with additional peaks at 380, 430, and 735 cm−1.23 Heiba et al. also reported a split in the main v1 and v2 modes, with the seven frequencies in their study recorded at 406, 419, 436, 481, 493, 582, and 667 cm−1.53 Their findings indicated that these frequencies were influenced by the ratio of cations. The frequency at 667 cm−1, which had a very low intensity, was not identified in some of their samples, aligning with our findings. Frequencies lower than 400 cm−1 were not reported in their study due to the limitations of their instrument.
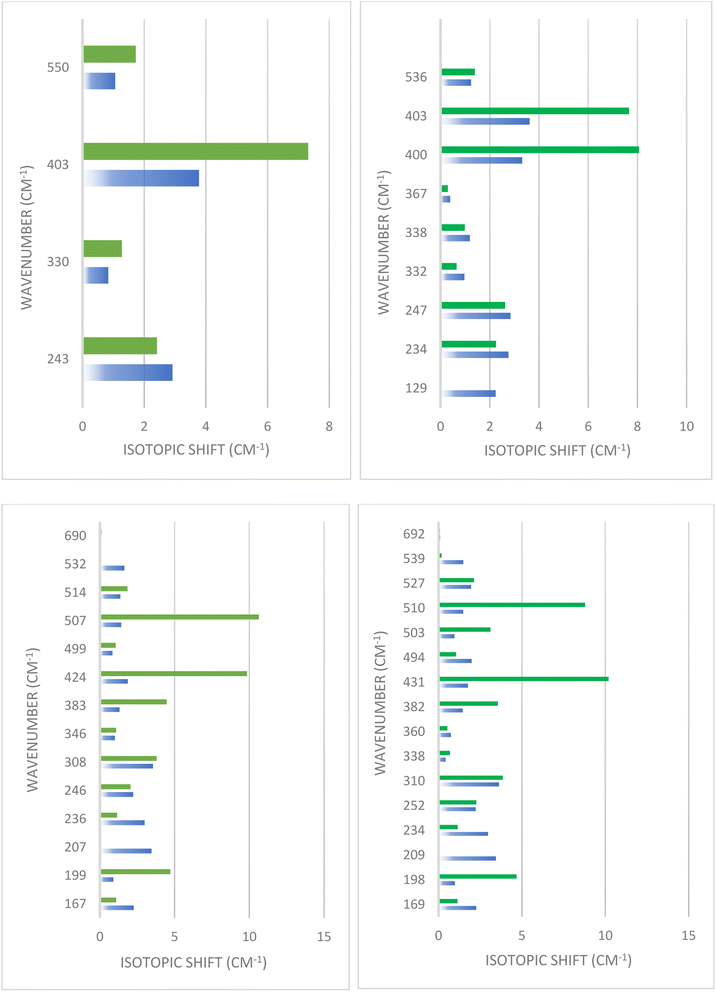
In order to delve deeper into the contribution of cations in the observed modes, we computed the spectra of isotopic substitutions (56Fe → 58Fe and 24Mg → 26Mg). As seen in Fig. 5, the vibrations of cations in their sites are highly correlated, making it challenging to interpret the spectra by categorizing the observed modes into A-site and B-site. In both FM and AFM (X = 0), the most noticeable shift was observed for the normal mode at approximately 400 cm−1. The largest shift occurred with the 26Mg substitution, which was 7–8 cm−1, while the 58Fe substitution resulted in a shift of approximately 3.5 cm−1. In FM and AFM of (X = 1), where all the Mg atoms transition to the octahedral site, a significant shift was also observed with the 26Mg substitution at 424 and 507 cm−1 mode in FM and 431 and 510 cm−1 modes in AFM. This shift was considerable, at about 10 cm−1. The modes at (199, 308, and 383 cm−1) in FM and their corresponding modes at (198, 310, and 382 cm−1) in AFM, shifted with 26Mg by 3.6–4.7 cm−1, indicating the influence of these modes by the lighter atom (Mg). Moreover, the 58Fe substitution also shifted the two modes at 308 and 207 cm−1 in FM, and the modes at 310 and 209 cm−1 in AFM by 3.5 cm−1.
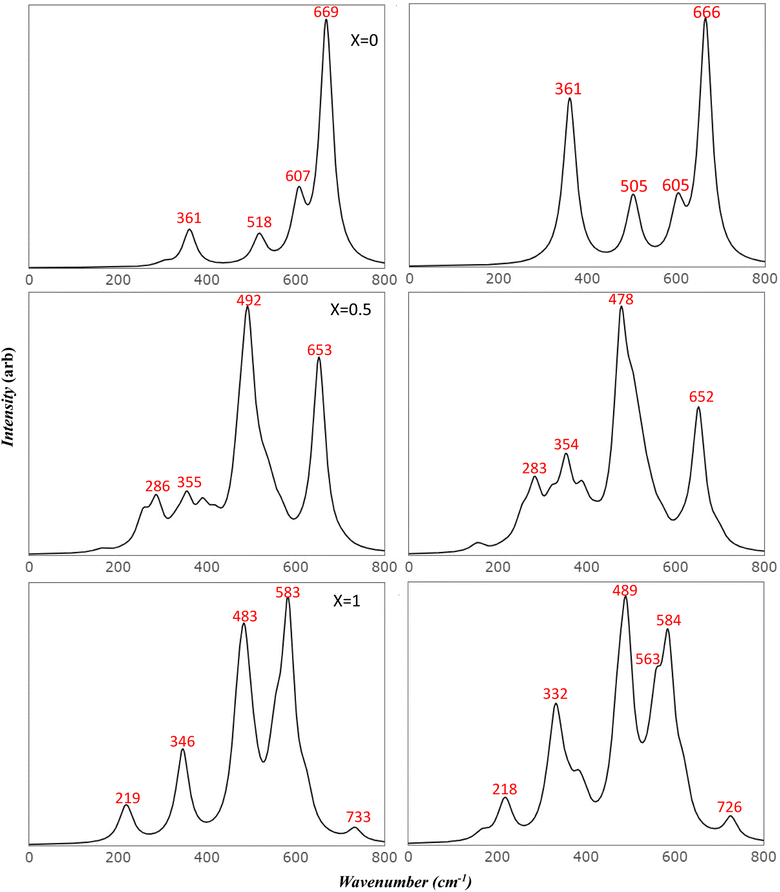
In the examination of scattered Raman (Fig. 6), the five modes predicted by group theory are discerned in FM (X = 0.0) at the following frequencies: 669 cm−1 for A1g; 607, 518, and 302 cm−1 for triply degenerate T2g symmetry; and 361 cm−1 for doubly degenerate Eg symmetry. Analysis of these modes reveals that the peaks at 302 cm−1 and 607 cm−1 encompass all the cations, specifically including the bending mode of O–Mg–O and Fe–O–Mg, in addition to the Fe–O–Fe bending detected at 606.6 cm−1.
The peak at 361 cm−1 implicates the stretching mode of Fe–O–Fe, O–Fe–O, and Fe–O–Mg, along with the bending mode of O–Mg–O and Fe–O–Mg. The peak at 518 cm−1 solely corresponds to the stretching mode of O–Mg–O and Fe–O–Mg bonds. The peak with the highest intensity and frequency, at 667 cm−1, is associated with the stretching mode of Mg–O and the bending mode of Fe–O–Mg. The impact of AFM spin ordering on Raman spectra is evident in both frequencies and intensities. For example, the peak at 302 cm−1 is shifted by 4 cm−1 (to 298 cm−1) and its intensity is halved, while the second peak at 361 cm−1 remains stationary but its intensity increases fivefold. The most significant shift is observed with the 518 cm−1 peak, which shifts to a lower frequency by 13 cm−1 (to 505 cm−1) with a doubling in intensity. This peak combines with a shoulder at 500 cm−1, leading to peak broadening. Minor shifts to lower frequencies are seen with 607 and 669 cm−1, by about 2 cm−1, accompanied by a minor decrease in their intensities.
Upon conversion to an inverse structure, the spectra undergo splitting over a broad region and show emerging new peaks, indicative of the deformation of the cubic structure. Starting with FM (X = 1), the spectra display ten peaks appearing in the entire calculated region. New twin peaks emerge at 213 and 221 cm−1, with small intensities related to the bending mode of O–Mg–O, Fe–O–Fe, and O–Fe–O. The peak at 346 cm−1, shifted from the corresponding doubly degenerate peak in FM (X = 0) at 361 cm−1 by 15 cm−1, displays a high correlation between cations, involving similar modes to those found at 361 cm−1.
The mid-range features three split peaks at 470, 485, and 505 cm−1. The peaks at 470 and 485 cm−1 are related to the stretching mode of Fe–O–Mg and O–Fe–O, and the second peak at 485 cm−1 additionally involves the bending mode of O–Fe–O and Fe–O–Fe. The third peak at 505 cm−1 is correlated to iron only, involving the stretching mode of both Fe–O–Fe and O–Fe–O. Another group of three peaks at 554, 583, and 622 cm−1 appear in the high-frequency region, along with a small peak at the edge of the spectra at 734 cm−1. The peak at 554 cm−1 resonates with the same stretching modes as the 470 cm−1 peak, but also includes the bending of O–Fe–O. Meanwhile, the 583 and 622 cm−1 peaks incorporate the same stretching modes as the 505 cm−1 peak, but with the additional bending of Fe–O–Fe and O–Mg–O, respectively. The peak at 734 cm−1 is related to the bending of Fe–O–Mg and Fe–O–Fe and the stretching of the Fe–O bond.
Alterations in spin arrangement in AFM (X = 1) also affect the Raman spectra, prompting shifts for most peaks and activating only three peaks due to slight deformation. Small new twin peaks appear at 162 and 169 cm−1, and another at 527 cm−1. No further splitting occurs for other peaks; instead, they undergo shifts as listed in Table 5. One of the most notable features in AFM spectra is the significant intensity increase of a group of peaks in the region of 300 cm−1 (329, 338, 360, 384, and 397 cm−1), four of which had almost zero intensity in FM. The small peak at 503 cm−1 merges with the 490 cm−1 peak to form one broad peak. The peak at 734 cm−1 in FM can be seen as an indication of the present inverse structure as it stands in a flat region in the normal spectra. Its large shift (8 cm−1) with the change in spin order can be useful for tracking phase changes under experimental conditions. Most of the studies reported in Table 5 detected this peak.
| Sy | Ref. 55 | Ref. 27 | Ref. 10 | Ref. 28 | Ref. 16 | Ref. 29 | Current study | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (X = 0) | (X = 1) | ||||||||||||
| 200 °C | 1000 °C | 500 °C | Sy | FM | AFM | Sy | FM | AFM | |||||
| T2g (1) | 217 | 217 | 209 | 202 | 216 | 217 | 215 | T2g (1) | 302 | 298 | B3g | 213 | 215 |
| Ag | 221 | 222 | |||||||||||
| B2g | 224 | 224 | |||||||||||
| Eg | 333 | 329 | 326 | 307 | 331 | 326 | 335 | Eg | 361 | 361 | B1g | 316 | 329 |
| B2g | 320 | 338 | |||||||||||
| B3g | 332 | 360 | |||||||||||
| 367 | B1g | 345 | 384 | ||||||||||
| Ag | 346 | 397 | |||||||||||
| T2g (2) | 486 | 480 | 475 | 462 | 483 | 487 | 400 | T2g (2) | 518 | 505 | B2g | 470 | 472 |
| Ag | 485 | 490 | |||||||||||
| 480 | 500 | B3g | 505 | 503 | |||||||||
| T2g (3) | 554 | 548 | 535 | 499 | 546 | 550 | 560 | T2g (3) | 607 | 605 | B2g | 554 | 557 |
| Ag | 583 | 585 | |||||||||||
| 646 | 590 | B3g | 622 | 619 | |||||||||
| A1g | 715 | 704 | 700 | 693 | 707 | 630 | 670 | A1g | 669 | 667 | Ag | 734 | 726 |
| 703 | 715 | ||||||||||||
The comparison of the obtained frequencies for both normal and inverted structures with available experimental data reveals a better alignment with the inverted structure. The breadth of the experimental peaks can be represented by resetting the full width half maximum value from 8 to 35 cm−1, as executed in the IR section (Fig. 7). Wang et al.55 predicted seven modes at frequencies of 217, 333, 390, 486, 554, 646, and 715 cm−1. These predictions are detailed in Table 5. The researchers attributed the additional peak at 646 cm−1 to the order–disorder effect within the structure. However, they provided no further explanation for the presence of the peak at 390 cm−1, which is also found in the simulated AFM Mg ferrite spectra (refer to Table 5). Our simulated spectra, with a FWHM of 35 cm−1, bear a significant resemblance to those of Wang et al. Frequencies of the modes are found at 218, 332, 489, 563, 584, 619, and 727 cm−1. The minor peak at 618 cm−1 merges with the 583 cm−1 peak in our study. The low intensity of these peaks could account for their absence in most of the studies listed in Table 5.10,27,28 Nakagomi et al. predicted seven modes similar to those identified by Wang et al. Yet, they attributed the peak at 670 cm−1 to the substitution of iron (Fe) atoms at tetrahedral sites with magnesium (Mg) atoms.29 They proposed that the substantial mass difference between Fe3+ and Mg2+ ions cause the A1g mode to split into two: one being attributable to Mg2+ (715 cm−1) and the other to Fe3+ ions (670 cm−1). They quantified the ion distribution at the tetrahedral sites based on the fluctuation in the integrated intensity of both modes relative to the total spectrum. Feng et al. identified a clear splitting into eight modes, including Eg and T2g (3), which further split into four peaks. They attributed the two highest peaks to A1g.16 Their frequency values align with our findings, but the assignments they reported do not. The peak at 619 cm−1, which resulted from the T2g (3) split in our study, closely matches their value at 630 cm−1. It's evident that the deformation from the cubic structure in inverse spinel leads to the degeneration of most modes and activates new modes in the Mg ferrite spectra. This finding aligns with experimental results10 and suggests that the assignments provided in existing literature need to be reassessed considering our simulated data.
4. Conclusion
This study delves into a comprehensive theoretical analysis based on density functional theory, examining the influence of inversion degree and spin arrangement of magnesium ferrite on multiple attributes including geometry, energy, electronic structure, and the frequencies and intensities of both IR and Raman spectra. We found that the inverse structure with anti-ferromagnetic order emerges as the ground structure, with relative energy being 0.21 and 0.41 eV (B3LYP) compared to the ferromagnetic order of (X = 0) and (X = 1), respectively. Our findings uncover the profound effect of inversion on the lattice structure, leading to deformation that significantly impacts the calculated IR and Raman spectra, inducing noteworthy shifting and splitting. The four IR frequencies with T1u symmetry calculated for the typical cubic structure of (X = 0) (243, 330, 403, and 550 cm−1) split over a wide spectral region upon inversion (X = 1). These frequencies are further influenced by the spin order, leading to a significant shift that provides valuable insights into phase transition under varying experimental conditions. Our isotopic calculations reveal an intricate relationship between the Mg and Fe vibrational modes. Despite the large correlation detected, some specific modes are predominantly influenced by the lighter Mg atom rather than the Fe atom, attributable to the substantial mass discrepancy, irrespective of the degree of inversion. This results in a significant shift (7–10 cm−1) obtained by Mg26 substitution with (403 cm−1) in the normal structure and (424, 507 cm−1) alongside corresponding modes (431, 510 cm−1) in FM and AFM, respectively, in the inverse structure. This can be construed as evidence of this mode's correlation to the Mg cation. Even though the IR peak at 690 cm−1 is of low intensity, its detection can be attributed to the inverse structure since no corresponding peak exists in this region in the normal phase. The simulated Raman spectra, which demonstrate splitting, elucidate a substantial amount of experimental data that detected more than five modes for Mg ferrite. Consequently, the provided assignments were reevaluated, taking into account the reduction in symmetry caused by lattice deformation. Similar to IR, the unique peak detected at the highest frequency region (727 cm−1) in Raman spectra can be considered as evidence for inverting the spinel structure. Unlike the 690 cm−1 peak in IR, this peak has a detectable intensity and is observed in most of the experimental data. In summary, this study invites us into a world where the inversion degree and spin arrangement of magnesium ferrite display substantial impacts on the material's properties. The findings not only contribute to the scientific understanding of these materials but also open up new alleys for exploration, fostering future developments in material science.Author contributions
Dr Tahani Saad Almutairi contributed in conceptualizing and designing the study, curating data, performing the formal analysis, leading the investigation, drafting the manuscript, and revising it critically for important intellectual content.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author extends his thanks to Taibah University and the Deanship of Scientific Research for their generous support, offering both essential facilities and an encouraging research atmosphere that contributed to conducting this study within the Department of Chemistry.References
- A. Goldman, Modern Ferrite Technology, Springer Science & Business Media, 2006 Search PubMed.
- R. Ranga, A. Kumar, P. Kumari, P. Singh, V. Madaan and K. Kumar, Mater. Charact., 2021, 178, 111269 CrossRef CAS.
- K. K. Kefeni, T. A. Msagati and B. B. Mamba, Mater. Sci. Eng., B, 2017, 215, 37–55 CrossRef CAS.
- N. R. Su, P. Lv, M. Li, X. Zhang, M. Li and J. Niu, Mater. Lett., 2014, 122, 201–204 CrossRef CAS.
- W. Tang, Y. Su, Q. Li, S. Gao and J. K. Shang, Water Res., 2013, 47, 3624–3634 CrossRef CAS PubMed.
- P. Hankare, S. Jadhav, U. Sankpal, R. Patil, R. Sasikala and I. Mulla, J. Alloys Compd., 2009, 488, 270–272 CrossRef CAS.
- J. Zhang, M. Yan, G. Sun, X. Li and K. Liu, J. Alloys Compd., 2021, 889, 161673 CrossRef.
- S. Verma, P. A. Joy, Y. B. Khollam, H. S. Potdar and S. B. Deshpande, Mater. Lett., 2004, 58, 1092–1095 CrossRef CAS.
- Y. Hou, F. Zuo, A. Dagg and P. Feng, Angew. Chem., Int. Ed., 2013, 52, 1248–1252 CrossRef CAS PubMed.
- M. I. Baraton, G. Busca, V. Lorenzelli and R. J. Wllley, J. Mater. Sci. Lett., 1994, 13, 275–279 CrossRef CAS.
- N. Sivakumar, A. Narayanasamy, J. M. Greneche, R. Murugaraj and Y. S. Lee, J. Alloys Compd., 2010, 504, 395–402 CrossRef CAS.
- M. Gateshki, V. Petkov, S. K. Pradhan and T. Vogt, J. Appl. Crystallogr., 2005, 38, 772–779 CrossRef CAS.
- Y.-L. Liu, Z.-M. Liu, Y. Yang, H.-F. Yang, G.-L. Shen and R.-Q. Yu, Sens. Actuators, B, 2005, 107, 600–604 CrossRef CAS.
- A. Pradeep, P. Priyadharsini and G. Chandrasekaran, J. Magn. Magn. Mater., 2008, 320, 2774–2779 CrossRef CAS.
- S. Jesus Mercy, D. Parajuli, N. Murali, A. Ramakrishna, Y. Ramakrishna, V. Veeraiah and K. Samatha, Appl. Phys. A: Mater. Sci. Process., 2020, 126, 1–13 CrossRef.
- Y. Feng, S. Li, Y. Zheng, Z. Yi, Y. He and Y. Xu, J. Alloys Compd., 2017, 699, 521–525 CrossRef CAS.
- V. Šepelák, D. Baabe, F. J. Litterst and K. D. Becker, J. Appl. Phys., 2000, 88, 5884–5893 CrossRef.
- A. Bloesser, H. Kurz, J. Timm, F. Wittkamp, C. Simon, S. Hayama, B. Weber, U. P. Apfel and R. Marschall, ACS Appl. Nano Mater., 2020, 3, 11587–11599 CrossRef CAS.
- T. P. Sumangala, I. Pasquet, L. Presmanes, Y. Thimont, C. Bonningue, N. Venkataramani, S. Prasad, V. Baco-Carles, P. Tailhades and A. Barnabé, Ceram. Int., 2018, 44, 18578–18584 CrossRef.
- N. K. Thanh, T. T. Loan, N. P. Duong, L. N. Anh, D. T. T. Nguyet, N. H. Nam, S. Soontaranon, W. Klysubun and T. D. Hien, Phys. Status Solidi A, 2018, 215, 1700397 CrossRef.
- A. Franco, T. E. Pereira Alves, E. C. De Oliveira Lima, E. Da Silva Nunes and V. Zapf, Appl. Phys. A: Mater. Sci. Process., 2009, 94, 131–137 CrossRef CAS.
- M. G. Ferreira Da Silva and M. A. Valente, Mater. Chem. Phys., 2012, 132, 264–272 CrossRef CAS.
- R. Waldron, Phys. Rev., 1955, 99, 1727 CrossRef CAS.
- W. White and B. DeAngelis, Spectrochim. Acta, Part A, 1967, 23, 985–995 CrossRef CAS.
- T. K. Pathak, N. H. Vasoya, V. K. Lakhani and K. B. Modi, Ceram. Int., 2010, 36, 275–281 CrossRef CAS.
- E. Katsnelson, A. Karoza, L. Meleshchenko, V. Pankov and B. Khavkin, Phys. Status Solidi B, 1987, 141, 599–609 CrossRef CAS.
- F. Naaz, H. K. Dubey, C. Kumari and P. Lahiri, SN Appl. Sci., 2020, 2, 808 CrossRef CAS.
- P. Prajapat, S. Dhaka and H. S. Mund, J. Electron. Mater., 2021, 50, 4671–4677 CrossRef CAS.
- F. Nakagomi, S. W. da Silva, V. K. Garg, A. C. Oliveira, P. C. Morais and A. Franco, J. Solid State Chem., 2009, 182, 2423–2429 CrossRef CAS.
- H. H. Kora, M. Taha, A. A. Farghali and S. I. El-Dek, Metall. Mater. Trans. A, 2020, 51, 5432–5443 CrossRef CAS.
- R. Dom, R. Subasri, K. Radha and P. H. Borse, Solid State Commun., 2011, 151, 470–473 CrossRef CAS.
- T. S. Almutairi, ACS Omega, 2023, 8, 36999–37010 CrossRef CAS PubMed.
- L. I. Granone, A. C. Ulpe, L. Robben, S. Klimke, M. Jahns, F. Renz, T. M. Gesing, T. Bredow, R. Dillert and D. W. Bahnemann, Phys. Chem. Chem. Phys., 2018, 20, 28267–28278 RSC.
- R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre and P. d'Arco, et al., Int. J. Quantum Chem., 2014, 114, 1287–1317 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1992, 3, 2155–2160 CrossRef.
- C. Adamo and V. Barone, Chem. Phys. Lett., 1998, 298, 113–119 CrossRef CAS.
- A. V Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- F. S. Gentile, W. C. Mackrodt, N. L. Allan and R. Dovesi, Phys. Chem. Chem. Phys., 2020, 22, 20612–20617 RSC.
- M. De La Pierre, R. Orlando, L. Maschio, K. Doll, P. Ugliengo and R. Dovesi, J. Comput. Chem., 2011, 32, 1775–1784 CrossRef CAS PubMed.
- M. Catti, G. Valerio and R. Dovesi, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 7441–7450 CrossRef CAS PubMed.
- M. Towler, N. Allan, N. M. Harrison, V. Saunders, W. Mackrodt and E. Apra, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 5041 CrossRef CAS PubMed.
- M. Catti, A. Pavese, R. Dovesi and V. R. Saunders, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 9189 CrossRef CAS PubMed.
- C. M. Zicovich-Wilson, F. Pascale, C. Roetti, V. R. Saunders, R. Orlando and R. Dovesi, J. Comput. Chem., 2004, 25, 1873–1881 CrossRef CAS PubMed.
- R. D. F. Pascale, C. M. Zicovich-Wilson, F. Lopez, B. Civalleri and R. Orlando, J. Comput. Chem., 2004, 25, 888–897 CrossRef PubMed.
- L. Maschio, B. Kirtman, M. Rérat, R. Orlando and R. Dovesi, J. Chem. Phys., 2013, 139, 164101 CrossRef PubMed.
- L. Maschio, B. Kirtman, R. Orlando and M. Rèrat, J. Chem. Phys., 2012, 137, 204113 CrossRef PubMed.
- J. Kurian and M. J. Mathew, J. Magn. Magn. Mater., 2018, 451, 121–130 CrossRef CAS.
- S. K. Pradhan, S. Bid, M. Gateshki and V. Petkov, Mater. Chem. Phys., 2005, 93, 224–230 CrossRef CAS.
- A. Franco and M. Silva, J. Appl. Phys., 2011, 109, 07B505 CrossRef.
- K. Kirchberg, A. Becker, A. Bloesser, T. Weller, J. Timm, C. Suchomski and R. Marschall, J. Phys. Chem. C, 2017, 121, 27126–27138 CrossRef CAS.
- R. Köferstein, T. Walther, H. Dietrich and S. G. Ebbinghaus, J. Mater. Sci., 2013, 48, 6509–6518 CrossRef.
- C. E. Rodríguez Torres, G. A. Pasquevich, P. M. Zélis, F. Golmar, S. P. Heluani, S. K. Nayak, W. A. Adeagbo, W. Hergert, M. Hoffmann, A. Ernst, P. Esquinazi and S. J. Stewart, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 104411 CrossRef.
- Z. K. Heiba and M. B. Mohamed, J. Mater. Sci.: Mater. Electron., 2019, 30, 786–796 CrossRef CAS.
- D. Narsimulu, B. N. Rao, M. Venkateswarlu, E. S. Srinadhu and N. Satyanarayana, Ceram. Int., 2016, 42, 16789–16797 CrossRef CAS.
- Z. Wang, P. Lazor, S. Saxena and H. C. St O, Mater. Res. Bull., 2002, 37, 1589–1602 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra07339d |
| This journal is © The Royal Society of Chemistry 2024 |