Exploring optoelectronic and photocatalytic properties of X₂AgBiY₆ (X = NH₄, PH₄, AsH₄, SbH₄ and Y = Cl, Br): a DFT study

Abstract

Ab initio calculations have been used to investigate lead-free double-perovskites (DPs) X₂AgBiY₆ (X = NH₄, PH₄, AsH₄, SbH₄ and Y = Cl, Br) for solar-cell-based energy sources. The most recent and improved Becke–Johnson potential (TB–mBJ) has been proposed for the computation of optoelectronic properties. Theoretical and calculated values of the lattice constants obtained by applying the Wu–Cohen generalized gradient approximation (WC-GGA) were found to be in good agreement. The computed bandgap values of (NH₄)₂AgBiBr₆ (1.574 eV) and (SbH₄)₂AgBiBr₆ (1.440 eV) revealed their indirect character, demonstrating that they are suitable contenders for visible light solar-cell (SC) technology. Properties like the refractive index, light absorption, reflection, and dielectric constant are all explained in terms of the optical ranges. Within the wavelength range of 620–310 nm, the maximum absorption band has been identified. Additionally, we discover that all chemicals investigated herein have photocatalytic capabilities that can be used to efficiently produce hydrogen at cheap cost using solar water splitting by photocatalysts. In addition, the stability of the compounds was examined using the calculation of mechanical properties.

---

1. Introduction

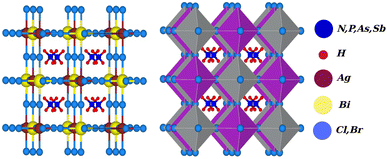
Due to the development of high efficiency and inexpensive materials, the past two decades have been crucial for the study of perovskite solar cells (PSC). Power conversion efficiencies (PCEs) for perovskite solar cells of up to 24.5% have been reported, which are comparable with PCEs for silicon (Si)-based solar cells.^1,2 Recent perovskite solar cells function similarly to absorber materials made of an inorganic halide perovskite (HP) and a lead-based organic halide. Geisz et al.³ produced a multi-junction solar cell (SC) with a productivity greater than 47.1%, which is 11.1% higher than with thin-film-based solar cells. In extremely efficient solar cell applications, including the production of solar fuel and solar hydrogen, hybrid organic–inorganic halide perovskites CH₃NH₃PbX₃ (X = Cl, Br, and I) have gained attention.^4–6 On the other hand, lead-based halide perovskites have challenges with stability, as well as containing a hazardous material (lead), which limits the applications of these materials on a broad scale. Finding reliable and Pb-free alternative materials is therefore necessary to solve these issues. Therefore, halide double perovskites have received a lot of attention as a result.^7–17 Halide double perovskites are a vast class of quaternary halides. Opportunities for new solar and photovoltaic materials have been offered by the wide geometric range of these materials. However, when a large number of compounds are examined to determine which are most promising in terms of energy, structure, and electrical properties for solar cell applications, the work grows more challenging. As opposed to the unstable solar absorbent substance CH₃NH₃PbI₃ (MAPI), which contains Pb, halide double perovskite compounds like Cs₂AgBiX₆ (X = Cl and Br) have gained a lot of interest, leading to a number of experimental and theoretical studies.^18,19 Filip et al.^20,21 suggested other cation possibilities from hypothetical perovskites such as NH₄, PH₄, AsH₄, SbH₄, NCl₄, PF₄, Ch₃PH₃, etc. The thermodynamic stability of numerous halide double perovskites was predicted by Han and his colleagues using density functional theory (DFT).²² All-double perovskite inorganic materials have been investigated as a potential replacement for lead-based perovskites due to their non-toxic qualities and three-dimensional structures. Giustino and Snaith have predicted the formation of new halide double perovskites.¹⁷ From those suggested materials, we selected one class as X₂AgBiY₆ (X = NH₄, PH₄, AsH₄, SbH₄ and Y = Cl, Br) with the exception of F and I because of the corresponding substantial bandgap instability. A predicted view of the crystal structure of the stable double perovskite material X₂AgBiY₆ is illustrated in Fig. 1. In this paper, we investigated the structural, electronic, photocatalytic, optical, and mechanical characteristics of X₂AgBiY₆X₂AgBiY₆.

Fig. 1 Predicted crystal structure of X₂AgBiY₆ (X = NH₄, PH₄, AsH₄, SbH₄ and Y = Cl, Br).

2. Computational details

We used the WIEN2k program to carry out our computations using the full-potential linearized augmented plane wave plus local orbitals (FP-LAPW + lo) approach, which constitutes a component of DFT.²³ A more accurate exchange-correlation potential flavour can be acquired using the Wu–Cohen generalized gradient approximation (WC-GGA), and used to evaluate the properties of the material.²⁴ In order to determine an accurate bandgap, we used the WC-GGA with the modified Becke–Johnson (mBJ) correction.^25,26 For other semiconductors, especially lead halide perovskites, in the past,^27–31 the mBJ approach produced encouraging band topologies and bandgap values when compared to experimental results. In order to apply the mBJ strategy across WC-GGA to our hypothesized compounds, we first applied it to the experimental data for Cs₂AgBiX₆ (X = Cl and Br), and after that, we implemented this plan for our compounds X₂AgBiY₆. Electronic and optical characteristics are estimated using k-meshes of 8 × 8 × 8 and 15 × 15 × 15. All structures are optimized when the energy convergence tolerance is 10⁻⁵ Ry.

3. Results and discussion

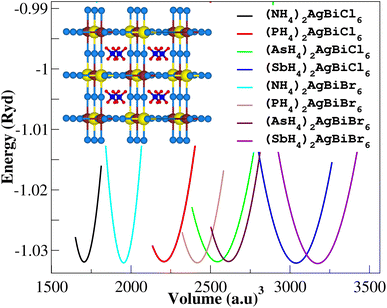
The structural characteristics of a compound play a significant role in understanding its varied physical properties. All eight potential compounds for the double perovskite X₂AgBiY₆ (X = NH₄, PH₄, AsH₄, SbH₄ and Y = Cl, Br) that we predicted are grouped into four different categories: NH₄-, PH₄-, AsH₄-, and SbH₄-based compounds.

Firstly, we performed relaxation as the organic components contain hydrogen. Then, using volume optimization, we were able to extract structural parameters such as the bulk modulus B (GPa) and lattice constant a (Å). Experimental values of the Cs₂AgBiX₆ lattice parameter (X = Cl and Br) has been used as a starting point. Table 1 displays the structural characteristics of the hypothetical compounds as determined using the Birch–Murnaghan equation of states.³² The optimization of X₂AgBiY₆ is presented in Fig. 2. The optimized lattice constants for all compounds range from 10.03 Å to 12.33 Å, which is quite close to the lattice constants of other experimentally synthesized double perovskites, like Cs₂AgBiCl₆ and Cs₂AgBiBr₆, which are 10.77 Å and 11.27 Å, respectively.¹⁸ (NH₄)₂AgBiCl₆ has the greatest optimal bulk modulus, B, of all the compounds with a value of 75.55 GPa. (Sb₄)₂AgBiBr₆, on the other hand, has the lowest B value of 27.15 GPa, demonstrating the durability of these double perovskites. Results for these optimized compounds cannot be compared to any theoretical or experimental data. After adjusting the lattice constant, these compounds can be characterized using bandgap values that are comparable to the best hybrid organic–inorganic perovskites.

Table 1 Lattice parameters, bond distances between A and H (A = N, P, As, and Sb) and bandgaps of halide double perovskites X₂AgBiY₆ (X = NH₄, PH₄, AsH₄, SbH₄ and Y = Cl, Br)

Materials	Bond distance d(A–H) (Å)	Lattice parameter (Å)	Bulk modulus B (GPa)	Bandgap (without SOC) Eg (eV)	Bandgap (with SOC) Eg (eV)	Bandgap hybrid (mBJ + SOC) Eg (eV)
(NH4)2AgBiCl6	1.08	10.03	75.55	1.51	1.36	2.32
(NH4)2AgBiBr6	1.12	10.50	66.87	0.97	0.87	1.75
(PH4)2AgBiCl6	1.39	10.94	46.77	1.78	1.43	2.42
(PH4)2AgBiBr6	1.43	11.26	44.39	1.28	1.03	1.95
(AsH4)2AgBiCl6	1.45	11.47	36.41	1.83	1.52	2.29
(AsH4)2AgBiBr6	1.46	11.56	38.95	1.36	1.23	2.15
(SbH4)2AgBiCl6	1.66	12.15	26.18	1.80	1.44	2.00
(SbH4)2AgBiBr6	1.69	12.32	27.15	1.31	1.03	1.44

---

Fig. 2 Volume optimization curves of X₂AgBiY₆.

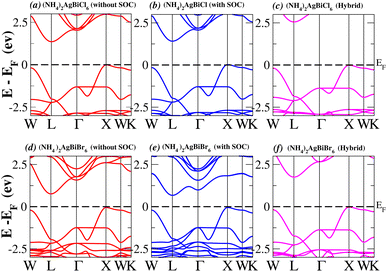
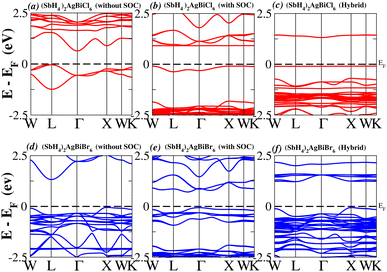
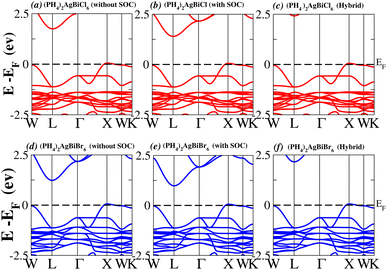
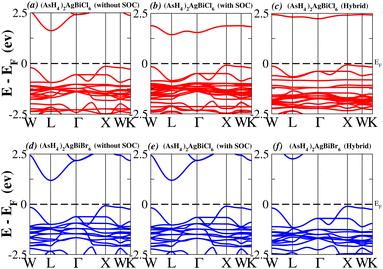
In order to analyse the electrical behavior of the materials, the band structures are essential. We can study the materials’ electronic nature by using band structures to determine if they are metallic or semiconducting, etc. The electronic band structure may successfully clarify the physical characteristics of solids including their optical behavior and resistivity, and this knowledge can further assist in the design of solid-state devices like solar cells and transistors, among other applications. In order to comprehend their electronic structure, we calculated the band structures of X₂AgBiY₆ (X = NH₄, PH₄, AsH₄, SbH₄ and Y = Cl, Br). We have observed a definite increase in their bandgap when their bond distance increases going from N to Sb. This is mostly caused by the compound’s growing number of deep shells. All of the compounds’ bandgaps were computed using an intuitive self-consistent field (SCF) model that took into account spin–orbit coupling (SOC), and on top of that, we used the mBJ technique to adjust the bandgap value to correspond with the experimental values. As a benchmark, we first recalculated the experimental bandgap values for Cs₂AgBiCl₆ and Cs₂AgBiBr₆, which are 2.77 eV and 2.19 eV, respectively.¹⁸ We have determined the bandgaps for Cs₂AgBiBr₆ to be 1.16 eV without SOC, 0.961 eV with SOC, and 2.17 eV with mBJ + SOC. For Cs₂AgBiCl₆, however, the bandgap values are 2.63 eV with mBJ + SOC, 1.40 eV with SOC, and 1.69 eV without SOC. For the first-Brillouin-zone results depicted in Fig. 3 and 4, the X₂AgBiY₆ electronic band structures were investigated at a high-symmetry point (X = Cl, Br). The band structures revealed an indirect bandgap for the DPs that included the conduction band’s L minima and valence band’s X and maxima at the L–X equilibrium point. On both a theoretical and practical level, lead-free DPs exhibit an indirect bandgap. Since we recently determined the bandgaps for (NH₄)₂AgBiBr₆ (1.58 eV) and (SbH₄)₂AgBiBr₆ by using mBJ + SOC to achieve bandgap values near to the MAPI experimental value, we were able to acquire indirect bandgaps comparable to MAPI.³³ Therefore, we draw the conclusion that the FP-LAPW + lo approach significantly underestimates bandgap values in the double perovskites until the addition of mBJ + SOC. In order to replace MAPI at room temperature, we must therefore find a material that is lead-free and has a bandgap value that is almost comparable to 1.6 eV.³⁴ Table 1 provides calculated bandgap values calculated with and without SOC, and with mBJ and SOC, for all materials. Referring to Table 1, it becomes evident that only (NH₄)₂AgBiBr₆ (1.58 eV) and (SbH₄)₂AgBiBr₆ have small bandgap values of 1.75 eV and 1.44 eV, respectively, for mBJ + SOC. On the other hand, the bandgap values for the rest of the compounds exceed 1.80 eV, as shown in Table 1. These materials exhibit a very high bandgap when mBJ + SOC is applied, rendering them inappropriate for solar cell applications, although they are fit for photocatalytic applications.

Fig. 3 Band structure of (NH₄)₂AgBiY₆.

Fig. 4 Band structure of (SbH₄)₂AgBiY₆.

We determined bandgap values for X₂AgBiY₆ materials without SOC, with SOC, and with the hybrid calculation, as shown in Table 1. According to Fig. 3(a) and (b), and 4(a) and (b), (NH₄)₂AgBiBr₆’s bandgap value is 0.97 eV without SOC, and 0.88 eV with SOC, and similarly for (SbH₄)₂AgBiBr₆, the bandgap value is 1.32 eV without SOC, and 1.036 eV with SOC, which indicates that SOC not only reduces the bandgap values but also causes splitting the of the conduction band minima (CBM). We were able to use SOC to detect a small reduction in the bandgap values for (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆ of up to 94 meV and 277 meV, respectively. The band structures for (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆ were subsequently calculated using the hybrid model [see Fig. 3(f) and 4(f)]. The calculated indirect bandgap values for (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆ are 1.75 eV and 1.44 eV, respectively. When we calculated the bandgaps of PH₄ and AsH₄ cations with Cl or Br using the hybrid method (shown in Fig. 5 and 6), they were higher than 2 eV because SOC did not strongly effect the splitting of the CBM, as shown in Table 1. The bandgap values of (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆ are closer to the values of CH₃NH₃PbX₃ (X = Cl, Br, I) determined experimentally. We can create an effective semiconductor solar cell material with bandgaps in the region between 1.0 and 1.8 eV. Electrons can be discharged in this bandgap range without generating a significant quantity of heat. Even though the indirect bandgap for double perovskite was recently discovered. While some materials have bandgap values that fall within the specified range, pressure-induced bandgap tuning may be used to achieve bandgap values that are nearly 1.5 eV.

Fig. 5 Band structure of (PH₄)₂AgBiY₆.

Fig. 6 Band structure of (AsH₄)₂AgBiY₆.

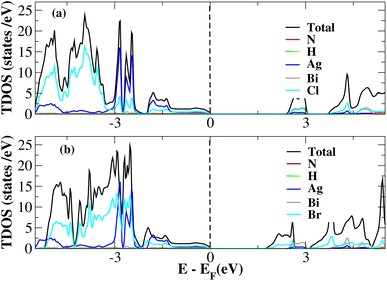
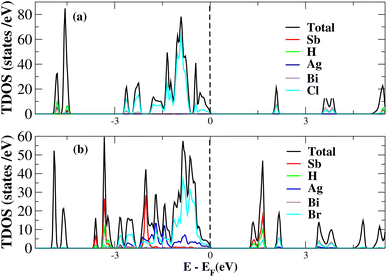
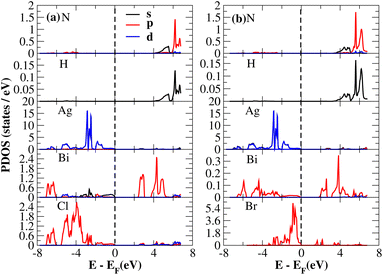
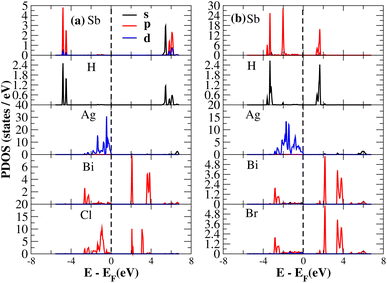
After investigating the band structures, a study of the electrical characteristics followed. The bandgap between the valence band and the conduction band in the Fermi level in these materials causes them to exhibit semiconducting characteristics, as indicated by the plot of the total density of states (TDOS) of (NH₄)₂AgBiY₆ (Y = Cl, Br) and (SbH₄)₂AgBiY₆ (Y = Cl, Br) in Fig. 7 and 8, respectively. A chemical difference serves as the main cause of the indirect bandgap, and the presence of the Ag atom’s 4d state contributes to the compact bandgap in X₂AgBiY₆. For the X₂AgBiY₆ compounds, the partial density of states (PDOS) comprises the antibonding states of the Ag atom’s 4d orbitals and Br atom’s 4p orbitals, as well as the valence band maxima.

Fig. 7 Total DOS of (NH₄)₂AgBiY₆.

Fig. 8 Total DOS of (SbH₄)₂AgBiY₆.

The PDOS of (NH₄)₂AgBiY₆ (Y = Cl, Br) and (SbH₄)₂AgBiY₆ (Y = Cl, Br) are depicted in Fig. 9 and 10, respectively. The PDOS provides details about how certain atoms contribute to structural stability. For the X₂AgBiY₆ compounds, the PDOS comprises the antibonding states of the Ag atom’s 4d orbitals and Br atom’s 4p orbitals as well as the valence band maxima. The 6p-state of Bi and the 4p-state of Cl/Br antibonding states formed the DP compounds in PDOS. This demonstrates how the H-s orbital for material slightly recedes. This demonstrates H-s orbital contribution is deep in the valence band. Important contributions come from the (Ag-d), (Bi-p), and (Cl/Br-p) states, which are depicted in Fig. 9 and 10. Both of these DPs can be used for indirect bandgap engineering in solar cell applications.

Fig. 9 Partial DOS of (NH₄)₂AgBiY₆.

Fig. 10 Partial DOS of (SbH₄)₂AgBiY₆.

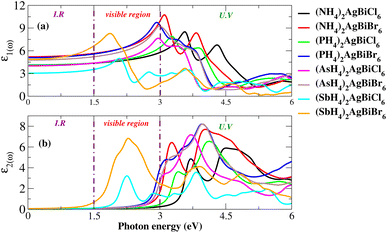
For an understanding of the importance of the predicted materials for solar cell applications, their optical properties were rigorously studied. For solar cell applications, we focused on two compounds, namely (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆. Research was undertaken into the optical performance of the transition from the valence band to the conduction band. The interaction of light and objects reveals optical characteristics. For optoelectronic devices, the strength of light absorption and emission depends on the transition between and within bands. Research on the relationship between optoelectronic characteristics and the dielectric function, absorption coefficient, complex refractive-index, and reflectivity R is available. The dielectric functions are described by ε(ω) = ε₁(ω) + iε₂(ω). Fig. 11(a and b) show the dielectric function plot with an energy range of 0 to 6 eV. The dielectric constant has two parts: the real part, represented by ε₁, and the imaginary part, represented by ε₂. The 0 Hz limit of the ε₁ spectrum exclusively describes the electronic component of the dielectric function, its most significant component. In Fig. 11(a), ε₀ increased from 3 to 5.7. Peaks at 1.75 eV for (SbH₄)₂AgBiBr₆ and 3.2 eV for (NH₄)₂AgBiBr₆ are the highest-energy peaks that have been recorded for these compounds. Thus, according to Penn’s model,^35,36 the bandgap and static-dielectric constant ε₀ are related to one another. A possible inter-band transition caused by light-energy absorption has been connected to ε₂. This can be seen in Fig. 11(b), where light absorption mostly targets the visible portions of the two predicted molecules. (SbH₄)₂AgBiBr₆’s smaller bandgap polarizes electron transfer in the conductance band and improves the photovoltaic outcomes. An extensive analysis of ε₁ and ε₂ revealed that both (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆ were capable of absorbing light with a substantial wavelength amplitude in the energy range of 1 to 4 eV. These combinations should not be ignored as they work well with a variety of solar cell technologies.

Fig. 11 Dielectric function for X₂AgBiY₆.

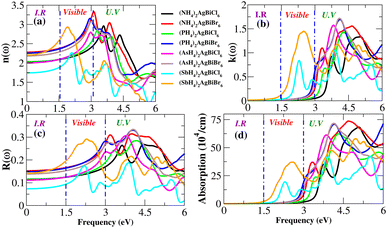
Light absorption is expressed by the absorption coefficient. In the visible spectrum, absorption weakened in the material under investigation. The obtained value of the absorption coefficient for the calculated compounds is illustrated in Fig. 12(d). The chemical compounds (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆ apparently have high absorption coefficients, as indicated by their strong absorption peaks with heights of 37 × 10⁴ cm⁻¹ at 2.8 eV and 70 × 10⁴ cm⁻¹ at 4.7 eV, respectively. Due to the DFT-based approximation, the effects of ε₂ and α(ω) have been compared to a lesser overestimation for the absorption coefficient peak.^37,38 In the case of opto-electronic applications, the refractive index n(ω) and reflectivity R(ω) have been important factors that characterize the right kind of material.

Fig. 12 Optical properties (n, k, R, absorption) of X₂AgBiY₆.

For (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆, n(ω) and R(ω) have been displayed in Fig. 12(a and c). (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆ have static refractive index values of 2.4 eV and 2.2 eV, respectively. The peak value is constant since the value of n(ω) is a copy of ε₁. According to Fig. 12(c), (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆ have full reflection R(ω) values of 0.07 and 0.05, respectively. According to Drude’s model,³⁹ those materials light waves in the visible area may be superluminal for both materials. Following a thorough examination of those DP’s optical properties, it was discovered that their significant absorption in the visible to UV spectrum enhances the likelihood that they could be used in solar cell systems. The dissipation of electromagnetic waves in materials is referred to as K(ω). The trends of n(ω) and K(ω) of (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆, respectively, are found to be very similar to those of the real and imaginary parts of the dielectric functions, especially where the peaks are located, indicating that the calculated results are in complete compliance with the relationships between the optical parameters (Table 2).

Table 2 Optical parameters of (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆

Parameters	(NH4)2AgBiBr6	(SbH4)2AgBiBr6
ε1(0)	3.80	5.7
n(0)	2.5	2.2
R(0)	0.07	0.05
k(0)	4.6	2.7

---

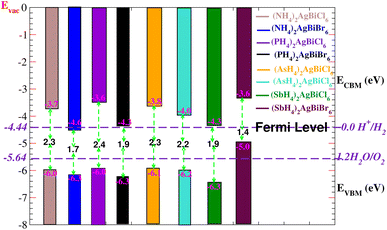
Solar energy can be effectively used by semiconductors with an appropriate bandgap in order to split water molecules and produce hydrogen,^40,41 therefore, clean renewable energy can be generated using photocatalytic water splitting. The electrons (holes) reduce (oxidize) water during the photocatalytic reaction.⁴² Therefore, the semiconductor’s bandgap needs to be greater than 1.23 eV (Fig. 13). Mulliken electronegativity is used to study photocatalytic water splitting for X₂AgBiY₆. E_VBM = χ − E_elec + 0.5 E_g and E_CBM = E_VBM + E_g.^43,44 Photocatalytic water splitting for X₂AgBiY₆ is studied using Mulliken electronegativity (χ), standard electrode potential on the hydrogen scale (E_elec = 4.5 eV), bandgap (E_g), energies of valence (E_VBM), and conduction (E_CBM) band edge potentials at pH = 0. It is noticeable that the standard oxidation and reduction potentials on the hydrogen scale for photocatalytic water splitting are −4.44 eV (set as the Fermi level) and −5.64 eV, respectively. To determine the band-edge positions of the conduction band (CB) and valence band (VB) with reference to standard oxidation on the hydrogen scale, the Fermi level is set to −4.44 eV.⁴⁵

Fig. 13 Photocatalytic properties of X₂AgBiY₆. The standard oxidation potential V_O2/H2O and standard reduction potential V_H2/H⁺ for water splitting are −5.67 eV and −4.44 eV (with the latter set as the Fermi level), respectively.

At pH = 0, the VB and CB are set to 1.23 eV and 0 eV correspondingly, which correspond to −5.67 eV and −4.44 eV.⁴⁴ The VB and CB potentials were estimated for X₂AgBiY₆ using the mBJ + (WC-GGA) functional range. The borders of the common redox band satisfy the conditions for water splitting at pH = 0. Out of eight compounds, six compounds show very good photocatalytic properties. (NH₄)₂AgBiBr₆ is not good for reduction purposes and (SbH₄)₂AgBiBr₆ is not good for oxidation purposes. On the other hand, all materials except these two have potentials more positive than the necessary VB potential, indicating good reactions for the oxidation of water. Furthermore, it is evident from Fig. 13 that six materials under study exhibit positions for the E_VB band edges that are outside of the reduction potentials that are energetically appropriate. Thus, we reach the conclusion that these materials under consideration are viable options for the industrial generation of solar hydrogen.

Effective elastic constants are crucial for appropriate practical applications of a material. The stability of a structure and a material’s reaction to outside forces are both described by the elastic constant. Table 3 lists the computed elastic constants of X₂AgBiY₆. Experimental results are not accessible for comparison with our predicted values. Both materials satisfy the C₁₁ > 0, C₄₄ > 0, C₁₁ + 2C₁₂ > 0, C₁₁ − C₁₂ > 0 and C₁₂ > B > C₁₁ stability criteria for cubic crystals.^46,47 This demonstrates the elastic stability of both the materials listed above against deformation forces. The elastic constant is being studied in order to calculate the mechanical characteristics using the conventional relations mentioned in Table 3.^48,49 The material’s plastic deformation in response to applied stress is measured using the shear modulus G_H. The fact that (NH₄)₂AgBiBr₆ has higher Young’s modulus (Y) and shear modulus (G_H) values than (Sb₄)₂AgBiBr₆ proves that it is stiffer and offers more resistance to plastic deformation. The B/G (Pugh ratio) reveals the ductile and brittle behavior of a material.⁵⁰ It is evident from Table 3 that all materials are ductile because their B/G ratios are greater than 1.75 (the crucial number). The positive or negative values of Cauchy pressure can also be used to indicate a material’s ductile or brittle nature (C′′ = C₁₂ − C₄₄). The positive value of C′′ (in Table 3) also indicates good ductility of (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆. The Poisson’s ratio (v) shows how resistant a crystal is to compression. Due to the low values of v, all materials are determined to be stable in the presence of shear stress. Table 3 lists the values of the anisotropic constant (A) for (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆. The deviation of A from unity can be used to gauge the anisotropy of a material. It is evident from the table that the anisotropic factor is less than unity, and as a result, the properties of the material alter in various crystallographic directions. The shear constant C indicates the material’s dynamic stability against tetragonal distortion. For dynamic stability, C must be bigger than 0 (positive values).⁵¹ As shown in Table 3, the fact that all materials have values of C that are greater than 0 shows that they are mechanically stable.

Table 3 Elastic lattice parameters of X₂AgBiY₆

Compound	C11	C12	C44	GV	GR	GH	Y	B/G	C′′	ν	A	C′
(NH4)2AgBiCl6	79.19	22.70	18.36	22.31	21.35	21.83	56.76	1.90	4.34	0.27	0.65	28.24
(NH4)2AgBiBr6	84.73	31.04	19.02	22.15	21.53	21.84	58.73	2.25	5.02	0.30	0.70	26.84
(PH4)2AgBiCl6	77.97	28.51	21.98	23.08	23.00	23.04	59.13	1.95	6.52	0.28	0.88	24.72
(PH4)2AgBiBr6	82.98	31.31	24.11	24.80	24.77	24.79	63.58	1.94	7.20	0.27	0.93	25.83
(AsH4)2AgBiCl6	73.37	29.66	21.54	21.66	21.66	21.70	55.88	2.04	8.12	0.28	0.98	21.85
(AsH4)2AgBiBr6	74.83	27.15	21.52	22.45	22.39	24.43	57.37	1.91	5.64	0.27	0.90	23.84
(SbH4)2AgBiCl6	72.21	28.84	20.26	20.83	20.81	20.83	53.85	2.0	8.54	0.29	0.93	21.68
(SbH4)2AgBiBr6	73.38	26.95	19.18	20.79	20.61	20.70	52.30	2.12	7.78	0.28	0.82	23.21

---

4. Conclusions

Double perovskites X₂Ag¹⁺Bi³⁺X₆ (X = NH₄, PH₄, AsH₄, SbH₄, and Y = Cl, Br) were investigated using density functional theory. Investigations were done on the structural, electronic, optical, photocatalytic, and elastic properties. These compounds’ bandgaps were computed. From these compounds, only (NH₄)₂AgBiBr₆ and (SbH₄)₂AgBiBr₆ had bandgaps of 1.76 eV and 1.44 eV, respectively. The remaining materials all exhibit bandgap values greater than 2 eV when the mBJ adjustment is applied. In contrast to partial density of states results, which show Cl’s p-orbital bands and Sb’s s-orbital bands, the total density of state (DOS) results present Cl and Br as significant contributors to the valence band maxima (VBM) and Ag as a contributor to the conduction band minima (CBM). We investigated optical characteristics to determine the absorption coefficients of X₂AgBiY₆ (NH₄, PH₄, AsH₄, SbH₄ and Y = Cl, Br) and we learned that, based on the bandgap values and optical absorption, (SbH₄)₂AgBiBr₆ is the best suited option among all other examined compounds for solar cell use. We determined that six compounds are suitable for redox reactions based on their photocatalytic characteristics. The stability, indirect bandgap value, and optical absorption values that are close to MAPI make these perovskites a good choice for lead-free hybrid solar cells. Their stability has been established by their mechanical characteristics.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors extend their appreciation to the Deanship of Scientific Research, King Saud University for funding through the Vice Deanship of Scientific Research Chairs; Research Chair of Prince Sultan Bin Abdulaziz International Prize for Water. The author Y. Saeed would like to thank Higher Education Comission (HEC) for providing a grant under NRPU–15844.

References

1. J. Tong, Z. Song, D. H. Kim, X. Chen, C. Chen, A. F. Palmstrom, P. F. Ndione, M. O. Reese, S. P. Dunfield, O. G. Reid, J. Liu, F. Zhang, S. P. Harvey, Z. Li, S. T. Christensen, G. Teeter, D. Zhao, M. M. Al-Jassim, M. F. A. M. van Hest, M. C. Beard, S. E. Shaheen, J. J. Berry, Y. Yan and K. Zhu, Science, 2019, 364, 475.
2. P. R. Varadwaj, Phys. Chem. Chem. Phys., 2020, 22, 24337.
3. J. F. Geisz, M. A. Steiner, N. Jain, K. L. Schulte, R. M. France, W. E. McMahon, E. E Perl and D. J. Friedman, IEEE J. Photovoltaics, 2018, 8, 626–632.
4. J. Chen, X. Cai, D. Yang, D. Song, J. Wang, J. Jiang, A. Ma, S. Lv, M. Z. Hu and C. Ni, J. Power Sources, 2017, 355, 98–133.
5. M. J. Fang, C. W. Tsao and Y. J. Hsu, J. Phys. D: Appl. Phys., 2020, 53, 143001–143026.
6. Y. H. Chiu, T. H. Lai, M. Y. Kuo, P. Y. Hsieh and Y. J. Hsu, APL Mater., 2019, 7, 080901.
7. Z. Yi, N. H. Ladi, X. Shai, H. Li, Y. Shen, M. Wang, V. Sharma, S. K. Singh and S. M. Mobin, Nanoscale Adv., 2019, 1, 1276–1289.
8. H. He, X. Lu, E. Hanc, C. Chen, H. Zhang and L. Lu, J. Mater. Chem. C, 2020, 8, 1494–1516.
9. R. Kour, S. Arya, S. Verma, J. Gupta, P. Bandhoria, V. Bharti, R. Datt and V. Gupta, Global Chall., 2019, 3, 1900050.
10. D. Zhou, T. Zhou, Y. Tian, X. Zhu and Y. Tu, J. Nanomater., 2018, 2018, 8148072.
11. M. Palummo, E. Berrios, D. Varsano and G. Giorgi, ACS Energy Lett., 2020, 5, 457–463.
12. X. G. Zhao, G. Volonakis, A. A. Haghighirad, R. L. Milot, W. H. Sio, M. R. Filip, B. Wenger, M. B. Johnston, L. M. Herz, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2017, 8, 772–778.
13. Z. Xiao, K. Z. Du, W. Meng, J. Wang, D. B. Mitzi and Y. Yan, J. Am. Chem. Soc., 2017, 139, 6054–6057.
14. F. Wei, Z. Deng, S. Sun, F. Zhang, D. M. Evans, G. Kieslich, S. Tominaka, M. A. Carpenter, J. Zhang and P. D. Bristowe, Chem. Mater., 2017, 29, 1089–1094.
15. J. H. Yang, Y. Fu, D. Yang, Q. Xu, L. Yu, S. H. Wei and L. Zhang, J. Am. Chem. Soc., 2017, 139, 2630–2638.
16. J. Liang, C. Wang, Y. Wang, Z. Xu, Z. Lu, Y. Ma, H. Zhu, Y. Hu, C. Xiao, X. Yi, G. Zhu, H. Lv, L. Ma, T. Chen, Z. Tie, Z. Jin and J. Liu, J. Am. Chem. Soc., 2016, 138, 15829–15832.
17. F. Giustino and H. J. Snaith, ACS Energy Lett., 2016, 1, 1233–1240.
18. E. T. McClure, M. R. Ball, W. Windl and P. M. Woodward, Chem. Mater., 2016, 28, 1348–1354.
19. M. R. Filip, S. Hillman, A. A. Haghighirad, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2016, 7, 2579–2585.
20. M. R. Filip, G. Eperon, H. J. Snaith and F. Giustino, Nat. Commun., 2014, 5, 5757.
21. M. R. Filip, C. Verdi and F. Giustino, J. Phys. Chem. C, 2015, 119, 25209.
22. D. Han, T. Zhang, M. Huang, D. Sun, M.-H. Du and S. Chen, APL Mater., 2018, 6, 084902.
23. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k; an Augmented Plane Wave Plus Local Orbital Program for Calculating Crystal Properties, Vienna University of Technology, Austria, 2001.
24. Z. Wu and R. E. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235116.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
26. E. Engel and S. H. Vosko, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13164.
27. Z. Ali, I. Ahmed, I. Khan and B. Amin, Intermetallics, 2012, 31, 287.
28. G. Murtaza, I. Ahmed, B. Amin and M. Zahid, Opt. Mater., 2011, 33, 553.
29. H. Jiang, J. Chem. Phys., 2013, 138, 134115.
30. J. A. Camargo-Martinez and R. Baquero, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195106.
31. R. A. Jishi, O. B. Ta and A. A. Sharif, J. Phys. Chem. C, 2014, 118, 28344–28349.
32. F. Birch, Phys. Rev., 1947, 71, 809–824.
33. Y. Saeed, B. Amin, H. Khalil, F. Rehman, H. Ali, M. I. Khan, A. Mahmood and M. Shafiq, RSC Adv., 2020, 10, 17444–17451.
34. N. R. Kumar and R. Radhakrishnan, Mater. Lett., 2018, 227, 289–291.
35. M. Hachemaoui, R. Khenata, A. Bouhemadou, A. H. Reshak, D. Rached and F. Semari, Curr. Opin. Solid State Mater. Sci., 2009, 13, 105–111.
36. F. Rehman, A. Dahshan, H. A. Yakout, M. Shariq, P. Ahmed and Y. Saeed, J. Comput. Electron., 2022, 21, 119.
37. M. Zia ur Rehman, S. A. M. Abdelmohsen, E. A. Mahmoud, M. Usman Saeed, M. Idress, M. Shafiq, B. Amin and Y. Saeed, Mater. Sci. Semicond. Process., 2022, 151, 106993.
38. M. K. Gerges, M. Mostafa and G. M. Rashwan, Int. J. Latest Res. Eng. Technol., 2016, 2(4), 42–49.
39. P. Drude, Zur elektronentheorie der metalle, Ann. Phys., 1900, 306(3), 566–613.
40. K. Maeda and K. Domen, J. Phys. Chem. Lett., 2010, 1, 2655–2661.
41. R. M. Navarro Yerga, M. C. Alvarez Galvan, F. Del Valle, J. A. Villoria de la Mano and J. L. Fierro, ChemSusChem, 2009, 2, 471–485.
42. V. Artero, M. Chavarot-Kerlidou and M. Fonte-cave, Angew. Chem., Int. Ed., 2011, 50, 7238–7266.
43. J. Liu, X. Fu, S. Chen and Y. Zhu, Appl. Phys. Lett., 2011, 99, 191903.
44. H. L. Zhuang and R. G. Hennig, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 115314.
45. H. Din, M. Idrees, A. Albar, M. Shafiq, I. Ahmad, C. V. Nguyen and B. Amin, Phys. Rev. B, 2019, 100, 165425.
46. J. Liu, X. Fu, S. Chen and Y. Zhu, Appl. Phys. Lett., 2011, 99, 191903.
47. M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon, Oxford, 1954.
48. M. Shafiq, S. Arif, I. Ahmad, S. Jalali Asadabadi, M. Maqbool and H. A. R. Aliabad, J. Alloys Compd., 2015, 618, 292.
49. M. Shafiq, I. Ahmad and S. J. Asadabadi, J. Appl. Phys., 2014, 116, 103905.
50. S. F. Pugh, Philos. Mag., 1954, 45, 823–843.
51. F. Ladwig and Y. A. Chang, J. Appl. Phys., 2003, 94, 979.

---