Open Access Article
Open Access ArticleAdsorption of molecular hydrogen on Be3Al2(SiO3)6-beryl: theoretical insights for catalysis, hydrogen storage, gas separation, sensing, and environmental applications
Waqas Amber Gill a,
Norah Alhokbanyb and
Muhammad Ramzan Saeed Ashraf Janjua
a,
Norah Alhokbanyb and
Muhammad Ramzan Saeed Ashraf Janjua *c
*c
aDepartamento de Química Física, Universidad de Valencia, Avda Dr Moliner, 50, E-46100 Burjassot, Valencia, Spain
bDepartment of Chemistry, King Saud University, Riyadh 11451, Saudi Arabia
cDepartment of Chemistry, Government College University Faisalabad, Faisalabad 38000, Pakistan. E-mail: Janjua@gcuf.edu.pk; Dr_Janjua2010@yahoo.com
First published on 25th January 2024
Abstract
Employing a combination of Density Functional Theory (DFT) calculations and Molecular Dynamics (MD) simulations, the adsorption of molecular hydrogen (H2) on Be3Al2(SiO3)6-beryl, a prominent silicate mineral, has been studied. The crystal structure of beryl, which consists of interconnected tetrahedral and octahedral sites, provides a fascinating framework for comprehending H2 adsorption behavior. Initial investigation of the interaction between H2 molecules and the beryl surface employed DFT calculations. We identified favorable adsorption sites and gained insight into the binding mechanism through extensive structural optimizations and energy calculations. H2 molecules preferentially adsorb on the exposed oxygen atoms surrounding the octahedral sites, producing weak van der Waals interactions with the beryl surface, according to our findings. To further investigate the dynamic aspects of H2 adsorption, MD simulations employing a suitable force field were conducted. To precisely represent interatomic interactions within the Be3Al2(SiO3)6-beryl–H2 system, the force field parameters were meticulously parameterized. By subjecting the system to a variety of temperatures, we were able to obtain valuable information about the stability, diffusion, and desorption kinetics of H2 molecules within the beryl structure. The comprehensive understanding of the H2 adsorption phenomenon on Be3Al2(SiO3)6-beryl is provided by the combined DFT and MD investigations. The results elucidate the mechanisms underlying H2 binding, highlighting the role of surface oxygen atoms and the effect of temperature on H2 dynamics. This research contributes to a fundamental understanding of hydrogen storage and release in beryllium-based silicates and provides valuable guidance for the design and optimization of materials for hydrogen storage, catalysis, gas separation, sensing and environmental applications.
1. Introduction
The efficient storage and release of molecular hydrogen (H2) is of utmost importance in various fields, including renewable energy and transportation sectors.1,2 Silicate minerals, with their abundant and diverse structures, have emerged as promising candidates for hydrogen storage materials due to their potential for high volumetric storage capacity.3,4 In particular, Be3Al2(SiO3)6-beryl, a prominent silicate mineral, exhibits a unique crystal structure comprising interconnected tetrahedral and octahedral sites, offering an intriguing framework for exploring hydrogen adsorption behavior.5In this research paper, we investigate the adsorption behavior of H2 over Be3Al2(SiO3)6-beryl using a combination of density functional theory (DFT) calculations, molecular dynamics (MD) simulations, and force field analysis.6 DFT, a quantum mechanical method, provides a powerful tool to understand the electronic structure, energetics, and adsorption properties of materials at the atomic scale.7 By employing DFT calculations, we aim to investigate the adsorption sites and energetics of H2 molecules within the silicate's framework. Furthermore, DFT allows us to analyze the electronic properties of Be3Al2(SiO3)6-beryl, shedding light on the fundamental mechanisms governing H2 adsorption.7 To complement the DFT results and capture the dynamical behavior of H2 molecules, molecular dynamics (MD) simulations are conducted.8 MD simulations provide insights into the thermodynamic properties, diffusion kinetics, and overall stability of H2 adsorption within the zeolite structure. By studying the time evolution of the system, we can observe the interactions between H2 molecules and silicates, contributing to a comprehensive understanding of the adsorption process.8 In addition to DFT and MD, we incorporate force field analysis to validate the accuracy and reliability of our simulation results.9,10 Force fields, empirical mathematical models, are commonly used to describe interatomic interactions within a system.11 By comparing the results obtained from DFT calculations and MD simulations with those derived from the force field, we can assess the level of agreement and provide insights into the validity of our computational approach.9,10
Previous studies have explored the adsorption of H2 on silicate materials, providing valuable insights into the interaction mechanisms and storage capacities. For instance, a comprehensive review on hydrogen storage in beryllium-based silicates, highlighting the potential of these materials and the challenges associated with their practical implementation.12 H2 adsorption on different silicate surfaces, revealing the influence of surface chemistry and crystallographic orientation on the adsorption behavior investigated by DFT calculation.13 Hydrogen diffusion in silicate minerals, demonstrating the importance of temperature and structural features in governing the mobility of H2 molecules by the utilization of MD simulation.14
We present a set of systematic potentials that characterize the interactions between molecular hydrogen and Be3Al2(SiO3)6-beryl using the Improved Lennard-Jones (ILJ) potential. These potentials strike a balance between accuracy and simplicity, making them suitable for molecular dynamics simulations. Molecular dynamics simulations will be used to compute second virial coefficients in order to compare the effectiveness of the proposed force fields. We can evaluate the effectiveness of the various force fields by comparing these results to experimental values reported in scientific literature. In addition, we will use precise techniques, including density functional theory (DFT), to predict the preferred interaction sites of gas molecules on Be3Al2(SiO3)6-beryl and determine the optimal orientation of molecular hydrogen.
In Section 2, we will describe the computational specifics used for this investigation. The focus of Section 3 will be the analysis of the derived potential energy surface, while Section 4 will describe the molecular dynamics simulation. In the concluding section, Section 5, the study's findings will be summarized.
2. Computational details
The widely used Lennard-Jones (LJ) potential is often employed to describe the adsorption of gases on silicates, graphene, metal organic frame works and zeolites.15,16 However, the LJ potential is known to have deficiencies at both short and long ranges.17–19 To overcome these limitations, Pirani et al. proposed an Improved Lennard-Jones (ILJ)17,18 potential that addresses the shortcomings of the LJ model. The ILJ potential introduces an additional parameter, enhancing its flexibility and accuracy. It has demonstrated excellent performance in capturing dispersion interactions in noble gas systems and has shown efficacy in high angular resolution and energy conditions, accurately reproducing vibrational springs. Through careful parameter selection, the ILJ potential proves particularly valuable for molecular dynamics simulations, especially for non-covalent interactions.18,19 Its simplicity and accuracy make it a useful tool for accurately representing the adsorption behavior of gases on Be3Al2(SiO3)6-beryl. In many cases, electrostatic contributions to the interaction are incorporated using a coulombic expression, where partial charges are assigned to the system.20,21 However, the inclusion of these partial charges is often done without thorough consideration of the actual improvement in accuracy achieved by this term. It is important to note that the assigned partial charges lack true physical significance, as they are not quantum observables. Furthermore, there is often limited evidence to suggest that their inclusion significantly impacts the obtained results. The Improved Lennard-Jones (ILJ) interaction potentials utilized in this study were derived from first principles calculations performed at the dispersion-corrected density functional theory level. Specifically, the B97D functional, which incorporates an empirical dispersion term, was employed. The B97D functional is recognized as a robust approach among semi-empirical generalized gradient approximation (GGA) functionals, offering efficiency and precision in studying large systems that interact via dispersion forces.22 While the B97D functional has demonstrated its value in accurately describing non-covalent interactions,22–25 it is important to note that its performance may not be universally reliable for all systems.In this study, we utilize the Improved Lennard-Jones (ILJ) potential to construct a series of force fields suitable for assessing van der Waals interactions, particularly within the Be3Al2(SiO3)6-beryl and molecular hydrogen system. Additionally, we explore the impact of the electrostatic component on the force field parameters by incorporating various charge schemes such as Hirshfeld,26 CHelpG,27 MBS (Minimum Basis Set),28 MK (Merz–Kollman),29 NBO (Natural Bonding Orbitals),30 evaluating their effectiveness and feasibility.
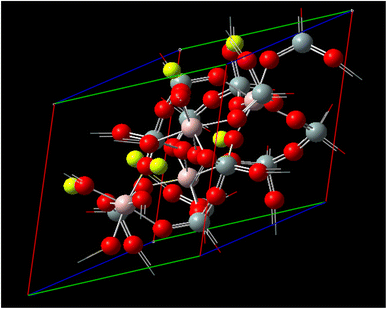
To account for the fact that Be3Al2(SiO3)6-beryl is an infinite molecule, we employed truncated system for the single point energy calculations. This model was designed to be large enough to capture the essential interactions. Previous studies have demonstrated that Be3Al2(SiO3)6-beryl can serve as a suitable model for silicates in B97D calculations. All monomers were initially optimized at the B3LYP/6-31G** level.31,32 In Table 1, the distances of the cell matrix are 9.21 Å, −4.605 Å, 7.97609 Å and 9.17 Å, respectively, for Be3Al2(SiO3)6-beryl. The cell parameters are A = 9.21 Å with α = 90°, B = 9.21 Å with β = 90° and C = 9.17 Å with γ = 120° and with the cell volume 673.62660 Å3. Subsequently, these optimized structures were treated as rigid in all subsequent interaction energy calculations.
| x | y | z | Parameters | Angles | |
|---|---|---|---|---|---|
| A | 9.21000 | 0.00000 | 0.00000 | 9.21000 | α = 90° |
| B | −4.60500 | 7.97609 | 0.00000 | 9.21000 | β = 120° |
| C | 0.00000 | 0.00000 | 9.17000 | 9.17000 | γ = 120° |
Fig. 1 illustrates the representation of a crystal lattice in crystallography, where a unit cell is commonly utilized to describe the crystal structure. The unit cell serves as the smallest repeating unit that encompasses the entire crystal lattice. It is defined by three parameters: the lengths of its edges (A, B, and C) and the angles between them (α, β, γ). The parameters A, B, and C correspond to the lengths of the edges of the unit cell, determining the size of the unit cell in each direction. Typically, these values are expressed in angstroms (Å) or picometers (pm). On the other hand, α, β, and γ denote the angles between the edges of the unit cell, influencing the shape and symmetry of the unit cell. Specifically, α represents the angle between edges B and C, β denotes the angle between edges A and C, and γ indicates the angle between edges A and B. These angles are measured in degrees. Be3Al2(SiO3)6-beryl, a specific type of silicate, exhibits a distinctive framework structure composed of interconnected channels and cages. The unit cell parameters (A, B, and C) and angles (α, β, γ) describe the arrangement of atoms within the crystal lattice of Be3Al2(SiO3)6-beryl. By knowing the specific values of A, B, C, α, β, and γ, crucial information regarding the size, shape, and symmetry of the Be3Al2(SiO3)6-beryl crystal structure can be deduced. These parameters play a vital role in understanding the crystallographic properties and can be employed to unravel various physical and chemical characteristics associated with Be3Al2(SiO3)6-beryl.
The energy calculations for the molecular hydrogen over Be3Al2(SiO3)6-beryl system, were performed using Gaussian 09 (ref. 33) and the EMSL Basis Set Exchange. The calculations were based on the B97D/TZV2P22,31 level. This specific combination of the B97D functional and the split-valence triple-zeta basis set with two polarizations (TZV2P) has been previously determined as adequate for accurately representing polarization effects in comparable systems.34,35
A total of 50 random orientations33 for the H2 molecule were generated by fixing Be3Al2(SiO3)6-beryl. Each orientation was then meticulously scanned for intermolecular distances ranging from 2.5 to 12.0, with a focus on sampling near the equilibrium distance. There was a total of 25 distances considered, which encompassed all 50 relative orientations. Using the B97D/TZV2P method, the interaction energy for each of the 1250 conformations was then calculated.
3. Potential energy surface
It is common to divide a potential energy surface into distinct components, such as electrostatic and non-electrostatic forces, when constructing one. For the potential energy surface of H2 over Be3Al2(SiO3)6-beryl, electrostatic forces result from coulombic interactions between charged particles within molecules, while non-electrostatic forces result from van der Waals interactions between neutral particles. The total potential energy can be expressed as the sum of electrostatic and non-electrostatic contributions if these components are treated separately and their separability is assumed. This assumption simplifies the construction procedure and facilitates the independent management of each contribution.To facilitate efficient calculation of potential energy contributions, it is assumed that both parts of the potential energy surface can be represented as sums over A and B molecule centres. The interactions between two molecules can be described in a straightforward and computationally efficient manner by totaling the contributions from each atom or centre in both molecules. It is essential to observe, however, that these assumptions may not apply to all molecular systems, and that certain circumstances may necessitate the use of advanced methods.
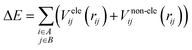 | (1) |
There are different ways to describe the resulting interactions between molecules, which can include coulombic sums over assigned atomic charges. The coulombic sum is given by
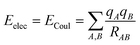 | (2) |
In the potential energy surface, distinct contributions, such as electrostatic and non-electrostatic forces, can be identified. Coulombic interactions between charged particles within the molecules generate electrostatic forces, whereas van der Waals forces between inert particles are responsible for the non-electrostatic forces.
| Vtot(R) = Vnelec(R) + Velec(R) = VILJ(R) + VCoul(R) | (3) |
In molecular simulations, the ILJ potential is used as a model to characterize the non-electrostatic portion of the potential energy surface. In molecular simulations, non-electrostatic interactions are typically attributed to van der Waals forces caused by fluctuations in the electron cloud encircling atoms and molecules.
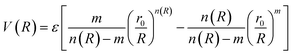 | (4) |
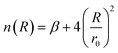 | (5) |
In Table 2, the higher value for βAlH is 7.893, indicating a stronger attractive interaction between aluminum (Al) and hydrogen (H). On the other hand, the lower value for βAlH is 7.356. The higher value for βBeH is 7.982, indicating a stronger attractive interaction between beryllium (Be) and hydrogen (H). The lower value for βBeH is 7.521. The higher value for βSiH is 8.853, indicating a stronger attractive interaction between silicon (Si) and hydrogen (H). The lower value for βSiH is 8.264. The higher value for βOH is 7.813, indicating a stronger attractive interaction between oxygen (O) and hydroxyl (OH) groups. It is worth noting that there is a discrepancy in the fifth value (7.637), which may or may not be considered an anomaly. The higher values of βAlH, βBeH, βSiH, and βOH represent stronger attractive interactions between the respective elements (Al, Be, Si, or O) and hydrogen (H) or hydroxyl (OH) groups. The lower values indicate relatively weaker attractive interactions.
| Parameters | Fitted | Hirshfeld | CHelpG | MBS | MK | NBO |
|---|---|---|---|---|---|---|
| qH (e−) | 0.419 | 0.291 | 0.443 | 0.416 | 0.426 | 0.568 |
| βAlH | 7.356 | 7.482 | 7.367 | 7.528 | 7.651 | 7.893 |
| εAlH (kJ mol−1) | 0.127 | 0.265 | 0.346 | 0.156 | 0.398 | 0.219 |
| rAlH (Å) | 3.364 | 3.389 | 3.462 | 3.375 | 3.521 | 3.502 |
| βBeH | 7.851 | 7.982 | 7.634 | 7.911 | 7.521 | 7.964 |
| εBeH (kJ mol−1) | 0.269 | 0.625 | 0.347 | 0.512 | 0.275 | 0.488 |
| rBeH (Å) | 3.761 | 3.964 | 3.931 | 3.826 | 3.725 | 3.673 |
| βSiH | 8.264 | 8.759 | 8.853 | 8.561 | 8.672 | 8.379 |
| εSiH (kJ mol−1) | 0.162 | 0.199 | 0.178 | 0.166 | 0.137 | 0.182 |
| rSiH (Å) | 3.658 | 3.782 | 3.621 | 3.873 | 3.918 | 3.653 |
| βOH | 7.571 | 7.639 | 7.452 | 7.527 | 7.637 | 7.813 |
| εOH (kJ mol−1) | 0.025 | 0.096 | 0.035 | 0.067 | 0.085 | 0.053 |
| rOH (Å) | 3.529 | 3.628 | 3.693 | 3.575 | 3.782 | 3.556 |
| R2 | 0.994 | 0.995 | 0.993 | 0.998 | 0.994 | 0.992 |
| MAES (kJ mol−1) | 0.412 | 0.727 | 0.448 | 0.467 | 0.481 | 0.458 |
The higher value for εAlH is 0.346 kJ mol−1, indicating a deeper potential well for the interaction between aluminum (Al) and hydrogen (H). The lower value for εAlH is 0.127 kJ mol−1. The higher value for εBeH is 0.625 kJ mol−1, indicating a deeper potential well for the interaction between beryllium (Be) and hydrogen (H). The lower value for εBeH is 0.269 kJ mol−1. The higher value for εSiH is 0.853 kJ mol−1, indicating a deeper potential well for the interaction between silicon (Si) and hydrogen (H). The lower value for εSiH is 0.162 kJ mol−1. The higher value for εOH is 0.096 kJ mol−1, indicating a deeper potential well for the interaction between oxygen (O) and hydroxyl (OH) groups. The lower value for εOH is 0.025 kJ mol−1. Higher values of εAlH, εBeH, εSiH, and εOH represent deeper potential wells, indicating stronger attractive interactions between the respective elements (Al, Be, Si, or O) and hydrogen (H) or hydroxyl (OH) groups. Conversely, lower values indicate shallower potential wells and relatively weaker attractive interactions. These values help characterize the depth of the interaction potentials, which are important for understanding molecular interactions and behaviors.
The higher value for rAlH is 3.462 Å, indicating a larger distance at which the potential between aluminum (Al) and hydrogen (H) reaches zero. The lower value for rAlH is 3.364 Å. The higher value for rBeH is 3.964 Å, indicating a larger distance at which the potential between beryllium (Be) and hydrogen (H) reaches zero. The lower value for rBeH is 3.673 Å. The higher value for rSiH is 3.918 Å, indicating a larger distance at which the potential between silicon (Si) and hydrogen (H) reaches zero. The lower value for rSiH is 3.621 Å. The higher value for rOH is 3.782 Å, indicating a larger distance at which the potential between oxygen (O) and hydroxyl (OH) groups reaches zero. The lower value for rOH is 3.529 Å. Higher values of rAlH, rBeH, rSiH, and rOH represent larger distances at which the potential between the respective elements (Al, Be, Si, or O) and hydrogen (H) or hydroxyl (OH) groups reaches zero. Conversely, lower values indicate smaller distances. These values provide information about the range of the interactions and help understand the spatial extent over which the attractive forces are effective.
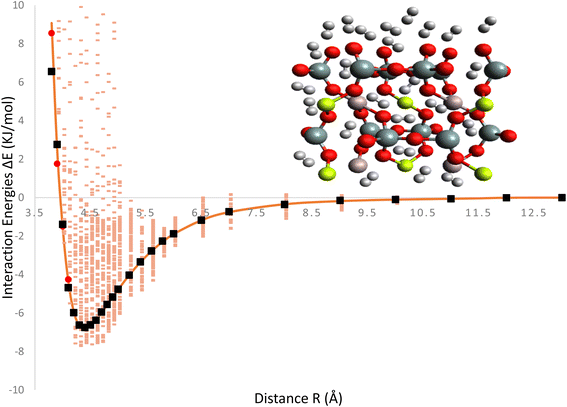
The Fig. 2, represent interaction energies and charges related to the ILJ potential and its fitting to a specific system. Interaction energies (pink) represent the calculated interaction energies between the H2/Be3Al2(SiO3)6-beryl system and some other entities, likely obtained through the B97D/TZV2P method. The pink color indicates that these energies are derived from calculations. Red points represent averaged interaction energies obtained from random conformations of the H2/Be3Al2(SiO3)6-beryl system. Each point represents an averaged energy value derived from multiple conformations of the system. Orange solid line represents the optimized ILJ potential. It is obtained by fitting the ILJ potential to the interaction energies calculated or averaged from the H2/Be3Al2(SiO3)6-beryl system. The optimized ILJ potential aims to best capture and reproduce the observed interaction energies. Black points represent the Hirshfeld charges of the H2/Be3Al2(SiO3)6-beryl system. Hirshfeld charges are a type of atomic charge calculation method. The ILJ potential is also fitted to these charges, meaning that it tries to reproduce the observed charges using its parameters. The Fig. 2, shows the fitting of an ILJ potential to interaction energies and atomic charges in the H2/Be3Al2(SiO3)6-beryl system. The pink interaction energies are calculated, the red points represent averaged energies from random conformations, the orange line represents the optimized ILJ potential, and the black point represents the Hirshfeld charges. This analysis helps in understanding the system's behavior and developing a potential energy model that accurately represents its interactions.
Mean Absolute Error (MAE) is a metric used to evaluate the accuracy of the ILJ potential's fit to the interaction energies or charges of the H2/Be3Al2(SiO3)6-beryl system as shown in Fig. 3. The MAE measures the average magnitude of the deviations between the predicted values (obtained from the fitted ILJ potential) and the observed values (the calculated or average interaction energies and the Hirshfeld charges). For each data point, the absolute differences between predicted and observed values are computed to determine the MAE. This value represents the mean absolute error. The MAE measures how well the ILJ potential fits the observed data, with smaller values indicating a superior fit. The MAE can be utilized to assess the efficacy of the ILJ potential and compare various potential models. It enables researchers to evaluate the accuracy with which the potential reproduces the interaction energies or charges and offers insight into the quality of the fitting procedure. By minimizing the MAE, one seeks to identify the set of ILJ potential parameters that best represents the observed data, resulting in a more precise description of the system's behavior.
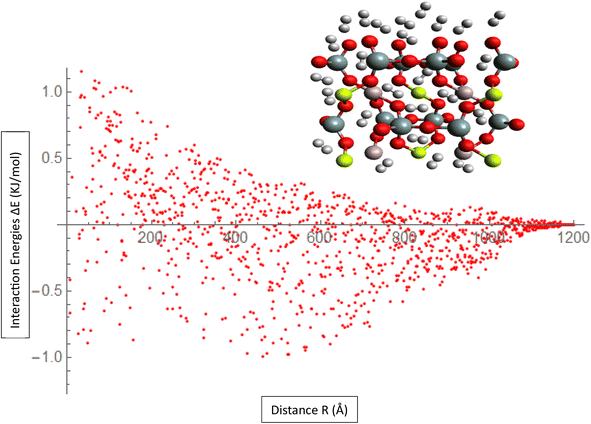 | ||
| Fig. 3 Fitting ILJ potential to the H2/Be3Al2(SiO3)6-beryl system, including evaluation of interaction energies, charges, and MAE. | ||
4. Molecular dynamics simulation
The adsorption of H2 on Be3Al2(SiO3)6-beryl,36 which is a type of silicate mineral composed of beryllium, aluminum, and silicon, can be studied using molecular dynamics simulations. We create a virtual model of the Be3Al2(SiO3)6-beryl surface and the H2 molecules. By employing mathematical equations and force fields that describe the interactions between atoms, the simulation calculates the movements and forces acting on each atom during the simulation timeframe. Through molecular dynamics simulations, we can observe how individual H2 molecules approach and interact with the Be3Al2(SiO3)6-beryl surface. The simulations37 can provide insights into the adsorption process, including the binding energies between the H2 molecules and the Be3Al2(SiO3)6-beryl surface, the distribution of adsorbed H2 molecules, and the dynamics of the system. By analyzing the simulation results, we can derive important information such as the adsorption energy, which indicates the strength of the interaction between H2 and Be3Al2(SiO3)6-beryl. They can also investigate the diffusion of H2 molecules on the Be3Al2(SiO3)6-beryl surface, which provides insights into the mobility and stability of the adsorbed H2. These simulations can help to understand the fundamental mechanisms38 of H2 adsorption on Be3Al2(SiO3)6-beryl and evaluate its potential as an adsorbent material for hydrogen storage or other applications. They can provide valuable insights into the thermodynamics and kinetics of the adsorption process and guide experimental studies.DL_POLY39 was utilized for molecular dynamics calculations. The microcanonical (NVE) ensemble used periodic boundary conditions in the x, y, and z directions under standard conditions (273 K and 1 atm). A timestep of 1 fs was utilized for a run time of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, including an equilibration of 3
000 steps, including an equilibration of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, resulting in a total run time of 5 ns, while monitoring of temperature and energy demonstrated convergence. To assure the standard density of methane, the van der Waals and coulombic cutoffs were set to 18 Å, and 100H2 molecules were randomly distributed in a cube with 160 Å sides.
000 steps, resulting in a total run time of 5 ns, while monitoring of temperature and energy demonstrated convergence. To assure the standard density of methane, the van der Waals and coulombic cutoffs were set to 18 Å, and 100H2 molecules were randomly distributed in a cube with 160 Å sides.
We have calculated the diffusion coefficient using the following Einstein equation:
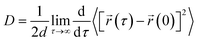 | (6) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (τ) is the position of the particle of interest at time τ. The term 〈[
(τ) is the position of the particle of interest at time τ. The term 〈[![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (τ) −
(τ) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (0)]2〉 is called the mean squared displacement (MSD) and varies linearly over time. To assure accurate statistics, we calculated the diffusion coefficient from five distinct starting configurations and sampled two million MSD values versus time for each starting configuration. We evaluated the diffusion coefficient over one million different time origins by dividing timestep 1 to one million, then timestep 2 to one million, and so on. The adsorption behavior of hydrogen molecules on Be3Al2(SiO3)6-beryl was investigated using two different calculation approaches by density functional theory (DFT) and molecular dynamics (MD) simulations. The obtained results are summarized in Table 2, which includes the distances between the adsorbed hydrogen molecules and the silicate surface, as well as the corresponding configurational energies (Ecfg) in kilojoules per mole (kJ mol−1).
(0)]2〉 is called the mean squared displacement (MSD) and varies linearly over time. To assure accurate statistics, we calculated the diffusion coefficient from five distinct starting configurations and sampled two million MSD values versus time for each starting configuration. We evaluated the diffusion coefficient over one million different time origins by dividing timestep 1 to one million, then timestep 2 to one million, and so on. The adsorption behavior of hydrogen molecules on Be3Al2(SiO3)6-beryl was investigated using two different calculation approaches by density functional theory (DFT) and molecular dynamics (MD) simulations. The obtained results are summarized in Table 2, which includes the distances between the adsorbed hydrogen molecules and the silicate surface, as well as the corresponding configurational energies (Ecfg) in kilojoules per mole (kJ mol−1).
In Table 3, the distance obtained from the DFT calculation is 2.352 Å. This distance represents the separation or bonding arrangement between the relevant atoms or molecules in the system. The configurational energy obtained from the DFT calculation is −27.58 kJ mol−1. Configurational energy refers to the potential energy of the system associated with a specific arrangement or configuration of the atoms or molecules. In this case, the negative value indicates that the system is in a stable or energetically favorable state with respect to this configuration. The distance obtained from the MD simulation is 2.338 Å. This distance represents the average separation between the relevant atoms or molecules during the simulation at the specified temperature. The configurational energy obtained from the MD simulation at a temperature of 273.15 K is −17.29 kJ mol−1. This energy value represents the potential energy associated with the system's configuration during the simulation under the given conditions. The DFT approach yielded a distance of 2.352 Å, while the MD simulation resulted in a slightly shorter distance of 2.338 Å. The small difference in distance indicates a minor variation in the molecular arrangement or interatomic distances between the two methods. It's important to note that this discrepancy could arise from inherent differences in the underlying methodologies, approximations, or computational models used in DFT and MD. The configurational energy obtained from the DFT approach is −27.58 kJ mol−1, whereas the MD simulation resulted in a lower value of −17.29 kJ mol−1. This significant difference in energy can be attributed to several factors. DFT calculations typically provide more accurate electronic structure information but might not capture certain dynamic or thermodynamic effects present in MD simulations. Additionally, the different parameterizations and potential functions used in the two methods can contribute to variations in the calculated energies.
| Types of calculation | Distances (Å) | Ecfg (kJ mol−1) |
|---|---|---|
| DFT approach | 2.352 | −27.58 |
| MD (T = 273.15 K) | 2.338 | −17.29 |
The adsorption behavior of hydrogen molecules on beryl's can be studied through the use of both density functional theory (DFT) calculations and molecular dynamics (MD) simulations. The trustworthiness of both approaches is highlighted by the fact that the predicted distances are compatible with one another when defining the spatial arrangement of the species that have been adsorbed. When looking at adsorption processes, it is essential to take into account both electronic structure calculations and dynamic impacts because the configurational energy values are so different from one another.
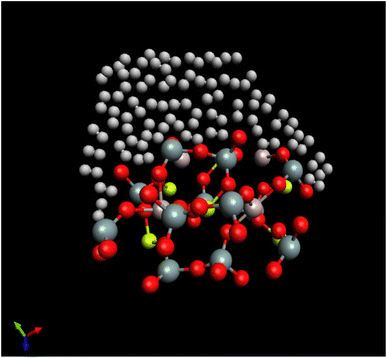
A snapshot refers to a particular moment or instant in time during a simulation where the positions and orientations of the particles or molecules are recorded. The “last configuration” indicates that this snapshot captures the arrangement of the system's particles at the end of the simulation run. H2/Be3Al2(SiO3)6-beryl system being simulated, composed of H2 molecules interacting with the Be3Al2(SiO3)6-beryl surface. Beryl is a mineral composed of beryllium aluminum silicate, and in this context, it serves as the surface interacting with the H2 molecules. The simulation is conducted at a temperature of 273.15 K. The random white-brown dumbbells are a visual representation of the H2 molecules present in the system. They indicate that the H2 molecules are distributed randomly and may exhibit different orientations and positions. The H2 molecules are shown to be located above or interacting with the Be3Al2(SiO3)6-beryl surface. This suggests that the simulation is focused on studying the behavior of the H2 molecules in relation to the surface and their potential interactions or adsorption onto the beryl surface (Fig. 4).
5. Conclusion
This study investigated the adsorption of molecular hydrogen (H2) on Be3Al2(SiO3)6-beryl, an important silicate mineral, using a combination of Density Functional Theory (DFT) calculations and Molecular Dynamics (MD) simulations. Through extensive structural optimizations and energy calculations using DFT, the study identified favorable adsorption sites and elucidated the binding mechanism. The results revealed that H2 molecules form mild van der Waals interactions with the exposed oxygen atoms surrounding the octahedral sites of the beryl surface. To investigate the dynamic aspects of H2 adsorption, MD simulations were conducted with a force field that precisely represented the interatomic interactions within the system and was meticulously parameterized. By subjecting the Be3Al2(SiO3)6-beryl–H2 system to a range of temperatures, valuable information regarding the stability, diffusion, and desorption kinetics of H2 molecules within the beryl structure was obtained. The combined DFT and MD investigations provided a thorough comprehension of the H2 adsorption phenomenon and shed light on the underlying mechanisms, highlighting the role of surface oxygen atoms and the impact of temperature on H2 dynamics. In addition, the study demonstrated that the Improved Lennard-Jones (ILJ) potential utilized in the MD simulations was in excellent accord with the DFT calculations and observed system behavior. This agreement enhances the precision and dependability of the simulation method utilized in this study. This study contributes to the fundamental understanding of hydrogen storage and release in beryllium-based silicates, providing valuable insights for the design and optimization of materials for a variety of applications, including hydrogen storage, catalysis, gas separation, sensing, and environmental applications. The findings emphasize Be3Al2(SiO3)6-beryl's potential as a candidate material for hydrogen-related applications and pave the way for future research in this area.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their sincere appreciation to Researchers Supporting Project number (RSP2024R253), King Saud University, Riyadh, Saudi Arabia.References
- A. M. Abdalla, S. Hossain, O. B. Nisfindy, A. T. Azad, M. Dawood and A. K. Azad, Energy Convers. Manage., 2018, 165, 602–627 CrossRef CAS.
- D. Teichmann, W. Arlt and P. Wasserscheid, Int. J. Hydrogen Energy, 2012, 37(23), 18118–18132 CrossRef CAS.
- X. W. Sun, Y. X. Zhang and D. Losic, J. Mater. Chem. A, 2017, 5(19), 8847–8859 RSC.
- Y. Li, Z. Y. Fu and B. L. Su, Adv. Funct. Mater., 2012, 22(22), 4634–4667 CrossRef CAS.
- M. J. Rosseinsky, Microporous Mesoporous Mater., 2004, 73(1–2), 15–30 CrossRef CAS.
- J. Rouquerol, F. Rouquerol, P. Llewellyn, G. Maurin and K. S. W. Sing, Adsorption by Powders and Porous Solids: Principle, Methodology and Applications, Academic Press, 2013 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 2nd edn, 2017 Search PubMed.
- B. Smit and T. L. M. Maesen, Nature, 2008, 451(7179), 671–678 CrossRef CAS PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulations: from Algorithms to Applications, Academic Press, San Diego, 3rd edn, 2023 Search PubMed.
- D. Dubbeldam, S. Calero, T. J. H. Vlugt, R. Krishna, T. L. Maesen, E. Beerdsen and B. Smit, Phys. Rev. Lett., 2004, 93(8), 088302 CrossRef CAS PubMed.
- J. A. Armstrong and M. T. Weller, J. Am. Chem. Soc., 2010, 132(44), 15679–15686 CrossRef CAS PubMed.
- S. A. Mian, L. C. Saha, J. Jang, L. Wang, X. Gao and S. Nagase, J. Phys. Chem. C, 2010, 114(48), 20793–20800 CrossRef CAS.
- I. C. Bourg and C. I. Steefel, J. Phys. Chem. C, 2012, 116(21), 11556–11564 CrossRef CAS.
- C. D. Wu, T. H. Fang, J. Y. Lo and Y. L. Feng, J. Mol. Model., 2013, 19(9), 3813–3819 CrossRef CAS PubMed.
- K. V. Kumar, K. Preuss, L. Lu, Z. X. Guo and M. M. Titirici, J. Phys. Chem. C, 2015, 119, 22310–22321 CrossRef CAS.
- F. Pirani, M. Albertí, A. Castro, M. M. Teixidor and D. Cappelletti, Chem. Phys. Lett., 2004, 394(1–3), 37–44 CrossRef CAS.
- F. Pirani, S. Brizi, L. F. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2008, 10(36), 5489–5503 RSC.
- A. Lombardi and F. Palazzetti, J. Mol. Struct.: THEOCHEM, 2008, 852(1–3), 22–29 CrossRef CAS.
- M. Albertí, A. Aguilar, J. M. Lucas and F. Pirani, J. Phys. Chem. A, 2012, 116(22), 5480–5490 CrossRef PubMed.
- M. K. Rana, H. S. Koh, H. Zuberi and D. J. Siegel, J. Phys. Chem. C, 2014, 118(6), 2929–2942 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27(15), 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25(12), 1463–1473 CrossRef CAS PubMed.
- R. Peverati and K. K. Baldridge, J. Chem. Theory Comput., 2008, 4(12), 2030–2048 CrossRef CAS PubMed.
- L. M. Roch and K. K. Baldridge, Phys. Chem. Chem. Phys., 2017, 19(38), 26191–26200 RSC.
- H. Liu, G. Qi, Q. Song and H. Wang, J. Photochem. Photobiol., A, 2018, 354, 119–126 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113(18), 6378–6396 CrossRef CAS PubMed.
- J. Autschbach, ChemPhysChem, 2009, 10(11), 1757–1760 CrossRef CAS PubMed.
- M. M. Ghahremanpour, P. J. Van Maaren and D. Van Der Spoel, Sci. Data, 2018, 5(1), 1–10 CrossRef PubMed.
- F. Weinhold and C. R. Landis, Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, 2005, p. 760 Search PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100(8), 5829–5835 CrossRef.
- M. Metcalf, J. Reid and M. Cohen, Modern Fortran explained, Oxford University Press, New York, 2011 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian-09 Revision D.01, 2009 Search PubMed.
- B. S. Mallik, I. W. Kuo, L. E. Fried and J. I. Siepmann, Phys. Chem. Chem. Phys., 2012, 14(14), 4884–4890 RSC.
- K. Srinivasu and S. K. Ghosh, J. Phys. Chem. C, 2012, 116(48), 25184–25189 CrossRef CAS.
- H. Hao, Y. Cao, L. Li, G. Fan and J. Liu, Appl. Surf. Sci., 2021, 537, 147926 CrossRef CAS.
- S. Caratzoulas, D. G. Vlachos and M. Tsapatsis, J. Am. Chem. Soc., 2006, 128(2), 596–606 CrossRef CAS PubMed.
- Y. Zhou, D. Hou, H. Manzano, C. A. Orozco, G. Geng, P. J. Monteiro and J. Liu, ACS Appl. Mater. Interfaces, 2017, 9(46), 41014–41025 CrossRef CAS PubMed.
- W. Smith and T. R. Forester, J. Mol. Graphics, 1996, 14(3), 136–141 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |