Open Access Article
Open Access ArticlePhysical properties of vacancy-ordered double perovskites K2TcZ6 (Z = Cl, Br) for spintronics applications: DFT calculations
Huda A. Alburaiha,
Sadia Nazir*b,
N. A. Noor *c,
A. Laref
*c,
A. Laref d and
M. Musa Saad H.-E.e
d and
M. Musa Saad H.-E.e
aPhysics Department, College of Science, Princess Nourah Bint Abdulrahman University, 11671 Riyadh, 12211, Saudi Arabia
bDepartment of Physics, University of Lahore, Pakistan
cDepartment of Physics, RIPHAH International University, Campus Lahore, Pakistan. E-mail: naveedcssp@gmail.com
dDepartment of Physics and Astronomy, College of Science, King Saud University, Riyadh, 11451, King Saudi Arabia
eDepartment of Physics, College of Science and Arts in Al-Muthnib, Qassim University, Al-Muthnib 51931, Saudi Arabia
First published on 8th January 2024
Abstract
Vacancy-ordered double perovskites (DPs) are emerging materials for spintronics due to their stable structures and non-toxic properties. In this study, we conducted a comprehensive investigation into the role of 4d electrons in Tc to understand their impact on the ferromagnetic properties of K2TcY6 (Y = Cl, Br). We have employed a modified Back and Johnson potential to assess electronic and magnetic characteristics and utilized the BoltzTraP code to investigate thermoelectric effects. Experimental lattice constants confirmed the presence of stable structures and formation energy estimates affirmed their thermodynamic stability. The Heisenberg model and density of electron states (DOS) at the Fermi level provides insights into Curie temperature and spin polarization. The presence of ferromagnetism is evident in the density of states, reflecting the transition of electron spins that support the exchange mechanism. The study delves into how electron functionality influences the control of ferromagnetism, considering exchange constants, exchange energies, hybridization process and the crystal field energies. Moreover, the exploitation of magnetic moments from Tc to K and Cl/Br sites takes precedence in driving ferromagnetism by exchanging electron spins rather than forming magnetic clusters. Additionally, to explore the optical characteristics of the compounds, we investigated their optical absorption, dielectric constants and refractive index within the energy range of 0–10 eV, ensuring absorption across both the visible and ultraviolet regions. Finally, we delve into the impact of the thermoelectric effect on both thermoelectric performance and spin functionality, taking into account factors such as the Seebeck coefficient, power factor, and electronic conductivity.
1. Introduction
Over the last two decades, there has been significant research interest in the field of room temperature ferromagnetism in semiconductors, primarily because of its potential applications in non-volatile memory, quantum computing and spintronics.1–5 Ferromagnetism in semiconductors holds the promise of facilitating the transmission of spin-polarized electrons, a crucial requirement in spintronics.6 Initial reports suggesting the possibility of a Curie temperature above room temperature in materials like GaN and ZnO7 led to several experimental studies claiming the existence of room temperature ferromagnetism.8–11 Furthermore, ferromagnetism has been identified in a range of non-magnetic semiconductor samples through the introduction of the creation of atomic defects and non-magnetic elements.12–21 This phenomenon is commonly referred to as d0 ferromagnetism.22 In such cases, the source of magnetism is distinct from the partially filled 4d or f-orbital electrons. The investigation of ferromagnetic characteristics has become a technological necessity for future advancements, given that spin-polarized currents have the ability to flow, unlike the unpolarized currents found in traditional electronic devices. As a result, researchers have reported the presence of ferromagnetic characteristics in perovskite materials.23 However, the applicability of perovskites on a broader scale is hindered by the presence of toxic constituent elements and stability concerns.24To address these limitations, researchers have undertaken studies on ferromagnetism in various A2BB′X6 type double perovskites (DPs).25–27 The half-metallic DP Sr2FeMoO6 has demonstrated a magnetic transition at temperature 410 K, as reported in ref. 28. This finding highlights the potential of such materials to unveil magnetic characteristics at higher temperatures.28 In a more recent experimental study of Pr2FeCrO6, researchers observed a magnetic transition occurring at 550 K. This finding was supported by the observed changes in magnetic susceptibility, dielectric constant and resistivity as a function of temperature.29,30 Double perovskite materials have been extensively explored for their magnetic and thermoelectric characteristics using a Density Functional Theory (DFT) approach, including compounds like Ba2FeMoO6 and Dy2CoMnO6.31,32 Double perovskite structures with a vacancy ordering are created by replicating the conventional ABX3 perovskite configuration and subsequently eliminating half of the B-type cations.33 These DPs are appealing because of their resemblance to perovskites in terms of structure and their impressive material characteristics, stemming from their broad range of constituent ion compositions and the potential for tilting in the [BX6]2− octahedra.34–36 Recently, DPs with cubic vacancy ordering in the A2BX6 structure have been employed in light absorption applications.37
Researchers are also engaged in theoretical investigations of these vacancy-ordered DPs to explore their half-metallic ferromagnetic characteristics.38 Moreover, vacancy-ordered DPs with ferromagnetic properties are worth exploring for potential applications in thermoelectric systems.39 Using DFT calculations, spin dependent DPs Rb2(Tc,Mo)X6 (X = Cl, Br) are investigated for spintronic applications due to the role of Mo/Tc atom 4d electrons and show all DPs ferromagnetic characteristics.40 Mustafa et al.,41 systematically explored the ferromagnetic characteristics in DPs Rb2(Os/Ir)Cl/Br6 using density functional theory. Their analysis of the computations shows that electron spin causes ferromagnetism to be induced by crystal field energy. The structural formula of K2TcY6 (Y = Cl or Br) suggests the potential for ferromagnetism in these vacancy-ordered DPs. These investigated DPs are gaining prominence as novel materials in the realm of spintronic applications, including the realization of phenomena such as dynamic random-access memories (DRAM), swift quantum computing, spin valves, magnetic switches and the giant magneto-resistance effect (GMR). In such devices, properties are controlled by manipulating the spin of electrons rather than altering their charge, making these materials faster and more versatile. Additionally, these materials find use in power-harvesting tools such as thermoelectric generators.
The investigation of these DPs is motivated by their full spin polarization, substantial magnetic coupling and enduring ferromagnetism, making them promising candidates for spintronic devices. Particularly, these DPs present the intriguing feature of maintaining ferromagnetic properties at temperatures exceeding room temperature, while simultaneously exhibiting ultralow thermal conductivity.42,43 Moreover, Cs2AgFeCl6 is subjected to magnetic and transport analysis employing the TB-mBJ potential, and its thermoelectric features are elucidated through a figure of merit scale.44,45 This study includes the comprehensive first-principles calculations to explore the magnetic characteristics within the DPs K2TcY6 (Y = Cl, Br). Experimental findings46 regarding K2TcY6 suggest that the Tc atom is a promising candidate for generating a substantial magnetic moment and ferromagnetic spin ordering in initially non-magnetic materials. Consequently, the K2TcY6 (Y = Cl, Br) DPs may exhibit intriguing electronic properties, which could play a crucial role in advancing the field of spintronics within these direct bandgap semiconductors. We have further examined the impact of their ferromagnetic nature on the thermoelectric properties by analyzing key thermoelectric parameters computed using the BoltzTraP code.47 Moreover, our results clearly demonstrate semiconducting ferromagnetic nature of these compounds and ultralow values of κe that can prove useful for application of these materials in spintronic and thermoelectric devices.
2. Method of calculations
The DFT gives the absolute information of the compounds' properties before recognizing them for being utilized in useful manufacturing of various devices. BoltzTraP codes were brought into use for thermoelectric analysis whereas the Wien2k code48 was employed for the evaluation of the structural, magnetic and spin-polarized electronic features. The optimization for AFM and FM states along with structural properties were conducted by PBEsol in the FP-LAPW method.49 Although the PBEsol accurately determines the lattice parameters as well as the energies of the system, it is unable to evaluate their band gaps and electronic behavior. For that reason, TB-mBJ potential were employed as an entire package for the improvement of band gap on which the compounds' physical features relies.50 In the whole potential method, the electronic gap system was divided into interstitial regions and muffin-tin corresponding to the plane wave and spherical harmonic solutions. In addition, RMT × Kmax = 8.0 was set by holding the radius of the muffin tin sphere as well as the wave vector in the opposite lattice. A k-mesh of 20 × 20 × 20 was employed for the iterative energy conversion approach within the first Brillouin zone. The above-mentioned k-mesh performed the convergence of the whole observed system. As a default setup, the other two fundamental factors such as angular momentum![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) max = 10 and Gaussian factor Gmax = 16. The convergence of energy was the sequence of 10−4 Ry. The charge convergence obtained from TB-mBJ, alongside the ground state energy, serves as the input for the BoltzTraP code, a classical transport theory-based tool for studying transport properties.
max = 10 and Gaussian factor Gmax = 16. The convergence of energy was the sequence of 10−4 Ry. The charge convergence obtained from TB-mBJ, alongside the ground state energy, serves as the input for the BoltzTraP code, a classical transport theory-based tool for studying transport properties.
3. Results and discussion
3.1 Structural properties
Fig. 1 shows the structural nature of the observed compounds (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225)) in cubic phase. The left part in the Fig. 1 presents the polyhedral form whereas the right one displays ball format. The geometric and atomic configurations are ensured by the unit cell. Amongst the octahedral of M(Cl/Br)6, the K atoms are located. The octahedral form for every atom is kept by the 12-fold composition order of Cl/Br atoms. The Tc atoms lie in the middle position of every octahedron of Cl/Br atoms. Further, the Wyckoff positions for Tc, Cl/Br and K are 4a (0, 0, 0), 24e (0.20, 0, 0), and 8c (0.25, 0.25, 0.25), respectively. The obtained values of the lattice constants (a0) determined through Murnaghan equation of state and found comparable to experimental lattice constant.46 From Table 1, it is clear when the ionic radius increases, the a0 also starts increasing from Cl to Br containing compound. On the other hand, it is also evident from Table 1 that the larger electronegativity value of Cl causes it to have large value of formation energy compared to K2TcBr6. As the increasing values of a0 reduces the density of the structures, the bulk modulus (B0), quite contrary to a0, starts decreasing from Cl to Br.
m (225)) in cubic phase. The left part in the Fig. 1 presents the polyhedral form whereas the right one displays ball format. The geometric and atomic configurations are ensured by the unit cell. Amongst the octahedral of M(Cl/Br)6, the K atoms are located. The octahedral form for every atom is kept by the 12-fold composition order of Cl/Br atoms. The Tc atoms lie in the middle position of every octahedron of Cl/Br atoms. Further, the Wyckoff positions for Tc, Cl/Br and K are 4a (0, 0, 0), 24e (0.20, 0, 0), and 8c (0.25, 0.25, 0.25), respectively. The obtained values of the lattice constants (a0) determined through Murnaghan equation of state and found comparable to experimental lattice constant.46 From Table 1, it is clear when the ionic radius increases, the a0 also starts increasing from Cl to Br containing compound. On the other hand, it is also evident from Table 1 that the larger electronegativity value of Cl causes it to have large value of formation energy compared to K2TcBr6. As the increasing values of a0 reduces the density of the structures, the bulk modulus (B0), quite contrary to a0, starts decreasing from Cl to Br.
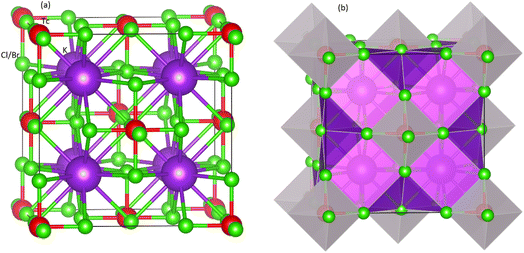 | ||
| Fig. 1 Unit cell of double perovskites K2TcX6 (X = Cl, Br) (a) ball format and (b) polyhedral format. Purple, red and green spheres show K, Tc, and X atoms, respectively. | ||
3.2 Curie temperature and structural stability
The graphs of the volume and augmented energy in anti-ferromagnetic (AFM) and in ferromagnetic (FM) states have been plotted in Fig. 2a–c. The estimation and comparison of the energies affirmed in Rydberg for AFM and FM states was done from the bottom. For FM, the highest omission of energy was observed as compared with AFM states. Thus, more suitability in the FM state is believed for the K2TcX6 (X = Cl, Br).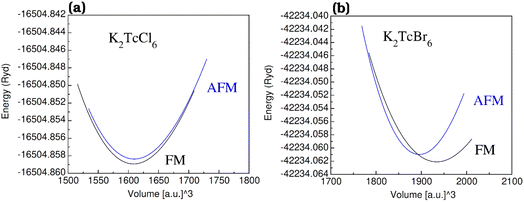 | ||
| Fig. 2 The energy (in term of Ryd) vs. volume (in term of [a.u]3) plots of double perovskites (a) K2TcCl6 and (b) K2TcBr6 in ferromagnetic (FM) and anti-ferromagnetic (AFM) phases. | ||
Further, formation energy helped illustrating the thermodynamic behavior while employing a reasonable chemical relation:50
| ΔHf = Etotal(KaTcbXc) − aEK − bETc − cEX | (1) |
3.3 Spin polarized electronic properties and magnetic behavior
The band structure (BS) for spin-down (↓) as well as spin-up (↑) orientations were computed using TB-mBJ potential for illustrating the ferromagnetism and spin polarization for DPs K2TcCl6 and K2TcBr6 (see Fig. 4a and b). Fermi-level (EF) remains within the insulating region between conduction band (CB) and valence band (VB) of for spin-down (↓) for both DPs. On the other hands, the states stay at EF for K2TcCl/Br6 in spin-up (↑). Resultantly, our compounds exhibited semiconducting ferromagnetic DPs that is assumed a necessary factor in spintronics. Spin-up (↑) channel indicate direct bandgap nature having bandgap values are 3.3 eV and 2.7 eV for K2TcCl6 and K2TcBr6 respectively. Both double perovskites studied in this work have earlier been studied with theoretical calculations and have been shown to have band gaps above 1 eV. However, accurate determination of band gap with TB-mBJ functional has not been reported which we have done for the first time. Although no experimental data is available for comparison, our calculated values of band gaps for the two systems are better than those reported by Berri et al.,52 and materials project database.53 The larger exchange interaction value causes the larger semiconducting gap that ensures the larger ferromagnetism.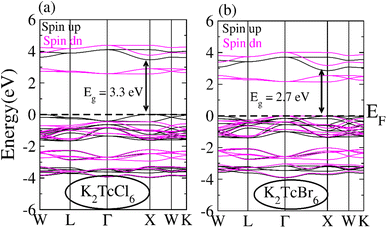 | ||
| Fig. 4 Band structures calculated for (a) K2TcCl6 and (b) K2TcBr6 for spin up (black line) and spin down (pink line) using mBJ potential. | ||
Total density of states (TDOS) along with partial density of states of Tc, K and Cl/Br atoms are calculated and represented in Fig. 5 and 6. TDOS also represent the semiconducting ferromagnetic behavior according to spin down (↓) and spin up (↑) calculated DOS. From PDOS, we see a major role of the burly hybridization of 3p/4p-Cl/Br electrons with 4-d states electrons of Tc in justifying the ferromagnetic interface [see Fig. 5 and 6].
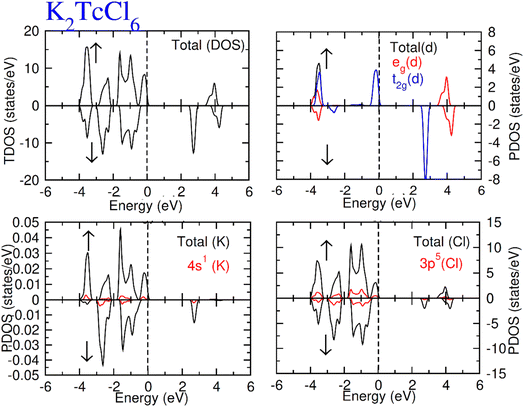 | ||
| Fig. 5 Total DOS and partial DOS for DP K2TcCl6 with K, Tc and Cl atoms in spin up (↑) and spin down (↓). | ||
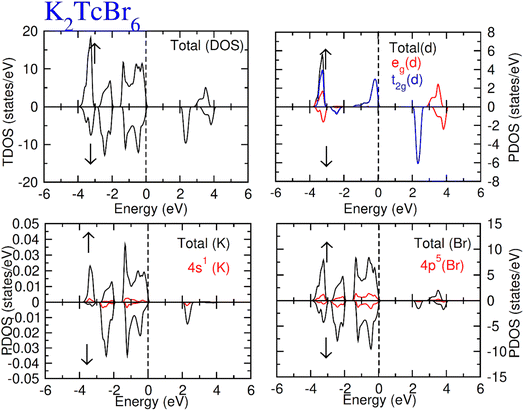 | ||
| Fig. 6 Total DOS and partial DOS for DP K2TcBr6 with K, Tc and Br atoms in spin up (↑) and spin down (↓). | ||
The 4d states of Tc are sum of 4d-t2g and 4d-eg states. The black color from 4d states overlapped by the red and blue color in the plot of the 4d-t2g and 4d-eg states from which it is confirmed the complete division of the 4d states into degenerated states. The 4d-Tc states are separated in five degenerated states. Three states (dzx, dyz and dxy) out of five degenerate states recombined to triplet-t2g-states. On the other hand, the rest of the two states (dz2 and dx2–y2) recombined to doublet-eg-states and lie at the highest energy-states. The hybridization of t2g states with 3p/4p-Cl/Br is found to observe at EF level in spin-up (↑). While at −3.2 eV, the hybridization of t2g and eg states was noted with p states of Cl/Br atom both (↓) and (↑) channels. However, the t2g significantly contribute to hybridization with p from −0.4 eV at EF. Further, there was interaction between t2g states and p states of Cl/Br in (↓), which generated exchange energies (Δ(d), Δ(pd)) and crystal field energy (ΔCF). The limitations of the studied compounds for ferromagnetism are also known through these energies. The calculation of the ΔCF was performed of the energy differences among degenerated states of Tc by the equation; ΔCF = t2g − eg. Nevertheless, Δ(d) was estimated from differences of 4d states of (↓) and (↑) for Tc. The same (Δ(d)) also ensured the existence of ferromagnetism. Δ(d) holding larger value than that of ΔCF (see Table 2) confirms the ferromagnetism in the compounds in hand. The stable ferromagnetism is vilified by the negative value of Δ(pd), due to lower energy operating through energy forbidden region in (↓).54
| Parameters | K2TcCl6 | K2TcBr6 |
|---|---|---|
| ΔEcry | 3.2 | 2.9 |
| Δx(d) | 5.4 | 5.0 |
| Δx(pd) | −0.6 | −0.4 |
| Noα | −0.39 | −0.33 |
| Noβ | −0.53 | −0.38 |
The major contribution of the partial sub states 3p/4p of Cl/Br, 4d of Tc, and 4s of K is confirmed by the electronic arrangements of Br [Ar] 4s23d104p5, Cl [Ne] 3s23p5, Tc [Kr] 4d55s2, and K [Ar] 4s1. The band edge splitting at CB and VB caused by the mentioned partially filled states are represented as exchange constants (Noβ and Noα). The p–d interactions are attributed to Noβ whereas s–d states interactions are related to Noα by the relation as under:
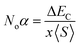 | (2) |
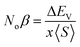 | (3) |
The ΔEV is the valence band edge (VBE) difference whereas ΔEC is the conduction band edge (CBE) difference for (↓) and (↑) channels. x represents the concentration of Tc and 〈S〉 is symbolized for the value of magnetic moment.55,56 Noβ remains negative whereas Noα stays positive for normal wave functions that become just like stationary waves afterwards, which reverts the sign of Noα, by being trapped into deep potential through quantum confinement effect, (see Table 2). The exchange mechanism helps lowering the energy of the compounds while stabilizing the ferromagnetism; hence, the Noβ becomes more outstanding for ferromagnetism. Our results show that exchange mechanism is responsible for ferromagnetic interaction for the two double perovskites. This is based on the computed s–d exchange-constant (Noα), p–d exchange constant (Noβ), exchange splitting Δx(d) and crystal field energy for DPs K2TcX6 (X = Cl, Br) reported in Table 2.
The role electronic spins in magnetic moment (MM) along FM for K2TcCl6 and K2TcBr6 is explained in Table 3. The absolute polarization is shown by the integer values of MM. Further, the exchange of electrons spin is confirmed by the electronic shift from Tc to K, Cl/Br. In addition, Tc and MM is increased by the empty places at Tc, which becomes their outstanding properties for spintronics. The solitude electrons configuration along with MM connects neighboring polarized atoms, increasing broad-range FM through RKKY exchange model.57 The shift of MM towards nonmagnetic sites (Rb, Cl/Br) from magnetic elements (Tc) is generated by the hybridization between 3p/4p-Cl/Br and 4d-Tc. The ferromagnetism is shown for Cs2MoCl6 along with node ring electrons in BS.58 The potency of spin–orbit coupling of A2TaCl6 because of octahedral of halogen ions and substantial ionicity, Jeff = 3/2 of 5d was studied by Ishikawa et al.59 Consequently, 100% spin polarization is exhibited by the integer values of MM, which is the major contribution of Tc (see Table 3).
| Parameters | K2TcCl6 | K2TcBr6 |
|---|---|---|
| Mtot (μB) | 2.999 | 2.999 |
| MK (μB) | 0.006 | 0.008 |
| MTc (μB) | 2.259 | 2.215 |
| MCl/Br (μB) | 0.061 | 0.056 |
| MInt (μB) | 0.373 | 0.442 |
3.4 Optical properties
Fig. 7a–f show the elaboration of the optical parameters, which depend on bandgap (BG). These compounds become very imperative for being utilized in optoelectronics just because of having direct BG of ferromagnetic DPs K2TcX6 as it limits the de-excitation along with direct electronic transition to CB from VB. In addition, changeability in band gap further formulates them for being employed in a range of other device applications. K2TcBr6 and K2TcCl6 possessing the values of absorption of light energy 2.7 eV and 3.3 eV for BGs goes down in UV and visible spectrum.60,61 The optical parameters have been analyzed in the form of real as well as imaginary parts of dielectric constants ε1(ω) and ε2(ω). The polarization and dispersion of light is symbolically and quantitatively measured by ε1(ω). Fig. 7a clearly displays its observed value ε1(ω) at ω = 0, reaching at 3.9 after increasing from 3.2 when Cl was changed to Br. The increasing value of ε1(0) due to changing the halide ions causes the reduction in BG from 3.3 to 2.7 exactly satisfying the Penn's model ε1(0) ≈ 1 + (ħωp/Eg)2.62 The polarization and dispersion of light energy becomes comparatively high due to resonance peaks of the ε1(ω) that have different peak sets, as at 4.3/3.0 eV and at 2.5/1.0 eV. The variation in refractive index n(ω) also changes the speed decay of light while passing through compounds. The behavior of ε1(ω) and n(ω) has also been proven to be alike (see Fig. 7b). The n(0) has been observed through the equation n(0)= (ε1(0))1/2, (see Table 1). The change of anions enhances the values of n(0), however, largely the relation with ε1(0) remains secured. Further, Krammer–Kronge formulism was used to determine ε2(ω) from ε1(ω).63 The absorbed light energy in a compound is symbolized by ε2(ω). Therefore, its higher value due to huge absorption is believed to be incredible for optoelectronic applications. It obtained value has been displayed in Fig. 7c. Its critical values were recorded as 2.2 eV and 3.2 eV showing the band gap of K2TcBr6 and K2TcCl6 correspondingly. Similarly, the absorption bands observed for K2TcBr6 and K2TcCl6 are 2.5 to 3.5 eV and 4.0 to 4.5 eV accordingly. K2TcBr6 is certified by the recorded bands for visible regions and K2TcCl6 for UV as well. The absorption bands were also formed by the electronic transitions at 3.8 eV onwards, 3.0 to 4.0 eV and 4.2 to 4.8 eV. However, generally the first absorption bands are strongly preferred for optoelectronics.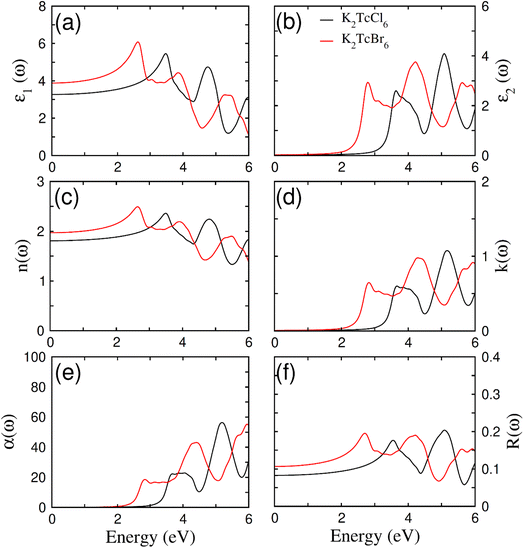 | ||
| Fig. 7 The calculated (a) real part ε1(ω), (b) imaginary part ε2(ω), (c) refraction n(ω), (d) extinction co-efficient k(ω), (e) absorption α(ω), (f) reflectivity R(ω) of DPs K2TcCl6 and K2TcBr6. | ||
Fig. 7d shows the recorded values of absorption coefficient α(ω). A similar trend of α(ω) as that of ε2(ω) was found to observe. It was so because the both (α(ω) and ε2(ω)) have representation of absorption of light. There is also a bit overestimation in the obtained values of absorptions and optical bands gap due to DFT. When Cl is replaced by Br, the absorption bands move towards lower energy. The modeling of band gap causes this shift towards lower values. The k(ω) represents to be the fictional of refraction as ε2(ω). It represents the decayed part of light energy (see Fig. 7d). In addition, it has two consecutive sets of peaks; the first one at 2.8/4.4 and the second one at 3.6/5.2 for Br/Cl correspondingly. The obtained values proved to be in accordance with ε2(ω) and α(ω).64 The reflected part of energy from the surface of the compound is known as reflectivity R(ω). Its frequency dependent value and static value R(0) have been expressed in Fig. 7f. Its static value R(0) started increasing by replacing the Cl with Br. The uppermost peak value of R(ω) remained below 0.21 that was much smaller as compared with the absorption of light energy in the compounds.
3.5 Thermoelectric properties
Thermoelectric features are generally investigated for the better understanding of their effects on thermoelectric performance and electronic spin in specific compounds. Any thermoelectric compound is believed to possess heavier elements to restrain the phonons transport.65,66 The ideal thermoelectric compounds also possess ultralow thermal conductivity (κe), electric conductivity (σ), and extensive Seebeck coefficient (S). The temperature limit for the computed parameters is from 200 K to 800 K. In this regard, power factor (σS2) was computed to assay the performance of DPs K2TcCl6 and K2TcBr6. In accordance with the classical Boltzmann theory, the collision rate of time for electronic gas was set as 10−14 s. Thus, the division of the κe and the σ was taken in terms of 10−14 s [see Fig. 8a–f]. The combination of all three parameters (κe, σ, S) for (↓) and (↑) is taken by the following equation:47| κ = κ(↑) + κ(↓)/2 | (4) |
| S = S(↑)σ(↑) + S(↓)σ(↓)/σ(↑) + σ(↓) | (5) |
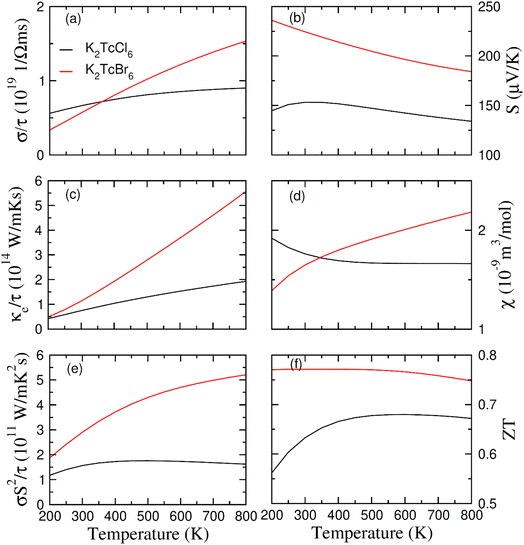
The above written relation shows the means of the both spin formations. Fig. 8a shows the computed values of σ. There is a difference between the thermoelectric factors of Tc based double perovskites as Tc possesses the electrons in odd numbers (5) in 4d orbitals. Its values increases at 200 K and 800 K from 0.6/0.3 × 1019 (Ω−1 m−1 s−1) to 0.9/1.6 × 1019 (Ω−1 m−1 s−1) respectively. The values of σ are more for Br based DPs than that of Cl based DPs at 400–800 K. It is so because the free carriers are increased in numbers by increasing the size of ions. Quite contrary to the values of σ, the κe starts increasing at 200 K to 800 K from 0.4/0.5 × 1014 W m−1 K−1 s−1 to 1.9/5.5 × 1014 W m−1 K−1 s−1 for K2Tc(Cl/Br)6. It is so because the lattice disturbance and the flow of carriers is increased by thermal effect (see Fig. 8c). Here, due to the restrictions of classical theory of Boltzmann, the merely electronic contribution to thermal conductivity was investigated whereas we could not touch the lattice disturbance. The comparison of σ and κe was performed through the κ/σ that is set as 10−6 in order to evaluate the relative effect.67 The ultralow values of κe provide the room for the compounds to be the best for spintronic and thermoelectric projects.
The potential gradient for thermoelectric measured through S is presented in Fig. 8b. The value of S became positive for K2Tc(Cl/Br)6 at 200–800 K, showing the p-type character. With increasing temperature from 200 K to 800 K, the values of S reduced from 148/230 mV K−1 to 130/180 mV K−1 for K2Tc(Cl/Br)6. The variation of the susceptibility of K2Tc(Cl/Br)6 as depicted in Fig. 8d, manifest an opposite trend. For K2TcCl6, the value of χ decreases up to 400 K then becomes constant to reach approximately value of 1.6 × 10−9 m3 mol−1 at 800 K. For K2TcCl6, the value of χ increases steadily up to 800 K then attains almost a steady approximately value of 2.3 × 10−9 m3 mol−1.
From the analysis of the computed values of power factor (PF) (see Fig. 8e), it is clear that its values are lowest for K2TcCl6 and highest for K2TcBr6. Therefore, Br based DP is believed to be more suitable for being used in thermoelectric device applications as compared with the Cl based DP. Additionally, the PF, mathematically equivalent to σS2, is calculated consequently, by utilizing these Seebeck coefficients in conjunction with the structural factor, one can determine the figure of merit, which fundamentally characterizes the efficacy of any thermoelectric material. When calculating the thermal efficiency (ZT) (see Fig. 8f), it exhibited a pattern similar to that of PF, for both studied DPs. This underscores the potential of both DPs as promising thermoelectric materials for a wide array of thermoelectric purposes.
4. Conclusion
To sum up, we have conducted a systematic evaluation of ferromagnetism and its impact on the functionality of electrons in the double perovskites (DPs) K2TcY6 (Y = Cl, Br) with the aim of exploring their potential applications in energy harvesting and spintronic devices. Primarily, our examination of cubic spinel structures of the investigated double perovskites in both ferromagnetic (FM) and antiferromagnetic (AFM) states has affirmed that with higher energy release the FM states are more energetically stable. Their structural and thermodynamic stability in FM states has also been corroborated by the tolerance factor and formation energy assessment. Moreover, the Heisenberg model corroborates that Tc remains above room temperature, while the larger exchange-energies in comparison to crystal field energy, coupled with the double exchange model, point towards the presence of ferromagnetism resulting from spin functionality and hybridization, as opposed to clustering. The prevailing negative exchange-constants exert a significant influence through the quantum confinement effect, effectively confining the electron wavefunction within a deep potential well. This negative pd exchange-interaction, coupled with the shift of magnetic moments from Tc to the K and Cl/Br sites, is a result of exchange mechanism that reduces the system's energy and bolsters the stability of ferromagnetism. From our results it can be seen that the band gaps of K2TcBr6 and K2TcCl6 are 2.2 eV and 3.2 eV, respectively. Since these values are in the UV region, one can expect these materials to be suitable for optical devices operating in UV region of electromagnetic spectrum. Absorption spectra have been observed in both the UV and visible regions for double perovskites containing Cl and Br anions. Furthermore, the presence of unpaired electrons in Tc enhances electrical conductivity and the performance of K2TcBr6-based double perovskites surpasses that of K2TcCl6-based DP. Moreover, our computed properties exhibit semiconducting ferromagnetic DPs that is assumed a necessary factor in spintronics devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors express their gratitude to Princess Nourah Bint Abdulrahman University Researchers Supporting Project (Grant No. PNURSP2024R70), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.References
- T. Dietl, A ten-year perspective on dilute magnetic semiconductors and oxides, Nat. Mater., 2010, 9, 965 CrossRef CAS PubMed.
- S. Bhatti, R. Sbiaa, A. Hirohata, H. Ohno, S. Fukami and S. N. Piramanayagam, Spintronics based random access memory: a review, Mater. Today, 2017, 20(9), 530–548 CrossRef.
- I. Žutić, J. Fabian and S. Das Sarma, Spintronics: Fundamentals and applications, Rev. Mod. Phys., 2004, 76(2), 323–410 CrossRef.
- G. A. Medvedkin, T. Ishibashi, T. Nishi and K. Hayata, Room temperature ferromagnetism in novel diluted magnetic semiconductor Cd1-xMnxGeP2, Jpn. J. Appl. Phys., 2000, 39, L949 CrossRef CAS.
- S. D. Sarma, Spintronics: A new class of device based on electron spin, rather thanon charge, may yield the next generation of microelectronics, Am. Sci., 2001, 89, 516 CrossRef.
- K. Ando, Seeking room-temperature ferromagnetic semiconductors, Science, 2006, 312, 1883–1885 CrossRef CAS PubMed.
- T. Dietl, H. Ohno, F. Matsukura, J. Cibert and D. Ferrand, Zener model description of ferromagnetism in zinc-blende magnetic semiconductors, Science, 2000, 287, 1019–1022 CrossRef CAS PubMed.
- P. Sharma, A. Gupta, K. V. Rao, F. J. Owens, R. Sharma, R. Ahuja, J. M. O. Guillen, B. Johansson and G. A. Gehring, Ferromagnetism above room temperature in bulk andtransparent thin films of Mn-doped ZnO, Nat. Mater., 2003, 2(10), 673–677 CrossRef CAS PubMed.
- R. K. Kittilstved, N. S. Norberg and D. R. Gamelin, Chemical manipulation of high-Tcferromagnetism in ZnO diluited magnetic semiconductor, Phys. Rev. Lett., 2005, 94, 147209 CrossRef PubMed.
- A. Sundaresan, R. Bhargavi, N. Rangarajan, U. Siddesh and C. N. R. Rao, Ferromagnetism as a universal feature of nanoparticles of the otherwisenonmagnetic oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 161306(R) CrossRef.
- D. Sanyal, M. Chakrabarti, T. K. Roy and A. Chakrabarti, The origin of ferromagnetismand defect-magnetization correlation in nanocrystalline ZnO, Phys. Lett. A, 2007, 371(5–6), 482–485 CrossRef CAS.
- H. Pan, J. B. Yi, L. Shen, R. Q. Wu, J. H. Yang, J. P. Feng, J. Ding, L. H. Van and J. H. Yin, Room-temperature ferromagnetism in carbon-doped ZnO, Phys. Rev. Lett., 2007, 99, 127201 CrossRef CAS PubMed.
- H. Luitel, P. Chettri, A. Tiwari and D. Sanyal, Experimental and first principle study of room temperature ferromagnetism in carbon-doped rutile TiO2, Mater. Res. Bull., 2019, 110, 13–17 CrossRef CAS.
- H. Luitel, M. Chakrabarti, A. Sarkar, S. Dechoudhury, D. Bhowmick, V. Naik and D. Sanyal, Ab-initio calculation and experimental observation of room temperatureferromagnetism in 50 keV nitrogen implanted rutile TiO2, Mater. Res. Express, 2018, 5, 026104 CrossRef.
- H. Luitel and D. Sanyal, Ab initio calculation of magnetic properties in B, Al, C, Si, N, Pand As-doped rutile TiO2, Int. J. Mod. Phys. B, 2017, 31, 1750227 CrossRef CAS.
- H. Luitel, S. Roy and D. Sanyal, Ab-initio calculation of magnetic properties of P and Asdoped SnO2, Computational Condensed Matter, 2018, 14, 36–39 CrossRef.
- H. Luitel and D. Sanyal, Ferromagnetism in p-block elements doped ZnO: An ab-initio approach, Computational Condensed Matter, 2019, 19, 00376 CrossRef.
- H. Luitel, S. Roy, M. Chakrabarti, P. Chettri, A. Tiwari, V. Naik and D. Sanyal, Room temperature ferromagnetism in boron-doped oxides: a combined first-principle and experimental study, Philos. Mag. Lett., 2020, 100(4), 141–153 CrossRef CAS.
- S. Wang, L. Pan, J.-J. Song, W. Mi, J.-J. Zou, L. i. Wang and X. Zhang, Titanium defected undoped anatase tio 2 with p-type conductivity, room-temperature ferromagnetism, and remarkable photocatalytic performance, J. Am. Chem. Soc., 2015, 137(8), 2975–2983 CrossRef CAS PubMed.
- D. Sanyal, M. Chakrabarti, P. Nath, A. Sarkar, D. Bhowmick and A. Chakrabarti, Room temperature ferromagnetic ordering in 4 MeV Ar5+ irradiated TiO2, J. Phys. D: Appl. Phys., 2013, 47, 025001 CrossRef.
- H. Luitel, A. Sarkar, M. Chakrabarti, S. Chattopadhyay, K. Asokan and D. Sanyal, Positron annihilation lifetime characterization of oxygen ion irradiated rutile TiO2, Nucl. Instrum. Methods Phys. Res., Sect. B, 2016, 379, 215–218 CrossRef CAS.
- M. Venkatesan, C. B. Fitzgerald and J. M. D. Coey, Unexpected magnetism in a dielectric oxide, Nat. Commun., 2004, 430, 630 CrossRef CAS PubMed.
- J. M. D. Coey, ferromagnetism, Solid State Sci., 2005, 7(6), 660–667 CrossRef CAS; R. Masrour, E. K. Hlil, M. Hamedoun and A. Benyoussef, Electronic and magnetic properties of MnAu nanoparticles, J. Magn. Magn. Mater., 2014, 354, 159–162 CrossRef.
- H. H. Fang, R. Raissa, M. Abdu-Aguye, S. Adjokatse, G. R. Blake, J. Even and M. A. Loi, Photophysics of organic-inorganic hybrid Lead iodide perovskite single crystals, Adv. Funct. Mater., 2015, 25, 2346–2347 CrossRef.
- H. Z. Lin, C. Y. Hu, P. H. Lee and A. Z. Z. Yan, et al., Half-metallic property induced by double exchange interaction in the double perovskite Bi2BB′O6 (B, B′ = 3d transitional metal) via first-principles calculations, Materials, 2019, 12, 1844 CrossRef CAS PubMed.
- H. E. M. Musa Saad and S. S. Althoyai, Half-metallic and insulating natures in Ru-based ordered double perovskite oxides Ba2XIIIRuVO6 (X = V, Cr) induced by 3d-t2gn orbital filling, Mater. Chem. Phys., 2017, 190, 230–240 CrossRef.
- A. Hossain, P. Bandyopadhyay and S. Roy, An overview of double perovskites A2B′ B′′ O6 with small ions at A site: synthesis, structure and magnetic properties, J. Alloys Compd., 2018, 740, 414–427 CrossRef CAS.
- K. I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Room-temperature magnetoresistance in an oxide material with an ordered double-perovskite structure, Nature, 1998, 395, 677 CrossRef CAS.
- Y. Krockenberger, K. Mogare, M. Reehuis, M. Tovar, M. Jansen and G. Vaitheeswaran, Sr2CrOsO6: end of a spin-polarized metal-insulator transition by 5d band filling, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 020404 CrossRef.
- S. Ravi, High Curie temperature and room temperature magnetoresistance in Pr2FeCrO6 material for spintronics applications, Mater. Lett., 2020, 278, 128448 CrossRef CAS.
- O. Ramdane, M. Labidi, R. Masrour, S. Labidi, M. Ellouze and R. Rehamnia, Study of structural, electronic, and magnetic properties of cubic and tetragonal Ba2FeMoO6, J. Supercond. Novel Magn., 2023, 36, 373–387 CrossRef CAS.
- M. Bessimou and R. Masrour, Magnetocaloric effect and magnetic properties of Dy2CoMnO6: Monte Carlo study, Philos. Mag., 2023, 103, 56–66 CrossRef CAS.
- A. E. Maughan, A. M. Ganose, D. O. Scanlon and D. O. Neilson, Perspectives and design principles of vacancy-ordered double perovskite halide semiconductors, Chem. Mater., 2019, 31, 1184–1195 CrossRef CAS.
- Q. Mahmood, G. Nazir, A. Rahim, J. Alzahrani, A. I. Aljameel, G. Murtaza, A. Aldayyat, H. Albalawi, A. Mera and B. Ul Haq, Impact of 5d electrons on half metallic ferromagnetism, and thermoelectric properties of Cs2Z(Cl/Br)6 (Z = Os, Ir) for spintronic applications, Mater. Chem. Phys., 2022, 288, 126414 CrossRef CAS.
- M. B. Gray, J. D. Majher, N. P. Holzapfel and P. M. Woodward, Exploring the stability of mixed-halide vacancy-ordered quadruple perovskites, Chem. Mater., 2021, 33, 2165–2172 CrossRef CAS.
- M. M. S. Karim, A. M. Ganose, L. Pieters, W. W. W. Leung, J. ade, L. Zhang, D. O. Scanlon and R. G. Palgrave, Anion distribution, structural distortion, and symmetry-driven optical band gap bowing in mixed halide Cs2SnX6 vacancy ordered double perovskites, Chem. Mater., 2019, 31, 9430–9444 CrossRef CAS PubMed.
- B. Lee, A. Krenselewski, S. I. Baik, D. N. Seidman and R. P. H. Chang, Solution processing of air-stable molecular semiconducting iodosalts, Cs2SnI6−xBrx, for potential solar cell applications, Sustainable Energy Fuels, 2017, 1(4), 710–724 RSC.
- A. E. Maughan, A. M. Ganose, M. M. Bordelon, E. M. Miller, D. O. Scanlon and J. R. Neilson, Air-stable molecular semiconducting iodosalts for solar cell applications: Cs2SnI6 as a hole conductor, J. Am. Chem. Soc., 2016, 138, 8453–8464 CrossRef CAS PubMed.
- M. Faizan, S. H. Khan, G. Murtaza, A. Khan and A. Laref, Electronic and magnetic properties of alkali metal chlorides A2MCl6 (A = K, Rb, Cs; M = Mn, Mo): a density functional theory study, Int. J. Mod. Phys. B, 2019, 33, 1950072 CrossRef CAS.
- Q. Mahmood, First-principles calculations to investigate role of 4d electrons spin (Mo/Tc) in half metallic ferromagnetism, and thermoelectric characteristics of Rb2(Tc, Mo)X6 (X =Cl, Br), Ceram. Interfaces, 2023, 49, 25121–25129 CrossRef CAS.
- G. M. Mustafa, M. Hassan, N. M. Aloufi, S. Saba, S. Al-Qaisi, Q. Mahmood, H. Albalawi, S. Bouzgarrou, H. H. Somaily and A. Mera, Half metallic ferroamgnetism, and transport properties of vacancy ordered double perovskites Rb2(Os/Ir)X6 (X= Cl, Br) for spintronic application, Ceram. Interfaces, 2022, 48, 23460–23467 CrossRef CAS.
- R. Ullah, M. A. Ali, G. Murtaza, A. Khan and A. Mahmood, Ab initio study for the structural, electronic, magnetic, optical, and thermoelectric properties of K2OsX6 (X = Cl, Br) compounds, Int. J. Energy Res., 2020, 44, 9035–9049 CrossRef CAS.
- M. A. Ali, G. Murtaza and A. Laref, Exploring the ferromagnetic half metallic nature of Cs2NpBr6 via spin polarized density functional theory, Chin. J. Phys., 2020, 29, 066102 CrossRef CAS.
- K. Radja, B. L. Farah, A. Ibrahim, D. Lamia and I. Fatima, et al., Investigation of structural, magneto-electronic, elastic, mechanical and thermoelectric properties of novel lead-free halide double perovskite Cs2AgFeCl6: first-principles calculations, J. Phys. Chem. Solids, 2022, 167, 110795–110802 CrossRef CAS.
- A. Gherriche, A. Bouhemadou, Y. Al-Douri, S. Bin-Omran, R. Khenata and M. A. Hadi, Ab initio exploration of the structural, elastic, electronic and optical properties of a new layered perovskite-type oxyfluoride: CsSrNb2O6F, Mater. Sci. Semicond. Process., 2021, 131, 105890–105900 CrossRef CAS.
- M. Elder, J. E. Fergusson, G. J. Gainsford, J. H. Hickford and B. R. Penfold, Potassium pentachlorohydroxytechnetate(iv), J. Chem. Soc. A, 1967, 1423–1425 RSC.
- G. K. H. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, an Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Vienna University of Technology, Austria, 2001 Search PubMed.
- F. Tran and P. Blaha, Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- F. Tran Koller and P. Blaha, Merits and limits of the modified Becke-Johnson exchange potential, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195134 CrossRef.
- W. Yi, G. Tang, X. Chen, B. Yang and X. Liu, qvasp: A flexible toolkit for VASP users in materials simulations, Comput. Phys. Commun., 2020, 257, 107535 CrossRef CAS.
- S. Berri and N. Bouarissa, Electronic Structure and Optical Spectra of Halide Perovskites A2BCl6 [(A= Cs; B= Se, Sn, Te, Ti, Zr) and (A= K; B= Pd, Pt, Sn)] for Photovoltaic and Optoelectronic Applications, Phys. Status Solidi B, 2023, 2300280 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, D. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- C. W. Zhang and S. Yan, First-principles prediction of half-metallic ferromagnetism inCu-doped ZnS, J. Appl. Phys., 2010, 107, 043913 CrossRef.
- Y. F. Li, K. C. Zhang and Y. Liu, Spin-orbital coupling, and magnetic properties of Irbaseddouble perovskites with different 5dn (n = 3, 4, 5) states, Phys. Lett., 2019, 383, 558–565 CrossRef CAS.
- Q. Mahmood, S. A. Ali, M. Hassan and A. Laref, First principles study offerromagnetism, optical and thermoelectric behaviors of AVO3 (A = Ca, Sr, Ba)perovskites, Mater. Chem. Phys., 2018, 211, 428–437 CrossRef CAS.
- L. Brey, M. J. Calderón, S. Das Sarma and F. Guinea, Mean-field theory for doubleperovskites: coupling between itinerant electron spins and localized spins, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 094429 CrossRef.
- T. Zhang, D. Hara and S. Murakami, Unique surface-state connection between Weyland nodal ring fermions in ferromagnetic material Cs2MoCl6, Phys. Rev. Res., 2021, 3, L042037 CrossRef CAS.
- H. Ishikawa, T. Takayama, R. K. Kremer, J. Nuss, R. Dinnebier, K. Kitagawa, K. Ishii and H. Takagi, Ordering of hidden multipoles in spin-orbit entangled 5d1 Tachlorides, Phys. Rev. B, 2019, 100, 045142 CrossRef CAS.
- T. H. Flemban, V. Singaravelu, A. A. S. Devi and I. S. Roqan, Homogeneous vertical ZnOnanorod arrays with high conductivity on an in situ Gd nanolayer, RSC Adv., 2015, 5(115), 94670–94678 RSC.
- B. Xin, N. Alaal, S. Mitra, A. Subahi, Y. Pak, D. Almalawi and N. Alwadai, Identifyingcarrier behavior in ultrathin indirect-bandgap CsPbX3 nanocrystal films for use inUV/visible-blind, Small, 2020, 16(43), 2004513 CrossRef CAS PubMed.
- D. R. Penn, Wave-number-dependent dielectric function of semiconductors, Phys. Rev., 1962, 128, 2093–2097 CrossRef CAS.
- S. Al-Qaisi, R. Ahmed, B. U. Haq, D. Rai and S. Tahir, A comprehensive first-principlescomputational study on the physical properties of lutetium aluminum perovskiteLuAlO3, Mater. Chem. Phys., 2020, 250, 123148 CrossRef CAS.
- B. U. Haq, S. AlFaify, T. A. Alrebdi, R. Ahmed, S. Al-Qaisi, M. Taib, G. Naz and S. Zahra, Investigations of optoelectronic properties of novel ZnO monolayers: A firstprinciplesstudy, Mater. Sci. Eng., B, 2021, 265, 115043 CrossRef.
- D. Singh, M. Sajjad, J. A. Larsson and R. Ahuja, Results Phys., 2020, 19, 103584 CrossRef.
- N. Tayebi, K. Bidai, M. Ameri, S. Amel, I. Ameri, Y. Al-Douri and D. Varshney, Pressureand temperature dependence of the structural, elastic, and thermodynamicproperties of potassium telluride: first-principles calculations, Chin. J. Phys., 2017, 55, 769–779 CrossRef CAS.
- B. Ul Haq, S. AlFaify, T. Alshahrani, R. Ahmed, Q. Mahmood, D. M. Hoat and S. A. Tahir, Investigations of thermoelectric properties of ZnO monolayers from thefirst-principles approach, Phys. E, 2021, 126, 114444 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |