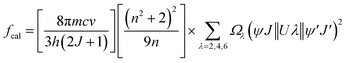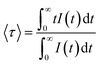DOI:
10.1039/D3RA08015C
(Paper)
RSC Adv., 2024,
14, 2070-2079
Influence of barium substitution on the physical, thermal, optical and luminescence properties of Sm3+-doped metaphosphate glasses for reddish orange light applications
Received
22nd November 2023
, Accepted 6th December 2023
First published on 9th January 2024
Abstract
Our present study focuses on examining the thermal, structural and luminescent characteristics of sodium barium metaphosphate glasses doped with Sm3+. Glass samples with molar compositions (100 − y)[(50P2O5)–(50-xNa2O)–(xBaO)]–ySm2O3, where x = 20, 25, 30, 35, 40 and y = 0.3 and 1% were first synthesized by conventional melt quenching and later dehydroxylated under a constant N2 flow to ensure final glasses with a very high degree of chemical and optical homogeneity and free of water. Upon the addition of BaO and Sm2O3, refractive index, molar mass, density, glass transition temperature and dilatometric softening temperature exhibited an increase, whereas the coefficient of thermal expansion showed a decrease. The FTIR spectra analysis reveals a network depolymerization that intensifies with rising BaO concentration, ultimately transitioning from a modifier oxide to a glass-forming element, at higher BaO concentrations. All doped samples exhibited prominent absorption bands in the visible (VIS) and near-infrared (NIR) regions, as revealed by the optical absorption spectra. The Na2O modifier demonstrated greater influence on Sm3+ emission compared to BaO, a phenomenon that can explained by the moderation of the local ligand field strength resulting from this substitution. With an increase in Sm2O3 concentration from 0.3 to 1 mol%, the experimental lifetimes of the 4G5/2 level decrease, primarily attributed to the presence of energy transfer mechanisms. A discussion of Judd–Ofelt parameter analysis and glass radiation properties will be presented.
1. Introduction
Nowadays, optical materials based on trivalent lanthanide ions are being widely applied in various technological applications such as photonic displays, communications devices, laser materials, hole burning high-density memories, optical storage, etc.1–6 Therefore, the special features of glassy matrices, such as low production cost, better thermal stability, mechanical strength, and chemical durability, make them more suitable as host materials than crystalline compounds. Phosphate-based glasses are recognized as significant materials in certain applications due to their favorable characteristics, including high solubility for rare-earth ions with minimal clustering effects, low melting temperature, low glass transition temperature, high thermal expansion coefficient, and biocompatibility.7,8 Based on previous investigations,9 the addition of barium oxide to phosphate glasses enhances thermal stability, the ability to form glass structures, and chemical resistance. It also reduces thermal expansion and phonon frequencies, thereby improving the internal quantum efficiency of luminescent materials. Barium-containing glass has been around since the earliest days of glass science, with a number of important applications such as its relevancy for making: materials to adapt optical properties, gamma ray shielding materials, barrier of plasma display ribs,10 sulphate-bearing high level liquid waste,11 and gamma ray shielding.12,13 Barium phosphates, whether in crystalline or glassy form, are significant in photonic applications when doped with rare-earth or transition metal ions. Additionally, the addition of small quantities of barium oxide or barium sulfate to the composition of bioactive materials imparts radio-opacity to the implants.11 RE3+ ions doped phosphate glasses were used in optical fibres,14 vitrification of radio-active waste,15 tissue engineering16 and many other applications. The Sm3+ ion is well suited for doping due of their excited energy level 4G5/2 level which shows greater quantum efficiency with various quenching emission channels,17 and presents strong reddish-orange emission, owns sufficient energy to provoke photodynamic reaction. The reddish light region is highly effective at penetrating human tissue 50 to 200% more deeply than blue or green light. Therefore, glasses doped with Sm3+ ions could find applications in high-power laser sources emitting reddish-orange light for the treatment of cancer. Additionally, the effective energy gap of Sm3+-doped glass at 560 nm has various applications in daytime running lights and traffic signals. Consequently, the Sm3+ ion was chosen as the doping element for the current work. Recently, Naick et al. investigated the optical absorption spectra of trivalent samarium ions doped phosphate glasses with Li2O, MgO, CaO, SrO and BaO as modifiers for visible orange-red photonic domains.18 Several researchers have explored different optical absorption analysis of phosphate and sulfophosphate glasses doped with Sm3+ ions.19 It has been observed that within these glass matrices, there is a conversion of oxygen atoms from bridging to non-bridging positions. Hence, in this present work, we prepared Na2O–BaO–P2O5 glasses doped with 0.3 and 1.0 mol% Sm2O3 by conventional melt quenching synthetic method. In glass compositions featuring network modifier ions with low field strength, an intriguing phenomenon emerges: the fluorescence lifetime of doped rare earth ions experiences a substantial enhancement as the concentration of network modifiers increases in both alkali and alkaline earth glasses.20–22 This phenomenon underscores the pivotal role of the network modifier in influencing the optical behavior of rare earth-doped glasses. In our investigation, we specifically target the influence of BaO on the physical and optical attributes of glasses. Our primary focus lies in exploring the coordination dynamics between high field strength Na+ and Ba2+ cations within glass networks. Understanding the impact of these two modifiers on the phosphate network is crucial as the spectroscopic properties of rare earth ions heavily rely on their local environment. Thus, altering the Sm3+ ions sites within the glass matrix could potentially intensify their emission. Through this exploration, we aim to uncover fundamental principles that not only enhance our comprehension of material properties but also offer potential insights for optimizing the optical characteristics, particularly in the context of reddish-orange laser applications.
2. Materials and methods
Glasses with composition (1 − y)((50 − x)Na2O–xBaO–50P2O5)–ySm2O3, in mol% with x = 20, 25, 30, 35, 40 and y = 0.3 and 1, were obtained by melt and quenching from batches synthesized by mixing reagent grade chemicals, Na2CO3, BaCO3, (NH4)2HPO4, and Sm2O3. In the first step, the batches were placed in porcelaine crucibles and slowly calcined overnight up to 450 °C. Then, they were melted for 2 h at temperatures of 900–1100 °C depending on the composition. A second melting of each glass was performed to obtain homogeneous and dehydroxylated glasses. This last was performed on about 5 g of each original glass in a graphite crucible, using a constant nitrogen flow within a tube furnace and, in the present case, at 750 °C for 6 h, following the methodology described in a previously published procedure in ref. 23.
The FTIR spectra were recorded on PerkinElmer Spectrum 100 spectrometer between 750 and 5000 cm−1 on plane parallel square samples of about 1 cm2 and between 1 and 2 mm thick. This analysis was performed to investigate the structural modifications resulting from changes in the glass composition and to evaluate the hydroxyl groups in the glasses before and after re-melting, thereby confirming the efficiency of our glass synthesis method. The density (ρ) of the glass compounds was measured at room temperature using the Archimedes principle, with ethanol as the immersion liquid. The molar volume (Vm) of glass samples was calculated dividing the molar mass of each composition by its density. The dilatometric softening point (Td), glass transition temperature (Tg), and coefficient of thermal expansion (CTE) were measured from very small glass pieces using a differential dilatometer (Netzsch Gerätebau model 402 EP). Dilatometry measurements were performed in the temperature range of 20 to 680 °C at a heating rate of 10 °C min−1. The refractive index (n) was measured at room temperature using an Abbe refractometer, with monobromo-naphthalene serving as the contact liquid. The measurements were performed at a wavelength of 589 nm. The optical absorption spectra were captured in the ultraviolet, visible, and near-infrared (UV-Vis-NIR) region spanning from 200 to 2000 nm. A UV-Vis-NIR spectrophotometer (Shimadzu, UV-3600) was employed for this purpose. The emission spectra and lifetime were measured with a fluorescence spectrophotometer FS5, equipped with a 150 W Xenon lamp. Then, the emission was detected using a Hamamatsu R928P photomultiplier.
3. Results and discussion
To demonstrate the effectiveness of our glass synthesis method, we recorded FTIR spectra from 20BaSm1 glass sample before and after re-melting in the spectral range of 2600–5000 cm−1, as shown in Fig. 1(a). It is worth noting that the spectra display a broad IR absorption band spanning from 2680 to 3400 cm−1, which is likely attributed to P–O–H stretching vibrations. The decrease in this signal in the re-melted sample suggests the breakdown and disruption of hydroxyl groups in the glass. Moreover, in the range of 3450 to 3650 cm−1, the OH stretching mode undergoes a substantial reduction upon re-melting the glass in a nitrogen (N2) atmosphere. This observation further indicates a significant decrease in the water content of the glasses due to the thermal treatment under a continuous N2 flow. Based on the FTIR measurements, the absorption coefficient of hydroxyl ions in the glasses, αOH (cm−1), was evaluated, using eqn (1), following the methodology described in ref. 24 and 25.| | |
αOH = −log(T5000/T3000)t
| (1) |
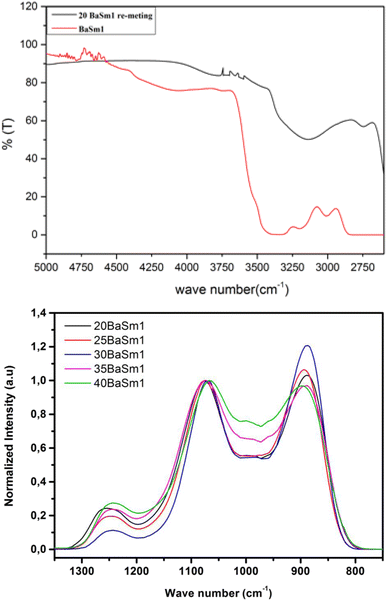 |
| | Fig. 1 FTIR spectra of the BaSm-1 glasses. | |
The results obtained were summarized in Table 1. The results indicate a reduction in the absorption coefficient of OH ions in the glass samples that underwent re-melting under a continuous N2 flow at 750 °C for 6 hours. It's important to note that the dehydroxylation process is thermally activated, as evidenced by the consistent decrease in OH content. The dehydroxylation method through a second melting under N2 has proven to be very effective in removing traces of water from the glasses as shown by the small OH absorption confidents at 3000 cm−1.
Table 1 Absorption coefficient of hydroxyl ions, αOH (cm−1), in the glasses before and after dehydroxylation
| Glass |
Density (g cm−3) |
Tg (°C) |
Td (°C) |
CTE (10−6 K−1) |
Refractive index |
| 20BaSm0.3 |
2.99 |
310.3 |
343.0 |
18.5 |
1.5275 |
| 25BaSm0.3 |
3.09 |
326.3 |
359.5 |
16.6 |
1.5379 |
| 30BaSm0.3 |
3.20 |
334.8 |
379.6 |
15.6 |
1.5465 |
| 35BaSm0.3 |
3.32 |
360.9 |
497.6 |
14.8 |
1.5589 |
| 40BaSm0.3 |
3.42 |
374.1 |
426 |
14.7 |
1.5738 |
| 20BaSm1 |
3.03 |
337.6 |
354.4 |
17.0 |
1.5197 |
| 25BaSm1 |
3.14 |
352.6 |
369.4 |
16.0 |
1.5429 |
| 30BaSm1 |
3.26 |
367.1 |
384.7 |
15.1 |
1.5509 |
| 35BaSm1 |
3.35 |
360.9 |
497.6 |
14.8 |
1.5595 |
| 40BaSm1 |
3.48 |
374.1 |
426 |
14.7 |
1.5739 |
Examining the FTIR spectra of BaSm-1 glasses within the 750–1350 nm range (Fig. 1(b)) provides valuable insights into the structural modifications resulting in the glass composition changes. The structural framework is predominantly characterized by the presence of PO4 tetrahedral units, with its features notably influenced by the incorporation of BaO into the glass matrix. Within the spectra, a prominent band appearing around 890 cm−1, indicating the asymmetric stretching vibration of P–O bonds, νas (P–O–P).26,27 Around 1075 cm−1, another significant band arises, though the specific vibrational mode of vs (P–O–P) of both Q2 and Q1 units.28 The band at approximately 1250 cm−1 is associated with the asymmetric stretching vibration of P–O–P bonds, νas (P–O–P).26 Between 950 and 1030 cm−1, multiple shoulders are detected and they were assigned to vs (PO32−) in Q1 units.29 According to the spectral data, an increase in the BaO content from 20 to 30 mol% results in a higher proportion of Q2 units at the expense of Q1 units. This can be confirmed from the increase in the band at 890 cm−1 with the reduction in the band at 1250 cm−1. These findings suggest that the phosphate chain depolymerizes as BaO substitutes Na2O content. As the barium content continues to increase, an inverse trend becomes apparent. This indicates that this element primarily serves as a modifier oxide only at relatively low concentrations, transitioning into a glass-forming element at higher concentrations. In this context, we are well-positioned to conduct an effective exploration of the spectroscopic features of RE elements, specifically Sm3+, in response to variations in the degree of depolymerization and polymerization within the phosphate matrix.
Physical properties of series A, Na2O–BaO–P2O5-0.3 Sm2O3 (BaSm-0.3) and series B, Na2O–BaO–P2O5-1Sm2O3 (BaSm-1) of glasses are gathered in Table 2, density, dilatometric softening temperature, glass transition temperature, coefficient of thermal expansion and refractive index. The density and refractive index of the glass samples exhibit an increase as the BaO content increases. This can be attributed to the higher molar mass of BaO in comparison to Na2O and the higher electronic density of Ba2+ ions compared to Na+ ions. In agreement with FTIR analyses, these factors contribute to the hindrance of light waves passing through the glass samples.11–30 The relationship between the refractive index of the glass and its density variation with BaO content is governed by the Lorentz–Lorentz equation.31 This equation establishes a direct correlation between the refractive index and density of the glass.11 The 1 to 2% difference in the values of the physical properties between the two sets of glasses can be explained by the mass percentage increase of samarium oxide. Table 2 presents the dilatometric softening temperature (Td), coefficient of thermal expansion (CTE) and glass transition temperature (Tg) values corresponding to different glass compositions. These data are also graphically illustrated in Fig. 2. Glass transition temperature of series A rises from 310 to for 374 °C for the glasses containing between 20 and 40 mol% of BaO and it is comprised between 337 and 390 °C in series B for similar contents of BaO. The dilatometric softening temperature exhibits a similar pattern of variation to that observed in the glass transition temperature across all the studied glass series. The coefficient of thermal expansion shows an opposite trend in the two glass series with a minimum of 14.7 × 10−6 K−1 for the compositions with 40 mol% BaO. The higher ionic field strength of Ba2+ modifier ions (0.49) compared to Na+ ones (0.19) strengthens the glass network through more covalent Ba–O–P bonds when Na2O is systematically substituted by BaO, causing the observed increase in the Tg and Td characteristic temperatures as well as the decrease in the CTE. The addition of a 1 mol% Sm2O3 instead of 0.3 in glasses of series B produces a similar effect on the thermal properties though minor increase in magnitude, with an increment of between 10 to 20 °C in the Tg values.
Table 2 Refractive index, density, glass transition temperature (Tg), dilatometric softening temperature (Td) and coefficient of thermal expansion coefficient (CTE)
| Glass sample |
αOH (cm−1) As-prepared samples |
αOH (cm−1) Re-melted sample |
| 20BaSm0.3 |
2.88 |
0.86 |
| 25BaSm0.3 |
2.53 |
0.86 |
| 30BaSm0.3 |
2.93 |
0.91 |
| 35BaSm0.3 |
2.12 |
0.30 |
| 40BaSm0.3 |
2.76 |
0.84 |
| 20BaSm1 |
2.47 |
0.54 |
| 25BaSm1 |
2.61 |
0.74 |
| 30BaSm1 |
2.94 |
0.65 |
| 35BaSm1 |
2.75 |
0.52 |
| 40BaSm1 |
2.84 |
0.71 |
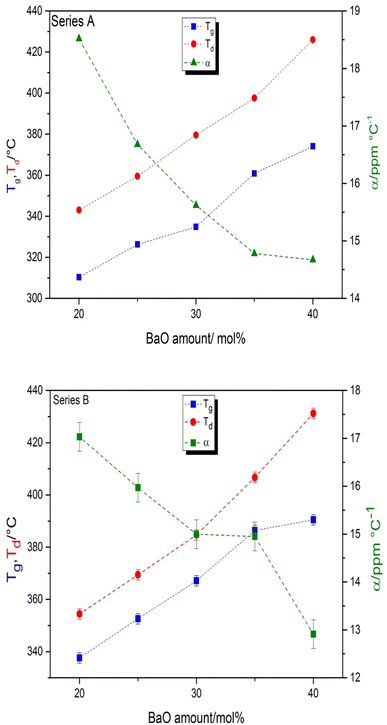 |
| | Fig. 2 Compositional dependence of glass transition temperature, Tg, dilatation softening temperature, Td, and the coefficient of thermal expansion in the glass series A: Na2O–BaO–P2O5–0.3Sm2O3 and in the glass series B: Na2O–BaO–P2O5–1Sm2O on the BaO content. The error in the values of Tg and Td is smaller than the symbol size. | |
The UV-Vis-NIR absorption curves of series A and series B glasses are plotted in Fig. 3 and 4, respectively. From these spectra, it is evident that all glass samples exhibit 13 absorption bands that share the same characteristics, with the exception of variations in band intensities. Hence, in both series of glasses, the absorption bands are observed at specific wavelengths: 318, 333, 345, 361, 375, 402, 439, 480, 945, 1079, 1230, 1378, 1483, 1530 and 1589 nm, these bands correspond to transitions from the ground state 6H5/2 to various excited states, including 4P3/2, 4G9/2, 3H7/2, 4D3/2,5/2, 6P7/2, 4F7/2 + 6P3/2, 4M17/2 + 4G9/2 + 4I9/2, 4M11/2 + 4I11/2,13/2, 6F11/2, 6F9/2, 6F7/2, 6F5/2, 6F3/2, 6H15/2 and 6F1/2, respectively.25,32 The Judd–Ofelt theory was employed to examine the spectroscopic properties of the glass samples. This involved calculating parameters such as the oscillator strength (f), radiative lifetime, J–O parameters (Ω2, Ω4, and Ω6), radiative transition possibility (AR), and branching ratio (βR).33 The calculated oscillator strength (fcal) of an electric dipole–dipole absorption transition from the initial state (ψj) to the final state (ψ′j′) of depends on three Ωλ parameters (λ = 2, 4 and 6) given by:34
| |
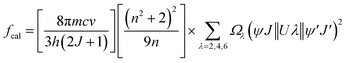 | (2) |
where
λ is the mean wavelength of the observed transition,
m is the electron mass,
n the refractive index,
c is the light velocity,
Ωλ the JO parameters, ‖
Uλ‖
2 are the doubly reduced squared matrix elements of a unit tensor operator, which are considered from the intermediate coupling approximation for the transition from
ψj to
ψ′
j′ and (
n2 + 2)
2/9
n is the Lorentz local field correction factor. The experimental oscillator strength (
fexp) of any absorption transition may be determined by determining the absorbance of each band as follow:
35| | |
fexp = 4.318 × 10−9∫ε(v)dv,
| (3) |
Here
ε(
v) represents the molar absorption coefficient and can be estimated by Beer–Lambert's equation.
Table 3 provides the experimental and calculated oscillator strengths for electronic transition observed in the absorption analysis. The reported values indicate that the oscillator strength values are approximately similar for most of the bands. This suggests that the non-symmetric component of the electric field acting on the Sm
3+ ions in the glasses is nearly identical for the majority of the transitions. In addition, the transition from
6H
5/2 to
6F
9/2 located at 1079 nm with the highest magnitude of
fexp and
fcal, is considered as the hypersensitive transition.
36 Table 4 lists the Judd–Ofelt (JO) parameters obtained in this study and compare them with those reported for Sm
3+-doped glass materials. As seen from
Table 4, the magnitude of trends of
Ωy parameters for BaSm0.3 glasses follow the order
Ω4 >
Ω6 >
Ω2. In general, the magnitude of the
Ω2 parameter is influenced by the local structure and asymmetry surrounding the RE ions, with a strong dependence on the covalency between RE
3+ ions and their ligand anions. The values of
Ω4 and
Ω6 are associated with the viscosity of the glass matrix and the vibronic transitions of the RE ions bound to the ligand atoms.
37,38 The comparisons of
Ω2 parameter of the present glasses with other Sm
3+ doped glasses show a higher value for our glasses, especially for the glasses containing 40 mol% of BaO. This suggests that the glass exhibits a highly asymmetric environment around the Sm
3+ ions. Conversely, the glass's lasing efficiency is evaluated using the spectroscopic quality factor (
χ), which is defined as the ratio of
Ω4 to
Ω6.
18 A smaller
Ω4/
Ω6 ratio indicates a more intense laser transition from the
4G
5/2 state to the
6H
7/2 state. The spectroscopic quality factor (
χ) value for our glasses was found to be approximately 1.16, which is the smallest compared to the other glasses mentioned in
Table 4. This shows that the closure transition is more than in other host glass. Consequently, the results show that our glasses appear to be better for the fabrication of photonic devices.
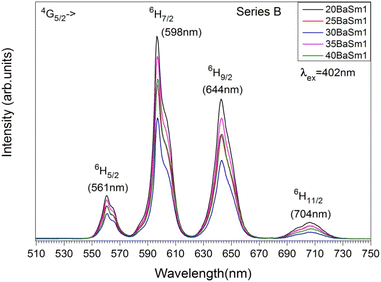
Fig. 5 and
6 displays the emission spectra of series A and B glasses, respectively, collected in the range 510–750 nm with an excitation at 402 nm. The excitation wavelength matches with the
6H
5/2 →
4F
7/2 transition which shows to be the most sensitive among the absorption bands. Four emission bands, centered at 561, 598, 644, and 703 nm, have been observed for all Sm
3+ doped glasses. They correspond to the transitions
4G
5/2 →
6H
5/2,
4G
5/2 →
6H
7/2,
4G
5/2 →
6H
9/2 and
4G
5/2 →
6H
11/2 respectively. For both Sm
3+ concentrations, the emission spectra show that the transition
4G
5/2 →
6H
7/2 (598 nm) has maximum fluorescence intensity, which illustrates that the glasses are potential candidates for reddish-orange emission. The transition follows the selection rule of Δ
J = ±1, making it partly allowed for electric dipole (ED) transitions but primarily allowed for magnetic dipole (MD) transitions. The
4G
5/2 →
6H
5/2 transition, despite having Δ
J = 0, also includes a contribution from magnetic dipole (MD) transitions. On the other hand, the
4G
5/2 →
6H
9/2 and
4G
5/2 →
6H
11/2 transitions are purely allowed for electric dipole (ED) transitions. The intensity of these transitions is sensitive to the variations in the local structure surrounding the rare earth ion.
39 The electric dipole (ED) transition from
4G
5/2 to
6H
9/2 at 644 nm exhibits a higher intensity compared to the magnetic dipole (MD) transition from
4G
5/2 to
6H
5/2 at 561 nm. This suggests the presence of asymmetric sites for the Sm
3+ ions in the glass.
40
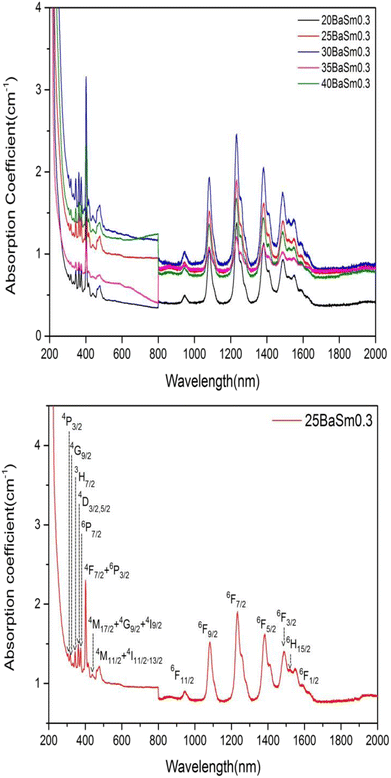 |
| | Fig. 3 The absorption spectra of series A glasses for (a) all concentrations and (b) 25 mol% of BaO and 0.3 mol % of Sm2O3. | |
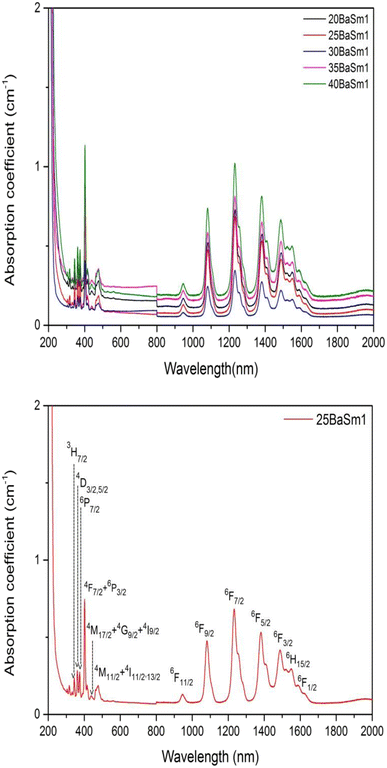 |
| | Fig. 4 The absorption spectra of series B glasses for (a) all concentrations and (b) 25 mol% of BaO and 1 mol% of Sm2O3. | |
Table 3 Experimental and calculated oscillator strengths (×10−6) of phosphate glasses doped 0.3% of samarium
| Transition from 6H5/2 to lower energy state |
20BaSm0.3 |
25BaSm0.3 |
30BaSm0.3 |
35BaSm0.3 |
40BaSm0.3 |
| fexp |
fcal |
fexp |
fcal |
fexp |
fcal |
fexp |
fcal |
fexp |
fcal |
| 4F7/2 |
1.059 |
0.040 |
1.059 |
0.040 |
1.059 |
0.040 |
1.059 |
0.041 |
1.059 |
0.041 |
| 4I13/2 |
1.627 |
1.653 |
1.627 |
1.654 |
1.628 |
1.654 |
1.627 |
1.658 |
1.627 |
1.662 |
| 6F11/2 |
3.246 |
3.140 |
3.248 |
3.170 |
3.284 |
3.170 |
3.284 |
3.151 |
3.284 |
3.132 |
| 6F9/2 |
5.311 |
5.589 |
5.351 |
5.650 |
5.352 |
5.646 |
5.535 |
5.689 |
5.535 |
5.731 |
| 6F7/2 |
3.670 |
3.419 |
3.717 |
3.456 |
3.718 |
3.454 |
3.813 |
3.495 |
3.908 |
3.536 |
| 6F5/2 |
0.599 |
0.5476 |
0.653 |
0.553 |
0.654 |
0.553 |
0.653 |
0.559 |
0.653 |
0.565 |
| 6F3/2 |
1.405 |
0.246 |
1.513 |
0.248 |
1.405 |
0.248 |
1.405 |
0.251 |
1.405 |
0.254 |
| 6H15/2 |
3.464 |
0.016 |
3.592 |
0.016 |
3.464 |
0.016 |
3.464 |
0.016 |
3.463 |
0.016 |
Table 4 J–O intensity parameters (×10−20 cm2) of BaSm0.3 phosphate glasses
| Glass system |
Ω2 |
Ω4 |
Ω6 |
Trend of Ωy |
Ω4/Ω6 (χ) |
Reference |
| 20BaSm0.3 |
1.13 |
10.92 |
9.36 |
Ω4 > Ω6 > Ω2 |
1.166 |
Present |
| 25BaSm0.3 |
1.13 |
11.04 |
9.46 |
Ω4 > Ω6 > Ω2 |
1.167 |
Present |
| 30BaSm0.3 |
1.13 |
11.05 |
9.47 |
Ω4 > Ω6 > Ω2 |
1.169 |
Present |
| 35BaSm0.3 |
1.14 |
11.26 |
9.57 |
Ω4 > Ω6 > Ω2 |
1.176 |
Present |
| 40BaSm0.3 |
1.23 |
11.88 |
9.70 |
Ω4 > Ω6 > Ω2 |
1.224 |
Present |
| 69.5 NH4H2PO4–15Na2CO3 –15Ba2CO3–0.5Sm2O3 |
0.30 |
4.08 |
3.68 |
Ω4 > Ω6 > Ω2 |
1.94 |
28 |
| NSBaP |
0.33 |
8.60 |
3.92 |
Ω4 > Ω6 > Ω2 |
2.19 |
29 |
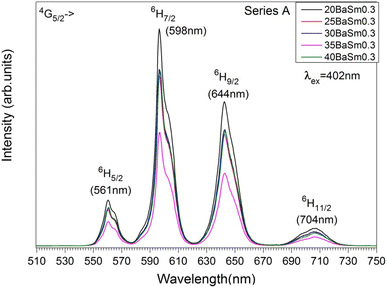 |
| | Fig. 5 The emission spectra of series A glasses. | |
 |
| | Fig. 6 The emission spectra of series B glasses. | |
Although the addition of BaO induces depolymerization in the phosphate network, surprisingly, it was found that the emission intensity of series A glasses first decrease when BaO content increases from 20 to 35 mol% and then increases with the further increase in BaO concentration. On the other hand, for series B, the intensity of luminescence decreases with the rise of BaO concentration initially until x = 30, then quench up to 35 and finally decrease to 40% of BaO. Therefore, glasses with 20% BaO have the maximal luminescence intensity for series A and B. This trend correlates perfectly with the degree of polymerization in the phosphate glass. In fact, an increase in the degree of compactness and polymerization of the phosphate network leads to a corresponding rise in Sm3+ emission, and vice versa. It should be noted that an inverse trend in emission intensity is typically observed with the depolymerization of the phosphate network, as reported in earlier studies.41,42 These results can likely be explained by the moderation of the local ligand field strength due to the modification of the glass network resulting from the replacement of Na+ with Ba2+. In this context, Na+ cations with the higher field strength exhibit a greater preference for coordination with NBOs compared to Ba2+ cations. Consequently, an increase in Ba2+ concentration results in a decreased competition for NBO coordinations, leading to a weakening of the coordination with Sm3+ ions. This mechanism clearly elucidates the reduced Sm3+ emission observed in glasses with Ba2+ as network modifier ions, particularly in comparison to the relatively high field strength cations of Na+.43 The radiative transition probability (AR), fluorescent branching ratio (βR), and lifetime (τR) for the emission peaks of Sm3+ ions in the glass samples were determined using previously published equations.40 The calculated values for the radiative transition probability (AR) and branching ratio (βR) for the 4G5/2 → 6H7/2 transition were found to be higher than those of other transitions. These values are presented in Table 5. The βR values obtained were 0.693 for 20BaSm0.3 and 0.582 for 20BaSm1. These values indicate that our samples have a high potential to be used as a laser gain medium for 598 nm emission due to their high lasing power, low laser threshold, and suitability for laser applications.44,45 The obtained luminescence lifetimes of the 4G5/2 level of the glass samples are gathered in Table 6. The luminescence decays were measured by exciting the samples at 402 nm and collecting the emitted light at 598 nm. As an illustration, Fig. 7 exhibits the experimental decay curves for the 35BaO–0.3Sm and 35BaO–1Sm samples. The decays of the samples doped with 0.3 mol% of Sm3+ can be reasonably approximated by single exponential functions. In contrast, the decays of the samples doped with 1 mol% of Sm3+ deviate from a single exponential function and exhibit a reduction in lifetimes. The lifetime values in Table 6 for our compounds doped with 1 mol% represents the average lifetime, investigated using the eqn (4):
| |
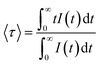 | (4) |
where,
I (
t) is the luminescence intensity at time
t corrected for the background. As shown in
Table 6, lifetime values in glasses doped with 1 mol% Sm
2O
3 are smaller than those in the 0.3 mol% counterparts, which can be due to concentration quenching effects. However, it is noteworthy that the emission lifetime values of the
4G
5/2 level are comparable to the maximum values reported in the literature for similar concentrations of Sm
3+ ions in glass systems,
46,47 underscoring the efficiency of the re-melting process. Specifically, the reduced presence of hydroxyl groups leads to a decrease in possible non-radiative relaxation processes for Sm
3+ ions, thereby extending the lifetime duration. On the other hand, there are not significant differences in the lifetime values from the BaO/Na
2O substitution. Shortened lifetimes and deviation from a single exponential function are characteristic of the presence of a concentration extinction mechanism in the lifetime of
4G
5/2 level as concentration rises. The experimental decay time of the
4G
5/2 level is determined by a combination of probabilities for both radiative and nonradiative processes. Non-radiative phenomena comprise non-radiative multiphonon relaxation and cross-relaxation energy transfer, as well as impurity-induced quenching. Considering the significant energy difference of approximately 7000 cm
−1 between the
4G
5/2 and the immediately lower level
6F
11/2, it is anticipated that non-radiative decay
via multiphonon emission would be minimal. Hence, the decrease in lifetime with increasing concentration can be primarily attributed to cross-relaxation energy transfer processes such as (
4G
5/2;
6H
5/2) → (
6F
11/2;
6F
5/2) and (
4G
5/2;
6H
5/2) → (
6F
9/2;
6F
7/2).
18,48 The values of radiative lifetime decrease from 2.98 to 2.93 for 20BaSm0.3 and 40BaSm0.3 glass respectively. It is clear that the
4G
5/2 level's radiative lifetime was continuously longer than the observed lifetime, which gets smaller as Sm
3+ concentration rises. This decrease can be attributed to non-radiative energy transfer processes.
Table 7 presents a comparison of the quantum efficiency (
η) values of the glass samples with the values reported above. The results show that the
η values for the
4G
5/2 level of the 30BaSm0.3 glass are higher than for the other glasses. Based on the obtained lifetime and quantum efficiency results, we conclude that they are promising and serve as a foundation for the development of efficient red luminophores suitable for display and illumination applications.
Table 5 Emission band position (λp, nm), radiative transition probability (A, s−1), and calculated branching ratios (βr) for the excited 4G5/2 level of BaSm0.3 phosphate glasses
| Emission transition |
Transition parameters |
20BaSm0.3 |
25BaSm0.3 |
30BaSm0.3 |
40BaSm0.3 |
| 4G5/2 → 6H5/2 |
λp |
561 |
561 |
561 |
561 |
| A |
14.53 |
14.62 |
14.62 |
14.58 |
| βr |
0.043 |
0.043 |
0.043 |
0.042 |
| 4G5/2 → 6H7/2 |
λp |
598 |
598 |
598 |
598 |
| A |
232.94 |
235.47 |
235.39 |
235.95 |
| βr |
0.693 |
0.695 |
0.695 |
0.694 |
| 4G5/2 → 6H9/2 |
λp |
644 |
644 |
644 |
644 |
| A |
88.44 |
88.33 |
88.29 |
89.02 |
| βr |
0.263 |
0.261 |
0.260 |
0.262 |
Table 6 Lifetime values obtained under excitation at 402 nm collecting the luminescence at 598 nm
| Sample |
Lifetime (ms) |
| 20BaO_Sm 0.3% |
2.69 |
| 25BaO_Sm 0.3% |
2.69 |
| 30BaO_Sm 0.3% |
2.68 |
| 35BaO_Sm 0.3% |
2.67 |
| 40BaO_Sm 0.3% |
2.64 |
| 20BaO_Sm1% |
1.15 |
| 25BaO_Sm1% |
1.14 |
| 30BaO_Sm1% |
1.15 |
| 35BaO_Sm1% |
1.16 |
| 40BaO_Sm1% |
1.15 |
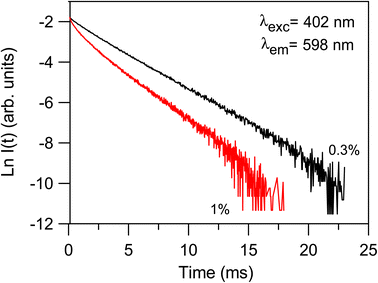 |
| | Fig. 7 Semi-logarithmic plot of the fluorescence decay of the 4G5/2 level for the 35BaO–0.3Sm ad 35BaO–1Sm samples obtained by exciting at 402 nm and collecting the luminescence at 598 nm. | |
Table 7 Radiatives lifetimes τrad, measured lifetimes τmeas and quantum efficiencies (η)
| Glass system |
τmeas of 4G5/2 (ms) |
τrad of 4G5/2 (ms) |
η (%) |
Reference |
| 20BaSm0.3 |
2.69 |
2.98 |
90.26 |
Present |
| 25BaSm0.3 |
2.69 |
2.95 |
91.18 |
Present |
| 30BaSm0.3 |
2.68 |
2.95 |
90.84 |
Present |
| 35BaSm0.3 |
2.67 |
2.94 |
90.81 |
Present |
| 40BaSm0.3 |
2.64 |
2.93 |
90.10 |
Present |
| 69.5 NH4H2PO4–15Na2CO3 –15Ba2CO3–0.5Sm2O3 |
2.01 |
3.41 |
58.89 |
28 |
| NSBaP |
1.74 |
2.40 |
72.5 |
29 |
| NNS05 |
2.06 |
2.9 |
71 |
30 |
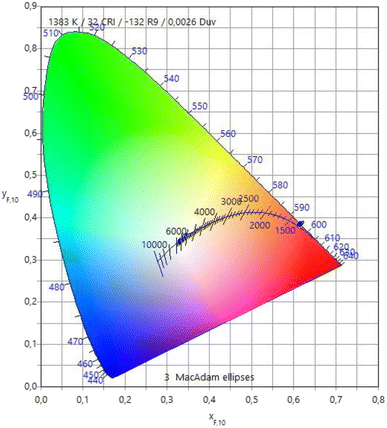
Fig. 8 depicts the variations in luminescent colors of the glass samples, analyzed using the Commission Internationale de l'Eclairage 1931 (CIE) chromaticity diagram. The CIE chromaticity coordinates (x, y) and associated color temperatures (CCT, K) of the examined glass samples have been computed and tabulated in Table 8. Upon substituting Na2O with BaO content, all glass samples exhibit a nearly identical red color, showcasing prominent reddish-orange tints with CIE coordinates. Additionally, they demonstrate lower CCT values corresponding to the temperature of the closest Planckian black-body radiator to the operating point on the chromaticity diagram.49 These findings strongly indicate the potential of the examined glasses as phosphors, generating reddish-orange light for solid-state devices.
 |
| | Fig. 8 CIE chromaticity diagram of the prepared glasses. | |
Table 8 The CIE chromaticity coordinates (x, y) and associated color temperatures (CCT, K) of the examined glass samples
| |
x |
y |
CCT |
| 20BaOSm1 |
0.6077 |
0.3916 |
1383 |
| 25BaOSm1 |
0.6057 |
0.3934 |
1401 |
| 30BaOSm1 |
0.6044 |
0.3942 |
1411 |
| 35BaOSm1 |
0.6075 |
0.3918 |
1385 |
| 40BaOSm1 |
0.6091 |
0.3902 |
1370 |
4. Conclusions
In summary, this investigation explored the impact of barium and samarium oxide additions on the physical, thermal, optical and luminescence characteristics of metaphosphate glasses. The density and refractive index of glass compounds rise with increasing BaO element. Furthermore, the properties values for the glasses doped with 1 mol% Sm2O3 are found to be higher than those of glasses doped with 0.3 mol% Sm2O3. The glass transition and dilatometric softening temperatures increased when BaO was substituted for Na2O, while the coefficient of thermal expansion decreased. The analysis of FTIR spectra indicates an increasing network depolymerization with the BaO addition, with a transition from a modifier oxide to a glass-forming element for high BaO levels. The absorption spectral profiles of the glass samples exhibit similar characteristics, with the only variation being the intensities of the bands. The photoluminescence emission of BaSm0.3 glasses has higher intensity than the BaSm1 glasses, which shows that BaSm0.3 glasses have less non-radiative energy transfer processes. Moreover, the emission spectra of all glasses presented a strong reddish orange emission at 598 nm, under 402 nm excitation, with the highest intensity for the glasses with 20 mol% of BaO. Finally the lifetime of the 4G5/2 level show similar values with the rise of BaO content and decreases with increasing Sm2O3 content mainly attributed to the existence of cross-relaxation processes. Further, the method used for dehydroxylation of the glasses increased the lifetimes which is the result of a strong reduction in non-radiative relaxation mechanism involving OH groups. It is concluded that current glasses may be a good candidate for displaying colors or visible lasers in the red-orange spectral region.
Data availability
The datasets generated or analyzed during the current study are available from the corresponding author on reasonable request.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors thank funding through projects MAT2017-87035-C2-1-P/-2-P from Agencia Estatal de Investigación, PID2020-115419GB-C21/C22 from Agencia Estatal de Investigación MCINN/AEI/10.13039/501100011033 and PIBA18-24 (Basque Country Government). The researchers would like to acknowledge Deanship of Scientific Research, Taif University.
References
- A. H. Almuqrin, A. Kumar, J. F. M. Jecong, N. Al-Harbi, E. Hannachi and M. I. Sayyed, Optik, 2021, 247, 167792 CrossRef CAS.
- N. Alharbiy, Z. Y. Khattari, Y. S. Rammah and A. Saleh, J. Mater. Sci.: Mater. Electron., 2023, 34, 191 CrossRef CAS.
- G. R. Dillip, C. M. Reddy, M. Rajesh, S. Chaurasia, B. D. P. Raju and S. W. Joo, Bull. Mater. Sci., 2016, 39, 711–717 CrossRef CAS.
- M. Rajesh, T. Gowthami, N. J. Sushma, B. Kamala and B. D. P. Raju, Infrared Phys. Technol., 2018, 90, 221–229 CrossRef.
- N. Srinivasa Rao, M. Rajesh, S. Kumaresan, G. Rajasekhara Reddy, K. Prasad, B. Deva Prasad Raju and S. Dhanapandian, Appl. Phys. A, 2020, 126, 1–6 CrossRef.
- S. S. Hajer, M. K. Halimah, Z. Azmi and M. N. Azlan, Chalcogenide Lett., 2014, 11, 553–566 Search PubMed.
- N. Chanthima, Y. Tariwong, M. Djamal and J. Kaewkhao, Mater. Today, 2018, 5, 15034–15039 CAS.
- P. Laporta, S. Taccheo, S. Longhi, O. Svelto and C. Svelto, Opt. Mater., 1999, 11, 269–288 CrossRef CAS.
- K. Nanda, R. S. Kundu, I. Pal, R. Punia and N. Kishore, J. Alloys Compd., 2016, 676, 521–526 CrossRef CAS.
- G. Pal Singh and D. P. Singh, J. Mol. Struct., 2012, 1012, 137–140 CrossRef CAS.
- H. Mrabet, M. Atef and I. Khattech, Mater. Chem. Phys., 2020, 239, 122087 CrossRef CAS.
- N. Al-Harbi, M. I. Sayyed, R. Kurtulus, M. Kamışlıoğlu, A. Kumar, A. M. S. Alhuthali, T. Kavas and Y. Al-Hadeethi, J. Mater. Sci.: Mater. Electron., 2021, 32, 11649–11665 CrossRef CAS.
- N. Al-Harbi, M. I. Sayyed, A. Kumar, K. A. Mahmoud, O. I. Olarinoye, A. M. S. Alhuthali and Y. Al-Hadeethi, J. Mater. Sci.: Mater. Electron., 2021, 32, 12371–12382 CrossRef CAS.
- S. Jiang, T. Luo, B. Hwang and F. Smekatala, J. Non-Cryst. Solids, 2000, 263–264, 364–368 CrossRef.
- M. G. Mesko and D. E. Day, J. Nucl. Mater., 1999, 273, 27–36 CrossRef CAS.
- M. N. Rahaman, D. E. Day, B. S. Bal, Q. Fu, S. B. Jung, L. F. Bonewald and A. P. Tomsia, Acta Biomater., 2011, 7, 2355–2373 CrossRef CAS PubMed.
- I. Jlassi, S. Mnasri and H. Elhouichet, J. Lumin., 2018, 199, 516–527 CrossRef CAS.
- B. N. Naick, V. R. Prasad, S. Damodaraiah, A. V Reddy and Y. C. Ratnakaram, Opt. Mater., 2019, 88, 7–14 CrossRef.
- S. Hussain, R. J. Amjad, M. Tanveer, M. Nadeem, H. Mahmood, A. Sattar, A. Iqbal, I. Hussain, Z. Amjad, S. Z. Hussain, S. A. Siddique and M. R. Dousti, Glass Phys. Chem., 2017, 43, 538–547 CrossRef CAS.
- A. Herrmann, S. Kuhn, M. Tiegel, C. Rüssel, J. Korner, D. Klopfel, J. Hein and M. C. Kaluza, J. Mater. Chem. C, 2014, 2, 4328–4337 RSC.
- A. Herrmann, M. Tewelde, S. Kuhn, M. Tiegel and C. Rüssel, J. Non-Cryst. Solids, 2018, 502, 190–197 CrossRef CAS.
- S. Kuhn, M. Tiegel, A. Herrmann, C. Rüssel, S. Engel, C. Wenisch, S. Graf, F. A. Müller, J. Korner, R. Seifert, F. Yue, D. Klopfel, J. Hein and M. C. Kaluza, J. Appl. Phys., 2015, 118, 103104–103109 CrossRef.
- F. Muñoz and R. Balda, Int. J. Appl. Glass Sci., 2019, 10, 157–161 CrossRef.
- H. Ebendorff-heidepriem and D. Ehrt, Glastech. Ber. Glass Sei. Technol., 1995, 68, 139–146 CAS.
- H. Ebendorff-Heidepriem, W. Seeber and D. Ehrt, J. Non-Cryst. Solids, 1993, 163, 74–80 CrossRef CAS.
- M. Ennouri, L. Kuusela, J. Ifa, B. Gelloz, L. Petit and H. Elhouichet, Materials, 2019, 12, 3516 CrossRef CAS PubMed.
- I. Konidakis, C.-P. E. Varsamis, E. I. Kamitsos, D. M oncke and D. Ehrt, J. Phys. Chem., 2010, 114, 9125–9138 CAS.
- J. A. Wilder and J. E. Shelby, J. Am. Ceram. Soc., 1984, 67, 438–444 CrossRef CAS.
- R. K. Brow, J. Non-Cryst. Solids, 2000, 263, 1–28 CrossRef.
- N. Chanthima, J. Kaewkhao, C. K. Jayasankar and W. Lertlop, Mater. Today: Proc., 2018, 5, 15049–15053 CAS.
- H. A. Lorentz, Ann. Phys., 1880, 245, 641–665 CrossRef.
- W. T. Carnall, P. R. Fields and K. Rajnak, J. Chem. Phys., 1968, 49, 4424–4442 CrossRef CAS.
- M. Monisha, M. S. Murari, M. I. Sayyed, K. Naregundi, N. Al-Harbi and S. D. Kamath, J. Non-Cryst. Solids, 2023, 599, 121971 CrossRef CAS.
- B. M. Walsh, Judd–Ofelt Theory: Principles and Practices, ed. Brian M. Walsh, 2006, pp. 403–433 Search PubMed.
- L. Li, Z. Leng, W. Zi and S. Gan, J. Electron. Mater., 2014, 43, 2588–2596 CrossRef CAS.
- S. Chahar, V. B. Taxak, M. Dalal, S. Singh and S. P. Khatkar, Mater. Res. Bull., 2016, 77, 91–100 CrossRef CAS.
- I. Jlassi, S. Mnasri and H. Elhouichet, J. Lumin., 2018, 199, 516–527 CrossRef CAS.
- H. Largot, K. E. Aiadi, M. Ferid, S. Hraiech, C. Bouzidi, C. Charnay and K. Horchani-naifer, Phys. B, 2019, 552, 184–189 CrossRef CAS.
- C. Madhukar Reddy, B. Deva Prasad Raju, N. John Sushma, N. S. Dhoble and S. J. Dhoble, Renewable Sustainable Energy Rev., 2015, 51, 566–584 CrossRef CAS.
- A. Langar, C. Bouzidi, H. Elhouichet, B. Gelloz and M. Férid, Displays, 2017, 48, 61–67 CrossRef CAS.
- M. Ennouri, L. Petit and H. Elhouichet, Opt. Mater., 2022, 131, 112610 CrossRef CAS.
- L. Kuusela, A. Veber, N. G. Boetti and L. Petit, Materials, 2020, 13(3), 527 CrossRef CAS PubMed.
- A. Herrmann, A. A. Assadi, R. Lachheb, M. Zekri, A. Erlebach, K. Damak, R. Maalej, M. Sierka and C. Rüssel, Acta Mater., 2023, 249, 118811 CrossRef CAS.
- N. Luewarasirikul and J. Kaewkhao, Mater. Today: Proc., 2017, 4, 6224–6233 Search PubMed.
- C. Bouzidi, M. Ferhi, H. Elhouichet, M. Ferid, M. Ferhi, H. Elhouichet and M. Ferid, J. Lumin., 2016, 179, 230–235 CrossRef CAS.
- R. Turki, M. Zekri, A. Herrmann, C. Rüssel, R. Maalej and K. Damak, J. Alloys Compd., 2019, 806, 1339–1347 CrossRef CAS.
- S. Ghosh and S. Jana, J. Lumin., 2023, 263, 119980 CrossRef CAS.
- S. Damodaraiah, V. Reddy Prasad and Y. C. Ratnakaram, Luminescence, 2018, 33, 594–603 CrossRef CAS PubMed.
- T. Erdem, S. Nizamoglu, X. W. Sun and H. V. Demir, Opt. Express, 2010, 18, 340 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article