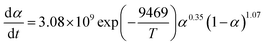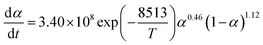Open Access Article
Open Access ArticleLow viscosity and low temperature curing reactive POSS/epoxy hybrid resin with enhanced toughness and comprehensive thermal performance†
Ruiyan Han,
Xiaoyan Ma *,
Lifeng Cai,
Zongwu Zhang,
Yiliang Fang and
Jian Wang
*,
Lifeng Cai,
Zongwu Zhang,
Yiliang Fang and
Jian Wang
School of Chemistry and Chemical Engineering, Northwestern Polytechnical University, Xi'an 710072, PR China. E-mail: m_xiao_yana@nwpu.edu.cn
First published on 1st March 2024
Abstract
The mechanical and high-temperature resistance properties of epoxy resins cured at low temperatures (Tcuring ≤ 100 °C) are often inferior, and the most toughening modification methods for epoxy resins tend to compromise thermal resistance, which significantly limit the practical applications of it. Therefore, this work reported a low viscosity and low-temperature curing epoxy hybrid resin system (OPEP), adopting E-51 as a resin matrix, liquid anhydride (MHHPA) as a curing agent, tertiary amine (DMBA) as a curing accelerator, and reactive octa-epoxy terminated polyhedral oligomeric silsesquioxane (OG-POSS) as a toughening modifier. Results demonstrated that the OPEP system has excellent processability with low viscosity and long processing window period and satisfies the practical requirements of low-temperature curing. The OG-POSS exhibits superior compatibility and reactivity with the resin matrix, and its addition slightly reduces the Eα of the curing reaction and has a certain promotive effect on the curing of epoxy resin. In addition, the curing reaction rate of the OPEP resin complies with the Šesták–Berggren autocatalytic kinetics model. The impact strength, flexural strength, tensile strength, and elongation at break of the OPEP resin reached a maximum of 15.55 kJ m−2, 121.65 MPa, 90.36 MPa, and 2.48%, representing increases of 55.97%, 3.1%, 64.68%, and 26.51% compared to those of the pure resin, respectively. Notably, due to the heat-resistant inorganic silicon cage structure of OG-POSS, the thermal decomposition temperature (Td5), glass transition temperature (Tg), and heat distortion temperature (THDT) of the OPEP0.02 resin were 313.2 °C, 123.7 °C, and 102.0 °C, showing increases of 13.0 °C, 2.3 °C, and 6.8 °C compared to the pure resin, respectively, which is difficult to achieve for the general thermosetting resin toughening modification method. This research utilized organic–inorganic nanohybrid materials (POSS) to optimize the toughness and thermal stability of the resin in a coordinated manner, providing guidance for the preparation of high-performance epoxy resins that cure at low temperatures.
1. Introduction
Epoxy resin is endowed with a range of exceptional properties due to its unique structure, including excellent chemical resistance, high modulus, and high glass transition temperature, among others. Consequently, it finds extensive application in various sectors such as adhesives, coatings, and aerospace.1–6 Liquid anhydride, as one of the typical curing agents for epoxy resin, has the advantages of low viscosity and low curing reaction heat, which enables the epoxy/anhydride system to exhibit excellent processability.7–9 However, due to the low reactivity between epoxy and anhydride groups, traditional epoxy/anhydride systems typically require curing under high-temperature conditions to produce products with superior mechanical and thermal stability.10 Due to the elevated curing temperatures, there are not only high requirements for equipment and processes, but it also presents challenges in terms of cost reduction.11,12 On the other hand, epoxy resins cured under low-temperature conditions (Tcuring ≤ 100 °C) often result in cured products with inferior mechanical and thermal stability.13–15 Therefore, based on the practical requirements in production for curing at low temperatures, developing a low viscosity and low curing temperature epoxy resin that has the characteristics of high toughness and high thermal stability holds significant application value, promoting the further use of epoxy resin in the industry.Epoxy resin, a typical thermosetting resin characterized by a three-dimensional network structure, is known for its shortcoming of poor toughness, which limits its applications in various engineering fields.16 Hence, methods to toughen epoxy resin have consistently been one of the focal points in high-performance composite materials research. In recent years, researchers have proposed various methods to enhance the toughness of epoxy resins, such as rubber elastomers,17 thermoplastic resins,18 hyperbranched polymers,10,19–25 or nanoparticles,26–29 etc. While these approaches have achieved significant improvements in the toughness of epoxy resins, most come at the expense of their thermal resistance or other properties, which hinders the further application of epoxy resin. Bian et al.30 modified the epoxy/BN composite material with carboxyl-terminated nitrile rubber, resulting in a toughness increase of about 32% for the modified system. However, both the glass transition temperature and thermal stability decreased.
Nanoparticles, distinguished by their minuscule size, large specific surface area, and high surface energy, possess distinct physicochemical properties that are entirely different from macroscopic materials. They can be used as common reinforcing and toughening fillers in resin-based composite materials.26,31,32 The toughening mechanism involves the interaction between nanoparticles and the epoxy groups at the interface. When this interaction force exceeds the van der Waals forces, crazes form, which can absorb the energy of deformation occurring in the epoxy resin. Additionally, the crazes can also act to blunt and hinder the propagation of cracks, thereby achieving toughening. Nanoparticles are categorized based on their material types into organic particles,33 inorganic particles,34 and organic–inorganic hybrid particles.35
Polyhedral oligomeric silsesquioxane (POSS), a typical nano-caged structured organic–inorganic hybrid material, has attracted significant interest from the scientific community in recent years.36 The general formula for POSS is (RSiO1.5)n (where R represents an organic substituent, and n can be 6, 8, 10, etc.). The interior comprises an inorganic framework (core) made of Si–O–Si bonds, while the exterior is covered by organic substituents (shell). It is precisely because of this unique core–shell structure that POSS combines the advantages of organic particles (processability, flexibility) with those of inorganic particles (heat resistance, high modulus). POSS can be classified into reactive POSS and non-reactive POSS based on the type of organic substituent. Furthermore, through chemical modification and physical blending, organic–inorganic hybrid nanocomposites can be synthesized for diverse applications.37–40 Reactive POSS can participate in the curing reaction of epoxy resin, achieving dispersion at the molecular level, which enhances its compatibility within the epoxy matrix. This characteristic addresses the drawback of inorganic nanomaterials and non-reactive POSS, which tend to agglomerate in resin matrices.41,42 Mishra et al.36,43 incorporated POSS molecules with different organic substituents (trisilanol phenyl and glycidyl) into the epoxy resin system. Among them, the glycidyl POSS demonstrated exceptional compatibility and reactivity with the epoxy resin. The modified resin's fracture toughness and fracture energy were increased by 130% and 400%, respectively. Meanwhile, the trisilanol phenyl POSS, being a non-reactive type, interacted with the epoxy resin through hydrogen bonding and π–π interactions. However, its mechanical property enhancement was limited, and it tended to agglomerate at higher concentrations.
Herein, in order to satisfy the practical requirements in production to cure at low temperatures and develop a new high-temperature resistant and high toughness epoxy, this study firstly determined a low viscosity and low-temperature curable (Tcuring ≤ 100 °C) epoxy resin system (E-51/MHHPA/DMBA). Subsequently, using reactive octa-epoxy terminated POSS (OG-POSS) as a toughener for modified hybrid epoxy resin (OPEP), and its processability, curing reactivity, mechanical properties, and comprehensive thermal performance were researched. This work aims to provide a new approach for the preparation of low viscosity, low curing temperature and high-performance epoxy resin, potentially broadening its application domains.
2. Experimental section
2.1. Materials
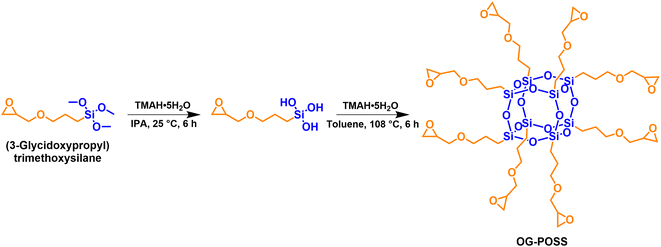
Epoxy resin (E-51) was supplied by SINOPEC Baling Petrochemical Co., Ltd (China). Methylhexahydrophthalic anhydride (MHHPA) was purchased from Adamas-beta Chemical Reagent Co., Ltd (China). N,N′-Dimethylbenzylamine (DMBA) and tetramethylammonium hydroxide pentahydrate (TMAH·5H2O) were analytical grade reagents purchased from Shanghai Macklin Biochemical Technology Co., Ltd (China). KH-560 was purchased from Dinghai Plastic Chemical Co., Ltd (China). Isopropanol (IPA) and toluene were chemical grade reagents purchased from Chengdu Kelong Chemical Co., Ltd (China). Sodium chloride and anhydrous magnesium sulfate were analytical grade chemicals purchased from Sinopharm Chemical Reagent Co., Ltd (China). All chemicals were used directly without further purification or treatment.The octa-epoxy terminated polyhedral oligomeric silsesquioxane (OG-POSS) was synthesized in the laboratory, with an epoxy value of 0.56 mol (100 g)−1. The synthesis route of OG-POSS is shown in Fig. 1, and the details, synthesis and characterization, are described in the ESI S1.†
2.2. Preparation of OPEP hybrid resin
At room temperature, E-51, OG-POSS, MHHPA, and DMBA were meticulously mixed to achieve a homogeneous blend. The mixture was then degassed at 60 °C for 30 minutes, resulting in a faint yellow transparent liquid. Subsequently, the prepolymer was poured into a preheated mold and constantly degassed in a vacuum oven at 60 °C for 30 minutes. This was followed by curing at 90 °C for one day. Finally, the sample was allowed to cool naturally to room temperature, yielding the OG-POSS modified hybrid epoxy resin (OPEP). It is noteworthy to mention that the weight ratios of OG-POSS to E-51 were 0, 0.01, 0.02, 0.05, and 0.10, and they were labeled as EP, OPEP0.01, OPEP0.02, OPEP0.05, and OPEP0.10, respectively.2.3. Measurements
Fourier transform infrared (FT-IR) spectra was measured with Bruker TENSOR 27 (Germany). 1H-NMR, 13C-NMR and 29Si-NMR spectra were recorded on a Bruker AVANCE 400 MHz NMR instrument. Viscosity was measured with NDJ-5S Bruker Dimension Icon (Germany). Curing kinetics analysis was performed by Mettler-Toledo DSC 3 under a nitrogen atmosphere. The impact, bending, and tensile experiments of the resins were determined in accordance with the ISO 179-2010, ISO 178-2010 and GB/T 2567-2021 standards, respectively, using a ZBC-4 pendulum impact tester (China), a CMT 6303 electronic universal testing machine (China) and a CMT 7204 electronic universal testing machine (China). The impact profile analysis was carried out using ZEISS Sigma 300 (Germany) Scanning Electron Microscopy (SEM), and the accelerating voltage was 10 kV. Atomic Force Microscope (AFM) was measured with Bruker Dimension Icon (Germany). Energy Dispersive Spectroscopy (EDS) was measured with OXFORD Xplore. X-ray Photoelectron Spectroscopy (XPS) was measured with Kratos AXIS Ultra DLD (UK). Thermal gravimetric analysis (TGA) was performed by STA 449F3 (Germany) and the test temperature, under argon atmosphere, increasing from 40 °C to 800 °C at the heating rate of 10 °C min−1. Dynamic mechanical analysis (DMA) was performed by DMA 242E (Germany) and the test temperature increasing from 30 °C to 200 °C at the heating rate of 5 °C min−1. The Heat Distortion Temperature (HDT) was determined using an INSTRON C-HV6M-000 instrument and the test temperature, under a load of 1.80 MPa, increasing from 25 °C to 300 °C at the heating rate of 2 °C min−1, in accordance with ISO 75 standards.3. Results and discussion
3.1. Processability and curing reactivity of OG-POSS in OPEP hybrid resin
Based on the practical requirements, this study initially determined a low viscosity and low-temperature curing (Tcuring ≤ 100 °C) epoxy resin system (E-51/MHHPA/DMBA), which is described in detail in the ESI S2.† The initial curing temperature (Ti) of systems containing curing accelerator was all less than 100 °C in the DSC curves (as shown in the Table 1 and Fig. S2(a)†), which provides a theoretical possibility for the low-temperature curing of epoxy resin. Particularly, the addition of liquid anhydride (MHHPA) apparently reduces the viscosity of the system (the viscosity of E-51 at 25 °C is 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 mPa s), as shown in the Table S1,† indicating a long processing window period, which lays the foundation for further preparation of modified hybrid resins. Moreover, the measurement results of viscosity (Table S1†) and gel time (Fig. S2(b)†) indicate that the addition of OG-POSS has no significant effect on the curing process of the resin, which enables OPEP hybrid resin to have the similar excellent processability as pure resin, holding significant application value. Therefore, a strategy is proposed to adopt the reactive organic–inorganic nanomaterial (OG-POSS) as a toughening modifier, which led to the creation of the modified hybrid resin (OPEP) to improve its overall performance.
940 mPa s), as shown in the Table S1,† indicating a long processing window period, which lays the foundation for further preparation of modified hybrid resins. Moreover, the measurement results of viscosity (Table S1†) and gel time (Fig. S2(b)†) indicate that the addition of OG-POSS has no significant effect on the curing process of the resin, which enables OPEP hybrid resin to have the similar excellent processability as pure resin, holding significant application value. Therefore, a strategy is proposed to adopt the reactive organic–inorganic nanomaterial (OG-POSS) as a toughening modifier, which led to the creation of the modified hybrid resin (OPEP) to improve its overall performance.
| Samples | β (K min−1) | Ti (°C) | Tp (°C) | Tf (°C) | ΔH (J g−1) |
|---|---|---|---|---|---|
| EP | 0 | 93.9 | 135.9 | 168.7 | — |
| 5 | 99.5 | 144.9 | 181.4 | 260.63 | |
| 10 | 103.8 | 156.7 | 195.5 | 247.60 | |
| 15 | 110.0 | 164.2 | 207.5 | 210.02 | |
| OPEP0.02 | 0 | 71.1 | 135.7 | 170.7 | — |
| 5 | 81.0 | 145.1 | 183.1 | 261.11 | |
| 10 | 91.2 | 158.2 | 201.5 | 273.28 | |
| 15 | 101.5 | 165.8 | 210.5 | 241.78 |
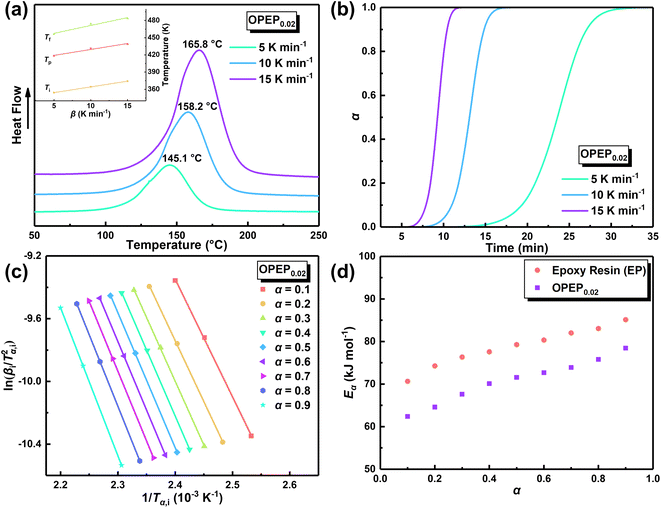
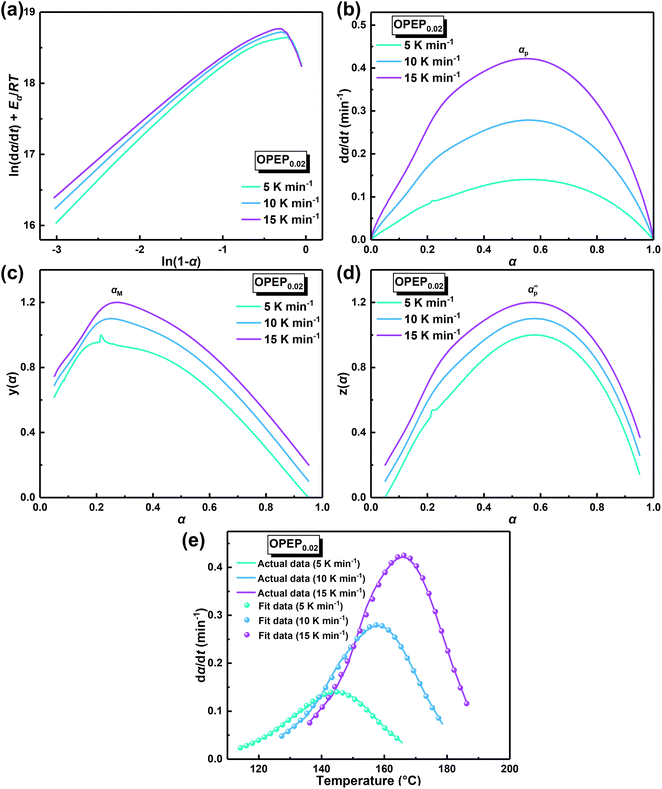
The physical properties of cured epoxy resin products are determined by their structural composition and the curing process. Therefore, to obtain high-performance resins, it is particularly crucial to conduct an in-depth study of curing reactivity. Non-isothermal Differential Scanning Calorimetry (DSC) method was used to study the curing behavior of the samples under different heating rates. The DSC curve at different heating rates of OPEP0.02 (Fig. 2(a)) is noticeably smooth, featuring a single and relatively symmetrical exothermic curing peak, which indicates excellent compatibility between OG-POSS and resin matrix. Furthermore, combining with the FT-IR spectra (Fig. S2c†) that show the disappearance of the stretching vibration peak of the epoxy group's skeleton in the OPEP system after complete curing, it can be concluded that the reactive OG-POSS can participate in the curing reactions of the resin matrix to form a homogeneous hybridization.
By integrating the exothermic peak and using the extrapolation method (β = 0 K min−1), non-isothermal curing reaction heat (ΔH), the initial curing temperature (Ti), peak temperature (Tp), and final temperature (Tf) can be determined, as shown in Table 1. It is apparent that the initial temperature (Ti) of the OPEP0.02 has decreased by about 20 °C compared to the pure system, suggesting that the epoxy groups of the reactive OG-POSS participate in the curing reaction, playing a certain promotive role in the low-temperature curing stage. However, the peak temperature (Tp) does not change significantly, indicating that the introduction of the modifier does not essentially affect the resin's curing process, exhibiting good processing performance. The trend of the conversion rate (α) over time at different heating rates is the same (Fig. 2(b)), with the growth rate initially slow, then increasing more quickly, and finally slowing down until the curing is complete. At the start, as the reaction proceeds and the temperature rises, the rate of increase in conversion rate accelerates. In the later stages of the reaction, the concentration of reactive groups decreases and the crosslinking density increases, causing the growth of the conversion rate to slow down.
As a matter of fact, the actual curing process of epoxy resins involves many elementary reactions (including mass transfer and diffusion processes), thereby exhibiting a complex curing mechanism, which means the activation energy (Eα) varies as the curing reaction proceeds.44,45 Therefore, in accordance with the International Confederation for Thermal Analysis and Calorimetry (ICTAC), the iso-conversional method (Kissinger–Akahira–Sunose (KAS) method, eqn (1)) generally is employed for studying the relationship between the activation energy and the conversion rate.46,47
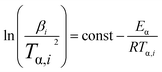 | (1) |
The nth-order kinetic model (eqn (2) and (3)) serves as the simplest form of phenomenological model and is frequently utilized for investigating the non-isothermal curing reaction kinetics of epoxy resins.47–49
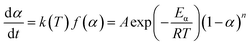 | (2) |
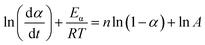 | (3) |
The term dα/dt represents the curing rate, min−1; k(T) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Eα/RT), where k(T) is the reaction rate constant, which is a function of temperature and follows the Arrhenius equation; f(α) = (1 − α)n is the mathematical equation for the nth-order kinetic model; n is the order of the reaction.
exp(−Eα/RT), where k(T) is the reaction rate constant, which is a function of temperature and follows the Arrhenius equation; f(α) = (1 − α)n is the mathematical equation for the nth-order kinetic model; n is the order of the reaction.
In order to ascertain the conformity of the selected model with objective reality, it is necessary to subject it to reasonable and essential validation. Therefore, in this study, the nth-order kinetic model was initially validated by eqn (3), which was derived by taking the logarithm of both sides of eqn (2). Specifically, by plotting the experimental data obtained from non-isothermal DSC for ln(dα/dt) + Eα/RT and ln(1 − α), it can be inferred that the nth-order kinetic model provides a satisfactory description of the curing behavior of the resin if there is a strong linear correlation between ln(dα/dt) + Eα/RT and ln(1 − α), as shown in Fig. 3(a). It is evident that there is no linearly correlation between ln(dα/dt) + Eα/RT and ln(1 − α), indicating that the actual curing reaction of epoxy resin, which is a multi-step process due to occurring phenomena such as phase separation, gelation, and vitrification with an exceptionally complex reaction mechanism, may not accurately be described by traditional model-fitting methods (e.g. nth-order kinetic model).45,49 Therefore, the non-model fitting method was employed to conduct a more in-depth investigation into the kinetics of the resin, which is known for its advantages of not being constrained by model selection and applicable to complex reaction systems, while enabling direct estimation of the kinetic parameter values and reducing the uncertainty associated with model selection and parameter estimation.47
In accordance with Málek's non-model fitting method,50–53 firstly, the Eα calculated previously (shown in Fig. 2(d) and Table 2) was used to construct the y(α) function (eqn (4)) and the z(α) function (eqn (5) and (6)), followed by normalizing the data through mathematical processing.
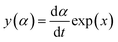 | (4) |
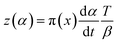 | (5) |
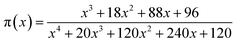 | (6) |
Within this context, x represents the reduced activation energy (x = Eα/RT); π(x) represents the temperature integral.51 Subsequently, the dα/dt − α, normalized y(α) − α, and normalized z(α) − α curves were plotted individually, enabling the determination of the conversion rates corresponding to the maximum dα/dt, the normalized y(α)max, and the normalized z(α)max, respectively represented as αp, αM, and αp∞, as shown in Fig. 3(b)–(d) and Table 2. Eventually, a suitable kinetic model was selected based on the relationship among αp, αM, and αp∞, and model parameters were determined. Therefore, as seen from Fig. 3(b), the dα/dt exhibits a trend of increasing and then decreasing with the α, reaching a maximum value at a certain intermediate moment (αp = 0.552). However, it is evident from the nth-order kinetic expression (eqn (2)) that the initial curing rate is supposed to be the highest, clearly contradicting the actual curing process, which further substantiates the evidence that the nth-order kinetic model is inadequate in describing the curing behavior of epoxy resins. Furthermore, at a certain intermediate moment, the curing rate dα/dt reaches its maximum value, which is consistent with the S-shaped curve observed in the α − t graph (Fig. 2(b)), indicating that the curing reaction of the OPEP0.02 system exhibits autocatalytic characteristics, with the intermediate products accelerating the progress of the reaction.54 Fig. 3(c) and (d) presents the curves of normalized y(α) − α and normalized z(α) − α, where the curves at heating rates of 10 K min−1 and 15 K min−1 are shifted upward by 0.1 and 0.2 units along the vertical axis, respectively, with the values of αM and αp∞ being 0.246 and 0.581. Hence, based on the non-model-fitting approach proposed by Málek, where it is evident that αM, αp, and αp∞ satisfy αM < αp < αp∞, and αp∞ ≠ 0.632, it can be considered that the curing reaction of the OPEP0.02 system conforms to the autocatalytic kinetics model (Šesták–Berggren, eqn (7) and (8)), denoted as SB (m, n).55
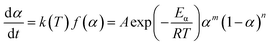 | (7) |
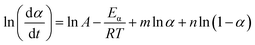 | (8) |
The mathematical equation for the autocatalytic kinetic model is f(α) = αm (1 − α)n, where m and n are the orders of the reaction. Subsequently, the SB model parameters are determined using the non-linear fitting method to obtain a complete curing reaction rate, as shown in Table 2. The correlation coefficient (R2) of the solved model parameters is all above 0.997, which indicates that the Málek method not only addresses the uncertainty of kinetic parameters during the solution process but also ensures the uniqueness of the rate equation in non-isothermal curing processes. Furthermore, the results of model validation (Fig. 3(e)) demonstrate excellent agreement between the model-fitted data and the actual data over a wide temperature range. Therefore, the SB model accurately describes and predicts the curing behavior of the OPEP system.
To delve deeper into the curing process, this study utilized Fourier Transform Infrared (FT-IR) and Differential Scanning Calorimetry (DSC) techniques to monitor the curing progression of the resin, thereby ensuring the complete curing of the hybrid resin. Fig. 4(a) illustrates the FT-IR spectral changes of the OPEP0.02 system at different stages of heating. Before curing, the absorption peak at 904 cm−1 corresponds to the stretching vibration of epoxy group's skeleton in E-51 and OG-POSS and the absorption peaks at 1859 ∼ 1788 cm−1 correspond to the stretching vibration of the carbonyl groups in the anhydride curing agent (MHHPA). As the curing reaction progresses, it becomes evident that the absorption peaks of the epoxy groups and the carbonyl groups gradually weaken and eventually disappear, while the absorption peak at around 1700 cm−1, attributed to the stretching vibration of ester groups, gradually strengthens. The curing reaction of the OPEP system follows a stepwise alternating polymerization mechanism, in which the tertiary amine accelerator (DMBA) acts as an anionic catalyst. Initially, it undergoes an attack on MHHPA, leading to the formation of zwitterionic pairs as active intermediates. Subsequently, the acyloxy anion within the structure of these pairs, serving as a nucleophilic center, further attacks the epoxy groups in E-51 or OG-POSS molecules, resulting in the formation of ester groups and a new alkoxide anion. This anion undergoes chain extension, branching, and crosslinking processes with the carbonyl groups in MHHPA and the epoxy groups in E-51 or OG-POSS in the aforementioned order, repeating alternately, thereby resulting in the formation of a three-dimensional crosslinked network structure, as shown in Fig. 4(c).56,57
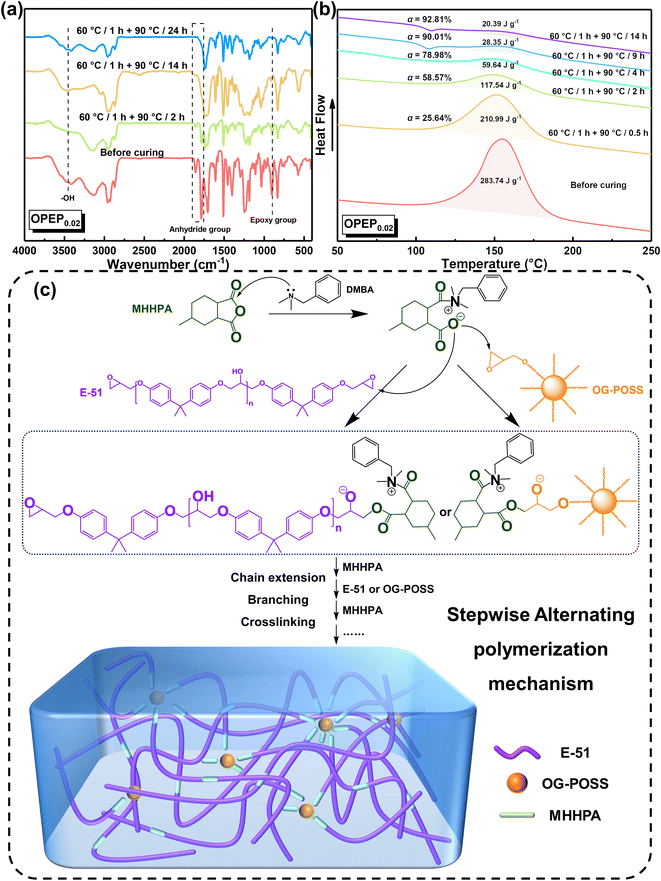 | ||
| Fig. 4 (a) The on-line FTIR spectra of OPEP0.02 sample; (b) the on-line DSC curve of OPEP0.02 sample; (c) curing mechanism diagram of OPEP. | ||
Fig. 4(b) displays the DSC curves of the OPEP0.02 system at different heating stages, and by integrating the peak areas, the corresponding reaction enthalpies (HS) for different heating stages can be obtained, where the total reaction enthalpy (HT) of the uncured OPEP0.02 system is 283.74 J g−1. It is evident that the heat released during the curing reaction gradually decreases as the reaction progresses. By calculating the degree of crosslinking (Cr) corresponding to different curing stages using the eqn (9), it can be observed that at 90 °C for 14 hours, the Cr reaches 92.81% and the FT-IR absorption peaks (Fig. 4(a)) of epoxy groups under this condition still can be observed. However, when cured at 90 °C for 24 hours, the absorption peak of the epoxy groups nearly disappears, indicating that this system has been completely cured. In summary, the curing process for the OPEP0.02 system is 60 °C for 1 hour followed by 90 °C for 24 hours, which meets the requirements for low-temperature curing. Herein, Cr represents the degree of crosslinking, %; HT is the total reaction heat before curing, J g−1; HS is the reaction heat of partial curing, J g−1.
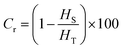 | (9) |
3.2. Mechanical properties of OPEP hybrid resin
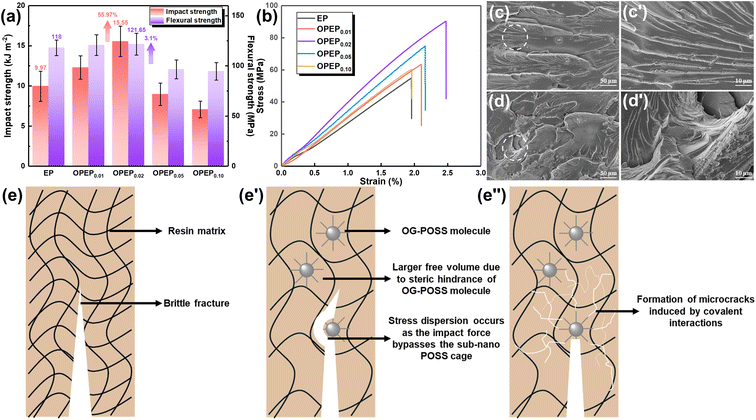
Epoxy resin, as a traditional thermosetting resin, has the shortcoming of poor toughness, and while typical toughening methods can achieve significant improvements in the toughness of epoxy resins, most of them may result in a decrease in thermal performance, hence developing the high toughness and high thermostability epoxy resins and holding significant application prospect. Fig. 5(a) and (b) displays the mechanical properties of EP and OPEP, indicating that as the content of OG-POSS increases, the mechanical properties first enhance and then decline. When 2 wt% of OG-POSS is incorporated, the impact strength, flexural strength, tensile strength, and elongation at break of the resins reach their maximum values of 15.55 kJ m−2, 121.65 MPa, 90.36 MPa, and 2.48% respectively, which are increases of 55.97%, 3.1%, 64.68%, and 26.51% compared to the pure resin. The internal structure of OG-POSS comprises a rigid inorganic silicon cage (with significant steric hindrance), while being externally coated by flexible chains. As a result, when the sample is subjected to an impact, the impact force can only circumvent the POSS cage-like structure. On one hand, this facilitates stress dispersion, preventing defect growth and crack formation. On the other hand, it increases the distance between molecular chains in the OPEP hybrid resin, leading to enhanced flexibility of the chain segments, thereby improving its toughness (Fig. 5(e′)). Simultaneously, octa-epoxy-terminated POSS, as a reactive organic–inorganic hybrid nanoparticle, can be covalently bonded with epoxy matrix to induce the formation of crazes, thereby achieving toughening (Fig. 5(e′′)). Moreover, the synergistic effect arising from the inherent elastic vibrations of the silicon cage, combined with the flexibility of the external chain segments, significantly contributes to the enhanced toughness of the material.39,40,58–61Furthermore, the uniform dispersion of rigid nano-fillers in the resin matrix is a prerequisite and key factor in achieving high toughness.41,43,58–60 Therefore, the dispersity of the modifier in the matrix was further studied through Atomic Force Microscopy (AFM), Energy Dispersive Spectroscopy (EDS), and X-ray Photoelectron Spectroscopy (XPS), as illustrated by the results in Fig. 6. Within a 2.0 × 2.0 μm area, the average surface roughness (Rq) of OPEP0.02 is 0.277 nm (Fig. 6(a)), and phase images (Fig. 6(b)) show no distinct second-phase interface, indicating that the modified resin surface is relatively smooth and that the added OG-POSS is uniformly mixed with the resin matrix. At the same time, the EDS spectra (Fig. 6(c)) clearly reveal that silicon atoms are uniformly dispersed within the resin matrix, which suggests that the covalent bonds formed by the epoxy groups in OG-POSS during the curing reaction enhance the interaction between the inorganic silicon cage and the organic matrix. This overcomes the issue of POSS's propensity to agglomerate at high loads. Moreover, in the wide spectrum XPS of OPEP0.02 (Fig. 6(d)), peaks at 532.6 eV, 284.6 eV, 152.6 eV, and 101.6 eV correspond to the characteristic peaks of O 1s, C 1s, Si 2s, and Si 2p, respectively. From the fine spectra of O 1s (Fig. 6(e)) and Si 2p (Fig. 6(f)), the characteristic peaks at 534.4 eV and 103.2 eV can be attributed to the Si–O–Si and O–Si–C bonds, further proving that the modifier containing the inorganic silicon cage participates in curing reaction and remains stable within the cured hybrid resin. This provides a solid process foundation for the modified resin to possess superior thermal and mechanical properties.
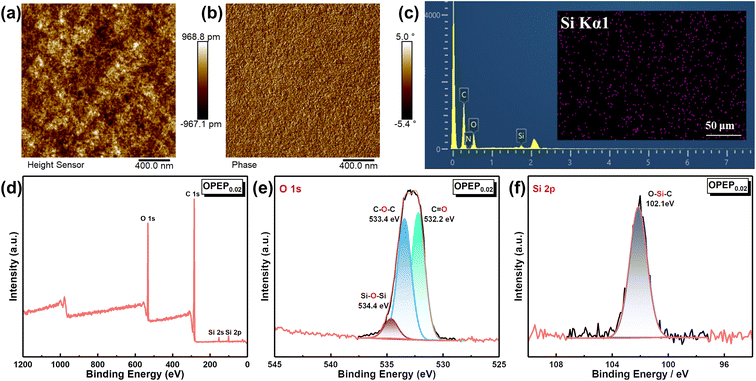 | ||
| Fig. 6 (a and b) The surface morphology and phase diagrams of OPEP0.02 sample; (c) the EDS mapping of OPEP0.02 sample; (d–f) the XPS spectrum of OPEP0.02 sample. | ||
However, the addition of an excessive amount of OG-POSS can reduce the mechanical properties of the resin, leading to diminished toughness. The primary reason for this decline is that a high loading of OG-POSS can degrade its dispersion within the resin matrix, making it prone to clustering and forming defects. This leads to stress concentration, which in turn diminishes the toughness of the material. Fig. 5(c) and (d) presents an analysis of the impact fracture morphologies of both EP and OPEP0.02 hybrid resins. It is evident that the pure resin displays a typical brittle fracture characterized by smooth fracture surfaces, sharp fracture edges, and a singular crack direction. In contrast, with the introduction of OG-POSS, there is an increase in the roughness of the impact fracture surface, with numerous toughening whirls and stress-whitening areas becoming apparent. These regions allow the material to absorb a significant amount of energy during the failure process, enhancing its impact strength. Moreover, POSS, as a type of nanomaterial, can induce micro-cracks during the failure process. Serving as initiation sites, these micro-cracks can absorb a considerable amount of fracture energy, thereby elevating the toughness of the material.60
3.3. Comprehensive thermal properties of OPEP hybrid resin
The thermal stability of various epoxy systems was investigated using Thermal Gravimetric Analyzer (TGA), with the results shown in Fig. 7(a) and (b). Clearly, the incorporation of an appropriate amount of OG-POSS can enhance the initial decomposition temperature (Td5) of the resin to a certain extent, bolstering its thermal stability. Specifically, the Td5 of OPEP0.02 is 313.2 °C, which is an increase of 13 °C compared to the pure resin. Besides, the heat index temperature (Ts) of OPEP0.02 is 176.7 °C, slightly higher than EP (as shown in Table 3). Essentially, OG-POSS contains an inorganic silicon cage skeleton structure, as well as bonds with high bond energy, namely Si–O and Si–C bonds, which are crucial factors to ensure the thermal stability of the material.2,62,63 However, if the amount of OG-POSS added is too high (as in OPEP0.10), clustering of POSS can occur, making it challenging to chemically bond with the organic resin. At the same time, the introduction of a large number of inorganic components can degrade the thermal stability of the modified resin.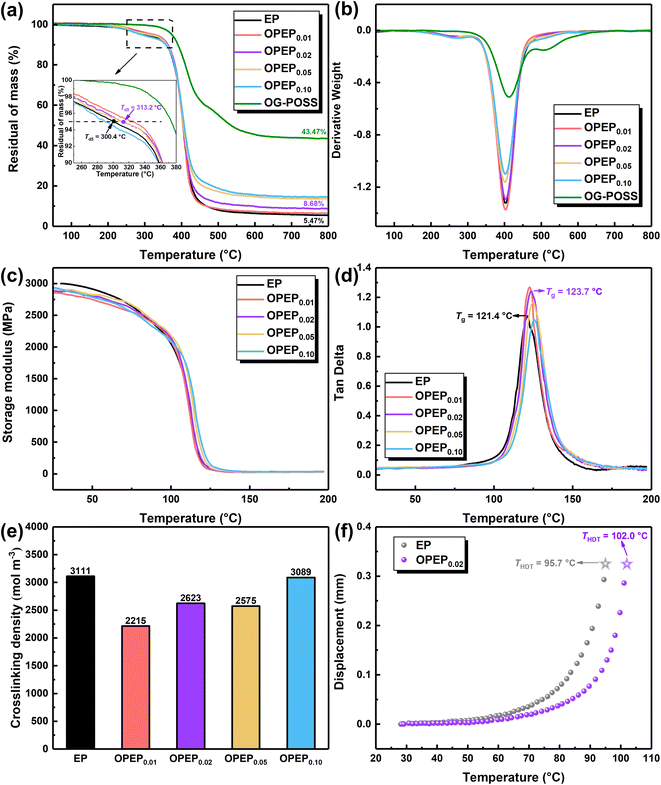 | ||
| Fig. 7 TGA (a and b), DMA (c and d), crosslinking density (e) and heat distortion temperature (HDT) (f) of EP and OPEP. | ||
| Sample | n | Td5a [°C] | Td30a [°C] | Tsa [°C] | Y800a [%] | Tgb [°C] | THDTc [°C] | Impact strength [kJ m−2] | Elongation at break [%] | ρb [mol m−3] |
|---|---|---|---|---|---|---|---|---|---|---|
| a Obtained from TGA, Ts = 0.49 × [Td5 + 0.6 × (Td30 − Td5)].b Obtained from DMA, ρ = E′/[2(1 + γ)RT], where γ is Poisson's ratio assumed as 0.5 for incompressible networks; R is gas constant; T is related to Tg + 40 °C and E′ is the storage modulus of materials at Tg + 40 °C.c Obtained from HDT-VICAT. | ||||||||||
| EP | — | 300.4 | 390.5 | 173.6 | 5.47 | 121.4 | 95.7 | 9.97 ± 1.87 | 1.96 ± 0.2 | 3111 |
| OPEPn | 0.01 | 326.1 | 390.5 | 178.8 | 6.50 | 122.7 | — | 12.30 ± 1.46 | 2.11 ± 0.3 | 2215 |
| 0.02 | 313.2 | 392.1 | 176.7 | 8.68 | 123.7 | 102.0 | 15.55 ± 1.90 | 2.48 ± 0.2 | 2623 | |
| 0.05 | 310.5 | 391.2 | 175.9 | 13.73 | 125.0 | — | 8.96 ± 1.40 | 2.16 ± 0.4 | 2575 | |
| 0.10 | 289.4 | 392.2 | 172.0 | 14.55 | 125.7 | — | 7.07 ± 1.05 | 1.96 ± 0.1 | 3089 | |
To study the overall performance of modified resin and the interaction between resin matrix and nano-fillers, the dynamic thermomechanical properties of the materials were analysed through Dynamic Mechanical Analysis (DMA). The results are shown in Fig. 7(c)–(e). Fig. 7(c) and (e) display the storage modulus and crosslink density of different epoxy systems. Compared to the pure system, the storage modulus and crosslink density of the OPEP system (at ambient temperature in the glassy state) both decrease. OG-POSS has an intrinsic cage-like hollow structure and externally longer flexible segments (γ-Glycidoxypropyl). When it is added to the resin, the distance between molecular chains increases, leading to an increase in free volume. Consequently, the resin's storage modulus and crosslink density decrease. Furthermore, as the concentration of OG-POSS is increased, the number of reaction crosslinking points (epoxy group) also increases, resulting in an increase in crosslink density, which leads to a slight rise in storage modulus.64 Fig. 7(d) shows the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curve of different epoxy systems. The peak magnitude reflects the internal frictional resistance overcome by the material under alternating stress during deformation. In general, the temperature corresponding to the peak indicates the glass transition temperature (Tg) of the polymer system. Evidently, a single tan
δ curve of different epoxy systems. The peak magnitude reflects the internal frictional resistance overcome by the material under alternating stress during deformation. In general, the temperature corresponding to the peak indicates the glass transition temperature (Tg) of the polymer system. Evidently, a single tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak suggests that OG-POSS nanoparticles and the resin matrix have good compatibility and no phase separation occurs. As the content of OG-POSS increases, the crosslink density also increases (leading to more rigid structures), making chain movement more difficult. This results in an increase in the glass transition temperature, where Tg (OPEP0.02) = 123.7 °C, slightly higher than that of the pure resin.
δ peak suggests that OG-POSS nanoparticles and the resin matrix have good compatibility and no phase separation occurs. As the content of OG-POSS increases, the crosslink density also increases (leading to more rigid structures), making chain movement more difficult. This results in an increase in the glass transition temperature, where Tg (OPEP0.02) = 123.7 °C, slightly higher than that of the pure resin.
Additionally, the heat distortion temperature (THDT, reflecting the material's resistance to deformation at a certain temperature; a higher THDT indicates that the material has better deformation resistance at high temperatures, implying better thermal stability) of the EP and OPEP0.02 systems was studied, as shown in Fig. 7(f). The THDT of the OPEP0.02 system is 102 °C, which is an increase of 6.8 °C compared to the pure resin. In summary, the introduction of reactive epoxy-group POSS significantly enhances the mechanical properties without compromising its heat resistance, which balances the contradiction between strengthening, toughening, and thermal stability in resin-based composite materials.
4. Conclusions
In this study, the reactive octa-epoxy-terminated polyhedral oligomeric silsesquioxane (OG-POSS), as a toughening modifier, was adopted, leading to the creation of an innovative hybrid epoxy resin that can be cured at low temperatures and demonstrates exceptional toughness and thermal stability. Due to the introduction of epoxy groups, OG-POSS demonstrates remarkable compatibility with the resin matrix, and its addition marginally diminishes the Eα of the curing reaction, simultaneously promoting the curing of the epoxy resin. In addition, the curing reaction rate of the OPEP resin complies with the Šesták–Berggren autocatalytic kinetics model. With 2 wt% addition of OG-POSS, the impact strength, flexural strength, tensile strength, and elongation at break of the modified system reach a maximum of 15.55 kJ m−2, 121.65 MPa, 90.36 MPa, and 2.48%, showing an increase of 55.97%, 3.1%, 64.68%, and 26.51% compared to those of the pure resin, respectively. Notably, Td5, Tg, and THDT are 313.2 °C, 123.7 °C, and 102 °C, with an increase of 13 °C, 2.3 °C, and 6.8 °C compared to the pure resin, respectively. In conclusion, this research paves the way for the development of a novel epoxy resin that cures at low temperatures while maintaining high toughness and thermal stability. Utilizing reactive organic–inorganic nano-hybrid materials (POSS), we have synergistically optimized the toughness and thermal stability of the resin, thereby balancing the inherent trade-off between enhanced toughness and thermal stability. The resulting hybrid resin exhibits superior overall performance, signifying its significant potential and applicability across various industries.Author contributions
Ruiyan Han: conceptualization, formal analysis, writing – original draft. Xiaoyan Ma: conceptualization, writing – review & editing. Lifeng Cai: investigation. Zongwu Zhang: investigation. Yiliang Fang: investigation. Jian Wang: investigation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the support from Key R & D Program and Key Industry Chain Project of Shaanxi Province, PR China (2019ZDLGY06-02-01), the Special Project for the Transformation of Achievements in Universities of Xianyang City (L2023-ZDKJ-QCY-SXGG-GY-002).References
- H. Dong, Y. Qiao, S. Peng, Y. Li, Y. Zhen, W. Tan, Q. Cheng and Y. Wang, Prog. Org. Coat., 2023, 183, 107817 CrossRef CAS.
- A. Abbasi, A. Salimi, H. Bouhendi and M. Karimi, Int. J. Adhes. Adhes., 2023, 124, 103368 CrossRef CAS.
- E. R. Ghomi, S. N. Khorasani, M. S. Koochaki, M. Dinari, S. Ataei, M. H. Enayati, O. Das and R. E. Neisiany, J. Adv. Res., 2023, 43, 137–146 CrossRef PubMed.
- P. P. Vijayan, K. Formela, M. R. Saeb, P. G. Chithra and S. Thomas, J. Coat. Technol. Res., 2022, 19, 269–284 CrossRef.
- N. Farzanehfar, A. Taheri, F. Rafiemanzelat and O. M. Jazani, Chem. Eng. J., 2023, 471, 144428 CrossRef CAS.
- Z. Zhou, S. Pourhashem, Z. Wang, J. Duan, R. Zhang and B. Hou, Chem. Eng. J., 2022, 439, 135765 CrossRef CAS.
- Y. Liu, Z. Du, C. Zhang, C. Li and H. Li, J. Appl. Polym. Sci., 2007, 103, 2041–2048 CrossRef CAS.
- T. Yang, C. Zhang, J. Zhang and J. Cheng, Thermochim. Acta, 2014, 577, 11–16 CrossRef CAS.
- T. Yang, C. Zhang, X. Hou, J. Cheng and J. Zhang, High Perform. Polym., 2016, 28, 854–860 CrossRef CAS.
- J. Zhang, Q. Guo and B. Fox, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 417–424 CrossRef CAS.
- C. Bao, Y. Wang, R. T. Mushtaq, K. Zhang, X. Li and X. Chen, Polym. Test., 2022, 116, 107783 CrossRef CAS.
- A. Gu, Polym. Adv. Technol., 2005, 16, 563–566 CrossRef CAS.
- H. Li, G. Chen, H. Su, D. Li, L. Sun and J. Yang, Eur. Polym. J., 2019, 112, 792–798 CrossRef CAS.
- K. H. Lee and D. G. Lee, Compos. Struct., 2008, 86, 37–44 CrossRef.
- J. Cheng, J. Li and W. Yang, J. Appl. Polym. Sci., 2009, 114, 1976–1983 CrossRef CAS.
- J. S. Jayan, A. Saritha and K. Joseph, Polym. Compos., 2018, 39, E1959–E1986 CrossRef CAS.
- S. Xu, X. Song and Y. Cai, Materials, 2016, 9, 640 CrossRef PubMed.
- G. Xu, L. Tan, K. Liu, R. Yang, Y. Nie, X. Fang and G. Chen, Polym. Eng. Sci., 2023, 63, 1772–1780 CrossRef CAS.
- X. Mi, N. Liang, H. Xu, J. Wu, Y. Jiang, B. Nie and D. Zhang, Prog. Mater. Sci., 2022, 130, 100977 CrossRef CAS.
- Q. Yu, Y. Liang, J. Cheng, S. Chen, A. Zhang, M. Miao and D. Zhang, ACS Omega, 2017, 2, 1350–1359 CrossRef CAS PubMed.
- K. Yang, Y. Long, J. Luo, S. Zhang, W. Feng, W. Tian and H. Yan, Chem. Eng. J., 2024, 481, 148662 CrossRef CAS.
- S. Chen, Z. Xu and D. Zhang, Chem. Eng. J., 2018, 343, 283–302 CrossRef CAS.
- F. Wei, J. Zhang, C. Wu, M. Luo, B. Ye, H. Zhang, J. Wang, M. Miao, T. Li and D. Zhang, Macromolecules, 2023, 56, 5290–5305 CrossRef CAS.
- J. Zhang, X. Mi, S. Chen, Z. Xu, D. Zhang, M. Miao and J. Wang, Chem. Eng. J., 2020, 381, 122719 CrossRef CAS.
- L. Zhong, Y. Hao, J. Zhang, F. Wei, T. Li, M. Miao and D. Zhang, Macromolecules, 2022, 55, 595–607 CrossRef CAS.
- C. Chen, R. S. Justice, D. W. Schaefer and J. W. Baur, Polymer, 2008, 49, 3805–3815 CrossRef CAS.
- M. Y. Khalid, A. Kamal, A. Otabil, O. Mamoun and K. Liao, Chem. Eng. J. Adv., 2023, 16, 100537 CrossRef CAS.
- Y. Zhang, K. Yang, R. Liu, J. Yao and H. Yan, Chem. Eng. J., 2023, 460, 141773 CrossRef CAS.
- Z. Chen, M. Zhang, P. Ren, Z. Lan, Z. Guo, H. Yan, Y. Jin and F. Ren, Chem. Eng. J., 2023, 466, 143086 CrossRef CAS.
- X. Bian, R. Tuo, W. Yang, Y. Zhang, Q. Xie, J. Zha, J. Lin and S. He, Polymers, 2019, 11, 1548 CrossRef CAS PubMed.
- M. M. Y. Zaghloul, M. M. Y. Zaghloul and M. Fuseini, Polym. Adv. Technol., 2023, 34, 3438–3472 CrossRef CAS.
- M. Zamanian, M. Mortezaei, B. Salehnia and J. E. Jam, Eng. Fract. Mech., 2013, 97, 193–206 CrossRef.
- J. Chen, A. J. Kinloch, S. Sprenger and A. C. Taylor, Polymer, 2013, 54, 4276–4289 CrossRef CAS.
- M. H. Kothmann, R. Zeiler, A. R. de Anda, A. Brüeckner and V. Altstädt, Polymer, 2015, 60, 157–163 CrossRef CAS.
- X. Zhao, Y. Li, W. Chen, S. Li, Y. Zhao and S. Du, Compos. Sci. Technol., 2019, 171, 180–189 CrossRef CAS.
- K. Mishra, G. Pandey and R. P. Singh, Polym. Test., 2017, 62, 210–218 CrossRef CAS.
- Z. Niu, Y. Xin, L. Wang, S. Shen, X. Ma, B. Chen, C. Wang, F. Chen, C. Zhang and X. Hou, J. Mater. Sci. Technol., 2023, 141, 199–208 CrossRef CAS.
- Y. Xin, Z. Niu, S. Shen, X. Ma, F. Chen, L. Wang, B. Chen, C. Wang, C. Zhang and X. Hou, Ceram. Int., 2023, 49, 4919–4928 CrossRef CAS.
- Z. Zhang, Y. Zhou, Y. Yang, X. Ma, L. Xuan and X. Wu, Compos. Sci. Technol., 2023, 231, 109825 CrossRef CAS.
- Y. Zhou, Z. Zhang, P. Wang and X. Ma, Composites, Part A, 2022, 162, 107136 CrossRef CAS.
- J. Yang, Y. Zhang, M. Hao, J. Zhi and X. Qian, Polymer, 2023, 268, 125719 CrossRef CAS.
- R. Yıldırım, M. S. Ullah, H. Koçoğlu, M. Ün, N. Y. Çakır, G. Demir, D. Çetin, G. Urtekin, G. Özkoç, O. Mert and M. Kodal, ACS Omega, 2023, 8, 47034–47050 CrossRef PubMed.
- K. Mishra and R. P. Singh, Polym. Compos., 2018, 39, E2445–E2453 CAS.
- J. S. Martin, J. M. Laza, M. L. Morrás, M. Rodríguez and L. M. León, Polymer, 2000, 41, 4203–4211 CrossRef CAS.
- C.-S. Chern and G. W. Poehlein, Polym. Eng. Sci., 2010, 27, 788–795 CrossRef.
- H. E. Kissinger, J. Res. Natl. Bur. Stand., 1956, 57, 217–221 CrossRef CAS.
- S. Vyazovkin, A. K. Burnham, J. M. Criado, L. A. Pérez-Maqueda, C. Popescu and N. Sbirrazzuoli, Thermochim. Acta, 2011, 520, 1–19 CrossRef CAS.
- J. Macan, I. Brnardić, S. Orlić, H. Ivanković and M. Ivanković, Polym. Degrad. Stab., 2006, 91, 122–127 CrossRef CAS.
- J. Sun and J. Wang, J. Therm. Anal. Calorim., 2014, 118, 571–578 CrossRef CAS.
- J. Málek, Thermochim. Acta, 1992, 200, 257–269 CrossRef.
- G. Hou, J. Gao, C. Tian and X. Wu, Mater. Chem. Phys., 2014, 148, 236–244 CrossRef CAS.
- N. Sbirrazzuoli, Y. Girault and L. Elégant, Thermochim. Acta, 1995, 249, 179–187 CrossRef CAS.
- X. Tan, L. Zeng, Q. Liao, G. Zhang, X. Wu, J. Wang and R. Xu, Thermochim. Acta, 2017, 657, 197–202 CrossRef CAS.
- J. Y. Lee, M. J. Shim and S. W. Kim, Thermochim. Acta, 2001, 371, 45–51 CrossRef CAS.
- X. Huang and B. Patham, J. Appl. Polym. Sci., 2013, 127, 1959–1966 CrossRef CAS.
- O. Vryonis, S. Riarh, T. Andritsch and A. S. Vaughan, Polymer, 2021, 213, 123312 CrossRef CAS.
- Y. Han, Z. Wang, S. Zhao and J. Wang, Measurement, 2019, 145, 600–610 CrossRef.
- W. Xie, S. Guo, Y. Liu, R. Chen and Q. Wang, Composites, Part B, 2020, 203, 108437 CrossRef CAS.
- Z. Chen, M. Gu, F. Wang, C. Gao, P. Liu, Y. Ding, S. Zhang and M. Yang, Mater. Chem. Phys., 2019, 225, 181–186 CrossRef CAS.
- C. Xin, X. Ma, F. Chen, C. Song and X. Qu, J. Appl. Polym. Sci., 2013, 130, 810–819 CrossRef CAS.
- Z. Zhang, Y. Zhou, L. Cai, L. Xuan, X. Wu and X. Ma, Chem. Eng. J., 2022, 439, 135740 CrossRef CAS.
- H. Dodiuk, S. Kenig, I. Blinsky, A. Dotan and A. Buchman, Int. J. Adhes. Adhes., 2005, 25, 211–218 CrossRef CAS.
- E. Ayandele, B. Sarkar and P. Alexandridis, Nanomaterials, 2012, 2, 445–475 CrossRef CAS PubMed.
- Q. Lian, H. Chen, Y. Luo, Y. Li, J. Cheng and Y. Liu, Polymer, 2022, 247, 124754 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra08390j |
| This journal is © The Royal Society of Chemistry 2024 |