Diethylenetriamine-functionalized reduced graphene oxide having more amino groups for methylene blue removal

Abstract

To obtain a high-performance amino-functionalized graphene, a new aminated graphene was prepared through a substitution reaction between chlorine-functionalized reduced graphene oxide and diethylenetriamine. The product exhibits high nitrogen content uniformly distributed in its sheets, with diethylenetriamine covalently attached to these sheets. The C–N bond in the product was certified by the Fourier transform infrared spectrum, which implies the successful attachment of diethylenetriamine to the graphene sheets. The average interlayer spacing is 0.42 nm. Diethylenetriamine features many more amino groups that act as ligands and spacers during adsorption and layer stacking processes. Compared with the adsorption capacities of reduced graphene oxide (77.1 mg g⁻¹) and activated carbon (46.7 mg g⁻¹), the product exhibits higher adsorption capacity (291.4 mg g⁻¹). The adsorption process fits the quasi-first-order model and Langmuir model. Physical adsorption plays a primary role in the adsorption process. The amino group of the product easily reacts with other chemicals, making it a useful intermediate for other graphene materials.

---

1 Introduction

Aminated graphene, including aminated graphene oxide (GO) and aminated reduced GO (RGO), are important graphene derivatives.^1,2 The amino group possesses a certain degree of alkalinity and high reactivity because of its lone pair of electrons. Compared with graphene, GO, and RGO, aminated graphene possesses excellent properties that invoke considerable attention.^3–5

Some composites contained amino groups; although the amine was not directly attached to the graphene sheet, these composites still exhibited high performance. For example, the Chen group prepared polyaniline/nano-Fe₃O₄/graphene composites, which displayed a broad band of electromagnetic wave absorption.⁶

The amino group was directly attached to the graphene sheet through the commonly used reaction between the carboxylic acid of GO and the amino group of other compounds. The products or composites possessed excellent properties. These compounds might include 1-aminopropyl-3-methylimidazolium chloride,⁷ 1,4-phenylenediamine or 2,3,5,6-tetramethyl-1,4-phenylenediamine,^8,9 amino-modified MXene (3-trimethoxysilylpropan-1-amine modified MXene),¹⁰ ethylenediamine,^11–13 4,4′-diaminodiphenylmethane,¹⁴ and amino acids (e.g., alanine, tyrosine, and cysteine).¹⁵

The epoxide of GO can also react with an amino group that is also attached directly or indirectly to the graphene sheet. These amino groups might be present in NH₂-boron dipyrromethenes¹⁶ and amino acids.¹⁷ Although Jana et al. did not mention the substitution reaction of epoxide, it probably reacted with the amino group of ethylenediamine during the synthetic process.¹³

In fact, the epoxide and carboxylic acid of GO can simultaneously react with the amino group of various compounds, such as polyethylenimine,¹⁸ diethylenetriamine,¹⁹ butylamine,²⁰ and polyaniline,²¹ under different conditions.

Although some authors did not explain the type of modification reaction, composites or materials still exhibited excellent performance. Readers might speculate about one or two of the previously mentioned reactions. Additionally, the carboxylic acid and amino group can easily form hydrogen bond or electrostatic interaction. The graphene sheet and modifier can form π–π stacking or π–π conjugated system. These interactions are also useful procedures for amine-modified graphene. For instance, the modifier could be polyaniline^22–25 or pyridine.²⁶

Other procedures were adopted to attach amines to the graphene sheet. Merkoçi et al. prepared cysteamine-modified graphene through the substitution reaction of F on fluorographene with amino groups on cysteamine. The product contained free thiol groups, which made cysteamine-modified graphene-carbon electrode with good sensitivity to Cd²⁺.²⁷ Amino-functionalized RGO was also acquired using an amino–silane coupling agent (3-trimethoxysilylpropan-1-amine) and GO.

Although some methods have been used for the preparation of aminated graphene, a more feasible and practical method is still needed urgently. The bond between C and Cl in chlorine-functionalized RGO (ClRGO)²⁸ can react with ethylenediamine,²⁹ mercaptoacetic acid,³⁰ and glycine.³¹ To prepare a high-performance aminated graphene, diethylenetriamine-functionalized RGO (TARGO) was prepared through the reaction between diethylenetriamine and ClRGO. TARGO contains more amino groups that act as ligands and spacers during the adsorption and layer stacking processes. Methylene blue (MB) is a commonly used organic dye that is exceedingly difficult to decompose in waste streams under visible-light irradiation. However, it can be decomposed under some high-performance catalysts.^32,33 Herein, it is selected as a model dye for the adsorption test.

2 Experiment

2.1 Materials

GO (1 mg mL⁻¹) and diethylenetriamine were donated by the Ctron Advanced Material Co., Ltd, (Xinxiang, China). Other raw materials of chemical grade were provided by the Henan Rayhope Graphene Application Technology Research Institute Co., Ltd, (Xinxiang, China).

2.2 Preparation of TARGO

The preparation of ClRGO has been reported in previous literature.²⁸ ClRGO (0.51 g) is dispersed in furanidine (48 mL) using ultrasound for 3 h. Diethylenetriamine (3 mL) is added to the suspension under reflux conditions. The suspension is heated and stirred for 24 h. The TARGO is filtered and cleaned seven times with distilled water and furanidine. A windless drying box is used for drying process (41 °C, 49 h), thereby yielding a black powder product (0.42 g).

2.3 Batch adsorption

Each adsorption test was conducted in a constant temperature cradle set at a specific temperature. The concentration of each solution was measured using a UV/vis spectrometer (663 nm), and the solutions were examined at desired time.

2.4 Sample tests

Microscopic morphology was obtained using field emission scanning electron microscopy (FEI-QUANTAFEG 250) and high-resolution transmission electron microscopy (HRTEM, FEI Talos F200X). Functional groups were characterized by Fourier transform infrared (FT-IR) spectra using FTS-40. The chemical structure was also analyzed by Raman spectroscopy (Renishaw inVia) with an exciting laser wavelength of 532 nm. The crystallinity of TARGO was characterized by X-ray diffraction analysis (XRD) using a Bruker D8 Advance instrument with Cu Kα (λ = 1.5406 Å). The elemental composition of TARGO was acquired through X-ray photoelectron spectroscopy (XPS) using the K-Alpha X-ray photoelectron spectrometer system (hν = 1486.6 eV). The Emmett–Brunauer–Teller (BET) and Barrett–Joyner–Halenda methods were used with an ASAP 2020 V3.01H (Micromeritics, USA) to measure the pore volume and specific surface area.

3 Results and discussion

3.1 Characteristics of TARGO

SEM (Fig. 1a) and HRTEM (Fig. 1b) clearly depict the micromorphology of TARGO, where TARGO sheets curl up and form folds, suggesting that the product might be a few-layer graphene. To reduce surface energy, single-layer and few-layer graphene easily form folds. In addition, the attachment of diethylenetriamine to the sheet is favorable to the formation of folds. The atoms in the sheet connected to diethylenetriamine are sp³ carbons, which increase folds or twists. Diethylenetriamine, possessing more lone pair electrons, repels the electrons in the TARGO sheet, thereby further increasing folds. The presence of diethylenetriamine in TARGO improves its adsorption performance.

Fig. 1 SEM image (a) and HRTEM image (b) of TARGO, HAADF-STEM images, and elemental mappings of TARGO (c–f).

Fig. 1c–f show the corresponding elemental mappings of TARGO. The nitrogen content is approximately 8.12 at%, indicating a high nitrogen content. The nitrogen distribution appears uniform in the elemental mappings in Fig. 1d, implying that diethylenetriamine reacts smoothly with ClRGO. If diethylenetriamine does not react, then it might dissolve in solvent. Diethylenetriamine is hydrophilic, while the graphene sheet is lipophilic. The residual diethylenetriamine on the sheet may accumulate into droplets, and they can be removed by washing.

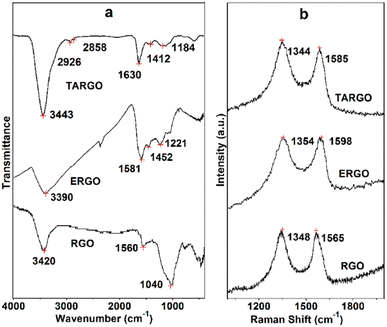
The FT-IR spectrum of TARGO is exhibited in Fig. 2a. For comparison, related spectra of ethylenediamine-functionalized RGO (ERGO) and RGO are also included in Fig. 2a. The spectra of TARGO and ERGO exhibit similarities. The band at 3443 cm^−l represents the N–H stretch. The bands at 2926 cm^−l and 2858 cm^−l correspond to the C–H stretch of –CH₂–. The band at 1630 cm^−l indicates the N–H bond vibration. The bands at 1412 cm^−l and 1184 cm^−l represent the C–N stretch. The prominent N–H band and weak C–H band confirm the displacement reaction between diethylenetriamine and ClRGO.

Fig. 2 FT-IR (a) and Raman (b) spectra of TARGO.

The Raman spectrum of TARGO is exhibited in Fig. 2b. The G band at 1585 cm^−l corresponds to the sp² C of the graphitic phase. The D band at 1344 cm^−l is associated with the sp³ C of crystal imperfections and disorders in TARGO. Notably, the D band is stronger than the G band, and the intensity ratio of D/G is approximately 1.5. In addition, diethylenetriamine was grafted onto the TARGO sheet, and the amount of sp³ C was augmented. The sheet stacking of TARGO might be more disordered, thereby reducing the crystallinity of TARGO.

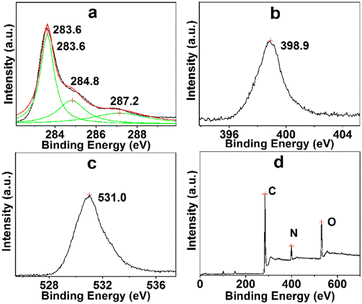
The essential component and electronic state of the atoms in TARGO were analyzed using XPS, as shown in Fig. 3. The binding energies at 283.6, 284.8, and 287.2 eV connect to the sp² carbon, C–N and C–O, and carboxy group, respectively (Fig. 3a). The binding energy at 398.9 eV corresponds to N (Fig. 3b). The binding energy at 531.0 eV connects to O (Fig. 3c). The TARGO contains C (75.52 at%), N (9.40 at%), and O (15.08 at%) elements, as displayed in the survey spectrum in Fig. 3d. The essential component of TARGO also proves that diethylenetriamine has been successfully attached on the TARGO sheet through displacement reaction between ClRGO and diethylenetriamine.

Fig. 3 Binding energies of C (a), N (b), O (c), and survey spectrum of TARGO (d).

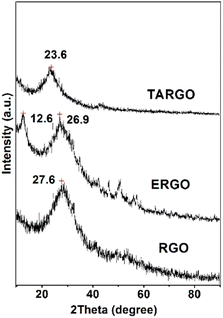
The diffraction analysis of TARGO is exhibited in Fig. 4. Compared with ERGO and RGO, the 2-theta angle of TARGO is approximately at 23.6°. The interlayer spacing of TARGO (0.42 nm) is wider than that of ERGO (0.38 nm), which may possibly improve the adsorption performance of TARGO. Diethylenetriamine attached to a sheet acts as pillaring agent during the sheet stacking process. The close proximity of sheets in a highly compact manner is difficult to achieve, and then the interlayer spacing of TARGO is enlarged. Adsorbate might easily come into the inner of adsorbent TARGO, and its adsorption capacity might be enhanced.

Fig. 4 XRD spectrum of TARGO and those of relevant materials (e.g., ERGO and RGO).

The TARGO was characterized using nitrogen sorption to determine the specific surface area and pore volume. The nitrogen adsorption–desorption isotherm exhibits a characteristic IUPAC type-IV curve, indicating the presence of numerous pores in the fabricated material (Fig. 5a). The surface areas of the TARGO and RGO are 293.2 m² g⁻¹ and 319.9 m² g⁻¹, respectively. These values were obtained by fitting the isotherm to the BET model. The pore volumes of TARGO and RGO are 0.443 cm³ g⁻¹ and 0.278 cm³ g⁻¹, respectively. Porosities of TARGO and RGO are further confirmed by porosity distribution analysis based on the original DFT (Fig. 5b). The incremental pore volume of TARGO is higher than that of RGO within the range of 14–100 nm. Although TARGO exhibits a smaller surface area than RGO, its improved pore sizes are favorable for enhancing MB adsorption.

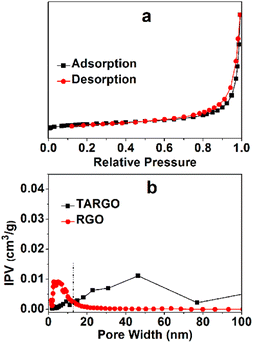Fig. 5 Typical nitrogen adsorption and desorption of TARGO (a) and pore size distribution curves of TARGO and RGO (b), IPV = incremental pore volume.

3.2 Adsorption

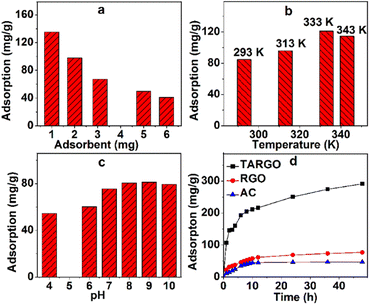
Extrinsic factors have evident effects on the adsorption performance of TARGO, especially the adsorbent dosage, temperature, and acidity–alkalinity of solution.

The amount of adsorbent that affects adsorption performance is displayed in Fig. 6a. The amount of TARGO is 1.0, 2.0, 3.1, 5.0, and 6.0 mg in a 100 mL MB solution (10 mg L⁻¹). The total amount of adsorbate MB remains constant. As the dosage of adsorbent increases, adsorption velocity is expedited, while adsorption capacity decreases. For convenience, 2.0 mg of adsorbent will be adopted in the next experiment.

Fig. 6 Adsorbent dosage (a) (MB concentration = 12 mg L⁻¹, 200 mL, adsorption time = 5 h, pH = 7, room temperature), temperature (b) (MB concentration = 10 mg L⁻¹, 200 mL, adsorption time = 2 h, pH = 7), and pH value (c) (MB concentration = 10 mg L⁻¹, 200 mL, adsorption time = 4 h, room temperature) affect the adsorption process and adsorption capacities of TARGO, RGO, and AC (d) (MB concentration = 8 mg L⁻¹, 100 mL, pH = 8, room temperature).

Adsorption temperature has a distinct influence on adsorption performance. The temperature parameters of the experiment were set as 293 K, 313 K, 333 K, and 343 K, and the corresponding adsorptions at different temperatures are displayed in Fig. 6b. Adsorbate diffusion is mainly controlled by temperature. As temperature increases, the diffusion of adsorbate also intensifies, making it easier for the adsorbate to reach the surface and macropores of TARGO. From 293 K to 333 K, adsorption increases with temperature. When temperature exceeds a certain value, adsorbate diffusion is exacerbated, adsorbate easily leaves from TARGO, and the desorption process of MB intensifies. At 343 K, adsorption capacity is lower than that at 333 K. For the next experiment, temperatures of 293 K, 313 K, and 333 K will be used.

Fig. 6c shows the adsorption values at different pH values. Adsorption increases from pH = 4 to 9. In acidic conditions, hydrogen ions bind to the amino groups, forming the ammonium radicals. Ammonium radical and MB⁺ are positive and repel each other. At neutral and alkaline conditions, MB⁺ can combine lone pair electrons of amino group instead hydrogen ions. Adsorption slightly decreases from pH = 9 to 10. In strong alkaline conditions, MB can form dimers and trimmers. The pH = 8–9 is adopted in the experiment.

Fig. 6d shows the adsorption of RGO, active carbon (AC), and TARGO at room temperature. The adsorption capacity of AC is approximately 46.7 mg g⁻¹. The adsorption capacity of TARGO is approximately 291.4 mg g⁻¹ or four times higher than that of RGO (77.1 mg g⁻¹). Moreover, the adsorption capacity of TARGO was higher than those of other adsorbents reported in Table 1.

Table 1 Adsorption capacities to MB for some porous materials, graphene-based materials reported in the literature

Adsorbent	Adsorbing capacity (mg L^−1)	Reference
Porous SiO2	74	34
SBA-15	45	35
MGC	66	36
FGS	73	37
Zeolite-rGO	53	38

---

3.3 Kinetic model of adsorption

The adsorption kinetics model provides useful information and identifies the rate-determining step of adsorption process. Three kinetic models are used to describe the adsorption data in a non-equilibrium state.

In most kinetic studies of adsorption, quasi-first and quasi-second-order rate equations have been adopted synchronously. Often, one is considered better than the other according to the differences in the correlation coefficient and calculated adsorption quantity.

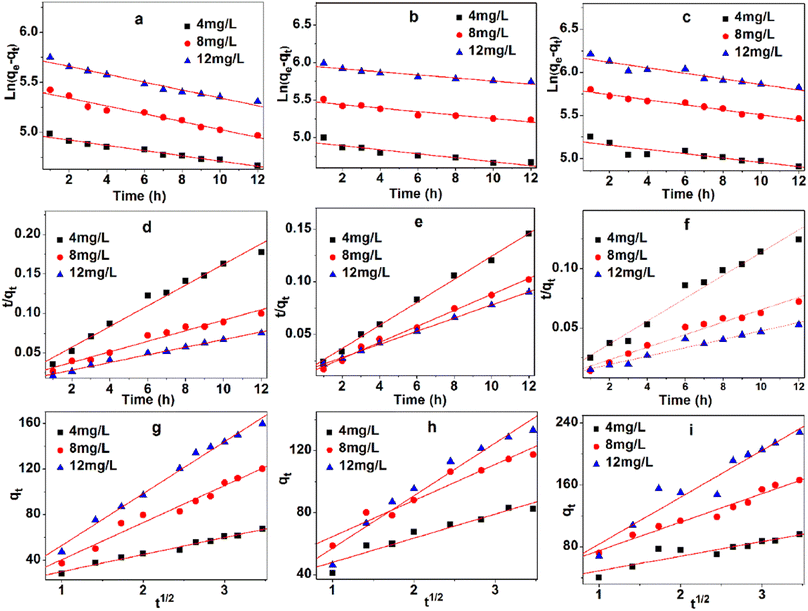
Fig. 7a–c and Table 2 show the linear fitting results of quasi-first-order model for three different concentrations (4, 8, and 12 mg L⁻¹) at three temperatures (293 K, 313 K, and 333 K). This model exhibits high linear correlation coefficient at three experimental temperatures in Table 2. The differences between the maximum adsorption capacity of the estimated value (q_est) and the experimental value (q_exp) can be accepted. The kinetics process can be described by the quasi-first-order model.

Fig. 7 Three kinetic models, quasi-first-order model of 293 K (a), 313 K (b), and 333 K (c); quasi-second order model of 293 K (d), 313 K (e), 333 K (f), and intraparticle diffusion model of 293 K (g), 313 K (h), and 333 K (i).

Table 2 Pseudo-first-order ln(q_e – q_t) = ln(q_e) – k₁t

Temperature	Concentration (mg L^−1)	Parameters			R^2
		K1 (×10^−2 min^−1)	Qest (mg g^−1)	qexp (mg g^−1)
293 K	4	2.63	144.8	174.3	0.971
	8	3.91	226.0	264.2	0.959
	12	3.95	310.7	361.3	0.967
313 K	4	2.67	140.7	189.3	0.876
	8	2.32	241.4	306.2	0.902
	12	2.05	387.2	445.1	0.892
333 K	4	2.52	182.5	231.7	0.802
	8	3.21	335.8	434.9	0.914
	12	3.23	483.9	565.4	0.902

---

Fig. 7d–f and Table 3 show the linear fitting results of quasi-second-order model for three different concentrations (4, 8, and 12 mg L⁻¹) at three temperatures (293 K, 313 K, and 333 K). This model possesses the highest linear correlation coefficient at three experimental temperatures in Table 3, because of its high fault tolerance. Marginal differences were observed between q_est and q_exp.

Table 3 Pseudo-second-order t/q_t = 1/k₂q_e² + t/q_e

Temperature	Concentration (mg L^−1)	Parameters			R^2
		K2 (×10^−3 min^−1)	Qest (mg g^−1)	qexp (mg g^−1)
293 K	4	5.50	76.3	174.3	0.980
	8	1.80	149.3	264.2	0.968
	12	1.23	208.3	361.3	0.990
313 K	4	7.97	91.7	189.3	0.996
	8	4.77	131.6	306.2	0.994
	12	2.45	161.3	445.1	0.999
333 K	4	5.36	104.2	231.7	0.975
	8	1.72	188.7	434.9	0.962
	12	1.01	258.7	565.4	0.955

---

The intraparticle diffusion model is commonly used to explore the diffusion mechanism in adsorbents. Although the intraparticle diffusion model exhibits moderate correlation coefficient at three experimental temperatures in Table 4 and Fig. 7g–i, it is not suitable for describing the MB adsorption on TARGO. The values of K_dif and C increase with temperature. None of the fitted lines are found across the origin, implying that the intraparticle diffusion partly affects the adsorption process but is not the only rate-determining step.

Table 4 Intraparticle diffusion q_t = k_dif t^1/2 + C

Temperature	Concentration (mg L^−1)	Parameters		R^2
		Kdif (mg g^−1 h^−1/2)	C (mg g^−1)
293 K	4	15.0	15.0	0.985
	8	32.5	18.02	0.971
	12	45.5	7.43	0.989
313 K	4	15.5	32.5	0.924
	8	23.3	41.4	0.946
	12	33.9	23.2	0.956
333 K	4	18.9	23.0	0.838
	8	36.8	38.3	0.969
	12	60.6	22.9	0.926

---

3.4 Isothermal adsorption model

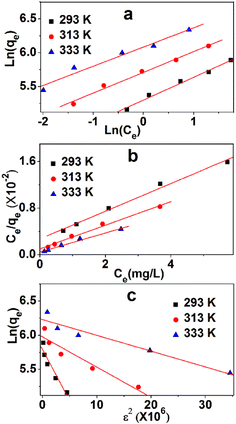
To analyze the adsorption mechanism, the equilibrium data of the adsorption process were described by three commonly used isothermal adsorption models, namely, Langmuir, Freundlich, and Dubinin–Radushkevich (Du–Ra) model.

The Langmuir isotherm might be the most prominent and widely applied equation used to explain the adsorption equilibrium. Fig. 8a shows the linearity of C_e/q_e and C_e. The data and relevant constants are displayed in Table 5. The main parameter of the Langmuir equation that shows the shape of the isotherm curve is R_L, a dimensionless parameter that can be obtained in Table 4. The adsorption isotherm was irreversible when the amount of R_L was zero, and a desirable isotherm could be obtained if it was between zero and one. If R_L is much larger than one, then an undesirable absorption isotherm will be achieved. The values of R_L are between zero and one, which indicates a favorable process. The values of q_e at 293 K, 313 K, and 333 K are 416.7, 500.0, and 625.0 mg g⁻¹, respectively. The linear correlation coefficients (0.991, 0.981, 0.987) are high, which show the strong linear dependence of C_e/q_e and C_e. The adsorption process can be described by the Langmuir model.

Fig. 8 Three isothermal adsorption models, namely, Langmuir (a), Freundlich (b), and Du–Ra (c).

Table 5 Constants and parameters derived from three adsorption isotherm models

Models and equations	Constants		293 K	313 K	333 K
	qm (mg g^−1)		416.7	500.0	625.0
Langmuir	b (L mg^−1)		1.13	0.500	0.313
Ce/qe = 1/qmb + Ce/qm	RL	C0 = 4 mg L^−1	0.181	0.333	0.444
RL = 1/(1 + bC0)		C0 = 8 mg L^−1	0.0996	0.200	0.285
		C0 = 12 mg L^−1	0.0687	0.143	0.210
	R^2		0.991	0.981	0.987
Freundlich	KF (mg g^−1 (L mg^−1)^1/n)		200.5	301.8	438.8
ln(qe) = ln(KF) + (1/n)ln(Ce)	n^−1		0.336	0.305	0.284
	R^2		0.989	0.989	0.967
Dubinin–Radushkevich	qs (×10^−3 mol g^−1)		0.88	1.05	1.36
ln(qe) = ln(qs) – Bε^2	B (mol^2 kJ^−2 × 10^−8)		15.0	4.42	2.31
ε = RT ln(1 + 1/Ce)	E (kJ mol^−1)		1.83	3.36	4.65
E = (2B)^−1/2	R^2		0.916	0.918	0.939

---

The Freundlich model is also used to describe the adsorption process. The linearities of ln(q_e) and ln(C_e) at three temperatures are shown in Fig. 8b, whereas data and relevant constants are displayed in Table 5. The constants of the model, K_F ((mg g⁻¹)/(mg L⁻¹)ⁿ) and n (dimensionless), can be calculated based on the graph. These values indicate the amount of MB adsorption per unit of equilibrium concentration and the distribution of the MB particles bound to the TARGO surface. A smaller 1/n value indicates a more feasible adsorption process. The linear correlation coefficients (0.989, 0.989, 0.987) are low, demonstrating the weak linear dependence between ln(q_e) and ln(C_e).

Du–Ra model is generally introduced to identify physical or chemical adsorption. The adsorption data were analyzed using this model. The linearities of ln(q_e) and ε² at three temperatures are shown in Fig. 8c, and the data and relevant constants are displayed in Table 5. The linear correlation coefficients (0.916, 0.918, 0.939) in three isothermal adsorption models are the lowest. The average adsorption energies at 293 K, 313 K, and 333 K are 1.83, 3.36, and 4.65 kJ mol⁻¹, respectively. These values suggest that physical adsorption is primary in the adsorption process.

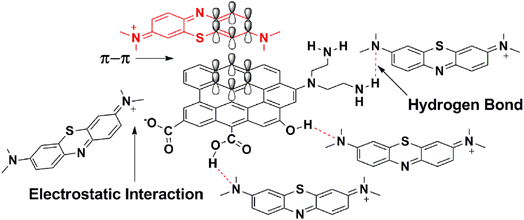
TARGO comprises carbon rings with a sp² hybrid that can form a π–π link with aromatic dyes, such as MB (Fig. 9). Three possible modes of hydrogen bonding can occur between the TARGO and MB. The amine functional groups in MB can form hydrogen bonds with the amino, carboxylic, and hydroxyl groups of TARGO. Additionally, some carboxylic groups can form carboxylate ions. The carboxylate ion can form electrostatic interaction with MB⁺.

Fig. 9 Mechanism for the adsorption of MB on TARGO.

3.5 Recovery and reusability of TARGO

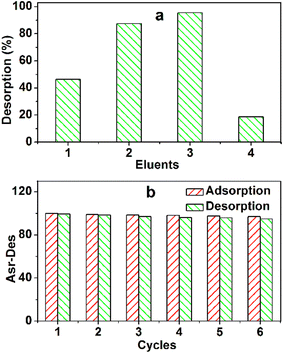
The recovery procedure is simple. First, MB-loaded TARGO (100 mg g⁻¹) was mixed with four different eluents for 12 h (Fig. 10a). The desorption rates of ethanol (95%), 0.1 M HCl/ethanol (10 : 90, v/v), 0.1 M HCl/ethanol (20 : 80, v/v), and water are 46.4%, 87.5%, 98.5%, and 18.7%, respectively. This experiment adopted the 0.1 M HCl/ethanol (20 : 80, v/v) as an eluent.

Fig. 10 (a) Desorption efficiency of pre-adsorbed MB. Desorption solution: ethanol (1), 0.1 M HCl/ethanol (10 : 90, v/v) (2), 0.1 M HCl/ethanol (20 : 80, v/v) (3), and water (4); adsorbed MB = 100 mg g⁻¹, mass of adsorbent = 4.0 mg, volume of eluent = 200 mL, room temperature. (b) Reusability of TARGO. Adsorption condition: mass of adsorbent = 4 mg, MB concentration = 30 mg L⁻¹, contact time = 4 h, room temperature; desorption condition: volume of eluent = 200 mL, contact time = 12 h, room temperature.

The reusability of TARGO is also a crucial factor for an adsorbent. The adsorption–desorption process was conducted six times (Fig. 10b). The adsorption capacities are 100, 98.8, 98.4, 98.1, 97.6, and 96.8 mg g⁻¹. The desorption amounts are 99.2, 98.3, 96.9, 96.1, 95.8, and 94.9 mg g⁻¹. The changes in different adsorption capacities and desorption amounts are small, suggesting that TARGO might exhibit considerable stability for potential applications.

4 Conclusion

TARGO was prepared to increase the number of amino groups and produce new aminated graphene. The product was characterized by SEM, HRTEM, FT-IR, Raman, XPS, and XRD. The TARGO has high nitrogen content, that is, 8.1 at% (by elemental mapping) or 9.4 at% (by XPS). The C–N bond in TARGO was certified by FT-IR, and the stretching C–N is at 1412 cm⁻¹ and 1184 cm⁻¹. Compared with RGO, the D band of TARGO is stronger, and the amount of sp³ carbon is increased. The adsorption capacity of TARGO for MB is high, which is approximately fourfold of RGO. Amine easily reacts with other chemical compounds, and TARGO will be a useful intermediate material used for preparing graphene materials.

Author contributions

Shijie Li: Formal analysis, investigation, data curation. Jingwen Liu: Methodology, formal analysis. Chao Xu: Formal analysis, investigation. Mingliang Zhang: Formal analysis, resources. Liangliang Chu: Conceptualization, methodology. Jianwei Zhou: Formal analysis, writing – review & editing, funding acquisition. Chubei Wang: Investigation, writing–review & editing, project administration.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work has been funded by the He'nan Science and Technology Department (No. 232102230096), the Foundation of He'nan Educational Committee (No. 22B150014), the Xinxiang University Leading Academic Discipline Project (No. 3922210001, 108220223002), and the Xinxiang University Innovation Projects (No. 20210001).

References

1. X. Y. Feng, J. Wang, P. Cai, Z. X. Yang, J. Shen, Y. C. Zhang and X. F. Zhang, Colloid. Surface. A, 2021, 625, 126977,  DOI:10.1016/j.colsurfa.2021.126977.
2. B. A. Arenas-Blanco, G. R. Cepeda-Marín, R. Cabanzo-Hernández and E. Mejía-Ospino, Colloid. Surface. A, 2022, 647, 129034,  DOI:10.1016/j.colsurfa.2022.129034.
3. N. J. Liu, H. Liang, W. Tian, C. C. Li, Q. Q. Gao, N. N. Wang, R. B. Guo and Z. L. Mo, Colloid. Surface. A, 2022, 649, 129367,  DOI:10.1016/j.colsurfa.2022.129367.
4. R. S. Juang, C. T. Hsieh, T. A. Lin, Y. C. Shao and Y. A. Gandomi, Colloid. Surface. A, 2023, 132426,  DOI:10.1016/j.colsurfa.2023.132426.
5. J. Oliva, A. I. Martinez, A. I. Oliva, C. R. Garcia, A. Martinez-Luevanos, M. Garcia-Lobato, R. Ochoa-Valiente and A. Berlanga, Appl. Surf. Sci., 2018, 436, 739–746,  DOI:10.1016/j.apsusc.2017.12.084.
6. X. L. Song, X. N. Chen, G. J. Gou, H. R. Xu, Z. Y. Zhang, L. Y. Cui, T. X. Peng and S. B. Zhu, Macromol. Mater. Eng., 2022, 307, 2200512,  DOI:10.1002/mame.202200512.
7. J. Y. Li, M. Z. Kan, L. Liu, L. Zheng and S. P. Wen, Ind. Eng. Chem. Res., 2023, 62, 11618–11625,  DOI:10.1021/acs.iecr.3c01161.
8. P. T. Zhang, X. Y. Liu, P. Y. Zuo, P. K. Mi and Q. X. Zhuang, ACS Appl. Nano Mater., 2023, 6, 1696–1706,  DOI:10.1021/acsanm.2c04630.
9. W. He, J. C. Du, L. H. Liu, Q. Sun, Z. Y. Song, J. Ma, D. Cao, W. W. Lim, S. U. Hassan and J. T. Liu, RSC Adv., 2023, 13, 10168–10181,  10.1039/D3RA00617D.
10. F. X. Yang, Y. Huang, X. P. Han, S. Zhang, M. Yu, J. P. Zhang and X. Sun, ACS Appl. Nano Mater., 2023, 6, 3367–3377,  DOI:10.1021/acsanm.2c05150.
11. F. Ghaffari, E. Salehi and F. Heidary, Ind. Eng. Chem. Res., 2023, 62, 8911–8925,  DOI:10.1021/acs.iecr.3c01091.
12. R. Narukulla, U. Ojha and T. Sharma, Colloid. Surface. A, 2022, 641, 128594,  DOI:10.1016/j.colsurfa.2022.128594.
13. A. Das, N. Mukherjee and T. Jana, ACS Appl. Nano Mater., 2023, 6, 6365–6379,  DOI:10.1021/acsanm.3c00834.
14. N. Kumar Das, S. Santra, P. K. Naik, M. S. Vasa, R. Raj, S. Bose and T. Banerjee, ACS Sustain. Chem. Eng., 2023, 11, 5376–5389,  DOI:10.1021/acssuschemeng.2c06325.
15. M. Mukhtar, M. Mubeen, A. Ul-Hamid, S. Erten Ela and A. Iqbal, Phys. Chem. Chem. Phys., 2023, 25, 17410–17419,  10.1039/D3CP00947E.
16. G. Reina, G. M. Beneventi, R. Kaur, G. Biagiotti, A. Cadranel, C. Ménard-Moyon, Y. Nishina, B. Richichi, D. M. Guldi and A. Bianco, Chem. Eur. J., 2023, 31, e202300266,  DOI:10.1002/chem.202300266S.
17. S. Mantovani, T. D. Marforio, S. Khaliha, A. Pintus, A. Kovtun, F. Tunioli, L. Favaretto, A. Bianchi, M. L. Navacchia, V. Palermo, M. Calvaresi and M. Melucci, Environ. Sci.: Water Res. Technol., 2023, 9, 1030–1040,  10.1039/D2EW00871H.
18. S. Pilato, S. Moffa, G. Siani, F. Diomede, O. Trubiani, J. Pizzicannella, D. Capista, M. Passacantando, P. Samorì and A. Fontana, ACS Appl. Mater. Interfaces, 2023, 15, 14077–14088,  DOI:10.1021/acsami.3c00216.
19. K. S. Wang, C. H. Wu, C. H. Huang, Y. W. Cheng, R. J. Jeng and T. Y. Liu, ACS Appl. Polym. Mater., 2023, 5, 1765–1774,  DOI:10.1021/acsapm.2c01871.
20. N. Palaniappan, I. Cole, A. Kuznetsov, F. Caballero-Briones and S. Manickam, Mater. Adv., 2023, 4, 1125–1134,  10.1039/D2MA01054B.
21. Z. X. Hou, J. J. Li, C. Y. Qu, W. Li and K. Wang, Energy Technol., 2023, 11, 2201447,  DOI:10.1002/ente.202201447.
22. H. Y. Fu, B. Gao, J. H. Li, Z. Liu, Q. H. Yin, Z. B. Feng and A. R. Kamali, New J. Chem., 2023, 47, 11001–11014,  10.1039/D3NJ01332D.
23. X. Zhao, X. T. Meng, H. Q. Zou, Z. H. Wang, Y. D. Du, Y. Shao, J. Qi and J. S. Qiu, Adv. Funct. Mater., 2022, 33, 2209207,  DOI:10.1002/adfm.202209207.
24. Z. Y. Lin, J. D. Zhong, R. Y. Sun, Y. Z. Wei, Z. H. Sun, W. Y. Li, L. Y. Chen, Y. R. Sun, H. B. Zhang, J. H. Pang and Z. H. Jiang, Adv. Sci., 2023, 10, 2302654,  DOI:10.1002/advs.202302654.
25. M. Li, H. Chen, C. Guo, S. S. Qian, H. P. Li, Z. Z. Wu, C. Xing, P. Xue and S. Q. Zhang, Adv. Energy Mater., 2023, 13, 2300646,  DOI:10.1002/aenm.202300646.
26. Y. Z. Zhao, Y. B. Hu, S. P. Zhang, S. Wang, A. L. Zhang, B. Liang and S. X. Li, Polym. Compos., 2022, 43, 9131–9142,  DOI:10.1002/pc.27091.
27. Q. Y. Yang, E. P. Nguyen, D. Panáček, V. Šedajová, V. Hrubý, G. Rosati, C. de C. Castro Silva, A. Bakandritsos, M. Otyepka and A. Merkoçi, Green Chem., 2023, 25, 1647–1657,  10.1039/D2GC02978B.
28. C. B. Wang, J. W. Zhou and L. L. Chu, RSC Adv., 2015, 5, 52466–52472,  10.1039/C5RA05618G.
29. J. Y. Zhang, C. B. Wang and J. W. Zhou, Environ. Eng. Sci., 2017, 34, 394–400,  DOI:10.1089/ees.2016.0262.
30. C. B. Wang, X. F. Ma, F. F. Duo, J. W. Zhou, Z. J. Wang and J. X. Huang, Mater. Sci. Eng., B, 2019, 245, 9–16,  DOI:10.1016/j.mseb.2019.05.004.
31. C. B. Wang, G. Y. Ma, J. W. Zhou, M. L. Zhang, X. F. Ma, F. F. Duo, L. L. Chu, J. X. Huang and X. M. Su, Appl. Organomet. Chem., 2019, 33, e5077,  DOI:10.1002/aoc.5077.
32. N. Pariona, M. Herrera-Trejo, J. Oliva and A. I. Martinez, J. Nanomater., 2016, 3427809,  DOI:10.1155/2016/3427809.
33. C. R. Garcia, J. Oliva, D. Chavez, E. Viesca-Villanueva, Y. Tejada-Velasquez, A. I. Mtz-Enriquez and L. A. Diaz-Torres, Top. Catal., 2022, 65, 1102–1112,  DOI:10.1007/s11244-022-01690-7.
34. R. Y. Cui, Y. Lin, J. C. Qian, Y. Y. Zhu, N. Xu, F. Chen, C. B. Liu, Z. Y. Wu, Z. G. Chen and X. Zhou, ACS Sustainable Chem. Eng., 2017, 5, 347–3487,  DOI:10.1021/acssuschemeng.7b00170.
35. Z. Y. Wu, Q. Y. Lu, W. H. Fu, S. Wang, C. B. Liu, N. Xu, D. T. Wang, Y. M. Wang and Z. G. Chen, New J. Chem., 2015, 39, 985–993,  10.1039/C4NJ01473A.
36. P. F. Wang, M. H. Cao, C. Wang, Y. H. Ao, J. Hou and J. Qian, Appl. Surf. Sci., 2014, 290, 116–124,  DOI:10.1016/j.apsusc.2013.11.010.
37. N. W. Li, M. B. Zheng, X. F. Chang, G. B. Ji, H. L. Lu, L. P. Xue, L. J. Pan and J. M. Cao, J. Solid State Chem., 2011, 184, 953–958,  DOI:10.1016/j.jssc.2011.01.014.
38. J. Y. Zhu, Y. M. Wang, J. D. Liu and Y. T. Zhang, Ind. Eng. Chem. Res., 2014, 53, 13711–13717,  DOI:10.1021/ie502030w.

---