Open Access Article
Open Access ArticlePredicting band gaps of ABN3 perovskites: an account from machine learning and first-principle DFT studies†
Swarup
Ghosh
and
Joydeep
Chowdhury
 *
*
Department of Physics, Jadavpur University, 188, Raja S.C. Mallick Road, Kolkata 700032, India. E-mail: joydeep72_c@rediffmail.com; joydeep.chowdhury@jadavpuruniversity.in
First published on 20th February 2024
Abstract
The present paper is primarily focused on predicting the band gaps of nitride perovskites from machine learning (ML) models. The ML models have been framed from the feature descriptors and band gap values of 1563 inorganic nitride perovskites having formation energies <−0.026 eV and band gaps ranging from ∼1.0 to 3.1 eV. Four supervised ML models such as multi-layer perceptron (MLP), gradient boosted decision tree (GBDT), support vector regression (SVR) and random forest regression (RFR) have been considered to predict the band gaps of the said systems. The accuracy of each model has been tested from mean absolute error, root-mean-square error and determination coefficient R2 values. The bivariate plots between the predicted and input band gaps of the compounds for both the training and test datasets have also been estimated. Additionally, two ABN3-type nitride perovskites CeBN3 (B = Mo, W) have been selected and their electronic band structures and optoelectronic properties have been studied from density functional theory (DFT) calculations. The band gap values of the said compounds have been estimated from DFT calculations at PBE, HSE06, G0W0@PBE, G0W0@HSE06 level of theories. The present study will be helpful in exploring the ML models in predicting the band gaps of nitride perovskites which in turn may bear potential applications in photovoltaic cells and optical luminescent devices.
1. Introduction
Perovskites are ternary compounds with general chemical formula ABX3 where “A” and “B” are cationic elements and “X” can be either oxygen or halogens in anionic forms. While “A” atoms are located in the cuboctahedral cavities of the crystal, “X” atoms on the other hand form corner sharing BX6 octahedra. These compounds are known to show fascinating physical and chemical properties and find extensive applications in the fabrications of solar, fuel cells, energy conversion and optoelectronic devices.1–10 Moreover, perovskites containing heavy fermionic elements, that show Rashba splittings, find promising applications in spintronics.11–14Despite considerable successes of oxide and halide perovskites, recently much attention has been focused on the synthesis and first-principle calculations of nitride perovskites having general formula ABN3.15–19 Of late, ABN3 find potential applications as topological insulators, photovoltaic cells and are being successfully used as optical luminescent materials.18,20,21 The primary driving force behind the realization of ABN3 stems from their extraordinary electronic, optical and magnetic properties of nitride compounds. For example, 2D hexagonal boron nitride is used in 5G wireless technology.22 Vanadium nitride (VN), niobium nitride (NbN) and tantalum nitride (TaN) compounds are commonly employed in the fabrications of high – Tc superconductors, supercapacitors and batteries.23–27
Barring several attributes, syntheses of nitride perovskites are experimentally challenging as their synthetic protocols demand oxygen free environment.28 Despite this limitation, successful preparations of ThTaN3, LaWN3, LaReN3, LaMoN3, CeMoN3, CeWN3, YMoN3 and YWN3 systems have so far been reported.28–31 Readers who are interested in their synthesis procedures are referred to the literature28–31 as depicted under reference section. Interestingly, these nitride perovskites find wide applications as topological insulators, spintronics and microelectromechanical devices.21,30,32
Considering the enormous applications of nitride perovskites, in silico approaches alone or in conjunction with experiments have been successfully applied to predict the structure–function relationships of these compounds. A combined minima hopping method and density functional theory (DFT) calculations have been performed to predict the crystal structures and band gaps (Eg) of twenty-one ABN3 perovskites such as LaBN3 (B = Re, W, Mo, Tc, Os, Cr, Mn, Co), SrBN3 (B = Re, W, Tc), CaBN3 (B = Re, W, Mo, Tc), BaBN3 (B = Re, W) and YBN3 (B = Re, W, Mo, Tc).19 Those systems were observed to be thermodynamically stable and proposed to have excellent chances of being experimentally accessible.19 Recently, the first-principle DFT calculations have been carried out to calculate the magnetic moments and thermodynamic stabilities of some rare-earth nitride perovskites ABN3 (A = La, Ce, Pr, Nd, Pm, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu and B = Re, W) and suggested their numerous technological applications in the domain of nitride materials.16 In this regard DFT is now recognized to be an elegant approach to estimate the electronic and optoelectronic properties of the materials under study. Both the electronic as well the optoelectronic properties are primarily guided by the band gaps of the materials. While DFT calculations with local density approximation (LDA) and generalized gradient approximation (GGA) underestimate Eg values,33–36 the unscreened hybrid and Perdew–Burke–Ernzerhof–Hartree–Fock exchange (PBE0) functionals overestimate band gap energies of the compounds relative to their experimental counterparts.37–39 In this regard DFT calculations, as accomplished from single-shot GW (G0W0) approximation using hybrid exchange-correlation (XC) functionals such as Heyd–Scuseria–Ernzerhof (HSE), Becke-3-parameter-Lee-Yang-Parr (B3LYP) and B3PW91 are known to predict the Eg values of the compounds close to the experimental results.14,33,40–48 The major pitfalls of such calculations are that they are computationally demanding and need high end servers to run them. In this context, the machine learning (ML) is now considered as an effective alternative route to avoid the inherent computational costs linked with DFT calculations and helps in establishing a simple model between the characteristics features of materials and the target variable (here Eg).49–60 Although ML approach is successfully implemented recently to predict the band gaps of oxide, halide perovskites and double perovskite compounds,61–66 no such report is found in predicting the band gaps of nitride perovskites.
Considering the above issues in mind, the present paper is aimed to predict the band gaps of ABN3 perovskites from ML models. The DFT studies have been performed to estimate the electronic band structures, Eg values and optoelectronic properties of two new nitride perovskites CeBN3 (B = Mo, W). The manuscript has been organized in the following manner. In Section 2, the computational methodology, which includes ML methods and first-principle DFT calculations, has been discussed. Cleaning and preprocessing of data for ABN3 perovskites have been shared in Section 3.1. In section 3.2, the training and validation of ML models have been deliberated. Section 3.3 is devoted to understand the structural properties and stabilities of two newly discovered nitride perovskite compounds CeBN3 (B = Mo, W). Section 3.4 is framed with the calculations of electronic band structures and band gaps of CeBN3 compounds using different level of theories in DFT calculations. The corresponding optoelectronic properties have also been highlighted in the Section 3.5. Overall conclusions of this work have been discussed under Section 4.
2. Computational methodology
2.1. Machine learning models
To predict the band gaps of nitride perovskite compounds, the ML models such as support vector regression (SVR), gradient boosted decision tree (GBDT), random forest regression (RFR) and multi-layer perceptron (MLP) algorithms have been considered. The input data consist of material descriptors of nitride perovskites and their corresponding target variables Eg. The algorithms have been realized using the Scikit-learn software package within the Python 3.9 framework.67 The parameters of the algorithms have been optimized and the model performances have been estimated using the grid search of the average root-mean-square error (RMSE) of each model validation set. The Eg values have been predicted from SVR model using the following mathematical relation:53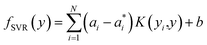 | (1) |
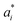 are non-negative multipliers for each observation yi. K is the kernel or radial basis function which is used to calculate the difference between training (yi) and predicted (y) values of band gaps. “b” can be estimated from the Lagrange function.
are non-negative multipliers for each observation yi. K is the kernel or radial basis function which is used to calculate the difference between training (yi) and predicted (y) values of band gaps. “b” can be estimated from the Lagrange function.
The Eg values, so predicted from the GBDT algorithm, are represented using the following expression:53
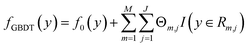 | (2) |
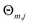 are the number of regression trees, number of leaf nodes of the trees and the best fitting value respectively for each set of leaf nodes Rm,j.
are the number of regression trees, number of leaf nodes of the trees and the best fitting value respectively for each set of leaf nodes Rm,j.
Using RFR model the predicted Eg can be represented as:53
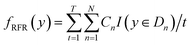 | (3) |
The Eg values, so predicted from neural network based MLP framework, can be expressed using the following mathematical function:53
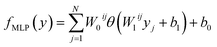 | (4) |
The characteristics of each model have been estimated from the Pearson correlation coefficient (p) which is expressed as:68
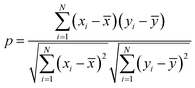 | (5) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) and ȳ are their respective average values. N represent total number of samples in the training set. The accuracy of each ML model has been determined from RMSE, mean absolute error (MAE) and evaluation coefficient (R2) values. RMSE, MAE and R2 have been calculated using the following relations:
and ȳ are their respective average values. N represent total number of samples in the training set. The accuracy of each ML model has been determined from RMSE, mean absolute error (MAE) and evaluation coefficient (R2) values. RMSE, MAE and R2 have been calculated using the following relations: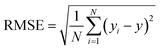 | (6) |
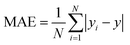 | (7) |
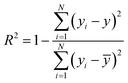 | (8) |
2.2. First-principle DFT calculations
The first-principle calculations have been carried out under the DFT framework within Quantum ESPRESSO (QE) software.69–71 The crystal structures of CeBN3 (B = Mo, W) compounds have been primarily optimized using “variable-cell relaxation” method followed by Broyden–Fletcher–Goldfarb–Shanno scheme.72–75 The Born Oppenheimer molecular dynamics (BOMD) simulations have then been performed at T = 300 K on the supercell structures (2 × 2 × 2) of the compounds, so obtained from the optimized unitcell geometries of the said systems. BOMD simulations have been accomplished from the NPT ensemble whose temperature is controlled by the Nose–Hoover thermostat. The projector augmented wave (PAW) pseudopotentials76 have been included to consider the electron–ion interactions and the exchange-correlation (XC) term of the pseudopotential has been implemented from Perdew–Burke–Ernzerhof (PBE) XC functional77 which is known as a parameterization form of GGA. The valence electrons of Ce, B (B = Mo, W) and N atoms have been considered as plane wave with kinetic energy cut-off of 80 Ry. Each crystal structure is allowed to optimize until the Hellmann–Feynman force attains a value <10−3 Ry Bohr−1 for total electronic energy difference <10−8 Ry at P = 0 GPa. A gamma-centered k-point mesh of 10 × 10 × 10 grid under Monkhorst–Pack scheme has been set for geometry optimization and self-consistent-field (SCF) calculations.The electronic band structures of CeBN3 crystal systems have been estimated from different level of theories such as PBE, HSE06, G0W0@PBE and G0W0@HSE06 in the DFT calculations. The optoelectronic properties of the said compounds have been calculated from SCF method as employed in QE software.78 The optical broadening of 0.15 eV has been considered for estimating the optoelectronic parameters which include complex dielectric function [ε(ω)], absorption coefficient [α(ω)] and optical conductivity [σ(ω)].
3. Results and discussions
3.1. Data cleaning and pre-processing for machine learning
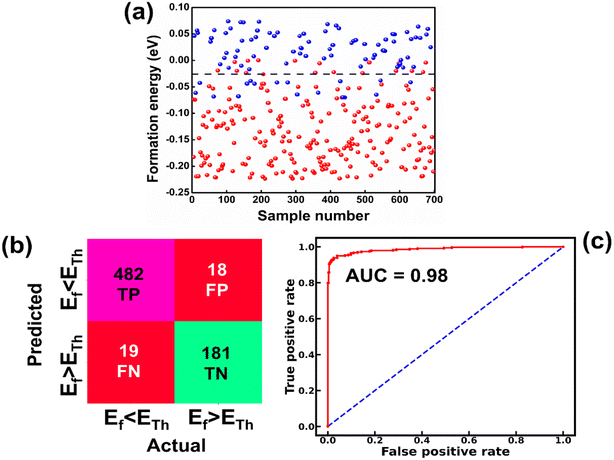
The raw data of inorganic ABN3-type perovskite compounds have been obtained from the available literature.15–19,21,28–31,79,80 By selecting all possible combinations of cations as “A” and “B”, a set of 5566 inorganic ABN3-type perovskites have been initially selected for model evaluation. Lead (Pb) containing perovskites in all combinations, due their inherent toxic characters, are not considered in the above mentioned dataset. In the next step, the samples have been primarily identified according to their respective formation energies (Ef). Using support vector classification (SVC), the samples are then categorized by eliminating those candidates which show Ef > thermal excitation energy (ETh ∼ −0.026 eV) at room temperature (T = 300 K).57 To implement SVC, initially 5566 samples have been randomly divided into 4866 (∼87%) and 700 (∼13%) samples as training and test set, respectively. Fig. 1(a) shows the Ef as a function of sample number of the test dataset as obtained from SVC algorithm. From Fig. 1(a), it is observed that the samples are segregated into Ef < ETh and Ef > ETh classes. The merit of this SVC algorithm is then tested from confusion matrix and receiver operating characteristics (ROC) curve.55 The results are shown in Fig. 1(b) and (c) respectively. From Fig. 1(b), the correctly identified compounds with Ef < ETh and Ef > ETh classes are observed to be 482 [true positive (TP)] and 181 [true negative (TP)], respectively. However, the number of incorrectly identified samples under Ef < ETh and Ef > ETh classes are found to be 18 [false positive (FP)] and 19 [false negative (FN)], respectively. Out of 700 test dataset, it is found that only 5% samples (37 out of 700) have been misclassified, which in turn suggests the reliability of the SVC model to segregate the samples into their respective classes. The F1 score of the model, as attained from confusion matrix, is mathematically expressed as: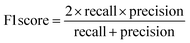 | (9) |
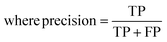 | (10) |
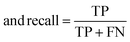 | (11) |
The F1 score is calculated to be 96.2% which also suggests the better performance of the said model. The ROC curve, as depicted in Fig. 1(c), represents the relation between the TP rate (sensitivity) and FP rate (1 – specificity). From Fig. 1(c), the area under curve (AUC) is estimated to be 0.98. The AUC closer to 1 further signifies the excellent segregation between the Ef < ETh and Ef > ETh classes.
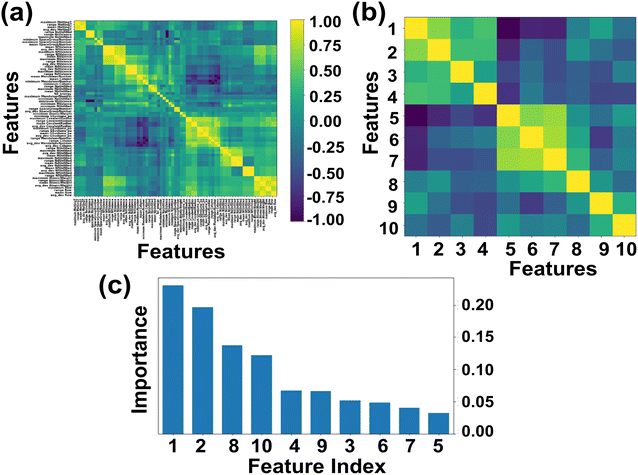
Here we primarily focused on ABN3 compounds which bear potential applications as photovoltaic and optical luminescent materials, the selection space has thus been further narrowed down to 1563 samples which exhibit Eg values spanning in the range from 1.0 to 3.1 eV. The Eg of the compounds in general are linked with the proposed 145 feature descriptors which include electronegativity, atomic weight, covalent radius, d valence electrons etc.57,81 Out of 145 feature descriptors, 117 feature attributes of ABN3 perovskites have been initially framed for the target variable Eg. The list of 117 features such as Mendeleev number, electronegativity, covalent radius, d valence electrons etc. are shown in Table S1 (ESI).† With these 117 features, the Pearson correlation heatmap is constructed and the result is shown in Fig. 2(a). The features having absolute correlation values <0.89 and with multiple collinearities between them have been eliminated. The final top 10 feature descriptors which include electronegativity, d valence electrons, formation energy, p valence electrons, Mendeleev number, specific volume of ground state, mean covalent radius, space group number, melting temperature and atomic weight, have been selected using the de-correlation method for further model evaluation. The heatmap portraying the evaluated top 10 feature descriptors and their order of importance are shown in Fig. 2(b) and (c), respectively. From Fig. 2(c), it is clearly seen that the electronegativity, d valence electrons and mean covalent radius show predominant contributions in predicting Eg values of the ABN3 compounds.
The correlations between Eg and electronegativity, mean covalent radius and d valence electrons can be rationalized. Electronegativity is a measure of ability to attract electrons of two bonded atoms towards their valence electrons. This ability results the delocalized distribution of valence electrons, which in turn influences the nature of the bonding as well as the Eg values of the compounds.82–84 The mean covalent radii of the constituent atoms are intrinsically linked with the electronegativity of the system. Systems with constituent atoms having larger mean covalent radii thus result in decrease in electronegativity of the compounds in general.85 Hence, the mean covalent radius is considered as an important feature descriptor in modulating the Eg values of the systems. The d valence electrons play major roles in the formation of energy bands in the electronic band structure and has direct impact on the Eg of the materials. Larger number of d valence electrons can realign the Fermi energy level (EF) through p-d and s-d hybridizations, which in turn may alter the Eg values of the compounds.57
3.2. Machine learning model training and validation
To precisely predict the band gaps of ABN3-ype perovskite compounds, four ML models such as SVR, MLP, GBDT and RFR have been considered. The accuracy of each model has been tested by selecting their respective hyperparameters. The list of hyperparameters of each model are shown in Table 1. From the dataset of 1563 ABN3 perovskites and their top 10 feature descriptors (vide supra), 1363 (∼87%) samples have been randomly selected for training and the rest 200 (∼13%) samples have been set for testing of each model. The random selection has been considered two times for each model to confirm the statistical validity of the results. The performance of ML model has been estimated by calculating the RMSE, MAE and R2 values. The RMSE, MAE and R2 values of each model for the test dataset, so attained from the 10-dimensional feature space, are illustrated in Table 1.| Models | Hyperparameters | MAE | RMSE | R 2 |
|---|---|---|---|---|
| MLP | Solver = adam, alpha = 1 × 10−8, tol = 1 × 10−6, max_iter = 5000, random_state = 0 | 0.16 | 0.22 | 0.74 |
| GBDT | n_estimators = 2000, max_depth = 30, min_samples_split = 2 | 0.10 | 0.15 | 0.90 |
| SVR | C = 50, gamma = 10, epsilon = 0.05, kernel = ‘rbf' | 0.08 | 0.13 | 0.91 |
| RFR | max_depth = 30, min_samples_split = 2, n_estimators = 2000, min_samples_leaf = 1, random_state = 0 | 0.03 | 0.11 | 0.94 |
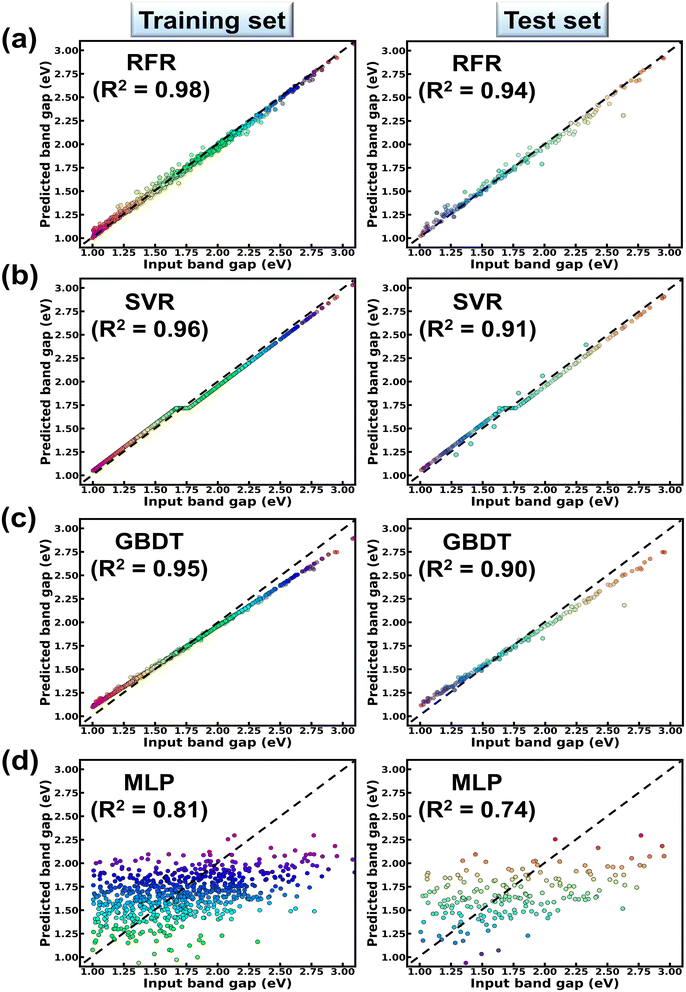
From Table 1, it is observed that while RFR predicts the Eg values of the compound with 3% MAE; SVR, GBDT and MLP predict the same Eg within MAEs of 8%, 10% and 16% respectively. From Table 1, the RFR algorithm shows lowest RMSE (=0.11 eV) and highest R2 (=0.94) values in contrast to other models. R2 (RMSE) values of GBDT, SVR and MLP models are estimated to be 0.90 (0.15 eV), 0.91 (0.13 eV) and 0.74 (0.22 eV) respectively. These results collectively suggest the reliability of the RFR model in predicting the band gaps of ABN3-type perovskite compounds. The bivariate plots from the RFR model showing both the predicted, input band gap values for the training and testing datasets are illustrated in Fig. 3(a). From Fig. 3(a), strong linear correlation [with R2 = 0.98 (training set) and 0.94 (test set)] between the predicted and input Eg values have been observed in both the training and test datasets. This result further justifies the accuracy of RFR model in predicting the band gaps of ABN3 perovskites. The corresponding bivariate plots between the predicted and input values of Eg, as accomplished from SVR, GBDT and MLP ML models, are also shown in Fig. 3(b–d) respectively. From Fig. 3(b–d), moderate to weak linear correlations between the predicted and input Eg values have been observed as the model goes from SVR, GBDT to MLP algorithms. The above results as a whole suggest the superiority of the RFR algorithm as an effective ML model is predicting the band gaps of ABN3 compounds in contrast to SVR, GBDT and MLP algorithms.
Besides, two newly synthesized nitride perovskites CeMoN3 and CeWN3, as reported elsewhere28 and whose band gaps are yet to be explored, have been selected for first-principle DFT calculations. Their electronic band structures, Eg values and optoelectronic properties have been studied from DFT calculations. The Eg values of the said systems have been predicted from both the DFT as well as RFR ML model to verify the accuracy of ML model in predicting Eg values of ABN3 compounds.
3.3. Crystal structures and stabilities of the CeBN3 (B = Mo, W) compounds
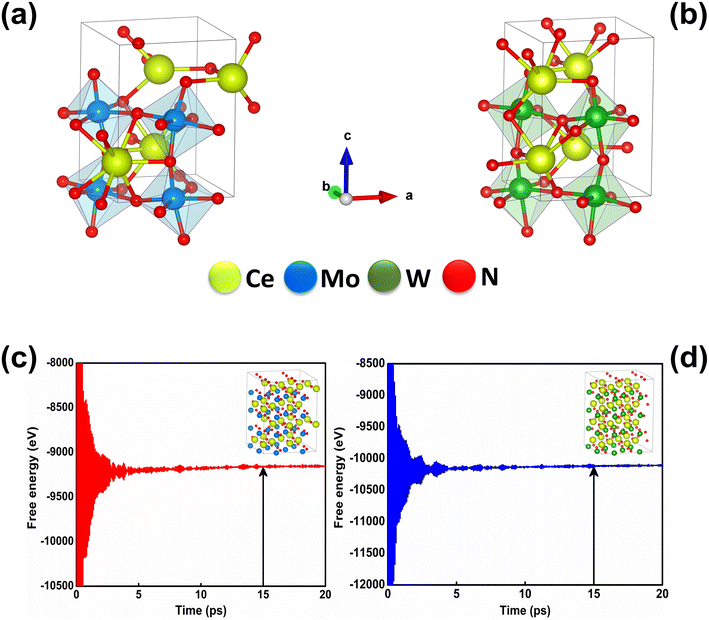
At room temperature (T = 300 K) and under ambient pressure (P = 0 GPa), CeBN3 (B = Mo, W) crystalize to primitive orthorhombic phase and belong to Pmc21 space group symmetry with space group no. 26. The optimized unitcell geometries of the compounds, as obtained from first-principle DFT calculations with GGA-PBE level of theory, are shown in the upper panel of Fig. 4. The lattice parameters of the CeMoN3 (CeWN3) crystal system have been estimated to be a = 5.789 Å (5.686 Å), b = 5.854 Å (5.667 Å) and c = 7.776 Å (8.027 Å) which are in close agreement with the experimentally determined X-ray diffraction data as reported elsewhere.28 From Fig. 4(a and b), it is observed that B (=Mo, N) and N atoms form several distorted octahedral environments within the crystal structure and B atom, which is located at the center of each BN6 octahedron, is found to be shifted towards the apical N atom. The distorted octahedron, aka pyramidal coordination and large c/a ratio of CeBN3 may result large spontaneous ferroelectric polarization in the systems under study.86,87 The ferroelectric polarization values of CeMoN3 and CeWN3 compounds are estimated to be ∼47.24 and 49.68 μC cm−2 respectively along the direction of crystallographic c-axis. To comprehend the thermal stabilities of the compounds at T = 300 K, the BOMD simulations have been performed over a time span of 20 ps under time step of 1 fs. Temporal variations of free energies of CeBN3 systems at T = 300 K are shown in the lower panel of Fig. 4. The free energies (F) of the compounds have been estimated using the following relation:88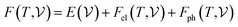 | (12) |
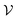 signifies the supercell volume at temperature T,
signifies the supercell volume at temperature T, 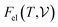 and
and 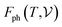 are the free energies of the electrons and phonons respectively.
are the free energies of the electrons and phonons respectively. 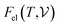 can be estimated using the following mathematical relation:89,90
can be estimated using the following mathematical relation:89,90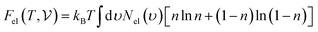 | (13) |
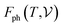 has been calculated under the thermodynamic integration approach90,91 and is expressed as:
has been calculated under the thermodynamic integration approach90,91 and is expressed as: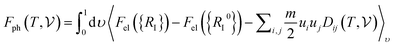 | (14) |
3.4. Estimations of Eg values for CeBN3 (B = Mo, W) compounds
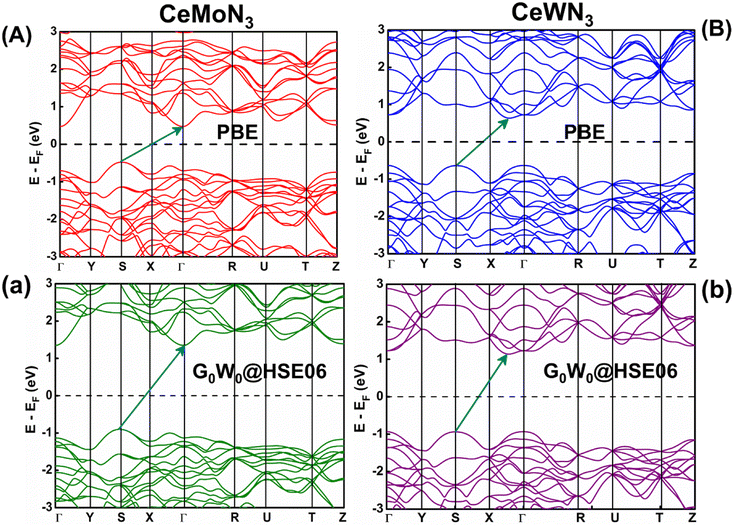
The E–k diagrams of CeBN3 systems for B = Mo, W along Γ → Y → S → X → Γ → R → U → T → Z high-symmetry direction have been estimated from DFT calculations at PBE, HSE06, G0W0@PBE and G0W0@HSE06 level of theories. The results are shown in Fig. 5 and S1 (ESI).† The estimated Eg values of the compounds from the corresponding E–k diagrams are shown in Table 2. Interestingly the E–k diagrams for both CeMoN3 and CeWN3 compounds show the existence of indirect band gaps ranging from 0.94–1.60 and 1.00–1.81 eV, respectively. Presence of indirect band gaps with gap openings in the range 0.94–1.81 eV may render their applications in photovoltaics.92–96 In this connection it may be relevant to mention that while the PBE functional is known to underestimate the Eg values of the systems in general,14,33–36,40,41,43 the HSE06 functional on the other hand can predict the Eg values of the compounds in close agreement with the experimental observations.14,33,40,45,97 The HSE06 XC energy functional (EHSE06XC) is mathematically expressed as:98| EHSE06XC = 1/4EHF, SRX(ω) + 3/4EPBE, SRX(ω) + EPBE, LRX(ω) + EPBEC | (15) |
| Level of theories | Band gaps (eV) | |
|---|---|---|
| CeMoN3 | CeWN3 | |
| PBE | 0.94 | 1.00 |
| HSE06 | 1.57 | 1.80 |
| G0W0@PBE | 1.46 | 1.71 |
| G0W0@HSE06 | 1.60 | 1.81 |
The Eg values of CeMoN3 and CeWN3 compounds are predicted to be ∼1.55 and 1.76 eV from RFR ML model for the G0W0@HSE06 input of 1.60 and 1.81 eV respectively. While the DFT calculations at HSE06 and G0W0@HSE06 level of theories can closely predict the experimentally observed Eg values of the systems within <1% error,40,42,45,48,97,99,100 the predicted Eg values of CeBN3 (B = Mo, W) compounds as obtained from RFR ML model are estimated within an error of ∼3% with standard deviation of ∼0.035. The selective choice of G0W0@HSE06 level of theory in the DFT calculation as input for the prediction of band gaps is thus meaningful, given its efficacy in reproducing the experimental band gaps of many such compounds as reported elsewhere.14,101–103
3.5. Optical properties of CeBN3 (B = Mo, W) systems
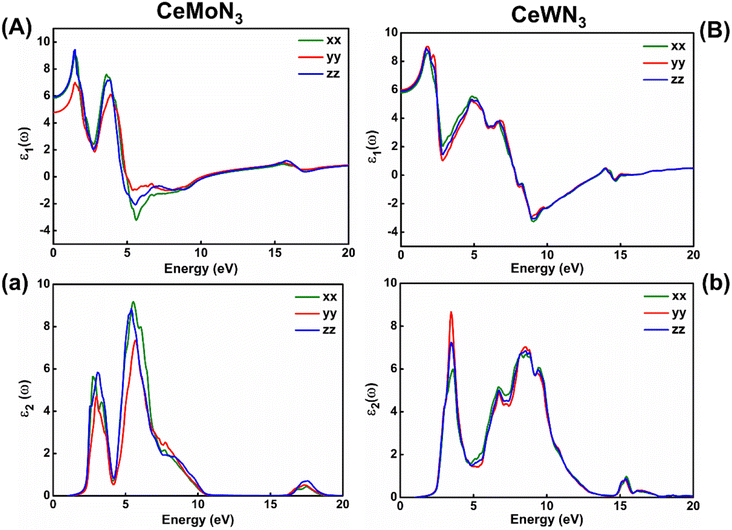
Electronic band structures are intrinsically linked with the optoelectronic properties of the systems in general. The optoelectronic properties of CeBN3 (B = Mo, W) crystal systems have been estimated from the frequency (ω) dependent complex dielectric function [ε(ω)]. Since, the Pmc21 phase of the compounds is structurally anisotropic, the incident electromagnetic (EM) field components along the direction of a, b and c-crystallographic axes are designated as xx, yy and zz, respectively in the consequent calculations. Fig. 6(A) and (B) show the variations of real part of ε(ω) [ε1(ω)] as a function of incident EM wave energy (ẼM), so obtained from G0W0@HSE06 level of theory, for CeMoN3 and CeWN3 compounds respectively. From the upper panel of Fig. 6, static values of ε1(ω) [ε1(0)] have been estimated to be ∼5.85 (5.80), 4.77 (5.99) and 5.93 (5.90) for CeMoN3 (CeWN3) system along xx, yy and zz polarization directions respectively of the incident EM wave. These non-zero values of ε1(0) for all the three polarization directions indicate their semiconducting nature so attained from the E–k diagrams [vide ante, Fig. 5]. The most intense structure band of ε1(ω) for CeMoN3 (CeWN3) compound is obtained at ẼM ∼1.45 (1.85) eV which corresponds to maximum dispersion of the EM wave. However, beyond ẼM ∼3.75 (6.86) eV, ε1(ω) values of CeMoN3 (CeWN3) system gradually decrease and attain negative values within the energy window ẼM ∼4.72 (7.86)–10.42 (13.39) eV. The negative values of ε1(ω) signify metallic Drude – like behaviour of the compounds within the said energy windows.42,43,104ε 2(ω) is known to correlate directly with the band gaps of the compounds in general. Fig. 6(a) and (b) depict the variations of ε2(ω) as a function of ẼM for CeMoN3 and CeWN3 systems respectively, so attained from G0W0@HSE06 level of theory. From Fig. 6(a and b) the critical or take-off values of ε2(ω) have been observed at ẼM ∼1.60 (1.81) eV for CeMoN3 (CeWN3) compound for all the three polarization directions. The critical or take-off values of ε2(ω) are in exact agreement with the Eg values of the systems, as obtained from the G0W0@HSE06 level of theory (vide ante, Table 2). Interestingly, the take-off values of ε2(ω) are found to be independent of polarization directions of EM wave. Moreover, finite values of ε2(ω) between ẼM ∼2.30 (2.40) and 10.01 (12.50) eV for CeMoN3 (CeWN3) crystal corroborate strong attenuation of the incident EM wave inside the crystal systems within the said energy window.42,43
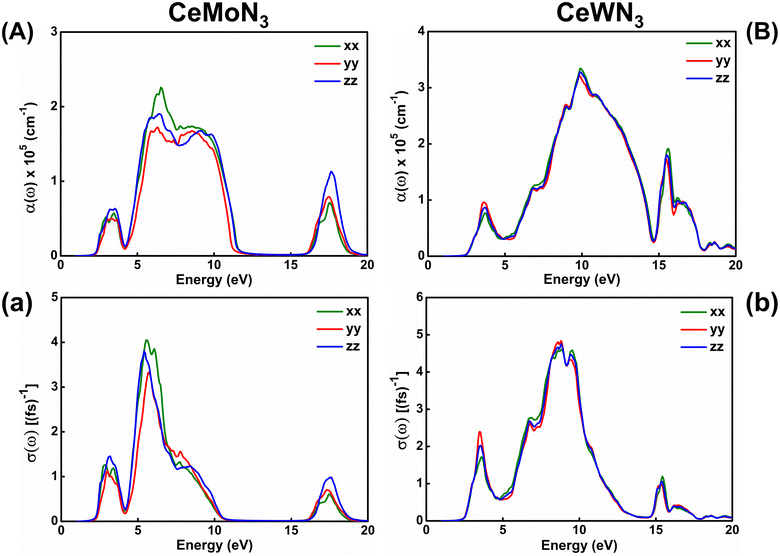
The response of strong attenuation of the incident EM wave inside the CeBN3 (B = Mo, W) compounds, so reflected in the ε2(ω)–ẼM plots (Fig. 6), can also be attributed from their absorption coefficients [α(ω)] and optical conductivities [σ(ω)]. Fig. 7 shows the variations of α(ω) and σ(ω) as function of ẼM for the referred systems. Akin to ε2(ω)–ẼM plots, the critical values of both α(ω) and σ(ω) are found at ẼM ∼1.60 (1.81) eV for CeMoN3 (CeWN3) crystal system for all the three polarization directions. Hence the estimations of α(ω) and σ(ω) help to recheck the Eg values as obtained from electronic band structures and ε2(ω)–ẼM plots. From Fig. 7, finite values of α(ω)/σ(ω) have been observed within ẼM ∼2.30/2.30 to 11.43/10.01 eV, 16.47/16.55 to 18.77/18.64 eV and 2.40/2.40 to 17.90/12.50 eV for CeMoN3 and CeWN3 compounds, respectively. The finite values of α(ω) and/or σ(ω) within the specified energy window signify large opacity and high optical conductivity of the said systems.42,43 Moreover, the high transparency of CeMoN3 (CeWN3) compound within the energy window ∼0–1.60 eV (0–1.81 eV) has also been noticed in α(ω)–ẼM and σ(ω)–ẼM plots (Fig. 7). The high transparency of the said systems covering visible and Infrared (IR) regions of the EM wave may promote them as potential candidates for optical luminescent materials and IR detectors.43,105,106
4. Conclusions
The band gaps of ABN3 perovskites have been predicted from ML models based on the feature descriptors. The dataset of 1563 ABN3 perovskites, which show Ef < −0.026 eV and Eg values spanning in the range from 1.0 to 3.1 eV, have been selected from initial 5566 samples for ML model evaluation. The Eg values of the compounds are found to be linked with 117 feature descriptors. The top 10 feature descriptors have been selected by eliminating those features which show absolute correlation values <0.89 and low rank of importance. Correlations between the band gap and the topmost 3 features such as electronegativity, mean covalent radius and d valence electrons have also been discussed. Four supervised ML models such as MLP, GBDT, SVR and RFR have been considered to predict the band gaps of these nitride perovskite compounds. The accuracy of each model has been tested from MAE, RMSE and R2 values. The RFR algorithm shows lowest RMSE (=0.11 eV) and highest R2 (=0.94) values in comparison to other models. R2 values and the corresponding bivariate plots suggest the superiority of RFR algorithm as an effective ML model is predicting the band gaps of ABN3 perovskites in contrast to SVR, GBDT and MLP algorithms. Two newly synthesized ABN3-type perovskites CeBN3 (B = Mo, W) have been further chosen and their electronic band structures and optoelectronic properties have been studied from DFT calculations. The Eg values of CeBN3 (B = Mo, W) compounds have been estimated from DFT calculations at PBE, HSE06, G0W0@PBE and G0W0@HSE06 level of theories. The Eg values of CeMoN3 and CeWN3 compounds have been predicted to be 1.55 and 1.76 eV from RFR algorithm for the G0W0@HSE06 input of 1.60 and 1.81 eV respectively. The Eg values of the systems have also been verified from their respective optoelectronic parameters such as ε2(ω), α(ω) and σ(ω). We believe that this study will help to unveil the efficacy of ML models in predicting the band gaps of nitride perovskites which in turn will bear potential applications as photovoltaic and optical luminescent materials.Data availability
The data and codes that support the findings of this study are available on reasonable request from corresponding author.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Authors would like to thank the National Supercomputing Mission (NSM) for providing computing resources of ‘PARAM Kamrupa’ at IIT Guwahati, which is implemented by C-DAC and supported by the Ministry of Electronics and Information Technology (MeitY) and Department of Science and Technology (DST), Government of India. Swarup Ghosh sincerely acknowledges the University Grants Commission (UGC), Government of India for providing the senior research fellowship (NET) award.References
- Z. Shi and A. H. Jayatissa, Materials, 2018, 11, 729 CrossRef.
- P. Tonui, S. O. Oseni, G. Sharma, Q. Yan and G. Tessema Mola, Renewable Sustainable Energy Rev., 2018, 91, 1025–1044 CrossRef CAS.
- M. Aldamasy, Z. Iqbal, G. Li, J. Pascual, F. Alharthi, A. Abate and M. Li, Phys. Chem. Chem. Phys., 2021, 23, 23413–23427 RSC.
- B. V. Politov, E. P. Antonova, E. S. Tropin, D. A. Osinkin, A. Y. Suntsov and V. L. Kozhevnikov, Renewable Energy, 2023, 206, 872–878 CrossRef CAS.
- Y. Zhou, X. Guan, H. Zhou, K. Ramadoss, S. Adam, H. Liu, S. Lee, J. Shi, M. Tsuchiya, D. D. Fong and S. Ramanathan, Nature, 2016, 534, 231–234 CrossRef CAS PubMed.
- A. Raj, S. Sharma, D. V. Singh, A. Kumar, R. K. Chourasia, J. M. Siqueiros, O. R. Herrera, A. Anshul and M. Kumar, Phys. B, 2024, 673, 415504 CrossRef CAS.
- L. Polavarapu, M. A. Loi, H. Zeng and J. M. Luther, Nanoscale, 2023, 15, 15075–15078 RSC.
- A. Balilonda, Z. Li, Y. Fu, F. Zabihi, S. Yang, X. Huang, X. Tao and W. Chen, J. Mater. Chem. C, 2022, 10, 6957–6991 RSC.
- R. Wang, J. Wang, S. Tan, Y. Duan, Z.-K. Wang and Y. Yang, Trends Chem., 2019, 1, 368–379 CrossRef CAS.
- D. Luo, X. Li, A. Dumont, H. Yu and Z.-H. Lu, Adv. Mater., 2021, 33, 2006004 CrossRef CAS PubMed.
- H. C. Koo, S. B. Kim, H. Kim, T.-E. Park, J. W. Choi, K.-W. Kim, G. Go, J. H. Oh, D.-K. Lee, E.-S. Park, I.-S. Hong and K.-J. Lee, Adv. Mater., 2020, 32, 2002117 CrossRef CAS.
- M. Kepenekian and J. Even, J. Phys. Chem. Lett., 2017, 8, 3362–3370 CrossRef CAS PubMed.
- M.-Y. Liu, Q.-Y. Chen, C. Cao and Y. He, Phys. Chem. Chem. Phys., 2019, 21, 2899–2909 RSC.
- S. Ghosh and J. Chowdhury, Mod. Phys. Lett. B, 2023, 38, 2330003 CrossRef.
- C. Gui, J. Chen and S. Dong, Phys. Rev. B, 2022, 106, 184418 CrossRef CAS.
- J. A. Flores-Livas, R. Sarmiento-Pérez, S. Botti, S. Goedecker and M. A. L. Marques, JPhys Mater., 2019, 2, 025003 CrossRef CAS.
- B. F. Grosso, D. W. Davies, B. Zhu, A. Walsh and D. O. Scanlon, Chem. Sci., 2023, 14, 9175–9185 RSC.
- V.-A. Ha, H. Lee and F. Giustino, Chem. Mater., 2022, 34, 2107–2122 CrossRef CAS.
- R. Sarmiento-Pérez, T. F. T. Cerqueira, S. Körbel, S. Botti and M. A. L. Marques, Chem. Mater., 2015, 27, 5957–5963 CrossRef.
- T. K. Ng, J. A. Holguin-Lerma, C. H. Kang, I. Ashry, H. Zhang, G. Bucci and B. S. Ooi, J. Phys. D: Appl. Phys., 2021, 54, 143001 CrossRef CAS.
- M.-C. Jung, K.-W. Lee and W. E. Pickett, Phys. Rev. B, 2018, 97, 121104 CrossRef CAS.
- M. Kim, E. Pallecchi, R. Ge, X. Wu, G. Ducournau, J. C. Lee, H. Happy and D. Akinwande, Nat. Electron., 2020, 3, 479–485 CrossRef CAS.
- I. Ashraf, S. Rizwan and M. Iqbal, Front. Mater., 2020, 7, 181 CrossRef.
- W. Lengauer, J. Phys. Chem. Solids, 1988, 49, 59–63 CrossRef CAS.
- Y. M. Shy, L. E. Toth and R. Somasundaram, J. Appl. Phys., 2003, 44, 5539–5545 CrossRef.
- S. P. Chockalingam, M. Chand, J. Jesudasan, V. Tripathi and P. Raychaudhuri, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 214503 CrossRef.
- V. M. Pan, V. G. Prokhorov, V. A. Komashko, G. G. Kaminsky, M. A. Kousenetsov and C. G. Tretiatchenko, IEEE Trans. Magn., 1989, 25, 2000–2003 CrossRef CAS.
- R. Sherbondy, R. W. Smaha, C. J. Bartel, M. E. Holtz, K. R. Talley, B. Levy-Wendt, C. L. Perkins, S. Eley, A. Zakutayev and G. L. Brennecka, Chem. Mater., 2022, 34, 6883–6893 CrossRef CAS.
- N. E. Brese and F. J. DiSalvo, J. Solid State Chem., 1995, 120, 378–380 CrossRef CAS.
- K. R. Talley, C. L. Perkins, D. R. Diercks, G. L. Brennecka and A. Zakutayev, Science, 2021, 374, 1488–1491 CrossRef CAS.
- S. D. Kloß, M. L. Weidemann and J. P. Attfield, Angew. Chem., Int. Ed., 2021, 60, 22260–22264 CrossRef PubMed.
- S. Bandyopadhyay, A. Paul and I. Dasgupta, Phys. Rev. B, 2020, 101, 014109 CrossRef CAS.
- S. Ghosh, R. R. Banik and J. Chowdhury, Indian J. Theor. Phys., 2021, 69, 43–68 Search PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B, 1991, 44, 943–954 CrossRef CAS.
- H. Xiao, J. Tahir-Kheli and W. A. Goddard III, J. Phys. Chem. Lett., 2011, 2, 212–217 CrossRef CAS.
- I. N. Yakovkin and P. A. Dowben, Surf. Rev. Lett., 2007, 14, 481–487 CrossRef CAS.
- D. S. Lambert and D. D. O'Regan, Phys. Rev. Res., 2023, 5, 013160 CrossRef CAS.
- S. Tomić and N. M. Harrison, AIP Conf. Proc., 2010, 1199, 65–66 CrossRef.
- D. Wing, G. Ohad, J. B. Haber, M. R. Filip, S. E. Gant, J. B. Neaton and L. Kronik, Proc. Natl. Acad. Sci. U.S.A., 2021, 118, e2104556118 CrossRef CAS PubMed.
- S. Ghosh, S. Sarkar and J. Chowdhury, Mater. Chem. Phys., 2022, 276, 125379 CrossRef CAS.
- R. Ray Banik, S. Ghosh and J. Chowdhury, Phys. Scr., 2023, 98, 045920 CrossRef CAS.
- S. Ghosh and J. Chowdhury, Mater. Sci. Eng., B, 2022, 284, 115903 CrossRef CAS.
- R. R. Banik, S. Ghosh and J. Chowdhury, Phys. Scr., 2023, 98, 105914 CrossRef CAS.
- S. Śmiga and L. A. Constantin, J. Phys. Chem. A, 2020, 124, 5606–5614 CrossRef.
- A. J. Garza and G. E. Scuseria, J. Phys. Chem. Lett., 2016, 7, 4165–4170 CrossRef CAS PubMed.
- H. Einollahzadeh, R. S. Dariani and S. M. Fazeli, Solid State Commun., 2016, 229, 1–4 CrossRef CAS.
- J. M. Crowley, J. Tahir-Kheli and W. A. Goddard III, J. Phys. Chem. Lett., 2016, 7, 1198–1203 CrossRef CAS PubMed.
- Y. Duan, L. Qin, L. Shi and G. Tang, Comput. Mater. Sci., 2015, 101, 56–61 CrossRef CAS.
- S. Chowdhury, S. Ghosal, D. Mondal and D. Jana, J. Phys. Chem. Solids, 2022, 170, 110909 CrossRef CAS.
- E. Bedolla, L. C. Padierna and R. Castañeda-Priego, J. Phys.: Condens. Matter, 2021, 33, 053001 CrossRef CAS.
- S. Chibani and F.-X. Coudert, APL Mater., 2020, 8, 080701 CrossRef CAS.
- C. Gao, X. Yang, M. Jiang, L. Chen, Z. Chen and C. V. Singh, Phys. Chem. Chem. Phys., 2022, 24, 4653–4665 RSC.
- Y. Zhang, W. Xu, G. Liu, Z. Zhang, J. Zhu and M. Li, PLoS One, 2021, 16, e0255637 CrossRef CAS PubMed.
- A. Halder, A. Ghosh and T. S. Dasgupta, Phys. Rev. Mater., 2019, 3, 084418 CrossRef CAS.
- Y. Zhuo, A. Mansouri Tehrani and J. Brgoch, J. Phys. Chem. Lett., 2018, 9, 1668–1673 CrossRef CAS PubMed.
- Y. Tang, H. Chen, J. Wang and X. Niu, Phys. Chem. Chem. Phys., 2023, 25, 18086–18094 RSC.
- M. Gao, B. Cai, G. Liu, L. Xu, S. Zhang and H. Zeng, Phys. Chem. Chem. Phys., 2023, 25, 9123–9130 RSC.
- H. J. Kulik, T. Hammerschmidt, J. Schmidt, S. Botti, M. A. L. Marques, M. Boley, M. Scheffler, M. Todorović, P. Rinke, C. Oses, A. Smolyanyuk, S. Curtarolo, A. Tkatchenko, A. P. Bartók, S. Manzhos, M. Ihara, T. Carrington, J. Behler, O. Isayev, M. Veit, A. Grisafi, J. Nigam, M. Ceriotti, K. T. Schütt, J. Westermayr, M. Gastegger, R. J. Maurer, B. Kalita, K. Burke, R. Nagai, R. Akashi, O. Sugino, J. Hermann, F. Noé, S. Pilati, C. Draxl, M. Kuban, S. Rigamonti, M. Scheidgen, M. Esters, D. Hicks, C. Toher, P. V. Balachandran, I. Tamblyn, S. Whitelam, C. Bellinger and L. M. Ghiringhelli, Electron. Struct., 2022, 4, 023004 CrossRef CAS.
- O. Allam, B. W. Cho, K. C. Kim and S. S. Jang, RSC Adv., 2018, 8, 39414–39420 RSC.
- F. Wang, Z. Yang, F. Li, J.-L. Shao and L.-C. Xu, RSC Adv., 2023, 13, 31728–31737 RSC.
- V. Gladkikh, D. Y. Kim, A. Hajibabaei, A. Jana, C. W. Myung and K. S. Kim, J. Phys. Chem. C, 2020, 124, 8905–8918 CrossRef CAS.
- G. Pilania, A. Mannodi-Kanakkithodi, B. P. Uberuaga, R. Ramprasad, J. E. Gubernatis and T. Lookman, Sci. Rep., 2016, 6, 19375 CrossRef CAS PubMed.
- A. Talapatra, B. P. Uberuaga, C. R. Stanek and G. Pilania, Commun. Mater., 2023, 4, 46 CrossRef CAS.
- V. Vakharia, I. E. Castelli, K. Bhavsar and A. Solanki, Phys. Lett. A, 2022, 422, 127800 CrossRef CAS.
- S. Priyanga G, M. N. Mattur, N. Nagappan, S. Rath and T. Thomas, J. Mater., 2022, 8, 937–948 Search PubMed.
- Z. Wan, Q.-D. Wang, D. Liu and J. Liang, New J. Chem., 2021, 45, 9427–9433 RSC.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- J. Hauke and T. Kossowski, Quaest. Geogr., 2011, 30, 87–93 Search PubMed.
- P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. de Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105 CrossRef CAS PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- D. F. Shanno, Math. Comput., 1970, 24, 647–656 CrossRef.
- D. Goldfarb, Math. Comput., 1970, 24, 23–26 CrossRef.
- R. Fletcher, Comput. J., 1970, 13, 317–322 CrossRef.
- C. G. Broyden, IMA J. Appl. Math., 1970, 6, 76–90 CrossRef.
- A. Dal Corso, Comput. Mater. Sci., 2014, 95, 337–350 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- A. Benassi, PWSCF ’s epsilon.x user's manual, https://www.researchgate.net/profile/Nowzar-Soltani/post/Can_anyone_answer_this_question_on_the_optical_properties_of_the_Epsilon_calculations/attachment/59d623046cda7b8083a1d75b/AS%3A310495943299072%401451039409313/download/eps_man.pdf) Search PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- J. Hu, S. Stefanov, Y. Song, S. S. Omee, S.-Y. Louis, E. M. D. Siriwardane, Y. Zhao and L. Wei, npj Comput. Mater., 2022, 8, 65 CrossRef.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj Comput. Mater., 2016, 2, 16028 CrossRef.
- K. Li, Y. Li and D. Xue, Funct. Mater. Lett., 2011, 04, 217–219 CrossRef CAS.
- A.-S. Om Kumar, V. Shukla and S. K. Srivastava, J. Sci.: Adv. Mater. Devices, 2019, 4, 158–162 Search PubMed.
- K. Li, C. Kang and D. Xue, Mater. Res. Bull., 2012, 47, 2902–2905 CrossRef CAS.
- M. Rahm, P. Erhart and R. Cammi, Chem. Sci., 2021, 12, 2397–2403 RSC.
- S. Bandyopadhyay and I. Dasgupta, Phys. Rev. B, 2021, 103, 014105 CrossRef CAS.
- T. Ahmad, K. Jindal, M. Tomar and P. K. Jha, Phys. Chem. Chem. Phys., 2023, 25, 5857–5868 RSC.
- S. Ghosh and J. Chowdhury, Phase Transitions, 2023, 96, 446–463 CrossRef CAS.
- R. Phillips, Crystals, Defects and Microstructures: Modeling across Scales, Cambridge University Press, Cambridge, 2001 Search PubMed.
- B. Grabowski, P. Söderlind, T. Hickel and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 214107 CrossRef.
- B. Grabowski, T. Hickel and J. Neugebauer, Phys. Status Solidi B, 2011, 248, 1295–1308 CrossRef CAS.
- J. Kangsabanik, M. K. Svendsen, A. Taghizadeh, A. Crovetto and K. S. Thygesen, J. Am. Chem. Soc., 2022, 144, 19872–19883 CrossRef CAS.
- S. Halder, R. A. Kumar, R. Maity and T. P. Sinha, Ceram. Int., 2023, 49, 8634–8645 CrossRef CAS.
- O. I. Malyi and C. M. Acosta, J. Phys. Chem. C, 2020, 124, 14432–14438 CrossRef CAS.
- R. Anbarasan, J. K. Sundar, M. Srinivasan and P. Ramasamy, Comput. Condens. Matter, 2021, 28, e00581 CrossRef.
- Y. Kang, Y. Youn, S. Han, J. Park and C.-S. Oh, Chem. Mater., 2019, 31, 4072–4080 CrossRef CAS.
- R. R. Pela, M. Marques and L. K. Teles, J. Phys.: Condens. Matter, 2015, 27, 505502 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- P. Borlido, J. Schmidt, A. W. Huran, F. Tran, M. A. L. Marques and S. Botti, npj Comput. Mater., 2020, 6, 96 CrossRef CAS.
- S. Matsuishi, D. Iwasaki and H. Hosono, J. Solid State Chem., 2022, 315, 123508 CrossRef CAS.
- P. Bhumla, D. Gill, S. Sheoran and S. Bhattacharya, J. Phys. Chem. Lett., 2021, 12, 9539–9546 CrossRef CAS PubMed.
- K. Demmouche and J. Coutinho, Int. J. Mod. Phys. B, 2018, 32, 1850328 CrossRef CAS.
- Y. Kang, G. Kang, H.-H. Nahm, S.-H. Cho, Y. S. Park and S. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 165130 CrossRef.
- M. I. Naher and S. H. Naqib, Sci. Rep., 2021, 11, 5592 CrossRef CAS PubMed.
- R. Reisfeld, Opt. Mater., 2010, 32, 850–856 CrossRef CAS.
- L. Su, X. Fan, T. Yin, H. Wang, Y. Li, F. Liu, J. Li, H. Zhang and H. Xie, Adv. Opt. Mater., 2020, 8, 1900978 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra00402g |
| This journal is © The Royal Society of Chemistry 2024 |