Assessing the efficacy of aluminum metal clusters Al₁₃ and Al₁₅ in mitigating NO₂ and SO₂ pollutants: a DFT investigation

Abstract

The present investigation delves into the adverse environmental impact of atmospheric pollutant gases, specifically nitrogen dioxide (NO₂) and sulfur dioxide (SO₂), which necessitates the identification and implementation of effective control measures. The central objective of this study is to explore the eradication of these pollutants through the utilization of aluminum Al₁₃ and Al₁₅ metal clusters, distinguished by their unique properties. The comprehensive evaluation of gas/cluster interactions is undertaken employing density functional theory (DFT). Geometric optimization calculations for all structures are executed using the ωB97XD functional and the Def2-svp basis set. To probe various interaction modalities, gas molecule distribution around the metal clusters is sampled using the bee colony algorithm. Frequency calculations employing identical model chemistry validate the precision of the optimization calculations. The quantum theory of atoms in molecules (QTAIM) and natural bond orbital (NBO) methodologies are applied for the analysis of intermolecular interactions. This research establishes the robust formation of van der Waals attractions between the investigated gas molecules, affirming aluminum metal clusters as viable candidates for the removal and control of these gases.

---

1. Introduction

Sulfur dioxide (SO₂) and nitrogen dioxide (NO₂) are deleterious gases with pronounced implications for both human health and environmental integrity.^1–3 SO₂ emanates predominantly from the combustion of sulfur-laden fossil fuels, such as coal and oil.^4,5 Consequently, power plants and industrial facilities that utilize these fuels contribute significantly to atmospheric SO₂ concentrations. This emission not only raises concerns for air quality and human health but also underscores the environmental impact of energy production.^6,7 Upon release into the atmosphere, SO₂ undergoes reactions with other compounds, precipitating the formation of fine particulate matter and thereby contributing to atmospheric pollution.^2,8 Prolonged exposure to heightened concentrations of SO₂ poses a significant threat to respiratory health,⁹ manifesting in conditions such as asthma¹⁰ and bronchitis.¹¹ Conversely, NO₂, another byproduct of combustion processes, also engenders the formation of fine particulate matter and ground-level ozone, exacerbating broader air quality concerns.^12,13 Persistent exposure to elevated NO₂ levels is associated with respiratory ailments and the exacerbation of pre-existing conditions. Moreover, both SO₂ and NO₂ are implicated in the acidification of soil and water bodies,¹⁴ thereby instigating ecological imbalances and adversely affecting aquatic ecosystems.¹⁵ Mitigating emissions of these pollutants is imperative to uphold human health standards and preserve environmental equilibrium.

Diverse materials have been applicated in the mitigation of gases within various environmental contexts, notably in the realms of air purification and industrial procedures. For instance, activated carbon,¹⁶ distinguished by its expansive surface area and porous structure, is extensively utilized for gas adsorption owing to its capacity to entrap and retain a spectrum of pollutants, including volatile organic compounds and malodorous gases.^17,18 Zeolites, crystalline aluminosilicate minerals, manifest selective adsorption properties, rendering them efficacious in the removal of specific gases and contaminants.^19,20 Besides, metal–organic frameworks represent a contemporary material class characterized by tunable structures, proffering elevated surface areas and customized functionalities conducive to gas adsorption and separation.^21,22 Furthermore, scrubbers employing liquid agents like sodium hydroxide or calcium oxide demonstrate proficiency in adsorbing and neutralizing acidic gases such as sulfur dioxide.²³ Molecular sieves,²⁴ silica gels,²⁵ and activated alumina²⁶ are other important materials used as gas removal compounds. The selection of gas removal materials is contingent upon factors such as the targeted gas pollutants, operational conditions, and the desired efficacy of the removal process. Ongoing research and advancements in material science persist in broadening the spectrum of options for efficacious gas removal across diverse applications.

Within the scope of adsorbing materials, aluminum metallic clusters have emerged as a compelling frontier, garnering significant attention from researchers globally.²⁷ The distinctive properties and behaviors of these clusters have rendered them particularly intriguing. Notably, possessing an expansive surface-to-volume ratio, these nanoclusters exhibit a plethora of remarkable attributes that set them apart from their bulk aluminum counterparts.^28,29 Their diminutive size and augmented surface area result in a profusion of active sites conducive to catalyzing chemical reactions, thereby establishing them as highly efficient catalysts for a diverse array of chemical transformations.³⁰ Moreover, the utilization of synthesis techniques such as physical vapor deposition, chemical vapor deposition, and cluster beam methods facilitates the precise tailoring of aluminum nanocluster structures, encompassing control over their size, shape, and composition. This exceptional tunability empowers researchers to delve into the intricate interplay between structure and properties.^31–33 Aluminum nanoclusters exhibit versatile applications across various disciplines. As a catalyst, their noteworthy catalytic activities prove advantageous for the creation of innovative and efficient catalysts, thereby impacting diverse industrial processes.³⁴ Additionally, the incorporation of these nanoclusters into electronic systems presents a potential avenue for the advancement of electronic components characterized by enhanced performance and miniaturization.^27,35,36

Broadly speaking, the employment of atomic metal clusters of transition metals, coupled with diverse nanocages, represents a prevalent approach in the utilization of material for the adsorption and regulation of polluting gases, the purification of liquids, and the remediation of environmental contaminants. Mohammadi et al.³⁷ have demonstrated the potential of atomic clusters of gold and silver to adsorb the atmospheric polluting gases, specifically highlighting their impact on SO₂ and NO₂. Furthermore, a research conducted by the same group has unveiled the efficacy of zinc and zinc oxide clusters in the adsorption and containment of gases, including carbon dioxide, etc.³⁸ In a distinct investigation, Hussain et al.³⁹ have undertaken fundamental research to elucidate the interaction dynamics between B₁₂N₁₂ nanocage and Phosgene gas. In a research by Guardado et al.⁴⁰ the prominent role of lithium atomic clusters in hydrogen gas storage has been highlighted. Numerous instances exemplify the pivotal role played by metal clusters, oxides,⁴¹ hydrides,⁴² and hydroxides,⁴³ serving as highly pragmatic advanced materials primarily deployed in the fabrication of electronic devices,⁴⁴ drug delivery systems,^45,46 water purification technologies,⁴⁷ and respiratory air purification methodologies,^48,49 among other applications.

Aluminum metal clusters are poised as versatile assets with considerable utility across a spectrum of applications, particularly in the area of sensor innovation and gas purification technologies.⁵⁰ Their unique electronic and chemical properties endow them with a diverse array of functionalities. In the domain of gas sensing, aluminum clusters serve as pivotal sensing elements, interacting with gas molecules to effect changes in electrical conductivity, optical characteristics, or surface reactivity.⁵¹ This inherent adaptability facilitates the discernment of a wide gamut of gases, including those of a hazardous nature, within industrial, environmental, and medical contexts. Furthermore, aluminum clusters assume a catalytic role, expediting chemical reactions essential to the mitigation of pollutants, thereby bolstering the efficacy of gas abatement methodologies for air decontamination and environmental remediation efforts.⁵² Moreover, the integration of aluminum clusters into porous substrates or nanocomposite matrices augments their capacity for gas adsorption, particularly towards species such as carbon dioxide, sulfur dioxide, and volatile organic compounds. This enhancement is of paramount significance in curtailing the emission of pollutants from industrial sources, vehicular exhausts, and indoor environments. Additionally, aluminum-based materials, inclusive of metal clusters, are under scrutiny for their potential in hydrogen storage applications. In this capacity, these clusters function as adept hydrogen adsorbents, enabling the reversible storage and release of hydrogen gas for utilization in fuel cell technologies and other energy-centric endeavors.^53–55

The objective of the upcoming research is to use quantum mechanical calculations to study intermolecular interactions of SO₂ and NO₂ gases onto the exterior surface of aluminum atomic clusters of Al₁₃ and Al₁₅. In addition, the methodology employed for computing adsorption energy is explicated, accompanied by a brief theoretical discourse on various facets of the calculations. For the computational scrutiny of the specified systems, the initial imperative lies in determining the stable ground state of aluminum clusters. A comprehensive elucidation of the procedures for generating and identifying the most stable ground state, predicated upon the energy content of atomic clusters, is provided in Section 3.1. Section 3.2 delves into the electronic structure of the aforementioned clusters. Sections 3.3 and 3.4 of this study encompass an analysis of the interactions between the gas and the cluster, employing various methodologies such as natural bond orbital (NBO) and quantum theory of atoms in molecules (QTAIM). The examination involves a comprehensive investigation into the nature of these interactions. Subsequently, in Section 4, a succinct summary of the research findings will be presented. This final section encapsulates the overarching conclusions derived from the analytical processes conducted in the preceding sections.

2. Computational details

The ωB97XD functional, with a dispersion correction term, effectively predicts electronic structure and energetics, considering repulsive and interactive electron influences, notably addressing long-range van der Waals interactions. Hence, employing the ωB97XD functional.⁵⁶ This approach extends the functionality of the prevalent ωB97 functional by amalgamating the empirical long-range correction (LC) articulated by Handy and Cohen with the PBE functional pioneered by Perdew, Burke, and Ernzerhof. The incorporation of dispersion corrections within the ωB97XD framework serves to accommodate van der Waals interactions, pivotal for an accurate depiction of non-covalent interplays among molecules, encompassing dispersion forces, π–π stacking, and hydrogen bonding. These enhancements in dispersion corrections substantially augment the fidelity of the method, especially in scenarios where non-covalent interactions wield pronounced influence, as observed in molecular aggregates, supramolecular complexes, and biomolecular systems. By integrating dispersion corrections, ωB97XD furnishes a more equitable portrayal of both short-range exchange–correlation interactions and long-range dispersion interactions, thereby engendering enhanced precision in the prognosis of diverse molecular attributes, spanning molecular geometries, energies, reaction barriers, and intermolecular interactions. This method excels in noncovalent interaction studies, reaction energies, pathways, and spectroscopic characteristics.^57–59

The Def2-svp basis set is recognized for accuracy in diverse chemical configurations, combines functions for valence electrons with polarization functions to address electron correlation effects and is chosen for its comprehensive coverage, elucidating complex interplays among molecular components, which is suitable for intermediate-sized molecules and moderately correlated systems.^60,61 The research focuses on optimizing the geometries of Al₁₃ and Al₁₅ clusters, along with gaseous NO₂ and SO₂ species, and conducting frequency analysis to ensure the stability of complexes/monomers. The Def2-SVP (SVP stands for single valence with polarization) and Def2-TZVPP (TZVPP stands for triple zeta valence with polarization and diffuse functions) basis sets are both widely used in computational chemistry for quantum mechanical calculations. These basis sets are designed to provide increasingly accurate descriptions of molecular electronic structure by systematically including more basis functions. The Def2-SVP basis set includes a moderate number of basis functions, usually sufficient for calculations on small to medium-sized molecules. It comprises a single valence set with additional polarization functions to account for electron correlation effects and diffuse functions to capture the electronic behavior in regions of low electron density. On the other hand, the Def2-TZVPP basis set is more extensive, incorporating triple zeta valence quality functions with additional polarization and diffuse functions. This allows for a more accurate representation of the electronic wavefunction and can yield more precise results, especially for larger and more complex molecular systems. The advantage of using the Def2-SVP basis set lies primarily in its computational efficiency without compromising significantly on accuracy. Since it contains fewer basis functions compared to Def2-TZVPP, calculations using Def2-SVP typically require less computational resources in terms of memory and CPU time. This makes Def2-SVP particularly advantageous for preliminary studies, high-throughput screenings, or when computational resources are limited. Additionally, the moderate size of the Def2-SVP basis set can sometimes lead to more stable and reliable convergence behavior in electronic structure calculations compared to larger basis sets, especially for systems where electronic correlation effects are not dominant.

The investigation and analysis of the electronic characteristics of the structures mentioned above have been a subject of scholarly discourse. The focus of this examination primarily centers on the evaluation of the frontier molecular orbitals (FMOs). To achieve a comprehensive understanding of the nature of intermolecular interactions, analyses based on the quantum theory of atoms in molecules (QTAIM) and natural bond orbital (NBO) methodologies have been implemented. The geometry structures of the gaseous species NO₂ and SO₂ were constructed using Gauss View software,⁶² with optimization and stability evaluations conducted through the Gaussian 09 package.⁶³ The extraction of precise geometric arrangements for the aluminum clusters Al₁₃ and Al₁₅ was accomplished using the ABCluster 3.1.⁶⁴ This software incorporates a sophisticated module for the automated allocation of two gas molecules and clusters to disparate spatial coordinates. These spatial arrangements, hereinafter referred to as “configurations,” undergo geometric optimization to identify those demonstrating utmost stability in relation to their ground state energy content. Selected configurations are then subjected to further analysis. The NBO 3.1 software,⁶⁵ integrated into the Gaussian 09 package, was employed for executing NBO and QTAIM calculations. Additionally, the Multiwfn⁶⁶ package was utilized to elucidate and visualize the resultant findings based on electronic structure analyses.

The quantification of adsorption energy (E_ads) is contingent upon the intricate framework of supramolecular theory referred to eqn (1).^67,68 This methodology involves the energy contributions originating from both the self-contained cluster and the targeted gaseous entity. The amalgamation of these two distinct magnitudes results in the subsequent deduction of the aggregated energy value characterizing the gas@cluster configurations. Additionally, it is demonstrated that the correction pertaining to zero-point energy (ZPEC) is concurrently administered, and this correction is derived through frequency calculations.

E_ads = E_complex − (E_gas + E_cluster) + ΔE_ZPEC (1)

In this context, the symbol E_ads represents the adsorption energy, while E_gas denotes the cumulative energy contained within the gas adsorbate. E_cluster signifies the aggregated energy encompassing the aluminum atom-based metallic cluster, and E_complex indicates the energetic constitution of the comprehensive gas/cluster complex. Notably, in this specific correlation, the parameter ΔE_ZPEC assumes paramount significance. This is crucial as the zero-point energy is inherently integrated into the adsorption energy association, providing a comprehensive elucidation of the energies under examination.

The method employed for ascertaining the optimal structure of Al₁₃ and Al₁₅ clusters involved the initial generation of 10 000 geometries for each structural isomers of a cluster utilizing specialized ABCluster software, with subsequent determination of their total energy employing the CHARMM force field.⁶⁹ Subsequently, isoenergies were subjected to a screening process, and a representative sample was chosen for each energy level. In the subsequent stage, 1000 structures were subjected to semi-empirical calculations using the xtb software,⁷⁰ and the total energy of these systems was computed utilizing the PM7 method. Ultimately, 100 structures characterized by the most stable energy levels were identified and submitted to the Gaussian software for DFT calculations. This sequential approach facilitated a comprehensive exploration of the energy landscapes of the respective clusters, contributing to the identification of structurally the most stable configurations. Ultimately, the selection process led to the identification of the most stable cluster, and its corresponding XYZ structure is presented in Table S1 within the (ESI†) section. It is to note that all clusters have been thoroughly already examined at 273 K and 1 atmospheric pressure using Gaussian Package.

3. Results and discussion

3.1 Geometry optimization

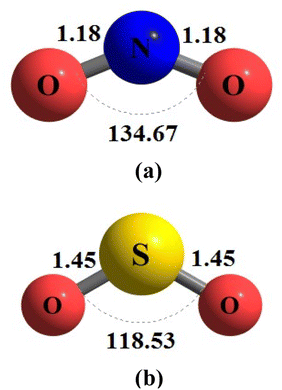
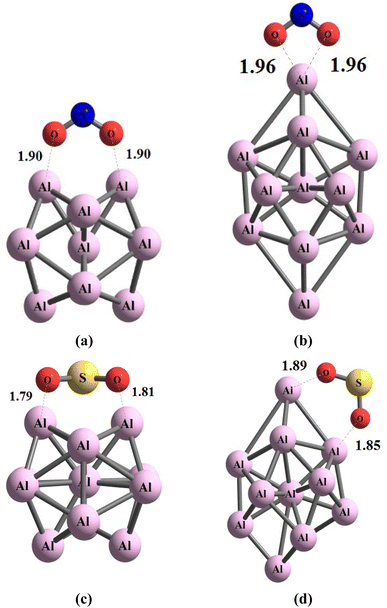
During the initial computational stage, it is imperative to verify the spatial morphology of aluminum clusters to identify their most stable configuration. The inherent lack of symmetry in these clusters complicates the determination of their optimal structure. Consequently, a specialized software ABCluster⁶⁴ has been designed to address this challenge. This software facilitates the generation of diverse spatial shapes, which can then be transmitted as input files to the Gaussian 09 (ref. 63) software for subsequent DFT calculations. This research does not delve into the intricacies of the artificial bee colony algorithm, which is employed in the software; however, the comprehensive descriptions of the bee colony algorithm can be found in relevant ref. 64, 71 and 72.

In Fig. 1, section (a), presents data on the bond length and interatomic angle of the NO₂ molecule, wherein the interatomic angle measures 134.67 Radians (rad), and the oxygen–nitrogen bond length is quantified at 1.18 Angstroms (Å). Subsequently, Fig. 1b depicts corresponding metrics for the SO₂ molecule, revealing an interatomic angle of 118.53 rad and a sulfur–oxygen bond length of 1.45 Å. The observed reduction in the interatomic angle in the SO₂ molecule can be attributed to an increasement of lone pair electrons within the valence layer of the sulfur atom. Subsequent computations demonstrate alterations in these bond lengths and angles as a consequence of interactions with aluminum clusters. Fig. 2 depicts the structural representations of aluminum clusters comprising 13 and 15 atoms in part (a) and (b), respectively. Given the intricate nature of these structures, involving numerous angles and varied bond lengths, the XYZ coordinates corresponding to these clusters have been systematically tabulated in Table S1.† Subsequently, utilizing a graphic tool, a comprehensive visualization of these structures has been generated, allowing for a detailed examination of pertinent structural information. Symmetry plays a pivotal role in dictating the stability of molecular configurations, exemplified by aluminum clusters such as Al₁₃ and Al₁₅. Al₁₃, characterized by its pronounced symmetry, assumes an icosahedral geometry, thereby facilitating optimal aluminum atom packing, thereby mitigating repulsive forces and augmenting stability. Conversely, Al₁₅, owing to its larger size, tends to manifest a more intricate and asymmetrical configuration, leading to less efficient atom packing and potentially heightened internal strain. Consequently, the stability of Al₁₅ typically pales in comparison to that of Al₁₃. In essence, the heightened symmetry inherent in Al₁₃ significantly bolsters its stability relative to the less symmetrical Al₁₅ cluster, as symmetry profoundly influences atom arrangements within the cluster, thereby modulating their interactions and overall stability characteristics.

Fig. 1 This illustration seeks to explain the detailed shapes of (a) nitrogen dioxide (NO₂) and (b) sulfur dioxide (SO₂) using the optimization method ωB97XD/Def2-svp. In the visual representation, the measurements are given in Angstroms (Å) for bond lengths and Radian (rad) for angles.

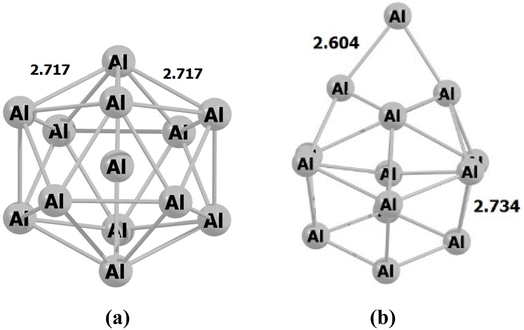Fig. 2 The figure illustrates an scheme of the geometry of the structures associated with (a) Al₁₃ and (b) Al₁₅ through optimization utilizing the ωB97XD/Def2-svp method. The values are in Å.

The disparate interaction characteristics of SO₂ gas with aluminum clusters, contingent upon whether the interaction occurs from the side of the sulfur atom or the oxygen atoms, result in distinct adsorption energies (E_ads). Furthermore, the outer surface of aluminum clusters exhibits diverse adsorption sites, necessitating a comprehensive examination of the entire cluster environment. Consequently, it becomes imperative to systematically investigate the adsorption energies of SO₂ or NO₂ gas molecules around the cluster molecule from various orientations. This investigative process, conventionally labor-intensive, has prompted the development of a specialized module within the ABCluster software. This module facilitated the automated generation of diverse gas@cluster configurations, streamlining the exhaustive exploration of adsorption energies under varying spatial arrangements. The investigation entails the consideration of a myriad of gas@cluster configurations, necessitating the determination of their respective adsorption energies to identify the most stable configuration. The methodology employed for discerning the most stable gas@cluster configuration mirrors the approach delineated earlier for determining aluminum cluster isomers. This consistent methodological framework has been systematically applied, resulting in the identification and documentation of 10 stable configurations, which are detailed in the ESI† section, specifically outlined in Table S1.† It is pertinent to elucidate that the nomenclature “gas@cluster_n” signifies the desired configuration indexed by n.

The examination of adsorption behaviors of NO₂ and SO₂ onto aluminum clusters, specifically Al₁₃ and Al₁₅, reveals intriguing insights into the stability of the resulting structures and their respective adsorption energies. The adsorption energies of NO₂ and SO₂ gases on clusters Al₁₃ and Al₁₅ exhibit variability contingent upon the spatial orientation of the respective molecules. The tabulated values in Table 1 elucidate this discrepancy, revealing a range of adsorption energies between −2.61 and −3.1 eV for NO₂ gas adsorption on the aluminum cluster with 13 atoms. Notably, the configuration NO₂@Al₁₃_4 (i.e. −3.1 eV) emerges as the most stable configuration within this context. Fig. 3, part (a), provides a visual representation of this system, although it is advisable to reference Table S1† for a more comprehensive understanding and a superior spatial visualization in graphical interfaces such as Gauss View. This approach allows for the observation and tracking of atomic angles, interatomic distances, and dihedral angles. The comprehensive presentation of such information within the textual narrative is deemed impractical and would not match the efficacy of a graphical interface. The variance in adsorption energy values observed between Al₁₅ clusters and NO₂ gas molecules spans from −2.49 to −3.97 eV, with these respective values corresponding to configurations NO₂@Al₁₅_6 and NO₂@Al₁₅_1. In Fig. 3, part (b), a schematic representation is presented illustrating the orientation of the NO₂ gas molecule on the outer surface of the Al₁₅ cluster, wherein the maximum adsorption energy is attained, signifying its optimal stability. Upon comparing the optimal configurations of Al₁₃ and Al₁₅ clusters in their interactions with NO₂ gas, it is deduced that the aluminum cluster composed of 15 atoms exhibits a superior adsorption capacity in comparison to its 13-atom counterpart which enables Al₁₅ to effectively hold NO₂ on it surface. The aluminum cluster composed of 15 atoms exhibited a better ability to accept electrons with a higher electrophilicity value η (eV) of 2.61 eV.

Table 1 The electronic structure parameters acquired through DFT calculations employing the ωB97XD/Def2-svp computational framework encompass an array of fundamental quantities: the HOMO energy (ε_HOMO), LUMO energy (ε_LUMO), the energy gap between the HOMO and LUMO orbitals (HLG), the chemical potential (μ), chemical hardness (η), electrophilicity index (ω), total electronic energy expressed in Hartree units (HF), and the adsorption energy (E_ads) pertaining to interactions between gaseous molecules and aluminum clusters

Systems	εHOMO (eV)	εLUMO (eV)	HLG (eV)	μ (eV)	η (eV)	ω	EE (HF)	Eads (eV)
Al13	−7.1261	−2.0126	5.1136	4.5693	2.5568	4.0830	−3150.595438	—
Al15	−5.6140	−1.9794	3.6346	3.7967	1.8173	3.9659	−3635.319898	—
NO2	−10.0282	−0.2057	9.8225	5.1170	4.9112	2.6657	−204.848691	—
SO2	−11.2848	−1.5842	9.7006	6.4345	4.8503	4.2681	−548.2876908	—
NO2@Al13_1	−7.0597	−2.0526	5.0072	4.5561	2.5036	4.1457	−3355.554484	−3.0029
NO2@Al13_2	−7.1223	−2.2256	4.8967	4.6740	2.4483	4.4614	−3355.539934	−2.6070
NO2@Al13_3	−7.0611	−2.0536	5.0074	4.5574	2.5037	4.1477	−3355.554484	−3.0029
NO2@Al13_4	−6.8690	−2.1813	4.6877	4.5251	2.3439	4.3682	−3355.558329	−3.1075
NO2@Al13_5	−7.1231	−2.2248	4.8983	4.6740	2.4492	4.4599	−3355.539942	−2.6072
NO2@Al13_6	−7.0603	−2.0531	5.0072	4.5567	2.5036	4.1467	−3355.554484	−3.0029
NO2@Al13_7	−7.0595	−2.0523	5.0072	4.5559	2.5036	4.1452	−3355.554484	−3.0029
NO2@Al13_8	−7.0608	−2.0528	5.0080	4.5568	2.5040	4.1463	−3355.554484	−3.0029
NO2@Al13_9	−7.1229	−2.2256	4.8972	4.6742	2.4486	4.4614	−3355.539931	−2.6069
NO2@Al13_10	−7.1337	−1.7111	5.4227	4.4224	2.7113	3.6066	−3355.551638	−2.9255
NO2@Al15_1	−7.1672	−1.9394	5.2279	4.5533	2.6139	3.9658	−3840.314374	−3.9670
NO2@Al15_2	−6.6331	−1.8838	4.7492	4.2584	2.3746	3.8184	−3840.294603	−3.4290
NO2@Al15_3	−7.0437	−2.2245	4.8191	4.6341	2.4096	4.4562	−3840.296942	−3.4927
NO2@Al15_4	−6.5343	−2.1606	4.3737	4.3474	2.1868	4.3213	−3840.277461	−2.9626
NO2@Al15_5	−6.6649	−1.8975	4.7674	4.2812	2.3837	3.8445	−3840.309092	−3.8233
NO2@Al15_6	−6.7898	−2.1347	4.6551	4.4623	2.3275	4.2775	−3840.260096	−2.4900
NO2@Al15_7	−7.0328	−2.2346	4.7982	4.6337	2.3991	4.4748	−3840.296952	−3.4929
NO2@Al15_8	−6.5917	−2.0332	4.5585	4.3125	2.2792	4.0797	−3840.283349	−3.1228
NO2@Al15_9	−6.4388	−1.8814	4.5574	4.1601	2.2787	3.7974	−3840.287373	−3.2323
NO2@Al15_10	−6.9520	−2.3130	4.6390	4.6325	2.3195	4.6259	−3840.295392	−3.4505
SO2@Al13_1	−6.5525	−2.6360	3.9165	4.5942	1.9583	5.3892	−3698.983339	−2.7269
SO2@Al13_2	−6.6366	−1.9775	4.6591	4.3070	2.3296	3.9815	−3698.991228	−2.9415
SO2@Al13_3	−6.8907	−3.6240	3.2667	5.2574	1.6334	8.4611	−3698.918967	−0.9752
SO2@Al13_4	−7.2034	−2.1119	5.0915	4.6576	2.5458	4.2607	−3698.889817	−0.1820
SO2@Al13_5	−6.6096	−1.8297	4.7800	4.2197	2.3900	3.7251	−3699.014201	−3.5666
SO2@Al13_6	−6.6369	−1.9783	4.6586	4.3076	2.3293	3.9830	−3698.991235	−2.9417
SO2@Al13_7	−6.6175	−1.8305	4.7870	4.2240	2.3935	3.7272	−3699.014199	−3.5666
SO2@Al13_8	−6.6113	−1.8281	4.7832	4.2197	2.3916	3.7225	−3699.014199	−3.5666
SO2@Al13_9	−6.6344	−1.9764	4.6580	4.3054	2.3290	3.9794	−3698.991233	−2.9417
SO2@Al13_10	−6.8875	−3.6599	3.2275	5.2737	1.6138	8.6171	−3698.918964	−0.9751
SO2@Al15_1	−6.5033	−1.8354	4.6678	4.1693	2.3339	3.7241	−4183.741918	−3.6553
SO2@Al15_2	−6.4382	−1.7121	4.7261	4.0752	2.3630	3.5139	−4183.729714	−3.3232
SO2@Al15_3	−6.4352	−1.7108	4.7244	4.0730	2.3622	3.5114	−4183.729714	−3.3232
SO2@Al15_4	−6.0015	−1.7290	4.2725	3.8652	2.1362	3.4968	−4183.719169	−3.0362
SO2@Al15_5	−6.4379	−1.7119	4.7261	4.0749	2.3630	3.5135	−4183.729715	−3.3232
SO2@Al15_6	−6.2739	−1.9094	4.3644	4.0916	2.1822	3.8359	−4183.767472	−4.3506
SO2@Al15_7	−6.4276	−1.6460	4.7816	4.0368	2.3908	3.4080	−4183.732452	−3.3977
SO2@Al15_8	−6.9063	−2.1647	4.7416	4.5355	2.3708	4.3383	−4183.717038	−2.9783
SO2@Al15_9	−6.4369	−1.7121	4.7247	4.0745	2.3624	3.5138	−4183.729715	−3.3232
SO2@Al15_10	−6.4184	−1.6414	4.7770	4.0299	2.3885	3.3996	−4183.732399	−3.3963

---

Fig. 3 This figure aims to explain the geometric arrangements of (a) NO₂@Al₁₃, (b) NO₂@Al₁₅, (c) SO₂@Al₁₃, and (d) SO₂@Al₁₅ using the optimization method ωB97XD/Def2-svp. The visual representation displays measurements in Å.

Concerning the adsorption of SO₂ gas on the Al₁₃ cluster, it is observed that the lowest adsorption energy corresponds to configuration SO₂@Al₁₃_4, with a value of −0.18 eV, while the highest energy is associated with configuration SO₂@Al₁₃_8, yielding a value of −3.57 eV. Notably, the range of adsorption energy variations for SO₂ is found to be more extensive than that for NO₂ on the external surface of the Al₁₃ cluster. The underlying rationale for this discrepancy lies in the spatial orientation and the nature of interaction between the two molecular species. This underscores the significance of the orientation of valence layer orbitals of the interacting species, as the ease with which electrons can be accommodated in bonded electrons profoundly influences the intensity of the interaction. Consequently, the juxtaposition of the valence layer orbitals assumes a pivotal role in modulating the strength of interaction between SO₂ and the Al₁₃ cluster. The final system under investigation pertains to the interaction between SO₂ gas and an aluminum cluster comprising 15 atoms. Within the scope of the 10 scrutinized configurations, the configuration denoted as SO₂@Al₁₅_8 exhibits the lowest adsorption energy, quantified at −2.98 eV, while configuration SO₂@Al₁₅_6 attains the highest value at −4.35 eV. The spatial arrangement of the SO₂ gas molecule in conjunction with the Al₁₃ cluster is illustrated in Fig. 3, part (c), and similarly, in part (d), the depiction extends to the same gas juxtaposed onto the aluminum cluster comprising 15 atoms. Upon scrutinizing the adsorption energies derived from these configurations, it becomes evident that the most robust interaction is manifested in the case of the SO₂ species and the Al₁₅ cluster.

It is imperative to acknowledge that the validity of each optimized molecular configuration has been substantiated through frequency calculations, wherein the absence of negative or imaginary frequencies signifies that the optimized structures at the extremum point pertain to the respective local minima. Table 2 provides a comprehensive compilation of all pertinent details derived from thermochemical computations. Additionally, a spectrum of thermochemical parameters, including thermal energy (TE), heat capacity (C_V), and total entropy (S), is systematically presented, furnishing an extensive dataset for the scrutiny and reflection of researchers.

Table 2 The thermochemical parameters, derived from frequency calculations at the ωB97XD/Def2-svp calculation method of study. These encompass the incorporation of a zero-point correction to the energy, expressed in Hartree units (HF), as well as the consideration of thermal energy in kilocalories per mole (kcal mol⁻¹). Additionally, the values of heat capacity, denoted in calories per mole per k (cal mol⁻¹ k⁻¹), and the quantification of entropy, expressed in calories per mole per k (cal mol⁻¹ k⁻¹)

Systems	ZPEC (HF)	TE (kcal mol^−1)	CV (cal mol^−1 k^−1)	S (cal mol^−1 k^−1)
Al13	0.0218	24.782	61.097	132.777
Al15	0.0242	28.625	72.091	151.074
NO2	0.0095	7.767	6.728	57.224
SO2	0.0072	6.458	7.433	59.329
NO2@Al13_1	0.0329	34.183	72.376	152.296
NO2@Al13_2	0.0318	33.885	73.305	158.562
NO2@Al13_3	0.0329	34.183	72.378	152.293
NO2@Al13_4	0.0331	34.069	72.330	147.962
NO2@Al13_5	0.0318	33.893	73.280	157.861
NO2@Al13_6	0.0329	34.183	72.374	152.267
NO2@Al13_7	0.0329	34.183	72.375	152.285
NO2@Al13_8	0.0329	34.183	72.379	152.292
NO2@Al13_9	0.0318	33.882	73.312	158.743
NO2@Al13_10	0.0320	33.962	73.174	156.721
NO2@Al15_1	0.0360	38.245	82.822	170.247
NO2@Al15_2	0.0363	38.085	82.837	163.019
NO2@Al15_3	0.0351	37.979	83.666	172.509
NO2@Al15_4	0.0346	37.805	83.936	174.061
NO2@Al15_5	0.0369	38.282	82.400	161.244
NO2@Al15_6	0.0362	38.531	83.072	172.842
NO2@Al15_7	0.0352	37.984	83.654	172.259
NO2@Al15_8	0.0357	38.142	83.140	171.082
NO2@Al15_9	0.0360	38.236	82.854	169.617
NO2@Al15_10	0.0352	37.398	81.641	165.674
SO2@Al13_1	0.0315	32.8020	72.883	146.172
SO2@Al13_2	0.0289	32.0450	74.617	154.653
SO2@Al13_3	0.0301	32.7400	73.933	158.716
SO2@Al13_4	0.0296	33.0170	74.400	170.079
SO2@Al13_5	0.0301	32.3530	73.750	149.842
SO2@Al13_6	0.0289	32.0430	74.618	154.608
SO2@Al13_7	0.0301	32.3480	73.763	149.872
SO2@Al13_8	0.0301	32.3530	73.753	149.880
SO2@Al13_9	0.0290	32.0490	74.607	154.592
SO2@Al13_10	0.0300	32.1540	71.961	152.376
SO2@Al15_1	0.0335	36.541	84.118	167.290
SO2@Al15_2	0.0333	36.549	84.262	167.679
SO2@Al15_3	0.0333	36.551	84.257	167.653
SO2@Al15_4	0.0332	36.496	84.344	168.639
SO2@Al15_5	0.0333	36.549	84.261	167.701
SO2@Al15_6	0.0330	36.203	84.427	165.639
SO2@Al15_7	0.0331	36.473	84.399	169.217
SO2@Al15_8	0.0326	36.624	84.616	177.921
SO2@Al15_9	0.0333	36.548	84.261	167.667
SO2@Al15_10	0.0331	36.476	84.383	168.920

---

3.2 Electronic structure

In the preceding section, we addressed the influence of different orientations of gas molecules around an aluminum cluster on adsorption energies. The electron redistribution within molecules results in an uneven electron distribution, with one part exhibiting greater electron density and another part demonstrating lower density. This phenomenon prompts an exploration of molecular reactivity. Logically, when a highly reactive portion of a gas molecule interfaces with a larger segment of a reactive cluster, a more robust interaction ensues between the participating species, leading to heightened adsorption energy. Additionally, the alignment of gas and cluster orbitals in the correct spatial orientation is a critical consideration, necessitating an examination of the electronic structure of the involved species. Theoretical explanations pertaining to conceptual density functional theory (CDFT) are provided in the ESI† section. In brief, it is observed that in the analysis of highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO), a smaller energy gap corresponds to increased reactivity of the species. Additionally, a higher electrophilic index (ω) value indicates greater reactivity for a given species. These indices afford a global assessment of the reactivity of two molecules in relation to each other. However, this analysis does not concern itself with determining the specific region of a molecule exhibiting greater reactivity.

Upon closer examination of the data presented in Table 1, it becomes evident that the ω values for aluminum clusters consisting of 13 and 15 atoms are distinctive, yet equally noteworthy, with respective magnitudes of 4.0830 and 3.9659. The presented data unequivocally indicates nearly identical reactivity between the two clusters under consideration, with Al₁₃ exhibiting a slightly elevated level. Nevertheless, it is reasonable to assert, with a high degree of approximation, that the global reactivity of the two clusters is essentially equivalent. Based on the electrophilicity index values obtained for NO₂ gas (2.7) and SO₂ gas (4.3), it is observed that the latter exhibits higher reactivity. It is crucial to underscore that the proper spatial alignment, orbital interaction, and promotion of charge transfer processes collectively contribute to the enhancement of adsorption energy. The findings derived from the adsorption energies, as presented in the preceding section, indicate that the maximum adsorption energy is achieved by SO₂ gas in conjunction with the aluminum cluster Al₁₅. Furthermore, the outcomes from the reactivity analysis align consistently with this observation, affirming the accurate prediction of the aforementioned conclusion.

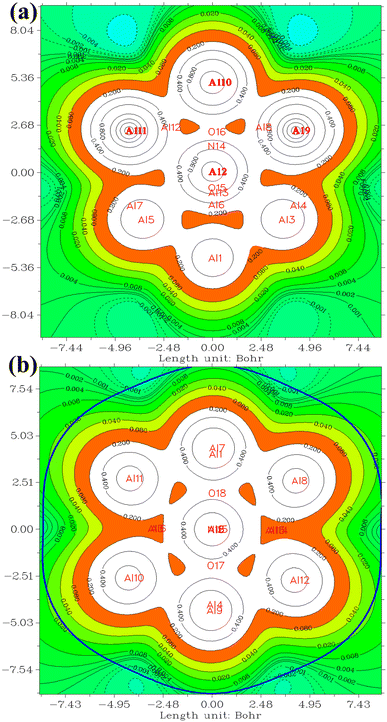
Electrostatic potential (ESP) map serves as valuable tools for elucidating the distribution of electric charge within a molecule or molecular system. In Fig. 4 and 5 the positive and negative regions are depicted by solid and dashed lines respectively. These maps, which visualize the electrostatic potential on a molecular surface, offer crucial insights into diverse facets of a molecule's chemical and physical attributes. The key information derived from ESP maps are details concerning charge distribution, aiding in the identification of regions with positive and negative charges that are pivotal for comprehending chemical reactivity and interactions. Additionally, these maps provide indications of molecular dipole moments, enabling an understanding of molecular polarity and its impacts on various properties. The identification of functional groups is facilitated by specific patterns in electrostatic potential maps, contributing to the interpretation of a molecule's chemical nature. Furthermore, ESP maps assist in predicting sites conducive to nucleophilic and electrophilic attacks in chemical reactions by highlighting regions with high and low electron density, respectively. Hydrogen bonding patterns, essential for predicting and explaining molecular interactions, are discernible through these maps. The inclusion of solvent molecules in electrostatic potential calculations allows for an understanding of a molecule's interaction with its environment and provides insights into solvation effects.

Fig. 4 The ESP for (a) NO₂@Al₁₃, (b) NO₂@Al₁₅. The positive and negative regions are depicted by solid and dashed lines respectively. Atomic symbols are employed to denote the positive and negative ESP values. The threshold is set at 0.2, while iso-surface values are represented at 0.001.

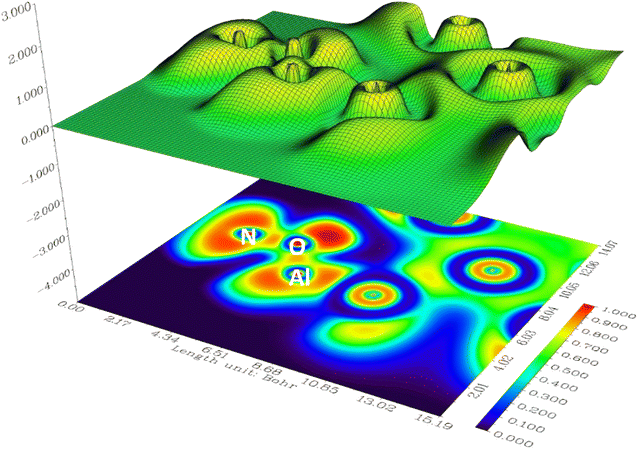
In the investigation of gas/cluster systems, the determination of electrophilic and nucleophilic sites within the adsorptive molecule often involves the utilization of ESP maps. The preceding section elucidated the process of sampling adsorption sites within the cluster molecule, wherein a comprehensive examination and sampling of the entire cluster were conducted. Subsequently, adsorption energy was calculated throughout the entirety of the cluster, resulting in a more extensive database than that derived solely from reactivity analysis. Reactivity analysis, conducted to identify electron-filled sites within the absorber molecule, entails placing the gas molecule in these identified areas and subsequently calculating the adsorption energy. Fig. 4 illustrates the interaction of NO₂ gas with the cluster from the oxygen atom side, demonstrating a peak in the ESP map data. A similar observation is discernible in Fig. 5 concerning the interaction with SO₂ gas.

Fig. 5 The ESP for (a) SO₂@Al₁₃, (b) SO₂@Al₁₅. The positive and negative regions are depicted by solid and dashed lines respectively. Atomic symbols are employed to denote the positive and negative ESP values. The threshold is set at 0.2, while iso-surface values are represented at 0.001.

3.3 NBO analysis

In computational chemistry, both natural bond orbital (NBO) analysis and Hartree–Fock (HF) theory constitute indispensable tools, each serving distinct purposes with inherent advantages. Unlike the delocalized depiction offered by HF theory, which encompasses the entire molecule, NBOs present a localized and chemically intuitive representation of electron density, focusing on specific atoms or bonds for enhanced clarity in understanding chemical bonding. Furthermore, NBO analysis facilitates a more straightforward interpretation of chemical bonds compared to the often-challenging interpretation of HF orbitals, particularly for complex molecules. Notably, NBO analysis excels in identifying and quantifying charge transfer, aiding in the comprehension of electron flow during chemical reactions, a feature less explicit in HF calculations. Additionally, while HF theory provides information about molecular orbitals, it may fall short in quantifying the strength of individual bonds, a limitation addressed by NBO analysis, which includes data on stabilization energies, thereby offering a quantitative measure of bond strength. Moreover, NBO results prove instrumental in predicting reactive sites within a molecule, contributing valuable insights into reaction mechanisms. Lastly, NBOs uniquely permit the quantification of electron delocalization, providing valuable information on the spread of electrons across multiple atoms or regions in a given molecular system.^73–75

Derived from electronic structure calculations, NBOs offer insights into the natural electron configurations associated with specific atoms or bonds within a molecule. By emphasizing localized orbitals, NBOs provide an intuitive and clear representation of electron distribution, enabling a comprehensive understanding of chemical bonding. The concept of “natural electron configuration” within NBO analysis pertains to the electron distribution in these localized NBOs, each with a defined electron occupancy. This analysis facilitates the identification of charge transfer, elucidates bonding characteristics, and quantifies the energetic stability of each orbital through occupancy and stabilization energy assessments. Additionally, NBO analysis enables the quantification of delocalization, shedding light on electron spread across different molecular regions.

Both NO₂ and SO₂ gases exhibit neutrality when considered in isolation, with distributed partial charges resulting in an overall charge of zero. The sulfur atom within the SO₂ molecule carries a partial charge of 1.56, whereas each oxygen atom in this compound bears a charge of −0.78, as outlined in Table 3. Similarly, the partial charges for the nitrogen atom within the NO₂ molecule are 0.54, and for each oxygen atom in the same molecule, the charge is −0.27. The distribution of electrons within the valence layer orbitals of each atom is presented in the natural electron configuration section of Table 3. Both analyses presented in this table furnish valuable data for comparing the isolated state of the specified gases with those engaged in interactions with aluminum clusters.

Table 3 Natural electron configurations as well as natural charges values for isolated gases and gases in the interaction with clusters at the ωB97XD/Def2-svp calculation level. By comparing the values in both types of analysis for the specified gases, it is possible to see the process of charge transfer after gas adsorption on the surface of aluminum clusters

System	Atom	Natural electron configuration	Natural charge
NO2	N	[Core] 2S (1.17) 2p (3.21) 3S (0.03) 3p (0.03) 3d (0.02)	0.5402
	O	[Core] 2S (1.74) 2p (4.52) 3p (0.01) 3d (0.01)	−0.2701
	O	[Core] 2S (1.74) 2p (4.52) 3p (0.01) 3d (0.01)	−0.2701
SO2	S	[Core] 3S (1.62) 3p (2.62) 4S (0.05) 3d (0.12) 4p (0.02)	1.5600
	O	[Core] 2S (1.83) 2p (4.94) 3d (0.01)	−0.7800
	O	[Core] 2S (1.83) 2p (4.94) 3d (0.01)	−0.7800
NO2@Al13_2	N	[Core] 2S (1.46) 2p (3.09) 3S (0.03) 3p (0.02) 3d (0.02)	0.3762
	O	[Core] 2S (1.72) 2p (5.04) 3p (0.01)	−0.7759
	O	[Core] 2S (1.71) 2p (4.52) 3S (0.01) 3p (0.01) 3d (0.01)	−0.2543
NO2@Al15_1	N	[Core] 2S (1.43) 2p (3.06) 3S (0.01) 3p (0.02) 3d (0.02)	0.4515
	O	[Core] 2S (1.71) 2p (4.80) 3p (0.01) 3d (0.01)	−0.5200
	O	[Core] 2S (1.71) 2p (4.80) 3p (0.01) 3d (0.01)	−0.5197
SO2@Al13_8	S	[Core] 3S (1.60) 3p (3.29) 4S (0.01) 3d (0.06) 4p (0.02)	1.0116
	O	[Core] 2S (1.76) 2p (5.29)	−1.0571
	O	[Core] 2S (1.76) 2p (5.28)	−1.0479
NO2@Al15_6	S	[Core] 3S (1.72) 3p (3.40) 4S (0.01) 3d (0.04) 4p (0.02)	0.8184
	O	[Core] 2S (1.76) 2p (5.27)	−1.0425
	O	[Core] 2S (1.79) 2p (5.37)	−1.1773

---

To ascertain the direction of charge transfer during the adsorption process—whether it occurs from the gas to the cluster or vice versa—a scrutiny of the algebraic sum of partial charges in the gas molecules suffices. As evident from the presented table, isolated gas molecules exhibit neutrality, with the algebraic sum of their partial charges equating to zero, as previously noted. Following the adsorption process, examination of NO₂@Al₁₃_2 configuration reveals that the sum of partial charges for gas atoms assume a value of −0.65. This observation indicates that a charge transfer has transpired from the Al₁₃ cluster to the NO₂ gas. One of the oxygen atoms within the gas molecule has exhibited a heightened significance in the charge transfer mechanism. Evidently, its partial charge has escalated from −0.27 to −0.78, concomitant with a modification in its associated orbital from 2p (4.52) to 2p (5.04). Furthermore, the 3d (0.01) subshell of this oxygen atom is found to be entirely unoccupied, with its electron density redistributed across alternative orbitals. The adsorption of NO₂ on an Al₁₅ cluster exhibits a similar behavior, albeit with a marginal reduction in the intensity of charge transfer. The algebraic summation of partial charges on NO₂ gas atoms in the NO₂@Al₁₅_1 configuration yields a value of −0.59, indicating a slight attenuation compared to the preceding system's value of −0.65. Furthermore, alterations in the distribution of electron density within orbitals are discernible in this system. Specifically, the 2p orbital population for oxygen atoms has undergone an elevation from 4.52 to 4.80, while a noteworthy modification involves the upgrade of the nitrogen atom's 2S orbital from 1.17 to 1.43, as evident in the table.

The magnitude of charge transfer from aluminum clusters to SO₂ gas surpasses that observed with NO₂ gas, as evident in configuration SO₂@Al₁₃_8. The cumulative sum of partial gas charges equates to −1.09, indicating a notably substantial charge transfer. There are pronounced alterations in electron distribution within the orbitals, resulting in the complete vacuity of the 3d (0.01) orbital. Conversely, in oxygen atoms, the 2p orbitals have experienced an elevation from 4.94 to 5.29. Moreover, significant alteration have occurred in the valence layer of the sulfur atom, transitioning from [3S (1.62), 3p (2.62), 4S (0.05), 3d (0.12), 4p (0.02)] to [3S (1.60), 3p (3.29), 4S (0.01), 3d (0.06), 4p (0.02)]. In the NO₂@Al₁₅_6 system, pronounced charge transfer has been observed, reaching a maximum of −1.4. Notably, the 2p orbital of the oxygen atoms has undergone enhancement (i.e. 4.94 to 5.37), while the valence electron distribution of the sulfur atom has undergone a substantial transformation, resulting in the configuration of 3S (1.72), 3p (3.40), 4S (0.01), 3d (0.04), and 4p (0.02).

3.4 QTAIM analysis

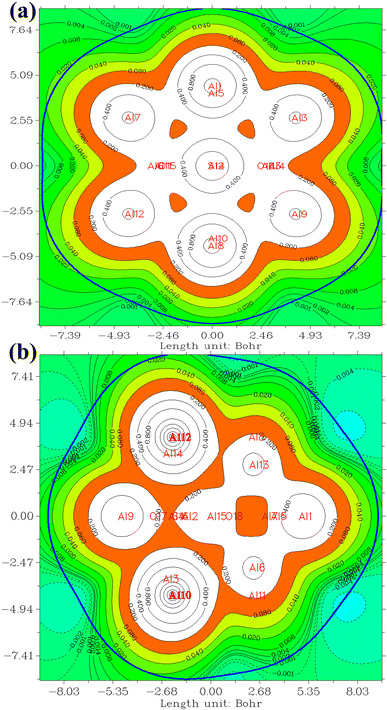
The QTAIM methodology meticulously examines the characteristics and features of chemical bonds within molecular entities, providing an understanding of the spatial distribution of electron density and its topological aspects. The determination of electron density originates from quantum mechanical computations and encompasses the probability of locating an electron at a specific spatial coordinate. The QTAIM methodology is intricately complex and posits an alternative conceptualization of atomic interactions surpassing conventional chemical bonding. Detailed exposition is eschewed in this context, as numerous sources are available for the thorough examination of the theory.^76,77 The ensuing discussion will focus exclusively on the interpretation of the results acquired. A concise introduction to this theory is attempted in the ESI† section for reference.

Table 4 presents data concerning bond critical points (3, −1). A detailed analysis reveals electron density values within the narrow range of 0.03 to 0.045. This range serves as a crucial indicator of the strength and resilience of the intermolecular bonds dictating the behavior of the examined system. Notably, the electron density of bond critical points between NO₂ and Al clusters is consistently lower than that of points between SO₂, implying a more robust interaction between SO₂ and Al clusters. This observation aligns with the higher adsorption energies of SO₂. Of particular interest is the pervasive negative sign characterizing electron density Laplacian throughout the system. This distinctive attribute enhances the favorable nature of the system's electronic structure. Negative Laplacian indicate regions of maximum electron accumulation, reinforcing the significance of intermolecular forces governing interactions within the system. Fig. 6 provides a visual representation of bond critical points in the NO₂@Al₁₃ system. The minutely varied electron density values, coupled with the consistently negative Laplacian, underscore the intricate dynamics of intermolecular interactions within the system.

Table 4 The parameters derived from the examination of the quantum theory of atoms in the molecules, encompassing the electron density ρ(r), Laplacian electron density ∇²ρ(r), kinetic energy density (G(r)), potential energy density (V(r)), the ratio denoted as G(r)/|V(r)|, electron localization function (ELF), and localized orbital locator (LOL) acquired through the application of ωB97XD/Def2-svp model chemistry

Systems	Bond	ρ(r)	∇^2 ρ(r)	G(r)	V(r)	G(r)/|V(r)|	ELF	LOL
NO2@Al13_2	O⋯Al	0.0374	−0.0122	0.0101	−0.0233	0.4343	0.7422	0.2206
	O⋯Al	0.0368	−0.011	0.0092	−0.0212	0.4348	0.4135	0.1725
NO2@Al15_1	O⋯Al	0.0367	−0.0085	0.0093	−0.0206	0.4484	0.7699	0.2243
	O⋯Al	0.0366	−0.0023	0.0092	−0.019	0.4849	0.7604	0.2230
SO2@Al13_8	O⋯Al	0.036	−0.0066	0.009	−0.0197	0.4584	0.7301	0.2191
	O⋯Al	0.0392	−0.0055	0.0136	−0.0286	0.4761	0.7262	0.2187
SO2@Al15_6	O⋯Al	0.0395	0.0133	0.0169	−0.0304	0.5549	0.6736	0.2117
	O⋯Al	0.0439	−0.0094	0.0156	−0.0336	0.4650	0.6951	0.2147

---

Fig. 6 The depiction explores critical points (3, −1) and the interatomic relationships, revealing how aluminum atoms in the Al₁₃ cluster interact with oxygen atoms in the NO₂ gas molecule (NO₂@Al₁₃_2).

The index G(r)/|V(r)|, serves as an essential metric for revealing insights into the robustness of the bond formed between gas and aluminum clusters. Consider the case of the Al₁₃ cluster and its interaction with NO₂ gas, where a value of 0.43 is observed, slightly below the critical threshold of 0.5. As explained in ESI,† these numerical outcomes indicate the covalent nature of the interactions. For the Al₁₅ cluster interacting with NO₂ gas, the index exhibits values of 0.44 and 0.48, resembling a strong affinity between the aluminum cluster and NO₂ gas molecules. Notably, this finding reinforces the established trend, corroborating previous meticulous analyses. It is noteworthy that the subtle disparity in favor of the Al₁₃ cluster, as observed in these investigations, aligns with knowledge from prior inquiries.

The investigation of the interaction between SO₂ gas and aluminum atomic clusters is examined through a comprehensive QTAIM analysis, aimed at elucidating the intricacies of this phenomenon. The results derived from this analysis reveal significant insights, particularly demonstrating that the intermolecular interactions between the gas and clusters exhibit characteristics akin to covalent bonds. By meticulous examination of the interaction between SO₂ and the Al₁₃ atomic cluster, the G(r)/|V(r)| index attains a noteworthy value of 0.37 at its maximum potency. The exploration of the adsorption process of this gas on the Al₁₃ cluster reveals additional data points, with values of 0.45 and 0.47, underscoring the profound nature of the gas/cluster interaction. Similarly, the investigation into the interaction of SO₂ gas with the Al₁₅ cluster yields compelling observations. In this context, the G(r)/|V(r)| index manifests values of 0.46 and 0.55, further substantiating the robust nature of the bond formed during this process. Additionally, the G(r)/|V(r)| of SO₂@Al_13/15 exceeds that of NO₂@Al_13/15, aligning with the adsorption energies and indicating the increased stability of SO₂ adsorption on the Al cluster. Notably, the G(r)/|V(r)| of SO₂@Al₁₅ surpasses others, corresponding to its highest adsorption energy.

In the context of these findings, it becomes evident that both SO₂ gases are intricately entangled within the potential field of these aluminum clusters. The established bond exhibits remarkable strength, resisting facile attempts to disassociate it. The robustness of the gas-cluster bond holds paramount significance and presents substantial potential in addressing the deleterious environmental effects associated with these gases. Given the profound implications of this research, its applications are diverse. The newfound understanding of the formidable strength and stability of these gas-cluster interactions opens promising avenues for utilizing Al clusters as potent absorbents, offering a means to alleviate the environmental impact of SO₂ gases. Innovative approaches leveraging these clusters hold great promise in fostering a cleaner and more sustainable future.

The electron localization function (ELF) serves as a valuable tool for scrutinizing the electron density distribution within a given molecular entity. Its utility extends to the provision of insights into the extent of electron localization or delocalization, thereby facilitating the identification of regions characterized by varying degrees of electron pairing strength. The interpretation of ELF results hinges upon the consideration of specific parameters, including low ELF values, which approximate zero and denote regions of electron delocalization, such as those found in aromatic systems or conjugated π systems. Conversely, high ELF values, approximating one, indicate localized regions where electrons are tightly bound or strongly paired, as observed around atoms participating in covalent bonds or lone pairs. Furthermore, ELF proves instrumental in the analysis of weak interactions, such as van der Waals forces or hydrogen bonding, with high ELF values in hydrogen bonding regions signifying pronounced electron localization.^78,79 The LOL exhibits comparable expressions to the ELF. Specifically, the chemically significant regions highlighted by both LOL and ELF demonstrate qualitative similarities. However, Jacobsen⁸⁰ has pointed out that LOL imparts a more decisive and clearer depiction than ELF. While LOL can be interpreted kinetically, similar to ELF, it also lends itself to an interpretation based on localized orbitals which leads to the clusters suitable for the eradication of pollutants.

Table 4 displays ELF values for the investigated systems, consistently indicating elevated and nearly unitary values. This observation suggests that the interatomic interactions within these systems are predominantly of a covalent nature. For instance, in NO₂@Al₁₃_2 system, the ELF attains a value of 0.7422, underscoring the robust and covalent nature of the bond between oxygen and aluminum atoms. Fig. 7 has been included to enhance comprehension, where regions corresponding to O–Al and N–O bonds are highlighted in red, denoting the presence of covalent interatomic interactions. Furthermore, the red coloring surrounding nitrogen (N) and oxygen (O) atoms signifies the existence of lone pairs of electrons. The tabular data reveals that interactions involving gas atoms and aluminum clusters exhibit a pronounced strength, indicating a proximity to covalency. This deduction aligns with the findings of the preceding section's topological analysis, wherein similarly robust interactions were anticipated.

Fig. 7 The illustration of shaded surface map with projection ELF of NO₂@Al₁₃_2 system. The red region around N and O atoms indicates the lone pair electrons. The region between Al–O and N–O indicates covalent bonds. Calculations are performed at ωB97XD/Def2-svp level of study.

4. Conclusions

This study investigates the intricate molecular interactions between NO₂ and SO₂ gases with Al₁₃ and Al₁₅ clusters. The clusters, characterized by adsorption energies surpassing the 2.0 eV threshold, display significant potential for efficiently eliminating noxious gases, making them viable candidates for further examination. Through systematic optimization of geometric configurations and rigorous analyses, valuable insights emerge. The electrophilicity index proves crucial in assessing cluster reactivity, with the SO₂ gas demonstrating superior reactivity due to its compact arrangement. Natural electron configuration and natural charge analyses reveal the nature of charge transfer through gas/cluster interactions, with the SO₂/Al₁₅ system exhibiting intensive charge transfer properties. QTAIM analysis provides detailed insights into the robust covalent bonding between both gases and aluminum clusters, indicating exceptional bond strength. G(r)/|V(r)| index values further underscore the substantial bonding affinity of SO₂ gas with both Al₁₃ and Al₁₅ clusters. These findings show promise in mitigating environmental pollution from SO₂ gases, suggesting the potential application of clusters as adsorbents. Employing a comprehensive array of analytical tools, this study enhances our understanding of gas-cluster interactions, presenting new possibilities for environmental and industrial contexts. Further exploration using advanced computational methods holds the potential to unveil deeper insights, contributing to a cleaner and more sustainable future.

Author contributions

Sajida Riffat Laraib: investigation, methodology, validation, writing – original draft, review & editing. Ji Liu: conceptualization, funding acquisition, supervision, writing – original draft, review & editing. Yuan-gu Xia: validation, writing – review & editing. Yang-wen Wu: validation, funding acquisition, writing – review & editing. Mohsen Doust Mohammadi: methodology, formal analysis. Nayab Fatima Noor: methodology, formal analysis. Qiang Lu: conceptualization, funding acquisition, writing – review & editing.

Conflicts of interest

There is no conflict of interest for this manuscript.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (52376182, 52276189); Natural Science Foundation of Jiangsu Province (BK20221248); China Postdoctoral Science Foundation (2022M721131); and Fundamental Research Funds for the Central Universities (2023JC009).

References

1. D. Burtraw and E. Mansur, Environ. Sci. Techonl., 1999, 33, 3489–3494.
2. S. Oesch and M. Faller, Corros. Sci., 1997, 39, 1505–1530.
3. D. O. Johns and W. S. Linn, Inhalation Toxicol., 2011, 23, 33–43.
4. V. Perraud, J. R. Horne, A. S. Martinez, J. Kalinowski, S. Meinardi, M. L. Dawson, L. M. Wingen, D. Dabdub, D. R. Blake and R. B. Gerber, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13514–13519.
5. J. A. De Gouw, D. D. Parrish, G. J. Frost and M. Trainer, Earth's Future, 2014, 2, 75–82.
6. S. M. Serbula, J. S. Milosavljevic, J. V. Kalinovic, T. S. Kalinovic, A. A. Radojevic, T. L. A. Trujic and V. M. Tasic, Sci. Total Environ., 2021, 777, 145981.
7. B. Kamarehie, M. Ghaderpoori, A. Jafari, M. Karami, A. Mohammadi, K. Azarshab, A. Ghaderpoury, A. Alinejad and N. Noorizadeh, J. Adv. Environ. Health Res., 2017, 5, 44–50.
8. B. Long, J. L. Bao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 8091–8100.
9. P. Orellano, J. Reynoso and N. Quaranta, Environ. Int., 2021, 150, 106434.
10. A. L. Reno, E. G. Brooks and B. T. Ameredes, Environ. Health Insights, 2015, 9, 13–25.
11. Y. Khajeamiri, S. Sharifi, N. Moradpour and A. Khajeamiri, J. Air Pollut. Health, 2021, 5(4), 243–258.
12. Y.-K. Park and B.-S. Kim, Chem. Eng. J., 2023, 461, 141958.
13. B. Yang, K. M. Zhang, W. D. Xu, S. Zhang, S. Batterman, R. W. Baldauf, P. Deshmukh, R. Snow, Y. Wu and Q. Zhang, Environ. Sci. Technol., 2018, 52, 4574–4582.
14. Q. Yu, T. Zhang, X. Ma, R. Kang, J. Mulder, T. Larssen and L. Duan, Environ. Sci. Technol., 2017, 51, 9498–9506.
15. A. Bouwman, D. Van Vuuren, R. Derwent and M. Posch, Water, Air, Soil Pollut., 2002, 141, 349–382.
16. H.-C. Shin, J.-W. Park, K. Park and H.-C. Song, Environ. Pollut., 2002, 119, 227–236.
17. D. Das, V. Gaur and N. Verma, Carbon, 2004, 42, 2949–2962.
18. M. P. Cal, M. J. Rood and S. M. Larson, Sep. Purif. Technol., 1996, 10, 117–121.
19. M. W. Ackley, S. U. Rege and H. Saxena, Microporous Mesoporous Mater., 2003, 61, 25–42.
20. M. Ozekmekci, G. Salkic and M. F. Fellah, Fuel Process. Technol., 2015, 139, 49–60.
21. N. A. Khan, Z. Hasan and S. H. Jhung, J. Hazard. Mater., 2013, 244, 444–456.
22. J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504.
23. Y. Sun, E. Zwolińska and A. G. Chmielewski, Crit. Rev. Environ. Sci. Technol., 2016, 46, 119–142.
24. C. C. Lin, K. A. Dambrowitz and S. M. Kuznicki, Can. J. Chem. Eng., 2012, 90, 207–216.
25. J. Lee, S. Han and T. Hyeon, J. Mater. Chem., 2004, 14, 478–486.
26. S. I. Alhassan, L. Huang, Y. He, L. Yan, B. Wu and H. Wang, Crit. Rev. Environ. Sci. Techonl., 2021, 51, 2051–2085.
27. A. Schnepf and H. Schnöckel, Angew. Chem., Int. Ed., 2002, 41, 3532–3554.
28. J. Demuynck, M. M. Rohmer, A. Strich and A. Veillard, J. Chem. Phys., 1981, 75, 3443–3453.
29. J. Koutecky and P. Fantucci, Chem. Rev., 1986, 86, 539–587.
30. S. Nigam and C. Majumder, Appl. Surf. Sci., 2021, 547, 149160.
31. G. Linti and H. Schnöckel, Coord. Chem. Rev., 2000, 206, 285–319.
32. Z. Luo, A. Castleman Jr and S. N. Khanna, Chem. Rev., 2016, 116, 14456–14492.
33. P. Dumitraschkewitz, S. S. Gerstl, L. T. Stephenson, P. J. Uggowitzer and S. Pogatscher, Adv. Eng. Mater., 2018, 20, 1800255.
34. S. Das, S. Pal and S. Krishnamurty, J. Phys. Chem. C, 2014, 118, 19869–19878.
35. V. S. Zharinov, T. Picot, J. E. Scheerder, E. Janssens and J. Van de Vondel, Nanoscale, 2020, 12, 1164–1170.
36. A. Datta, S. S. Mallajosyula and S. K. Pati, Acc. Chem. Res., 2007, 40, 213–221.
37. M. D. Mohammadi, N. Patsalidis, S. Bhowmick, V. A. Harmandaris and G. Biskos, RSC Adv., 2023, 13, 18014–18024.
38. M. D. Mohammadi, H. Louis, U. G. Chukwu, S. Bhowmick, M. E. Rasaki and G. Biskos, ACS Omega, 2023, 8, 20621.
39. S. Hussain, R. Hussain, M. Y. Mehboob, S. A. S. Chatha, A. I. Hussain, A. Umar, M. U. Khan, M. Ahmed, M. Adnan and K. Ayub, ACS Omega, 2020, 5, 7641–7650.
40. A. Guardado, I.-R. Marisol, R. Mayén-Mondragón and M. Sánchez, J. Mol. Graph. Model., 2023, 122, 108491.
41. A. Azari, R. R. Kalantary, G. Ghanizadeh, B. Kakavandi, M. Farzadkia and E. Ahmadi, RSC Adv., 2015, 5, 87377–87391.
42. M. Krstić, A. Zavras, G. N. Khairallah, P. Dugourd, V. Bonačić-Koutecký and A. Richard, Int. J. Mass Spectrom., 2017, 413, 97–105.
43. F. Zare, M. Ghaedi, A. Daneshfar, S. Agarwal, I. Tyagi, T. A. Saleh and V. K. Gupta, Chem. Eng. J., 2015, 273, 296–306.
44. M. Mil’vidskii and V. Chaldyshev, Semiconductors, 1998, 32, 457–465.
45. K. Bhattacharyya and S. Mukherjee, Bull. Chem. Soc. Jpn., 2018, 91, 447–454.
46. R. Sinha, G. J. Kim, S. Nie and D. M. Shin, Mol. Cancer Ther., 2006, 5, 1909–1917.
47. B. Huang, Z. Wu, H. Zhou, J. Li, C. Zhou, Z. Xiong, Z. Pan, G. Yao and B. Lai, J. Hazard. Mater., 2021, 412, 125253.
48. J. B. DeCoste and G. W. Peterson, Chem. Rev., 2014, 114, 5695–5727.
49. N. Vershinin, I. Balikhin, O. Efimov, E. Kabachkov and E. Kurkin, J. Phys. Conf., 2018, 1134, 012067.
50. N. S. King, L. Liu, X. Yang, B. Cerjan, H. O. Everitt, P. Nordlander and N. J. Halas, ACS Nano, 2015, 9(11), 10628–10636.
51. R. Leuchtner, A. Harms and A. Castleman Jr, J. Chem. Phys., 1991, 94(2), 1093–1101.
52. R. Jones, Phys. Rev. Lett., 1991, 67(2), 224.
53. J. Akola, M. Manninen, H. Häkkinen, U. Landman, X. Li and L. S. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(19), 13216.
54. J. Akola, H. Häkkinen and M. Manninen, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(7), 3601.
55. D. Cox, D. Trevor, R. Whetten, E. Rohlfing and A. Kaldor, J. Chem. Phys., 1986, 84(8), 4651–4656.
56. J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
57. D. Jacquemin, E. A. Perpete, I. Ciofini and C. Adamo, Theor. Chem. Acc., 2011, 128, 127–136.
58. N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924.
59. N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110.
60. A. Hellweg and D. Rappoport, Phys. Chem. Chem. Phys., 2015, 17, 1010–1017.
61. J. Witte, J. B. Neaton and M. Head-Gordon, J. Chem. Phys., 2017, 146, 234105.
62. R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 6.1, Semichem Inc., Shawnee Mission, KS, 2016.
63. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
64. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181.
65. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241.
66. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
67. S. Grimme, J. Antony, T. Schwabe and C. Mück-Lichtenfeld, Org. Biomol. Chem., 2007, 5, 741–758.
68. D. Phlip, Adv. Mater., 1996, 8(10), 866–868.
69. B. R. Brooks, C. L. Brooks III, A. D. Mackerell Jr, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels and S. Boresch, J. Comput. Chem., 2009, 30, 1545–1614.
70. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wires. Comput. Mol. Sci., 2021, 11, e1493.
71. D. Karaboga and B. Akay, Appl. Math. Comput., 2009, 214, 108–132.
72. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010.
73. F. Weinhold and C. R. Landis, Chem. Educ. Res Pract., 2001, 2, 91–104.
74. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
75. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
76. R. F. Bader, Chem. Rev., 1991, 91, 893–928.
77. R. F. Bader, Monatsh. Chem., 2005, 136, 819–854.
78. E. Matito, B. Silvi, M. Duran and M. Sola, J. Chem. Phys., 2006, 125, 024301.
79. F. Hao, R. Armiento and A. E. Mattsson, J. Chem. Phys., 2014, 140, 18A536.
80. H. Jacobsen, Can. J. Chem., 2008, 86, 695–702.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra00708e

---