The stability of CsPb(Br_xCl_1−x)₃ all-inorganic mixed halide perovskites

Abstract

The use of mixed halide perovskites in the preparation of blue light-emitting diodes (LEDs) is considered to be the most effective and direct approach. However, the introduction of chlorine (Cl) element might raise stability issues in the system and lead to low efficiency, thereby impeding the development of deep blue light-emitting diodes with high efficiency and stability. Determining the alloy concentration and the atomic distribution of bromine–chlorine (Br–Cl) mixed systems is essential for further application of deep blue light-emitting diodes. In this work, we have systematically investigated the stability of bromine–chlorine (Br–Cl) mixed alloy systems in various substitution configurations using high-throughput theoretical calculations. Based on this, we have examined the relationship between configuration stability and three aspects: the type of octahedra, the orientation of the octahedra and the Pb–X–Pb distortion angle in the configuration.

---

1 Introduction

All-inorganic CsPbX₃ (X = I or X = Br or X = Cl) perovskites have demonstrated potential in various optoelectronic applications such as solar cells, light-emitting diodes, photodetectors, and lasers.^1–5 Especially in the perovskite light-emitting diodes (PeLEDs), a lot of attention has been attracted because of their superior optoelectronic properties, including solution processability,⁶ high photoluminescence quantum yield (PLQY), narrow emission,⁷ long charge-carrier diffusion length,⁸ high defect tolerance⁹ and facile color tunability.¹⁰ Recent progress has shown that perovskite LEDs with near-infrared, red, and green emissions have reached over 20% external quantum efficiency (EQE),^3,11,12 However, as one of the primary colors, the performance of blue, sky blue, and deep blue PeLEDs still lags far behind,^13–15 which makes industrial full-color devices a challenge.

In general, there are mainly two experimental strategies, dimensional tuning and composition engineering, used to achieve blue emission in the range of 420–495 nm.¹⁶ Despite the progress in achieving blue, sky blue light emission through bandgap modulation via dimensional tuning to generate quantum confinement effects,^17–19 the introduction of large organic cations and/or over-capped ligands during the modulation process leads to the deterioration of the electronic properties of the system, which is unfavorable for the realization of efficient and stable perovskite LEDs. Compared with dimensional control, composition engineering provides a more direct approach to modulating bandgap.^20,21 A typical example is the use of mixed-halide perovskites, where the blue emission is regulated by adjusting the ratio of halide anions in the system. This method enables direct modulation of the bandgap of 3D perovskite materials,^6,22 thereby avoiding the influence of residual organic components on the electronic properties of the system. However, the preparation of deep blue perovskite LEDs still faces obstacles, such as phase segregation, poor color stability, limited solubility of inorganic Cl salts in precursor solutions,^13,23–25 and the presence of deep defect energy levels associated with Cl ions,²⁶ which hinder the application of this method.

To study the mixed alloy system composed of bromine and chlorine, it is crucial to determine the crystal structure of CsPbX₃ (X = Br or X = Cl), the identification of whose crystal phase type varies across different experiments as evidenced by Table S1 (see ESI).† Several previous studies have proposed that CsPbBr₃ undergo an orthorhombic-to-tetragonal phase transition at 88 °C and a tetragonal-to-cubic phase transition at 130 °C.²⁷ CsPbCl₃ retains its orthorhombic crystal structure below 42 °C and experiences a tetragonal-to-cubic phase transition at 47 °C.²⁸ According to this, it is anticipated that the system would exhibit an orthorhombic phase at room temperature. However, due to the wide bandgap, CsPbX₃ (X = Br or X = Cl) perovskites do not exhibit obvious color changes during phase transition, unlike hybrid organic–inorganic perovskites, and the XRD spectra of cubic and orthorhombic phases exhibit significant resemblance. These characterization challenges result in divergent opinions on the obtained experimental results. Different opinions suggest that discrepancies in material growth environments and preparation process, or surface energy may enable the stable presence of the cubic phase or coexistence of two phases at room temperature.^10,29–31 At present, a comprehensive explanation for this issue remains elusive. Therefore, the impact of various phases should be considered to employ stoichiometric engineering in the system's alloying process and modify the system's bandgap by manipulating the Cl element content, particularly for the implementation of blue light emission using the chemical vapor anion exchange (CVAE) technique.

In this paper, we have systematically investigated the structural stabilities of CsPb(Br_xCl_1−x)₃ all-inorganic mix-halide perovskite based on the first-principles calculations. It is shown that when the initial crystal structure transforms from the cubic phase to the orthorhombic phase, the distribution of Cl elements in the corresponding bromine–chlorine alloy system shifts from a random distribution to an ordered distribution. A relatively larger Pb–Cl–Pb average distortion angle is conducive to a decrease in formation energy. In the highly symmetric cubic phase, an unordered distribution of Cl elements is beneficial for angle distortion. As the crystal's symmetry becomes lower, the ordered configurations can facilitate the Pb–Cl–Pb angle distortion, thereby reducing formation energy. This allows the regulatory role of local ordering arrangement on the formation energy of the configurations to become apparent. Moreover, the introduction of Cl elements into the excessively distorted orthorhombic alloy system leads to a reduction in bond angle distortion, which results in an increase of formation energy and induces instability of the alloy system. Our results will provide a theoretical reference for the preparation of highly efficient and stable blue light devices.

2 Computational method

The first-principles calculations based on density-functional theory were performed using the VASP code³² with the projector-augmented-wave (PAW) method. The Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation was used to describe the exchange–correlation interaction.^33,34 The atomic positions and cell size are fully relaxed for each configuration. Cutoff energy for the basis functions was set to 520 eV and the Γ-centered k-point meshes with a grid of spacing 0.02 × 2π Å⁻¹ is employed for Brillouin zone sampling. Geometric optimization is halted when the residual atomic forces on the atoms drop below 0.01 eV Å⁻¹ and the final energies are calculated in a subsequent static calculation. To simulate the bromine–chlorine all-inorganic mixed halide perovskite alloy system, we consider a cell of 20 atoms generated with the Hermite normal form matrices,³⁵ and all inequivalent configurations were obtained by using the SAGAR package.³⁶

For the stability of different alloy systems, the formation energy of different configurations is calculated as follows:

ΔH_j = E_j − (1 − x)E_CsPbBr3 − xE_CsPbCl3

where ΔH_j represents the formation energy of configuration j, and E_j represents the total energy of configuration j. E_CsPbBr3 and E_CsPbCl3 represent the total energy of pure Br and pure Cl phase required for generating configuration j respectively. Generally, a negative formation energy suggests that a compound is energetically stable, while a positive formation energy means the occurrence of phase separation.

3 Results and discussion

We have found that Cl element tends to be ordered distributed in the orthorhombic and tetragonal alloy systems, while the distribution is not ordered in cubic alloy system as shown in Section 3.1. Besides the type and orientation of octahedra, we consider the effect of the connection between octahedra and octahedra on the formation energy of the structure as shown in Section 3.2. Section 3.3 attempts to explain why orthorhombic alloy systems with high Cl concentrations cannot exist stably from the perspective of order and bond angles.

3.1 Ground state configuration characteristics

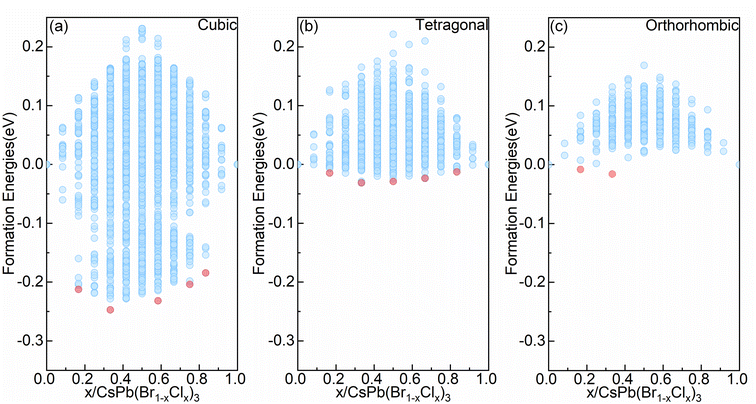
The tolerance factor, taking into account the types of elements and the atomic radii, is frequently used in the literature to evaluate the stability of perovskite structures.^37,38 However, it cannot reflect the influence of different configurations (e.g. atomic coordination environment or motif arrangement) on the stability of the structure at the microscopic level. Note that configuration information plays an important role in theoretical calculations, and different configurations can significantly impact the stability of the system. To comprehensively investigate the stability of mixed halide alloy systems, we consider various possible bromo–chloro mixed configurations from the three commonly observed phases in all-inorganic perovskite. The Fig. 1 exhibits the convex hull of formation energy for all symmetry-nonequivalent configurations deriving from three crystal phases, cubic (Pm3̄m symmetry), tetragonal (I4/mcm symmetry), and orthorhombic (Pnma symmetry), reflecting the relative stability among various configurations.

Fig. 1 The formation energy convex hull plots of symmetry-nonequivalent configurations in the CsPb(Br_xCl_1−x)₃ mixed halide alloy systems for three main perovskite phases: the symmetry-nonequivalent configurations from (a) cubic (b) tetragonal (c) orthorhombic phase and the red dots represent convex points configurations.

At the same Cl concentration, as shown in Fig. 1, different configurations can lead to significant variations in formation energy. From Fig. 1(a) to (c), as symmetry decreases, the range of formation energy influenced by configurations decreases. For the cubic alloy system with the highest symmetry, there is the widest range of formation energy influenced by configurations, reaching approximately 500 meV per cell (c.f. Fig. 1(a)). However, for the orthorhombic alloy system (c.f. Fig. 1(c)), the range in which configurations affect the formation energy is restricted to approximately 180 meV per cell. Moreover, it can be seen from Fig. 1 that the three alloy systems all contain negative formation energy configurations. For the orthorhombic alloy system (c.f. Fig. 1(c)), there are convex point configurations when the alloy concentration of Cl is no greater than 0.333. Meanwhile, the formation energy becomes positive as the Cl concentration continues to increase. For the cubic and tetragonal alloy system (c.f. Fig. 1(a) and (b)), there are convex point configurations with more different concentrations. This indicates that the configurations with higher Cl content become relatively unstable in the orthorhombic alloy system but can maintain stable in the cubic and tetragonal alloy systems, which offers advantages for effectively enhancing Cl content via compositional engineering to achieve wide bandgap blue light emission. Above all, obtaining higher Cl concentrations is more challenging in the orthorhombic alloy system, compared with the cubic and tetragonal alloy system. Note that, the lowest formation energy configuration in the cubic and tetragonal alloy systems also appears with a Cl concentration of 0.333, consistent with the observation in the orthorhombic alloy system. Previous study provided an explanation for this phenomenon.³⁹

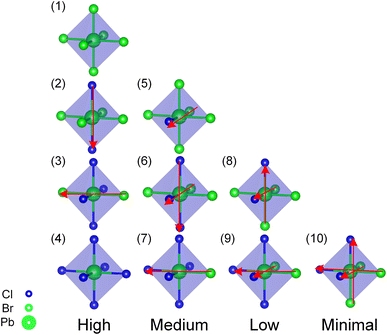
In order to clarify the effect of Cl distributions on structural stability, a comparative study was carried out to focus on the Pb atoms coordination environment (PbBr_6−yCl_y) for the stable convex point configurations among the three alloy systems according to convex hull. Using the type and orientation of the PbBr_6−yCl_y octahedra motif as shown in Fig. 2, we classify the PbBr_6−yCl_y octahedra motif into four categories, high, medium, low, and minimal, based on how symmetry the Cl elements are distributed in the octahedra, and the spatial orientation of the same type PbBr_6−yCl_y is uniquely represented by the vector (red arrows) summation in the figure. Among the cubic alloy convex point configurations (c.f. Fig. 3(a–e)), there is more than one type of PbBr_6−yCl_y octahedra motifs in the structure, and the same type octahedra motif's orientation are not all parallel to each other in one configuration, besides that the distribution of Cl elements in one octahedron has a certain randomness, with the presence of low symmetric distribution of Cl elements in one octahedron (c.f. Fig. 2 Low symmetry octahedra), which means that the distribution of Cl elements in the cubic alloy system is more homogeneous. However, in the convex point configurations of the orthorhombic and tetragonal alloy systems (c.f. Fig. 3(f–l)), the PbBr_6−yCl_y octahedra motif of the configuration was symmetry equivalent, that is, the configuration only contained one type of octahedra motif, and the same type octahedra motif's orientation is all parallel to each other in one configuration, besides that the Cl elements in one octahedron tended to be relatively symmetric distributed (c.f. Fig. 2 high and medium symmetry octahedra). This implies that the arrangement of the Cl elements in the structure does not exhibit a random distribution but rather adheres to a certain ordered distribution.

Fig. 2 Classification of the Pb atoms coordination environment (PbBr_6−yCl_y) octahedra motif according to the distribution way of Cl elements in one octahedron: type (1–4) high, type (5–7) medium, type (8–9) low, type (10) minimal symmetry distribution. The orientation of the same type octahedra in one configuration is determined by the vector (red arrows) summation. Type (1) and (4) octahedra motif orientation is always the same in one configuration.

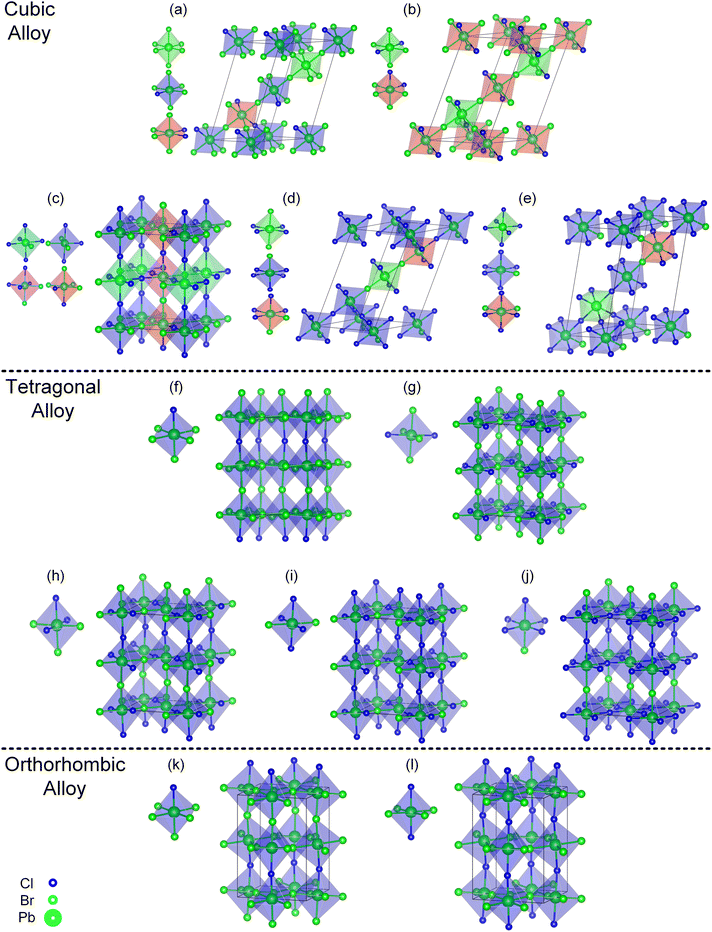Fig. 3 Convex point configurations of the cubic, tetragonal, and orthorhombic alloy systems. Cubic alloy system (a–e), tetragonal alloy system (f–j), orthorhombic alloy system (k–l), and different types of octahedra in one configuration are labeled with different colors special low symmetric type octahedra represented in red and pink. The lowest formation energy configurations (b), (g) and (l) for different alloy systems are consistent with previous studies,^39–41 for ease of viewing, the Cs atoms have not been depicted. The chemical formula is as follows (a), (f) and (k) CsPbBr_0.833Cl_0.167 (b), (g) and (l) CsPbBr_0.667Cl_0.333 (h) CsPbBr_0.500Cl_0.500 (c) CsPbBr_0.417Cl_0.583 (i) CsPbBr_0.333Cl_0.667 (d) CsPbBr_0.250Cl_0.750 (j) and (e) CsPbBr_0.167Cl_0.833.

Combined with Fig. 1 and 3(b), (g) and (l), three alloy systems reach the lowest formation energy at the same alloy concentration, but the arrangement way of Cl elements in the corresponding configuration was not consistent, indicating that the stable configuration should be influenced by the crystal structure of the system. Therefore, we calculated the formation energies of the ordered configurations (an ordered configuration means that it contains only one type of octahedra motif, this type of octahedra must also belong to high or medium symmetry motif, and the orientation of the octahedra in the configuration is parallel to each other) within the three alloy systems. The locations of the ordered configurations in the convex hull diagrams of each alloy system are displayed in Fig. S1(a)–(c).† It can be observed that in the orthorhombic and tetragonal alloy systems (c.f. Fig. S1(b) and (c)),† at a certain concentration, the lowest formation energies configuration belongs to the ordered configurations. However, in the cubic alloy system (c.f. Fig. S1(a)†), the formation energies of ordered configurations are generally significantly higher compared to the lowest formation energy configuration at the corresponding concentration. The ordered configurations that can stably exist in the orthorhombic and tetragonal alloy systems become unstable in the cubic alloy system, which indicates that other factors will influence the formation energy of the configurations besides ordering. The variation of the crystal structure will lead to the redistribution of Cl atoms within the structure. From the cubic to orthorhombic phase, the decrease of crystal symmetry results in the ordered distribution of Cl elements in alloy system, which provides insight for the observed phenomenon of phase separation in mixed-halide perovskite experimental observations.

To study the dynamical stabilities, we have performed molecular simulations for a total time of 20 ps and a time interval of 1 fs at high temperature, with 160 atoms of the (b), (g) and (l) (c.f. Fig. 3) convex point configurations. As shown in the Fig. S14,† the energy fluctuation of configuration (b) and (g) at 500 K is small, indicating a relatively dynamic stability of the configuration. In contrast, the energy fluctuation of configuration (l) is larger, suggesting that configuration (l) becomes less stable at high temperature. From an energy perspective, at 500 K, the average energy of configuration (l) is higher than that of configuration (b) and (g), indicating that the orthorhombic convex point configuration (l) becomes unstable at high temperature. This is different from the situation at 0 K, where the energy of the orthorhombic convex point configuration (l) is lower than that of the tetragonal and cubic convex point configurations of (b) and (g).

3.2 Distortion effect on structural stabilities

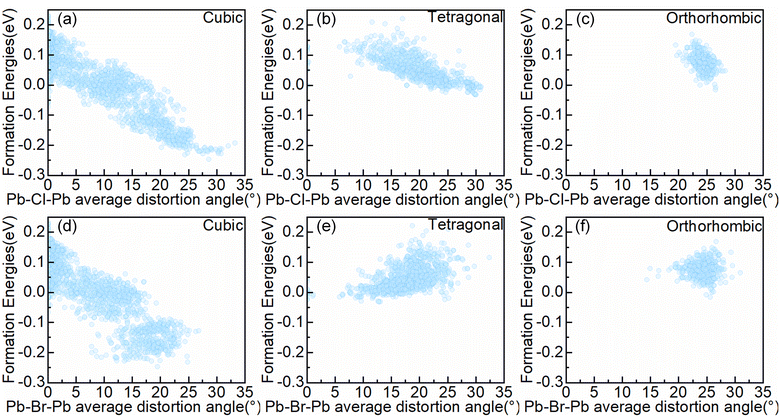
To further analyze the impact of interactions between octahedra in the system on structural stability, we focused on the bond angles of the system, which represent the connectivity characteristics between octahedra motifs. Firstly, we quantified the degree of bond angle distortion in the configurations. The Pb–X–Pb (X = Br or X = Cl) distortion angle is defined as 180°-∠Pb–X–Pb (The ∠Pb–X–Pb angle depict in Fig. S2.†). The Pb–X–Pb (X = Br or X = Cl or X = Br/Cl) total distortion angle is defined as the sum of all Pb–X–Pb distortion angles in the configuration, and the Pb–X–Pb average distortion angle is defined as the Pb–X–Pb total distortion angle divided by the number of X in the configuration. An optimized configuration's distortion angle will be obtained. The relationship between the Pb–X–Pb (X = Br or X = Cl) average distortion angle and the formation energy in symmetry-nonequivalent configurations, as shown in Fig. 4.

Fig. 4 The relationship between the Pb–X–Pb (X = Br or X = Cl) average distortion angle and the formation energy in symmetry-nonequivalent configurations, (a) and (d) cubic (b) and (e) tetragonal (c) and (f) orthorhombic alloy system.

As can be seen from Fig. 4, the atomic distribution and cell type give rise to disparate magnitudes of the Pb–X–Pb (X = Br or X = Cl) average distortion angle. For the cubic alloy system, the configuration can manipulate the Pb–Cl–Pb average distortion angle in the range of 0 to 33.24°, and modulate the Pb–Br–Pb average distortion angle in the range of 0 to 26.81°, corresponding to the range of formation energy from −247.1 meV per cell to 231.3 meV per cell. Thus, the range of the Pb–Br–Pb average distortion angle variations is smaller than the range of the Pb–Cl–Pb average distortion angle variations. Within the tetragonal alloy system, the configuration can manipulate the Pb–Cl–Pb average distortion angle in the range of 0 to 30.94°, and modulate the Pb–Br–Pb average distortion angle in the range of 0 to 32.39°, in accordance with the range of formation energy from −31.3 meV per cell to 221.5 meV per cell. The range of variations of the Pb–Cl–Pb average distortion angle is comparable to that of Pb–Br–Pb. For the orthorhombic alloy system, the configuration can manipulate the Pb–Cl–Pb average distortion angle in the range of 19.46° to 28.29°, as well as modulating the Pb–Br–Pb average distortion angle in the range of 14.32° to 30.96°. So the range of the Pb–Br–Pb average distortion angle variations is greater than the range of the Pb–Cl–Pb average distortion angle variations, which corresponds to the range of formation energy restricted from −16.0 meV per cell to 168.8 meV per cell.

In addition, Fig. 4 shows the correlation between the Pb–X–Pb (X = Cl or X = Br) average distortion angle and the formation energy of the configurations. It is apparent that the formation energy of configurations in the cubic alloy system (c.f. Fig. 4(a)) exhibits a strong correlation with the Pb–Cl–Pb average distortion angle, where the formation energy decreases as the Pb–Cl–Pb average distortion angle increases. A similar phenomenon has also been observed in the tetragonal alloy systems (c.f. Fig. 3(b)), while the relationship becomes not easily observable in the orthorhombic alloy system (c.f. Fig. 3(c)). It may be due to the small changes in angles in the orthorhombic alloy system. For a particular concentration, the correlation is also maintained (c.f. Fig. S3–5†), which means a relatively higher Pb–Cl–Pb average distortion angle enhances the structural stability.

Due to the requirement of maintaining corner-sharing connectivity in the perovskite structure, there is an upper limit on the Pb–X–Pb (X = Br/Cl) average distortion angles,⁴² corresponding to the maximum Pb–X–Pb (X = Br/Cl) average distortion angle around 25° in different alloy systems (c.f. Fig. S6†). As the symmetry decreases from cubic to orthorhombic alloy systems, most alloy configurations tend to cluster in regions with larger angles of the Pb–X–Pb (X = Br/Cl) average distortion, while the range of adjustable Pb–X–Pb (X = Br/Cl) average distortion angles in the configuration significantly narrows. Combined with Fig. 4 and S6,† for the cubic alloy systems, when the Pb–X–Pb (X = Br/Cl) average distortion angle in the configuration is much smaller than the upper limit, the increment in the Pb–Cl–Pb average distortion angle will also coordinately contribute to the promotion of the Pb–Br–Pb average distortion angle. However, when the Pb–X–Pb (X = Br/Cl) average distortion angle approaches the upper limit, it will require sacrificing the magnitude of certain Pb–Br–Pb distortion angles to further increase the Pb–Cl–Pb average distortion angle, thereby decreasing the configuration formation energy (c.f. Fig. 4(a) and (d)). For the orthorhombic and tetragonal alloy systems, the distortion angles in the corresponding alloy system will initiate from a large value, and the Pb–Br–Pb average distortion angle exhibits a decreasing trend with the reduction of the formation energy (c.f. Fig. 4(b), (e) and (c), (f)). For a particular concentration, the same phenomenon was observed (c.f. Fig. S7–9†). Therefore, the Pb–Cl–Pb average distortion angle is more important than the Pb–Br–Pb average distortion angle in decreasing the formation energy. Moreover, as shown in Fig. S4 and S5,† in the orthorhombic and tetragonal alloy system, ordered configurations can provide a larger Pb–Cl–Pb average distortion angle, which means ordered configurations benefit for Pb–Cl–Pb angle distortion but not the case in cubic alloy system (c.f. Fig. S3†). Meanwhile, we find that the cubic alloy convex point configurations have the largest Pb–X–Pb (Br/Cl) average distortion angle at the corresponding concentration (c.f. Fig. S10†). Above all, it can be concluded that the degree of distortion in bond angles would significantly affect the formation energy of the system, particularly in the cubic alloy system.

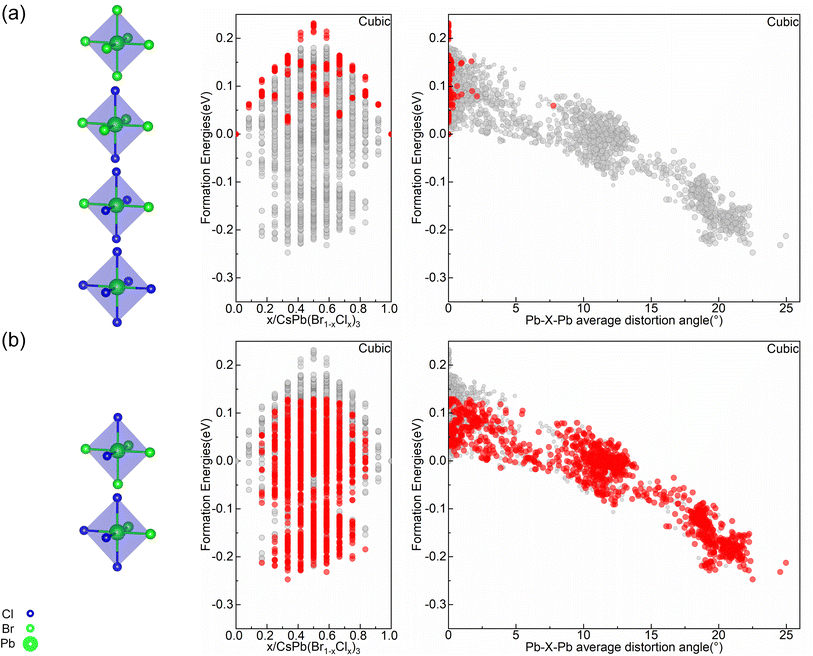
To explain the cubic alloy system have relatively low symmetry octahedral motifs compared with orthorhombic and tetragonal alloy systems at the convex point configurations. The relationship between formation energy and octahedral types as well as distortion angle has been studied. As shown in Fig. 5(a), in the cubic alloy system, when configuration only consists of high symmetric octahedra, their formation energies are located at the top of the convex hull. All of these structures have positive formation energies with minimal distortion angles. While configurations containing low symmetric octahedra, as shown in Fig. 5(b), show a notable decrease in the formation energy accompanied by a significant increase in the distortion angle within the structure. It indicates that in the cubic alloy system, these configurations formed by the stacking of octahedra with high symmetric distribution are relatively unstable, and only having the highly symmetric octahedra motifs does not benefit for angle distortion. The introduction of low symmetric octahedra can effectively adjust the distortion angles and increase the stability of the system. In the highly symmetric cubic phase, a relatively random distribution of Cl elements is conducive to destroying the symmetry of the structure, thereby increasing the level of distortion in the Pb–X–Pb (X = Br/Cl) bond angles throughout the entire configuration. This explains the fact that the cubic alloy convex point configurations are composed of multiple types of octahedra motifs, with the presence of low symmetric distribution of Cl elements in one octahedron motif, as reflected in Fig. 3(a–e). Therefore, the correlation between stability and bond angle distortion which reveals the conflict between symmetric and bond angle distortion in cubic alloy systems.

Fig. 5 Cubic alloy system: (a) the position of the configuration (marked by the red dot) only consisting of high symmetric octahedra in the convex hull and in the Pb–X–Pb (X = Br/Cl) average distortion angle diagram (b) the position of the configuration (marked by the red dot) containing low symmetric octahedra in the convex hull and in the Pb–X–Pb (X = Br/Cl) average distortion angle diagram.

One significant distinction among the three alloy systems lies in the extent to which altering the alloy configuration can influence the Pb–X–Pb (X = Br or X = Cl) distortion angle of the structure. For the orthorhombic and tetragonal alloy system (c.f. Fig. S11 and 12†) exhibits small differences in the Pb–X–Pb (X = Br/Cl) average distortion angle variations among different configurations. Hence, it is not easy to distinguish the formation energies of the diverse configurations only based on the distortion angle. It is known that the Pb–X–Pb (X = Br/Cl) average distortion angle represents the level of distortion in bond angles throughout the entire configuration, reflecting global information rather than local arrangement information. As shown in Fig. S13(a),† the lowest formation energy configurations at various concentrations in the cubic alloy system all contain low symmetric octahedra, while these configurations become unstable in orthorhombic and tetragonal alloy systems, and by the orthorhombic alloy system, the formation energies of such configurations are all positive (c.f. Fig. S13(b) and (c)†). Besides that, in the tetragonal alloy system (c.f. Fig. S1(e)†) even though some unordered configurations can obtain higher Pb–X–Pb (X = Br/Cl) bond angle distortions with respect to ordered configurations, none of these structures are convex configurations. Therefore, in addition to bond angles, the local ordering arrangement is also substantial for the formation energy of the orthorhombic and tetragonal alloy configurations.

Unlike in orthorhombic and tetragonal alloy systems, the different configurations in cubic alloy can significantly change the magnitude of the Pb–X–Pb (X = Br/Cl) average distortion angle, and the Pb–X–Pb (X = Br/Cl) average distortion angle will dramatically affect the formation energy of the configuration. Therefore, the formation energy of the cubic alloy configuration is predominantly governed by distortion angle. But the effect of orderliness on the formation energy can also be demonstrated. As observed in Fig. S10,† the formation energy of configurations with the same concentration and the same Pb–X–Pb (X = Br/Cl) average distortion angle can also vary within a certain range. This implies that both the type and orientation of the octahedra in the configuration will affect the formation energy of the configuration. In Fig. S1(a),† among configurations with similar Pb–X–Pb (X = Br/Cl) distortion angles, these ordered configurations predominantly occupy the lower boundary of the formation energy. Although these structures are not the configurations with the lowest formation energy at the corresponding concentrations in the cubic alloy system, in terms of the Pb–X–Pb (X = Br/Cl) distortion angle dimension, the formation energy of these ordered configurations is generally lower than those with similar distortion angle configurations. The same phenomenon is also observed in the orthorhombic and tetragonal alloy systems (c.f. Fig. S1(e) and (f)†).

3.3 Instability of orthorhombic high Cl concentration alloy

Up to this point, we have systematically analyzed the relationship between the types of octahedra, the octahedra orientation, and the level of distortion of bond angles in the configurations with stability. Another question is why the configuration becomes unstable at high Cl concentrations in the orthorhombic system. As shown in Fig. S1(c),† the ordered configurations exist at high Cl concentrations in the orthorhombic alloy system, and the configurations with the lowest formation energies at the corresponding concentrations are the ordered configurations, but these ordered configurations all have positive formation energies, which indicates that the ordered configurations in orthorhombic alloy system become unstable at high Cl concentrations. To address this, we evaluated the Pb–X–Pb (X = Br/Cl) average distortion angles within various concentration configurations of the three alloy systems, which is employed to reflect how the bond angles will change in alloy systems with different concentrations of Cl elements.

As shown in Fig. 6, in both tetragonal and cubic alloy systems, the mean value of the Pb–X–Pb (X = Br/Cl) average distortion angles for all configurations at different concentrations exhibits an initial increase followed by a decrease as the concentration ascends. However, in the orthorhombic alloy system, the mean value of the Pb–X–Pb (X = Br/Cl) average distortion angles for all configurations at different concentrations decreases consistently as the concentration increases. When the concentration of Cl in the configuration exceeds 0.333, there is no configuration where the Pb–X–Pb (X = Br/Cl) average distortion angle is greater than that of the pure orthorhombic CsPbBr₃ configuration. This implies that due to the excessive distortion of the orthorhombic structure, the introduction of more Cl elements will reduce rather than increase the overall bond angle distortion in the orthorhombic alloy system. Therefore, for the orthorhombic alloy system, we deduce that the decrease in formation energy due to the ordered arrangement of Cl element in the structure is insufficient to offset the increase in formation energy caused by the reduction in global bond angle distortion, destabilizing the configurations with high Cl concentrations in the orthorhombic system.

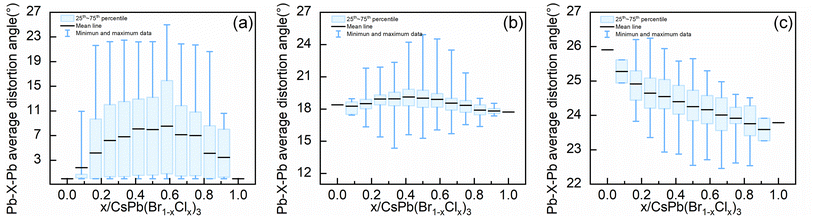Fig. 6 The mean value of the Pb–X–Pb (X = Br/Cl) average distortion angle within various concentration configurations of the (a) cubic (b) tetragonal and (c) orthorhombic alloy systems.

4 Conclusions

In summary, we have investigated the relative stability of different configurations within three alloy systems using the first-principles calculations. The results indicate that the different mechanisms of structural stability in the orthorhombic (tetragonal) and cubic alloy systems are mainly due to the contribution to the structural stability of the ordered arrangement of the octahedra and the large distortion angles caused by the different distribution of the Cl atoms. The type and orientation of octahedra in the crystal structure of different symmetries not only affect the distribution of Cl elements but also influence the extent of distortion in bond angles within the structure. Cubic alloy system's configurations formation energy is predominantly governed by distortion angle, a relatively unordered low symmetry distribution of Cl elements is conducive to the bond angle distortion, only highly symmetric octahedral motifs and ordered configurations are not benefit for the angle distortion. Therefore, the distribution of Cl elements in the ground state configuration is relatively unordered. As the symmetry decreases, the ordered distribution of Cl elements in the tetragonal and orthorhombic alloy configurations becomes apparent in reducing the formation energy, and ordered configurations will benefit for the Pb–Cl–Pb angle distortion. Thus, Cl elements tend to be orderly distributed in the tetragonal and orthorhombic configurations. Furthermore, excessive distortion of the orthorhombic structure leads to a situation where the introduction of more Cl elements does not further increase the average distortion angle of the system but instead reduces it, making high Cl concentration configurations in the orthorhombic alloy system no longer stable. Our study will be helpful for further research of the all-inorganic mixed halide perovskite systems.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was supported by the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2021A1515010328), Science and Technology Program of Guangzhou (Grant No. 202201010090) and the Key-Area Research and Development Program of Guangdong Province (Grant No. 2020B010183001).

References

1. G. Li, Z. Su, L. Canil, D. Hughes, M. H. Aldamasy, J. Dagar, S. Trofimov, L. Wang, W. Zuo, J. J. Jerónimo-Rendon, M. M. Byranvand, C. Wang, R. Zhu, Z. Zhang, F. Yang, G. Nasti, B. Naydenov, W. C. Tsoi, Z. Li, X. Gao, Z. Wang, Y. Jia, E. Unger, M. Saliba, M. Li and A. Abate, Science, 2023, 379, 399–403.
2. Y. Jiang, C. Sun, J. Xu, S. Li, M. Cui, X. Fu, Y. Liu, Y. Liu, H. Wan, K. Wei, T. Zhou, W. Zhang, Y. Yang, J. Yang, C. Qin, S. Gao, J. Pan, Y. Liu, S. Hoogland, E. H. Sargent, J. Chen and M. Yuan, Nature, 2022, 612, 679–684.
3. K. Lin, J. Xing, L. N. Quan, F. P. G. De Arquer, X. Gong, J. Lu, L. Xie, W. Zhao, D. Zhang, C. Yan, W. Li, X. Liu, Y. Lu, J. Kirman, E. H. Sargent, Q. Xiong and Z. Wei, Nature, 2018, 562, 245–248.
4. J. Miao and F. Zhang, J. Mater. Chem. C, 2019, 7, 1741–1791.
5. Y. Wang, X. Li, J. Song, L. Xiao, H. Zeng and H. Sun, Adv. Mater., 2015, 27, 7101–7108.
6. A. Sadhanala, S. Ahmad, B. Zhao, N. Giesbrecht, P. M. Pearce, F. Deschler, R. L. Z. Hoye, K. C. Gödel, T. Bein, P. Docampo, S. E. Dutton, M. F. L. De Volder and R. H. Friend, Nano Lett., 2015, 15, 6095–6101.
7. S. De Wolf, J. Holovsky, S.-J. Moon, P. Löper, B. Niesen, M. Ledinsky, F.-J. Haug, J.-H. Yum and C. Ballif, J. Phys. Chem. Lett., 2014, 5, 1035–1039.
8. S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–344.
9. J. Kang and L.-W. Wang, J. Phys. Chem. Lett., 2017, 8, 489–493.
10. L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696.
11. Y. Cao, N. Wang, H. Tian, J. Guo, Y. Wei, H. Chen, Y. Miao, W. Zou, K. Pan, Y. He, H. Cao, Y. Ke, M. Xu, Y. Wang, M. Yang, K. Du, Z. Fu, D. Kong, D. Dai, Y. Jin, G. Li, H. Li, Q. Peng, J. Wang and W. Huang, Nature, 2018, 562, 249–253.
12. Y. Hassan, J. H. Park, M. L. Crawford, A. Sadhanala, J. Lee, J. C. Sadighian, E. Mosconi, R. Shivanna, E. Radicchi, M. Jeong, C. Yang, H. Choi, S. H. Park, M. H. Song, F. De Angelis, C. Y. Wong, R. H. Friend, B. R. Lee and H. J. Snaith, Nature, 2021, 591, 72–77.
13. Z. Li, Z. Chen, Y. Yang, Q. Xue, H.-L. Yip and Y. Cao, Nat. Commun., 2019, 10, 1027.
14. G. Zou, Z. Li, Z. Chen, L. Chu, H. Yip and Y. Cao, Adv. Funct. Mater., 2021, 31, 2103219.
15. L. Zhang, Y. Jiang, Y. Feng, M. Cui, S. Li, X. Fu, H. Hsu, C. Qin and M. Yuan, Angew. Chem. Int. Ed., 2023, 62, e202302184.
16. G. Zou, Z. Chen, Z. Li and H.-L. Yip, Acta Phys. Chim. Sin., 2021, 37, 2009002.
17. Y. Jiang, C. Qin, M. Cui, T. He, K. Liu, Y. Huang, M. Luo, L. Zhang, H. Xu, S. Li, J. Wei, Z. Liu, H. Wang, G.-H. Kim, M. Yuan and J. Chen, Nat. Commun., 2019, 10, 1868.
18. J. Xing, Y. Zhao, M. Askerka, L. N. Quan, X. Gong, W. Zhao, J. Zhao, H. Tan, G. Long, L. Gao, Z. Yang, O. Voznyy, J. Tang, Z.-H. Lu, Q. Xiong and E. H. Sargent, Nat. Commun., 2018, 9, 3541.
19. Y. Dong, Y.-K. Wang, F. Yuan, A. Johnston, Y. Liu, D. Ma, M.-J. Choi, B. Chen, M. Chekini, S.-W. Baek, L. K. Sagar, J. Fan, Y. Hou, M. Wu, S. Lee, B. Sun, S. Hoogland, R. Quintero-Bermudez, H. Ebe, P. Todorovic, F. Dinic, P. Li, H. T. Kung, M. I. Saidaminov, E. Kumacheva, E. Spiecker, L.-S. Liao, O. Voznyy, Z.-H. Lu and E. H. Sargent, Nat. Nanotechnol., 2020, 15, 668–674.
20. Y. J. Yoon, Y. S. Shin, H. Jang, J. G. Son, J. W. Kim, C. B. Park, D. Yuk, J. Seo, G.-H. Kim and J. Y. Kim, Nano Lett., 2021, 21, 3473–3479.
21. M. Karlsson, Z. Yi, S. Reichert, X. Luo, W. Lin, Z. Zhang, C. Bao, R. Zhang, S. Bai, G. Zheng, P. Teng, L. Duan, Y. Lu, K. Zheng, T. Pullerits, C. Deibel, W. Xu, R. Friend and F. Gao, Nat. Commun., 2021, 12, 361.
22. N. K. Kumawat, A. Dey, A. Kumar, S. P. Gopinathan, K. L. Narasimhan and D. Kabra, ACS Appl. Mater. Interfaces, 2015, 7, 13119–13124.
23. M. Zirak, E. Moyen, H. Alehdaghi, A. Kanwat, W.-C. Choi and J. Jang, ACS Appl. Nano Mater., 2019, 2, 5655–5662.
24. S. Colella, E. Mosconi, P. Fedeli, A. Listorti, F. Gazza, F. Orlandi, P. Ferro, T. Besagni, A. Rizzo, G. Calestani, G. Gigli, F. De Angelis and R. Mosca, Chem. Mater., 2013, 25, 4613–4618.
25. S. Shi, Y. Wang, S. Zeng, Y. Cui and Y. Xiao, Adv. Opt. Mater., 2020, 8, 2000167.
26. D. P. Nenon, K. Pressler, J. Kang, B. A. Koscher, J. H. Olshansky, W. T. Osowiecki, M. A. Koc, L.-W. Wang and A. P. Alivisatos, J. Am. Chem. Soc., 2018, 140, 17760–17772.
27. P. Cottingham and R. L. Brutchey, Chem. Mater., 2018, 30, 6711–6716.
28. S. Plesko, R. Kind and J. Roos, J. Phys. Soc. Jpn., 1978, 45, 553–557.
29. F. Yang, C. Wang, Y. Pan, X. Zhou, X. Kong and W. Ji, Chin. Phys. B, 2019, 28, 056402.
30. Q. A. Akkerman, G. Rainò, M. V. Kovalenko and L. Manna, Nat. Mater., 2018, 17, 394–405.
31. M. C. Brennan, M. Kuno and S. Rouvimov, Inorg. Chem., 2019, 58, 1555–1560.
32. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
33. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
35. G. L. W. Hart and R. W. Forcade, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 224115.
36. C.-C. He, J.-H. Liao, S.-B. Qiu, Y.-J. Zhao and X.-B. Yang, Comput. Mater. Sci., 2021, 193, 110386.
37. A. M. Glazer, Acta Crystallogr. B Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392.
38. K. Thesika and A. Vadivel Murugan, Inorg. Chem., 2020, 59, 6161–6175.
39. W.-J. Yin, Y. Yan and S.-H. Wei, J. Phys. Chem. Lett., 2014, 5, 3625–3631.
40. J. S. Bechtel and A. Van Der Ven, Phys. Rev. Mater., 2018, 2, 045401.
41. L. Cheng, C. Yi, Y. Tong, L. Zhu, G. Kusch, X. Wang, X. Wang, T. Jiang, H. Zhang, J. Zhang, C. Xue, H. Chen, W. Xu, D. Liu, R. A. Oliver, R. H. Friend, L. Zhang, N. Wang, W. Huang and J. Wang, Research, 2020, 2020, 2020–9017871.
42. M. R. Filip, G. E. Eperon, H. J. Snaith and F. Giustino, Nat. Commun., 2014, 5, 5757.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra00818a

---