Open Access Article
Open Access ArticleMagnetoresistance (MR) properties of magnetic materials
Okvarahireka Vitayaya
a,
Phahul Zhemas Zul Nehan
a,
Dicky Rezky Munazat
a,
Maykel T. E. Manawan
bc and
Budhy Kurniawan
 *a
*a
aDepartment of Physics, Universitas Indonesia, Depok, 16424, Indonesia. E-mail: budhy.kurniawan@sci.ui.ac.id
bResearch Center for Advanced Materials, BRIN, Serpong 15314, Indonesia
cFaculty of Defense Technology, Indonesia Defense University, Bogor 16810, Indonesia
First published on 11th June 2024
Abstract
In this review, the classification of magnetic materials exhibiting magnetoresistive properties is the focus of discussion because each material possesses different magnetic and electrical properties that influence the resulting magnetoresistance (MR) values. These properties depend on the structure and mechanism of the material. In this overview, the classification of magnetic materials with different structures is examined in several material groups, including the following: (1) perovskite structure (ABO3), (2) alloy, (3) spinel structure, and (4) Kagome magnet. This review summarizes the results of each material's properties based on experimental findings, and serves as a reference for studying the characteristics of each material.
1. Introduction
Magnetoresistance (MR) is the response of a conductor's resistance to an external magnetic field and is associated with the mechanism of charge carrier scattering.1 The properties of MR are classified into four types, anisotropic magnetoresistance (AMR), giant magnetoresistance (GMR), tunneling magnetoresistance (TMR), and colossal magnetoresistance (CMR). Research on magnetoresistance began with the discovery of the anisotropic magnetoresistance (AMR) effect by William Thomson (Lord Kelvin) in 1856. In his research, William Thomson conducted tests on several samples, including iron, nickel, and brass, to determine the conductivity of each material under the influence of various magnetic field orientations. Thomson found no change in resistance owing to the influence of the magnetic field in brass. However, in iron and nickel materials, an increase in resistance occurred in parallel magnetic field orientations, whereas in perpendicular magnetic field orientations, the resistance decreased. This forms the basis of the magnetoresistance phenomenon. However, in its early discovery, only a 2% decrease in the resistance occurred under the influence of low magnetic fields at room temperature. However, this study did not show any significant development in the MR phenomenon. It wasn't until the early 1970s that the demand for magnetic data storage systems increased, which drove increased research in the field of magnetic sensors.2 In the 1970s, research related to TMR began to emerge. Julliere first studied the TMR effect in 1975. He discovered a magnetic tunnel junction (MTJ) in the Fe/Ge–O/Co multilayer, which showed an MR value of 14% at a temperature of 4.2 K. Subsequently, Maekawa and Gafvert also observed TMR. However, research related to TMR has received little attention for more than a decade because there was not studied further at room temperature. MR properties regained attention in 1988 with the discovery of the giant magnetoresistance (GMR) phenomenon in magnetic multilayers.3 In 1988, GMR was first reported in thin Fe/Cr layers within nanometer structures containing various types of ferromagnetic metals, and practically, GMR was used in hard disk drives (HDD).4 This research pushed the boundaries of William Thomson's previous, enabling the generation of larger resistance changes. The results from the Fe–Cr–Fe layers showed resistance changes of 10% to 50% at low temperatures. This remarkable finding was acknowledged by the 2007 Nobel Prize in Physics. Despite being a highly significant discovery, there are constraints in the development of GMR. Some of these include the experimental samples they created involving complex production methods, such as the single-crystal growth method to form uniform film layers. However, the production method is not suitable for large-scale production. The best results were obtained at low temperatures (50% at 4 K by Fert and 10% at 5 K by Grunberg).2 The mechanism of the GMR differs from that of the AMR. Magnetization in ferromagnetic materials arises from the spin-splitting effect, resulting from the quantum exchange interaction between electrons. The spin-split band structure leads to different spin-up and spin-down states at the Fermi level, resulting in changes in conductivity properties. In AMR, the difference in resistance because of the application of magnetic field orientations parallel or perpendicular result from of the difference in the scattering cross-sectional area induced by electron spin–orbit coupling. In contrast, the GMR is based on the spin-dependent scattering effect, which explains the anomalies in solid ferromagnetic materials with impurities. The solution lies in the “two-channel model,” which treats spin-up and spin-down electrons as relatively independent conduction channels, where spin-flip scattering between the two channels is neglected. Because of the spin-polarized band structure of ferromagnetic transition metals, the mean free path of electrons is much smaller, as electrons can transition to partially filled d states, leading to stronger scattering and higher resistivity. The unfilled d states are also responsible for ferromagnetism, thus establishing a direct relationship between the electrical transport and magnetic properties.5 GMR technology opens up opportunities for various applications, such as position sensors, biomagnetism, magnetic random access memory (MRAM), and current sensors. In 1993, the first automotive sensor emerged, more than four years before using GMR in read-head sensors for hard disks. MR sensors have also been applied in a wider range of fields, from the automotive sectors to biophysics. In recent years, GMR have been developed for current sensors, storage function sensors, and biotechnology applications. Colossal magnetoresistance (CMR) is relatively new compared with other MR effects.2 CMR is typically associated with spin polarization induced by a magnetic field, resulting in reduced spin scattering and resistance. CMR is related to the double-exchange (DE) mechanism, which has potential commercial applications in magnetic storage media.6It has been reported that MR has been increasingly drawing attention in the past few decades because of its wide-ranging applications.15–18 One application of the MR effect is in computer memory and storage technology.19 In sensor systems, the MR effect is also widely utilized, such as in biosensing, biochips, and the emerging field of “spintronics” commonly known as spin electronics or magnetoelectronics. This field focuses on investigating the spin properties of electrons to enhance the efficiency of electronic devices and to discover new properties.20 Magnetic materials with high MR values and Curie temperatures (TC) close to room temperature exhibit promising prospects for applications in the manufacturing of uncooled infrared bolometers and magnetic sensor devices.21 In its development, several material structures that exhibit good MR values have been discovered, including perovskite materials,7–9,22,25 alloy,13,17,23 Kagome magnets,10,13–16,24 and spinel.11,12,26,27,29 In the past few decades, perovskite materials in manganese oxide compounds with mixed valence states have become one of the most intriguing research topics in the study of magnetic materials. This is because of their highly varied multifunctional properties in terms of magnetism, making them suitable for diverse applications such as magnetic refrigeration, spintronics, and solid oxide fuel cells (SOFC). However, what makes them particularly interesting are the intrinsic phase differences based on various interactions related to the coexistence of regions with significantly different magnetic, electrical, and structural characteristics. The fundamentals of the interplay between the electronic and magnetic phase states have been extensively studied and have garnered much attention. This can explain a wide range of phenomena in all strongly correlated electron systems in the presence of phase coexistence.28 Based on a comprehensive review of the MR phenomena from the various material groups above, this review will discusses the interconnected properties of each material that influence the resulting MR values. The characteristics of these materials were based on conducted previously experimental data, providing a reference for determining material types with superior properties and demonstrating the best MR values.
2. Magnetoresistance classification
2.1 Giant magnetoresistance (GMR)
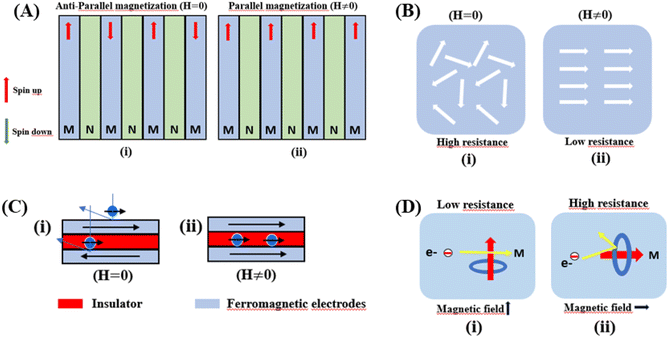
Giant magnetoresistance (GMR) is a phenomenon in which the resistance of a material can rapidly change owing variations in the external magnetic field.29 GMR has excellent potential as a magnetic field sensor, possessing both magnetic and electrical properties. It has been widely developed for various applications such as sensor measurements, current sensing, linear and rotational position sensors, data storage, and magnetic random access memory (MRAM).30 The GMR system candetect extremely low magnetic fields.31 GMR is a quantum mechanical effect that was first observed in 1988 in thin-film materials consisting of multiple layers of ferromagnetic Fe separated by non-magnetic Cr.32 Giant magnetoresistance (GMR) is defined as the ratio (RAP − RP)/RP, where RAP is the resistance in antiparallel materials and RP is the resistance of parallel materials. The GMR effect is utilized to change the magnetization orientation in adjacent magnetic metal layers, where the film thickness must be smaller than the average free path of the electrons. Fig. 1A(i) shows that when the magnetic layers are anti-parallel, it results in a higher probability of scattering because spin-up and spin-down electrons scatter more strongly, resulting in higher resistivity. In contrast Fig. 1A(ii) shows that when the magnetic layers are parallel, the current is mostly carried by spin-up, which can easily pass through the material layers experiencing weak scattering, resulting in lower resistance.33 The electrical transport properties are influenced by three parameters, namely: spin-dependent scattering within the layers, spin scattering at the interfaces between layers, and resistivity dependent on the magnetization orientation in the magnetic layers.34 Electrons in magnetic materials exhibit different resistances and average free path lengths owing differences in the density of states at the Fermi level (N(EF)) for two different spin states when an external magnetic field is applied.The GMR effect is generally explained by spin-dependent electron scattering. In the case of ferromagnetic layers with parallel magnetization directions, only one type of electron is strongly scattered, resulting in low resistivity. In the case of antiparallel magnetization directions, both types of electrons were significantly scattered, resulting in high resistivity.35 GMR is not only found in magnetic multilayers but also in magnetized metallic grains, such as Co or Fe. The grain size nanoscale and the magnetic moments of the grains are nearly isolated from each other.36 As in the study by John et al., the Co20Cu80 sample shows an MR value of 18% with the application of a magnetic field of 50 kOe.37
2.2 Colossal magnetoresistance (CMR)
Colossal magnetoresistance (CMR) is the extraordinary increase in electrical conductivity in the presence of a magnetic field. CMR is classified into two types based on origin: intrinsic CMR and extrinsic CMR. In intrinsic CMR, perovskite manganite is formed by the double exchange mechanism and is typically observed at relatively high magnetic field scales and narrow temperature ranges. On the other hand, extrinsic CMR, or what is called low field magnetoresistive (LFMR), is usually found in polycrystalline materials and arises owing to irregular grain boundaries. This extrinsic MR effect is caused by spin-polarized tunneling (SPT) or spin-dependent scattering (SDS) during electron transport across the grain boundaries. LFMR is temperature-independent and occurs at low magnetic fields. LFMR was observed over a wide temperature range below the Curie temperature (TC). LFMR increased with decreasing grain size. This is because a higher number of grain boundaries will increase spin disturbances, acting as electron scattering centers and resulting in a high resistance without applying a magnetic field. Then, with the application of a small magnetic field, it can initially align irregular spins, reducing electron scattering and resulting in LFMR.38–41 Fig. 1B(i) is associated with the spin polarization induced by the magnetic field, which inhibits spin scattering and reduces electrical resistance. A characteristic of CMR materials is their ability to rapidly align magnetic spins, thereby reducing electron scattering and electrical resistance in the material. This condition makes the material highly conductive (Fig. 1B(ii)).42The CMR phenomenon cannot be solely explained by the double exchange (DE) mechanism. The CMR is also influenced by several interactions, such as the Jahn–Teller (JT) polaron and phase separation. The CMR effect is categorized into two types, namely intrinsic MR and extrinsic MR. Intrinsic MR which are expressive at high magnetic fields, whereas extrinsic MR is significantly more pronounced at low magnetic fields (<0.2 T).22 CMR is explained by the concept of double exchange (DE), which considers the transfer of electrons or holes between two Mn atoms through the 2p orbital of oxygen atoms as intermediaries. There is also a polaronic effect related to the dynamic distortion of octahedral MnO6.43 Polarons involves collective electron motions in a distorted lattice that serve as key transport features in manganite materials. In the development of CMR, studies related to polarons, such as polaron ordering and the transition from polaron transport to metal transition. Among various interactions, two basic types of electron-lattice coupling are important in manganites. One of these is the influence of the crystal structure on electron transportation and bonding. Different ion radii at the A sites result in different internal pressures on the Mn–O–Mn bonds. This lattice distortion leads to the transition from the ideal cubic structure to hexagonal, rhombohedral, and orthorhombic structures, which can affect the Mn–O–Mn bond angles (<180°) because of the influence of rigid rotations of the MnO6 octahedra. This results in a reduction in the width of the eg conduction band, conductivity, and ferromagnetic DE.44 The distortion at the Mn site is key to explaining the mechanism of the polaron transition.45 The electronic and lattice properties are highly influenced by the distribution of Mn–O bond lengths. The distorted Mn–O bonds above TC are consistent with Jahn–Teller distortions in the MnO6 octahedra.46 During the electron transfer process, there is a dynamic and cooperative influence of the Jahn–Teller type of distortion. Conduction in manganites is described by electron transfer, for example, from Mn3+ ions to the nearest Mn4+ ion orbitals through the 2p orbital of oxygen. When the electron spin t2g from Mn combines in a ferromagnetic manner, the conduction band opens when there is a regular exchange of Mn3+/Mn4+ sites. The ease of conduction depends on the Mn–O–Mn angle approaching 180°, which improve the conductivity. The Mn–O–Mn angle depended on the size of the A cation. The transition from a paramagnetic insulator to ferromagnetic metal around TC with the application of a magnetic field is explained by the alignment of electron spins at the t2g level, allowing electron transport at the eg level.47 In thin films, the resistivity is twice that of the crystal and six times that of the intrinsic resistivity of the stoichiometric bulk material. This indicates that the resistance of the grain boundary was dominant. The resistivity of the thin films can be expressed as Ri + Rgb, Ri is the intrinsic resistance, and Rgb = n × rgb/A, represents the extra resistance because of n grain boundaries in a sample of cross-sectional area A.48
2.3 Tunneling magnetoresistance (TMR)
Tunneling magnetoresistance (TMR) has an effect similar to that of GMR, however TMR includes a non-magnetic insulating layer (instead of a conducting layer). The insulating layer typically has 1–2 nm thickness, which allows electrons to tunnel through it. This type of sensor is known as the magnetic tunnel junction (MTJ). The materials used for the insulating layer are typically Al2O3, Ga2O3, MgO, and graphene. TMR sensors can detect micro to nanosized particles. MTJs exhibit the most sensitive magnetic resistance, with an MR ratio of 20–50%.31In the TMR effect, electrons move from one ferromagnetic (FM) layer to another through the tunneling effect. In this tunneling process, electrons find a free path to the tunnel in the parallel magnetization direction, making the electron transport process easier than antiparallel magnetization when the electron state at the barrier is polarized (Fig. 1C(i) and (ii)). The TMR effect can be defined as (RAP − RP)/RP, where RAP is the resistance of antiparallel materials and RP is the resistance of parallel materials. The TMR effect was first observed by Julliere in 1975 when a tunnel junction between two FM films (Fe–Ge–Co tunnel junction) was created. The key point of the TMR phenomenon is the dependence of the tunnel resistance of ferromagnetic junctions on the orientation of magnetic moments. This effect is similar to that of GMR in magnetic multilayers, where the resistance depends on the orientation of magnetic moments separated by nonmagnetic metallic layers. The TMR effect is typically observed in simple planar junctions and also exists in more complex junctions, such as mesoscopic double-barrier junctions, and junctions including granular systems.49
Magnetic Tunnel Junctions (MTJs) exhibiting Tunneling Magnetoresistance (TMR) have become the core of modern magnetic storage. Most of MTJs use FeCo alloy magnetic electrodes that are body-centered cubic (BCC)-centered, and directly interfacing with the MgO barrier (FeCo MgO-MTJs). The resulting TMR ratio exceeded 1000% in the polycrystalline FeCo/Mg MTJs at cryogenic temperatures. This thousandfold effect is attributed to the nearly complete spin polarization of tunneling electrons in the energy band of the Bloch electronic states. The TMR value can rival that of MTJs with half-metal electrodes such as Co2 (Mn, Fe) Si.50
2.4 Anisotropic magnetoresistance (AMR)
The anisotropic magnetoresistance (AMR) effect results in electrical conductivity that depends on the magnetization orientation and the current density vector. In ferromagnetic materials, the resistivity is high when the magnetic field is parallel to the current, and the resistivity was low when the magnetic field is perpendicular to the current.31 AMR was first discovered in the ferromagnetic (FM) metals Ni and Fe by William Thomson in 1856.51 The AMR effect is defined as the difference between ρ∥ (resistivity when the magnetic moment M is parallel to the electric current i) and ρ⊥ (resistivity when M is perpendicular to i), defined as Δρ = ρ∥ − ρ⊥.An increase in spin-dependent scattering causes the increase in AMR. Increasing magnetization also enhances the TMR because it results in increased spin polarization. AMR is not only influenced by temperature but also by lattice distortions caused by doping.52
The AMR effect is often observed in various types of thin films of ferromagnetic metals and alloys such as Fe, Co, and Ni.53 The anisotropic resistance in Ni–Fe and Ni–Co alloys depends on the orientation of the magnetic moment related to the direction of the electric current arising from spin–orbit coupling. In Fig. 1D(i), it is shown that if M (magnetic moment perpendicular to i and spin–orbit parallel to i), the cross-sectional area for the resulting scattering is small, leading to low resistance. Conversely, in Fig. 1D(ii), if M is parallel to i and spin–orbit is perpendicular to i, the cross-sectional area for scattering is large, resulting in high a resistance.
3. Parameters that affect magnetoresistance
3.1 Magnetic parameters
With the application of a magnetic field, there is a decrease in resistivity, particularly under saturating magnetic fields. In Fig. 2A and B, the resistivity rapidly decreases, followed by a rapid increase in magnetization values. This is based on a double-exchange interaction mechanism. In this mechanism, the alignment of the Mn spin directions leads to an increased electrical conductivity. Conversely, it becomes difficult for electron transfer between ion difficult to cross domain walls in different magnetization directions, resulting in high resistivity. Under a strong magnetic field, the magnetic domains tended to align with the field direction. As a result, electrons can easily cross the domain-wall boundaries, leading to a decrease in resistivity and an increase in the MR value.54 Magnetization increases owing to the rotation of the magnetic domains influenced by the magnetic field. Simultaneously, this causes a sharp decrease in the resistance, underpinning the negative MR values at high magnetic fields.55 Furthermore, at decrease in ferromagnetic coercivity (Hc) occurs with an increase in grain size, indicating a transformation from a multi-domain state to a single-domain state in the ferromagnetic grains.56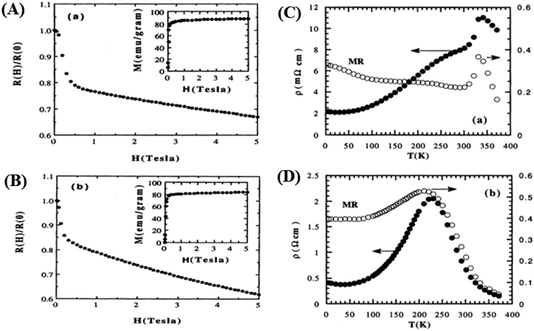 | ||
| Fig. 2 [A] Field dependence of relative resistivity and magnetization at 5 K for, La0.67Ba0.33MnO2.99 and [B] La0.67Ba0.33MnO2.90). Reprinted with permission from the American Physical Society.54 Curves of resistivity (filled circles) and MR ratio (empty circles) against temperature for [C] La0.67Ba0.33MnO2.99 and [D] La0.67Ba0.33MnO2.90. Reprinted with permission from the American Physical Society.54 | ||
3.2 Electrical parameters
Applying a magnetic field, significantly decreases the resistivity across the entire temperature range. The decrease in resistivity resulted in an increase in the MR value. In Fig. 2C and D with a 5 T magnetic field, the maximum MR value occurs at a temperature of 330 K, which is slightly lower than the peak resistivity at around 340 K. The MR experiences a slight increase as the temperature decreases. This indicates a correlation between the magnetization and resistivity of the material. Under the influence of a magnetic saturation field, the resistivity decreases significantly, whereas at fields above the saturation level, the resistance decreases more slowly than at low fields.54 This is because the magnetic field deflects the charge carriers (electrons) and aligns the magnetic spins in the manganite compound. Therefore, the resistivity decreases when electrons move under the influence of DE, causing a shift in the transition metal–insulator (TMI) characteristics.224. Classification of magnetoresistance materials groups
4.1 Perovskite structure material (ABO3)
Research on perovskite manganite materials has seen significant developments in the past few decades. Perovskite materials based on manganese oxide have the general formula R1−xAxMnO3, where R is a rare earth element, and A is a divalent element (Fig. 3A). Doping manganese with other elements results in superior properties, with theoretical calculations indicating the presence of additional multiferroic magnetic phases.57 Some manganite perovskite materials that show MR values include manganite perovskites based on LaMnO3 (46 and 58–60) and NdMnO3.22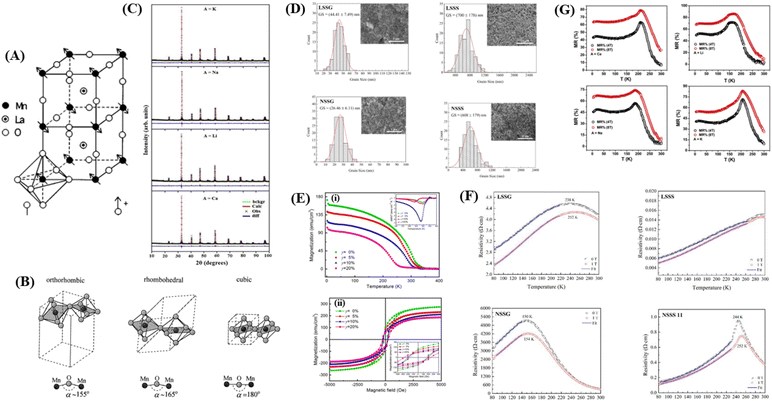 | ||
| Fig. 3 [A] Perovskite structure LaMnO3. Reprinted with permission from the American Physical Society.147 [B] Schematic arrangement of octahedral MnO6. Reprinted with permission from the Elsevier.67 [C] Rietveld for XRD pattern of La0.5Nd0.15Ca0.25A0.1MnO3). Reprinted with permission from the Elsevier.148 [D] Grain size distribution histogram and FESEM micrographs of manganite samples (https://doi.org/10.3390/, Open source MDPI).22 [E] (i) Magnetization versus temperature (500 Oe) of LSMZO film. The inset shows the temperature derivative of magnetization (dM/dT) curve. (ii) Hysteresis loop of LSMZO film recorded at 10 K Reprinted with permission from the Elsevier.87 [F] shows the electrical resistivity as a function of temperature for LSMO and NSMO manganites under an applied magnetic field of 0 and 1 T).22 [G] Plot of magnetoresistance (MR%) as a function of temperature (T) for La0.5Nd0.15Ca0.25A0.1MnO3) (https://doi.org/10.3390/coatings11030361, open source MDPI).22 | ||
Similar to the study by Mahesh et al., that La1−xAxMnO3 (A = Ca, Sr) exhibits a remarkably large negative magnetoresistance with a doping range of 0.2 ≤ x ≤ 0.5. Dynamic or static Jahn–Teller effects plays a crucial role in explaining the colossal magnetoresistance (CMR) effect in perovskite materials such as manganese oxides.61 The mixed valence state, between Mn3+ and Mn4+, can be enhanced by the fractional substitution of La3+ sites with divalent alkaline earth ions, influencing the magnetic transition temperature in the system. This transition can be explained by the double exchange (DE) interaction between Mn3+ and Mn4+ ions. This affects the system in the MnO6 octahedral, where ion doping causes distortion in the Mn–O plane, leading to significant changes in the structural and transport properties. LaMnO3 perovskite exhibits a varied phase diagram owing to changes in electron behavior in the 3-d orbital. This behavior arises from the complex exchange involving charge, spin, orbital, and lattice degrees of freedom.62 The undoped LaMnO3 parent compound exhibited a different crystal structure. There are two phases at room temperature, distorted orthorhombic and trigonal. Atom substitution at specific sites can influence the vibrational properties of the base material based on bond strength, mass, and ionic radii. Notably the insulating state in LaMnO3 changes, displaying metallic behavior at room temperature by adjusting the doping ratio. This indicates that the structural phase transition acts as a trigger for the metal–insulator transition.63
Manganite perovskite materials exhibit diverse properties, owing to their unique electromagnetic properties, such as interactions between the spin, charge, and orbitals.7 The addition of doping is usually employed to control the spontaneous exchange bias (SEB) effect. For instance, partial substitution of Ba in La1.5Sr0.5−xBaxCoMnO6 enhances the SEB effect. This effect can be further improved with concentrations of Sr or Ba, relating to changes in the balance between the crystal field and Coulomb repulsion acting on Co, affecting its spin state, leading Co to pair with Mn ions. The combination of Co and Mn becomes crucial for the spin state, and presence of the spin glass (SG) phase. When magnetic Co ions are substituted with non-magnetic Ga3+, it weakens the spin interaction of CO+–O2−–Mn+ (ferromagnetic interaction) and generates other interactions such as Co3+–O2−–Co3+ (antiferromagnetic interaction), resulting in a decrease in Curie temperature (TC).8 In La0.5Sr0.5FeO3−δ (LSFO), the material crystallizes in a perovskite structure because the substitution of Sr for La creates oxygen vacancies and electron holes to maintain electronegativity. In addition, the insertion of oxygen ions entering LSFO also lead to changes in the concentration of Fe3+ and oxygen vacancies. This results in a rapid oxygen diffusion rate and enhances the capacitance based on oxygen anions.64
Numerous studies have been conducted on hole-doped manganite materials, showing complex phases of orbital/spin/charge, and ferromagnetic (FM) – antiferromagnetic (AFM) dependent on the doping percentage (x) and temperature, where x represents the concentration of Mn4+ ions or the percentage of doping of divalent atoms. In the antiferromagnetic insulator LaMnO3 compound of type A, doping with divalent ions such as Ca, Sr, and Ba transforms its antiferromagnetic insulator properties into ferromagnetic metal by varying the ratio of Mn3+ and Mn4+. It was found that at a doping concentration x = 0.3, the concentration of Mn4+ reached a level where the double exchange (DE) mechanism between Mn3+–O–Mn4+ dominated the super exchange interaction between Mn3+–O–Mn3+ and Mn4+–O–Mn4+. This indicates significant colossal magnetoresistance (CMR) in the Curie temperature (TC) region.65
The following sections describe the crystal structure and morphology, electrical properties, magnetic properties, and MR of several perovskite materials.
From Fig. 3B, it is evident that there are distortions and structural changes in LSMO that are highly dependent on the concentration and radii of the substituting ions. Fig. 3B, also shows that the MnO6 octahedral bonds undergo distortion, indicating a change in the bond lengths of the Mn–O–Mn ions. According to the Double Exchange (DE) theory, changes in d〈Mn–O〉 and 〈Mn–O–Mn〉 influence the bandwidth (W). A decrease in W weakens the DE interaction between Mn3+–O–Mn4+ owing to a reduction in electron mobility caused by an increase in the d〈Mn–O〉 length and a decrease in the 〈Mn–O–Mn〉 angle. Here, W is determined using the equation:68
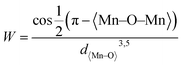 | (1) |
As an example, the X-ray diffraction (XRD) results of the perovskite material (LMO) with the composition La0.5Nd0.15Ca0.25A0.1MnO3, where (A = Ca, Li, Na, and K), as shown in Fig. 3C using the solid-state reaction method, revealed that the material has an orthorhombic crystal structure in the Pbnm space group. In Fig. 3C, sharp and intense peaks are observed, consistent with the perovskite structure, indicating good sample crystallinity with no detected secondary phases. Different ion substitutions (Ca, Li, Na, and K) lead to changes in the unit cell volume of the material. With Na ion substitution, the unit cell volume decreased, whereas samples substituted with K ions showed a significant increase. This is because the average ionic radius of Na+ is smaller than that of Ca+ and K+ ions. The average size of crystals is determined using the Scherrer equation as follows:
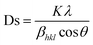 | (2) |
When the ionic radii of the dopant atoms at the A sites increase, the internal pressure decreases, reducing the distortion of the MnO6 octahedra. This increases the Mn–O–Mn angle, lattice parameter, and unit cell volume. The increase in the unit cell volume causes a decrease in the density owing to the increased molecular mass. As the radius of A increases, there is a decrease in the Mn–O bond length. An increase in the Mn–O–Mn bond angle compensates for the reduction in Mn–O bond length. This is because the spaces in the cell are filled with larger-radius A-site cations, and the increased compressive stress shortens the Mn–O–Mn bond in the MnO6 octahedra, which is related to the Mn–O–Mn and Mn–O bond lengths. The level of distortion in the unit cell structure was measured by the Goldschmidt tolerance factor (t) using the following equation:
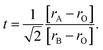 | (3) |
The tolerance factor is a term related to the bond-length mismatch of the A–O and B–O bonds, which are associated with the ionic radii. Distortions tend to disappear at high temperatures because of the greater thermal expansion of the A–O bond lengths. When t > 1, the A–O bonds undergo compressed, whereas the B–O bonds are under tension.70 The influence of the tolerance factor is a major factor affecting the magnetic properties of materials, such as affecting TC and Tρ. This is related to the DE interaction, which was influenced by the ratio of Mn3+ to Mn4+. A stronger DE results in a higher Tρ. There are three factors that greatly affect Tρ, including the hole carrier density controlled by the ratio [Mn3+]/[Mn4+], [rA], and cation mismatch (σ2) determined by the equation:
σ2 = ∑yir2i − 〈rA〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2
| (4) |
In study by Munazat et al.,79 the material La0.7Ba0.1Ca0.1Sr0.1MnO3, synthesized using the sol–gel and wet mixing (WM) methods, showed that the grain size of the MW sample was smaller than that of the SG sample. This is evidenced by the XRD and SEM results indicating that the crystallite and grain size of WM are smaller than those of SG. Both the samples were subjected to the same heat treatment. This difference can be attributed to the SG method being carried out under neutral pH conditions, whereas the WM method was performed under acidic conditions because of the precursor was dissolved in nitric acid. This indicates that pH and the use of a chelating agent are important parameters that influence the resulting grain size. In perovskite synthesis, the grain size is influenced by chemical reactions under pH conditions.80
In a study by Das et al., it wass also stated that grain growth increases with increasing sintering temperature, leading to a reduction in grain boundaries. The effect of sintering temperature on grain size showed a similar influence on the XRD results. Significant differences in grain shape were observed by synthesizing CoFe2O4 materials with varying the sintering temperature from 300 °C to 1200 °C, grain shapes such as spheres (T = 300 °C), pyramids (CFO – 450 °C), (T = 600 °C), lamellae (T = 750 °C), octahedra (T = 900 °C), and truncated octahedra (T = 1200 °C) were observed, with uniform grain shapes in all samples. It is estimated that different grain shapes have a significantly impact on the material's physical properties.81 The increase in grain size because of the temperature rise is caused by the coalescence of crystallites at higher temperatures.82 By increasing the sintering temperature, the grains were enlarged and the porosity was gradually reduced. The porosity of materials can lead to crystallographic defects and significantly affect the material's physical properties.83
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe, and there is a decrease in the saturation magnetization (Ms) and an increase in coercive field (Hc) with increasing Zn content (Fig. 3E(ii)). Hc depends heavily on the microstructure of the ferromagnetic material, such as structural mismatches and defects that affect the magnetic domains. Substitution of Zn2+ ions can induce internal strain at Mn sites because of the large ionic radius mismatch between Zn2+ and Mn3+/Mn4+, resulting in lattice distortion, including the rotation of MnO6 octahedra and a decrease in Mn–O distance and Mn–O–Mn angle. Doping also distorts of the Mn–O–Mn angle, making it smaller, and increasing the Mn–O distance distribution. This suggests that increasing mismatch in the substituted cation size leads to a decrease in Tc, as well as metal–isolator transition temperature in perovskite manganites.87
000 Oe, and there is a decrease in the saturation magnetization (Ms) and an increase in coercive field (Hc) with increasing Zn content (Fig. 3E(ii)). Hc depends heavily on the microstructure of the ferromagnetic material, such as structural mismatches and defects that affect the magnetic domains. Substitution of Zn2+ ions can induce internal strain at Mn sites because of the large ionic radius mismatch between Zn2+ and Mn3+/Mn4+, resulting in lattice distortion, including the rotation of MnO6 octahedra and a decrease in Mn–O distance and Mn–O–Mn angle. Doping also distorts of the Mn–O–Mn angle, making it smaller, and increasing the Mn–O distance distribution. This suggests that increasing mismatch in the substituted cation size leads to a decrease in Tc, as well as metal–isolator transition temperature in perovskite manganites.87The magnetoresistance (MR) properties of perovskite materials are highly interesting, leading to investigations regarding MR determined by the decrease in the electrical resistivity of the material under the influence of an external magnetic field. The strong MR effect results from the coexistence of ferromagnetism and metallic conductivity. The percentage of magnetoresistance is defined as % MR = (ρ0 − ρ(H))/ρ0 × 100%, where ρ(0) is the resistivity at zero field and ρ(H) is the resistivity under an applied magnetic field. In the study by Kumar et al., the %MR values for La0.5Nd0.15Ca0.25A0.1MnO3 (A = Ca, Li, Na, and K) in Fig. 3G were found to be 80%, 87%, 75%, and 84% for samples doped with Ca, Li, Na, and K at the TMS with the application of an 8 T magnetic field. The highest magnetoresistive effect observed around TMS is attributed to the increased ferromagnetic interaction because of the alignment of parallel spins in the Mn–O–Mn coupling. Additionally, significant MR effect was observed at low temperatures, which could be attributed to the influence of carrier scattering at the grain boundaries.92 When electrons move from one grain to another, they encounter insulation barriers between grains, and each can scatter the electrons because of the reduced connectivity between the grains or surface contamination. A strong magnetic field can overcome strong electron scattering, resulting in high magnetoresistance at low temperatures.93
The external CMR is related to grain boundaries, which can be explained by spin-polarized tunneling and spin-dependent scattering. Many efforts have been made to enhance CMR in materials, one of which is creating manganite composite materials with have a secondary phase as an insulator. Several studies have reported an increase in MR values.43,94,95 Additionally, vacancy substitution in manganite materials can also enhance the MR value.96,97
4.2 Alloy
Several alloy groups that show the phenomenon of MR, including Ni–Mn based,98 Co–Fe,50 and Ni–Cu.99 In Ni–Mn–Z-based alloys, the magnetic moment (ΔM) can be significantly enhanced by the addition of a fourth element, composition adjustment, and heat treatment. Specifically, doping with Fe/Co atoms can act as a “ferromagnetic activator” inducing the alignment of magnetic moments (of Mn–Mn nearest neighbors), resulting in ferromagnetic behavior and creating a strong magnetostructural coupling state. For instance, in the study conducted by Zhang et al., the Ni41Mn43Sn10Co6 alloy showed a ΔM value of 90 A m2 kg−1 under the influence of a 5.0 T magnetic field, which is significantly larger than that of the Ni47Mn43Sn10 alloy without Co doping (ΔM = ∼16 A m2 kg−1)17 In addition, ΔM was found to experience a significant increase with the substitution of Ni by 4.2% with Fe in the Ni50Mn38.0Sn12.0 alloy, specifically from 16 A m2 kg−1 to 58 A m2 kg−1.100 However, the magnetocaloric effect (MCE) associated with the first-order martensitic transformation characterized by a large isothermal magnetic entropy change (ΔSM) shows a narrow operating temperature range of approximately 1–5 K, which poses a barrier to the practical application of this alloy for magnetic refrigeration. To expand the operating temperature range with refrigeration capacity (RC), strategies such as reducing the material size (thin films or microwires) need to be implemented.101 In the study by Zhang et al., using the material Ni46.8Mn38.1Sn11.6Fe3.5, the highest negative magnetoresistance (MR) values were observed, reaching 40.8% at 261 K and 26.7% at 275 K during the cooling and heating processes.102The following sections describe the crystal structure and morphology, electrical properties, magnetic properties, and MR of several alloy materials.
In Fig. 4A, it can be observed that a single phase in the Mn1.9Co0.1Sb alloy is obtained after substituting Co with a tetragonal Cu2Sb structure (space group P4/nmm) with lattice parameters a = 4.1048 Å and c = 6.4770 Å, obtained from Rietveld refinement. The unit cell volumes whereas V = 109.137 Å, and c/a = 1.577. The lattice parameters for the Mn2Sb alloy were a = 4.07 Å and c = 6.54 Å. The results indicate that substituting Co is increase the lattice parameter a and decreasing c in the Mn1.9Co0.1Sb alloy. There was a decrease in c/a by 1.8%, an increase in volume by 0.7%, and a contradictory change in a and c, suggesting anisotropic deformation of the crystal lattice in the Co-substituted Mn2Sb alloy.
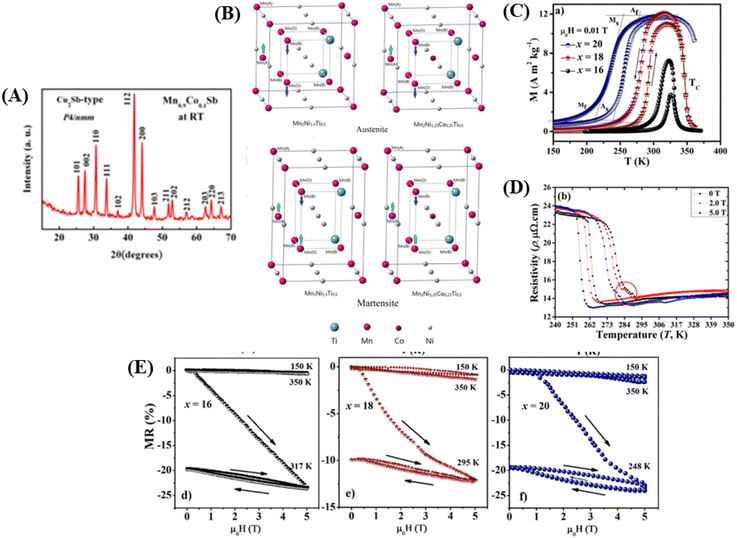 | ||
| Fig. 4 [A] XRD pattern for Mn1.9Co0.1Sb alloy at room temperature. Reprinted with permission from the AIP Publishing,104 [B] Heusler alloy supercell model Mn2Ni1.5Ti0.5 and Mn2Ni1.25Co0.25Ti0.5) Reprinted with permission from the Elsevier.116 [C] M–T curve for alloys Ni50−x(FeCo)xMn37Ti13 (x = 16, 18 and 20) with 0.01 T). Reprinted with permission from the Elsevier.98 [D] Electrical resistance curve (ρ–T) with respect to material temperature Ni43Mn41Co5Sn11 at 0, 2.0 and 5.0 T). Reprinted with permission from the Elsevier.102 [E] MR is field-dependent throughout the martensite phase respectively, the magneto-structural transition of temperature and the austenite phase, respectively to x = 16, 18, 20 sampel. Reprinted with permission from the Elsevier.98 | ||
Furthermore, there are alloys with Heusler structures that have the composition X2YZ, where X and Y are transition metal elements, and Z is an sp-element. The main group element Z occupies four different crystal locations, namely A (0, 0, 0), B (0.25, 0.25, 0.25), C (0.5, 0.5, 0.5), and D (0.75, 0.75, 0.75), resulting in an ordered structure. An example of a Heusler alloy was found in the study by Ma et al., where the material Mn50Ni50−xTix had a cubic structure, and the Ni atoms enter the Mn site (C). This is based on the “valence electron counting rule” in Heusler alloys, which states that transition metal atoms with more valence electrons prefer to occupy A and C sites.106 Crystal structures of Heusler alloys can be classified into two types: half (or semi-) with the chemical formula XYZ and full Heusler with the formula X2YZ, where X and Y are transition metal elements and Z is an sp-element. In Full-Heusler compound system, when the valence of X is larger than Y, the atomic sequence becomes X–Y–X–Z along the diagonal direction of the cubic cell, and its structure is more commonly known as L21. However, when the valence of Y is the largest, the atomic sequence becomes X–X–Y–Z, known as the inverse-Heusler alloy.107 Heusler alloys (HA) have become interesting materials for development owing to several advantages, including high Curie temperature (TC), half metallicity, shape memory effect, thermoelectric properties, and ferromagnetism.108–111 Owing to these advantages, HA is widely applied as spin filter, GMR materials, tunnel junctions, transducers, energy technology, spin valve, memory device, multiferroic, and for magnetocaloric effect. HAs have a large thermoelectric coefficient, which allows them to efficiently convert heat energy into electrical energy.112,113
A supercell model of a Heusler alloy is depicted in Fig. 4B, specifically for the materials Mn2Ni1.5Ti0.5 and Mn2Ni1.25Co0.25Ti0.5. The arrows on the Mn atoms indicate the sequence of spin moments. In the austenitic state, it behaves as ferromagnetic (FM), whereas in the martensitic state, it behaves as an antiferromagnetic (AFM).114
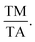 115 The e/a ratio was found to decrease with the content of (FeCo)x, as indicated by the TM/TA shifting towards lower temperatures. In the Ni–Mn–Ti system, Mn occupies the Ti site in the D position with antiferromagnetic (AFM) coupling with Mn at the B site, which is nearest to the austenitic and martensitic phases.116 In this material, Co–Fe acts as an “FM activator” and transforms Mn (B)–Mn (D) AFM into Mn (B)–Fe/Co (A, C)–Mn (D) with ferromagnetic exchange coupling in the Heusler alloy system (A (0,0,0), B (¼, ¼, ¼), C (½, ½, ½), D (¾, ¾, ¾)). It has also been reported that Co doping has a more significant effect on increasing FM exchange than Fe doping, but it increases hysteresis loss. Therefore, simultaneous Fe–Co substitution results in higher FM exchange interactions, decreased TM, and increased hysteresis TC.117
115 The e/a ratio was found to decrease with the content of (FeCo)x, as indicated by the TM/TA shifting towards lower temperatures. In the Ni–Mn–Ti system, Mn occupies the Ti site in the D position with antiferromagnetic (AFM) coupling with Mn at the B site, which is nearest to the austenitic and martensitic phases.116 In this material, Co–Fe acts as an “FM activator” and transforms Mn (B)–Mn (D) AFM into Mn (B)–Fe/Co (A, C)–Mn (D) with ferromagnetic exchange coupling in the Heusler alloy system (A (0,0,0), B (¼, ¼, ¼), C (½, ½, ½), D (¾, ¾, ¾)). It has also been reported that Co doping has a more significant effect on increasing FM exchange than Fe doping, but it increases hysteresis loss. Therefore, simultaneous Fe–Co substitution results in higher FM exchange interactions, decreased TM, and increased hysteresis TC.1174.3 Spinel material
Materials with a spinel structure formulated as AB2X4 (Fig. 5A) exhibit interesting ground states associated with the interactions of charge, spin, and orbital degrees of freedom, strongly coupled with the lattice. In the B-sublattice, complexity arises owing to the competition between direct nearest neighbor (NN) and ferromagnetic (FM) interactions and exchanges between next-nearest neighbors (NNN), and antiferromagnetic (AFM) interactions. Therefore, the FM and AFM states depend on the separation of B sites.10 As an example, compounds based on chromium (Cr) with the formula ACr2X4 (where A represents a transition metal and X includes the elements S, Se, or Te) various of physical properties. These properties arise from the complex interplay between structural, spin, charge, and orbital degrees of freedom.12 In this spinel structure, the FM state arises from the superexchange (SE) interactions between 3d electrons of Cr ions mediated by oxygen. The exchange interaction between s and d electrons results in substantial spin in the electronic band. The dependence on the strength of spin–orbit coupling and exchange separation leads to spinel materials exhibiting magnetic semiconductor behavior.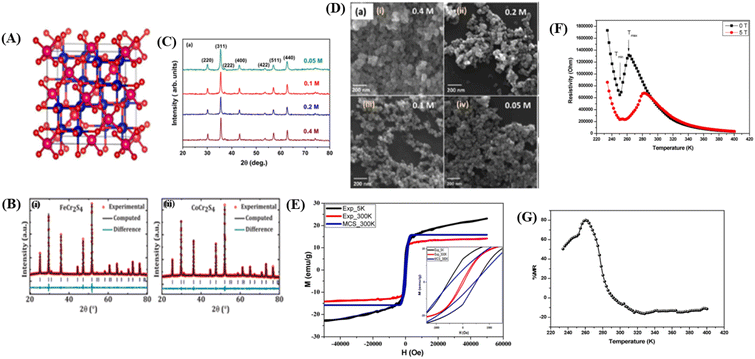 | ||
| Fig. 5 [A] The crystal structure of the spinel. Reprinted with permission from the Elsevier.11 [B] Rietveld refinement of powder X-ray diffraction pattern (i) FeCr2S4 and (ii) CoCr2S4. Reprinted with permission from the Elsevier.121 [C] X-ray diffraction data of Fe3O4 nanoparticles prepared using different concentrations of precursor). Reprinted with permission from the Elsevier.122 [D] FESEM images showing the surface morphology of Fe3O4 nanoparticles prepared from different precursor concentrations). Reprinted with permission from the Elsevier.122 [E] Experimental and theoretical magnetic hysteresis circles of SnFe2O4 nanoparticles). Reprinted with permission from the Elsevier.11 [F] Dependence of electrical resistivity of SnFe2O4 on temperature under different magnetic fields. Reprinted with permission from the Elsevier.11 [G] Magnetoresistance versus temperature for SnFe2O4 nanoparticles. Reprinted with permission from the Elsevier.11 | ||
Chromium-based compounds, represented as ACr2X4 (where A represents a transition metal and X represents S, Se, or Te), are currently of significant interest owing to their diverse physical properties. The physical properties of these materials arise from the complex interplay between their structure, spin, charge, and orbital degrees of freedom. For example, CuCr4X4 is a metal, CdCr2Se4 is a semiconductor, HgCr2Se4 (n-type) is a semi-metal showing ferromagnetic behavior, MnCr2Se4 a semiconductor with ferromagnetic properties, and ZnCr2S4 is an insulator with antiferromagnetic characteristics. Some of these materials are of interest because of their ferromagnetic ordering and the emergence of semimetallicity predicted by band structure calculations. The FM order arises from the superexchange (SE) interaction between the 3d electrons of Cr ions mediated by anions. The SE interaction between s and d electrons results in substantial spin splitting from the electronic band. This is dependent on the strength of spin–orbit coupling and exchange splitting. Sayyan et al. reported that FeCr3Te4 underwent a ferrimagnetic (FIM) transition at a critical temperature (Tc) of 123 K. This result indicates that the FIM interaction in FeCr2Te4 emerges because of the FM interaction between antiferromagnetic Cr–Fe–Cr layers being magnetically coupled. This compound also exhibits Hall effect anomalies at temperatures <123 K, primarily dominated by the extrinsic skew-scattering mechanism rather than intrinsic Karpus–Luttinger or extrinsic hopping mechanisms.12
The following is a presentation of the crystal structure and morphology, electrical properties, magnetic properties, and MR of several spinel materials.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. For example, in the case of SnFe2O4, this cubic spinel structure can be clearly identified through X-ray diffraction (XRD) analysis,11 MCr2S4 (M = Fe & Co),121 and Fe3O4.122 For example, in the study conducted by Dey et al.,121 using the compounds FeCr2S4 and CoCr2S4 with spinel structures synthesized through the solid-state reaction method, the XRD results in Fig. 5B, refined using Rietveld refinement, showed that the materials have a cubic FCC spinel structure (No. 277). The atomic positions in the unit cell were determined as 8a Fe (0, 0, 0), 16c Cr (0.625, 0.625, 0.625, 0.625), and 32e S (x = y = z= 0.3841920 (4)) for FeCr2S4 and 8a Co (0, 0, 0), 16c Cr (0.625, 0.625, 0.625), and 32e S (x = y = z = 0.3779778 (4)) for CoCr2S4 (Fig. 5B(i)). The XRD plot also indicated that both materials have a single-phase without impurities. The lattice parameters for each material are a = b = c = 9.9984 (2) Å for FeCr2S4 and a = b = c = 9.9263 (2) Å for CoCr2S4 (Fig. 5B).
m space group. For example, in the case of SnFe2O4, this cubic spinel structure can be clearly identified through X-ray diffraction (XRD) analysis,11 MCr2S4 (M = Fe & Co),121 and Fe3O4.122 For example, in the study conducted by Dey et al.,121 using the compounds FeCr2S4 and CoCr2S4 with spinel structures synthesized through the solid-state reaction method, the XRD results in Fig. 5B, refined using Rietveld refinement, showed that the materials have a cubic FCC spinel structure (No. 277). The atomic positions in the unit cell were determined as 8a Fe (0, 0, 0), 16c Cr (0.625, 0.625, 0.625, 0.625), and 32e S (x = y = z= 0.3841920 (4)) for FeCr2S4 and 8a Co (0, 0, 0), 16c Cr (0.625, 0.625, 0.625), and 32e S (x = y = z = 0.3779778 (4)) for CoCr2S4 (Fig. 5B(i)). The XRD plot also indicated that both materials have a single-phase without impurities. The lattice parameters for each material are a = b = c = 9.9984 (2) Å for FeCr2S4 and a = b = c = 9.9263 (2) Å for CoCr2S4 (Fig. 5B).In the study conducted by Roy et al., it was found that there is a significant difference in lattice parameters because of variations in material concentration. The crystal size of Fe3O4 material (Fig. 5C) with a concentration of 0.4 M was approximately 34 nm, whereas for a concentration of 0.05, the crystal size was approximately 23 nm.122 Higher lattice strain occurs in materials with smaller crystal sizes, resulting from lower precursor concentrations. Small crystal sizes can lead to larger grain boundaries and higher defect concentrations. Defects can introduce imperfections in the crystal, causing intrinsic strain in the lattice.114
4.4 Kagome magnet
Magnets with a Kagome lattice structure have long been studied in condensed matter physics. The Kagome lattice forms a two-dimensional honeycomb network of triangles at various angles. Because of its unique lattice geometry, Kagome magnets to exhibit diverse topological states and phenomena.15 In the compound RMn6Sn6, if the R element can be entirely replaced by elements such as Li, Mg, or Ca, it will result in ferromagnetic properties. The lower the valence of Li, Mg, and Ca, the fewer valence electron systems there will be. Therefore, by controlling the magnetic and electronic states, it possible to achieve a larger anomalous Hall effect and observe other phenomena. To investigate these phenomena, the Kagome lattice with d-electrons needs to be studied, designed to enhance the large numbers massive Dirac fermions in the ferromagnetic state.13 By incorporating spin–orbit coupling and magnetism, the system can exhibit various nontrivial electronic or magnetic topological states, such as magnetic Weyl fermions, quantized anomalous Hall states, and spin structures.14In the rare-earth Kagome magnet family ReMn6Sn6 (where Re is a rare-earth element) with a layered hexagonal structure, rich magnetic states and a nontrivial band structure topology is observed (Fig. 6A).134 These materials typically consist of two magnetic sublattices from different layers: (1) a Kagome magnetic sublattice by Mn ions, and (2) a Kagome magnetic sublattice by rare-earth ions. Interlayer magnetic interactions drive various magnetic structures and produce complex magnetic phase diagrams. One example of such a material is TmMn6Sn6. TmMn6Sn6 forms a hexagonal structure with space group P6/mmm, consisting of Mn3Sn Kagome planes separated by two Sn3 layers and two inequivalent Sn2Tm layers. Than light rare-earth elements such as Y, Tm is a heavy rare-earth element with 4f electrons and strong spin–orbit coupling, leading to stronger magnetic interactions capable of producing more complex magnetic states.16 The Kagome magnet with the formula RMn6Sn6 (R = lanthanide) has recently been extensively studied because of its significance in magnetic transport properties for exploring new magnetic ground states and topological phases. The quasi-two-dimensional magnetic structure leads to strong intralayer coupling and weak interlayer coupling, which is highly sensitive to the sublattice properties. Than non-rare-earth Kagome materials such as MgMn6Sn6 and LiMn6Sn6, rare-earth metal compositions RMn6Sn6 exhibit more complex and tunable magnetic properties. By varying the R site, the magnetic properties can change dramatically. When R = Y, Sc, and Lu, the RMn6Sn6 system shows antiferromagnetic (AFM) behavior, whereas when R = Gd–Ho, the materials exhibit ferrimagnetic (FIM) behavior. Among the rare-earth metal alloys RMn6Sn6, TmMn6Sn6 exhibits a more complex magnetic structure than other alloys because of its dual magnetic sublattices and non-collinear magnetic structure with a Néel temperature TN = 350 K. The exchange coupling interaction between neighboring Tm and Mn is antiferromagnetic (AFM). This Kagome magnet shows a transition temperature above room temperature (TC), but the resulting magnetoresistance (MR) values are in the range of 6% to −3% over the temperature range of 10 K to 300 K with an applied magnetic field parallel to the sample of 6 T.25
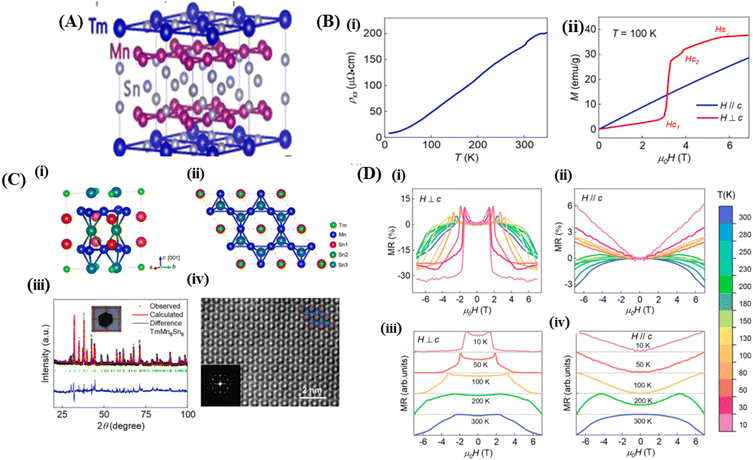 | ||
| Fig. 6 [A] Crystal structure of Kagome (TmMn6Sn6). Reprinted with permission from the Physical Review B.16 [B] (i) Crystal structure of TmMn6Sn6. (ii) The TmMn6Sn6 crystal structure is depicted in the illustration arranged along the [001] direction (iii) XRD pattern of TmMn6Sn6, (iv) l STEM image of TmMn6Sn6. Reprinted with permission from the Elsevier.25 [C] (i) Resistivity versus temperature with current along the ab-axis. (ii) M(H) curves for H∥c and H⊥c magnetic fields at 100 K. Reprinted with permission from the Elsevier.25 [D] (i) and (ii) Magnetoresistance to field at various temperatures measured with H⊥c and (ii) and (iv) H∥c Reprinted with permission from the Elsevier.25 | ||
The following describes the crystal structure, magnetic properties, electrical properties, and MR of Kagome magnets.
| Sample | Magnetic properties | Electrical properties | MR | Method | Ref. | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ms (emu g−1) | Hc | Tc (K) | ρ(H) (Ω cm) | Tρ (K) | |MR| (%) | TMR (K) | (μ0H) B | |||
| La0.8MnO3−δ | 45.71 | — | 268 | 0.2 | 260 | 90 | 260 | 5 T | Ceramic classical | 149 |
| La0.85MnO3 | 80 | — | 270 | 300 | 250 | 74 | 260 | 5 T | SS | 150 |
| La0.7Sr0.3MnO3 | 50 | — | >300 | 1.854 | 252 | 2 | 300 | 0.2 T | SG | 22 |
| La0.7Sr0.3MnO3 | — | — | >300 | 3.77 × 10−3 | >300 | 2 | 300 | 1 T | SS | 22 |
| La0.875Sr0.125MnO3 | — | — | — | 0.029 | 290 | 32.22 | 273.22 | 1 T | SG-spin coating | 151 |
| La0.850Sr0.150MnO3 | — | — | — | 0.012 | 300 | 42.85 | 290.95 | 1T | SG-spin coating | 151 |
| La0.875Sr0.175MnO3 | — | — | — | 0.010 | 325 | 31.36 | 307.23 | 1T | SG-spin coating | 151 |
| La0.800Sr0.200MnO3 | — | — | — | 0.008 | 350 | 25.76 | 315.64 | 1T | SG-spin coating | 151 |
| La0.67Sr0.33MnO3 | 2.35 | 50 | 300 | 0.1 | 300 | 25 | 300 | 10 T | SS | 56 |
| La0.8Sr0.2MnO3 | — | — | — | 0.01 | 300 | 27 | 200 | 0.5 T | SS | 39 |
| La0.67Sr0.33MnO3 | — | — | 350 | 28 | 230 | 20 | 300 | 6 T | Citrate gel | 152 |
| La0.67Sr0.33MnO3 | 32 | — | >350 | 0.325 | 300 | 99 | 300 | 1 T | SG | 153 |
| La0.67Sr0.33Mn0.95Fe0.05O3 | 15 | — | 350 | 1.6 | 225 | 97.5 | 300 | 1 T | SG | 153 |
| La0.67Sr0.33Mn0.90Fe0.10O3 | 4 | — | 350 | 1000 | — | 100 | 300 | 1 T | SG | 153 |
| La0.67Sr0.33Mn0.85Fe0.15O3 | 2 | — | 350 | 2500 | — | 100 | 300 | 1 T | SG | 153 |
| La0.7Ca0.3MnO3 | — | — | 250 | 0.06 | 200 | 0.05 | 180 | 0.3 T | SS | 40 |
| La0.75Ca0.25MnO3 | — | — | 350 | 40 | 270 | 80 | 250 | 4 T | — | 154 |
| La0.72Ca0.28MnO3 | — | — | — | 0.015 | 290 | 57.1 | 260 | 1 T | SG | 21 |
| La0.7Ca0.3MnO3 | — | — | — | 0.012 | 285 | 57.2 | 263 | 1T | SG | 21 |
| La0.67Ca0.33MnO3 | — | — | — | 0.008 | 295 | 68.6 | 270 | 1T | SG | 21 |
| La0.65Ca0.35MnO3 | — | — | — | 0.009 | 290 | 65.2 | 269 | 1T | SG | 21 |
| La0.675Ca0.375MnO3 | — | — | — | 0.012 | 280 | 56 | 261 | 1 T | SG | 21 |
| La0.65Ca0.35MnO3 | — | — | — | 0.29 | 225 | 57 | 260 | 8 T | SS | 69 |
| La0.65Ca0.30Ba0.05MnO3 | — | — | — | 0.37 | 140 | 55 | 260 | 8 T | SS | 69 |
| La0.65Ca0.25Ba0.10MnO3 | — | — | — | 0.51 | 225 | 45 | 280 | 8 T | SS | 69 |
| La0.65Ca0.20Ba0.10MnO3 | — | — | — | 0.15 | 270 | 43 | 290 | 8 T | SS | 69 |
| La0.65Ca0.15Ba0.15MnO3 | — | — | — | 0.09 | 180 | 32 | 300 | 8 T | SS | 69 |
| La0.67Ca0.33MnO3 | 60 | 0.01 T | 252.8 | 0.15 | 215.7 | 40.4 | 250 | 3 T | SS | 7 |
| La0.67Ca0.33MnO3 | — | — | — | 0.0375 | 275 | 39.97 | 264.78 | 1 T | SS | 155 |
| La0.67Ca0.33MnO3 | — | — | — | 0.022 | 275 | 54.27 | 263.80 | 1 T | SG | 155 |
| La0.75Ca0.25MnO3 | — | — | 350 | 40 | 280 | 80 | 250 | 4 T | Mixing stoichiometric | 156 |
| La0.7Ca0.3MnO3 | — | — | — | 0.2 | 260 | 18 | 77 | 3.6 T | SG | 38 |
| La0.7Ca0.3MnO3 | — | — | 320 | 80 | 250 | 5 | 300 | 1 T | Citrate gel method | 157 |
| La0.7Ca0.3MnO3 | — | — | 320 | 60 | 250 | 20 | 300 | 3 T | Citrate gel method | 157 |
| La0.7Ca0.3MnO3 | — | — | 320 | 45 | 250 | 40 | 300 | 7 T | Citrate gel method | 157 |
| La0.7Ca0.3MnO3 | — | — | 234 | 8 | 125 | 22 | 80 | 1 T | Pyrophoric reaction process | 158 |
| La0.7Ca0.3MnO3 | — | — | 234 | 8 | 125 | 22 | 80 | 1 T | Pyrophoric reaction process | 158 |
| La0.99Na0.01MnO3 | — | — | 210 | 0.175 | 240 | 75 | 240 | 1 T | SS | 159 |
| La0.99Na0.01MnO3 | — | — | — | 0.10 | 260 | 60 | 240 | 3 T | SS | 159 |
| La0.99Na0.01MnO3 | — | — | — | 0.075 | 290 | 50 | 240 | 5 T | SS | 159 |
| La0.98Na0.02MnO3 | — | 225 | 0.10 | 250 | 70 | 250 | 1 T | SS | 159 | |
| La0.98Na0.02MnO3 | — | — | — | 0.06 | 270 | 55 | 250 | 3 T | SS | 159 |
| La0.98Na0.02MnO3 | — | — | — | 0.05 | 300 | 30 | 250 | 5 T | SS | 159 |
| La0.95Na0.05MnO3 | — | 240 | 0.075 | 260 | 70 | 260 | 1 T | SS | 159 | |
| La0.95Na0.05MnO3 | — | — | — | 0.05 | 280 | 52 | 260 | 3 T | SS | 159 |
| La0.95Na0.05MnO3 | — | — | — | 0.04 | 290 | 28 | 260 | 5 T | SS | 159 |
| La0.8Na0.2MnO3 | — | — | — | 7.5 × 10−5 | 350 | 15 | 320 | 2 T | SS | 96 |
| La0.8Na0.2MnO3 | — | — | — | 8 × 10−5 | 330 | 25 | 340 | 5 T | SS | 96 |
| La0.8Na0.15□0.05MnO3 | — | — | — | 1.6 × 10−5 | 340 | 22 | 320 | 2 T | SS | 96 |
| La0.8Na0.15□0.05MnO3 | — | — | — | 2.0 × 10−5 | 320 | 38 | 320 | 5 T | SS | 96 |
| La0.8Na0.1□0.1MnO3 | — | — | — | 1.4 × 10−5 | 310 | 35 | 300 | 2 T | SS | 96 |
| La0.8Na0.1□0.1MnO3 | — | — | — | 1.9 × 10−5 | 300 | 50 | 300 | 5 T | SS | 96 |
| La0.8□0.15MnO3 | — | — | — | 6.0 × 10−5 | 300 | 40 | 280 | 2 T | SS | 96 |
| La0.8□0.15MnO3 | — | — | — | 9.0 × 10−5 | 290 | 60 | 290 | 5 T | SS | 96 |
| La0.9K0.1MnO3 | — | — | — | 0.030 | 300 | 43.03 | 286.3 | 1T | SG | 160 |
| La0.85K0.15MnO3 | — | — | — | 0.028 | >300 | 46.39 | 294.03 | 1T | SG | 160 |
| La0.8K0.2MnO3 | — | — | — | 0.025 | >300 | 37.49 | 294.6 | 1T | SG | 160 |
| La0.75K0.25MnO3 | — | — | — | 0.020 | >300 | 35.16 | 295.43 | 1T | SG | 160 |
| La0.7K0.3MnO3 | — | — | — | 0.017 | >300 | 26.76 | 296.4 | 1T | SG | 160 |
| La0.833K0.167MnO3 | 90 | — | 277 | 2.5 | 250 | 0.4 | 320 | 5.5 T | SG | 161 |
| La0.67K0.33MnO3 | — | — | 325 | 22 | 290 | 40 | 300 | 6 T | SG | 58 |
| La0.95K0.05MnO3 | — | — | 260.45 | 0.339 | 239.8 | 0.40 | 300 | 0.8 T | Thermolysis of an aqueous | 162 |
| La0.90K0.10MnO3 | — | — | 287.43 | 0.281 | 261.9 | 2.82 | 300 | 0.8 T | Thermolysis of an aqueous | 162 |
| La0.85K0.15MnO3 | — | — | 309.76 | 0.189 | 276.0 | 4.53 | 300 | 0.8 T | Thermolysis of an aqueous | 162 |
| LaMnO3+δ | — | — | 150 | 5.00 | 150 | 0.07 | 175 | 0.6 T | Precursor-based synthetic | 163 |
| La0.95 K0.05MnO3+δ | — | — | 235 | 1.2 | 230 | 0.08 | 225 | 0.6 T | Precursor-based synthetic | 163 |
| La0.85K0.15MnO3 | 44.34 | 31.252 G | 360 | 0.1 | 289 | 6 | 300 | 1 T | SS | 164 |
| La0.85K0.15MnO3 | 34.58 | 29.115 G | 360 | 1.1 | 289 | 3.5 | 300 | 1 T | SG | 164 |
| La0.85K0.15MnO3 | 23.56 | 10.986 G | 320 | 11 | 258 | 8 | 300 | 1 T | Co-precipitation | 164 |
| (La0.5Pb0.5)MnO3 | — | — | — | 0.02 | >300 | 18 | 300 | 5 T | SG | 165 |
| (La0.6Pb0.4)0.95MnO3 | — | — | — | 0.022 | >300 | 20 | 300 | 5 T | SG | 165 |
| (La0.8Pb0.2)0.9MnO3 | — | — | — | 0.0325 | >300 | 24 | 300 | 5 T | SG | 165 |
| La0.5Pb0.5MnO3 | — | — | — | 1.26 | 225 | 2.5 | 300 | 1.5 T | SS | 145 |
| La0.8Ca0.2MnO3 | — | — | 241 | 0.075 | 290 | 28 | 250 | 2 T | SS | 97 |
| La0.8Ca0.1□0.1MnO3 | — | — | 264 | 0.03 | 240 | 27 | 260 | 2 T | SS | 97 |
| La0.8□0.2MnO3 | — | — | 259 | 0.225 | 240 | 10 | 270 | 2 T | SS | 97 |
| La0.5Nd0.15Ca0.35MnO3 | 75 | — | 204 | 0.3 | 200 | 63 | 208 | 4 T | Via ceramic | 148 |
| La0.5Nd0.15Ca0.25Li0.1MnO3 | 80 | — | 169 | 10 | 160 | 72 | 171 | 4 T | Via ceramic | 148 |
| La0.5Nd0.15Ca0.25Na0.1MnO3 | 90 | — | 263 | 20 | 180 | 57 | 184 | 4 T | Via ceramic | 148 |
| La0.5Nd0.15Ca0.25K0.1MnO3 | 100 | — | 266 | 0.2 | 240 | 71 | 207 | 4 T | Via ceramic | 148 |
| La0.7Ba0.1Ca0.1Sr0.1MnO3 | 95 | — | 330.81 | 0.012 | 250 | 32 | 275 | 7 T | SG | 68 |
| La0.7Ba0.1Ca0.1Sr0.1MnO3 | 93 | — | 316.17 | 0.008 | 275 | 32.5 | 274 | 7 T | WM | 68 |
| Nd0.7Sr0.3MnO3 | 5 | — | 255 | 1293 | 154 | 1 | 300 | 0.2 T | Chemical citrate-gel route | 22 |
| Nd0.7Sr0.3MnO3 | — | — | 270 | 5.33 × 10−2 | 252 | 2 | 300 | 0.2 T | Chemical citrate-gel route | 22 |
| Nd0.67Ca0.33MnO3 | — | — | — | 9 × 103 | 120 | 20 | 250 | 7 T | SG | 72 |
| Nd0.67Sr0.33MnO3 | — | — | — | 9 | 250 | 18 | 225 | 7 T | SG | 72 |
| Nd0.67Pb0.33MnO3 | — | — | — | 15 | 175 | 80 | 150 | 7 T | SG | 72 |
| Nd0.67Ba0.33MnO3 | — | — | — | 500 | 150 | 90 | 90 | 7 T | SG | 72 |
| (Pr1/3Sm2/3)2/3Sr1/3MnO3 | 3.5 | — | 150 | 4 | 156 | 95 | 150 | 8 T | Chemical citrate-gel route | 138 |
| (Pr1/3Sm2/3)2/3Sr1/3MnO3 | 3.5 | — | 150 | 6 | 156 | 90 | 150 | 6 T | Chemical citrate-gel route | 138 |
| (Pr1/3Sm2/3)2/3Sr1/3MnO3 | 3.5 | — | 150 | 7 | 156 | 82 | 150 | 4 T | Chemical citrate-gel route | 138 |
| (Pr1/3Sm2/3)2/3Sr1/3MnO3 | 3.5 | — | 150 | 8 | 156 | 64 | 150 | 2 T | Chemical citrate-gel route | 138 |
| (Pr1/3Sm2/3)2/3Ba1/3MnO3 | 2.5 | — | 200 | 12 | 150 | 100 | 50 | 8 T | Chemical citrate-gel route | 138 |
| (La1/3Sm2/3)0.67Ba0.33MnO3 | 3.2 | — | 175 | 5 × 105 | 70 | 100 | 100 | 8 T | Chemical citrate-gel route | 166 |
| (La1/3Sm2/3)0.67Ba0.23Sr0.1MnO3 | 3.5 | — | 175 | 104 | 75 | 90 | 100 | 8 T | Chemical citrate-gel route | 166 |
| (La1/3Sm2/3)0.67Ba0.13Sr0.2MnO3 | 3.5 | — | 175 | 103 | 100 | 100 | 110 | 8 T | Chemical citrate-gel route | 166 |
| (La1/3Sm2/3)0.67Sr0.33MnO3 | 3.4 | — | 175 | 10 | 200 | 80 | 200 | 8 T | Chemical citrate-gel route | 166 |
| La0.833Li0.167MnO3 | 70.1 | 145 | 113 | 0.1 | 75 | 86.8 | 75 | 5 T | SG | 59 |
| La0.85K0.15MnO3 | 23.56 | 10.986 G | 320 | 11 | 258 | 8 | 300 | 1 T | Co-precipitation | 164 |
| (La0.5Pb0.5)MnO3 | — | — | — | 0.02 | >300 | 18 | 300 | 5 T | SG | 165 |
| La0.7Ca0.3MnO3 | — | — | 234 | 8 | 125 | 22 | 80 | 1 T | Pyrophoric reaction process | 158 |
| La0.99Na0.01MnO3 | — | — | 210 | 0.175 | 240 | 75 | 240 | 1 T | SS | 159 |
| La0.99Na0.01MnO3 | — | — | — | 0.10 | 260 | 60 | 240 | 3 T | SS | 159 |
| La0.99Na0.01MnO3 | — | — | — | 0.075 | 290 | 50 | 240 | 5 T | SS | 159 |
| La0.98Na0.02MnO3 | — | 225 | 0.10 | 250 | 70 | 250 | 1 T | SS | 159 | |
| La0.98Na0.02MnO3 | — | — | — | 0.06 | 270 | 55 | 250 | 3 T | SS | 159 |
| La0.98Na0.02MnO3 | — | — | — | 0.05 | 300 | 30 | 250 | 5 T | SS | 159 |
| La0.95Na0.05MnO3 | — | 240 | 0.075 | 260 | 70 | 260 | 1 T | SS | 159 | |
| La0.95Na0.05MnO3 | — | — | — | 0.05 | 280 | 52 | 260 | 3 T | SS | 159 |
| La0.95Na0.05MnO3 | — | — | — | 0.04 | 290 | 28 | 260 | 5 T | SS | 159 |
| La0.8Na0.2MnO3 | — | — | — | 7.5 × 10−5 | 350 | 15 | 320 | 2 T | SS | 96 |
| La0.8Na0.2MnO3 | — | — | — | 8 × 10−5 | 330 | 25 | 340 | 5 T | SS | 96 |
| La0.833Na0.167MnO3 | 84.2 | 66 | 308 | 1.6 | 309 | 33.7 | 309 | 5 T | SG | 59 |
| La0.833Ag0.167MnO3 | 75.2 | 40 | 296 | 0.8 | 299 | 37.4 | 299 | 5 T | SG | 59 |
| La0.833K0.167MnO3 | 76.7 | 83 | 320 | 1.6 | 328 | 27.2 | 328 | 5 T | SG | 59 |
| La0.80Sm0.05Na0.15MnO3 | — | — | — | 2.25 | 280 | 10 | 250 | 8 T | SS | 167 |
| La0.80Sm0.05Na0.15MnO3 | — | — | — | 1.6 | 290 | 18 | 250 | 4 T | SS | 167 |
| La0.80Sm0.05Na0.15MnO3 | — | — | — | 0.8 | 300 | 9 | 250 | 2 T | SS | 167 |
| La0.75Sm0.1Na0.15MnO3 | — | — | — | 0.8 | 250 | 40 | 250 | 8 T | SS | 167 |
| La0.75Sm0.1Na0.15MnO3 | — | — | — | 0.7 | 250 | 25 | 250 | 4 T | SS | 167 |
| La0.75Sm0.1Na0.15MnO3 | — | — | — | 0.6 | 250 | 12 | 250 | 2 T | SS | 167 |
| La0.70Sm0.15Na0.15MnO3 | — | — | — | 0.9 | 250 | 64 | 250 | 8 T | SS | 167 |
| La0.70Sm0.15Na0.15MnO3 | — | — | — | 0.8 | 250 | 52 | 250 | 4 T | SS | 167 |
| La0.70Sm0.15Na0.15MnO3 | — | — | — | 0.6 | 250 | 40 | 250 | 2 T | SS | 167 |
| Y0.15Ca0.85MnO3 | 1.5 | — | 150 | 0.12 | 80 | 50 | 100 | 5 T | SS | 168 |
| Y0.15Ca0.85MnO3 | 1.5 | — | 150 | 0.07 | 90 | 60 | 100 | 7 T | SS | 168 |
| Gd0.15Ca0.85MnO3 | 3 | — | 180 | 0.0065 | 90 | 50 | 100 | 5 T | SS | 168 |
| Gd0.15Ca0.85MnO3 | 3 | — | 180 | 0.0045 | 110 | 60 | 100 | 7 T | SS | 168 |
| Dy0.15Ca0.85MnO3 | 2.5 | — | 140 | 0.0075 | 100 | 50 | 100 | 5 T | SS | 168 |
| Dy0.15Ca0.85MnO3 | 2.5 | — | 140 | 0.0065 | 100 | 60 | 100 | 7 T | SS | 168 |
| (La0.7Ca0.3MnO3) | — | — | — | 100 | 225 | 0.7 | 225 | 5 T | SG | 43 |
| (La0.7Ca0.3MnO3)0.95:0.05ZrO2 | — | — | — | 225 | 120 | 0.9 | 140 | 5 T | SG | 43 |
| (La0.7Ca0.3MnO3)0.9:0.1ZrO2 | — | — | — | 120 | 120 | 0.8 | 160 | 5 T | SG | 43 |
| (La0.7Ca0.3MnO3)0.8:0.2ZrO2 | — | — | — | 225 | 160 | 0.8 | 140 | 5 T | SG | 43 |
| (La0.7Ca0.3MnO3)0.6:0.4ZrO2 | — | — | — | 40 | 200 | 0.8 | 200 | 5 T | SG | 43 |
| La0.8Ag0.2MnO3 | — | — | 285 | 3.714 × 10−6 | 289 | 5 | 220 | 0.7 T | SS | 90 |
| (0.985)La0.8Ag0.2MnO3/0.015BFO | — | — | 283 | 1.294 × 10−6 | 282 | 8 | 230 | 0.7 T | SS | 90 |
| (0.975)La0.8Ag0.2MnO3/0.025BFO | — | — | 282 | 3.519 × 10−6 | 278 | 6 | 240 | 0.7 T | SS | 90 |
| (0.965)La0.8Ag0.2MnO3/0.035BFO | — | — | 274 | 10.53 × 10−6 | 272 | 18 | 280 | 0.7 T | SS | 90 |
| La0.7Sr0.3MnO3 | 63 | — | 360 | 2.5 ×104 | 275 | 0.25 | 300 | 3 T | SS | 94 |
| Sample | Magnetic properties | Electrical properties | MR | Method | Ref. | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ms (emu g−1) | Hc | TC (K) | ρ(H) (Ω cm) | Tρ (K) | |MR| (%) | TMR (K) | (μ0H) B | |||
| (Co0.79Mn0.21)0.92Fe0.08 | 1550 | — | — | — | — | 200 | 350 | — | Arc melting | 50 |
| (Co0.79Mn0.21)0.83Fe0.17 | 1550 | — | — | — | — | 290 | 370 | — | Arc melting | 50 |
| (Co0.79Mn0.21)0.74Fe0.26 | 1450 | — | — | — | — | 280 | 400 | — | Arc melting | 50 |
| (Co0.79Mn0.21)0.65Fe0.35 | 1400 | — | — | — | — | 220 | 430 | — | Arc melting | 50 |
| (Co0.79Mn0.21)0.55Fe0.45 | 1600 | — | — | — | — | 200 | 440 | — | Arc melting | 50 |
| Ni34(FeCo)16Mn37Ti13 | 40 | — | 330 | 1.3 | 280 | 25.4 | 317 | 5 T | Arc melting | 98 |
| Ni32(FeCo)18Mn37Ti13 | 58 | — | 346 | 1.3 | 275 | 12.9 | 317 | 5 T | Arc melting | 98 |
| Ni30(FeCo)20Mn37Ti13 | 65 | — | 369 | 1.4 | 200 | 23.7 | 248 | 5 T | Arc melting | 98 |
| Ni92Cu8 | 0.8 | — | — | — | — | 1.4 | — | 1 T | Electrochemical deposition | 99 |
| Ni75Cu25 | 1.0 | — | — | — | — | 10 | — | 1 T | Electrochemical deposition | 99 |
| Ni54Cu46 | 0.9 | — | — | — | — | 0.8 | — | 1 T | Electrochemical deposition | 99 |
| Ni46.8Mn38.1Sn11.6Fe3.5 | — | — | — | 13 | 268 | 47 | 262 | 5 T | Induction melting | 102 |
| Ni46.8Mn38.1Sn11.6Fe3.5 | — | — | — | 14 | 276 | 25 | 262 | 2 T | Induction melting | 102 |
| Ni2Mn1.4Sn0.6 | 60 | — | — | 200 | 160 | 16 | 170 | 5 T | Argon arc melting | 120 |
| Ni45Co5Mn36.5In13.5 | — | — | 300 | 0.8 | 200 | 80 | 230 | 5 T | Arc melting | 114 |
| Ni40Co6Fe4Mn33Al17 | 211 | — | 348 | 0.06 | 250 | 35 | 230 | 3 T | Melting high purity | 117 |
| Ni40Co4Fe6Mn33Al17 | 173 | — | 297 | 0.015 | 220 | 28 | 190 | 3 T | Melting high purity | 117 |
| Ni40Co2Fe8Mn33Al17 | 127 | — | — | 0.005 | 170 | 15 | 150 | 3 T | Melting high purity | 117 |
| Ni43Mn41Co5Sn11 | — | — | — | — | — | 20 | 280 | 1 T | Arc melting high purity | 118 |
| Mn1.9Co0.1Sb | 40 | — | — | — | 170 | 46 | 136 | 5 T | Arc melting | 104 |
| Ni45Mn43CrSn11 | 50 | — | 300 | 28 | 250 | 70 | 250 | 5 T | Arc melting | 105 |
| Ni50Mn37Sn13 | — | — | 300 | 108 | 320 | 24 | 320 | 5 T | Arc melting | 169 |
| Ni50Mn36Sn14 | — | — | 220 | 120 | 250 | 42 | 250 | 5 T | Arc melting | 169 |
| Ni50Mn35Sn15 | — | — | 180 | 90 | 180 | 42 | 180 | 5 T | Arc melting | 169 |
| Ni50Mn36Sn16 | — | — | 100 | 40 | 100 | 34 | 100 | 5 T | Arc melting | 169 |
| Sample | Magnetic properties | Electrical properties | MR | Method | Ref. | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ms (emu g−1) | Hc | TC (K) | ρ(H) (Ω cm) | Tρ (K) | |MR| (%) | TMR (K) | (μ0H) B | |||
| a SG (sol–gel), SS (solid-state reaction), wet-mixing (WM). | ||||||||||
| FeCr2Te4 | — | — | — | 1.1 | >300 | 3.2 | 140 | 9 T | SS | 12 |
| FeCr2Te4 | — | — | — | 1.1 | >300 | 2.4 | 140 | 7 T | SS | 12 |
| FeCr2Te4 | 2.2 | — | 123 | 1.1 | >300 | 1.4 | 140 | 5 T | SS | 12 |
| FeCr2S4 | 24 | 50 kOe | 170 | 48 | 175 | 17 | 165 | 50 kOe | SS | 121 |
| CoCr2S4 | 27 | 50 kOe | 225 | 7 × 107 | 150 | 10.2 | 165 | 50 kOe | SS | 121 |
| ZnFe2O4 | 10 | — | — | 11 | 150 | 9 | 200 | 9 T | SS | 130 |
| Zn0.8Co0.2Fe2O4 | 50 | 0.3 T | 170 | 36 | 150 | 12 | 200 | 9 T | SS | 130 |
| Zn0.6Co0.4Fe2O4 | 120 | 0.2 T | >300 | 43 | 150 | 16 | 200 | 9 T | SS | 130 |
| ZnFe2O4 | — | — | — | — | — | 4 | 250 | 9 T | SS | 131 |
| Zn0.9Ni0.1Fe2O4 | 30 | 005 T | — | — | — | 6.25 | 250 | 9 T | SS | 131 |
| Zn0.8Ni0.2Fe2O4 | 60 | 0.05 T | 150 | — | — | 5 | 250 | 9 T | SS | 131 |
| Zn0.7Ni0.3Fe2O4 | 100 | 0.05 T | — | — | — | 7 | 250 | 9 T | SS | 131 |
| Zn0.6Ni0.4Fe2O4 | 140 | 0,05 T | — | — | 9 | 250 | 9 T | SS | 131 | |
| Ni0.6Mn0.4Fe2O4 | 51.76 | 229 | — | — | 0.43 | 502 | 0.57 T | SS | 132 | |
| Ni0.2Mn0.8Fe2O4 | 58.13 | 210 | — | — | 1,24 | 438 | 057 T | SS | 132 | |
| SnFe2O4 | 14.17 | 36,11 Oe | 760 | 7 × 105 | 280 | 80.10 | 260 | 5 T | Solvo-thermal | 11 |
| Fe3O4 | 87.5 | 100 Oe | — | — | — | 2.13 | >300 | 5 kOe | Co-precipitation | 122 |
| FeCr1.95Ga0.05S4 | — | — | 180 | 90 | — | 0.5 | 250 | 0.5 T | SS | 173 |
| FeCr1.9Ga0.1S4 | — | — | 180 | 15 | — | 0.32 | 250 | 0.5 T | SS | 173 |
| FeCr1.85Ga0.15S4 | — | — | 180 | 8 | — | 0.25 | 250 | 0.5 T | SS | 173 |
| FeCr1.8Ga0.2S4 | — | — | 180 | 5 | — | 0.2 | 250 | 0.5 T | SS | 173 |
| FeCr1.7Ga0.3S4 | — | — | 200 | 3 | — | 0.22 | 250 | 0.5 T | SS | 173 |
| FeCr1.6Ga0.4S4 | — | — | 200 | 8 | — | 0.32 | 250 | 0.5 T | SS | 173 |
| CdCr2S4 | 6 | — | 85 | 120 | 125 | 55 | 90 | 9 T | Chemical transport reaction | 174 |
| Fe2.5Zn5O4 | 12 | — | — | — | — | 30 | 300 | 1.2 T | Pulsed laser deposition | 175 |
| Fe2.5Mn5O4 | 50 | — | — | — | — | 90 | 300 | 1.2 T | Pulsed laser deposition | 175 |
| Sample | Magnetic properties | Electrical properties | MR | Method | Ref. | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ms (emu g−1) | Hc | TC (K) | ρ(H) (Ω cm) | Tρ (K) | |MR| (%) | TMR (K) | (μ0H) B | |||
| CoSn | — | — | 5 | — | — | 105 | 3 | 8 T | Arc melting | 176 |
| Co0.8Fe0.2Sn | — | — | 17 | — | — | 8.4 | 3 | 8 T | Arc melting | 176 |
| Co0.7Fe0.3Sn | — | — | 26 | — | — | 3.7 | 3 | 8 T | Arc melting | 176 |
| Co0.6Fe0.4Sn | — | — | — | — | — | 2.7 | 3 | 8 T | Arc melting | 176 |
| Co3In2S2 | — | — | — | 20 | 50 | 0.3 | 20 | 8 T | Flux method | 177 |
| (Co0.97Fe0.03)3In2S2 | — | — | — | 44 | 50 | 0.175 | 50 | 8 T | Flux method | 177 |
| Fe3Sn2 | 2.0 μB/Fe | — | 320 | 250 | 400 | 2 | 40 | 9 T | Self-flux | 178 |
| YMn6Sn6 | 1.5 μB/Fe | — | 400 | 0.08 | 400 | 24 | 40 | 9 T | Sn flux methods | 179 |
| YMn6Sn5.93Ga0.07 | 2 μB/Fe | — | 400 | 0.06 | 400 | 14 | 40 | 9 T | Sn flux methods | 179 |
| YMn6Sn5.87Ga0.13 | 2 μB/Fe | — | 400 | 0.058 | 400 | 7.5 | 40 | 9 T | Sn flux methods | 179 |
| YMn6Sn5.78Ga0.22 | 2 μB/Fe | — | 400 | 0.05 | 400 | 21 | 40 | 9 T | Sn flux methods | 179 |
| YMn6Sn5.70Ga0.30 | 2 μB/Fe | — | 400 | 0.045 | 400 | 7 | 40 | 9 T | Sn flux methods | 179 |
| YMn6Sn5.39Ga0.61 | 2 μB/Fe | — | 400 | 0.045 | 400 | 7.5 | 40 | 9 T | Sn flux methods | 179 |
| Ni3In2S2 | — | — | — | 0.4 | 300 | 16 | 2 | 10 T | SS | 180 |
| Yb0.5Co3Ge3 | — | — | — | 15 | 300 | 12.5 | 3 | 10 T | Sn flux | 181 |
Based on the MR parameter data above, it can be concluded that there are several criteria for obtaining materials with high MR values, including the following:
1. Magnetic properties
(a) High saturation magnetization (Ms) value
(b) Low coercivity (Hc) value
(c) TC near room temperature
2. Electrical properties
(a) Large resistivity change value
(b) Tρ near room temperature
3. Low external magnetic field required (Table 5).
| Material group | Magnetic properties | Electrical properties | Low (μ0H) B external | |||
|---|---|---|---|---|---|---|
| a | b | c | a | b | ||
| a ✓ = meets the criteria, — = not meeting the criteria. | ||||||
| Perovskite | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Alloy | ✓ | — | ✓ | — | ✓ | ✓ |
| Spinel | ✓ | ✓ | — | — | — | — |
| Kagome | — | — | ✓ | ✓ | ✓ | — |
5. Electrical transport mechanism
To study the electron transport mechanism in materials, Nguyen et al. utilized a theoretical model to describe it. In the paramagnetic region, at high temperatures (T > Tρ), the conductivity of manganites is generated through the thermally activated hopping of charge carriers localized in the form of small polaron. Therefore, the transport characteristics are described by two models: the variable-range hopping (VRH) model and the small polaron hopping (SPH) mechanism when T < θD/2, where θD/2 is the Debye temperature, which is the temperature at which the resistivity deviates from linearity in the plot ln(ρ/T) versus 1/T. The conductivity mechanism in the range of θD/2 < T < Tρ is analyzed using the VRH model, whereas for the range above θD/2 it is described using the SPH model. In the SPH model, there are two different mechanisms, namely, adiabatic and non-adiabatic, as presented in the following equations:
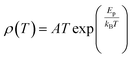 | (5) |
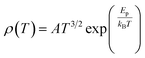 | (6) |
In the study by Das et al.,135 resistivity data were also analyzed using the small-polaron hopping model with different models, as follows:
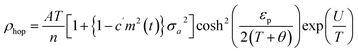 | (7) |
Eqn (5) represents adiabatic small polaron hopping, and eqn (6) represents non-adiabatic small polaron hopping, where A is the residual resistivity, Ep is the activation energy of the polaron, is the band gap the polaron must overcome to transfer to the next site, which includes the activation energy required for free charge carriers (WD) and the energy that stimulates carriers to hop (WH), kB is the Boltzmann constant.
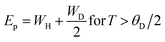 | (8) |
| WH = Ep − Es | (9) |
In this case, the Holstein criterion can determine whether the polaron-hopping conduction is adiabatic or non-adiabatic. The Holstein criterion states that adiabatic and non-adiabatic mechanisms can be identified by comparing the polaron bandwidth (J) with the critical polaron energy bandwidth (ϕ), where the values of J and ϕ are determined from the following equations:
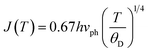 | (10) |
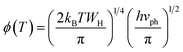 | (11) |
The temperature-dependent resistivity relationship can also be explained using the variable range hopping (VRH) model for the temperature range Tρ < T< θD, which is described by the following equation:
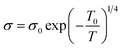 | (12) |
Furthermore, in the study by Asthana et al.,138 it was mentioned that the transport data in the semiconducting regime of the material can be analyzed using Mott variable range hopping (Mott-VRH) with the following equation:
ρ = ρ0m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(T0m/T)1/4 exp(T0m/T)1/4
| (13) |
On the other hand, in the metallic region (T0 ≤ Tρ), the electron transport mechanism is described by one of the following equations:
| ρ(T) = ρ0 + ρ2.5T2.5 | (14) |
| ρ(T) = ρ0 + ρ2T2 + ρ4.5T4.5 | (15) |
| ρ(T) = ρ0 + ρ2T2 + ρ5T5 | (16) |
In the research of Khlifi et al., it was shown that in the paramagnetic region, at high temperatures (T > Tρ), the electrical conduction mechanism in the magnetic material (La0.8Ca0.2−x□xMnO3) is governed by the adiabatic mechanism of small polaron hopping (SPH),139 where
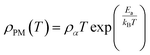 | (17) |
At low temperatures (T < Tρ), Khlifi et al., used ρFM(T) from eqn (15). The fitting results can be seen in Fig. 7 (A), showing a simulation of the resistivity vs. temperature curve using the formulas ρPM(T) in the insulating phase (red line) and ρFM (T) (green line).
 | ||
| Fig. 7 [A] Resistivity variation as a function of temperature in the zero plane (symbol) for samples x = 0.00, x = 0.10 and x = 0.20, and resistivity fit Reprinted with permission from the Elsevier.97 [B] Resistivity fit according to eqn (7) for x = 0.00, x = 0.10 and x = 0.20 samples in the temperature range between 0 and 100 K. Reprinted with permission from the Elsevier.97 [C] Volume fraction of ferromagnetic phase (f) against temperature for different samples: x = 0.00, x = 0.10 and x = 0.20 under applied magnetic field of 0; 2 and 5 T) Reprinted with permission from the Elsevier.97 [D] Experimental (symbols) and calculated (lines) electrical resistivity as a function of temperature of x = 0.00, x = 0.10 and x = 0.20 samples under the application of 0; 2 and 5 T magnetic field). Reprinted with permission from the Elsevier.97 [E] The thermal variation of the thermoelectric power (S) of material La0.5Pb0.5MnO3 with two different grain sizes, S1 and S3, (B = 0 and 1.5 T) at low temperature. [F] Plot of S as a function of temperature, the solid lines represent the best fitting curves with the equation S = S0 + S1.5 T 1.5 + S4 T 4. [G] Variation of thermopower S as a function of inverse temperature 1/T, solid lines are the best fits to Mott's SPH model eqn (28). Reprinted with permission from the AIP Publishing.145 [H] (i) The calculated normalized resistivity at a specific temperature is plotted as a function of magnetic field strength and orientation relative to the crystal c-axis (θ) (ii) the calculated dependence of normalized resistivity rotating in the yz plane is shown by solid lines, compared with the experimental results obtained from the slab sample (iii and iv) the calculated angle dependence of normalized resistivity rotating in three perpendicular planes (from y to x, z to y, and z to x direction) is depicted, compared with the experimental results (represented by symbols) obtained from the slab and square-rod samples, respectively.146 Open source PNAS. [I] The Ts depends on the spin (+ and −) for ferromagnetic junctions in the free-electron model. Reprinted with permission from the Elsevier.36 | ||
From the curve, it can be observed that the minimum resistivity is obtained at a temperature of 40 K. The scattering mechanism cannot explain the resistivity at lower temperature ranges (<40 K). This indicates that the contribution of other behaviors influences the resistivity at low temperatures. Essentially, this behavior is caused by strong correlation effects, related to the disordered system.140 The origin of this low-temperature behavior is analyzed by considering scattering mechanisms such as the Kondo effect and electron–electron interactions.141 To explain these mechanisms, experimental measurements are fitted with equations:
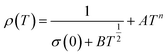 | (18) |
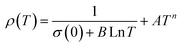 | (19) |
Eqn (18) depends on electron–electron interactions, and eqn (19) depends on the influence of scattering like the Kondo effect. Here, r (0) represents the residual conductivity, the term BT1/2 corresponds to correlated electron–electron interactions, and the term B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ln (T) represents the contribution because of the spin dependence of scattering, like the Kondo effect. Eqn (18) is used for samples with a 0 T field effect, whereas eqn (19) is used for samples under 2 and 5 T fields. Fig. 7B shows a good fit between the equation results and experimental data. This concludes that the mechanism responsible for the increase in resistivity at low temperatures is sensitive to the applied magnetic field, regulated by Kondo-like scattering, which is consistent with the results obtained by Xu et al. in the compounds La2/3Ca1/3MnO3 and electron–electron interactions.142
Ln (T) represents the contribution because of the spin dependence of scattering, like the Kondo effect. Eqn (18) is used for samples with a 0 T field effect, whereas eqn (19) is used for samples under 2 and 5 T fields. Fig. 7B shows a good fit between the equation results and experimental data. This concludes that the mechanism responsible for the increase in resistivity at low temperatures is sensitive to the applied magnetic field, regulated by Kondo-like scattering, which is consistent with the results obtained by Xu et al. in the compounds La2/3Ca1/3MnO3 and electron–electron interactions.142
Meanwhereas, percolation approach is used for the electrical transport mechanism in the temperature range of 5–400 K, assuming that the material is composed of paramagnetic (PM) and ferromagnetic (FM) regions. In this approach, the electrical resistivity of the system is determined by the variation in the volume fraction of ferromagnetic regions (f). Thus, the resistivity is expressed by the equation:
| ρ(T) = ρFMf + ρPM(1 − f) | (20) |
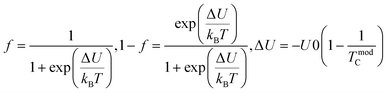 | (21) |
Then the equation ρ(T) becomes:
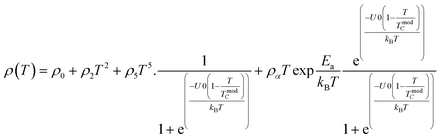 | (22) |
From Fig. 7C, it can be explained that f(T) eqn (22) below the metal–insulator transition temperature, with a strong dominance of the FM fraction. Then, the volume fraction of FM reduces to zero, transitioning from the ferromagnetic metal state to the paramagnetic insulator state. The temperature-dependent variation of f confirms that it follows a Boltzmann distribution, being one below the transition temperature and 0 above the transition temperature.
Thus, the temperature-dependent resistivity variation for all temperature ranges can be expressed using the following equation:
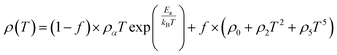 | (23) |
Fig. 7D shows that the experimental results are in accordance with the equation, even with the influence of external magnetic fields of 0 T, 2 T, and 5 T. This result aligns with the research of Gamzatov et al.143
In the GMR effect, there are several mechanisms to consider related to the transition between antiferromagnetic (AF) and ferromagnetic (F) states. One mechanism is spin-dependent scattering of conduction electrons, associated with a decrease in relaxation time in the AF state. This mechanism generally leads to GMR in magnetic multilayers. GMR depends on both spin and electron conduction. GMR mechanisms not only assume that electron scattering occurs because of irregularities at layer boundaries; another possible GMR mechanism involves variations in the Fermi surface through metamagnetic transitions, resulting from the formation of superzone gaps in the AF state. To explain the origin of GMR mechanisms, measurements of transport properties such as the Hall effect and thermoelectric power are required. Hall resistivity in magnetic materials is divided into two types: normal Hall resistivity and extraordinary Hall resistivity. Normal Hall resistivity provides information about the Fermi surface, such as carrier concentration and the k-dependence of conduction electron scattering. The extraordinary Hall effect provides information about the asymmetry of scattering. Meanwhereas, thermoelectric power is a derivative of the energy density of states and the relaxation time of conduction electrons. In the research of Kobayashi et al.,144 showed the curves of ρ(T) at μ0H = 0 T and M(T) at μ0H = 0.1 T exhibit large hysteresis, indicating a first-order transition between AF and F states. At high magnetic field applications, the transition is no longer observed. The results shows that both the normal and extraordinary components at 9 T magnetic field application. Asymmetric scattering affecting the Hall effect can be classified into two mechanisms: the skew scattering proportional to ρ and the side-jump scattering proportional to ρ2. The extraordinary Hall coefficient Rs for the ferromagnetic state can be described as follows:
| Rs = aρ + bρ2 | (24) |
| Rs/ρ = a + bρ | (25) |
Kobayashi et al. explained in their research the relationship between thermoelectric power (S) and temperature under the influence of magnetic fields of 0 and 9 T. At 0 T magnetic field, the curve forms hysteresis indicating a first-order transition. In the ferromagnetic state, S is negative at high temperatures. However, applying a 9 T magnetic field, the ferromagnetic state is observed across the entire temperature range, with S being negative and temperature-dependent. For higher temperatures, the value of S is nearly the same at 0 T and 9 T magnetic fields. According to the Mott equation, the thermoelectric power (S) is formulated as follows:
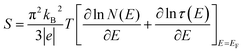 | (26) |
There is a relationship between thermoelectric power (S) and temperature for manganite samples with the influence of grain size. In the study by Banerjee et al.,145 by preparing La0.5Pb0.5MnO3 samples with variations of S1 (heated at 900 °C for 48 h), S2 (the grounded powder was palletized and annealed again at 900 °C for 24 h), and S3 (the well-ground powder is then palletized and annealed at 940 °C for 25 h), grain sizes (S3 > S2 > S1). The curves of S versus temperature (B = 0.0T and 1.5T) in Fig. 7E for samples S1 and S3 show differences in the S value because of grain size influence. In sample S3, which has lower resistivity, the S value at low temperatures is relatively smaller (S < 2 mV) than sample S1. Additionally, samples S1 and S3 also show an increase in S at low temperatures because of the applied magnetic field. Thermoelectric power (S) data dependent on magnetic field in the ferromagnetic region also indicate a contribution from magnons.
Similar to the resistivity data at low temperatures (T < Tρ), the values of S (B = 0.0 T and 1.5 T) for the ferromagnetic phase are adjusted according to the following equation:
| S = S0 + S1.5T1.5 + S4T4 | (27) |
To understand polaronic transport in the paramagnetic phase (T > Tρ), it's necessary to note that the previous S data did not fit well at high temperatures. Therefore, the Mott equation at high temperatures becomes.
Bagian Atas Formulir
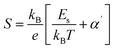 | (28) |
In the AMR effect, we can quantitatively explain it using a phenomenological model influenced by crystal anisotropy. Assuming that the resistivity under the influence of a magnetic field parallel and perpendicular to the c-axis in the crystal is ρ∥ and ρ⊥, their relationship can be described as follows:
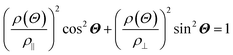 | (29) |
Like in Fig. 7H(i), it shows the short-to-long axial ratio representing the uniaxial resistivity ratio as α = ρ∥/ρ⊥, the resistivity is normalized as in the following equation:
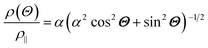 | (30) |
AMR is fully determined by the ratio α, if the anisotropy is too weak α = 1 is assumed. Therefore, the resistivity can be formulated as follows:
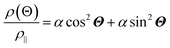 | (31) |
The equation describes a symmetric sinusoidal function of the angle Θ.
In Fig. 7H(ii) and (iii), there is an asymmetry from peak to valley with a broader valley width. Fig. 7H(ii) exhibits a very good agreement between theoretical and experimental results, forming a clearly asymmetric line shape, which provides justification for eqn (31). This emphasizes that AMR also displays asymmetry in the form of ρ(Θ)/ρ0. The phenomenological model shows consistency across all experimental AMR data for all magnetic field rotations in various sample planes. Fig. 7H(iii) demonstrates excellent agreement between theoretical and experimental results from the slab sample (with dimensions 3.8 × 0.85 × 0.15 mm3). Each component satisfies eqn (31) and exhibits the same values across the samples. Fig. 7H(iv) depict the agreement of the adjusted parameters with the data ρ(Θ)/ρ0 from square-rod sample (with dimensions 7.0 × 0.85 × 0.85 mm3). The conformity between experimental data and theoretical results indicates a very good fit, despite disregarding other contributions, such as Lorentzian MR.146
Next, in the TMR effect, we need to consider a one-dimensional free electron model to investigate the process of electron tunneling through a barrier. Next, we need to calculate the transmission probability for electrons from the left electrode with the energy required to penetrate the barrier towards the right electrode. The required energy (E) is measured from the bottom of the energy band, and its magnitude depends on spin when the electrode is ferromagnetic, expressed as Es, where s = + (majority spin) and s = − (minority spin).
Then, the barrier potential is denoted by ϕ determined from the Fermi energy and d (barrier thickness). Further, the rate of decrease in the wave function at the barrier can be calculated using the following equation:
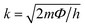 | (32) |
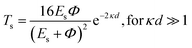 | (33) |
The values of Ts are plotted as a function of ϕ/E+ to obtain the value of E+/E−. Fig. 7I shows that the sign of the spin polarization of the transmission coefficient (Ts) depends on ϕ/E+.
The difference between the transmission coefficients in parallel (P) and antiparallel (AP) alignments of magnetization also needs to be evaluated, which can be calculated using a generalized calculation such as the conductance ΓP and ΓAP P for P and AP alignments of the magnetization, as in the following equation:
| ΓP(AP) ∝ 1 + (−)P2 | (34) |
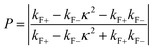 | (35) |
The value of P needs to be evaluated by calculating kFs, where P is very small (only a few percent) than experimental measurements involving the factor |k2 − kF+kF−|. To obtain a quantitative comparison between experimental and theoretical values of P, numerical calculations of P should be more realistic, incorporating the effects of disorder at, for example, junction interfaces.36
6. Conclusions, challenges and perspectives
The magnetoresistive (MR) properties are highly unique characteristics of magnetic materials and have various applications in different technological fields. MR is observed in several material groups, including perovskites, alloys, spinels, and Kagome magnets. Comparing the properties of each material group, perovskite materials exhibit superior MR values, supported by various magnetic and electrical parameters. Perovskite materials show ideal magnetization curves with high saturation magnetization, low coercivity, and a critical temperature (Tc) close to room temperature. Electrically, perovskite materials can undergo significant changes in resistivity when an external magnetic field is applied. Therefore, perovskite materials are intriguing for development because of their excellent MR properties and the ability to operate at room temperature without the need for cooling.However, there are still challenges for the widespread potential applications of perovskite materials. Perovskites will exhibit good magnetic properties, electrical properties, and magnetoresistance whereas having Tc near room temperature if substituted with the right cations, both at A and B sites, considering the radii of the substituting elements that will influence the electron transport mechanism in the perovskite material. Therefore, perovskite materials have great potential for further development to enhance their properties and create materials with superior characteristics.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors gratefully acknowledge the PMDSU Scholarship for Okvarahireka Vitayaya and the financial support under grant “Penelitian Dasar Unggulan Perguruan Tinggi 2024” NKB-677/UN2.RST/HKP.05.00/2024.References
- X. Y. Qu, X. F. Gou and T. G. Wang, Comput. Mater. Sci., 2021, 193, 110406 CrossRef CAS.
- R. Weiss, R. Mattheis and G. Reiss, Meas. Sci. Technol., 2013, 24, 1–17 Search PubMed.
- S. Yuasa, J. Phys. Soc. Jpn., 2008, 77, 1–13 CrossRef.
- K. Takanashi, Spintron. Next Gener. Innov. Devices, 2016, 1–20 Search PubMed.
- Y. Tian and S. Yan, Sci. China: Phys., Mech. Astron., 2013, 56, 2–14 Search PubMed.
- A. P. Ramirez, J. Phys.: Condens.Matter, 1997, 9, 8171–8199 CrossRef CAS.
- S. B. Li, C. B. Wang, H. X. Liu, L. Li, Q. Shen, M. Z. Hu and L. M. Zhang, Mater. Res. Bull., 2018, 99, 73–78 CrossRef CAS.
- H. Zhang, W. Chen, L. Xie, H. H. Zhao and Q. Li, Curr. Appl. Phys., 2022, 35, 58–66 CrossRef.
- V. P. Jovanović, H. Raffy, Z. Z. Li, G. Reményi and P. Monceau, Phys. Rev. B, 2021, 103, 1–9 CrossRef.
- J. Hemberger, T. Rudolf, H. A. Krug Von Nidda, F. Mayr, A. Pimenov, V. Tsurkan and A. Loidl, Phys. Rev. Lett., 2006, 97, 2–5 CrossRef PubMed.
- O. Mounkachi, L. Fkhar, R. Lamouri, E. Salmani, A. El hat, M. Hamedoun, H. Ez-Zahraouy, E. K. Hlil, M. Ait Ali and A. Benyoussef, Ceram. Int., 2021, 47, 31886–31893 CrossRef CAS.
- S. Routh, I. Kar, A. Low, S. Ghosh and T. Bhowmik, Phys. Lett. A, 2023, 468, 129101 CrossRef.
- L. Ye, M. Kang, J. Liu, F. Von Cube, C. R. Wicker, T. Suzuki, C. Jozwiak, A. Bostwick, E. Rotenberg, D. C. Bell, L. Fu, R. Comin and J. G. Checkelsky, Nature, 2018, 555, 638–642 CrossRef CAS PubMed.
- M. Kang, L. Ye, S. Fang, J. You, A. Levitan, M. Han and J. I. Facio, Nat. Mater., 2020, 19, 163–169 CrossRef CAS PubMed.
- D. Chen, C. Le, C. Fu, H. Lin, W. Schnelle, Y. Sun and C. Felser, Phys. Rev. B, 2021, 103, 144410 CrossRef CAS.
- B. Wang, E. Yi, L. Li, J. Qin, B. Hu, B. Shen and M. Wang, Phys. Rev. B, 2022, 106, 1–7 Search PubMed.
- X. Zhang, H. Zhang, M. Qian and L. Geng, Sci. Rep., 2018, 8, 1–11 Search PubMed.
- Z. Guo, H. T. Hahn, H. Lin, A. B. Karki and D. P. Young, J. Appl. Phys., 2008, 104, 1–5 Search PubMed.
- W. J. Gallagher and S. S. P. Parkin, IBM J. Res. Dev., 2006, 50, 5–23 CAS.
- A. Brataas and P. J. Kelly, Phys. Rep., 2006, 427, 157–255 CrossRef CAS.
- X. Yu, S. Jin, X. Guan, Y. Yan, K. Wu, L. Zhao and X. Liu, J. Alloys Compd., 2022, 890, 161788 CrossRef CAS.
- L. N. Lau, K. P. Lim, A. N. Ishak, N. B. Ibrahim and M. Miryala, Coating, 2021, 11, 1–15 Search PubMed.
- S. Sarkar, M. De Raychaudhury, I. Dasgupta and T. Saha-Dasgupta, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 2–5 Search PubMed.
- F. Canepa, M. Napoletano, C. Lefevre and G. Venturini, Phys. B, 2003, 334, 68–74 CrossRef CAS.
- C. Liu, H. Zhang, Z. Li, Y. Yan, Y. Zhang, Z. Hou and X. Fu, Surf. Interfaces, 2023, 39, 102866 CrossRef CAS.
- B. Shi, Z. Zhang, Y. Liu, J. Su, X. Liu, X. Li, J. Wang, M. Zhu, Z. Yang, J. Xu and Y. F. Han, J. Catal., 2020, 381, 150–162 CrossRef CAS.
- K. K. Kefeni, T. A. M. Msagati, T. T. Nkambule and B. B. Mamba, Mater. Sci. Eng. C, 2020, 107, 110314 CrossRef CAS PubMed.
- B. Rajyaguru, K. Gadani, M. J. Keshvani, D. Dhruv, A. D. Joshi, K. Asokan, R. J. Choudhary, D. M. Phase, N. A. Shah and P. S. Solanki, Mater. Res. Bull., 2023, 170, 112548 CrossRef.
- S. Fan, C. Zhou, H. Xu, J. Xu, H. M. Wen, J. Q. Xiao and J. Hu, J. Alloys Compd., 2022, 910, 164729 CrossRef CAS.
- Z. Wang, L. Chen, S. Li, J. Ying, F. Tang, G. Gao, D. Cortie, X. Wang and R. Zheng, npj Quantum Mater., 2021, 53, 1–8 Search PubMed.
- V. Nabaei, R. Chandrawati and H. Heidari, Biosens. Bioelectron., 2017, 86, 69–86 Search PubMed.
- M. N. Baibich, J. M. Broto, A. Fert, F. N. Van Dau, F. Petroff, P. Eitenne, G. Creuzet, A. Friederich and J. Chazelas, Phys. Rev. Lett., 1988, 61, 2472–2475 CrossRef CAS PubMed.
- C. Chappert, A. Fert and F. N. Van Dau, Nat. Mater., 2007, 3, 1–36 Search PubMed.
- P. M. Levy, S. Zhang and A. Fert, Phys. Rev. Lett., 1990, 65, 1643–1646 CrossRef CAS PubMed.
- K.-M. H. Lenssen, D. J. Adelerhof, H. J. Gassen, A. E. T. Kuiper and J. B. A. D. van Zon, Sens. Actuators, 2000, 85, 1–8 CrossRef CAS.
- J. ichiro Inoue, GMR, TMR and BMR, Nanomagnetism and Spintronics, 2009 Search PubMed.
- C. L. C. John, Q. Xiao and J. Samuel Jiang, Phys. Rev. Lett., 2008, 70, 2008–2011 Search PubMed.
- P. K. Siwach, R. Prasad, A. Gaur, H. K. Singh, G. D. Varma and O. N. Srivastava, J. Alloys Compd., 2007, 443, 26–31 CrossRef CAS.
- P. Kameli, H. Salamati and A. Aezami, J. Alloys Compd., 2008, 450, 7–11 CrossRef CAS.
- D. H. Manh, P. T. Phong, T. D. Thanh, L. V. Hong and N. X. Phuc, J. Alloys Compd., 2010, 499, 131–134 CrossRef CAS.
- L. K. Pah, W. Y. Jing, N. Jamaluddin, A. N. Ishak, H. X. Tong, L. L. Nguong, M. M. A. Kechik, C. S. Kien and A. H. Shaari, Mater. Today: Proc., 2023, 3–6 Search PubMed.
- I. K. Yu Zhang1, Y. Ni1, H. Zhao1, S. Hakani2, F. Ye3, L. DeLong4 and G. Ca, Nature, 2022, 611, 467–472 CrossRef PubMed.
- D. Das, A. Saha, S. E. Russek, R. Raj and D. Bahadur, J. Appl. Phys., 2003, 93, 8301–8302 CrossRef CAS.
- C. Jooss, L. Wu, T. Beetz, R. F. Klie, M. Beleggia, M. A. Schofield, S. Schramm, J. Hoffmann and Y. Zhu, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 13597–13602 CrossRef CAS PubMed.
- G. Subías, J. Blasco, V. Cuartero, S. Lafuerza, L. Simonelli, G. Gorni, M. Castro and J. García, Phys. Rev. B, 2023, 107, 1–13 CrossRef.
- C. H. Booth, F. Bridges, G. H. Kwei, J. M. Lawrence, A. L. Cornelius and J. J. Neumeier, Phys. Rev. Lett., 1998, 80, 853–856 CrossRef CAS.
- A. Dhahri, J. Mol. Struct., 2023, 3, 136592 Search PubMed.
- J. M. D. Coey, A. E. Berkowitz, L. Balcells, F. F. Putris and F. T. Parker, Appl. Phys. Lett., 1998, 72, 734–736 CrossRef CAS.
- J. Barnaś and W. Rudziński, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 1–10 Search PubMed.
- T. Ichinose, J. Ikeda, Y. Onodera, T. Tsuchiya, K. Z. Suzuki and S. Mizukami, J. Alloys Compd., 2023, 960, 170750 CrossRef CAS.
- H. Gu, X. Zhang, H. Wei, Y. Huang, S. Wei and Z. Guo, Chem. Soc. Rev., 2013, 42, 5907–5943 RSC.
- H. S. Alagoz, J. Desomberg, M. Taheri, F. S. Razavi, K. H. Chow and J. Jung, Appl. Phys. Lett., 2015, 106, 082407 CrossRef.
- J. Velev, R. F. Sabirianov, S. S. Jaswal and E. Y. Tsymbal, Phys. Rev. Lett., 2005, 94, 1–4 CrossRef PubMed.
- R. L. Greene, H. L. Ju, J. Gopalakrishnan, J. L. Peng, L. Qi, G. C. Xiong and T. Venkatesan, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 6143–6146 CrossRef PubMed.
- A. Gupta and J. Z. Sun, J. Magn. Magn. Mater., 1999, 200, 24–43 CrossRef CAS.
- I. P. Muthuselvam and R. N. Bhowmik, J. Alloys Compd., 2012, 511, 22–30 CrossRef CAS.
- G. Giovannetti, S. Kumar, J. Van Den Brink and S. Picozzi, Phys. Rev. Lett., 2009, 103, 1–4 Search PubMed.
- A. Goktas, I. H. Mutlu and A. Kawashi, Thin Solid Films, 2012, 520, 6138–6144 CrossRef CAS.
- S. Joseph and K. V. Saban, Ceram. Int., 2019, 45, 6425–6439 CrossRef CAS.
- E. S. Bozin, W. G. Yin, R. J. Koch, M. Abeykoon, Y. S. Hor, H. Zheng, H. C. Lei, C. Petrovic, J. F. Mitchell and S. J. L. Billinge, Nat. Commun., 2019, 10, 1–7 CrossRef CAS PubMed.
- R. Mahesh, R. Mahendiran, A. K. Raychaudhuri and C. N. R. Rao, J. Solid State Chem., 1995, 114, 297–299 CrossRef CAS.
- K. Kuepper, M. C. Falub, K. C. Prince, V. R. Galakhov, I. O. Troyanchuk, S. G. Chiuzbaian, M. Matteucci, D. Wett, R. Szargan, N. A. Ovechkina, Y. M. Mukovskii and M. Neumann, J. Phys. Chem. B, 2005, 109, 9354–9361 CrossRef CAS PubMed.
- J. Ahmad, H. Abbas, S. H. Bukhari, M. T. Jamil, U. Nissar, J. A. Khan and S. A. Ali, J. Ovonic Res., 2018, 14, 429–439 CAS.
- Y. Tang, F. Chiabrera, A. Morata, A. Cavallaro, M. O. Liedke, H. Avireddy, M. Maller, M. Butterling, A. Wagner and M. Stchakovsky, ACS Appl. Mater. Interfaces, 2022, 14, 18486–18497 CrossRef CAS PubMed.
- S. Koner, S. Satapathy, P. Deshmukh, R. K. Sharma, P. K. Sahoo and S. K. Majumder, J. Alloys Compd., 2023, 968, 172249 CrossRef CAS.
- O. Y. Gorbenko, O. V. Melnikov, A. R. Kaul, A. M. Balagurov, S. N. Bushmeleva, L. I. Koroleva and R. V. Demin, Mater. Sci. Eng., B, 2005, 116, 64–70 CrossRef.
- T. Manabe, T. Fujimoto, I. Yamaguchi, W. Kondo, I. Kojima, S. Mizuta and T. Kumagai, Thin Solid Films, 1998, 323, 99–104 CrossRef CAS.
- D. R. Munazat, B. Kurniawan, D. S. Razaq, K. Watanabe and H. Tanaka, Phys. B, 2020, 592, 412227 CrossRef CAS.
- S. O. Manjunatha, A. Rao, T. Y. Lin, C. M. Chang and Y. K. Kuo, J. Alloys Compd., 2015, 619, 303–310 CrossRef CAS.
- J. B. Goodenough, J. Less-Common Met., 1986, 116, 83–93 CrossRef CAS.
- Y. Kalyana Lakshmi, G. Venkataiah, M. Vithal and P. Venugopal Reddy, Phys. B, 2008, 403, 3059–3066 CrossRef.
- G. Venkataiah and P. V. Reddy, Solid State Commun., 2005, 136, 114–119 CrossRef CAS.
- G. Venkataiah, V. Prasad and P. Venugopal Reddy, J. Alloys Compd., 2007, 429, 1–9 CrossRef CAS.
- X. Xiao, S. L. Yuan, Y. Q. Wang, G. M. Ren, J. H. Miao, G. Q. Yu, Z. M. Tian, L. Liu, L. Chen and S. Y. Yin, Solid State Commun., 2007, 141, 348–353 CrossRef CAS.
- T. D. Thanh, L. H. Nguyen, D. H. Manh, N. V. Chien, P. T. Phong, N. V. Khiem, L. V. Hong and N. X. Phuc, Phys. B, 2012, 407, 145–152 CrossRef CAS.
- R. Rozilah, N. Ibrahim and A. K. Yahya, Solid State Sci., 2019, 87, 64–80 CrossRef CAS.
- S. W. Ng, K. P. Lim, S. A. Halim and H. Jumiah, Results Phys., 2018, 9, 1192–1200 CrossRef.
- A. E. Danks, S. R. Hall and Z. Schnepp, Mater. Horiz., 2016, 3, 91–112 RSC.
- D. R. Munazat, B. Kurniawan, D. S. Razaq, K. Watanabe and H. Tanaka, Phys. B, 2020, 592, 412227 CrossRef CAS.
- Z. Wu, W. Zhou, W. Jin and N. Xu, AIChE J., 2006, 52, 769–776 CrossRef CAS.
- A. Das, K. Kumar Bestha, P. Bongurala and V. Gorige, Nanotechnology, 2020, 31, 335716 CrossRef CAS PubMed.
- J. Massoudi, M. Smari, K. Nouri, E. Dhahri, K. Khirouni, S. Bertaina, L. Bessais and E. K. Hlil, RSC Adv., 2020, 10, 34556–34580 RSC.
- A. Swain, P. S. Anil Kumar and V. Gorige, J. Magn. Magn. Mater., 2019, 485, 358–368 CrossRef CAS.
- H. Chen, C. Jin, X. Song, P. Wang, L. Chen and H. Bai, Appl. Surf. Sci., 2021, 569, 151032 CrossRef CAS.
- H. Cheng, H. Chen, C. Jin and H. Bai, J. Magn. Magn. Mater., 2023, 565, 170300 CrossRef CAS.
- U. K. Sinha, A. Sahoo and P. Padhan, J. Alloys Compd., 2023, 952, 170037 CrossRef CAS.
- L. Yin, C. Wang and Q. Shen, Ceram. Int., 2023, 49, 1–9 CrossRef.
- R. C. Bhatt, S. K. Singh, P. C. Srivastava, S. K. Agarwal and V. P. S. Awana, J. Alloys Compd., 2013, 580, 377–381 CrossRef CAS.
- N. Panwar, I. Coondoo, R. S. Singh and S. K. Agarwal, J. Alloys Compd., 2010, 507, 439–442 CrossRef CAS.
- N. Ibrahim and A. K. Yahya, Ceram. Int., 2013, 39, S181–S184 CrossRef CAS.
- J. Lloyd-Hughes, C. D. W. Mosley, S. P. P. Jones, M. R. Lees, A. Chen, Q. X. Jia, E. M. Choi and J. L. MacManus-Driscoll, Nano Lett., 2017, 17, 2506–2511 CrossRef CAS PubMed.
- M. Kumar Verma, N. Dutt Sharma, S. Sharma, N. Choudhary and D. Singh, Mater. Res. Bull., 2020, 125, 110813 CrossRef CAS.
- A. De Andrés, M. García-Hernández and J. L. Martínez, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 7328–7334 CrossRef.
- P. T. Phong, D. H. Manh, N. V. Dang, L. V. Hong and I. J. Lee, Phys. B, 2012, 407, 3774–3780 CrossRef CAS.
- B. Rajyaguru, K. Gadani, M. J. Keshvani, D. Dhruv, A. D. Joshi, K. Asokan, R. J. Choudhary, D. M. Phase, N. A. Shah and P. S. Solanki, Mater. Res. Bull., 2024, 170, 112548 CrossRef CAS.
- M. Wali, R. Skini, M. Khlifi, M. Bekri, E. Dhahri and E. K. Hlil, Ceram. Int., 2016, 42, 5699–5706 CrossRef CAS.
- M. Khlifi, E. Dhahri and E. K. Hlil, J. Alloys Compd., 2014, 587, 771–777 CrossRef CAS.
- S. Samanta, S. Ghosh, S. Chatterjee and K. Mandal, J. Alloys Compd., 2022, 910, 164929 CrossRef CAS.
- A. Costas, C. Florica, E. Matei, M. E. Toimil-Molares, I. Stavarache, A. Kuncser, V. Kuncser and I. Enculescu, Beilstein J. Nanotechnol., 2018, 9, 2345–2355 CrossRef CAS PubMed.
- H. Zhang, M. Qian, X. Zhang, L. Wei, F. Cao, D. Xing, X. Cui, J. Sun and L. Geng, J. Alloys Compd., 2016, 689, 481–488 CrossRef CAS.
- A. S. R. Modak, Appl. Phys., 2019, 125 Search PubMed.
- H. Zhang, X. Zhang, Y. Xiao, M. Yang, Z. Xu, Z. Yao, M. Qian, L. Zhang, L. Yin and D. Jia, Intermetallics, 2022, 149, 107651 CrossRef CAS.
- S. C. Ma, D. H. Wang, Z. C. Zhong, J. M. Luo, J. L. Xu and Y. W. Du, Appl. Phys. Lett., 2013, 102, 3–7 Search PubMed.
- S. C. Ma, D. Hou, Y. Y. Gong, L. Y. Wang, Y. L. Huang, Z. C. Zhong, D. H. Wang and Y. W. Du, Appl. Phys. Lett., 2014, 104, 1–6 Search PubMed.
- S. Pandey, A. Quetz, A. Aryal, I. Dubenko, D. Mazumdar, S. Stadler and N. Ali, Magnetochemistry, 2017, 3, 1–7 CrossRef.
- L. Ma, W. H. Wang, C. M. Zhen, D. L. Hou, X. D. Tang, E. K. Liu and G. H. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 1–9 Search PubMed.
- X. Y. Z. X. Cr, Y. Co, Z. Al, S. K. Mohanta, Y. Tao, X. Yan, G. Qin and V. Chandragiri, J. Magn. Magn. Mater., 2017, 430, 65–69 CrossRef.
- X. P. Wei, Y. L. Zhang, X. W. Sun, T. Song, P. Guo, Y. Gao, J. L. Zhang, X. F. Zhu and J. B. Deng, J. Alloys Compd., 2017, 694, 1254–1259 CrossRef CAS.
- H. Arshad, M. Zafar, S. Ahmad, M. Rizwan, M. I. Khan, S. S. A. Gillani, C. B. Cao and M. Shakil, Mod. Phys. Lett. B, 2019, 33, 1950389 CrossRef CAS.
- S. A. Khandy, I. Islam, D. C. Gupta and A. Laref, J. Solid State Chem., 2019, 270, 173–179 CrossRef CAS.
- H. Xie, H. Wang, C. Fu, Y. Liu, G. J. Snyder, X. Zhao and T. Zhu, Sci. Rep., 2014, 4, 1–6 Search PubMed.
- M. Shakil, S. Mushtaq, I. Zeba, S. S. A. Gillani, M. I. Khan, H. Arshad and M. Rafique, Phys. B, 2021, 602, 412558 CrossRef CAS.
- C. Felser, L. Wollmann, S. Chadov, G. H. Fecher and S. S. P. Parkin, APL Mater., 2015, 3, 041518 CrossRef.
- L. Chen, F. X. hu, J. Wang, J. Shen, J. Zhang, J. R. Sun, B. G. Shen, J. H. Yin and L. Q. Pan, J. Appl. Phys., 2010, 107, 2472 Search PubMed.
- R. Sahoo, A. K. Nayak, K. G. Suresh and A. K. Nigam, Appl. Phys., 2011 Search PubMed.
- Z. Ni, X. Guo, X. Liu, Y. Jiao, F. Meng and H. Luo, J. Alloys Compd., 2019, 775, 427–434 CrossRef CAS.
- Y. Wu, H. Xuan, S. Agarwal, Y. Xu, T. Zhang, L. Feng, H. Li, P. Han, C. Zhang, D. Wang, F. Chen and Y. Du, Phys. Status Solidi A, 2018, 215, 1–7 Search PubMed.
- S. C. Ma, D. H. Wang, Z. C. Zhong, J. M. Luo, J. L. Xu and Y. W. Du, Appl. Phys. Lett., 2013, 102, 1–6 Search PubMed.
- R. Kainuma, W. Ito, R. Y. Umetsu, K. Oikawa and K. Ishida, Appl. Phys. Lett., 2008, 93, 2008–2010 CrossRef.
- S. Chatterjee, S. Giri, S. Majumdar and S. K. De, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 1–5 Search PubMed.
- K. Dey, A. Indra, A. Karmakar and S. Giri, J. Magn. Magn. Mater., 2020, 498, 166090 CrossRef CAS.
- S. Roy, H. R. Nikhita, G. V. Varshini, A. Kumar Patra, R. B. Gangineni and S. Angappane, J. Magn. Magn. Mater., 2022, 557, 169468 CrossRef CAS.
- H. Sharifi Dehsari, A. Halda Ribeiro, B. Ersöz, W. Tremel, G. Jakob and K. Asadi, CrystEngComm, 2017, 19, 6694–6702 RSC.
- G. U. Kulkarni, K. R. Kannan and T. Arunarkavalli, Phys. Rev., 1994, 49, 4–7 Search PubMed.
- I. M. Obaidat, B. Issa and Y. Haik, Nanomaterials, 2014, 5, 63–89 CrossRef PubMed.
- O. Mounkachi, M. Hamedoun and A. Benyoussef, J. Supercond. Novel Magn., 2017, 30, 3035–3038 CrossRef CAS.
- S. Ju, K. W. Yu and Z. Y. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 1–8 Search PubMed.
- A. Gaur and G. D. Varma, J. Phys.: Condens.Matter, 2006, 18, 8837–8846 CrossRef CAS.
- I. A. Abdel-Latif, A. M. Ahmed, H. F. Mohamed, S. A. Saleh, J. A. Paixão, K. A. Ziq, M. K. Hamad, E. G. Al-Nahari, M. Ghozza and S. Allam, J. Magn. Magn. Mater., 2018, 457, 126–134 CrossRef CAS.
- A. K. M. Akther Hossain, H. Tabata and T. Kawai, J. Magn. Magn. Mater., 2008, 320, 1157–1162 CrossRef CAS.
- A. K. M. A. Hossain, M. Seki, T. Kawai and H. Tabata, J. Appl. Phys., 2004, 96, 1273–1275 CrossRef.
- J. Hu, H. Qin, Y. Wang, Z. Wang and S. Zhang, Solid State Commun., 2000, 115, 233–235 CrossRef CAS.
- L. Fkhar, K. El Maalam, M. Hamedoun, A. El Kenz, A. Benyoussef, P. Lachkar, E. K. Hlil, A. Mahmoud, F. Boschini, M. Ait Ali and O. Mounkachi, Mater. Res. Express, 2020, 7, 9 Search PubMed.
- W. Ma, X. Xu, J. Yin, H. Yang, H. Zhou, Z. Cheng and Y. Huang, Phys. Rev. Lett., 2021, 3–8 Search PubMed.
- D. Das, C. M. Srivastava, D. Bahadur, A. K. Nigam and S. K. Malik, J. Phys.: Condens.Matter, 2004, 16, 4089–4102 CrossRef CAS.
- L. H. Nguyen, L. X. Hung, N. X. Phuc, P. H. Nam, L. T. T. Ngan, N. V. Dang, L. V. Bau, P. H. Linh and P. T. Phong, J. Alloys Compd., 2020, 849, 1–10 Search PubMed.
- M. Viret, L. Ranno and J. Coey, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 8067–8070 CrossRef CAS.
- S. Asthana, D. Bahadur, A. K. Nigam and S. K. Malik, J. Phys.: Condens.Matter, 2004, 16, 5297–5307 CrossRef CAS.
- M. Khlifi, E. Dhahri and E. K. Hlil, J. Alloys Compd., 2014, 587, 771–777 CrossRef CAS.
- M. Ziese, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 7–10 Search PubMed.
- G. Cao, Y. Li, J. Zhang, S. Cao, C. Cai and X. Shen, J. Appl. Phys., 2010, 107, 2–7 Search PubMed.
- Y. Xu, J. Zhang, G. Cao, C. Jing and S. Cao, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 2–7 Search PubMed.
- A. G. Gamzatov and I. K. Kamilov, J. Alloys Compd., 2012, 513, 334–338 CrossRef CAS.
- Y. Kobayashi, K. Muta and K. Asai, J. Phys.: Condens.Matter, 2001, 13, 3335–3346 CrossRef CAS.
- A. Banerjee, S. Pal, S. Bhattacharya, B. K. Chaudhuri and H. D. Yang, J. Appl. Phys., 2002, 91, 5125–5134 CrossRef CAS.
- R. W. Li, H. Wang, X. Wang, X. Z. Yu, Y. Matsui, Z. H. Cheng, B. G. Shen, E. W. Plummere and J. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 14224–14229 CrossRef CAS PubMed.
- Z. S. Popović and F. R. Vukajlović, Phys. Rev. Lett., 1996, 76, 960–963 CrossRef PubMed.
- M. Kumar Verma, N. Dutt Sharma, S. Sharma, N. Choudhary and D. Singh, Mater. Res. Bull., 2020, 125, 110813 CrossRef CAS.
- R. Dhahri and F. Halouni, J. Alloys Compd., 2004, 381, 21–25 CrossRef CAS.
- R. Suryanarayanan, J. Berthon, I. Zelenay, B. Martinez, X. Obradors, S. Uma and E. Gmelin, J. Appl. Phys., 1998, 83, 5264–5269 CrossRef CAS.
- X. Yu, S. Jin, H. Li, X. Guan, X. Gu and X. Liu, Appl. Surf. Sci., 2021, 570, 151221 CrossRef CAS.
- G. Venkataiah, Y. K. Lakshmi, V. Prasad and P. V. Reddy, J. Nanosci. Nanotechnol., 2007, 7, 2000–2004 CrossRef CAS PubMed.
- Y. Zhou, X. Zhu and S. Li, Ceram. Int., 2017, 43, 3679–3687 CrossRef CAS.
- A. P. Ramirez, S. W. Cheong and P. Schiffer, J. Appl. Phys., 1997, 81, 5337–5342 CrossRef CAS.
- X. Yu, H. Li, K. Chu, X. Pu, X. Gu, S. Jin, X. Guan and X. Liu, Ceram. Int., 2021, 47, 13469–13479 CrossRef CAS.
- P. Schiffer, A. P. Ramirez, W. Bao and S. W. Cheong, Phys. Rev. Lett., 1995, 75, 3336–3339 CrossRef CAS PubMed.
- G. Venkataiah, J. C. A. Huang and P. Venugopal Reddy, J. Magn. Magn. Mater., 2010, 322, 417–423 CrossRef CAS.
- P. Dey and T. K. Nath, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–14 CrossRef.
- R. Das and R. Mahendiran, Ceram. Int., 2021, 47, 393–399 CrossRef CAS.
- S. Jin, X. Gu, X. Yu, X. Guan, Y. Yan, K. Wu, L. Zhao, Y. Zhu, S. Sun, J. Liu, J. Hu, J. Zhao, L. Kong, W. Yang, Q. Chen, P. Kameli and X. Liu, Appl. Surf. Sci., 2022, 589, 152905 CrossRef CAS.
- W. Jian, J. Magn. Magn. Mater., 2012, 324, 2183–2187 CrossRef CAS.
- S. Das and T. K. Dey, Solid State Commun., 2005, 134, 837–842 CrossRef CAS.
- Y. Ng-Lee, F. Sapiña, E. Martinez-Tamayo, J. V. Folgado, R. Ibañez, D. Beltrán, F. Lloret and A. Segura, J. Mater. Chem., 1997, 7, 1905–1909 RSC.
- K. Y. Pan, S. A. Halim, K. P. Lim, W. M. W. Y. Daud, S. K. Chen and M. Navasery, J. Mater. Sci.: Mater. Electron., 2013, 24, 1869–1874 CrossRef CAS.
- G. Popov, J. Goldsmith and M. Greenblatt, J. Solid State Chem., 2003, 175, 52–58 CrossRef CAS.
- S. Asthana, A. K. Nigam, S. K. Malik and D. Bahadur, J. Alloys Compd., 2008, 450, 136–141 CrossRef CAS.
- D. Varshney and N. Dodiya, J. Mater. Res., 2014, 29, 1183–1198 CrossRef CAS.
- L. Dhal, E. Andharia, N. Shukla, T. Geetha Kumary, A. K. Nigam, S. K. Malik, P. N. Santhosh and R. Nirmala, J. Magn. Magn. Mater., 2019, 474, 215–220 CrossRef CAS.
- I. D. Mahmud Khan, A. K. Pathak, M. R. Paudel and N. A. Shane Stadler, J. Magn. Magn. Mater., 2008, 320, L21–L25 CrossRef.
- X. Zhang, Z. Liu, Q. Cui, Q. Guo, N. Wang, L. Shi, H. Zhang, W. Wang, X. Dong, J. Sun, Z. Dun and J. Cheng, Phys. Rev. Mater., 2022, 6, 1–9 Search PubMed.
- X. Wei, C. Tian, H. Cui, Y. Li, S. Liu, Y. Feng, J. Cui, Y. Song, Z. Wang and J. H. Chen, 2D Mater., 2023, 10, 1–10 Search PubMed.
- D. Huang, H. Li, B. Ding, X. Xi, J. Gao, Y. C. Lau and W. Wang, Appl. Phys. Lett., 2022, 121, 232404 CrossRef CAS.
- K. Jin, G. He, X. Zhang, S. Maruyama, S. Yasui, R. Suchoski, J. Shin, Y. Jiang, H. S. Yu, J. Yuan, L. Shan, F. V Kusmartsev, R. L. Greene and I. Takeuchi, Nat. Commun., 2015, 6, 7183 CrossRef CAS PubMed.
- C. P. Sun, C. L. Huang, C. C. Lin, J. L. Her, C. J. Ho, J. Y. Lin, H. Berger and H. D. Yang, Appl. Phys. Lett., 2010, 96, 4–6 Search PubMed.
- H. Aireddy, S. Guchhait and A. K. Das, J. Magn. Magn. Mater., 2022, 556, 169438 CrossRef CAS.
- K. Vijay, L. S. S. Chandra, K. Ali, A. Sagdeo, P. Tiwari, M. K. Chattopadhyay, A. Arya and S. Banik, Appl. Phys. Lett., 2023, 122, 233103 CrossRef CAS.
- M. A. McGuire, Q. Zhang, H. Miao, W. Luo, M. Yoon, Y. Liu, T. Yilmaz and E. Vescovo, Chem. Mater., 2021, 33, 9741–9749 CrossRef CAS.
- Q. Wang, S. Sun, X. Zhang, F. Pang and H. Lei, Phys. Rev. B, 2016, 94, 1–5 Search PubMed.
- C. Q. Xu, T. W. Heitmann, H. Zhang, X. Xu and X. Ke, Phys. Rev. B, 2021, 104, 1–8 Search PubMed.
- H. Fang, M. Lyu, H. Su, J. Yuan, Y. Li, L. Xu, S. Liu, L. Wei, X. Liu, H. Yang, Q. Yao, M. Wang, Y. Guo, W. Shi, Y. Chen, E. Liu and Z. Liu, Sci. China Mater., 2023, 66, 2032–2038 CrossRef CAS.
- Y. Wang, G. T. McCandless, X. Wang, K. Thanabalasingam, H. Wu, D. Bouwmeester, H. S. J. Van Der Zant, M. N. Ali and J. Y. Chan, Chem. Mater., 2022, 34, 7337–7343 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |