Open Access Article
Open Access ArticleEnhancing the charge transport and luminescence properties of ethyl 4-[(E)-(2-hydroxy-4-methoxyphenyl)methyleneamino]benzoate through complexation: a DFT and TD-DFT study†
Dinyuy Emmanuel Kiven a,
Fritzgerald Kogge Bine
a,
Fritzgerald Kogge Bine b,
Nyiang Kennet Nkungli
b,
Nyiang Kennet Nkungli a,
Aymard Dider Tamafo Fouegue
a,
Aymard Dider Tamafo Fouegue c,
Stanley Numbonui Tasheh
c,
Stanley Numbonui Tasheh a and
Julius Numbonui Ghogomu
a and
Julius Numbonui Ghogomu *ad
*ad
aDepartment of Chemistry, Faculty of Science, The University of Bamenda, P. O. Box 39, Bambili, Bamenda, Cameroon. E-mail: ghogsjuju@hotmail.com
bDepartment of Fundamental and Cross-cutting Sciences, National Advanced School of Public Works, P. O. Box 510, Yaounde, Cameroon, ghogsjuju@hotmail.com
cDepartment of Chemistry, Ecole Normale Superieure, Université de Bertoua, P. O. Box 652, Bertoua, Cameroon
dDepartment of Chemistry, Research Unit of Noxious Chemistry and Environmental Engineering, Faculty of Science, University of Dschang, P. O. Box 67, Dschang, Cameroon
First published on 11th June 2024
Abstract
Organic light emitting diode (OLED) and organic solar cell (OSC) properties of ethyl 4-[(E)-(2-hydroxy-4-methoxyphenyl)methyleneamino]benzoate (EMAB) and its Pt2+, Pd2+, Ni2+, Ir3+, Rh3+, and Zn2+ complexes have been theoretically studied herein. Geometry optimizations have been performed via the r2SCAN-3c composite method while single-point calculations have been carried out at the PBE0-D3(BJ)/def2-TZVP level of theory. Results have shown that complexation with selected metal ions improves hole and electron transfer rates in Pt[EMAB]2 and Rh[EMAB]2+. Specifically, the hole transport rate of Pt[EMAB]2, (kct(h) = 6.15 × 1014 s−1), is found to be 44 times greater than that of [EMAB], (kct(h) = 1.42 × 1013 s−1), whereas electron transport rate of Pt[EMAB]2, (kct(e) = 4.6 × 1013 s−1) is 4 times that of EMAB (kct(e) = 1.1 × 1013 s−1). Charge mobility for holes and electrons are equal to 19.182 cm2 V−1 s−1 and 1.431 cm2 V−1 s−1 respectively for Pt[EMAB]2, and equal to 4.11 × 10−1 cm2 V−1 s−1 and 3.43 × 10−1 cm2 V−1 s−1 for EMAB respectively. These results show that, charge transport in EMAB can be tuned for better performance through complexation with transition metals such as Pt2+. OSC properties of the complexes were also studied by comparing their HOMO/LUMO energies with those of (6,6)-phenyl-C61-butyric acid methyl ester (PCBM) and poly(3-hexylthiophene) (P3HT). It turned out that the energy gap of EMAB reduced significantly upon complexation from 2.904 eV to 0.56 eV in [Rh(EMAB)2]+ and to a lesser extent in the other complexes. The energy values of the HOMOs remained higher than those of PCBM while those of the LUMOs were found to be greater than that of P3HT with the exception of [Rh(EMAB)2]+. These findings show that the aforementioned species are good electron donors to PCBM. The open circuit voltage, VOC, of the compounds ranged between 0.705 × 10−19 V and 6.617 × 10−19 V, values that are good enough for practical usage in OSC applications. The UV-visible absorption spectra revealed absorption maxima well below 900 nm in all compounds, vital in the efficient functioning of solar cells. In general, this study has shown that platinoid complexation of EMAB can successfully modify both its OLED and OSC properties, making them better precursors in the electronic industry.
1 Introduction
Burgeoning world population has led to an unprecedented rise in the pursuit of better energy-saving lighting devices necessitating the search and manufacture of low-cost, environmentally friendly and low energy consuming lighting devices or their precursors.1,2 Organic electroluminescent materials have attracted wide attention in both academia and industry as a result of their pre-eminence as light emitting materials in flat screen displays.3,4 Organic electronic materials have found extensive applications in organic light-emitting diodes (OLEDs), optoelectronics, display and lighting technologies, phototransistors, smartphones, TV applications, personal computers, photodetectors, and bio-imaging.4–7 Their applications in displays are due to several unique advantages such as low cost, high contrast, good colour range, flexibility, wide viewing angle, fast response time, low driving voltage, low weight, low-temperature maintenance, and absence of toxic metals.6,8–10 In their mode of operation, OLED devices transform electrical energy into light. OLED materials encompass a sequential multilayer arrangement of thin organic films (an emissive layer (EL), a hole-transport layer (HTL) and an electron transport layer (ETL)), all in the middle of two electrodes, assembled via a variety of high technologies.1,2,9A proficient HTL material is endowed with adequate hole injection and high hole mobility, which are primordial properties for effective transmission of charge carriers towards the emissive layer.11,12 Moreover, the HTL material is expected to exhibit a highest occupied molecular orbital (HOMO) energy of about 4.5 eV. This HOMO energy facilitates hole injection from the anode into the emissive layer. In addition, an appropriate lowest unoccupied molecular orbital (LUMO) energy level limits the injection of electrons from EL to HTL.11 Similarly, a good ETL material is expected to possess a suitable HOMO and LUMO energy levels capable of accommodating the potential energy barrier, thus minimizing electron injection, lowering the operating voltage and making its hole-blocking ability significant.11,13
Within the framework of OLED manufacture and design, N,N-diphenyl-N,N-bis(3-methyl phenyl) (1,1-biphenyl)-4,4-diamine (TPD) is the routinely used hole transport layer, whereas tris(8-hydroxyquinolinato) aluminium (Alq3) is the habitually used electron transport layer prototype.12,13 Polymers and π-conjugated molecules are outstanding for organic-based electronics, owing to their efficient light emission and charge transport properties.14,15 Among organic materials used for OLED fabrication, Schiff bases have been portrayed as one of the most important photo-luminescent class of organic compounds, with promising electron transport and emission properties.9
Schiff bases, especially the D–π–A types have been remarkable in the manufacture of OLEDs because they are easily synthesisable and modifiable.16,17 Although Schiff bases are good electroluminescent materials, they are completely organic and thermally unstable. This obstructs their successful application in displays, lighting and other purposes and consequently their marketability.7 Again, OLEDs usually wear out through dark spot degradation, catastrophic failure and intrinsic degradation. Additionally, a noticeable band is always recorded in the luminescence spectrum of organic polymers, diminishing pure colour production ability.18,19 These setbacks have therefore motivated the search for more stable electroluminescent materials or their precursors for the manufacture of OLEDs.4 Important factors to look out for when searching materials for OLED fabrication include thermal stability, structural rearrangement resistance, and low chemical degradation. Although pure OLEDs have been commercialized as flat panel displays in the past, only single excitons have been involved because emission from spin triplet state is forbidden by spin selection rules (i.e. phosphorescence is not possible) at room temperature.9,20,21 Transition metal complexes are generally stable and heat resistant; properties highly searched for in OLED design and fabrication.3,17 Moreover, effective phosphorescence in late transition metal-Schiff base complexes at room temperature is associated with the heavy atom effect, which is responsible for promoting spin–orbit coupling (SOC). Maximizing the inter-system crossing (ISC) from the singlet state (with a 25% probability of emission) to the triplet state (with a 75% probability of emission), significantly improves their quality.4,17,22
In the same vein, transition metal complexes, especially platinoid complexes of iridium (Ir), platinum (Pt) and palladium (Pd) demonstrate high stability, are easily purified, and can function as both electron transporters and light emitters with excellent brightness.4,11,23 Schiff bases and their associated transition metal complexes have been widely explored for their applications in diverse areas such as nonlinear optics, molecular/metal ion sensing, dye-sensitized solar cells, molecular magnetism and photoluminescence.2,3 Also, the ease of synthesis of both Schiff base ligands and their metal complexes offers an additional advantage. Luminescent metal–organic compounds possessing functional emissive ligands represent an upcoming class of luminescent materials owing to their attributes of both organic dyes (tuneable and intense emission), and transition-metal-based emitters (high photostability, large absorption–emission Stokes shifts, long emission lifetime, and tuneable excited states).24–26
To harvest both singlet and triplet excitons, which are responsible for high performance in OLEDs, heavy transition metals have generally been used in the emissive layer. Heavy metal ions including Ir(III), Rh(III), Pt(II) and Pd(II) have shown such characteristics and have been used in the manufacture of phosphorescent organic light-emitting devices possessing both singlet and triplet excitons.4,27–29 When both singlet and triplet excited states are involved, excitons are maximized theoretically to yield phosphorescent OLEDs with close to 100% internal quantum efficiency.17,30 Iridium(III) has short lifetimes of triple excitons and therefore distinguishes itself as one of the best candidates for phosphorescent OLEDs. Moreover, Iridium metal is less expensive compared to other metals routinely used for OLEDs fabrication.31 Transition metal complexes of Schiff bases are generally stable, owing to numerous binding sites such as nitrogen of the imine group, and oxygen of the carbonyl group which makes them more useful.3
Equally, zinc complexes of azomethine ligands exhibit good electron transport ability, high fluorescence quantum yields, and excellent thermal stability.32–35 Zinc has been shown to produce white OLEDs (WhOLEDs) owing to its d10 configuration, and its Schiff base complexes have been proven to possess interesting luminescent properties.2,36,37 Lastly, zinc(II) complexes, are cheap and universal electroluminescent materials, which have frequently yielded a higher quantum emission than free ligands.2,38 Since they are simple to acquire and are easily modifiable, Schiff bases and their metal complexes have been extensively developed. Bearing in mind that transition metal coordination would probably boost the mechanical, luminescent and the thermal stability properties of these molecules, the continuous design of more and more metal–organic based materials with high efficiency for OLEDs is urgent. Fortunately, theoretical studies can be employed in investigating these properties at reduced costs compared to the expensive traditional experimental approaches, notably the spectroradiometer and integrating sphere methods.
Like OLED technology, organic solar cell (OSC) technology has attracted significant attention in this era where green energy is highly solicited due to the adverse effects of fossil fuels. Organic solar cells (OSCs) are photovoltaic devices that convert sunlight into electrical energy. In contrast to conventional silicon-based solar cells, which utilize inorganic materials, OSCs employ carbon-based organic molecules or polymers to absorb and convert sunlight into electrical energy. Organic solar cells have captured both academic and industrial interest owing to their advantages such as lightweight, flexibility and roll-to-roll fabrication capabilities.39 OSC devices with improved light trapping properties are particularly important for electrical energy applications.7,40 Although enormous progress has been made in the search and development of new materials, the low efficiency and thermal stability of small organic electronics materials remain a problem for their application.7 It is therefore necessary to develop new versatile organic materials with high efficiency for OLEDs and OSCs, which are more stable and capable of functioning as better light emitters, absorbers and charge transporters.41 Although a great deal of diverse OSC materials have been designed and developed, transition metal complexes have been given very little attention. Schiff base metal complexes are promising in the realm of OSCs. The coordination of transition metals with Schiff bases is readily attainable, and usually results in enhanced charge transfer, mechanical properties, and reduced energy gaps. Consequently, they are emerging as promising acceptor materials for OSCs.42 Pasa and colleagues explored the optoelectronic characteristics of a Schiff base ligand and its metal complexes, and observed a reduction in band gap and intriguing charge transfer properties. These features of Schiff base complexes hold significant promise for potential application in solar cell fabrication.43
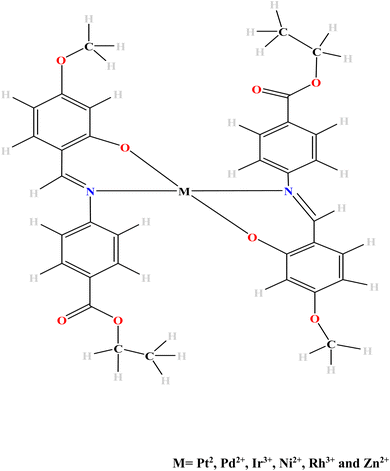
The aim of this study therefore has been to theoretically investigate the effects of some transition metal complexation on the OLED and OSC properties of the planar Schiff base “ethyl 4-[(E)-(2-hydroxy-4-methoxyphenyl)methyleneamino]benzoate” herein duped EMAB. The metal ions of Pt(II), Pd(II), Ir(III), Ni(II) and Zn(II) were chosen for their ability to improve charge transfer properties and thermal stability when complexed with Schiff bases.4,6,7 Also, some of these metal ions were chosen based on their reported ability to attain triplet excited states which leads to Inter System Crossing, a prerequisite for phosphorescence. Interestingly, EMAB and its copper complex were synthesized and characterized by Pahonţu and coworkers in 2015.44 Moreover, the effects of metal complexation on the luminescent properties of the Schiff base under study are yet to be investigated to the best of our knowledge. The result of this investigation would provide knowledge on molecular species or precursors for the manufacture of cheaper, more durable, and environmentally friendly electronic materials. The density functional theory (DFT) method (and its time-dependent extension (TD-DFT)) have been used in this investigation because they are a good compromise between computational time and accuracy while concurrently taking into account electron correlation.45,46 Fig. 1 shows the proposed mode of complexation between EMAB and the selected metal ions. This mode of complexation was proposed because EMAB is a Schiff base and will use only the O and N atoms close to each other for complexation. Given the bulky nature of EMAB is very bulky, it will be difficult to obtain octahedral structures due to steric hindrance reason why only complexes with coordination number of 4 have been modelled and studied herein.
2 Computational details and the theory
2.1 Effects of complexation on organic light-emitting diode (OLED) properties of EMAB
The effects of complexation on the OLED properties of the ligand and its selected complexes were studied by first carrying out geometry optimization of the species using the ORCA 5.0 program package.47 The Density functional theory was chosen herein because it has been proven to be suitable for studying coordination compounds.45,46 Due to the large number of atoms in the molecules studied, pre-optimization was carried out using the Semi-empirical Quantum Mechanical (SQM) extended Tight-Binding (XTB) density functional method. The Avogadro 1.2.1 visualization program was used to prepare input files for all computations.49 After pre-optimization and frequency calculation with the XTB method, the level of theory was augmented, and re-optimization and frequency calculation were carried out with the Swiss Army Knife composite electronic structure (r2SCAN-3c) method well embedded in ORCA 5 package.48 This functional contains the mGGA functional, r2SCAN-3c where “3c” denotes the three corrections-(refitted) gCP (geometrical counterpoise correction), the D4 correction, and the modification of the basis set. This method was chosen because of its advantages over other mGGAs. The mGGA r2SCAN describes electron-correlation effects in a more advanced way, resulting in improved conformational energies, thermochemistry, and refined covalent bond lengths. Moreover, self-interaction error, which most approximate functionals suffer from is reduced.50,51 This functional is also more numerically robust and precise than its predecessor (SCAN). Lastly, the r2SCAN-3c composite is competitive with more demanding approaches for thermochemistry and conformational energies such as B3LYP and PBE0 functionals, owing to its broader range of applications.52 To ascertain that geometry optimization yielded reliable and stable structures (minima on the PES), vibrational frequencies were calculated for all optimized structures at the same level of theory as that used for geometry optimization. Analysis revealed no imaginary frequencies, affirming the reliability of the structures as minima on the PES.Transition metal ions with partially filled d-orbitals are known to demonstrate multiple spin states. As a result, spin state analysis was carried out by optimizing each complex at all possible spin states at the r2SCAN-3c level and determining the single point energies at r2SCAN-3c, PBE0/def2TZVP and M06/def2TZVP levels of theory respectively for comparison. The spin states with the lowest energies were then adopted for subsequent calculations. Based on the r2SCAN-3c optimized geometries, single-point energy calculations were also performed with the hybrid-GGA functional; PBE0 together with the Ahlrich's basis set def2-TZVP.51,53,54
The PBE0 functional has been used herein owing to its accurately and agreement with previous experimental results as well as theoretical results obtained at the B3LYP/6-311++g** level of theory in estimating geometrical parameters of EMAB.44,55 Moreover, literature indicates that the PBE0 functional, especially when combined with the Def2-TZVP basis set yields good energies for transition metals.9,51 Long-range dispersion corrections were done via the Grimme's dispersion correction along with the Becke-Johnson damping D3(BJ) scheme.56 To determine the reorganization energies, single point calculations were carried out on the neutral, anionic and cationic structures at the RIJ-COSX-PBE0D3(BJ)/def2-TZVP level of theory. RI-J signifies the resolution of the identity approximation, and COSX refers to the chain of spheres approximation.54 In this study, property determination was done step by step, by involving the initial screening which was carried out at tight-binding level, followed by structural refinement, and finally energy calculations with inexpensive low-level DFT, and energy re-ranking with a high-level method.52
Two models have been widely used to describe charge transfer properties within entities; the coherent band model and the incoherent hopping model.57 The band model is useful for ordered organic crystals, where there exists full delocalization of charge carriers at low temperatures.57,58 At elevated temperatures (above 150 K), charge carriers are localized, intermolecular forces weaken, and the band model becomes less relevant. As a result, the hopping model becomes more useful in describing charge transfer rates in organic systems. The hopping model is described by the Marcus' theory, via the following equation59
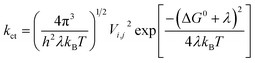 | (1) |
The reorganization energy, λ is the energy needed to destabilize the reactant and its solvent molecules, from their relaxed nuclear configurations to the relaxed nuclear configurations of the product and its associated solvent molecules.60 It is clear from (1) that charge transfer rate depends directly on the square of the transfer integrals and is inversely proportional to the reorganization energy. Therefore, large transfer integrals and smaller reorganization energies are expected to boost the rate of charge transfer. However, re-organization energy is the main parameter determining charge hopping rate, which is generally sectionalized into λinternal and λexternal.5,6 The internal reorganization energy is a measure of the structural change between the ionic and neutral states of a molecule, while the external re-organization energy depicts the effect of the surrounding medium on charge transfer.61 Essentially, λexternal is not as great as λinternal.62 Presently, attention is focused on λinternal, since the species under study are isolated and are all in the gas phase. The reorganization energy for the electron λe and hole λh of the entities studied herein were determined from the following relations.5,6,60
| λe = (E0− − E−−) + (E0− − E00) | (2) |
| λh = (E0+ − E++) + (E0+ − E00) | (3) |
The transfer integral Vi,j describing the ability of the holes and electrons to move from molecule i to j, is a fundamental criterion to consider in charge transfer studies, especially in semiconducting materials.63 Indeed, it reveals the interaction strength between two close species involved in charge transfer.58 Two popular methods are generally used to determine charge transfer rates; they are the direct and the indirect methods. The former determines Vi,j from the electronic coupling element of the two wavefunctions which describe the donor and acceptor species, while the latter otherwise termed the Energy-Splitting-in-Dimer (KT-ESD) is based on Koopman's theorem (KT). In the KT-ESD method, Vi,j for the hole and the electron are both computed as half the energy of the HOMOs and LUMOs of two molecular dimers containing species i and j as shown in eqn (4) and (5) respectively.
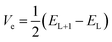 | (4) |
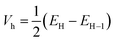 | (5) |
It is worth noting that complete overlap was observed for the ligand and partial overlap for the complexes. The energy of each dimer was obtained by carrying out single point energy calculations for each neutral complex at the PBE0-D3(BJ)/def2-TZVP level of theory, with the RIJCOSX approximation.
In order to determine the stability, which is usually desirable for OLED fabrication,5 Chemical hardness; a measure of a species' ability to resist reaction, was calculated using the relationship
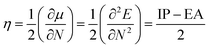 | (6) |
The IP and EA, are adiabatic and are calculated as the energy difference between the cationic and neutral species and as the energy difference between the anionic and neutral species respectively.
The ionization potential and electron affinity were obtained using eqn (7) and (8)
| IP = E(M+) − E(M0) | (7) |
| EA = E(M0) − E(M−) | (8) |
| ΔEint = Ecomplex − (2EL + EMn+) | (9) |
Lastly, the charge transfer mobility, an essential parameter for charge transfer rate studies was determined using Einstein's relation depicted in eqn (10).
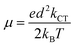 | (10) |
2.2 Effects of complexation on the organic solar cell properties of EMAB
The ability of EMAB and its designed complexes to serve as materials for OSCs was determined as follows: Firstly, the HOMO and LUMO energies, (EHOMO and ELUMO), the band gaps (EHOMO–ELUMO), major FMO-based performance parameters; the open circuit voltage (VOC) and the energy driving force (ΔEL−L) were computed, where (ΔEL−L) is the difference between the LUMO energy levels of the donor (EMAB's complexes) and the standard acceptor (6,6)-phenyl-C61-butyric acid methyl ester PCBM. The open circuit voltage was determined using the following relation:| VOC = EdonorHOMO − EacceptorLUMO − 0.3 | (11) |
The energy driving force, ΔEL−L determines the dissociation efficiency of an exciton at the donor/acceptor interface in OSCs. ΔEL−L was calculated using eqn (12). We note here that the numerical value of ΔEL−L must be above the threshold value of 0.3 eV; to ease dissociation.65
| ΔEL−L = LUMOdonor − LUMOacceptor | (12) |
For EMAB and its complexes VOC and ΔEL−L were obtained by carrying out single point energy calculations with the r2SCAN-3c optimized structures at the RIJCOSX-PBE0-D3(BJ)/def2TZVP level of theory. The energy level of the HOMO indicates its ability to donate electrons, while the LUMO energy indicates its ability to act as an electron acceptor.66 To visualize the HOMO and LUMO charge distributions, frontier molecular surfaces of EMAB and its complexes were generated using Avogadro 1.2.1 visualization program.44 Also, the absorption spectra, and the maximum electronic absorption wavelength, λmax of each complex have been computed. The TD-DFT method was used to calculate electronic absorption properties at the CAM-B3LYP/def2-TZVP level of theory in the gas phase, based on the r2SCAN-3c optimized ground state geometries. Indeed, range-separated hybrid functionals like CAM-B3LYP exhibit suitability not only for conjugated systems with n → π* and π → π* electronic transitions but also for molecules characterized by significant charge transfer, such as transition metal complexes.67,68 It is worth noting that 10 excited states were computed for each species. Lastly, the density functional theory (DFT) method and its time-dependent extension (TD-DFT) were used in this study owing to the good compromise between computational cost and accuracy they offer, together with the considerable treatment of electron correlation.45,46
3 Results and discussion
3.1 Effects of complexation on OLED properties of EMAB
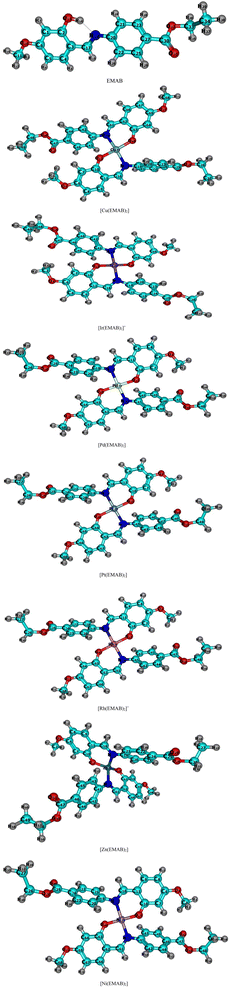 | ||
| Fig. 2 Optimized structures of EMAB and its designed complexes studied at the r2SCAN-3c level of theory. | ||
It can be seen from Fig. 2 that the EMAB forms somewhat square planar complexes with the exception of [Zn(EMAB)2], which has a distorted tetrahedral structure. Some geometric parameters of EMAB, computed at the PBE0(D3)BJ/def2-TZVP level of theory were compared with experimental data from Pahonţu and co-workers.44 In addition, these parameters were also compared with theoretical parameters computed at the B3LYP/6-311++g** level of theory and the agreement between these parameters was close to 100%.55 Moreover, some geometric parameters of the copper complex of EMAB, which was synthesized by Pahontu and co-workers were computed and compared with those of EMAB as shown in Table 1.
| Selected structural parameters | Theoretical value/level of theory | Experimental value | ||
|---|---|---|---|---|
| B3LYP/6-311++g** | PBE0-D3(BJ)/def2-TZVP | |||
| EMAB | EMAB | Cu[EMAB]2 | Cu[EMAB]2 | |
| Bond length (Å) | ||||
| N18–C17 | 1.297 | 1.29 | 1.302 | 1.284 |
| C2–C1 | 1.394 | 1.388 | 1.401 | 1.386 |
| C1–C6 | 1.398 | 1.393 | 1.38 | 1.382 |
| N39–Cu77 | — | — | 2.025 | — |
| Cu77–O40 | — | — | 1.9 | — |
| Cu77–N17 | — | — | 2 | — |
| Cu77–O15 | — | — | 1.9 | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Bond angle (°) | ||||
| C30–O32–C33 | 117 | 115.9 | 115.9 | 116.8 |
| O32–C33–C34 | 111 | 111.2 | 111 | 107.4 |
| O32–C30–C27 | 112.5 | 112.2 | 112.4 | 112.4 |
| O31–C30–O32 | 123.3 | 123.6 | 123.5 | 122.7 |
| O31–C30–C27 | 124.1 | 124.2 | 124.1 | 124.9 |
| C21–C20–N18 | 118 | 118 | 119.2 | 116.9 |
| C22–C20–N18 | 122.9 | 122.8 | 121.1 | 125 |
| C17–N18–C20 | 121.1 | 120.8 | 118 | 122 |
| N18–C17–C3 | 122.4 | 122.1 | 127 | 122.3 |
| O15–C2–C3 | 121.3 | 121.2 | 123.6 | 121.1 |
| O15–C2–C1 | 118.6 | 118.7 | 118.6 | 118.3 |
| O10–C6–C1 | 123.8 | 123.8 | 123.3 | 124.7 |
| O10–C6–C5 | 115.4 | 115.1 | 115.5 | 114.5 |
| C6–O10–C11 | 119.1 | 118.2 | 118.4 | 117.6 |
| N39–Cu77–O40 | — | — | 92.9 | — |
| N39–Cu77–O15 | — | — | 90.7 | — |
| N17–Cu77–O15 | — | — | 91.4 | — |
| N17–Cu77–O40 | — | — | 93.3 | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Hydrogen bond parameters | ||||
| O15–H16 (Å) | 1 | 1 | 0.9 | |
| N18–H16 (Å) | 1.7 | 1.7 | 1.9 | |
| O15–H16–N18 (°) | 147.6 | 148.9 | 140.7 | |
Results from Table 1 have revealed excellent agreement between experimental data and data obtained from calculations studies at the B3LYP/6-311++g**.44,55 Moreover, the Cu–N and Cu–O bond lengths obtained theoretically fall within the range of acceptable values of 1.9–2.1 Å and 1.8–2 Å respectively.69 Since these geometrical parameters fall within the acceptable range, we proceeded to use the PBE0-D3(BJ)/Def2-TZVP level of theory to predict the parameters of the modelled complexes. Some parameters of EMAB and its complexes were selected and presented in Table 2.
| Geometric parameter | [Ir(EMAB)2]+ | [Pd(EMAB)2] | [Rh(EMAB)2]+ | [Zn(EMAB)2] | [Pt(EMAB)2] | [Ni(EMAB)2] |
|---|---|---|---|---|---|---|
| Bond length (Å) | ||||||
| N17-M77 | 2.001 | 2.035 | 2.022 | 2.013 | 2.028 | 1.909 |
| N39-M77 | 2.021 | 2.027 | 2.025 | 2.016 | 2.021 | 1.904 |
| O40-M77 | 1.961 | 1.997 | 1.927 | 1.927 | 2.010 | 1.786 |
| O15-M77 | 1.969 | 1.993 | 1.925 | 1.923 | 2.006 | 1.838 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Bond angle (°) | ||||||
| N17-M77-O15 | 91.1 | 91.0 | 89.6 | 96.4 | 91.7 | 92.3 |
| N17-M77-O40 | 88.9 | 89.5 | 90.8 | 115.8 | 88.8 | 87.7 |
| N39-M77-O40 | 91.6 | 91.8 | 90.1 | 96.3 | 92.1 | 92.9 |
| N39-M77-O15 | 88.3 | 87.7 | 89.3 | 113.7 | 87.0 | 87.1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Dihedral angle (°) | ||||||
| C41–N39-M77-O15 | −11.0 | −12.0 | −9.6 | −40.0 | −9.5 | −16.3 |
| C41–N39-M77-N17 | 71.4 | 50.9 | 32.5 | 69.8 | 47.1 | 59.8 |
The optimized structure of the ligand exhibits some degree of planarity, rigidity and stabilization arising from the intermolecular hydrogen bond O15–H16⋯N18 with hydrogen bond length 1.702 A and O–H⋯N bond angle 148.92°. Non-conventional hydrogen bonds of the form C–H⋯O are observed in nearly all the metal complexes. These non-covalent interactions contribute to the rigidity and planarity of the investigated compounds, which in turn, are likely to enhance intramolecular charge transfer thereby reinforcing photo-physical and electronic properties of the molecules.70,71
From the values of bond angles in Table 2, it is clear that the geometry adopted by the metal complexes is approximately square planar apart from the [Zn(EMAB)2] which is nearly tetrahedral. In all cases, the geometries of the complexes slightly deviate from the 90° bond angles of perfect square planar species and 109.5° of perfect tetrahedral structures. These recorded deviations from perfect planarity or tetrahedral structures about the central metal ions may be due to electron cloud repulsion between benzene rings in each structure (ligand) and due to the Jahn Teller distortions, which causes a distortion in molecular structure and lowers the energy of the molecule.72 Furthermore, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond length (1.29 Å) in the ligand is smaller than that obtained in all complex structures (>1.3 Å), indicating that complexation increases the C
N bond length (1.29 Å) in the ligand is smaller than that obtained in all complex structures (>1.3 Å), indicating that complexation increases the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond length. Among the complexes studied, metal–ligand bond lengths in [Ni(EMAB)2] are the shortest indicating higher stability compared to other complexes.
N bond length. Among the complexes studied, metal–ligand bond lengths in [Ni(EMAB)2] are the shortest indicating higher stability compared to other complexes.
In this study, metal–oxygen and metal–nitrogen bond lengths in the designed molecules were also compared with experimental values.73,74 It is well known that transition metal–nitrogen bond lengths range between 1.9 and 2.03 Å, while metal–oxygen bond lengths range between 1.7 and 2.2 Å. The calculated bond lengths for these structures, at the PBE0D3(BJ)/def2TZVP level of theory are presented in Table 3, alongside the corresponding experimental values.
| Bond lengths | Theoretical value/Å | Experimental value/Å |
|---|---|---|
| Pd–N | 2.02 | 2.03 |
| Pd–O | 1.99 | 2.01 |
| Ni–N | 1.80 | 2.00 |
| Ni–O | 1.80 | 1.95 |
| Rh–N | 2.02 | 2.07 |
| Rh–O | 1.92 | 2.03 |
| Zn–N | 2.01 | 2.07 |
| Zn–O | 1.92 | 1.95 |
| Cu–N | 2.02 | 2.01 |
| Cu–O | 1.92 | 1.94 |
| Pt–O | 2.01 | 2.01 |
| Pt–N | 2.02 | 2.00 |
Results obtained from the comparison between theoretical and experimental parameters in Table 3 have revealed that the level of theory used for determining the geometrical parameters is satisfactory, since theoretical results agree with experiment.
| Complex | Spin multiplicity | Level of theory | Energy/kcal mol−1 |
|---|---|---|---|
| Pd2+ | 1 | r2SCAN-3c | −2153.8785 |
| PBE0 | −2152.7215 | ||
| M06 | −2153.6785 | ||
| 3 | r2SCAN-3c | −2153.8210 | |
| PBE0 | −2152.6564 | ||
| M06 | −2153.5728 | ||
| Pt2+ | 1 | r2SCAN-3c | −2145.3235 |
| PBE0 | −2144.137 | ||
| M06 | −2145.0331 | ||
| 3 | r2SCAN-3c | −2145.2567 | |
| PBE0 | −2144.0597 | ||
| M06 | −2144.9523 | ||
| Ir3+ | 1 | r2SCAN-3c | −2130.0956 |
| PBE0 | −2128.9081 | ||
| M06 | −2129.7920 | ||
| 3 | r2SCAN-3c | −2130.0900 | |
| PBE0 | −2128.9497 | ||
| M06 | −2129.8308 | ||
| 5 | r2SCAN-3c | −2130.0019 | |
| PBE0 | −2128.8539 | ||
| M06 | −2129.7342 | ||
| Rh3+ | 1 | r2SCAN-3c | −2136.3114 |
| PBE0 | −2135.1428 | ||
| M06 | −2136.0365 | ||
| 3 | r2SCAN-3c | −2136.3059 | |
| PBE0 | −2135.1457 | ||
| M06 | −2136.0307 | ||
| 5 | r2SCAN-3c | −2136.2343 | |
| PBE0 | −2135.0616 | ||
| M06 | −2135.9524 |
Results obtained in Table 4 indicate that the most stable spin state for Pt2+ and Pd2+ is the +1 state, by virtue of their low energy minima. In the case of Ir3+, results show the most stable spin state of +3, while the +1-spin state is the lowest for the Rh3+. Zinc has a filled d orbital and therefore would not exhibit multiple spin states. Nickel on the other hand would not exhibit multiple spin states since is not a heavy d-block metal.
3.1.2.1 Reorganization energy and charge transport. Reorganization energy analysis is crucial in charge transport studies.40 The calculated reorganization energies for hole/electron transport for EMAB and its metal complexes are displayed in Table 5 together with those of N,N-diphenyl-N,N-bis(3-methyl phenyl)(1,1-biphenyl)-4,4-diamine (TPD)65 and tris(8-hydroxyquinolinato)aluminium (Alq3)12,60 as references for hole and electron transport materials, respectively.
| Species | λh (eV) | λe (eV) | λtotal (eV) |
|---|---|---|---|
| EMAB | 0.375 | 0.612 | 0.987 |
| [Pt(EMAB)2] | 0.185 | 0.481 | 0.666 |
| [Pd(EMAB)2] | 0.136 | 0.489 | 0.625 |
| [Zn(EMAB)2] | 30.192 | 30.164 | 60.356 |
| [Ir(EMAB)2]+ | 0.653 | 0.925 | 1.578 |
| [Rh(EMAB)2]+ | 0.171 | 0.215 | 0.386 |
| [Ni(EMAB)2] | 0.147 | 1.12 | 1.267 |
| TPD | 0.290 | — | — |
| Alq3 | — | 0.276 | — |
The information that was used to calculate the reorganization energies for the hole and the electron is found in ESI.† It is important to note that reorganization energy is easily estimated theoretically as compared to experimental procedures using spectrochemical and electrochemical methods. Equally, theoretical calculations provide flexibility in exploring different parameters that contribute to the reorganization energy such as molecular structure, external electric field, which are not easily manipulated in experiments.
Generally, molecules with high values of reorganization energies will be poor transporters of holes/electrons, while those with smaller values of reorganization energies will be good transporters. From the results in Table 5, numerical values of λh in EMAB complexes reveal that they are good hole transport materials except for the zinc complex. This is because all values of λh for EMAB's complexes are less than that of TPD, apart from [Zn(EMAB)2] and [Ir(EMAB)2]+. Thus the latter will serve as a mild hole transport material. This is obvious because the [Zn(EMAB)2] complex has a somewhat tetrahedral structure which usually hinders charge transfer rate, unlike the other square planar complexes which enhance charge transport.74 It should be noted also that EMAB, by virtue of its high reorganization energy value for both the hole and the electron will be a mild charge transport material. According to the ranking for λh, [Pd(EMAB)2] < [Ni(EMAB)2] < [Rh(EMAB)2]+ < [Pt(EMAB)2] < [Ir(EMAB)2]+ < EMAB < [Zn(EMAB)2], it is clear that complexation improves the hole transport properties of the ligand because the λh values are significantly lower than those of the prototype molecule TPD. Although the ligand itself is a mild hole transport material, this property further diminishes when the ligand is complexed with zinc and iridium. Therefore, complex formation between transition metals and ligands such as EMAB can play a significant role in tuning the hole transport properties of the ligand by either significantly improving it as in Pd2+, Ni2+, Rh3+ and Pt2+ or diminishing it as in Zn2+ and Ir3+. From Table 5, numerical values for reorganization energies for the electron λe in EMAB complexes are like or lower than those of the prototype to some extent. The [Rh(EMAB)2]+ complex proved to be the best electron transport material due to its low λe value. Although the complexes have reorganization energies closer to those of the ligand, the zinc complex has a very high value. This suggests that the electron transfer rate in these complexes apart from the zinc complex is improved through complexation. The estimated λe values follow the order: [Rh(EMAB)2]+ < [Pt(EMAB)]2 < [Pd(EMAB)2] < (EMAB) < [Ir(EMAB)2]+ < [Ni(EMAB)2] < [Zn(EMAB)2]. From this ordering and λe values in Table 5, it is glaring that transition metal complexation can tune electron transport properties of organic molecules. Our results have also indicated (from reorganization energy values) that among the complexes studied, Rh(III) complex [Rh(EMAB)2]+ (λe = 0.215 eV) is the best electron transport material, while [Pd(EMAB)2], (λh = 0.136) is the best hole transport material. Consequently, most of the complexes studied are potential charge transport materials for the manufacture of OLEDs. Moreover, some studies have reported that the smaller the sum of the total reorganization energy, the higher the short circuit current density which in turn improves charge transfer rate.66 From Table 5, the sum of reorganization energies is relatively small, except that of [Zn(EMAB)2]. The total reorganization energy classification is as follows: [Rh(EMAB)2]+ < [Pd(EMAB)2] < [Pt(EMAB)2] < [Ir(EMAB)2]+ < [(EMAB)] < [Ni(EMAB)] < [Zn(EMAB)2]. Therefore, the rate of charge transfer is expected to follow this order. The hole and electron reorganization energy results obtained for the Zn[EMAB]2 and Ir[(EMAB)2]+ significantly deviate from the standard values (about 100 times and 3 times greater than the standard respectively).
3.1.2.2 Charge transfer integrals and charge transport. When transfer integrals are on average smaller than the reorganization energies as the case in pure organic molecules, Marcus' theory is suitable for carrying out charge transfer studies with the molecules. Transfer integrals were calculated using the Marcus' theory because the entities are predominantly organic. It is also important to note that the higher the value for charge transfer integral, the higher the molecule's ability to transfer charge. The computed charge transfer integral values for both the hole and electron transport processes of the investigated species are listed in Table 6.
| Species | Ve (eV) | Vh (eV) |
|---|---|---|
| EMAB | 0.11 | 0.14 |
| [Pt(EMAB)2] | 0.12 | 0.10 |
| [Pd(EMAB)2] | 0.12 | 0.10 |
| [Rh(EMAB)2]+ | 0.06 | 0.01 |
| [Ni(EMAB)2] | 0.13 | 0.11 |
Transfer integrals for the electrons range between 0.06 and 0.13 eV following the order [Rh(EMAB)2]+ < EMAB < [Pt(EMAB)2] = [Pd(EMAB)2] < [Ni(EMAB)2], while that for the hole range from 0.01–0.14 eV in the order [Rh(EMAB)2]+ < [Pt(EMAB)2] = [Pd(EMAB)2] < [Ni(EMAB)2] < EMAB. Although the values for transfer integrals are considerably large for the ligand, the corresponding results for reorganization energy are larger than that of the prototypes Alq3 and TPD and therefore EMAB can be considered as a moderate electron/hole transport molecule.
From Table 6, metal chelation with EMAB increases the value of transfer integrals for the electron in most cases studied but diminishes the hole transport properties in all cases. Moreover, the ligand itself is a good hole and electron transport material by virtue of its high transfer integral values. Based on the reorganization energies, complexation between EMAB and Pd2+, Ni2+ and Pt2+ increases its hole transport properties while complexation with Rh3+ improves its electron transport properties. Based on transfer integrals, complexing EMAB with Ni2+, Pd2+ and Pt2+ increases transfer integrals for the electrons, thus making them suitable electron transport materials for the fabrication of OLED devices.
3.1.2.3 Charge transfer rate and charge transfer mobility. Marcus' theory relates charge transfer rate to both transfer integrals and reorganization energies. Therefore, studying charge transfer integrals or reorganization energies independently cannot indicate the best species for the fabrication of OLED materials or their precursors. Herein therefore, the charge transfer rates for EMAB and its studied metal complexes have been computed. Charge transfer rate simultaneously accounts for the reorganization energy and charge transfer integrals of the studied species as seen in eqn (1). Also, charge mobility, another useful parameter in evaluating the performance of OLED materials has been calculated based on Einstein's relation eqn (10). The charge transfer rate and mobility calculated have been presented in Table 7.
| Species | kct(h) × 1013 s−1 | kct(e) × 1013 s−1 | uh (cm2 V−1 s−1) | ue (cm2 V−1 s−1) |
|---|---|---|---|---|
| EMAB | 1.412 | 1.1 | 0.441 | 0.343 |
| [Pd(EMAB)2] | 4.03 | 0.32 | 1.26 | 0.010 |
| [Pt(EMAB)2] | 61.5 | 4.6 | 19.182 | 1.435 |
| [Rh(EMAB)2]+ | 0.13 | 1.84 | 0.035 | 0.574 |
| [Ni(EMAB)2] | 12.7 | 0.00046 | 3.963 | 0.00014 |
Our results unambiguously reveal that complexation between EMAB and majority of the metal ions under investigation increases the hole transfer rate, while the electron transfer rate increases significantly only for [Pt(EMAB)2] and [Rh(EMAB)2]+.
Charge transfer rates for the hole range from 0.13 × 1013 s−1 to 61.5 × 1013 s−1 and follow the order [Rh(EMAB)2]+ < EMAB < [Pd(EMAB)2] < [Ni(EMAB)2] < [Pt(EMAB)2]. The charge transfer rate for the electrons follows the order [Ni(EMAB)2] < [Pd(EMAB)2] < EMAB < [Rh(EMAB)2]+ < [Pt(EMAB)2]. From the foregoing observations, it can be seen that [Pt(EMAB)2]+ is a fascinating ambipolar material for the fabrication of OLED devices since the complex exhibits improved charge transport properties, both for the hole and the electron, compared to the ligand. As expected, charge mobility varies in the same manner as the charge transfer rate. A large value for charge mobility indicates the ease with which charges (holes/electrons) move. For the species under study, the hole mobility rate increases generally with complexation for most of the metals. Charge mobility rate follows the trend [Rh(EMAB)2]+ < EMAB < [Pd(EMAB)2] < [Ni(EMAB)2] < [Pt(EMAB)2] for both the hole and the electron. At this juncture, it can be concluded that the [Pt(EMAB)2] is the best charge transporter amongst the species studied. It is therefore recommended as a good precursor for the manufacture of charge transport for OLED devices.
3.1.2.4 Effect of complexation on charge transfer rate and stability. Investigations on luminescent and/or charge transport properties of materials requires some basic idea or knowledge of their stability. In fact, materials that are chemically and thermally stable are desirable for OLED fabrication.5 Chemical hardness, which is the measure of the ability of a species to resist reaction or the ability to resist exchange in electrons has been calculated through conceptual density functional theory and listed in Table 8, along with the corresponding values for ionization potential, electron affinity, and their change in interaction energies.
| Species | EL (eV) | EH (eV) | Eg (eV) | IP (eV) | EA (eV) | η (eV) | ΔEint (eV) |
|---|---|---|---|---|---|---|---|
| EMAB | −2.657 | −5.561 | 2.904 | 7.370 | 1.120 | 3.120 | 0.000 |
| [Pd(EMAB)2] | −2.540 | −4.700 | 2.160 | 6.558 | 1.100 | 2.700 | −0.977 |
| [Pt(EMAB)2] | −2.478 | −4.534 | 2.056 | 5.124 | 2.340 | 1.400 | −26.997 |
| [Rh(EMAB)2]+ | −7.621 | −8.181 | 0.560 | 9.754 | 6.620 | 1.600 | −25.906 |
| [Ni(EMAB)2] | −2.705 | −4.487 | 1.782 | 6.582 | 1.490 | 2.550 | −0.990 |
Table 8 reveals that the compounds [Pd(EMAB)2], [Pt(EMAB)2] and [Rh(EMAB)2]+ have small energy gaps and are therefore expected to have the most outstanding photophysical properties.66 In addition, metal complexation by EMAB is observed to have generally reduced the both the HOMO and LUMO energies, except those of [Rh(EMAB)2]+. Furthermore, the energy gaps of the complexes in all cases are smaller than that of the ligand. This indicates that the ease of electron transfer would generally increase with complexation since a low energy gap facilitates electron jump from the HOMO to the LUMO, a primordial factor for photoluminescence. Based on energy gap, EMAB and its complexes are ranked as follows: [Rh(EMAB)2]+ < [Ni(EMAB)2] < [Pt(EMAB)2] < [Pd(EMAB)2] < EMAB. Therefore, metal complexation increases the ease of charge transfer from the HOMO to LUMO and thus OLED properties. The studied complexes of EMAB have higher electron affinity than EMAB and their ionization potentials are higher or very close to that of the ligand. Ionization potentials follow the ranking [Pt(EMAB)2] < [Pd(EMAB)2] < [Ni(EMAB)2] < EMAB < [Rh(EMAB)2]+, while the electron affinity classification varies thus: [Pd(EMAB)2] < EMAB < [Ni(EMAB)2] < [Pt(EMAB)2] < [Rh(EMAB)2]+.
In OSC fabrication, both strong electron donors and acceptors are essential for efficient charge generation and separation. Electron donor materials typically require a low ionization potential and a high HOMO energy level, while electron acceptors should possess a high electron affinity and a low LUMO energy level. Thus, achieving a balance between the donor and acceptor properties is critical for optimizing device performance.
From our results, [Pt(EMAB)2] has the lowest ionization potential, indicating its high electron releasing ability and thus its suitability as an electron donor for OSC technology. Conversely, [Rh(EMAB)2]+, with the highest ionization potential value, is the least effective electron donor and therefore unsuitable for this purpose. Ionization potential is found to generally decrease upon complexation, except in the case of [Rh(EMAB)2]+, suggesting that complexation enhances electron donation. Additionally, in most cases, complexation increases electron affinity, with [Rh(EMAB)2]+ exhibiting the highest potential as an electron acceptor. Consequently, the complexes investigated could serve as electron acceptors in OSC production.
Interestingly, [Pt(EMAB)2] demonstrates potential as both an electron donor and acceptor, based on its ionization potential and electron affinity values. However, before final conclusions can be drawn regarding the suitability of [Pt(EMAB)2] and [Rh(EMAB)2]+ as electron donor and acceptor, respectively, for OSC fabrication, other relevant factors and properties must be considered.
From Table 8, it can be observed that the ligand has the highest η value. This clearly indicates that the ligand is kinetically more stable and therefore less reactive than its corresponding complexes studied. Among the complexes studied, [Pd(EMAB)2] is the most kinetically stable while [Rh(EMAB)2]+ is the least kinetically stable. It is equally important to note that complexation of the various metals with EMAB reduces chemical stability to some degree. Furthermore, the relative stability of EMAB's complexes was studied by determining their interaction energies ΔEint. This energy was calculated using the supramolecular approach and is presented in Table 8. The more negative the ΔEint value, the more stable the compound. Indeed, the negative values in Table 8 indicate that the formation process of the complex ions from the ligand and the various metal ions is energetically favoured. To sum up, the relatively high η values for [Pt(EMAB)2], [Ni(EMAB)2] and [Rh(EMAB)2]+ indicate that they are fairly stable and can be used as precursors for the construction of OLED devices.
Generally, materials with LUMO energies below the threshold value of −2.7 eV often exhibit a limited capacity for accepting and transporting charges efficiently, which can lead to lower power conversion efficiency (PCE) in OSCs. It can be seen that apart from the LUMO energy of [Rh(EMAB)2]+ which is well below −2.7 eV and that of [Ni(EMAB)2] which is approximately −2.7 eV, the LUMO energies of the investigated compounds are above the threshold value. Interestingly, PCE limitation in investigated compounds with EL ≤ −2.7 eV is significantly mitigated by their relatively low HOMO–LUMO energy gaps, which can enhance their charge transport capabilities. Other charge transport pathways such as metal-to-ligand charge transfer (MLCT) and/or ligand-to-metal charge transfer (LMCT) are likely in these metal complexes, further mitigating the PCE limitation.
3.2 Effect of complexation on photovoltaic (organic solar cell) properties
Charge transfer in organic solar cells is determined by the donor–acceptor efficiency which in turn is directly dependent on the HOMO and LUMO energy levels of the donor and acceptor. In order to have effective charge transfer within a molecule, the HOMO and LUMO energies of the molecule must be higher than that of (6,6)-phenyl-C61-butyric acid methyl ester (PCBM), for which the HOMO is −6.1 eV and the LUMO is −3.75 eV and lower than that of Poly(3-hexylthiophene) (P3HT) for which the HOMO is −4.65 eV and the LUMO is −2.13 eV,7,66,67 which are reference electron acceptor and donor materials respectively.Table 9 shows the energy levels of the HOMO and LUMO, the energy gap, the open circuit voltage, and the variation in LUMO energy for EMAB and its studied metal complexes in addition to the VOC and EL−L values. It is worthy of note that, PCBM the electron acceptor prototype for OSCs has been used for comparison because of its stability, its capacity to accept electrons, and its suitable energy level.68 From Table 9, the energy gaps for all EMAB complexes are smaller than those of the ligand, indicating that the HOMO–LUMO energy gap is reduced upon complexation. This can lead to increased effective charge transfer from the donor to the acceptor. Also, the energy gaps are observed to range between 0.56 eV and 2.904 eV and show the following trend: [Rh(EMAB)2]+ < [Ni(EMAB)2] < [Pt(EMAB)2] < [Pd(EMAB)2] < EMAB. Relatively small band gaps of the complexes indicate their relative ease with which electrons can be promoted from the HOMOs to the LUMOs. Based on band gap analysis, EMAB is the least reactive and thus the most stable among the molecules studied. Also, the energy values of the HOMOs are higher than that of PCBM with the exception of [Rh(EMAB)2]+, while the LUMO energy values are higher than that of P3HT besides [Rh(EMAB)2]+. Consequently, these species apart from [Rh(EMAB)2]+ are good electron donors to PCBM by virtue of their HOMO–LUMO energy values. As a matter of fact, all studied molecules stand out as potential donors, since the process of promoting electrons from the valence to the conduction band of the PCBM is feasible and thus good for donor materials applications in organic solar cells technology. Fig. 3 shows iso-surfaces of the frontier molecular orbitals (FMOs) of EMAB and its complexes computed at PBE0-D3(BJ)/def2-TZVP level of theory in gas phase, along with the corresponding HOMO–LUMO energy gaps.
| Species | EHOMO | ELUMO | Egap | VOC (eV) | VOC (×10−19 V) | ΔEL−L |
|---|---|---|---|---|---|---|
| EMAB | −5.561 | −2.657 | 2.904 | 1.500 | 2.408 | 1.100 |
| [Pd(EMAB)2] | −4.700 | −2.540 | 2.160 | 0.650 | 1.041 | 1.210 |
| [Pt(EMAB)2] | −4.534 | −2.478 | 2.056 | 0.480 | 0.769 | 1.2700 |
| [Rh(EMAB)2]+ | −8.181 | −7.621 | 0.560 | 4.130 | 6.617 | −3.85 |
| [Ni(EMAB)2] | −4.487 | −2.705 | 1.782 | 0.440 | 0.705 | 1.030 |
| PCBM | −6.100 | −3.750 | — | — | — | — |
| P3HT | −4.650 | −2.130 | 2.520 | 0.600 | 0.961 | 1.620 |
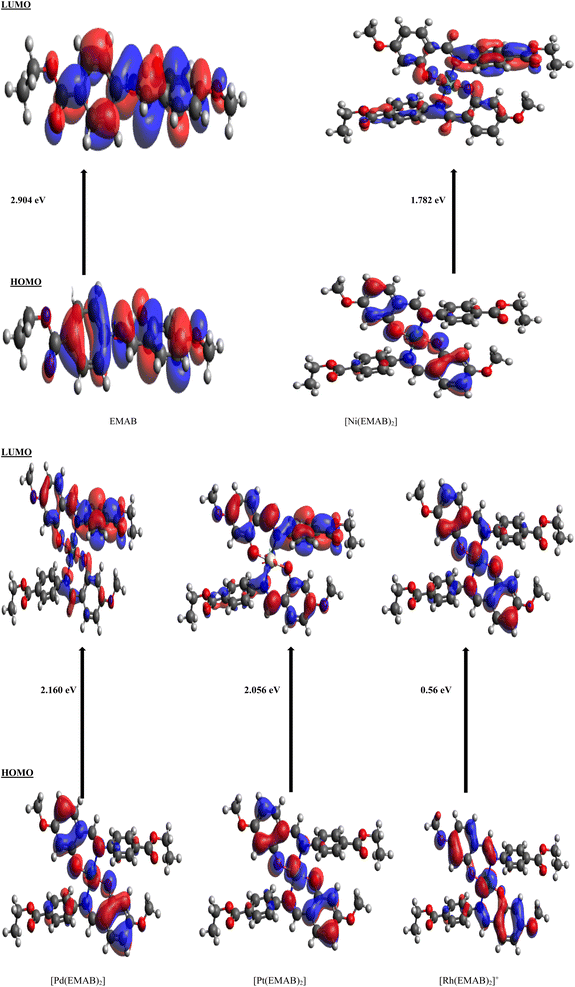 | ||
| Fig. 3 Iso-surfaces of the FMOs of EMAB and its complexes computed at PBE0-D3(BJ)/def2-TZVP level of theory in gas phase. | ||
A discernible shift in electron density is not apparent from EMAB's HOMO and LUMO distributions, unlike the case with [Pd(EMAB)2], [Ni(EMAB)2] and [Pt(EMAB)2], where there is a clear shift in electron distribution when transitioning from the HOMO to the LUMO. This highlights the fact that metal ion complexation by EMAB can enhance intramolecular charge transfer from one part of the molecule to another. In the case of [Rh(EMAB)2]+, there is no significant difference in electron distribution between the HOMO and the LUMO. This indicates that, despite a smaller HOMO–LUMO band gap, intramolecular charge transfer within the molecule is somewhat limited.
| Species | Transition | λmax (nm) | fosc | Assignment/% contribution | Energy (eV) |
|---|---|---|---|---|---|
| EMAB | S0 → S1 | 307.6 | 1.0090 | H → L (66%) | 3.785 |
| [Pd(EMAB)2] | S0 → S10 | 271.5 | 0.9348 | H → L+2 (84%) | 4.566 |
| [Pt(EMAB)2] | S0 → S8 | 288.8 | 0.6936 | H−1 → L+1 (66%) | 3.870 |
| [Rh(EMAB)2]+ | S0 → S10 | 538.0 | 0.3321 | H−2 → L (73%) | 2.219 |
| [Ni(EMAB)2] | S0 → S5 | 273.4 | 0.4075 | H → L (37%) | 4.534 |
The wavelength for a good photovoltaic material should ideally be low for substantial energy absorption.70 For optimal absorption efficiency, an OSC should exhibit absorption onsets that align with the higher-energy regions of the solar spectrum, usually in the visible and near ultraviolet regions. From Table 10, absorption maxima for the molecules are in the order [Pd(EMAB)2] > [Ni(EMAB)2] > [Pt(EMAB)2] > EMAB > [Rh(EMAB)2]+.
EMAB exhibits a maximum absorption peak in its spectra at 307.6 nm, corresponding to excitation energies of 3.785 eV with an oscillator strength (fosc) of 1.0090. This band corresponds to the molecular orbital transition H → L.
The complexes [Pd(EMAB)2], [Ni(EMAB)2] and [Pt(EMAB)2] show absorption maxima at 271.5, 273.4 and 288.8 nm in their spectra, corresponding to excitation energies 4.566 eV, 4.534 eV and 3.870 eV, with oscillator strengths fosc 0.9348, 0.4075 and 0.6936, respectively. These bands correspond to the molecular orbital transitions H → L+2, H → L and H−1 → L+1, respectively. These species are found to have the lowest absorption frequencies, corresponding to the greatest energies.
These results are so fascinating because they show that complexation between EMAB and the chosen metal ions can significantly alter the absorption frequency. There is a significant drop in the absorption frequency in the complexes [Pt(EMAB)2], [Ni(EMAB)2] and [Pd(EMAB)2]. Thus, these complexes, based on their absorption frequencies will carry more energy per photon than EMAB and its other complexes. This will greatly increase the efficiency and therefore energy conversion with materials produced using these complexes.
On the other hand, [Rh(EMAB)2]+ complex of EMAB shows absorption spectra maxima band at 538.0 nm, corresponding to the excitation energy of 2.219 eV with oscillator strength fosc 0.3321. These values correspond to the molecular orbital transition H−2 → L. These results show that the absorption energy is significantly reduced and therefore the amount of energy absorbed per photon will be lower.
Although this absorption frequency is higher than that of the parent molecule, it is still within the range at which visible light can be absorbed. Therefore, this complex can still be useful for the fabrication of OSC devices owing to its better mechanical properties owing to the presence of the metal centre.
These values are well below 900 nm, the maximum acceptable wavelength value for photovoltaics. It is also clear from Table 10 that the excitation energies increase as the wavelength reduces, as expected. As mentioned earlier, complexation is observed to increase absorption maxima in some cases (red shift) as in [Rh(EMAB)2]+ and reduces in other cases (blue shift) as in [Pd(EMAB)2], [Ni(EMAB)2] and [Pt(EMAB)2]. This shows that complexation can conveniently be used to modify the absorption wavelength of a molecule to our interest. When the absorption wavelength is increased, absorption is more in the visible region. It must be indicated that, high-energy photovoltaics offer the advantage of extracting more energy from the sun i.e. by using materials that absorb more energy per photon. Photovoltaic materials containing top layers that absorb in the UV region (more energy), while the inner layers absorb at the visible and the innermost layer absorbs at the visible region, offer the advantage of absorbing energy at a range of frequencies. From the foregoing observations, complexing EMAB with metals can tune the absorption wavelength of EMAB, making it useful as a precursor for the fabrication of photovoltaic materials that absorb radiation at a range of frequencies, thus maximizing the amount of energy absorbed (especially during rainy days) from the sun ranging from the UV through visible regions. From the foregoing observations, complexation of EMAB with majority of the metal ions studied can significantly alter the charge transport properties of the molecule and make it a better precursor to the fabrication of OLED and OSC devices, especially the [Pd(EMAB)2], [Ni(EMAB)2] and [Pt(EMAB)2] complexes.
4 Conclusion
Theoretical investigations using density functional theory (DFT) and its time-dependent variant (TD-DFT) have been performed to explore the organic light-emitting diode (OLED) and organic solar cell (OSC) properties of EMAB and its complexes with transition metals (Pt, Pd, Zn, Ir, Rh and Ni). It has been found that transition metal complexation significantly enhances the suitability of EMAB for use in OLEDs and OSCs. According to the results derived from Marcus' theory, the complex [Pt(EMAB)2] emerges as the most effective transporter of both holes and electrons with a hole transfer rate (kct(h) = 6.15 × 1014 s−1) about 44 times greater than that of EMAB (kct(h) = 1.42 × 1013 s−1). Also, Pt[EMAB]2 exhibits the best electron transport rate (4.6 × 1013 s−1) that is about 4 times greater than that of EMAB (1.1 × 1013 s−1). It is clear from the calculated hole and electron charge mobility for Pt[EMAB]2 (19.182 cm2 V−1 s−1 and 1.435 cm2 V−1 s−1) and for EMAB (4.41 × 10−1 cm2 V−1 s−1 and 3.43 × 10−1 cm2 V−1 s−1, respectively) that the charge transport properties of EMAB are tuneable via transition metal coordination, with Pt[EMAB]2 being the best charge transporter. To evaluate the applicability of the investigated compounds in OSCs, their HOMO and LUMO energies were compared with those of (6,6)-phenyl-C61-butyric acid methyl ester (PCBM) and poly(3-hexylthiophene) (P3HT). With the exception of [Rh(EMAB)2]+, the HOMO energies were higher than that of PCBM and the LUMO energies were higher than that of P3HT, indicating that these molecules can be efficient electron donors to PCBM. UV-visible absorption studies revealed absorption maxima λmax between 271 nm and 538 nm, in the order: [Pd(EMAB)2] > [Ni(EMAB)2] > [Pt(EMAB)2] > EMAB > [Rh(EMAB)2]+. Accordingly, complexation of EMAB with some transition metal ions can shift its maximum absorption wavelength, which can be beneficial for the manufacture of photovoltaic materials.Data availability
The data used to support the study's conclusions are contained in the ESI† file and the article.Author contributions
Conceptualization, investigation, writing-original draft, software: D. E. K.; writing – original draft, investigation, revision, editing, software: F. K. B.; writing – original draft, revision, editing investigation, software N. K. N.; writing – original draft, investigation: A. D. T. F; writing – original draft, Investigation, software: S. N. T.; conceptualization, supervision, validation: J. N. G.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We highly acknowledge the financial support (research modernization allowance) from the Ministry of Higher Education of Cameroon.References
- A. F. Henwood, A. K. Bansal and D. B. Cordes, Solubilised bright blue-emitting iridium complexes for solution processed OLEDs, J. Mater. Chem., 2016, 4, 3726–3737, 10.1039/c6tc00151c.
- S. Kagatikar and D. Sunil, Schiff bases and their complexes in organic light emitting diode application, J. Electron. Mater., 2021, 50, 1–16, DOI:10.1007/s11664-021-09197-9.
- A. Sarwar, M. B. Shamsuddin and H. Lingtang, Synthesis, characterization and luminescence studies of metal-diimine complexes, Mod. Chem. Appl., 2018, 6, 1–7, DOI:10.4172/2329-6798.1000262.
- A. N. Gusev, M. A. Kiskin and E. V. Braga, et al., Schiff base zinc (II) complexes as promising emitters for blue organic light-emitting diodes, ACS Appl. Electron. Mater., 2021, 3, 3436–3444, DOI:10.1021/acsaelm.1c00402.
- F. Sun and R. Jin, DFT and TD-DFT study on the optical and electronic properties of derivatives of 1, 4-bis (2-substituted-1, 3, 4-oxadiazole) benzene, Arabian J. Chem., 2017, 10, 2988–2993, DOI:10.1016/j.arabjc.2013.11.037.
- C. H. A. Alongamo, N. K. Nkungli and J. N. Ghogomu, DFT-based study of the impact of transition metal coordination on the charge transport and nonlinear optical (NLO) properties of 2-{[5-(4-nitrophenyl)-1, 3, 4-thiadiazol-2-ylimino] methyl} phenol, Mol. Phys., 2019, 117, 2577–2592, DOI:10.1080/00268976.2019.1576932.
- C. I. L. Alongamo, S. N. Tasheh and N. K. Nkungli, Structural, electronic, and charge transport properties of new materials based on 2-(5-mercapto-1, 3, 4-oxadiazol-2-yl) phenol for organic solar cells and light emitting diodes by DFT and TD-DFT, J. Chem., 2022, 1155, 1–15, DOI:10.1155/2022/1802826.
- B. X. Yang, C. Yao and G. Zhou, Highly efficient phosphorescent materials based on platinum complexes and their application in organic light-emitting devices (OLEDs), Platinum Met. Rev., 2013, 57, 2–16, DOI:10.1595/147106713X659019.
- B. Derkowska-Zielinska, M. Barwiolek and C. Cassagne, Nonlinear optical study of Schiff bases using Z-scan technique, Opt Laser. Technol., 2020, 124, 1–7, DOI:10.1016/j.optlastec.2019.105968.
- N. M. de Amorim Lima, H. J. Camargo Avila and C. F. do Nascimento Marchiori, et al., Light-emitting porphyrin derivative obtained from a subproduct of the cashew nutshell liquid: A promising material for OLED applications, Materials, 2019, 12, 1–16, DOI:10.3390/ma12071063.
- U. Giovanella, M. Pasini, and C. Botta, Organic Light-Emitting Diodes (OLEDs): working principles and device technology, Applied Photochemistry: when Light Meets Molecules, 2016, DOI:10.1007/978-3-319-31671-0_3.
- M. Rahman and M. Moniruzzaman, Fundamentals of Organic Light Emitting Diode, Paper Presented at: Proceedings of 10th Global Engineering, Science and Technology Conference, 2015 Search PubMed.
- B. C. Lin, C. P. Cheng and Z.-Q. You, et al., Charge transport properties of tris (8-hydroxyquinolinato) aluminum (III): Why it is an electron transporter, J. Am. Chem. Soc., 2017, 127, 66–67, DOI:10.1021/ja045087t.
- E. Mainimo, G. Ejuh and J. Ndjaka, Effect of metalation on some graphene nanoribbons for potential application as donor in organic photovoltaic cells, J. Mater. Sci.: Mater. Electron., 2019, 31, 21923–21933, DOI:10.1007/s10854-020-04696-7.
- M. Raftani, T. Abram and W. Loued, The optoelectronic properties of π-conjugated organic molecules based on terphenyl and pyrrole for BHJ solar cells DFT/TD-DFT theoretical study, Curr. Chem. Lett., 2021, 10, 489–502, DOI:10.5267/j.ccl.2021.4.002.
- R. Jin, X. Zhang and W. Xiao, Theoretical studies of photophysical properties of D–π–A–π–D-type diketopyrrolopyrrole-based molecules for organic light-emitting diodes and organic solar cells, Molecules, 2021, 25, 1–13, DOI:10.3390/molecules25030667.
- B. Blondel, F. Delarue and M. Lopes, Investigation of a sterically hindered Pt (II) complex to avoid aggregation-induced quenching: Applications in deep red electroluminescent and electrical switching devices, Synth. Met., 2017, 227, 106–116, DOI:10.1016/j.synthmet.2017.02.021.
- C. Murawski, K. Leo and M. C. Gather, Efficiency roll-off in organic light-emitting diodes, Adv. Mater., 2013, 25, 6801–6827, DOI:10.1002/adma.201301603.
- H. Lee, J. Lee and J.-I. Lee, Improvement of colour gamut in bottom-emission organic light-emitting diodes using micro-cavity structure embedded cathodes, Electronics, 2018, 7, 1–9, DOI:10.3390/electronics7090155.
- A. Köhler and H. Bässler, Triplet states in organic semiconductors, Mater. Sci. Eng., R, 2009, 66, 71–109, DOI:10.1016/j.mser.2009.09.001.
- J. Zhang, F. Zhao and X. Zhu, New phosphorescent platinum (II) Schiff base complexes for PHOLED applications, J. Mater. Chem., 2012, 32, 16448–16457, DOI:10.1016/j.mser.2009.09.001.
- Y. Yao, H.-Y. Yin and Y. Ning, Strong fluorescent lanthanide salen complexes: photophysical properties, excited-state dynamics, and bioimaging, Inorg. Chem., 2019, 58, 1806–1814, DOI:10.1021/acs.inorgchem.8b02376.
- T. Yu, W. Su and W. Li, et al., Synthesis, crystal structure and electroluminescent properties of a Schiff base zinc complex, Inorg. Chim. Acta, 2006, 359, 2246–2251, DOI:10.1016/j.ica.2006.01.019.
- H. Tanaka, S. Tokito and Y. Taga, Novel metal–chelate emitting materials based on polycyclic aromatic ligands for electroluminescent devices, J. Mater. Chem., 1998, 8(9), 1999–2003, 10.1039/a803308k.
- R. C. Evans, P. Douglas and C. J. Winscom, Coordination complexes exhibiting room-temperature phosphorescence: Evaluation of their suitability as triplet emitters in organic light emitting diodes, Coord. Chem. Rev., 2006, 250, 2093–2126, DOI:10.1016/j.ccr.2006.02.007.
- X. Xu, X. Yang and J. Zhao, Recent advances in solution-processable dendrimers for highly efficient phosphorescent organic light-emitting diodes (PHOLEDs), Asian J. Org. Chem., 2015, 4, 394–429, DOI:10.1002/ajoc.201402266.
- E. Zysman-Colman, Iridium (III) in Optoelectronic and Photonics Applications, John Wiley & Sons, 2017 Search PubMed.
- J. Kalinowski, V. Fattori and M. Cocchi, Light-emitting devices based on organometallic platinum complexes as emitters, Coord. Chem. Rev., 2011, 225, 2401–2425, DOI:10.1016/j.ccr.2011.01.049.
- E. V. Puttock, J. D. Fradgley, D. S. Yufitet and J. G. Williams, A family of readily synthesised phosphorescent platinum (II) complexes based on tridentate N^ N^ O-coordinating Schiff-base ligands, Dalton Trans., 2019, 48, 15012–15028, 10.1039/c9dt03156a.
- A. Odod, E. Nikonova and S. Y. Nikonov, Electroluminescence of zinc complexes in various OLED structures, Russ. Phys. J., 2017, 60, 7–13, DOI:10.1007/s11182-017-1038-2.
- M. Ibrahim-Ouali and F. Dumur, Recent advances on metal-based near-infrared and infrared emitting OLEDs, Molecules, 2019, 24, 1–39, DOI:10.3390/molecules24071412.
- A. Steinegger, O. S. Wolfbeis and S. M. Borisov, Optical sensing and imaging of pH values: Spectroscopies, materials, and applications, Chem. Rev., 2020, 120, 12357–12489, DOI:10.1021/acs.chemrev.0c00451.
- A. Gusev, E. Braga and Y. Baluda, Structure and tuneable luminescence in polymeric zinc compounds based on 3-(3-pyridyl)-5-(4-pyridyl)-1, 2, 4-triazole, Polyhedron, 2020, 191, 1–9, DOI:10.1016/j.poly.2020.114768.
- H. Genç Bilgiçli, A. T. Bilgicli and A. Günsel, Turn-on fluorescent probe for Zn2+ ions based on thiazolidine derivative, Appl. Organomet. Chem., 2011, 3, 3436–3444, DOI:10.1002/aoc.5624.
- L. Kafi-Ahmadi, A. P. Marjani and M. Pakdaman-Azari, Synthesis, characterization and antibacterial properties of N, N’-Bis (4-dimethylaminobenzylidene) benzene-1, 3-diamine as new Schiff base ligand and its binuclear Zn (II), Cd (II) complexes, S. Afr. J. Chem., 2018, 71, 151–159, DOI:10.17159/0379-4350/2018/v71a20.
- B. Naskar, R. Modak and D. K. Maiti, et al., A Schiff base platform: structures, sensing of Zn (II) and PPi in aqueous medium and anticancer activity, Dalton Trans., 2017, 46, 9498–9510, 10.1039/c7dt01932g.
- Y.-Z. Xie, G.-G. Shan and P. Li, et al., A novel class of Zn (II) Schiff base complexes with aggregation-induced emission enhancement (AIEE) properties: Synthesis, characterization and photophysical/electrochemical properties, Dyes Pigm., 2013, 96, 467–474, DOI:10.1016/j.dyepig.2012.09.020.
- D. J. Golding, N. Carter and D. Robinson, et al., Crystallisation-Induced Emission Enhancement in Zn (II) Schiff Base Complexes with a Tuneable Emission Colour, Sustainability, 2020, 12, 95–99, DOI:10.3390/su12229599.
- Y. Tong, Z. Xiao and X. Du, et al., Progress of the key materials for organic solar cells, Sci. China: Chem., 2020, 63, 1–8, DOI:10.1007/s11426-020-9726-0.
- C. H. C. Wallace, K. C. Wai and Y. Yuping, Recent advances in transition metal complexes and light-management engineering in organic optoelectronic devices, Adv. Mater., 2014, 26, 5368–5398, DOI:10.1002/adma.201306133.
- C. Duan and L. Ding, The new era for organic solar cells: small molecular donors, Sci. Bull., 2020, 42, 060502, DOI:10.1016/j.scib.2020.05.019.
- T. Akitsu, B. Miroslaw and S. Sudarsan, “Photo functions in Hybrid Systems of Schiff Base Metal Complexes and Metal or Semiconductor (Nano) Materials, Int. J. Mol. Sci., 2022, 23, 1005, DOI:10.3390/ijms231710005.
- S. Pasa, Y. S. Ocak, H. Temel and T. Kilicoglu, “Synthesis, characterization, and catalytic behavior in the Suzuki reaction of Schiff base and its complexes and the optical properties of nickel complex used in the fabricationof a photodiode, Inorg. Chim. Acta, 2013, 405, 493–504, DOI:10.1016/j.ica.2013.02.038.
- E. Pahonţu, D.-C. Ilieş and S. Shova, et al., Synthesis, characterization, crystal structure and antimicrobial activity of copper (II) complexes with the Schiff base derived from 2-hydroxy-4-methoxybenzaldehyde, Molecules, 2015, 20, 5771–5792, DOI:10.3390/molecules20045771.
- C. J. Cramer and D. G. Truhlar, Density functional theory for transition metals and transition metal chemistry, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816, 10.1039/b907148b.
- E. G. Lewars, Introduction to the theory and applications of molecular and quantum mechanics, Computational Chemistry, 2011, DOI:10.1007/978-90-481-3862-3.
- F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606, DOI:10.1002/wcms.1606.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671, DOI:10.1021/acs.jctc.8b01176.
- M. D. Hanwell, D. E. Curtis and D. C. Lonie, et al., Avogadro: an advanced semantic chemical editor, visualization, and analysis platform, J. Cheminf., 2012, 4, 1–17, DOI:10.1186/1758-2946-4-17.
- P. Verma and D. G. Truhlar, Status and challenges of density functional theory, Trends Chem., 2020, 2, 302–318, DOI:10.1016/j.trechm.2020.02.005.
- S. Grimme, J. G. Brandenburg and C. Bannwarth, et al., Consistent structures and interactions by density functional theory with small atomic orbital basis sets, J. Chem. Phys., 2015, 143, 054107, DOI:10.1063/1.4927476.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465, DOI:10.1002/jcc.21759.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305, 10.1039/b508541a.
- F. Neese, F. Wennmohs and A. Hansen, et al., Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange, Chem. Phys., 2009, 356, 98–109, DOI:10.1016/j.chemphys.2008.10.036.
- D. E. Kiven, N. K. Nkungli and S. N. Tasheh, In silico screening of ethyl 4-[(E)-(2-hydroxy-4-methoxyphenyl) methyleneamino] benzoate and some of its derivatives for their NLO activities using DFT, R. Soc. Open Sci., 2023, 10, 1–24, DOI:10.1098/rsos.220430.
- E. Caldeweyher, C. Bannwarth and S. Grimme, Extension of the D3 dispersion coefficient model, J. Chem. Phys., 2017, 147, 034112, DOI:10.1063/1.4993215.
- D. Geng, Y. Chen and Y. Chen, et al., High oxygen-reduction activity and durability of nitrogen-doped graphene, Energy Environ. Sci., 2011, 4, 760–764, 10.1039/c0ee00326c.
- J.-L. Brédas, J. P. Calbert,D. da Silva Filho, et al., Organic semiconductors: A theoretical characterization of the basic parameters governing charge transport, Proceedings of the National Academy of Sciences, 2002, DOI:10.1073/pnas.092143399.
- R. A. Marcus, Chemical and electrochemical electron-transfer theory, Annu. Rev. Phys. Chem., 1964, 15, 155–196, DOI:10.1146/annurev.pc.15.100164.001103.
- D. P. McMahon and A. Troisi, Evaluation of the external reorganization energy of polyacenes, J. Phys. Chem. Lett., 2010, 1, 941–946, DOI:10.1021/jz1001049.
- G. R. Hutchison, M. A. Ratner and T. J. Marks, Hopping transport in conductive heterocyclic oligomers: reorganization energies and substituent effects, J. Am. Chem. Soc., 2005, 127, 2339–2350, DOI:10.1021/ja0461421.
- D. L. Cheung and A. Troisi, Theoretical study of the organic photovoltaic electron acceptor PCBM: Morphology, electronic structure, and charge localization, J. Phys. Chem., 2010, 114, 20479–20488, DOI:10.1021/jp1049167.
- V. Coropceanu, H. Li and P. Wingetet al, Electronic-structure theory of organic semiconductors: charge-transport parameters and metal/organic interfaces, Annu. Rev. Mater. Res., 2013, 43, 63–87, DOI:10.1146/annurev-matsci-071312-121630.
- M. Ottonelli, M. Piccardo and D. Duce, et al., Tuning the photophysical properties of pyrene-based systems: A theoretical study, J. Phys. Chem., 2012, 116, 611–630, DOI:10.1021/jp2084764.
- N. A. Wazzan, A DFT/TDDFT investigation on the efficiency of novel dyes with ortho-fluorophenyl units (A1) and incorporating benzotriazole/benzothiadiazole/phthalimide units (A2) as organic photosensitizers with D–A2–π–A1 configuration for solar cell applications, J. Comput. Electron., 2019, 18, 375–395, DOI:10.1007/s10825-019-01308-4.
- F. Bella, S. Galliano and G. Piana, et al., Boosting the efficiency of aqueous solar cells: A photoelectrochemical estimation on the effectiveness of TiCl4 treatment, Electrochim. Acta, 2019, 302, 31–37, DOI:10.1016/j.electacta.2019.01.180.
- T. Yanai, D. P. Tew and N. C Handy, A new hybrid exchange–correlation functional using the oulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57, DOI:10.1016/j.cplett.2004.06.011.
- J. Creutzberg and E. Hedegård, Investigating the influence of relativistic effects on absorption spectra for platinum complexes with light-activated activity against cancer cells, Phys. Chem. Chem. Phys., 2020, 22, 27013–27023, 10.1039/D0CP05143H.
- O. C. Gagne and F. C. Hawthorne, Bond-length distributions for ions bonded to oxygen: Results for the transition metal and quantification of the factors underlying bond-length variation in organic solids, IUCrJ, 2020, 7, 581–629, DOI:10.1107/S2052252520005928.
- I. Chérif, H. Raissi, K. Abiedh and B. Gassoumi, et al., Computational studies on optoelectronic and nonlinear optical properties of para-substituted nitrobenzofurazan compound, Mater. Today Commun., 2023, 35, 106133, DOI:10.1016/j.mtcomm.2023.106133.
- B. Abdelaziz, I. Chérif, B. Gassoumi, S. Patanè and S. Ayachi, Linear and nonlinear optical responses of nitrobenzofurazan-sulfide derivatives: DFT-QTAIM investigation on twisted intramolecular charge transfer, J. Phys. Chem., 2023, 127, 9895–9910, DOI:10.1021/acs.jpca.3c04277.
- M. A. Halcrow, Jahn–Teller distortions in transition metal compounds, and their importance in functional molecular and inorganic materials, Chem. Soc. Rev., 2013, 42(4), 1784–1795, 10.1039/c2cs35253b.
- A. Nimmermark, L. Öhrström and J. Reedijk, Metal–ligand bond lengths and strengths: are they correlated? A detailed CSD analysis, Z. für Kristallogr. - Cryst. Mater., 2013, 228, 311–317, DOI:10.1524/zkri.2013.1605.
- G. L. Miessler and D. A. Tarr, Inorganic Chemistry, Pearson, Boston, 5th edn, ISBN 129202075X, 2013 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The supplementary file contains the optimized geometrical coordinates of the studied compounds, data used to calculate reorganization energies and UV-visible spectra. See DOI: https://doi.org/10.1039/d4ra02250e |
| This journal is © The Royal Society of Chemistry 2024 |